1
Wydział Elektroniki Mikrosystemów i Fotoniki
Politechnika Wrocławska
Fizyka dla elektroników 2
Nr ćwiczenia:
Temat:
44A
Pomiar zależności oporu metali i półprzewodników od temperatury
Termin zajęć
Prowadzący
Sprawozdanie wykonał
Ocena
Wt., 9 III 2010
Godz. 15.15-16.45
Dr inż. Ewa
Oleszkiewicz
Andrzej Głowacki 163968
I.
Cel ćwiczenia
Pomiar wartości oporu metali i półprzewodników w funkcji temperatury oraz
wyznaczenie temperaturowego współczynnika rezystancji metalu i szerokości przerwy
energetycznej półprzewodnika.
II.
Spis przyrządów
•
Multimetr cyfrowy METEX M-3850
•
Urządzenie zawierające grzejnik, regulator temperatury, wentylator oraz badane próbki
III.
Wyniki i opracowanie pomiarów
(błędy bezwzględne były przybliżane do pierwszej cyfry znaczącej w górę, o ile wstępne
przybliżenie nie zmieniało ich wartości o więcej niż 10% - w przeciwnym wypadku do dwóch
cyfr znaczących)
W sprawozdaniu wykonano analizę pomiarów dla próbek 1 (metal) i 4 (półprzewodnik)
a)
Metal
Ogrzewanie:
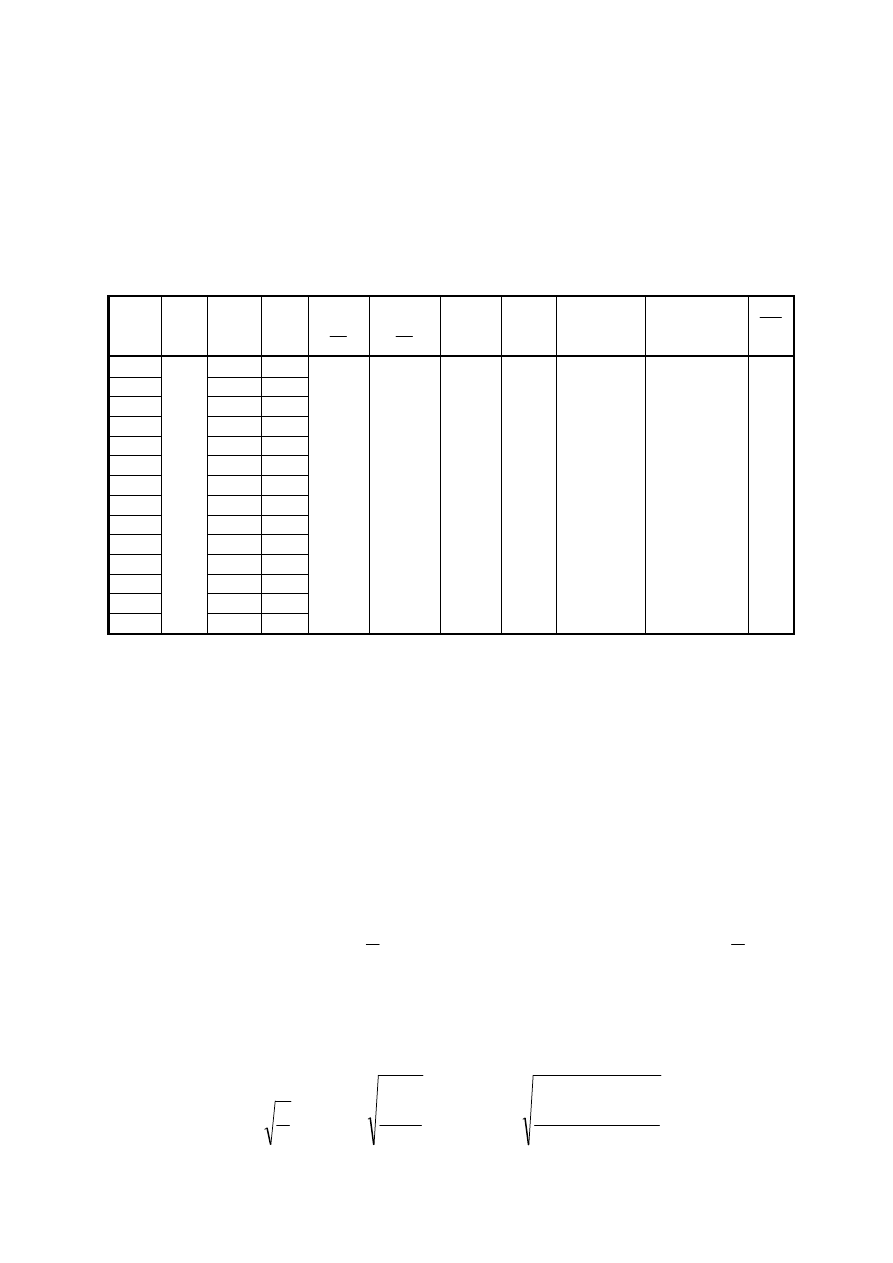
Tabela 1 – Wyniki pomiarów i obliczeń dla metalu podczas ogrzewania
t
[°C]
∆
t
[°C]
R
m
[Ω]
∆
R
m
[Ω]
a
°
Ω
C
∆
a
°
Ω
C
b
[Ω]
∆
b
[Ω]
α
[°C
-1
]
∆
α
[°C
-1
]
α
α
∆
[%]
30,3
114,4 ±0,7
35,4
115,6 ±0,7
40,8
116,4 ±0,7
45,2
118,4 ±0,7
50,5
119,7 ±0,7
55,5
121,5 ±0,8
60,5
122,3 ±0,8
65,2
124,2 ±0,8
70,5
125,5 ±0,8
75,2
127,6 ±0,8
80,6
128,7 ±0,8
85,4
131,0 ±0,8
90,5
131,9 ±0,8
95,2
134,0 ±0,8
100,5
±1,0
135,0 ±0,8
0,3036 ±0,0022 104,55 ±0,15 2,904
3
10
−
⋅
±0,026
3
10
−
⋅
±0,9
2
Oznaczenia:
t
–
wskazana temperatura
R
m
– zmierzona rezystancja metalu
a, b
– współczynniki prostej postaci
b
at
R
+
=
, wyznaczonej metodą regresji liniowej
α
–
temperaturowy współczynnik rezystancji
Ochładzanie:
Tabela 2 – Wyniki pomiarów i obliczeń dla metalu podczas ochładzania
t
[°C]
∆
t
[°C]
R
m
[Ω]
∆
R
m
[Ω]
a
°
Ω
C
∆
a
°
Ω
C
b
[Ω]
∆
b
[Ω]
α
[°C
-1
]
∆
α
[°C
-1
]
α
α
∆
[%]
33,5
114,8 ±0,7
35,0
115,6 ±0,7
44,7
118,6 ±0,7
50,5
120,5 ±0,8
54,8
121,6 ±0,8
60,2
123,7 ±0,8
65,2
125,3 ±0,8
70,4
126,4 ±0,8
75,3
128,2 ±0,8
80,4
129,9 ±0,8
85,2
131,1 ±0,8
90,1
133,1 ±0,8
94,7
134,1 ±0,8
100,5
±1,0
135,0 ±0,8
0,3084 ±0,0014 104,85 ±0,10 2,941
3
10
−
⋅
±0,017
3
10
−
⋅
±0,6
Wykorzystane wzory i przykładowe obliczenia:
Niepewno
ść
pomiaru rezystancji obliczona została zgodnie z niedokładno
ś
ci
ą
miernika,
przykładowo:
]
[
7
,
0
]
[
674
,
0
1
,
0
8
,
114
005
,
0
1
%
5
,
0
Ω
≈
Ω
=
+
⋅
=
+
=
∆
dgt
rdg
R
m
Jako,
ż
e nie była znana dokładno
ść
termometru wbudowanego w zestaw laboratoryjny, za
niepewno
ść
pomiaru temperatury przyj
ę
to typow
ą
dla termometrów cyfrowych niedokładno
ść
równ
ą
±1,0 °C.
Współczynniki prostej postaci
b
at
R
m
+
=
wyznaczone zostały na podstawie punktów
pomiarowych metod
ą
regresji liniowej. W tym celu wykorzystano nast
ę
puj
ą
ce wzory:
Γ
⋅
−
=
∑
∑
∑
=
=
=
1
1
1
1
n
i
i
n
i
i
n
i
i
i
y
x
y
x
n
a
,
Γ
⋅
−
=
∑
∑
∑
∑
=
=
=
=
1
1
1
1
1
2
n
i
i
i
n
i
i
n
i
i
n
i
i
y
x
x
y
x
b
,
gdzie:
n –
liczba punktów pomiarowych,
x
i
– i-ty pomiar temperatury,
y
i
– i-ty pomiar rezystancji,
oraz
2
1
1
2
−
=
Γ
∑
∑
=
=
n
i
i
n
i
i
x
x
n
. Niepewno
ś
ci współczynników a i b obliczone zostały
nast
ę
puj
ą
co:
Γ
=
∆
n
a
y
σ
,
Γ
=
∆
∑
=
n
i
i
y
x
b
1
2
σ
, gdzie
(
)
2
1
2
−
−
−
=
∑
=
n
b
ax
y
n
i
i
i
y
σ
.
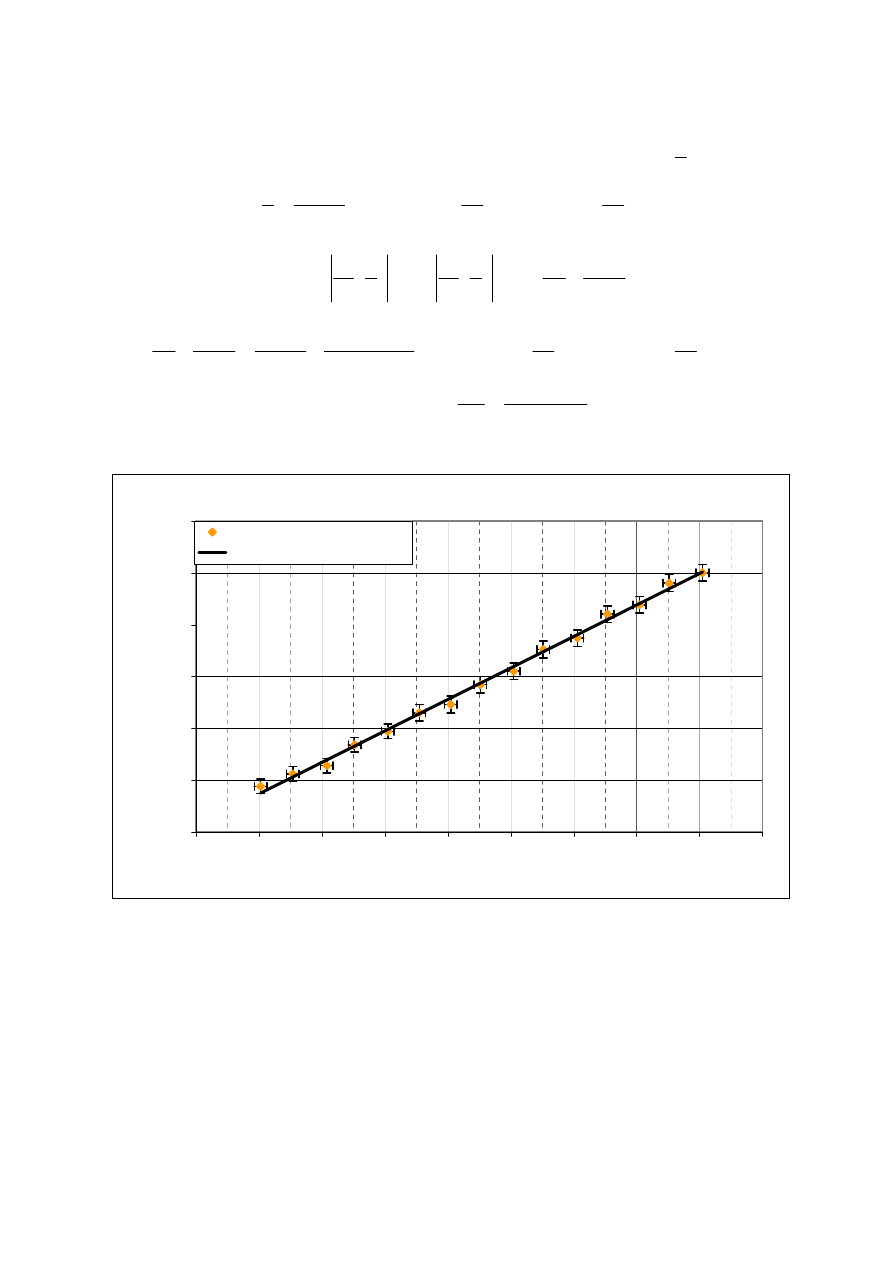
3
Dla metalu zachodzi równość
(
)
0
0
1
)
(
R
t
R
t
R
t
R
o
m
+
=
+
=
α
α
, zatem
α
0
R
a
=
,
0
R
b
=
.
Temperaturowy współczynnik rezystancji wyznaczyć więc można jako:
b
a
=
α
. Przykładowo
dla ochładzania:
°
⋅
≈
°
=
=
=
−
C
C
b
a
1
10
941
,
2
1
00294134
,
0
85
,
104
3084
,
0
3
α
.
Niepewno
ść
pomiarow
ą
temperaturowego współczynnika rezystancji wyznaczono metod
ą
ró
ż
niczki
zupełnej:
2
b
b
a
b
a
b
b
a
b
a
b
a
a
∆
⋅
+
∆
=
∆
⋅
∂
∂
+
∆
⋅
∂
∂
=
∆
α
.
Przykładowo
dla
ochładzania:
°
⋅
≈
°
⋅
=
⋅
+
=
∆
⋅
+
∆
=
∆
−
−
C
C
b
b
a
b
a
1
10
017
,
0
1
10
6158
,
1
85
,
104
10
,
0
3084
,
0
85
,
104
0014
,
0
3
5
2
2
α
.
Wzgl
ę
dna niepewno
ść
pomiaru współczynnika:
[%]
6
,
0
005780
,
0
10
941
,
2
10
017
,
0
3
3
≈
=
⋅
⋅
=
∆
−
−
α
α
Przedstawienie wyników na wykresach:
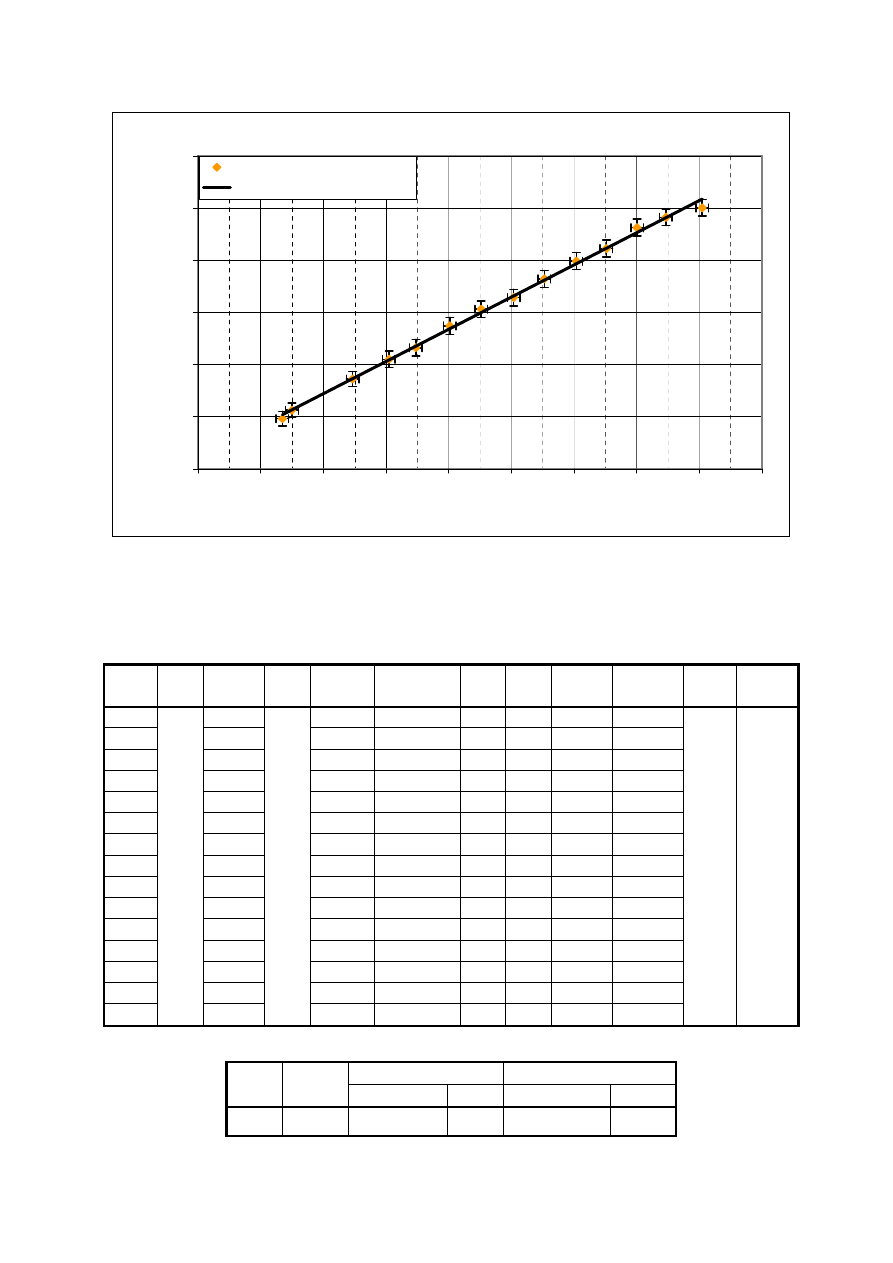
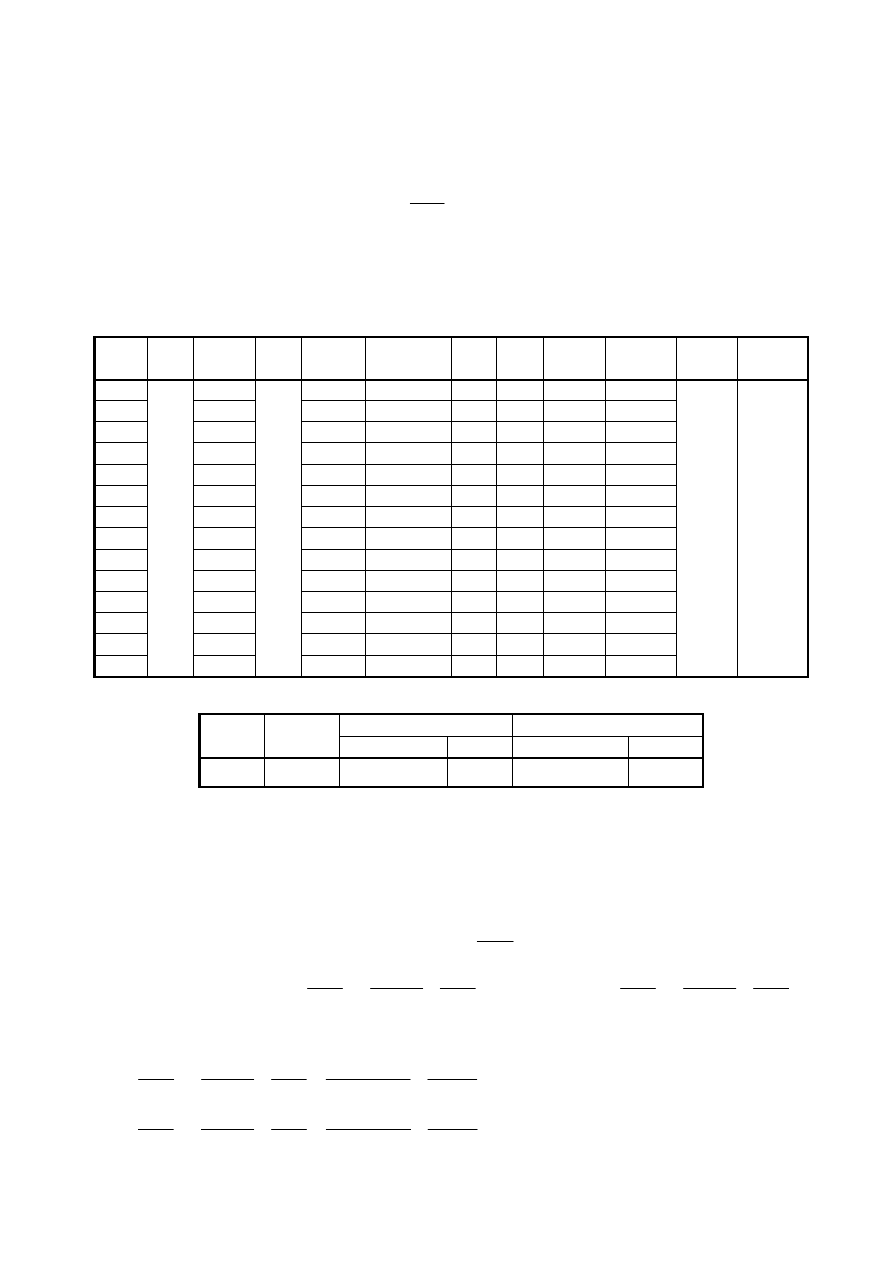
Ogrzewanie
R = 0,3036t + 104,55
110,0
115,0
120,0
125,0
130,0
135,0
140,0
20
30
40
50
60
70
80
90
100
110
t [°C]
R
[
Ω
]
Punkty pomiarowe
Liniowy (Punkty pomiarowe)
4
Ochładzanie
R = 0,3084t + 104,85
110,0
115,0
120,0
125,0
130,0
135,0
140,0
20
30
40
50
60
70
80
90
100
110
t [°C]
R
[
Ω
]
Punkty pomiarowe
Liniowy (Punkty pomiarowe)
b)
Półprzewodnik
Ogrzewanie:
Tabela 3 – Wyniki pomiarów i obliczeń dla półprzewodnika podczas ogrzewania
t
[°C]
∆
t
[°C]
T
[K]
∆
T
[K]
1000/T
[K
-1
]
∆
(1000/T)
[K
-1
]
R
s
[Ω]
∆
R
s
[Ω]
lnR
s
∆
lnR
s
A
[K]
∆
A
[K]
30,3
303,45
3,295
±0,011
99,5 ±0,7 4,6002 ±0,0071
35,4
308,75
3,239
±0,011
91,8 ±0,7
4,520
±0,008
40,8
313,85
3,186
±0,011
80,6 ±0,7
4,389
±0,009
45,2
318,55
3,139
±0,010
71,3 ±0,7
4,267
±0,010
50,5
323,25
3,094
±0,010
62,7 ±0,7
4,138
±0,011
55,5
328,75
3,042
±0,010
58,5 ±0,8
4,069
±0,014
60,5
333,35
3,000
±0,009
51,3 ±0,8
3,938
±0,016
65,2
338,55
2,954
±0,009
47,2 ±0,8
3,854
±0,017
70,5
343,35
2,912
±0,009
41,3 ±0,8
3,72
±0,02
75,2
348,55
2,869
±0,009
38,2 ±0,8
3,643
±0,021
80,6
353,35
2,830
±0,008
33,4 ±0,8
3,509
±0,024
85,4
358,55
2,789
±0,008
30,5 ±0,8
3,418
±0,026
90,5
363,25
2,753
±0,008
27,0 ±0,8
3,30
±0,03
95,2
368,45
2,714
±0,008
24,9 ±0,8
3,215
±0,032
100,5
±1,0
373,35
±1,0
2,678
±0,008
21,9 ±0,8
3,09
±0,04
2,461 ±0,021
Tabela 4 – Ostateczne wyniki obliczeń dla półprzewodnika (ogrzewanie)
E
g
∆
E
g
A
[K]
∆
A
[K]
[J]
[eV]
[J]
[eV]
2,461
±
0,021 6,80
20
10
−
⋅
0,424
±
0,06
20
10
−
⋅
±
0,004
5
Oznaczenia:
t
–
wskazana temperatura
T – temperatura w Kelwinach
R
s
– zmierzona rezystancja półprzewodnika
A
– nachylenie prostej postaci
B
T
A
R
+
=
)
1000
(
ln
, wyznaczonej metodą regresji liniowej
E
g
– wyznaczona przerwa energetyczna półprzewodnika
Ochładzanie:
Tabela 5 – Wyniki pomiarów i obliczeń dla półprzewodnika podczas ochładzania
t
[°C]
∆
t
[°C]
T
[K]
∆
T
[K]
1000/T
[K
-1
]
∆
(1000/T)
[K
-1
]
R
s
[Ω]
∆
R
s
[Ω]
lnR
s
∆
lnR
s
A
[K]
∆
A
[K]
33,5
306,65
3,261
±0,011
89,7 ±0,7
4,496
±0,008
35,0
308,15
3,245
±0,011
86,5 ±0,7 4,4601 ±0,0081
45,0
318,15
3,143
±0,010
66,2 ±0,7
4,193
±0,011
50,2
323,35
3,093
±0,010
58,5 ±0,7
4,069
±0,012
55,3
328,45
3,045
±0,010
51,7 ±0,7
3,945
±0,014
59,2
332,35
3,0089
±0,0091
47,0 ±0,8
3,85
±0,02
65,2
338,35
2,956
±0,009
41,8 ±0,8
3,73
±0,02
70,4
343,55
2,911
±0,009
36,7 ±0,8
3,603
±0,022
75,3
348,45
2,870
±0,009
33,9 ±0,8
3,523
±0,024
80,4
353,55
2,828
±0,008
30,7 ±0,8
3,424
±0,026
85,2
358,35
2,791
±0,008
27,5 ±0,8
3,314
±0,030
90,1
363,25
2,753
±0,008
24,5 ±0,8
3,199
±0,033
94,7
367,85
2,718
±0,008
22,2 ±0,8
3,100
±0,036
100,2
±1,0
373,35
±1,0
2,6785
±0,0072
21,9 ±0,8
3,086
±0,037
2,4972 ±0,0025
Tabela 6 – Ostateczne wyniki obliczeń dla półprzewodnika (ochładzanie)
E
g
∆
E
g
A
[K]
∆
A
[K]
[J]
[eV]
[J]
[eV]
2,4972
±
0,0025 6,895
20
10
−
⋅
0,4304
±
0,007
20
10
−
⋅
±
0,0005
Wykorzystane wzory i przykładowe obliczenia:
Niepewności pomiarów temperatury i rezystancji zostały wyznaczone tak samo jak dla metalu.
Temperatura na Kelwiny została przeliczona wg zależności:
[ ] [ ]
15
,
273
+
°
=
C
t
K
T
.
Niepewność wyrażona w Kelwinach pozostała taka sama.
Niepewność po przeliczeniu skali temperatury (
T
1000
) wyznaczona została w nast
ę
puj
ą
cy
sposób: „w gór
ę
” jako
T
T
T
T
1000
1000
1000
−
∆
−
=
∆
+
, oraz „w dół”
T
T
T
T
1000
1000
1000
−
∆
+
=
∆
−
.
Obie warto
ś
ci były bardzo zbli
ż
one, wi
ę
c jako ostateczn
ą
niepewno
ść
przyj
ę
to wi
ę
ksz
ą
z nich.
Przykładowo dla ochładzania:
]
[
011
,
0
]
[
010669
,
0
65
,
306
1000
0
,
1
65
,
306
1000
1000
1000
1000
1
1
−
−
+
≈
=
−
−
=
−
∆
−
=
∆
K
K
T
T
T
T
]
[
011
,
0
]
[
0105999
,
0
65
,
306
1000
0
,
1
65
,
306
1000
1000
1000
1000
1
1
−
−
−
−
≈
−
=
−
+
=
−
∆
+
=
∆
K
K
T
T
T
T

6
Ostatecznie więc
]
[
011
,
0
1000
1
−
±
=
∆
K
T
.
Podobną metodą wyznaczona została niepewność po przeliczeniu skali rezystancji:
( )
s
s
s
s
R
R
R
R
ln
)
ln(
ln
−
∆
+
=
∆
+
,
( )
s
s
s
s
R
R
R
R
ln
)
ln(
ln
−
∆
−
=
∆
−
(jako ostateczna większa z
nich). Przykładowo dla ochładzania:
( )
008
,
0
00777
,
0
)
7
,
89
ln(
)
7
,
0
7
,
89
ln(
ln
)
ln(
ln
≈
=
−
+
=
−
∆
+
=
∆
+
s
s
s
s
R
R
R
R
( )
008
,
0
00783
,
0
)
7
,
89
ln(
)
7
,
0
7
,
89
ln(
ln
)
ln(
ln
−
≈
−
=
−
−
=
−
∆
−
=
∆
−
s
s
s
s
R
R
R
R
Ostatecznie:
008
,
0
ln
±
=
∆
s
R
Nachylenie A prostej postaci
B
T
A
R
s
+
⋅
=
1000
ln
, wyznaczone zostało w analogiczny
sposób jak dla metalu (metod
ą
regresji liniowej)
Γ
⋅
−
=
∑
∑
∑
=
=
=
1
1
1
1
n
i
i
n
i
i
n
i
i
i
y
x
y
x
n
A
, przy
czym w tym wypadku x
i
oznacza i-t
ą
warto
ść
postaci
T
1000
, natomiast y
i
i-t
ą
warto
ść
postaci
s
R
ln
. Równie
ż
niepewno
ść
nachylenia prostej została wyznaczona w analogiczny sposób jak
dla metalu.
Dla półprzewodników w zakresie badanych temperatur zale
ż
no
ść
rezystancji od temperatury
jest
postaci:
⋅
=
kT
E
R
T
R
g
s
s
2
exp
)
(
0
,
logarytmuj
ą
c
obie
strony
otrzymamy:
s
g
s
g
s
R
T
k
E
R
kT
E
R
0
3
0
ln
1000
2
10
ln
2
ln
+
⋅
⋅
=
+
=
−
(k – stała Boltzmanna). Zatem wyznaczone
nachylenie prostej równe jest:
k
E
A
g
2
10
3
⋅
=
−
. Przerw
ę
energetyczn
ą
badanego półprzewodnika
wyznaczy
ć
wi
ę
c mo
ż
na jako:
]
[
10
2
3
J
k
A
E
g
⋅
⋅
=
, co wyrazi
ć
mo
ż
na w eV:
19
10
602177
,
1
]
[
]
[
−
⋅
=
J
E
eV
E
g
g
.
Przykładowo dla ogrzewania:
]
[
10
80
,
6
]
[
10
79531
,
6
461
,
2
10
3806
,
1
2
10
2
10
20
20
23
3
3
J
J
A
k
E
g
−
−
−
⋅
≈
⋅
=
⋅
⋅
⋅
⋅
=
⋅
⋅
=
oraz w przeliczeniu na eV:
]
[
424
,
0
]
[
42413
,
0
]
[
10
602176
,
1
10
79531
,
6
19
20
eV
eV
eV
E
g
≈
=
⋅
⋅
=
−
−
.
Niepewno
ść
pomiaru przerwy energetycznej wyznaczona została metod
ą
ró
ż
niczki zupełnej:
(
)
A
k
A
A
k
A
E
g
∆
⋅
⋅
=
∆
⋅
⋅
⋅
∂
∂
=
∆
2
10
2
10
3
3
.
Przykładowo
dla
procesu
ogrzewania:
]
[
004
,
0
]
[
10
06
,
0
]
[
10
05798
,
0
021
,
0
10
3806
,
1
2
10
2
10
20
20
23
3
3
eV
J
J
A
k
E
g
±
≈
⋅
±
≈
⋅
±
=
⋅
⋅
⋅
⋅
=
∆
⋅
⋅
=
∆
−
−
−
7
Przedstawienie wyników na wykresach:
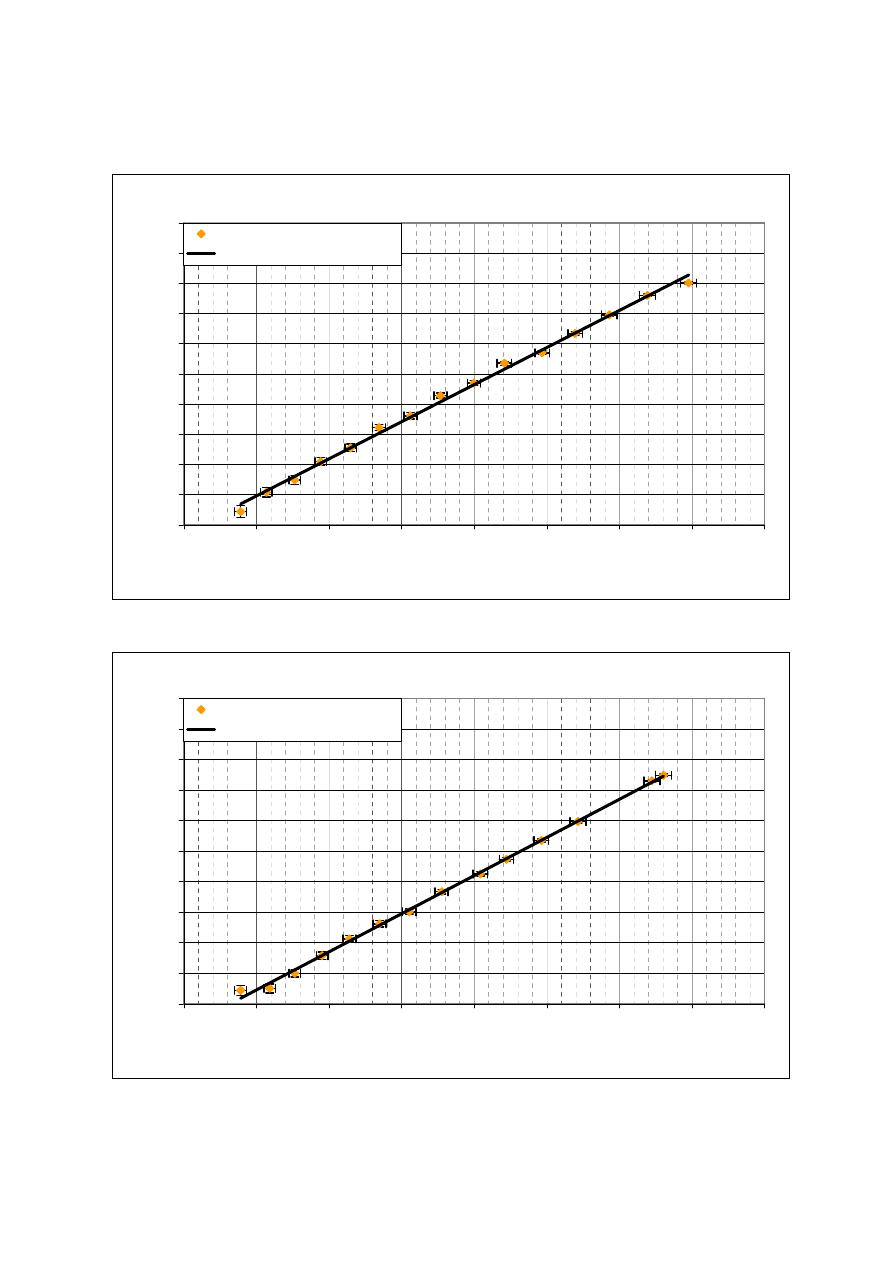
Ogrzewanie
lnR = 2,461(1000/T) - 3,454
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
4,8
5,0
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
1000/T [K
-1
]
ln
R
Punkty pomiarowe
Liniowy (Punkty pomiarowe)
Ochładzanie
lnR = 2,4972(1000/T) - 3,6526
3,0
3,2
3,4
3,6
3,8
4,0
4,2
4,4
4,6
4,8
5,0
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
1000/T [K
-1
]
ln
R
Punkty pomiarowe
Liniowy (Punkty pomiarowe)

8
IV.
Wnioski
Otrzymana dla badanej próbki metalu wartość temperaturowego współczynnika
rezystancji jest nieco mniejsza niż dla miedzi czy złota (dla miedzi wynosi ok.
1
3
10
9
,
3
−
−
°
⋅
C
,
natomiast dla złota
1
3
10
4
,
3
−
−
°
⋅
C ), wynik jest jednak prawidłowego rzędu. Również wartość
wyznaczonej przerwy energetycznej badanej próbki półprzewodnika jest z zakresu
dopuszczalnych dla półprzewodników wartości. W obu wypadkach wyniki otrzymane dla
ogrzewania i ochładzania są bardzo zbliżone i biorąc pod uwagę wyznaczone niepewności są
niesprzeczne. Niewielkie różnice wynikać mogą z dynamicznych zmian temperatury
(szczególnie w początkowych fazach ogrzewania i ochładzania), które sprawiały pewne
trudności pomiarowe. Wyznaczone charakterystyki (dla metalu
)
(t
R
m
, dla półprzewodnika
)
1000
(
ln
T
R
s
) s
ą
wyra
ź
nie liniowe, punkty pomiarowe niewiele odbiegaj
ą
od prostych
wyznaczonych metod
ą
regresji liniowej – to z kolei przeło
ż
yło na niewielkie niepewno
ś
ci
współczynników wyznaczonych prostych, a wi
ę
c równie
ż
ostatecznych wyników. Warto
równie
ż
zauwa
ż
y
ć
,
ż
e niedokładno
ś
ci przyrz
ą
dów pomiarowych nie miały wpływu na
niepewno
ś
ci ostatecznych wyników – wpływ na to miało jedynie rozproszenie punktów
pomiarowych wzgl
ę
dem aproksymowanych prostych.
Wyszukiwarka
Podobne podstrony:
fiza
sila termoelektryczna, Transport i Logistyka (AM) 1 (semestr I), Fizyka, fiza laborki (rozwiązania),
AKCELE~2, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, wsm1, FIZA, FIZAII
poprawa druk, Uczelnia, sem I, fiza, LABORATORIUM, Nowe laborki, Ciecz
Fifyka komputerowa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
kationy, Polibuda, II semestr, fizyka, FIZA, lab, Chemia laborki, chemia ogolna nie organiczna
Sprawko 48-fiza, Fizyka
fiza tematy cw, Biotechnologia i, Rok I, Fizyka i biofizyka
WYKRES73, 1 STUDIA - Informatyka Politechnika Koszalińska, Labki, fizyka1, fiza, fizyka
302brudnopis fiza, Polibuda, studia, S12, Fiza, Lab
badanie fotokom˘rki2, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
badanie fotokom˘rki1, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
307 (2), Politechnika Poznańska (PP), Fizyka, Labolatoria, fiza sprawka, optyka
DRGHARMNSS, Polibuda, Fiza, Fizyka sprawozdania (burdel jak cholera), struna2
Pomia napięcia powierzchniowego, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, spr
fiza egz44
więcej podobnych podstron