Analiza wariancji c.d.

Zasada działania, testy post-hoc, 

kontrasty, wieloczynnikowa ANOVA 

z interakcjami, efekty proste

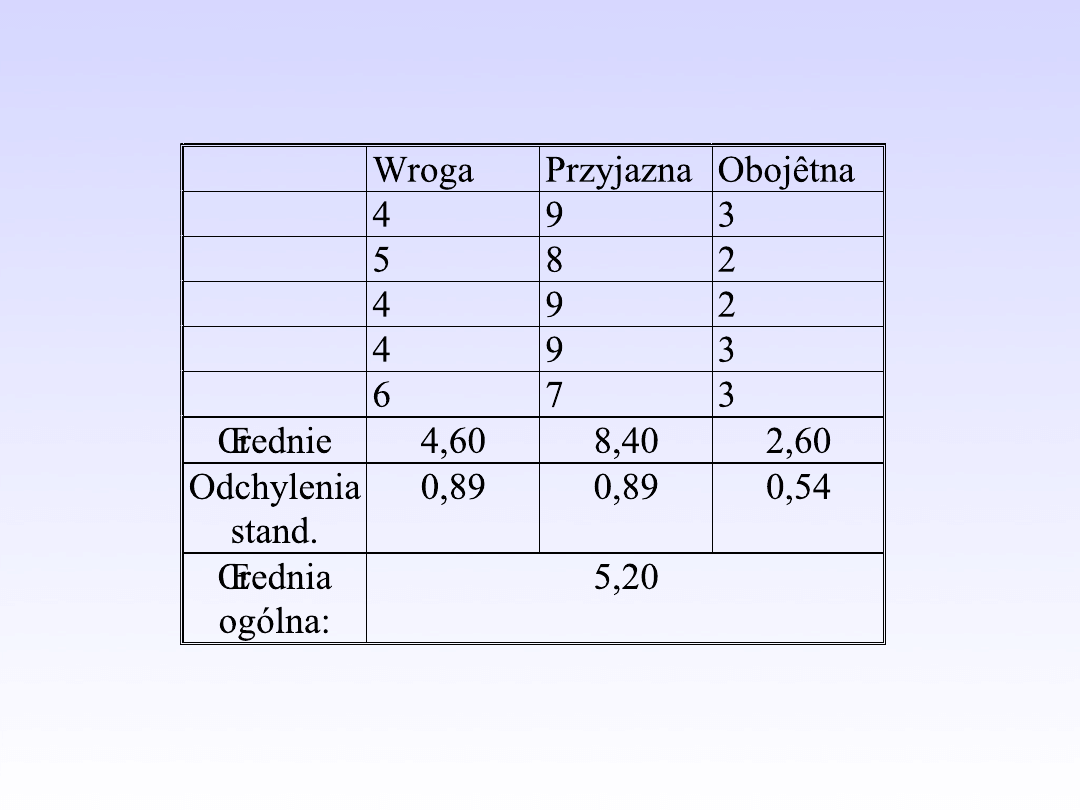
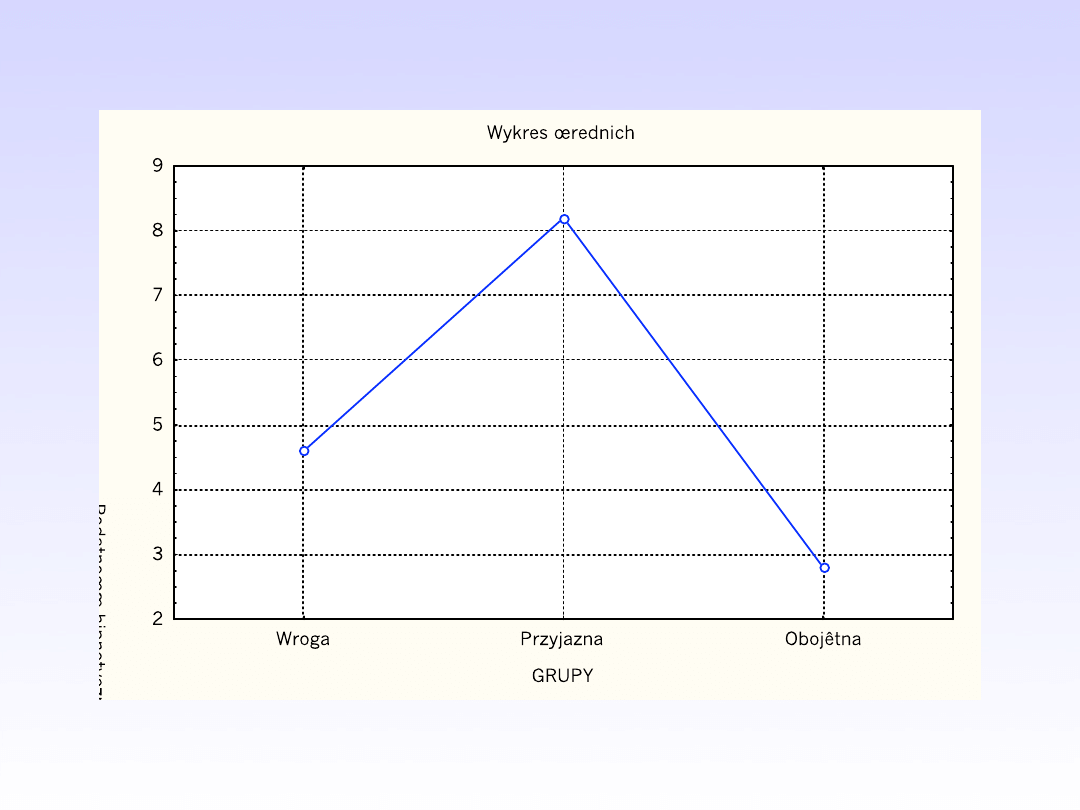
• Podstawowa idea analizy wariancji: 

porównywanie zmienności poszczególnych 
wyników wewnątrz grup ze zmiennością 
średnich z grup

• = Porównywanie średnich kwdratów 

odchyleń wewnątrzgrupowch ze średnim 
kwadratem odchyleń międzygrupowych

• Jeśli analiza wariancji przyniosła „istotne” 

wyniki, to wiemy tylko tyle, że w badanych 
grupach występują jakieś istotne różnice. 
Nie wiemy natomiast, która grupa od której 
się różni. Żeby dowiedzieć się czegoś 
więcej na temat natury tych różnic, trzeba 
przeprowadzić dalsze analizy.

• Jeden ze sposobów na dalszą analizę: 

porównania wielokrotne między średnimi 
za pomocą testów post-hoc

• Error rate per comparison: 

prawdopodobieństwo, że w danej 
(pojedynczej) analizie popełniony zostanie 
błąd I rodzaju

• Error rate familywise: 

prawdopodobieństwo, że w serii analiz 
zostanie popełniony przynajmniej jeden 
błąd I rodzaju

• Np. dla serii trzech analiz, w których α=0,05, 

prawdoppdobieństwo błędu I rodzaju wynosi 1 - (1 - α)

c  

= 

1 - .95

3

 = .1426

Konserwatywność / liberalność 

(testu statystycznego)

• Testy konserwatywne - działają "ostrożnie", 

stosunkowo rzadziej popełniamy przy ich 
użyciu błąd I rodzaju, ale częściej błąd II 
rodzaju

• Testy liberalne - działają "śmiało"; 

stosunkowo rzadziej popełniamy przy ich 
użyciu błąd II rodzaju, ale częściej błąd I 
rodzaju

Procedura Bonferoniego

• Zmodyfikowanie poziomu istotności 

poprzez podzielenie go  przez liczbę 
dokonywanych porównań

• Np. jeśli mamy 3 grupy (czyli 3 

porównania), to α=0,05 / 3 = 0,017

• Test ten staje się bardzo konserwatywny 

przy większej liczbie grup do porównania

Test Najmniejszej Istotnej 

Różnicy Fishera (LSD)

• Wg Fishera, jeśli test ogólny F przyniósł 

istotne wyniki, można wykonać serię testów 
t badających wszystkie możliwe różnice 
między średnimi

• Test ten jest najbardziej liberalny ze 

wszystkich testów post-hoc

• Można go polecić tylko w sytuacji, kiedy są 

trzy grupy do porównania

Test Newmana-Keulsa

• Jest testem liberalnym
• Utrzymuje α=0,05 tylko, jeśli są trzy grupy 

do porównań

• Dla czterech i pięciu grup, α=0,10, dla 

sześciu i siedmiu: α=0,15

• Zalecany tylko dla trzech grup do porównań

Test Tukeya

• raczej konserwatywny
• utrzymuje poprawny poziom α = 0,05 bez 

względu na liczbę grup do porównań

REGWQ

• Ryan, Einot, Gabriel, Welch q test
• raczej liberalny
• ogólna logika podobna do testu 

Bonferroniego, ale zrealizowana inaczej: 
α

κ

 = α/(k/r), gdzie k = liczba porównań, r = 

liczba średnich, z których dwie 
porównywane są najmniejsze i największe

• utrzymuje poprawny poziom α bez względu 

na liczbę porównań

test Scheffe'go

• bardzo konserwatywny
• raczej wyszedł obecnie z użycia

Kontrasty

• Kontrast to suma ważona pewnej liczby 

średnich, gdzie suma wag jest równa zero

• Stosowane do wykonywania porównań 

zaplanowanych (w tym np. efektów 
prostych) oraz do szczególnego rodzaju 
porównań wielokrotnych

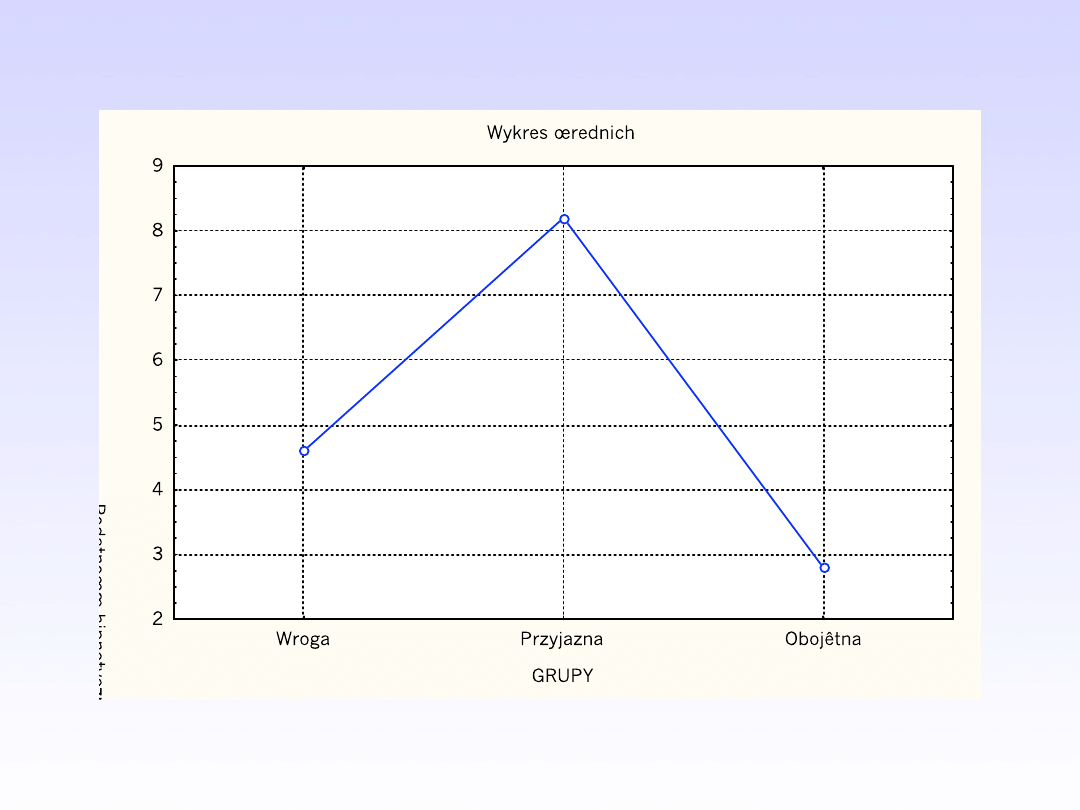
Kontrasty jako technika porównań 

wielokrotnych

• Odchylenie: porównanie odchyleń od 

średniej ogólnej zmiennej zależnej (dla 
każdego poziomu z wyjątkiem jednego)

• Różnica: porównanie poziomów zmiennej 

ze średnią z poprzedzających poziomów tej 
zmiennej 

• Helmerta: porównanie poziomów zmiennej 

ze średnią z następnych poziomów tej 
zmiennej 

• Prosty: porównywanie każdego poziomu 

zmiennej z poziomem kryterialnym

• Powtarzany: porównywanie każdego 

poziomu zmiennej z poziomem 
poprzedzającym

• Wielomianowy - analiza trendów

Jednoczynnikowa ANOVA - podsumowanie

• Służy do wykrywania różnic średnich między trzema 

lub więcej grupami

• Opiera się na porównywaniu zmienności 

wewnątrzgrupowej ze zmiennością średnich z grup

• Istotny wynik testu F analizy wariancji znaczy tylko 

tyle, że co najmniej jedna średnia jest różna od co 
najmniej jednej innej, ale nie mówi, która od której

• Żeby dowiedzieć się, które średnie różnią się od 

których, wykonuje się porównania wielokrotne, np. za 
pomocą testów post-hoc (jest to tzw. podejście a 
posteriori)

Podejście "a posteriori" a 

podejście "a priori"

• Jeśli z góry istniały bardzo ścisłe hipotezy 

dotyczące tego, które średnie mają się od których 
różnić i w którą stronę, to można i należy 
pominąć etap testu ogólnego F, i zamiast niego 
wykonać serię porównań zaplanowanych.

• Porównania zaplanowane to kontrasty testujące 

różnice między określonymi parami średnich

• Stosując podejście "a priori" nie używa się testów 

post-hoc