U

niwersytet

T

echnologiczno-

P

rzyrodniczy

w Bydgoszczy

W

ydział

T

elekomunikacji i

E

lektrotechniki

Z

akład

E

lektroenergetyki

Laboratorium Inżynierii materiałowej

Instrukcja do ćwiczenia:

Badanie materiałów ferromagnetycznych

(wersja „beta” – proszę o uwagi do instrukcji)

Opracowali

dr inż. Maria Derecka, mgr inż. Sebastian Zakrzewski

Bydgoszcz, 2012 r.

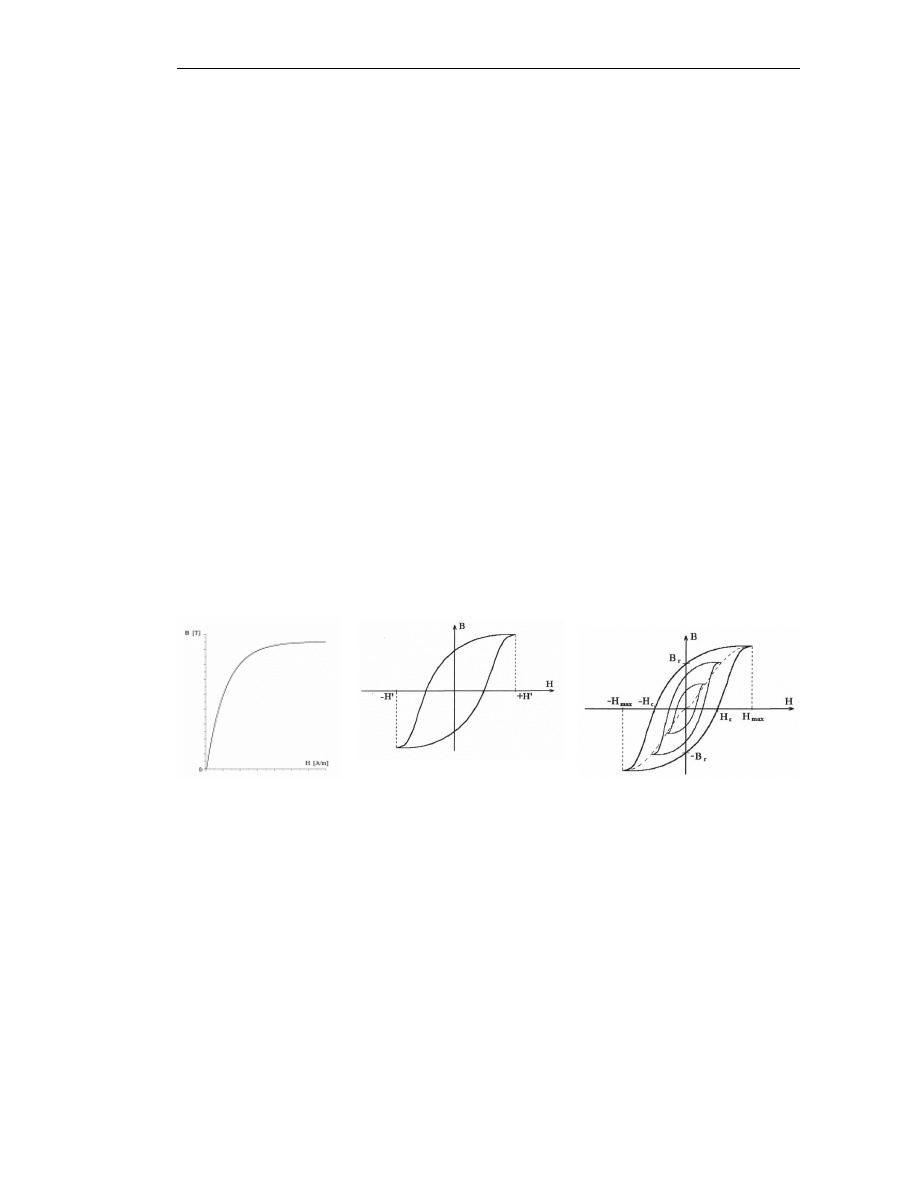
Badanie materiałów ferromagnetycznych (wersja „beta”)

1

I. Cel ćwiczenia

02.03.10

Celem

ćwiczenia jest:

•

utrwalenie pojęć i charakterystyk używanych do opisu właściwości magnetycznych materia-
łów,

•

poznanie magnetycznych właściwości materiałów używanych w elektrotechnice przez do-
ś

wiadczalne badania ich próbek,

•

poznanie ilościowych charakterystyk materiałów magnetycznych decydujących o ich zastoso-
waniach w konstrukcji urządzeń elektrycznych.

II.

Podstawowe wiadomości

Należy przypomnieć sobie następujące zagadnienia omawiane na wykładach:

• właściwości dia-, para- i ferromagnetyków;
• pierwotna krzywa magnesowania materiału ferromagnetycznego;
• pętla histerezy i charakterystyczne pojęcia z nią związane;
• straty mocy czynnej na histerezę i prądy wirowe.

Pierwsze magnesowanie próbki materiału ferromagnetycznego, od stanu określonego wartościa-

mi H = 0 i B = 0, przy monotonicznie rosnącej wartości natężenia prądu magnesującego, odbywa
się według krzywej przedstawionej na rys. la. Przy cyklicznym przemagnesowywaniu materiału
ferromagnetycznego przy wartości natężenia pola magnetycznego od –H

′ do +H′ charakterystyka

B

= f(H) ma kształt krzywej zamkniętej zwaną pętlą histerezy (rys. 1b).

Powtarzając proces cyklicznego przemagnesowywania przy coraz to większych wartościach H’

otrzymuje się rodzinę pętli histerezy oraz graniczną pętle histerezy odpowiadającą wartości natęże-
nia pola magnetycznego ±H

max

przy którym osiąga się stan nasycenia w materiale ferromagnetycz-

nym (rys. 1c).

a)

b)

c)

Rys. 1. Charakterystyki magnesowania materiału ferromagnetycznego :

a) krzywa pierwotna
b) pętla histerezy powstała wskutek cyklicznego przemagnesowywania przy zmianie pola magnetycz-

nego od – H

’

do + H

’

i z powrotem do – H

’

c) rodzina pętli histerezy i charakterystyka komutacyjna - linia przerywana.

Graniczna pętla histerezy, po wcześniejszym namagnesowaniu materiału do stanu nasycenia, od-

cina na osi rzędnych wartość indukcji szczątkowej B

r

tj. indukcji, jaka pozostaje w zamkniętym

rdzeniu magnetycznym bezpośrednio po przerwaniu obwodu magnesującego, a na osi odciętych
określa wartość ujemnego natężenia pola – H

c

potrzebnego do całkowitego usunięcia indukcji

szczątkowej. Natężenie – H

c

nazywane jest natężeniem powściągającym (koercją). Wierzchołki

pętli histerezy wyznaczają podstawową charakterystykę magnesowania (linia przerywana na rys.
1c) podawaną w literaturze w postaci wykresów lub tablic.

Bezwzględną przenikalnością magnetyczną

µ

danego materiału nazywamy iloraz:

Badanie materiałów ferromagnetycznych (wersja „beta”)

2

H

B

=

µ

(1)

Względna przenikalność magnetyczna jest określona jako:

0

µ

µ

µ

=

r

(2)

przy czym:

µ

0

=4

π⋅10

-7

H/m - przenikalność magnetyczna próżni.

Przenikalność magnetyczna materiałów ferromagnetycznych zależy od indukcji magnetycznej B

w obwodzie magnetycznym.

Materiały magnetycznie miękkie charakteryzują się małym natężeniem koercji (50 - 100 A/m).

Do produkcji magnesów trwałych używa się materiałów magnetycznie twardych. W specjalnych
stopach magnetycznych natężenie koercji jest rzędu kilkudziesięciu tysięcy A/m.

Zmieniający się okresowo w materiale magnetycznym strumień magnetyczny powoduje powsta-

nie strat mocy ze względu na histerezę i prądy wirowe. Straty mocy w watach na kilogram stali
spowodowane histerezą są równe:

8

2

10

100

−

⋅

=

B

f

k

P

h

h

∆

(3)

Spowodowane zaś prądami wirowymi:

8

2

2

10

100

−

⋅

=

∆

B

f

k

P

w

w

(4)

gdzie: f - częstotliwość zmian indukcji magnetycznej, B - indukcja magnetyczna [T], k

h

i k

w

:

- dla stali z dużą zawartością krzemu o grubości 0,5 mm - k

h

=3, k

w

= 1,2,

- dla stali o grubości 0,35 mm – k

h

= 2,4, k

w

= 0,6.

Można wykazać [1], że w obwodzie magnetycznym strata energii spowodowana histerezą, na je-

den cykl przemagnesowania i na jednostkę objętości wynosi:

∫

⋅

=

∆

dB

H

P

v

(5)

Pole powierzchni wewnątrz pętli histerezy jest więc miarą strat energii na jeden cykl przemagne-

sowania i na jednostkę objętości.

III. Układ pomiarowy

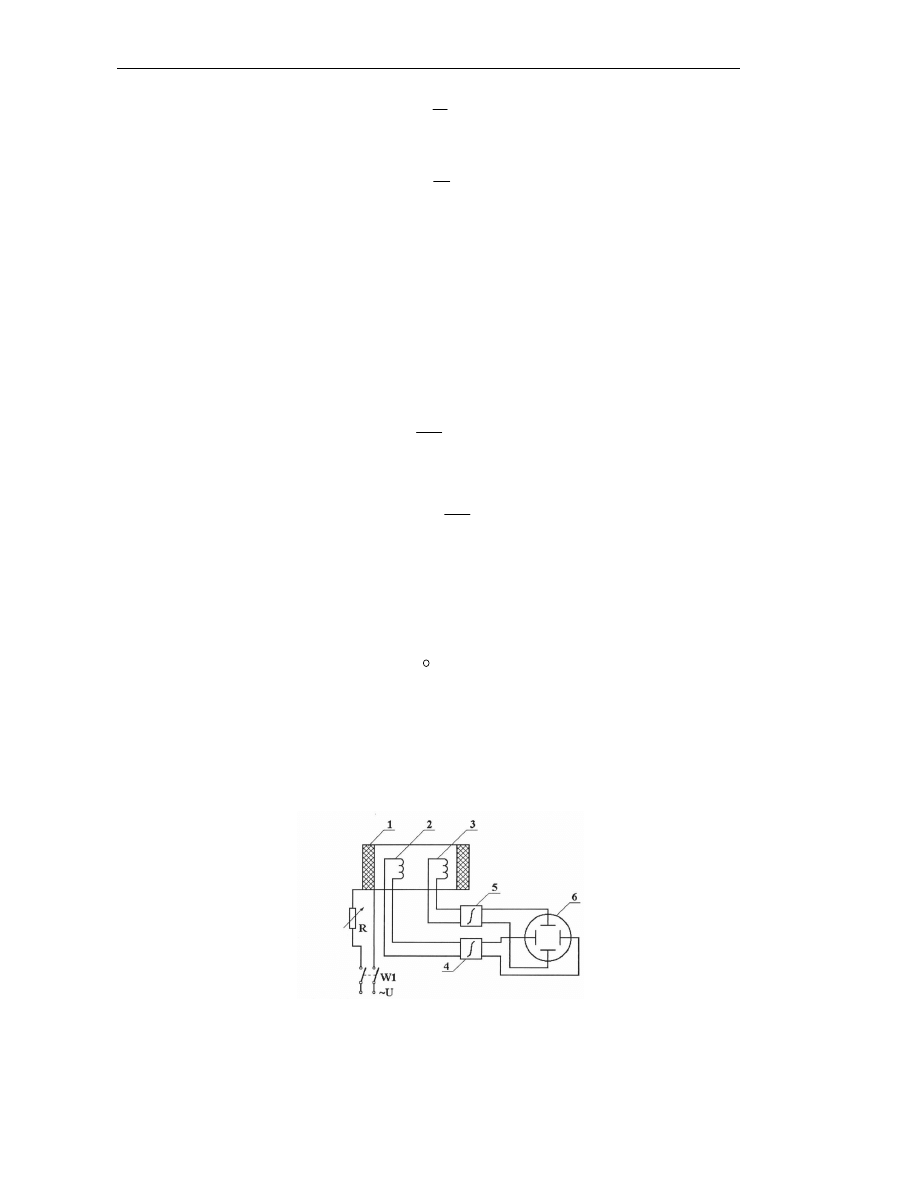
Schemat ideowy układu pomiarowego przedstawiono na rys. 2.

Rys. 2. Schemat układu pomiarowego (ferrometru). Objaśnienia: 1, 2, 3 - cewki, 4, 5 - układy całkujące, 6 -
oscyloskop.

W praktycznie jednorodnym, przemiennym polu magnetycznym H cewki 1 zasilanej napięciem

przemiennym o częstotliwości 50 Hz umieszczone są dwie jednakowe cewki 2 i 3.

Badanie materiałów ferromagnetycznych (wersja „beta”)

3

Siła elektromotoryczna (SEM) na zaciskach cewki 2, w której znajduje się próbka badanego ma-

teriału magnetycznego, jest proporcjonalna do pierwszej pochodnej indukcji B w próbce, natomiast
SEM na zaciskach cewki 3 jest proporcjonalna do pierwszej pochodnej natężenia pola magnetycz-
nego H wytworzonego przez prąd I płynący przez cewkę 1.

Na podstawie zależności (5) moc tracona w jednostce objętości próbki materiału na przemagne-

sowanie wynosi:

1

k

S

f

P

s

v

⋅

⋅

=

∆

(6)

gdzie: S

s

- pole powierzchni zawarte wewnątrz pętli histerezy w mm

2

, k

1

- stała ferrometru.

Przyjmując

k

f

k

=

1

(7)

otrzymuje się:

k

S

P

s

v

⋅

=

∆

(8)

IV. Przebieg ćwiczenia

IV.1. Czynności przygotowawcze

A.

Przygotowanie stanowiska pomiarowego

Na rys. 3 pokazano wygląd stanowiska.

oscyloskop

wyłącznik

cewka

próbka

Rys. 3. Wygląd stanowiska.

Czynności, które należy wykonać:

•

włączyć napięcie wyłącznikiem znajdującym się na tablicy zasilającej,

•

włączyć napięcie zasilania oscyloskopu wyłącznikiem SIEĆ (na górnej ściance, z lewej strony),

•

po uzyskaniu plamki świetlnej strumienia na ekranie oscyloskopu można przystąpić do na-
stawienia wzmocnienia odchylania pionowego i poziomego: w otwór cewki wkładać kolej-
no wszystkie próbki materiałów magnetycznych, które mają być badane, aby ustalić, która
próbka powoduje największe odchylenia pionowe strumienia na ekranie oscyloskopu,

•

tak wybraną próbkę należy ponownie włożyć w otwór cewki po czym nastawić wzmocnienie
odchylania poziomego (gałka: X zewn. wzm.) i odchylania pionowego (gałka: A) tak, aby po-
wierzchnia wewnętrzna krzywej B = f(H) była możliwie duża i obraz pętli histerezy mieścił się
na ekranie oscyloskopu. Ferrometr należy uważać za wyskalowany. Położenie pokręteł A oraz
X zewn. wzm. w czasie pomiarów nie może być zmieniane.

Badanie materiałów ferromagnetycznych (wersja „beta”)

4

B. Przygotowanie komputera i ściąganie kopii ekranu oscyloskopu

Włączyć komputer.

Uruchomić edytor tekstów Word (do dokumentu tekstowego będziemy wklejać kopie ekranu

oscyloskopu zawierające poszczególne pętle histerezy, stanowiące wyniki poszczególnych badań w
ferrometrze). Na pulpicie zapisać plik Worda pod nazwą zawierającą datę wykonywania ćwiczenia
oraz kod grupy wykonującej ćwiczenie.

Uruchomić program WaveStar (skrót w menu Start). Zadeklarować typ oscyloskopu wybierając

w menu

Instrument/Select/Scope,

a następnie Tek TDS210.

Wejść w zakładkę Select/RS -232 Setting i wybrać port Com1 (można dla pewności wykonać

Test). Potwierdzić przez OK.

Następnie wejść w zakładkę Picture 1. Nacisnąć przycisk Acquire (oznaczony symbolem prze-

biegu prostokątnego). Czekać cierpliwie do pojawienia się kopii ekranu oscyloskopu. Następnie
wykonać Print Screen i po przełączeniu się na plik Worda wkleić tę kopię ekranu do pliku opisując
próbkę materiału magnetycznego symbolem podanym na próbce. Przygotować arkusz dla następnej
próbki wybierając Insert/Picture

IV.2. Badania

Porównanie właściwości magnetycznych różnych materiałów

W otwór cewki wkładać kolejno wszystkie dostępne próbki materiałów i za każdym razem ścią-

gnąć przebieg pętli histerezy do komputera jak opisano w punkcie IV.1.B.

Obserwowanie wpływu naprężenia mechanicznego na przebieg pętli histerezy

W otwór cewki włożyć próbkę oznaczoną jako D, a następnie:

•

ś

ciągnąć przebieg pętli histerezy do komputera jak opisano w punkcie IV.1.B.,

•

odkształcić próbkę według wskazówek prowadzącego ćwiczenie,

•

ś

ciągnąć przebieg pętli histerezy do komputera jak opisano w punkcie IV.1.B.

V.

Opracowanie wyników badań

Wyniki należy opracować wykorzystując informacje o próbce wzorcowej A (patrz załącznik).

V.1. Obliczenie maksymalnej indukcji i pola powściągającego

Znamy wykres pętli histerezy próbki A oraz wiemy iż: indukcja nasycenia B

max-A

= 1,4 T, natę-

ż

enie powściągające H

c-A

= 30 Am

-1

.

To pozwala wyznaczyć indukcję nasycenia B

max-Z

oraz natężenie powściągające H

c-Z

dla dowol-

nej próbki Z. Mianowicie

A

max

Z

max

A

max

Z

max

Y

Y

B

B

−

−

−

−

=

(9)

A

c

Z

c

A

c

Z

c

X

X

H

H

−

−

−

−

=

(10)

gdzie Y

max-A

, Y

max-Z

– rzędne [mm] odpowiadające indukcji nasycenia odpowiednio próbki A i próbki Z, uzy-

skane z wykresu pętli histerezy; X

c-A

, X

c-Z

– odcięte [mm] odpowiadające natężeniu powściągającemu odpo-

wiednio próbki A i próbki Z, uzyskane z wykresu pętli histerezy.

Badanie materiałów ferromagnetycznych (wersja „beta”)

5

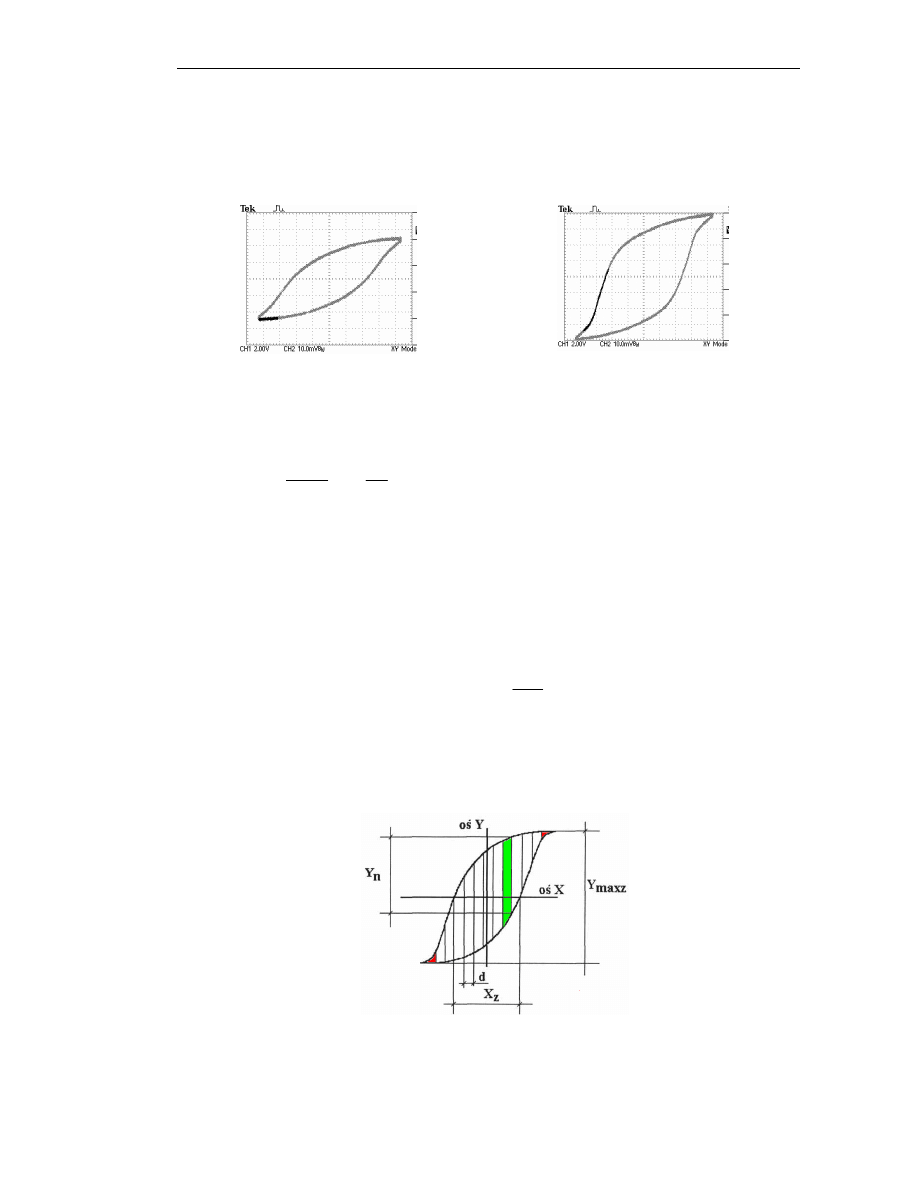
Przykład obliczeń maksymalnej indukcji.

Na rys. 4 a i 4b pokazano pętle histerezy materiałów A i Z. Z tych wykresów można odczytać

wartości rzędnych, które odpowiadają maksymalnej indukcji obydwu próbek. Następnie odczytane
wartości wstawiamy do wzoru (9).

a)

b)

Rys. 4. Pętle histerezy a) materiału A, rzędna odpowiadająca indukcji maksymalnej Y

max-A

=

2,5 cm b) ma-

teriału Z, rzędna odpowiadająca indukcji maksymalnej Y

max-z

=

4 cm

Zgodnie ze wzorem (9) mamy

24

2

5

2

4

4

1

,

,

,

Y

Y

B

B

A

max

Z

max

A

max

Z

max

=

=

=

−

−

−

−

T

Podobnie obliczamy natężenie pola powściągające (pole koercji).

V.2. Obliczenie strat na histerezę

Znamy także straty na histerezę próbki A, wynoszą one

∆P

gA

= 2,52 W/kg. Po obliczeniu pola

powierzchni pętli histerezy próbki A (wyrażonego w mm

2

) oraz pola powierzchni pętli histerezy

próbki Z (wyrażonego w mm

2

) możemy obliczyć straty na histerezę dowolnej próbki Z:

A

s

Z

s

A

g

Z

g

S

S

P

P

−

−

−

−

=

∆

∆

(11)

Sposób obliczenia pola powierzchni pętli histerezy (wyrażonego w mm

2

) pokazano na rys. 5.

Pętla histerezy została podzielona na m+1 podobszarów, których kształt - oprócz dwóch narożnych
(wypełnione kolorem czerwonym) – można przybliżyć za pomocą kształtu rombu (jeden z nich
wypełniony kolorem zielonym).

Rys.5. Ilustracja do sposobu obliczania pola powierzchni pętli histerezy

Pole powierzchni rombu można przybliżyć obliczeniem

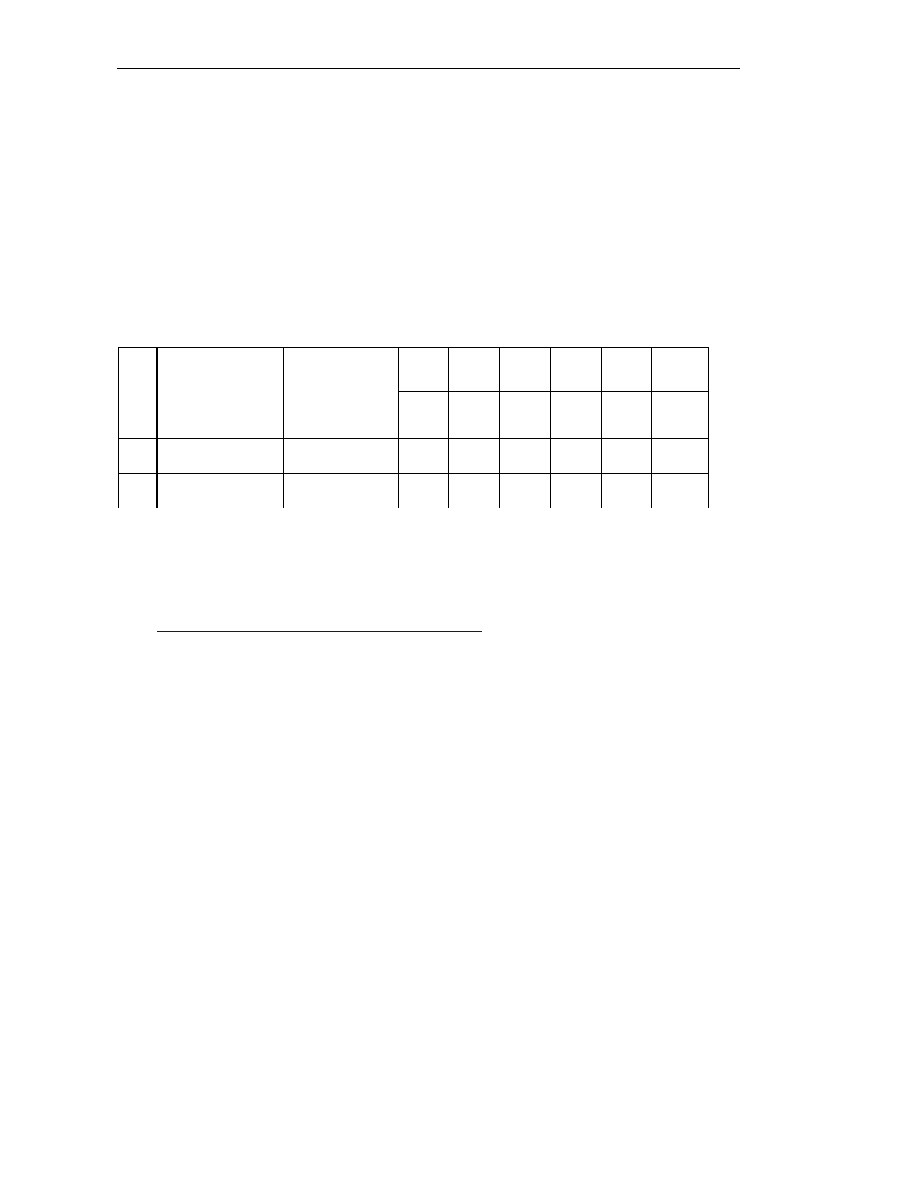
Badanie materiałów ferromagnetycznych (wersja „beta”)

6

n

rombu

dY

S

=

(12a)

pole powierzchni dwóch trójkątów

1

2

dY

S

=

∆

(12b)

Tak więc pole powierzchni pętli histerezy [mm

2

] S

s

można oszacować jako

∑

=

=

m

n

n

s

Y

d

S

1

(12)

gdzie: Y

n

[mm] przedstawiono na rys. 5.

Wyniki obliczeń przedstawić w tabeli 1. Pod pozycją 1 należy zanotować parametry próbki

wzorcowej materiału magnetycznego (A).

Tab. 1. Wyniki obliczeń

S

s

Y

max

X

z

B

max

H

c

∆P

g

Lp

Rodzaj ba-

danego ma-

teriału

Oznaczenie

mm

2

mm

mm

T

A/m

W/kg

Literatura

[1] Celiński Z. - Materiałoznawstwo elektrotechniczne. Oficyna Wydawnicza Politechniki Warszawskiej,

Warszawa, 2005 r.

[2] http://www.mat-fiz.p.lodz.pl/fizyka/kurs/ferro/ferrop.html

Badanie materiałów ferromagnetycznych (wersja „beta”)

7

Załącznik 1

Opis próbek materiałów ferromagnetycznych.

Powierzchnia przekroju każdej próbki wynosi 9 mm

2

.

Długość próbek l = 25 cm.

A - Próbka wzorcowa. Pakiet blach transformatorowych o zawartości krzemu 4%, indukcja nasyce-

nia B

max-A

= 1,4 T, natężenie powściągające H

c-A

= 30 A/m, straty na histerezę

∆P

g-A

= 2,52

W/kg [1] lub

∆P

v1-A

= 19,1 W/dcm i masa właściwa m

w

-A

= 7,6 kg/dcm

3

.

B - Pakiet blach prądnicowych o zawartości krzemu 1%, ciętych równolegle do kierunku

walcowania. Masa właściwa m

w

-B

= 7,85 kg/dcm

3

.

C - Pakiet blach prądnicowych o zawartości krzemu 1%, ciętych prostopadle do kierunku

walcowania. Masa właściwa m

w-C

= 7,85 kg/dcm

3

.

D - Pakiet drutów ze stali pospolitej, miękkiej o zawartości węgla 0,2%, m

w

--D

= 7,85 kg/dcm

3

.

E - Pakiet z drutu "fortepianowego" (D 85 A) o zawartości węgla 1%, m

w

-E

= 7,8 kg/dcm

3

.

H - Pakiet z drutu sprężynowego" (D 90) o zawartości węgla 0,9%, m

w

-H

= 7,8 kg/dcm

3

.

M - Pakiet z drutu ze stali miękkiej m

w-M

= 7,8 kg/dcm

3

.

N - Pręt ferrytowy o masie właściwej m

w-N

=

4,61 kg/dcm

3

.