
METROLOGIA ELEKTRYCZNA I ELEKTRONICZNA
SEMESTR II
1. W
IELKOŚCI
I
JEDNOSTKI
PODSTAWOWE
W
UKŁADZIE
SI................................................................................................3
2. W
ZORCE
NAPIĘCIA
REZYSTANCJI
I
POJEMNOŚCI
;
BUDOWA
I
WŁAŚCIWOŚCI
........................................................................4
3. P
ODZIAŁ
I
DEFINICJE
BŁĘDÓW
I
NIEPEWNOŚCI
POMIARU
................................................................................................6
4. B
ŁĄD
WSKAZANIA
MIERNIKA
ELEKTROMECHANICZNEGO
...............................................................................................6
5. B
UDOWA
I
ZASADA
DZIAŁANIA
MIERNIKA
MAGNETOELEKTRYCZNEGO
..............................................................................7
6. W
YPROWADZIĆ
WZÓR
NA
MOMENT
SKRĘCAJĄCY
W
MIERNIKU
MAGNETOELEKTRYCZNYM
....................................................8
7. W
PŁYW
TEMPERATURY
NA
WSKAZANIA
MIERNIKÓW
MAGNETOELEKTRYCZNYCH
................................................................8
8. Z
MIANY
ZAKRESÓW
POMIAROWYCH
AMPEROMIERZY
I
WOLTOMIERZY
MAGNETOELEKTRYCZNYCH
.........................................9
9. W
YPROWADZIĆ
WZÓR
NA
MOMENT
SKRĘCAJĄCY
W
MIERNIKU
PROSTOWNIKOWYM
...........................................................10
10. W
PŁYW
KSZTAŁTU
KRZYWEJ
PRZEBIEGU
MIERZONEGO
NA
WSKAZANIA
MIERNIKA
PROSTOWNIKOWEGO
..............................12
11. B
UDOWA
,
ZASADA
DZIAŁANIA
I
WŁAŚCIWOŚCI
MIERNIKÓW
TERMOELEKTRYCZNYCH
.......................................................13
12. B
UDOWA
,
ZASADA
DZIAŁANIA
I
WŁAŚCIWOŚCI
MIERNIKÓW
ELEKTROMAGNETYCZNYCH
...................................................14
13. W
YPROWADZIĆ
WZORY
NA
MOMENT
SKRĘCAJĄCY
MIERNIKÓW
ELEKTROMAGNETYCZNYCH
PRZY
PRĄDZIE
STAŁYM
I
ZMIENNYM
............................................................................................................................................................................14
14. Z
MIANY
ZAKRESÓW
POMIAROWYCH
AMPEROMIERZY
I
WOLTOMIERZY
ELEKTROMAGNETYCZNYCH
.....................................15
15. W
PŁYW
CZĘSTOTLIWOŚCI
I
OBCYCH
PÓL
MAGNETYCZNYCH
NA
WSKAZANIA
MIERNIKÓW
ELEKTROMAGNETYCZNYCH
...........16
16. B
UDOWA
,
ZASADA
DZIAŁANIA
I
WŁAŚCIWOŚCI
MIERNIKÓW
ELEKTRODYNAMICZNYCH
.....................................................17
17. Z
MIANY
ZAKRESÓW
POMIAROWYCH
AMPEROMIERZY
I
WOLTOMIERZY
ELEKTRODYNAMICZNYCH
.......................................18
18. W
PŁYW
CZYNNIKÓW
ZEWNĘTRZNYCH
NA
WSKAZANIA
MIERNIKÓW
ELEKTRODYNAMICZNYCH
..........................................19
19. B
UDOWA
I
ZASADA
DZIAŁANIA
WATOMIERZA
ELEKTRODYNAMICZNEGO
........................................................................19
20. W
YPROWADZIĆ
WZÓR
NA
MOMENT
SKRĘCAJĄCY
W
WATOMIERZU
ELEKTRODYNAMICZNYM
..............................................20
21. P
ODAĆ
DEFINICJĘ
STAŁEJ
WATOMIERZA
PRZY
PRĄDZIE
PRZEMIENNYM
,
WYJAŚNIĆ
POJĘCIE
„
COS
ϕ
ZN
”
WATOMIERZA
.............21
22. W
YPROWADZIĆ
WZÓR
NA
BŁĄD
„
OD
KĄTA
γ
”
W
WATOMIERZU
ELEKTRODYNAMICZNYM
.................................................21
23. Z
MIANY
ZAKRESÓW
POMIAROWYCH
WATOMIERZA
ELEKTRODYNAMICZNEGO
.................................................................22
24. P
OMIAR
MOCY
CZYNNEJ
PRZEBIEGÓW
ODKSZTAŁCONYCH
WATOMIERZEM
ELEKTRODYNAMICZNYM
....................................23
25. W
PŁYW
CZĘSTOTLIWOŚCI
NA
WSKAZANIA
WATOMIERZA
ELEKTRODYNAMICZNEGO
.........................................................23
26. B
UDOWA
I
ZASADA
DZIAŁANIA
GALWANOMETRU
STATYCZNEGO
..................................................................................24
27. W
YPROWADZIĆ
WZÓR
NA
MOMENT
HAMUJĄCY
–
CEWKOWY
W
GALWANOMETRZE
STATYCZNYM
.......................................24
28. D
EFINICJE
,
WZORY
I
PRZYKŁADOWE
WARTOŚCI
WIELKOŚCI
CHARAKTERYZUJĄCYCH
GALWANOMETR
STATYCZNY
..................25
29. W
ARUNKI
REZONANSU
GALWANOMETRU
WIBRACYJNEGO
..........................................................................................26
30. N
ARYSOWAĆ
KRZYWĄ
REZONANSU
I
ZDEFINIOWAĆ
SZEROKOŚĆ
REZONANSU
W
GALWANOMETRZE
WIBRACYJNYM
................27
31. N
ARYSOWAĆ
SCHEMAT
BLOKOWY
,
OPISAĆ
ZASADĘ
DZIAŁANIA
I
WYPROWADZIĆ
WZÓR
NA
N
X
W
WOLTOMIERZU
CYFROWYM
O
PRZETWARZANIU
IMPULSOWO
-
CZASOWYM
....................................................................................................................28
32. N
ARYSOWAĆ
SCHEMAT
BLOKOWY
,
OPISAĆ
ZASADĘ
DZIAŁANIA
I
WYPROWADZIĆ
WZÓR
NA
N
X
W
WOLTOMIERZU
CYFROWYM
Z
PODWÓJNYM
CAŁKOWANIEM
......................................................................................................................................29
33. N
ARYSOWAĆ
SCHEMAT
BLOKOWY
,
OPISAĆ
ZASADĘ
DZIAŁANIA
I
WYPROWADZIĆ
WZÓR
NA
N
X
W
WOLTOMIERZU
CYFROWYM
PRZETWARZAJĄCYM
NAPIĘCIE
W
CZĘSTOTLIWOŚĆ
...........................................................................................................30
34. N
ARYSOWAĆ
SCHEMAT
BLOKOWY
I
OPISAĆ
ZASADĘ
DZIAŁANIA
WOLTOMIERZA
KOMPENSACYJNEGO
..................................31
35. O
PISAĆ
KOMPENSACJĘ
NAPIĘCIA
10,5V
W
WOLTOMIERZUKOMPENSACYJNYM
O
KOMPENSACJI
WAGOWEJ
O
WAGACH
23, 22,
21, 20..................................................................................................................................................................31
36. Z
ASADA
DZIAŁANIA
WOLTOMIERZY
CYFROWYCH
NAPIĘCIA
PRZEMIENNEGO
...................................................................32
37. N
ARYSOWAĆ
SCHEMAT
WOLTOMIERZA
CYFROWEGO
NAPIĘCIA
PRZEMIENNEGO
Z
KOMPENSACJĄ
WARTOŚCI
SKUTECZNEJ
........33
38. K
LASY
DOKŁADNOŚCI
I
DOKŁADNOŚĆ
POMIARU
WOLTOMIERZAMI
CYFROWYMI
.............................................................34
39. W
YJAŚNIĆ
POWSTAWANIE
BŁĘDU
ZLICZANIA
...........................................................................................................35
40. C
YFROWY
POMIAR
REZYSTANCJI
. N
ARYSOWAĆ
SCHEMAT
BLOKOWY
I
PODAĆ
ODPOWIEDNIE
WZORY
DLA
JEDNEGO
Z
CYFROWYCH
MIERNIKÓW
REZYSTANCJI
........................................................................................................................35
41. Z
ASADA
DZIAŁANIA
KOMPENSATORÓW
O
REGULOWANEJ
REZYSTANCJI
.........................................................................36
1

42. D
EKADA
PODWÓJNA
F
EUSSNERA
..........................................................................................................................37
43. Z
ASADA
DZIAŁANIA
KOMPENSATORA
O
REGULOWANYM
PRĄDZIE
................................................................................37
44. K
OMPARATOR
TERMOELEKTRYCZNY
......................................................................................................................38
46. W
ARUNKI
PEŁNEJ
KOMPENSACJI
W
KOMPENSATORACH
PRĄDU
PRZEMIENNEGO
..............................................................39
45. K
OMPARATOR
MOMENTÓW
..................................................................................................................................39
46. W
ARUNKI
PEŁNEJ
KOMPENSACJI
W
KOMPENSATORACH
PRĄDU
PRZEMIENNEGO
..............................................................40
47. Z
ASADA
DZIAŁANIA
KOMPENSATORA
PRĄDU
PRZEMIENNEGO
O
WSPÓŁRZĘDNYCH
BIEGUNOWYCH
......................................40
48. Z
ASADA
DZIAŁANIA
KOMPENSATORA
O
WSPÓŁRZĘDZNYCH
PROSTOKĄTNYCH
................................................................41
49. B
UDOWA
I
ZASADA
DZIAŁANIA
PRZEKŁADNIKA
PRĄDOWEGO
(
NAPIĘCIOWEGO
)..............................................................41
50. P
ODAĆ
DEFINICJE
PRZEKŁADNI
ZWOJOWEJ
,
RZECZYWISTEJ
I
ZNAMIONOWEJ
PRZEKŁADNIKA
PRĄDOWEGO
(
NAPIĘCIOWEGO
)...43
51. W
YJAŚNIĆ
POJĘCIE
POPRAWKI
ZWOJOWEJ
...............................................................................................................43
52. P
ODAĆ
DEFINICJE
BŁĘDÓW
PRZEKŁADNIKA
PRĄDOWEGO
ORAZ
ICH
ZWIĄZEK
Z
KLASĄ
PRZEKŁADNIKA
(
NAPIĘCIOWEGO
).......43
54. S
KUTKI
ROZWARCIA
OBWODU
WTÓRNEGO
PRZEKŁADNIKA
PRĄDOWEGO
.......................................................................44
55. Z
ASADA
DZIŁANIA
I
WŁAŚCIWOŚCI
PRZEKŁADNIKA
LEM.........................................................................................44
56. N
ARYSOWAĆ
SCHEMAT
UKŁADU
DO
POMIARU
NATĘŻENIA
PRĄDU
(
NAPIĘCIA
)
PRZY
UŻYCIU
PRZEKŁADNIKA
,
PODAĆ
WZORY
NA
WIELKOŚĆ
MIERZONĄ
I
BŁĄD
POMIARU
........................................................................................................................45
57. Z
ASADA
DZIAŁANIA
WATOMIERZA
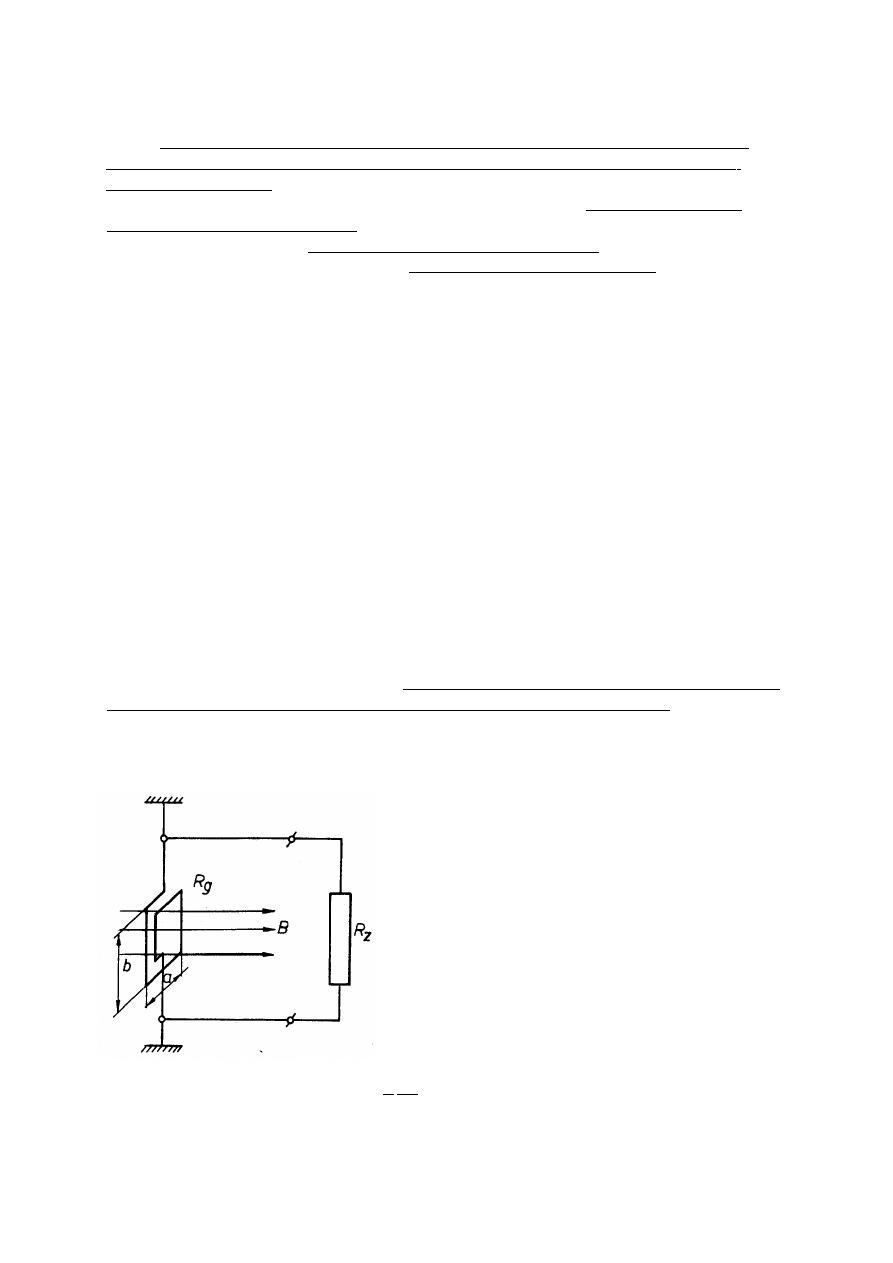
HALLOTRONOWEGO
..............................................................................................46
58. P
OMIAR
MOCY
UKŁADU
JEDNOFAZOWEGO
PRZY
POPRAWNIE
MIERZONYM
PRĄDZIE
(
NAPIĘCIU
),
PODAĆ
WZORY
NA
P,Q,S
I
BŁĘDY
METODY
POMIARU
..........................................................................................................................................47
2
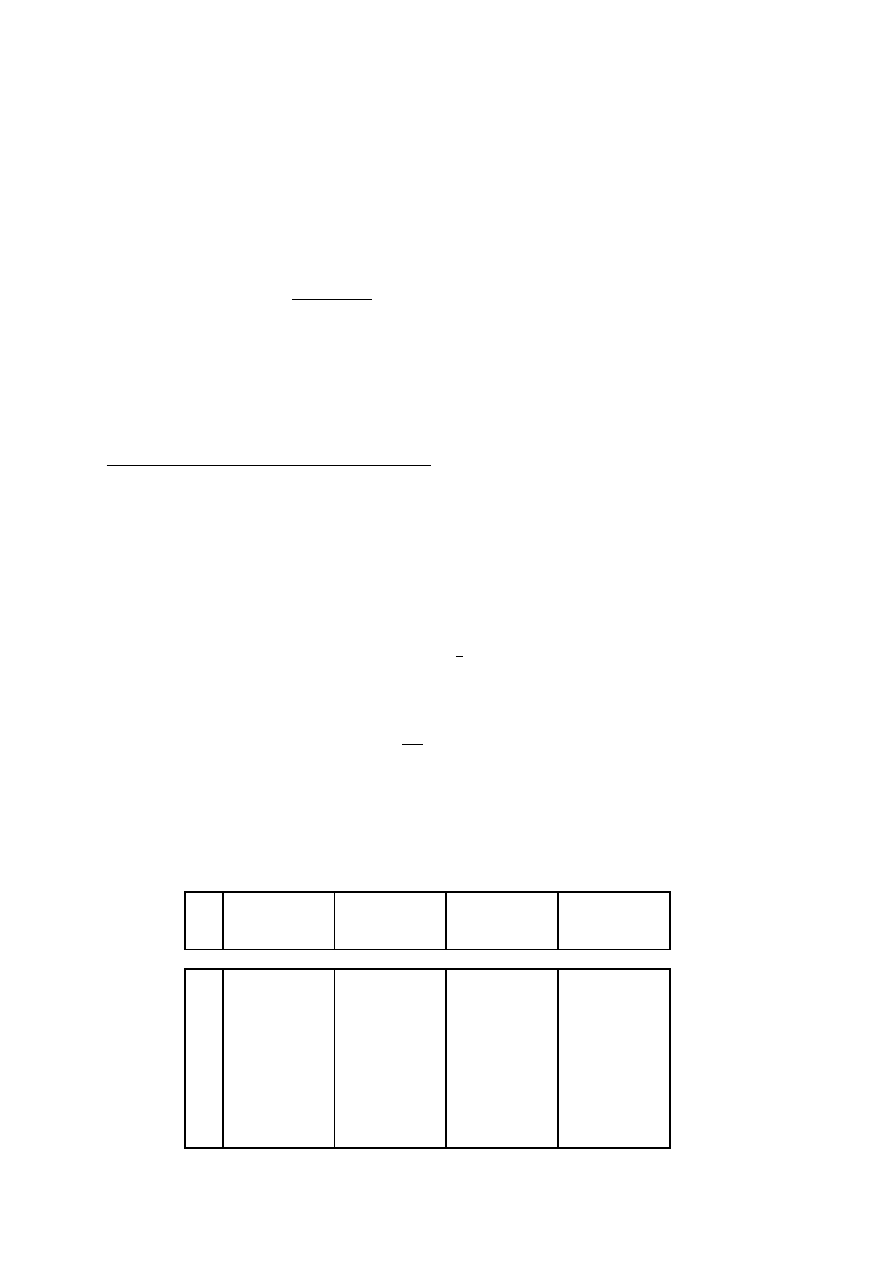
1. Wielkości i jednostki podstawowe w układzie SI.
Wstęp teoretyczny:
Wielkość – jest to cecha zjawiska lub ciała, którą można wyznaczyć jakościowo i ilościowo.
Wielkość mierzona – wielkość poddana mierzeniu.
Jednostka miar – umownie przyjęta wartość danej wielkości służąca do porównania z
wartością mierzoną.
Wartość wielkości mierzonej – liczba określająca ile razy dana wielkość mierzona jest
większa od wartości jednostki podstawowej.
Układ wielkości – zbiór wszystkich wielkości występujący w danej dziedzinie. Wielkości te
powiązane są równaniami wiążącymi prawa przyrody.
W Polsce obowiązuje Międzynarodowy Układ Jednostek Miar, oznaczony w skrócie SI.
Układ SI jest oparty na siedmiu podstawowych jednostkach miar i dwóch
uzupełniających, które wystarczają do ustalenia jednostek wszystkich wielkości
geometrycznych, mechanicznych, cieplnych, elektrycznych, magnety-cznych, świetlnych,
akustycznych i promieniowań jonizujących.
Wielkości podstawowych nie definiujemy. Za pomocą nich natomiast określa się inne
wielkości nazwane wielkościami pochodnymi. Na przykład w układzie SI prędkość liniowa
jest wielkością pochodną określaną ilorazem wielkości podstawowych długości i czasu.
Jednostki miary wielkości pochodnych nazywane pochodnymi jednostkami miar wywodzą
się od podstawowych jednostek miar.
Cecha układu SI jest to, że jednostkę miary jakiejkolwiek wielkości pochodnej otrzymuje się
przez podstawienie, do wzoru definicyjnego tej wielkości, oznaczeń odpowiednich
podstawowych jednostek miar. Na przykład jednostkę miary prędkości liniowej otrzymuje się
podstawiając we wzorze definicyjnym
t
l
v
=
zamiast oznaczenia literowego długości l jej jednostkę miary 1m, a zamiast czasu t jednostkę
miary czasu 1s
1
1
1
1
−
⋅
=
s
m
s
m
czyli metr na sekundę.
Układy jednostek miar mające opisaną cechę nazywa się spójnymi układami
jednostek miar.
Układ SI jest spójnym układem jednostek miar, to znaczy że pochodne jednostki miar są
wyrażone za pomocą jednostek miar podstawowych, wzorem definicyjnym, w którym
współczynnik liczbowy jest równy jedności.
Lp.
Nazwa
wielkości
Oznaczenie
literowe
Nazwa
jednostki
miary
Oznaczenie
jednostki
miary
Jednostki podstawowe
1
2
3
4
5
6
7
Długość
Masa
Czas
Natężenie
prądu
elektrycznego
Temperatura
Światłość
Ilość materii
L
M
T
I
T
I
Metr
Kilogram
Sekunda
Amper
Kelwin
Kandela
Mol
m
kg
s
A
K
cd
mol
3
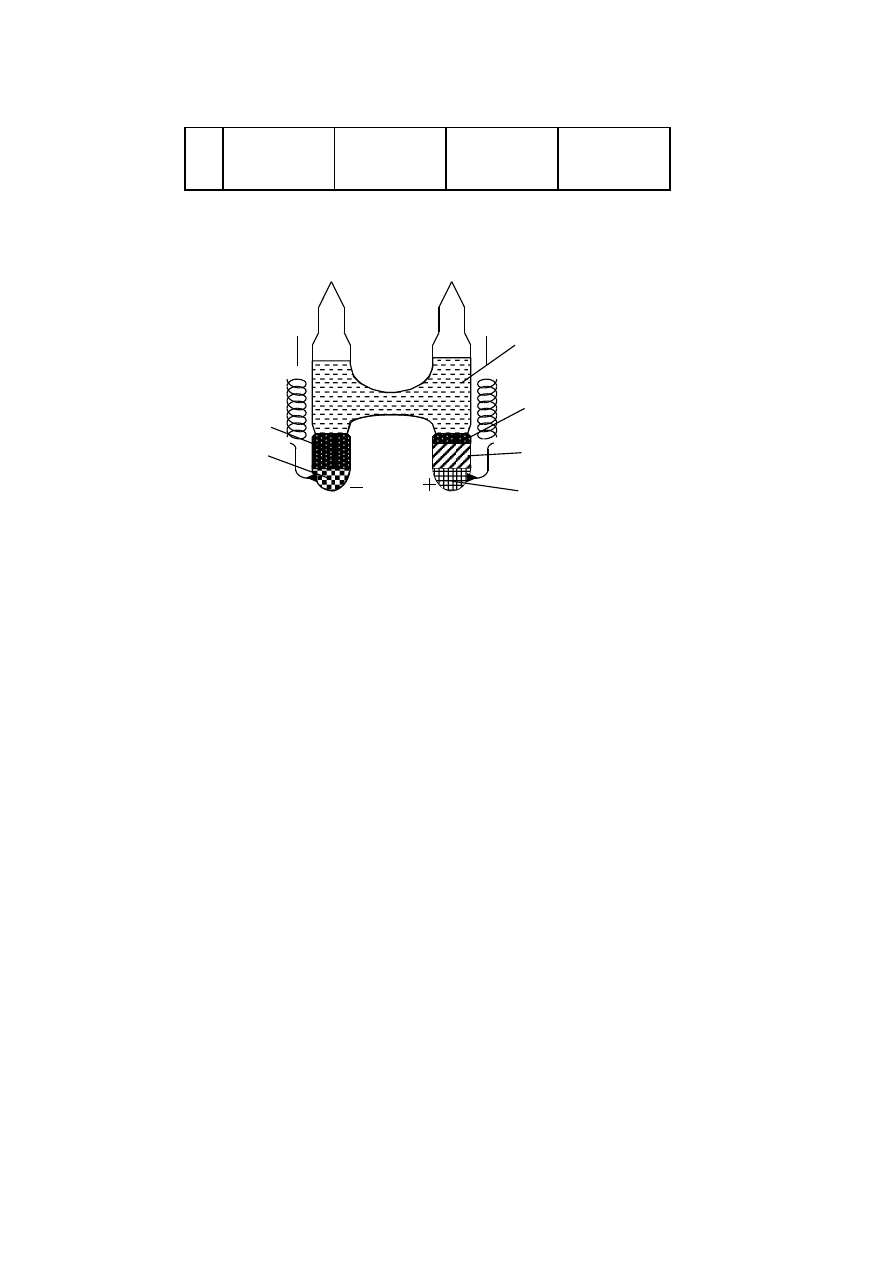
Jednostki uzupełniające
8
9
Kąt płaski
Kąt bryłowy
α
lub inne
grec.
ω
(
Ω
)
Radian
Steradian
Rad
sr
2. Wzorce napięcia rezystancji i pojemności; budowa i właściwości
Wzorcem napięcia, a ściślej – siły elektromotorycznej, jest ogniwo Westona. Istnieją dwa
typy ogniw wzorcowych: nasycone (częściej stosowane) i nienasycone.
Elektrolitem w ogniwie jest nasycony roztwór siarczanu kadmu, elektrodą dodatnią rtęć
metaliczna, zaś elektrodą ujemną amalgamat kadmu i rtęci. Pasta z rtęci, siarczanu
rtęciowego, umieszczona nad elektrodą dodatnią, pełni rolę depolaryzatora. Krystaliczny
siarczan kadmu zapewnia utrzymywanie elektrolitu w stanie nasycenia. Całość zamknięta jest
w szklanym naczyniu w kształcie litery H z zatopionymi w dolnej części drucikami
platynowymi stanowiącymi wyprowadzenia elektrod. Całość zamknięta jest w obudowie z
blach lub tworzywa sztucznego. Tak zbudowane ogniwo ma w temperaturze t=20
0
C siłę
elektromotoryczną (SEM) E
W20
=1,01865V. Zakres zmian temperatur pracy ogniwa Westona
wynosi 4-40
0
C, zmiana SEM wraz z temperaturą – około 0,004%/K. Ogniwo nie powinno być
obciążone prądem większym niż 1
µ
A. Rezystancja wewnętrzna ogniwa jest rzędu 400-500
Ω
.
Istnieją także nienasycone ogniwa Westona, gdzie elektrolitem jest w nich nienasycony
roztwór siarczanu kadmu. Ich SEM wynosi (E=1,0190V) i charakteryzują się kilkakrotnie
mniejszym wpływem temperatury na wartość SEM oraz mniejszą rezystancją wewnętrzną, a
także mniejszą wrażliwością na wstrząsy. Wadą jest mniejsza stałość w czasie.
Podstawowym elementem elektronicznych wzorców napięcia jest dioda Zenera, uzupełniona
układami stabilizacji napięcia i temperatury. Wzorzec 1V charakteryzuje się błędem nie
większym niż 0,0001%, roczną zmianą napięcia również mniejszą niż 0,0001%. Oraz
temperaturowym współczynnikiem zmian napięcia rzędu 0,001%/K. Dopuszczalny prąd
obciążenia 10mA. Wykonuje się także regulowane źródła napięcia wzorcowego z
dokładnością 0,01% i obciążalnością do kilkudziesięciu miliamperów. Zalety wzorców
elektronicznych: możliwość uzyskania dowolnej wartości napięcia wzorcowego, duża
obciążalność, odporność na przeciążenia, dobra stabilność czasowa i temperaturowa,
niewrażliwe na oddziaływania mechaniczne. Wady: kłopoty w otrzymywaniu powtarzalnych
właściwości poszczególnych egzemplarzy i odpowiedniej kontrolowanej stabilności.
Wzorcami rezystancji są oporniki wykonane z dużą starannością z materiałów oporowych.
4
Budowa nasyconego ogniwa
Westona
Hg
Hg
2
SO
Kryształy
CdSO
4
+
Roztwór
Cd SO
4
CdSO
4
+
Cd+Hg
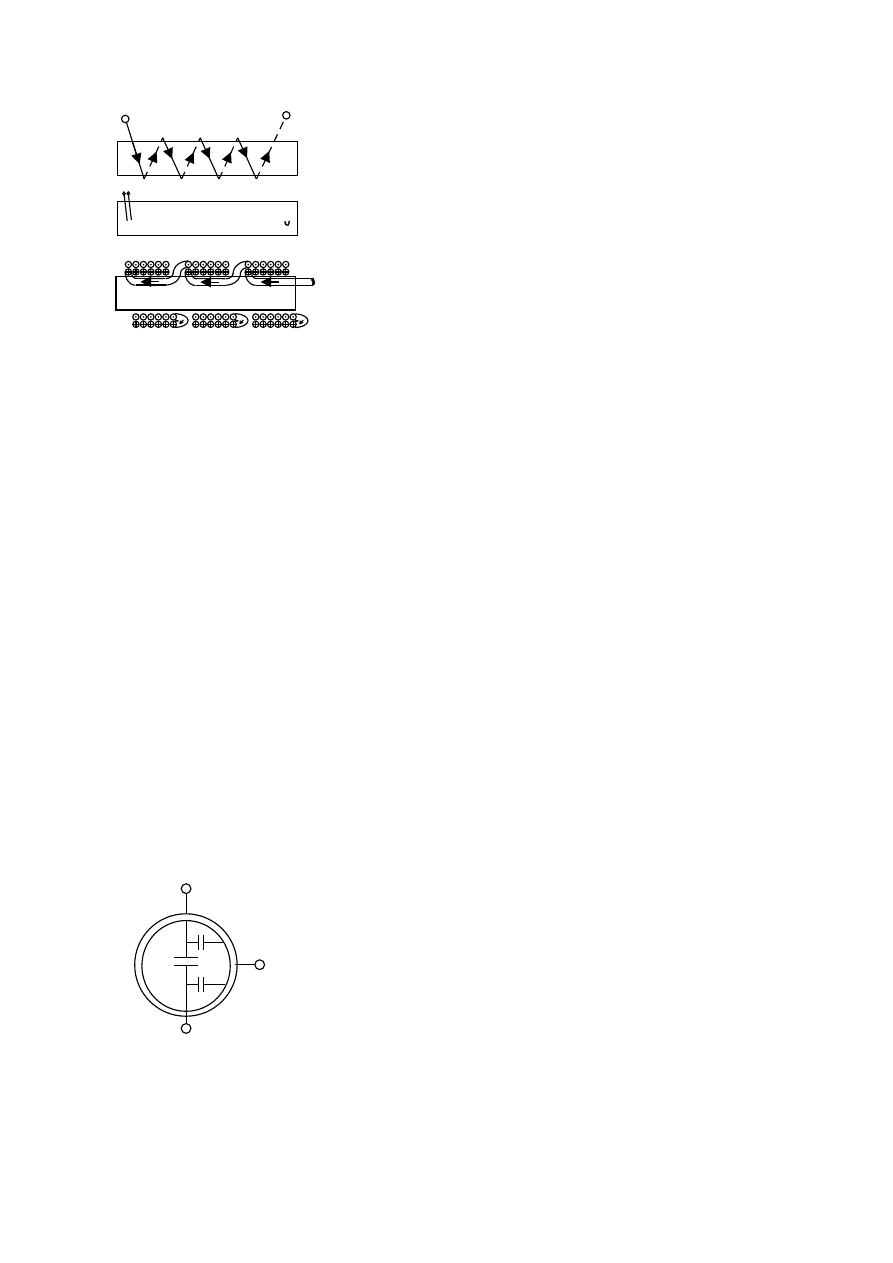
Schemat zastępczy kondensatora
wzorcowego ekranowanego.
I,II – zaciski łączeniowe
C
12
– pojemność wzorcowa
C
10
, C
20
– pojemności cząstkowe elektrod
względem ekranu
II
I
0
C
1
C
2
C
1
Wzorce rezystancji powinny spełniać następujące wymagania: stałość rezystancji w czasie,
niezależność od temperatury, mała STE (siła termoelektryczna) względem miedzi.
Wymagania te spełnione są przez właściwy dobór materiału z którego wykonywany jest
opornik. Najczęściej jest nim manganin w postaci taśmy lub drutu. Innym materiałem
używanym do budowy oporników wzorcowych jest konstantan.. Dla zapewnienia stałości
rezystancji w czasie przeprowadza się starzenie materiału oporowego: sztuczne (wygrzewanie
przez kilkadziesiąt godzin w temperaturze 100-150
0
C), naturalne (długotrwałe
przechowywanie w normalnych warunkach). Przy prądzie przemiennym konieczne jest
spełnienie dwóch dodatkowych wymagań : niezależność rezystancji od częstotliwości, kąt
fazowy jest równy zero. Przy prądzie przemiennym schemat zastępczy opornika składa się z
szeregowego połączenia rezystancji i indukcyjności oraz równoległego połączenia
pojemności. Wymaga to brania pod uwagę takich zjawisk jak: naskórkowość (zwiększająca
wartość rezystancji wraz ze wzrostem częstotliwości). Dla prądu przemiennego opornik
stanowi więc impedancję, charakteryzowaną kątem fazowym
ϕ
, lub też stałą czasową
τ
(określa szybkość narastania prądu).
Oporniki wzorcowe stałe wykonywane są w szeregu: 10
-4
-10
-3
-10
-2
-10
-1
-1-10-10
2
-10
3
-10
4
-10
5
Ω
. Opornbiki o wartościach
≤
0,1
Ω
mają 2 pary zacisków (zewnętrzne-służą do
doprowadzania prądu, zaś zewnętrzne są zaciskami potencjałowymi). Dokładność oporników
wzorcowych jest rzędu 10
-2
-10
-3
%, klasy dokładności: 0,001-0,002-0,01-0,02-0,05.
Oporniki regulowane stanowią zestawy cewek oporowych umieszczonych we wspólne
obudowie. Mogą być wykonane w układzie wagowym lub dekadowym. Dokładność
oporników regulowanych: 0,01-0,02-0,05-0,1-0,2-0,5. Oporniki mają na ogół: 4 dekady x1-
x10-x100-x1000
Ω
, 6 dekad x0,1-x1,x10,x100,x1000,x10000
Ω
, rzadziej 8dekad.
Wzorce pojemności. Podstawowymi wzorcami pojemności są kondensatory powietrzne o
prostych geometrycznie kształtach elektrod, dla których wartość pojemności można określić z
dużą dokładnością na drodze obliczeniowej.
Buduje się wzorcowe kondensatory powietrzne o pojemnościach 100pF-10000pFi
dokładności do 0,01. Współczynnik stratności tg
δ≈
10
-5
, zmiana pojemności pod wpływem
temperatury 0,001%/K. Napięcie znamionowe 250-500V. Kondensatory o większej
5
Sposoby nawijania
oporników:
nawinięcie płaskie
nawinięcie bifilarne

pojemności (1nF-10
µ
F) wykonuje się z dielektrykiem mikowym (względna przenikalność
elektryczna
ε
r
=4-8) lub styrofleksowym (
ε
r
=2,2). Wzorcowe kondensatory mikowe i
styrofleksowe są wykonywane jako stałe i regulowane (dekadowe). Kondensatory wzorcowe
umieszczane są w ekranujących obudowach metalowych.
3. Podział i definicje błędów i niepewności pomiaru.
Błędy pomiarów podzielić można na trzy zasadnicze grupy:
błędy systematyczne – powtarzają się niezależnie od liczby wykonywanych pomiarów.
Zalicza się do nich
błąd metody – są powodowane takimi czynnikami jak: rezystancja przewodów
pomiarowych, rezystancja przewodów łączeniowych (przy pomiarze mostkiem
Wheatstone’a), rezystancja przejścia na stykach, siły termoelektryczne, sprzężenia indukcyjne
i pojemnościowe między elementami układu pomiarowego, upływ prądu przez izolację
elementów układu pomiarowego
błędy wywołane niedokładnością przyrządów, takich jak mierniki, oporniki, cewki i
kondensatory, wynikają z faktu, iż żaden przyrząd nie jest idealny. Zarówno mierniki jak i
inne przyrządy używane w pomiarach mają określoną dokładność, co oznacza, że
zagwarantowana jest największa różnica między wartością wskazywaną a wartością
rzeczywistą.
błędy wywołane czynnikami postronnymi pochodzą od: zewnętrznych pół
magnetycznych, zewnętrznych pól elektrycznych, temperatury otoczenia, warunków
mechanicznych (wstrząsy, ruch powietrza), warunków atmosferycznych (ciśnienie,
wilgotność).
błędy przypadkowe – mogą się zmieniać przy powtarzaniu pomiaru. Do tej grupy
zalicza się: błędy spowodowane przypadkowo zmieniającymi się czynnikami zewnętrznymi,
błąd odczytu
błędy grube – zawarte są w wynikach pomiarów znacznie odbiegających od innych
wyników tej samej serii. Przyczyną ich są awarie przyrządów lub nieuwaga obserwatora.
Wyników pomiarów obarczonych błędem grubym nie bierze się po prostu pod uwagę przy
obliczaniu wartości wielkości mierzonej i dokładności pomiaru.
4. Błąd wskazania miernika elektromechanicznego.
Błąd wskazania miernika (
δ
w
) jest to największy błąd względny jaki może zostać popełniony
przy pomiarze konkretnej wartości wielkości badanej
δ
w
gr
w
W
=
∆
*100%
podstawiając
∆
gr
gr
W
=
⋅
δ
max
100
otrzymujemy
δ
δ
w
gr
w
W
W
=
max
%
.
Gdzie
∆
gr
– graniczna wartość błęd,u
δ
gr
– błąd graniczny, liczbowo równy klasie miernika,
W
w
wartość wskazywana, W
max
– maksymalna wartość zakresu przyrządu pomiarowego.
Błąd wskazania jest tym mniejszy im bardziej wartość mierzona jest zbliżona do zakresu
miernika (wartości znamionowej). Wynika stąd wniosek, że dla zapewnienia odpowiedniej
dokładności zakres przyrządu powinien być tak dobrany, aby uzykać możliwie duże
wychylenie wskazówki (2/3 łuku pomiarowego).
6
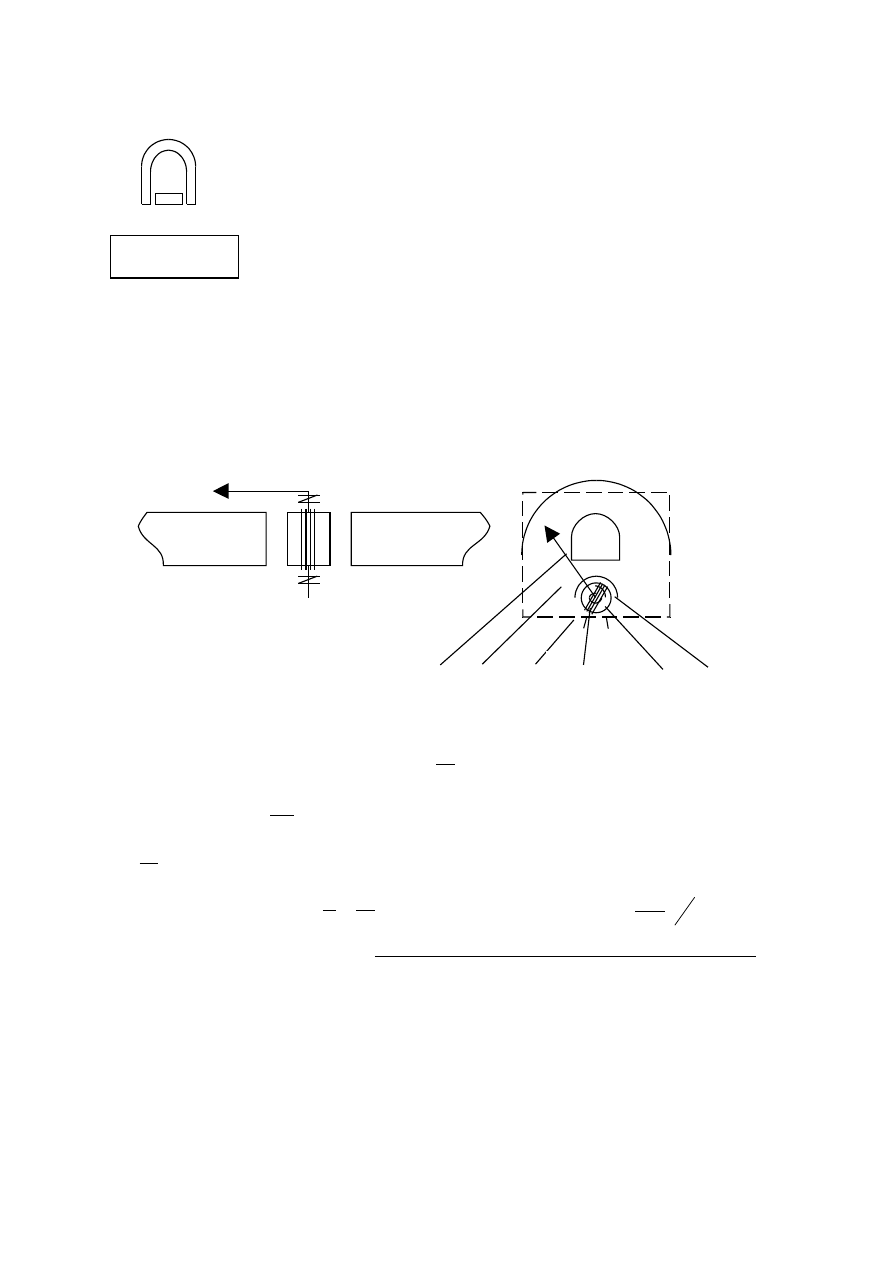
Przetwornik
magnetoelektryczny
5. Budowa i zasada działania miernika magnetoelektrycznego.
W przetwornikach magnetoelektrycznych źródłem momentu
napędowego jest wzajemne oddziaływanie stałego pola magnetycznego i
uzwojenia, przez które płynie prąd. Organem ruchomym może być
zarówno miniaturowy magnes trwały umieszczony wewnątrz
nieruchomej cewki, jak i lekka cewka znajdująca się w nieruchomym
polu magnesu trwałego. Najczęściej spotyka się drugie rozwiązanie (rys),
w którym magnes trwały 1 wraz z nabiegunnikami 2 i rdzeniem 3
stanowią ciężkie elementy nieruchome, służące do wytworzenia w
szczelinie powietrznej 4, pola magnetycznego o promieniowym kierunku i stałej wartości
niezależnej od położenia (czyli od kąta
α
). Organem ruchomym jest cewka 5, nawinięta
cienkim (0,02...0,1mm) izolowanym przewodem miedzianym(rzadziej aluminiowym). Cewka
jest ułożyskowana w taki sposób, aby jej oś obrotu pokrywała się z osią geometryczną
szczeliny obwodu magnetycznego. Do cewki jest przymocowana wskazówka oraz masy
dodatkowe tak dobrane, że środek ciężkości całego organu ruchomego znajduje się na osi
obrotu. Dwie sprężyny spiralne (czasem taśmy zawieszenia) doprowadzają prąd do cewki i są
jednocześnie źródłem momentu zwrotnego.
W stanie równowagi mamy :
Z
S
M
M
=
X
D
J
α
φ
⋅
=
⋅
0
X
D
J
α
φ
⋅
=
0
Czułość miernika
dJ
d
S
α
=
informuje jak zmieni się wychylenie przy zmianie prądu. Ale
const
D
S
=
=
0
φ
, gdzie
φ
0
– całkowity stumień skojarzony z cewką, D – współczynnik
sprężyny. Stała miernika
const
D
S
C
=
=
=
0
1
φ
czyli
X
C
J
α
⋅
=
⇒
[ ]
dz
A
J
C
ZN
ZN
α
=
Ponieważ stała miernika C jest stała, podziłka miernika magetoelektrycznego jest liniowa.
Przy zmianie kierunku prądu płynącego przez cewkę zmienia się kierunek momentu
napędowego i odchylenia organu ruchomego, dlatego oznaczenia (+ i -) umieszczone na
zaciskach określają jednoznacznie kierunek właściwy (tj. dający prawidłowe odchylenie).
Prąd wewnątrz przetwornika powinien płynąć od zacisku dodatniego (+) do ujemnego (-).
Buduje się również przetworniki o dwustronnym odchylaniu, mające wskaz zerowy w
środku podziałki. Przy dodatnim (zgodnym z oznaczeniami) kierunku prądu dają one
odchylenie dodatnie (w prawo), a przy zmianie kierunku prądu następuje zmiana kierunku
odchylenia (w lewo).
7
N
S
1
2
3
4
5
6
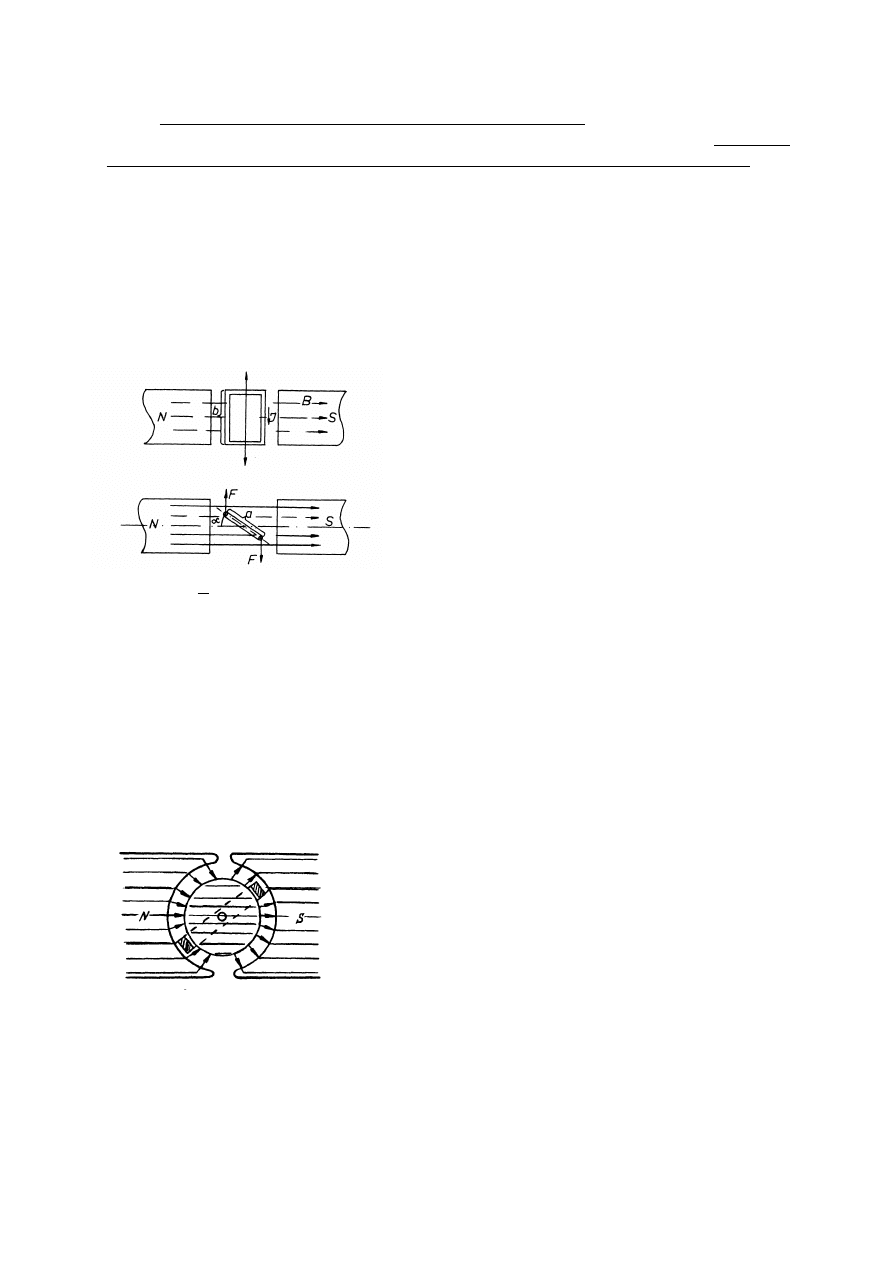
Organ ruchomy przetwornika magnetoelektrycznego ma stosunkowo dużą
bezwładność i duży (kilka di kilkunastu sekund) okres drgań własnych, dlatego może być
stosowany tylko do przetwarzania wartości stałych lub zmieniających się bardzo wolno (jest
to przetwarzanie statyczne). Dla częstotliwości powyżej 20 Hz miernik pokazuje wartość
średnią. Tłumienie jest wytwarzane przez prądy płynące w ramce.
Mierniki magnetoelektryczne to głównie amperomierze i woltomierze. Maksymalny prąd to
25mA, tak mała wartość spowodowany jest tym, że jest on doprowadzany za pośrednictwem
sprężyn (wytrzymałość cieplna).
6. Wyprowadzić wzór na moment skręcający w mierniku magnetoelektrycznym.
W mierniku magnetoelektrycznym cewka o wymiarach a,b o z zwojach umieszczona jest w
polu magnetycznym magnesu trwałego o indukcji B.
Przez cewkę płynie prąd I. Przepływ tego prądu
powoduje powstanie sił działających na boki cewki
b:
l
I
B
F
⋅
⋅
=
gdzie długość czynna cewki o z
zwojach wynosi :
b
z
l
⋅
=
Siły działające na cewkę tworzą parę sił, której
moment wynosi:
α
α
α
α
cos
M
:
y
Otrzymujem
cewką
z
skojarzony
strumieńt
-
z
zwojem
jednym
z
skojarzony
strumieńt
-
s
B
cewki
ia
powierzchn
-
S
b
a
:
cos
cos
cos
2
2
0
0
⋅
⋅
Φ
=
Φ
=
⋅
Φ
Φ
=
⋅
=
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
=
⋅
⋅
=
I
ponieważ
a
b
z
I
B
a
F
a
F
M
Jak widać moment napędowy
zależy od kąta obrotu, co jest niekorzystne. Aby zniwelować tą zależność stosuje się
odpowiednie zabiegi konstrukcyjne, aby przebieg linii sił pola był radialny tj. kąt między
liniami sił pola i bokiem a wynosi 0. Wtedy zależność ta przechodzi w:
I
M
⋅
Φ
=
0
Momentowi napędowemu przeciwdziała moment
zwracający wynoszący
α
⋅
=
k
M
Z
gdzie k jest stałą
zwracania sprężyny. Po porównaniu równań stronami
można przekonać się, że w mierniku magnetoelektrycznym
kąt wychylenia jest wprost proporcjonalny do
przepływającego prądu.
7. Wpływ temperatury na wskazania mierników magnetoelektrycznych.
Zmiany temperatury wpływają na następujące wielkości:
•
Strumień skojarzony z cewką
φ
0
– maleje ze wzrostem temperatury ~ 0,2%/10K
•
Stała zwracania D – maleje ze wzrostem temperatury ~ 0,4%/10K
8
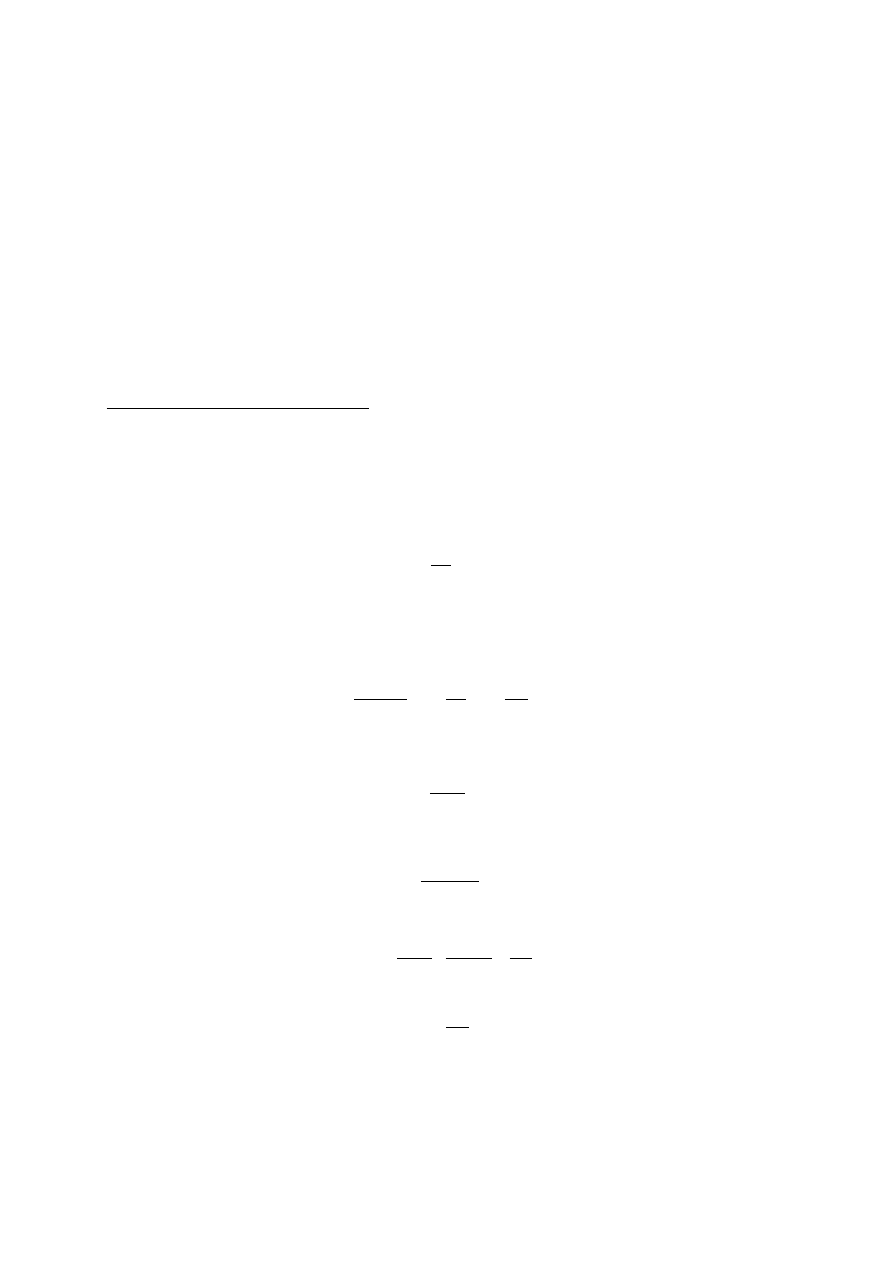
•
Rezystancja cewki wykonanej z przewodu miedzianego rośnie ze wzrostem temperatury o
4%/10K
Na skutek tych zmian wskazania miernika maleją ze wzrostem temperatury o około
4%/10K. Aby temu zapobiec stosuje się układy kompensacyjne. Są to oporniki wykonane z
manganinu, materiału o rezystancji praktycznie niezależnej od temperatury. Wartość
oporników manganinowych oraz ich sposoby włączenia zapewniają ograniczenie wpływu
temperatury. Zgodnie z przepisami normalizacyjnymi błąd spowodowany zmianami
temperatury
±
10K nie powinien przekraczać wartości błędu podstawowego wynikającego z
klasy miernika.
8. Zmiany zakresów pomiarowych amperomierzy i woltomierzy
magnetoelektrycznych
Rozszerzenie zakresu amperomierza
Czynność ta polega na zbocznikowaniu ustroju miernika rezystorem o niewielkie rezystancji.
Dzięki temu przez cewkę miernika płynie tylko część mierzonego prądu, reszta płynie przez
bocznik:
B
A
I
I
I
+
=
(1)
gdzie I
– prąd badany; I
A
–prąd płynący przez ustrój; I
B
– prąd płynący przez bocznik
podstawowym parametrem opisującym rozszerzenie zakresu amperomierza jest mnożnik m:
A
I
I
m
=
(2)
Na mocy NPK możemy zapisać:
B
B
A
A
R
I
R
I
*
*
=
(3)
gdzie R
A
jest rezystancją ustroju pomiarowego, R
B
jest rezystancją bocznika
Uwzględniając w równaniu 2 równania 1 i 3 otrzymujemy wzór na mnożnik m:
B
A
A
B
A
B
A
R
R
1
I
I
1
I
I
I
m
+
=
+
=
+
=
(4)
Przekształcając wzór 4 możemy wyznaczyć wartość rezystancji bocznika w zależności od
mnożnika:
1
m
R
R
A
B
−
=
(5)
Poprzez dołączenie bocznika do ustroju zmieni się rezystancji zestawu widziana z punktu
widzenia obwodu badanego.
B
A
B
A
Z
R
R
R
R
R
+
=
*
(6)
Uwzględniając wzór 5 we wzorze 6 otrzymany:
m
R
m
R
1
m
1
m
R
R
A
A
2
A
Z
=
−
−
=
*
*
Moc wydzielana (pobierana z obwodu) na zestawie
A
A
2
A
A
2
A
Z
2
mP
R
I
m
m
R
I
m
R
I
P
=
=
=
=
*
*
)
*
(
*
gdzie P
A
– moc wydzielana na ustroju amperomierza przed zmianą zakresu
Miliamperomierz łączy się do zacisków napięciowych bocznika za pomocą specjalnych
przewodów. Zaciski prądowe służą do podłączenie do obwodu badanego. Wielkości
charakteryzujące bocznik to prąd znamionowy, znamionowy spadek napięcia, klasę bocznika
oraz numer miernika z którym konkretny bocznik współpracuje.
9

Rozszerzenie zakresu woltomierza
Woltomierz magnetoelektryczny jest to ustrój magnetoelektryczny (wykorzystywany jako taki
do pomiaru prądu) z wmontowanym rezystorem wewnętrznym R
w
. Suma rezystancji rezystora
wewnętrznego R
W
i rezystancji sprężyn doprowadzających prąd RS do ustroju oraz
rezystancja cewki RC stanowią rezystancję woltomierza Rv.
W
S
C
V
R
R
2
R
R
+
+
=
Pod wpływem napięcia mierzonego U przez miernik popłynie prąd Iv
V
V
R
U
I
=
Prąd ten jest ograniczony ze względów termicznych więc przy pomiarach większych napięć w
szereg z woltomierzem należy włączyć rezystor dodatkowy RD.
Mnożnikiem zakresu nazywamy wielkość:
V
U
U
m
=
gdzie U jest napięciem mierzonym a UV jest napięciem odkładającym się na właściwym
mierniku czyli na rezystancji RV,
m
R
R
1
R
R
R
R
I
R
R
I
U
U
V
D
V
D
V
V
V
D
V
V
V
=
+
=
+
=
+
=
)
(
Z powyższej zależności możemy wyznaczyć wielkość rezystancji dodatkowej R
D
w
zależności od mnożnika m:
)
(
1
m
R
R
V
D
−
=
Rezystancja zestawu z punku widzenia obwodu badanego wyniesie:
V
V
V
D
V
z
R
m
R
1
m
R
R
R
R
*
)
(
=
−
+
=
+
=
Natomiast moc pobierana z układu (wydzielana na mierniku i rezystorze dodatkowym):
V
V
2
v
V
2
v
2
z
2
P
m
R
U
m
mR
U
m
R
U
P
*
=
=
=
=
Gdzie P
V
jest mocą wydzielaną na mierniku przed zmianą zakresu
9. Wyprowadzić wzór na moment skręcający w mierniku prostownikowym
Miernik prostownikowy stanowi połączenie miernika magnetoelektrycznego z
prostownikiem. Zadaniem prostownika jest przetworzenie prądu przemiennego na prąd stały
lub pulsujący, który mierzony jest miernikiem magnetoelektrycznym. Do prostowania są
używane najczęściej prostowniki półprzewodnikowe – krzemowe lub germanowe, rzadziej
miedziowe. Parametrami charakteryzującymi prostowniki są: maksymalne napięcie wsteczne,
maksymalny prąd przewodzenia, maksymalna wartość prądu wyprostowanego, maksymalna
temperatura obudowy, pojemność własna, częstotliwość graniczna (tzn. częstotliwość, przy
której wartość prądu wyprostowanego maleje do 20% wartości prądu przy małej
częstotliwości), sprawność prostowania ( współczynnik prostowania)
k
I
I
R
R
p
f
r
r
f
=
=
(gdzie, I
f
,
I
r
, R
f
, R
r
prąd i rezystancja w kierunku przewodzenia i zaporowym)
Prostowanie średnie
Przy ujemnym półokresie napięcia prąd w
kierunku zaporowym jest pomijalnie mały.
10
R
Schemat obwodu prostowania
średniego
Zakrzywienie na początku charakterystyki powoduje, że podziałka miernika
prostownikowego jest na początku zagęszczona.
Wartość średnia
k
k
– współczynnik kształtu,
k
s
– współczynnik szczytu .
Prostowanie szczytowe
Kondensator C jest ładowany przez prostownik do
napięcia bliskiego amplitudzie U
m
mierzonego
napięcia. Im mniejszy jest prąd rozładowania
kondensatora – i
c
tym mniejsza jest różnica między
napięciem u
c
i U
m
.
Amperomierze i woltomierze.
11
u t
T
u t dt
U
T
U t dt
u t dt
k
U
U
U
U
T
śr
T
T
k
śr
m
( )
( )
( )
( )
=
=
=
=
∫
∫
∫
1
1
0
0
2
0
U =
1
T
k
s
kszt. przebiegu
u(t)
sinus
0
2
sin prost 1- p
sin prosr 2 - p
prostokąt
trójkąt
pioksztatny
.
,
,
,
,
,
,
,
,
,
,
U
U
k
k
U
U
U
U
U
U
U
U
U
U
U
U
U
U
śr
k
s
m
m
m
m
m
m
m
m
m
m
m
m
m
m
π
π
π
π
π
1
2
111 1 41
1
1
1
2
1 57 2 00
2
2
1
2
111 1 41
0
1
1
0
1
2
1
3
115 1 73
0
1
2
1
3
115 1 73
a)
b)
c)
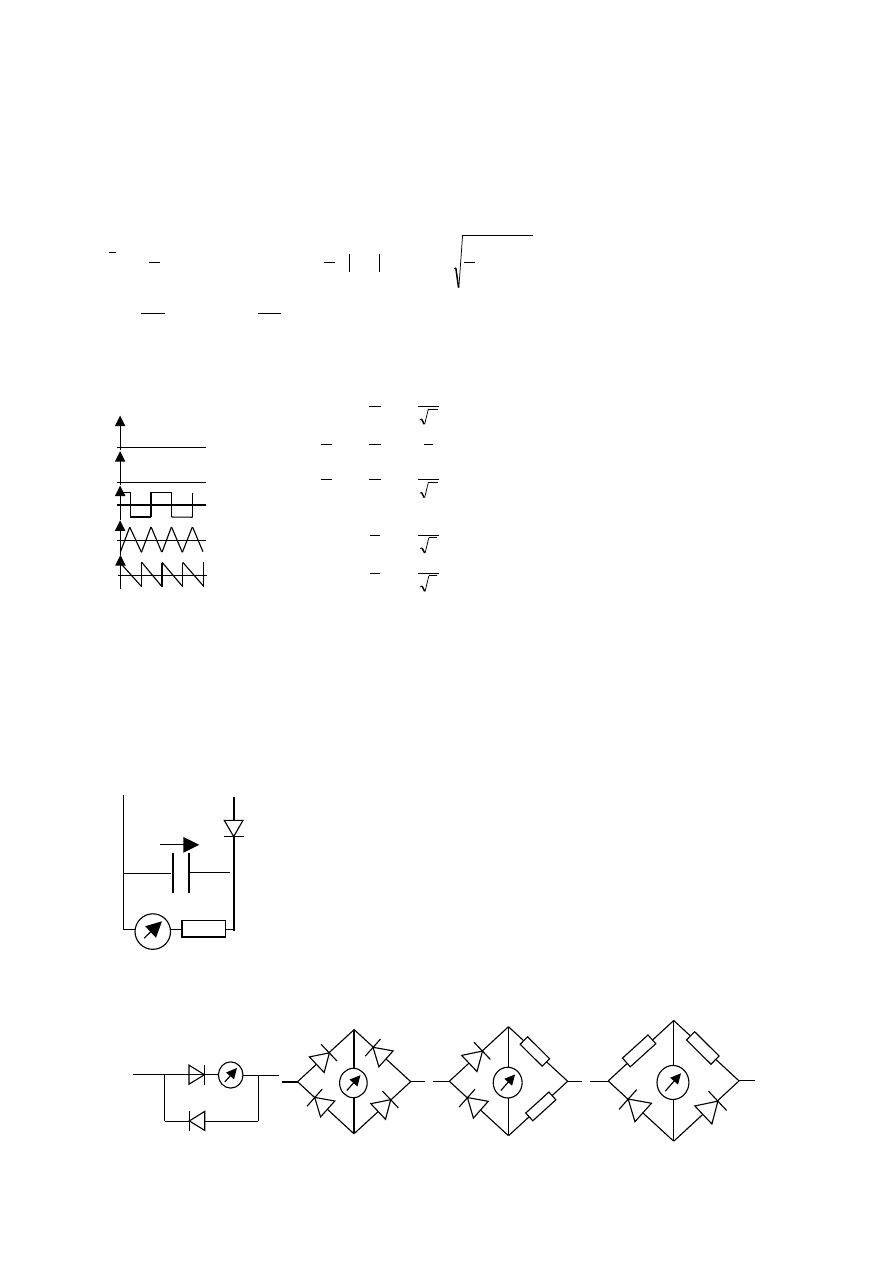
d)
Połączenie prostowników z miernikiem przy prostowaniu średnim: a) prostowanie półokresowe, b)
prostowanie pełnookresowe w układzie Graetza, c) prostowanie pełnookresowe w układzie mostkowym
stosowane w woltomierzach, amperomierzach i miernikach uniwersalnych, d) prostowanie pełnookresowe
w układzie mostkowym stosowane w amperomierzach do pomiaru większych prądów.
U
c
i
p
R
C
i
c
Schemat
obwodu
prostowania
szczytowego

W układach przedstawionych na rysunku przez cewkę organu ruchomego miernika
magnetoelektrycznego przepływa pulsujący prąd wyprostowany. Powstaje zatem pulsujący
moment skręcający. Ponieważ moment bezwładności organu ruchomego jest tak duży, że ruch
jego nie nadąża za zmianami momentu napędowego, wskazówka ustawia się w położeniu
odpowiadającym wartości średniej tego momentu, a zatem i wartości średniej prądu. Przy
prądzie sinusoidalnym będą obowiązywały zależności:
- chwilowy moment skręcający
m
i
I
t
n
m
=
=
Φ
Φ
0
0
*
*
sin
ω
- średni moment skręcający:
M
T
m dt
T
I
tdt
I
I
n
n
T
m
T
m
śr
śr
=
=
=
=
∫
∫
2
2
2
0
2
0
0
2
0
0
/
/
sin
Φ
Φ
Φ
ω
π
Wskazania mierników magnetoelektrycznych z prostownikiem są proporcjonalne do wartości
średniej mierzonego prądu. Ponieważ znajomość wartości skutecznej ma duże znaczenie
praktyczne, dlatego też mierniki te są skalowane w wartościach skutecznych dla przebiegu
sinusoidalnego, czyli dla współczynnika kształtu k
k
=1,11.
10. Wpływ kształtu krzywej przebiegu mierzonego na wskazania miernika
prostownikowego.
Miernik prostownikowy jest przyrządem służącym do pomiaru napięcia lub
natężenia prądu przemiennego, wykorzystuje przy tym prostownik półprzewodnikowy. Przez
przetwornik przepływa prąd pulsujący (okresowy prąd jednokierunkowy). Moment napędowy
jest w każdej chwili proporcjonalny do chwilowej wartości prądu, ale bezwładność i tłumienie
organu ruchomego powodują, że ustalone odchylenie
α
jest proporcjonalne do średniej
wartości momentu, zatem proporcjonalne do średniej wartości prądu płynącego przez
przetwornik
W obwodach prądu przemiennego jako wartości charakterystyczne napięcia i prądu
stosuje się wartości skuteczne, toteż podziałkę miernika skaluje się w wartościach
skutecznych, przy założeniu, że wielkości mierzone mają przebiegi sinusoidalne o znanym
współczynniku kształtu
11
,
1
2
2
2
2
≈
=
=
=
π
π
m
m
śr
k
I
I
I
I
k
Podziałka jest wykonana w taki sposób (zmniejszona ilość działek), że wartości
odczytane są 1,11 razy większe od wartości średnich prądu, czyli przy przebiegu
sinusoidalnym są równe wartością skutecznym. Tak wykonana podziałka traci ważność
przy przebiegach odkształconych. Posługiwanie się przyrządem prostownikowym przy
pomiarze wartości skutecznej przebiegu odkształconego powoduje powstanie błędu zależnego
od współczynnika kształtu przebiegu k
K
. Błąd procentowy dla miernika mierzącego wartości
sinusoidalne (1,11)
12
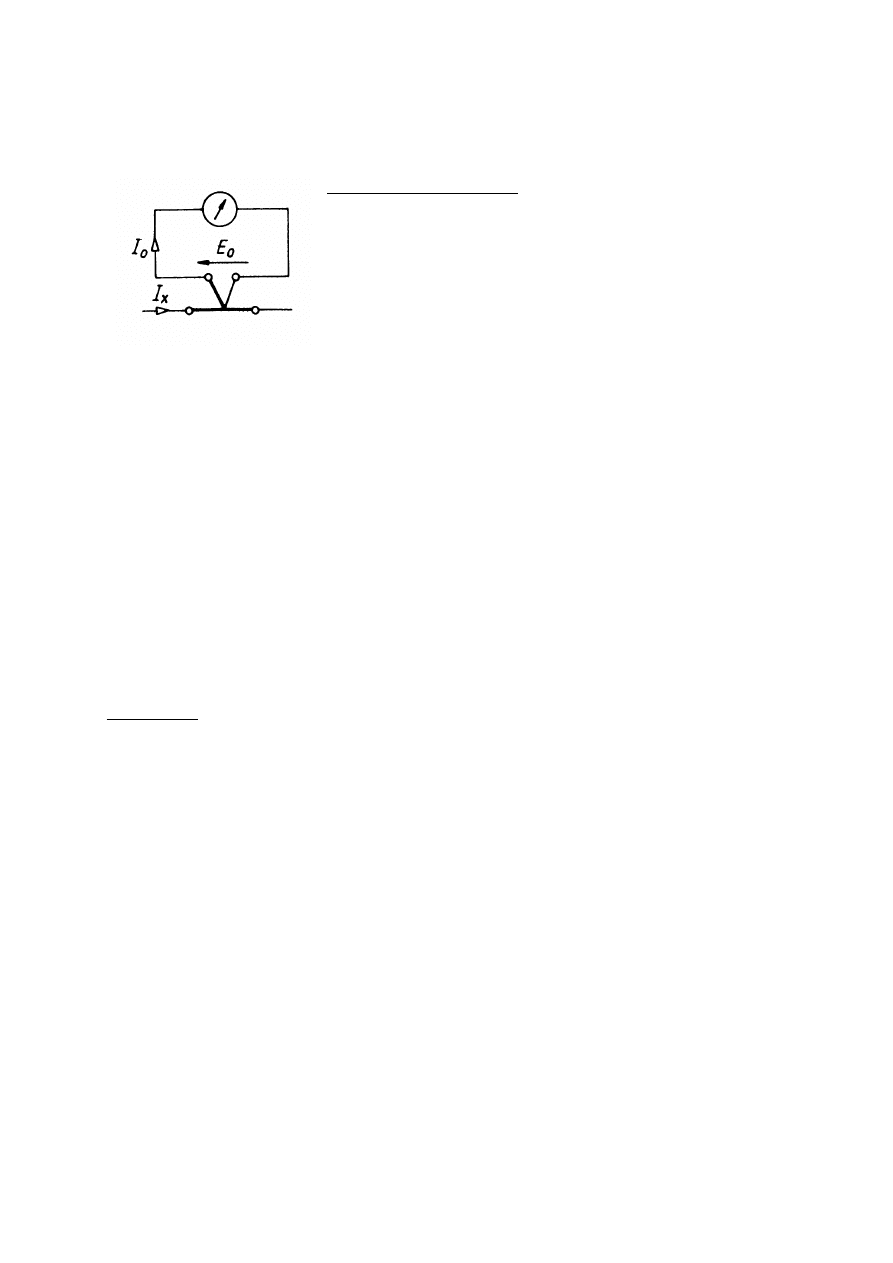
11. Budowa, zasada działania i właściwości mierników termoelektrycznych.
Mierniki termoelektryczne zaliczają się do urządzeń mierzących wartości prądu
przemiennego.
Budowa i zasada działania
Miernik termoelektryczny stanowi połączenie miernika
magnetoelektrycznego z przetwornikiem termoelektrycznym,
składającym się z termoelementu i grzejnika.
Grzejnik o rezystancji R mierzonym prądem nagrzewa spoinę
termoelementu, różnica temperatur powoduje powstanie siły
termoelektrycznej, która jest następnie mierzona. Prąd I
0
płynący przez ustrój, a więc i wychylenie organu ruchomego są
proporcjonalne do kwadratu wartości skutecznej prądu mierzonego (P = I
2
R prop. do różnicy
temp.). Podziałka miernika ma, więc przebieg nieliniowy. Ponieważ napięcie
termoelektryczne E
0
jest małe, 10
÷
12 mV, więc miernik magnetoelektryczny jest
miliwoltomierzem wyskalowanym w amperach. Woltomierze termoelektryczne są budowane
rzadziej niż amperomierze. Pobierają one z obwodu mierzonego prąd, który rozgrzewa
termoelement. Zasada działania jest identyczna jak amperomierza.
Termoogniwo składa się z dwóch wykonanych z różnych metali tak, aby napięcie powstałe
przy różnicy temperatur między końcami była jak największa. Najczęściej używane są
następujące termoogniwa: konstantan – chromel, konstantan – żelazo.
Grzejnik może być nieizolowany od termoogniwa lub izolowany. Przy budowie grzejnik
dobiera się go ze względu na możliwość wydzielania ciepła i małą intensywność zjawiska
naskórkowości i pojemności własne, natomiast termoogniwo ze względu na napięcie
termoelektryczne.
Właściwości
- (+) mierzą wartość skuteczną niezależnie od kształtu przebiegu
- (-) na pomiar wpływ ma temperatura otoczenia – zmienia się temperatura grzejnika i
napięcie termoelektryczne
- (+) mierzą prądy do częstotliwości przebiegu 100 MHz (nawet 1GHz) i napięcia do 50
MHz. Zakres ten ograniczają błędy dodatkowe wynikające ze zjawiska naskórkowości
oraz pojemności grzejnika i przewodów łączących (klasy amperomierzy : 1; 1,5; 2,5 –
błędy temperaturowe nie przekraczają 1 %)
- (-) nieliniowy przebieg skali urządzenia, – aby zlinearyzować jej przebieg stosuje się
mierniki ze wzmacniaczami z pętlą sprzężenia.
- (-) w przypadku woltomierzy wadą jest duży pobór mocy. Dla amperomierza spadek
napięcia na grzejniku wynosi 0,2
÷
2 V.
Mierniki termoelektryczne stosuje się do pomiaru przebiegów o dużej częstotliwości. Przy
częstotliwości technicznej używa się ich wtedy, gdy przebieg jest znacznie odkształcony.
13

12. Budowa, zasada działania i właściwości mierników elektromagnetycznych.
W przetwornikach elektromagnetycznych moment napędowy powstaje w wyniku
wzajemnego przyciągania się lub odpychania rdzeni wykonanych z miękkiego materiału
ferromagnetycznego pod wpływem pola magnetycznego wytwarzanego przez cewkę, przez
którą płynie mierzony prąd.
Ze względu na konstrukcję organu ruchomego rozróżnia się dwa typy mierników:
•
O rdzeniu wciąganym
•
O rdzeniach odpychanych
Rdzenie te są magnesowane polem magnetycznym wytworzonym przez przetwarzany
prąd. Ponieważ działanie powstałych w taki sposób elektromagnesów nie zależy od kierunku
prądu, przetworniki elektromagnetyczne można stosować zarówno do prądu stałego, jak i
przemiennego. Ze względu jednak na stosunkowo dużą moc pobieraną nie stosuje się ich w
układach prądu stałego (przetworniki magnetoelektryczne są pod tym względem znacznie
lepsze), lecz prawie wyłącznie do pomiarów w obwodach prądu zmiennego. Są one bardzo
rozpowszechnione ze względu na prostą budowę i mały koszt wytwarzania.
Wśród wielu rozwiązań obecnie najczęściej stosuje się przetworniki dwurdzeniowe mające
cewkę okrągłą. Jeden rdzeń jest unieruchomiony przez zamocowanie do nieruchomej cewki,
drugi jest połączony mechanicznie z osią przetwornika. Moment zwrotny wytwarza jedna
sprężyna spiralna. Moment napędowy powstaje na skutek odpychania się rdzeni znajdujących
się w tym samym polu magnetycznym, a więc magnesowanych jednakowo. Siły odpychające
są zależne od indukcji magnetycznej w obu rdzeniach i ich wzajemnej odległości. Rdzenie
nie są magnetycznie nasycone. Wytworzone przez cewkę pole magnetyczne jest
proporcjonalne do natężenia prądu. Zatem moment napędowy jest proporcjonalny do
kwadratu natężenia prądu i jest zależny od odchylenia (zmieniająca się odległość rdzeni).
Zależność momentu od odchylenia można zmienić przez zmianę kształtu rdzeni.
Wykorzystuje się to do uzyskania podziałki o wymaganym charakterze. Podziałka miernika
elektromagnetycznego nie jest równomierna. Przy czym możemy rozróżnić następujące jej
rodzaje: a) podziałka równomierna (od 10% wartości końcowej zakresu), b) podziałkę
przeciążoną (podziałka zagęszczona na końcu), c) podziałkę kwadratową (zagęszczoną na
początku). Odchylenie ustalone jest proporcjonalne do wartości średniej momentu
napędowego, czyli do średniej z kwadratów wartości chwilowych prądu, tzn. do kwadratu
wartości skutecznej prądu, bez względu na kształt przebiegu. Parametrem charakterystycznym
przetwornika jest liczba amperozwojów. Amperomierze wykonywane są jako bezpośrednie
(cały prąd płynie przez cewkę na której są odczepy dla różnych zakresów) na zakres od 1mA
do 350A. Nie stosuje się boczników. Aby otrzymać woltomierz wystarczy do amperomierza
włączyć szeregowo rezystor.
13. Wyprowadzić wzory na moment skręcający mierników
elektromagnetycznych przy prądzie stałym i zmiennym
Prąd stały
Energia pola magnetycznego cewki określona jest wyrażeniem:
2
LI
2
1
A
=
gdzie I jest prądem płynącym przez cewkę
14

obrót organu ruchomego o d
α
powoduje zmianę indukcyjności cewki o dL i przyrost energii
zgromadzonej przez cewkę o dA
2
I
dL
2
1
dA
*
=
Praca wykonana przy obrocie cewki o kąt d
α
jest równa iloczynowi momentu skręcającego i
kąta d
α
(z fizyki wiadomo że wykonanie pracy równe jest zmianie energii)
α
=
d
M
dA
S
*
α
=
d
dL
I
2
1
M
2
S
Jak widać moment skręcający jest wprost proporcjonalny do kwadratu prądu płynącego przez
ustrój. Jak widać wraz ze zmiana kąta o d
α
następuje zmiana indukcyjności własnej o dL w
wyniku wciągnięcia lub wypchnięcia z cewki blaszki wykonanej z materiału magnetycznego.
Prąd zmienny
W poprzednim podpunkcie zostało wyprowadzenie wyrażenie na moment skręcający przy
prądzie stały. Analogiczne wyrażenie jesteśmy w stanie zapisać dla wartości chwilowych
momentu i prądu sinusoidalnie zmiennego płynącego przez ustrój
α
ω
=
α
=
d
dL
2
t
I
d
dL
2
i
m
2
m
2
S
)
sin
(
Jednak ze względu na bezwładność ustroju należy rozważać średni moment skręcający jaki
będzie działał na ustrój. Wielkość tę możemy oznaczyć jako:
α
=
α
=
α
ω
=
=
∫
∫
d
dL
I
2
1
d
dL
I
4
1
dt
d
dL
2
t
I
T
1
dt
m
T
1
M
2
2
m
T
0
2
m
T
0
S
ŚR
S
)
sin
(
gdzie:
2
I
I
m
=
- wartość skuteczna prądu.
A wiec średni moment skręcający jest wprost proporcjonalny do kwadratu wartości skutecznej
prądu, tak więc miernik wyskalowany prądem stałym powinien wskazywać przy prądzie
zmiennym sinusoidalnym wartość skuteczną tego prądu, lecz nie zawsze tak jest ze względu
na szerokość pętli histerezy materiałów z których ustrój pomiarowy został wykonany.
14. Zmiany zakresów pomiarowych amperomierzy i woltomierzy
elektromagnetycznych.
Zmianę zakresów pomiarowych w amperomierzach elektromagnetycznych uzyskuje się
przez zmianę liczby zwojów cewki, przy czym należy pamiętać, że liczba amperozwojów
powodująca pełne odchylenie organu ruchomego jest stała dla danego miernika
(Iz)
n
= const
Na cewce znajdują się odczepy tak aby spełniony był powyższy warunek.
Przykładowo mamy:
15
Z1
Z2
Z3
0
25A
5
A
1
A
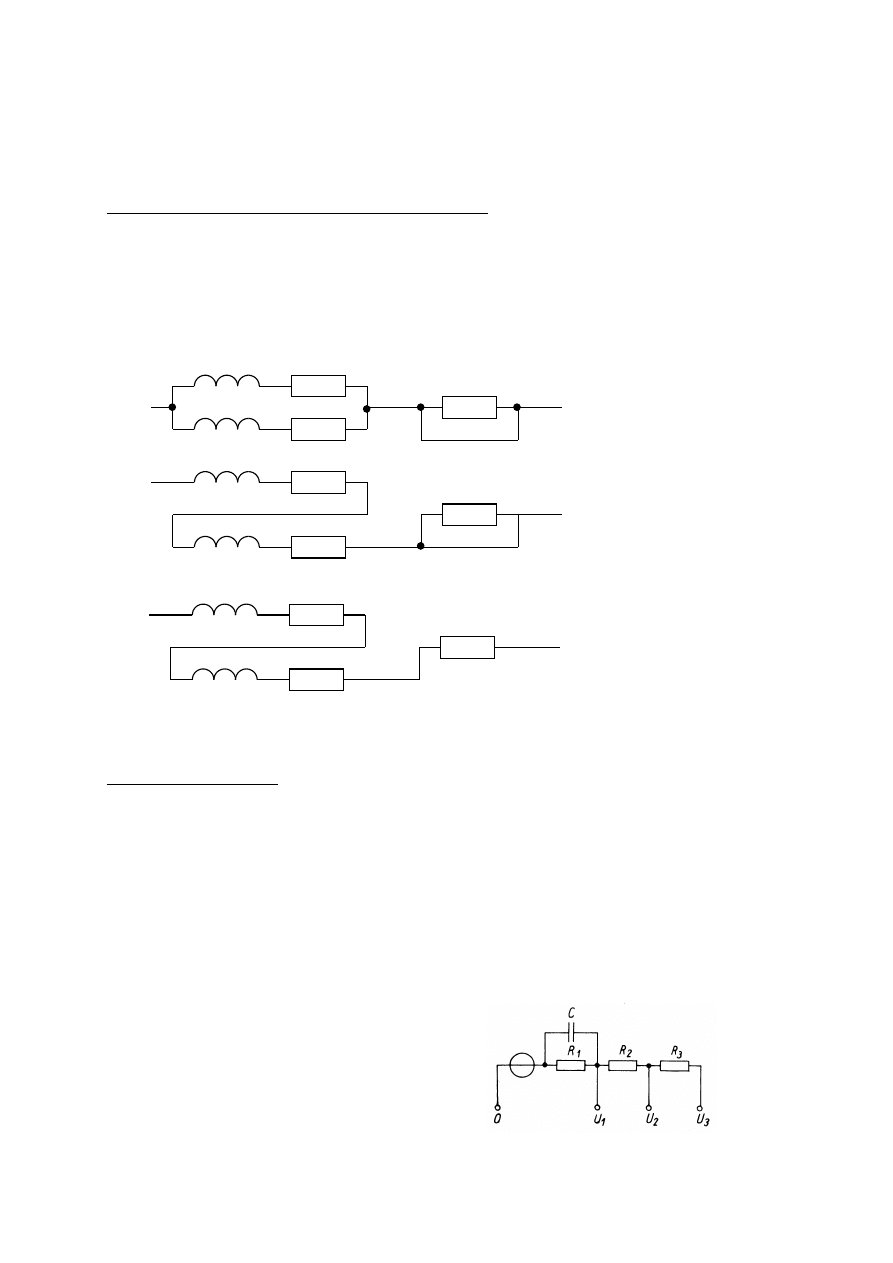
(
)
(
)
const
A
z
z
z
A
z
z
A
z
=
+
+
=
+
=
⋅
1
5
25
3
2
1
2
1
1
Niech Iz = 250Az
Wtedy z
1
= 10, z
2
= 40, z
3
= 200
W amperomierzach e-m nie stosuje się boczników ze względu na trudności występujące
przy kompensacji wpływów temperatury i częstotliwości a także już dużą rezystancję cewki.
Zmianę zakresów pomiarowych w woltomierzach elektromagnetycznych uzyskuje się przez
zastosowanie oporników dodatkowych tym sposobem można zwiększyć zakres do 4xU
n
. Aby
uzyskać większy zakres przełącza się szeregowo albo równolegle dwie identyczne cewki
woltomierza. Dla dwóch rezystorów dodatkowych uzyskujemy zwiększenie ilość zakresów.
15. Wpływ częstotliwości i obcych pól magnetycznych na wskazania mierników
elektromagnetycznych.
Błąd częstotliwościowy
W częściach metalowych ustroju pomiarowego znajdujących się w zasięgu pola
magnetycznego cewki zasilanej prądem przemiennym indukują się prądy. Pole magnetyczne
wytworzone przez te prądy osłabia pole cewki, w wyniku, czego następuje zmniejszenie
wskazania. Ze względu na dopuszczalną wartość tego błędu górna granica zakresu
częstotliwościowego wynosi około 1,5 kHz.
W przypadku stosowania dodatkowych oporników połączonych szeregowo z miernikiem (np.
w woltomierzach) dodatkowym źródłem błędu jest ten opornik. Wraz ze zmianą
częstotliwości zmienia się moduł impedancji zarówno cewki miernika jak i dodatkowego
posobnika. Gdy rośnie częstotliwość mierzonego przebiegu rosną również wspomniane
impedancje, więc występuje błąd ujemny (zmniejszenie wskazań) Uwaga:Ze względu na
reaktancję cewki nie stosuje się boczników w
amperomierzach.
Przykład korekcji błędu częstotliwości:
16
Rd
R
R
z
z
Dla 75V
Rd
Dla 150V
Rd
Dla 300V
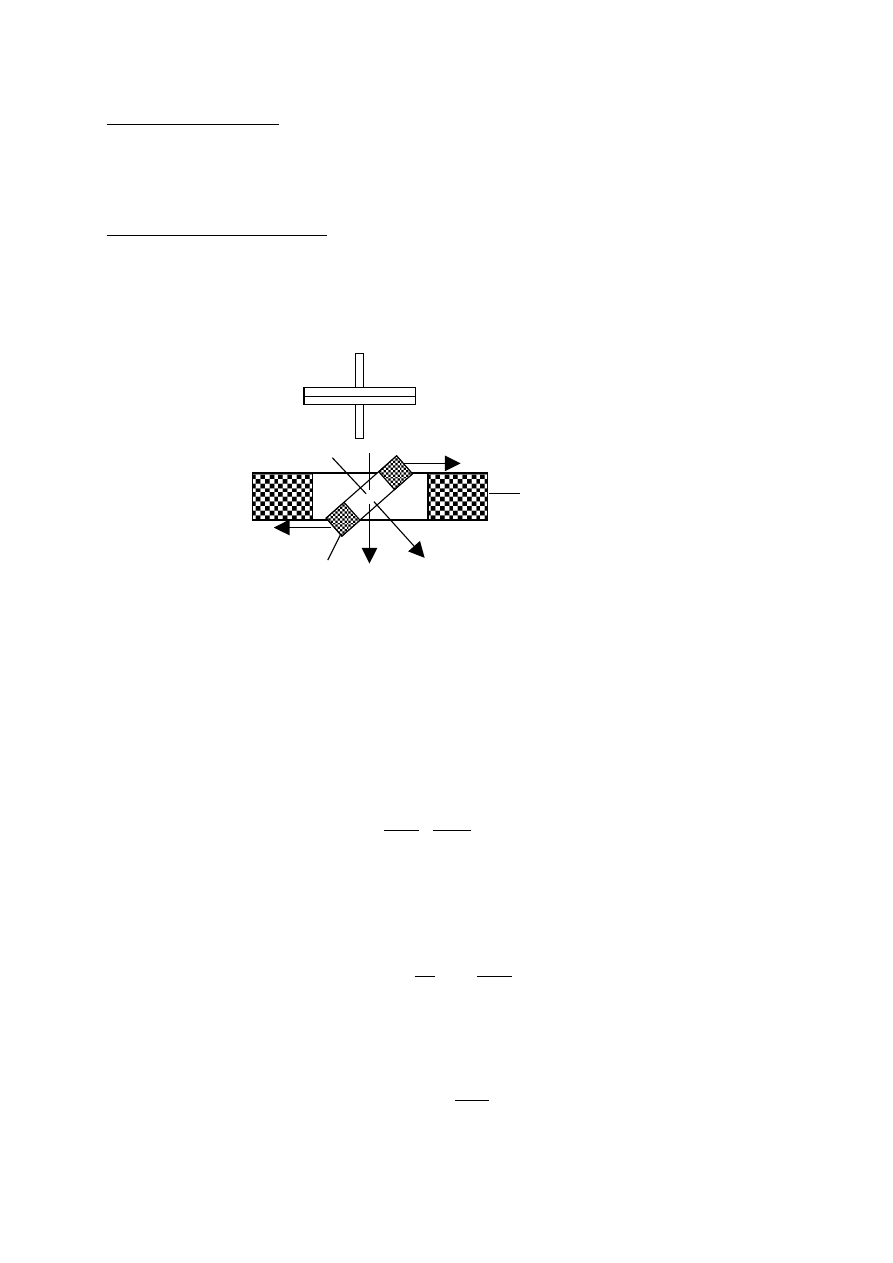
Obce pola magnetyczne
Indukcja pola w cewce ustroju wynosi od kilku do kilkunastu militesli. Nawet niewielkie
zewnętrzne pola magnetyczne w istotny sposób wpływają na odchylenie organu ruchomego.
Mierniki elektromagnetyczne muszą być, więc ekranowane.
Kształt przebiegu mierzonego
Nie ma wpływu na pomiar, gdy przebieg nie jest zanieczyszczony impulsami. Mierzona jest
zawsze wartość skuteczna.
16. Budowa, zasada działania i właściwości mierników elektrodynamicznych.
Działanie miernika elektrodynamiczznego jest oparte na wykorzystaniu sił występujących
między przewodami, przez które płyną prądy. W polu magnetycznym wytworzonym przez
prąd płynący przez cewkę nieruchomą umieszczona jest cewka ruchoma. Prąd do cewki
ruchomej jest doprowadzany za pomocą spiralnych sprężyn, które wytwarzają jednocześnie
oment zwrotny. Na osi obrotu cewki ruchomej umocowana jest wskazówka oraz tłumik i
korektor zera. Między blokami cewek występują siły wytwarzające moment napędowy, który
powoduje obrócenie cewki ruchomej w takim kierunku, aby strumienie magnetyczne obu
cewek dodawały się. Moment napędowy jest proporcjonalny do przyrostu energii
magnetycznej miernika przy obrocie organu ruchomego o kąt d
α
. Enrgię można wyrazić za
pomocą zależności:
A
I L
I L
I I M
=
+
+
1
2
1
2
2
2
1 2
12
2
2
Gdzie L
1
– indukcyjność własna cewki nieruchomej, L
2
– indukcyjność własna cewki
ruchomej, M
12
– indukcyjność wzajena obu cewek, I
1
– prąd w cewce nieruconej, I
2
– prąd w
cewce ruchomej.
Zakładając, że prądy w cewkach są wymuszone i nie zmieniają się w czasie potrzebnym do
obrotu cewki ruchomej o kąt d
α
, można obliczć wartość momentu napędowego:
M
dA
d
I I
dM
d
n
=
=
α
α
1 2
12
.
Warunkiem wykorzystania ustroju elektrodynamicznego jako amperomierz jest utrzymanie
niezmiennego stosunku między prądem mierzonym, a prądami w cewkach. Najprostszym
rozwiązaniem jest szeregowe połączenie cewek (stosowane przy małych prądach I
≤
0,5A).
Moment napędowy wówczas wynosi
M
I
dM
d
n
=
2
12
α
.
17
1
F
F
2
H1
H2
Symbol miernika
elektrodynamiczne
go
Szkic budowy
ustroju
elektrodynamiczne
go
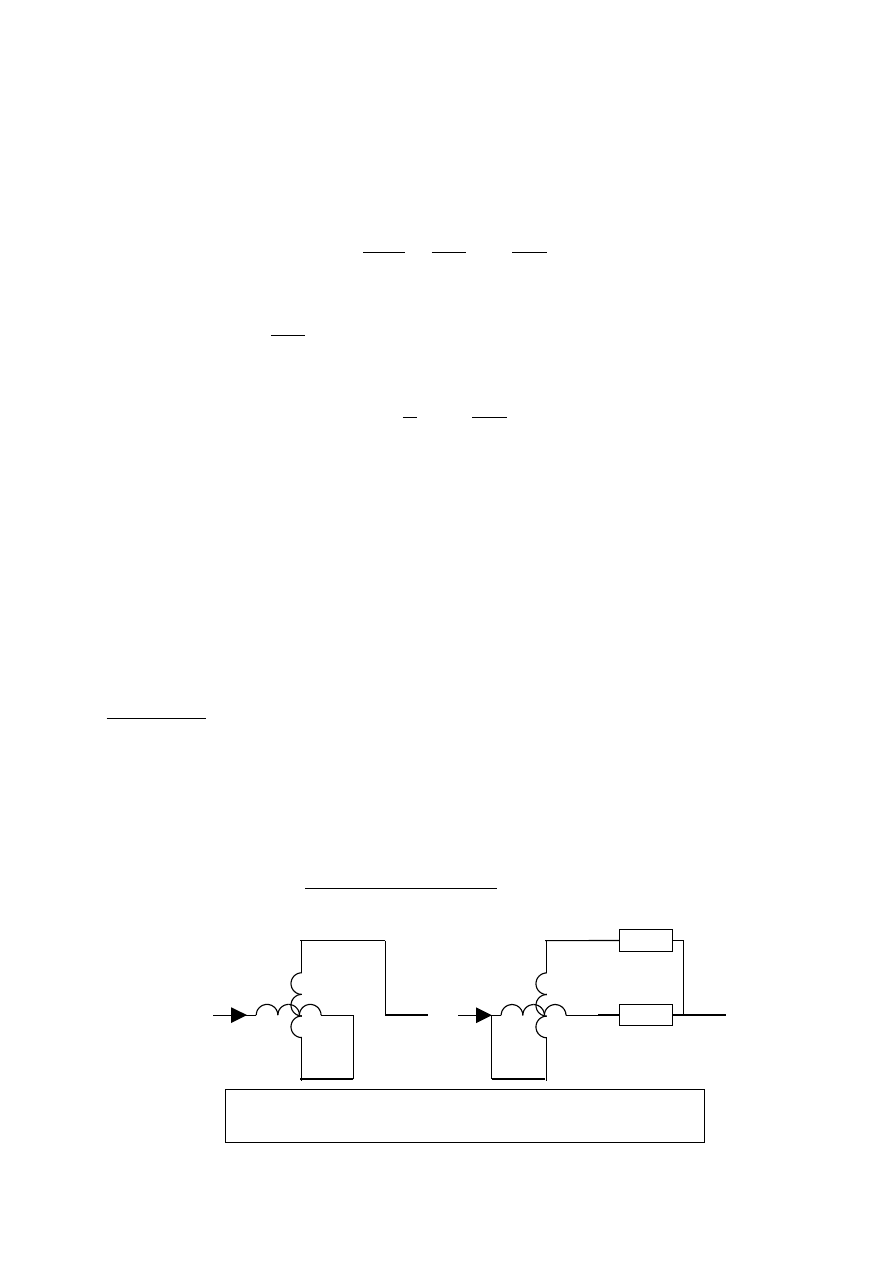
Prądy większe od 0,5A mierzy się przy równoległym połączeniu obu cewek. Amperomierze
elektrodynamiczne budowane są w klasach dokładności: 0,1 , 0,2 , 0,5. Najmniejszy zakres
wynosi 1mA, największy 50A. Moc pobierana przez miernik 2-10W.
Woltomierze elektrodynamiczne buduje się łącząc szeregowo cewki i włączając szeregowo
opornik. Napięcie na woltomierzu wynosi U=I*R
V
. Podstawiając do wzoru na moment
napędowy otrzymujemy wzór opisujący odchylenie
α
α
α
=
=
1
2
12
2
12
D R
U
dM
d
cU
dM
d
*
*
.
Najmniejszy zakres pomiarowy wynosi 7,5V, największy 750V. Pobór mocy 5-
15VA.Podziałka miernika elektrodynamicznego jest kwadratowa. Charakter podziałki można
zmienić przez zmianę
dM
d
12
α
- kształtujemy odpowiednio pole cewki ruchomej. Można
uzyskać podziałkę równomierną od około 10% długości podziałki.
Odchylenie organu ruchomego przy prądzie przemiennym określa zależność
α
α
=
1
1 2
12
D
I I co
dM
d
Ψ
.
Gdzie
Ψ
- kąt przesunięcia fazowego między prądami w cewkach. Dla
Ψ
=0 wyrażenie jest
takie samo jak dla prądu stałego. Dla 90
0
<
Ψ
<180
0
następuje zmiana kierunku odchylenia.
Warunkiem uzyskania ustalonego odchylenia jest jednakowa częstotliwość prądu w cewkach.
Woltomierze i amperomierze są używane jako mierniki laboratoryjne. Zaletą ich jest
możliwość wzorcowania prądem stałym. Wdą wysoki koszt produkcji i mała odporność na
przeciążenia. Znajdują zastosowanie jako watomierze.Wpływ czynników zewnętrznych na
pomiary miernikami elektrodynamicznymi: temperatura (zastosowane są sprężyny zwrotne),
obce pola magnetyczne, częstotliwość (indukowane prądy wirowe wytwarzają własne pole
magnetyczne), kształt przebiegu mierzonego.
17. Zmiany zakresów pomiarowych amperomierzy i woltomierzy
elektrodynamicznych.
Amperomierz
Dla prądów do 0,5 A pomiaru dokonuje się przy szeregowym połączeniem obu cewek
miernika. Powyżej tego prądu stosuje się połączenie równoległe cewek. W celu zachowania
niezmiennego stosunku prądów w cewkach przy zmianach temperatury oraz zgodności faz
między prądami przy pomiarze prądu przemiennego, szeregowo z cewkami włącza się
oporniki wykonane np. z manganianu. Amperomierze wielozakresowe mają cewki
nieruchome, podzielone na 2 lub 4 sekcje. W tym ostatnim przypadku łącząc sekcje
szeregowo, równolegle lub szeregowo – równolegle, otrzymuje się 3 zakresy pomiarowe o
stosunku prądów 1 – 4 – 2. Boczników nie stosuje się. Zakresy od 1mA do 50A.
18
Z1
Z2
Z1
Z2
R1
R2
Rys. 17.1 Rodzaje połączeń cewek amperomierza
elektrodynamicznego
a) połączenie szeregowe, b) połączenie równoległe
a)
b)

Woltomierze
Woltomierze wielozakresowe mają oporniki dodatkowe (zwiększające zakres maksymalnie do
4xU
n
ze względu na pobór mocy) lub cewkę nieruchomą podzieloną na 2 albo 4 przełączane
sekcje. Najmniejszy zakres pomiarowy wynosi 7,5 V a największy 750V
18. Wpływ czynników zewnętrznych na wskazania mierników
elektrodynamicznych.
Błędy częstotliwościowe powstają w wyniku:
•
Indukowania się prądów wirowych (podobnie jak w miernikach elektromagnetycznych).
Prądy te wytwarzają własny moment przeciwny do momentu napędowego cewki.
Powoduje to mniejsze wychylenie wskazówki. Aby przeciwdziałać powstawaniu prądów
wirowych elementy konstrukcyjne są wykonywane z materiałów ceramicznych.
•
Zmiany reaktancji cewek. Jest ona początkowo mała i rośnie wraz ze wzrostem
częstotliwości. Powoduje to zmniejszenie prądu w obwodzie. W watomierzach ponadto
wzrost reaktancji obwodu napięciowego przyczynia się do wzrostu kąta przesunięcia
między prądem a napięciem w tym obwodzie, co jak wiadomo powoduje powstawanie
dodatkowego błędu. (Błąd od kąta
γ
).
•
Wzajemnej indukcyjności cewek miernika. Powoduje ona indukowanie się w obu
obwodach prądów i napięć, które wytwarzają dodatkowy moment napędowy.
Obce pola magnetyczne
Mierniki tego typu są wrażliwe na obce pola, ponieważ indukcja własna miernika (cewek)
jest niewielka. Dlatego też ustroje pomiarowe powinny być ekranowane. Ważne jest, że pola
magnetyczne stałe są szkodliwe podczas pomiaru wartości stałych (np. prądu stałego). Przy
pomiarach wartości przemiennych szkodliwe są pola zmienne.
Kształt przebiegu mierzonego
Nie ma wpływu na wskazania o ile błędy powodowane harmonicznymi są małe.
Temperatura
Błędy wynikają ze zmiany sprężystości sprężynek zwrotnych. Nie przekraczają one 0,01
÷
0,02%/
°
C. Dla pomiarów napięcia błędy te są najczęściej kompensowane przez rezystory
dodatkowe.
Mierniki elektrodynamiczne pracują z powodzeniem jako woltomierze (10
÷
500 kHz),
amperomierze (10
÷
10 kHz), jednak głównie są stosowane jako watomierze (10
÷
10 kHz).
Błędy częstotliwościowe są praktycznie niezauważalne do 500 Hz. Dolna granica wskazań
wynika z drgań wskazówki.
19. Budowa i zasada działania watomierza elektrodynamicznego.
Watomierz elektrodynamiczny stosuje się do pomiaru mocy czynnej, głównie w
obwodach prądu przemiennego. Cewka nieruchoma przetwornika stanowi obwód prądowy
watomierza, który włącza się szeregowo w przewód doprowadzający prąd do odbiornika.
Cewka ruchoma uzupełniona rezystorem dodatkowym R
d
tworzy obwód napięciowy, który
włącza się równolegle na napięcie odbiornika.
Wartość średnia momentu napędowego, a zatem i odchylenie są proporcjonalne do mocy
czynnej odbiornika. Podziałka watomierza jest równomierna.
19

Stałe konstrukcyjne przetwornika (wymiary, liczba zwojów, stałe sprężyn) są tak
dobrane, że pełne odchylenie organu ruchomego powstaje wówczas, gdy:
•
Do obwodu napięciowego przyłoży się napięcie o wartości znamionowej,
•
Przez obwód prądowy płynie prąd o wartości znamionowej,
•
Kosinus kąta fazowego między napięciem i prądem jest równy wartości znamionowej (cos
ϕ
najczęściej wynosi 1, wartość różną od jedności podaje się na podzielni)
Stałą watomierza oblicza się z wzoru:
[ ]
dz
W
I
U
P
C
n
n
n
n
max
max
cos
α
ϕ
α
=
=
zaś moc mierzoną
[ ]
W
C
P
⋅
=
α
W przypadku pomiaru mocy czynnej prądu odkształconego, w mierniku wytwarzane są
momenty tylko przez prądy o jednakowych częstotliwościach w obu cewkach. Przy takich
samych odkształceniach w cewce prądowej i napięciowej moment napędowy jest
proporcjonalny do sum mocy poszczególnych harmonicznych. Miernik wskazuje prawidłowo,
niezależnie od kształtu krzywej, jeśli tylko zachowuje małe błędy częstotliwościowe.
Kierunek odchylenia organu ruchomego watomierza zależy od kierunku prądów płynących w
cewkach. Dlatego początek cewki prądowej watomierza łączy się tak, aby był zwrócony w
kierunku dopływu energii, a początek cewki napięciowej łączy się z początkiem lub końcem
cewki prądowej. Najczęściej najmniejszy zakres prądowy watomierza wynosi 0,5A Obydwa
obwody watomierza są skonstruowane w taki sposób, że wytrzymują trwałe przeciążenie
wynoszące 20%.
20. Wyprowadzić wzór na moment skręcający w watomierzu
elektrodynamicznym
Moment skręcający jest proporcjonalny do przyrostu energii magnetycznej miernika przy
obrocie organu ruchomego o kąt d
α
. Energia magnetyczna miernika elektrodynamicznego
który jest zbudowany z dwóch cewek poruszających się względem siebie wyraża się wzorem.
12
2
1
2
2
2
1
2
1
M
I
I
2
L
I
2
L
I
A
*
*
+
+
=
gdzie : I
1
- prąd płynący przez cewkę L
1
I
2
- prąd płynący przez cewkę L
2
M
12
– indukcyjność wzajemna cewek L
1
i L
2
α
=
α
=
d
M
I
I
d
dA
M
12
2
1
S
*
*
Konkretnie dla watomierzy stosuje się oznaczenia we wzorze jak niżej:
α
=
d
M
I
I
M
12
w
w
S
N
P
*
*
gdzie: I
Wp
– prąd płynący przez cewkę prądową watomierza
I
Wn
– prąd płynący przez cewkę napięciowa watomierza
)
(
*
*
*
α
=
f
I
I
c
M
N
P
w
w
n
S
Często także do opisu momentu skręcającego watomierza elektrodynamicznego stosuje się
wzór przedstawiony powyżej.
Dla prądu przemiennego wyznacza się średni moment skręcający opisany wzorem
)
(
*
cos
*
*
*
α
Ψ
=
f
I
I
c
M
N
P
w
w
n
SR
S
20

ψ
γ
ϕ
gdzie: wartości pradów są wartościami skutecznymi:
Ψ
- kąt przesunięcia fazowego między prądami w cewkach watomierza
21. Podać definicję stałej watomierza przy prądzie przemiennym, wyjaśnić
pojęcie „ cos
ϕ
zn
” watomierza.
W watomierzu elektrodynamicznym wskazanie w stanie ustalonym opisane jest zależnością:
P= c
w
*
α
gdzie c
w
– stała watomierza ;
α
- wychylenie (wskazywana działka, wartość). Stała
watomierza wyznaczana jest z warunków znamionowych i jest określona następująco:
zn
zn
Wzn
Wzn
W
I
U
c
α
ϕ
cos
)
(
)
(
⋅
⋅
=
oznaczenia : U
Wzn
– znamionowa wartość napięcia obwodu napięciowego
I
Wzn
– znamionowa wartość prądu obwodu prądowego
α
zn
– znamionowa liczba działek
cos
ϕ
zn
jest znamionowym współczynnikiem mocy watomierza;
ϕ
zn
jest to kąt między prądem
obwodu prądowego i napięciem obwodu napięciowego taki, że przy jednoczesnym
osiągnięciu wartości znamionowych tych wielkości wskazanie watomierza jest równe
znamionowemu (wskazuje moc znamionową przy prądzie znamionowym i znamionowym
napięciu oraz współczynniku mocy). Najczęściej buduje się watomierze tak by cos
ϕ
zn
= 1,
jednak dla celów specjalnych (pomiar małych mocy) współczynniki mocy mogą wynosić:
0,8; 0,5; 0,1 ; 0,05.
Ważne jest, aby kąt przesunięcia pomiędzy napięciem i prądem obwodu napięciowego (
γ
) był
jak najmniejszy, ponieważ istotnie wpływa on na powstawanie błędów pomiaru (patrz pkt 22
– błąd od kąta
γ
)
22. Wyprowadzić wzór na błąd „od kąta
γ
” w watomierzu elektrodynamicznym
Jak widać kat
γ
jest kątem przesunięcia fazowego między
napięciem a prądem płynącym przez cewkę napięciową
watomierza
Moment skręcający watomierza przy prądzie przemiennym
określa się wzorem:
)
(
*
cos
*
*
*
α
Ψ
=
f
I
I
c
M
N
P
w
w
n
SR
S
Z punktu widzenia prądu przemiennego obwód napięciowy
poza rezystancją posiada pewną reaktancję, a więc moduł
impedancji zapisuj się jako:
(
)
2
w
2
w
W
N
N
N
L
R
Z
ω
+
=
Z tego powodu prąd płynący przez cewkę napięciową będzie
opóźniony względem napięcia o pewien kąt
γ
N
N
w
w
Z
R
=
γ
cos
Prąd płynący przez tą cewkę można określić poprzez:
γ
=
=
cos
N
N
N
N
N
w
w
w
w
w
R
U
Z
U
I
a wiec moment skręcający ostatecznie opisywany jest zależnością
21
)
(
*
)
cos(
*
cos
*
*
α
γ
−
ϕ
γ
=
f
R
U
I
c
M
N
N
P
w
w
w
n
SR
S
przy czym: (
ϕ
-
γ
)=
Ψ
A więc aby watomierz mierzył moc czynną musi być spełniona zależność:
(
)
ϕ
=
γ
−
ϕ
γ
cos
cos
*
cos
Zależność ta jest spełniona tylko w dwóch przypadkach
γ
=0 i
γ
=
ϕ
Wtedy moment skręcający jest proporcjonalny do mocy mierzonej.
W praktyce dąży się aby
γ
=0 niestety nie udaje się tego osiągnąć i
γ≠
0 i wynosi kilka minut co
niestety wprowadza błąd do pomiarów mocy zwany błędem „od kata
γ
”. Błąd ten wynosi
(
)
1
2
−
γ
γ
ϕ
+
γ
=
ϕ
ϕ
−
γ
−
ϕ
γ
=
δ
γ
cos
*
sin
*
tg
cos
cos
cos
cos
*
cos
Biorąc pod uwagę że kąt
γ
jest bardzo mały i przyjmując pewne złażenia możemy to
wyrażenie uprościć
radianach
w
kat
to
gdzie
1
r
r
γ
γ
≈
γ
≈
γ
sin
,
cos
ϕ
γ
=
−
ϕ
γ
+
=
δ
γ
tg
*
tg
*
r
r
1
1
a dla kąta zapisanego w stopniach
ϕ
γ
=
δ
γ
tg
*
*
,000291
0
Jak widać wartość błędu „od kata
γ
” zależy od charaktery odbiornika którego mocz czynna
jest mierzona. Dla odbiorników rezystancyjnych (
ϕ
=0) kat ten wynosi 0, niestety wraz z
dążeniem cos
ϕ
do zera wartość błędu „od kąta
γ
” rośnie.
23. Zmiany zakresów pomiarowych watomierza elektrodynamicznego.
Zmiany zakresu pomiarowego w watomierzach elektrodynamicznych można dokonać na dwa
sposoby.
Przy stosunkowo małych napięciach i prądach w obwód napięciowy możemy włączyć
dodatkowe oporniki. Zmianę zakresów prądowych realizuje się natomiast poprzez podział na
sekcje i odpowiednie ich połączenie.
Przy bardzo dużych prądach lub napięciach możemy watomierz podłączyć za pomocą
przekładników. Możemy wyróżnić dwie metody połączeń; połączenie półpośrednie (dla dużej
wartości prądu) i pośrednie, ( gdy prąd i napięcie osiągają duże wartości).
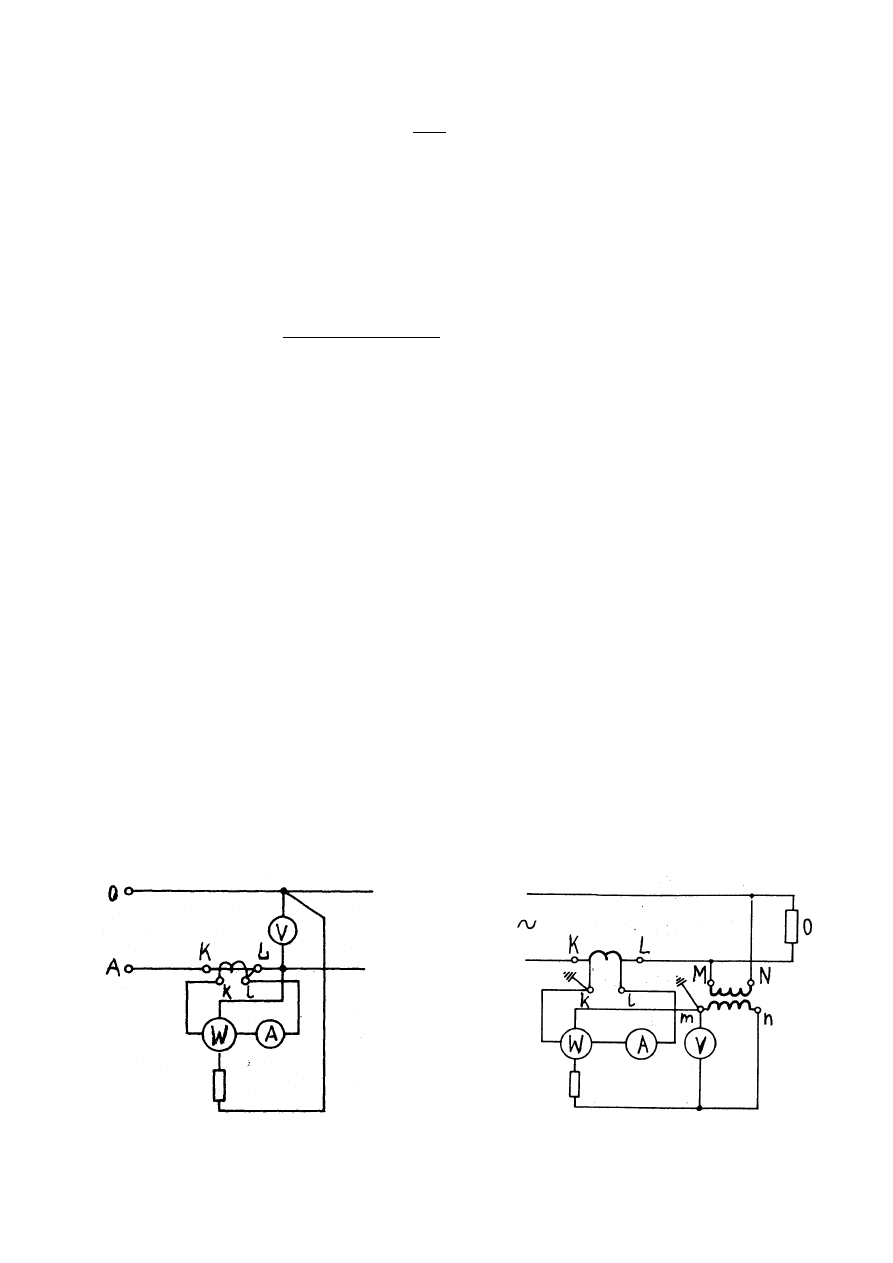
Schemat połączenia półpośredniego
Schemat połączenia pośredniego
22

Warto zauważyć, że w obu przypadkach można zastosować układ poprawnie mierzonego
napięcia lub prądu.
24. Pomiar mocy czynnej przebiegów odkształconych watomierzem
elektrodynamicznym
Jeżeli do jednej z cewek doprowadzimy przebieg sinusoidalny
t
I
i
1
Pm
P
w
w
ω
=
sin
*
a do drugiej przebieg zawierający harmoniczne
(
)
(
)
k
w
1
w
w
t
k
I
t
I
i
Nmk
1
Nm
N
Ψ
+
ω
+
Ψ
+
ω
=
sin
*
sin
*
To średni moment skręcający opisany będzie wzorem
(
)
(
)
[
]
dt
t
k
I
t
I
t
I
T
1
M
T
0
k
w
1
w
w
SR
S
Nmk
1
Nm
1
Pm
∫
Ψ
+
ω
+
Ψ
+
ω
ω
=
sin
*
sin
*
*
sin
*
i po przekształceniu wyniesie:
(
)
dt
t
I
t
I
T
1
M
T
0
1
w
w
SR
S
1
Nm
1
Pm
∫
Ψ
+
ω
ω
=
sin
*
*
sin
*
Upraszcza się on w ten sposób gdyż:
(
)
∫
=
Ψ
+
ω
ω
T
0
k
w
w
0
dt
t
k
I
t
I
T
1
Nmk
1
Pm
sin
*
*
sin
*
Jak widać w tym przypadku średni moment skręcający jest wprost proporcjonalny do mocy
czynnej częstotliwości podstawowej.
Przy pomiarze mocy czynnej prądów odkształconych w mierniku wytwarzane są momenty
skręcające tylko przez prądy i napięcia o tych samych częstotliwościach.
Przy takich samych częstotliwościach prądów w cewce prądowej i napięciowej moment
skręcający watomierza jest proporcjonalny do sumy mocy poszczególnych harmonicznych
∑
∞
=
ϕ
+
=
1
k
k
k
k
0
0
I
U
I
U
P
cos
*
gdzie: U
o
,I
o
– składowa stał napięcia i prądu
U
k
,I
k
– wartość skuteczna prądu i napięcia k-tej harmonicznej
ϕ
k
–przesunięcie fazowe między prądem i napięciem k-tej harmonicznej
25. Wpływ częstotliwości na wskazania watomierza elektrodynamicznego.
Istotny wpływ na dokładność wskazań watomierzy ma błąd częstotliwościowy. Jego źródłem
jest przede wszystkim indukcyjność cewki napięciowej. Indukcyjność ta jest rzędu kilku
milihenrów. Już przy częstotliwościach sieciowych wuwołuje ona odczuwalne opóźnienie
prądu I
U
w cewce względem napięcia U na zaciskach obwodu napięciowego. Stąd przy
indukcyjnym obciążeniu obwodu, do którego włączono watomierz wskazania zależą nie od
cos
ϕ
lecz od cos(
ϕ
-
ε
), gdze
ε
-kąt przesunięcia między napięciem U, a prądem I
U
. Kąt
ε
zależy
od częśtotliwości. Korekcja tego błedu polega na zbocznikowaniu opornika szeregowego w
obwodzie napięciowym kondensatorem o pojemności tak dobranej, aby reaktancja tego
obwodu była równa zero.
23
U
I
I
ε
ϕ
Wykres
wektorowy
watomierza
26. Budowa i zasada działania galwanometru statycznego.
Galwanometr statyczny jest to przyrząd o ustroju magnetoelektrycznym o bardzo
dużej czułości, przeznaczony do wykrywania i pomiaru małych prądów (rzędu 10
-8
A) i
napięć stałych (10
-6
V).
Różnice konstrukcyjne między miernikami magnetoelektrycznymi a
galwanometrami wynikają z tego, że w konstrukcji galwanometru położono szczególny
nacisk na uzyskanie dużej czułości (czułość „S” : stosunek odchylenia do prądu) rezygnując z
dokładności przetwarzania. Zwiększenie czułości uzyskuje się przez zwiększenie momentu
napędowego, ale przede wszystkim przez zmniejszenie momentu zwrotnego. W tym celu
sprężyny zwrotne zastąpiono taśmami z brązu berylowego, a tradycyjną wskazówkę –
wskazówką świetlną, która umożliwia pomiar małego kąta wychylenia: układ optyczny może
być wewnętrzny lub zewnętrzny. Zewnętrzny jest lepszy ze względu na dłuższą drogę
optyczną.
Właściwości galwanometru charakteryzują parametry:
C
I
[A/dz] – stała prądowa, natężenie prądu odchylającego wskazówkę o jedną działkę;
C
U
[V/dz] – stała napięciowa, napięcie, które przyłożone do galwanometru wraz z szeregowo
dołączoną rezystancją krytyczną odchyla wskazówkę o jedną działkę
R
g
(
Ω
) – rezystancja wewnętrzna galwanometru
R
kr
(
Ω
) – rezystancja krytyczna jest to wartość rezystancji obwodu zewnętrznego, który
należy dołączyć do zacisków galwanometru, aby powstało tłumienie krytyczne
dające najkrótszy czas ustalania się organu ruchomego,
T
O
[s] – okres drgań własnych nietłumionych galwanometru.
C
A
– stała energetyczna
Oraz klasa (0,5; 1; 1,5; 2; 2,5; 5).
Ze względu na dużą czułość galwanometru i możliwość łatwego uszkodzenia nie włącza się
go do obwodu bezpośrednio, lecz za pośrednictwem układów znieczulających. Są to
wielostopniowe rezystory dodatkowe lub wielostopniowe boczniki powiększające stałą
napięciową lub prądową galwanometru. Galwanometr statyczny jest stosowany zwykle jako
wskaźnik równowagi w zerowych metodach pomiaru prądów i napięć stałych.
27. Wyprowadzić wzór na moment hamujący – cewkowy w galwanometrze
statycznym
Rysunek przedstawia zasadę powstawania momentu
hamującego cewkowego w galwanometrze
statycznym. Moment hamujący cewkowy jest
głównym elementem momenty tłumiącego.
Oznaczenia na rysunku:
R
Z
–rezystancja zastępcza badanego obwodu
R
g
– rezystancja cewki galwanometru
a,b – wymiar cewki o z zwojach
Cewka o rezystancj R
g
porusza się w polu
magnetycznym o indukcji B pochodzącym od
trwałego magnesu. Na skutek ruchu cewki, indukuj się
w niej siła elektromotoryczna e:
BlV
e
=
gdzie
l- długość (aktywna) cewki l=2b*z
V- prędkość poruszania się cewki
dt
d
2
a
V
α
=
A więc siła elektromotoryczna indukowana w poruszającej się cewce wynosi:
24
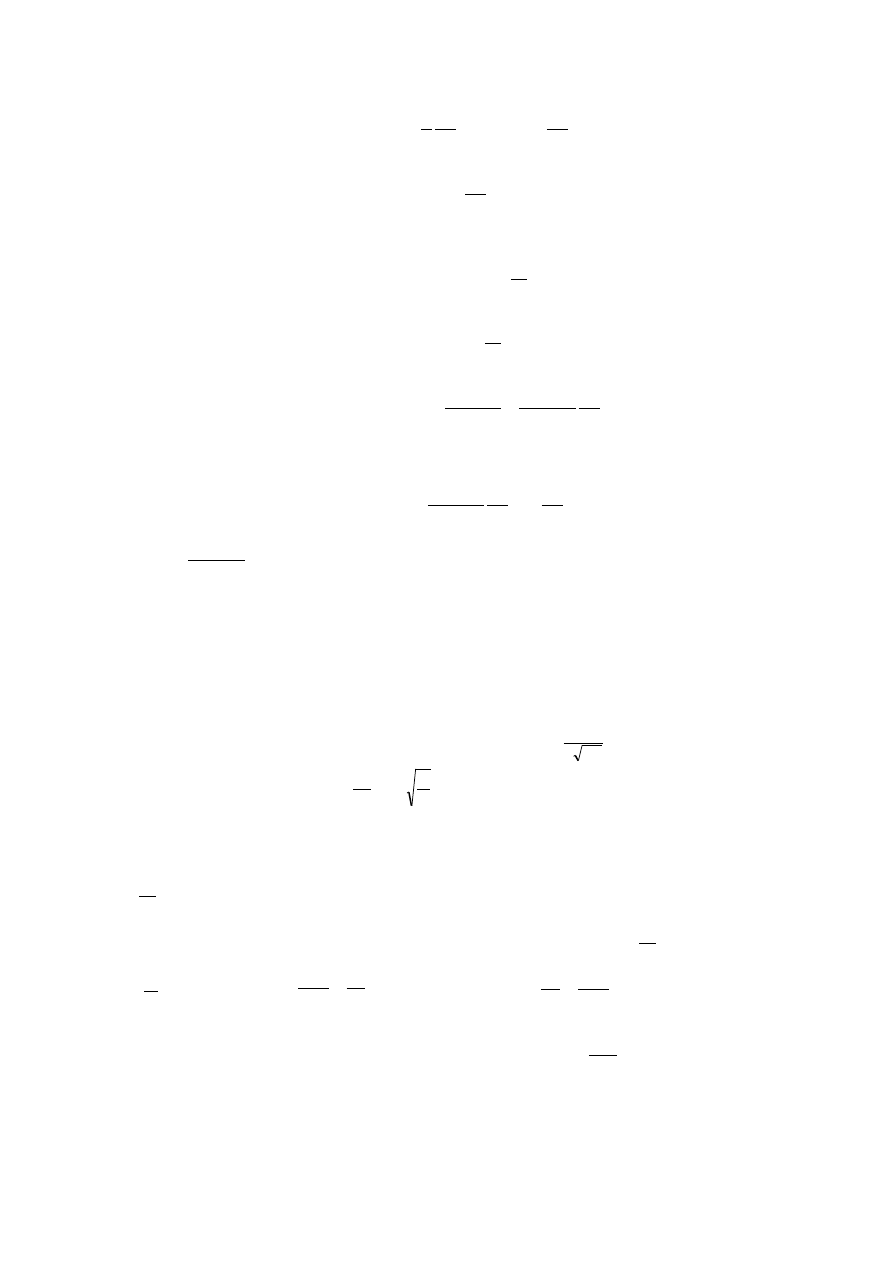
dt
d
z
ab
B
dt
d
2
a
z
b
2
B
e
α
=
α
=
*
*
*
*
*
*
Wprowadzając pojęcie strumienia skojarzonego
Φ
0
=B*ab*z
dt
d
e
0
α
Φ
=
*
Jednocześnie ponieważ obwód pomiarowy jest zamknięty to pod wpływem siły
elektromotorycznej popłynie prąd i możemy zapisać równanie:
dt
di
L
R
R
i
e
z
g
*
)
(
*
+
+
=
gdzie L – indukcyjność cewki galwanometru
Jednocześnie należy zauważyć że
dt
di
L
R
R
i
z
g
*
)
(
*
> >
+
wiec z pewnym przybliżeniem
możemy zapisać:
(
)
dt
d
R
R
R
R
e
i
R
R
i
e
z
g
0
z
g
z
g
α
+
Φ
=
+
=
⇒
+
≅
*
Kierunek prądu i jest taki że współdziałając z polem magnetycznym magnesu trwałego
wytwarza moment hamujący:
dt
d
K
dt
d
R
R
i
M
z
g
2
0
0
h
α
=
α
+
Φ
=
Φ
=
*
gdzie:
z
g
2
0
R
R
K
+
Φ
=
jest stała tłumienia
28. Definicje, wzory i przykładowe wartości wielkości charakteryzujących
galwanometr statyczny.
Parametry galwanometru statycznego:
R
kr
(R
zkr
) – rezystanacja (zewnętrzna) krytyczna – jest to rezystancja, przy której organ
ruchomy porusza się ruchem aperiodycznym krytycznym
R
JD
kr
= Φ
0
2
2
Okres wahań swobodnych
T
J
D
0
0
2
1
2
=
=
π
ω
π
Czułość prądowa S
i
i napięciowa S
u
– liczba działek o jaką odchyli się organ ruchony do
prądu, napięcia który spowoduje to wychylenie Czułość prądowa (10
6
-10
11
mm/A),
napięciowa (10
4
-10
7
mm/V)
S
a
I
i
g
=
, a – odchylenie wskazówki galwanometru [mm], I
g
– prąd płynący przez
galwanometr, odwrotnością czułości prądowej jest stała prądowa C
I
C
S
I
I
=
1
S
a
U
U
=
, U=I
g
R
g
stąd
S
a
I R
S
R
U
g g
I
g
=
=
, stała napięciowa
C
S
I R
a
C R
U
U
g g
I g
=
=
=
1
Klasa galwanometru – oznaczenie stałości jego wskazań: 0,5 , 1 , 1,5 , 2,5 , 5
Stała energetyczna – iloczyn najważniejszych stałych
C
C C T
W s
dz
A
I U
=
⋅
0
2
25
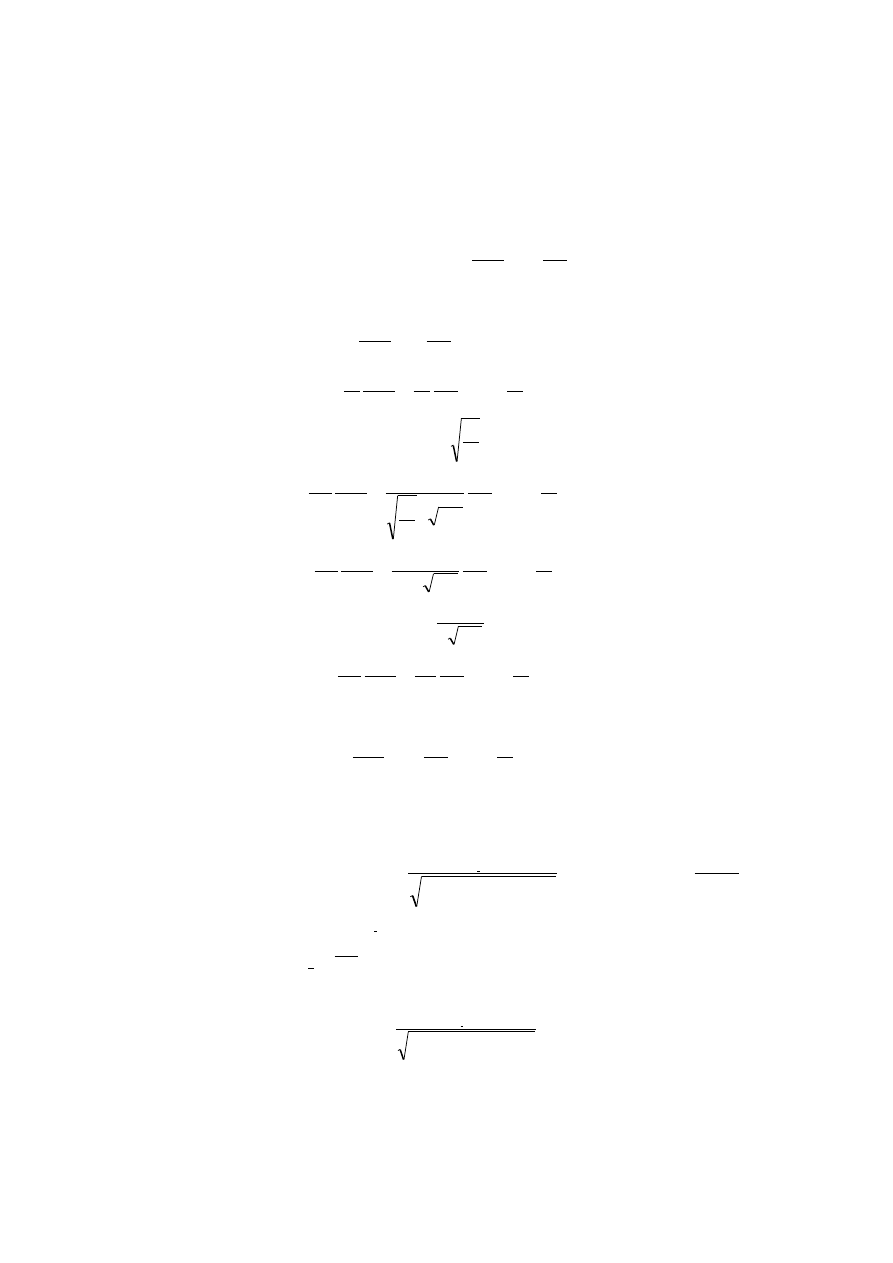
29. Warunki rezonansu galwanometru wibracyjnego
Galwanometr wibracyjny pracuje w tzw. „reżimie rezonansów”. Służy do wykrycia i
pomiarów małych prądów przemiennych. Dzielą się na – pętlicowe (cewka zredukowana do
jednej pętli, oparta na dwóch pryzmatach, przy zmianach położenia pryzmatu, zmieniają się
drgania własne galwanometru). Przy wielu zwojach zwiększa się czułość a zmniejsza drgania
własne galwanometru.
tumiąum
moment
i
bezwadnośe
moment
napęapęd
moment
n
zwracająwr
moment
dt
d
K
dt
d
J
M
D
α
α
α
−
−
=
⋅
2
2
n
M
D
dt
d
K
dt
d
J
=
⋅
+
+
α
α
α
2
2
n
M
D
dt
d
D
K
dt
d
D
J
1
2
2
=
+
+
α
α
α
J
D
=
0
ω
n
M
D
dt
d
JD
J
D
K
dt
d
1
1
2
2
2
0
=
+
⋅
+
α
α
α
ω
n
M
D
dt
d
JD
K
dt
d
1
1
0
2
2
2
0
=
+
⋅
+
α
α
ω
α
ω
JD
K
b
2
=
n
M
D
dt
d
b
dt
d
1
2
1
0
2
2
2
0
=
+
+
α
α
ω
α
ω
t
⋅
=
0
ω
τ
n
M
D
d
d
b
d
d
1
2
2
2
=
+
+
α
τ
α
τ
α
załóżmy że mierzony jest prąd określony równaniem i(t) = J
m
sin
η
t, gdzie
η
- częstotliwość
względna
η
=
ω
/
ω
0
Wychylenie określa równanie
( )
(
)
(
)
−
−
⋅
+
−
=
2
2
2
2
1
2
sin
2
1
n
bk
arctan
b
I
S
t
m
i
η τ
η
η
α
Gdzie S
i
– czułość dla prądu stałego
_
I
S
i
α
=
I_ - natężenie prądu stałego
Wychylenie jest maksymalne dla sin(...) = 1 czyli
(
)
(
)
2
2
2
2
1
η
η
α
b
I
S
m
i
m
+
−
=
I
m
= const
Otrzymujemy dwa przypadki
1)
ω
- regulowane
ω
0
, b – stałe
26

0
=
ω
α
d
d
m
z czego po rozwiązaniu otrzymujemy
2
0
2
1
b
−
=
ω
ω
warunek rezonansu dla
którego szerokość pasma będzie największa
( )
m
i
m
I
b
b
S
⋅
−
=
2
max
1
2
α
0
1
2
≥
−
b
b < 0,7
2)
ω
= const
ω
0
– regulowane (poprzez zmianę D)
2
2
2
2
2
0
1
D
k
D
j
D
I
m
m
ω
ω
φ
α
+
−
⋅
=
0
1
2
2
2
2
2
=
+
−
dD
D
k
D
j
D
d
ω
ω
j
D
2
ω
=
jest to drugi warunek rezonansu
0
ω
ω
=
=
J
D
0
ω
ω =
30. Narysować krzywą rezonansu i zdefiniować szerokość rezonansu w
galwanometrze wibracyjnym.
Wykres zależności amplitudy drgań organu ruchomego od częstotliwości drgań własnych f
0
zwany jest krzywą rezonansu.
Szerokość rezonansu s określa się za
pomocą wzoru:
%
100
2
%
100
1
2
1
•
−
=
•
−
=
r
r
r
f
f
f
f
f
f
s
gdzie:
27
f
f1 fr f2
L max
(1/2) * L max
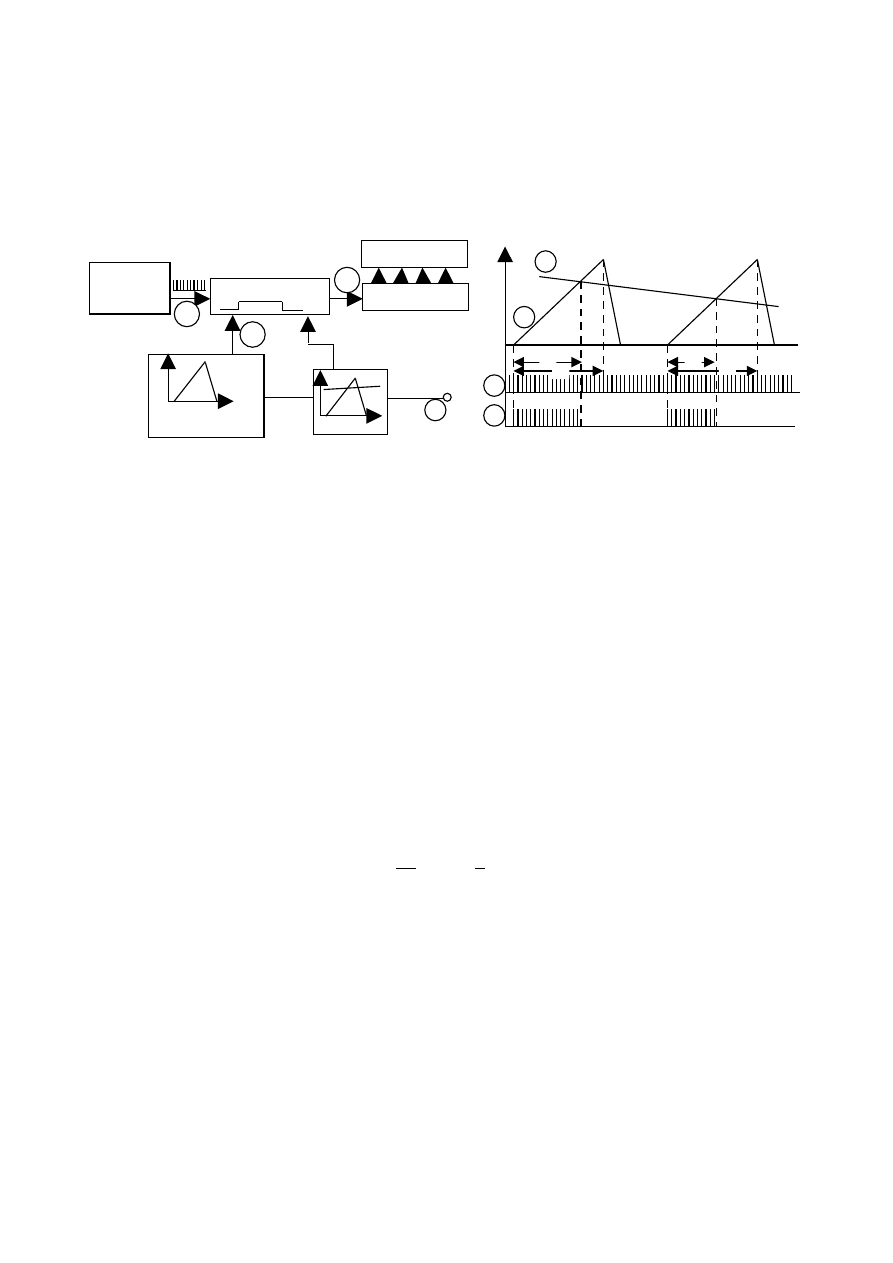
f
r
– częstotliwość drgań własnych, przy której występuje rezonans; f
1
,f
2
– częstotliwość drgań
własnych, przy której częstotliwość pasma świetlnego maleje do połowy pasma przy
rezonansie. W praktyce szerokość rezonansu to około 1%.
31. Narysować schemat blokowy, opisać zasadę działania i wyprowadzić wzór
na N
x
w woltomierzu cyfrowym o przetwarzaniu impulsowo-czasowym.
Napięcie mierzone U
x
jest podawane na komparator. W komparatorze napięcie U
x
jest
porównywane z napięciem wzorcowym U
N
, liniowo narastającym, z generatora napięcia
wzorcowego. Początek narastania tego napięcia jest wyznaczany impulsem start (z układu
sterowania). Impuls “start” powoduje wyzerowanie licznika impulsów oraz otwiera bramkę
elektroniczną, dzięki czemu impulsy o częstotliwości f
N
z generatora impulsów wzorcowych
są podawane na licznik , gdzie są zliczane. Zzliczanie impulsów trwa do momentu zrównania
napięcia piłokształtnego U
N
z mierzonym U
x
, wtedy na wyjściu komparatora pojawia się
impuls “stop” zamykający bramkę. Stan licznika jest wyświetlany w postaci cyfrowej w
urządzeniu odczytowym.
Licznik zliczył N
x
impulsów o częstotliwości f
N
wypełniających przedział czasu T
x
N
x
=f
N
*T
x
.
Napięcie wzorcowe piłoksztłtne opisane jest zależnością
U
N
=k*t,
przy czy k jest szybkością zmian tego napięcia. Po czasie T
x
U
N
k*T
x
=U
x
ponieważ
T
N
f
N
k
f U
x
x
N
x
w x
=
⇒
=
1
.
Woltomierz mierzy wartość chwilową. Liczba impulsów zliczanych przez licznik jest
proporcjonalna do wartości mierzonego napięcia.Dokładność pomiaru woltomierzami tego
typu jest stosunkowo mała i zależy od : liniowości napięcia wzorcowego, stabilności
częstotliwości generatora, czułości komparatora.
28
start
stop
start
stop
T
X
T
X
U
1
2
3
4
T
N
T
N
t
0
t
1
t
1
t
0
t
2
Zespół odczytowy
Licznik
impulsów
Układ bramkujący
Generator
impulsów
wzorcowyc
U
N
t
Generator napięcia
wzorcoweg
U
N
U
X
U
t
komparator
3
4
2
start
stop
U
X
1
Woltomierz cyfrowy o przetwarzaniu impulsowo czasowym; schemat funkcyjny,
przebiegi czasowe wyjaśniające zasadę działania
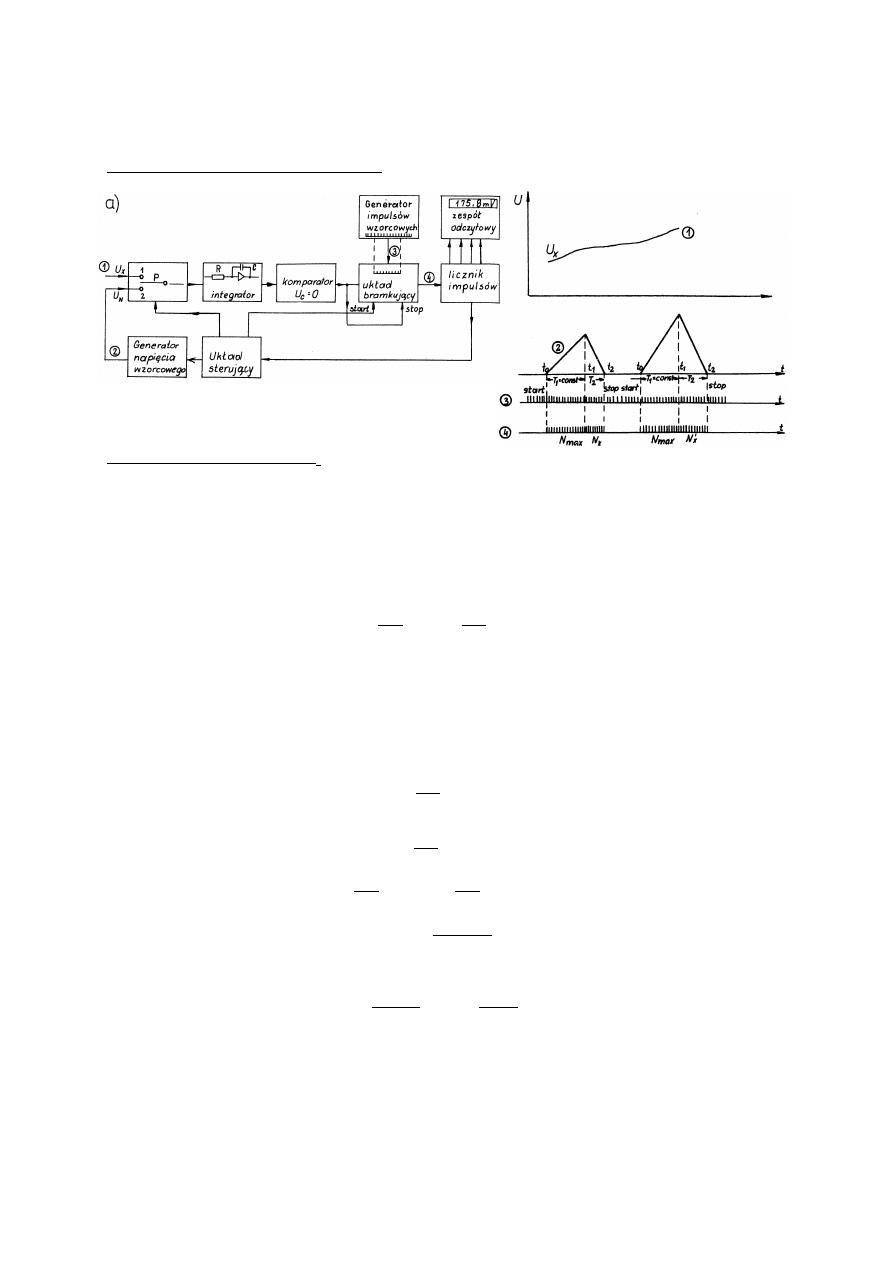
32. Narysować schemat blokowy, opisać zasadę działania i wyprowadzić wzór
na N
x
w woltomierzu cyfrowym z podwójnym całkowaniem
Schemat blokowy i przebiegi czasowe
Zasada działania i wzór na N
x
Okład sterujący w chwili t
0
zeruje licznik, otwiera układ bramkujący impulsy z generatora
wzorcowego i przełącza przełącznik w pozycję 1 i podaje badane napięcie U
x
na integrator
czyli układ całkujący. Badane napięcie U
x
jest całkowane przez stały okres T
1
do chwili t
1
do
momentu zapełnienia licznika. Nachylenie krzywej narastającej na wyjściu integratora jest
wprost proporcjonalne do napięcia badanego U
x
. W chwili t
1
(po czasie T
1
) na wyjściu
integratora panuje napięcie U
1
1
SR
X
t
t
x
1
T
u
RC
1
dt
u
RC
1
U
1
0
*
=
=
∫
gdzie RC jest stała integratora.
Ostatni impuls z generatora wzorcowego zeruje licznik, przełącza przełącznik w pozycję 2
podając napięcie wzorcowe U
0
(stałe o takiej polaryzacji aby zmniejszać napięcie na wyjściu
integratora) na wejście integratora. W momencie t
2
(po czasie T
2
)
napięcie na wyjściu
integratora jest równe 0 i komparator wysyła sygnał do zamknięcia bramki.
∫
=
−
2
1
t
t
0
1
0
dt
u
RC
1
U
0
T
U
RC
1
U
2
0
1
=
−
*
2
0
1
xSR
T
U
RC
1
T
u
RC
1
*
*
*
=
0
1
xSR
2
U
T
u
T
*
=
w
2
x
f
T
N
*
=
xSR
0
xSR
0
w
1
x
u
U
N
u
U
f
T
N
*
*
*
max
=
=
Jak widać liczba impulsów zliczana w czasie rozładowywania integratora jest zależna tylko i
wyłącznie od napięcia u
x
. Jak widać miernik ten jest miernikiem wartości średniej za okres
całkowania..
Błąd woltomierzy tego typu jest powodowany głównie przez stabilność napięcia wzorcowego
U
0
. Dokładność pomiaru nie zależy od liniowości integratora oraz stabilności generatora
29
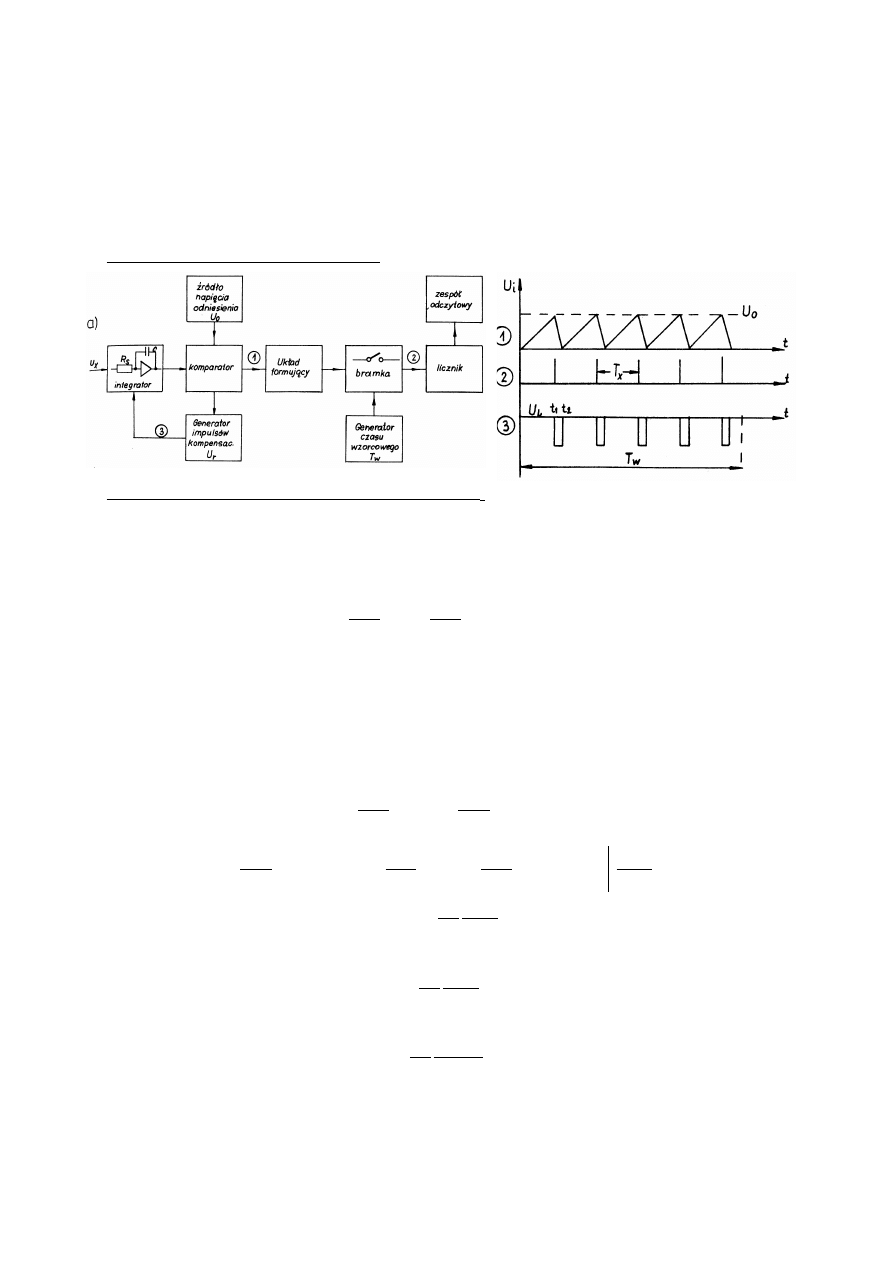
impulsów wzorcowych. Mierniki tego typu są odporne na zakłócenia przemienne
symetryczne o ile czas pomiaru jest wielokrotnością okresu zakłócenia.
Dokładność mierników z podwójnym całkowaniem 0,05%
÷
0,02%
33. Narysować schemat blokowy, opisać zasadę działania i wyprowadzić wzór
na N
x
w woltomierzu cyfrowym przetwarzającym napięcie w częstotliwość
Przebiegi czasowe i schemat blokowy
Opis zasady działania i wyprowadzenie wzoru na N
x
Na początek należy zauważyć że układ całkujący (integrator) ma dwa oddzielne wejścia (z
dzielnymi rezystorami dla napięcia badanego R
x
i dla napięcia rozładowującego R
r
.
Badane napięcie U
x
podawane jest do integratora przez rezystor R
x
i po czasie T
1
osiąga
napięcie
0
0
1
xSR
x
t
t
x
x
I
U
t
t
U
C
R
1
U
C
R
1
U
1
0
=
−
=
=
∫
)
(
*
Po osiągnięciu napięcia na wyjściu integratora poziomu równego
U
0
komparator daje impuls
do układu formowania (gdzie formowany jest impuls o szerokości
∆
t) oraz do układu
generowania impulsu rozładowującego. Układ ten rozładowuje integrator (sprowadza
napięcie na wyjściu integratora do zera) w czasie
∆
t. Należy zwrócić uwagę że napięcie
badane jest ciągle podawane na integrator. Ponieważ w chwili (t
1
+
∆
t) lub inaczej t
2
napięcie
na wyjściu integratora napięcie ma być równe 0 więc możemy zapisać równanie:
0
dt
U
C
R
1
dt
U
C
R
1
U
t
t
t
x
x
t
t
t
r
r
0
1
1
1
1
=
+
−
∫
∫
∆
+
∆
+
C
R
U
0
t
U
C
R
1
t
U
C
R
1
t
t
U
C
R
1
x
xSR
xSR
x
r
r
0
1
xSR
x
:
*
*
)
(
*
=
∆
+
∆
−
−
0
t
U
U
R
R
t
t
t
xSR
r
r
x
0
1
=
∆
−
∆
+
−
*
)
(
należy zwrócić uwagę że wielkość (t
1
-t
0
+
∆
t) równa jest odstępowi między impulsami T
x
t
U
U
R
R
T
xSR
r
r
x
x
∆
=
*
Częstotliwość impulsów f
x
jest odwrotnością czasu T
x
xSR
r
x
r
x
U
t
U
1
R
R
f
∆
=
*
Impulsy o częstotliwości wprost proporcjonalnej do badanego napięcia (a właściwie jego
wartości średniej) są zliczane przez wzorcowy okres czasu T
w
.
30
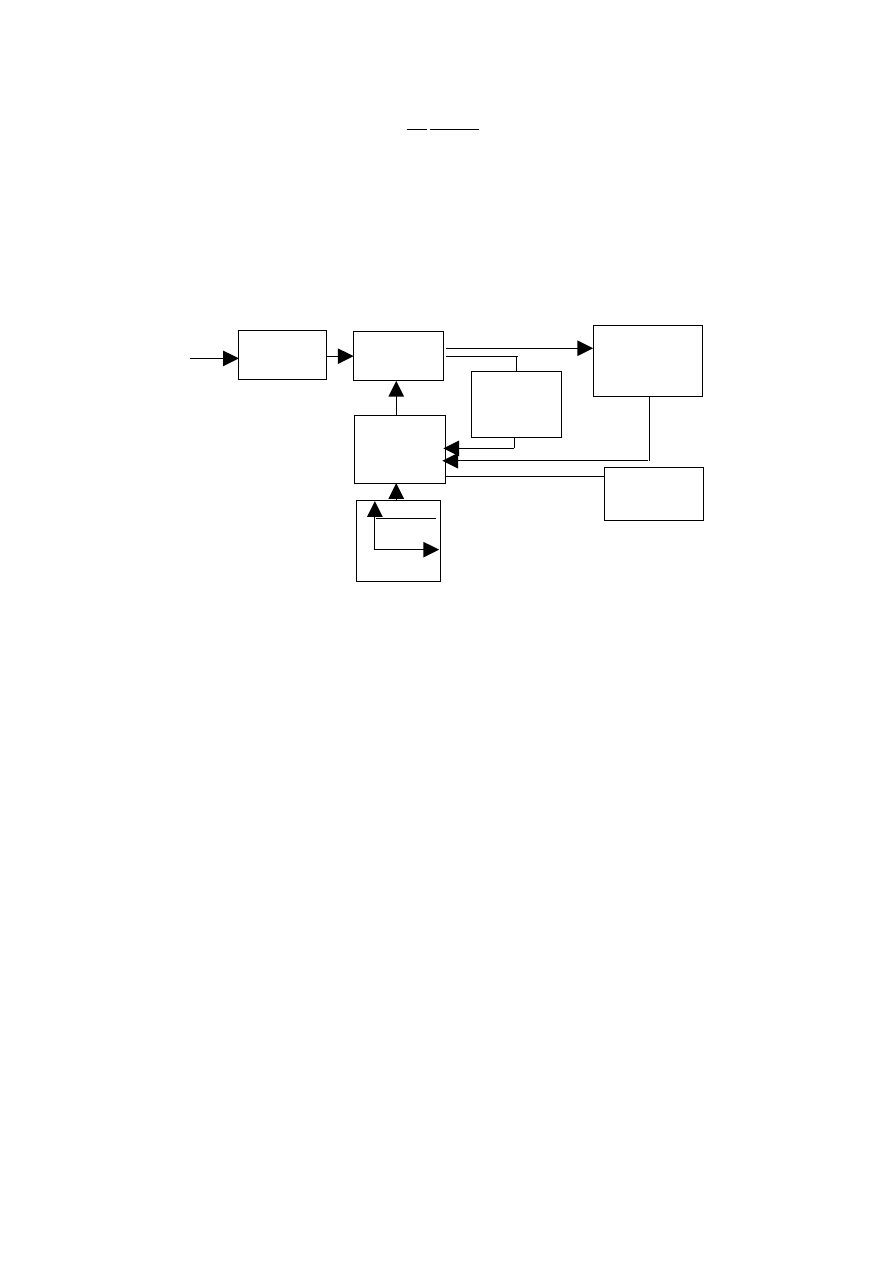
xSR
r
W
x
r
x
U
t
U
T
R
R
N
*
*
∆
=
Ponieważ miernik mierzy wartość średnia napięcia to jest odporny na zakłócenia przemienne.
Dokładność pomiaru zależy od dokładności dozowania napięcia rozładowującego U
R
,
liniowości integratora, stabilności napięcia odniesienia U
o
, oraz od szybkości i dokładności
działania komparatora.
Dokładność mierników tego typu to 0,01%
÷
0,1%
34. Narysować schemat blokowy i opisać zasadę działania woltomierza
kompensacyjnego.
Woltomierze cyfrowe napięć stałych o przetwarzaniu kompensacyjnym należą do
najdokładniejszych. Zasada ich pracy polega na porównywaniu napięcia mierzonego U
x
ze
skokowo zmieniającym się napięciem wzorcowym U
N
. Ze względu na algorytm zmian
napięcia wzorcowego, woltomierze kompensacyjne dzieli się na woltomierze z kompensacją
równomierną i na woltomierze z kompencacją wagową. W woltomierzach z kompensacją
równomierną napięcie wzorcowe ma przebieg schodkowy, przy czym zmiana napięcia
odbywa się równomiernymi przyrosami
∆
U
N
. W woltomierzach z kompensacją wagową
proces porównywania przypomina ważenie wedłu określonego programu.
Obwód wejściowy zawiera filtr dolnoprzepustowy, eliminujący zakłócenia zmienne.
Dyskretny dzielnik napięcia to szereg oporników wzorcowych o odpowiednich wartościach
zasilanych ze źródła napięcia wzorcowego. Detektor różnicowy reaguje na różnicę napięć na
jego wejściach. Układ sterujący wytwarza impulsy taktowe, które powodują kolejne
podawanie napięć wzorcowych odpowiadających poszczególnym wagom 2
3
, 2
2
, 2
1
, 2
0
.
35. Opisać kompensację napięcia 10,5V w woltomierzukompensacyjnym o
kompensacji wagowej o wagach 2
3
, 2
2
, 2
1
, 2
0
Jako pierwsze zostaje podane napięcie odpowiadające najwyższemu rzędowi, czyli 2
3
. Dla
omawianego przykładu 2
3
=8V. Ponieważ U
N
<U
x
(napięcie wzorcowe jest mniejsze od
napięcia mierzonego ) impuls z detektora powoduje wytworzenie w układzie sterującym
nowego impulsu, który wysyłany jest do dyskretnego dzielnika napięć wzorcowych. W
wyniku tego impulsu w następnym takcie do poprzedniego napięcia wzorcowego zostaje
dodane napięcie wzorcowe niższego rzędu 2
2
=4V. Ponieważ U
N
>U
x
wobec czego detektor
różnicowy działa na układ sterujący, a ten z kolei na dyskretny dzielnik napięcia tak, że w
następnym takcie napięcie wzorcowe rzędu 2
2
=4V zostaje odjęte, a w kolejnym takcie
dołączone zostaje napięcie niższego rzędu, w tym przypadku 2
1
=2V. Ponieważ U
N
<U
x
31
Obwody
wejściowe
Detektor
różnicowy
Dyskretny
dzielnik
napięcia
Skasować
ostatni
skok
Zapamiętać
stan U
N
dodać
następny skok
U
X
U
X
>U
N
U
X
<U
N
Źródło napięcia
wzorcowego
U
N
t
Zespół
odczytowy
Uproszczony schemat funkcyjny woltomierza cyfrowego z

(napięcie wzorcowe jest mniejsze od napięcia mierzonego ) impuls z detektora powoduje
wytworzenie w układzie sterującym nowego impulsu, który wysyłany jest do dyskretnego
dzielnika napięć wzorcowych. W wyniku tego impulsu w następnym takcie do poprzedniego
napięcia wzorcowego zostaje dodane napięcie wzorcowe niższego rzędu 2
0
=1V. Ponieważ
U
N
>U
x
wobec czego detektor różnicowy działa na układ sterujący, a ten z kolei na dyskretny
dzielnik napięcia tak, że w następnym takcie napięcie wzorcowe rzędu 2
0
=1V zostaje odjęte.
W tym momencie wszystkie stopnie w tej dekadzie się wyczerpały więc układ sterujący
uruchamia następną, niższą dekadę czyli 0,1 x (2
3
+2
2
+2
1
+2
0
)V. Proces równoważenia trwa
według opisanego algorytmu aż do pełnej kompensacji lub po porównaniu z całum zbiorem
napięć wzorcowych. Wartość napięcia
U
x
=(1*2
3
+0*2
2
+1*2
1
+0*2
0
)
+ 0,1 x (0*2
3
+1*2
2
+0*2
1
+1*2
0
)V=10,5V
36. Zasada działania woltomierzy cyfrowych napięcia przemiennego.
Cyfrowy pomiar napięć przemiennych może odbywać się, podobnie jak analogowy przez
zmianę wartości, którą chcemy zmierzyć na napięcie stałe. Stosuje się w tym celu najczęściej
przetworniki prostownikowe wartości średniej, skutecznej, szczytowej na napięcia stałe.
Podstawową wadą wszystkich woltomierzy prostownikowych jest zależność wskazań od
kształtu przebiegu oraz to, że dolna częstotliwość badanego przebiegu jest ograniczona
poprzez stałą rozładowania kondensatora w układzie prostownika.
Mierniki małych napięć buduje się jak na (rys. c) - oznaczenia mierników analogowych
należy w tym przypadku traktować jako mierniki cyfrowe!
Przykładowy przetwornik (prostownik wartości szczytowej)
Zasada działania:
Napięcie badane
ładuje kondensator
przez dodatni
półokres. Przez
kolejny półokres
napięcie na
kondensatorze jest
utrzymywane dzięki
nieprzewodzącej w
tym przypadku
32
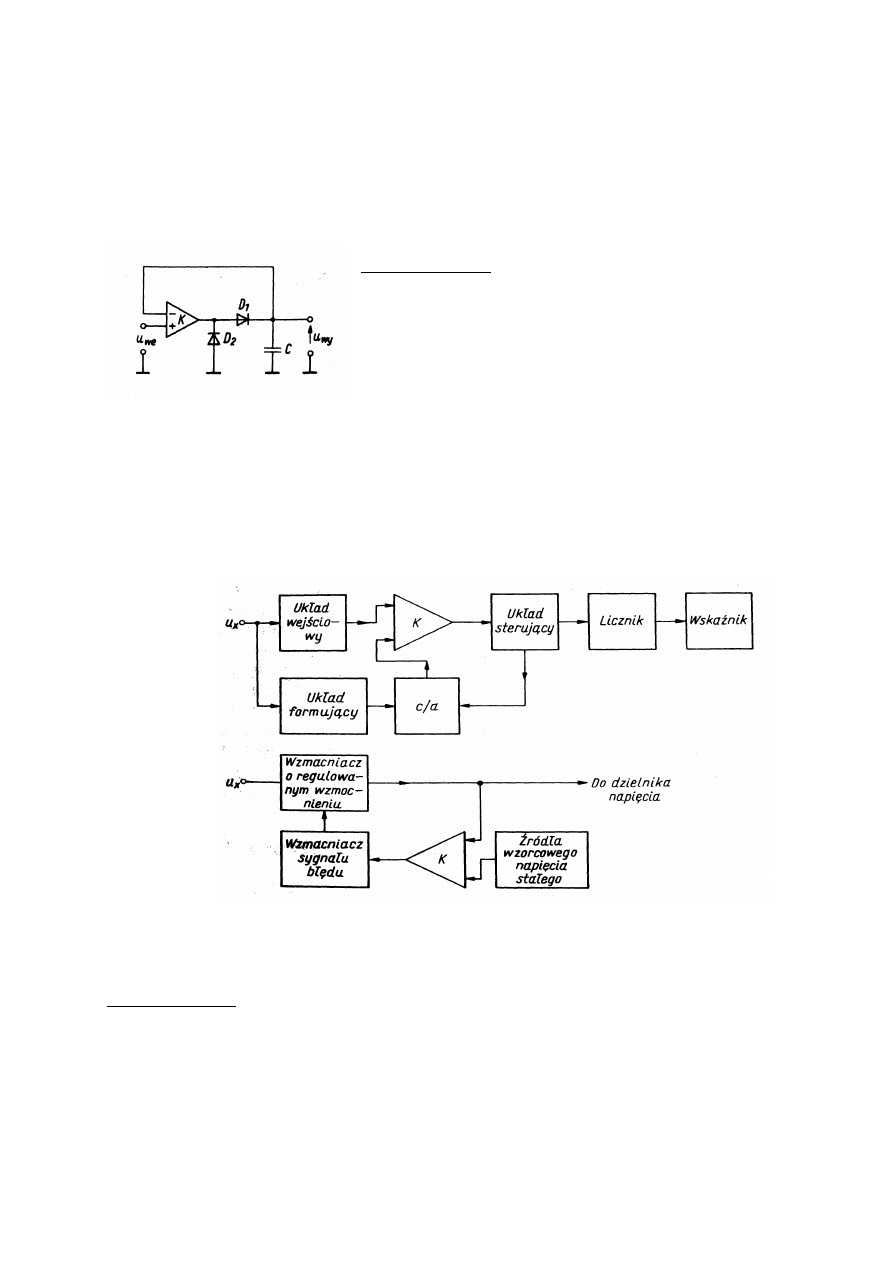
diodzie – częściowo jednak prąd z kondensatora jest pobierany poprzez ustrój pomiarowy
(modelowany przez R
0
). Dokładność układu jest w dużym stopniu zależna od parametrów
zastosowanych elementów.
Znacznie lepsze efekty uzyskuje się w układach zawierających wzmacniacze operacyjne
jednak zawęża się wówczas pasmo częstotliwości.
Zasada działania:
Wzmacniacz pobiera ze źródła badanego napięcia tylko
prąd polaryzacyjny. Czas narastania napięcia na wyjściu
wzmacniacza zależy tylko od jego możliwości prądowych
a nie od stałej czasowej jak w przypadku poprzednim.
Ponadto wzmacniacz jest włączony jako wtórnik
napięciowy jednak w taki sposób by zniwelować spadek
napięcia polaryzacji diody.
37. Narysować schemat woltomierza cyfrowego napięcia przemiennego z
kompensacją wartości skutecznej.
Tego typu woltomierze stosuje się przy pomiarze przebiegów odkształconych. (Powody
budowania tych mierników na podstawie pytania 36).
Główną trudnością przy budowie tego typu mierników jest brak źródeł napięć wzorcowych
odtwarzających kształt napięcia mierzonego w całym zakresie częstotliwości pracy przyrządu.
Można to ominąć tworząc napięcie kompensujące z mierzonego.
Zasada działania:
Napięcie mierzone podawane jest na wejście komparatora oraz wejście układu formującego.
Układ ten nie zmieniając kształtu przebiegu przetwarza go w taki sposób, aby otrzymać
napięcie wyjściowe o stałej wartości skutecznej przy zmianach napięcia mierzonego w
szerokim zakresie.
33
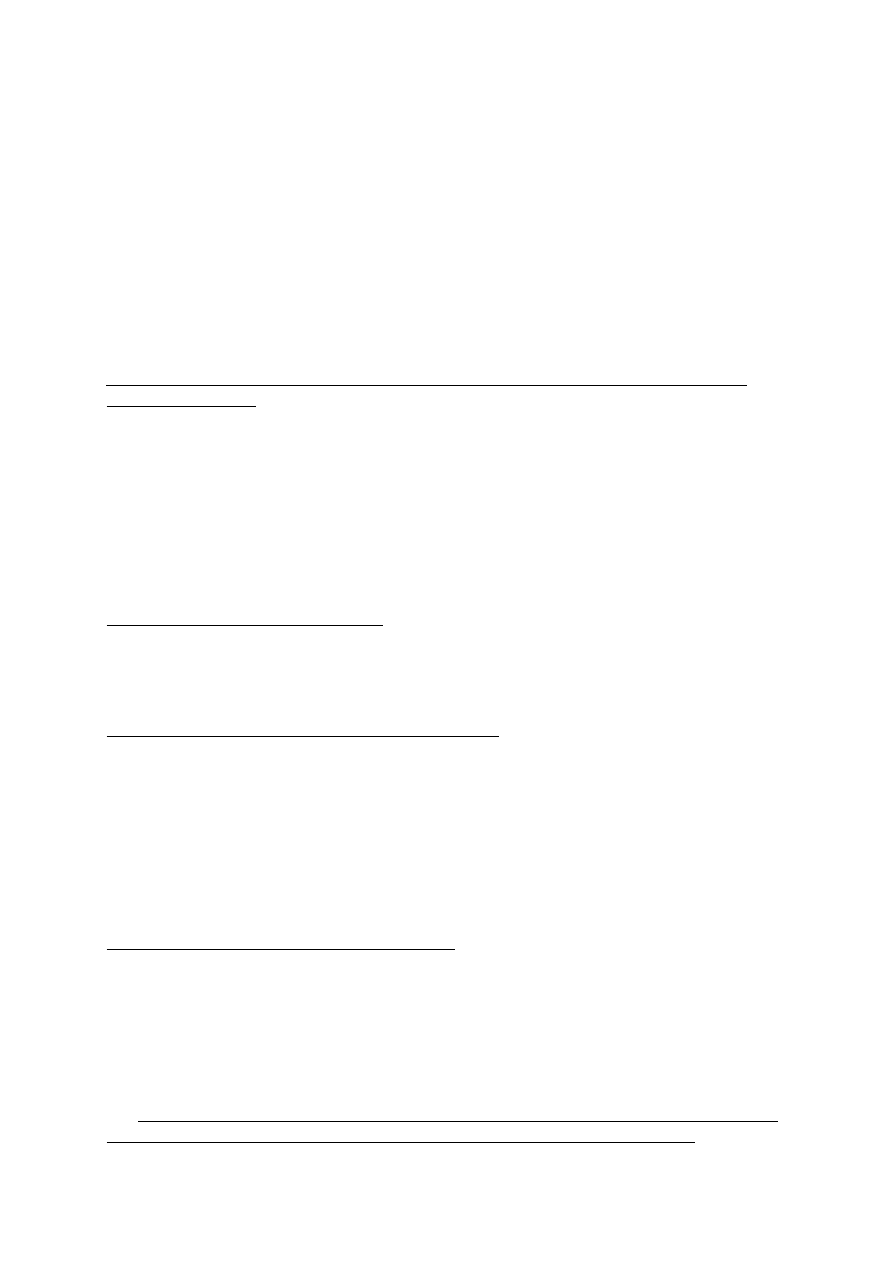
Wartość skuteczna napięcia wyjściowego z układu formującego jest porównywana z
wzorcowym napięciem stałym. Wzmocnienie wzmacniacza jest zmieniane do momentu
zrównania się wartości skutecznych tych napięć.
Tak formowane napięcie jest podawane przez przetwornik c/a do układu porównywania. Jeśli
napięcie kompensujące jest różne od mierzonego to następuje zmiana współczynnika podziału
dzielnika (przetwornik c/a). Operacje te są powtarzane dopóki napięcia mierzone i
kompensujące nie zrównają się. Odczyt wartości skutecznej mierzonego napięcia odbywa się
na podstawie stanu dzielnika (c/a) oraz stopnia podziału w obwodzie wejściowym.
Woltomierze tego typu mają błąd 0,05% do 0,1% w paśmie częstotliwości akustycznych.
38. Klasy dokładności i dokładność pomiaru woltomierzami cyfrowymi.
Woltomierz o przetwarzaniu impulsowo – czasowym
(metoda zwana też jako metoda
zliczania impulsów)
Dokładność pomiaru jest stosunkowa mała i zależy:
•
Od liniowości napięcia wzorcowego,
•
Od stabilności częstotliwości generatora impulsów wzorcowych,
•
Od czułości komparatora
Woltomierz mierzy wartość chwilową. Przyrządy tak działające, mają prostą budowę.
Wykonane są na zakresy od 1mV do 1kV. Graniczny błąd wskazań tego typu woltomierzy jest
±
0,1%
±
1 cyfra. Ten drugi wskaźnik to błąd zliczania.
Woltomierz o podwójnym całkowaniu.
Błąd tego typu woltomierzy jest uwarunkowany stabilnością i dokładnością napięcia
wzorcowego U
0
, a prawie wcale nie zależy od dokładności generatora wzorcowego. W
woltomierzach tego typu jest osiągana dokładność rzędu od 0,05% do 0,02%
Woltomierz o przetwarzaniu napięcia w częstotliwość.
Z uwagi na to, że woltomierz reaguje na wartość średnią napięcia, nie jest on czuły na zakłócenia w
postaci okresowego sygnału symetrycznego (składowa stała tego przebiegu jest zero). Składowa analogowa
błędu pomiaru tego typu woltomierzy jest rzędu od
±
0,01% do
±
0,1%. O dokładności pomiaru decydują :
•
Dokładność dozowań ładunków rozładowujących,
•
Nieliniowość integratora
•
Niestabilność procesów przejściowych na początku i końcu całkowania
•
Niestabilność napięcia U
0
•
Błąd komparatora
Woltomierze p przetwarzaniu kompensacyjnym.
Przyczyny błędów charakterystycznych tylko dla woltomierzy kompensacyjnych to :
•
Niestabilność i niedokładność napięć wzorcowych
•
Próg czułości detektora różnicowego.
Produkowane woltomierze kompensacyjne mają błąd pomiaru rzędu tysięcznej części
procenta.
Uogólnienie
Zakresy woltomierzy cyfrowych zawierają się w granicach od 1mV do 1kV. Najczęściej
spotykane klasy dokładności: 0,1% i 0,01%, przy istnieją także 0,005% i 0,001%.
34
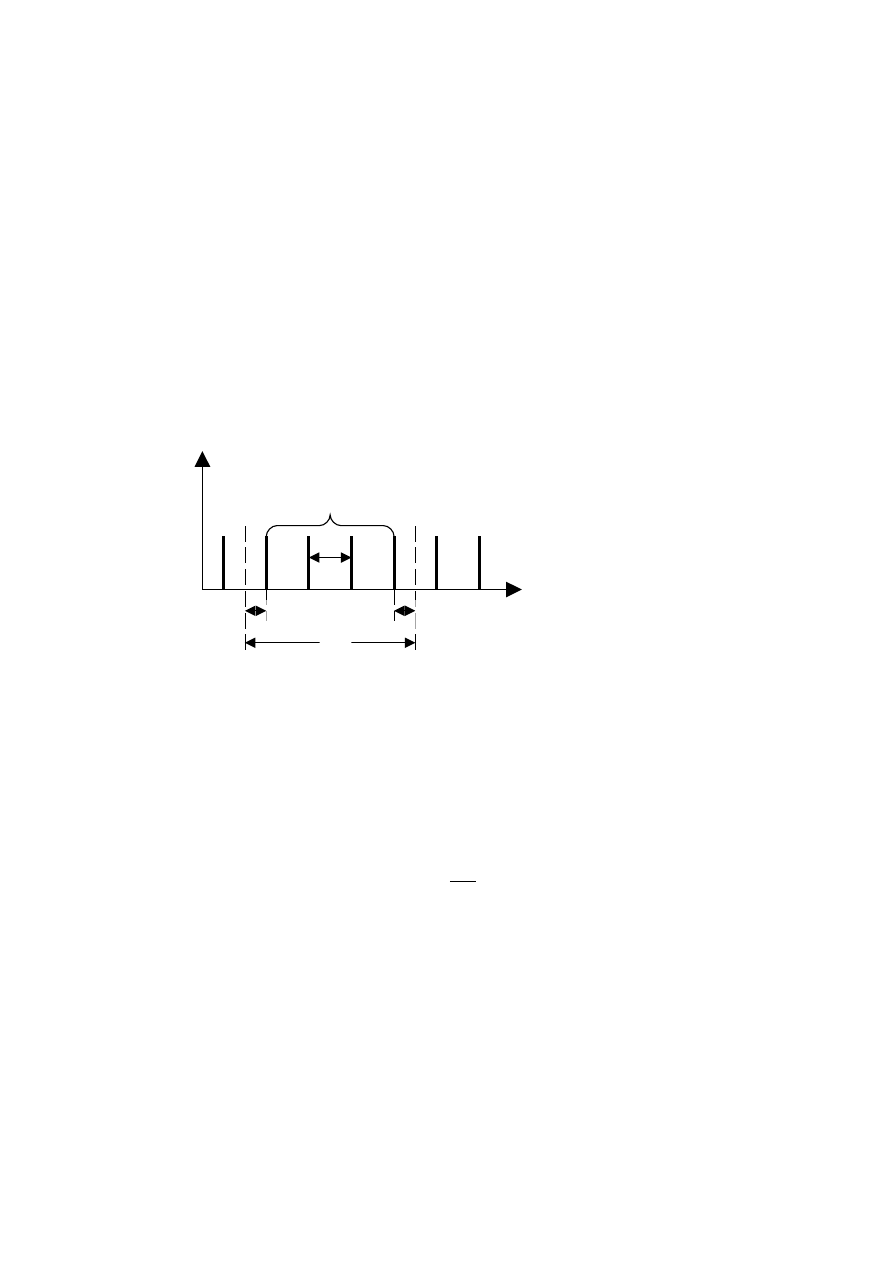
39. Wyjaśnić powstawanie błędu zliczania.
Błędy w przyrządach cyfrowych można podzielić na analogowe i cyfrowe. Podział
taki wynika ze struktury miernika, który jest urządzeniem hybrydowym: analogowym i
cyfrowym.
Błędy analogowe są wynikiem niedoskonałości budowy i działania przetwornika
analogowo – cyfrowego. Podobnie jak w przyrządach analogowych, rozróżnia się błędy
analogowe podstawowe (błąd nieliniowości charakterystyki przetwarzania, czyli zależności
sygnały wyjściowego od wejściowego) i dodatkowe (wynikają ze zmiany warunków pracy:
temperatury i czasu starzenia się elementów).
Składowa cyfrowa błędu w miernikach cyfrowych jest wynikiem procesu zliczania.
Przyczyną jego jest przypadkowe „ułożenie” się względem siebie czasu zliczania i impulsów
zliczanych. Powstanie błędu zliczania dla przypadku stałej częstotliwości pokazano na
rysunku.
W czasie T
X
licznik zlicza N
X
impulsów, tyle samo co w czasie N
X
T
O
+
∆
t
1
-
∆
t
2
, a wskazanie
przyrządu będzie równe N
X
T
O
, więc błąd zliczania
∆
Tx
= N
X
T
O
- N
X
T
O
-
∆
t
1
+
∆
t
2
=
∆
t
2
-
∆
t
1
ponieważ
∆
t
1
<
∆
t
2
, lub odwrotnie, to maksymalna wartość błędu będzie równa:
(
∆
Tx
)
max
=
±
T
O
odpowiada to „zgubieniu” jednego impulsu lub zliczeniu o jeden impuls za dużo.
Równoznaczne jest to błędowi bezwzględnemu zliczania:
∆
Nx
=
±
1 impuls
lub względnemu
X
N
N
X
1
±
=
δ
Błąd całkowity przyrządu podaje się jako błędów: analogowego i cyfrowego.
c
a
pc
δ
δ
δ
+
=
Składowa analogowa jest podstawą do określenia klasy miernika cyfrowego. Przyrządy
cyfrowe są budowane w klasach 0,01; 0,02; 0,05; 0,1; 0,2; 0,5; 1. Składowa analogowa jest
proporcjonalna do wartości wskazanej, cyfrowa jest składową stałą.
40. Cyfrowy pomiar rezystancji. Narysować schemat blokowy i podać
odpowiednie wzory dla jednego z cyfrowych mierników rezystancji.
Jako cyfrowe mierniki rezystancji buduje się mierniki z przetwarzaniem rezystancji na
napięcie i rezystancji na proporcjonalny przedział czasu.
35
N
X
T
O
T
O
T
X
∆
T
1
∆
T
2
U
t
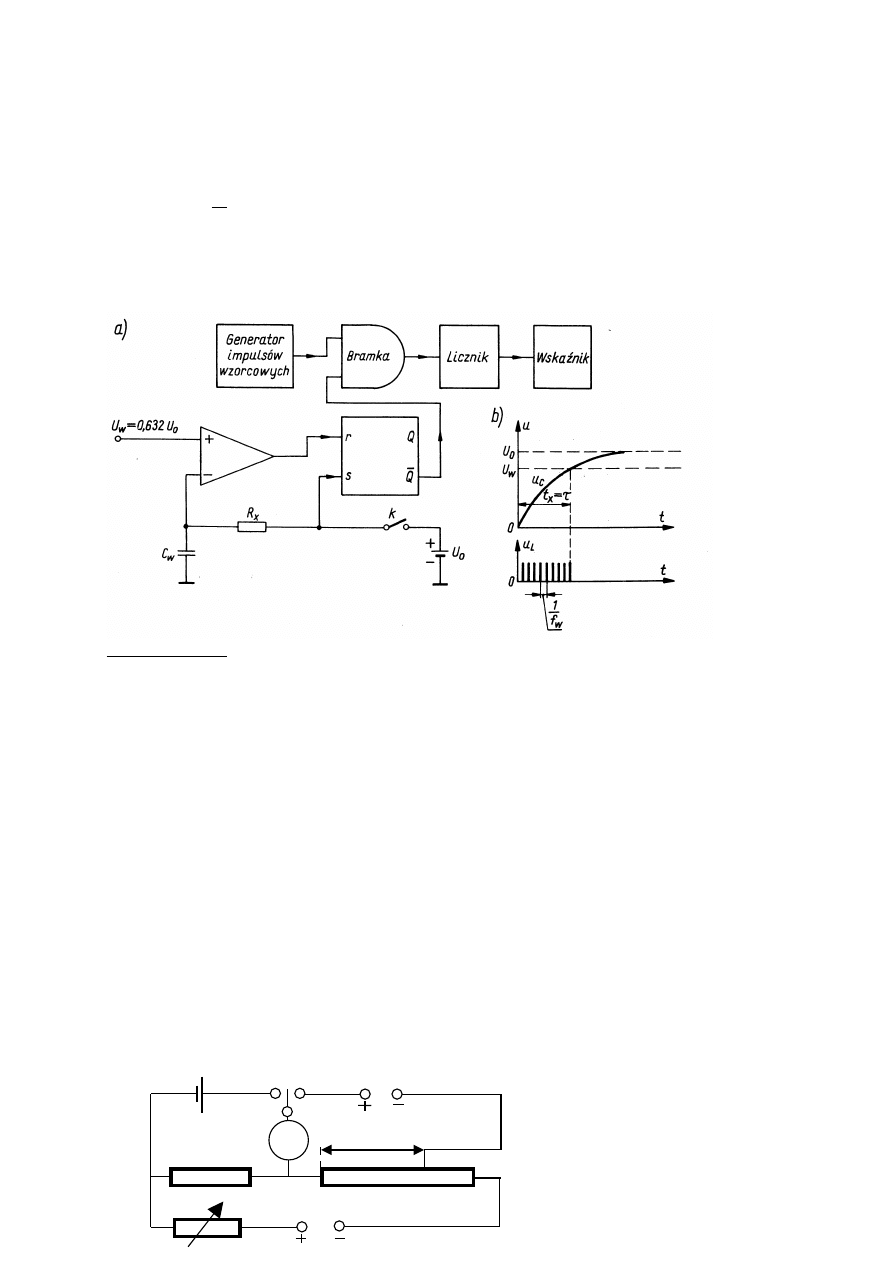
Miernik z przetwarzaniem rezystancji w proporcjonalny przedział czasu.
W metodzie tej wykorzystuje się stany nieustalone występujące w dwójniku RC przy
ładowaniu lub rozładowywaniu kondensatora. Zmiany napięcia na ładowanym kondensatorze
następują zgodnie ze wzorem:
−
=
−
RC
t
c
e
U
u
1
0
Schemat takiego miernika przedstawia rysunek:
Zasada działania
Po zamknięciu klucza k przerzutnik przechodzi do stanu 1 i rozpoczyna się zliczanie
impulsów. Kończy się ono po zamknięciu bramki. Bramka zostanie zamknięta, gdy:
RC
t
tzn
U
U
e
U
u
x
w
c
=
=
=
=
−
=
τ
gdy
.
632
,
0
)
1
(
0
1
0
Jeśli zmienimy wartość rezystora na R
x
> R zwiększy się stała czasowa układu i zliczanie
będzie trwało dłużej (aż do spełnienia warunków j.w.) więc zostanie zliczona większa liczba
impulsów.
Liczba impulsów zliczonych przez licznik w czasie t:
(
)
X
W
X
X
W
X
R
C
f
N
C
R
t
t
f
N
⋅
⋅
=
⋅
=
⋅
=
:
wię
ale
Zaletą tego typu mierników jest to, że przy zmianie elementu wzorcowego na opornik
mierzona może być pojemność C
X
. Błąd pomiaru nie przekracza przeważnie 0,1
÷
0,5 %.
41. Zasada działania kompensatorów o regulowanej rezystancji.
Schemat kompensatora o stałym prądzie pomocniczym I
p
i regulowanej rezystancji
kompensacyjnej R
k
przedstawia rysunek.
36
U
p
R
R
R
I
p
E
N
P
1
2
R
U
U
X
G
Schemat połączeń
kompensatora napięcia
stałego o regulowanej
rezystancji

W kompensatorze tym wartość prądu pomocniczego ustala się na podstawie porównania
spadku napięcia, wywołanego tym prądem na oporniku wzorcowym R
E
, z siłą
elektromotoryczną ogniwa wzorcowego Westone’a E
n
. W tym celu przełącznik P ustawia się
w położeniu 1 i reguluje rezystorem R
r
dopóty, dopóki galwanometr nie wskaże stanu
kompensacji, wówczas E
n
=I
p
*R
E
. Napięcie badane U
x
mierzy się w położeniu przełącznika P
w pozycji 2. Stan kompensacji uzyskuje się przez regulację suwakiem opornika R
k
. Gdy
galwanometr wskaże zero, wówczas U
x
=I
p
*R
u
, po podstawieniu pierwszego wzoru do
drugiego otrzymujemy
U
E
R
R
x
n
U
E
=
*
. Wzór jest słuszny gdy mamy pewność, że wartość prądu
pomocniczego podczas pomiaru nie uległa zmianie. Dlatego też po skompensowaniu napięcia
badanego należy przełączyć przełącznik P w pozycję 1 i sprawdzić, czy galwanometr
pokazuje zreo. Oczywistym jest, że przy zmianie wartości prądu pomocniczego I
p
należy
powtórzyć pomiar po wyregulowaniu prądu I
p
do wartości wymaganej. Wartość prądu
pomocniczego I
p
powinna być taka, aby wynik mógł być odczytywany bezpośrednio w
jednostkach napięcia. Warunek ten jest spełniony gdy R
E
=E
n
*10
n
wtedy dla stanu kompensacji
U
x
=R
u
*10
-n
.
42. Dekada podwójna Feussnera
Obok przedstawiono zasadę budowy podwójnej
dekady Feussnera. Skład się ona z dwóch bloków
po 10 rezystorów o jednakowej wartości R
połączonych jak pokazano na rysunku.
Niezależnie od położenia przełącznika przez
dekadę płynie jednakowy prąd pomocniczy I
P
gdyż zawsze płynie on przez 10 rezystorów.
Dekady możemy ze sobą łączyć (tzn. połączyć
drugą dekadę Feussnera z rezystorami o
rezystancji 0,1R). W ostatniej dekadzie łączymy
ze sobą „prawe” przewody przez które płynie
prąd pomocniczy I
p
aby zamknąć obwód prądowy. Do „lewych” przewodów pierwszej
dekady podłączamy jakieś wzorcowe źródło napięcie wymuszające przepływ znanego prądu
pomocniczego I
p
. Napięcie kompensujące zdejmujemy zawsze z górnego zestawu rezystorów.
Napięcie kompensacyjne zdjęte z dekady z rezystorami R jest równie iloczynowi prądu
pomocniczego, liczby wybranych rezystorów i ich rezystancji R.
Dekad podwójna Feussnera jest elementem na którym opiera się budowa wielu komparatorów
o stałym prądzie pomocniczym (zmiennej rezystancji).
43. Zasada działania kompensatora o regulowanym prądzie.
Kompensatory o regulowanym prądzie zaliczamy do układów pomiarowych prądu stałego.
Wykonuje się jeszcze kompensatory o stałym prądzie roboczym. Ogólnie metoda
kompensacyjna pomiaru napięcia polega na takim dobraniu napięcia (wyjściowego
przyrządu) by nie różniło się ono od napięcia mierzonego. Miernik, najczęściej galwanometr
wskazuje różnicę między tymi napięciami.
37
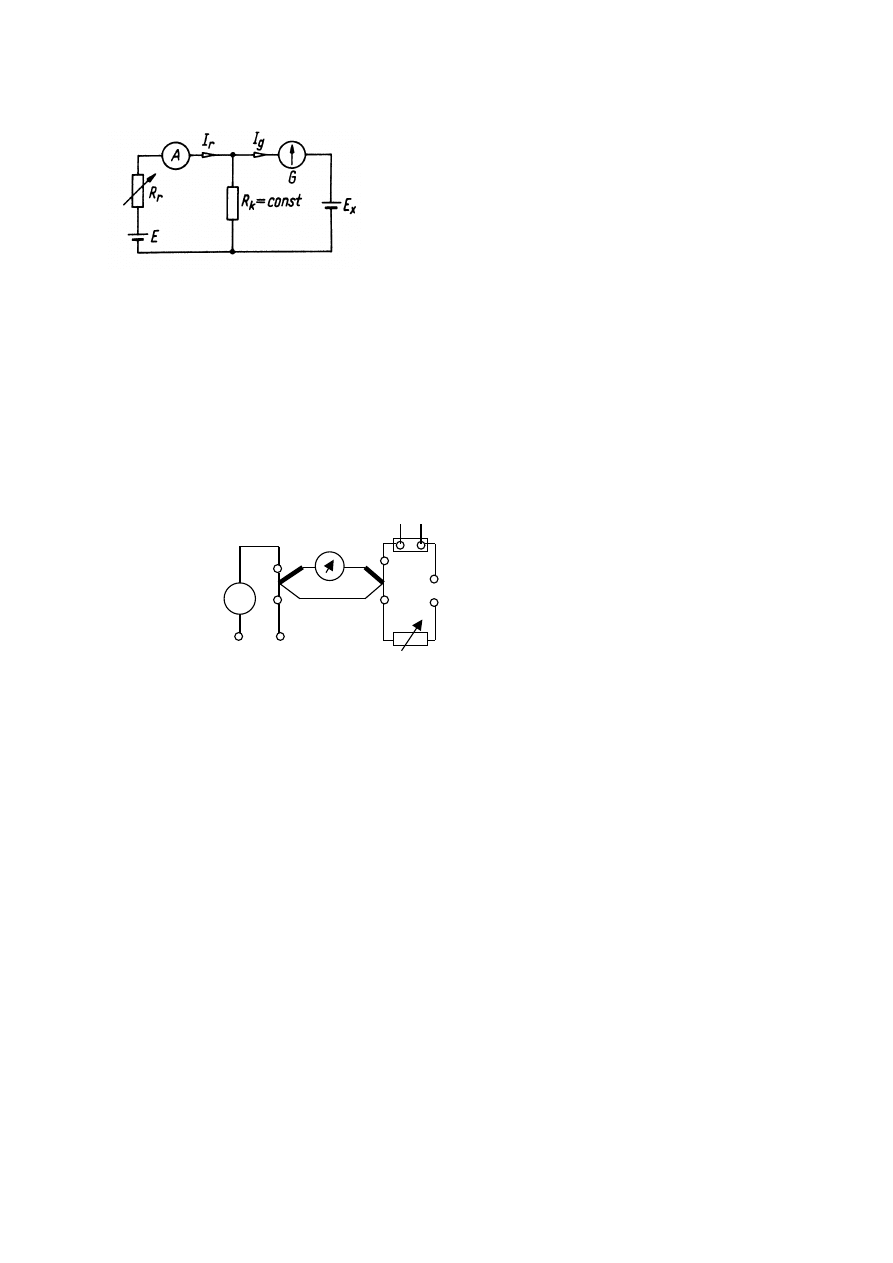
Zasadę działania tego kompensatora o regulowanym prądzie wyjaśnia schemat:
Wartość prądu roboczego I
r
, regulowaną opornikiem R
r
,
mierzy amperomierz. Napięcie mierzone E
x
porównuje
się ze spadkiem napięcia na stałym oporniku
wzorcowym R
k
. W układzie skompensowanym (I
g
= 0)
mierzone napięcie można wyznaczyć następująco :
k
r
x
R
I
E
⋅
=
Głównym składnikiem błędu pomiaru jest błąd wprowadzany przez amperomierz, stąd
kompensatory o regulowanym prądzie pomocniczym są budowane najczęściej jako
kompensatory techniczne ( klasy 0,1; 0,2 ; 0,5). Z powodzeniem zastępuje się te przyrządy
miernikami elektronicznymi, które posiadają klasy porównywalne lub lepsze i podobnie jak
kompensatory nie pobierają prądu z układu pomiarowego.
44. Komparator termoelektryczny.
W komparatorach z czujnikami jako czujniki są używane przetworniki termoelektryczne,
ogniwa fotoelektryczne i oporniki o ujemnym współczynniku cieplnym. Największe
zastosowanie znajdują komparatory z dwoma jednakowymi przetwornikami
termoelektrycznymi.
Jeden z grzejników przetwornika łączy się w obwód prądu przemiennego, a drugi w obwód
prądu stałego.Prąd stały mierzony kompensatorem, nastawia się tak, aby nie było różnicy
między siłami termoelektrycznymi. Wskaźnikiem kompensacji jest galwanometr statyczny.Do
kontroli wskazana jest zamiana przetworników – po zamianie stan równowagi nie powinien
ulec zmianie. Wtedy wartość skuteczna prądu przemiennego równa się wartości prądu
stałego. Komparatory pozwalają na pomiar wartości skutecznych prądu przemiennego o
częstotliwości technicznej (komparatory momentu napędowego) i do około 100kHz
(komparatory z czujnikami termoelektrycznymi), z błędem nie przekraczającym 1%. Wadą
jest pobór mocy z obwodu kontrolowanego, oraz niemożność jednoczesnego pomiaru kąta
przesunięcia fazowego. Używa się ich przede wszystkim do sprawdzania dokładności
wskazań precyzyjnych przyrządów prądu przemiennego oraz do dokładnych pomiarów
wartości skutecznych prądu i napięcia, do nastawiania prądu pomocniczego w
kompensatorach napięcia przemiennego.
38
~
=
R
n
Do kompensatora
mA
J
X
J
n
Kompensator z
przetwornikami
termoelektrycznymi
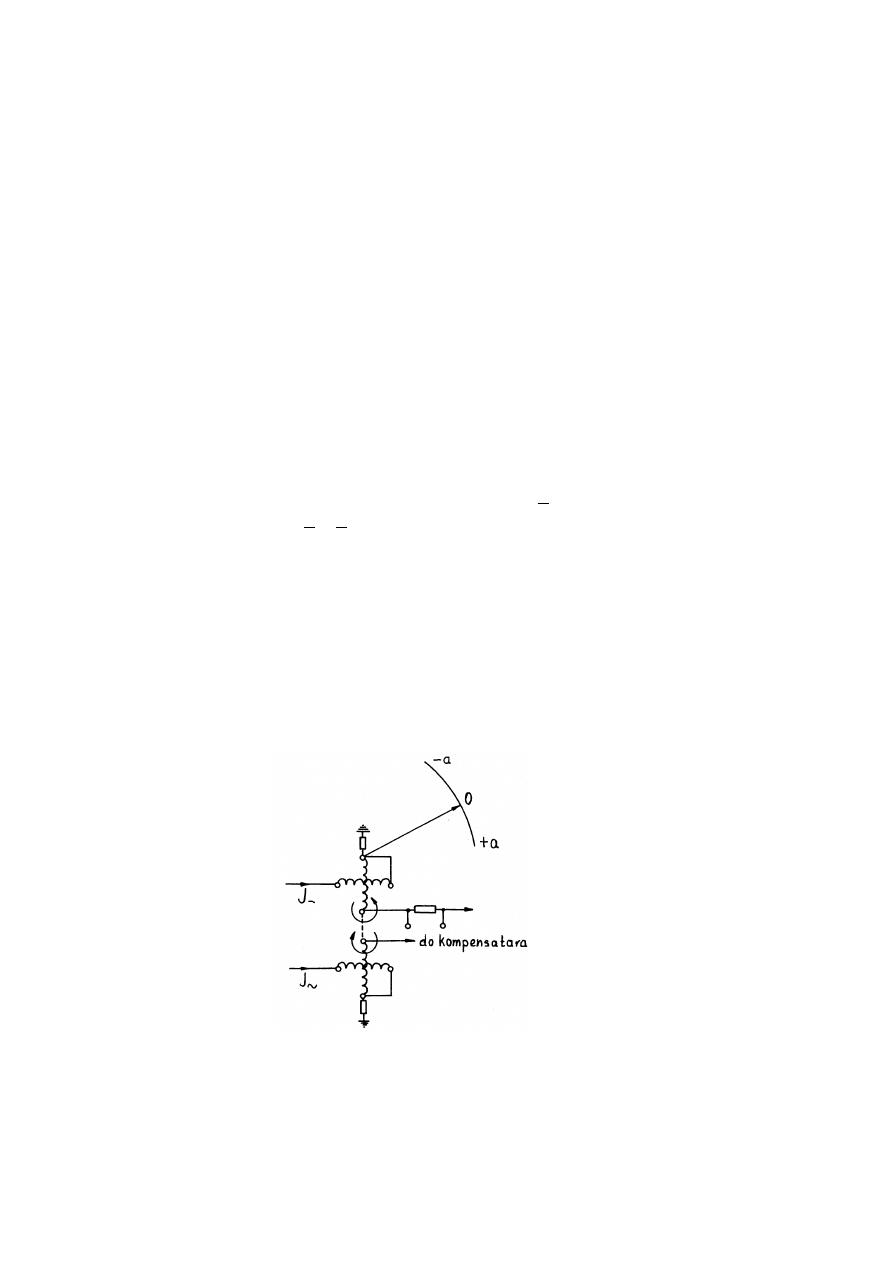
46. Warunki pełnej kompensacji w kompensatorach prądu przemiennego.
W kompensatorach napięć przemiennych dla uzyskania pełnej kompensacji wymagane jest
spełnienie 4 warunków dotyczących obu napięć: mierzonego i wzorcowego.
a)
równość częśtotliwości napięcia mierzonego i kompensującego (f
x
=f
k
). Warunek
ten spełniamy zasilając kompensator i obwód kontrolowany z tego samego źródła
prądu.
b) jednakowe kształty krzywych obu napięć. Ten warunek jest trudny do spełnienia
ponieważ elementy nielinioew układu pomiarowego , obce pole magnetyczne itp.
w różny sposób zniekształcają krzywe napięć i prądów. W praktyce równowaga
dotyczy tylko I-ej harmonicznej odkształconego napięcia badanego. Uzyskuje się
to stosując selektywne wskaźniki równowagi, kosztem zmniejszenia dokładności
pomiaru.
c)
Jednakowe wartości modułów obu napięć (U
x
=U
k
)
d)
Przesunięcie faz między napięciami 0 180
0
(
ϕ
x
=-
ϕ
k
).
Zależnie od sposobu przeprowadzenia regulacji modułu i fazy rozróżnia się dwa typy
kompensatorów: o współrzędnych biegunowych i współrzędnych prostokątnych.W
kompensatorach o współrzędnych biegunowych moduł napięcia wzorcowego jest regulowany
opornikiem kompensacyjnym, a kąt przesuwnikiem fazowym. Natomiast w kompensatorach o
współrzędnych prostokątnych wektor napięcia mierzonego
U
X
jest sumą geometryczną
dwóch napięć składowych
U
1
i
U
2
, stale przesuniętych względem siebie o kąt 90
0
i
regulowanych osobno.
45. Komparator momentów.
Według zasady działania komparatory można podzielić na dwie grupy:
- komparatory momentu napędowego
- komparatory czujnikowe
W komparatorach momentu napędowego na wspólnej osi pracują dwa ustroje pomiarowe o
przeciwnie skierowanych momentach napędowych. Przez jeden z ustrojów przepływa prąd
przemienny, a przez drugi prąd stały, którego wartość jest mierzona np. kompensatorem prądu
stałego. Używa się tu dwóch ustrojów elektrodynamicznych (rys) lub ustroju
elektrodynamicznego dla prądu przemiennego i magnetoelektrycznego dla prądu stałego.
Różnice między momentami odczytywane są za pomocą wskazówki świetlnej. W chwili
równowagi, wartość skuteczna prądu przemiennego jest równa wartości prądu stałego.
39
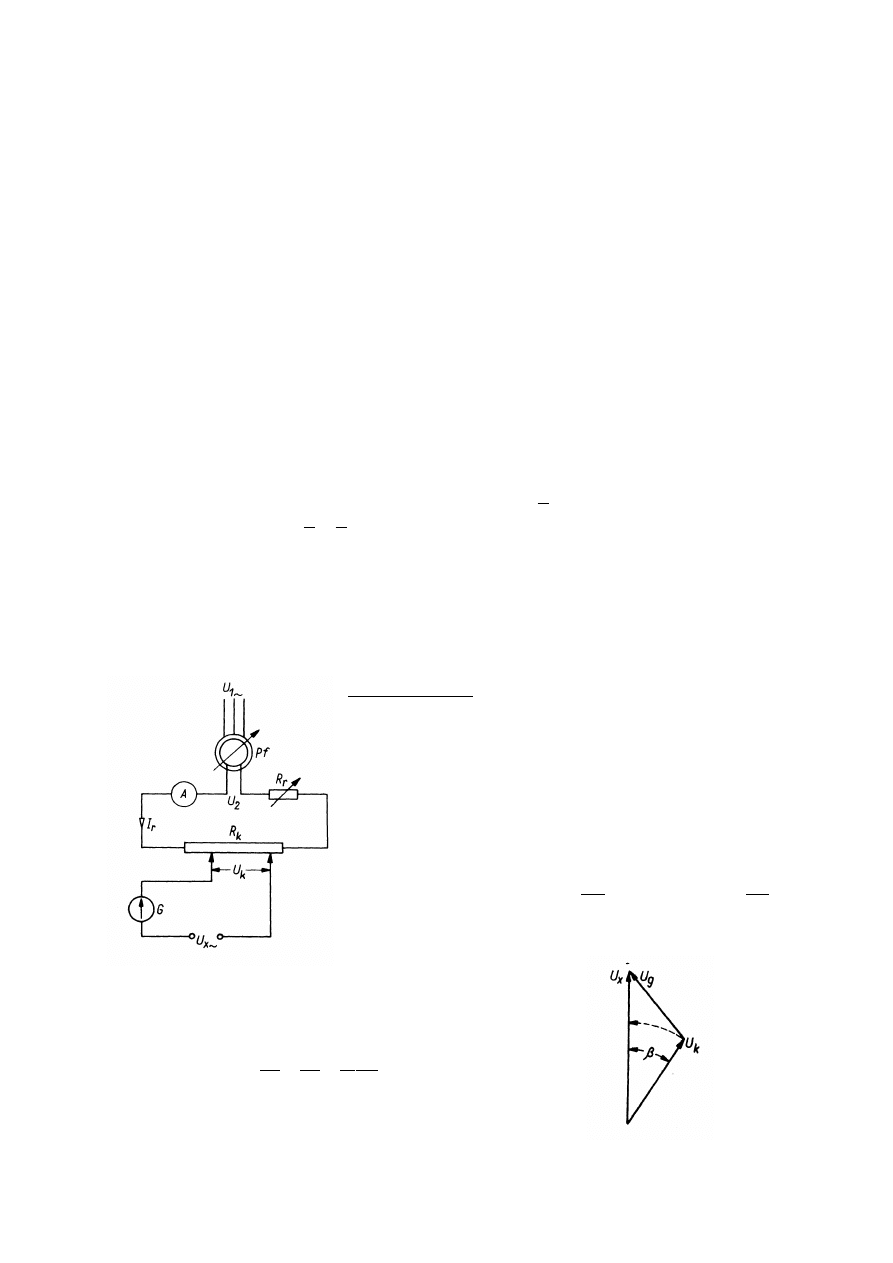
46. Warunki pełnej kompensacji w kompensatorach prądu przemiennego.
W kompensatorach napięć przemiennych dla uzyskania pełnej kompensacji wymagane jest
spełnienie 4 warunków dotyczących obu napięć: mierzonego i wzorcowego.
e)
równość częśtotliwości napięcia mierzonego i kompensującego (f
x
=f
k
). Warunek
ten spełniamy zasilając kompensator i obwód kontrolowany z tego samego źródła
prądu.
f) jednakowe kształty krzywych obu napięć. Ten warunek jest trudny do spełnienia
ponieważ elementy nielinioew układu pomiarowego , obce pole magnetyczne itp.
w różny sposób zniekształcają krzywe napięć i prądów. W praktyce równowaga
dotyczy tylko I-ej harmonicznej odkształconego napięcia badanego. Uzyskuje się
to stosując selektywne wskaźniki równowagi, kosztem zmniejszenia dokładności
pomiaru.
g)
Jednakowe wartości modułów obu napięć (U
x
=U
k
)
h)
Przesunięcie faz między napięciami 0 180
0
(
ϕ
x
=-
ϕ
k
).
Zależnie od sposobu przeprowadzenia regulacji modułu i fazy rozróżnia się dwa typy
kompensatorów: o współrzędnych biegunowych i współrzędnych prostokątnych.W
kompensatorach o współrzędnych biegunowych moduł napięcia wzorcowego jest regulowany
opornikiem kompensacyjnym, a kąt przesuwnikiem fazowym. Natomiast w kompensatorach o
współrzędnych prostokątnych wektor napięcia mierzonego
U
X
jest sumą geometryczną
dwóch napięć składowych
U
1
i
U
2
, stale przesuniętych względem siebie o kąt 90
0
i
regulowanych osobno.
47. Zasada działania kompensatora prądu przemiennego o współrzędnych
biegunowych.
(W punkcie 46 zostały omówione warunki pełnej kompensacji dla prądu przemiennego.)
Układ kompensatora tego typu przedstawia rysunek.
Zasada działania:
Układ pomiarowy zasilany jest za pomocą przesuwnika
fazowego. Amperomierz (wartość skuteczna) służy do
kontroli stałości prądu roboczego w czasie i jego wartości.
Jako przyrząd wskazujący stan skompensowania stosuje się
przeważnie galwanometr wibracyjny dostrojony najczęściej
na częstotliwość techniczną.
Prąd roboczy ustawiany jest za pomocą opornika
regulowanego R
r
. Napięcie na galwanometrze jest różnicą
wektorów napięcia mierzonego
X
U i kompensującego
K
U .
Kąt fazowy
β
zmienia się tak by napięcie U
g
miało jak
najmniejszą wartość:
Można to zaobserwować na
galwanometrze. Gdy to nastąpi oba napięcia będą w fazie.
Następnie opornikiem R
K
zmienia się moduł napięcia U
K
do
stanu, gdy galwanometr wskaże zero. Wówczas układ będzie w
stanie równowagi tj.
K
r
k
x
R
I
U
U
=
=
.
Kompensatory napięcia przemiennego stosuje się do pomiaru
wartości skutecznej napięcia sinusoidalnego oraz fazy bez
poboru prądu z układu badanego. Dokładność kompensatorów
40
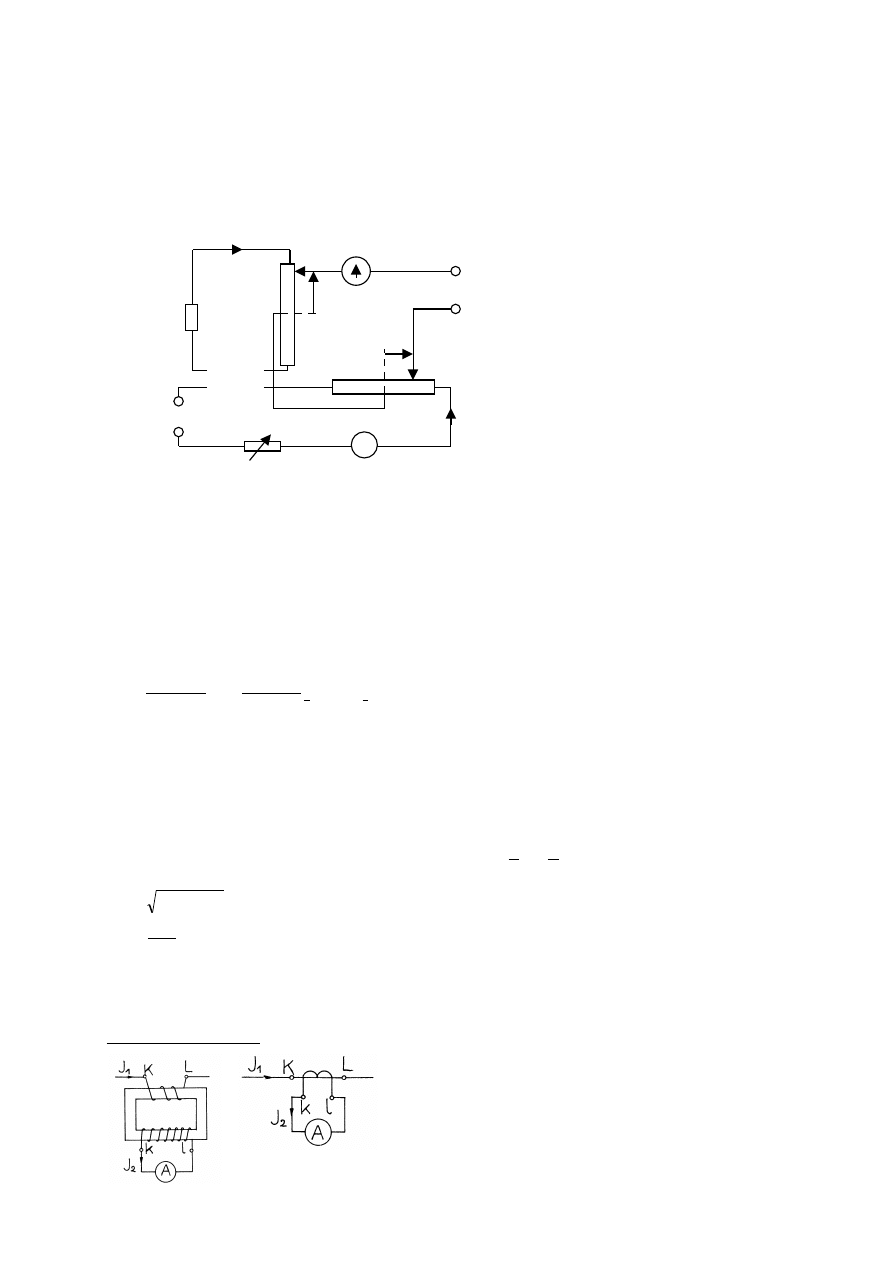
napięcia przemiennego jest dużo mniejsza niż kompensatorów napięcia stałego (1 %) i
dlatego nie są one szeroko stosowane. Często lepsze wyniki daje zastosowanie przyrządów
elektronicznych. Zaletą tych urządzeń jest fakt, że za ich pomocą można zmierzyć kąt
przesunięcia fazowego (z tarczy przesuwnika).
48. Zasada działania kompensatora o współrzędznych prostokątnych.
Kompensator ma dwa obwody kompensujące, połączone ze sobą za pomocą transformatora
powietrznego T. W prawidłowo wyregulowanym kompensatorze, napięcia na opornikach
kompensacyjnych R
K1
i R
K2
są przesunięte w fazie względem siebie o 90
0
. Środki oporników
kompensacyjnych są ze sobą połączone, dzięki czemu napięcia kompensujące U
K1
i U
K2
mogą
być regulowane od +U
Kn
do 0 i do –U
Kn
, to znaczy, że oba napięcia kompensujące mogą
zmieniać fazę o 180
0
. Prąd pierwotny I
R1
zależy od napięcia zasilającego oraz od impedancji
obwodu pierwotnego. Wartość tego prądu może być nastawiona opornikiem R
r
a
kontrolowana amperomierzem elektromagnetycznym mierzącym wartość skuteczną. Prąd
wtórny I
R2
wynika z napięcia E
2
indukowanego w uzwojeniu wtórnym transformatora
powietrznego T o indukcyjności wzajemnej M i rezystancji obwodu wtórnego
I
E
R
R
j
M
R
R
I
jcI
R
k c
k c
R
R
2
2
2
2
2
2
1
1
=
+
= −
+
= −
ω
przy czym R
k2c
– całkowita rezystancja opornika
kompensacyjnego. Kompensację mierzonego napięcia U
x
osiąga się przez zmianę nastawień
oporników kompensacyjnych R
K1
i R
K2
.
Stan kompensacji
wykazuje selektywny elektroniczny
wskaźnik równowagi lub galwanometr wibracyjny. Równoważenie wymaga teoretycznie
dwóch operacji: nastawienia opornikiem R
K1
napięcia U
K1
, przy którym galwanometr
wskazuje minimum wychylenia, a następnie opornikien R
K2
zmienia się napięcie U
K2
, aż do
sprowadzenia wskazania galwanometru do zera. W układzie skompensowanym , a więc gdy
napięcie galwanometru U
g
=0 zachodzi równość napięć
U
U
X
K
=
. Moduł napięcia
kompensującego oblicza się ze składowych prostokątnych U
K1
=I
R1
R
K1
i U
K2
=I
R2
R
K2
U
U
U
K
K
K
=
+
1
2
2
2
. Fazę napięcia mierzonego względem prądu I
R1
wyznacza się z zależności
tg
U
U
K
K
β =
2
1
49. Budowa i zasada działania przekładnika prądowego (napięciowego)
Przekładnik prądowy
Obok przedstawiono budowę i symbol przekładnika
prądowego. Niestety na rysunkach znajdują tylko stare
oznaczenia zacisków. Z tej chwili częściej podaje się
nowe które odpowiadają w następujący sposób
starym:
41
I
r2
I
r1
R
2
R
r
R
k2
R
k1
U
k2
U
k1
U
x~
U~
G
A
T
Uproszczony układ kompensatora
pracującego we współrzędnych
prostokątnych
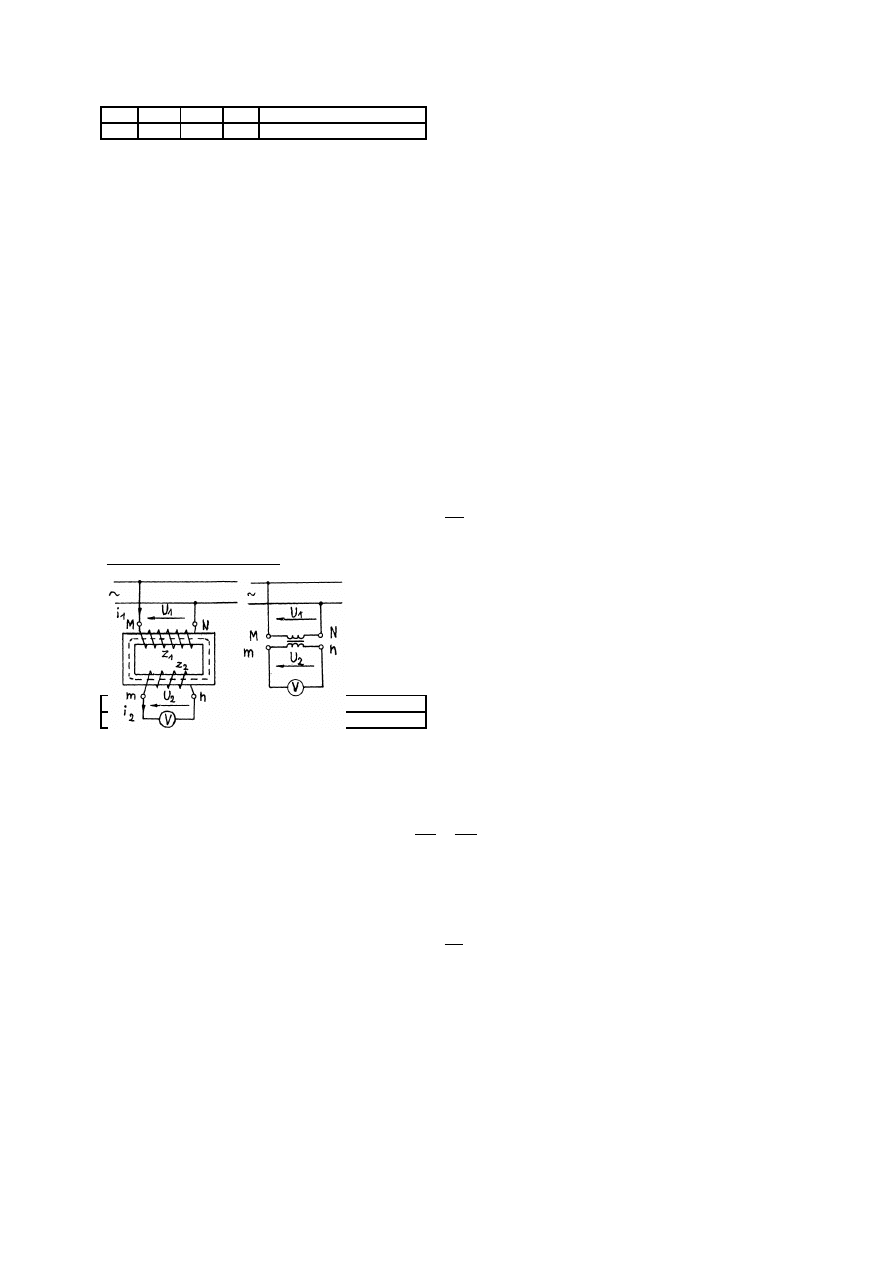
K
L
K
l
Oznaczenia stare
P
1
P
2
S
1
S
2
Oznaczenia nowe
Dużymi literami (lub P) oznacza się uzwojenie pierwotna, a małymi literami (lub S) oznacza
się uzwojenie wtórne.
Przekładniki prądowe są to urządzenia zbliżone do transformatorów mocy lecz w odróżnieniu
od nich są przystosowane do pracy w stanie bliskim stanowi zwarcia. Posiadają dwa
uzwojenia starannie od siebie odizolowane nawinięte na rdzeniu z blach ferromagnetycznych.
Ich zasada działania jest identyczna jat transformatora tzn. pod wpływem zmiennego prądu w
uzwojeniu pierwotnym powstaje strumień magnetyczny (zmienny) który powoduje
wyidukowanie siły elektromotorycznej po stronie wtórnej, dzięki czemu w obwodzie
zamykanym przez amperomierz popłynie prąd.
Ze względu na w stanie bliskim stanowi zwarcia można pominąć magnesowania i możemy
zapisać przybliżoną zależność:
2
2
1
1
I
z
I
z
=
gdzie I
1
,I
2
– są wartościami skutecznymi prądów odpowiednio w uzwojeniu pierwotnym i
wtórnym
z
1
,z
2
– są ilościami zwojów odpowiednio po stronie pierwotnej i wtórnej
Z tej zależności z pewnym błędem jesteśmy w stanie wyznaczyć prąd płynący przez
uzwojenie pierwotne:
2
1
2
1
I
z
z
I
≈
Przekładnik napięciowy
Obok przedstawiono budowę, sposób podłączania oraz
symbol przekładnika napięciowego. Przekładnik
napięciowy jest transformatorem pomiarowym pracującym
w stanie bliskim stanowi jałowemu. Rysunki zawierają
tylko oznaczenia stare tabelka pokazuje także oznaczenia
nowe:
M
N
m
n
Oznaczenia stare
A
B
a
b
Oznaczenia nowe
Zaciski oznaczane dużymi literami są zaciskami uzwojenia pierwotnego.
Ze względu na znikomy prąd płynący w uzwojeniu wtórnym możemy zapisać przybliżoną
zależność:
2
2
1
1
z
U
z
U
=
gdzie U
1
,U
2
– napięcia odpowiednio po stronie pierwotnej i wtórnej
z
1
,z
2
– są ilościami zwojów odpowiednio po stronie pierwotnej i wtórnej
Z tej zależności z pewnym błędem jesteśmy w stanie wyznaczyć:
2
2
1
1
U
z
z
U
≈
42

50. Podać definicje przekładni zwojowej, rzeczywistej i znamionowej
przekładnika prądowego (napięciowego)
Przekładnik prądowy
Dla przekładnika prądowego zachodzi zależność (patrz pytanie 49):
2
1
2
1
I
z
z
I
⋅
≈
- wartości z
indeksem jeden dotyczą strony pierwotnej. Stosunek z
2
/z
1
nosi nazwę przekładni zwojowej
przekładnika.
Stosunek rzeczywistych wartości I
1
oraz I
2
jest nazywany rzeczywistą przekładnią prądową.
Zależy ona od wartości prądu pierwotnego (I
1
) oraz impedancji obciążenia. Wpływ prądu
pierwotnego na przekładnię jest spowodowany nieliniowością charakterystyki magnesowania
rdzenia. Dlatego w praktyce operuje się przekładnią prądową znamionową – równą
stosunkowi wartości znamionowych prądów pierwotnego i wtórnego :
n
n
In
I
I
k
2
1
=
.
Przekładnik napięciowy
Pojęcia te definiuje się podobnie jak dla przekładnika prądowego.
Przekładnią napięciową (zwojową) nazywamy stosunek liczby zwojów uzwojenia
pierwotnego i wtórnego przekładnika. Podobnie jak dla przekładników prądowych
definiowana jest przekładnia rzeczywista niestety nie jest ona stała w całym zakresie pracy
(zależy od napięcia pierwotnego i obciążenia), dlatego też do wyznaczenia napięcia
pierwotnego wykorzystuje się przekładnię znamionową będącą ilorazem wartości
znamionowych napięć przekładnika.
n
n
Un
U
U
k
2
1
=
Mierzoną wartość można określić z zależności U
1
= k
Un
* U
2
.
51. Wyjaśnić pojęcie poprawki zwojowej.
Pojęcie poprawki zwojowej związane jest z błędem napięciowym w przekładniku
napięciowym. Jeśli znamionowa przekładnia napięciowa jest równa zwojowej to błąd
napięciowy jest zawsze ujemny na skutek występujących spadków napięcia na przekładniku.
W produkowanych przekładnikach uzwojenie wtórne ma często nieco większą liczbę zwojów
z
2
(uzwojenie wtórne) niż wynikałoby to z ostatniego wyrażenia. Uzyskany w ten sposób
przyrost napięcia U
2
może skorygować spadki napięcia na uzwojeniach przekładnika i
doprowadzić błąd napięciowy do zera lub nawet do wartości dodatnich. Dobierając, więc
stosunek z
1/
z
2
można błąd napięciowy sprowadzić do odpowiednio małych wartości; mówi się
wtedy o wprowadzeniu poprawki zwojowej.
Podobnie poprzez dobór przekładni zwojowej w przekładniku prądowym można
skompensować błąd prądowy przekładnika. Można tak dobrać przekładnię, że dla pewnych
obciążeń będzie on równy zeru.
52. Podać definicje błędów przekładnika prądowego oraz ich związek z klasą
przekładnika (napięciowego)
Różnica między przekładnią znamionową(stałą) a przekładnią rzeczywistą jest błędem
prądowym przekładnika prądowego lub błędem napięciowym w przypadku przekładnika
napięciowego.
1
1
2
I
I
I
I
I
N
−
ϑ
=
δ
*
1
1
2
U
U
U
U
U
N
−
ϑ
=
δ
*
43
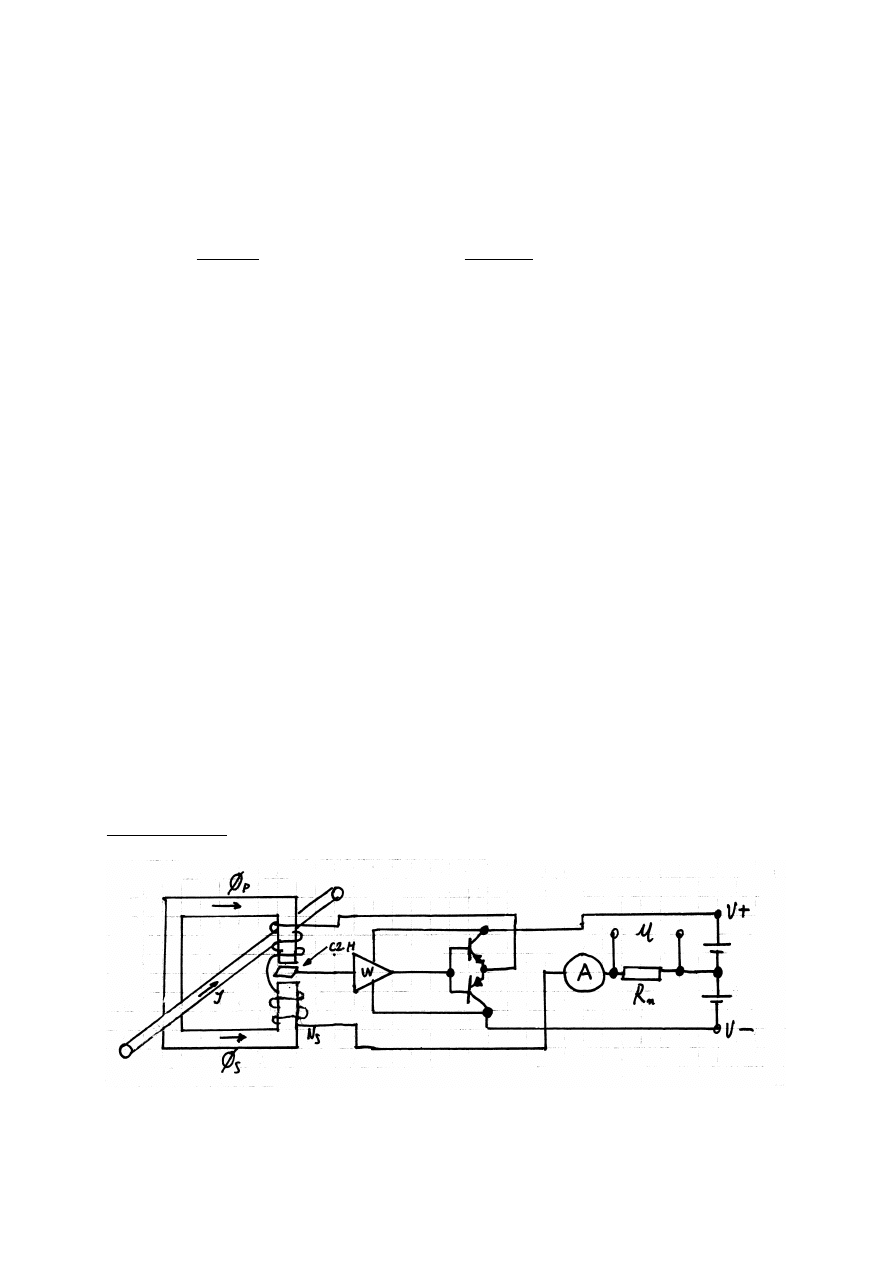
Równanie po prawej stronie jest wyrażeniem na błąd prądowy przekładnika prądowego gdzie
ϑ
IN
jest przekładnią znamionową a I
1
i I
2
wartości skuteczne prądów odpowiednio w
uzwojeniu pierwotnym i wtórnym. Prawe równanie opisuje błąd napięciowy przekładnika
napięciowego gdzie
ϑ
UN
jest przekładnią znamionową a U
1
i U
2
wartości skuteczne napięć
odpowiednio w uzwojeniu pierwotnym i wtórnym.
Dzieląc lewe równanie przez I
2
a prawe przez U
2
otrzymamy następujące zależności:
I
I
I
I
N
ϑ
ϑ
−
ϑ
=
δ
U
U
U
U
N
ϑ
ϑ
−
ϑ
=
δ
gdzie
ϑ
I
jest rzeczywistą przekładnią przekładnika prądowego, a
ϑ
U
jest rzeczywistą
przekładnika napięciowego.
Klasa przekładnika jest równa procentowemu błędowi prądowemu przy 100% prądu
znamionowego.
Podobny związek zachodzi dla przekładnika napięciowego.
Błąd kątowy
γ
I
przekładnika prądowego jest to kąt mierzony w minutach między wektorem
prądu pierwotnego I
1
, a odwróconym wektorem prądu wtórnego I
2
.
Dla przekładnika napięciowego błąd kątowy
γ
U
definiuje się jako kąt mierzony w minutach
między wektorem napięcia pierwotnego a odwróconym wektorem napięcia wtórnego.
Błąd kątowy ma wpływ przy pomiarach mocy i energii. Błąd ten wynika ze strat energii w
rdzeniu.
54. Skutki rozwarcia obwodu wtórnego przekładnika prądowego.
Rozwarcie obwodu wtórnego przekładnika prądowego podczas pracy powoduje znaczne
zwiększenie strumienia magnetycznego, co jest przyczyną indukowania dużego napięcia
(nawet rzędu kilowoltów!) po stronie wtórnej. Cały prąd jest prądem magnesującym.
Następuje przesunięcie punktu pracy – magnesowanie a także skutki cieplne. Dlatego należy
zapamiętać: Nie wolno podczas przepływu prądu w obwodzie pierwotnym rozwierać
obwodu wtórnego przekładnika prądowego. W razie potrzeby wykonania przełączenia w
obwodzie wtórnym, należy zawsze zewrzeć zaciski k-l.
55. Zasada dziłania i właściwości przekładnika LEM
Przekładniki LEM są nowym typem przekładników opracowanym przed 25 laty przez francuską firmę.
W stosunku do tego urządzenia używa się nazwy przekładnik z tzw. zerowym (skompensowanym) strumieniem
magnetycznym. Budowa przekładnika prądowego tego typu jest następująca:
Zasada działania
Przez rdzeń przechodzi przewód z prądem I. W rdzeniu indukuje się strumień magnetyczny
Φ
P
. W rdzeniu wykonana jest szczelina w której umieszczony jest czujnik Halla (Cz H). Czujnik
ten mierzy strumień magnetyczny. Jeżeli taki występuje to sygnał z czujnika traktowany jest
44

jako sygnał błędu. Sygnał ten jest wzmacniany przez wzmacniacz W i podawany na
tranzystory pracujące jako klucze. Otwarcie jednego z nich (naraz otwierany jest tylko jeden)
powoduj przepływ prądu przez cewkę o N
S
zwojach nawiniętą na rdzeniu. Prąd płynący przez
cewkę powoduje powstawanie strumienia
Φ
S
. Kierunek płynięcia prądu przez cewkę jest
uzależniony od tego który z tranzystorów jest aktualnie otwarty. Tranzystory są tak otwierany
aby prąd płynący przez cewkę powodował pojawienie się strumienia
Φ
S
skierowanego
przeciwnie do
Φ
P
. Układ dąży do stanu aby całkowity strumień magnetyczny w rdzeniu był
równy 0 (stąd nazwa przekładnika). Wtedy:
S
S
N
I
I
*
=
gdzie: I – wartość skuteczna prądu w przewodzie
I
s
– wartość skuteczna odczytana z amperomierza
Właściwościami charakteryzującymi ten rodzaj przekładników a zarazem ich zaletami są:
- niewielkie wymiary
- nie pobierają energii z układu (niestety potrzebują źródeł zasilania)
- prąd i
s
ma taki sam kształt co prąd i
- szeroki zakres częstotliwościowy (od 0 do kilku kHz)
- dosyć duża dokładność 0,1%
÷
1%
- szeroki zakres temperatur pracy -25
°
C
÷
70
°
C
56. Narysować schemat układu do pomiaru natężenia prądu (napięcia) przy
użyciu przekładnika, podać wzory na wielkość mierzoną i błąd pomiaru
Pomiar prądu
Obok przedstawiono układ do pomiaru prądu przy użyciu
przekładnika radowego.Prąd płynacy przez odbiornik R
o
okręsla się wzorem
A
n
o
I
K
I
I
*
=
gdzie K
nI
jest prerzekładnią zanmionowa prezkładnika, I
2
jest
wskazaniem amperomierza.
Względny bład pomiaru okręsla się wzorem
δ
+
δ
±
=
∆
+
∆
±
=
∆
A
NA
Agr
I
A
A
n
n
o
o
I
I
I
I
K
K
I
II
I
/
gdzie:
∆
K
nI
– bład bezwzględny przekładni czyli róznica między przekładnią zanmionową, a
rzeczywistą,
∆
I
A
bład względny wskazań amperomierza,
δ
I
– bład względny pradowy
przekładnika,
δ
Igr
bład względny graniczny miernika.
Pomiar napięcia
Napięcie na odbiorniku U
o
równe jest:
v
n
o
U
K
U
U
*
=
gdzie K
nU
jest przekładnią znamionową przekładnika
Natomiast względny błąd pomiaru wyraża się wzorem
δ
+
δ
±
=
∆
+
∆
±
=
∆
V
NV
Vgr
U
V
v
n
n
o
o
U
U
U
U
K
K
U
U
IU
U
gdzie:
∆
K
nV
– bład bezwzględny przekładni czyli róznica między przekładnią zanmionową,
a rzeczywistą,
∆
U
V
bład względny wskazań wolomierza,
δ
U
– bład względny napięciowy
przekładnika,
δ
Vgr
bład względny graniczny miernika.
45
A
S
2
(l)
S
1
(k)
P
1
(K)
P
2
(L)
R
o
I
o
I
A
A
(M)
B
(N)
b
(n)
a
(m)
V
U
o
U
V
R
o
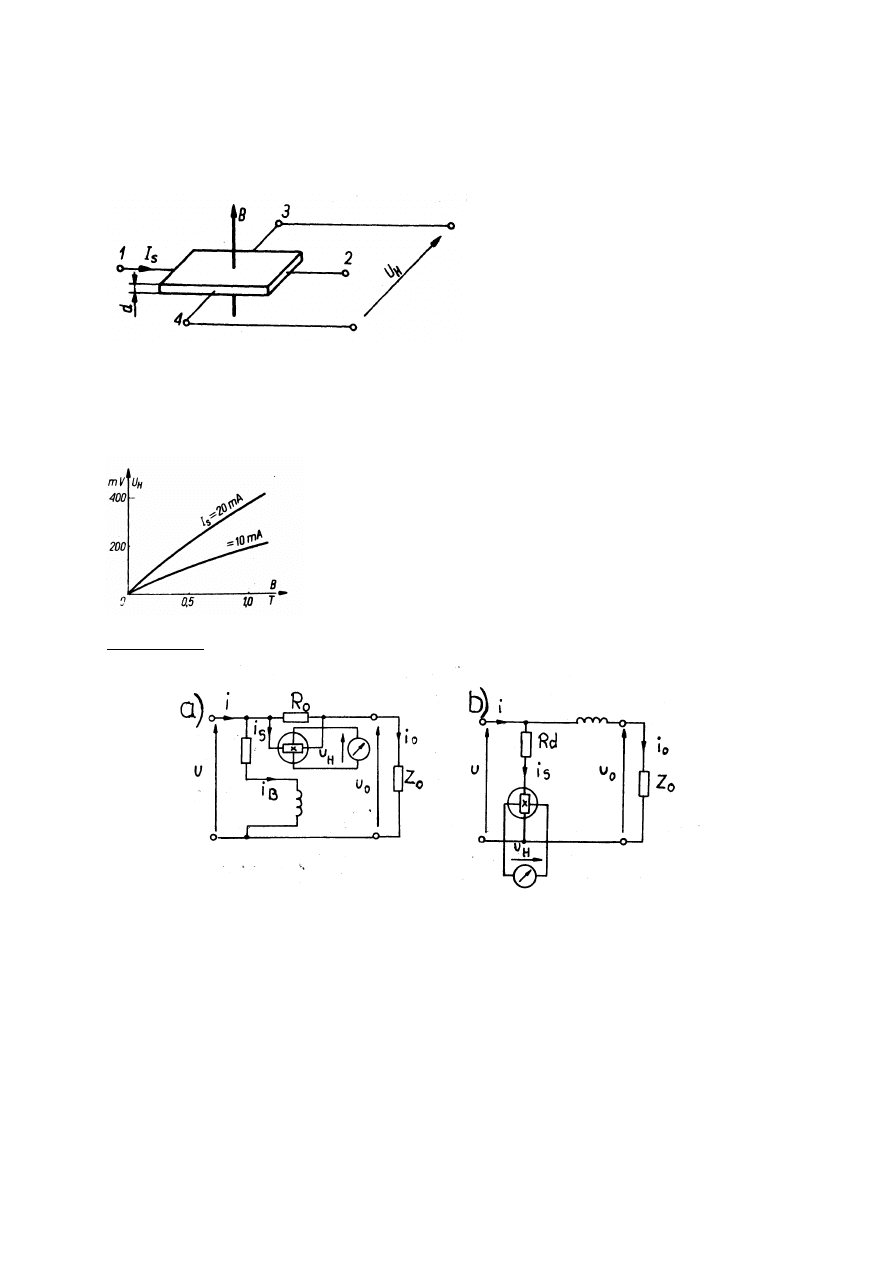
57. Zasada działania watomierza hallotronowego.
Hallotron jest półprzewodnikowym elementem mnożącym. Jest to cienka płytka o dwóch
wzajemnie prostopadłych parach elektrod.
Jeśli płytkę, umieszczoną w polu
magnetycznym, którego wektor indukcji
jest skierowany prostopadle do
płaszczyzny przetwornika, zasilimy
prądem sterującym I
s
to na
wyprowadzeniach 3 i 4 powstanie
napięcie halla. Powstanie również pole
elektryczne o takim natężeniu E
H
, że
zrównoważy siłę pola magnetycznego.
W przypadku stałego pola magnetycznego i stałego prądu sterującego napięcie halla jest stałe
w czasie. Jeśli natomiast, choć jedna z tych wielkości jest przemienna to napięcie wyjściowe
jest również przemienne o takiej samej częstotliwości jak wielkość wejściowa.
W watomierzach wykorzystuje się jednak inną zależność. Otóż, gdy indukcja pola
magnetycznego wzbudzającego oraz prąd sterujący mają tę samą
częstotliwość, ale są przesunięte w fazie o stały w czasie kąt
ϕ
to
napięcie wyjściowe zawiera dwie składowe: stałą i przemienną o
podwójnej częstotliwości.
Zależność napięcia halla od prądu sterującego i indukcji:
Układy pracy
Na rys przedstawiono dwa typowe układy pracy watomierza hallotronowego. W układzie a)
natężenie pola magnetycznego jest proporcjonalne do napięcia zasilającego układ zaś prąd
sterujący jest pośrednio uzależniony od prądu odbiornika i
0
. Rysunek b) przedstawia
zależność odwrotną.
ϕ
Dokładność tego typu mierników jest tego samego rzędu, co dokładność mierników
elektrodynamicznych (przy stosowaniu kompensacji temperaturowej), natomiast zakres
częstotliwości pracy może dochodzić do kilkuset kilo herców
46
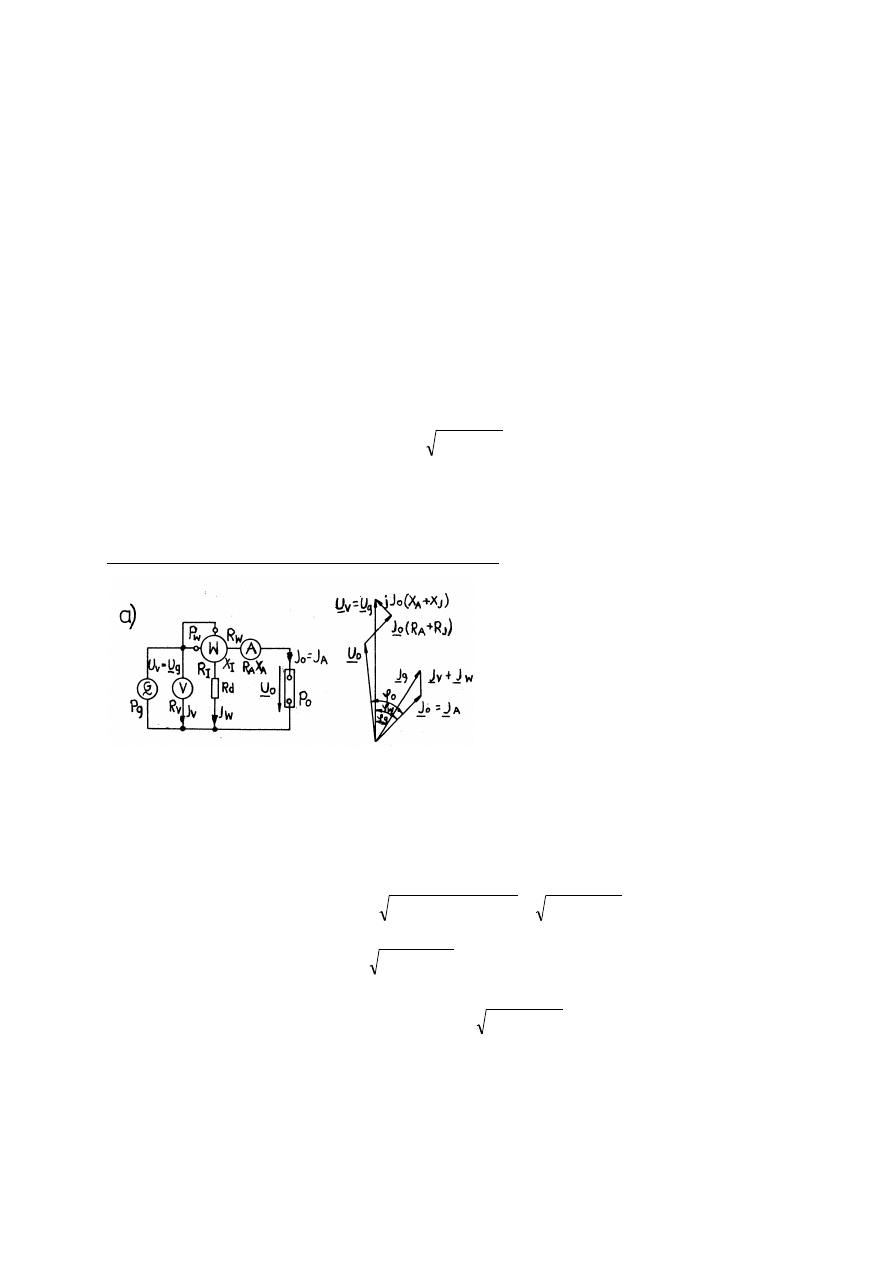
58. Pomiar mocy układu jednofazowego przy poprawnie mierzonym prądzie
(napięciu), podać wzory na P,Q,S i błędy metody pomiaru
Przy pomiarze mocy przy użyciu woltomierza, amperomierza i watomierza poza mocą
obwodu badanego mierzymy moc wydziela na obwodach prądowych lub napięciowych
mierników (zależnie od sposobu włączenia mierników). Dlatego przy pomiarach
precyzyjnych należy uwzględnić poprawki. Natomiast przy pomiarach technicznych poprawki
(pomiary te wykonuje przy założeniu się że mierniki są idealne pod względem
energetycznym) te można pominąć i wtedy moc czynna osiąga wartość
w
o
P
P
=
′
gdzie P
w
jest wskazaniem watomierza, P’
0 –
przybliżona moc czynna odbiornika
Moc pozorna:
A
v
o
I
U
S
*
=
′
gdzie S’
o
– przybliżona moc pozorna odbiornika, U
v
wskazanie woltomierza, I
A
wskazanie
amperomierza
Moc bierna:
2
o
2
o
o
P
S
Q
′
−
′
=
′
gdzie Q’
o
– jest mocą pozorną watomierza (modułem).
Błędy tej metody pomiaru polegają na powiększaniu mocy odbiornika o mocy wydzielane na
miernikach. Przy pomiarach mocy dużych dokładność taka jest wystarczająca, natomiast przy
pomiarach mocy mniejszych należy uwzględnić poprawki co jest jednak uciążliwe
Układ pomiarowy przy „zadanym” prądzie odbiornika
W układzie tym moc czynna odbiornika
wskazywana przez watomierz
powiększona jest o moc czynną
wydzieloną na rezystancji cewki
prądowej watomierza i rezystancje
amperomierza więc rzeczywista moc
odbiornika opisywana jest wzorem:
)
(
I
A
2
A
w
o
R
R
I
P
P
+
−
=
gdzie : P
o
– moc czynna odbiorników, I
A
– prąd wskazywany przez amperomierz, R
A
– rezystancja amperomierza, R
I
–rezystancja
cewki prądowej watomierza.
Aby wyznaczyć moc bierną należy z wykresu wektorowego wyznaczyć iloczyn U
o
sin
ϕ
0
U
o
sin
ϕ
0
=U
v
sin
ϕ
w
-I
A
(X
A
+X
I
)
gdzie X
I
– reaktancja cewki prądowej watomierza, X
A
- reaktancja cewki amperomierza
oraz
2
w
2
A
2
v
w
2
2
A
2
V
r
A
V
P
I
U
1
I
U
I
U
−
=
ϕ
−
=
ϕ
)
cos
(
sin
*
ostatecznie moc pozorna odbiornika
)
(
I
A
2
A
2
w
2
A
2
v
o
X
X
I
P
I
U
Q
+
−
−
=
Moc pozorną odbiornika możemy wyliczyć z zależności:
[
]
2
I
A
2
A
2
w
2
A
2
v
2
I
A
2
A
w
2
o
2
o
2
o
X
X
I
P
I
U
R
R
I
P
Q
P
S
+
−
−
+
+
−
=
+
=
)
(
)
(
47
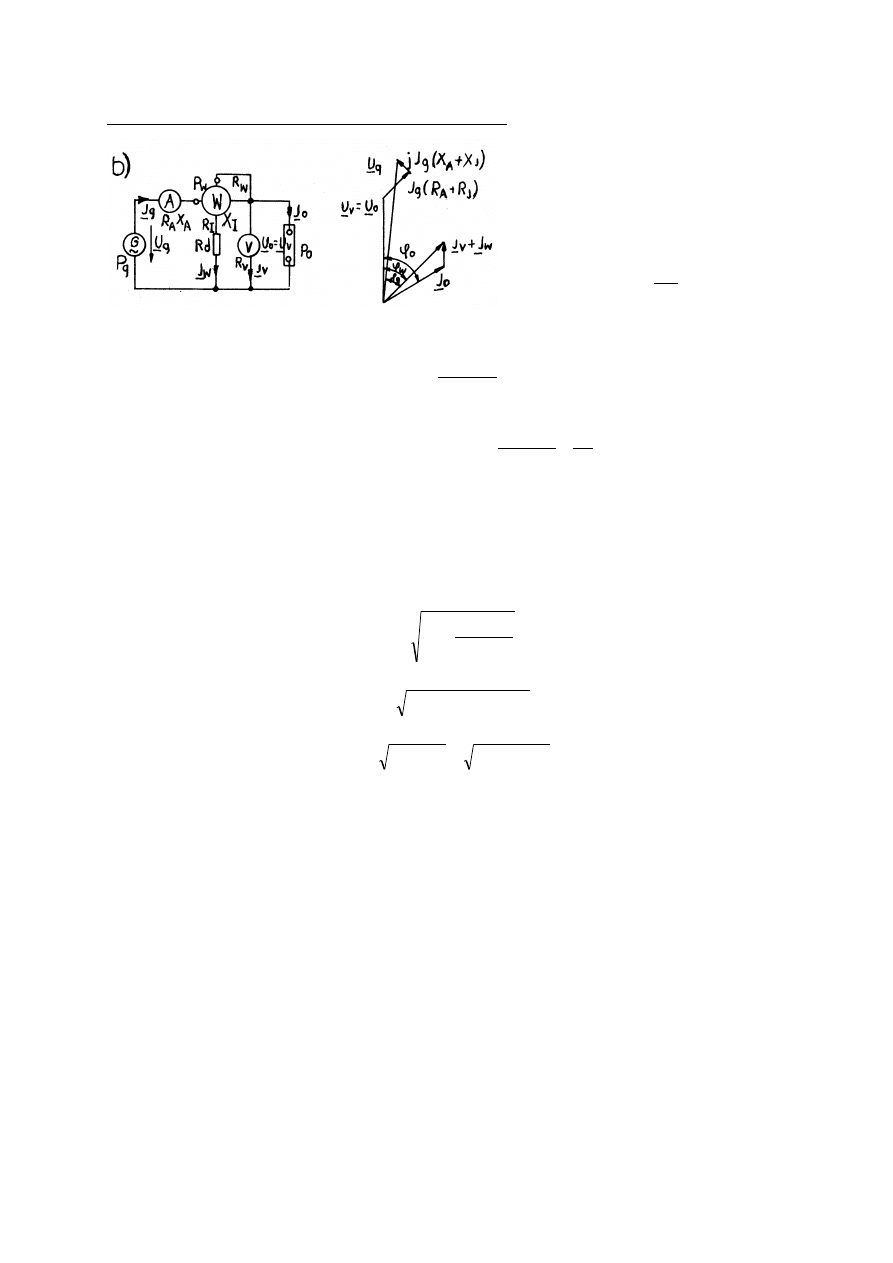
Układ pomiarowy przy „zadanym” napięciu odbiornika
W obwodzie tym mocz czynna
wskazywana przez watomierz
powiększona jest w stosunku do
mocy czynnej pobieranej przez
odbiornik o moc wydzieloną na
cewce woltomierza
v
2
v
V
R
U
P
=
oraz o moc wydzielona na
napięciowym obwodzie watomierza
d
w
2
v
w
R
R
U
P
V
+
=
Dlatego moc czynna odbiornika określa się wzorem:
+
+
−
=
−
−
=
v
d
w
2
v
w
v
w
w
o
R
1
R
R
1
U
P
P
P
P
P
V
Gdzie P
w
– wskazanie watomierza, U
v
wskazanie woltomierza, (R
w
+R
d
) rezystancja obwodu
napięciowego watomierza, R
v
– rezystancja woltomierza
W celu wyznaczenia mocy pozornej odbiornika należy wyznaczyć prąd odbiornika I
o
z
zależności odczytanej z wykresu wektorowego
0
w
v
o
2
w
v
2
o
2
A
I
I
I
I
I
I
I
ϕ
+
+
+
+
=
cos
)
(
)
(
Skąd po przekształceniach
2
v
2
o
2
w
2
A
o
U
P
P
I
I
−
−
=
Moc pozorną oblicza się z zależności
)
(
2
o
2
w
2
V
2
A
0
P
P
U
I
S
−
−
=
Moc pozorna natomiast obliczamy z zależności
2
w
2
v
2
A
2
o
2
o
o
P
U
I
P
S
Q
−
=
−
=
48
Document Outline
- METROLOGIA ELEKTRYCZNA I ELEKTRONICZNA
- 1. Wielkości i jednostki podstawowe w układzie SI.
- 2. Wzorce napięcia rezystancji i pojemności; budowa i właściwości
- 3. Podział i definicje błędów i niepewności pomiaru.
- 4. Błąd wskazania miernika elektromechanicznego.
- 5. Budowa i zasada działania miernika magnetoelektrycznego.
- 6. Wyprowadzić wzór na moment skręcający w mierniku magnetoelektrycznym.
- 7. Wpływ temperatury na wskazania mierników magnetoelektrycznych.
- 8. Zmiany zakresów pomiarowych amperomierzy i woltomierzy magnetoelektrycznych
- 9. Wyprowadzić wzór na moment skręcający w mierniku prostownikowym
- 10. Wpływ kształtu krzywej przebiegu mierzonego na wskazania miernika prostownikowego.
- 11. Budowa, zasada działania i właściwości mierników termoelektrycznych.
- 12. Budowa, zasada działania i właściwości mierników elektromagnetycznych.
- 13. Wyprowadzić wzory na moment skręcający mierników elektromagnetycznych przy prądzie stałym i zmiennym
- 14. Zmiany zakresów pomiarowych amperomierzy i woltomierzy elektromagnetycznych.
- 15. Wpływ częstotliwości i obcych pól magnetycznych na wskazania mierników elektromagnetycznych.
- 16. Budowa, zasada działania i właściwości mierników elektrodynamicznych.
- 17. Zmiany zakresów pomiarowych amperomierzy i woltomierzy elektrodynamicznych.
- 18. Wpływ czynników zewnętrznych na wskazania mierników elektrodynamicznych.
- 19. Budowa i zasada działania watomierza elektrodynamicznego.
- 20. Wyprowadzić wzór na moment skręcający w watomierzu elektrodynamicznym
- 21. Podać definicję stałej watomierza przy prądzie przemiennym, wyjaśnić pojęcie „ coszn” watomierza.
- 22. Wyprowadzić wzór na błąd „od kąta ” w watomierzu elektrodynamicznym
- 23. Zmiany zakresów pomiarowych watomierza elektrodynamicznego.
- 24. Pomiar mocy czynnej przebiegów odkształconych watomierzem elektrodynamicznym
- 25. Wpływ częstotliwości na wskazania watomierza elektrodynamicznego.
- 26. Budowa i zasada działania galwanometru statycznego.
- 27. Wyprowadzić wzór na moment hamujący – cewkowy w galwanometrze statycznym
- 28. Definicje, wzory i przykładowe wartości wielkości charakteryzujących galwanometr statyczny.
- 29. Warunki rezonansu galwanometru wibracyjnego
- 30. Narysować krzywą rezonansu i zdefiniować szerokość rezonansu w galwanometrze wibracyjnym.
- 31. Narysować schemat blokowy, opisać zasadę działania i wyprowadzić wzór na Nx w woltomierzu cyfrowym o przetwarzaniu impulsowo-czasowym.
- 32. Narysować schemat blokowy, opisać zasadę działania i wyprowadzić wzór na Nx w woltomierzu cyfrowym z podwójnym całkowaniem
- 33. Narysować schemat blokowy, opisać zasadę działania i wyprowadzić wzór na Nx w woltomierzu cyfrowym przetwarzającym napięcie w częstotliwość
- 34. Narysować schemat blokowy i opisać zasadę działania woltomierza kompensacyjnego.
- 35. Opisać kompensację napięcia 10,5V w woltomierzukompensacyjnym o kompensacji wagowej o wagach 23, 22, 21, 20
- 36. Zasada działania woltomierzy cyfrowych napięcia przemiennego.
- 37. Narysować schemat woltomierza cyfrowego napięcia przemiennego z kompensacją wartości skutecznej.
- 38. Klasy dokładności i dokładność pomiaru woltomierzami cyfrowymi.
- 39. Wyjaśnić powstawanie błędu zliczania.
- 40. Cyfrowy pomiar rezystancji. Narysować schemat blokowy i podać odpowiednie wzory dla jednego z cyfrowych mierników rezystancji.
- 41. Zasada działania kompensatorów o regulowanej rezystancji.
- 42. Dekada podwójna Feussnera
- 43. Zasada działania kompensatora o regulowanym prądzie.
- 44. Komparator termoelektryczny.
- 46. Warunki pełnej kompensacji w kompensatorach prądu przemiennego.
- 45. Komparator momentów.
- 46. Warunki pełnej kompensacji w kompensatorach prądu przemiennego.
- 47. Zasada działania kompensatora prądu przemiennego o współrzędnych biegunowych.
- 48. Zasada działania kompensatora o współrzędznych prostokątnych.
- 49. Budowa i zasada działania przekładnika prądowego (napięciowego)
- 50. Podać definicje przekładni zwojowej, rzeczywistej i znamionowej przekładnika prądowego (napięciowego)
- 51. Wyjaśnić pojęcie poprawki zwojowej.
- 52. Podać definicje błędów przekładnika prądowego oraz ich związek z klasą przekładnika (napięciowego)
- 54. Skutki rozwarcia obwodu wtórnego przekładnika prądowego.
- 55. Zasada dziłania i właściwości przekładnika LEM
- 56. Narysować schemat układu do pomiaru natężenia prądu (napięcia) przy użyciu przekładnika, podać wzory na wielkość mierzoną i błąd pomiaru
- 57. Zasada działania watomierza hallotronowego.
- 58. Pomiar mocy układu jednofazowego przy poprawnie mierzonym prądzie (napięciu), podać wzory na P,Q,S i błędy metody pomiaru
Wyszukiwarka
Podobne podstrony:
5 Podstawy Metrologii systemy pomiarowe
metrologia
kuran,Metrologia wielkosci geom Nieznany
oscyloskop metrologia cw6
Metrologia Elektryczna i Elektroniczna wykład 2
Podstawy Metrologii
Zadanie z pasowania otwarte, PWR Politechnika Wrocławska, podstawy metrologii, Wykłady 2011
1.10spis treci do cigi z metro, POLITECHNIKA (Łódzka), Metrologia, 1semestr
Program-3, Studia, Metrologia
ściąga metrologia (2), PWR mbm, Podstawy metrologii
MIERNIK ELEKTRODYNAMICZNY, Studia, Metrologia
Program-4, Studia, Metrologia
SPRAWOZDANIE NR 1, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 1
metrologia - błędy kształtu, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
Metrologia sciaga, Politechnika, Metrologia
LABMETS1, AGH IMIR Mechanika i budowa maszyn, II ROK, Metrologia Tyka Haduch, Metrologia, Metrologia
więcej podobnych podstron