
POLITECHNIKA WARSZAWSKA
WIECZOROWE STUDIA ZAWODOWE
RADIOKOMUNIKACJA I TECHNIKI MULTIMEDIALNE
Preskrypt wykładu
PODSTAWY METROLOGII
Wydanie 3 poprawione
Opracował: dr inż. Jerzy Olędzki
Warszawa 2003

2
Wykład 1
Wstęp do pomiarów
Wielkość, jednostka, wartość, system wielkości, system jednostek. O błędzie pomiaru i narzę-
dziach pomiarowych. O sygnałach i ich przetwarzaniu. Typowe elektryczne przyrządy pomia-
rowe.
Pojęcia podstawowe metrologii
Pomiar to doświadczenie, którego celem jest wyznaczenie pewnej liczby, zwanej war-
tością liczbową wielkości albo miarą wielkości. Tak jak liczność jest abstrakcyjną cechą
zbioru; tak wielkość jest abstrakcyjną cechą obiektów określonej kategorii, np. długość jest
cechą odcinków, masa jest cechą przedmiotów materialnych. Wartość liczbowa wielkości od-
noszącej się do wybranego obiektu jest liczbą równą stosunkowi tej wielkości do wielkości
przyjętej jako jednostka miary. Pomiar polega na porównywaniu pod względem mierzonej
wielkości badanego obiektu z obiektami o znanych wartościach tej wielkości, czyli wzorcami,
tak jak przy pomiarze długości linijką lub ważeniu za pomocą wagi dźwigniowej i odważni-
ków. Liczność jest cechą daną w sposób naturalny. Wielkość musi być najpierw
zdefiniowana, a mierzyć ją można dopiero po przyjęciu jednostki miary.
Metrologia jest nauką o pomiarach. Nazwa metrologia pochodzi od greckich słów
µετρον
–
miara i
λογος
– słowo, nauka. Zamiast metrologia używa się także nazwy miernictwo, od cza-
sownika mierzyć czyli wykonywać pomiary.
Wielkość (niekiedy opatruje się ją przymiotnikiem mierzalna) jest cechą zjawiska, ciała lub
substancji, którą można rozróżniać jakościowo i określać ilościowo. Przykłady wielkości: dłu-
gość – cecha odcinków, masa – cecha przedmiotów, ładunek elektryczny – cecha
przedmiotów naładowanych elektrycznie.
Wartość wielkości jest wyrażeniem ilościowym przejawu wielkości zwykle jako iloczynu
liczby (zwanej wartością liczbową wielkości) i jednostki miary wielkości. Tak określoną
wartość nazywa się także wartością mianowaną.
Jednostka miary wielkości jest określonym, umownie przyjętym przejawem wielkości, z któ-
rym porównuje się inne przejawy tej wielkości, w celu ich ilościowego wyrażenia w stosunku
do tego przejawu. Jednostce miary przyporządkowuje się wartość liczbową jeden.

3
O błędzie pomiaru i narzędziach pomiarowych
Nieodłączną cechą pomiaru jest jego niedokładność, co oznacza, że wartość zmierzona
~
x
(otrzymana w wyniku pomiaru) różni się na ogół od wartości prawdziwej x& wielkości mie-
rzonej. Miarą niedokładności pomiaru są błędy pomiaru: prawdziwy błąd pomiaru i graniczny
błąd pomiaru
.
Pomiary wykonuje się za pomocą narzędzi. Narzędzia charakterystyczne dla
pomiarów nazywają się narzędziami pomiarowymi. Do narzędzi pomiarowych należą: wzorce
miar
, przyrządy pomiarowe i przetworniki pomiarowe.
Wzorzec miary
jest narzędziem, substancją lub zjawiskiem fizycznym odtwarzającym,
w granicach określonej niedokładności, przejaw wielkości o określonej wartości. O wzorcu
miary (wielkości) mówi się, że odtwarza określoną wartość wielkości. Wzorzec jest wzorcem
jednomiarowym
, jeżeli odtwarza jedną tylko wartość wielkości i wzorcem wielomiarowym,
jeżeli odtwarza wiele wartości wielkości. Deklarowana wartość wielkości, którą odtwarza
wzorzec nazywa się wartością nominalną wzorca lub wskazaniem wzorca.
Przykład 1
(a)
Międzynarodowy prototyp metra przechowywany w Międzynarodowym Biurze Miar (BIPM) w Sèvres pod
Paryżem i wyskalowana linijka są wzorcami miar długości.
(b)
Międzynarodowy prototyp kilograma przechowywany w Międzynarodowym Biurze Miar (BIPM) w Sèvres
pod Paryżem i odważniki są wzorcami miary masy.
(c)
Opornik wzorcowy, kondensator wzorcowy, ogniwo wzorcowe są wzorcami miar wielkości elektrycznych.
(d)
Stałe punkty termometryczne Międzynarodowej Praktycznej Skali Temperatur są wzorcami temperatury.
Przyrząd pomiarowy
jest narzędziem pomiarowym przeznaczonym do wykonywania
pomiarów, samodzielnie lub w połączeniu z innymi urządzeniami, z udziałem lub bez udziału
człowieka, tworzącym zamkniętą całość konstrukcyjną. Najpopularniejszy przyrząd pomia-
rowy to przyrząd pomiarowy wskazujący czyli miernik, tj. przyrząd formujący sygnał przeno-
szący odczytywalną przez człowieka informację o wartości wielkości mierzonej. Sygnał for-
mowany przez miernik nazywa się wskazaniem miernika, a część miernika formująca wskaza-
nie – urządzeniem wskazującym. Nazwy mierników tworzy się przez dodanie końcówki -
omierz
do nazwy wielkości mierzonej (np. długościomierz, częstościomierz) lub do nazwy
jednostki mierzonej wielkości (np. amperomierz, woltomierz, sekundomierz).
Wskazanie miernika jest analogowe, jeżeli ma postać przesunięcia wskazówki wzdłuż
skali pomiarowej, przesunięcie wskazówki mierzy się porównując je ze wskazami (kreskami)
tworzącymi skalę, tak jak przy pomiarze długości wyskalowaną linijką, z tym, że linijka jest
4
wyskalowana w jednostkach długości, skala miernika zaś w jednostkach wielkości mierzonej.
Wskazanie jest cyfrowe, jeżeli ma postać ciągu wyświetlanych cyfr, reprezentujących wartość
liczbową wielkości mierzonej. Miernik o wskazaniu analogowym nazywa się miernikiem ana-
logowym
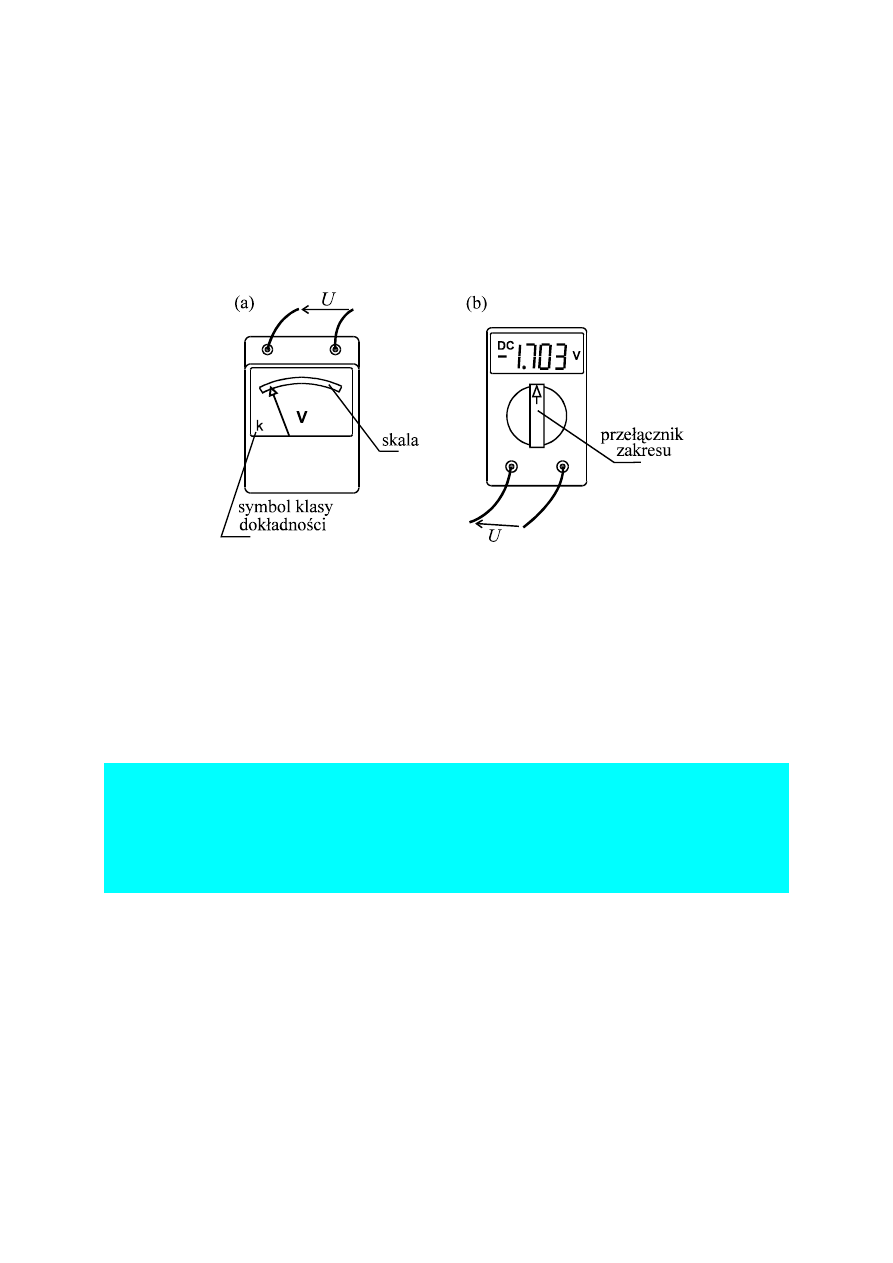
, miernik o wskazaniu cyfrowym – miernikiem cyfrowym. Na rys.1 schematycznie
pokazano widok woltomierza analogowego i woltomierza cyfrowego.
Rys.1. Woltomierz analogowy (a) i cyfrowy (b)
Miernik analogowy może mieć wskazanie analogowo-ciągłe, tzn. jego wskazówka, przy cią-
głych zmianach wielkości mierzonej, porusza się ruchem ciągłym, lub analogowo-dyskretne,
tzn. jego wskazówka, przy ciągłych zmianach wielkości mierzonej, porusza się ruchem
skokowym.
Przykład 2
(a)
Amperomierz magnetoelektryczny, termometr rtęciowy (wskazówką termometru rtęciowego jest koniec
słupa rtęci) i waga sprężynowa są miernikami analogowymi.
(b)
Zegar mechaniczny i kwarcowy są miernikami analogowo-dyskretnymi.
(c)
Woltomierz cyfrowy i częstościomierz cyfrowy są miernikami cyfrowymi.
Miernik wielkości x wskazuje wartość ~
x
tej wielkości (jest to wartość zmierzona lub
wskazanie miernika). Charakterystycznym dla miernika jest jego zakres pomiarowy
[X
min
, X
max
], tzn. przedział, wewnątrz którego mieści się wskazanie ~
x
miernika. Różnica gór-
nej granicy X
max
i dolnej granicy X
min
zakresu pomiarowego
X
X
X
mm
=
−
max
min
(1)
nazywa się długością zakresu pomiarowego i jest ważnym parametrem miernika. Zwykle za-
kres pomiarowy zaczyna się od zera [0, X
max
], długość takiego zakresu pomiarowego, równa

5
górnej granicy zakresu pomiarowego X
mm
= X
max
, jest nazywana wprost zakresem pomiaro-
wym, a zakres miernika określa się podając tylko X
max
. Dla mierników cyfrowych zakres po-
miarowy, zwykle zaczynający się od zera jest określony liczbą cyfr i wartością jednostki
ostatniego rzędu q czyli tzw. cyfrą. Wartość jednostki ostatniego rzędu q (zwana także
wartością cyfry, kwantem, czułością lub LSB od ang. least significant bit) jest podawana w
jednostkach wielkości mierzonej, równa się ona prawie zawsze dziesiętnej podwielokrotności
jednostki wielkości mierzonej. Zakres miernika cyfrowego może być podawany jako zakres
wielkości mierzonej [0, X
max
), częściej nawet jako X
max
, lub zakres wskazań cyfrowych [0,
N
max
), częściej nawet jako N
max
, przy czym zachodzi
X
N
q
max
max
=
(2)
a N
max
jest zwiększoną o jeden największą liczbą (nie uwzględniając przecinka, który wyzna-
cza wartość kwantu q) wskazywaną przez miernik. Stosuje się nazwy:
•
miernik M cyfrowy czyli miernik o M cyfrach mogących przyjmować wartości 0,1,...,9 każda;
dla takiego miernika N
max
= 10
M
,
•
miernik M i
1
/
2
cyfrowy czyli miernik o M cyfrach mogących przyjmować wartości 0,1,...,9
każda, i pierwszej mogącej przyjmować wartości 0 i 1; dla takiego miernika N
max
= 2
⋅
10
M
,
•
miernik M i 3/4 cyfrowy czyli miernik o M cyfrach mogących przyjmować wartości 0,1,...,9
każda, i pierwszej mogącej przyjmować wartości 0,1,2,4; dla takiego miernika N
max
= 5
⋅
10
M
.
Każdy miernik z natury jest niedokładny, wskazanie miernika x
~ różni się od wartości
prawdziwej x& wielkości mierzonej.
O sygnałach i ich przetwarzaniu
Sygnałem pomiarowym
będziemy nazywali sygnał przenoszący informację o wartości
wielkości mierzonej (ogólnie o tzw. mezurandzie) lub informację innego rodzaju niezbędną
dla realizacji pomiaru. Sygnał pomiarowy ma trzy elementy:
•
treść sygnału
czyli informację (wiadomość) przenoszoną przez sygnał,
•
nośnik sygnału
czyli zjawisko przenoszące treść sygnału, nośnik jest często utożsamiany z
wielkościami modelującymi zjawisko przenoszące informację, wielkości te są nazywane
wielkościami nośnymi
lub wprost nośnikami,

6
•
kod sygnału
czyli zależność między treścią a nośnikiem, zwykle kod ma postać zależności
między treścią a wartością nośnika, którą może być wartość wielkości nośnej, parametr roz-
kładu wielkości nośnej lub inna reprezentacja nośnika.
Treści sygnałów pomiarowych albo są liczbami rzeczywistymi, albo są sprowadzalne do liczb
rzeczywistych. W praktyce treść sygnału jest nazywana wprost sygnałem, a przez wartość
sygnału
rozumie się wartość treści sygnału.
Niektóre sygnały pomiarowe mają tę właściwość, że ich treści mogą być wyznaczone
przez człowieka za pomocą jego zmysłu wzroku. Sygnały te są nazywane sygnałami wizual-
nymi
lub wskazaniami, jeżeli są formowane przez przyrządy pomiarowe.
Szczególny rodzaj sygnału pomiarowego, tzw. sygnał naturalny, ma nośnik w postaci
pojedynczej wielkości fizycznej, treścią sygnału są zaś wartości liczbowe tej wielkości.
Jednym z sygnałów naturalnych jest wielkość mierzona. Bardziej złożoną postać mają
sygnały modulowane
, w których treść sygnału jest przenoszona przez parametr rozkładu
czasowego wielkości nośnej. Osobną grupę stanowią sygnały losowe, których nośniki są
modelowane procesami stochastycznymi, a treść jest przenoszona przez charakterystyki
probabilistyczne nośników.
Zależnie od natury fizycznej nośnika rozróżnia się sygnały elektryczne, optyczne, me-
chaniczne itp. Szczególne znaczenie, ze względu na łatwość formowania, kształtowania i
przesyłania mają sygnały elektryczne, chociaż można już obserwować wzrastające znaczenie
sygnałów optycznych przesyłanych światłowodami.
Przykład 3
(a)
Napięcie z ogniwa termoelektrycznego platyna - platyna-rod jest sygnałem prostym, wartości napięcia są
zależne od treści sygnału - różnicy temperatur złącza roboczego i złącza odniesienia.
(b)
Wskazanie przyrządu pomiarowego analogowego lub cyfrowego jest sygnałem wizualnym.
(c)
Sygnał o nośniku sinusoidalnie zmiennym x(t)
=
sin (2
π
f
+
ϕ
), w którym treść jest przenoszona przez
amplitudę A lub częstotliwość f lub fazę początkową
ϕ
jest sygnałem modulowanym amplitudowo lub czę-
stotliwościowo lub fazowo.
Wśród sygnałów pomiarowych wyróżnia się dwie grupy sygnałów: sygnały
analogowe i sygnały cyfrowe.
Sygnał analogowy jest to sygnał pomiarowy, którego treściami są liczby rzeczywiste,
a kod sygnału, tzn. zależność treści od nośników ma postać funkcji wartości lub parametrów
rozkładu czasowego wielkości nośnych. Wśród sygnałów analogowych rozróżnia się sygnały
analogowo-ciągłe
(zwane często wprost sygnałami analogowymi), których treści mogą przyj-
mować dowolne wartości z pewnego przedziału liczb rzeczywistych i sygnały analogowo-

7
dyskretne
(zwane także sygnałami kwantowymi), których treściami są tylko niektóre wartości
z pewnego przedziału liczb rzeczywistych. Kod sygnału analogowego, czyli zależność C
wartości treści x sygnału od wartości chwilowej u nośnika lub wartości chwilowych nośników
u
1
, u
2
,..., u
L
ma ogólną postać
)
,...,
,
(
lub
)
(
L
2
1
u
u
u
C
x
u
C
x
=
=
(3)
Dla sygnału naturalnego kod jest identycznością. Wygodniej jest jednak przedstawiać kod
jako
=
=
=
=
=
)
,...,
,
(
lub
)
(
nawet
a
,
zwykle
),
(
L
2
1
u
u
u
F
U
u
F
U
U
x
U
K
x
U
f
x
(4)
Gdzie f() – funkcja rzeczywista,
K
– współczynnik proporcjonalności,
U
– parametr nośnika (nośników) przenoszący treść sygnału,
F
() – operator określający parametr.
Parametrem kodu może być amplituda lub częstotliwość nośnika harmonicznego, wartość
skuteczna nośnika okresowo zmiennego itp. Dla sygnałów analogowo-ciągłych x jest zmienną
ciągłą (może przyjmować dowolne wartości), dla sygnału analogowo-dyskretnego – zmienną
dyskretną.
Przykład 4
(a)
Wielkość, której wartość jest przedmiotem pomiaru (czyli tzw. mezurandem), napięcie z ogniwa
termoelektrycznego jako sygnał o różnicy temperatur i wskazanie analogowego przyrządu pomiarowego są
sygnałami analogowo-ciągłymi.
(b)
Wskazanie zegarka mechanicznego i zegarka cyfrowego ze wskazaniem analogowym oraz sygnał wyj-
ściowy przetwornika cyfrowo-analogowego sygnału cyfrowego w napięcie są sygnałami analogowo-dys-
kretnymi.
Sygnał cyfrowy jest to sygnał pomiarowy, w którym treściami są liczby rzeczywiste
przedstawione w zapisie cyfrowym, a nośniki sygnału kodują poszczególne cyfry oddzielnie.
Zależnie od podstawy systemu zapisu liczby rozróżnia się sygnały jedynkowe czyli unitarne
1
,
sygnały dwójkowe
czyli binarne, sygnały dziesiętne czyli dekadowe, sygnały szesnastkowe
czyli heksadecymalne itd. Cyfry zapisu dziesiętnego mogą być kodowane w systemie
dwójkowym, co prowadzi do sygnału dwójkowo-dziesiętnego. Cyfry zapisu szesnastkowego
są zawsze kodowane w systemie dwójkowym.
1
Zapis jedynkowy, historycznie pierwszy system zapisu, operuje cyfrą o jednej wartości 1 i zapisuje liczbę
k jako ciąg k jedynek. Pierwowzorem zapisu jedynkowego był system nacięć na kiju. Elektryczny sygnał
w kodzie jedynkowym ma postać paczek impulsów, każda paczka sygnalizuje liczbę liczbą impulsów w paczce.

8
Szczególne znaczenie mają sygnały zero-jedynkowe czyli dwustanowe, najczęściej
o naturze elektrycznej. Sygnał zero-jedynkowy jest zbiorem sygnałów elementarnych (np.
napięć elektrycznych), z których każdy może przyjmować jeden z dwóch dopuszczalnych
stanów (np. napięcie bliskie zeru i napięcie bliskie wartości 5 V) umownie oznaczanych jako
„0” i „1” czyli tzw. „zero logiczne” i „jedynka logiczna”. Pojedynczy sygnał elementarny w
jego aspekcie informacyjnym jest nazywany bitem, sygnał zero-jedynkowy złożony z M
sygnałów elementarnych jest sygnałem M-bitowym. Wartością nośnika sygnału zero-
jedynkowego M bitowego jest ciąg zero-jedynkowy uporządkowany od bitu najmniej
znaczącego{a
0
, a
1
,..., a
M-2
, a
M-1
} lub uporządkowany od bitu najbardziej znaczącego
{b
1
, b
2
,..., b
M-1
, b
M
}, gdzie poszczególne bity am i bj mogą przyjmować wartości „0” lub „1”,
przy czym wygodnie jest utożsamiać „zero logiczne” z liczbą 0, a „jedynkę logiczną” z
liczbą 1. Sygnał M bitowy ma 2
M
różnych wartości nośnika - ciągów zero-jedynkowych. Kod
sygnału jest przyporządkowaniem liczb, stanowiących treści sygnału, ciągom zero-
jedynkowym, stanowiącym wartości nośnika sygnału. Jeżeli treścią sygnału jest liczba
naturalna k zapisana w systemie dwójkowym, to kod takiego najprostszego sygnału, zwanego
sygnałem dwójkowym w kodzie naturalnym
, można przedstawić jako
k
a
b
m
m
M
m
M
j
j
j
M
=
=
=
−
−
=
∑
∑
0
1
1
2
2
2
(5)
Sygnał dwójkowo-dziesiętny
, kodujący liczbę całkowitą k zapisaną ciągiem K cyfr
dziesiętnych d
M-1
, d
M-2
,..., d
1
, d
0
, jest sygnałem M = 4 K bitowym z bitami uporządkowanymi
w czwórki (zwane dekadami), z których każda koduje dwójkowo jedną cyfrę dziesiętną.
Rozróżnia się sygnały cyfrowe równoległe, w których poszczególne cyfry (lub bity)
przenoszone przez oddzielne nośniki (rozdział w przestrzeni), i sygnały cyfrowe szeregowe, w
których poszczególne cyfry (lub bity) przenoszone są w sekwencji czasowej przez jeden
nośnik (rozdział w czasie).
Zależnie od związków treści sygnału z czasem rozróżnia się sygnały pomiarowe ciągłe
w czasie i sygnały dyskretne w czasie. Sygnał ciągły w czasie jest to sygnał pomiarowy, któ-
rego nośniki są modelowane funkcjami czasu ciągłego, a treść sygnału jest określona dla każ-
dej chwili czasu. Sygnał dyskretny w czasie jest to sygnał pomiarowy, którego treść jest okre-
ślona dla wybranych chwil czasu.
Zależność treści x
sygnału ciągłego od czasu t modeluje się ciągłą funkcją czasu
x
t
=
f ( )
(6)

9
przy czym t jest zmienną rzeczywistą ciągłą i stąd mówi się o czasie ciągłym. Sygnał ciągły w
czasie może więc jednoznacznie odtwarzać treść o postaci funkcji rzeczywistej argumentu
rzeczywistego ciągłego.
Zależność treści x
sygnału dyskretnego od czasu modeluje się zwykle funkcją czasu
dyskretnego, tzn. przedstawia się ją w postaci ciągu { x(i) | i
∈
N } treści sygnału indeksowa-
nych numerem i (gdzie N – zbiór liczb całkowitych) kolejnych treści, zwanym czasem
dyskretnym.
Konstruuje się także modele sygnału dyskretnego w czasie przyjmując jako argument
czas ciągły. Modele takie oddają sposób przekazywania sygnału w czasie rzeczywistym. Z
tego punktu widzenia rozróżnić można dwie skrajne postaci sygnału dyskretnego:
•
sygnał impulsowy modelowany ciągiem wąskich impulsów w chwilach czasu ti o wysoko-
ściach równych kolejnym treściom x(i), zwykle impulsom tym nadaje się postać impulsów
Diraca
∑
∞
−∞
=
−
=
i
i
t
t
i
x
t
x
)
(
)
(
)
(
δ
(7)
gdzie
δ
(
)
t
t
i
−
- impuls d-Diraca w chwili
t
t
i
=
.
•
sygnał z „pamięcią” modelowany funkcją schodkową
[
)
x t
x i
t
t t
i
i
( )
( )
,
=
∈
+
dla
1
(8)
Obydwa typy sygnałów dyskretnych mają ten sam model w dziedzinie czasu ciągłego. Chwile
ti, nazywane chwilami próbkowania, są zwykle równoodległe od siebie, czas t między sąsied-
nimi chwilami próbkowania nazywa się czasem lub okresem próbkowania (lub repetycji) a
jego odwrotność częstotliwością próbkowania (lub repetycji). Chwile próbkowania są zwykle
wyznaczane przez dodatkową składową sygnału, zwaną sygnałem taktującym.
Sygnały analogowe mogą być ciągłe i dyskretne w czasie. Sygnały cyfrowe są prawie
zawsze sygnałami dyskretnymi w czasie z pamięcią.
Typowe elektryczne przyrządy pomiarowe
Typowymi przyrządami do pomiarów w obwodach prądu stałego są:
•
amperomierz czyli przyrząd do pomiaru natężenia prądu (zwykle zamiast nazwy natężenie
prądu używa się nazwy skróconej – prąd),
•
woltomierz czyli przyrząd do pomiaru napięcia,
•
omomierz czyli przyrząd do pomiaru rezystancji.
Typowymi przyrządami do pomiarów w obwodach prądu okresowo zmiennego są:
10
•
amperomierz czyli przyrząd do pomiaru prądu, prawie wyłącznie stosowane są amperomierze
mierzące wartość skuteczną prądu,
•
woltomierz czyli przyrząd do pomiaru napięcia, prawie wyłącznie stosowane są
woltomierze mierzące wartość skuteczną napięcia,
•
watomierz czyli przyrząd do pomiaru mocy czynnej, a ściślej wartości średniej okresowej
iloczynu napięcia i prądu,
•
częstościomierz czyli przyrząd do pomiaru częstotliwości napięcia okresowo zmiennego.
Oprócz wyżej wymienionych jako typowy przyrząd pomiarowy elektryczny można uznać
•
oscyloskop, zwany także oscylografem, czyli przyrząd odwzorowujący rozkład czasowy na-
pięcia krzywą narysowaną na ekranie.
Do końca lat sześćdziesiątych każdy z wymienionych ośmiu przyrządów był w zasadzie
budowany jako oddzielny przyrząd, obecnie przeważnie buduje się tzw.
•
multimetry czyli przyrządy łączące wiele funkcji, zawsze amperomierza i woltomierza
prądu stałego i zmiennego, omomierza i częstościomierza.
Amperomierz, jako przyrząd mierzący prąd, włącza się szeregowo w obwód badany
"przepuszczając" przez amperomierz mierzony prąd i (rys.2a). Amperomierz prądu stałego
mierzy wartość chwilową (stałą w czasie) prądu i (zwykle oznacza się ją symbolem I). Więk-
szość amperomierzy prądu okresowo zmiennego mierzy wartość skuteczną prądu I
rms
(zwykle
oznacza się ją także symbolem I, skrót "rms" pochodzi z ang.
root mean square value – pier-
wiastek z wartości średnio kwadratowej)
∫
−
=
=
t
T
t
t
i
T
I
I
d
rms
2
1
(9)
gdzie T – okres zmienności prądu.
Amperomierz jest dwójnikiem, dla prądu stałego opisuje się go rezystancją R
A
, dla prądu
zmiennego impedancją Z
A
(posiadającą zresztą zwykle przeważającą składową
rezystancyjną). Włączenie amperomierza do obwodu badanego zmienia wartość mierzonego
prądu i, stąd też od amperomierza wymaga się bardzo małej rezystancji (impedancji).

11
Rys.2. Włączanie mierników: (a) amperomierza, (b) woltomierza, (c) omomierza.
Woltomierz, jako przyrząd mierzący napięcie, włącza się równolegle do badanego
dwójnika "przykładając" do woltomierza mierzone napięcie u (rys.2b). Woltomierz prądu
stałego mierzy wartość chwilową (stałą w czasie) napięcia u (zwykle oznacza się ją symbolem U).
Większość woltomierzy prądu okresowo zmiennego mierzy wartość skuteczną napięcia Urms
(zwykle oznacza się ją także symbolem U
∫
−
=
=
t
T
t
t
u
T
U
U
d
rms
2
1
(10)
gdzie T – okres zmienności napięcia.
Woltomierz jest dwójnikiem, dla prądu stałego opisuje się go rezystancją R
V
, dla prądu
zmiennego impedancją Z
V
(zwykle modeluje się ją równolegle połączoną rezystancją R
V
i
pojemnością C
V
). Włączenie woltomierza do obwodu badanego zmienia wartość mierzonego
napięcia u, stąd też od woltomierza wymaga się bardzo dużej rezystancji i małej pojemności.
Amperomierze i woltomierze analogowe prądu stałego wymagają zwykle
odpowiedniej polaryzacji włączanego prądu i napięcia. Amperomierze i woltomierze cyfrowe
prądu stałego wskazują wartość wielkości mierzonej i jej polaryzację. Dla amperomierzy i
woltomierzy prądu zmiennego kierunek włączonego prądu i napięcia nie wpływa na
wskazanie miernika.
Omomierz, w odróżnieniu od amperomierza i woltomierza, jest dwójnikiem aktyw-
nym. Sposób przyłączania omomierza pokazano na rys.2c.
Watomierz, w odróżnieniu od amperomierza i woltomierza, jest czwórnikiem, ma
dwa obwody wejściowe: napięciowy i prądowy. Watomierz mierzy wartość średnią okresową
iloczynu napięcia u
WU
obwodu napięciowego watomierza i prądu i
WI
obwodu prądowego
∫
−
=
t
T
t
t
i
u
T
P
d
WI
WU
W
1
(11)
gdzie: P
W
– wskazanie watomierza, T – okres napięcia i prądu.
A
(b)
(c)
(a)
12
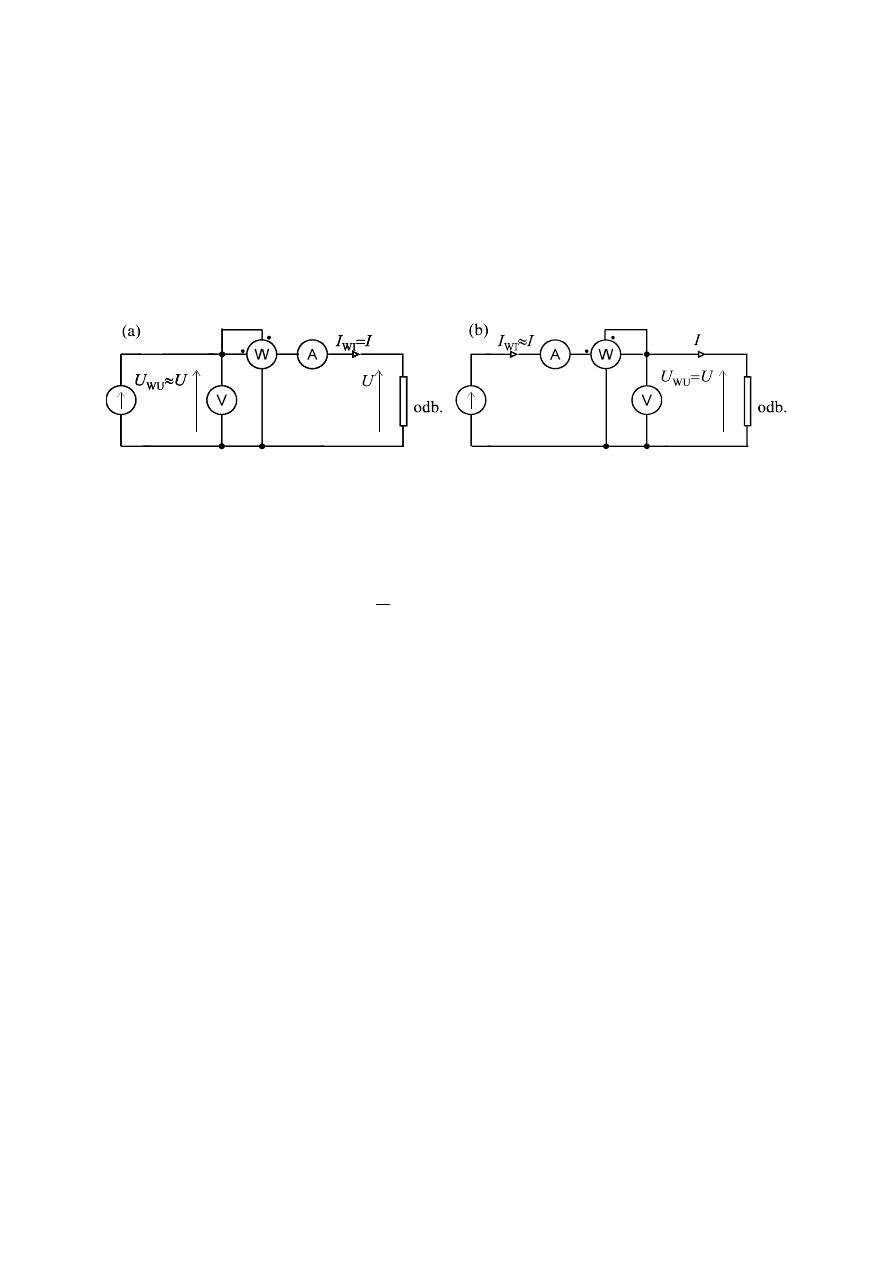
Aby watomierz mierzył moc czynną wydzielaną w dwójniku o napięciu u i prądzie i, włącza
się go obwodem napięciowym równolegle i obwodem prądowym szeregowo do badanego
dwójnika (rys.3). Możliwe są dwa układy połączeń: układ, w którym prądy watomierza i
odbiornika są równe (rys.3a) i układ, w którym napięcia watomierza i odbiornika są równe
(rys.3b). Zaniedbując nierówność napięć w układzie równo-prądowym i nierówność prądów
w układzie równo-napięciowym mamy
Rys.3. Dwa sposoby włączania watomierza przy pomiarze mocy odbiornika:
(a) równo-prądowy, (b) równo-napięciowy.
P
t
i
u
T
P
t
T
t
=
=
∫
−
d
W
1
(12)
a w szczególnym przypadku prądu harmonicznego
ϕ
cos
I
U
P
P
=
=
W
(13)
gdzie
ϕ
– przesunięcie fazowe między napięciem i prądem.
Przy
ϕ
=
±
1
/
2
π
wskazanie watomierza będzie zerowe przy niezerowym napięciu i prądzie;
stąd też, jeżeli obwody watomierza nie mają zabezpieczenia przed przeciążeniem, wskazane
jest włączanie do obwodu pomiarowego watomierza także woltomierza i amperomierza, jak
na rys3. Przy
ϕ
<
–
1
/
2
π
i
ϕ
>
1
/
2
π
wskazanie watomierza będzie ujemne (wskazówka
watomierza analogowego odchyla się w przeciwną stronę względem skali), w takim
przypadku należy zmienić kierunek prądu i
WI
obwodu prądowego watomierza albo kierunek
napięcia u
WU
obwodu napięciowego i wskazanie watomierza przyjmować jako ujemne.
Watomierz ma wyróżniony zacisk (kropka na rys.3) w obwodzie prądowym i napięciowym,
jeżeli przesunięcie fazowe między prądem wpływającym do wyróżnionego zacisku i
napięciem skierowanym do wyróżnionego zacisku spełnia
ϕ≤
1/2
π,
to wskazanie
watomierza jest dodatnie.
Częstościomierz włącza się do obwodu tak jak woltomierz.
13
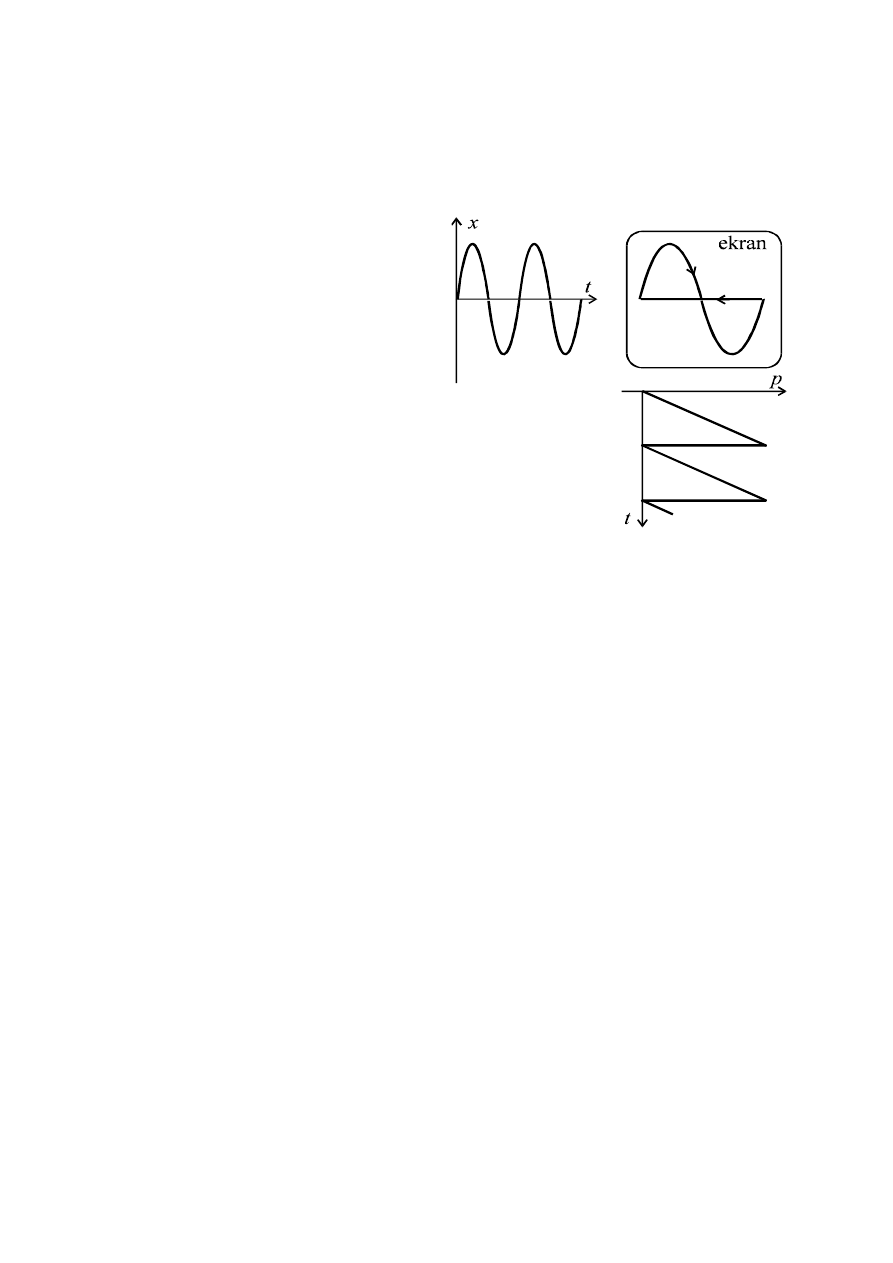
Oscyloskop, zwany także oscylografem, w swojej pierwotnej wersji był przyrządem
do obserwacji krzywej wykresu funkcji x(t) opisującej rozkład czasowy wielkości x okresowo
zmiennej. Urządzeniem wskazującym oscyloskopu jest ekran z ruchomą plamką świetlną.
Ruch plamki ma dwa stopnie swobody w
dwóch osiach prostokątnego układu
współrzędnych. Ruch w osi pionowej jest ste-
rowany wielkością x, ruch w osi poziomej –
specjalnie uformowaną wielkością okresową
p o piłozębnym rozkładzie czasowym (rys.4),
zwaną podstawą czasu. Jeżeli okres podstawy
czasu jest K-wielokrotnością okresu wielkości
obserwowanej, to na ekranie, wskutek nakła-
dania się ruchu plamki świetlnej, powstaje
obraz K okresów krzywej x(t). Okres pod-
stawy czasu jest dobierany przez mierzącego,
proces tego doboru nazywa się synchroniza-
cją. Tak właśnie działa oscyloskop kato-
dowy, zwany także oscyloskopem analo-
gowym.
Rys. 4. Powstawanie obrazu krzywej x(t) na ekranie
oscyloskopu (x okresowo zmienne).
Oscyloskop włącza się do badanego obwodu tak jak woltomierz.
W dalszych wykładach będziemy bardziej szczegółowo omawiali właściwości tych i
innych jeszcze elektrycznych przyrządów pomiarowych, sposoby ich wykorzystania do po-
miaru różnych wielkości w różnych sytuacjach. Stosunkowo mało miejsca będziemy
poświęcali budowie przyrządów pomiarowych, ograniczając się do krótkiego wyjaśnienia
zasady działania wybranych przyrządów.

14
Wykład 2
Pomiary w inżynierii
Typowe obiekty pomiarów. Pomiar jako identyfikacja parametryczna. Modelowanie struktury
i parametrów obiektu. O przetwornikach, czujnikach, systemach pomiarowych i komputerach.
Obiekty pomiarów
Właściwości obiektów fizycznych najogólniej modeluje się za pomocą cech abstrakcji
zwanych wielkościami. Wielkości te, choć nazywane fizycznymi, są w istocie wyidealizowa-
nymi cechami wyidealizowanych obiektów. Idealizacja obiektu, którego właściwość jest mo-
delowana wielkością polega między innymi na izolacji tej właściwości od innych właściwości
obiektu i jego otoczenia.
Zawęzimy pojęcie obiektu fizycznego do fragmentu rzeczywistości wyodrębnionego
ze swojego otoczenia wyraźnymi granicami, którymi są najczęściej powierzchnie nieciągłości
gęstości masy. Istnienie tych granic nie oznacza, że obiekt nie oddziałuje na otoczenie i nie
podlega jego oddziaływaniu. Przeciwnie, między obiektem a otoczeniem zachodzi wymiana
energii lub masy (ma miejsce dopływ energii promieniowania cieplnego czy energii prądu
elektrycznego, dopływ określonego surowca oraz wypływ określonego wyrobu). Punkty lub
obszary graniczne obiektu, przez które odbywa się wymiana energii lub masy, nazywa się
zwykle wejściami lub wyjściami, albo ogólnie - wrotami, obiektu.
Przepływ energii i masy przez wrota obiektu opisuje się za pomocą wielkości fizycz-
nych, takich jak strumień energii, strumień masy, strumień objętości lub gęstość energii, pole
prędkości przepływu, natężenie pola elektrycznego. Często wrota opisuje się parą skojarzo-
nych wielkości (takich jak siła i prędkość, prąd i napięcie), których iloczyn charakteryzuje
moc przepływającą przez wrota. W ogólnym przypadku wielkości opisujące wrota są zmienne
w czasie i zależne od współrzędnych przestrzennych.
Wśród wielkości opisujących wrota wyróżnimy:
(i) wielkości wejściowe, utożsamiane z przyczynami zjawisk zachodzących w obiekcie, a
nazywane także wymuszeniami,
(ii) wielkości wyjściowe, utożsamiane ze skutkami zjawisk zachodzących w obiekcie, a nazywane
także odpowiedziami,

15
(iii) wielkości wpływające, których wartości podlegają stabilizacji podczas operacji związanych z
tworzeniem i wykorzystaniem modelu obiektu,
(iv) czynniki zakłócające, których skutkiem jest występowanie rozbieżności między odpowiedzią
obiektu i odpowiedzią modelu na to samo wymuszenie; najczęściej przyporządkowuje się je
do wyjścia, mimo, że pojawiają się w różnych punktach modelowanego obiektu.
Model matematyczny obiektu jest jego opisem za pomocą liczb, zmiennych, zbiorów,
równań, funkcji, relacji, obrazów itd., umożliwiającym przewidywanie zachowania obiektu w
różnych warunkach. Jest to zawsze opis przybliżony w tym sensie, że tylko w przybliżeniu
pozwala przewidywać zachowanie modelowanego obiektu.
Każda gałąź techniki, każda dyscyplina nauki ma swoje typowe obiekty pomiarów. W
elektryce i telekomunikacji bada się np. obwód elektryczny i jego parametry, poszczególne
elementy tego obwodu, źródła i odbiorniki sygnałów, linie przesyłowe, uziemienia i
zerowania, właściwości elementów komutujących i wyłączających, właściwości materiałów
izolacyjnych, przewodzących, magnetycznych. Itp. , itd. W takich badaniach oprócz
pomiarów wielkości elektrycznych bardzo często występuje potrzeba wyznaczania wartości
wielkości nieelektrycznych. Można wymienić tu przykładowo pomiary temperatury,
wilgotności, przesunięć, naprężeń, ciśnienia, przepływu, emisji światła.
Pomiar jako identyfikacja parametryczna
Z punktu widzenia klasycznej teorii eksperymentu sposób uzyskania danych do
identyfikacji parametrów modelu jest nieistotny. Przy identyfikacji obiektów fizycznych dane
te są wynikiem doświadczenia: ich źródłem są przede wszystkim pomiary. We współczesnej
inżynierii i badaniach naukowych pozyskiwanie danych do identyfikacji (nastawianie lub
pomiary wartości wielkości wejściowych, pomiary wartości wielkości wyjściowych i
wpływających) oraz sama identyfikacja parametrów (obliczanie ich wartości) są coraz
częściej zachodzącymi na siebie ogniwami spójnego procesu. Ta spójność wynika zarówno z
faktu, że oba typy operacji są (lub mogą być) wykonywane przez ten sam system pomiarowy,
jak i z wzajemnych związków zachodzących między nimi: metoda identyfikacji może
warunkować sposób pomiaru i odwrotnie - metoda pomiarowa może wpływać na sposób
identyfikacji. Tak więc granica między pomiarami a identyfikacją parametryczną jest trudna,
a niekiedy wręcz niemożliwa do wytyczenia; co więcej - rozdzielne traktowanie pomiarów i
identyfikacji może grozić zagubieniem lub zaniedbaniem istotnych elementów procesu
poznawczego, któremu pomiary i identyfikacja służą.

16
Identyfikacja modelu obiektu jest ciągiem operacji mających na celu określenie
modelu matematycznego obiektu, tzn. wybór adekwatnej struktury modelu (identyfikacja
strukturalna) oraz wyznaczenie wartości jego parametrów (identyfikacja parametryczna).
Identyfikacja strukturalna jest zagadnieniem trudno algorytmizowanym: wybór struktury
modelu opiera się na ogół na przesłankach intuicyjnych, na precedensach technicznych i
doświadczeniach opisanych w literaturze przedmiotu.
Identyfikacją jest w istocie także pomiar wartości wielkości, pomiar rozkładu
wielkości i pomiar (wyznaczanie) charakterystyki zależności między wielkościami. Operacje
prowadzone są bowiem według tego samego schematu logicznego co identyfikacja
parametrów, ich podstawą jest model matematyczny obiektu (ściślej jego struktura), ich celem
jest uszczegółowienie ("wykończenie" lub "uzupełnienie") modelu konkretnego obiektu przez
wyznaczenie "brakujących" jego elementów - wartości lub rozkładów wielkości,
charakterystyk zależności między wielkościami, wartości parametrów modelu. Spostrzeżenie
to prowadzi do identyfikacyjno-parametrycznej koncepcji pomiaru, traktującej pomiar jako
identyfikację modelu matematycznego obiektu badanego, przy apriorycznie danej strukturze
tego modelu.
Przedstawimy zręby tej koncepcji. Załóżmy, że dany jest obiekt badany (mierzony)
oraz struktura modelu matematycznego tego obiektu, a celem pomiaru jest wyznaczenie
wartości (szeroko rozumianych - liczb, funkcji, ciągów liczb itd.) mezurandu m. Typ struktury
modelu zależy od rodzaju i charakteru mezurandu. Rozpatrzymy cztery typy struktur modelu
stanowiących podstawę czterech typów pomiarów, ograniczając się do modeli o jednym
wyjściu i jednym wejściu lub bez wejścia.
Jeżeli mezurandem jest wartość wielkości lub rozkład wielkości, to model mierzonego
obiektu jest modelem "bez wejścia" i można go przedstawić w postaci
=
∈
y
m
y
Y
(1)
przy czym Y jest przestrzenią zmienności wielkości y.
Jeżeli mezurandem jest reprezentacja wielkości, to model mierzonego obiektu jest mo-
delem "bez wejścia" i można go przedstawić w postaci
∈
=
∈
M
Y
m
y
F
m
y
),
(
(2)

17
Jeżeli mezurandem jest charakterystyka zależności między wielkością y a wielkością
x, to model mierzonego obiektu jest modelem o jednym wejściu (opisanym wielkością x) i
jednym wyjściu (opisanym wielkością y) i można go przedstawić w postaci
=
∈
∈
)
(
,
x
y
m
y
x
Y
X
(3)
Jeżeli mezurandami są parametry zależności między wielkościami x i y, to taki pomiar
jest równoznaczny z identyfikacją parametryczną. Modelem mierzonego obiektu jest model o
jednym wejściu (opisanym wielkością x) i jednym wyjściu (opisanym wielkością y) i można
go przedstawić w postaci
=
=
∈
∈
p
m
p
Y
X
0
)
,
,
(
,
y
x
H
y
x
(4)
gdzie: H - operator definiujący równanie modelu.
Operacje wyznaczania parametrów pewnych zależności są tradycyjnie nazywane po-
miarami (np. pomiar rezystancji, indukcyjności, pojemności), operacje wyznaczania parame-
trów innych zależności są z kolei traktowane jako operacje identyfikacji. Proponowany tu
sposób podejścia cechuje pełna jednolitość – wszystkie omówione tu operacje, także (3) i (4),
nazwiemy pomiarami.
Modelowanie struktury i parametrów obiektu
Model matematyczny obiektu oprócz wielkości opisujących wrota obejmuje
specyfikację matematyczną tych wielkości jako zmiennych oraz równanie modelu. Wielkości
specyfikuje się określając przestrzenie ich zmienności. Przestrzeniami tymi mogą być zbiory
liczb rzeczywistych albo klasy funkcji czasu lub współrzędnych przestrzennych.
Podział wielkości modelujących obiekt na wielkości wejściowe, wielkości wyjściowe,
wielkości wpływające i czynniki zakłócające wynika z filozofii modelowania
matematycznego, którą - w nieco uproszczony sposób - można sformułować następująco:
- model odwzorowuje tylko niektóre zjawiska lub właściwości obiektu (istotne z punktu widze-
nia przeznaczenia modelu), przedstawiając je w postaci równania modelu, wiążącego
wielkości wejściowe (modelujące przyczyny istotnych zjawisk zachodzących w obiekcie lub
czynniki odpowiedzialne za jego istotne właściwości) z wielkościami wyjściowymi
(modelującymi przejawy tych zjawisk lub właściwości);

18
- na zjawiska i właściwości istotne z punktu widzenia modelu mają także wpływ inne zjawiska
zachodzące w obiekcie i jego otoczeniu; w celu uniezależnienia się od wpływu tych zjawisk
ustala się ich natężenie, stabilizując wielkości wpływające;
- poznanie zjawisk w obiekcie ma zawsze ograniczony charakter i dlatego wielkości
wpływające nie opisują wszystkich zjawisk, a ich stabilizacja nie eliminuje wpływu innych
zjawisk na wyjścia; tę ograniczoną poznawalność obiektu uwzględnia się w modelu
wprowadzając doń czynniki zakłócające.
Biorąc pod uwagę charakter wielkości wejściowych i wyjściowych można podzielić
modele np. na statyczne i dynamiczne, stacjonarne i niestacjonarne, modele o stałych skupio-
nych i o stałych rozłożonych. Modele o stałych skupionych charakteryzują się niezależnością
wielkości wejściowych i wyjściowych od współrzędnych przestrzennych, podczas gdy w mo-
delach o stałych rozłożonych taka zależność ma miejsce przynajmniej dla niektórych z tych
wielkości. Modele statyczne charakteryzują się niezależnością wielkości wejściowych i wyj-
ściowych od czasu. Modele dynamiczne opierają się na założeniu, że przynajmniej niektóre z
tych wielkości są zmienne w czasie.
Najogólniej rozróżnia się dwa typy modeli obiektów:
- modele funkcyjne, traktujące modelowany obiekt jako całość („black box”) i opisujące go za
pomocą równań wiążących wielkości wejściowe i wyjściowe w dziedzinie czasu lub częstotli-
wości,
- modele o postaci kilkuelementowych obwodów zastępczych, których parametry są w bezpo-
średnim związku z poszukiwanymi charakterystykami modelowanych obiektów.
Oba typy modeli są zbieżne dla przypadków stosunkowo prostych - dwu, trzy elementowych.
Gdy liczba elementów obwodu zastępczego wzrasta, pojawia się problem jednoznacznego
wyznaczenia parametrów tych elementów. Problem ten nie ma rozwiązania ogólnego. Stąd -
dla takich przypadków - obserwuje się wyraźną tendencję do odchodzenia od modeli obwo-
dowych w stronę modeli funkcyjnych.
Dla uproszczenia rozważymy tylko modele o jednym wejściu x i jednym wyjściu y,
obejmujące wielkości niezależne od współrzędnych przestrzennych. Wielkość wejściową x(t)
i wyjściową y(t) będziemy nazywać, odpowiednio, sygnałem wejściowym i wyjściowym.
Struktura modelu powinna obejmować specyfikację przestrzeni sygnałów x(t) i y(t),
obejmującą w szczególności ograniczenia dotyczące zakresów wartości sygnałów i ich
pochodnych.
Model obiektu opisuje jego zachowanie i właściwości tylko w przybliżeniu. Spowodo-
wane jest to dwoma przyczynami: niedokładnością wyznaczenia parametrów modelu oraz

19
nieadekwatnością struktury modelu. Niedokładność wyznaczenia parametrów modelu jest
spowodowana przez:
- błędy przyjętej metody identyfikacji parametrów modelu oraz błędy jej realizacji (błędy obli-
czeń),
- błędy danych użytych do identyfikacji parametrów modelu.
Nieadekwatność struktury modelu wynika z zawsze ograniczonej poznawalności rzeczywisto-
ści (niekiedy wymuszona jest ograniczeniami technicznymi) i objawia się:
- pominięciem, wśród wielkości modelujących obiekt, czynników istotnych dla przebiegu
zjawisk w obiekcie i właściwości obiektu;
- niewłaściwą specyfikacją wielkości modelujących obiekt (wejściowych, wyjściowych i wpły-
wających);
- przyjęciem niewłaściwego typu równania modelu.
Rozważmy zagadnienia niedokładności i nieadekwatności modelu na przykładzie mo-
delu liniowego o jednym wejściu i jednym wyjściu. Założymy, że modelowany obiekt istnieje
w rzeczywistości, a wiedza o nim ma charakter empiryczny. Zamiast "prawdziwych" wartości
wielkości wejściowej x& , wyjściowej y& i wpływającej w
& (dla wygody ograniczymy się do
jednej wielkości wpływającej) obiektu (rys.1) znane są odpowiednie wartości zmierzone: x
~ ,
y
~ i w~ , przy czym
∆
+
=
∆
+
=
∆
+
=
~
~
~
w
w
w
y
y
y
x
x
x
&
&
&
&
&
&
(11)
gdzie:
x
∆
&
- błąd prawdziwy nastawienia wartości wielkości wejściowej,
y
∆
&
- błąd prawdziwy
pomiaru wartości wielkości wyjściowej,
w
∆
&
- błąd prawdziwy stabilizacji wielkości
wpływającej. Zamiast więc obiektu ("chmurka" na rys.1) dostępny jest tylko pewien jego
obraz składający się z wyników obserwacji i pomiarów (wielokąt na rys.1). Stanowią one
dane wejściowe do identyfikacji parametrów równania modelu i na ogół mogą być
uporządkowane w ciąg par odpowiadających sobie wartości
{
}
N
i
i
y
i
x
,...,
2
,
1
)
(
~
),
(
~
=
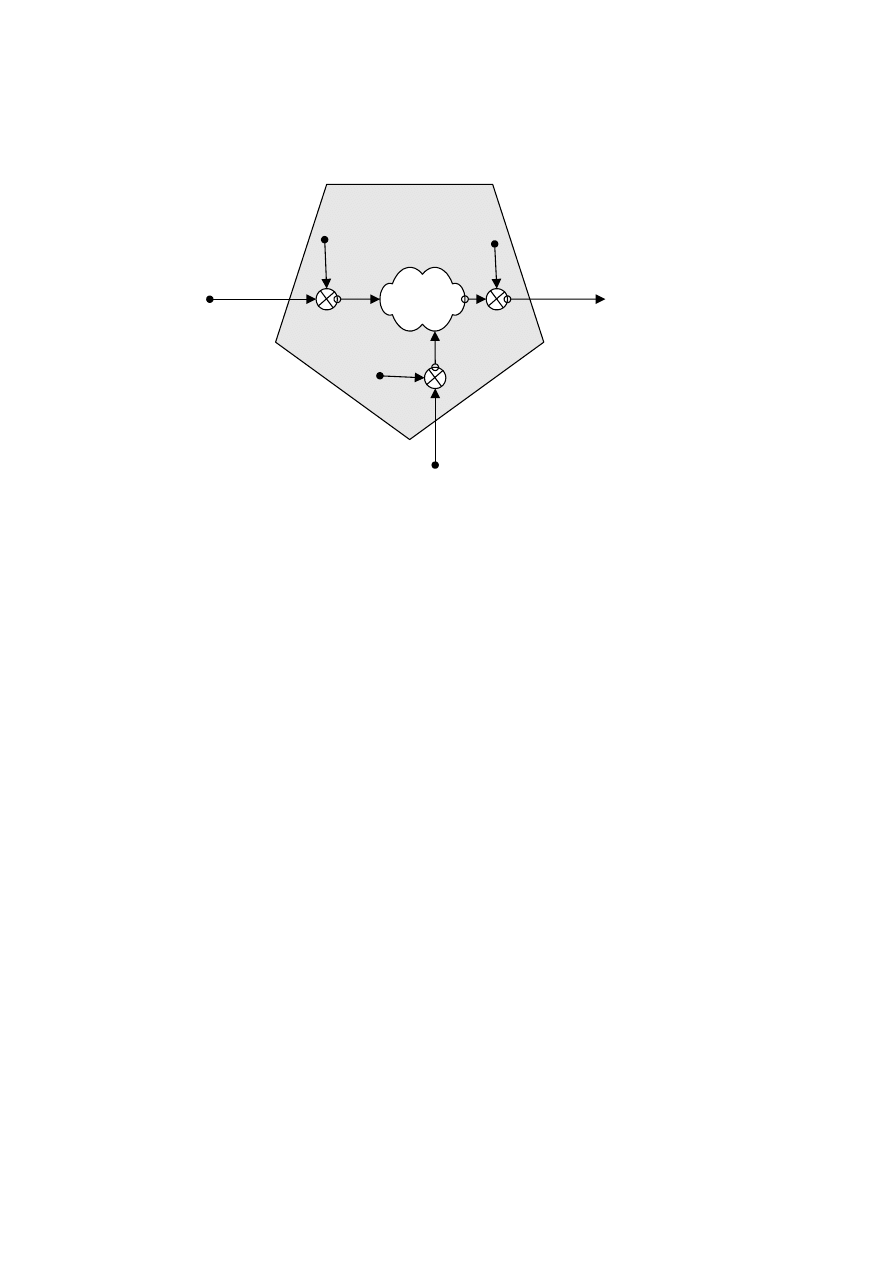
20
Rys.1. Identyfikacja parametrów modelu na podstawie wyników pomiarów
Załóżmy, że równanie modelu ma postać
R
X
⊂
∈
+
=
x
dla
x
a
a
y
1
0
(11)
Na podstawie zebranych danych
{
}
)
(
~
),
(
~
i
y
i
x
, stosując np. metodę najmniejszych kwadratów,
możemy wyznaczyć estymaty parametrów
0
ˆ
a i
1
ˆ
a
, którym odpowiada równanie modelu
x
a
a
y
1
0
ˆ
ˆ
ˆ
+
=
(12)
Zauważmy, że ze względu na błędy danych pomiarowych, możliwy błąd metody
identyfikacji, błędy obliczeniowe, a także - nieadekwatność przyjętej struktury modelu,
0
ˆ
a i
1
ˆ
a
są tylko estymatami parametrów, obarczonymi pewnymi błędami. Wpływ tych błędów na
jakość zidentyfikowanego modelu ocenia się według różnych kryteriów zależności od
przeznaczenia modelu. Najczęściej są to:
- błędy odwzorowania wielkości wyjściowej, odpowiadające zadanym wartościom wielkości
wejściowej,
- błędy odwzorowania wielkości wejściowej, odpowiadające zadanym wartościom wielkości
wyjściowej,
- błędy wyznaczonych parametrów modelu.
Ograniczmy nasze rozważania do tego pierwszego kryterium, definiując błąd wyznaczonego
modelu jako
O BIEKT
x
~
x
&
y
&
y
∆
&
w
~
w
&
w
∆
&
y
~
x
∆
&

21
y
x
a
a
y
y
&
&
&
&
−
+
=
−
=
1
0
ˆ
ˆ
ˆ
∆
(13)
Załóżmy wstępnie, że struktura modelu została wybrana w sposób adekwatny, tzn. istnieją
takie wartości
0
0
a
a
&
=
i
1
1
a
a
&
=
, dla których
X
∈
+
=
x
dla
x
a
a
y
&
&
&
&
&
1
0
(14)
Wówczas błąd zidentyfikowanego modelu przybiera postać
x
a
a
a
a
&
&
&
&
)
ˆ
(
ˆ
1
1
0
0
−
+
−
=
∆
(15)
i może być w całym przedziale zmienności wielkości x oszacowany przez liczbę
∆
)
zwaną
błędem granicznym modelu
x
a
a
a
a
x
)
ˆ
(
ˆ
sup
1
1
0
0
X
&
&
)
−
+
−
=
∈
∆
(16)
Y
-A
x
is
X-Axis
Y
-A
x
is
X-Axis
a)
b)
Rys.2. Przykład ilustrujący zagadnienie adekwatności modelu: a) dwie aproksymacje liniowe;
b) aproksymacja liniowa i kwadratowa
Na rys.2 przedstawiono linią przerywaną przykład charakterystyki (14); kropkami oznaczono
dane pomiarowe
{
}
)
(
~
),
(
~
i
y
i
x
, zaś linią ciągłą - wynik identyfikacji, tzn. charakterystykę li-
niową, której parametry
0
ˆ
a i
1
ˆ
a
wyznaczono na podstawie tych danych.
Załóżmy teraz, że struktura modelu liniowego jest nieadekwatna, ponieważ zadowalającą
zgodność z wynikami "bardzo dokładnych" pomiarów zapewnia dopiero równanie
kwadratowe
2
2
1
0
x
a
x
a
a
y
&
&
&
&
&
&
+
+
=
(17)

22
Przykład charakterystyki statycznej takiej postaci, danych pomiarowych oraz wyniku
identyfikacji przedstawiono na rys.2b. Błąd zidentyfikowanego modelu ma w tym wypadku
postać
R
,
)
ˆ
(
ˆ
2
2
1
1
0
0
∈
−
−
+
−
=
x
x
a
x
a
a
a
a
&
&
&
&
&
&
&
∆
(18)
Choć źródłem błędu modelu jest zarówno nieadekwatność struktury modelu jak
niedokładność identyfikacji jego parametrów, nie sposób ilościowo określić, w jakim stopniu
dwa te czynniki w nim partycypują. Co więcej, globalna ocena błędu modelowania postaci
(15) lub (18), czy nawet (16), jest w praktyce wysoce problematyczna ze względu na brak
wstępnej informacji o adekwatnej strukturze modelu i dokładnych wartościach jego
parametrów. Błędu modelu nie można także wyznaczyć ze wzoru (13), gdyż zamiast wartości
prawdziwych x& i y& znane są tylko przybliżone wartości x
~ , y~ . Błąd ten można jedynie
oszacować. W ogólności polega to na tym, że jako od- niesienia do oceny adekwatności i
niedokładności modelu Mp, który nazwiemy podstawowym, używa się albo odpowiednio
dokładnego obrazu obiektu Mo, albo doskonalszego modelu Mr, który nazwiemy
rozszerzonym (rys.3).
Obraz obiektu Mo jest tabelaryczną formą modelu obiektu; wartości wielkości wejściowej i
wyjściowej
{
}
)
(
~
),
(
~
i
y
i
x
, tworzące ten model, nie muszą (a nawet nie powinny) być identyczne
z wartościami, na podstawie których wyznaczono parametry modelu podstawowego.
Model rozszerzony Mr różni się tym od podstawowego, że ma bogatszą strukturę (większą
liczbę wielkości wejściowych, wyjściowych i wpływających, większą liczbę parametrów);
jego parametry zostały wyznaczone na podstawie dokładniejszych danych pomiarowych;
znane są błędy graniczne identyfikacji tych parametrów.
W obu przypadkach model podstawowy Mp jest porównywany nie z "rzeczywistością" ale z
innym modelem:
z Mo
y
y
~
ˆ
~
−
=
∆
(19)
bądź z Mr
y
y
(
(
−
=
ˆ
∆
(20)
Błędy
∆
~
i
∆
(
są traktowane jako estymaty błędu prawdziwego
∆
& .
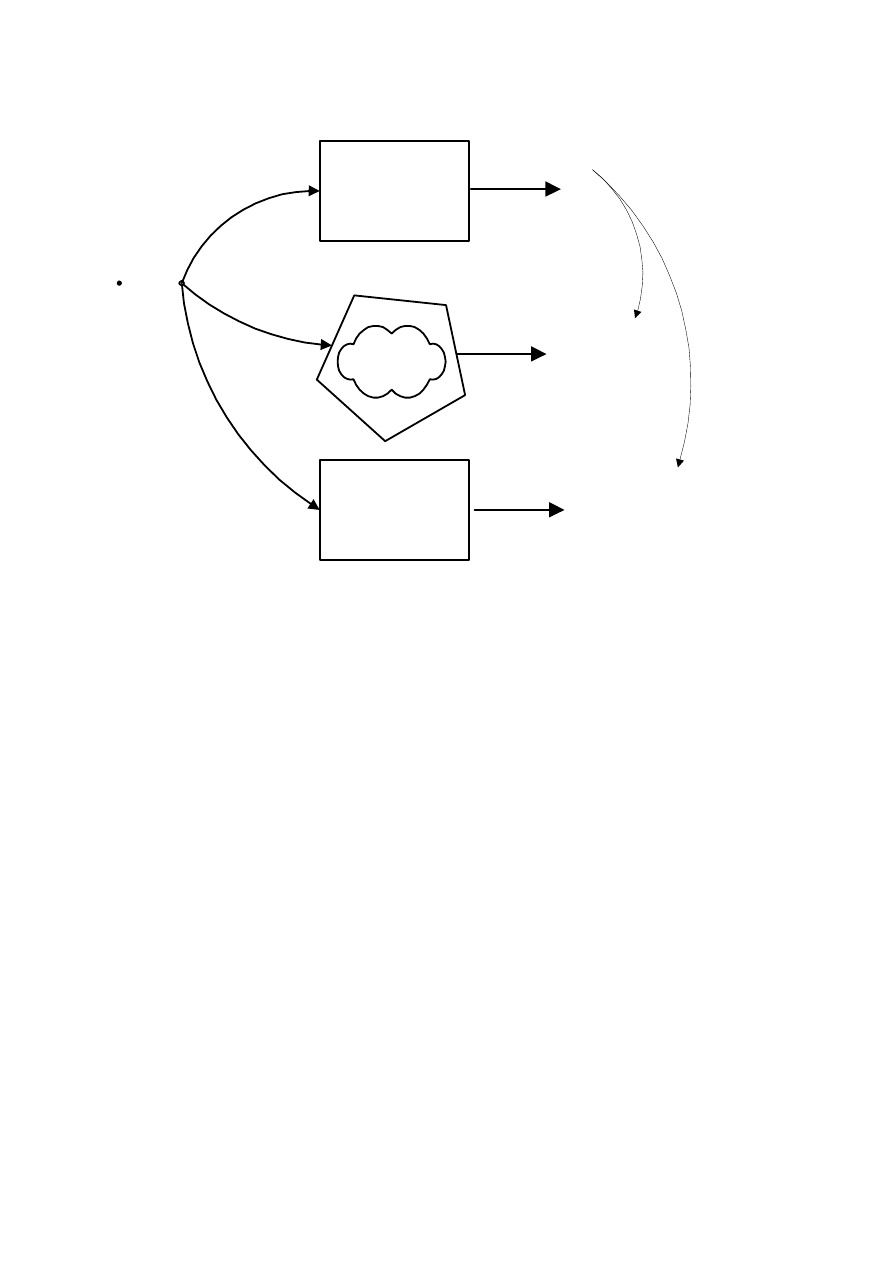
23
Rys.3. Wyznaczanie błędów modelu
Należy zdawać sobie sprawę z tego, że ocena nieadekwatności i niedokładności modelu pod-
stawowego Mp polega nie na wyznaczaniu błędu prawdziwego lecz jedynie na oszacowaniu
błędu granicznego. Z tego też powodu znacznie wygodniejsze jest porównywanie modelu
podstawowego Mp z modelem rozszerzonym Mr niż z obrazem obiektu Mo. Do oszacowania
błędu granicznego nie jest na ogół potrzebna znajomość pełnego modelu rozszerzonego:
wystarcza wyznaczenie tylko niektórych jego elementów.
O przetwornikach, czujnikach, systemach pomiarowych i komputerach
Urządzenie, które wytwarza sygnał elektryczny proporcjonalny do stanu fizycznego
lub wielkości fizycznej, jest zwykle zwane przetwornikiem. Ściślej mówiąc nazwa ta powinna
być zastrzeżona dla urządzeń, które przetwarzają jedną postać energii w drugą, np. energię
mechaniczną w energię elektryczną. Wynikałoby z tego, że urządzenie takie dla wytworzenia
sygnału elektrycznego na wyjściu powinno pobrać pewną porcję energii z otaczającego je
środowiska. Dla procesu pomiaru najkorzystniej jest jednak, gdy przetwornik otrzymuje
energię potrzebną do wytworzenia sygnału wyjściowego ze źródła zewnętrznego, nie zaś z
obiektu pomiaru. Przetwornik nie pobierający energii z mierzonego obiektu jest zwykle
MODEL
PODSTAWOWY
MODEL
ROZSZERZONY
x
OBIEKT
y
y
(
(
−
=
∆
y
~
y
y
(
y
y
~
~
−
=
∆

24
zwany czujnikiem, choć nie jest to wyróżnik terminologiczny stosowany konsekwentnie.
Równie często przyjmuje się, że czujnik jest tym elementem toru pomiarowego, który
bezpośrednio reaguje na wielkość mierzoną. Podstawową charakterystyką czujnika jest
charakterystyka przetwarzania wiążąca sygnał wyjściowy z sygnałem wejściowym. W
przetwarzaniu pomiarowym nie należy zatem brać dosłownie określenia „przetwarzanie”, np.
przetwarzanie temperatury na rezystancję. Chodzi tu jedynie o powiązanie funkcyjne dwóch
wielkości: wejściowej i wyjściowej. Każdej wartości wielkości wejściowej jest jednoznacznie
przyporządkowana ściśle określona wartość wielkości wyjściowej.
Najważniejsze wymagania stawiane czujnikom to:
- bardzo dobre charakterystyki jakościowe: stałość (powtarzalność) charakterystyki przetwa-
rzania, duża czułość na wielkość mierzoną, a mała na inne wielkości wpływające, duża moc
sygnału wyjściowego, mała moc szumów, szeroki zakres pomiarowy, możliwie słabe od-
działywanie na źródło sygnału mierzonego, duża dokładność, liniowość przetwarzania, duża
szybkość przetwarzania, brak histerezy;
- wysoka niezawodność pracy, długi czas „życia”, odporność na pasożytnicze wpływy ze-
wnętrzne;
- technologiczność konstrukcji: małe wymiary i ciężar, prosta konstrukcja, niski koszt własny.
Oczywistym jest, że wykonanie czujników, odpowiadających wszystkim przytoczo-
nym tu wymaganiom jest zadaniem niezwykle trudnym. Powoduje to, że - dla sprostania tym
wymaganiom - stosowane jest dziś dość często wspomaganie mikrokomputerowe. W szcze-
gólności mikrokomputer pozwala na zlinearyzowanie nieliniowej charakterystyki przetwarza-
nia, minimalizację wpływu szumów własnych czujnika i szumów zewnętrznych, korekcję
wpływu zmian temperatury otoczenia czujnika, korekcję wpływu zmian czułości i pełzania
zera, a także na autodiagnostykę czujnika. Obserwowane tendencje rozwoju konstrukcji czuj-
ników wskazują na coraz większą integrację czujnika z poprawiającymi jego jakość układami
współpracującymi. Przy wykorzystaniu technologii układów scalonych dużej skali integracji
do obudowy czujników wmontowywane są układy zasilania, wzmacniacze, przetworniki
analogowo-cyfrowe, mikrokomputery oraz układy interfejsu. Buduje się także czujniki gru-
powe. Połączenie kilku czujników w jednym korpusie pozwala na jednoczesne pomiary wielu
wielkości. Np. czujnik mierzący jednocześnie temperaturę i wilgotność jest szczególnie uży-
teczny w urządzeniach klimatyzacyjnych. Z drugiej strony nowe, ciekawe możliwości
powstają przy łączeniu czujnika z elementem wykonawczym (aktuatorem).
Zbieranie i przetwarzanie wyników pomiarów z wielu czujników (przetworników)
każe zastanowić się nad obecną i przyszłą rolą systemów pomiarowych. Jest wiele definicji

25
systemu pomiarowego, ale wydaje się, że wobec dość pośpiesznej ich ewolucji należy
powracać do źródłosłowu, tj. do złożenia definicji systemu jako uporządkowanego
wewnętrznie zbioru (tu środków technicznych) tworzącego pewną całość i przymiotnika
„pomiarowy”, czyli służący do pomiarów. W tym znaczeniu systemem pomiarowym będzie
zarówno linijka, miernik magnetoelektryczny, multimetr cyfrowy, jak i obsługiwany przez
komputer zestaw aparatury do zbierania danych pomiarowych z dużego obiektu
przemysłowego, czy stacja telemetrii kosmicznej rejestrująca wyniki pomiarów przesyłane z
Marsa.
Najstarsze systemy pomiarowe były obsługiwane wyłącznie przez człowieka - przez
niego były także odczytywane i rejestrowane wyniki pomiarów. Następnym etapem rozwoju
było powstanie systemów pomiarowych zapisujących wynik pomiaru samoczynnie - w
postaci analogowej lub cyfrowej. Dalszym krokiem naprzód było wyposażenie systemu w
programowane wejścia, pozwalające na sterowanie pracą systemu za pomocą sygnałów
cyfrowych generowanych z układu sterującego o sztywnych sekwencjach sygnałów
sterujących. Istotny przełom w rozwoju tych ostatnich stanowiło wprowadzenie w miejsce
układu sterującego, komputera, który nie tylko ustawia programowane wejścia elementów
systemu, lecz także odczytuje sygnały wprowadzane przez operatora oraz prowadzi złożone
niekiedy przetwarzanie sygnałów wyjściowych. Aby zapewnić właściwą pracę podzespołów
systemu konieczna jest normalizacja wszystkich środków technicznych tworzących system,
począwszy od wymiarów gabarytowych podzespołów systemu, poprzez konstrukcję
okablowania, a na poziomach sygnałów wyjściowych, kodach i konwencjach programowych
skończywszy. Stąd też obecnie podstawowym zadaniem przy konstruowaniu i eksploatacji
systemów pomiarowych jest zapewnienie odpowiedniej standaryzacji i kompatybilności
wymienionych środków. Przedstawiony tu kierunek rozwoju nie powinien jednak przesłaniać
faktu, że w praktyce w laboratoriach naukowych i przemysłowych, w kontroli produkcji i
urzędach miar są użytkowane systemy wszystkich wymienionych wyżej generacji.
Oddzielny rozdział zagadnień technicznych w konstruowaniu i eksploatacji systemów
pomiarowych, to współpraca operatora z systemem. Zdolność człowieka do wyciągania wnio-
sków ogólnych z wielu oddzielnych informacji, a także jego zdolności adaptacyjne, umożli-
wiające prawidłowe reagowanie na nieprzewidziane sytuacje, powodują, że systemy pomia-
rowe i dzisiaj i w przyszłości powinny w założeniach swej struktury i algorytmu działania, te
właśnie zdolności operatora uwzględniać. Skuteczne uczestniczenie operatora w działaniu
systemu wymaga wyprowadzenia i przedstawienia informacji w takiej postaci i za pomocą ta-
kich środków by powodować możliwie najmniejsze jego zmęczenie fizyczne i psychiczne. W

26
związku z tym istnieje konieczność zredukowania ilości informacji oraz przyjęcia takiego
sposobu wizualizacji, by nie przeciążyć zdolności percepcyjnej operatora. Jeśli przyjąć dla
współczesnych rozwiązań systemów pomiarowych określenie „inteligentne”, to abstrahując
od dość zawiłych prób oceny owej „inteligencji”, można zaryzykować stwierdzenie, że
podstawową jej miarą jest łatwość programowania i obsługi takiego systemu.

27
Wykład 3 i 4
Podstawowe pojęcia teorii błędów
Przedział niepewności. Błąd prawdziwy i graniczny; błąd bezwzględny, względny, sprowa-
dzony. Błędy systematyczne i przypadkowe. Przenoszenie błędów. Typowe przypadki szaco-
wania błędów. Ogólne procedury szacowania błędów.
1. Wprowadzenie
Pomiar jest zawsze operacją niedokładną, to znaczy estymata wartości prawdziwej
mezurandu otrzymana jako wynik pomiaru różni się na ogół od wartości prawdziwej, równość
estymaty i estymowanej wartości jest zdarzeniem wyjątkowym, a fakt jego zajścia pozostaje
nieznany. Istotą pomiaru jest jednak to, że
niedokładność wyniku pomiaru można zawsze
oszacować, to znaczy można zawsze określić graniczną odległość między znanym wynikiem
pomiaru a nieznaną wartością prawdziwą mezurandu.
Szacowanie niedokładności pomiaru jest jedną z podstawowych czynności, która po-
winna być wykonywana w procesie mierzenia. Niestety, jest jednak czynnością nie lubianą,
niedocenianą i wykonywaną, najoględniej mówiąc, nie najlepiej. Co gorsza, często mierzący
rezygnuje z oceny niedokładności wykonanego pomiaru. Dostępna literatura przedmiotu, za-
równo krajowa jak i zagraniczna, zagadnienia niedokładności pomiaru omawia wyrywkowo i
pobieżnie, traktując je raczej jako dodatek upiększający do "prawdziwej" metrologii, która
jest encyklopedią zasad działania i budowy narzędzi pomiarowych, dodatek wprawdzie
upiększający, ale praktycznie nieużyteczny.
Przedmiotem naszych rozważań będą pomiary, których mezurandami są wartości
wielkości fizycznych – wartości liczbowe lub wartości mianowane czyli iloczyny wartości
liczbowych i jednostki miary wielkości. Warto dodać, że pojęcie mezurandu (to, co jest
mierzone) jest uogólnieniem pojęcia wielkości mierzonej ale na poziomie naszych rozważań
może być z nim utożsamiane.
Przedmiotem rozważań jest zasadniczo niedokładność i błędy pomiaru, rozważania te
jednak odnoszą się do niedokładności i błędów innych operacji, np. tworzenia reprezentacji
cyfrowych liczb rzeczywistych, aproksymacji, obliczeń numerycznych, a także operacji skła-
dających się na pomiar.

28
2. Przedział niepewności. Błąd pomiaru
Pomiar jest zawsze niedokładny, tzn. wartość zmierzona mezurandu xˆ (tj.
wyznaczona w procesie pomiaru) różni się od wartości prawdziwej mezurandu x& . Oznacza to,
że wynik pomiaru jest liczbą przybliżoną, można więc go interpretować jako przedział [ xˆ ] w
przestrzeni liczb rzeczywistych czyli na osi liczbowej, wewnątrz którego znajduje się wartość
prawdziwa mezurandu
x&
∈
[ xˆ ]
(1)
Przedział ten można nazwać przedziałem niepewności wyniku pomiaru i dopatrywać się jego
analogii z przedziałem ufności estymaty parametru rozkładu zmiennej losowej. Przedział nie-
pewności wyniku pomiaru ustala się najczęściej jako przedział symetryczny
[ ]
]
ˆ
ˆ
,
ˆ
ˆ
[
ˆ
max
max
x
x
x
x
x
∆
+
∆
−
=
(2)
W ogólności wynik jakiegokolwiek pomiaru mezurandu x podawany jest w niezbyt
poprawnej formie matematycznej
x
x
x
ˆ
ˆ
max
∆
±
=
&
(3)
Wygodnie jest zawsze definiować
∆
x jako wielkość dodatnią, tak aby x +
∆
x było zawsze
największą prawdopodobną wartością wielkości mierzonej, a x -
∆
x było jej wartością
najmniejszą.
Wartości
xˆ
max
∆
±
nazywają się błędami granicznymi lub granicami błędu lub
niepewnościami granicznymi lub niepewnościami rozszerzonymi. Graficzną interpretację
przedziałowej postaci wyniku pomiaru pokazano na rys.1a.
Rys.1. Wynik pomiaru ma postać przedziału niepewności, wartość prawdziwa x& mezurandu leży
wewnątrz przedziału niepewności wyniku pomiaru (a), błąd prawdziwy
∆∆∆∆
x leży wewnątrz
przedziału niepewności błędu (b).
Błąd bezwzględny (prawdziwy i graniczny) wyraża się w jednostkach wielkości mierzonej;
błąd względny i odniesiony są ułamkami, najczęściej wyraża się je w procentach (%),
promilach (‰) lub w częściach milionowych (ppm).
Obok granicznych błędów pomiaru definiuje się prawdziwy błąd pomiaru

29
x
x
x
&
−
=
∆
ˆ
ˆ
(4)
Zachodzi
]
ˆ
,
ˆ
[
ˆ
max
max
x
x
x
∆
∆
−
∈
∆
(5)
przy czym przedział
]
ˆ
,
ˆ
[
max
max
x
x
∆
∆
−
można nazwać przedziałem niepewności błędu pomiaru.
Graficzną interpretację przedziału niepewności błędu pokazano na rys.1b. Przymiotnik
"prawdziwy" prawie zawsze, a przymiotnik "graniczny" bardzo często pomija się, i o jaki
błąd chodzi, wynika z kontekstu.
Błąd graniczny
xˆ
max
∆
powinien nazywać się błędem granicznym bezwzględnym, a
błąd prawdziwy
xˆ
∆
– błędem prawdziwym bezwzględnym, gdyż oprócz nich definiuje się
błąd prawdziwy względny
x
x
x
x
x
x
&
&
&
−
=
∆
=
ˆ
ˆ
ˆ
δ
(6)
i błąd graniczny względny
x
x
x
ˆ
ˆ
ˆ
max
max
∆
=
δ
(7)
Każdy przedział
]
ˆ
[
]
ˆ
[
x
x
⊃
∗
jest także przedziałem niepewności, a każdy
x
x
ˆ
ˆ
max
max
∆
>
∆
∗
jest
także błędem granicznym, sztuka jednak polega na określeniu możliwie wąskiego przedziału
niepewności i możliwie małego błędu granicznego.
W tak prostym doświadczeniu jak pomiar wysokości szafki łatwo można określić zakres od
x -
∆
x do x +
∆
x, w którym na pewno mieści się szukana wartość. Niestety w większości
pomiarów przeprowadzanych w nauce i inżynierii bardzo trudno sformułować taki wniosek.
W szczególności, jeśli pragniemy być całkowicie pewni, że mierzona wielkość leży pomiędzy
x -
∆
x i x +
∆
x, nasze oszacowanie daje zbyt dużą wartość
∆
x - tak, że staje się ona prawie
bezużyteczna. Aby tego uniknąć, wybieramy często taką wartość
∆
x, żeby powiedzmy w 70%
być pewnym, że szukana wielkość jest gdzieś między x -
∆
x i x +
∆
x. Nie możemy tego
zrobić bez szczegółowej znajomości praw statystyki, rządzących procesem pomiaru. Na razie
zadowólmy się zdefiniowaniem błędu
∆
x jako takiego, przy którym z „rozsądnym
prawdopodobieństwem" można powiedzieć, że mierzona przez nas wielkość leży gdzieś
pomiędzy x -
∆
x i x +
∆
x.

30
Przedział niepewności jest modelem niedokładności i jako model jest też niedokładny, tzn.
błędy graniczne wyznaczające przedział niepewności są także liczbami przybliżonymi.
Przedział niepewności wyniku pomiaru powinien być bezpieczny, to znaczy wartość
prawdziwa mezurandu powinna leżeć wewnątrz przedziału niepewności. Bezpieczeństwo
takie zapewnia się przyjmując szeroki przedział niepewności. Przedział niepewności wyniku
pomiaru powinien być realistyczny, to znaczy nie powinien być zbyt szeroki. Wymagania
bezpieczeństwa i realizmu są przeciwstawne. Ponieważ błędy graniczne są same obarczone
błędami, nie ma absolutnej pewności, że wartość prawdziwa mezurandu leży wewnątrz
przedziału niepewności. Im przedział niepewności jest szerszy, tym pewność ta jest większa.
Im przedział niepewności węższy, tym pewność ta mniejsza. Miarę stopnia pewności, że
wartość prawdziwa leży wewnątrz przedziału niepewności, wprowadza się nadając
przedziałowi niepewności sens probabilistyczny.
Probabilistyczna
interpretacja
przedziału
niepewności
wymaga
przyjęcia
hipotetycznego doświadczenia (hipotetycznego, to znaczy faktycznie nie wykonywanego, ale
precyzyjnie zdefiniowanego), którego wynikiem jest otrzymywanie przedziału niepewności
jako zdarzenia losowego. Powtarzając to doświadczenie otrzymuje się różne przedziały
niepewności, niektóre z nich obejmują wartość prawdziwą mezurandu, niektóre z nich
wartości prawdziwej nie obejmują. Owe hipotetyczne doświadczenie randomizujące przedział
niepewności można interpretować jako hipotetyczne powtarzanie pomiaru. Hipotetyczne
powtarzanie pomiaru powinno pozwalać oszacować od dołu prawdopodobieństwo 1
−
α
zachodzenia zdarzenia
[
]
{
}
α
−
≥
∆
+
∆
−
∈
1
ˆ
ˆ
,
ˆ
ˆ
Pr
max
max
x
x
x
x
x&
(8)
Prawdopodobieństwo
α
−
1
, przez analogię do przedziału ufności w statystyce, można nazy-
wać także poziomem ufności. Probabilistyczną zależność (8) można odnieść do błędu praw-
dziwego xˆ
∆
pisząc
[
]
{
}
α
−
≥
∆
∆
−
∈
∆
1
xˆ
,
xˆ
xˆ
Pr
max
max
(9)
Przedziały dane zależnościami (8) i (9) są przedziałami niepewności na poziomie
ufności (1–
α
), a błędy graniczne dane tymi zależnościami są błędami granicznymi na poziomie
ufności (1–
α
.)
Przedział niepewności
[
]
x
x
x
x
ˆ
ˆ
,
ˆ
ˆ
max
max
∆
+
∆
−
jest przedziałem losowym, a więc dla
każdego hipotetycznego pomiaru będzie na ogół inny. Niektóre z tych przedziałów będą
zawierały wartość prawdziwą mezurandu, a inne nie będą jej zawierały. Jednak w długiej serii

31
hipotetycznie powtórzonych pomiarów względna częstość przypadków, gdy przedział
niepewności zawiera wartość prawdziwą powinna być większa od 1
−
α
. W tym sensie 1
−
α
jest miarą zaufania, że określony dla jednego pomiaru przedział niepewności obejmuje
wartość prawdziwą.
Nie mówi się tu jednak o prawdopodobieństwie, że nieznana wartość prawdziwa
mezurandu będzie zawarta w jakimś stałym przedziale. Mówi się tu jedynie o
prawdopodobieństwie, że przedział losowy zawiera wartość prawdziwą. Losowość przedziału
niepewności oznacza, że dla każdego hipotetycznego pomiaru będzie na ogół inne xˆ i inne
∆
max
xˆ , co oznacza, że zarówno xˆ jak i
∆
max
xˆ są realizacjami zmiennych losowych.
Przedział
niepewności
wyniku
pomiaru
jest
przekonywującym
modelem
niedokładności pomiaru. Przedział niepewności może (
ale nie musi) mieć określony poziom
ufności. Jeżeli przy przedziale niepewności nie podano poziomu ufności, przyjmuje się, że
jest to przedział zdeterminowany w sensie zależności (1). Przedział niepewności określa się
za pomocą parametrów niepewności, przy czym parametr niepewności bywa nazywany
wprost niepewnością. Ściślej jednak, przez niepewność pomiaru należałoby rozumieć cechę
pomiaru polegającą na tym, że wynik pomiaru jest liczbą przybliżoną, tzn. ma postać
przedziału.
Doskonałą ilustracją pojęcia liczby przybliżonej i przedziału niepewności jest
zapisywanie liczb rzeczywistych za pomocą skończonej liczby cyfr czyli cyfrowa
reprezentacja liczb rzeczywistych i operacja zaokrąglania wartości liczbowych (p.3).
W praktyce zarówno błąd prawdziwy jak i błąd graniczny nazywa się wprost błędem,
a który jest to błąd, wynika z kontekstu. Podobnie pomija się przymiotniki bezwzględny i
względny, o jaki błąd chodzi, wskazują jednostki błędu. W zdaniu:
"długość przedmiotu zmierzono z błędem 1%"
i zdaniu równoważnym mu:
"błąd pomiaru długości przedmiotu wynosi 1%"
i podobnych im chodzi o graniczny błąd względny. Często także treść powyższych zdań prze-
kazuje się jako:
"długość przedmiotu zmierzono z niedokładnością (lub niepewnością) 1%"
"niedokładność (lub niepewność) pomiaru długości przedmiotu wynosi 1%".
Niekiedy zamiast terminu "niedokładność" w sensie granicznego błędu pomiaru używa się
terminu "dokładność", takie sformułowanie jest logicznie błędne. Symbole dodatkowe

32
odróżniające wartość zmierzoną i wartość prawdziwą, gdy występuje tylko jedna z nich,
pomija się zakładając, że znaczenie symbolu wynika z kontekstu.
Graniczny bezwzględny błąd pomiaru
∆
max
x i graniczny względny błąd pomiaru
δ
max
x
są miarami niedokładności pomiaru. Błąd bezwzględny jest miarą szczegółową, określającą
niedokładność, gdy ustalona jest wartość wielkości mierzonej i określony jest cel pomiaru.
Porównajmy na przykład pomiar długości obarczony błędem bezwzględnym 1 mm. Błąd taki
może być odpowiedni dla stolarza, jest nieosiągalny dla astronoma, a zbyt duży dla zegarmi-
strza. Pomiary obarczone błędem względnym 1% natomiast mogą zadowolić każdego z nich.
3. Cyfrowa reprezentacja liczb rzeczywistych i zaokrąglanie
Reprezentacja cyfrowa liczb rzeczywistych jest to operacja zastępowania liczb rze-
czywistych ich zapisami cyfrowymi czyli ciągami cyfr. Reprezentacja cyfrowa dziesiętna ma
postać ciągów cyfr z przecinkiem
d
d
d d
J
d
d
d
d
J
J
d
d
d d
d
d
d
J
J
K
K
K
K
J
J
K
K
J
J
−
−
−
−
+
−
−
−
+
=
>
<
1
2
1 0
1
2
1
1
2
1 0
1
1
0
00 0
0
0
...
(
)
( )
...
...
, (
)
( )
...
,
...
, (
)
( )
dla
a
dla
zer przed przecinkiem
b
dla
cyfr po przecinku
c
(10)
gdzie: D
K-1
= 1,2,...,9 – pierwsza cyfra znacząca,
d
k
= 0,1,...,9 dla k = J, J+1,...,K–2 (K > J+1) – pozostałe cyfry znaczące,
M = K–J – liczba cyfr znaczących,
k – numer pozycji, lub wprost pozycja, cyfry w zapisie,
J – pozycja ostatniej cyfry znaczącej, czyli cyfry, która może być różna od zera.
Cyframi znaczącymi danej liczby w zapisie dziesiętnym nazywamy wszystkie jej cyfry z
wyjątkiem początkowych zer. Np. liczba 14,00827 ma siedem cyfr znaczących, zaś liczba
0,000038 ma tylko dwie cyfry znaczące. Przecinka w zapisie (10) nie stawia się, jeżeli ostatnia
cyfra znacząca znajduje się na pozycji J
≥
0. Zapisowi (10) można nadać jednolitą postać
J
M
M
J
J
J
K
K
d
d
d
d
d
d
d
d
10
)
...
(
10
)
...
(
0
1
2
1
1
2
1
⋅
=
⋅
∗
∗
∗
−
∗
−
+
−
−
(11)
gdzie
∗
i
d (i 0,1,...,M–1) – cyfry numerowane począwszy od ostatniej znaczącej w lewo.
Zapisy (10) i (11) reprezentują dokładnie liczbę
∑
∑
−
=
−
=
∗
=
=
1
1
0
10
10
10
ˆ
K
J
k
M
i
i
i
J
k
k
d
d
x
(12)

33
Liczba xˆ istnieje dokładnie 9
⋅
10
K-J-1
począwszy od 10
K-1
do 10
K
–1, wszystkie są całkowitymi
wielokrotnościami 10
J
. Pozostałe liczby rzeczywiste z przedziału [10
K-1
, 10
K
) wyraża się
także ciągami (10) i (11), przyjmując zwykle, że ciąg reprezentujący dokładnie liczbę xˆ , jest
przybliżoną reprezentacją ~
x każdej liczby z przedziału
[
)
J
J
x
x
x
10
ˆ
,
10
ˆ
2
1
2
1
⋅
+
⋅
−
∈
&
(13)
Popełnia się w ten sposób błąd, którego wartość graniczna wynosi
J
10
2
1
⋅
.
Zauważmy, że nie jest możliwe jednoznaczne określenie błędu granicznego
reprezentacji (10), jeżeli nie jest znana liczba cyfr znaczących. Jeżeli bowiem d
J
= 0, to cyfra
ta może być potraktowana jako nieznacząca. Z tego względu zaleca się stosowanie zapisu
wykładniczego (11). Z tego samego powodu nie wolno pomijać w zapisie (10c) końcowych
zer znaczących.
Przykład 1
Następujące zapisy, choć dokładnie reprezentują tę samą liczbę, oznaczają różne liczby przybliżone x, ponieważ
odpowiadają im różne błędy graniczne:
129
⋅
102
⇒
x
∈
[12850; 12950)
∆
max = 50
1290
⋅
101
⇒
x
∈
[12895; 12905)
∆
max = 5
12900
⇒
x
∈
[12899,5; 12900,5)
∆
max = 0,5
12900,0
⇒
x
∈
[12899,95; 12900,05)
∆
max = 0,05
12900,00
⇒
x
∈
[12899,995; 12900,005)
∆
max = 0,005
Format stałoprzecinkowy ma postać (10), przy czym liczby M i J są ustalone i znane,
a każda z cyfr znaczących może przyjmować wartość 0, 1,...,9. W formacie stałoprzecinko-
wym można przedstawiać, ze stałym granicznym błędem bezwzględnym 0,5
⋅
10
J
, liczby rze-
czywiste x z przedziału w przybliżeniu [0, 10
M+J
), a ściślej z przedziału [–0,5
⋅
10
J
; 10
M+J
–
0,5
⋅
10
J
). Graniczny błąd względny jest w tym przedziale zmienny i zmienia się w zakresie
od 0,5
⋅
10
-M
(dla x
≈
10
M+J
) do
∞
(dla x = 0). Uzupełnienie zapisu (11) znakiem + lub – z
lewej strony umożliwia rozszerzenie zakresu reprezentowanych liczb do przedziału [–
10
M+J
, 10
M+J
).
Format zmiennoprzecinkowy zapisuje liczbę x w postaci
c
m
x
10
⋅
=
(14)
gdzie m
=
±
0, d
-1
d
-2
... d
-M
jest M-cyfrową mantysą z niezerową pierwszą cyfrą (d
-1
≠
0), a
c =
±
c
K-1
c
K-2
... c
0
jest K-cyfrową cechą z dowolnymi cyframi. Liczby M i K są ustalone i

34
znane. W formacie zmiennoprzecinkowym można przedstawiać liczby rzeczywiste o module
zawartym w przedziale od 0,1
⋅
10– (10
K
–1) do 10 (10
K
–1). Graniczny błąd bezwzględny
zapisu w formacie zmiennoprzecinkowym wynosi 0,5
⋅
10
-M
⋅
10 c, a graniczny błąd względny
zapisu zmienia się w przedziale od 0,5
⋅
10
-M
(dla x
≈
10 c) do 5
⋅
10
-M
(dla x = 0,1
⋅
10 c).
Zaokrąglanie jest operacją zastępowania cyfrowej reprezentacji x liczby rzeczywistej x& cy-
frową reprezentacją y tejże liczby x& , ale o mniejszej ilości cyfr znaczących. Liczbę x
będziemy nazywali liczbą zaokrąglaną, a liczbę y – liczbą zaokrągloną. Niech liczba
zaokrąglona y ma ostatnią cyfrę znaczącą na pozycji J, niech dalej liczba zaokrąglana x jest
zapisana w postaci ciągu cyfr (d
K-1
d
K-2
... d
J+1
d
J
, d
J-1
d
J-2
...)
⋅
10
J
. Zaokrąglanie normalne
jest określone zależnością
≥
+
⋅
<
⋅
=
=
−
+
−
−
+
−
−
5
dla
10
10
)
...
(
5
dla
10
)
...
(
)
(
round
1
1
2
1
1
2
1
J
J
J
J
J
K
K
J
J
J
K
K
J
d
d
d
d
d
x
d
d
d
d
x
y
(15)
gdzie round
J
() – operator zaokrąglania normalnego do ostatniej cyfry znaczącej na pozycji J.
Zaokrąglanie w górę polega na utworzeniu y przez odrzucenie wszystkich cyfr x po d
J
i
dodaniu doń 10
J
(jeżeli któraś z odrzuconych cyfr jest różna od zera) lub pozostawieniu tak
otrzymanej reprezentacji (jeżeli wszystkie odrzucone cyfry są zerami). Zaokrąglanie w dół
czyli obcinanie polega na utworzeniu y przez odrzucenie wszystkich cyfr x po d
J
. Bardziej
rozsądne jest stosowanie powyższych reguł nie bezpośrednio do x, lecz do round
J-1
(x).
Zasada zaokrąglania normalnego (15) odnosi się do liczby zaokrąglanej x, która jest
reprezentacją cyfrową liczby rzeczywistej, a więc jest obarczona granicznym błędem bez-
względnym 0,5
⋅
10
J-L
, gdzie L liczba odrzucanych cyfr. Zaokrąglanie zwiększa błąd do 0,5
⋅
10
J
.
Przykład 2
Zaokrąglić liczbę 1953,5091 do formatów z ostatnią cyfrą znaczącą kolejno na miejscach od trzeciego po prze-
cinku do czwartego przed przecinkiem.
Stosując (15) mamy kolejno: 1953,509; 1953,51; 1953,5; 1954; 195
⋅
101; 20
⋅
102; 2
⋅
103.
Odrębne zasady zaokrąglania stosuje się do liczb obarczonych błędami granicznymi
różnymi od 0,5
⋅
10
J-L
. Liczbę przybliżoną x
±
∆
max
x zaokrągla się do y
±
∆
max
y, gdzie y i
∆
max
y
są wyrażone w tym samym formacie, tak aby przedział [y –
∆
max
y, y +
∆
max
y] obejmował
35
przedział [x +
∆
max
x, x +
∆
max
x] i był mu najbliższy z obu stron. Często jednak poprzestaje się
na zaokrąglaniu normalnym x do y i na zaokrąglaniu do góry
∆
max
x do
∆
max
y.
Zaokrąglanie należy stosować ostrożnie i tylko w razie konieczności. Każda bowiem
operacja tego typu prowadzi do nieodwracalnych strat informacji. W przeszłości,
zaokrąglanie było stosowane w celu minimalizacji liczby cyfr znaczących danych,
przeznaczonych do dalszych obliczeń przy użyciu w najlepszym razie arytmometru
korbkowego. Upowszechnienie komputerów wyeliminowało niemal całkowicie tę motywację.
Pozostało jedynie zaokrąglanie danych przeznaczonych do publikacji, interpretacji przez
człowieka itp. Podając dane obarczone błędami estymatę wartości i graniczny błąd
bezwzględny wyraża się w tym samym formacie, przyjmując dla błędu jedną lub dwie cyfry
znaczące.
Warto tu podkreślić podstawowe zasady podawania błędów pomiaru, ponieważ zbyt
często dochodzi tu do nieporozumień. Jeśli mierzymy rezystancję opornika R z
rozdzielczością pozwalającą na otrzymanie wyniku czterocyfrowego, byłoby absurdem
podawanie odpowiedzi w postaci:
R = 29,82 ±0,02385
Ω
-
źle!!!
Przy bardzo dokładnych pomiarach można czasem podawać błędy z dwiema cyframi
znaczącymi, jednak dla potrzeb niezbyt zaawansowanej praktyki pomiarów można przyjąć
regułę, że błędy powinny być zaokrąglane do jednej cyfry znaczącej. Tak więc, jeśli z jakichś
rachunków otrzymujemy błąd
∆
x = 0,02385
Ω
, wynik ten powinien być zaokrąglony do
∆
x =
0,02
Ω
, rezultat pomiaru zaś należy przepisać w postaci
R = 29,82 ±0,02
Ω
- dobrze!!!
Od tej reguły jest tylko jeden istotny wyjątek. Otóż jeśli pierwszą cyfrą znaczącą błędu
∆
x
jest l, to lepiej zachować w zapisie
∆
x dwie cyfry znaczące zamiast jednej. Przypuśćmy na
przykład, że nasze obliczenia dają błąd
∆
x = 0,14. Zaokrąglenie tej wartości do
∆
x = 0,1
prowadziłoby do 40% zmniejszenia błędu, można zatem dowodzić, że mniej mylące byłoby
pozostawienie dwóch cyfr znaczących, czyli
∆
x =0,14. Ten sam argument można by
ewentualnie zastosować, kiedy pierwszą cyfrą znaczącą jest 2, nie działa ona jednak dla cyfr
większych.
Kiedy już oceniliśmy błąd pomiaru, należałoby się zastanowić, które z cyfr wartości
zmierzonej są znaczące. Wynik zapisany jako
C = 6051,78 ±30 nF

36
jest wprost niedorzeczny. Błąd 30 nF oznacza, że cyfra na trzecim miejscu liczby 6051,78 (a
więc 5) mogłaby być w rzeczywistości równa 2 lub 8. Jasne jest zatem, że ostatnie cyfry l, 7
oraz 8 nie mają zupełnie znaczenia i powinny zniknąć po zaokrągleniu. Poprawny zapis tego
wyniku powinien zatem wyglądać następująco:
C = 6050 ± 30 nF
Ogólna reguła może więc przyjąć następującą formę:
Ostatnia cyfra znacząca w każdym wyniku powinna być tego samego rzędu
(stać na tym samym miejscu dziesiętnym) co błąd.
Na przykład wynik 92,81 z błędem 0,3 powinien być zaokrąglony do 92,8 ±0,3. Jeśli błąd
równy jest 3, to ten sam rezultat należałoby zapisać jako 93±3, jeśli zaś błąd wynosi 30, to
odpowiedź powinna brzmieć 90 ±30.
Jest jeszcze jeden wyjątek od podanej tu reguły. Jeśli pierwsza cyfra błędu jest mała (l lub być
może 2), to mogłoby być właściwe pozostawienie w odpowiedzi jeszcze jednej cyfry
znaczącej. Przykładowo, wynik taki jak:
L = 27,6 ± l cm
jest zupełnie rozsądny. W tym przypadku należałoby się zgodzić, że jego zaokrąglenie do
28 ± l powodowałoby utratę informacji.
Zwróćmy uwagę, że wymiar błędu bezwzględnego jakiejkolwiek mierzonej wielkości jest taki
sam jak wymiar owej wielkości. Zapis, w którym jednostki (nF, cm
2
itd.) pojawiają się tylko
na końcu wyniku, będzie zatem bardziej czytelny i ekonomiczny. W ten sam sposób, jeśli
mierzona wartość jest tak duża bądź mała, że wymaga zastosowania zapisu wykładniczego (tj.
użycia formy 3•10
3
zamiast 3000), to prościej i czytelniej jest podać odpowiedź i błąd w tej
samej formie. Przykładowo wynik
Q = (1,61 ± 0,05)•10
-19
C
jest o wiele prostszy do odczytania i zrozumienia, niż gdyby był zapisany w postaci:
Q = 1,61•10
-19
C ± 5•10
-21
C
4. Szacowanie granicznego błędu pomiaru bezpośredniego. Model zdeterminowany.
Pomiar bezpośredni jest to pomiar, w którym estymatę mezurandu wyznacza się
wprost ze wskazania przyrządu pomiarowego. Błąd pomiaru bezpośredniego ma w przypadku
ogólnym trzy składowe: błąd instrumentalny wnoszony przez zastosowany przyrząd
pomiarowy, błąd odczytu popełniany przez człowieka przy odczytywaniu wskazania
przyrządu oraz błąd metody powodowany nieidealnym informatycznym sprzężeniem między

37
przyrządem a obiektem mierzonym
2
. Błąd prawidłowego odczytu wskazania przyrządu
cyfrowego jest równy zeru, błąd prawidłowego odczytu wskazania przyrządu analogowego
jest zwykle wliczany do błędu granicznego określonego w danych przyrządu, błąd metody
zależy od szczegółowych warunków danego pomiaru. Rozważać więc będziemy tylko błąd
instrumentalny.
Błąd instrumentalny można traktować jako błąd systematyczny, tzn. przyjmujący war-
tość niezmienną przy powtarzaniu pomiaru tej samej wartości mezurandu w identycznych wa-
runkach. Błąd instrumentalny
∆
x jest nieznany co do wartości, wiadomo o nim, że spełnia
warunek
∆
∆
x
x
≤
max
(16)
gdzie
∆
max
x
jest granicznym błędem przyrządu pomiarowego określonym przez wytwórcę.
Miernik wielkości x wskazuje wartość ~
x tej wielkości (jest to wartość zmierzona lub
wskazanie miernika). Charakterystycznym dla miernika jest jego zakres pomiarowy
[X
min
, X
max
], tzn. przedział, wewnątrz którego mieści się wskazanie ~
x miernika. Różnica gór-
nej granicy X
max
i dolnej granicy X
min
zakresu pomiarowego
X
X
X
mm
=
−
max
min
(17)
nazywa się długością zakresu pomiarowego i jest ważnym parametrem miernika. Zwykle za-
kres pomiarowy zaczyna się od zera [0, X
max
], długość takiego zakresu pomiarowego, równa
górnej granicy zakresu pomiarowego X
mm
= X
max
, jest nazywana wprost zakresem pomiaro-
wym, a zakres miernika określa się podając tylko X
max
. Dla mierników cyfrowych zakres po-
miarowy, zwykle zaczynający się od zera jest określony liczbą cyfr i wartością jednostki
ostatniego rzędu q. Wartość jednostki ostatniego rzędu q (zwana także wartością cyfry,
kwantem, czułością lub LSD od ang. least significant digit) jest podawana w jednostkach
wielkości mierzonej, równa się ona zawsze dziesiętnej podwielokrotności lub wielokrotności
jednostki wielkości mierzonej. Zakres miernika cyfrowego może być podawany jako zakres
wielkości mierzonej [0, X
max
), częściej nawet jako X
max
, lub zakres wskazań cyfrowych
[0, N
max
), częściej nawet jako N
max
, przy czym zachodzi
X
N
q
max
max
=
(18)
2
Innymi słowy, błąd metody powstaje wówczas, gdy przyrząd mierzy nie to, co powinien mierzyć; np.
woltomierz przy pomiarze napięcia źródła w stanie jałowym mierzy napięcie źródła obciążonego impedancją
woltomierza, woltomierz połączony ze źródłem "długimi" przewodami mierzy napięcie zniekształcone
zakłóceniami indukowanymi w przewodach.

38
a N
max
jest zwiększoną o jeden największą liczbą (nie uwzględniając przecinka, który
wyznacza wartość kwantu q) wskazywaną przez miernik. Stosuje się niekiedy nazwy:
•
miernik M cyfrowy czyli miernik o M cyfrach, mogących przyjmować wartości 0,1,...,9
każda, dla takiego miernika N
max
= 10
M
,
•
miernik M i
1
/
2
cyfrowy, w którym pierwsza cyfra może przyjmować wartości 0 i 1, a
pozostałe M cyfr – wartości 0,1,...,9 każda; dla takiego miernika N
max
= 2
⋅
10
M
,
•
miernik M i
3
/
4
cyfrowy, w którym pierwsza cyfra może przyjmować wartości 0,1,..., K–1,
(
)
2
9
< ≤
K
a pozostałe M cyfr może przyjmować wartości 0,1,...,9 każda, dla takiego
miernika N
max
= K
⋅
10
M
.
Każdy miernik z natury jest niedokładny, wskazanie miernika ~
x różni się od wartości
prawdziwej x& wielkości mierzonej. Niedokładność miernika opisuje nieznany prawdziwy
błąd wskazania i znany graniczny błąd instrumentalny miernika. Wytwórca gwarantuje, że
błąd prawdziwy wskazania miernika nie przekracza podanej przez niego wartości błędu
granicznego.
Dla elektrycznych mierników analogowych graniczny błąd bezwzględny i graniczny
błąd względny są określane zwykle przez klasę dokładności k przyrządu i wynoszą
=
=
∆
x
X
x
X
x
~
100
max
max
max
max
k
k
δ
(19)
Klasa dokładności k przyrządu jest granicznym błędem bezwzględnym wyrażonym w procen-
tach długości zakresu. Norma polska PN 84/E 06501 Mierniki elektryczne analogowe o dzia-
łaniu bezpośrednim i ich przybory ustala następujące klasy dokładności:
0,05; 0,1; 0,2; 0,5; 1; 1,5 i 2;5
Klasę dokładności podaje się na skali przyrządu.
Dla przyrządów cyfrowych graniczny błąd pomiaru (wskazania) określa się zwykle
jako sumę błędu
δ
R
podanego w procentach od wartości mierzonej (wskazanej) i błędu
wynikającego z braku pewności co do n ostatnich jednostek (kwantów) wskazania cyfrowego.
Ten drugi składnik błędu granicznego jest zwany błędem od długości zakresu
max
X
i czasem
jest podawany w procentach jako
δ
FS
(
δ
FS
= 100 n/N
max
). Często graniczny błąd przyrządu
cyfrowego zapisuje się stosując nazwy angielskie
δ
R
% rdg + n dgt lub
δ
R
% rdg +
δ
FS
%
3
.
3
R, rgd pochodzi od reading – odczyt, dgt od digit – cyfra, skrót FS pochodzi od Full Scale - pełny zakres.

39
Graniczny błąd bezwzględny pomiaru i graniczny błąd względny pomiaru dla tak opisanego
miernika cyfrowego wynoszą
+
±
=
+
±
=
+
±
=
+
±
=
∆
)%
100
(
)%
(
100
)
(
)
100
(
max
max
max
max
N
n
N
N
x
q
N
N
q
n
N
x
FS
R
R
R
FS
R
δ
δ
δ
δ
δ
δ
δ
(20)
gdzie: N - wskazanie cyfrowe wartości mierzonej bez uwzględniania przecinka.
Do wykresów błędów miernika analogowego i cyfrowego jeszcze wrócimy.
Przykład 3
(a)
Woltomierz analogowy o zakresie [0; 300 V] i klasie dokładności 0,5 wskazał:
(1) 295 V, (2) 153 V, (3) 101 V, (4) 32 V
Obliczyć graniczne błędy pomiaru bezwzględne i względne oraz podać wyniki pomiaru w pełnej postaci. Gra-
niczny bezwzględny błąd pomiaru jest jednakowy dla wszystkich pomiarów i wynosi
∆
max
U = 0,005
⋅
300 V = 1,5 V
Graniczne względne błędy pomiaru są różne dla różnych pomiarów, oblicza się je z (19).
(1)
U = 295,0 V
±
1,5 V
U
∈
[293,5 V; 296,5 V]
δ
maxU = 0,508%
≈
0,5%
(2)
U = 153,0 V
±
1,5 V
U
∈
[151,5 V; 154,5 V]
δ
maxU = 0,980%
≈
1,0%
(3)
U = 101,0 V
±
1,5 V
U
∈
[ 99,5 V; 102,5 V]
δ
maxU = 1,485%
≈
1,5%
(4)
U = 32,0 V
±
1,5 V
U
∈
[ 30,5 V; 33,5 V]
δ
maxU = 4,687%
≈
4,7%
Graniczny względny błąd pomiaru (4) jest zbyt duży, przeszło dziewięć razy większy niż w okolicy końca
zakresu, należałoby zastosować przyrząd o mniejszym zakresie.
(b)
Woltomierz czterocyfrowy o błędzie 0,05% rdg + 5 dgt (i o dekadowo zmienianych zakresach) wskazał na
zakresie 10 V:
(1) 9,837 V, (2) 6,667 V, (3) 1,017 V, (4) 0,333 V
Obliczyć graniczne błędy pomiaru bezwzględne i względne oraz podać wyniki pomiaru w pełnej postaci.
Zakres wskazań cyfrowych woltomierza wynosi Nmax = 10
4
V, wartość jego ostatniej cyfry, czyli kwant, –
q = 10–
3
V. Graniczne błędy pomiaru bezwzględny i względny oblicza się z (20).
(1)
∆
maxU = 9,919
⋅
10–3 V
≈
10
⋅
10–3 V U = 9,837 V
±
0,010 V
δ
maxU = 0,1008%
≈
0,1%
(2)
∆
maxU = 8,333
⋅
10–3 V
≈
8
⋅
10–3 V U = 6,667 V
±
0,008 V
δ
maxU = 0,1250%
≈
0,13%
(3)
∆
maxU = 5,509
⋅
10–3 V
≈
6
⋅
10–3 V U = 1,017 V
±
0,006 V
δ
maxU = 0,5416%
≈
0,54%
(4)
∆
maxU = 5,167
⋅
10–3 V
≈
5
⋅
10–3 V U = 0,333 V
±
0,005 V
δ
maxU = 1,5515%
≈
1,55%
Graniczny względny błąd pomiaru (4) jest zbyt duży, przeszło piętnaście razy większy niż w okolicy końca
zakresu - należałoby zastosować mniejszy zakres przyrządu.
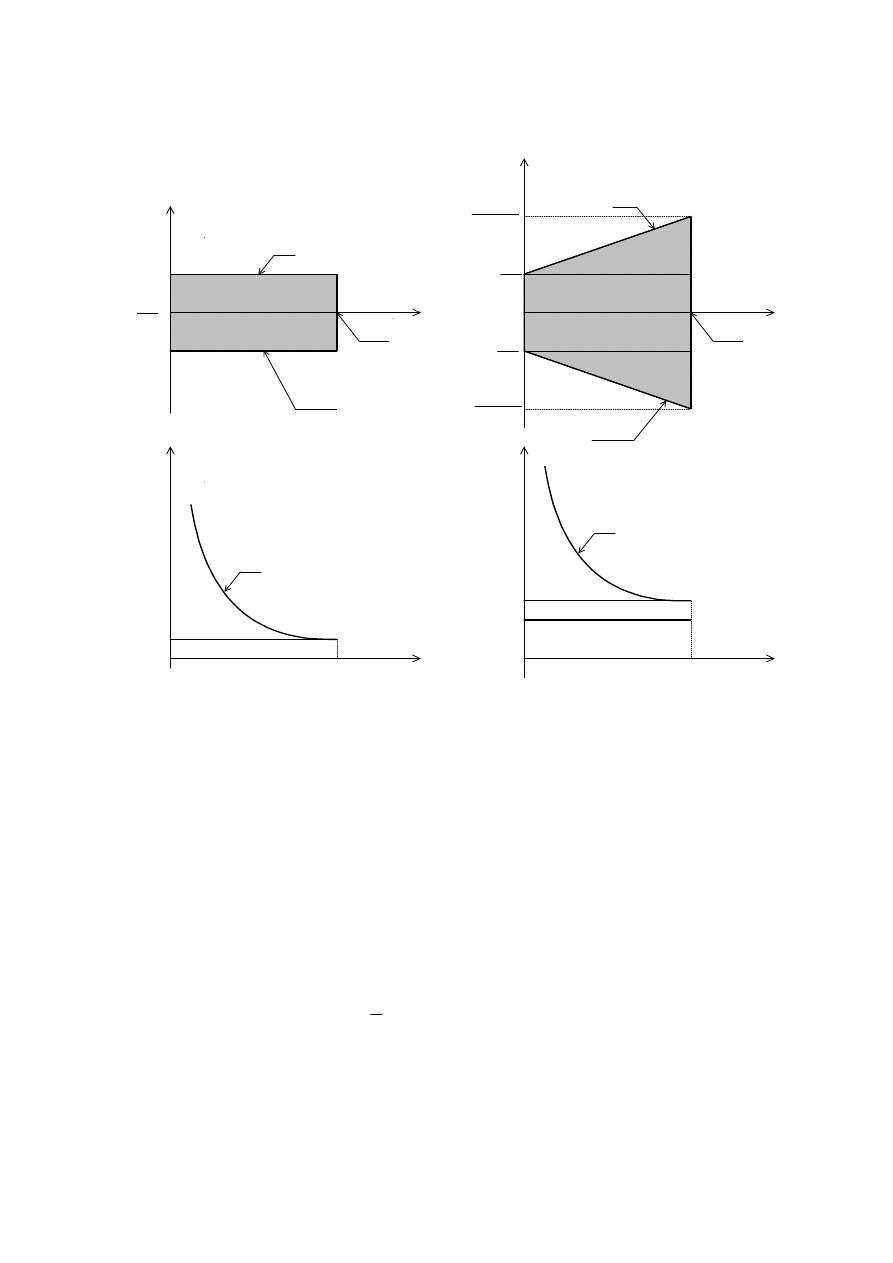
40
x
max
∆
x
max
∆
−
x
max
δ
max
X
max
X
100
FS
R
max
δ
δ
+
−
X
100
FS
R
max
δ
δ
+
X
100
FS
max
δ
X
100
FS
max
δ
X
−
x
max
∆
x
max
∆
−
max
X
max
k X
∗
max
k
-
X
∗
100
k
k
=
∗
x
max
δ
max
X
x
∆
x
δ
x
∆
x
δ
x
~
x
~
)
~
(x
N
)
~
(x
N
∗
k
(a)
(b)
FS
R
δ
δ
+
R
δ
Rys.2. Dopuszczalny obszar błędu bezwzględnego i górna połówka dopuszczalnego obszaru błędu
względnego: (a) miernika analogowego klasy k; (b) miernika cyfrowego o granicznym błędzie
δδδδ
R
%
odczytu +
δδδδ
FS
% długości zakresu; (błąd bezwzględny pomiaru miernikiem musi leżeć w obszarze
zaciemnionym!!!)
Z powyższych przykładów i analizy (19) oraz (20), a także z wykresów na rys.2 widać, że
niedokładność pomiaru zależy od wyboru zakresu miernika. Im wskazanie bliższe końca
zakresu, tym mniejszy graniczny względny błąd pomiaru. Możliwość zmniejszenia
granicznego błędu względnego poprzez wybór zakresu miernika jest uwarunkowany
asortymentem przyrządów, jakim dysponuje mierzący. Dla miernika analogowego jest
[
]
[
]
∈
∈
k
,
k
,
1
~
max
max
max
h
x
X
X
h
x
δ
(21)
tzn. jeżeli wskazanie przekracza 1/h-część zakresu, to błąd względny nie przekracza
h-krotnego błędu na końcu zakresu. Najczęściej przyjmuje się h = 4, co można na ogół

41
spełnić, gdyż zakresy mierników pozostają do siebie zwykle w stosunku 1:3:10. Mierniki
cyfrowe mają zakresy rozłożone dekadowo, przez co dla miernika cyfrowego jest
[
)
[
)
+
+
∈
∈
FS
R
FS
R
max
max
max
10
,
,
1
,
0
~
δ
δ
δ
δ
δ
x
X
X
x
(22)
Spełnienie powyższego wymaga takiego doboru zakres pomiarowego miernika cyfrowego,
żeby dla miernika
M cyfrowego pierwsza cyfra była niezerowa,
M i 1/2 cyfrowego zakazane były także kombinacje pierwszej i drugiej cyfry 00 i 01,
M i 3/4 cyfrowego zakazane były także kombinacje pierwszej i drugiej cyfry 00, 01,..., 0(K–1).
Współczesne mierniki cyfrowe mają oprócz ręcznego wyboru zakresu pomiarowego również
wybór automatyczny. Warunki (21) i (22) nie dotyczą zakresu najmniejszego.
5. Prawo propagacji błędów
Często wykonuje się pomiar pośredni wielkości y polegający na bezpośrednich pomia-
rach wielkości x
1
,..., x
M
, związanych z y znaną zależnością
)
,
,
(
1
J
x
x
f
y
K
=
(23)
i obliczeniu wartości y. W szczególnym przypadku pomiar pośredni y może polegać na
bezpośrednim pomiarze jednej tylko wielkości x i obliczeniu
y
f x
=
( )
(24)
Operacja wyznaczania błędu prawdziwego
∆
y wartości funkcji y w zależności od błędów
prawdziwych
∆
x
1
...,
∆
x
J
argumentów x
1
,..., x
J
nazywa się propagacją błędów lub składaniem
błędów lub przenoszeniem błędów, a formuła określająca tę zależność – prawem propagacji
(składania lub przenoszenia) błędów. Prawo przenoszenia błędów odnosi się także do sytuacji
ogólniejszej określania błędu wartości funkcji (23) obliczonej na podstawie niedokładnych ar-
gumentów obarczonych błędami dowolnego pochodzenia.
Najczęściej operuje się prawem składania błędów bezwzględnych w postaci zwanej
prawem różniczki zupełnej
∆
∆
y
K
x
m
m
M
m
=
=
∑
1
(25)

42
gdzie:
M
M
M
m
x
x
x
x
x
x
f
x
K
~
,
,
~
)
,
,
(
1
1
1
=
=
=
K
K
∂
∂
M
x
x
~
,
,
~
1
K
−
znane estymaty wartości argumentów.
lub prawem składania błędów względnych w postaci zwanej prawem różniczki logarytmicznej
δ
δ
y
k
x
m
m
M
m
=
=
∑
1
(26)
gdzie:
M
M
M
M
M
M
M
m
x
x
x
x
x
x
f
x
x
x
x
x
x
x
f
x
x
x
k
~
,
,
~
)]
,
,
(
[
ln
~
,
,
~
)
,
,
(
)
,
,
(
f
1
1
1
1
1
1
1
1
=
=
=
=
=
=
=
K
K
K
K
K
∂
∂
∂
∂
Prawo różniczki zupełnej wyprowadza się z definicji błędu bezwzględnego funkcji
)
~
,
,
~
(
)
~
,
,
~
(
)
,
,
(
)
~
,
,
~
(
~
1
1
1
1
1
M
M
M
M
M
x
x
x
x
f
x
x
f
x
x
f
x
x
f
y
y
y
∆
−
∆
−
−
=
=
−
=
−
=
∆
K
K
&
K
&
K
&
(27)
rozwijając
)
,...,
(
1
M
x
x
f
&
&
w szereg potęgowy wokół punktu
M
x
x
~
,...,
~
1
i pomijając wyrazy z błę-
dami w potędze większej niż jeden oraz z iloczynami błędów, jako znacznie mniejsze od
wyrazów z błędami w potędze pierwszej. Prawo różniczki logarytmicznej wyprowadza się z
definicji błędu względnego funkcji
)
~
,
,
~
(
)
,
,
(
1
1
M
M
x
x
f
y
x
x
f
y
y
y
y
K
&
K
&
&
∆
≈
∆
=
∆
=
δ
(28)
i prawa różniczki zupełnej. Zależności
)
,...,
(
1
M
x
x
f
y
&
&
&
=
i
M
x
x
&
& ,...,
1
są dokładnymi, ale niezna-
nymi, wartościami funkcji i argumentów, a
)
~
,...,
~
(
~
1
M
x
x
f
y
=
i
M
x
x
~
,...,
~
1
są niedokładnymi, ale
znanymi, wartościami funkcji i argumentów. Obydwa prawa można stosować, gdy spełniony
jest warunek pomijalności wyrazów z błędami w wyższych potęgach. Warunek ten nie jest
spełniony w pobliżu punktów zaniku pochodnych pierwszego rzędu.
Stosując prawa składania błędów dla najczęściej spotykanych funkcji (23), można wy-
prowadzić dla nich stosunkowo proste formuły zestawione w Tablicy 1. Błąd funkcji nie
umieszczonej w Tablicy 1 oblicza się albo stosując prawo różniczki zupełnej lub logarytmicz-
nej, albo, jeżeli funkcję tę można wyrazić jako kombinację funkcji prostych, stosując kolejno
reguły podane w Tablicy 1.

43
Tablica 1. Błędy niektórych funkcji
Funkcja
błąd funkcji
bezwzględny
∆
y lub względny
δ
y
y
K x
=
∆
∆
y
K
x
y
x
=
=
,
δ
δ
y
x
x
=
+
1
2
∆
∆
∆
y
x
x
=
+
1
2
y
x
x
=
−
1
2
∆
∆
∆
y
x
x
=
−
1
2
y
x x
=
1
2
δ
δ
δ
y
x
x
=
+
1
2
y
x
x
x
=
≠
1
2
2
0
,
δ
δ
δ
y
x
x
=
−
1
2
y
x
x
k
=
>
,
0
x
k
y
δ
δ
=
y
x
x
=
>
ln
,
0
δ
y
x
=
∆
y
x
a
x
a
=
>
>
log
,
,
0
0
δ
δ
y
a
x
=
1
ln
y
x
=
e
∆
y
x
=
δ
y
a
a
x
=
>
,
0
∆
y
a
x
=
ln
δ
y
x
x
=
<
sin
,
| |
1
2
π
∆
∆
y
x
x
=
cos
y
x
x
=
<
≤
cos ,
| |
0
1
2
π
∆
∆
y
x
x
= −
sin
y
x
=
arc tg
∆
∆
y
x
x
=
+
1
1
2
Przykład 2
Błąd funkcji
y
x
x x
=
arc cos
1
2 3
wyznaczymy wprowadzając zmienną pomocniczą
x
x
x x
y
=
=
1
2 3
cos
Teraz mamy
(
)
∆
∆
∆
∆
y
y
x x
x
x
x x
x
x
x x
x
x
y
x
x
x
= −
−
−
=
−
+
+
1
1
2
3
1
1
2
2
3
2
1
2
3
2
3
1
2
3
sin
sin
δ
δ
δ
gdyż
d
d
(arc cos
x
x
x
y
)
sin
= −
−
= −
1
1
1
2

44
Błąd funkcji
3
3
2
1
x
x
y
x
=
wyznaczymy logarytmując tę funkcję. Jest
ln
ln
ln
y
x
x
x
=
+
2
1
3
3
i dalej
δ
δ
y
y
x
x
x
x
x
x
x
x
=
=
+
=
+
=
∆
∆
∆
∆
(ln )
(
ln
)
( ln
)
ln
(
ln
)
(ln
)
2
1
3
2
1
2
1
3
3
3
[
]
=
+
+
=
+
+
=
+
+
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
2
1
1
2
3
2
1
1
1
2
3
2
1
2
1
2
3
3
3
3
ln
(ln
)
ln
(ln
)
ln
ln
δ
δ
δ
δ
δ
δ
δ
δ
∆
Błąd funkcji
y
x
x
x
x
=
−
1
2
2
2
3
2
2
4
obliczamy jako
δ
δ
δ
δ
y
x
x
x
x
x
x
x
x
x
x
x
x
y
x
x
x
x
y
x
x
x
x
x
x
x
x
=
−
=
−
−
=
−
=
−
=
1
2
1
2
2
2
3
2
2
4
1
2
1
2
2
2
3
2
2
4
1
2
2
2
3
2
2
4
2
1
2
2
2
3
2
2
4
2
1
2
2
2
1
2
2
2
3
2
2
4
3
2
2
4
1
2
1
2
∆
∆
∆
=
−
−
−
=
−
−
−
1
2
2
2
2
4
1
2
2
1
2
2
2
1
2
3
2
2
4
3
2
2
1
2
2
2
1
1
2
2
2
3
2
2
4
2
3
2
2
4
3
y
x
x
x
x
x
x
x
x
y
x
x
x
x
x
x
x
x
x
x
x
(
)
(
δ
δ
δ
δ
δ
δ
δ
6. Szacowanie granicznego błędu pomiaru pośredniego. Model zdeterminowany
Prawa i reguły z poprzedniego rozdziału odnoszą się do obliczania błędu prawdziwego
funkcji: bezwzględnego
∆
y lub względnego
δ
y. Na ich podstawie można dalej oszacować błąd
graniczny funkcji: bezwzględny
∆
max
y lub względny
δ
max
y w zależności od błędów
granicznych argumentów: bezwzględnych
∆
max
x
1
,...,
∆
max
x
M
lub względnych
δ
max
x
1
,...,
δ
max
x
M
.
Operacja ta nazywa się składaniem niepewności lub składaniem błędów granicznych.
Stosowane są dwie metody składania niepewności.
Metoda najgorszego rozłożenia zakłada najgorsze z możliwych rozłożenie błędów
∆
x
m
(lub
δ
x
m
) poszczególnych argumentów – wszystkie mają wartości skrajne
±
∆
max
x
m
(lub
±
δ
max
x
m
), ich moduły są równe błędom granicznym, a znaki takie, jak znaki odpowiadają-
cych im współczynników wrażliwości. Graniczny błąd pomiaru określa wzór
∆
∆
max
max
max
max
y
K
x
y
k
x
m
m
m
M
m
m
m
M
=
=
=
=
∑
∑
1
1
δ
δ
(29)
Metoda najgorszego rozłożenia daje oszacowanie zawyżone, ale pewne. Metodę najgorszego
rozłożenia stosuje się przy małej liczbie argumentów M i tam, gdzie zależy na dużej pewności
oszacowania przedziału niepewności.

45
Metoda losowego rozłożenia zakłada, bardziej realistycznie, że błędy systematyczne
estymat wartości poszczególnych wielkości wejściowych są rozłożone w różnych punktach
wewnątrz swoich przedziałów niepewności [-
∆
max
x
m
,
∆
max
x
m
], niekoniecznie na ich krańcach.
Losowe rozłożenie błędów systematycznych jest rozkładem zbioru błędów
J
x
x
∆
∆
,...,
1
, a nie
pojedynczych błędów
∆
x
j
. Graniczny błąd pomiaru określa wzór
4
∆
∆
max
max
max
max
(
)
(
)
y
K
x
y
k
x
m
m
m
M
m
m
m
M
=
=
=
=
∑
∑
3
3
2
2
1
2
2
1
δ
δ
(30)
Metodę losowego rozłożenia stosuje się przy większej liczbie argumentów obarczonych błę-
dami niezależnymi od siebie.
Przykład 3
Funkcja y jest iloczynem: (a) czterech, (b) dziewięciu, (c) dwudziestu pięciu i (d) stu argumentów, z których
każdy jest obarczony granicznym błędem względnym
δ
maxxm = 1%. Prawdziwy względny błąd funkcji jest
sumą prawdziwych względnych błędów wszystkich argumentów. Szacując graniczny względny błąd funkcji
δ
maxy metodą najgorszego rozłożenia otrzymuje się wartości: (a) 4%, (b) 9%, (c) 25% i (d) 100% (!!!), a sza-
cując metodą losowego rozłożenia: (a) 3,5%, (b) 5,2%, (c) 8,7% i (d) 18%.
7. Szacowanie granicznego błędu pomiaru bezpośredniego. Model losowy
Metodę szacowania niepewności pomiaru przedstawioną w p.4 i p.6 można stosować
przyjmując zdeterminowany model błędu pomiaru. Model ten może być zastosowany, jeżeli
wyniki pomiarów tej samej wartości mezurandu powtarzane w tych samych warunkach (takie
pomiary nazywają się pomiarami powtarzanymi w warunkach powtarzalności) są jednakowe.
Często zdarza się jednak, że pomiary powtarzane w warunkach powtarzalności różnią się mię-
dzy sobą. Niech wyniki pojedynczych powtarzanych pomiarów wynoszą x(1), x(2),..., x(N).
W takich sytuacjach przyjmuje się losowy model błędu pomiaru, zakładając, że wynik
pomiaru x jest obarczony błędem
∆
=
∆
x
, modelowanym zmienną losową. Błąd ten rozkłada
4
Zależność tę otrzymuje się zakładając równomierny rozkład błędów wewnątrz przedziału niepewności i
przyjmując tzw. trójsigmowy przedział ufności, co odpowiada wysokiemu poziomowi ufności 0,9973. Godząc
się z mniejszym poziomem ufności 0,916 można graniczny błąd pomiaru szacować z zależności
∆
∆
max
max
(
)
y
K
x
m
m
m
M
=
=
∑
2
2
1
lub
δ
δ
max
max
(
)
y
k
x
m
m
m
M
=
=
∑
2
2
1

46
się na dwie składowe: błąd systematyczny
ξ
=
∆
x
s
, niezmienny dla każdego pomiaru, i błąd
przypadkowy
∆
r
x
=
ε
będący zmienną losową o zerowej wartości oczekiwanej. Jest więc
ε
ξ
+
+
=
∆
+
=
x
x
x
&
&
(31)
Zmiennymi losowymi są x,
∆
i
ε
. Wartości oczekiwane tych zmiennych wynoszą
odpowiednio
0
)
(
,
)
(
,
)
(
=
=
∆
+
=
ε
ξ
ξ
E
E
x
x
E
&
(32)
Błąd systematyczny definiuje się jako wartość oczekiwaną błędu pomiaru powtarzanego w
warunkach powtarzalności, a błąd przypadkowy – jako centrowany (tzn. z zerową wartością
oczekiwaną) błąd pomiaru powtarzanego w warunkach powtarzalności.
O błędzie przypadkowym przyjmuje się zwykle, że jest zmienną losową o rozkładzie
normalnym z zerową wartością oczekiwaną i wariancją
2
σ
, zapisuje się to
ε
∈
N
(0,
σ
2
)
(33)
Wynik pomiaru jest także zmienną losową o rozkładzie normalnym
X
∈
N
(
ξ
+
x&
,
σ
2
)
(34)
gdzie
)
(
2
2
x
σ
σ
=
jest wariancją błędu przypadkowego i wariancją zmiennej losowej
modelującej wynik pojedynczego pomiaru. Błąd systematyczny spełnia
ξ
∈
[−
ξ
max
,
ξ
max
]
(35)
gdzie
ξ
max
max
=
∆
s
x jest granicznym błędem systematycznym. Najczęściej błąd
systematyczny jest błędem instrumentalnym, jego wartość graniczną
ξ
max wyznacza się z
danych o przyrządach pomiarowych.
Estymatą xˆ wartości prawdziwej mezurandu x& jest średnia arytmetyczna wyników
serii pojedynczych pomiarów
∑
=
=
N
n
n
y
N
y
1
)
(
1
,
∑
=
=
+
+
=
N
n
n
N
y
y
1
)
(
1
,
ε
ε
ε
ξ
&
(36)
obarczona błędem składającym się z błędu systematycznego
ξ
=
∆
yˆ
s
i błędu przypadkowego
ε
=
∆
yˆ
r
(równego średniej arytmetycznej błędów przypadkowych pojedynczych pomiarów)
spełniających

47
ξ
∈
[−
ξ
max
,
ξ
max
]
i
N
x
x
2
2
2
)
(
,
)]
(
,
0
[
N
σ
σ
σ
ε
=
∈
(37)
Odpowiednio do granicznego błędu systematycznego określa się graniczny błąd przypadkowy
jako połowę szerokości przedziału ufności na poziomie ufności
N
x
x
z
2
2
1
max
)
(
,
)
(
σ
σ
σ
ε
α
=
=
−
(38)
gdzie
α
−
1
z
jest kwantylem rzędu 1–
α
/2 rozkładu normalnego standaryzowanego
N
(0,1). Naj-
częściej przyjmuje się
3
1
=
−
α
z
(błąd trójsigmowy) z
99
,
0
9973
,
0
1
≈
=
−
α
lub
2
1
=
−
α
z
(błąd
dwusigmowy) z 1
0 9545
0 95
− =
≈
α
,
,
. Zwykle wariancja
2
σ
jest nieznana, wyznacza się jej
estymatę
s
x
N
x n
x
N
x n
n
N
n
N
2
2
1
2
1
1
1
1
1
( )
[ ( )
]
[
( )]
=
−
−
=
−
=
=
∑
∑
∆
d
(39)
gdzie
∆
d
x n
x n
x
( )
( )
=
−
jest odchyleniem wskazania od średniej arytmetycznej. Graniczny błąd
przypadkowy oblicza jako
ε
α
max
( ) ,
( )
=
=
−
z
s x
s
x
s
N
1
2
2
(40)
Formuła ta jest formułą przybliżoną, można ją uściślić zastępując kwantyle rozkładu normal-
nego kwantylami rozkładu t-Studenta. Graniczny błąd pomiaru oblicza się
max
max
max
ε
ξ
+
=
∆
y
(41)
czyli jako sumę granicznego błędu systematycznego i granicznego błędu przypadkowego. Ta-
kie liczenie granicznego błędu pomiaru odpowiada hipotetycznemu powtarzaniu serii pomia-
rów w warunkach powtarzalności, a więc zawsze tego samego błędu systematycznego. Ta
metoda szacowania niepewności będzie nazywana
metodą powtarzania błędu systematycz-
nego.
Często zachodzi potrzeba porównywania wyników pomiarów wykonywanych w róż-
nych laboratoriach. Wtedy lepiej jest obliczać graniczny błąd pomiaru
metodą randomizacji
i centryzacji błędu systematycznego, jako
3
)
(
ˆ
2
max
2
2
1
max
ξ
α
+
=
∆
−
y
s
z
x
(42)
co odpowiada hipotetycznemu powtarzaniu serii pomiarów, każdej z innym błędem systema-
tycznym, losowo wybieranym z równomiernego rozkładu błędu systematycznego w
przedziale
[−
ξ
max
,
ξ
max
].
Fizycznie taką sytuację można byłoby stworzyć wykonując każdą
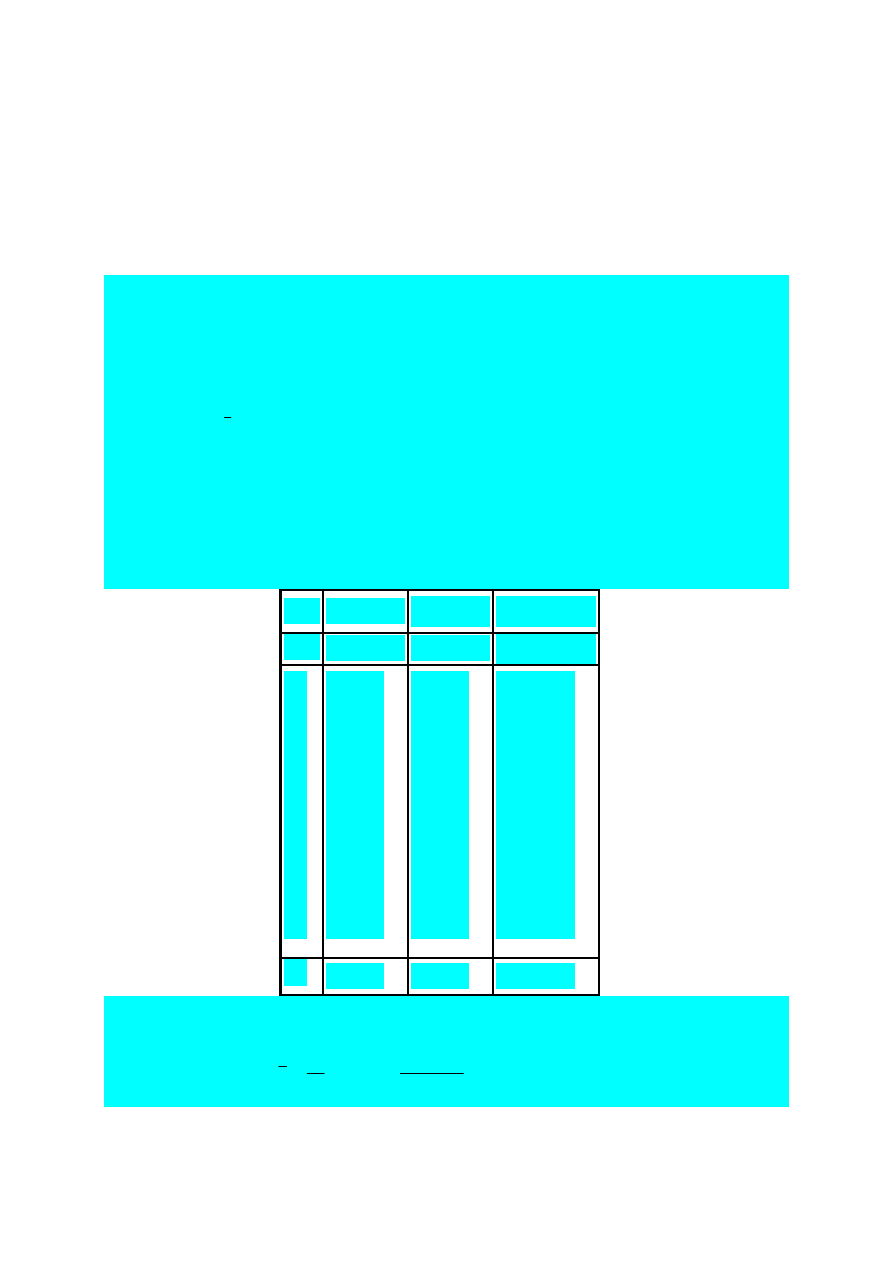
48
serię pomiarów innym przyrządem, losowo wybranym z populacji wszystkich przyrządów o
tym samym granicznym błędzie instrumentalnym
ξ
max
.
Przedstawioną metodykę obliczeń ograniczono do szacowania błędu granicznego bez-
względnego, bez trudu można ją rozszerzyć na szacowanie błędu granicznego względnego.
Przykład 4
Woltomierzem cyfrowym o maksymalnym wskazaniu cyfrowym 3999 i niedokładności (granicznym błędzie
pomiaru) 0,5% odczytu plus 3 jednostki ostatniego rzędu wykonano serię dziesięciu pomiarów napięcia. Wyniki
pomiarów podano w drugiej kolumnie tablicy. Tablica ta będzie tablicą wzorcową do rozwiązywania zadań
podobnego typu z zastrzeżeniem, że obecnie stosowane kalkulatory (nie mówiąc już o komputerach) pozwalają
otrzymać wartości
x
i s bez potrzeby wypełniania trzeciej i czwartej kolumny tablicy.
Pomiary powinny być wykonane (zgodnie z zasadami sztuki mierzenia) na zakresie 100,0 V, wartość cyfry
ostatniego rzędu (kwant) tego zakresu wynosi 0,1 V. Na podstawie danych o niedokładności woltomierza obli-
czamy graniczny błąd systematyczny jego wskazań
V
0,8
=
V
1
,
0
3
V
0
,
100
005
,
0
ˆ
s
max
×
+
×
=
∆
x
n
x(n)
∆
dx(n)
[
∆
xd(n)]2
V
V
V2
1
2
3
4
5
6
7
8
9
10
97,1
95,6
101,6
102,9
102,8
95,5
104,3
99,1
102,5
103,5
-3,4
-4,9
1,1
2,4
2,3
-5,0
3,8
-1,4
2,0
3,0
11,56
24,01
1,21
5,76
5,29
25,00
14,44
1,96
4,00
9,00
Σ
1004,9
-0,1
102,23
Na podstawie danych wyników pojedynczych pomiarów x(n) obliczamy
V
5
,
100
V
49
,
100
10
V
9
,
1004
)
(
1
1
=
=
=
=
∑
=
N
n
n
x
N
x

49
stąd obliczamy odchylenia od średniej
∆
d
x(n)= x(n)–
x
i ich sumę, której zerowa wartość (lub bliska zeru ze
względu na zaokrąglanie średniej arytmetycznej
x
) jest sprawdzianem poprawności obliczeń, a na jej podstawie
obliczamy estymatę wariancji błędu przypadkowego i wskazań
[
]
2
2
1
2
d
2
V
36
,
11
9
V
23
,
102
)
(
1
1
≈
=
∆
−
=
∑
=
N
n
n
x
N
s
,
oraz estymaty wariancji i odchylenia standardowego średniej arytmetycznej wskazań
2
2
2
2
V
136
,
1
10
V
36
,
11
)
(
=
=
=
N
s
x
s
,
V
1
,
1
V
066
,
1
)
(
≈
=
x
s
Obliczamy graniczny błąd pomiaru metodą powtarzania błędu systematycznego. Jest on sumą granicznego
błędu systematycznego i granicznego błędu przypadkowego
x
x
x
ˆ
ˆ
ˆ
r
max
s
max
max
∆
+
∆
=
∆
Graniczny błąd przypadkowy na poziomie ufności bliskim 0,95 obliczamy jako
V
2
,
2
)
(
2
ˆ
r
max
=
=
∆
x
s
x
i stąd ostatecznie
V
0
,
3
=
V
8
,
0
V
2
,
2
ˆ
ˆ
ˆ
r
max
s
max
max
+
=
∆
+
∆
=
∆
x
x
x
,
V
0
,
3
V
5
,
100
±
=
x&
Obliczamy graniczny błąd pomiaru metodą randomizacji i centryzacji błędu systematycznego przyjmując
dalej poziom ufności bliski 0,95
(
)
V
4
,
2
V
162
,
1
2
V
136
,
1
3
)
V
8
,
0
(
2
)
(
3
ˆ
2
ˆ
2
2
2
2
2
s
max
max
≈
×
=
+
=
+
∆
=
∆
x
s
x
x
,
V
4
,
2
V
5
,
100
±
=
x&
Otrzymaliśmy dwie różne wartości błędu granicznego, różnica między nimi wynosząca około 20%, wynikająca z
różnej interpretacji błędu granicznego, nie powinna nikogo przerażać, gdyż dopuszczalny błąd oszacowania
błędu jest rzędu dziesiątków procent.

50
Wykład 5, 6 i 7
Metody pomiarowe i narzędzia pomiarowe I
Przetwarzanie sygnałów pomiarowych i przetworniki pomiarowe. Model przetwornika analo-
gowego. Parametry charakterystyczne. Normalizacja błędów przetwarzania. Przetworze-
niowo-sygnałowy model pomiaru. Wzorzec i komparator. Komparacja równoczesna i nie
równoczesna - kompensacja i podstawienie. Pomiary analogowe.
1. Przetwarzanie sygnałów pomiarowych
Przetwarzaniem sygnałów pomiarowych nazywa się operację zamiany sygnału pomiarowego
w inny sygnał pomiarowy z zachowaniem, w granicach określonej niedokładności, ustalonego
związku między treściami obu sygnałów. Sygnał przetwarzany nazywa się sygnałem wejścio-
wym, sygnał przetworzony - sygnałem wyjściowym, związek między treściami sygnałów -
równaniem przetwarzania. Funkcja wyrażająca zależność treści sygnału wyjściowego od
treści sygnału wejściowego nazywa się funkcją przetwarzania. Funkcja wyrażająca zależność
treści sygnału wejściowego od treści sygnału wyjściowego nazywa się odwrotną funkcją
przetwarzania.
W niniejszych rozważaniach pominiemy na początku zagadnienia niedokładności przetwarza-
nia, rozważać więc będziemy przetwarzanie dokładne według równania przetwarzania. Odpo-
wiednio do wyróżnionych dwóch rodzajów sygnałów: analogowego i cyfrowego, wyróżnia
się cztery typy przetwarzania:
•
przetwarzanie analogowe,
•
przetwarzanie analogowo-cyfrowe,
•
przetwarzanie cyfrowo-analogowe,
•
przetwarzanie cyfrowe.
Przetwarzanie analogowe
jest przetwarzaniem sygnału analogowego w analogowy.
Równanie przetwarzania analogowego może mieć postać identyczności lub równania algebra-
icznego liniowego lub nieliniowego wiążącego treści sygnałów, ale może także mieć postać
równania różniczkowo-całkowego, zawierającego pochodne i całki rozkładów czasowych sy-
gnałów, lub równania różnicowego. Istnieje wiele rodzajów przetwarzania analogowego,
ograniczymy się do krótkiego omówienia kilku tylko rodzajów.

51
Najprostszym strukturalnie przetwarzaniem analogowym jest przetwarzanie skali
(wielkości) zwane także przetwarzaniem wartości (wielkości), w którym nie zmienia się ani
natura i rodzaj nośnika sygnału wejściowego i wyjściowego (np. wielkością nośną obydwu
sygnałów jest napięcie elektryczne lub ciśnienie płynu), ani rodzaj wartości nośnika (np. oby-
dwa sygnały są przenoszone przez wartości wielkości nośnych lub ich amplitudy), ani
wreszcie kody sygnałów. Funkcja przetwarzania skali jest funkcją wzajemnie jednoznaczną,
zwykle prostą proporcjonalnością.
Przetwarzanie (natury) wielkości jest przetwarzaniem analogowym, w którym zmienia
się natura nośników przetwarzanych sygnałów (np. z mechanicznej w elektryczną, z
termicznej w elektryczną). Przetwarzanie wielkości, jako przetwarzanie sygnałów
pomiarowych, jest aspektem informacyjnym przetwarzania energii (np. mechanicznej w
elektryczną, termicznej w elektryczną). Przetwarzaniu wielkości poddawane są zwykle
sygnały proste.
Równania przetwarzania wartości i przetwarzania wielkości sygnałów naturalnych
(dla których treść sygnału jest identyczna z wartością wielkości nośnej) mają postać
[
]
y
x
x
X
X
X
X
=
∈
=
+
g( )
mm
min
max
min
,
(1)
gdzie: x
−
wartość sygnału wejściowego (tzn. wartość chwilowa wielkości nośnej równa
treści sygnału),
y
−
wartość sygnału wyjściowego,
g(x)
−
prosta funkcja przetwarzania,
[X
min
, X
max
]
−
zakres przetwarzania sygnału wejściowego,
X
mm
−
długość zakresu przetwarzania.
Odniesienie przyrostu sygnału wyjściowego
∆
y do powodującej ten przyrost niewielkiej
zmiany sygnału wejściowego
∆
x nazywa się czułością (prostą) przetwornika
G
y
x
= ∆
∆
(2)
Niekiedy przetwornik opisuje się odwrotnym równaniem przetwarzania
[
]
x
y
y
Y
Y
Y
Y
=
∈
=
+
h( )
min
max
min
mm
,
(3)

52
gdzie:
x
−
wartość sygnału wejściowego,
y
−
wartość sygnału wyjściowego,
h(y)
−
odwrotna funkcja przetwarzania,
[Y
min
, Y
max
]
−
zakres przetwarzania sygnału wyjściowego,
Y
mm
−
długość zakresu przetwarzania.
Odniesienie niewielkiej zmiany sygnału wejściowego
∆
x do odpowiadającego jej przyrostu
sygnału wyjściowego
∆
y nazywa się czułością odwrotną przetwornika
H
x
y
=
∆∆∆∆
∆∆∆∆
(4)
Niektóre przetworniki mogą realizować zarówno operację przetwarzania prostego jak i od-
wrotnego. Dla takich przetworników funkcje g() i h() są funkcjami wzajemnie odwrotnymi.
Najchętniej stosuje się przetworniki liniowe o równaniu przetwarzania
y
G x
x
H y
=
=
(5)
gdzie:
G
H
=
1
−
czułość przetwornika liniowego
H
G
=
1
−
stała przetwarzania przetwornika liniowego
Przetwarzanie rozkładu
(wielkości) jest przetwarzaniem analogowym, w którym zmie-
nia się rozkład czasowy i widmowy wielkości nośnej, a co za tym idzie rodzaj wartości nośnej
przetwarzanych sygnałów. Stosuje się wiele rodzajów przetwarzania rozkładu (prostowanie,
modulacja, demodulacja, filtracja), niektóre z nich omówimy w dalszych częściach wykładu.
Kwantowanie
jest operacją polegającą na zamianie zmiennej rzeczywistej ciągłej x w
zmienną rzeczywistą dyskretną y w ten sposób, że dziedzinę argumentu dzieli x się zupełnie i
rozłącznie na przedziały i każdemu przedziałowi przyporządkowuje się jedną wartość y argu-
mentu z tego przedziału. Zwykle przedziały zmiennej kwantowanej x mają jednakową
długość, zwaną kwantem (niekiedy także nieprawidłowo rozdzielczością), są lewostronnie
domknięte, a wartościami zmiennej skwantowanej y są wartości centralne przedziału
y
x
q
x
q
=
=
+
Q
( )
E
1
2
(6)
gdzie: E()
−
funkcja entier (część całkowita liczby rzeczywistej),Q
−
operator kwantowania.
Jeżeli wartość zmiennej skwantowanej y przyjmuje się za reprezentację wartości zmiennej
ciągłej x, to popełnia się błąd kwantowania

53
∆
∆
Q
Q
= −
∈ −
y
x
q
q
(
,
]
1
2
1
2
(7)
gdzie:
1
2
q
−
jest granicznym błędem kwantowania.
Operacji kwantowania poddaje się najczęściej sygnały naturalne, wówczas x i y są
wartościami sygnału wejściowego i wyjściowego.
Próbkowanie jest operacją polegającą na zastąpieniu funkcji rzeczywistej x(t) argu-
mentu rzeczywistego ciągłego t, zwykle identyfikowanego z czasem, ciągiem indeksowanym
liczb rzeczywistych y(i), reprezentujących wartości tej funkcji w kolejnych, tak samo indekso-
wanych przedziałach argumentu, na które podzielona jest zupełnie i rozłącznie dziedzina
argumentu t. Liczba y(i) zastępująca wartość funkcji w danym przedziale, zwanym
przedziałem (lub okresem) próbkowania, nazywa się próbką funkcji. Indeks próbki i nazywa
się czasem dyskretnym, wartość próbki jest funkcją czasu dyskretnego. Najczęściej stosuje się
próbkowanie chwilowe równomierne, o stałej długości
τ
okresu próbkowania i próbkach
równych wartościom funkcji w początkach okresów próbkowania
y i
P x t
x i
( )
( )}
(
)
=
=
{
ττττ
(8)
gdzie: P
−
operator próbkowania.
Okres próbkowania
τ
jest charakterystycznym parametrem operacji próbkowania, jego od-
wrotność nazywa się częstotliwością próbkowania.
Operacja próbkowania (ang. sample) modeluje przetwarzanie sygnału analogowego
ciągłego w czasie w sygnał analogowy dyskretny w czasie. Operacja próbkowania może
łączyć się z operacją zapamiętywania (ang. sample and hold) polegającą na przetwarzania
sygnału analogowego ciągłego w czasie w sygnał analogowy dyskretny w czasie z pamięcią.
Ciąg próbek y(i) reprezentuje funkcję x(t) argumentu ciągłego, ale reprezentacja ta może być
niedokładna, tzn. sygnał x(t) i sygnał odtworzony z próbek mogą się różnić.
Jeżeli sygnał x(t)
ma widmo ograniczone częstotliwością f
max
, to można go dokładnie odtworzyć z próbek
chwilowych o częstotliwości próbkowania nie mniejszej niż 2 f
max
. Jest to twierdzenie o prób-
kowaniu (twierdzenie Shannona).
Przetwarzanie analogowo-cyfrowe
jest operacją przetwarzania sygnału analogowego
w cyfrowy. Sygnałem wejściowym przetwarzania analogowo-cyfrowego jest sygnał analo-
gowy, zwykle naturalny; sygnałem wyjściowym jest sygnał cyfrowy, dyskretny w czasie z pa-
mięcią, którego treścią jest cyfrowa reprezentacja ky wartości liczbowej x sygnału wejścio-
wego. Przetwarzanie analogowo-cyfrowe składa się z trzech operacji:

54
•
próbkowania sygnału analogowego, chwile próbkowania są wyznaczane przez sygnał taktu-
jący, którego częstotliwość, zwana częstotliwością próbkowania lub repetycji jest charakte-
rystycznym parametrem przetwarzania A/C;
•
kwantowania, kwant q jest drugim charakterystycznym parametrem przetwarzania A/C;
•
kodowania cyfrowego liczby kwantów ky; rodzaj kodu jest trzecią charakterystyczną cechą
przetwarzania A/C.
Zależnie od kodu sygnału wyjściowego stosuje się także nazwy przetwarzanie sygnału analo-
gowego w kod dwójkowy (lub dwójkowo-dziesiętny lub dziesiętny). Równanie przetwarzania
przetwornika analogowo-cyfrowego ma postać
[
)
[
)
k
x
q
x
X
k
N
y
y
=
+
∈
⊂
∈
⊂
E
1
2
0
0
,
,
,
,
max
max
R
N
(9)
gdzie:
x
−
sygnał wejściowy,
k
y
−
wartości liczbowe przenoszone przez sygnał wyjściowy,
q
X
N
=
max
max
−
kwant przetwarzania, zwany także rozdzielczością przetwornika.
Równanie przetwarzania przetwornika A/C w kod dwójkowy, czyli przetwornika A/C którego
sygnał cyfrowy koduje liczby kodem dwójkowym naturalnym, można także przedstawić w
postaci
∑
∑
=
−
−
=
=
=
+
P
j
j
j
P
i
i
i
b
X
a
q
q
x
q
1
1
0
2
2
2
1
max
E
(10)
gdzie:
{a
0
, a
1
,..., a
P
−
2
, a
P
−
1
} i {b
1
, b
2
,..., b
P
−
1
, b
P
}
−
bity sygnału wyjściowego,
P i q
X
P
=
−
2
max
−
liczba bitów sygnału wyjściowego i kwant przetwornika.
Analogiczne równanie można napisać dla przetwarzania A/C w kod dziesiętny.
Przetwarzanie cyfrowo-analogowe
jest operacją przetwarzania sygnału cyfrowego w
sygnał analogowy. Sygnałem wejściowym przetwarzania cyfrowo-analogowego jest sygnał
cyfrowy, którego treścią jest cyfrowa reprezentacja k
x
wartości liczbowej y sygnału wyjścio-
wego, sygnałem wyjściowym jest sygnał analogowo-dyskretny y, zwykle naturalny. Zależnie
od kodu sygnału wejściowego stosuje się także nazwę przetwarzanie kodu dwójkowego (lub
dwójkowo-dziesiętnego lub dziesiętnego) w sygnał analogowy. Równanie przetwarzania
przetwornika cyfrowo-analogowego ma postać

55
[
)
[
)
y
q k
k
N
y
Y
x
x
=
∈
⊂
∈
⊂
0
0
,
,
max
max
N ,
R
(11)
gdzie:
q
Y
N
=
max
max
−
kwant przetwarzania, zwany także rozdzielczością przetwornika.
Równanie przetwarzania przetwornika kodu dwójkowego, czyli przetwornika C/A którego sy-
gnał cyfrowy koduje liczby kodem dwójkowym naturalnym, można także przedstawić w postaci
y
q
a
Y
b
i
i
i
P
j
j
j
P
=
=
=
−
−
=
∑
∑
2
2
0
1
1
max
(12)
gdzie:
{a
0
, a
1
,..., a
P
−
2
, a
P
−
1
} i {b
1
, b
2
,..., b
P
−
1
, b
P
}
−
bity sygnału wejściowego,
P i q
Y
P
=
−
2
max
−
liczba bitów sygnału wejściowego i kwant przetwornika.
Przetwarzanie cyfrowo-analogowe, podobnie jak przetwarzanie analogowo-cyfrowe charakte-
ryzują: częstotliwość repetycji, kwant i kod sygnału cyfrowego.
Przetwarzanie cyfrowe
jest operacją przetwarzania sygnału cyfrowego lub sygnałów
cyfrowych w sygnał lub sygnały cyfrowe. Przetwarzanie cyfrowe obejmuje bardzo dużą klasę
operacji, począwszy od najprostszej, polegającej na zmianie kodu sygnału, do bardzo złożo-
nych, polegających na wykonywaniu obliczeń numerycznych na liczbach przenoszonych
przez sygnały. Przetwarzanie cyfrowe jest zwykle realizowane przez komputer.
Termin przetwornik pomiarowy
ma dwa znaczenia:
(i)
operatora realizującego operację przetwarzania sygnałów pomiarowych,
(ii)
narzędzia pomiarowego realizującego operację przetwarzania sygnałów pomiarowych, a
nie będącego przyrządem pomiarowym i wzorcem miary.
Przetworniki w znaczeniu (i) i (ii) dzieli się zależnie od rodzaju przetwarzania na:
•
przetworniki analogowe, nazywane przetwornikami A/A,
•
przetworniki analogowo-cyfrowe, nazywane przetwornikami A/C,
•
przetworniki cyfrowo-analogowe, nazywane przetwornikami C/A,
•
przetworniki cyfrowe, nazywane przetwornikami C/C.
Stosowane są dwa rodzaje modeli przetworników:
♦
modele dokładne, dane równaniami lub operatorami przetwarzania i
♦
modele z błędami, opisujące także niedokładność realizacji operatora przetwarzania.
W ramach niniejszego wykładu omawiać będziemy przetworniki analogowe w sensie (ii). Po-
zostałe typy przetworników omówimy w dalszych wykładach.

56
2. Przetworniki pomiarowe analogowe
Omawiać będziemy teraz przetworniki analogowe w sensie (ii), rozpoczynając od
przetwornika analogowego sygnału naturalnego w sygnał naturalny. Model takiego przetwor-
nika można łatwo uogólnić na inne typy przetworników.
Przetwornik analogowy sygnału naturalnego w naturalny
jest charakterystyczny
tym, że treściami obu jego sygnałów są wartości chwilowe wielkości nośnych, a kody
sygnałów są identycznościami, nie ma więc potrzeby rozróżniania treści i nośnika; x –
nazywane sygnałem wejściowym i y – nazywane sygnałem wyjściowym oznacza zarówno
treści jak i nośniki sygnałów. Rozróżnia się model statyczny i model dynamiczny
przetwornika. Elementy tych modeli opatrywane są przymiotnikami statyczny i dynamiczny,
np. statyczne równanie przetwarzania i dynamiczne równanie przetwarzania.
Model dokładny statyczny przetwornika sygnału naturalnego w sygnał naturalny jest
dany równaniami przetwarzania: prostym (1) lub odwrotnym (3) z zakresem przetwarzania
sygnału wejściowego [X
min
, X
max
] lub sygnału wyjściowego [Y
min
, Y
max
], najchętniej stoso-
wane są przetworniki liniowe o liniowym statycznym równaniu przetwarzania (5) i zakresami
przetwarzania [0, X
max
] lub [0, Y
max
]. Model statyczny z błędami tworzymy nakładając na
model dokładny (rys.1a) błędy bezwzględne prawdziwe przetwornika:
•
odniesiony do wyjścia (rys.1b)
)
(
g
~
x
y
y
y
y
&
&
&
−
=
−
=
∆
(13)
•
i odniesiony do wejścia (rys.1c)
x
y
x
x
x
&
&
&
−
=
−
=
∆
)
(
h
~
(14)
gdzie: x& i y&
−
wartości prawdziwe sygnału wejściowego i wyjściowego,
)
(
~
x
g
y
&
=
−
wartość sygnału wyjściowego obliczona z prostego równania przetwarzania,
)
(
h
~
y
x
&
=
−
wartość sygnału wejściowego obliczona z odwrotnego równania
przetwarzania.
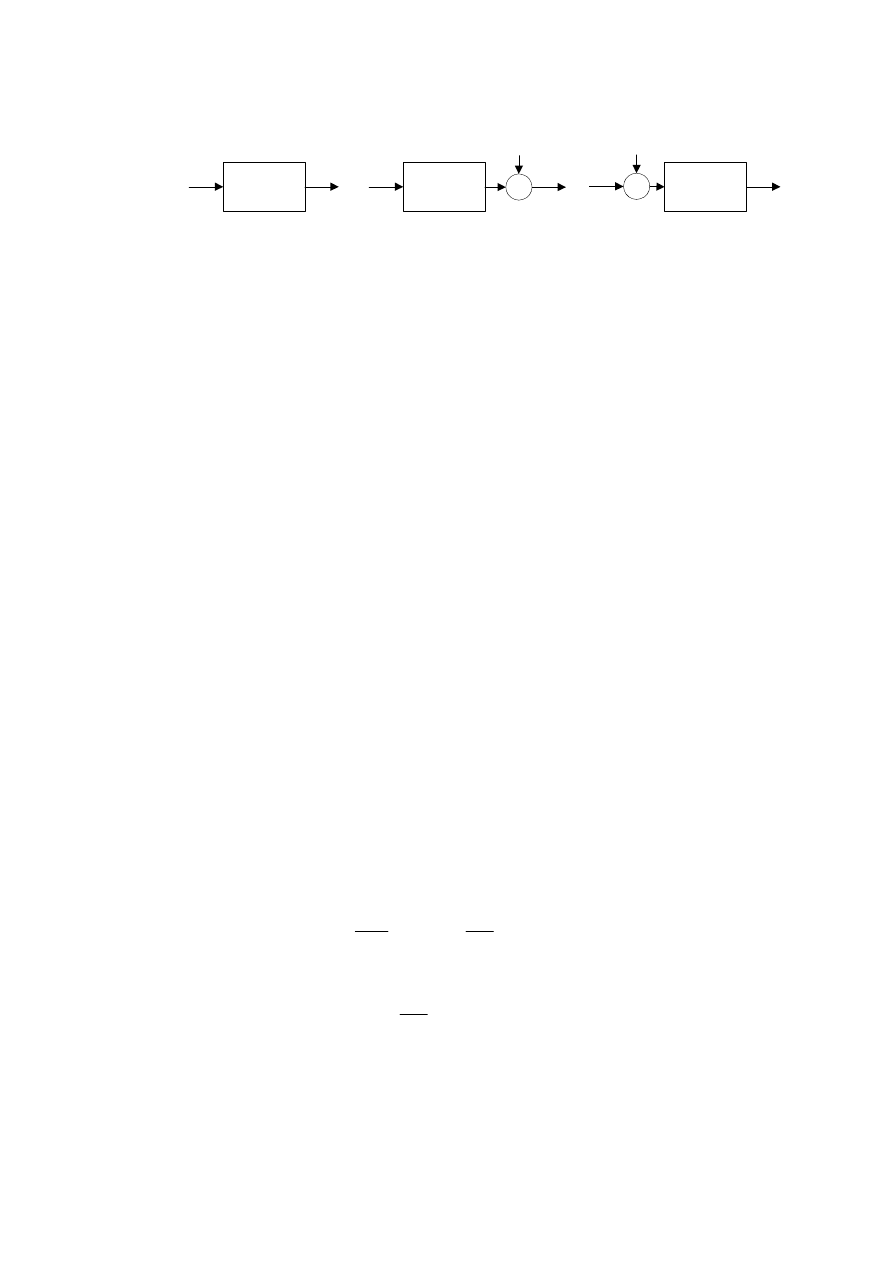
57
Rys.1. Modele statyczne przetwornika analogowego sygnału naturalnego w naturalny:
(a) model przetwornika dokładnego
(b) przetwornik z błędem odniesionym do wyjścia
(c) przetwornik z błędem odniesionym do wejścia
Błędy te są oczywiście nieznane co do wartości i jako takie nie mogą służyć do oceny niedo-
kładności. Miarą niedokładności przetwornika są błędy graniczne: bezwzględny i względny
odniesione do wyjścia i odniesione do wejścia. Błędy graniczne mogą zależeć od wartości
przetwarzanych sygnałów - wygodniej jest jednak zależność tę możliwie upraszczać. Mówi
się wówczas o normalizacji błędu granicznego. Najczęściej stosuje się określanie błędu bez-
względnego granicznego jako stałego w całym zakresie przetwarzania (normalizacja addy-
tywna), liniowo zmieniającego się wraz z wartością sygnału (normalizacja multiplikatywna) i
stanowiącego kombinację tych dwóch sposobów (normalizacja addytywno-multiplikatywna)
(
)
∆
∆
∆
∆
∆
max
max
max
/
/
y
y
y
y
y
y
y
a
m
a
m
= ±
= ±
= ±
+
δ
δ
100
100
(15)
gdzie:
∆
a
y
−
graniczny błąd bezwzględny addytywny odniesiony do wyjścia wyrażony w
jednostkach sygnału wyjściowego,
δ
m
−
graniczny błąd względny multiplikatywny wyrażony jako ułamek procentowy
długości zakresu przetwarzania sygnału wyjściowego Y
mm
.
Odpowiednio do granicznych błędów bezwzględnych określa się na podstawie powyższych
formuł graniczne błędy względne odniesione do wyjścia.
δ
δ
δ
δ
δ
δ
δ
max
max
max
%
= ±
= ±
= ±
= ±
+
∆
a
mm
a
m
m
mm
a
y
y
Y
y
Y
y
100
(16)
g( )
g( )
Σ
g( )
Σ
~
x
x&
∆
x
y&
y&
x&
~
y
∆
y
x
y
(a)
(b)
(c)

58
gdzie
δ
a
= (
∆
a
y/Y
mm
)100% jest zwany błędem sprowadzonym (odniesionym do zakresu prze-
twarzania Y
mm
). Błędy graniczne ustala się najczęściej dla błędów odniesionych do wyjścia, w
ten sam sposób można ustalać także graniczne błędy względne odniesione do wejścia.
Błędy bezwzględne prawdziwe i graniczne odniesione do wyjścia i odniesione do wej-
ścia są powiązane zależnościami
∆
∆
∆
∆
y
x
G x
y
x
G x
=
=
( ) ,
( )
max
max
(17)
gdzie: G(x) – czułość przetwornika, w ogólnym przypadku zależna od sygnału.
Dla błędów granicznych addytywnych (
∆
a
x,
∆
a
y) i multiplikatywnych (
δ
m
) odniesionych do
wyjścia i wejścia obowiązują zależności
|
)
(
)
(
g
|
,|
)
(
|
,|
)
(
|
mm
mm
x
G
x
x
x
G
Y
X
x
G
x
y
mx
my
ax
ay
a
a
=
=
=
∆
∆
δ
δ
δ
δ
(18)
gdzie: g(x) – prosta funkcja przetwarzania.
Dla przetwornika liniowego czułość G jest stała w całym zakresie pomiarowym, a ponadto
zachodzi
=
=
=
=
=
=
m
mx
a
ax
ay
x
y
x
y
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
my
max
max
,
,
(19)
Podział na błąd addytywny i multiplikatywny stosuje się niekiedy i dla błędów prawdziwych
+
∆
=
+
∆
=
∆
M
A
M
A
y
y
y
y
y
y
δ
δ
δ
100
100
/
(20)
szczególnie dla przetworników liniowych, dla których sygnał wyjściowy można wyrazić jako
≤
=
∆
≤
∆
∆
+
+
=
100
/
,
)
1
(
mm
0
0
G
M
G
Ay
Ay
Y
y
y
x
G
y
δ
δ
δ
δ
&
&
(21)
Błąd prawdziwy addytywny
x
G
x
G
y
y
A
A
0
0
∆
=
∆
=
∆
=
∆
nazywany bywa także błędem zera
przetwornika, a błąd prawdziwy multiplikatywny
%
100
G
δ
δ
δ
=
=
Mx
My
– błędem czułości lub
błędem nieliniowości przetwornika. Modele statyczne przetwornika idealizowanego i prze-
tworników z błędami przedstawiono na rys.1.
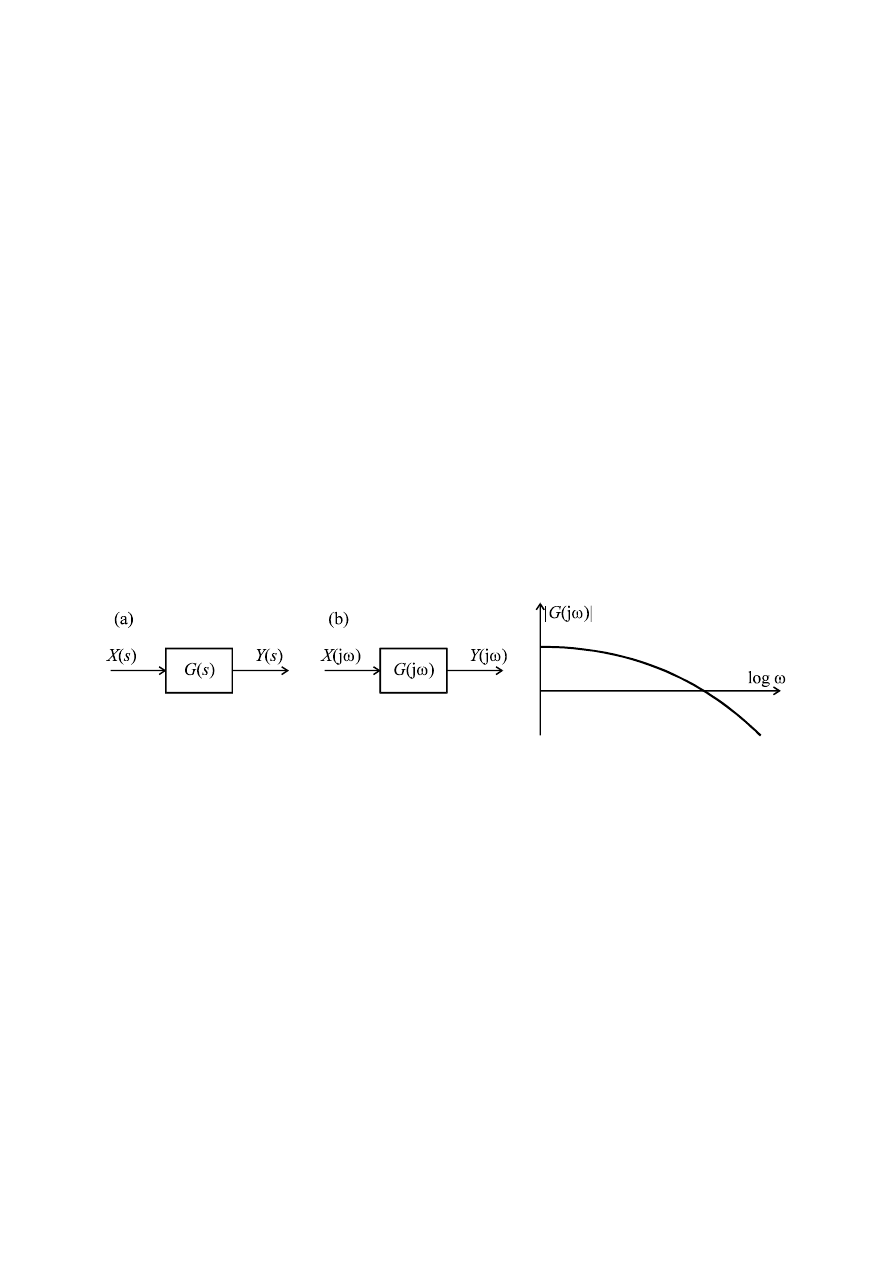
59
Model dynamiczny przetwornika sygnału naturalnego w naturalny opisuje właściwości
metrologiczne przetwornika w stanie, w którym przynajmniej jeden z sygnałów, wejściowy
lub wyjściowy, zmienia się w czasie. Przetwornik dokładny w stanie dynamicznym powinien
przetwarzać według statycznego równania przetwarzania; model dynamiczny, opisuje więc
niedokładności przetwornika spowodowane zmiennością sygnałów. Model dynamiczny kon-
struuje się zwykle jako model liniowy, który opisuje przetwornik w całym zakresie przetwa-
rzania dla przetworników liniowych, bądź tylko dla małych zmian sygnału wokół ustalonego
punktu przetwarzania. Model dynamiczny może być konstruowany:
(i)
w dziedzinie czasu, jest on wówczas dany przez równanie różniczkowe liniowe o stałych
współczynnikach,
(ii)
jako model operatorowy, jest on dany przez transmitancją operatorową przetwornika
równą stosunkowi transformat Laplace'a sygnału wyjściowego i wejściowego (rys 2a),
(iii)
w dziedzinie częstotliwości jako model widmowy, jest on wówczas dany przez transmi-
tancją widmową przetwornika równą stosunkowi transformat Fouriera sygnału wyjścio-
wego i wejściowego lub przez charakterystyki częstotliwościowe. (rys.2b).
Rys.2. Modele dynamiczne przetwornika analogowego sygnału naturalnego w naturalny:
(a) operatorowy, (b) widmowy z charakterystykami częstotliwościowymi.
Przetwornikami analogowymi sygnału naturalnego są przetworniki skali czyli prze-
tworniki wartości i przetworniki natury czyli przetworniki wielkości. Przetworniki te mają
charakterystyki częstotliwościowe zawsze opadające dla dużych częstotliwości, mają więc
zawsze ograniczone widmo przenoszenia sygnału. Model dynamiczny podaje się zwykle za
pomocą parametrów dynamicznych, którymi mogą być:
•
parametry transmitancji (stałe czasowe, częstotliwość drgań własnych, stopień tłumienia),
•
częstotliwość graniczna, definiowana zwykle jako częstotliwość, dla której czułość (czyli
stosunek amplitudy sygnału wyjściowego do amplitudy sygnału wejściowego) zmniejsza się
o 3 dB (czyli o około 30%),
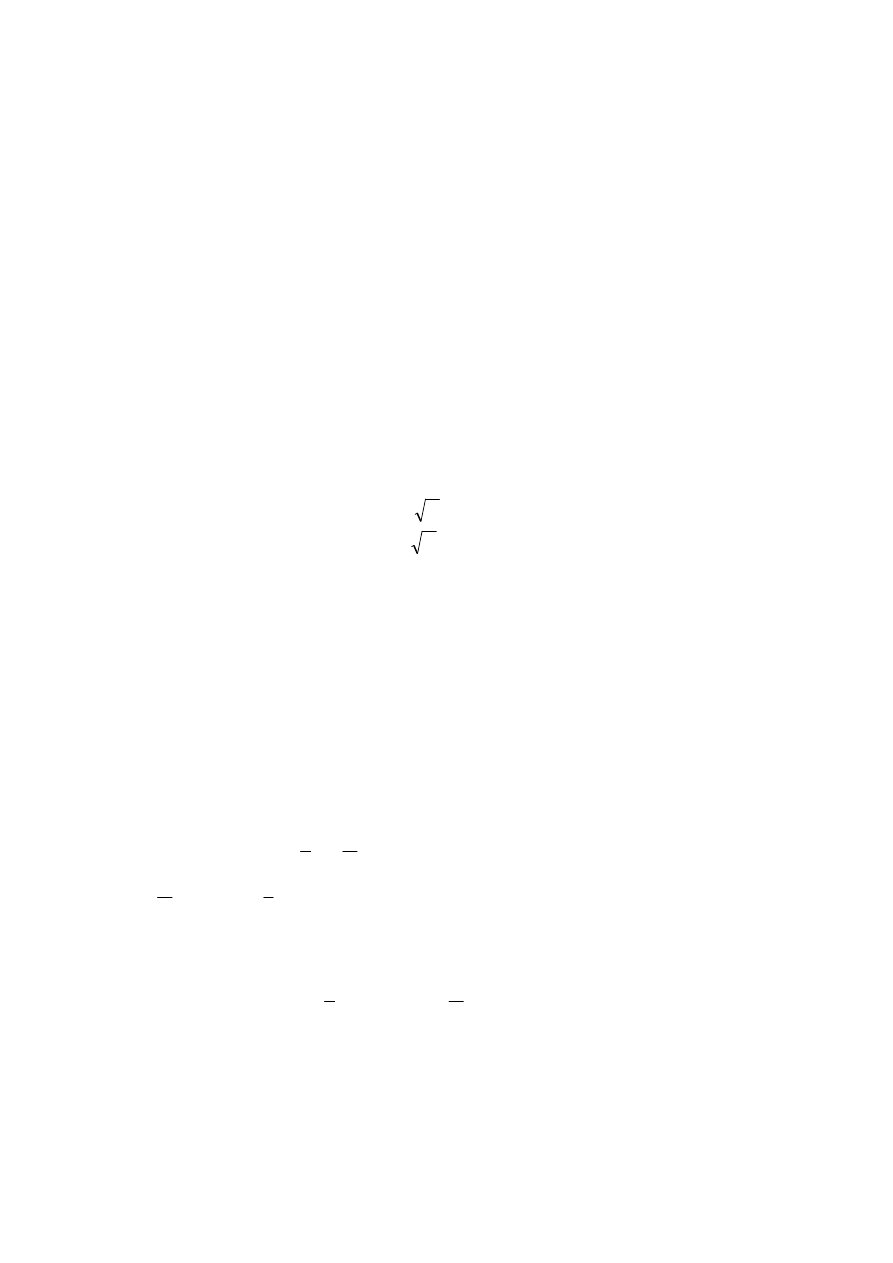
60
•
czas ustalenia odpowiedzi na wymuszenie skokowe, definiowany zwykle jako czas, po któ-
rego upływie odpowiedź nie różni się od wartości ustalonej o więcej niż ustalony jej
ułamek.
Przetworniki skali
są budowane prawie zawsze jako przetworniki liniowe. Przetwor-
niki skali elektryczne to przetworniki napięcia w napięcie lub natężenia prądu w natężenie
prądu. Przetworniki skali elektryczne dzieli się na przetworniki skali pasywne, budowane z
elementów pasywnych (oporników, kondensatorów) i przetworniki skali aktywne, mające w
swoich strukturach oprócz elementów pasywnych także i elementy aktywne (wzmacniacze opera-
cyjne).
Przetwornik skali sygnału harmonicznego
jest szczególnym rodzajem przetwornika
skali, przetwarza on sygnał harmoniczny wejściowy x(t) w sygnał harmoniczny wyjściowy
y(t)
x t
X
t
X
t
y t
Y
t
Y
t
x
x
x
x
( )
sin (
)
sin (
)
( )
sin (
)
sin (
)
max
max
=
+
=
+
=
+
=
+
ω ψ
ω ψ
ω ψ
ω ψ
2
2
(22)
gdzie: X
max
, Y
max
– amplitudy sygnałów,
X, Y – wartości skuteczne sygnałów,
ψ
x
,
ψ
y
– przesunięcia fazowe sygnałów.
Równanie przetwarzania można zapisywać w trzech postaciach: związków między warto-
ściami chwilowymi, związków między amplitudami i fazami oraz związków między
reprezentacjami zespolonymi sygnałów
=
=
=
=
)
c
(
)
b
(
,
)
a
(
)
(
)
(
X
G
Y
X
Y
t
x
G
t
y
x
y
ψ
ψ
(23)
gdzie: X
X
Y
Y
x
y
=
=
e
i
e
j
j
ψ
ψ
– reprezentacje zespolone sygnału wejściowego i wyjściowego.
G – czułość przetwornika (liczba rzeczywista).
Błąd przetwornika modeluje się zastępując równanie przetwarzania (23c) równaniem
X
G
Y
Y
&
&
ϕ
δ
∆
+
=
j
e
)
1
(
(24)
gdzie:
δ
Y
– błąd amplitudowy,
∆ϕ
– błąd fazowy.
Ograniczenie błędów ustanawia się osobno dla błędu amplitudowego i osobno dla błędu fazo-
wego w określonym paśmie częstotliwości, zwykle obustronnie ograniczonym.

61
Przetworniki (natury) wielkości
to przede wszystkim elektryczne czujniki pomiarowe,
wrócimy do nich w dalszej części wykładu.
Przykład 1
(a)
Potencjometr, dzielnik napięcia i wzmacniacz operacyjny są przetwornikami skali napięcia.
(b)
Przekładnik pomiarowy prądu zmiennego (zwany także transformatorem pomiarowym) jest przetwornikiem
skali sygnału harmonicznego przekładnik napięciowy – napięcia, przekładnik prądowy – natężenia prądu,
(c)
Termo-ogniwo jest przetwornikiem wielkości: temperatury w napięcie.
Model ogólny przetwornika analogowego
powinien rozróżniać treści sygnałów wej-
ściowego i wyjściowego x i y od nośników sygnałów wejściowego i wyjściowego u lub
u
1
, u
2
,..., u
J
i v lub v
1
, v
2
,..., v
K
. Nośniki związane są równaniem przetwarzania fizycznego
(nazywanym niekiedy równaniem ruchu przetwornika), treści związane są z nośnikami
poprzez kody
C
x
i
C
y
, a treści między sobą związane są równaniem przetwarzania (sygnałów)
=
=
=
=
=
=
=
)
(
)
,...,
(
C
)
(
C
)
,...,
(
C
)
(
C
0
)
,...,
,
,...,
(
K
0
)
,
(
K
1
1
1
1
x
y
v
v
y
v
x
u
u
x
u
x
v
v
u
u
v
u
K
y
y
J
x
x
K
J
g
lub
i
lub
lub
(25)
Gdzie K jest operatorem równania przetwarzania fizycznego. Równanie przetwarzania fizycz-
nego opisuje fizyczne działanie przetwornika polegające na przetwarzaniu i magazynowaniu
energii i masy; równanie przetwarzania sygnałów, opisujące informacyjne działanie przetwor-
nika, wynika z równania przetwarzania fizycznego. Działanie fizyczne przetwornika
sprowadza się często do zmiany rozkładu widmowego nośników, takie przetworniki można
nazwać przetwornikami rozkładu widmowego. Do szczególnie często używanych
elektrycznych przetworników rozkładu widmowego należą przetworniki parametrów
wielkości (napięć i prądów) okresowo zmiennych oraz filtry, przede wszystkim
dolnoprzepustowe.
Przetwornik parametru wielkości okresowo zmiennej
ma nośnik sygnału
wejściowego (napięcie lub natężenie prądu) u(t) okresowo zmienny z okresem T, treścią
sygnału wejściowego jest parametr nośnika: wartość szczytowa, wartość średnia
wyprostowana, wartość skuteczna itp., określona na okresie u(t) operatorem F. Sygnał
wyjściowy jest najczęściej naturalny (napięcie stałe lub prąd stały), tzn. treścią sygnału y jest
wartość chwilowa nośnika v. Przetwornik opisujemy równaniem
=
=
=
)
(
g
)]
(
[
x
v
y
t
u
x
F
(26)

62
Przetworniki parametrów wielkości okresowo zmiennych, podobnie jak przetworniki skali, dzieli się na
przetworniki pasywne i aktywne.
Przykład 2
Przetwornik wartości średniej napięcia zbudowany z prostownika dwu-połówkowego w układzie mostkowym z
kondensatorem bocznikującym wyjście jest przetwornikiem wartości średniej wyprostowanej napięcia okreso-
wego w napięcie stałe.
Równanie przetwarzania i graniczne błędy przetwornika wyznacza się w procesie kali-
bracji
polegającym na:
(1)
wprowadzeniu na wejście przetwornika sygnału o znanych treściach x(1), x(2),..., x(N),
(2)
zmierzeniu odpowiadających im treści sygnału wyjściowego y(1), y(2),..., y(N),
(3)
wyznaczeniu, na podstawie danych x(1), x(2),..., x(N); y(1), y(2),..., y(N) oraz granicznych
błędów pomiaru tych wartości, równania przetwarzania g(x) i granicznych błędów prze-
twornika addytywnych
∆
a
y
,
∆
a
x
, (lub
δ
a
y
,
δ
a
x
) i multiplikatywnych
δ
m
y
,
δ
m
x
, zależnie od
sposobu normowania błędu.
3. Elektryczne przyrządy pomiarowe
Przyrząd pomiarowy realizuje operację przetwarzania sygnału elektrycznego we wska-
zanie czyli w sygnał przenoszący informację o mezurandzie bezpośrednio odbieraną przez
człowieka. Będziemy tu zajmowali się przede wszystkim przyrządami wskazującymi czyli
miernikami, których wskazanie określa wartość liczbową wielkości mierzonej,
Mierniki, zależnie od rodzaju wskazania, można podzielić na mierniki analogowo-cią-
głe, zwane wprost analogowymi, mierniki analogowo-dyskretne i mierniki cyfrowe. Przed-
miotem naszych rozważań będą tu mierniki analogowe, zwane także miernikami wskazówko-
wymi. Mierniki cyfrowe i analogowo-dyskretne będą omawiane w następnych wykładach.
Za pierwowzór miernika wskazówkowego można uznać wagę sprężynową, składającą
się ze sprężyny, zamocowanej jednym końcem i z szalką przymocowaną do drugiego końca,
ruchomy koniec sprężyny jest zaopatrzony we wskazówkę, której przesunięcie l, równe od-
kształceniu sprężyny, można odczytać na skali. Przedmiot o masie m, umieszczony na szalce,
działa na sprężynę siłą ciężkości
F
g m
=
(27)
rozciągając ją o l, co powoduje powstanie siły sprężystości
F
D l
S
=
(28)

63
proporcjonalnej do odkształcenia sprężyny i skierowanej przeciwnie do F. Ustala się równo-
waga, gdy
F
F
=
S
(29)
dla przesunięcia wskazówki
l
g
D
m
=
(30)
gdzie: g – przyspieszenie ziemskie,
D – stała zwracania sprężyny.
Przesunięcie wskazówki (odchylenie) l jest miarą masy m, skalę sporządza się w jednostkach
masy w procesie kalibracji polegającym na znaczeniu przesunięć wskazówki dla znanych
mas.
Zasadniczym elementem konstrukcyjnym elektrycznego miernika wskazówkowego
jest elektryczny mechanizm pomiarowy, zwany także niekiedy elektrycznym ustrojem (lub
systemem) pomiarowym. Elektryczny mechanizm pomiarowy jest przetwornikiem wielkości
elektrycznej w, będziemy ją nazywali wielkością wejściową mechanizmu, w przesunięcie
α
(zwykle kątowe) ruchomej części mechanizmu, zwanej organem ruchomym, połączonego ze
wskazówką poruszającą się wzdłuż skali. Ruch organu ruchomego następuje wskutek
działania momentu napędowego M, zależnego od wielkości wskazywanej v i w ogólnym
przypadku od położenia
α
organu ruchomego
M
w
= γ
α
m
( , )
(31)
stanowiącej odpowiednik siły ciężkości rozciągającej sprężynę wagi. Ruchowi organu pod
wpływem momentu napędowego przeciwstawia się moment zwracający wytwarzany przez
spiralne sprężyny, proporcjonalny do kąta skręcenia
α
M
D
S
= α
(32)
Przy wielkości wskazywanej stałej w czasie organ ruchomy ustawia się w położeniu
ustalonym, w którym moment napędowy M zostaje zrównoważony momentem zwracającym
M
S
. Ustala się położenie
α =
g
m
( )
w
(33)
Wiele mechanizmów jest wystarczająco dokładnie opisanych równaniem liniowym
α =
G w
m
(34)

64
gdzie G
m
nazywa się czułością mechanizmu, a jej odwrotność, H
m
, – stałą mechanizmu. Z
odchylenia wskazówki mechanizmu można wyznaczyć wartość wielkości wejściowej.
Miernik wskazówkowy, oprócz mechanizmu pomiarowego, ma zwykle układ wej-
ś
ciowy, w którym następuje przetworzenie wielkości mierzonej x w wielkość wejściową
mechanizmu w, według równania
w
x
=
g
we
( )
(35)
często liniowego
w
G
x
=
we
( )
(36)
Stąd już cały miernik można opisać równaniem
α =
g ( )
x
(37)
często liniowym
α =
G x
(38)
gdzie g
we
() i G
we
– funkcja przetwarzania i czułość układu wejściowego,
g() i G – funkcja przetwarzania i czułość układu miernika.
Na podstawie odchylenia
α
wskazówki miernika i równania miernika (37) i (38) można wy-
znaczyć wartość wielkości mierzonej. Prawie zawsze jednak odchylenie wskazówki mierzy
się (odczytuje się) nie w jednostkach długości lub kąta, tylko według specjalnie
spreparowanej skali pozwalającej odczytywać wprost wartości wielkości mierzonej.
Pomiar długości i skala pomiarowa miernika
. Długość odcinka lub przesunięcie
wskazówki
α
mierzy się (odczytuje się) porównując go lub je ze skalą pomiarową długości
utworzoną przez N
max
wskazów wyznaczających wzorcowe odcinki o znanych długościach
α
n
n d
n
N
=
=
,
, ,...,
max
0 1
(40)
Odcinek między sąsiednimi wskazami nazywa się działką, a jego długość d, nazywana długo-
ś
cią działki i wybierana zwykle jako dziesiętna wielokrotność lub podwielokrotność jednostki
długości, jest charakterystycznym parametrem skali. Odczyt długości
α
polega na ustaleniu
odcinka wzorcowego
α
N
N d
=
(41)
najbliższego długością (mniejszego lub większego niż)
α
. Długość tego odcinka przyjmuje się
jako miarę długości odcinka (przesunięcia)
α
α α
≈
=
N
N d
(42)

65
Popełnia się błąd w ten sposób błąd
∆
∆
∆
α α
α
α
α
=
− ≈
≤
N
d
Q
Q
, |
|
1
2
(43)
gdzie
∆
Q
α
nazywa się błędem rozdzielczości (lub kwantowania) odczytu.
W rzeczywistości prawdziwa długość wzorcowego odcinka
α
N
jest obarczona błędem
wykonania skali
∆
S
α
N
(zwanym błędem skali lub błędem skalowania); przyjmując (42) popeł-
nia się więc błąd (prawdziwy) pomiaru długości
α
α
α
α
α
α
α
max
S
Q
S
∆
+
≤
∆
∆
+
∆
≈
−
=
∆
d
N
N
2
1
|
|,
(44)
gdzie
∆
Smax
α
jest granicznym błędem skali.
Często stosuje się odczyt z interpolacją, polegający na podziale w "myśli" działki, w
obrębie której znajduje się koniec odcinka mierzonego (wskazówka), na M równych poddzia-
łek (M
=
1,2,4,5) i przyjęciu
α α
≈
+
=
+
∗
∗
N
m
d
M
N
m
M
d
(45)
gdzie
α
N
∗
jest odcinkiem wzorcowym najbliższym
α
, ale niewiększym od
α
, a m (m
=1
,..., M–
1) jest numerem poddziałki, o końcu najbliższym końcowi
α
. Interpolacja zmniejsza M-
krotnie graniczny błąd kwantowania
|
|
∆
Q
∗
≤
α
1
2
d
M
(46)
Wskazy można stawiać nierównomiernie, tak że działki będą miały niejednakowe
długości d
n
α
n
j
j
n
d
=
=
∑
1
(47)
Jeżeli odcinkom
α
n
przyporządkowuje się wartości
θ
ς α
n
n
=
(
)
(48)
a n -tej działce tzw. wartość działki
q
n
n
n
=
−
−
θ
θ
1
(49)
to odcinkowi (odchyleniu wskazówki) można przyporządkować wartość

66
θ
N
n
n
N
q
=
=
∑
1
(50)
czyli zmierzyć go według innej skali pomiarowej
θ
, wtórnej do skali oryginalnej długości
α
,
związanej z nią transformacją
θ ς α
=
( )
(51)
gdzie
ς
() nazywa się funkcją skali. Jeżeli funkcję skali dobierze się tak, aby było
ς α
α
( )
( )
=
−
g
1
(52)
to będzie zachodziła formalna równość między wartością
θ
odchylenia wskazówki zmierzoną
według skali wtórnej (czyli skali miernika) a wartością wielkości mierzonej x. Zakres pomia-
rowy miernika i długość zakresu pomiarowego można określać w jednostkach długości
α
α
α
α
α
∈
=
[ ,
]
max
max
max
0
] = [0,
mm
N
N
(53)
lub jednostkach wielkości mierzonej
x
X
X
X
X
X
q
N
n
n
N
∈
=
−
=
=
∑
[
,
)]
min
max
max
min
max
max
] = [ (0), (
mm
ς
ς α
1
(54)
Zależnie od postaci funkcji skali rozróżnia się skale liniowe i skale nieliniowe, a wśród
tych ostatnich skale kwadratowe, logarytmiczne, wykładnicze itd. Skala jednostajna ma
wszystkie działki jednakowej długości d
n
=
d, skala równomierna ma wszystkie działki jedna-
kowej wartości q
n
=
q, skala regularna ma działki jednakowych długości i jednakowej warto-
ści. Skala regularna jest skalą liniową.
Błąd miernika
(ściśle: prawdziwy błąd bezwzględny miernika) zdefiniujemy
∆
x
x
= −
θ
(55)
gdzie:
θ
– odczytane wskazanie miernika,
x – wartość prawdziwa wielkości mierzonej.
Do analizy błędu miernika wrócimy w końcowej części wykładu. Użytkownika miernika inte-
resuje graniczny błąd miernika
∆
max
x, jest on wyznaczany przez wytwórcę i podawany w po-
staci błędu unormowanego. Najczęściej dla mierników wskazówkowych stosuje się
normalizację addytywną, ustalającą, że graniczny błąd bezwzględny miernika w całym
zakresie nie przekracza
δ
a
% długości X
mm
zakresu pomiarowego miernika. Dopuszczalna

67
dla miernika wartość błędu granicznego jest zwykle podawana w sposób umowny jako klasa
dokładności (patrz wykład 3 i 4).
Skalę miernika sporządza się w procesie skalowania, będącym szczególnym rodzajem
kalibracji, znamiennym tym, że efekt kalibracji tj. funkcję miernika g(x) (ściślej jej
odwrotność) materializuje się w postaci skali miernika. Skalowanie, oprócz sporządzenia
skali, obejmuje wyznaczenie błędów granicznych miernika. Trzeba pamiętać, że wytwórca
gwarantuje zachowanie właściwości miernika, a więc i błędu granicznego, tylko w
określonym czasie i przy zachowaniu określonych warunków eksploatacji i przechowywania.
Miernik po upływie czasu gwarancji powinien być poddany sprawdzeniu, czyli zabiegom
ustalającym czy jego aktualny błąd graniczny spełnia deklaracje wytwórcy, lub ponownej
kalibracji polegającej na ustaleniu aktualnych błędów granicznych.
Do niedawno mierniki wskazówkowe były najczęściej używanymi elektrycznymi
narzędziami pomiarowymi. I stąd też, w dostępnej literaturze przedmiotu (a trzeba pamiętać,
że pochodzi ona sprzed lat kilkunastu) mierniki wskazówkowe zajmują najwięcej miejsca.
Obecnie mierniki wskazówkowe są wypierane przez mierniki cyfrowe, w wielu jednak
laboratoriach stanowią one jeszcze znaczną część instrumentarium.
Przykład 3
(a)
Mechanizm magnetoelektryczny.
(b)
Mierniki magnetoelektryczne (zawierające mechanizmy magnetoelektryczne): amperomierz, woltomierz i
omomierz.
(c)
Mechanizm elektromagnetyczny.
(d)
Mechanizm elektrodynamiczny.

68
5. Wzorzec i komparator
Porównanie
jest operacją wykonywaną na obiektach fizycznych (np.
ω
1
i
ω
2
), mającą
na celu ustalenie relacji między przejawami (q
1
i q
2
) określonej cechy Q, której nośnikami są
te obiekty; w wyniku porównania stwierdza się zachodzenie jednej i tylko jednej spośród
następujących relacji:
(i) przejaw q
1
cechy Q w obiekcie
ω
1
jest "większy" niż przejaw q
2
cechy Q w obiekcie
ω
2
,
(ii) przejaw q
2
cechy Q w obiekcie
ω
2
jest "większy" niż przejaw q
1
cechy Q w obiekcie
ω
1
,
(iii) przejawy q
1
cechy Q w obiekcie
ω
1
i przejaw q
2
tej cechy w obiekcie
ω
2
są jednakowe,
tzn. obiekty
ω
1
i
ω
2
są równoważne pod względem cechy Q.
Każdy pomiar polega na porównaniu
nieznanych przejawów wybranej cechy
pewnego obiektu z wzorcowymi przejawami tej cechy, którym - zgodnie z uprzednio przyjętą
skalą pomiarową - przyporządkowano odpowiednie wartości. Nośnikiem przejawów
wzorcowych jest obiekt zwany wzorcem. Porównaniu z wzorcem może podlegać wprost
obiekt mierzony i wówczas do wykonania pomiaru może wystarczać samo tylko porównanie.
Taka metoda pomiarowa nazywa się metodą bezpośredniego porównania
.
Przykładem pomiaru metodą bezpośredniego porównania może być ważenie
przedmiotów na symetrycznej wadze dźwigniowej (rys.5). Pomiar polega na porównaniu pod
względem mierzonej cechy Q (masy) obiektu mierzonego
ω
x
z obiektami wzorcowymi
ω
i
(i = 1,2,...,M), odtwarzającymi przejawy q
i
wielkości Q, o znanych wartościach liczbowych
v
i
. Obiektem mierzonym jest więc w tym wypadku przedmiot ważony
ω
x
; wzorce o różnych
przejawach masy tworzy się przez łączenie na szali odważników 1, 2, 2, 5, 10, 20, 20, 50,
100 dag.
Wyniki porównania określa się zwykle nie w dziedzinie przejawów wielkości, ale w
dziedzinie wartości liczbowych wielkości. Wynik porównania obiektu mierzonego
ω
x
z
wzorcem
ω
i
można więc zapisać jako ustalenie zachodzenia jednej z trzech relacji
x v
x v
x = v
i
i
i
〉
〈
(56)
gdzie: x - wartość liczbowa mierzonego przejawu w obiekcie
ω
x
, v
i
- wartość liczbowa
przejawu odtwarzanego przez wzorzec
ω
i
.
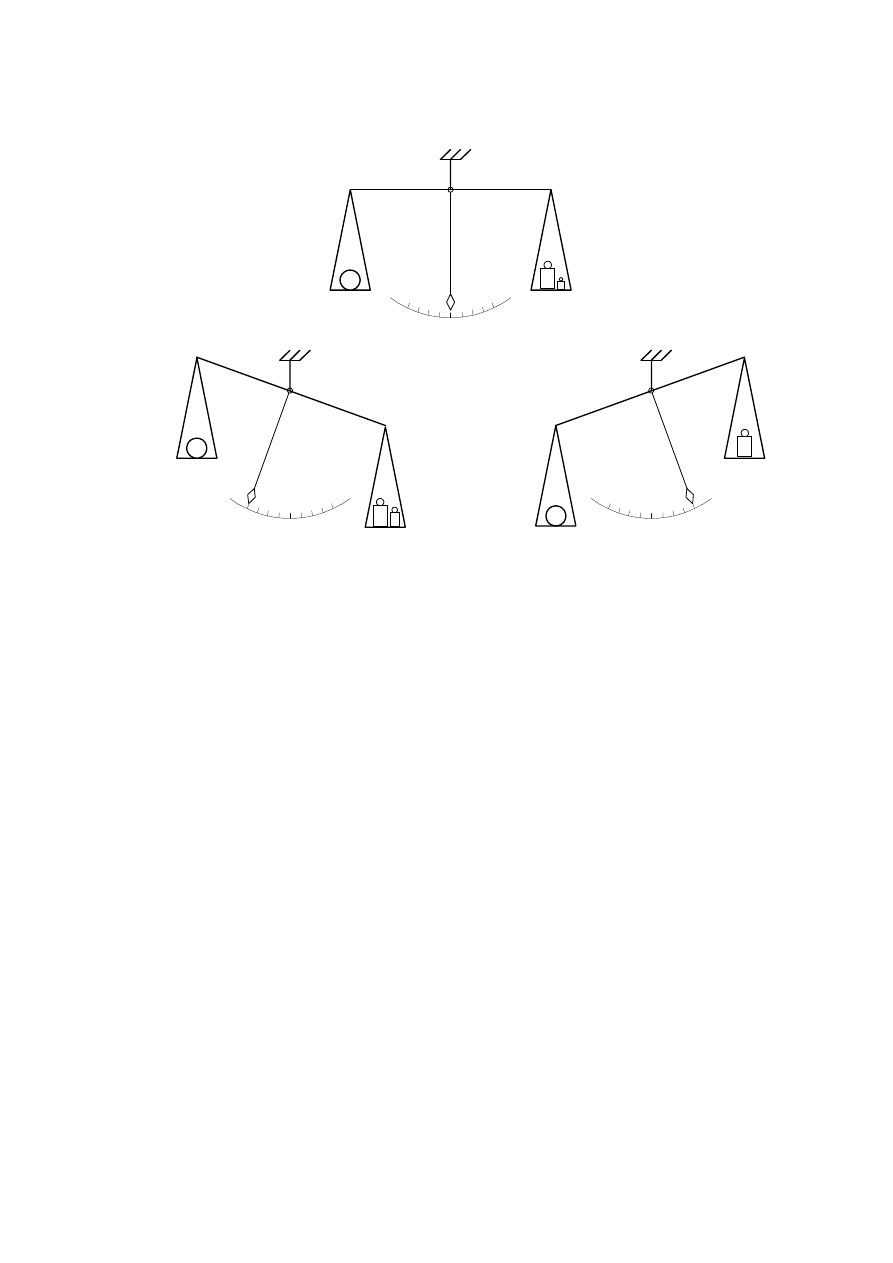
69
Rys.3 Ważenie przedmiotu na wadze dźwigniowej
Pomiar metodą bezpośredniego porównania
polega na kolejnym porównywaniu
obiektu mierzonego w z różnymi wzorcami, aż do znalezienia wzorca
ω
k
równoważnego pod
względem cechy Q z obiektem
ω
x
. Z równoważności tej wynika
x = v
k
(57)
Zwykle skala pomiarowa dana przez wzorce
ω
i
ma skończoną rozdzielczość, tj. odtwarza
tylko niektóre wartości v
i
(w rozważanym przykładzie ważenia odtwarza się tylko całkowite
wielokrotności 1 dag) i spełnienie (57) nie jest możliwe dla wszystkich x. Dąży się wtedy do
znalezienia dwóch sąsiednich wzorców
ω
l-1
i
ω
l
takich, że
V
l-1
< x < v
l
(58)
Za miarę przejawu cechy w obiekcie mierzonym przyjmuje się jedną z dwóch wartości: v
l-1
lub v
l
, zależnie od konwencji - bliższą, mniejszą lub większą.
W realizacji pomiaru metodą bezpośredniego porównania dość często jest (w
mniejszym lub większym stopniu) zaangażowany człowiek i odpowiednie narzędzie
pomiarowe. Powszechnie znana metoda oceny długości (lub odległości) "na oko" jest metodą
pomiarową bezpośredniego porównania, nie wymagającą stosowania narzędzi pomiarowych.
100
20
100
5
100
0
0
0
m
x
= 105 dag
m
x
< 120 dag
m
x
> 100 dag
m
x
m
x
m
x

70
Wzorce długości (odległości) istnieją w świadomości mierzącego; porównanie jest
wykonywane także w jego świadomości. Znakomita większość praktycznie wykonywanych
pomiarów wymaga jednak stosowania narzędzi, a rozwój techniki pomiarowej zmniejsza
zaangażowanie człowieka w realizacji pomiaru.
Dokonamy teraz krótkiego przeglądu stosowanych metod pomiaru i przetwarzania,
prowadząc
jednocześnie
uproszczoną
analizę
błędów
pomiaru
i
przetwarzania,
charakterystycznych dla tych metod.
6. Metoda kompensacyjna i metoda podstawieniowa
Porównanie wartości nieznanej z wzorcową tylko w nielicznych pomiarach jest
wykonywane wyłącznie za pomocą zmysłów człowieka (jak przy pomiarze długości "na oko"
lub linijką), znacznie częściej korzysta się z urządzeń technicznych zwanych komparatorami.
Można wyróżnić dwa rodzaje porównywania: równoczesne, wykonywane metodą
kompensacyjną, i nierównoczesne, wykonywane metodą podstawieniową (substytucyjną).
Należy zaznaczyć tu, że w terminologii równie często używa się określeń: „metoda
komparacji równoczesnej” i „metoda komparacji nierównoczesnej”.
Porównywanie metodą kompensacyjną polega na równoczesnym oddziaływaniu na
komparator dwóch porównywanych wielkości (sygnałów) tego samego rodzaju (np. dwóch
napięć, dwóch sił, dwóch strumieni świetlnych) i obserwacji pewnego, zachodzącego w
komparatorze zjawiska, którego natężenie jest wynikiem przeciwdziałania wielkości
porównywanych i które zanika wówczas, gdy wartości wielkości porównywanych są sobie
równe. Stan zaniku obserwowanego zjawiska nazywa się równowagą i stąd komparator
nazywany jest także wskaźnikiem równowagi.
Najprostszy model komparatora równoczesnego ma postać układu o dwóch wejściach
dla wielkości (sygnałów) porównywanych: x (mierzonej o nieznanej wartości) i v (wzorcowej
o znanej wartości), oraz jednym wyjściu formującym sygnał komparacji
r, przenoszący
informację o natężeniu zjawiska zachodzącego w komparatorze. W okolicy stanu równowagi
komparator można opisać równaniem
r = K
c
(x - v)
(59)
gdzie K
c
- czułość komparatora.
Pomiar metodą kompensacyjną (tzn. pomiar opierający się na porównaniu metodą
kompensacyjną) polega na wyznaczeniu wartości wielkości wzorcowej, sprowadzającej
komparator do równowagi. Wartość tę wyznacza się wprowadzając na jego wejście v wartości
wielkości wzorcowej v(1),v(2),... (rys.6) i obserwując odpowiadające im wartości sygnału

71
komparacji r(1), r(2),..., aż do znalezienia v(N) = v
0
, dla którego r(N) jest równe lub
wystarczająco bliskie zeru.
Wartość v(N) = v
0
przyjmuje się jako estymatę wartości mierzonej x.
Rys.4. Idea pomiaru metodą kompensacyjną.
Algorytm równoważenia, tzn. wyboru odpowiedniej wartości wielkości wzorcowej,
może być realizowany przez człowieka lub automat. W tym pierwszym przypadku sygnał
komparacji musi być dostosowany do zdolności percepcyjnych człowieka. Najczęściej stosuje
się komparatory wskazówkowe, których sygnał wyjściowy, czyli wskazanie, ma postać
odchylenia wskazówki od położenia równowagi. Takim właśnie komparatorem jest
wspomniana już waga dżwigniowa.
Przykład 4
(a) Waga dżwigniowa (patrz rys.5). Wielkościami porównywanymi są tu: masa ważona m
x
i masa odważników
m
v
; sygnałem komparacji r jest odchylenie (kątowe) wskazówki od pionu
r = K
w
(m
x
- m
v
)
przy czym K
w
jest współczynnikiem czułości wagi.
(b) Kompensator napięcia (rys.7). Napięcie mierzone U
x
jest porównywane z napięciem wzorcowym (czyli
kompensującym) U
v
, zbieranym z wyskalowanego dzielnika napięcia P; różnica napięć działa na galwanometr
G, spełniający funkcję wskażnika zera prądu (lub napięcia). Napięcie U
v
dobiera się (nastawiając dzielnik) tak,
aby galwanometr wskazał zanik prądu I w obwodzie. Wzór (64) przybiera w tym wypadku postać
I = K
k
(U
x
- U
v
)
gdzie K
k
jest współczynnikiem czułości kompensatora.
K
C
Człowiek
lub
automat
0
)
(
),...,
2
(
),
1
(
≅
N
r
r
r
0
)
(
),...,
2
(
),
1
(
v
N
v
v
v
=
x
v
0
ˆ
v
x
=
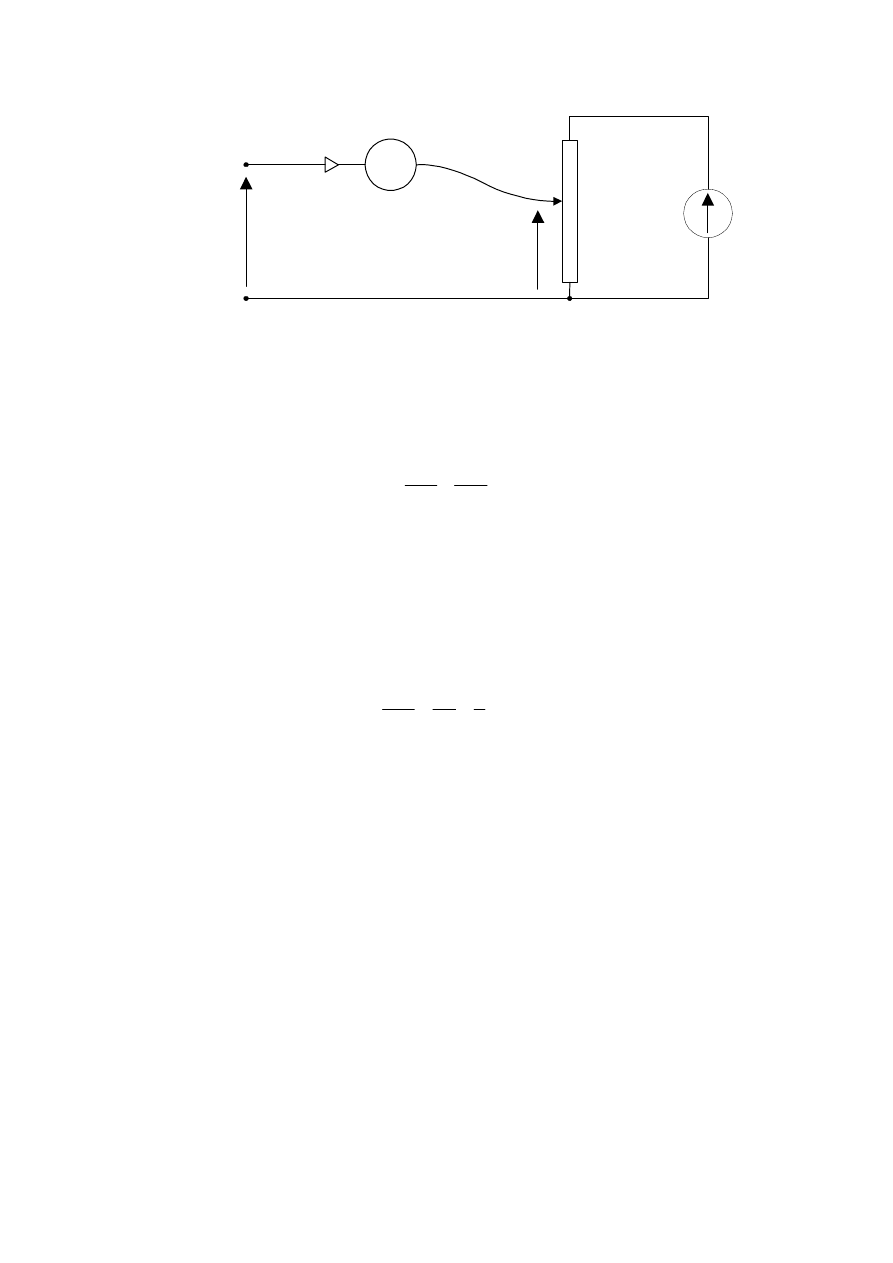
72
Rys.5. Kompensator napięcia - schemat ideowy
Błąd pomiaru metodą kompensacyjną.
Jeżeli jako estymatę wartości mierzonej x przyjmie
się wartość wielkości wzorcowej v
0
, której odpowiada sygnał komparacji o najmniejszym
module, to prawdziwy błąd pomiaru można określić jako
c
0
c
00
0
K
r
K
r
v
-
=
x
x
∆
−
∆
−
∆
∆
&
&
&
&
(60)
gdzie
∆
v
0
- błąd wielkości wzorcowej,
∆
00
r - błąd zera komparatora (niezerowy sygnał
komparacji odpowiadający stanowi równowagi),
∆
0x
r - błąd niezrównoważenia spowodowany
nieczułością oka obserwatora i skończoną rozdzielczością wielkości wzorcowej (równy
sygna- łowi komparacji w stanie uznanym za równowagę). Graniczny błąd pomiaru
odpowiadający (65) można oszacować następująco
u
2
1
K
d
K
r
+
v
=
x
c
c
00
+
+
∆
∆
∆
)
)
)
)
(61)
gdzie
∆
v - błąd graniczny wzorca,
∆
00
r - błąd graniczny zera komparatora, d - błąd graniczny
odczytu sygnału komparacji, wywołany skończoną rozdzielczością oka, u - kwant skali
pomiarowej (moduł różnicy między dwoma sąsiednimi wartościami wzorcowymi).
Jeżeli zero komparatora jest korygowane przed pomiarem, tzn. jeżeli istnieje
możliwość "zgrania" zerowego wskazania komparatora ze wskazaniem odpowiadającym
rzeczywistemu stanowi równowagi, to
∆
00
r = d. Taka możliwość istnieje dla wagi
dźwigniowej (równowaga przy nieobciążonych szalkach) i kompensatora napięcia z
galwanometrem (zerowy prąd w jego obwodzie); obydwa te przyrządy mają odpowiednie
urządzenia (korektory zera) do sprowadzania wskazania do zera.
Porównywanie metodą podstawieniową polega na zastępowaniu wartości mierzonej
przez znaną wartość tej samej wielkości, wybraną w ten sposób, aby skutek oddziaływania
obu tych wartości na komparator był jednakowy. Jako komparator może być zastosowany
G
I
U
x
U
v
E

73
przetwornik o sygnale wejściowym y i wyjściowym r, którego równanie przetwarzania ma
postać
r =
g
(y)
(62)
Wejście przetwornika - komparatora jest przełączane: w położeniu I poddawane jest ono
działaniu wartości mierzonej x, a w położeniu II - wartości wzorcowej v (rys.8). Pomiar
polega na zapamiętaniu sygnału r(x), odpowiadającego działaniu wartości x na komparator, a
następnie wprowadzeniu na wejście komparatora znanych wartości v(1),v(2),... i obserwacji
sygnałów r[v(1)], r[v(2)],..., aż do znalezienia wartości v(N) = v
0
, dla której sygnał r[v(N)]
jest równy lub wystarczająco bliski r(x). Wartość v(N) = v
0
przyjmuje się jako estymatę
wartości mierzonej x.
Rys.6. Idea pomiaru metodą podstawieniową
Błąd prawdziwy pomiaru metodą podstawieniową można określić jako
s
II
s
I
0
K
r
K
r
v
-
=
x
∆
−
∆
−
∆
∆
&
&
&
&
(63)
gdzie:
∆
I
r - błąd niepowtarzalności i niestałości sygnału wyjściowego komparatora (przy
dokładnie tych samych wartościach y wartości r mogą być nieznacznie różne wskutek
niekontrolowanych zmian parametrów konstrukcyjnych),
∆
II
r - błąd niezrównoważenia,
równy różnicy wyznaczonych sygnałów
g
(x) i
g
[(v
0
)], spowodowany dyskretnym
charakterem wzorca i błędem odczytu sygnału wyjściowego r, K
s
=
∆
r/
∆
y - czułość
przetwornika komparującego.
Jeżeli sygnał wyjściowy komparatora ma postać przesunięcia wskazówki wzdłuż
podziałki, to graniczny błąd pomiaru można określić jako
u
2
1
K
d
2
K
r
+
v
=
x
s
s
I
+
+
∆
∆
∆
)
)
)
)
(64)
przy czym
∆
I
r jest zwykle do pominięcia, a podwojenie d jest spowodowane dwukrotnym od-
czytaniem wskazania komparatora.
g
(
)
0
ˆ
)
(
)
(
),...,
1
(
v
x
x
N
v
v
(x)
r
=
=
=
g
g
g
x
v
0
)
(
),...,
2
(
),
1
(
v
N
v
v
v
=
y

74
Warto podkreślić, że do wyznaczenia wartości v
0
, estymującej x, nie jest potrzebna
znajomość funkcji przetwarzania
g
. Czułość komparatora K
s
(a również czułość K
c
przy
pomiarze metodą kompensacyjną) można wyznaczyć eksperymentalnie jako stosunek zmiany
wskazania komparatora w pobliżu stanu równowagi do wywołującej ją zmiany wielkości
wzorcowej v. Metoda podstawieniowa bywa często stosowana w połączeniu z metodą
kompensacyjną.
Przykład 5
(a) Ważenie metodą Bordy. Pomiar masy m polega tu na zrównoważeniu wagi za pomocą innej masy, o bliżej
nieznanej wartości, a następnie zastąpieniu masy m
x
odważnikami, doprowadzającymi wagę ponownie do stanu
równowagi.
(b) Pomiar wartości skutecznej prądu zmiennego. Ideę metody podstawieniowej dobrze ilustruje praca
komparatora termoelektrycznego (rys.9), stosowanego do pomiaru wartości skutecznej prądu zmiennego.
Skuteczna wartość prądu zmiennego równa się wartości prądu stałego, która w danym rezystorze wydzieli taką
samą ilość ciepła co prąd zmienny przepływający przez ten rezystor. Stąd też w pierwszym takcie,
przepuszczając mierzony prąd o wartości skutecznej I
x
przez rezystor sprzężony termicznie z ogniwem
termoelektrycznym, kompensuje się siłę termoelektryczną ogniwa za pomocą pomocniczego układu
kompensacji napięcia stałego - do stanu, w którym galwanometr wskaże zero. W drugim takcie przez rezystor
przepuszcza się prąd stały o wartości nastawianej tak, by galwanometr również wskazał zero. Sygnałem
komparacji r jest odchylenie galwanometru w drugim takcie, proporcjonalne do różnicy I
x
- I
v
. Dla r = 0 znana
dokładnie wartość I
v
prądu stałego stanowi wynik pomiaru wartości I
x
. Wartość I
v
przyjmuje się jako estymatę
wartości skutecznej I
x
. Idea tej metody jest wykorzystywana w wielu współczesnych całkowicie
zautomatyzowanych woltomierzach wartości skutecznej.
Rys.7. Komparacja nierównoczesna - schemat ilustrujący metodę pomiaru wartości skutecznej prądu
zmiennego.
I
p
E
T
U
B
E
G
i
x
I
v
Prąd okresowo zmienny
o wartości skutecznej I
x
Kalibrator
prądu stałego
0
0
ˆ
0
)
,
(
v
x
v
x
p
I
I
I
I
I
=
⇒
≅

75
7. Pomiary analogowe
Pomiary analogowe, można traktować jako realizację metody podstawieniowej.
Wykażemy, że każde przetwarzanie analogowe jest w istocie realizacją metody
podstawieniowej.
Rozważmy przetwornik analogowy sygnału analogowego x na sygnał analogowy y,
zakładając dla uproszczenia, że obydwa sygnały mają charakter naturalny, tzn. ich treściami
są wartości chwilowe nośników. Przetwornik ten może być użyty do odtwarzania sygnału x
na podstawie sygnału y - a więc do pomiaru - tylko wtedy, gdy znany jest jego model
matematyczny, obejmujący równanie lub charakterystykę przetwarzania, oraz model błędu
przetwarzania.
Z dotychczasowej analizy metody podstawieniowej (rys.8) wynika, że nieznaną
wartość x można wyznaczyć wprowadzając na wejście zamiast x znaną wartość v (sygnału
tego samego rodzaju) i dobierając ją tak, aby odpowiadający jej sygnał wyjściowy y(v) miał
taką samą wartość jak sygnał wyjściowy y(x) odpowiadający nieznanej wartości x na wejściu.
W praktyce idealna równowaga, tzn. równość y(v) = y(x) - nie może być spełniona; chociażby
ze względu na dyskretny charakter wielkości wzorcowej, którą dysponuje eksperymentator,
doprowadza się tylko do odpowiedniej bliskości y(v) i y(x). Warunkiem realizowalności
takiego sposobu postępowania jest możliwość zapamiętania wartości sygnału y(x).
Opisane postępowanie można odwrócić, tzn. zapamiętać szereg wartości sygnału
wyjściowego
y(v
1
), y(v
2
),...,y(v
M
),
odpowiadających
znanym
wartościom
sygnału
wejściowego v
1
,v
2
,...,v
M
, a wyznaczanie x sprowadzić do wskazania y(v
k
) najbliższego y(x).
Jest to procedura wzorcowania
przetwornika pomiarowego, czyli wyznaczania jego
charakterystyki przetwarzania w postaci tabelarycznej. Naturalnym uogólnieniem tej
procedury jest wyznaczanie (identyfikacja) charakterystyki przetwarzania w postaci
analitycznej.
W ten sposób pokazaliśmy, że identyfikacja charakterystyki (równania) przetwarzania
przetwornika analogowego i korzystanie z tej charakterystyki (równania) jest realizacją
porównania metodą podstawieniową. Prawdziwa pozostaje także analiza błędów i
wypływające z niej wnioski. Nasze rozważania miały charakter ogólny, nie wymagały np.
żadnych założeń dotyczących charakteru sygnału wyjściowego przetwornika. W
szczególnych przypadkach sygnał ten może być bezpośrednio dostępny dla zmysłów
człowieka. Takim sygnałem jest przesunięcie mechaniczne elementu nazywanego wskazówką
- czyli wychylenie wskazówki. Metodę pomiaru, w której wartość wielkości mierzonej
wyznaczana jest na podstawie wychylenia urządzenia wskazującego, określa się mianem

76
metody wychyłowej. Metoda wychyłowa jest realizowana przez powszechnie znane mierniki
wychyłowe.
Rys.8. Zasada działania wagi sprężynowej
Przykład 6
(a) Waga sprężynowa. Zasadę działania wagi sprężynowej przedstawia rys.10. Ciężar mg ważonego obiektu (m -
masa, g - przyśpieszenie ziemskie) powoduje wydłużenie sprężyny o l. Związek między ciężarem a
wydłużeniem sprężyny może być na ogół modelowany równaniem liniowym
mg = cl
gdzie c - stała sprężyny. Masę m można więc wyznaczyć na podstawie wydłużenia sprężyny l. Mamy tu do
czynienia z ciągiem przetworzeń:
- masa ⇒ siła,
- siła ⇒ wydłużenie,
- wydłużenie ⇒ obraz (wskazówka + podziałka),
- obraz ⇒ cyfra (w świadomości eksperymentatora).
Porównanie w wadze sprężynowej występuje w dwóch postaciach: jawnej - kiedy wyznacza się wydłużenie
sprężyny przez porównanie przesunięcia wskazówki z podziałką - i ukrytej - przy sporządzaniu podziałki, czyli
przy skalowaniu. Skalowanie w jednostkach masy polega w tym wypadku na umieszczeniu na szali odważników
o znanych masach i zaznaczeniu odpowiadających im wydłużeń sprężyny.
(b) Termometr rtęciowy. Zmiana wysokości poziomu rtęci w szklanej kapilarze termometru, np. wskutek
ogrzania, jest następstwem rozszerzania się rtęci. Słupek rtęci jest widoczny na tle podziałki oznaczonej według
przyjętej skali (interwałowej) temperatur. Pomiar temperatury sprowadza się do pomiaru długości słupka rtęci.
(c) Elektryczne przyrządy wskazówkowe do pomiaru napięcia, prądu, rezystancji, mocy itp.
(d) Czujniki elektryczne wielkości nieelektrycznych, takich jak: ciśnienie, przyspieszenie, temperatura,
wilgotność itp.
m
x
0
0
l

77
4. Przetworzeniowo-sygnałowy model pomiaru
Przetworzeniowo-sygnałowym modelem pomiaru będziemy nazywali model pomiaru
traktujący operację pomiaru jako złożoną operację przetwarzania sygnałów, którą można
przedstawić w postaci zbioru powiązanych ze sobą prostszych operacji przetwarzania
sygnałów pomiarowych. Innymi słowami model przetworzeniowo-sygnałowy przedstawia
pomiar jako zbiór operacji przetwarzania i odpowiednio, system pomiarowy, czyli
zorganizowany zbiór narzędzi realizujący pomiar, – jako zbiór przetworników (rozumianych
jako operatory przetwarzania). Wzajemne związki między operacjami przetwarzania tworzą
strukturę operacyjną pomiaru a wzajemne związki między przetwornikami – strukturę
operacyjną systemu pomiarowego. Poszczególne operacje i grupy operacji przetwarzania są
realizowane przez narzędzia pomiarowe, wzajemne związki między narzędziami tworzącymi
system pomiarowy tworzą strukturę instrumentalną systemu pomiarowego. Dalej będziemy
mówili wprost struktura pomiarowa, a o jaką strukturę chodzi będzie wynikało z kontekstu.
Model przetworzeniowo-sygnałowy traktuje pomiar jako przetwarzanie pochodzącego
z obiektu sygnału mierzonego, którego treścią jest wartość prawdziwa x& wielkości mierzonej
(ogólnie mezurand pomiaru), we wskazanie, którego treścią jest wartość zmierzona x
~
(ogólnie estymata mezurandu). Sygnał mierzony jest najczęściej sygnałem analogowym
naturalnym. Operator przetwarzania pomiaru, traktowanego jako złożona operacja
przetwarzania, można dekomponować, tworząc system operatorów prostszych o określonej
strukturze pomiarowej.
Ze względu na funkcje i miejsce w systemie operacji tworzących pomiar wyróżnia się
cztery rodzaje operacji przetwarzania:
(i)
przetwarzanie wstępne (ang. sensing od sensor – czujnik),
(ii)
kondycjonowanie sygnałów (ang. conditioning),
(iii)
przetwarzanie operacyjne (ang. signal processing),
(iv)
wskazywanie (ang. displaying).
Typowa struktura pomiaru ma postać łańcucha pomiarowego, składającego się z ciągu
następujących po sobie przetworników, tak połączonych, że sygnał wyjściowy poprzednika
jest sygnałem wejściowym następnika. Początek łańcucha tworzy operacja przetwarzania
wstępnego, koniec – operacja wskazywania. Wewnętrzne ogniwa łańcucha mogą na przemian
mieć charakter kondycjonowania i przetwarzania operacyjnego.
Przetwarzanie wstępne
jest składową operacją pomiaru, polegającą na przyjęciu z
obiektu mierzonego sygnału i uformowaniu na jego podstawie sygnału pomiarowego, z
którego jest wyznaczana wartość mezurandu. Przetwarzanie wstępne jest pierwszym

78
ogniwem łańcucha operacji przetwarzania składających się na pomiar. Przetwarzanie wstępne
jest często przetwarzaniem analogowym natury wielkości realizowanym instrumentalnie
przez czujnik.
Wskazywanie jest składową operacją pomiaru, polegającą na przetwarzaniu sygnału
pomiarowego we wskazanie, czyli sygnał przenoszący informację w sposób bezpośrednio
odbierany przez człowieka. Wskazywanie może przenosić informację o wartości wielkości
mierzonej i wówczas jest ostatnim ogniwem łańcucha pomiarowego. Wskazanie może także
przenosić inną informację niezbędną do wykonania pomiaru, np. o wartości sygnału
nierównowagi z komparatora i nastawionej wartości wielkości wzorcowej, tak jak w metodzie
pomiarowej zerowej, o której będziemy mówili w następnym wykładzie.
Wskazywanie jest
przetwarzaniem sygnału pomiarowego nazywanego sygnałem wskazywanym lub wielkością
wskazywaną we wskazanie. Sygnał wskazywany jest zwykle analogowy, wskazanie może być
analogowo-ciągłe, analogowo-dyskretne lub cyfrowe. Wskazywanie w klasycznym systemie
pomiarowym sprowadza się zwykle do pomiaru wielkości wskazywanej miernikiem
analogowym lub cyfrowym.
Kondycjonowanie (sygnałów pomiarowych) jest składową operacją pomiaru,
polegającą na przetwarzaniu sygnału pomiarowego celu dopasowania jego zakresu
zmienności, poziomu energii, rozkładu czasowego i kodu do następnego stopnia
przetwarzania. Kondycjonowanie może być przetwarzaniem analogowym, lub analogowo-
cyfrowym lub cyfrowym. Najczęściej jednak kondycjonowanie polega na dopasowaniu
zakresu przez przetwornik wartości.
Przetwarzanie operacyjne jest składową operacją pomiaru, polegającą na
przetwarzaniu jednego lub kilku sygnałów pomiarowych według równania przetwarzania
uznanego za matematycznie złożone. Ocena złożoności równania przetwarzania ma charakter
po części arbitralny. Na ogół za złożone przyjmuje się równania przetwarzania więcej niż
jednego sygnału, równania przetwarzania jednego sygnału nieliniowe (wyjąwszy
kwantowanie) i równania przetwarzania rozwiązywane numerycznie przez komputer.
Przetwarzanie operacyjne jest coraz częściej przetwarzaniem cyfrowym, realizowanym przez
komputer i jako takie nazywa się przetwarzaniem programowym.

79
Rys.9. Łańcuch trzech przetworników (a) i wypadkowy przetwornik równoważny (b)
Struktura łańcuchowa odpowiada superpozycji operatorów przetwarzania. Na rys.9
przedstawiono łańcuch trzech szeregowo połączonych przetworników o funkcjach
przetwarzania g
1
(), g
2
() i g
3
(). Schemat z rys.9a przedstawia model operacyjny łańcucha nie
uwzględniający błędów przetwarzania. Wypadkowa funkcja przetwarzania łańcucha ma
postać
( )
[
]
{
}
( )
y
x
x
x
=
=
=
g
g
g g
g g g
1
( )
3
2
1
3 2
(65)
gdzie g
3
g
2
g
1
() – superpozycja funkcji g
3
(), g
2
() i g
1
().
Dla przetworników liniowych o czułościach G
1
, G
2
i G
3
y
G x
G G G x
=
=
3
2
1
(66)
tj. czułość szeregowego połączenia przetworników liniowych jest równa iloczynowi czułości
przetworników.
Model struktury przetwarzania z błędami tworzymy wprowadzając addytywnie do jej
węzłów (czyli na połączenia wyjście poprzednika z wejściem następnika) błędy bezwzględne.
Błędy te modelują:
(i)
niedokładności przetwarzania przetwornika;
(ii)
zakłócenia sygnału powstające przy jego transmisji od wyjścia poprzednika do wejścia
następnika; zakłócenia te mogą być zewnętrznymi (pochodzącymi z otoczenia) i
wewnętrznymi (powodowanymi wzajemnym oddziaływaniem przetworników, np.
obciążeniem energetycznym wyjścia poprzednika przez wejście następnika);
(iii)
obciążenie informacyjne sygnału czyli błąd własny sygnału spowodowany np.
niedokładnością kodu, niedokładnością operacji formowania sygnału (dotyczy to sygnału
wejściowego).
Wprowadzone do struktury błędy mogą mieć charakter błędów prawdziwych lub granicznych.
Określenie niedokładności struktury obejmuje:
(1)
przeniesienie wszystkich błędów na wyjście (lub na wejście) łańcucha,
(2)
złożenie błędów,
(3)
określenie błędu granicznego.
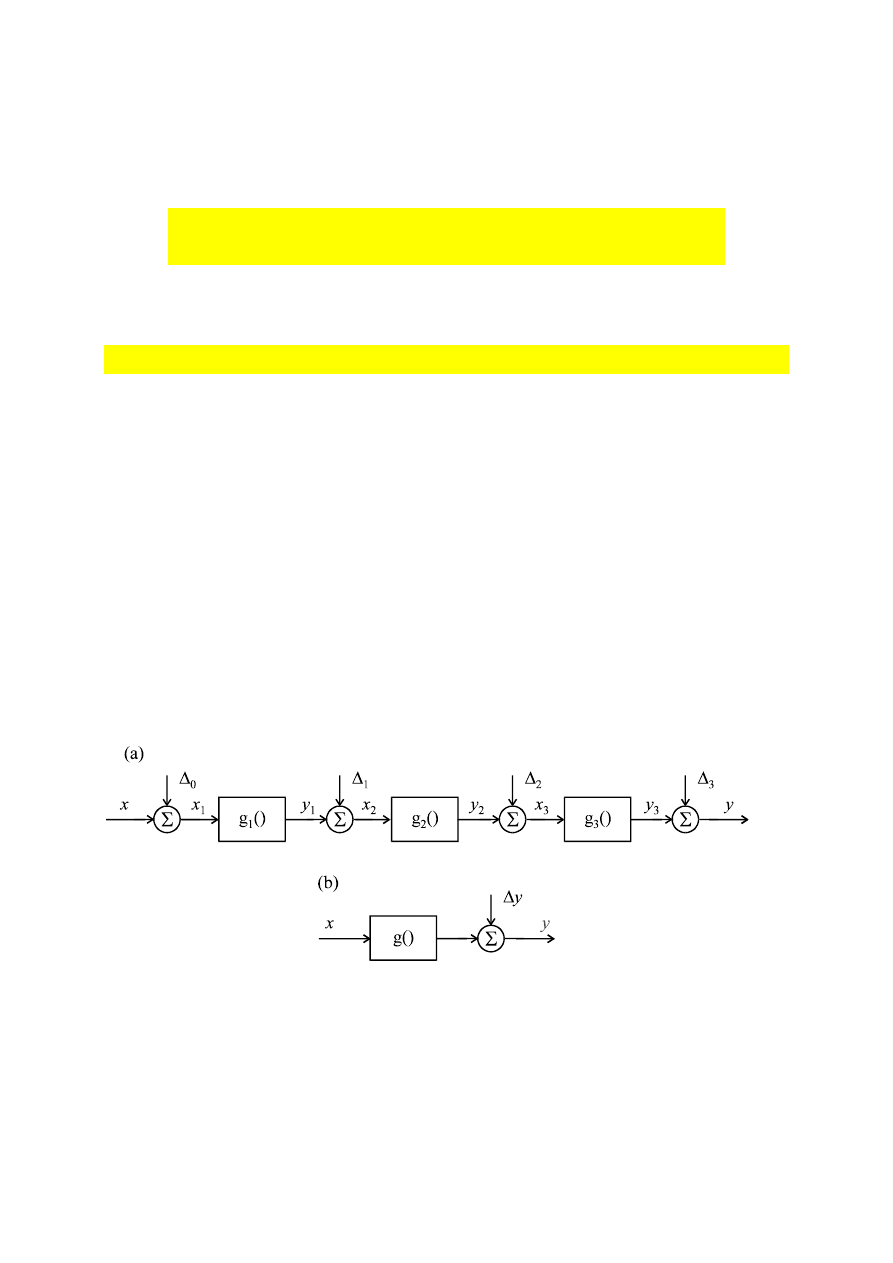
80
Pomocne przy gromadzeniu błędów na wejściu lub na wejściu łańcucha są reguły
przenoszenia błędu dane zależnościami (17), (18) i (19). Reguły te można sprowadzić do
jednej ogólnej reguły przenoszenia błędu bezwzględnego (prawdziwego i granicznego):
błąd bezwzględny przenosi się z wejścia na wyjście przetwornika mnożąc go
przez czułość, a z wyjścia na wejście – dzieląc przez czułość przetwornika
i jednej szczegółowej, określającej przenoszenie błędów względnych przez przetwornik
liniowy:
błąd względny przetwornika liniowego przenosi się bez zmiany z jednej strony na drugą
Obowiązuje zasada, że tam, gdzie tylko można, przenosi się błędy prawdziwe, składa je
sumując algebraicznie i na koniec określa błąd graniczny. Jeżeli dysponuje się tylko danymi o
błędach granicznych przetworników, to przenosi się błędy graniczne i składa według zasad
składania niepewności.
Na rys.10a przedstawiono strukturę łańcucha trójprzetwornikowego z addytywnie
wprowadzonymi błędami prawdziwymi
∆
0
,
∆
1
,
∆
2
i
∆
3
, przenosząc je na wyjście łańcucha i
składając poprzez sumowanie otrzymujemy (rys.10b)
∆
∆
∆
∆
∆
y
G G G
G G
G
=
+
+
+
3
2
1
0
3
2
1
3
2
3
(67)
przy czym dla uproszczenia pominięto zależność czułości od sygnałów G
1
(x
1
), G
2
(x
2
) i
G
3
(x
3
).
Rys. 10. Łańcuch trzech przetworników z błędami (a)
i wypadkowy przetwornik z błędem na wyjściu (b)
Jeżeli dane są błędy graniczne
∆
0max
,
∆
1max
,
∆
2max
i
∆
3max
, to błąd graniczny łańcucha można
oszacować albo według zasady najgorszego przypadku (patrz wykład 3 i 4)
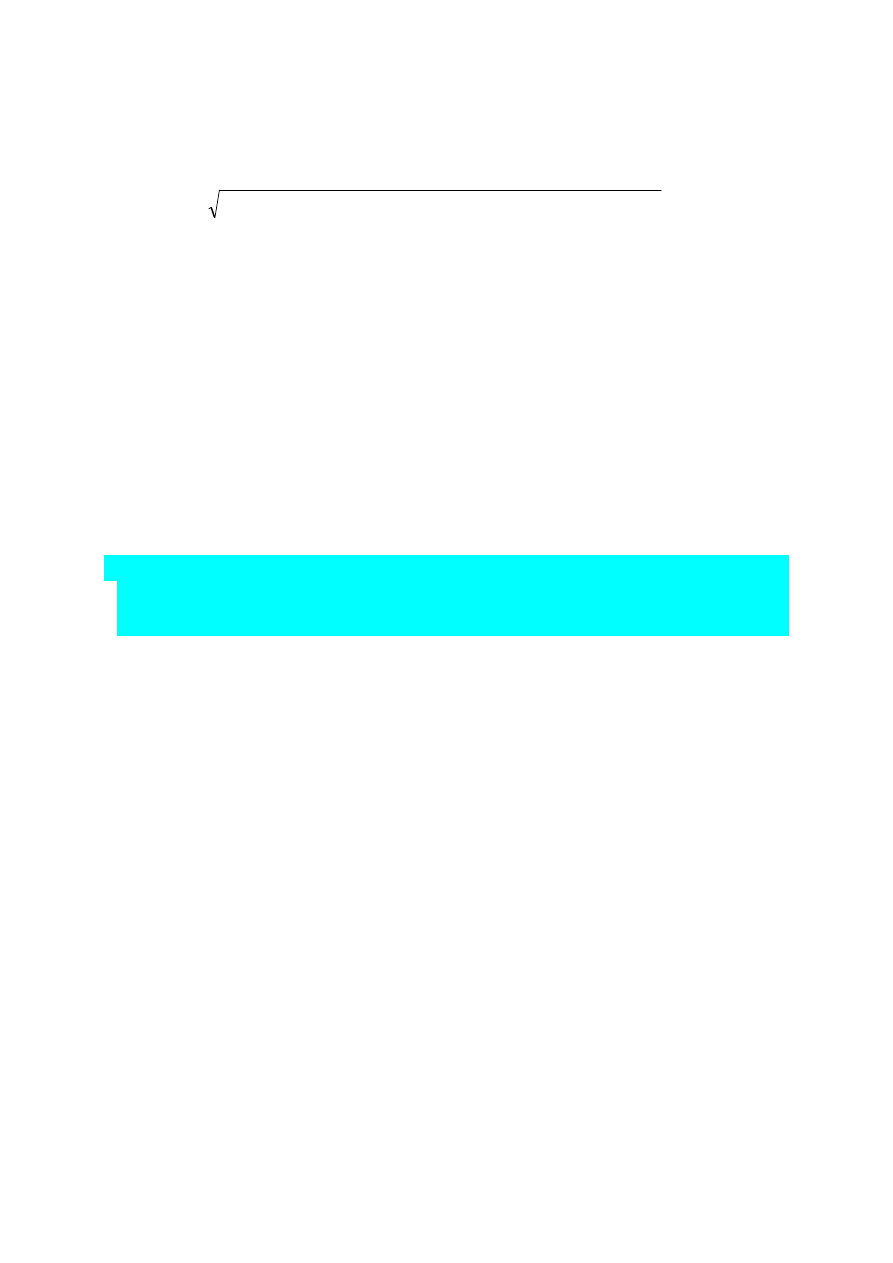
81
∆
∆
∆
∆
∆
max
max
max
max
max
|
|
|
|
|
|
y
G G G
G G
G
=
+
+
+
3
2
1
0
3
2
1
3
2
3
(68)
lub zasady pierwiastka z sumy kwadratów błędów
∆
∆
∆
∆
∆
max
max
max
max
max
(
)
(
)
(
)
y
G G G
G G
G
=
+
+
+
3
2
1
2
0
2
3
2
2
1
2
3
2
2
2
3
2
(69)
Należy jednak wyraźnie podkreślić, że zależności (68) i (69) mogą służyć tylko jako
orientacyjne miary niedokładności łańcucha przetwarzania, pierwsza całkowicie pewna, ale
zawyżona, druga mniej pewna, ale bardziej realistyczna. Graniczny błąd przetwarzania
określa się prawie zawsze poprzez kalibrację całego łańcucha.
Model przetworzeniowo-sygnałowy szczególnie dobrze nadaje się do opisu
elektrycznego przyrządu pomiarowego z przetwornikiem, którego szczególnym
przypadkiem jest miernik. Przyrząd taki ma strukturę łańcuchową z miernikiem elektrycznym
jako
elementem
końcowym,
w
rozwiązaniach
starszych
z
miliamperomierzem
magnetoelektrycznym, w rozwiązaniach współczesnych z woltomierzem cyfrowym napięcia
stałego.
Przykład 7
Przeprowadzić analizę błędu amperomierza magnetoelektrycznego z bocznikiem uwzględniając
temperaturową zależność rezystancji Rm i czułości Gm mechanizmu.

82
Wykład 8, 9 i 10
Metody pomiarowe i narzędzia pomiarowe II
Przetworniki
cyfrowo-analogowe.
Przetworniki
analogowo-cyfrowe.
Woltomierze
i
multimetry cyfrowe. Oscyloskopy cyfrowe.
1. Przetworniki cyfrowo-analogowe
Sygnał wejściowy przetwornika C/A i sygnał wyjściowy przetwornika A/C mają
postać cyfrową. Sygnały cyfrowe są reprezentowane przez odpowiednie kody cyfrowe,
stanowiące uporządkowane zbiory stanów dwójkowych: 0 lub 1. Najmniejszą jednostką
informacyjną kodu jest bit. Grupa bitów tworzy słowo cyfrowe a liczba bitów słowa określa
jego długość. Dowolna całkowita liczba dziesiętna może być zapisana w naturalnym kodzie
dwójkowym następująco:
N = a
n
2
n
+ a
n-1
2
n-1
+...+a
2
2
2
+ a
1
2
1
+ a
0
2
0
(1)
przy czym każdy współczynnik a może przyjmować wartość 1 lub 0. Podobnie dowolna
ułamkowa liczba dziesiętna może być przedstawiona w naturalnym kodzie dwójkowym w
postaci:
N = b
1
2
-1
+ b
2
2
-2
+ ... + b
j-1
2
-(j-1)
+ b
j
2
-j
=
b
j
j
j
M
2
1
−
=
∑
(2)
Np. słowo kodowe 101101 ma tu wartość:
(1x0,5) + (0x0,25) + (1x0,125) + (1x0,0625) + (0x0,03125) + (1x0,015625) = 0,703125
Jeśli nawet wszystkie bity miały by stan 1, to suma (2) nie dała by pełnej skali przetwarzania.
Otrzymujemy w takim przypadku liczbę (1 - 2
M
), tzn. Y
max
pomniejszoną o najmniej
znaczący bit (ang. LSB - last significant bit). Jeśli 10 bitowy przetwornik C/A ma Y
max
=
10V [patrz wzór (12) w tekście wykładów 5,6,7], to sygnał wyjściowy wyniesie (1 - 2
-10
)10V
= 9,99023V, przy czym LSB = 9,77mV.
W tablicy 1 zestawiono niektóre charakterystyczne wartości liczbowe naturalnego
kodu dwójkowego dla różnych długości słowa cyfrowego. Znajomość tych liczb jest pomocna
np. przy ocenie przydatności przetwornika A/C lub C/A w analizowanej strukturze systemu
pomiarowego.
Oprócz zapisu w naturalnym kodzie dwójkowym stosowany jest również zapis
dziesiętny kodowany dwójkowo (BCD - binary coded decimal). Porównanie tych dwóch
zapisów zestawiono w tablicy 2. W przetwornikach A/C pracujących w kodzie BCD
83
wprowadza się często dodatkowy bit na pozycji bardziej znaczącej niż MSB (ang. most
significant bit - najbardziej znaczący bit) - o wadze odpowiadającej Y
max
. Ten dodatkowy bit,
zwany bitem przekroczenia, zwiększa zakres przetwarzania przetworników A/C o 100%. tak
więc w przetworniku o pełnym dziesiętnym zakresie przetwarzania 999, bit przekroczenia
zakresu podwaja pełny zakres do 1999 (kod wyjściowy: 1 1001 1001 1001). Dodatkowy
zakres jest powszechnie oznaczany jako
1
/
2
cyfry i cały zakres w tym przypadku wynosi 3
1
/
2
cyfry.
Tablica 1. Niektóre charakterystyczne wartości liczbowe ułamkowego naturalnego kodu dwójkowego dla
różnych długości słowa cyfrowego
BIT
2
-n
1/2
n
(część)
dB
1/2
n
(dziesiętnie)
%
Ppm
FS
2
0
1
0
1,0
100
1000000
MSB
2
-1
1/2
-6
0,5
50
500000
2
2
-2
1/4
-12
0,25
25
250000
3
2
-3
1/8
-18,1
0,125
12,5
125000
4
2
-4
1/16
-24,1
0,0625
6,2
62500
5
2
-5
1/32
-30,1
0,03125
3,1
31250
6
2
-6
1/64
-36,1
0,015625
1,6
15625
7
2
-7
1/128
-42,1
0,007812
0,8
7812
8
2
-8
1/256
-48,2
0,003906
0,4
3906
9
2
-9
1/512
-54,2
0,001953
0,2
1953
10
2
-10
1/1024
-60,2
0,0009766
0,1
977
11
2
-11
1/2048
-66,2
0,00048828
0,05
488
12
2
-12
1/4096
-72,2
0,00024414
0,024
244
13
2
-13
1/8192
-78,3
0,00012207
0,012
122
14
2
-14
1/16384
-84,3
0,000061035
0,006
61
15
2
-15
1/32768
-90,3
0,0000305176
0,003
31
16
2
-16
1/65536
-96,3
0,0000152588
0,0015
15
17
2
-17
1/131072
-102,3
0,00000762939
0,0008
7,6
18
2
-18
1/262144
-108,4
0,000003814697
0,0004
3,8
19
2
-19
1/524288
-114,4
0,000001907349
0,0002
1,9
20
2
-20
1/1048576
-120,4
0,0000009536743
0,0001
0.95
Budowę przetwornika cyfrowo-analogowego można najprościej objaśnić przykładem
nastawnego dzielnika napięcia (rys.1). Jeżeli na analogowe wejście dzielnika podamy
napięcie wzorcowe E
w
, to sygnał wzorcowy U
w
na analogowym wyjściu będzie zależał
wprost proporcjonalnie od nastawionego współczynnika podziału. Sygnał U
w
będzie więc
reprezentował wartość liczbową (cyfrę N) współczynnika podziału.
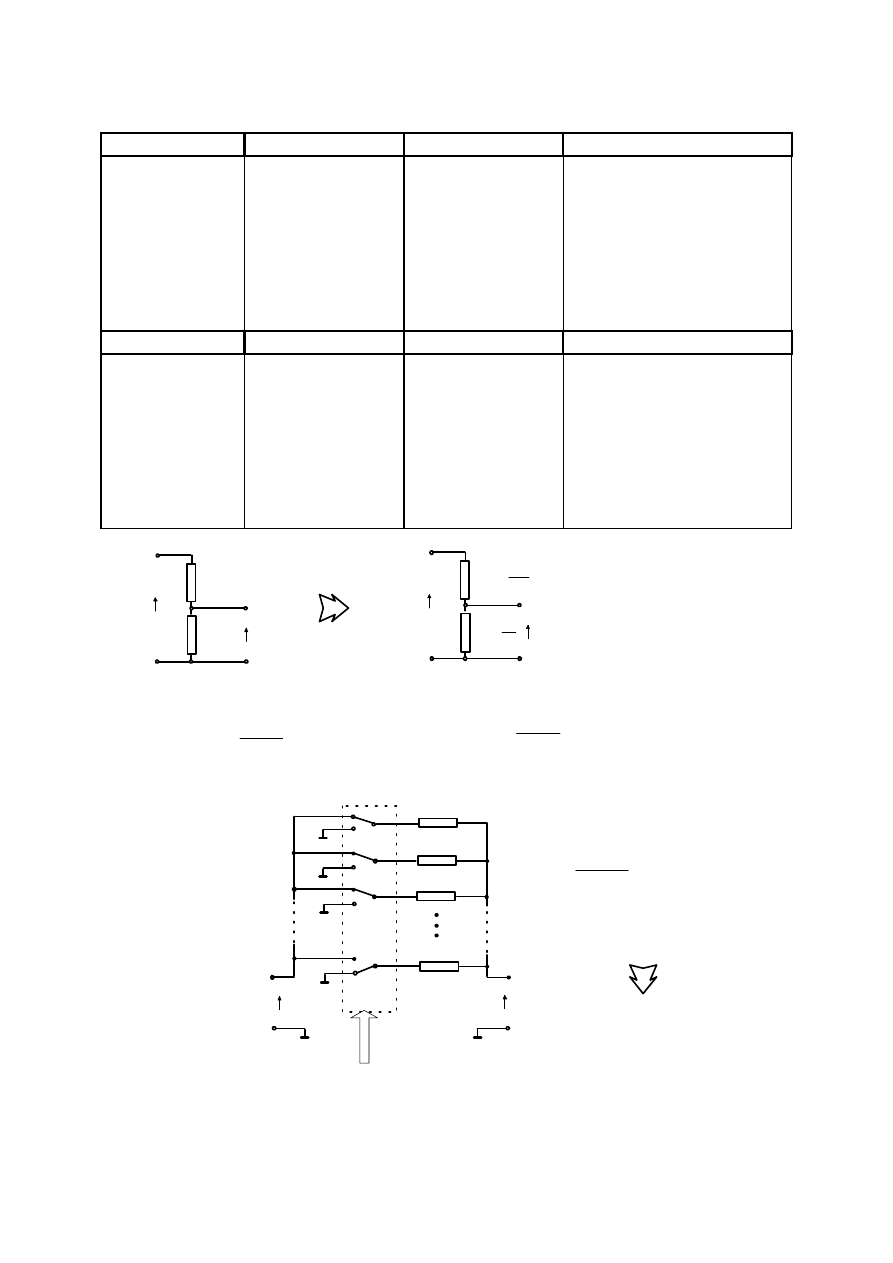
84
Tablica 2. Porównanie zapisu w naturalnym kodzie dwójkowym i w kodzie BCD
Skala
+10 V FS
+5 V FS
Kod dwójkowy
+FS - 1LSB
+9,9976
+4,9988
1111 1111 1111
+7/8 FS
+8,7500
+4,3750
1110 0000 0000
+3/4 FS
+7,5000
+3,7500
1100 0000 0000
+5/8 FS
+6,2500
+3,1250
1010 0000 0000
+1/2 FS
+5.000
+2,5000
1000 0000 0000
+3/8 FS
+3,7500
+1,8750
0110 0000 0000
+1/4 FS
+2,5000
+1,2500
0100 0000 0000
+1/8 FS
+1,2500
+0,6250
0010 0000 0000
0+1LSB
+0,0024
+0,0012
0000 0000 0001
0
0,0000
0,0000
0000 0000 0000
Skala
+10 V FS
+5 V FS
Kod dwójkowo-dziesiętny
+FS - 1LSB
+9,99
+4,95
1001 1001 1001
+7/8 FS
+8,75
+4,37
1000 0111 0101
+3/4 FS
+7,50
+3,75
0111 0101 0000
+5/8 FS
+6,25
+3,12
0110 0010 0101
+1/2FS
+5.00
+2,50
0101 0000 0000
+3/8 FS
+3,75
+1,87
0011 0111 0101
+1/4 FS
+2,50
+1,25
0010 0101 0000
+1/8 FS
+1,25
+0,62
0001 0010 0101
0+1LSB
+0,01
+0,00
0000 0000 0001
0
0,00
0,00
0000 0000 0000
Rys.1. Nastawny dzielnik napięcia jako przetwornik cyfrowo-analogowy
G
1
G
2
G
3
G
n
1
0
1
1
0
0
0
1
E
w
U
v
N
U
v
E
w
U
v
E
w
*
R
R
*
*
R
1
G
=
R
1
G
=
const
R
R
*
=
+
const
G
G
*
=
+
w
*
v
E
R
R
R
U
+
=
w
*
*
v
E
G
G
G
U
+
=
)
1
,
0
(
x
czym
przy
E
G
x
G
U
k
w
n
1
k
k
n
1
k
k
k
v
∈
=
∑
∑
=
=
w
v
NE
U
====
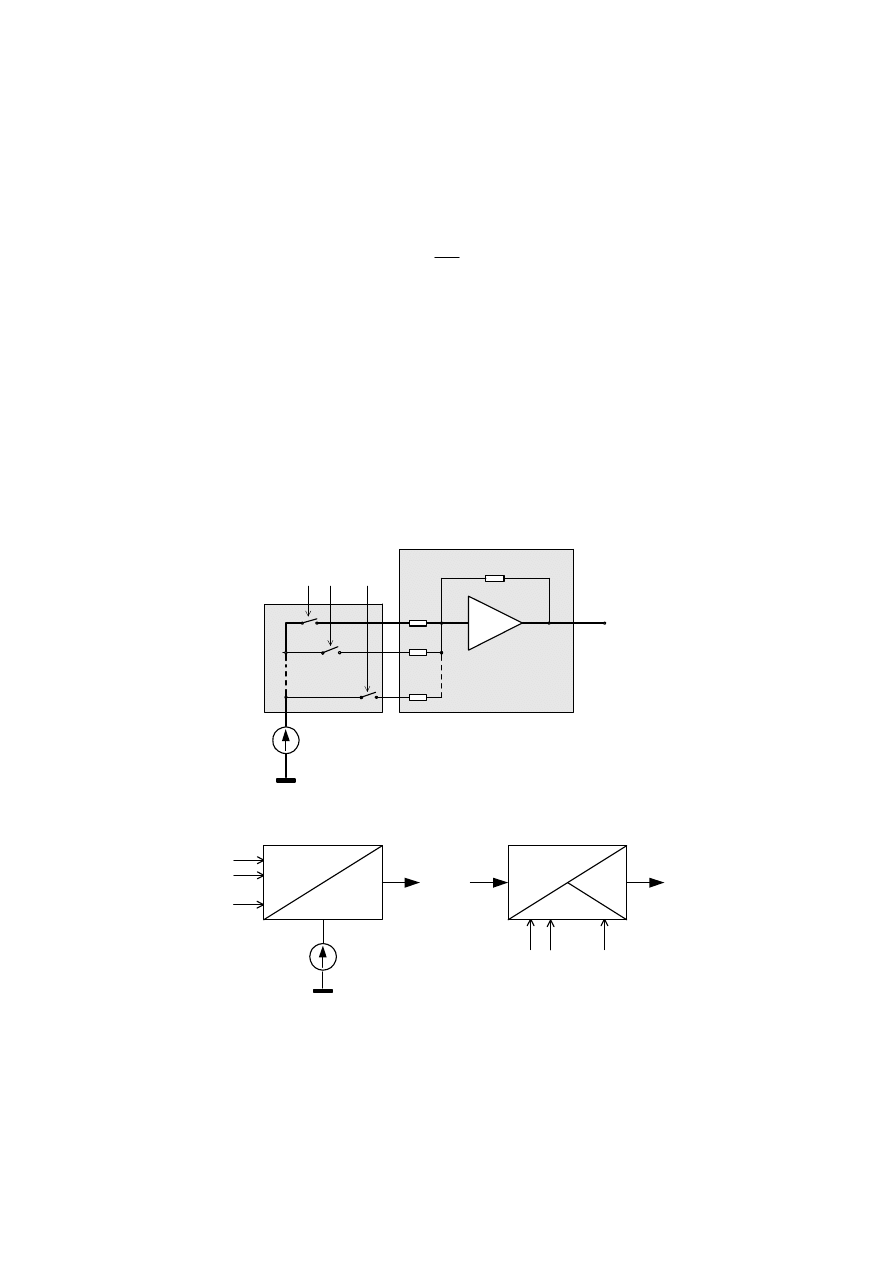
85
Przetwarzanie C/A można zilustrować także przykładem sumacyjnego przetwornika
napięcia elektrycznego, którego strukturę przedstawiono na rys.2a. Przyjętym modelem
wzmacniacza operacyjnego w tej strukturze jest idealne źródło napięciowe o nieskończonym
wzmocnieniu. Napięcie wyjściowe U
v
wyraża się tu wzorem
U
E
R
R
v
w
F
=
−
=
−
∑
b
p
p
p
P
2
0
1
(3)
w którym: E
w
- napięcie wzorcowe, R
F
,R,2R,...,2
P-1
R - rezystancje sumatora, b
0
b
1
...b
P-1
-
reprezentacja dwójkowa liczby przenoszonej przez sygnał wejściowy, dana przez stany
wyłączników: 0 - otwarty, 1 - zamknięty.
Zauważmy, że struktura z rys.2a może być interpretowana zarówno jako przetwornik C/A
(rys.2 b) jak też jako cyfrowo sterowany dzielnik napięcia (rys.2 c). Ta druga interpretacja jest
istotna wówczas, gdy przetwornik spełnia funkcję nastawnego wzorca napięcia, zwanego
kalibratorem napięcia.
Rys.2. Przetwornik cyfrowo-analogowy: a) przykład realizacji; b) schemat blokowy eksponujący funkcję
przetwarzania cyfrowo-analogowego; c) schemat blokowy eksponujący funkcję sterowanego
cyfrowo podziału napięcia.
Dla bliższego przedstawienia takich parametrów jak rozdzielczość q oraz zakres
przetwarzania Y
max
= FS (od ang. full scale) na rys.3a przedstawiono idealną charakterystykę
−∞
E
w
b
0
b
1
b
P-1
...
R
F
2R
2
P-1
R
R
sumator
U
v
...
..
.
E
w
U
v
U
v
C
C
A
A
A
E
w
b
0
b
0
b
1
b
1
b
P-1
b
P-1
b)
c)
a)
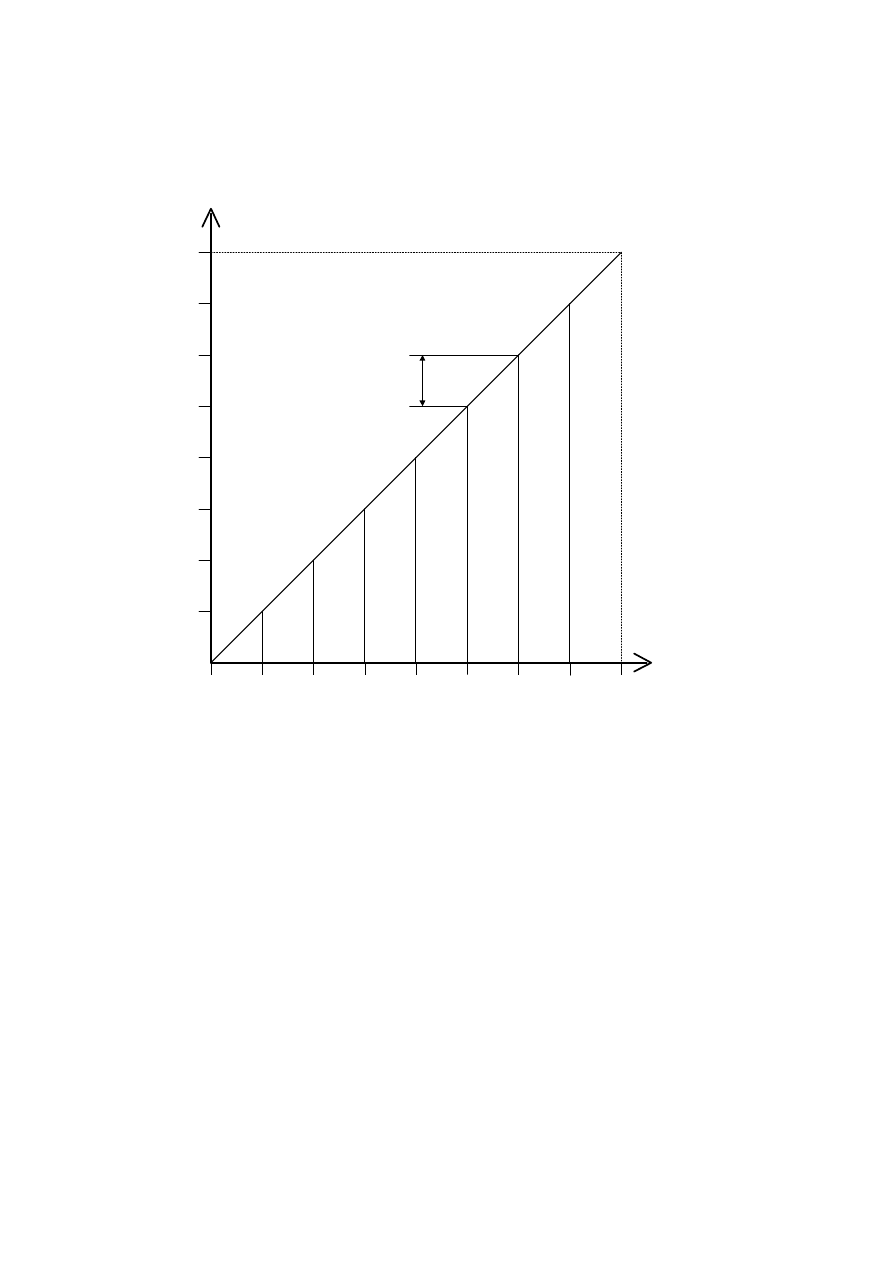
86
przetwarzania przetwornika C/A o rozdzielczości odpowiadającej 3 bitowej długości słowa. Z
charakterystyki tej wynika, że pełny zakres przetwarzania (FS) jest teoretyczną wartością
graniczną, nie osiągalną praktycznie.
Rys. 3. Charakterystyka przetwarzania 3-bitowego przetwornika C/A
Idealna charakterystyka przetwarzania daje odniesienie przy analizie i ocenie błędów
przetwornika C/A. Błędy związane z przesunięciem zera i zmianą nachylenia charakterystyki
definiowane są zgodnie z zasadami normalizacji błędów addytywnych i multiplikatywnych.
Błędy związane z nieliniowością charakterystyki mogą się ujawnić np. po przeprowadzeniu
procedury kalibracyjnej (skorygowaniu przesunięcia zera i zmiany nachylenia), tak, by oba
kalibrowane punkty (dolny i górny) leżały dokładnie na charakterystyce idealnej. Błędy
związane z nieliniowością charakterystyki przetwarzania w dobrym przetworniku nie
powinny przekraczać wartości
±
1
/
2
LSB.
2. Przetworniki analogowo-cyfrowe
U
000
N
001
010
100
101
110
111
011
1/8
FS
7/8
3/4
5/8
1/2
3/8
1/4
W
y
jś
c
ie
a
n
a
lo
g
o
w
e
w
o
d
n
ie
si
e
n
iu
d
o
k
o
ń
c
a
z
a
k
r
e
su
(
F
u
ll
S
c
a
le
)
Wejście cyfrowe
1 LSB

87
Ze względu na znaczne zróżnicowanie metod przetwarzania analogowo-cyfrowego ich
klasyfikacja oraz porównywanie parametrów natrafiają na duże przeszkody. Najczęściej
stosowanym kryterium podziału jest kryterium czasu przetwarzania. Według tego kryterium
metody przetwarzania A/C dzielą się na metody przetwarzające wartość chwilową sygnału
(zastosowanie w technice video, w oscyloskopach cyfrowych i analizatorach widma) oraz na
metody integracyjne - uśredniające wartość sygnału w czasie (zastosowanie w automatyce, w
woltomierzach i multimetrach cyfrowych). Do metod przetwarzających wartość chwilową
zalicza się np. metody bezpośredniego porównania i kolejnych przybliżeń (kompensacyjną).
Do metod integracyjnych zalicza się przede wszystkim metody podwójnego i wielokrotnego
całkowania oraz metody modulacji szerokości impulsu.
Metody przetwarzania A/C wartości chwilowej bliżej zilustrujemy przykładem
przetwornika napięcia (rys.4). Podstawowe bloki schematu to:
- komparator - porównuje dwa napięcia i stwierdza które z nich jest większe,
- cyfrowo sterowany dzielnik napięcia, czyli przetwornik C/A,
- układ sterujący - generuje sygnały cyfrowe sterujące procesem pomiaru,
- źródło napięcia wzorcowego, podawanego na sterowany dzielnik napięcia,
- rejestr cyfrowy - przechowuje informacje o kolejnych sygnałach cyfrowych w trakcie
realizacji procedury kolejnych przybliżeń.
Układ sterujący i cyfrowy rejestr aproksymacyjny wykonują operację „ważenia”, nastawiając
kolejne wartości „odważników” napięcia U
k
porównywanego w komparatorze z napięciem
U
x
. Proces pomiaru można zilustrować schematami ważenia dla pierwszego stopnia podziału
(rys4 b). Proces ten sprowadza się do sprawdzania relacji komparatora dla kolejnych wartości
U
k
(sumy wartości „odważników” na rys.4 b składane są z napięć: 0,8V; 0,4V; 0,2V i 0,1V).
Porównywanie rozpoczyna się od 0,8V. Sygnał wyjściowy komparatora (0 lub 1) decyduje o
włączeniu bądź wyłączeniu kolejnej wartości U
k
na stałe w danym cyklu rozwijania wzorca.
W przetwornikach cyfrowo-analogowych wielostopniowych istota tego procesu pozostaje
taka sama - po zakończeniu badania stopnia najwyższego następuje badanie stopni niższych
aż do wyznaczenia sumy napięć włączonych we wszystkich stopniach, w pełnym cyklu
rozwijania napięcia U
k
. Na przykład przy czterech stopniach wynik w rozpatrywanym
przykładzie (rys.4) mógłby wynosić: (0,4 + 0,07 + 0,005 + 0,0002) = 0,4752 V.
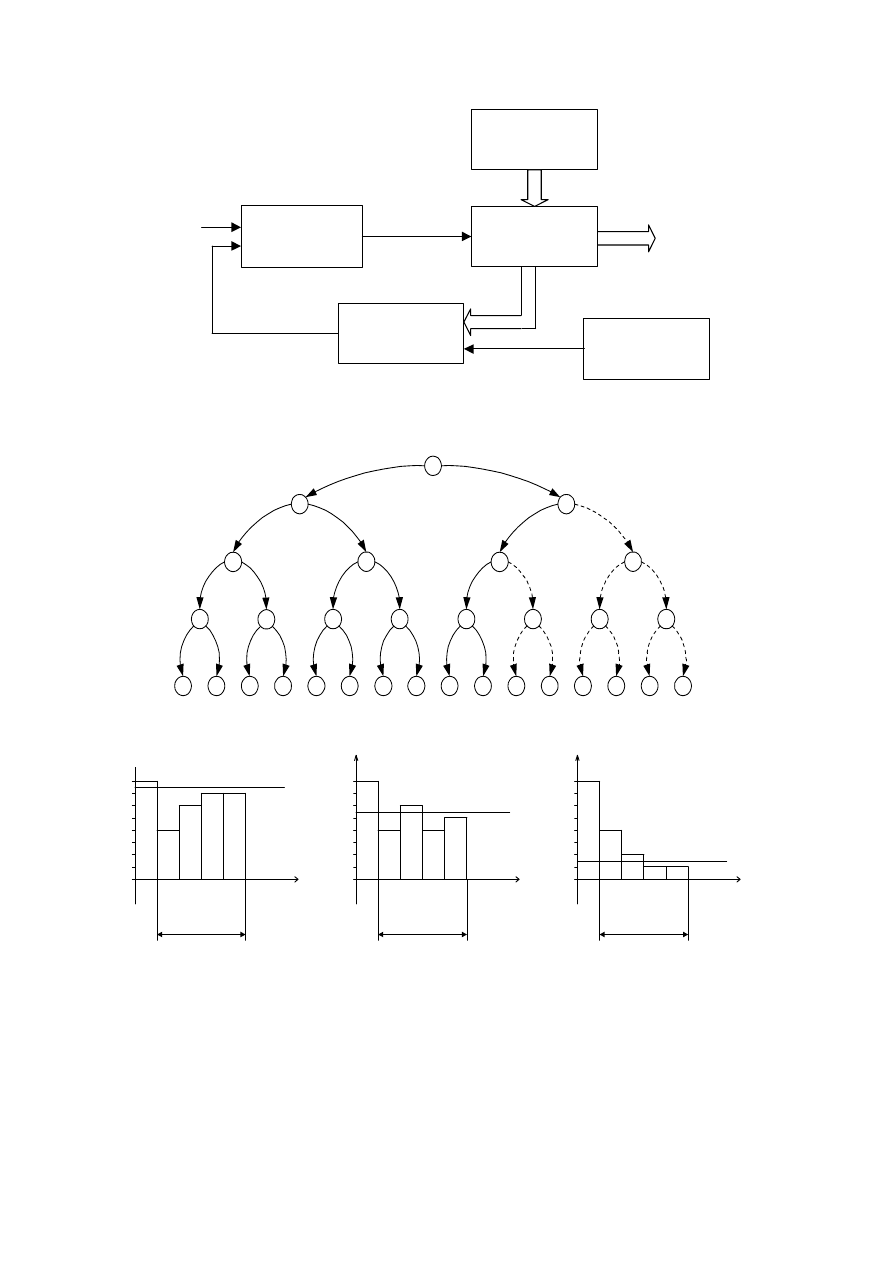
88
KO M PARAT O R
PRZET W O RNIK
C/A
U
x
Układ
steruj
ą
cy
Rejestr
cyfrow y
Ź
ródło napi
ę
cia
w zorcow ego
N
x
0,8
0,4
1,2
0,2
0,6
1,0
1,4
0,3
0,5
1,1
1,3
0,7
0,9
0,1
1,5
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
-
+
-
-
-
-
-
-
-
-
-
-
-
-
-
-
+
+
+
+
+
+
+
+
+
+
+
+
+
+
cykl 1-go stopnia
U
t
0
0,2
0,4
0,6
0,8
U
x
= 0,75
0
0,2
cykl 1-go stopnia
U
t
0
0,2
0,4
0,6
0,8
U
x
= 0,55
cykl 1-go stopnia
U
t
0,4
0,6
0,8
U
x
= 0,15
Rys. 4. Schemat blokowy przetwornika A/C realizującego metodę kolejnych przybliżeń (a) oraz schematy
ilustrujące „ważenie” (b) i odpowiadające mu zmiany napięcia na wyjściu przetwornika C/A
podawane na wejście komparatora (c)
Zasadę
działania przetwornika A/C integracyjnego, pracującego według metody
podwójnego całkowania ilustruje schemat przedstawiony na rys.5a. Napięcie mierzone
b)
c)
a)

89
przetwarzane jest na liczbę impulsów. Cykl pomiarowy przetwarzania składa się z trzech
powtarzających się kroków:
- pierwszy krok - zerowanie układu całkującego i zerowanie licznika,
- drugi krok - całkowanie napięcia U
x
w ściśle odmierzonym czasie T
i
,
- trzeci krok - całkowanie napięcia wzorcowego do chwili osiągnięcia poziomu zera na
wyjściu układu całkującego (rys.5 b).
Liczba N impulsów zliczonych przez licznik w czasie T
n
(3 krok) jest proporcjonalna do
napięcia U
x
zgodnie ze wzorem:
N
T f
U
U
i
w
x
w
=
(4)
w którym f
w
jest częstotliwością generatora impulsów, iloczyn T
i
f
w
jest pojemnością licznika
N
max
, tzn. maksymalną liczbą impulsów całkowicie go wypełniającą.. Wzór (4) jest słuszny,
jeżeli napięcie U
x
jest stałe w czasie i nie występują zakłócenia. W ogólnym przypadku wynik
pomiaru jest określony wzorem:
N
f
U
u t dt
w
w
x
T
i
=
∫
( )
0
(5)
tzn. wynik pomiaru jest proporcjonalny do wartości napięcia U
x
uśrednionej w okresie
całkowania T
i
. Ze wzoru (5) widać, że o dokładności pomiaru decyduje stałość w czasie
napięcia wzorcowego. W praktyce największe źródła błędów tkwią w stanach przejściowych
przy przełączaniu układu całkującego z napięcia mierzonego na napięcie wzorcowe. Kłopoty
z eliminacją wpływu owych stanów przejściowych spowodowały opracowanie dużej liczby
modyfikacji tej metody przetwarzania A/C.
Podobnie jak w przypadku przetworników C/A, charakterystykę przetwornika A/C
wygodnie jest przedstawić za pomocą charakterystyki idealnej (rys.6a). Analizę błędów tej
charakterystyki nieco komplikuje jej „schodkowy” przebieg. Niemniej jednak zasadnicze
objawy błędów mają taki sam charakter jak w przetwornikach C/A. Błąd przesunięcia zera (tj.
składowa addytywna błędu całkowitego) ilustruje charakterystyka pokazana na rys.6b, zaś
wpływ zmiany wzmocnienia (tj. składową multiplikatywną błędu całkowitego) pokazuje
rys.6c.
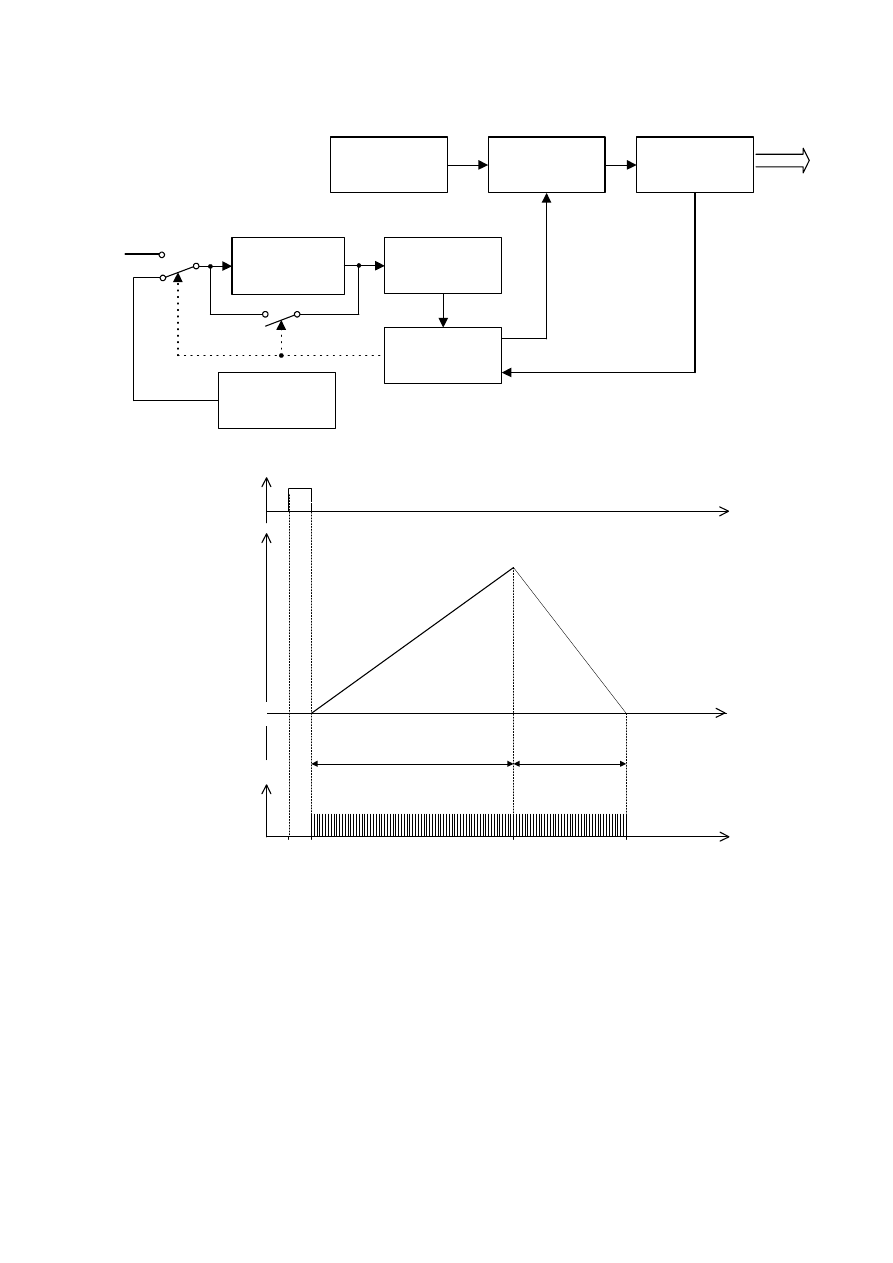
90
Układ
całkuj
ą
cy
Układ
steruj
ą
cy
U
x
G enerator
im pulsów
Detektor
zera
Ź
ródło
napi
ę
cia
w zorcow ego
N
x
Bram ka
Licznik
U
w
t
impuls startu
t
t
na
ch
yl
en
ie
p
ro
po
rc
jo
na
ln
e
do
U
x
na
ch
yl
en
ie
p
ro
po
rc
jo
na
ln
e
do
U
w
T
i
T
n
napięcie na
wyjściu
układu
całkującego
0
impulsy zliczane przez licznik
a)
b)
Rys. 5. Schemat blokowy przetwornika A/C pracującego wg metody podwójnego całkowania (a) oraz
przebiegi czasowe objaśniające tę metodę (b)
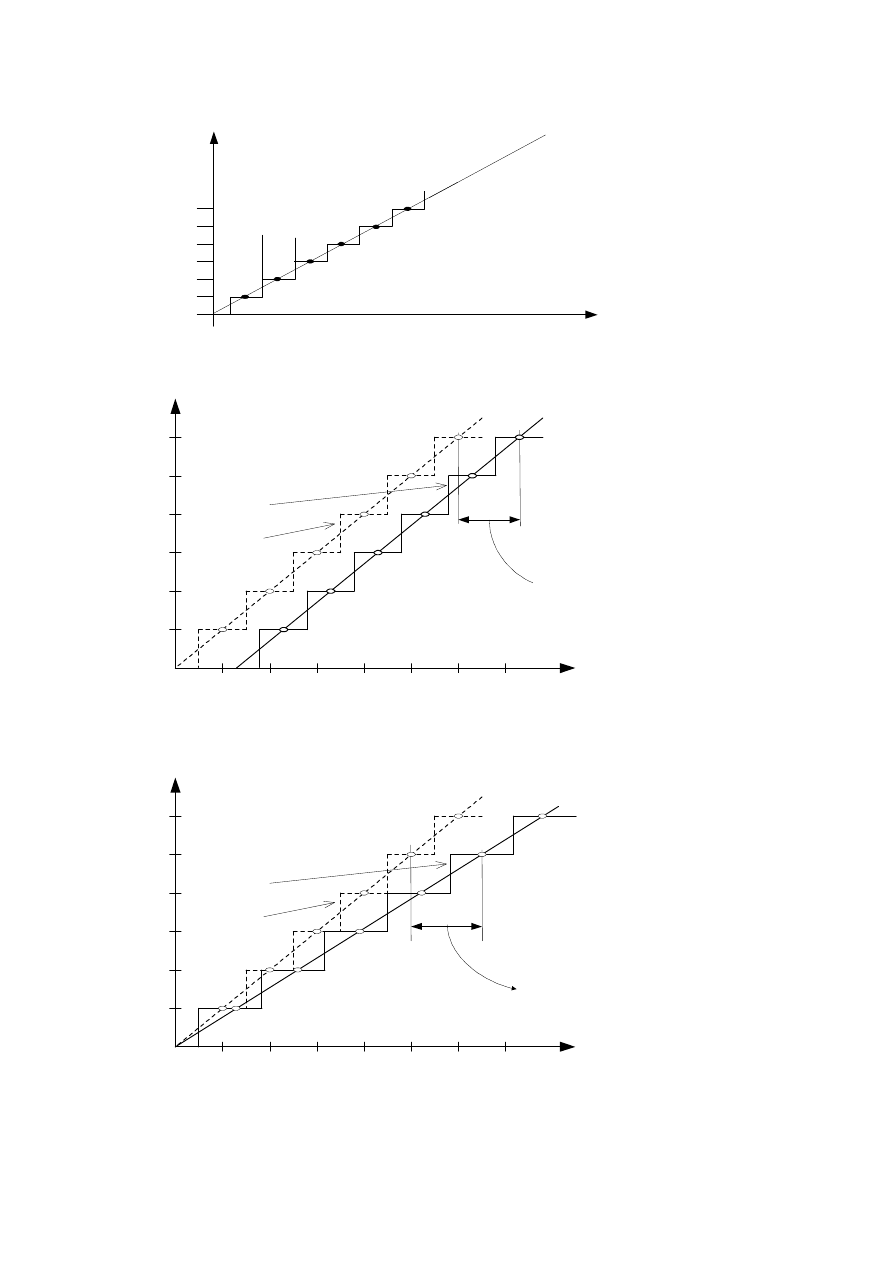
91
Rys. 6. Przykład charakterystyki idealnej przetwornika A/C 3-bitowego (a); wpływ składowej addytywnej
błędu (b); wpływ składowej multiplikatywnej błędu (c)
U
N
q
000
001
010
011
100
101
110
1/8
1/4
3/8
1/2
5/8
Bł
ą
d p rzes uni
ę
c ia
C ha ra ktery s ty ka
id ea lna
Ch arak te rys tyk a
rzec zywista
3/4
7/8
000
001
010
011
100
101
110
1/8
1/4
3/8
1/2
5/8
Bł
ą
d wzmoc nienia
C ha ra ktery s ty ka
id ea lna
Ch arak te rys tyk a
rzec zywista
3/4
7/8
000
001
010
011
100
101
110
N
N
U (FS)
U (FS)
a)
b)
c)

92
3. Woltomierze cyfrowe
Woltomierze cyfrowe zajmują w technice pomiarowej bardzo ważną, wręcz
„strategiczną”, pozycję. W wyniku ewolucyjnego procesu wyparły niemal całkowicie inne
przyrządy służące do pomiaru napięcia jak np. kompensatory i woltomierze
elektromechaniczne. Wchodzą w skład podstawowego wyposażenia niemal każdego
laboratorium pomiarowego, niezależnie od charakteru przeprowadzanych tam pomiarów.
Można z niewielką tylko przesadą powiedzieć, że - dysponując woltomierzem cyfrowym
napięć stałych i zmiennych - można zmierzyć dowolnie wybraną wielkość fizyczną. Można
dlatego, że czujniki i przetworniki pomiarowe rozmaitych wielkości fizycznych o
wyjściowym elektrycznym sygnale napięciowym należą do najpopularniejszych i najlepiej
zbadanych. W technice znajomość wartości napięcia, tak stałego jak i zmiennego, jest
niezbędna w prawie wszystkich pracach badawczych i konstrukcyjnych oraz w wielu
stanowiskach produkcji przemysłowej. Ponadto pomiary pośrednie rozmaitych wielkości
poprzez pomiary napięcia pozwalają dziś dość często na zastąpienie specjalizowanej i
kosztownej
aparatury
pomiarowej
woltomierzem
cyfrowym
współpracującym
z
mikrokomputerem za pośrednictwem standardowego interfejsu.
Struktura woltomierza
Każdy woltomierz cyfrowy można przedstawić za pomocą schematu blokowego jak
na rys.7. Na ogólną strukturę woltomierza składają się: obwód wejściowy, przetwornik A/C,
źródło napięcia wzorcowego, układ sterujący i urządzenie odczytowe. Obwód wejściowy
zawiera dzielnik napięcia i układ wzmacniacza o bardzo dużej rezystancji wejściowej.
Poziom sygnału wyjściowego tego wzmacniacza jest dopasowany do wejścia przetwornika
A/C. Wybór zakresu odbywa się poprzez zmianę nastawienia dzielnika napięcia. Układ
sterowania pozwala na dobór właściwego podzakresu automatycznie lub ręcznie. Przetwornik
A/C jest centralnym elementem struktury każdego woltomierza. Decyduje o liczbie cyfr
wyniku, błędzie pomiaru, odporności na zakłócenia i czasie pomiaru. Wokół wyboru
właściwego rozwiązania przetwornika A/C koncentrują się podstawowe prace projektowe
producentów woltomierzy. Urządzenie odczytowe jest coraz częściej wykonywane jako
specjalizowany monitor alfanumeryczny. Układ sterujący jest automatem cyfrowym
zapewniającym odpowiednią realizację algorytmów pomiaru i obsługi przyrządu. Steruje
również funkcjami autotestowania i autokalibracji.
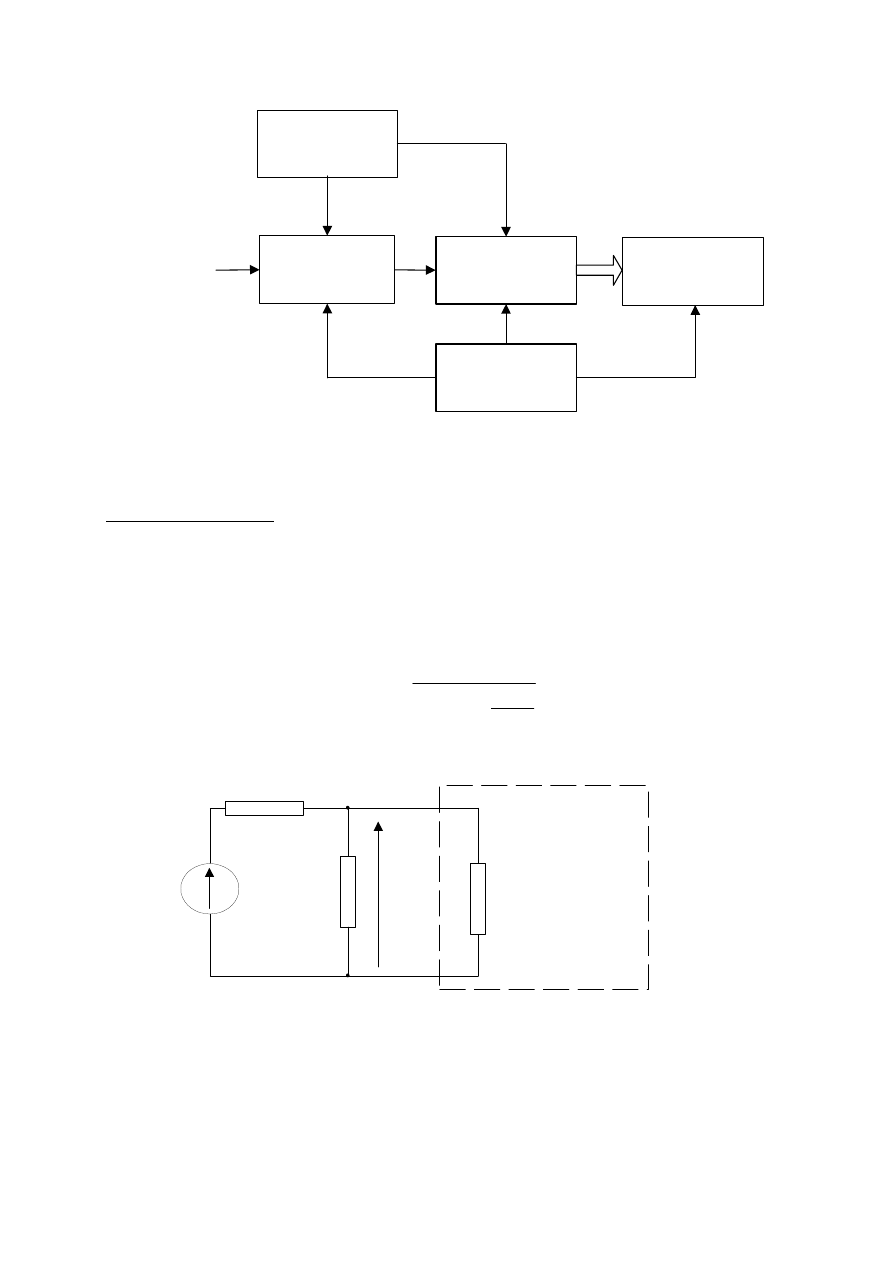
93
Rys. 7. Ogólna struktura woltomierza cyfrowego
Pomiary napięć stałych
Jednym z istotnych zagadnień przy pomiarze napięcia jest zagadnienie wpływu
skończonej wartości rezystancji R
v
wejścia woltomierza na wynik pomiaru napięcia.
Zagadnienie to można zilustrować obwodem pokazanym na rys.8. Napięcie wskazane przez
woltomierz wyraża się wzorem:
U
E
R
R
R
R R
R
v
o
s
o
s
o
v
=
+
+
(6)
U
v
E
R
s
R
o
R
v
Woltomierz
Rys. 8. Obwód ilustrujący wpływ rezystancji R
v
na wynik pomiaru napięcia
Wpływ rezystancji R
v
na wynik pomiaru będzie pomijalnie mały tylko przy spełnieniu
warunku R
v
>>
R
s
R
o
. Wtedy:
Obwód
wej
ś
ciowy
PRZETWORNIK
A/C
U
x
Układ
steruj
ą
cy
Urz
ą
dzenie
odczytowe
Ź
ródło napi
ę
cia
wzorcowego

94
U
E
R
R
R
v
o
s
o
≅
+
(7)
Typowe wartości rezystancji wejściowej dla dwóch wybranych woltomierzy cyfrowych (z
rozbudowanymi funkcjami multimetrycznymi) podano w tablicy 7.
Pomiary napięć zmiennych
Pomiar napięcia zmiennego odbywa się najczęściej drogą wstępnego przetworzenia
napięcia zmiennego (AC) na napięcie stałe (DC) i pomiaru tego ostatniego. Elementem
decydującym o dokładności pomiaru może okazać się przetwornik AC/DC. Napięcie zmienne
jest charakteryzowane najczęściej za pomocą wartości skutecznej. Jednakże dokładne
przetworzenie wartości skutecznej natrafia na zasadnicze trudności natury technicznej.
Znacznie prostsza jest realizacja przetwarzania wartości średniej - dlatego najtańsze
woltomierze wyposażane są w przetworniki wartości średniej. Wzgląd na potrzeby i żądania
użytkowników powoduje, że ich wskazania skalowane są w w wartości skutecznej. Dla
przebiegu sinusoidalnego zależność między wartością skuteczną a średnią jest ściśle
określona wzorem:
ś
r
sk
U
U
2
2
π
=
(8)
Dlatego też w instrukcjach użytkowania takich woltomierzy producenci zaznaczają, że
wskazania odpowiadają podanej dokładności pomiaru tylko dla przebiegów sinusoidalnych.
Przy pomiarach napięć odkształconych wskazania będą obarczone błędem, gdyż iloraz U
sk
/U
ś
r
będzie inny niż dla sinusoidy (patrz tablica 3).
W najdokładniejszych przetwornikach wartości skutecznej wykorzystywane są
zjawiska cieplne prądu elektrycznego, przy czym należy nadmienić, że otrzymanie dużej
dokładności przetwarzania wiąże się ze znaczną komplikacją układu przetwornika.
Woltomierze z takimi przetwornikami produkowane są w niewielkich ilościach i są bardzo
kosztowne. Ogniwem pośrednim pomiędzy dokładnymi przetwornikami "cieplnymi" a
przetwornikami wartości średniej skalowanymi w wartości skutecznej są monolityczne układy
wzmacniaczy operacyjnych realizujące definicyjne wyznaczanie wartości skutecznej drogą
operacji matematycznych na przetwarzanym sygnale analogowym. Stałonapięciowy sygnał
wyjściowy takich przetworników jest proporcjonalny do wartości skutecznej sygnału
wejściowego w dość dużym przedziale odkształceń od sinusoidy, charakteryzowanym zwykle
za pomocą współczynnika szczytu (ang. crest factor), t.j. odniesienia wartości szczytowej do
wartości skutecznej.
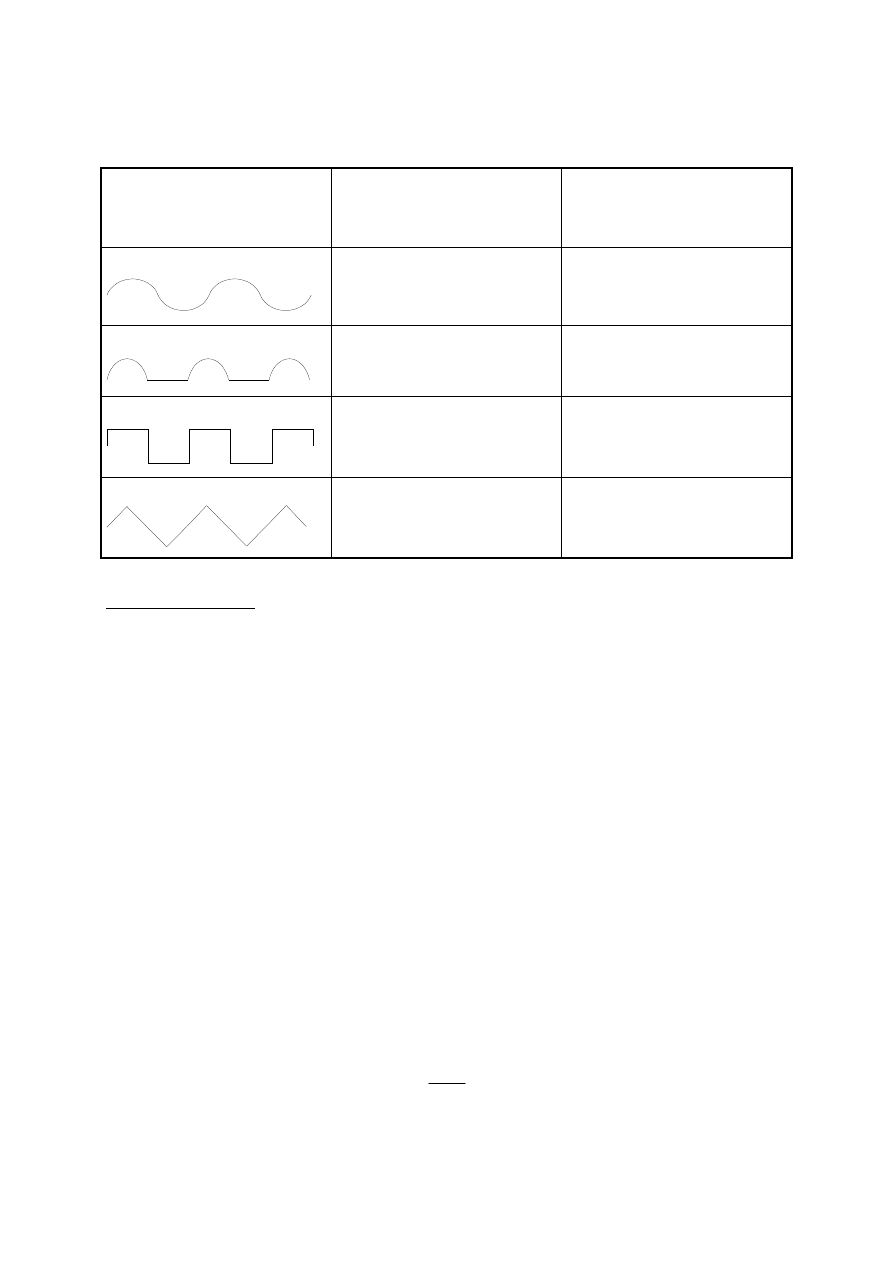
95
Tablica 3. Porównanie wskazań woltomierza reagującego na wartość średnią (ale wyskalowanego w
wartości skutecznej dla sygnału sinusoidalnego) i woltomierza reagującego na wartość
skuteczną dla kilku typowych kształtów sygnałów.
Kształt
(amplituda 1V)
Wskazanie woltomierza
wartości średniej
(wyskal. w wart. skutecznej)
Wskazanie woltomierza
wartości skutecznej
Sinusoida
0,707 V
0,707 V
pół-sinusoida
0,353 V
0,500 V
Prostokąt
1,110 V
1,000 V
Trójkąt
0,545 V
0,577 V
Parametry użytkowe
Do podstawowych parametrów użytkowych woltomierzy cyfrowych zaliczamy:
- zakres pomiaru (podzakresy),
- błąd pomiaru,
- rezystancję wejściową,
- współczynnik tłumienia sygnału nałożonego dla zakłóceń szeregowych i równoległych,
- czas trwania pomiaru (szybkość pomiaru),
- przeciążalność wejścia.
Typowe wartości parametrów użytkowych dwóch wybranych woltomierzy cyfrowych
(z rozbudowanymi funkcjami multimetrycznymi) zestawiono w tablicy 7.
Spośród wymienionych parametrów nieco uważniej należy potraktować błąd pomiaru. Błąd
pomiaru napięcia za pomocą woltomierza cyfrowego ocenia się na podstawie danych
producenta zawierających najczęściej dwie składowe:
- błąd pomiaru
δ
m
podany w procentach od wartości mierzonej (wskazanej) U
w
- błąd pomiaru podany w procentach od końca zakresu (pełnego wskazania) U
max
:
δ
FS
a
U
U
=
∆
max
%
100
(9)

96
Podział błędów na dwie grupy wynika z charakteru zależności rozmaitych czynników
powodujących błędy od wartości mierzonego napięcia. Graniczny błąd bezwzględny pomiaru
wyniesie:
100
/
)
(
max
max
FS
m
w
U
U
U
δ
δ
+
±
=
∆
(10)
natomiast graniczny błąd względny będzie opisany wzorem:
δ
δ
δ
max
max
max
%
%
=
= ±
+
∆
U
U
U
U
w
m
w
FS
100
(11)
We wzorach tych U
max
dla woltomierzy wielozakresowych jest górną granicą podzakresu
pomiarowego. Na rys.9 pokazano przykład charakterystyki błędu
δ
max
woltomierza
wielozakresowego.
Dość często przy opisie błędów woltomierza producent zamiast podania wartości błędu
wyrażonej w procentach od końca zakresu, wymienia wartość bezwzględną wyrażoną w
postaci n cyfr, przy czym n jest liczbą cyfr ostatniego pola odczytowego, np.:
δ
max
=
±
(0,02% + 2 cyfry)
(12)
co np. przy maksymalnym wskazaniu 19999 odpowiada zapisowi:
δ
max
max
,
,
%
= ±
+
0 02
0 01
U
U
w
(13)
Niekiedy producent podaje tylko błąd wyrażony w procentach od wartości mierzonej. Należy
w takim przypadku dodatkowo uwzględniać tzw. błąd kwantowania. Ponieważ mierzone
napięcie jest przedstawiane za pomocą skończonej liczby poziomów kwantowania, to jego
wartość rzeczywista jest zastępowana wartością najbliższą. W ogólnym przypadku błąd
kwantowania jest praktycznie równy najmniejszemu poziomowi kwantowania i powinien być
traktowany jako błąd w procentach od końca zakresu
δ
FS
. Na przykład dla woltomierza o
zakresie 100 V i maksymalnym wskazaniu 9999 bezwzględna wartość błędu kwantowania
równa się 0,01V. Natomiast względny błąd kwantowania przy pomiarze napięcia o wartości
np. 10 V wyniesie:
%
,
%
,
1
0
100
10
01
0
=
=
FS
δ
(14)
Prócz błędu granicznego należy liczyć się z błędami dodatkowymi, wśród których
najważniejszym jest błąd temperaturowy. Przy prowadzeniu pomiarów w warunkach
odbiegających od warunków znamionowych (bądź powszechnie przyjmowanych za
znamionowe) należy uważnie przestudiować dane producenta.
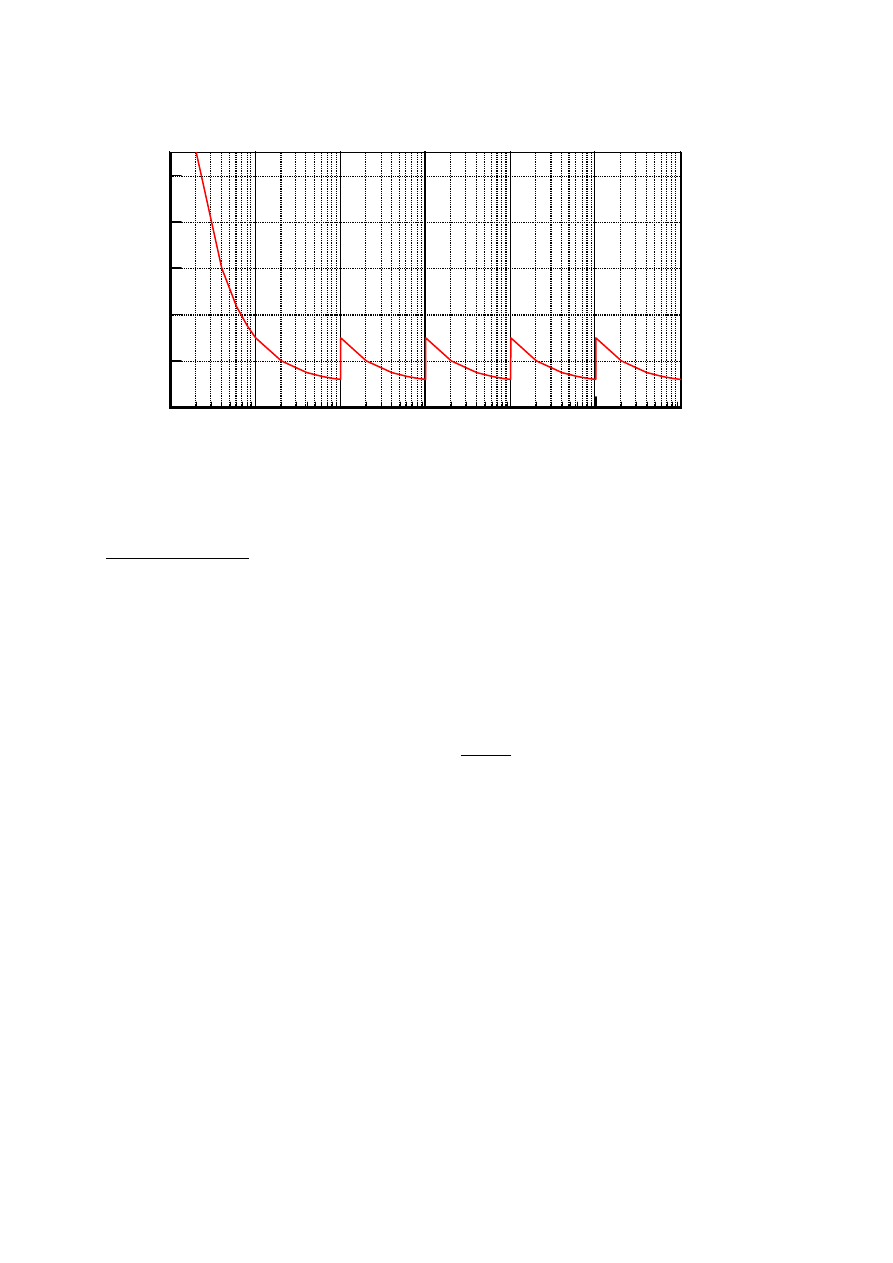
97
Rys. 9. Przykład charakterystyki błędu
δδδδ
max
woltomierza o podzakresach 0,1-1-10-100-1000V, odczycie
czterocyfrowym (9999), błędzie od wartości wskazanej
δδδδ
m
= 0,05%, błędzie od końca zakresu
δδδδ
FS
= 0,01%
Tłumienie zakłóceń
Zdolność do tłumienia zakłóceń nakładających się na przetwarzane napięcie
charakteryzowana jest zazwyczaj współczynnikiem tłumienia sygnału nałożonego WTSN.
Współczynnik ten określany jest stosunkiem amplitudy napięcia zakłócającego o przebiegu
sinusoidalnym U
z(max)
do maksymalnej wartości zmiany wskazania woltomierza
∆
max
U
spowodowanej zakłóceniem.
[ ]
WTSN = 20 log
U
U
dB
z(max)
max
∆
(15)
Pożądane jest aby wartość tego współczynnika była możliwie duża, zwłaszcza dla sygnałów o
częstotliwości 50 Hz.
O wpływie sygnałów zakłócających na wskazania decyduje usytuowanie źródeł
zakłóceń w stosunku do obwodu wejściowego woltomierza. Na rys.10a przedstawiono
schemat rozmieszczenia dwóch najczęściej występujących źródeł zakłóceń. Źródło E
NM
reprezentuje napięcie szumów i tętnień nakładających się na napięcie mierzone U
x
w
obwodzie wejściowym woltomierza. Źródło to zwane jest często źródłem zakłóceń
szeregowych.
Źródło E
CM
reprezentuje różnicę potencjałów między punktami uziemienia źródła U
x
i
woltomierza, wynikającą z charakterystycznych dla sieci energetycznej rozpływów prądów w
przewodach uziemiających. Na rys.10a pokazano drogę, którą źródło E
CM
oddziałuje na
wskazania woltomierza. Źródło Z
S
dołączone jest do woltomierza za pomocą dwóch
0,001
0,01
0,1
1
10
100
1000
0
0,1
0,2
0,3
0,4
0,5
δ
max
%
V
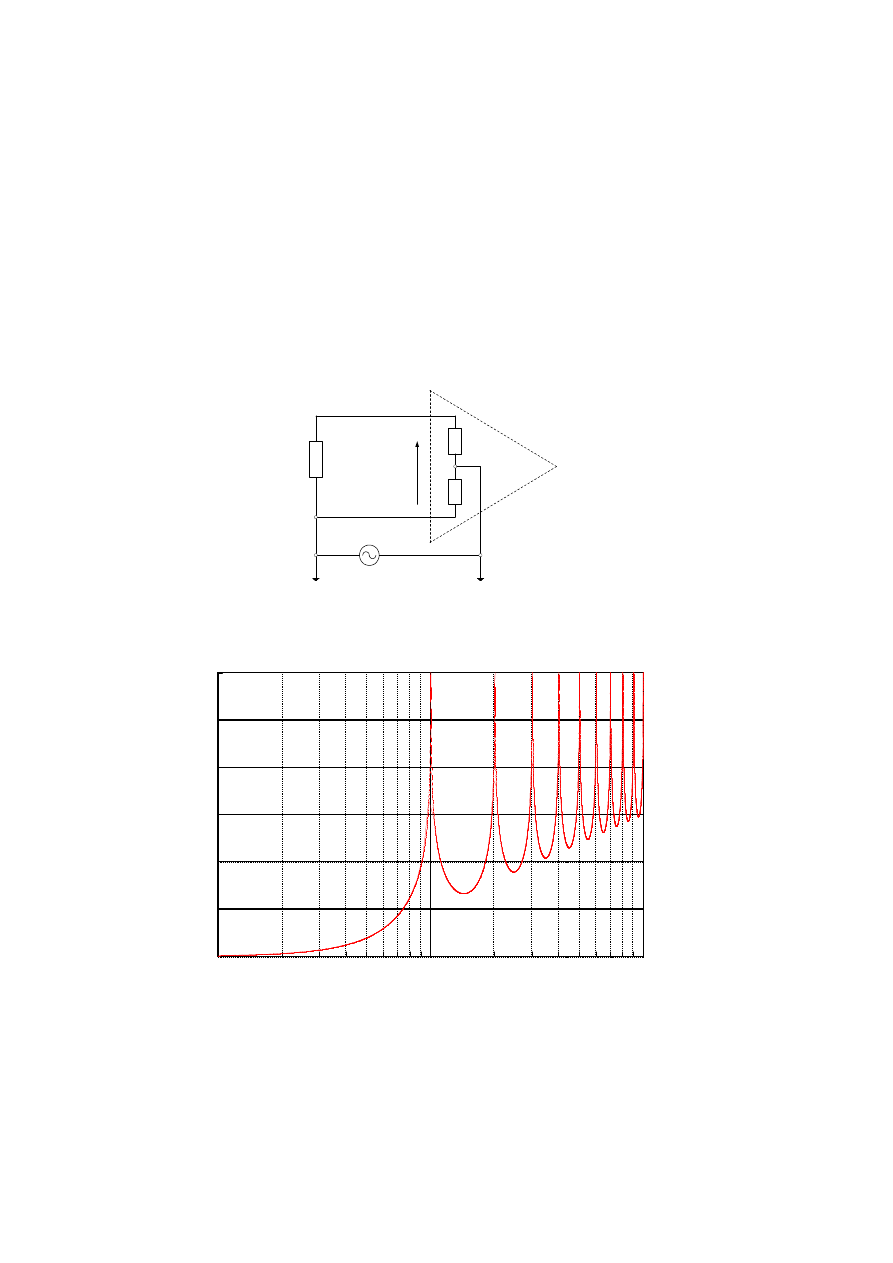
98
przewodów: tak zwanego przewodu „gorącego” i przewodu „zimnego”. Prawie cały prąd ze
źródła E
CM
płynie przewodem „zimnym” powodując spadek napięcia na jego rezystancji i
tym samym powstanie zakłócenia o charakterze szeregowym. Spadek napięcia na tej
rezystancji można ograniczać jedynie drogą zwiększania impedancji izolacji. Dlatego
tłumienie zakłóceń równoległych w woltomierzach cyfrowych o zakresach rzędu 100 mV
(zwłaszcza pracujących z zasilaczem sieciowym) realizuje się drogą wprowadzenia
specjalnego ekranu ochronnego do wnętrza obudowy woltomierza i trójprzewodowego
podłączenia źródła Z
S
.
Rys. 10. Usytuowanie źródeł zakłóceń przy pomiarach napięcia (a) i wykres tłumienia zakłóceń w funkcji
stosunku okresów T
i
/T
s
(b)
Z
s
Z
1
Z
2
ziemia źródła
ziemia przyrządu
E
CM
E
NM
a)
0,1
1
10
0
5
10
15
20
25
30
WTSN dB
T
i
/T
s
b)

99
Tłumienie zakłóceń szeregowych zależy od właściwości zastosowanej metody przetwarzania
napięcia a także od właściwości obwodów filtrujących w układzie wejściowym woltomierza.
Woltomierze całkujące, wskazujące wartość średnią napięcia w zadanym przedziale czasu,
uśredniają także zakłócenia nakładające się na napięcie mierzone. Np. niech napięcie na
wejściu woltomierza całkującego będzie:
u
we
(t) = U
x
+ U
s
sin
ω
s
t
(16)
przy czym U
s
sin
ω
s
t jest przebiegiem zakłócającym.
Wynik pomiaru jest tworzony zgodnie ze wzorem:
u
t dt
U dt
U
t dt
U
U
t
we
x
s
s
xœr
s
s
s
T
T
T
T
i
i
i
i
( )
sin
cos
=
+
=
+
∫
∫
∫
ω
ω
ω
0
0
0
0
(17)
Jeżeli okres całkowania T
i
jest równy okresowi sygnału zakłócającego T
s
, to drugi składnik w
wyniku całkowania sprowadza się do zera. Wobec tego dla przypadku, gdy okres T
i
jest
równy okresowi T
s
(bądź jest jego całkowitą wielokrotnością) tłumienie sygnałów
zakłócających jest nieskończenie duże. Na rys.10 pokazany jest wykres tłumienia w funkcji
ilorazu okresów T
i
/T
s
. Z wykresu widać, że
- wraz z odejściem T
i
od całkowitej wielokrotności T
s
tłumienie znacznie zmniejsza się,
- tłumienie jest tym większe im większe są okresy całkowania T
i
przy T
s
= const.

100
4. Multimetry cyfrowe
Multimetrami nazywamy przyrządy pomiarowe służące do pomiaru kilku wielkości.
Zestaw wielkości pozwala zwykle na zastosowanie multimetru w wydzielonym obszarze prac
inżynierskich lub naukowych. Od czasu gdy w 1975 roku pojawiły się na rynku pierwsze
modele multimetrów mikroprocesorowych obserwuje się intensywny rozwój tej grupy
przyrządów. Dzisiejsza oferta producentów - to pełna gama modeli prześcigających się
pomysłowością rozwiązań, obszarem pomiarowym, szybkością i dokładnością pomiarów, etc.
Wiele rozwiązań multimetrów pretenduje do miana najwyższych osiągnięć w dziedzinie
aparatury pomiarowej.
Podstawowe podziały klasyfikacyjne multimetrów wiążą się z ich strukturą
wewnętrzną oraz z cechami ergonomicznymi. I tak można wyróżnić multimetry z
przetwornikami
analogowo-cyfrowymi
integracyjnymi
(dość
rozbudowane
układy
kondycjonowania sygnałów po stronie analogowej, proste przetwarzanie po stronie cyfrowej)
oraz multimetry z przetwornikami analogowo-cyfrowymi próbkującymi (proste układy
kondycjonowania, dość skomplikowane przetwarzanie po stronie cyfrowej). Drugi bardzo
widoczny podział, to podział na multimetry podręczne (z reguły o wewnętrznym zasilaniu
bateryjnym) i multimetry laboratoryjne (z reguły wyposażone w bogate możliwości
współpracy systemowej).
Równolegle postępuje proces wyodrębniania się z grupy multimetrów ogólnego
zastosowania multimetrów przeznaczonych do zadań ściślej określonych. I tak np. dla
elektrotechniki motoryzacyjnej mamy multimetry samochodowe (ang. vehicle multimeters),
do badania układów cyfrowych - multimetry sygnaturowe (ang. signature multimeters), do
badania telefonicznych linii abonenckich - multimetry telekomunikacyjne (ang. subscriber’s
line multimeters), do obserwacji kształtu przebiegów czasowych sygnałów - multimetry
graficzne (ang. graphical multimeters).
Zastosowanie mikroprocesorów w wewnętrznej strukturze multimetru pozwoliło na
realizację wielu funkcji tzw. sztucznej inteligencji. Wiąże to się z takimi właściwościami jak
np. automatyczne wykonywanie złożonych procedur pomiarowych wymagających
podejmowania decyzji na podstawie kolejno otrzymywanych wyników pomiarów pośrednich
i posługiwania się pamięcią. Miarą tej "inteligencji" jest przede wszystkim łatwość obsługi i
programowania pracy przyrządu oraz obszar realizowanych procedur. Realizacja
adaptacyjnych
algorytmów
pomiaru,
poważne
ograniczenie
wpływu
czynników
pasożytniczych na wyniki pomiarów, zwiększenie niezawodności, możność pracy systemowej
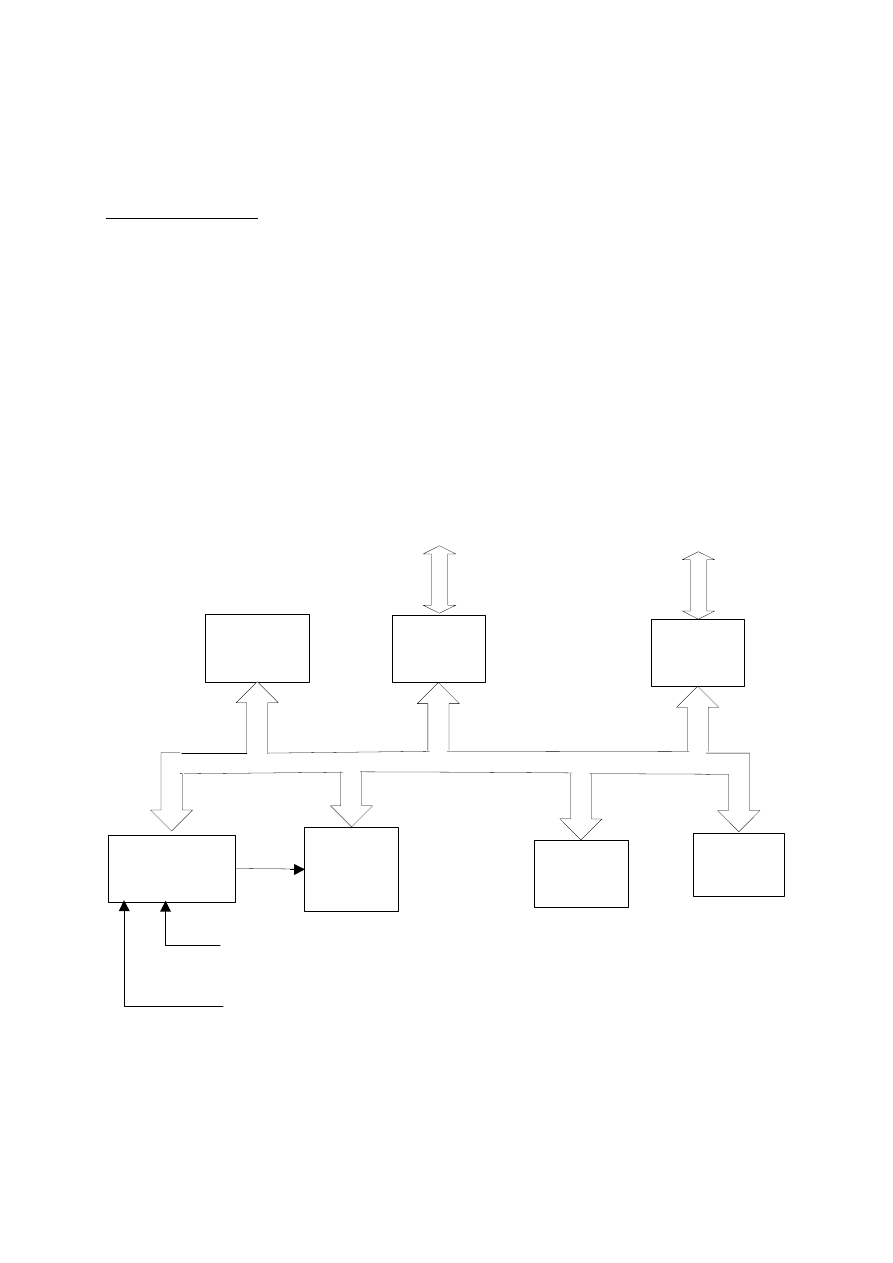
101
w różnych standardach interfejsów - wszystko to sprawia, że multimetry stanowią dziś
najlepszy przykład współczesnych osiągnięć techniki pomiarowej.
Struktura multimetru
Na rys.11 pokazana jest ogólna struktura typowego multimetru. Połączenia rysowane
podwójną linią reprezentują zbiór przewodów równoległych, służących cyfrowej organizacji
pracy multimetru. Są to tzw. szyny adresowe, szyny rozkazów i szyny danych. Sygnały
wejściowe poddawane są kondycjonowaniu, tj. takiemu przetwarzaniu wstępnemu, by
przetwornik A/C otrzymał na wejściu odpowiedni rodzaj i poziom sygnału (np. napięcie stałe
0
÷
10V). W zakres kondycjonowania wchodzi więc np. automatyczne wybieranie zakresu
multimetru zależnie od poziomu sygnału wejściowego, wstępne przetwarzanie analogowe
(np. rezystancja
→
napięcie stałe, wartość skuteczna napięcia zmiennego
→
napięcie stałe).
Mikroprocesor
Kondycjonowanie
sygnału
Przetwornik
analogowo-
cyfrowy
Pami
ęć
danych
(RAM)
INTERFEJS
IEC-625
Klawiatura
i
urz
ą
dzenie
odczytowe
Przetwarzanie
wyników
(RAM+ROM)
Wej
ś
cie
OPERATOR
STEROWNIK
(KONTROLER)
Rys.11. Ogólna struktura multimetru ze sterowaniem mikroprocesorowym
Spośród metod przetwarzania analogowo-cyfrowego najczęściej stosowane są trzy:
podwójnego lub wielokrotnego całkowania (dual slope, multiple slope), modulacji szerokości
impulsu (pulse width, delta-pulse modulation) i kolejnych przybliżeń (successive
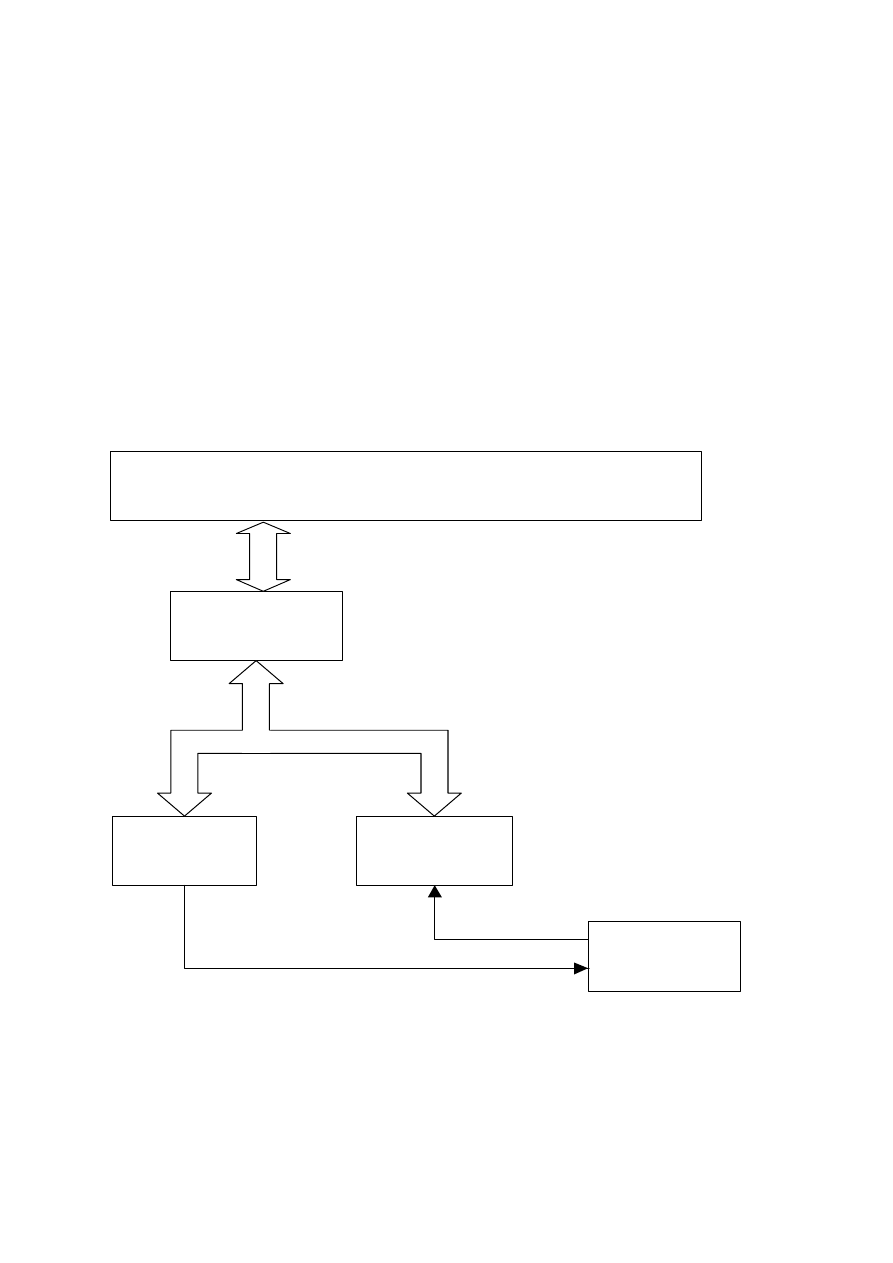
102
approximation). Wybór metody zależy na ogół od przyjętej rozdzielczości wyniku, zadanego
czasu przetwarzania oraz stopnia skojarzenia struktury przetwornika analogowo-cyfrowego ze
strukturą układu mikroprocesorowego.
Kontakt operatora z multimetrem odbywa się za pośrednictwem klawiatury i
urządzenia odczytowego (najczęściej niewielki monitor alfanumeryczny). W multimetrach
mikroprocesorowych dokonała się tu zasadnicza zmiana w odniesieniu do rozwiązań
„klasycznych”, związana z programową obsługą wyboru funkcji pomiaru. Ani jeden z
klawiszy nie jest bezpośrednio sprzężony z torem mierzonego sygnału. Płyta czołowa
multimetru, zwykle dotąd dość gęsto upakowana przełącznikami i pokrętłami, znacznie się
oczyściła, stając się jednocześnie układem peryferyjnym mikroprocesora.
KOMPUTER TYPU IBM PC
STEROWNIK
INTERFEJSU
IEC- 625
GENERATOR
MULTIMETR
BADANY
OBIEKT
SZYNA INTERFEJSU
Rys.12. Przykład zastosowania multimetru w komputerowym systemie pomiarowym
Blok przetwarzania wyników (pamięci ROM i RAM) pozwala na realizację typowych
operacji na wynikach pomiarów. Można wymienić tu obliczanie parametrów statystycznych
(wartość średnia, wariancja, odchylenie standardowe), obliczanie wartości wyników

103
pomiarów pośrednich, obliczanie wartości wyniku związane z wewnętrznymi procedurami
auto-zerowania i auto-kalibracji.
Blok pamięci danych (RAM) służy do bieżącego gromadzenia kolejnych wyników
pomiarów w celu dalszego ich opracowywania bądź rejestracji. Poważną zaletą tej pamięci
jest możliwość przeglądania kolejnych odczytów pomiarów przy nastawianej szybkości ich
repetycji (np. od 200 odczytów na sekundę do 1 odczytu na godzinę).
Interfejs transmisji danych w standardzie IEC-625 lub V-24 (RS-232) służy
współpracy multimetru z komputerem. Przykład struktury systemu pomiarowego
realizującego taką współpracę pokazany jest na rys.12.
Funkcje multimetrów
Zestawione w tablicy 4 funkcje pomiarowe charakteryzują grupę multimetrów tzw.
ogólnego zastosowania. Prócz wymienionych wielkości incydentalnie mogą pojawiać się i
takie, które poszerzając ofertę standardową stanowią „magnes” dla wahających się
nabywców.
Funkcje pomiarowe i funkcje dodatkowe (patrz tablica 5) uzupełnia typowy zestaw
parametrów charakterystycznych (tablica 6). Zestaw ten może stanowić podstawę do
porównań multimetrów między sobą oraz podstawę do oceny jakości przyrządu. W
przeszłości, w praktyce projektowania aparatury pomiarowej, posługiwano się tzw.
współczynnikami dobroci, pozwalającymi na ujawnienie ukrytych współzależności między
parametrami charakterystycznymi oraz na ujawnienie konstrukcji lepszej. Dziś nie tylko nie
dysponujemy współczynnikami dobroci, ale pojawiły się tak trudne elementy oceny jak np.
łatwość programowania i obsługi oraz zdolność przyrządu do pracy adaptacyjnej, tj. zdolność
do auto-optymalizacji swych parametrów przy zmianach warunków pomiaru.
W związku z dość dużą liczbą funkcji realizowanych w jednym przyrządzie oraz
złożonością jego struktury wzrasta waga kryterium niezawodności pracy. Prócz
zachowywania najdalej posuniętej staranności w selekcji elementów i podzespołów w
procesie montażu u producenta - jeszcze na etapie projektowania wbudowuje się w strukturę i
algorytmy pracy bloki i operacje auto-testowania, pozwalające na szybkie wykrywanie i
wymianę uszkodzonych części przyrządu.
Rośnie również waga kosztów rozumianych jednak dość szeroko, bo wynikających nie
tylko z ceny przyrządu w dniu zakupu, ale także z konieczności okresowego sprawdzania, czy
okresowej kalibracji. Wyraźny związek między parametrami charakterystycznymi a ceną

104
przyrządu może powodować w pewnych warunkach, że praktycznym współczynnikiem
jakości przyrządu będzie jego cena.
Tablica 4. Multimetry ogólnego zastosowania - funkcje pomiarowe
Wielkość mierzona
Uwagi
Napięcie stałe
pomiar wartości
Prąd stały
jw.
Napięcie zmienne
pomiar wartości średniej, skutecznej,
szczytowej, pomiar składowej stałej i
zmiennej, pomiar tylko składowej zmiennej
Prąd zmienny
jw.
Rezystancja
(konduktancja)
pomiar wartości przy prądzie stałym i przy
ustalonym poziomie sygnału pobudzającego
Częstotliwość
pomiar wartości w określonym przedziale
amplitudy sygnału badanego
Impedancja
(jej wybrane parametry np. L, C)
pomiar wartości przy ustalonej częstotliwości
i poziomie sygnału pobudzającego
Temperatura
pomiar wartości przy wykorzystaniu
czujników typu termopara lub rezystor
platynowy
Iloraz wielkości wejściowych
(np. iloraz dwóch napięć stałych)
pomiar wartości ilorazu w czasie
rzeczywistym

105
Tablica 5. Multimetry ogólnego zastosowania - funkcje dodatkowe
Funkcja
Uwagi
Współpraca systemowa
standardowe interfejsy np. IEC625/IEEE488,
V24/RS232, HPIL
Automatyczny wybór zakresu
jest zwykle stosowany równolegle z ręcznym
wyborem zakresu
Obliczenia:
- wprowadzanie z klawiatury nachylenia a i
przesunięcia b do charakterystyki skali,
- obliczanie odchylenia procentowego od
wartości wprowadzonej z klawiatury,
- obliczanie ilorazu,
- obliczanie różnicy,
- kompresja logarytmiczna,
- uśrednianie, filtracja,
- obliczenia statystyczne,
np. Y = aX + b
wynik w decybelach - dB
wartość średnia, wariancja, odchylenie
standardowe
Zapamiętywanie wyników
często przy nastawianej szybkości pomiarów
- np. od 1pom./godz. do 1000 pom./s, pamięć
typu “salwa” (burst memory)
Sygnalizowanie przekroczeń
HI/LO/PASS
Linearyzacja charakterystyk czujników i
przetworników współpracujących z
multimetrem
np. wielomianem 3 stopnia
Wyświetlanie wartości błędu
systematycznego
Wykrywanie połączeń galwanicznych
brzęczyk
Test diodowy
Wejście wielokanałowe
nazwa “multilogger”
Zegar, zadawanie odcinków czasu dla
wyzwalania pomiarów
106
Tablica 6. Multimetry ogólnego zastosowania - parametry charakterystyczne
Parametr
Uwagi
Zakres górny,
zakres dolny
obszar pomiarowy
Liczba cyfr wyniku
np. 5
1
/
2
Rozdzielczość
np. 1 LSD = 10
µ
V
Dokładność (błąd podstawowy)
składowa od wskazania + składowa od końca zakresu
Liniowość,
powtarzalność wskazań
na ogół parametry te są wliczane
do bł ę du podstawowego
Szybkość pomiaru (czas pomiaru)
np. 20 pom./s lub 50 ms
Poziom szumu wewnętrznego
np. 5
µ
V
Współczynniki tłumienia szumów
NMR, CMR, ECMR
Pasmo częstotliwości (błąd dodatkowy)
pomiary zmiennoprądowe
Współczynnik szczytu (błąd dodatkowy)
pomiary zmiennoprądowe
Rezystancja wejściowa
(pojemność wejściowa)
pomiary napięć
- przy pomiarach zmiennoprądowych
Spadek napięcia na zaciskach lub rezystancja
wejściowa
pomiary prądów
Prąd obciążenia obiektu pomiaru
pomiary rezystancji
Minimalna dopuszczalna wartość napięcia
wej.
pomiary częstotliwości
Przedział temperatur pracy
np. 0
÷
55
°
C
Moc pobierana ze źródła zasilania lub średni
czas pracy z podanym typem źródła
elektrochem.
Wymiary gabarytowe
także cechy ergonomiczne
Masa (ciężar)
także odporność na wstrząsy i udary

107
Tablica 7. Porównanie parametrów charakterystycznych dwóch multimetrów laboratoryjnych
Hewlett Packard 34401A
Keithley 2000
Liczba cyfr wyniku
4
1
/
2
...6
1
/
2
4
1
/
2
...6
1
/
2
Napięcie stałe
Błąd podstawowy
Rozdzielczość
Maks. szybkość pomiaru
Rezystancja wej.
100mV...1000V
35 ppm R + 5 ppm FS
100 nV
1000 pom./s
10M
Ω
lub do 10V>10G
Ω
100mV...1000V
30 ppm R + 5 ppm FS
100 nV
1850 pom./s
10M
Ω
, do 10V>10G
Ω
Napięcie zmienne TRMS
Błąd podstawowy
Pasmo
Współczynnik szczytu
Maks. szybkość pomiaru
Impedancja wej.
100mV...750V
0,06% R + 0,03% FS
3 Hz...300 kHz
maks. 5 : 1
50 pom./s
1M
Ω
/100pF
100mV...750V
0,06% R + 0,03% FS
3 Hz...300 kHz
maks. 5 : 1
30 pom./s
1M
Ω
/100pF
Inne funkcje
prąd stały i zmienny
rezystancja (2 i 4 przew.)
test diodowy
częstotliwość i okres
sprawdz. ciągłości obw.
podtrzymanie wyniku
przeliczanie wyniku
pamięć 512 odczytów
interfejs IEC-625 i V-24
prąd stały i zmienny
rezystancja (2 i 4 przew.)
test diodowy
częstotliwość i okres
temperatura
sprawdz. ciągłości obw.
podtrzymanie wyniku
przeliczanie wyniku
pamięć 1024 odczytów
interfejs IEC-625 i V-24
wejście 10-cio kanałowe
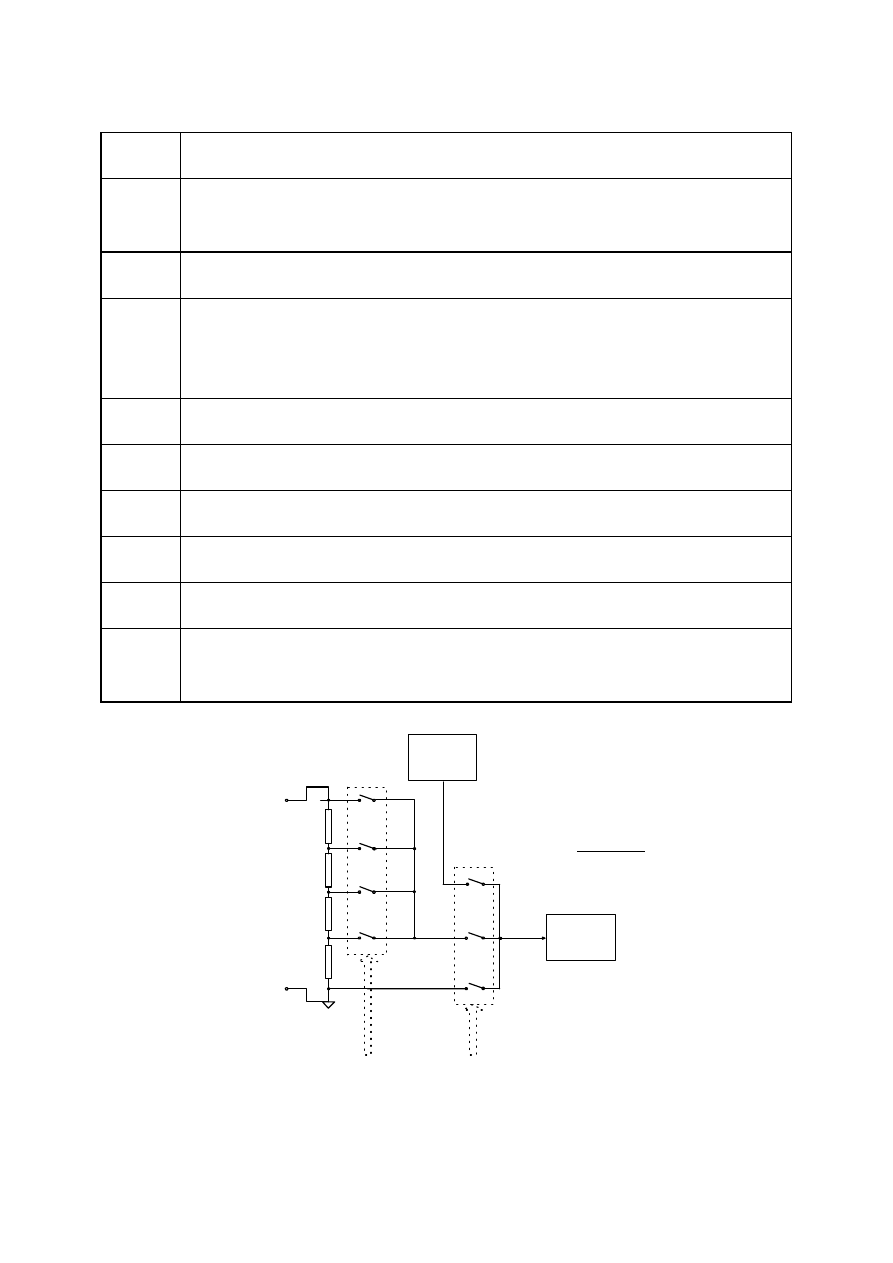
108
Tablica 8. Zestawienie środków konstrukcyjnych poprawiających jakość metrologiczną multimetrów
1.
Kalibracja cyfrowa - wprowadzanie do pamięci stałych kalibracji
2.
Auto-kalibracja, auto-zerowanie - cykliczne wprowadzanie poprawek do wskazań
określane wspólnie jako auto-korekcja
3.
Auto-testowanie (łącznie z sygnalizacją charakteru uszkodzeń)
4.
Zabezpieczenie wejść przed przeciążeniem oraz wskaźniki przeciążenia (w tym np.
wskaźnik przekroczenia dopuszczalnej wartości współczynnika szczytu przy
pomiarze wartości skutecznej)
5.
Uzupełnienie odczytu cyfrowego wskazaniem analogowym
6.
Zastosowanie wskaźników alfanumerycznych
7.
Rozdzielenie galwaniczne części analogowej i cyfrowej
8.
Ekran ochronny (guard)
9.
Wejście cztero-zaciskowe (pomiary małych rezystancji)
10.
Zastosowanie układów i podzespołów elektronicznych o minimalizowanym
poborze mocy (b. ważne przy zasilaniu bateryjnym)
Źródło
napięcia
wzorcowego
P rzetwornik
A/C
U
w
U
x
U
o
9M
900k
90k
10k
W e
o
w
o
x
'
x
w
U
U
U
U
2
U
:
V
2
U
−
−
=
=
Dla
Rys. 13. Schemat obwodu wejściowego multimetru ilustrujący metodę wprowadzania poprawki na
przesunięcie zera i zmianę wzmocnienia
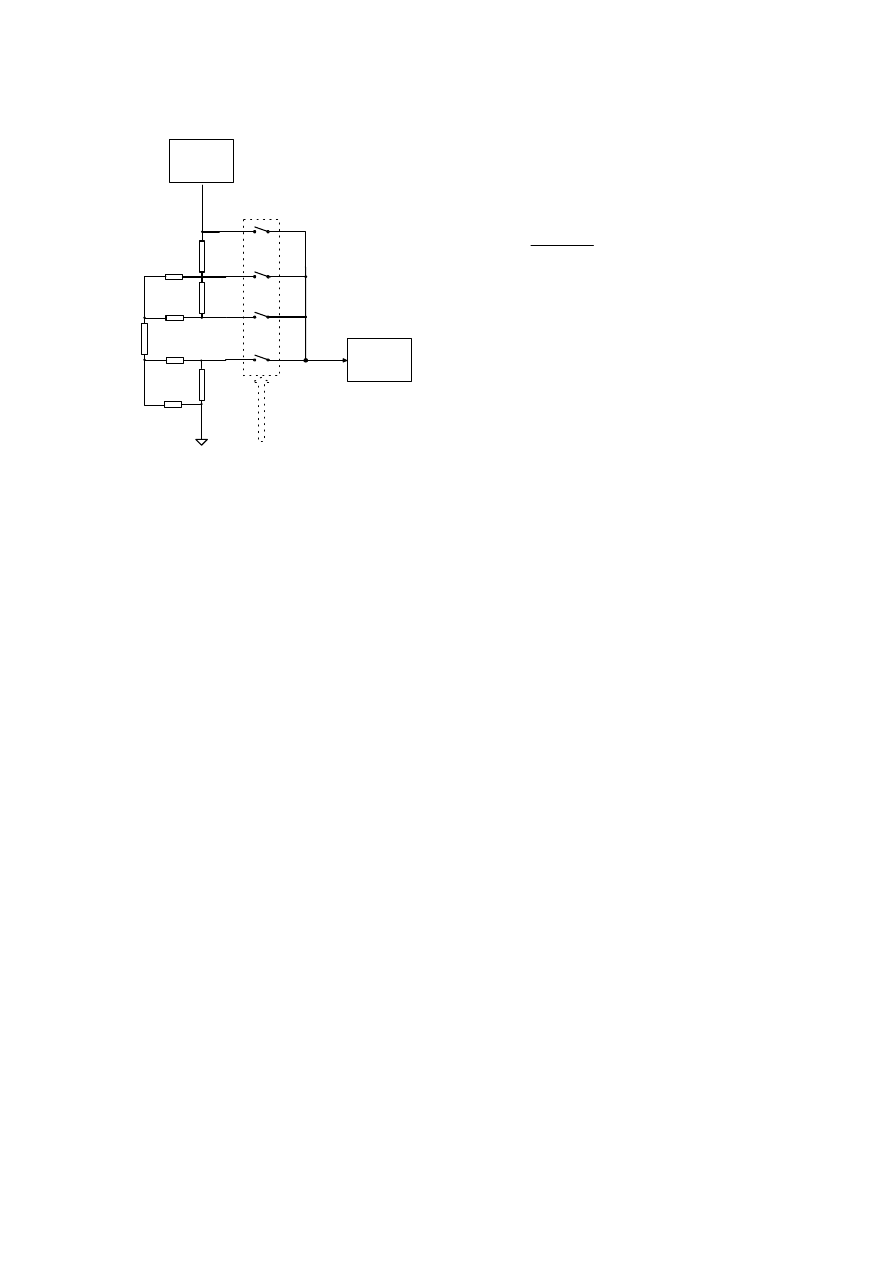
109
Rys.14. Cztero-zaciskowy pomiar rezystancji
Na rys.13 pokazano popularny sposób korekcji przesunięcia zera i zmiany wzmocnienia na
drodze programowej. Rys.14 ilustruje metodę cztero-zaciskowego pomiaru rezystancji. Dla
uproszczenia pominięto układ wyboru zakresu, przy czym należy zauważyć, że nie jest bez
znaczenia dla błędu pomiaru jaką wartość przyjmie rezystor wzorcowy R
w
i przy jakich
poziomach napięć pomiar będzie realizowany.
Jednym z podstawowych dylematów konstruktorów i producentów jest wybór funkcji
realizowanych bezpośrednio przez multimetr. Jest zawsze pewna granica między funkcjami,
które niewątpliwie należy włączyć do struktury wewnętrznej multimetru, a funkcjami, które
mogą być realizowane za pomocą sprzętu wspomagającego, interfejsu i komputera. Typowym
przykładem może być wielokanałowy układ wejścia (rys.15). Mamy tu do czynienia z trzema
możliwościami wyboru. Pierwsza - to włączenie tego układu do struktury wewnętrznej
multimetru, co pozwala na prostą realizację sterowania przełączaniem kanałów oraz eliminuje
konieczność skomplikowanej ochrony toru komutowanych sygnałów przed zakłóceniami.
Rozwiązanie to wybierane jest jednak dość rzadko, gdyż - zawyżając cenę przyrządu - czyni
go mało atrakcyjnym dla użytkowników nie wymagających wejścia wielokanałowego. Druga
możliwość, to podporządkowanie wielokanałowego układu wejścia komputerowi za
pośrednictwem interfejsu (rys.15a). Rozwiązanie takie jest wprawdzie do przyjęcia, ale
wymaga zwrócenia szczególnej uwagi na staranną ochronę toru sygnału analogowego na
łączeniu z wejściem multimetru. Ponadto mogą powstawać kłopoty związane ze sterowaniem
przełączaniem kanałów przy uwzględnianiu stanów nieustalonych, co prowadzi do
wydłużenia czasu komunikacji w procesie zbierania danych. Wreszcie trzecia możliwość, to
Źródło
napięcia
Przetwornik
A/C
U
1
U
2
U
3
2
1
4
3
w
x
U
U
U
U
R
R
−
−
=
U
4
R
w
R
R
x
R
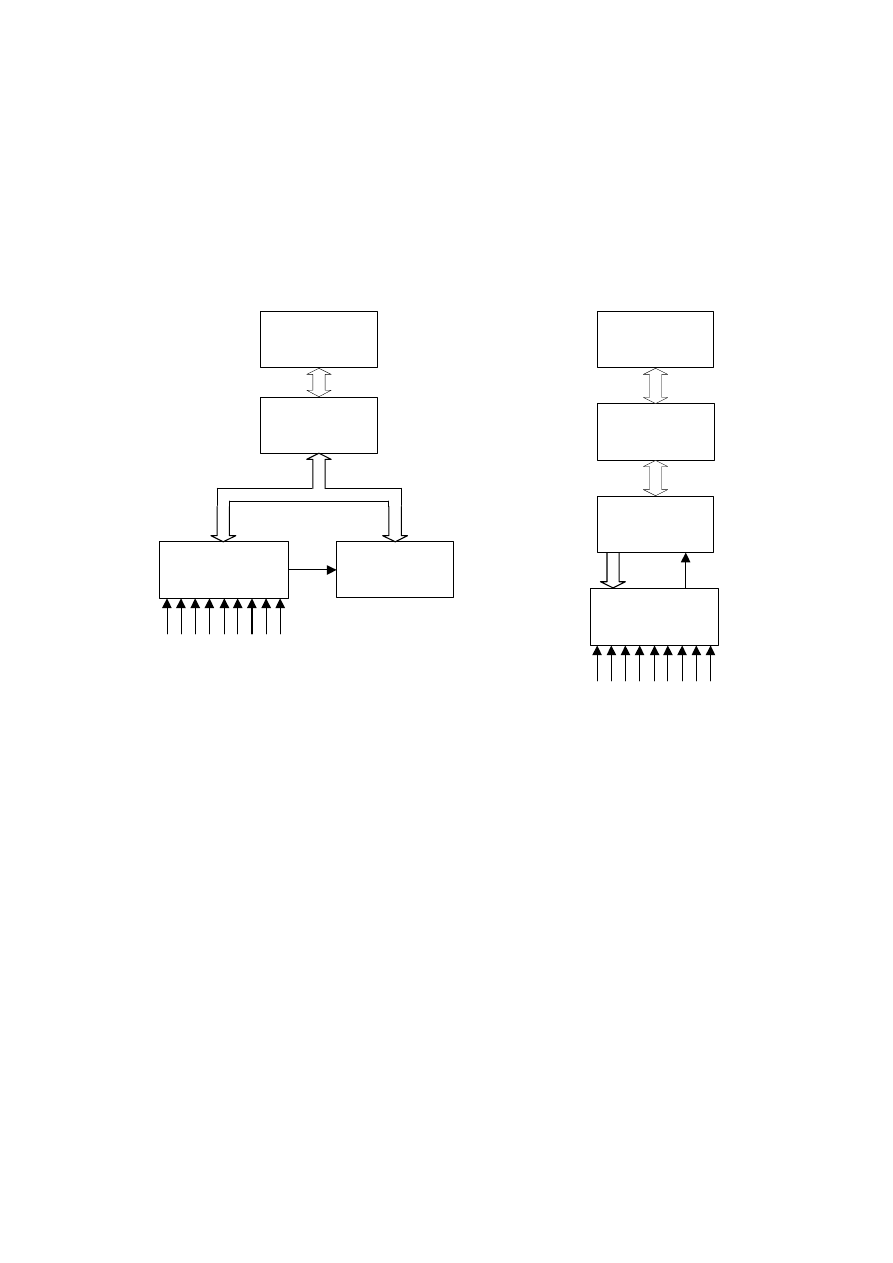
110
podporządkowanie układu przełączającego multimetrowi w strukturze hierarchicznej
(rys.15b). Z punktu widzenia komputera układ przełączający jest częścią multimetru, gdyż
sterowanie przełączaniem należy do multimetru, natomiast komputer decyduje jedynie o
wyborze kanału. W tym rozwiązaniu układ przełączający może być rozwiązany jako blok
opcjonalny, dołączany w obudowie przyrządu na życzenie użytkownika.
Rys. 15. Ilustracja do zagadnienia wyboru struktury sterowania układem komutującym przy pomiarach
wielokanałowych
Nie zawsze można dojść do tak jednoznacznego przedstawienia opcji jak wyżej.
Zmiany w sprzęcie współpracującym (komputery, interfejsy) wywierają duży, a będą
wywierać jeszcze większy wpływ na strukturę multimetrów. Pytanie - które funkcje należy
powierzyć multimetrowi, a które komputerowi? - pozostaje dość często bez wyraźnej
odpowiedzi. Zwolennicy rozwiązań ascetycznych starają się przerzucić „ile się da” funkcji na
komputer, motywując to z jednej strony oszczędnościami w sferze kosztów produkcji, z
drugiej zaś, wzrastającą elastycznością zastosowań. Wymaga to jednak rozbudowy dość
dużych narzędzi programowych projektowanych z myślą o użytkowniku niezbyt
Multimetr
Interfejs
Komputer
Komputer
Interfejs
Multimetr
a)
b)
Sterowanie
Pomiar
Układ
komutuj
ą
cy
Układ
komutuj
ą
cy
Wej
ś
cie
Wej
ś
cie

111
zaawansowanym, zwanych dziś zintegrowanymi środowiskami programowymi (będziemy o
tym mówili jeszcze w dalszych wykładach). Zwolennicy rozwiązań „bogatych” starają się
zmieścić możliwie dużą liczbę funkcji w strukturze wewnętrznej multimetru, przy
zapewnieniu prostego programowania, pozwalającego na obsługę przyrządu bez specjalnego
przygotowania. W skrajnych rozwiązaniach pojawia się tu problem „wodotrysku”.
5. Oscyloskopy cyfrowe
Najchętniej poznajemy zjawiska natury poprzez obserwację wzrokową. Pierwotnie
oscyloskop służył do obserwacji przebiegów czasowych napięcia elektrycznego (1897 - K.F.
Braun). W miarę upływu lat funkcję podstawową uzupełniano o pomiary amplitudy, okresu,
częstotliwości, fazy, a także o możliwość obserwowania i pomiarów rozmaitych sygnałów
elektrycznych w funkcji innych sygnałów elektrycznych (charakterografy). Lata ostatnie
zdominował intensywny rozwój oscyloskopów cyfrowych. Pozwalają one nie tylko na
obserwację i dość dokładne pomiary parametrów sygnałów w dziedzinie czasu, lecz także na
obserwację i pomiary parametrów sygnałów w dziedzinie częstotliwości. Charakterystyczne
jest tu przejmowanie przez oscyloskopy cyfrowe coraz większej liczby operacji
realizowanych dotąd przez przyrządy zwane analizatorami widma. Oscyloskopy cyfrowe
pozwalają dziś na realizację obszernego zestawu funkcji pomiarowych związanych z
obserwacją i analizą kształtów sygnałów.
Uproszczony schemat blokowy oscyloskopu cyfrowego przedstawiony jest na rys.16.
Pierwszy człon tego schematu zawiera dzielniki i wzmacniacze obwodu wejściowego (układy
kondycjonowania) oraz układ próbkujący, który realizuje funkcję próbkowania z pamięcią.
Jego konstrukcja decyduje o górnej granicy pomiarowego pasma częstotliwości sygnału
wejściowego. Próbka sygnału jest przetwarzana następnie w przetworniku a/c na siedmio lub
ośmiobitową liczbę. Liczby te gromadzone są w szybkiej pamięci, na przykład 1024 liczby w
każdym cyklu pomiarowym. Liczba próbek trafiająca na ekran jest uzależniana od przyjętej
podstawy czasu. Po zakończeniu cyklu pomiarowego mikroprocesor odczytuje owe liczby i
przetwarza je na zbiór przechowywany w pamięci kształtu sygnału, współpracującej wprost z
ekranem monitora. Mikroprocesor pozwala także na przesyłanie kształtu obserwowanego
sygnału do pamięci dyskowej, a następnie przywoływanie go dla porównań bądź dalszego
przetwarzania w celu uśrednienia, filtracji, otrzymania parametrów w dziedzinie
częstotliwości. Oscyloskopy wyposażane są zwykle w dwie pamięci ekranu; jedna, to
wymieniona pamięć kształtu, druga zaś jest pamięcią rastra. Dzięki separacji obrazów
statycznych i dynamicznych możliwe jest osiągnięcie szybszych „kasowań” przebiegów na
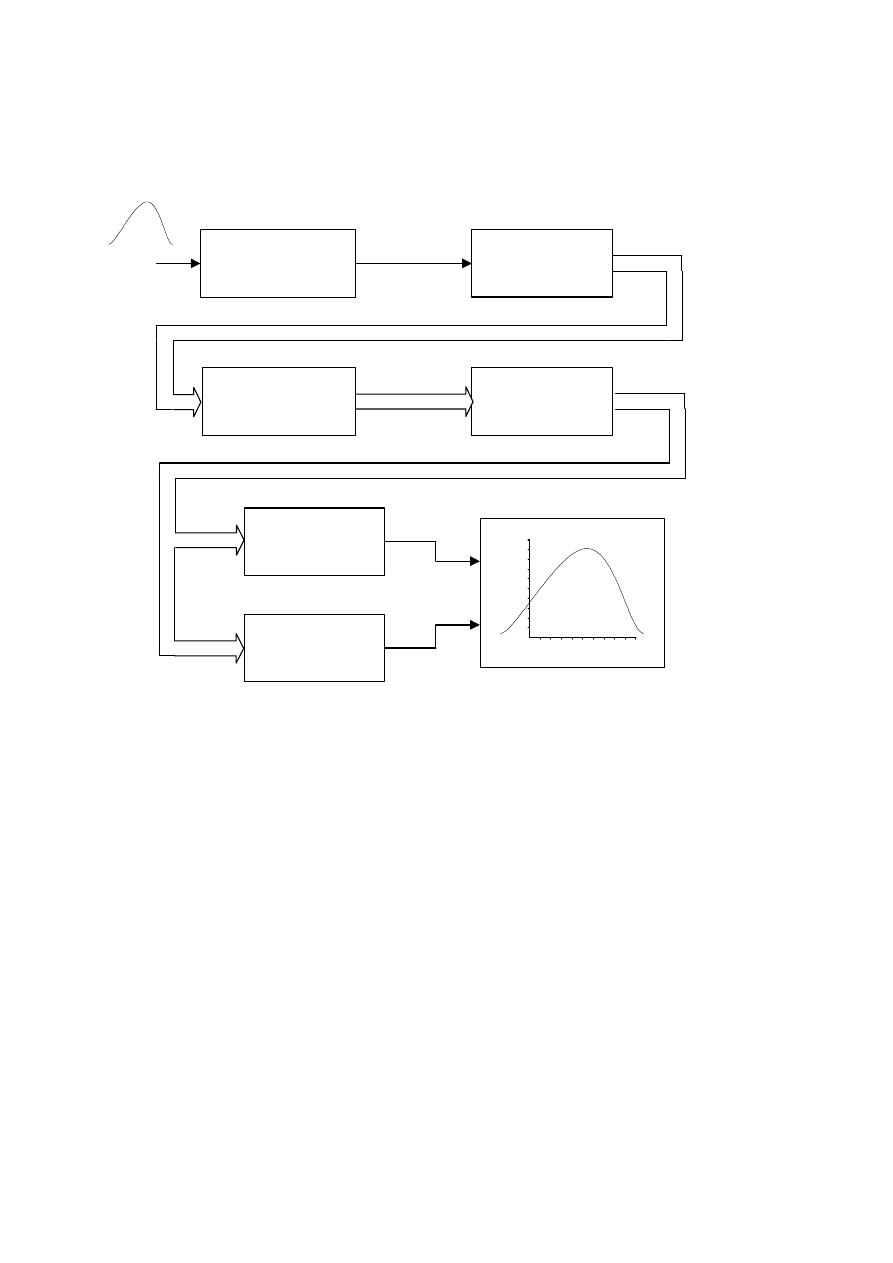
112
ekranie, gdyż oprogramowanie nie jest obciążane wyświetlaniem rastra. Dzięki temu możliwe
jest również niezależne sterowanie jaskrawością rastra i przebiegów.
Rys. 16. Uproszczony schemat blokowy oscyloskopu cyfrowego
Praca oscyloskopu cyfrowego jest nieodłącznie związana z procesem próbkowania
ciągłego przebiegu wejściowego. W wyniku tego procesu otrzymujemy funkcję odtwarzającą
zmienność wielkości wejściowej w postaci ciągu wartości próbek odpowiadających
wybranym chwilom czasu t. Proces zastępowania funkcji ciągłej x(t) ciągiem x
*
(t) nazywamy
dyskretyzacją lub kwantowaniem w czasie. Najczęściej próbki są rozłożone równomiernie w
czasie. Przedział
∆
t między sąsiednimi chwilami próbkowania nazywa się okresem
próbkowania, a jego odwrotność - częstotliwością próbkowania. Model matematyczny
próbkowania można zbudować za pomocą ciągu impulsów Diraca rozłożonych równomiernie
w czasie w odległości
∆
t:
h t
t
n t
n
( )
(
)
=
−
=−∞
∞
∑
δ
∆
(18)
Próbkowanie polega teraz na pomnożeniu funkcji ciągłej x(t) przez h(t):
Obwód wej
ś
ciowy
i
układ próbkuj
ą
cy
PRZETWORNIK
A/C
Pami
ęć
o du
ż
ej
szybko
ś
ci
Mikroprocesor
Pami
ęć
kształtu
sygnału
Pami
ęć
rastra
Y
-A
x
is
X-Axis
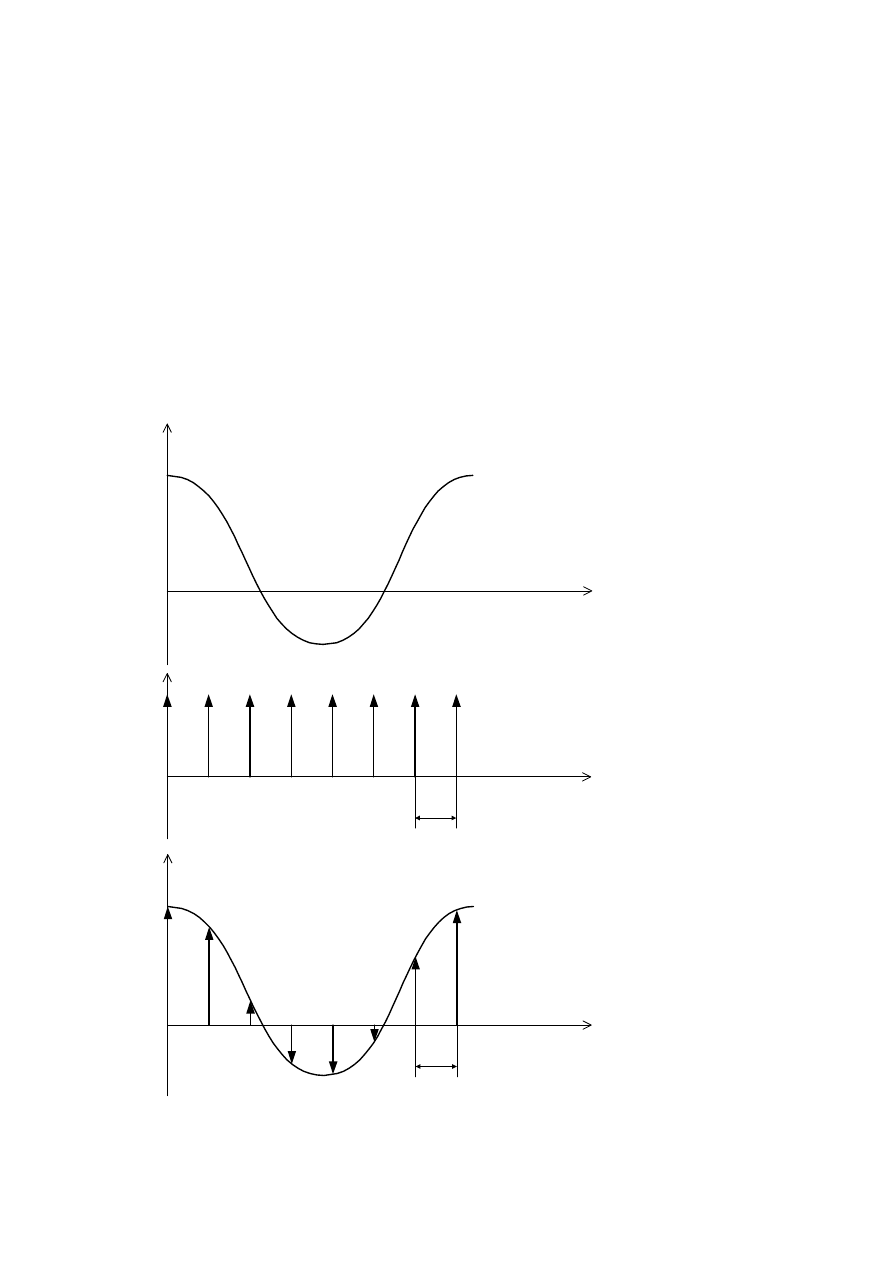
113
x
t
x t h t
x t
t
n t
n
*
( )
( ) ( )
( )
(
)
=
=
−
=−∞
∞
∑
δ
∆
(19)
i dalej
x
t
x n t
t
n t
n
*
( )
(
) (
)
=
−
=−∞
∞
∑
∆
∆
δ
(20)
Funkcja po dyskretyzacji jest ciągiem impulsów Diraca o powierzchniach równych
wartościom chwilowym próbek (ilustruje to rys.17). Pozornie przebieg po próbkowaniu
zawiera mniej informacji niż przebieg oryginalny. W rzeczywistości, jeżeli tylko spełnione są
warunki twierdzenia Shannona próbkowanie nie wprowadza strat informacji o przebiegu
wejściowym.
Rys. 17. Próbkowanie przebiegu ciągłego
∆
Τ
h(t)
t
x(t)
t
∆
Τ
t
x*(t)
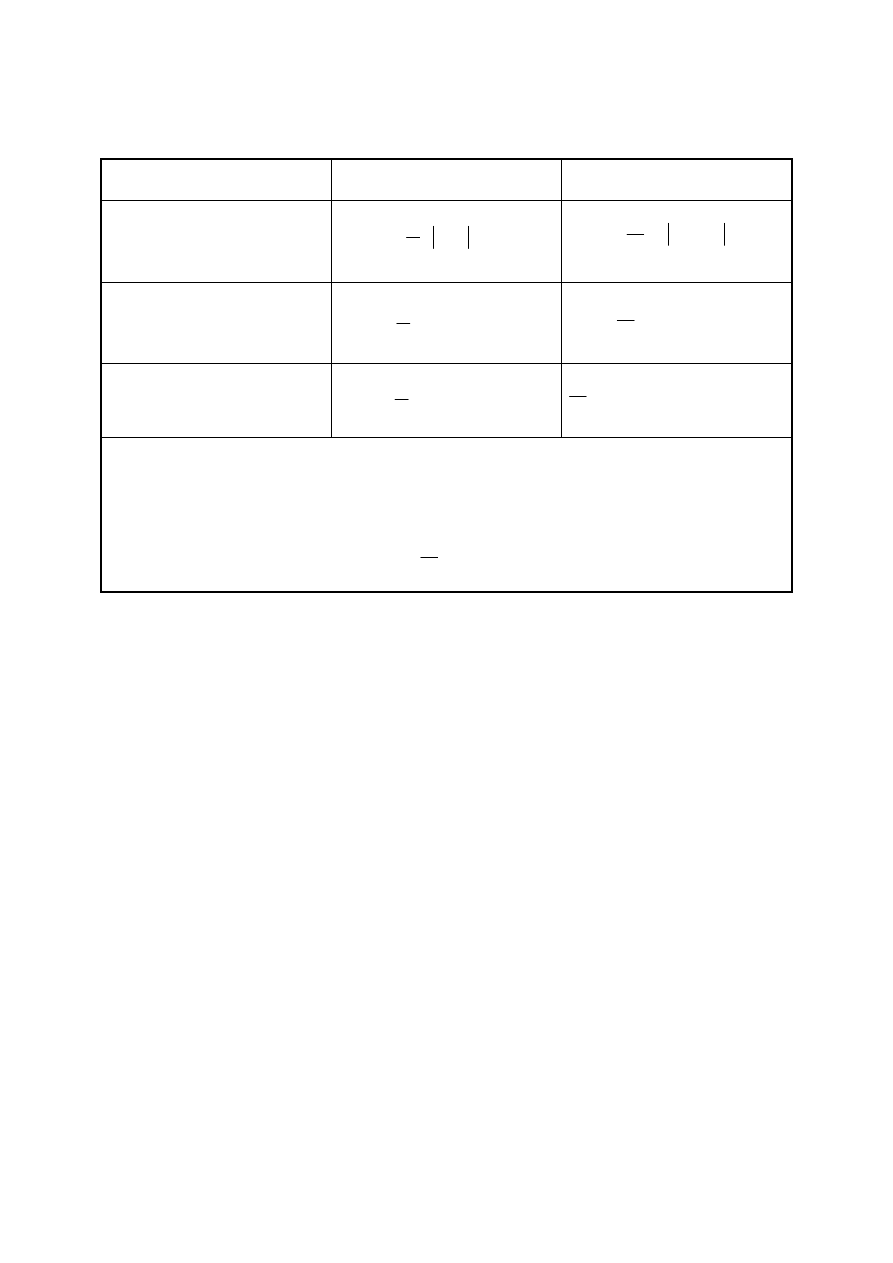
114
Tablica 9. Przykład wzorów definicyjnych i obliczeniowych wielkości elektrycznych wyznaczanych
metodą próbkowania
parametr
definicja
wzór obliczeniowy
napięcie
- wartość średnia
∫
T
dt
t
u
T
0
1
)
(
∑
−
=
∆
1
0
1
N
n
t
n
u
N
)
(
)
napięcie
- wartość skuteczna
2
1
0
2
1
/
)
(
∫
T
dt
t
u
T
2
1
1
0
2
1
/
)
(
∆
∑
−
=
N
n
t
n
u
N
)
moc czynna
∫
T
dt
t
u
t
i
T
0
1
)
(
)
(
∑
−
=
∆
∆
1
0
1
N
n
t
n
u
t
n
i
N
)
(
)
(
)
)
Oznaczenia:
u(t), i(t),
)
(
),
(
t
i
t
u
)
)
- wartości chwilowe napięcia i prądu, rzeczywiste i skwantowane,
T - okres sygnału, N - liczba próbek,
N
T
r
t
=
∆
(r - liczba próbkowanych okresów sygnału)
Równolegle z prezentacją przebiegów oscyloskop cyfrowy daje możliwość pomiaru
parametrów charakterystycznych tych przebiegów - amplitudy, okresu, częstotliwości, a także
wartości średniej, skutecznej, mocy (patrz tablica 9). Nie bez znaczenia jest także przyjazna
użytkownikowi prezentacja wyników pomiarów w odpowiednich miejscach monitorowego
rastra.

115
Wykład 11 i 12
Automatyzacja pomiarów
Struktury
systemów
pomiarowych.
Interfejsy
standardowe.
Procedury
pomiarów
systemowych. Oprogramowanie systemów. Przyrządy wirtualne.
1. Struktury systemów pomiarowych
Struktura i organizacja systemów pomiarowych są zależne od przeznaczenia, sposobu i
szybkości przetwarzania informacji, sposobu oddziaływania systemu na obiekt lub proces itp.
Przybliżenie problemów struktury i organizacji systemów pomiarowych w zasadzie jest moż-
liwe dopiero po dokonaniu podziału systemów, uwzględniając różne kryteria klasyfikacji
(rys.1).
Zależnie od głównego zadania pomiarowego rozróżnia się trzy grupy systemów
pomiarowych: obserwacyjne, pomiarowo-kontrolne i pomiarowo-diagnostyczne. Systemy
obserwacyjne (poznawcze, badawcze) stosowane są głównie w badaniach naukowych,
których celem jest doświadczalna weryfikacja hipotez naukowych. Podstawowy zbiór
otrzymywanych informacji jest na ogół wyprowadzany poza strukturę systemu dla operatora
kierującego eksperymentem. Systemy te wykorzystywane są w wielu dziedzinach nauki, jak:
elektronika, fizyka, chemia, mechanika, biologia, medycyna. Systemy pomiarowo-kontrolne
stanowią obecnie integralną część każdego procesu technologicznego. Procesy te
kontrolowane są zwykle poprzez pomiary parametrów wytwarzanych w trakcie procesu
obiektów, jak i parametrów urządzeń technologicznych służących do ich wyrobu. Kontrola ta
polegała dawniej na odczycie wskazań odpowiedniego zestawu przyrządów. Gdy liczba
kontrolowanych parametrów była znaczna, panowanie nad prawidłowością całego procesu
było kłopotliwe. Automatyzacja procesów technologicznych wymusiła w sposób oczywisty
automatyzację pomiarów, czyli wprowadzenie systemów pomiarowo-kontrolnych. Systemy
takie wykorzystują zwykle znaczne liczby czujników rozmieszczonych terytorialnie na całym
kontrolowanym obiekcie i przetworników formujących sygnały wykorzystywane dalej przez
regulatory sterujące procesem technologicznym. Głównym użytkownikiem tych systemów
jest przemysł.
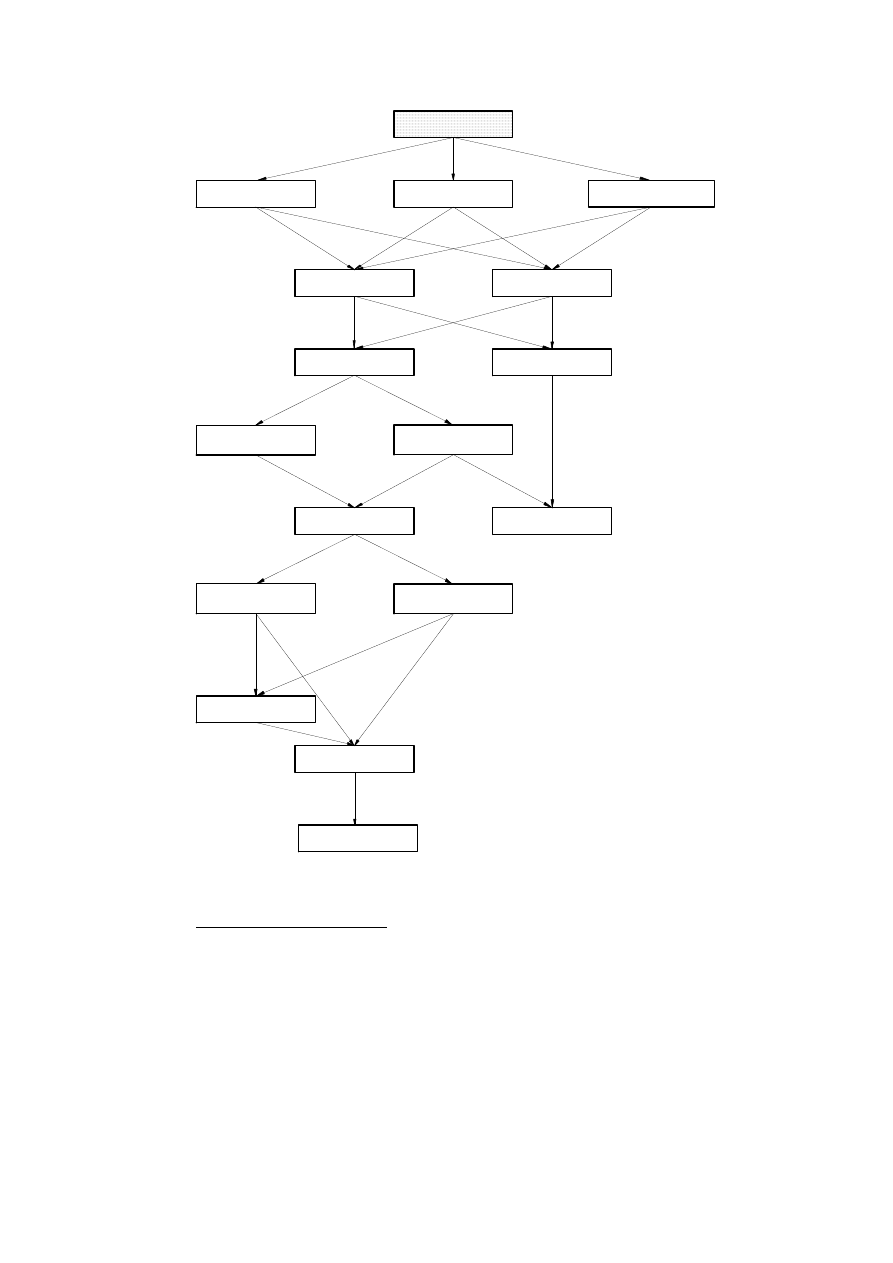
116
Rys. 1. Klasyfikacja systemów pomiarowych
Systemy pomiarowo-diagnostyczne służą detekcji, lokalizacji, identyfikacji lub predykcji
uszkodzeń obiektu na podstawie objawów charakterystycznych dla poszczególnych jego sta-
nów niezawodnościowych. Do podstawowych problemów diagnostyki należą metody wyzna-
czania różnego rodzaju testów i procedur diagnostycznych (czyli sposobów posługiwania się
testami w trakcie diagnozowania obiektu. Zależnie od charakteru obiektu wyróżnia się okre-
ślone rodzaje diagnostyki, jak np. diagnostyka techniczna czy diagnostyka medyczna. Celem
diagnozowania jest nie tylko stwierdzenie stanu obiektu, ale często również wskazanie nie-
PRACUJĄCE W CZASIE
RZECZYWISTYM
PRACUJĄCE W CZASIE
WŁASNYM
Z MODYFIKOWANYM
PROGRAMEM ODDZIAŁYWAŃ
AKTYWNE
SYSTEMY POMIAROWE
POMIAROWO-KONTROLNE
POMIAROWO-DIAGNOSTYCZNE
ROZŁOśONE
TERYTORIALNIE
PASYWNE
ZE STAŁYM
PROGRAMEM ODDZIAŁYWAŃ
BEZ OBRÓBKI DANYCH
Z OBRÓBKĄ DANYCH
Z REDUKCJĄ INFORMACJI
ADAPTACYJNE
Z SAMOKONTROLĄ
SKUPIONE
OBSERWACYJNE

117
zdatnego elementu, co z reguły wymaga testowania kontrolnego odpowiednio utworzonych
fragmentów systemu.
Każdy system pomiarowy może być zrealizowany w sposób skupiony lub rozłożony
terytorialnie. System może oddziaływać na badany obiekt w celu stworzenia odpowiednich
warunków do wykonania pomiaru. Wynika stąd podział na systemy aktywne (mogące
oddziaływać na obiekt) oraz pasywne, pozbawione tej możliwości. Oddziaływanie na obiekt
może się odbywać wg stałego programu (systemy aktywne z programem stałym) lub może
być uzależnione od aktualnie uzyskiwanych informacji (systemy aktywne ze sprzężeniem
zwrotnym, czyli z modyfikowanym programem oddziaływań uzależnionym od bieżących
wyników pomiaru). Potrzeba przetwarzania danych decyduje o obecności komputera w wielu
systemach pomiarowych. Przetwarzanie danych może odbywać się w czasie rzeczywistym,
czyli równolegle ze zbieraniem danych, lub z opóźnieniem w czasie, czyli w czasie własnym.
Systemy pracujące w czasie rzeczywistym wymagają szybkich algorytmów przetwarzania
danych, szybkich komputerów, procesorów sygnałowych oraz układów sprzęgających
(interfejsów) o dużej szybkości transmisji. Przetwarzanie danych, w tym nadmiarowych, wy-
dłuża czas wykonania pomiarów. Dlatego w wielu systemach zachodzi potrzeba redukcji nad-
miaru informacji. Może się to odbywać się w torze pomiarowym lub podczas przetwarzania.
Zmniejszenie prawdopodobieństwa powstania błędów oraz zwiększenie wiarygodności infor-
macji wyjściowej występuje w systemach z auto-kalibracją. Polega ona na sprawdzaniu sys-
temu lub jego części pod względem zachowania właściwości metrologicznych, a także po-
prawności wykonywania obliczeń. Pozytywny wynik testu, wykonanego na rozkaz operatora
lub zgodnie z założonym z algorytmem działania, jest równoznaczny z przyjęciem wyników
pomiaru za wiarygodne. Dalszym etapem rozwoju systemów są systemy adaptacyjne, a
zwłaszcza systemy mające możliwość automatycznej korekcji swoich charakterystyk. Wyko-
rzystuje się w nich wyniki auto-kalibracji do modyfikacji charakterystyk systemu, zgodnie ze
zmieniającymi się właściwościami sygnałów pomiarowych lub warunkami eksploatacji
systemu.
Stymulatorami postępu w budowie systemów pomiarowych są z jednej strony takie
potrzeby, jak zwiększenie szybkości pomiarów przy wzrastającym stopniu ich automatyzacji,
a także stała potrzeba zwiększania ich dokładności i niezawodności. Z drugiej strony rozwój
tych systemów jest stymulowany przez nowe możliwości, wynikające głównie z postępów
technologii mikrokomputerowej w coraz silniejszym powiązaniu z nowymi rozwiązaniami
scalonych układów przetworników analogowych i analogowo-cyfrowych.

118
Systemy pomiarowe charakteryzują się ogromną różnorodnością rozwiązań. Ograni-
czymy się tu do systemów, w których grupa urządzeń podłączona jest poprzez standardowy
układ sprzęgający (interfejs) do komputera typu PC, a do zbierania, przetwarzania i
prezentacji danych pomiarowych wykorzystywane są zwykle powszechnie stosowane w
świecie firmowe pakiety oprogramowania (klasyczne i tzw. zintegrowane).
Prace nad rozwojem komputerowych systemów pomiarowych rozpoczęto od prób
przeniesienia funkcji kontrolno-sterujących oraz obróbki wyników do wydzielonego urządze-
nia zwanego kontrolerem. Jednymi z pierwszych kontrolerów systemów pomiarowych były
kalkulatory programowalne firmy Hewlett-Packard (HP9820 i HP9830) wykorzystujące wła-
sny standard interfejsu HPIB (Hewlett-Packard Interface Bus), który później stał się standar-
dem dużych producentów aparatury pomiarowej, znanym jako interfejs GPIB (General Pur-
pose Interface Bus), następnie został standardem amerykańskim IEEE-488, a wreszcie stan-
dardem międzynarodowym IEC-625. Wraz z postępem technologii opracowano specjalizo-
wane układy bardzo dużej skali integracji VLSI umożliwiające proste sprzęganie kontrolerów
systemów pomiarowych z aparaturą pomiarową. Można było już konstruować tak małe
układy komunikacji przyrząd - system, że wbudowywano je bezpośrednio w przyrządy
pomiarowe (wcześniej stanowiły one odrębne urządzenia). Także popularność zaczęły
zdobywać komputery osobiste PC. Ze względu na ich uniwersalność, elastyczność, otwartą
architekturę, dostępność i duże możliwości (duża i szybka pamięć operacyjna i masowa,
urządzenia peryferyjne, łatwa komunikacja z użytkownikiem za pomocą klawiatury i
monitora, bogate oprogramowanie użytkowe i systemowe) postanowiono wykorzystać je jako
jednostki sterujące, zapewniające prawidłowy obieg informacji w systemie pomiarowym i
czasową koordynację pracy poszczególnych jego elementów. W związku z tym opracowano
komputerowe karty kontrolera ze standardowym układem interfejsu i odpowiednim
oprogramowaniem, dając w ten sposób początek systemom pomiarowym sterowanym
komputerowo. W komputerowym systemie pomiarowym poszczególne przyrządy połączone są
z kontrolerem za pomocą interfejsu, składającego się z pakietów interfejsu i zestawu
instrukcji sterujących.
Komputer jest podstawowym blokiem systemu pomiarowego, ale głównym
elementem wokół którego zbudowany jest system stał się interfejs systemu. Interfejs
praktycznie przesądza o strukturze systemu oraz - w dużym stopniu - o jego możliwościach i
ograniczeniach technicznych. Umożliwia realizację złożonych zadań pomiarowych, poprzez
koordynację i sterowanie pracą dołączonych urządzeń, oraz zapewnienie wymiany danych
pomiędzy nimi.

119
Powstało kilkanaście standardów interfejsów które znalazły
zastosowanie
w systemach pomiarowych, m.in.: RS-232C, RS-422, RS-485, CAMAC, IEC-625 (IEEE-
488), VME, a w ostatnich latach również VXI.
Największą popularność zdobył opracowany w 1978 roku interfejs IEEE-488
(międzynarodowa wersja - IEC-625). Główny obszar zastosowań tego standardu stanowią
systemy laboratoryjne, a także wybrane systemy przemysłowe. Interfejs ten umożliwia
łączenie przyrządów pomiarowych, sterujących i pomocniczych z komputerem nadzorującym
pracę systemu. Oferta urządzeń z interfejsem IEC-625 jest bardzo szeroka. Obejmuje ona
zarówno powszechnie stosowane przyrządy pomiarowe (z wyjątkiem najtańszych,
wyposażonych zwykle w interfejs RS-232), jak i specjalizowane urządzenia kontrolno-
pomiarowe (np. wysokiej klasy odbiorniki radiokomunikacyjne, sterowniki anten, itp.). Każde
z tych urządzeń może pracować również jako samodzielne urządzenie obsługiwane z płyty
czołowej. Szeroka jest także gama komputerów sterujących systemami IEC-625, poczynając
od komputerów osobistych takich jak: IBM PC czy Macintosh, a kończąc na stacjach
roboczych: Sun, NeXT, Apollo, IBM, DEC i in.
Interfejsy szeregowe (np. RS-232, RS-485) stosowane są w prostych systemach
pomiarowych składających się z kontrolera i przyrządu, jak również w systemach
pomiarowych o przetwarzaniu rozproszonym (szczególnie - z czujnikami inteligentnymi), w
których istnieje konieczność przesyłania danych na większe odległości. Zaletą systemów z
interfejsami szeregowymi jest ich niski koszt, wadą - mała prędkość transmisji danych.
Najbardziej zaawansowanym technicznie jest standard interfejsu VXI. Standard ten
(podobnie jak wycofywany z użycia CAMAC) przeznaczony jest do stosowania w moduło-
wych systemach kontrolno-pomiarowych, w których bloki funkcjonalne realizowane są w po-
staci modułów wsuwanych do standardowej obudowy. Moduły te nie mogą pracować poza
systemem. Systemy VXI zapewniają wysoką prędkość działania, są jednak bardzo kosztowne.
Stąd też zastosowania ich ograniczają się do tych obszarów, w których najważniejszym pro-
blemem jest bardzo duża szybkość działania całego systemu lub konieczność transmisji i
przetwarzania dużej liczby danych. Obszary takie znajdują się zarówno w badaniach nauko-
wych (np. badania bardzo szybkich przetworników), jak również w przemyśle (np. kontrola
działania elektrowni jądrowych, nadzorowanie lotu samolotów wojskowych, nadzór nad zło-
żonymi urządzeniami diagnostyki medycznej).

120
3. Interfejsy standardowe
Interfejs może być zdefiniowany jako połączenie (układ pośredniczący) między
rozważanym systemem a innym systemem lub częściami jakiegoś systemu przez które
przepływa informacja. Polska Norma PN-83/T-06536 rozróżnia pojęcia interfejsu i systemu
interfejsu. System interfejsu definiowany jest tu jako zbiór (niezależnych od urządzeń)
elementów mechanicznych, elektrycznych i funkcjonalnych koniecznych w procesie wymiany
informacji między urządzeniami. (rys.2).
System pomiarowy
System
interfejsu
JFn
JF2
JF3
JF1
Rys. 2. System pomiarowy a system interfejsu (JFn - jednostka funkcjonalna n)
Typowymi elementami systemu interfejsu są kable, złącza, nadajniki i odbiorniki linii, funkcje
interfejsowe z opisem logicznym, linie sygnałowe, zależności czasowe oraz zasady sterowania.
Należy wyraźnie podkreślić, że system interfejsu nie sprowadza się jedynie do
fizycznej warstwy (jak np. kable i złącza), ale obejmuje ogół środków zapewniających
dopasowanie mechaniczne, elektryczne i informacyjne oraz ustalających funkcjonalne relacje
między fizycznie odrębnymi częściami systemu, a także organizujących wymianę informacji
między nimi.
Wymiana danych między elementami systemu odbywa się poprzez kanał
transmisyjny, którego specyficzne właściwości zależą od fizycznej formy tego kanału (np.
przewód, światłowód, fale radiowe). Wymusza to konieczność użycia konwerterów między
elementem systemu a kanałem transmisyjnym (rys.3).
Na problem łączenia elementów systemu można spojrzeć nieco szerzej. Strukturę
wszystkich interfejsów w systemie można traktować jako pewien system komunikacyjny słu-
żący do wymiany danych między częściami systemu pomiarowego, które w tym układzie są
poza systemem komunikacyjnym. Zatem w tym podejściu do systemu interfejsu jest on - jako
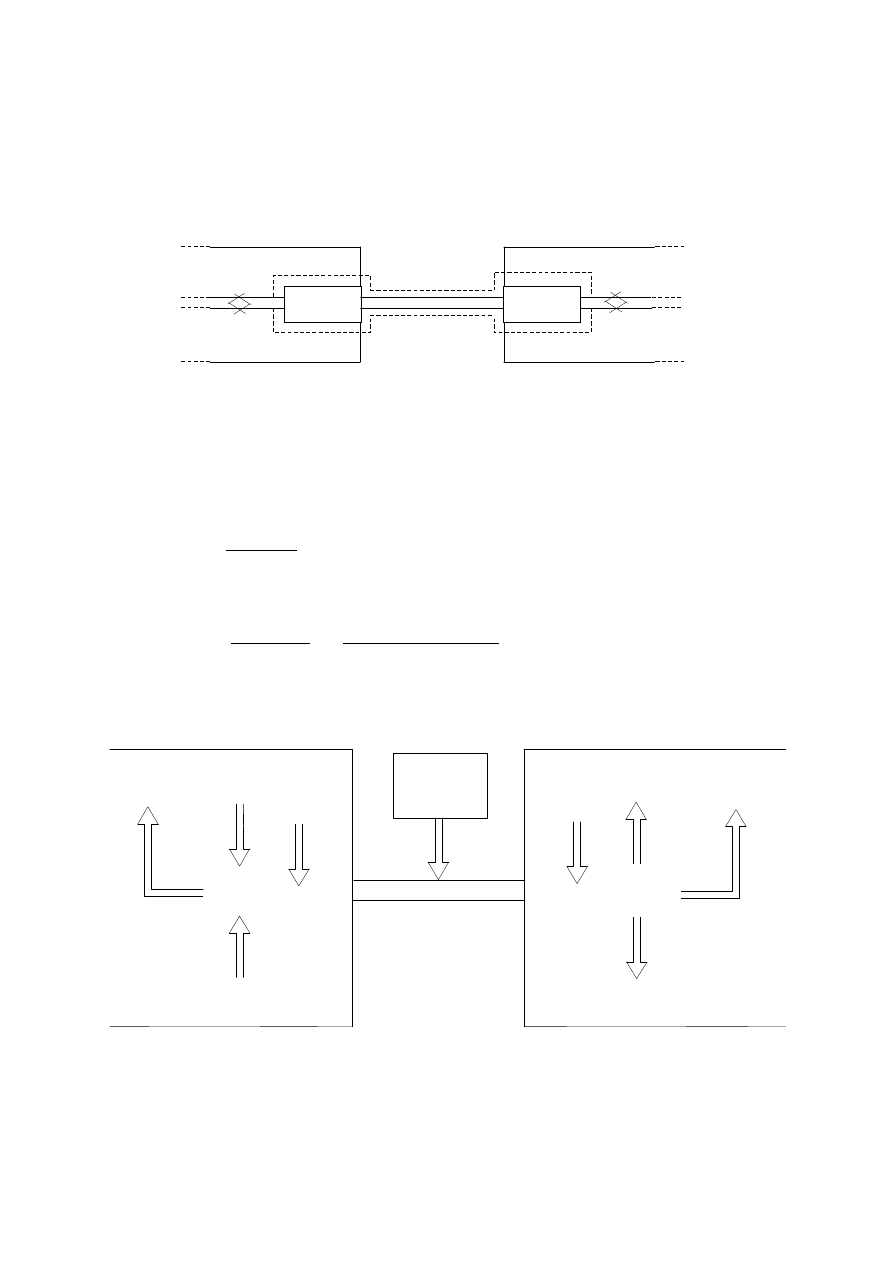
121
wydzielony system komunikacyjny, zwany wówczas siecią (ang. network) - podsystemem
systemu pomiarowego.
Uwaga: W systemach pomiarowych przyjmuje się często, że pod słowem "interfejs" rozumie
się "system interfejsu".
Kanał
transmisyjny
INTERFEJS
Konwerter
INTERFEJS
Konwerter
Rys. 3. Kanał interfejsu między dwoma jednostkami
Prawidłowa realizacja wymiany informacji między elementami systemu poprzez ich
interfejsy wymaga określenia funkcji interfejsu. Im system interfejsu jest bardziej złożony,
tym zbiór tych funkcji jest obszerniejszy. Ogólny schemat funkcji interfejsu zobrazowano
symbolicznie na rys.4 na przykładzie połączeń dwóch jednostek.
Funkcja konwersji dostosowuje typ danych w jednostce systemu do typu danych
stosowanego w kanale transmisyjnym, a w szczególności dopasowuje poziomy logiczne i
kody wszystkich informacji przesyłanych poprzez interfejs.
Funkcja kodowania i dekodowania adresu jest potrzebna w systemie wielo-
elementowym dla zapewnienia właściwego adresowania - tak, by dane sygnałów
informacyjnych i organizacyjnych docierały do właściwych miejsc systemu.
Rys.4. Funkcje interfejsu
Zarzadzanie
interfejsem
Buforowanie
Buforowanie
Przerwania
Przerwania
Synchronizacja
Synchronizacja
Konwersja
Konwersja
Kodowanie
adresu
Dekodowanie
adresu
Korekcja
błędów

122
Funkcja synchronizacji (ang. handshake) zapewnia wymaganą synchronizację
transmisji danych (ang. timing) między jednostkami poprzez kanał interfejsu, uwzględniając
ewentualne nieregularne lub przypadkowe opóźnienia w kanale.
Funkcja przerwania pozwala na zatrzymanie normalnej komunikacji, aby umożliwić
przesłanie specjalnych komunikatów - np. komunikatów zarządzania interfejsem.
Funkcja buforowania pozwala na odcięcie wyjścia nadajnika lub wejścia odbiornika,
gdy nie są one zdolne (z rozmaitych powodów) wysyłać lub odbierać dane, lub też, gdy kanał
transmisyjny nie jest w stanie przesyłać dostarczonych danych.
Funkcja zarządzania interfejsem jest potrzebna w rozbudowanych, złożonych syste-
mach interfejsu, aby zapewnić właściwe funkcjonowanie komunikacji w systemie. Operacje
realizowane przez tę funkcję, to np.: inicjacja interfejsu, obsługa przerwań, zabezpieczenia
przed przeciążeniem kanału transmisyjnego, itp.
Funkcja korekcji błędów pozwala na korekcję tych błędów w danych, które powstały
w wyniku wpływu zakłóceń w kanale transmisyjnym.
Opis konkretnego interfejsu zawiera nie tylko opis jego struktury topologicznej (tzn.
zespołu cech decydujących o konfiguracji systemu pomiarowego realizowanego przy
wykorzystaniu danego interfejsu) oraz funkcji interfejsu, ale również opis fizycznej natury
(warstwy), własności sygnałów oraz protokołu komunikacyjnego.
Łączenie elementów w system może być związane z koniecznością przezwyciężenia
szeregu trudności ze względu na różnorodność rozwiązań konstrukcyjnych zastosowanych
przez wytwórców przyrządów czy modułów pomiarowych. Wszystkie urządzenia wybrane do
realizacji systemu pomiarowego na dowolnym poziomie złożoności muszą spełniać warunki
zgodności metrologicznej, konstrukcyjnej, informacyjnej, itp. Dotyczy to zarówno
rozbudowanego systemu pomiarowego z komputerem jako kontrolerem, jak i czujnika o
sztucznej inteligencji, będącego również systemem pomiarowym, tyle że realizowanym w
innej technologii niż poprzedni i z innym kontrolerem (np. mikrokontrolerem).
Stopień wymaganej kompatybilności zależy od wielu czynników. Podstawowe wyma-
gania dotyczą:
- zgodności mechanicznej i konstrukcyjnej gniazd przyłączeniowych i rozmieszczenia
sygnałów w gnieździe,
- zgodności parametrów elektrycznych poszczególnych sygnałów,
- zgodności stosowanych kodów i protokołów komunikacyjnych,
- zgodności metod transmisji danych.

123
Firmy produkujące aparaturę pomiarową i urządzenia komputerowe podejmują próby
standaryzacji interfejsów pomiarowych, oferując jednocześnie bogatą gamę urządzeń wyposa-
żonych w jednolity system interfejsu. Niektóre z tych propozycji uzyskują akceptację szero-
kiej grupy znaczących w świecie producentów sprzętu pomiarowo-kontrolnego, stając się po-
czątkowo nieoficjalnym standardem, a po akceptacji międzynarodowych organizacji normali-
zacyjnych (np. IEC, IEEE) uzyskują rangę standardów światowych. W ten sposób powstał
m.in. standard IEC-625. Na podstawie zaleceń międzynarodowych tworzone są normy kra-
jowe przez organizacje narodowe (np. PN-83/T-06536 opisująca standard IEC-625). Przyjęcie
standardowego interfejsu zapewnia możliwość szybkiego zestawiania systemu pomiarowego
przy wykorzystaniu bloków produkowanych przez różne firmy, co znacznie obniża koszty
realizacji systemu. Spowodowało to, że obecnie zdecydowana większość projektowanych
systemów pomiarowych wykorzystuje standardowe lub quasi-standardowe interfejsy.
Klasyfikacja interfejsów ściśle zależy od przyjętych kryteriów. Brak jest
dominującego kryterium podziału interfejsów. Rozważmy zatem kilka kryteriów najczęściej
spotykanych.
Przyjmijmy jako pierwsze kryterium warstwę organizacyjną systemu. We współcze-
snych systemach pomiarowych można wyróżnić następujące warstwy:
A. warstwa sieci zarządzającej grupą systemów,
B. warstwa sterownika ( kontrolera ) systemu,
C. warstwa przyrządów ( bloków ) pomiarowych,
D. warstwa modułów funkcjonalnych.
Poszczególne warstwy współpracują ze sobą zgodnie z zasadami hierarchicznego sterowania,
tzn. warstwa wyższa zarządza elementami warstwy niższej.
Warstwa A jest nadrzędną w stosunku do pojedynczego systemu pomiarowego. Ty-
pową funkcją tej warstwy jest - oprócz zarządzania grupą systemów - analiza danych odbiera-
nych z systemów pomiarowych do celów monitorowania i sterowania całym nadzorowanym
procesem (np. procesem produkcyjnym). Do sterowania tą warstwą wykorzystywane są zwy-
kle rozbudowane komputery z najnowszymi typami procesorów (np. stacje robocze). Pracują
one zwykle w instalacjach sieciowych pod kontrolą wielodostępnych i wielozadaniowych sys-
temów operacyjnych klasy UNIX. Zatem na poziomie warstwy A możemy mówić o interfej-
sach sieciowych.
Warstwa B jest najwyższą dla pojedynczego systemu pomiarowego. Sterownik tej
warstwy bezpośrednio zarządza urządzeniami pomiarowymi (przyrządami lub kasetami

124
pomiarowymi) poprzez interfejs. Interfejsy na poziomie tej warstwy możemy nazwać
przyrządowymi (np. IEC-625) lub kasetowymi (np. CAMAC).
Warstwy C i D są obecnie domeną kontrolerów mikro-układowych, jak: mikroprocesory
(głównie jednoukładowe) i mikrokontrolery (czyli pojedyncze układy scalone stanowiące
kompletny stało-programowy system komputerowy). Mikrokontrolery zorientowane pomia-
rowo mają ponadto wbudowane przetworniki A/C, C/A, komutatory analogowe i inne typowo
pomiarowe bloki funkcjonalne. Interfejsy tej warstwy wykorzystują często magistralę mikro-
procesorową, dlatego też można mówić o interfejsach mikroprocesorowych. Drugą grupę
stosowanych tu interfejsów można nazwać mikro-interfejsami. Są to specjalne interfejsy
służące do łączenia mikrokontrolera ze scalonymi blokami funkcjonalnymi traktowanymi
jako zewnętrzne (z punktu widzenia mikrokontrolerów) mikroukłady pomiarowe. Jednym z
takich interfejsów jest szeregowy interfejs synchroniczny (ang. serial micro-interface),
określany w skrócie SMI. Operowanie pojęciem mikro-interfejsu jest szczególnie uprawnione
na poziomie warstwy D.
Podsumowując, przy przyjęciu jako kryterium podziału interfejsów warstwę organiza-
cyjną systemu można mówić o:
* interfejsach sieciowych,
* interfejsach przyrządowych,
* interfejsach kasetowych,
* interfejsach mikroprocesorowych,
* mikro-interfejsach.
Głównym polem naszego zainteresowania pozostaną interfejsy przyrządowe i kasetowe.
Kryterium zasięgu (czyli dopuszczalna długość połączeń wszystkich bloków systemu)
pozwala na wyodrębnienie grupy interfejsów o podobnych właściwościach. Można bowiem
zauważyć wyraźną zależność między zasięgiem interfejsu a szybkością transmisji,
odpornością na zakłócenia i złożonością konstrukcyjną interfejsu.
Interfejsy o małym zasięgu są zwykle bardzo rozbudowane. Wykorzystują one transmisję
równoległą długich słów (obejmujących nie tylko dane, ale np. rozkazy), co w sumie
zapewnia dużą szybkość transmisji informacji (dziesiątki MB/s). W interfejsach o średnim
zasięgu przesyłana informacja dzielona jest na 8 bitowe słowa (bajty); bity każdego bajtu
przesyłane są równolegle, bajty - kolejno jeden po drugim. Jest to więc transmisja szeregowo
- równoległa, tańsza od poprzedniej, ale odpowiednio wolniejsza (setki kB/s). W interfejsach
o dużym zasięgu dominuje transmisja szeregowa realizowana na możliwie prostym kanale
transmisyjnym (np. kabel dwużyłowy). Szybkość transmisji informacji jest tu niewielka
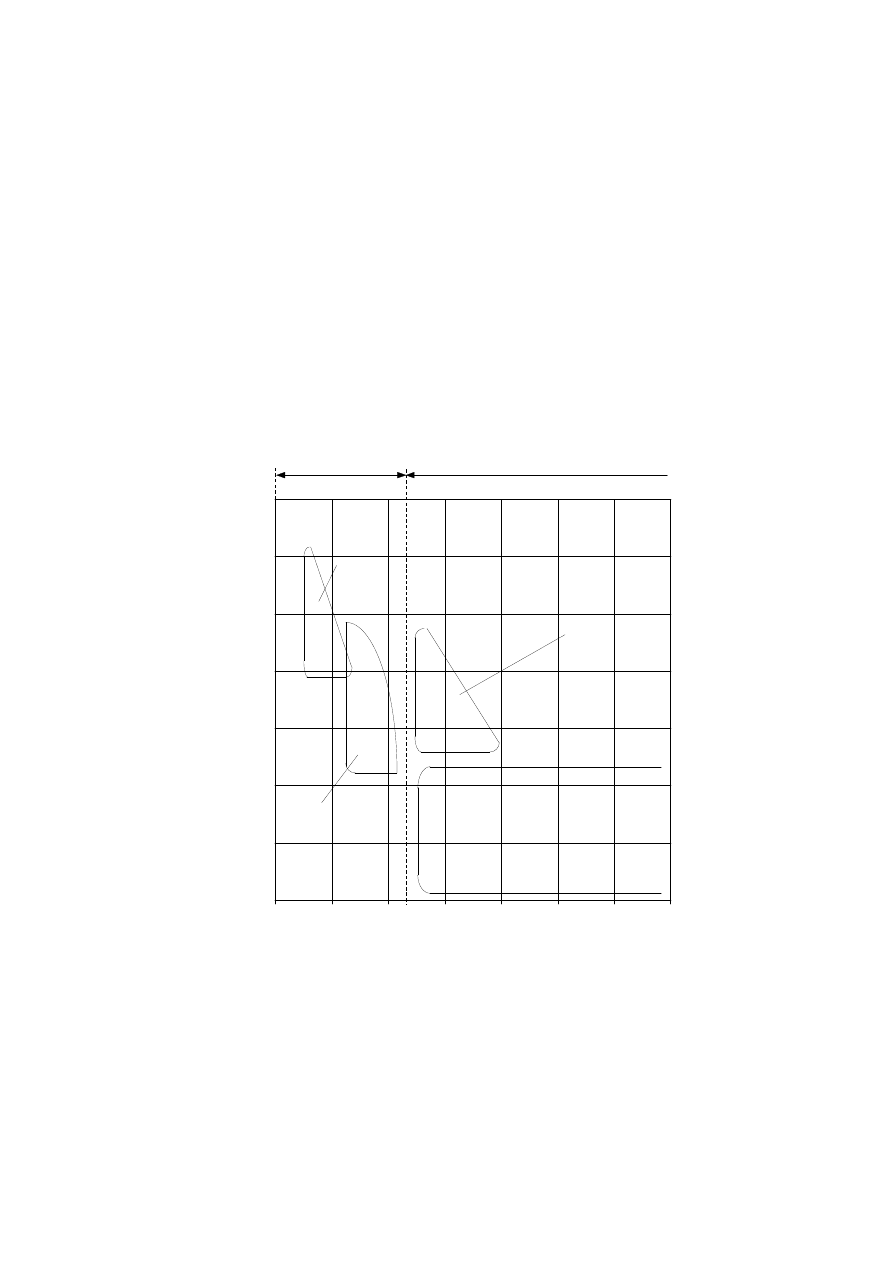
125
(dziesiątki kB/s); zależy ona od nośnika fizycznego i odległości między nadajnikiem a
odbiornikiem. Przy bardzo dużych odległościach wykorzystuje się sygnały modulowane oraz
specjalne metody kodowania i korekcji błędów transmisji. Przyjmując zasięg jako kryterium
podziału interfejsów można więc wyróżnić następujące grupy:
1.
interfejsy o małym zasięgu (kasetowe) - do 1 metra,
2.
interfejsy o średnim zasięgu (przyrządowe) - do kilkunastu metrów,
3.
interfejsy dużego zasięgu (lokalne sieci komputerowe) - do ok. 1km,
4.
interfejsy bardzo dużego zasięgu ( łącza telekomunikacyjne ).
Grupy te przedstawiono na rys.5 na płaszczyźnie zasięg/szybkość. Wspomniane w
poprzednim punkcie mikro-interfejsy można by określić jako interfejsy o bardzo małym
zasięgu.
1,00E-01
1,00E+01
1,00E+03
1,00E+05 [ m ]
1.00E+02
1.00E+04
1.00E+06
1.00E+08
[ bit/sek ]
VME
VXI
FASTBUS
CAMAC
IEEE 802.3 LAN
RS 422
RS 423
IEC 625
RS 232C
PCIB
HPIL
Dominuje transmisja
równoległa
Dominuje transmisja
szeregowa
4
3
2
1
Rys. 5. Położenie różnych systemów interfejsu na płaszczyźnie zasięg/szybkość:
1 - interfejsy kasetowe,
2 - interfejsy przyrządowe,
3 - lokalne sieci komputerowe,
4 - łącza telekomunikacyjne.
Przyjmując rodzaj sygnału w kanale transmisyjnym jako kryterium podziału
interfejsów, można je podzielić na:
* interfejsy typu "off-line"

126
* interfejsy analogowe,
* interfejsy cyfrowe szeregowe,
* interfejsy cyfrowe równoległe,
* interfejsy cyfrowe szeregowo-równoległe.
Najprostszym interfejsem można nazwać interfejs typu "off-line", w którym elementy
systemu nie są połączone bezpośrednio kanałem informacyjnym, a informacja umieszczona
na nośniku stałym (np. kartka papieru z wynikami pomiaru, czy dyskietka) przenoszona jest
między elementami systemu przez operatora lub użytkownika.
Interfejsy analogowe transmitują sygnały analogowe, w których użyteczna informacja
zawarta jest w amplitudzie (napięcia, prądu) lub w czasie (np. czas trwania impulsu, czy czę-
stotliwość sygnału). Transmisja ta najczęściej odbywa się między dwoma elementami
systemu (ang. point-to-point). Ponadto, transmisja danych może odbywać się między różnymi
elementami systemu z podziałem czasowym lub częstotliwościowym.
Transmisja z podziałem czasowym pozwala każdemu nadawcy zajmować kanał trans-
misyjny na ściśle określony czas w regularnych sekwencjach czasowych. Analogowe
interfejsy nie wykorzystujące przedstawionej wyżej możliwości przekazywania jednym
kanałem informacji od różnych nadawców wymagają na ogół znacznej ilości kabli
transmisyjnych (przewodów); np. w instalacjach chemicznych długość przewodów sięga
kilometrów, w samolotach waga miedzianych kabli staje się znacząca. W tych przypadkach
zwielokrotnienie kanałów transmisyjnych w torze transmisyjnym jest trudne z powodu
rozproszonego umiejscowienia wszystkich
nadawców informacji. Również koszt
dodatkowych modulatorów i demodulatorów, które odpowiednio przetwarzają sygnały
pomiarowe, może nie uzasadniać konieczności ich użycia.
Analogowe interfejsy zwykle realizują tylko kilka wybranych funkcji interfejsu.
Funkcja konwersji dostosowuje oryginalny sygnał pomiarowy (np. ciśnienie, temperatura) do
postaci standardowej, jaką najczęściej jest znormalizowany sygnał napięciowy lub prądowy.
Transmisja z podziałem częstotliwościowym wymaga modulatorów. Przy transmisji z
podziałem czasowym konieczna jest synchronizacja między odpowiednimi przełącznikami u
nadawców i odbiorców sygnałów.
Ze względu na trudności związane z łączeniem analogowych interfejsów w sieci, panuje
obecnie tendencja do zamiany sygnału analogowego na cyfrowy przy samym źródle sygnału
pomiarowego, tzn. bezpośrednio przy czujniku pomiarowym, aby możliwa była transmisja
cyfrowego sygnału poprzez interfejsy cyfrowe.

127
Interfejsy cyfrowe wykorzystują kodowane, binarne sygnały. Cyfrowe interfejsy szere-
gowe transmitują dane kodowane bit po bicie (jak np. w telegrafach czy teleksach).
Powszechnie wykorzystywany jest szeregowy interfejs RS-232 do komunikacji między
komputerem a urządzeniami peryferyjnymi. Interfejsy szeregowe stosowane są również w
systemach pomiarowych, a szczególnie w systemach o przetwarzaniu rozproszonym.
Wymagają one tylko 2 przewodów do sprzęgania urządzeń w system, co znacznie zmniejsza
koszt realizacji takiego systemu. Są wyjątkowo odpowiednie do transmisji cyfrowych danych
z czujników pomiarowych. Liczba czujników w systemie może być znaczna, a ponadto mogą
one być szeroko rozłożone terytorialnie, co pociąga za sobą konieczność prowadzenia długich
kabli. W takiej sytuacji im mniej liczna jest magistrala systemu, tym mniejszy jest koszt
systemu. Inne wykorzystanie interfejsu szeregowego, w mieszanej analogowo-cyfrowej
postaci, to zamiana sygnału napięciowego z czujnika na ekwiwalentną postać
częstotliwościową (przetwornik napięciowo-częstotliwościowy) i wysłanie tego binarnego ale
nie kodowanego sygnału poprzez dwuprzewodowy interfejs. Dla zwiększenia szybkości
transmisji danych możliwe jest wykorzystanie współosiowego kabla koncentrycznego. W
środowisku narażonym na silne zakłócenia elektryczne wskazane jest użycie kabli
światłowodowych. W miejsce przewodów może być zastosowane radiowe połączenie jako
forma kanału transmisyjnego - np. w komunikacji poprzez satelitę.
Cyfrowe interfejsy równoległe transmitują bity słowa równolegle, stąd konieczność
zwielokrotnienia linii sygnałowych w interfejsie. Wymagana jest oddzielna linia na każdy bit
słowa danych, a ponadto dodatkowe linie na synchronizację i specjalne funkcje, jak
adresowanie. Wszystkie te informacje transmitowane są jednocześnie (łącznie, w jednej
chwili). Prowadzi to do znacznej rozbudowy magistrali systemowej i w konsekwencji kable
interfejsu osiągają sporą grubość. W systemach pomiarowych interfejsy równoległe są
najczęściej stosowane w systemach modułowych, gdzie odległości między modułami
umieszczonymi w zwartej kasecie są bardzo małe, a zatem łączna długość przewodów
magistrali jest niewielka mimo znacznej liczby linii w magistrali. Cyfrowe interfejsy
równoległe stosowane są w systemach wymagających znacznej szybkości działania (np.
CAMAC, VME).
Pewną odmianą interfejsów równoległych są interfejsy szeregowo-równoległe, w któ-
rych pojedyncze znaki (np. cyfry, litery, adresy, rozkazy) przesyłane są znak po znaku (czyli
szeregowo), a bity danego znaku - równocześnie (czyli równolegle). Przykładem takiego in-
terfejsu jest IEC-625.
128
Magistrala systemu interfejsu jest drogą komunikacyjną między jednostkami systemu,
która stanowi jedną lub wiele linii sygnałowych systemu interfejsu, wykorzystywaną do prze-
kazywania komunikatów. Zwykle magistrala składa się ze zbioru szyn. Szyną magistrali na-
zwiemy podzbiór linii magistrali służących do przesyłania określonego rodzaju informacji,
(np. danych). W najprostszym przypadku szyna może składać się z jednej linii; wówczas na
ogół nazywamy ją linią interfejsu. Czasami szyny zwane są również magistralami, jednakże
celowe jest operowanie pojęciem szyny dla zaznaczenia niższego poziomu organizacyjnego
szyny w stosunku do magistrali. Szyna może być jednokierunkowa lub dwukierunkowa.
Szyną jednokierunkową informacje przesyłane są zawsze w jednym kierunku, (np. od
kontrolera do jednostki systemu). Szyną dwukierunkową mogą być przesyłane informacje w
obu kierunkach, przy czym o aktualnym kierunku transmisji decyduje na ogół kontroler
systemu.
Strukturę ogólną magistrali przedstawiono na rys.6. Magistrala może zawierać nastę-
pujące typy szyn danych:
- szyny równoległe,
- szyny gwiazdowe,
- szyny lokalne.
JF
JF
JF
JF
JF
KT
Rys. 6. Struktura ogólna magistrali
- szyna równoległa
- szyna gwiazdowa
- szyna lokalna
Szyna równoległa jest to grupa linii sygnałowych w układzie liniowym (inaczej: magi-
stralowym, równoległym). Każda z jednostek systemu połączona jest bezpośrednio ze wszyst-
kimi liniami szyny równoległej.
Szyna gwiazdowa jest to grupa linii sygnałowych w układzie gwiazdy z jednostką cen-
tralną (np. kontrolerem) jako "jądrem" szyny. Każda jednostka systemu połączona jest z

129
grupą linii (lub z jedną linią) szyny gwiazdowej, przy czym zbiory linii dołączonych do
poszczególnych jednostek są rozłączne.
Szyna lokalna jest to grupa linii sygnałowych łączących tylko dwie sąsiednie jednostki
systemu.
Poszczególne standardy interfejsów mogą być wyposażone we wszystkie powyższe typy szyn
lub w ich podzbiór. W magistrali mogą występować następujące główne grupy szyn:
•
szyny danych,
•
szyny adresowe,
•
szyny rozkazów,
•
szyny zarządzania (sterowania),
•
szyny zasilania.
Szyna danych służy do przesyłania: tekstów programujących pracę jednostek systemu,
wyników pomiarów lub słów stanu jednostek (np. bajtu statusu urządzenia). Liczba linii w
szynie danych od 1 (przy transmisji szeregowej) do wielokrotności 8 bitów (najczęściej 8, 16,
24, 32, bity).
Szyna adresowa wykorzystywana jest przez kontroler systemu do tworzenia
konfiguracji jednostek w celu przeprowadzenia transmisji danych. Konfiguracja ta
realizowana jest poprzez adresowanie jednostek do nadawania lub odbioru, inaczej mówiąc
poprzez wysyłanie adresów. Adresem nazwiemy cechę identyfikującą jednostkę funkcjonalną
systemu (całe urządzenie lub jego część). Nadajnikiem jest urządzenie lub jego część
(jednostka funkcjonalna), które wysyła na magistralę interfejsu komunikaty urządzenia.
Odbiorcą jest urządzenie (lub jego część), które odbiera komunikaty urządzeń przesyłane
magistralą interfejsową. Szyna adresowa może być typu równoległego lub gwiazdowego. W
pierwszym przypadku adresem jednostki jest słowo (czasem 2 słowa) wielo-liniowe (dla
każdej jednostki inne). Adresowanie polega na wysłaniu adresu na magistralę. Wszystkie
jednostki dołączone do magistrali odczytują adres. Do stanu zaadresowania przechodzi ta,
która identyfikuje się z tym adresem, tzn. stwierdzi zgodność adresu ustawionego na
magistrali z adresem przyporządkowanym jej przez operatora przed uruchomieniem systemu.
W drugim przypadku, każda jednostka ma swoją indywidualną linię adresową dołączoną do
kontrolera systemu. Adresowanie polega na ustawieniu przez kontroler stanu aktywnego na
linii odpowiadającej danej jednostce.
Szyna rozkazów służy do przesyłania komunikatów jedno- lub wielo-liniowych (tzw.
rozkazów) służących do zarządzania systemem interfejsu (komunikaty interfejsu) lub do wy-
wołania konkretnego zachowania się jednostki, do której dany komunikat został wysłany (ko-

130
munikat urządzenia). Rozkazy można podzielić na uniwersalne (wykonywane przez
wszystkie jednostki niezależnie od stanu zaadresowania) i adresowane (wykonywane tylko
przez te jednostki, które zostały odpowiednio zaadresowane do odbioru).
Szyny zarządzania służą do zapewnienia odpowiedniej koordynacji działania
wszystkich jednostek funkcjonalnych systemu. W systemie pomiarowym istnieje wielka
różnorodność szyn zarządzania. Mogą być one typu magistralowego (najczęściej) lub
gwiazdowego, ponadto jedno- lub wielo-liniowe. Wśród nich można wymienić kilka
najważniejszych. Są to szyny zerowania, synchronizacji, impulsów zegarowych, wyzwalania,
sterowania transmisją (hand-shake), przerwań, arbitrażu. Liczba linii szyn i sposób ich
wykorzystania zależy ściśle od danego standardu interfejsu, dlatego trudno w tym miejscu o
jakiekolwiek ogólne ich omówienie.
Szyny zasilania służą do doprowadzenia napięć zasilających podstawowe i
pomocnicze jednostki systemu. Szyny te są zwykle stosowane w interfejsach systemów
modułowych.
Wszystkie przedstawione wyżej szyny magistrali interfejsu występują w całości lub w
podzbiorach w poszczególnych standardach interfejsów. Ponadto część szyn może być
łączona w jedną szynę multiplikowaną.
4. Oprogramowanie systemów
Klasyczny sposób projektowania systemów pomiarowych polega na samodzielnym
opracowywaniu od podstaw programu sterującego przy wykorzystaniu do tego języków wy-
sokiego poziomu (Basic, Pascal, C), wzbogaconych o zestaw poleceń do komunikacji z kon-
trolerem, umożliwiających w prosty sposób wysyłanie i odbiór informacji od urządzeń.
Stopień trudności i przejrzystość pisanego programu zależą od tego, na jakim poziomie są
dostępne dla programisty instrukcje kontrolera i jak są one udokumentowane. Podobnie jest z
tekstami programującymi przyrządy pomiarowe. Konkretna realizacja zależy zatem od
użytego kontrolera i przyrządów.
Dużym krokiem na drodze do ujednolicenia i uproszczenia procesu projektowania
oraz uruchamiania systemów pomiarowych, było ustalenie przez największych światowych
producentów aparatury pomiarowej, przemysłowego standardu, określającego metody
programowania przyrządów pomiarowych. W ten sposób powstał standard instrukcji
programujących pracę przyrządów pomiarowych o nazwie SCPI (ang. Standard Commands
for Programmable Instruments). Definiuje on zestaw instrukcji, które niezależnie od
producenta, czy modelu przyrządu, pozwalają na pełne zaprogramowanie jego pracy,

131
uzależniając sposób programowania jedynie od realizowanego zadania pomiarowego. Ze
względu na to, że SCPI jest standardem instrukcji programujących, jest on niezależny
sprzętowo i może być używany w pracy nie tylko z systemem interfejsu w standardzie IEEE-
488, ale także innymi, jak: RS-232C czy VXI.
Kolejnym krokiem ułatwiającym projektowanie oprogramowania systemów pomiaro-
wych było powstanie tzw. zintegrowanych środowisk programowych, zawierających silne
mechanizmy wspomagania projektowania.
Znaczna moc obliczeniowa powszechnie dostępnych i stosunkowo tanich komputerów
typu IBM PC umożliwiła w ostatnich latach opracowanie bardzo rozbudowanych środowisk
programowych do komputerowego wspomagania projektowania systemów pomiarowych (np.
LabView, LabWindows, HP-VEE, HP-ITG, LabTech), radykalnie zmieniających podejście
do procesu projektowania systemów. Środowiska te posiadają bardzo silne mechanizmy
wspomagania projektowania z wykorzystaniem potężnie rozbudowanego graficznego
interfejsu z użytkownikiem (grafika "pomiarowa"). Podstawowe cechy tych środowisk są
następujące:
•
interakcyjność programu tworzenia oprogramowania użytkowego,
•
możliwość tworzenia na ekranie i wkomponowywania w oprogramowanie paneli sterują-
cych sprzętem pomiarowym (łącznie z panelami przyrządów "wirtualnych"),
•
możliwość generowania programu przez wywoływanie paneli funkcyjnych (np.
LabWindows) lub przez rysowanie schematu blokowego kodującego algorytm działania sys-
temu pomiarowego w postaci graficznej (np. LabTech, HP-VEE)
•
bogate biblioteki (m.in. sterowników przyrządów, dostępu do interfejsów pomiarowych,
analiz sygnałów pomiarowych),
Przedstawione własności środowisk programowych wyznaczają kierunek rozwoju kom-
puterowego wspomagania działań projektowych przy automatyzacji pomiarów.
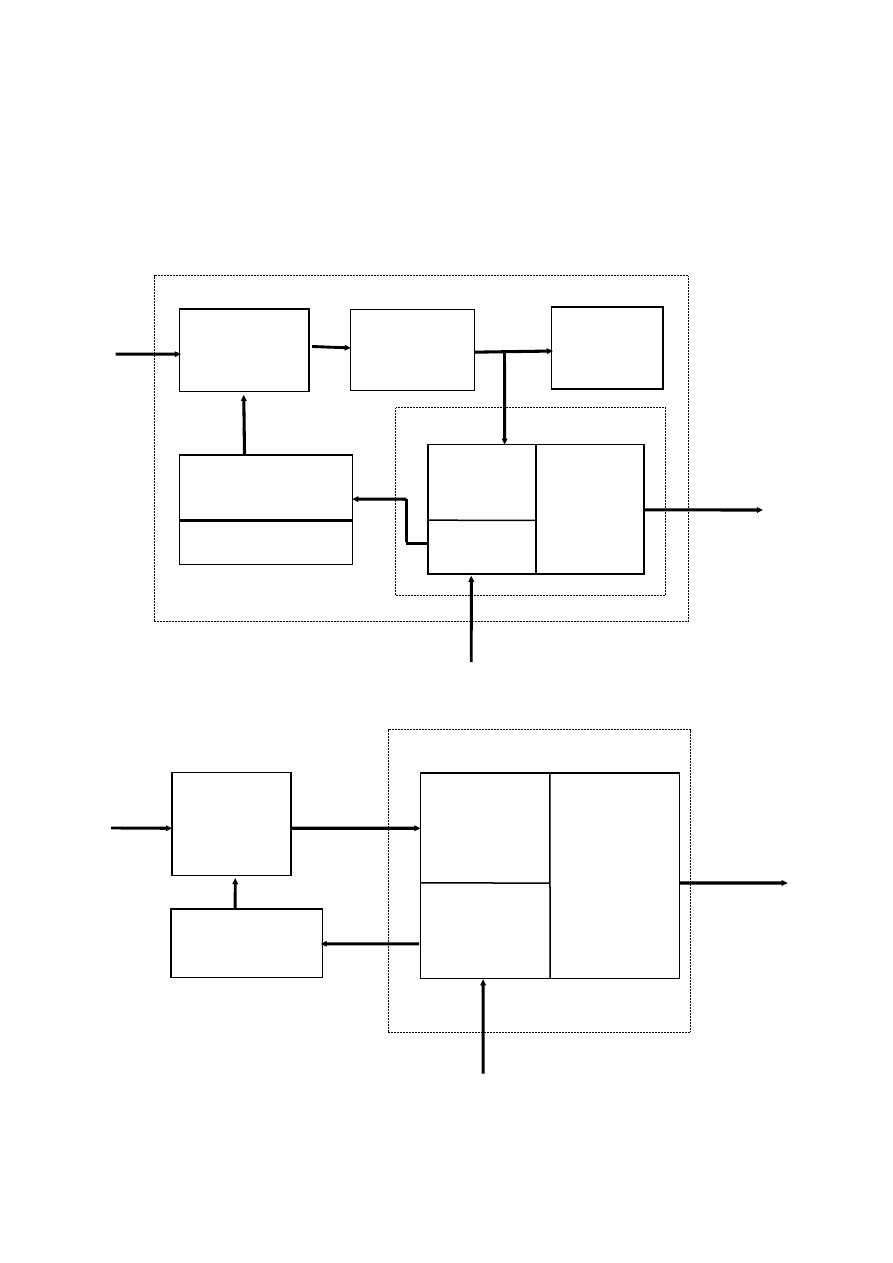
132
5. Przyrządy wirtualne
Przyrządy wirtualne stanowią kombinację odpowiednio oprogramowanego komputera
ogólnego przeznaczenia z przyrządami systemowymi lub urządzeniami pomiarowymi nowej
generacji (np. karty typu „plug-in”). Strukturę dwóch typów wirtualnych przyrządów pomia-
rowych przedstawiono w uproszczeniu na rys.7 i rys.8.
PC
Rys. 7. Struktura wirtualnego przyrządu pomiarowego wykorzystującego autonomiczny przyrząd pomia-
rowy (pominięto bloki interfejsów)
Rys. 8. Struktura wirtualnego przyrządu wykorzystującego bloki zbierania danych pomiarowych (pomi-
nięto bloki interfejsów)
PC
BLOK
PRZETWARZANIA
A/C
BLOK STEROWANIA
PRZETWARZANIE
C/C
STEROWANIE
GRAFICZNY
INTERFEJS
U
ś
YTKOWNIKA
( GUI )
OPERATOR
OBSERWATO
R
I/LUB
OPERATOR
OBSERWATOR
I/LUB
OPERATOR
PRZETWARZANIE
C/C
STEROWANIE
GRAFICZNY
INTERFEJS
U
ś
YTKOWNIKA
(GUI)
BLOK
PRZETWARZANIA
A/C
BLOK
WIZUALIZACJI
BLOK
STEROWANIA
NASTAWNIKI
OPERATOR
BLOK
PRZETWARZANIA
C/C

133
Przyrząd wirtualny można określić jako przyrząd składający się z komputera ogólnego
przeznaczenia i dołączonych do niego sprzętowych bloków funkcjonalnych (wewnętrznych
i/lub zewnętrznych), którego funkcje i możliwości określone są przez zarówno przez sprzęt,
jak i oprogramowanie, a obsługa odbywa się za pomocą ekranu komputerowego, klawiatury
i/lub myszy z wykorzystaniem graficznego interfejsu użytkownika.
Każdy z bloków sprzętowych - takich jak: pakiety zbierania danych, moduły VXI,
przyrządy IEC-625, i in. - jest dołączony do komputera albo jako karta typu „plug-in” wsta-
wiona bezpośrednio do komputera, albo jako urządzenie zewnętrzne poprzez interfejs. Przy-
rząd wirtualny może być projektowany i budowany zarówno przez producenta firmowego, jak
i przez użytkownika, który definiuje jego przeznaczenie i funkcje konstruując odpowiednie
oprogramowanie. Oprogramowanie to integruje komputer i pomiarowe bloki sprzętowe two-
rząc z nich przyrząd; jest ono zatem integralną częścią przyrządu wirtualnego.
W typowym torze pomiarowym można wyróżnić 3 główne elementy funkcjonalne:
- blok zbierania danych pomiarowych,
- blok analizy i przetwarzania danych pomiarowych,
- blok interfejsu użytkownika (sterowanie przyrządem i prezentacja wyników).
Wszystkie te elementy musi zawierać przyrząd pomiarowy, w tym również wirtualny, ale
realizacja techniczna poszczególnych funkcji może być różna, zależnie od typu przyrządu.
Cechą wirtualnego przyrządu pomiarowego jest jego otwarta architektura. Otwartość archi-
tektury oznacza m.in. dostęp do magistrali interfejsu łączącego komputer z częścią sprzętową.
W przypadku sprzętowych bloków funkcjonalnych wewnętrznych magistralą tą jest
magistrala mikroprocesorowa komputera, a w przypadku bloków zewnętrznych - najczęściej
magistrala jednego ze standardowych interfejsów pomiarowych (IEC-625, VXI, RS-232, RS-
485). Inną istotną cechą przyrządu wirtualnego jest funkcjonalna elastyczność i
rekonfigurowalność; oznacza to, że jeden sprzętowy blok funkcjonalny (lub ich zbiór)
umożliwia stworzenie szerokiego zbioru różnych przyrządów wirtualnych realizujących
bardzo różnorodne funkcje. Redukcja części sprzętowej przyrządu wirtualnego zarówno
zmniejszyła jego koszt, jak i skróciła czas jego opracowania i dalszych modyfikacji.
Projektowanie przyrządów wirtualnych wiąże się ze stworzeniem odpowiedniego
oprogramowania w komputerze ogólnego przeznaczenia. Strukturę oprogramowania tych
przyrządów można przedstawić symbolicznie jak na rys.9.
134
Sterowniki cz
ęś
ci sprz
ę
towej
Program obsługi panelu graficznego
IEC-625
VXI
komputera
szyna
RS-232
Panel graficzny przyrz
ą
du
Pomiary
Analiza
Prezentacja
S t e r o w n i k i i n t e r f e j s ó w
komputera
szyna
do cz
ęś
ci sprz
ę
towej
Rys. 9. Struktura oprogramowania wirtualnego przyrządu pomiarowego
Panel graficzny odwzorowuje na ekranie komputera płytę czołową przyrządu wirtual-
nego. Panel ten zawiera zbiór symboli graficznych, służących do obsługi przyrządu, takich
jak: przełączniki, pola znakowe lub numeryczne, wskaźniki, pola wykresów i inne.
Sterownik części sprzętowej (sterownik przyrządu) odwzorowuje funkcje przyrządu.
Stanowi go zbiór funkcji wykorzystywanych przy komunikacji z przyrządem (takich jak: pro-
gramowanie nastaw, wyzwalanie pomiaru, odbiór wyników, wyświetlanie wyników itp.).
Sterowniki interfejsów zawierają programy obsługi magistral interfejsów standardo-
wych (np. IEC-625, VXI, RS-232) lub/i niestandardowych (np. szyna komputera do której
dołączony jest pakiet akwizycji danych). Sterowniki interfejsów wykorzystywane są przez
sterowniki części sprzętowej, a te z kolei - przez program obsługi panelu graficznego.
Koncepcja projektowania oprogramowania przyrządu wirtualnego różni się od
koncepcji klasycznego projektowania oprogramowania. Koncepcja ta wykorzystuje
obiektowe podejście do programowania, tj. podejście pozwalające na budowę systemu
oprogramowania jako otwartego zbioru obiektów programowych wielokrotnego użycia.
Obiekty te reprezentują zarówno fizyczne bloki funkcjonalne, jak i procedury pomiarowe,
procedury przetwarzania danych oraz elementy graficznego interfejsu użytkownika.
Wszystkie te obiekty programowe mogą być reprezentowane w komputerze przez
odpowiednie symbole graficzne lub tekstowe.
Tworząc panel przyrządu wirtualnego operujemy obiektami przedstawionymi w formie gra-
ficznej (tzn. obiektami graficznymi) rozmieszczanymi na ekranie komputera i obsługiwanymi
za pomocą myszy. Struktura programu obsługi panelu jest zasadniczo różna od klasycznej.

135
Każde kliknięcie myszą na danym obiekcie graficznym powoduje powstanie tzw. zdarzenia.
Oprogramowanie obsługi panelu jest zatem zbiorem obsługi tych zdarzeń.
Narzędzia do projektowania przyrządów wirtualnych można podzielić na: podstawowe
(klasyczne języki wysokiego poziomu jak Basic, Pascal, C lub języki typu Visual Basic) i za-
awansowane
(zintegrowane
ś
rodowiska
programowe).
Obecnie
powszechnie
wykorzystywane są narzędzia zaawansowane. Integrują one funkcje sterowania pracą
systemu, gromadzenia i przetwarzania danych pomiarowych oraz prezentacji wyników, a
także oferują języki programowania wyższego rzędu (w tym graficzne), edytor, uruchamiacz
(ang. debugger) i rozbudowane mechanizmy wspomagające - upraszczające obsługę aparatury
pomiarowej i ułatwiające pisanie własnych programów sterujących pracą całego systemu
(koncepcja przyjazności dla użytkownika - user friendly). Takie specjalizowane pakiety
programowe
można
nazwać
zintegrowanymi
ś
rodowiskami
programowymi.
Najpopularniejszymi przedstawicielami powyższej idei są produkty firm: National
Instruments (LabWindows
®
for DOS, LabWindows
®
/CVI, LabView
®
), Hewlett-Packard
(HP VEE
®
), Keithley (TestPoint
®
). Środowiska te wykorzystują koncepcję programowania z
wykorzystaniem obiektów programowych. Projektowanie zarówno paneli jak i programów
ich obsługi realizowane jest tu poprzez wybór z bogatego menu tekstowego lub graficznego
odpowiednich opcji, a z nich - wymaganych funkcji lub symboli graficznych. Projektowanie
oprogramowania możliwe jest z wykorzystaniem klasycznych języków programowania (np. C
lub Basic) albo języków graficznych. Pierwszą możliwość zapewnia m.in. środowisko
LabWindows/CVI, drugą - m.in. LabView i HP VEE.
Ogólny sposób postępowania przy projektowaniu przyrządu wirtualnego z wykorzystaniem
zintegrowanych środowisk programowych polega na:
•
określeniu funkcji i parametrów przyrządu wirtualnego;
•
doborze części sprzętowej;
•
analizie sterownika części sprzętowej lub zaprojektowaniu własnego sterownika;
•
zaprojektowaniu panelu graficznego
-
przez wybór rodzajów obiektów graficznych (przełączniki, wyświetlacze, itp.);
-
przez wybór dla każdego z rodzajów obiektów konkretnego reprezentanta;
-
przez rozmieszczenie obiektów na panelu;
-
przez ustalenie wymiarów obiektów;
-
przez ustalenie kolorów obiektów, koloru tła, kroju liter, itp.;
•
zaprojektowaniu oprogramowania przyrządu wirtualnego
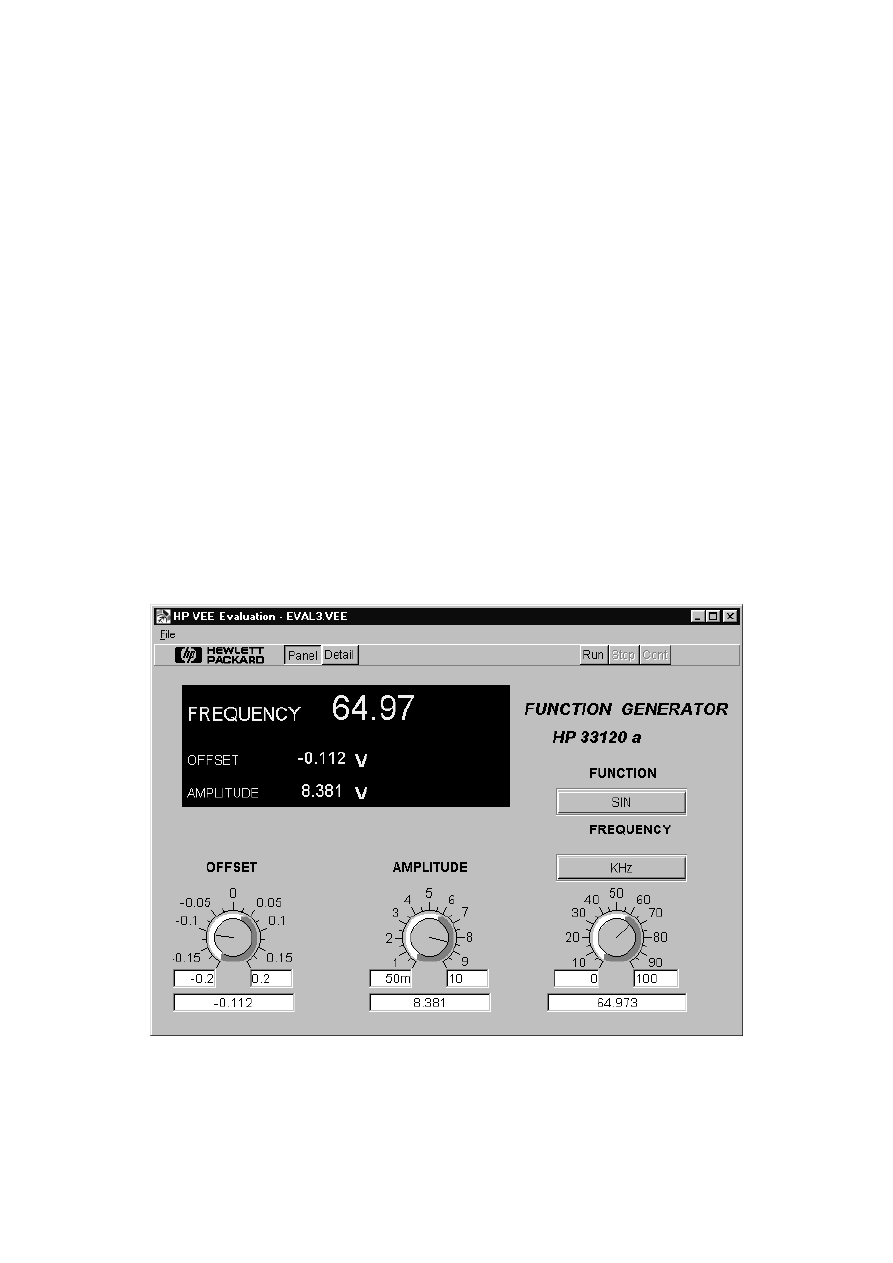
136
-
przez zbudowanie osnowy programu obsługi (zależnie od środowiska - graficznego lub
tekstowego),
-
przez uzupełnienie osnowy o procedury obsługi zdarzeń (graficzne - poprzez wybór ikon
z menu i połączenie ich „nitką”; lub tekstowe - poprzez wybór konkretnych funkcji z
menu i wstawienie automatycznie budowanych linii do odpowiednich miejsc osnowy
programu);
•
uruchomieniu oprogramowania.
Szczegółowy algorytm projektowania zależy od konkretnego zintegrowanego środowiska
programowego użytego przy projektowaniu. Na przykład w środowisku HP VEE projekt pa-
nelu poprzedzony jest zaprojektowaniem schematu blokowego przyrządu (w postaci graficz-
nej), pełniącego funkcję oprogramowania przyrządu - czyli etap projektowania oprogramowa-
nia występuje tu przed etapem projektowania panelu. Panel czołowy tworzony jest tu na pod-
stawie schematu blokowego. Na panelu tym mogą znajdować się tylko te obiekty, które wy-
stępują na schemacie blokowym. Przykłady rozwiązania projektu panelu pokazano na rys.10 i
rys.11.
kHz
Rys. 10. Przykład panelu graficznego wirtualnego generatora funkcji
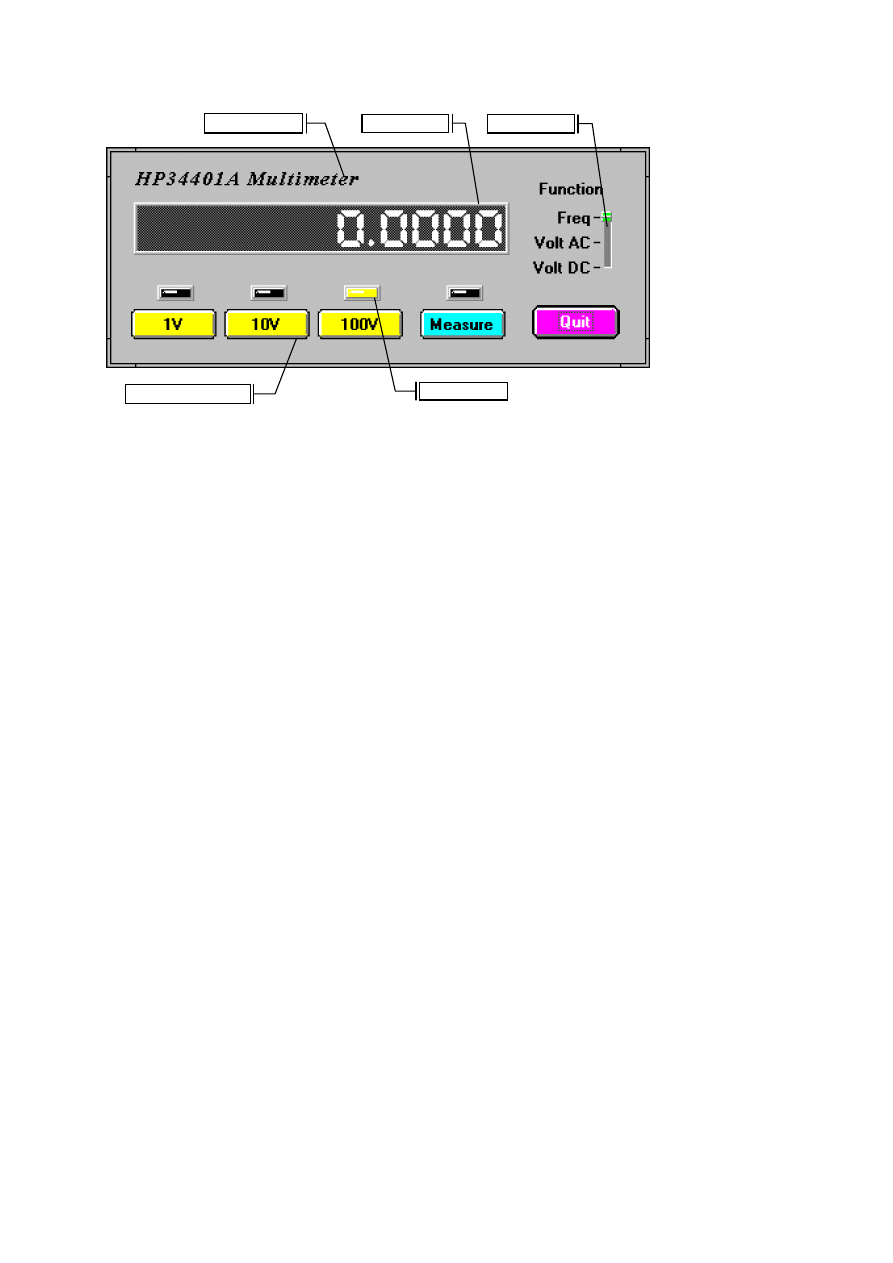
137
Numeric
Text Message
Ring
Command Button
LED
Rys. 11. Przykład panelu graficznego wirtualnego multimetru
Jedną z cech przyrządów wirtualnych jest możliwość ich projektowania bezpośrednio
przez użytkownika. Jednak coraz więcej firm oferuje gotowe przyrządy wirtualne, które naj-
częściej składają się z karty pomiarowej umieszczanej w komputerze lub w kasecie
pomiarowej oraz odpowiedniego oprogramowania. Coraz częściej pojawiają się również
przykłady rozwiązań przyrządów wirtualnych zawierających w panelu graficznym zarówno
część pomiarową jak i generacyjną. Część generacyjna może zawierać wyjście analogowe
i/lub cyfrowe. Przykładem mogą tu być przyrządy wirtualne firmy National Instruments,
prezentowane pod nazwą DAQInstruments. Jest to zestaw kilku kart: multimetru (5
1
/
2
cyfry),
generatora sygnałowego (16 MHz, rozdzielczość 12 bitów), oscyloskopu (pasmo 15 MHz ,
rozdzielczość 8 bitów), analizatora widma (dwu- lub cztero-kanałowy, pasmo 95 kHz),
uzupełnionych o odpowiednie oprogramowanie.

138
Wykład 13 i 14
Technika mierzenia
Przegląd zasad techniki mierzenia. Pisanie raportu. Przykład pełnego cyklu procesu pomia-
rowego: przygotowanie, wykonanie i opracowanie wyników.
1. Ogólne zasady mierzenia
Wychodząc z koncepcji pomiaru traktowanego jako identyfikacja parametryczna
(patrz wykład 2) można skonstruować ogólny model pomiaru (rys.1) oraz ogólny schemat
organizacji pomiaru (rys.2). Model obiektu opisuje jego zachowanie i właściwości tylko w
przybliżeniu - zaznaczono to graficznie na rys.1. Spowodowane to jest dwoma przyczynami:
niedokładnością wyznaczenia parametrów modelu oraz nieadekwatnością struktury modelu.
Aby wykonać pomiar należy:
1) przyjąć model obiektu i ustalić mezurandy (często model może być dany a priori);
2) przyjąć równanie modelu (relacja między pobudzeniem i odpowiedzią obiektu);
3) zaprojektować i zrealizować procedury generacji pobudzeń i odbierania oraz przetwarzania
sygnałów w systemie pomiarowym, prowadzące do wyznaczenia mezurandów.
Zarówno przyjęta koncepcja pomiaru jak i praktyka współczesnych pomiarów pocią-
gają za sobą konieczność uwzględniania w procesie pomiaru weryfikacji wyników (tj. weryfi-
kacji procedur odbierania i przetwarzania sygnałów pomiarowych), weryfikacji przyjętych
równań modelu oraz weryfikacji struktury modelu. Potrzeba weryfikacji wynika z błędów in-
strumentalnych wnoszonych przez system pomiarowy oraz z błędów jakimi może być obar-
czone równanie modelu, a także z błędów wynikających z przyjęcia niewłaściwej struktury
modelu. Wymienione tu przyczyny weryfikacji wymagają, by wykonywaniu pomiaru
towarzyszył proces o charakterze iteracyjnym, polegający na kolejnej eliminacji czynników
pasożytniczych i niedostatków koncepcyjnych. W procesie tym bardzo pomocne jest -
przedstawione w materiale wykładu 2 - pojęcie modelu rozszerzonego.
Projektowanie pomiaru powinno być poprzedzone próbą odpowiedzi na elementarne
pytania:
- Czego poszukuję? Jaka jest moja hipoteza?
- Jak dokładna powinna być odpowiedź?
- Jakie prawa fizyki dotyczą obiektu lub wielkości, które są badane?
- Jakie wielkości zmienne powinny być poddane sterowaniu lub stabilizacji?
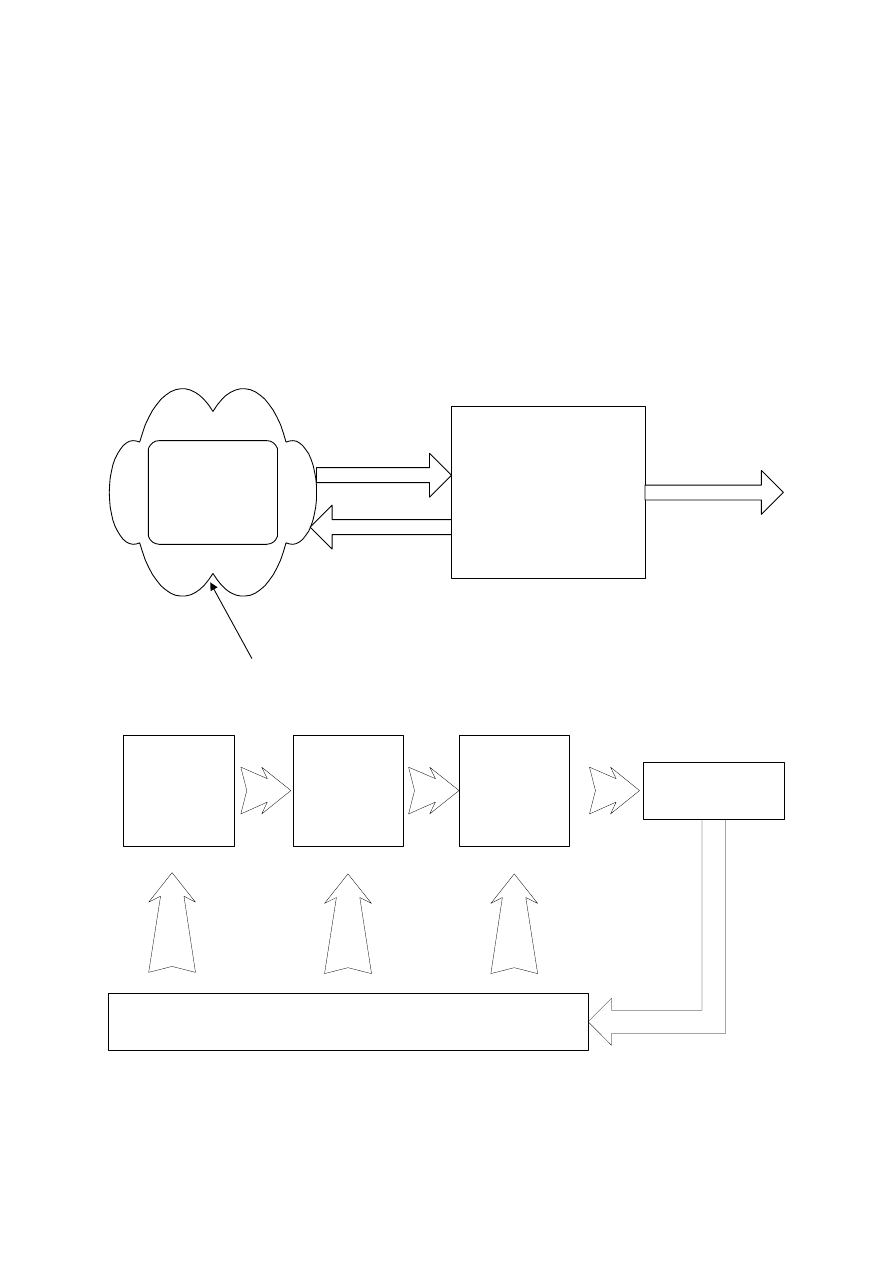
139
- Jakie wielkości powinny być mierzone? Jak dokładnie?
- Jakie środki techniczne (narzędzia) powinny być zastosowane?
- Ile informacji (danych) należy zgromadzić?
- Jakie procedury przetwarzania i analizy danych należy uruchomić?
- Jaką postać powinien przyjąć raport z przeprowadzonych pomiarów?
- Jakie są najskuteczniejsze sposoby prezentacji wyników?
- Czy postawione wymagania dadzą się zrealizować w granicach dostępnego budżetu i czasu?
Jest to - bez wątpliwości - lista pytań niekompletna, ale trudno mówić o sukcesie w
pomiarach bez ich postawienia.
SYSTEM
POMIAROWY
Cloud
MODEL
OBIEKTU
OBIEKT MIERZONY
pobudzenia
odpowiedzi
mezurandy
Rys.1. Ogólny model pomiaru
MODEL
OBIEKTU
MEZURANDY
RÓWNANIA
MODELU
SYSTEM
GENERACJI
POBUDZE
Ń
i
PRZETWARZANIA
SYGNAŁÓW
WERYFIKACJA
Rys.2. Ogólny schemat organizacji pomiaru

140
2. Pisanie raportu
Schemat raportu z pomiarów jest podobny do typowego schematu sprawozdania z
pracy naukowej, a jego podstawowe części, to
- Wstęp
- Metoda pomiarowa
- Wyniki
- Omówienie wyników, wnioski
- Literatura
We wstępie należy podać podstawowy cel pomiarów, a także sformułować hipotezę,
którą otrzymane wyniki potwierdzają lub podważają.
Opis metody pomiarowej powinien zawierać niezbędne schematy ilustrujące podsta-
wowe operacje przetwarzania sygnałów stosowane w przeprowadzonych pomiarach. Powinna
im towarzyszyć analiza błędów oraz uwagi dotyczące warunków otoczenia, czynników zakłó-
cających, zjawisk pasożytniczych itd., itp.
Wyniki należy podać bezbłędnie i wiernie, co nie oznacza jednak, że należy
przedstawić wszystkie otrzymane wyniki. Stosunkowo częstym niedociągnięciem jest
przepisywanie wszystkich wyników wprost z zapisów roboczych. Zapisy te należy
uporządkować i przedstawić je w formie tabel, wykresów lub diagramów. Końcowej
prezentacji wyników należy nadać taką formę, która w omówieniu wyników umożliwi
poparcie lub odrzucenie sprawdzanej hipotezy. Tabele, wykresy i diagramy powinny być
opisane szczegółowo i jednoznacznie, a także stanowić zamkniętą całość. Powinny
uzupełniać tekst omówienia wyników, a nie go zastępować.
W omówieniu wyników zasadniczym problemem jest rozstrzygnięcie, czy fakty po-
twierdzają wysuniętą na wstępie hipotezę. Jeżeli w trakcie pomiarów pojawią się inne warte
uwagi kwestie, należy także je tu omówić. Zestawienie otrzymanych wyników, analiza zareje-
strowanej informacji o warunkach pomiaru i powtórne przyjrzenie się właściwościom
zastosowanej metody pozwala na sformułowanie wniosków końcowych dotyczących
przedmiotu pomiarów oraz wniosków dotyczących metody, narzędzi i warunków pomiaru.
Końcowa postać raportu powinna się charakteryzować czytelnością tekstu oraz starannością
wykonania wykresów i rysunków. Powinna ponadto spełniać wymagania poprawności
językowej (terminologiczne, gramatyczne i stylistyczne). Pozycje literaturowe należy
cytować w taki sam sposób jak to jest przyjęte w publikacjach naukowych. Należy
wystrzegać się nieścisłości i nie mylić numerów odnośników w tekście.
Krótki ogólny przepis na pisanie raportu można przedstawić następująco:
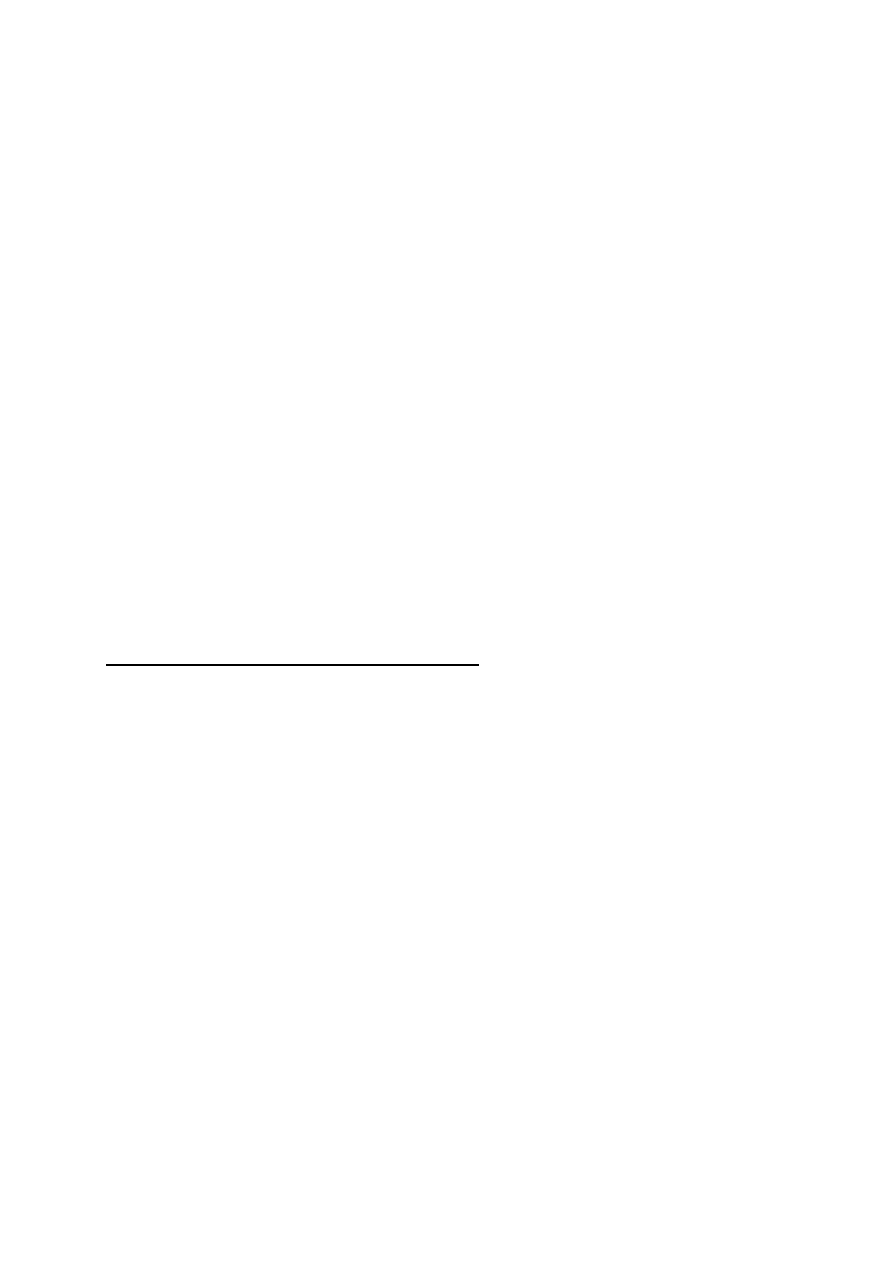
141
1. Zrób pisemny schemat raportu, tak szczegółowo, jak to tylko możliwe.
2. "Zamroź" ten schemat na pewien niezbyt długi czas, zajmując się innymi sprawami.
3. Wróć do schematu raportu i dokonaj zmian, które uznasz za niezbędne.
4. Napisz raport w postaci szkicowej tak szybko jak tylko możesz.
5. Po upływie mniej więcej tygodnia przeprowadź korektę i spróbuj poddać raport krytyce
zewnętrznej (np. kolegów).
6. Po ewentualnym uwzględnieniu uwag przepisz raport w postaci końcowej.
3. Przykład pełnego cyklu procesu pomiarowego
Przyjmijmy, że naszym zadaniem pomiarowym jest wyznaczenie indukcyjności cewki
bez rdzenia ferromagnetycznego w zakresie małych częstotliwości.
Cewki indukcyjne, zwane również induktorami, należą do podstawowych elementów obwo-
dów elektrycznych. Najważniejszym parametrem cewki jest indukcyjność własna. Jednostką
indukcyjności jest 1 henr (1 H = 1
Ω
s). Pojęcie indukcyjności własnej jest wykorzystywane
przy analizie różnych zjawisk fizycznych, np. przy określaniu energii magazynowanej w polu
magnetycznym, czy też przy określaniu impedancji cewki.
Przygotowanie pomiaru - wybór modelu obiektu
Najczęściej stosowanym modelem cewki dla małych częstotliwości, konstruowanym
przy uwzględnieniu strat energii, jest model przedstawiany w postaci dwójnika, złożonego z
połączonych szeregowo: indukcyjności L
s
i rezystancji R
s
(rys.3) - nazwijmy go modelem
podstawowym. Jego impedancja wyraża się wzorem:
Z
R
j L
s
s
s
=
+ ω
(1)
Zależnie od przeznaczenia spotyka się wiele różnych schematów zastępczych. Głównym
dążeniem przy ich tworzeniu jest, by dany model przybliżał możliwie dokładnie impedancję
cewki lub tylko jej indukcyjność w danym paśmie częstotliwości. Praktyka pokazała, że
niemożliwym jest zbudowanie dla cewki modelu uniwersalnego, który z jednakową
dokładnością odtwarzałby parametry w szerokim paśmie częstotliwości.
Zależnie od przyjętych granic błędu oraz celu, dla którego wartość indukcyjności jest
wyznaczana model przedstawiony na rys.3 może okazać się za mało dokładny. Można wtedy
przyjąć model rozszerzony, uwzględniający dodatkowo np. wpływ pojemności między-zwojo-
wych (rys.4). Przyrównując składowe czynną i bierną obu modeli można określić
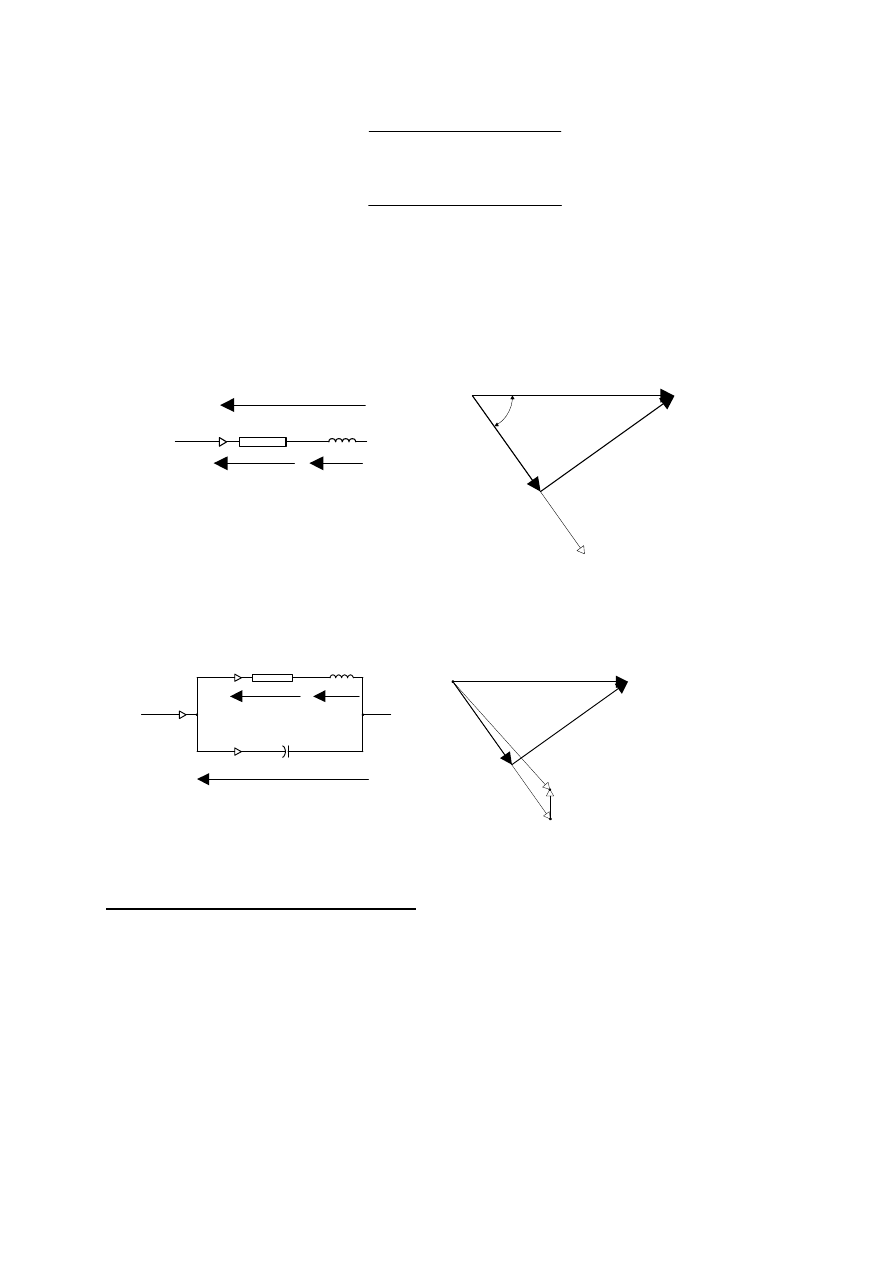
142
(
)
(
)
R
R
L C
R C
s
o
o
o
o
o
=
−
+
1
2
2
2
ω
ω
(2)
(
)
L
L
L C
R C
L C
R C
s
o
o
o
o
o
o
o
o
o
=
−
−
−
+
(
)
(
)
1
1
2
2
2
2
2
ω
ω
ω
(3)
Sposób połączenia elementów L
o
, C
o
i R
o
podyktowany jest tym, że straty w cewkach
bezrdzeniowych powstają głównie w przewodzie miedzianym, którym cewka jest nawinięta,
natomiast pole elektryczne (reprezentowane przez pojemność C
o
) występuje głównie między
zwojami i zaciskami, a więc bocznikuje cewkę.
Rys. 3. Model podstawowy cewki dla małych częstotliwości; a) schemat zastępczy, b) wykres wskazowy
R
o
L
o
C
o
U
R
U
L
U
I
I
L
I
C
a)
b)
U
U
L
U
R
I
I
C
I
L
Rys. 4. Model rozszerzony cewki dla małych częstotliwości; a) schemat zastępczy, b) wykres wskazowy
Przygotowanie pomiaru - wybór metody
Metody pomiaru indukcyjności w paśmie małych częstotliwości stanowią silnie
zróżnicowaną grupę. Zależnie od zakresu pomiaru i od wymaganej dokładności dokonuje się
wyboru metody i przyrządu. Prócz tego przy takim wyborze dużą rolę spełnia cena i
dostępność odpowiedniej aparatury. Ponieważ w licznych laboratoriach do popularnych
przyrządów o największej dostępności należy woltomierz, to naszą próbę pomiaru
indukcyjności podejmiemy nawiązując do tzw. metody trzech woltomierzy, znanej niemal od
R
s
L
s
U
R
U
L
I
U
U
L
a)
b)
I
U
R
U
ϕ
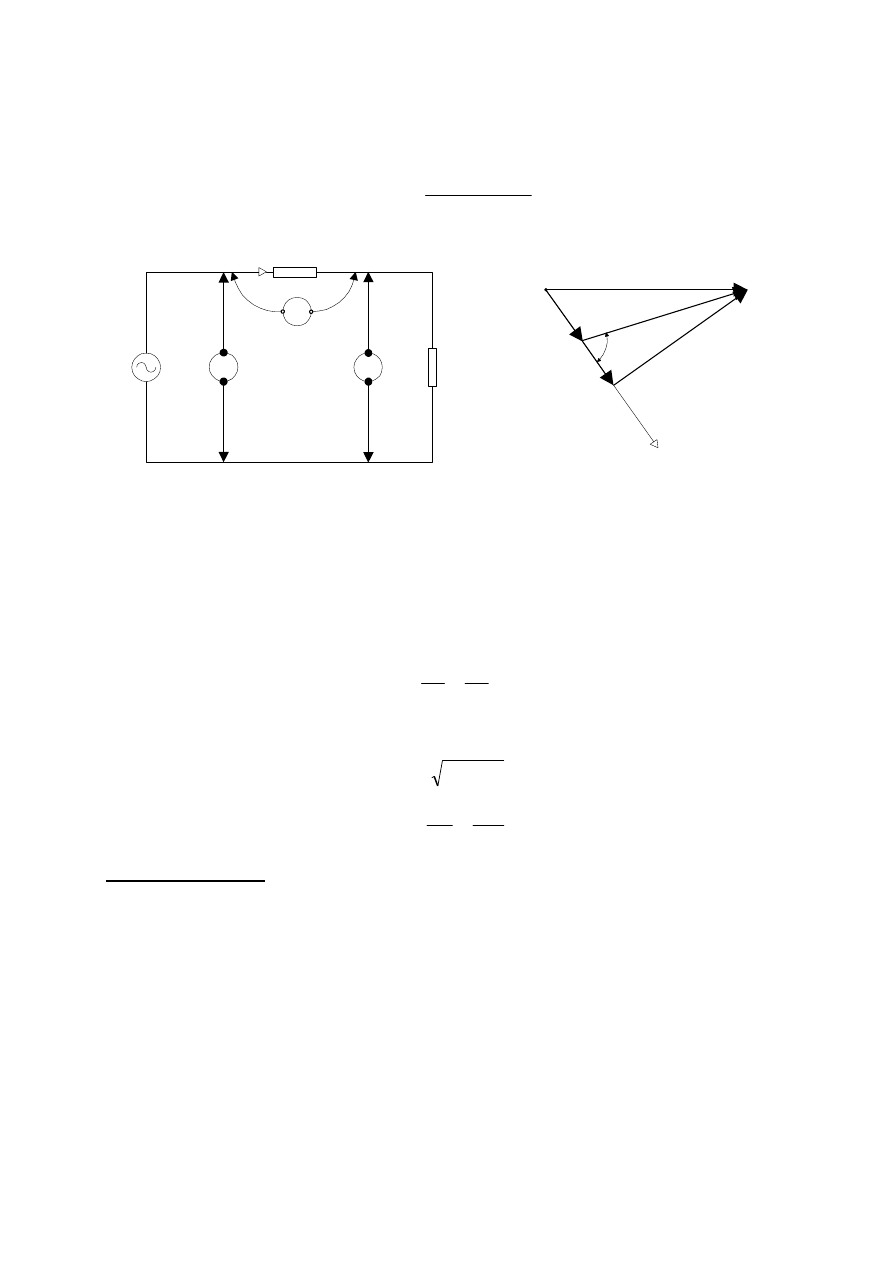
143
początków elektrycznej techniki pomiarowej. Zasadę tej metody ilustrują układ pomiarowy i
wykres wskazowy przedstawione na rys.5. Z wykresu wskazowego znajdujemy:
cos
ϕ
x
U
U
U
U U
=
−
−
1
2
2
2
3
2
2
3
2
(4)
Rys. 5. Metoda trzech woltomierzy przy wyznaczaniu parametrów modelu cewki; a) schemat układu
pomiarowego, b) wykres wskazowy ilustrujący ideę metody
Znając pulsację
ω
= 2
π
f (f -częstotliwość napięcia zasilającego układ pomiarowy), rezystancję
opornika wzorcowego R
w
oraz cos
ϕ
x
można wyznaczyć także impedancję Z
x
, rezystancję R
x
,
reaktancję X
x
oraz indukcyjność L
x
:
Z
U
I
U
U
R
x
w
=
=
3
3
2
(5)
R
Z
x
x
x
=
cos
ϕ
(6)
X
Z
R
x
x
x
=
−
2
2
(7)
L
X
X
f
x
x
x
=
=
ω
π
2
(8)
Wykonanie pomiaru
Mimo nazwy metody sugerującej udział trzech woltomierzy przy pomiarze, wszystkie
trzy napięcia można zmierzyć za pomocą jednego woltomierza. Stosowanie jej jest celowe
jednak tylko wtedy, gdy rezystancja wejściowa woltomierza jest dostatecznie duża w
odniesieniu zarówno do badanej impedancji jak i do rezystancji wzorcowej - wpływ
woltomierza na stan obwodu powinien być pomijalnie mały.
Przy potrzebie prowadzenia pomiarów wielokrotnych metoda ta stosunkowo łatwo
poddaje się automatyzacji przy wykorzystaniu komputera (rys.6). Przyrządy pracujące w sys-
temie, którego jednostką centralną jest np. komputer typu IBM PC, stanowią typowe wyposa-
a)
b)
R
w
V
I
V
V
U
2
U
1
U
3
Z
x
U
1
U
2
I
U
3
ϕ
x
U
Rx
U
Lx
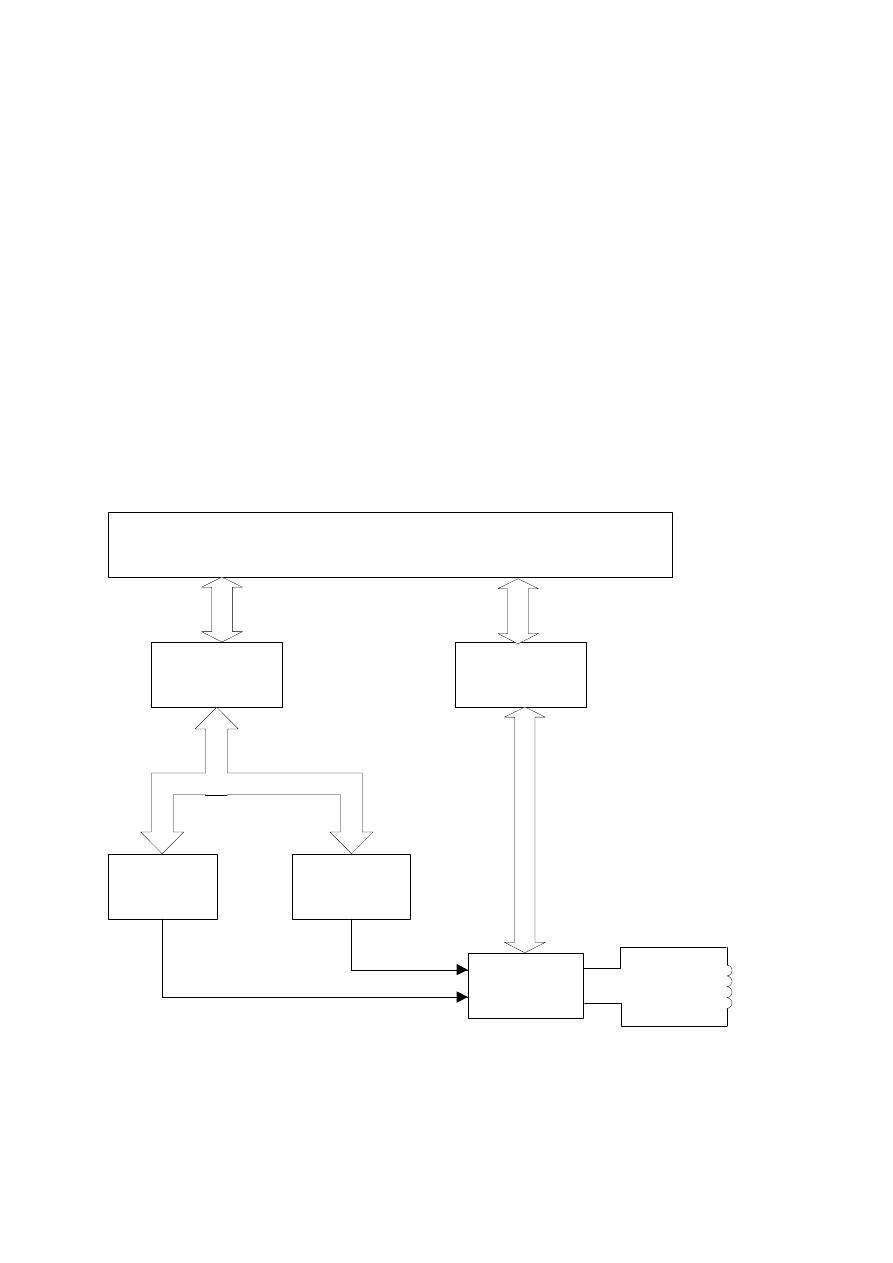
144
żenie laboratoriów naukowych i przemysłowych. Częstotliwość sygnału pomiarowego oraz
jego wartość mogą być ustawiane tak, by parametry badanego elementu były wyznaczane w
warunkach bardzo zbliżonych do jego warunków pracy. Blok 3V na rys.6 jest jedynie zesta-
wem rezystorów wzorcowych i kluczy sterowanych, za pomocą których wybierana jest war-
tość rezystancji R
w
oraz miejsce pomiaru napięcia (rys.7). Sterowanie kluczy w bloku 3V jest
zrealizowane za pomocą prostego uniwersalnego interfejsu I/O 8255. Zestaw rezystorów
można wykonać w technice cienkowarstwowej, pozwalającej na otrzymanie dużej stabilności
temperaturowej i czasowej i zminimalizowanych parametrów resztkowych (pojemność,
indukcyjność). Złożoność zadania pomiarowego metody wiąże się głównie z zagadnieniem
właściwego doboru wartości rezystancji wzorcowej R
w
oraz z estymacją wyników i błędów
granicznych. Można tu wkroczyć na grunt adaptacyjnych algorytmów pomiaru i metodę w
pełni zautomatyzować.
MIKROKOMPUTER TYPU IBM PC
KONTROLER
INTERFEJSU
IEC-625
UNIWERSALNY
INTERFEJS
PROGRAMOWANY
I/O 8255
GENERATOR
MULTIMETR
(woltomierz+cz
ę
so
ś
ciomierz)
BLOK 3V
Z
x
Rys. 6. Schemat blokowy systemu pomiarowego realizującego metodę trzech woltomierzy
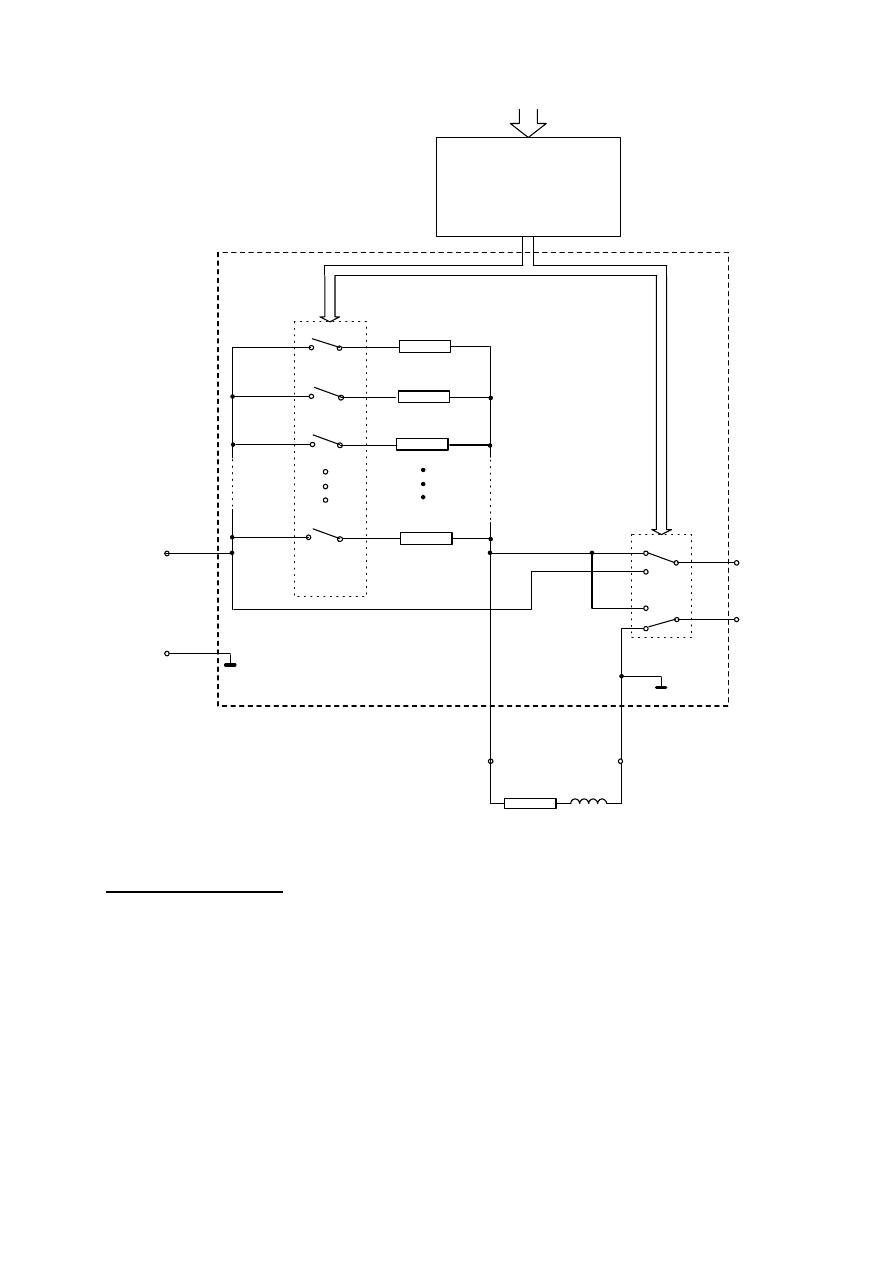
145
Rys. 7. Schemat połączeń wewnętrznych bloku 3V (patrz rys.6)
Opracowanie wyników
Podstawowe problemy właściwego opracowania wyników wiążą się z zastosowaniem
właściwych metod numerycznych przy obliczeniach wyznaczanych parametrów i szacowaniu
błędów. W rozpatrywanym przykładzie podstawowa trudność obliczeń wiąże się z
problemem tzw. dobrego uwarunkowania numerycznego zadania rozwiązywania trójkąta.
Najprościej to ujmując należy dążyć przy pomiarach (poprzez dobór wartości rezystora R
w
),
by wyznaczany trójkąt napięć miał ramiona o wartościach możliwie porównywalnych. Wtedy
błędy obliczeń i błędy systematyczne graniczne wyznaczanych parametrów, wynikające z
UNIWERSALNY
INTERFEJS
PROGRAMOWANY
I/O 8255
R
w2
R
w3
R
wn
R
w1
Z
x
Woltomierz
BLOK 3V
Generator
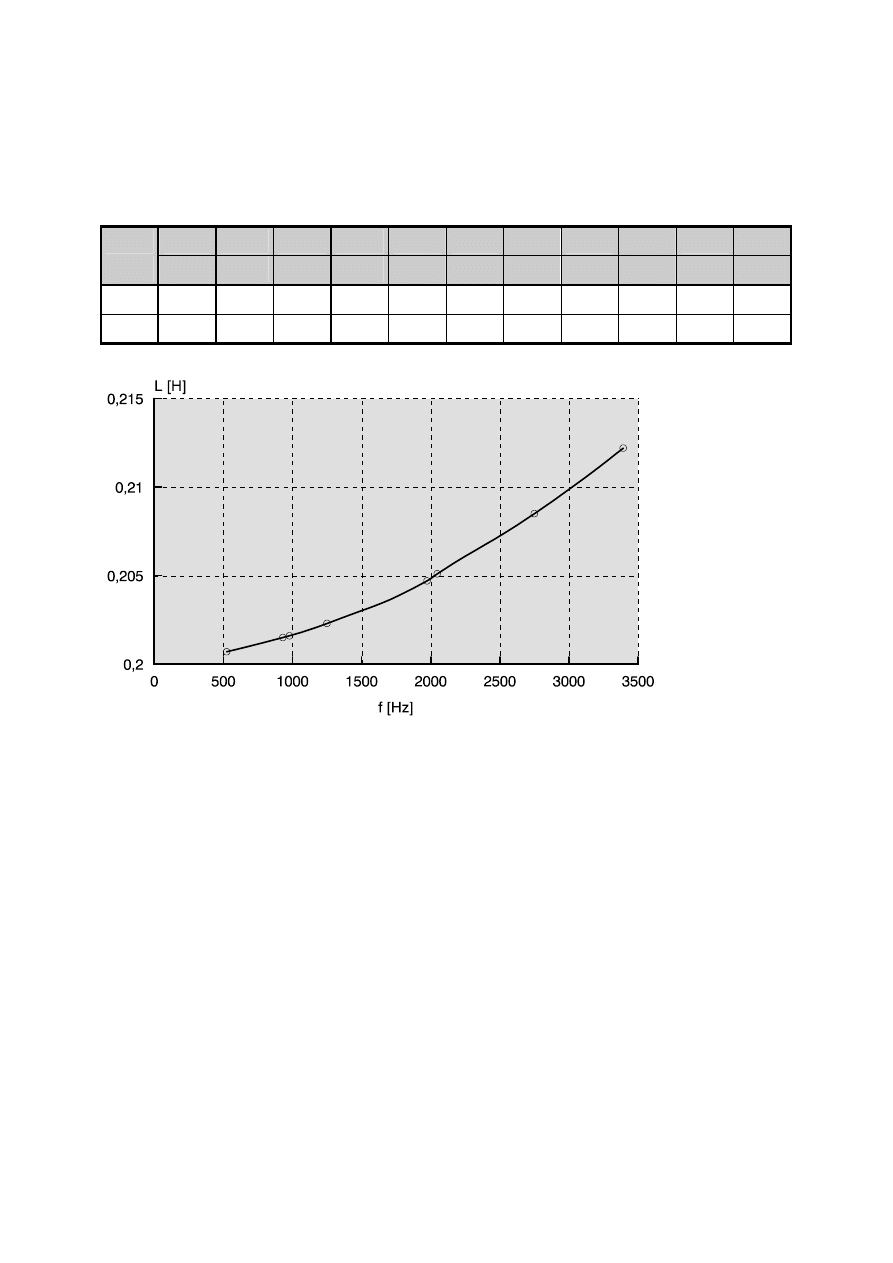
146
błędów systematycznych popełnianych przy pomiarach napięć i częstotliwości, będą
najmniejsze.
Tablica 1. Przykład zapisu wyników pomiarów metodą trzech woltomierzy
Lp.
f
U
1
U
2
U
3
R
w
Z
x
δδδδ
Zx
R
x
δδδδ
Rx
L
x
δδδδ
Lx
Hz
V
V
V
Ω
Ω
Ω
Ω
Ω
Ω
Ω
Ω
%
Ω
Ω
Ω
Ω
%
mH
%
1
50,0
9,13
2,41
8,22
10
34,1
±±±±
0,5
8,59
±±±±
1,4
105,1
±±±±
1,1
2
50,0
12,13
3,13
11,38
100
363,6
±±±±
0,5
40,0
±±±±
1,4
1150
±±±±
1,1
Rys. 8. Przykład prezentacji wyników pomiarów indukcyjności w funkcji częstotliwości
Przykład zapisu wyników pomiarów i obliczeń pokazuje tablica 1. Na rys.8 pokazano zaś
przykład prezentacji wyników pomiarów indukcyjności w funkcji częstotliwości - w postaci
graficznej. W tym przypadku wykres przedstawia funkcję w sposób bardziej poglądowy i ilu-
stracyjny niż wartości, które można by zestawić w tablicy. Wykres powinien być zawsze opa-
trzony informacją o osiach współrzędnych (wielkości, jednostki), zaś punkty zmierzone po-
winny być zaznaczone odpowiednimi symbolami (np. kółka, krzyżyki, iksy, trójkąty).

147
Spis treści
Wstęp do pomiarów (wykład 1).................................................................................... str. 2
Wielkość, jednostka, wartość, system wielkości, system jednostek. O błędzie pomiaru i narzę-
dziach pomiarowych. O sygnałach i ich przetwarzaniu. Typowe elektryczne przyrządy pomia-
rowe.
Pomiary w inżynierii (wykład 2)................................................................................. str. 14
Typowe obiekty pomiarów. Pomiar jako identyfikacja parametryczna. Modelowanie struktury
i parametrów obiektu. O przetwornikach, czujnikach, systemach pomiarowych i komputerach.
Podstawowe pojęcia teorii błędów (wykład 3 i 4)....................................................... str. 27
Przedział niepewności. Błąd prawdziwy i graniczny; błąd bezwzględny, względny, sprowa-
dzony. Błędy systematyczne i przypadkowe. Przenoszenie błędów. Typowe przypadki szacowa-
nia błędów. Ogólne procedury szacowania błędów.
Metody pomiarowe i narzędzia pomiarowe I (wykład 5, 6 i 7).................................. str. 50
Przetwarzanie sygnałów pomiarowych i przetworniki pomiarowe. Model przetwornika analo-
gowego. Parametry charakterystyczne. Normalizacja błędów przetwarzania. Przetworze-
niowo-sygnałowy model pomiaru. Wzorzec i komparator. Komparacja równoczesna i nierów-
noczesna - kompensacja i podstawienie. Pomiary analogowe.
Metody pomiarowe i narzędzia pomiarowe II (wykład 8, 9 i 10).............................. str. 82
Przetworniki
cyfrowo-analogowe.
Przetworniki
analogowo-cyfrowe.
Woltomierze
i
multimetry cyfrowe. Oscyloskopy cyfrowe.
Automatyzacja pomiarów (wykład 11 i 12).............................................................. str. 115
Struktury
systemów
pomiarowych.
Interfejsy
standardowe.
Procedury
pomiarów
systemowych. Oprogramowanie systemów. Przyrządy wirtualne.
Technika mierzenia (wykład 13 i 14)........................................................................ str. 138
Przegląd zasad techniki mierzenia. Pisanie raportu. Przykład pełnego cyklu procesu pomia-
rowego: przygotowanie, wykonanie i opracowanie wyników.

148
PODZIĘKOWANIE
Autor niniejszego opracowania serdecznie dziękuje prof. dr hab.
Januszowi Jaworskiemu i
dr inż.
Wiesławowi Winieckiemu za udostępnienie niepublikowanych tekstów i rysunków
dydaktycznych oraz za cenne sugestie dotyczące tak poszczególnych fragmentów wykładu
jak i całości.
Wyszukiwarka
Podobne podstrony:
5 Podstawy Metrologii systemy pomiarowe
Zadanie z pasowania otwarte, PWR Politechnika Wrocławska, podstawy metrologii, Wykłady 2011
ściąga metrologia (2), PWR mbm, Podstawy metrologii
Podstawy Metrologii Pomiary małych rezystancji za pomoca mostka 6 ramiennego Protokol
Wyznaczanie niepewności pomiarów, PWr W9 Energetyka stopień inż, II Semestr, Podstawy metrologii i t
Podstawy metrologii, Polibuda (MiBM), Semestr III, III semestr, od Arniego, 3 semester, sebastianowe
Podstawy Metrologii 12 2 BPPPA P
Struktura źródeł błędów w procesie pomiarowym, PWR Politechnika Wrocławska, podstawy metrologii, Wyk
Podstawy metrologii dr Czesław Jermak [ metody, def., tematy], metody-pom, Pierwszy pode metod, prze
Podstawy metrologii Wykład 4bBRAKNOTATEK
cw1, Semestr II, Podstawy metrologii, Sprawka
Podstawy Metrologii Pomiary małych rezystancji za pomoca mostka 6 ramiennego Instrukcja
Podstawy Metrologii 12 1 ZOS P
PODSTAWY METROLOGII pomiary HB
1 Podstawy Metrologii podstawy, wielkości i jednostki miary, SI
więcej podobnych podstron