1

Dr hab. inż. Michał LISOWSKI, prof. P.Wr.

[e-mail]

Uwaga: poniższe materiały maja charakter autorski na prawach rękopisu. Ich udostępnianie
bez zgody autora, a także rozpowszechnianie jest prawnie zabronione.

Wykład 4b

ZASADA DZIAŁANIA MIERNIKA MAGNETOELEKTRYCZNEGO

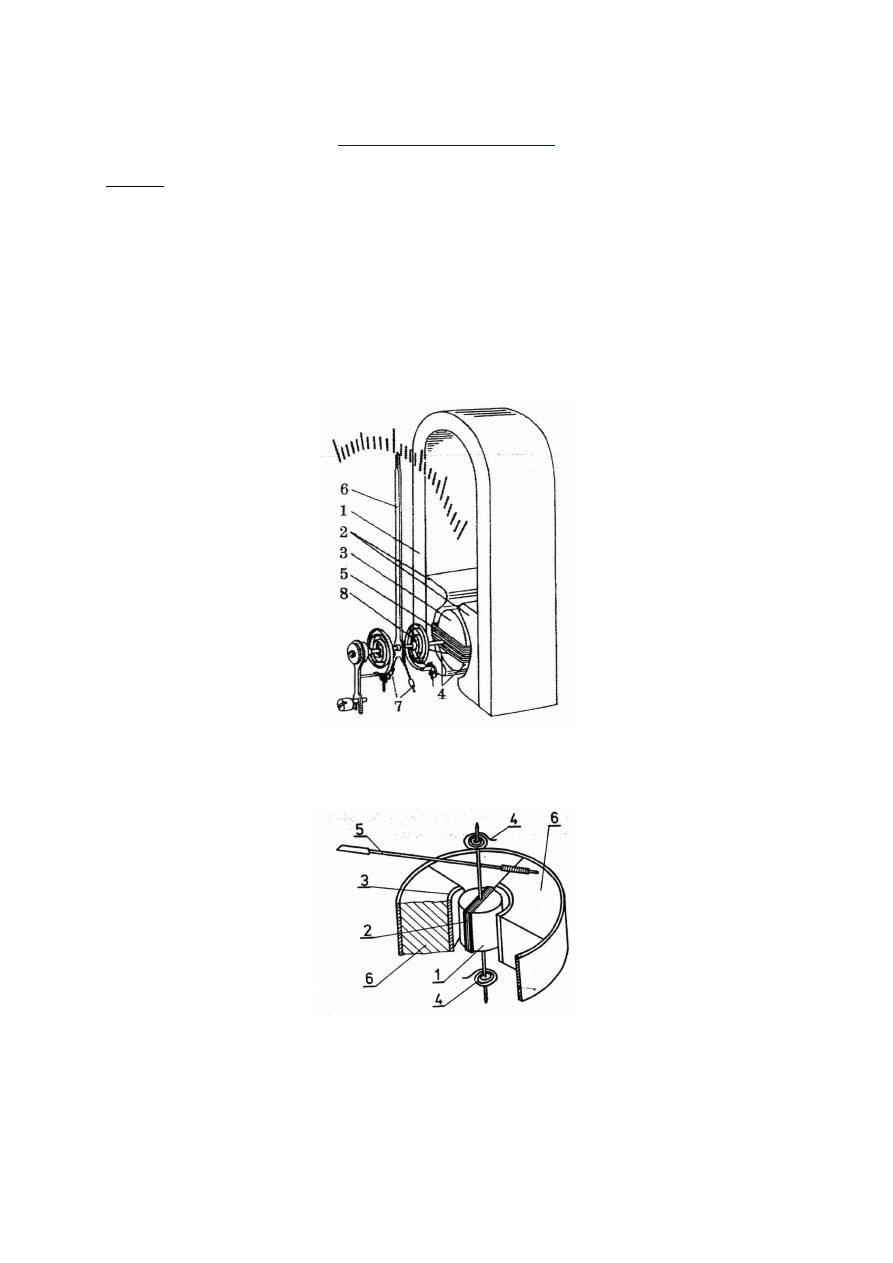
Budowę miernika magnetoelektrycznego z magnesem zewnętrznym pokazano na rys. 4.9, a
na rys. 4.10 przedstawiono budowę przyrządów magnetoelektrycznych, obecnie najczęściej
stosowanych, z magnesem wewnętrznym.

Rys. 4.9. Budowa miernika magnetoelektrycznego z magnesem zewnętrznym: 1 – magnes,

2 – nabiegunnik, 3 – rdzeń, 4 – szczelina powietrzna, 5 – cewka. 6 – wskazówka,

7 – przeciwwagi 8 – sprężynka zwrotna

Rys. 4.10. Budowa miernika magnetoelektrycznego z magnesem wewnętrznym: 1 – rdzeń,

2 – cewka ruchoma, 3 – nabiegunniki, 4 – sprężynka zwrotna, 5 – wskazówka, 6 – magnes

trwały

2

Prąd I przepływający przez cewkę o liczbie zwojów z i szerokości d, nawiniętą na

ruchomej ramce (rys. 4.11) znajdującej się w polu magnetycznym o indukcji B i szerokości
nabiegunnika l wywołuje moment obrotowy

M = IBzdl .

Sprężynka zwrotna, wskutek jej skręcenia, wytwarza moment zwrotny

M

z

= k

α

.

W stanie ustalenia się wskazań

M = M

z

, czyli IBzdl = k

α

.

Stąd

I = c

α

,

gdzie

c = k/(IBzdl).

Rys. 4. 11. Cewka nawinięta na ruchomej ramce

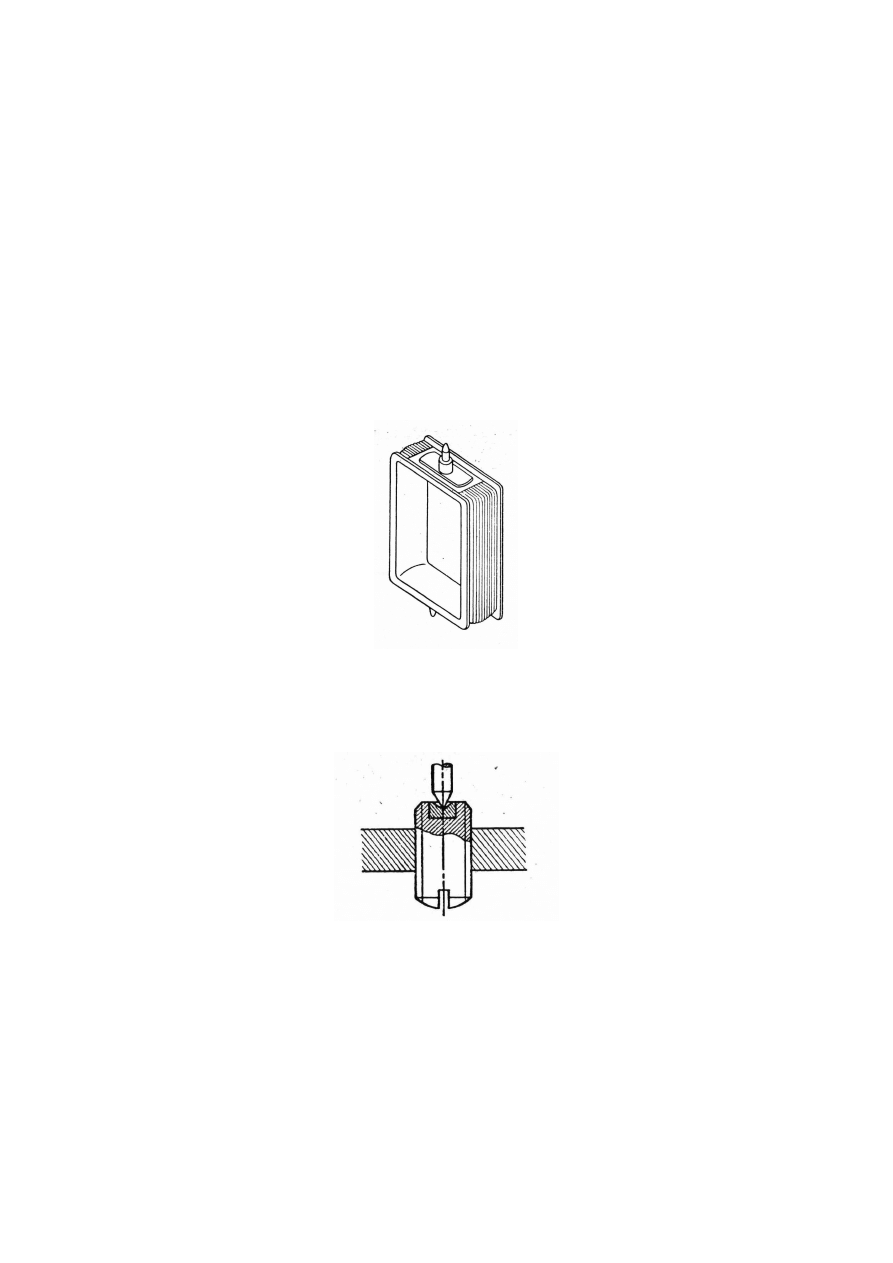
Czopy, z hartowanej stali węglowej, przyklejone do cewki ułożyskowane są łożyskach

z kamieni szlachetnych (syntetyczny szafir lub rubin), podobnie jak czopy w zegarkach
(rys.4.12).

Rys. 4.12. Czop i łożysko

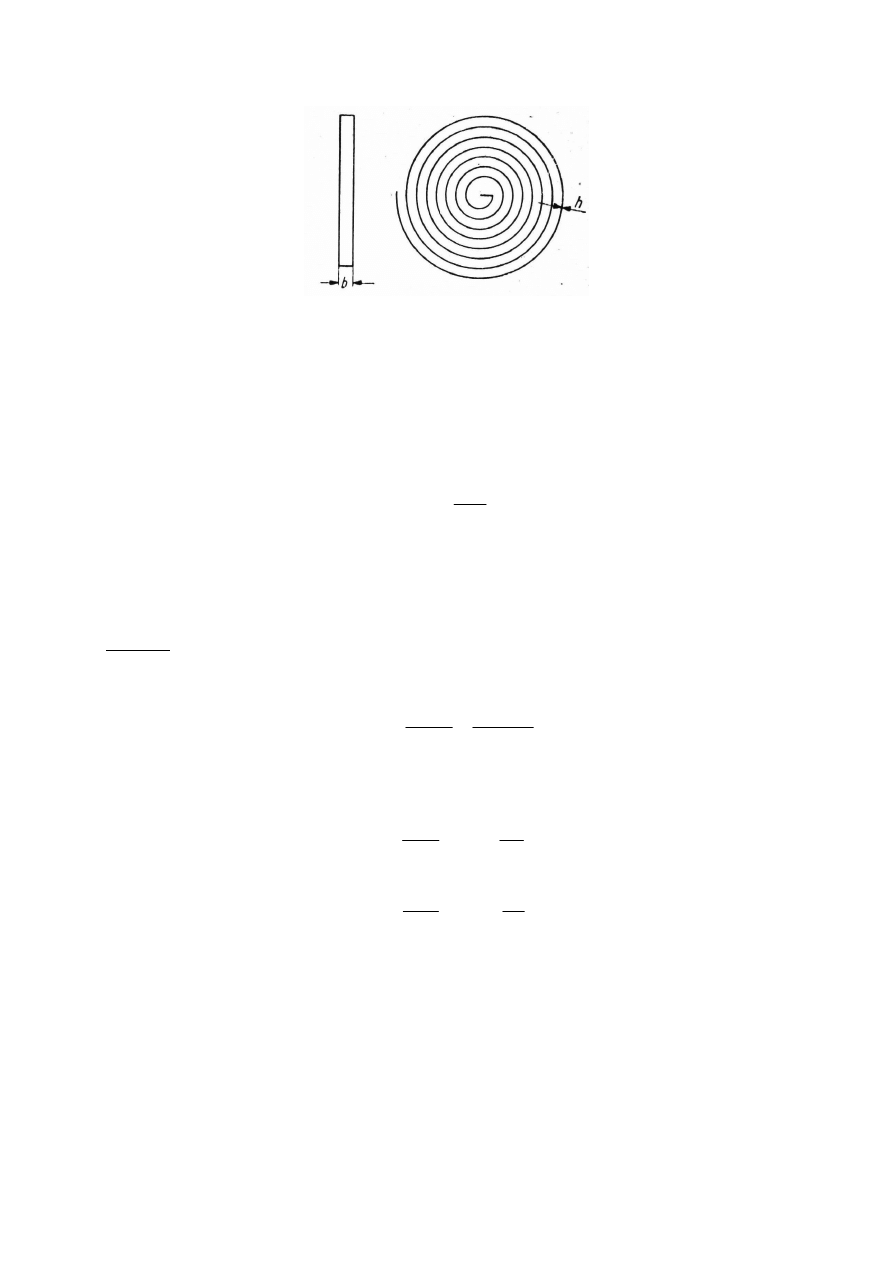
Sprężynki zwrotne (rys. 4.12) równocześnie służą jako doprowadzenia prądu do

uzwojenia cewki

3

Rys. 4.12. Sprężynka zwrotna

NIEDOKŁADNOŚĆ PRZYRZĄDÓW ANALOGOWYCH

Klasa przyrządu

.

X

X

X

kl

n

g

100

∆

δ

ch

=

≥

Klasy są znormalizowane szeregiem: 0,1; 0,2;0,5; 1; 1,5; 2,5

Najczęściej wartością umowna jest zakres pomiarowy.


Przykład
Przyrząd klasy 0,5 o

α

n

=100 dz.

Błąd graniczny wskazań przyrządu

Błąd przy dowolnym wskazaniu X

X

X

kl

X

X

X

n

g

=

∆

=

100

δ

.

lub

α

α

α

α

δα

n

g

kl

=

∆

=

100

.

Np. kl=0,5,

α

n

=150 dz. to dla

α

=10 dz. δ

α

=7,5 %,

α

=50 dz. δ

α

=1,5 %,

α

=100 dz. δ

α

=0,75 %,

α

=150 dz. δ

α

=0,5 %.

Dla wzorów nastawnych klasa odniesiona jest najczęściej do wartości nastawy i jest
wielokrotnością dziesiętną liczb

(1;2;5)10

k

,

gdzie k jest całkowitą liczbą niedodatnią.

.

dz

,

,

kl

n

g

5

0

100

100

5

0

100

±

=

⋅

=

⋅

=

∆

α

α

4

PRZYRZĄDY CYFROWE

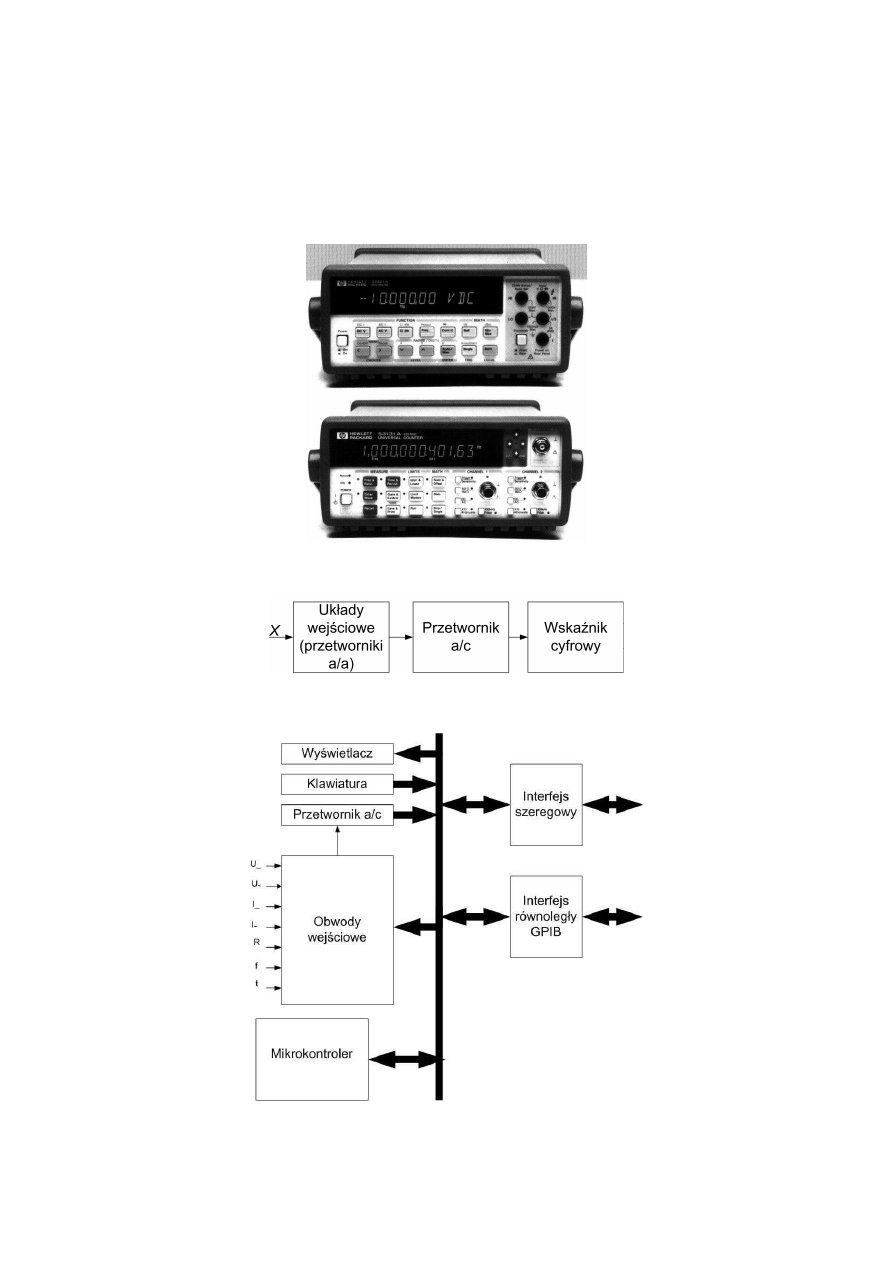
Przyrządy cyfrowe mają cyfrowe pole odczytowe, które dla przyrządów cyfrowych,

umożliwiają odczyt z dużą rozdzielczością (rys. 4.13). Ogólny schemat strukturalny przyrządu
cyfrowego pokazano na rys. 4.14. Przyrządy te obecnie przeważnie w swojej strukturze zawierają
mikroprocesory. Podstawowym elementem przyrządu cyfrowego jest przetwornik analogowo-cyfrowy
(rys. 4.16).

Rys. 4.13. Laboratoryjne multimetry cyfrowe

Rys. 4.14. Schemat strukturalny przyrządu cyfrowego

Rys. 4.15. Schemat strukturalny mikroprocesorowego przyrządu cyfrowego

5

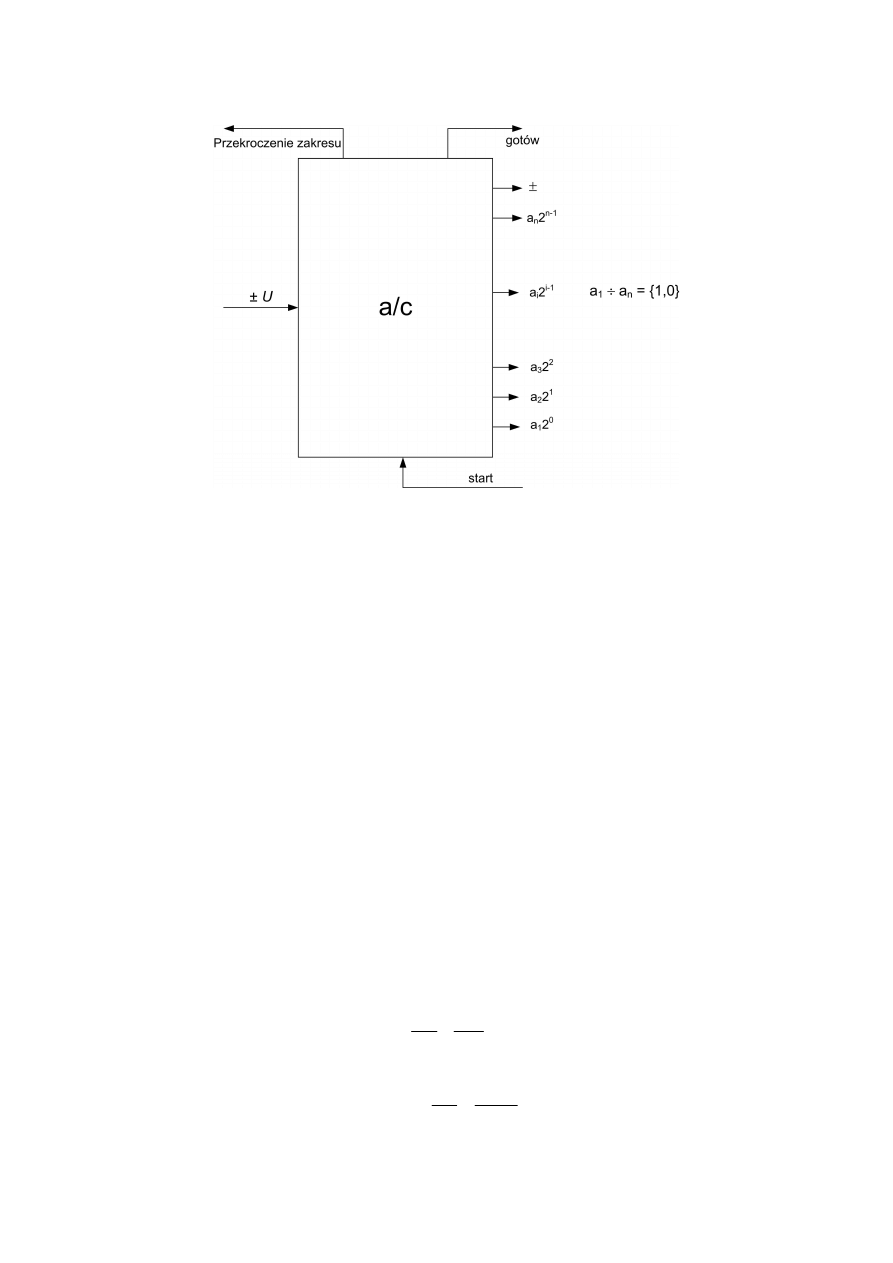
Rys. 4.16. Przetwornik analogowo-cyfrowy

Parametry określające właściwości przetworników a/c:

• zakres napięcia wejściowego,

najczęściej ±5 V lub ± 10 V,

• rezystancja wejściowa,

przeważnie rzędu 10

9

,

• przeciążalność (napięcie wejściowe, które nie powoduje jeszcze uszkodzenia przetwornika),

• niedokładność,

przeważnie ±(0,1 ÷ 0,002) %,

• rozdzielczość (liczba bitów),

4, 8, 16 bitów,

• czas przetwarzania,

od 0,1 s (wolne) do 10 ns (bardzo szybkie),

• rodzaj kodu,

najczęściej binarny,

• obciążalność wyjścia (przeważnie określana jest liczbą bramek, które można przyłączyć do

jednego wyjścia przetwornika),

• warunki użytkowania (zakres temperatury i wilgotności),

• zasada przetwarzania,

• technologia wykonania,

• topografia (rodzaj i rozmieszczenie wyprowadzeń),

• rozmiary,

• masa

NIEDOKŁADNOŚĆ PRZYRZĄDÓW CYFROWYCH

Błąd podstawowy ma dwie składowe: multiplikatywną i addytywną.

Np. dla zakresu 100 mV:

±0,015 % w.m. ±0,002 % w.k.p. ±3µV.

Dla danego wskazania błąd graniczny bezwzględny













∆

+

+

±

=

∆

X

bX

aX

X

of

n

g

100

100

,

a względny błąd graniczny













∆

+

+

±

=

100

X

X

X

X

b

a

X

of

n

δ

.

Może być podany także w postaci

6

±0,01 % w.m. ±1(2) cyfry.

Wówczas













∆

+

±

=

∆

X

n

n

aX

X

g

100

,













∆

+

=

100

n

n

a

X

δ

.

Przykład
V.C. ma niedokładność ±0,1 % ±1 cyfra.
Jeżeli wskazał U=85,1 mV, to

%

,

,

U

22

0

100

851

1

1

0

±

=













+

±

=

δ

,

dla U=2,1 mV

%

,

,

U

9

4

100

21

1

1

0

±

=













+

±

=

δ

.

PRZYRZADY REJESTRUJĄCE

REJESTRACJA ANALOGOWA (CIĄGŁA)

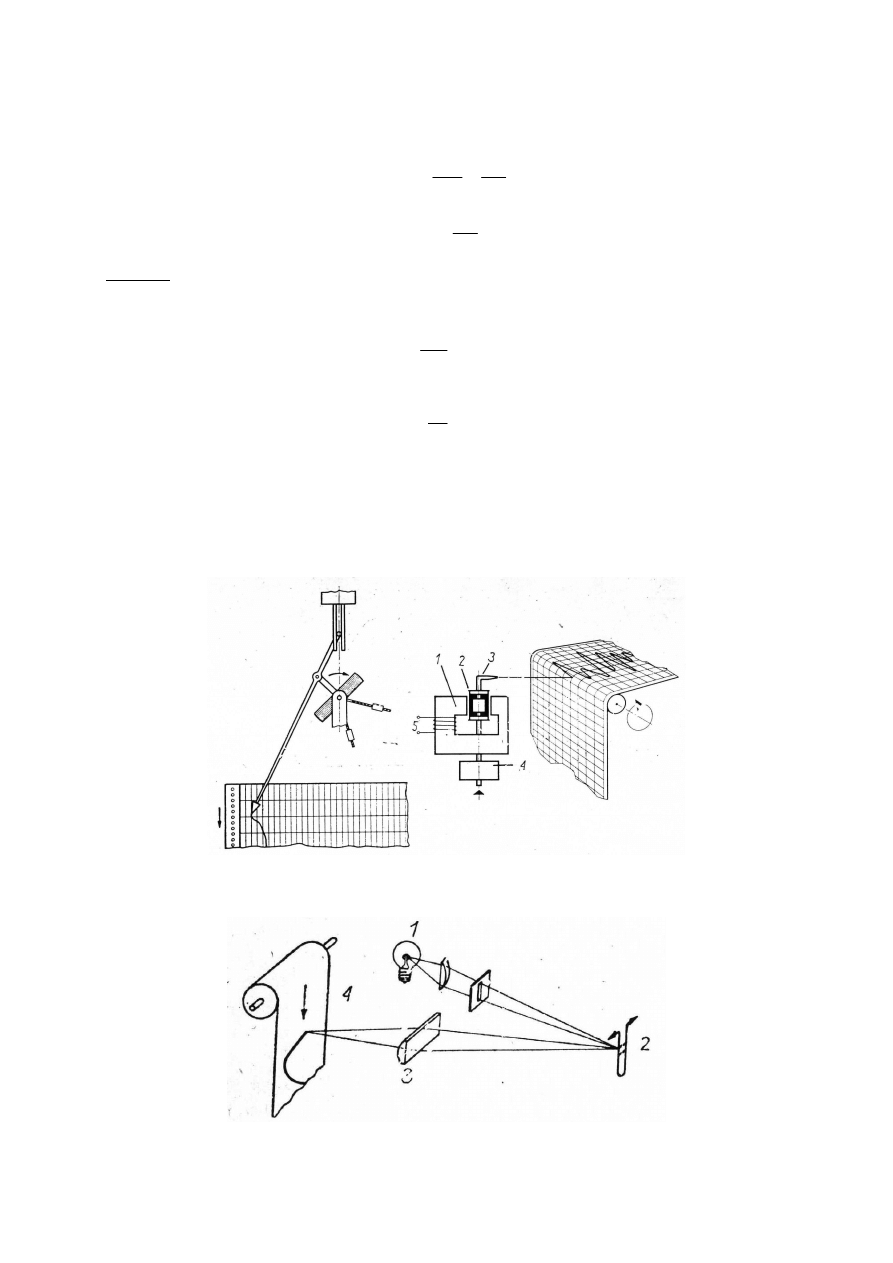
Rys. 4.17. Rejestratory atramentowe

Rys. 4.18. Oscylograf pętlicowy

7

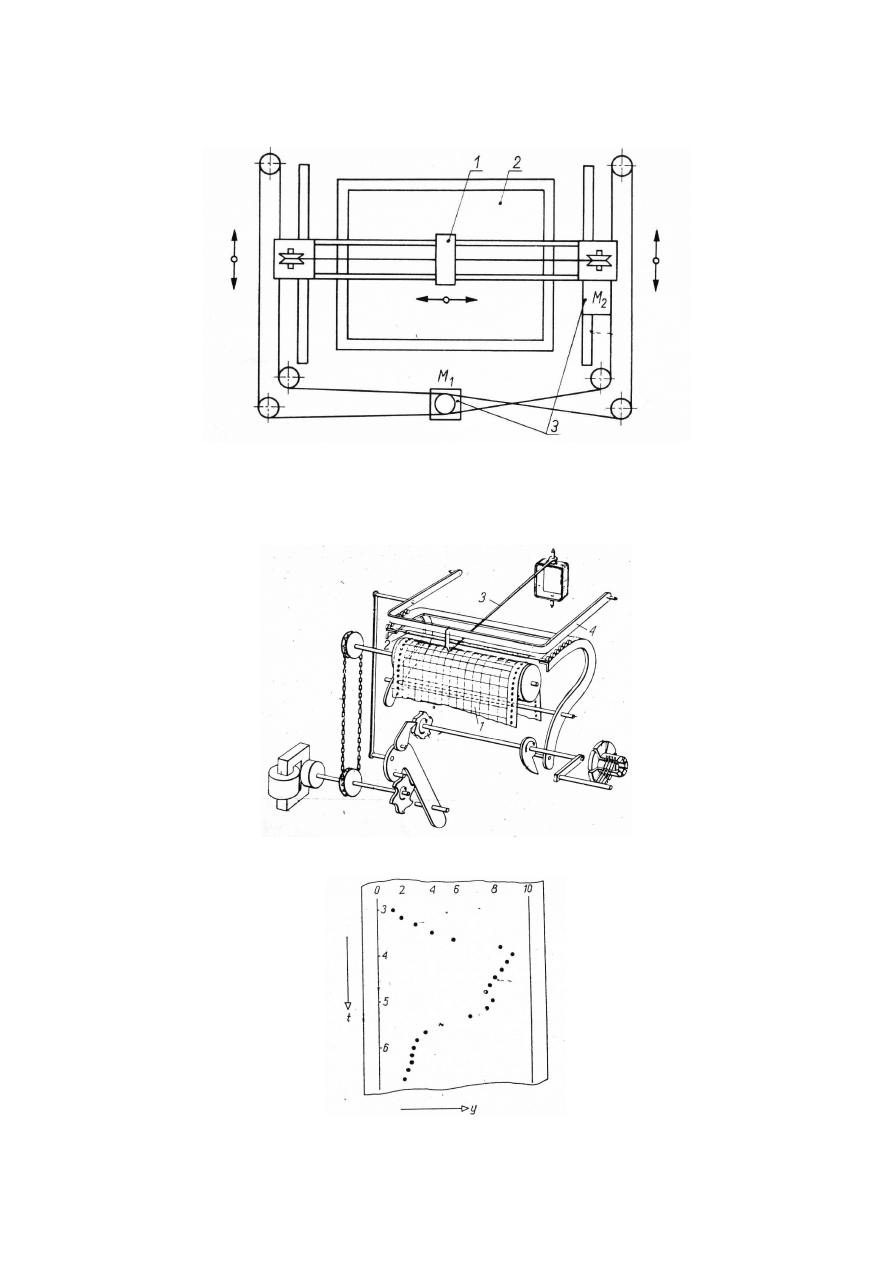
Rys. 4.19. Rejestrator X-Y

REJESTRATRACJA DYSKRETNA

Rys. 4.20. Rejestrator punktowy

Rys. 4.21. Rejestracja punktowa

8

Rys. 4.22. Rejestracja komputerowa

OSCYLOSKOPY

Dostępne są oscyloskopy analogowe i cyfrowe (dyskretne) oraz analogowo-cyfrowe,

tzn. takie które mogą pracować analogowo lub dyskretnie. Czasami mogą zawierać
wewnętrzną drukarkę (rys. 4.23).

Rys. 4.23. Oscyloskop cyfrowy z wewnętrzną drukarką