1

Dr hab. inż. Michał LISOWSKI, prof. P.Wr.

[e-mail]

Uwaga: poniższe materiały maja charakter autorski na prawach rękopisu. Ich udostępnianie
bez zgody autora, a także rozpowszechnianie jest prawnie zabronione.

Wykład 5

BŁĄD POMIARU

Bezwzględny błąd pomiaru jest różnicą miedzy wynikiem pomiaru a wartością

prawdziwą wielkości mierzonej:

∆

∆

∆

∆X = X

s

- X

p

,

gdzie: X

s

— wynik surowy,

X

p

— wartość prawdziwa wielkości mierzonej.

Ma on jakąś konkretną wartość, ale niestety nie zawsze jest ona znana, ponieważ we
wzorze definicyjnym występuje nie zawsze znana wartość prawdziwa.

Błąd pomiaru jest wskaźnikiem stopnia zgodności wyniku pomiaru i wartości

prawdziwej. Niestety wartość błędu nie jest dokładnie znana, lub nieznana, bowiem nie jest
znana dokładnie, lub wcale, wartość prawdziwa wielkości mierzonej.

Wynik surowy jest to wynik pomiaru przed korekcją błędu systematycznego.
Przy powtarzaniu pomiarów wartość błędu będzie się zmieniała, co uwidoczni się w

zmienności wyników X

s

, ponieważ błąd pomiaru jest wypadkową dwóch składowych:

• błędu systematycznego ∆

∆

∆

∆

s

X

,

• błędu przypadkowego ∆

∆

∆

∆

p

X,

czyli

∆

∆

∆

∆

X =

∆

∆

∆

∆

s

X

+ ∆

∆

∆

∆

p

X

Błąd systematyczny zdefiniowany jest następująco:

„Błąd systematyczny jest różnicą między wartością średnią

Χ

Χ

Χ

Χ

śr

z nieskończonej liczby

wyników pomiarów tej samej wielkości mierzonej, wykonanych w warunkach
powtarzalności, a wartością prawdziwą wielkości mierzonej

Χ

Χ

Χ

Χ

p

":

∆

∆

∆

∆

s

Χ

Χ

Χ

Χ

=

=

=

=

Χ

Χ

Χ

Χ

śr

−

−

−

−

Χ

Χ

Χ

Χ

p

.

Warunki powtarzalności obejmują: tę samą procedurę pomiarową, tego samego
obserwatora, ten sam przyrząd pomiarowy stosowany w tych samych warunkach, to samo
miejsce, powtarzanie w krótkich odstępach czasu. Błąd systematyczny ma stałą
powtarzającą wartość w czasie pomiaru. Stąd jego nazwa. Może on być wyeliminowany
przez wprowadzenie poprawki.

Błąd przypadkowy ma następującą definicję:

2

„Błąd przypadkowy jest różnicą między wynikiem pomiaru X a średnią

Χ

Χ

Χ

Χ

śr

z

nieskończonej liczby wyników pomiarów tej samej wielkości mierzonej, wykonanych
w warunkach powtarzalności":

∆

∆

∆

∆

p

Χ

Χ

Χ

Χ

=

=

=

=

Χ

Χ

Χ

Χ

−

−

−

−

Χ

Χ

Χ

Χ

śr

.

Błędy przypadkowe maja zawsze rozkład losowy (przypadkowy) i dlatego nie można

ich wyeliminować przez wprowadzenie poprawki. Ich wpływ na w wartość średnią wyników
pomiarów można zmniejszyć powtarzając wielokrotnie pomiary. Wartość średnia tych
wyników nie będzie obarczona błędami przypadkowymi, jeżeli liczba pomiarów będzie
nieskończenie duża.

Całkowity błąd pomiaru

∆

∆

∆

∆

Χ

Χ

Χ

Χ

=

=

=

= ∆

∆

∆

∆

s

Χ

Χ

Χ

Χ

+ ∆

∆

∆

∆

p

Χ

Χ

Χ

Χ

.

Względny błąd pomiaru zdefiniowany jest jako stosunek bezwzględnego błędu

pomiaru do wartości prawdziwej, czyli

p

X

X

X

∆

=

δ

lub

[%]

100

⋅

∆

=

p

X

X

X

δ

.

Jeżeli wartość prawdziwa nie jest znana, to wówczas do odniesienia błędu zamiast wartości
prawdziwej przyjmuje się wynik surowy (wartość zmierzoną) i powyższe wzory przyjmują
wówczas postać:

s

X

X

X

∆

=

δ

lub

[%]

100

⋅

∆

=

s

X

X

X

δ

.

POPRAWKA

Jeżeli znana jest wartość błędu systematycznego, to można go wyeliminować z

wyniku pomiaru poprzez wprowadzenie poprawki. Poprawka ma wartość błędu
systematycznego, ale ze znakiem przeciwnym:

p(X) = - ∆

∆

∆

∆

s

X

Zatem poprawka jest wartością dodawaną algebraicznie do surowego wyniku
pomiaru w celu skompensowania błędu systematycznego.

Wynik pomiaru po korekcji błędu systematycznego nazywamy wynikiem

poprawionym.

WZORCOWANIE PRZYRZĄDÓW

Błędy systematyczne przyrządów pomiarowych wyznacza się podczas ich wzorcowania.

W procesie wzorcowania przyrządów pomiarowych porównuje się wskazania przyrządu
badanego ze wskazaniami przyrządu wzorcowego. Przyrząd wzorcowy powinien być znacznie
dokładniejszy od przyrządu badanego (wzorcowanego). Różnica między wskazaniem przyrządu
badanego a przyrządu wzorcowego jest błędem wskazań przyrządu wzorcowanego. Podczas
pomiarów przyrządem wywzorcowanym wartość tego błędu ze znakiem przeciwnym możemy
dodać do wskazania przyrządu, ażeby uzyskać wynik poprawny.

3

Przykład świadectwa wzorcowania

LOGO FIRMY

NAZWA LABORATORIUM WZORCUJACEGO

tel:

fax:

ŚWIADECTWO WZORCOWANIA

Nr

Data wydania: 27 września 2005 r.

Liczba stron: 4

PRZEDMIOT
WZORCOWANIA

Woltomierz magnetoelektryczny 3 V 1500 Ω, klasy 0,5 napięcia stałego,
typ TLME – 2 firmy era, nr fab. 1111544 z opornikiem dodatkowym typ,
OD1 do miernika 3 V 1500 Ω klasy 0,2 o zakresach pomiarowych: 7,5 V,
15 V, 30 V, 75 V, 150 V, 300 V, 750 V, firmy ERA, nr fab. 20172.

ZGŁASZAJĄCY

Instytut Elektrotechniki, Oddział Technologii i Materiałoznawstwa
Elektrotechnicznego, Pracownia Pomiarów i Diagnostyki.

METODA
WZORCOWANIA

Metoda bezpośrednia i interpolacyjna – zgodnie z procedurą
wzorcowania analogowych przyrządów pomiarowych - PW-
1/IEL/OTiME/LB.

WARUNKI
ŚRODOWISKOWE

Temperatura otoczenia (23 ± 1) °C, wilgotność względna (58 ± 3) %.

DATA WYKONANIA
WZORCOWANIA

27 września 2005 r.

SPÓJNOŚĆ
POMIAROWA

Wyniki wzorcowania woltomierza magnetoelektrycznego zostały
odniesione do wzorca państwowego jednostki miary za pośrednictwem
multimetru cyfrowego firmy Hewlett Packard typu 34401A o nr fab.
314A56323 (świadectwo wzorcowania OUM we Wrocławiu).

WYNIKI
WZORCOWANIA

Podano na stronach 2 ÷ 3 niniejszego świadectwa.

NIEPEWNOŚĆ
WYNIKÓW
WZORCOWANIA

Niepewność pomiaru została określona zgodnie z dokumentem EA-4/02
Podane wartości niepewności stanowią niepewności rozszerzone przy
poziomie ufności 95 % i współczynniku rozszerzenia k=1,65 dla metody
bezpośredniej i k=2 dla metody interpolacyjnej.

ZGODNOŚĆ
Z WYMAGANIAMI

W wyniku wzorcowania stwierdzono, że na wszystkich wzorcowanych
zakresach błędy wskazań przyrządu nie przekraczają wartości,
określonych dopuszczalnym błędem podstawowym podanym przez
producenta.

Kierownik Laboratorium

Wzorcowania

Przyrządów Pomiarowych

Niniejsze świadectwo może być okazywane lub kopiowane tylko w całości.

4

METODA WZORCOWANIA

Dla zakresu 3 V wzorcowanie wykonano metodą bezpośrednia przez porównanie

wskazań przyrządu wzorcowanego ze wskazaniami cyfrowego woltomierza wzorcowego.
Wzorcowanie wykonano dla rosnących i malejących wartości wskazań przyrządu dla
wszystkich ocyfrowanych wskazów. W tabelach z wynikami pomiarów podano wartości
średnie dla każdego wskazania. Dla pozostałych zakresów wzorcowanie wykonano dla
końców każdego zakresu pomiarowego, a błędy wskazań w pozostałych punktach obliczono
metodą interpolacyjną.

WYNIKI WZORCOWANIA

Wyniki wzorcowania podano w tabelach 1 ÷ 3, w których oznaczono przez:

α

x

– wychylenie wzorcowanego miernika,

U

x

– wartość napięcia wskazana przez wzorcowany miernik,

U

w

– wartość poprawna napięcia (wzorcowa),

u(U

odcz

).– niepewność standardowa odczytu napięcia wskazanego przez

wzorcowany miernik,

u(U

w

) – niepewność standardowa wartości napięcia wskazanego przez

przyrząd wzorcowy,

∆α

x

– błąd bezwzględny wskazania wzorcowanego miernika wyrażony w

działkach,

U(∆α

x

) – niepewność rozszerzona wyznaczonej wartości błędu wskazań

wzorcowanego miernika wyrażona w działkach, określona przy
poziomie ufności 0,95,

∆

dop

α

x

– dopuszczalny błąd bezwzględny napięcia wzorcowanego miernika

wyrażony w działkach.

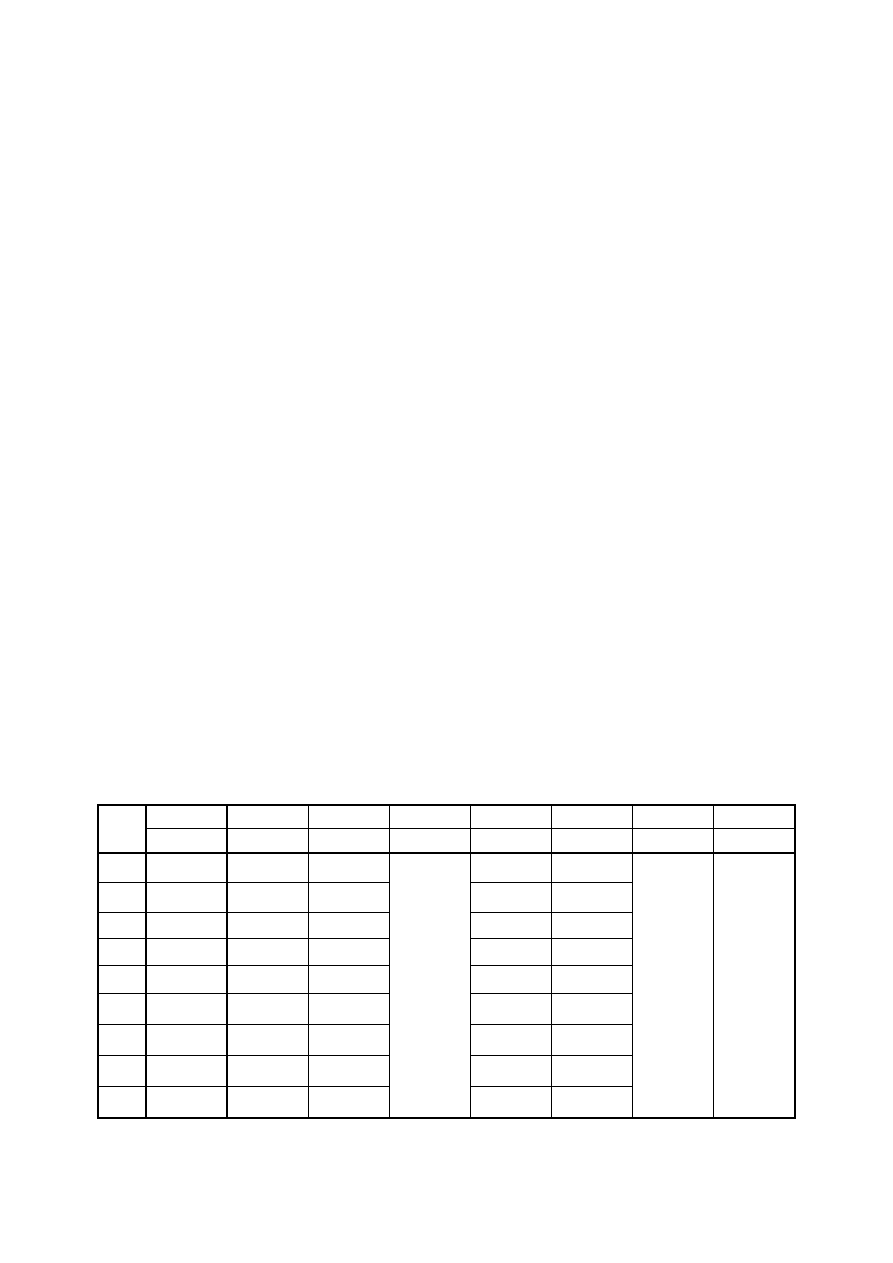
Tabela 1. Wyniki wzorcowania wraz z ich niepewnościami dla zakresu 3 V

α

x

U

x

U

w

u(U

odcz

)

u(U

w

)

∆α

x

U(∆α

x

)

∆

dop

α

x

L.p.

dz

V

V

V

V

dz

dz

dz

1.

0,0

0,000

0,00006

0,00000

0,0

2.

10,0

0,400

0,40145

0,00002

0,0

3.

20,0

0,800

0,80169

0,00004

0,0

4.

30,0

1,200

1,2014

0,0001

0,0

5.

40,0

1,600

1,6039

0,0001

-0,1

6.

50,0

2,000

2,0071

0,0001

-0,2

7.

60,0

2,400

2,4075

0,0001

-0,2

8.

70,0

2,800

2,8087

0,0001

-0,2

9.

75,0

3,000

3,0116

0,0024

0,0001

-0,3

0,1

±0,4

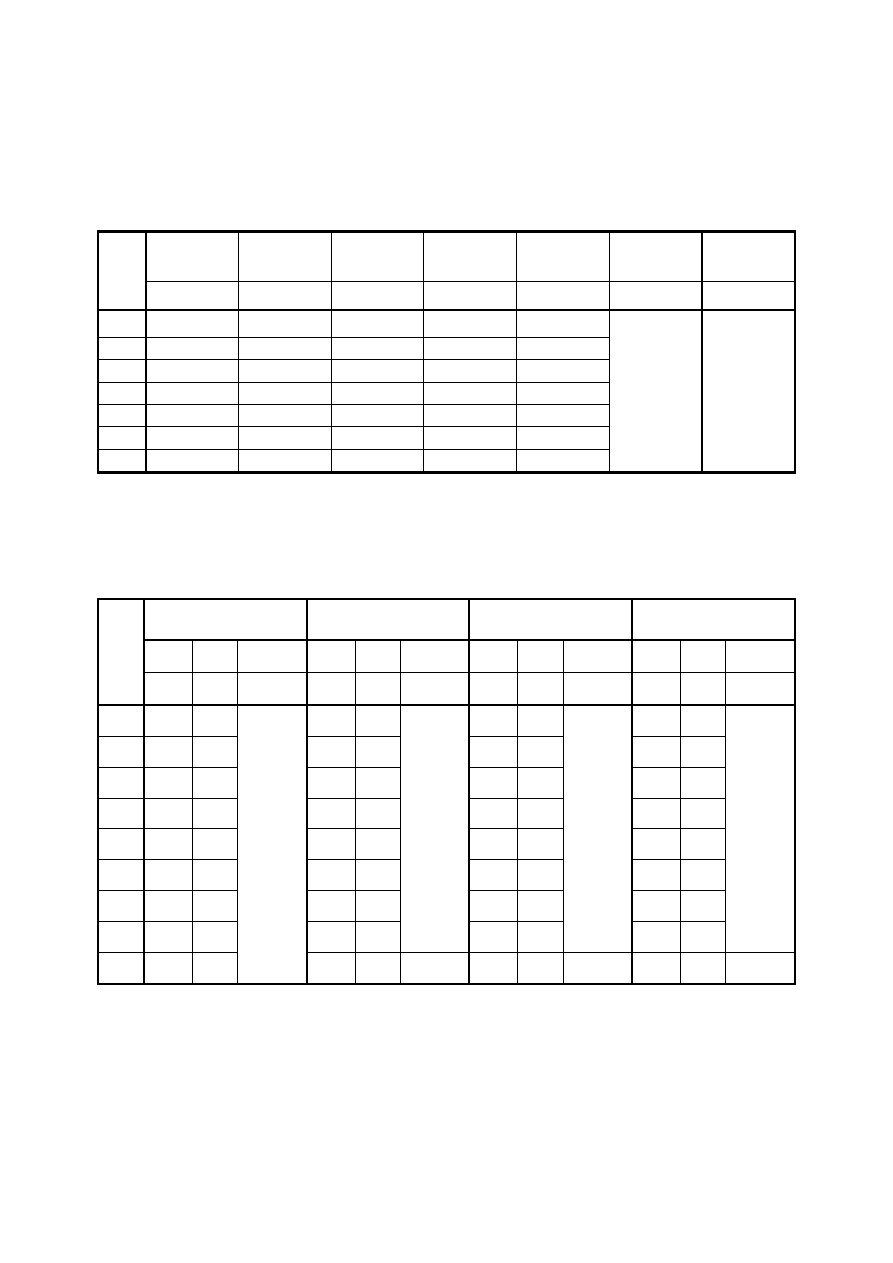
5

Tabela 2. Wyniki wzorcowania przyrządu dla pozostałych zakresów dla górnej granicy
zakresu pomiarowego (α

x

=75 dz)

U

x

U

wśr

u(U

odcz

)

u(U

w

)

∆α

x

U(∆α

x

)

∆

dop

α

x

L.p.

V

V

V

V

dz

dz

dz

1.

7,5

7,5273

0,01

0,0003

-0,3

2.

15

15,066

0,01

0,001

-0,3

3.

30

30,135

0,02

0,002

-0,3

4.

75

75,326

0,06

0,004

-0,3

5.

150

150,78

0,12

0,01

-0,4

6.

300

301,36

0,23

0,02

-0,3

7.

750

753,13

0,58

0,04

-0,3

0,1

±0,4

Tabela 3. Wyniki wzorcowania dla wszystkich zakresów przyrządu pomiarowego wyrażone

w działkach

Zakres 3 V

Zakres 7,5 V

Zakres 15 V

Zakres 30 V

α

x

∆α

x

U(∆α

x

)

α

x

∆α

x

U(∆α

x

)

α

x

∆α

x

U(∆α

x

)

α

x

∆α

x

U(∆α

x

)

L.p.

dz

dz

dz

dz

dz

dz

dz

dz

dz

dz

dz

dz

1.

0,0

0,0

0,0

0,0

0,0

0,0

0,0

0,0

2.

10,0 0,0

10,0 0,0

10,0 0,0

10,0 0,0

3.

20,0 0,0

20,0 0,0

20,0 0,0

20,0 0,0

4.

30,0 0,0

30,0 0,0

30,0 0,0

30,0 0,0

5.

40,0 -0,1

40,0 -0,1

40,0 -0,1

40,0 -0,1

6.

50,0 -0,2

50,0 -0,2

50,0 -0,2

50,0 -0,2

7.

60,0 -0,2

60,0 -0,2

60,0 -0,2

60,0 -0,2

8.

70,0 -0,2

70,0 -0,2

0,2

70,0 -0,2

0,2

70,0 -0,2

0,2

9.

75,0 -0,3

0,1

75,0 -0,3

0,1

75,0 -0,3

0,1

75,0 -0,3

0,1

6

Tabela 3. Ciąg dalszy

Zakres 75 V

Zakres 150 V

Zakres 300 V

Zakres 750 V

α

x

∆α

x

U(∆α

x

)

α

x

∆α

x

U(∆α

x

)

α

x

∆α

x

U(∆α

x

)

α

x

∆α

x

U(∆α

x

)

L.p.

dz

dz

dz

dz

dz

dz

dz

dz

dz

dz

dz

dz

1.

0,0

0,0

0,0

0,0

0,0

0,0

0,0

0,0

2.

10,0 0,0

10,0 0,0

10,0 0,0

10,0 0,0

3.

20,0 0,0

20,0 0,0

20,0 0,0

20,0 0,0

4.

30,0 0,0

30,0 0,0

30,0 0,0

30,0 0,0

5.

40,0 -0,1

40,0 -0,1

40,0 -0,1

40,0 -0,1

6.

50,0 -0,2

50,0 -0,3

50,0 -0,2

50,0 -0,2

7.

60,0 -0,2

60,0 -0,3

60,0 -0,2

60,0 -0,2

8.

70,0 -0,2

0,2

70,0 -0,3

0,2

70,0 -0,2

0,2

70,0 -0,2

0,2

9.

75,0 -0,3

0,1

75,0 -0,4

0,1

75,0 -0,3

0,1

75,0 -0,3

0,1

Uwaga: W tabeli 3 tłustym drukiem podano wyniki uzyskane metodą bezpośrednią

zamieszczone w tabeli 2.

Pomiary wykonał:

……………………………………

Sprawdził

Kierownik Laboratorium Wzorcowania

Przyrządów Pomiarowych

…………………………………………….....

dr hab. inż. Michał Lisowski

Wskazania przyrządu wzorcowego też są obarczone jakimiś błędami, często o nieznanych

wartościach, zatem i wyznaczone poprawki są obarczone jakimiś błędami, których wartości nie
znamy. Możemy tylko z pewnym prawdopodobieństwem oszacować granice tych błędów. Tak
oszacowane granice błędów nazywamy niepewnością pomiarów.

7

LEGALIZACJA PRZYRZĄDÓW

Legalizacja jest zespołem czynności objętych prawną kontrolą metrologiczną

przyrządów pomiarowych. Obejmuje ona sprawdzenie, stwierdzenie i poświadczenie
świadectwem legalizacji, że przyrząd pomiarowy spełnia wymagania określone w przepisach
prawnych. Legalizacji podlegają przyrządy pomiarowe, stosowane:
1) w ochronie zdrowia, życia i środowiska,
2) w ochronie bezpieczeństwa i porządku publicznego,
3) w ochronie praw konsumenta,
4) przy pobieraniu opłat, podatków i niepodatkowych należności budżetowych oraz ustalaniu

opustów, kar umownych, wynagrodzeń i odszkodowań, a także przy pobieraniu i ustalaniu
podobnych należności i świadczeń,

5) przy dokonywaniu kontroli celnej,
6) w obrocie (handlu).

Przyrządy pomiarowe podlegające legalizacji mogą być wprowadzane do obrotu i

użytkowane tylko wówczas, jeżeli posiadają odpowiednio ważną legalizację. Prawna kontrola
metrologiczna przyrządów pomiarowych jest wykonywana przez organy administracji miar
oraz, w zakresie udzielonych upoważnień, przez upoważnione akredytowane laboratoria
wzorcujące.

Świadectwa legalizacji wyglądają podobnie do świadectw wzorcowania. W rubryce

„zgodność z wymaganiami” powinno być powołanie się na odpowiednie przepisy prawne. W
świadectwach legalizacji mogą być pominięte wyniki tabelaryczne z konkretnymi
wartościami błędów.

DOKŁADNOŚĆ POMIARÓW

Według Międzynarodowego Słownika Podstawowych i Ogólnych Terminów

Metrologii: Dokładność pomiaru jest stopniem zgodności wyniku pomiaru z wartością
rzeczywistą (prawdziwą) wielkości mierzonej.

Dokładność pomiaru może być:

• duża,
• mała,
• wysoka,
• niska,
• większa,
• mniejsza,
• wyższa,
• niższa, itd.

Nie można jej wprost przyporządkować liczby.

Oprócz dokładności pomiaru istnieje pojęcie

niedokładność pomiaru.

Według normy

PN-71/N-020050 Metrologia. Nazwy i określenia:

niedokładność wyrażona przez zespół błędów granicznych, zawierający wszystkie błędy
systematyczne oraz graniczne błędy przypadkowe.

Istnieje także pojęcie błędu granicznego jako granic dopuszczalnych błędów, np.

przyrządu pomiarowego. Według Międzynarodowego Słownika Podstawowych i Ogólnych
Terminów Metrologii:

8

błędy graniczne dopuszczalne (przyrządu pomiarowego) są to, granice błędów
dopuszczalnych (przyrządu pomiarowego), czyli wartości skrajne błędów, dopuszczalne
przez warunki techniczne lub wymagania, dotyczące danego przyrządu pomiarowego.

NIEPEWNOŚĆ WYNIKÓW POMIARÓW

Każdy wynik pomiaru X powinien być podany wraz z obliczoną lub oszacowaną

niepewnością u(X), a więc w postaci

Wynik pomiaru, dla którego podano niepewność staje się wynikiem wiarygodnym,

gdyż informuje on o przedziale wartości


w którym z określonym prawdopodobieństwem znajduje się prawdziwa wartość mierzonej
wielkości X

p

.

Niepewność = wątpliwość

Niepewność oznacza wątpliwość co do wartości wyniku pomiaru. Międzynarodowy

słownik podstawowych i ogólnych terminów metrologii (tłumaczenie polskie: Główny Urząd
Miar, 1996) podaje: „Niepewność pomiaru – parametr, związany z wynikiem pomiaru,
charakteryzujący rozrzut wartości, które można w uzasadniony sposób przypisać
wielkości mierzonej”
W międzynarodowym przewodniku: Wyrażenie niepewności pomiaru (tłumaczenie polskie:
Główny Urząd Miar, 1999) czytamy:
„Niepewność pomiaru obrazuje brak dokładnej znajomości wartości wielkości
mierzonej. Wynik pomiaru po korekcji rozpoznanych dokładności systematycznych
pozostaje wciąż tylko estymatą wartości wielkości mierzonej, a to z powodu
niedoskonałości wynikającej z oddziaływań przypadkowych i niedoskonałej korekcji
oddziaływań systematycznych”

Norma dotycząca działalności laboratoriów badawczych i wzorcujących PN-EN

ISO/IEC 17025:2005 w p. 5.4.6.2 podaje:
„Laboratoria badawcze powinny mieć i stosować procedury szacowania niepewności
pomiarów”,
a w p. 5.10.3c:
„Sprawozdanie z badań powinno zawierać stwierdzenie, gdy ma to zastosowanie,
dotyczące oszacowanej niepewności pomiaru”.

( )

.

X

U

X

X

p

±

=

( )

( )

X

U

X

X

X

U

X

p

+

≤

≤

−