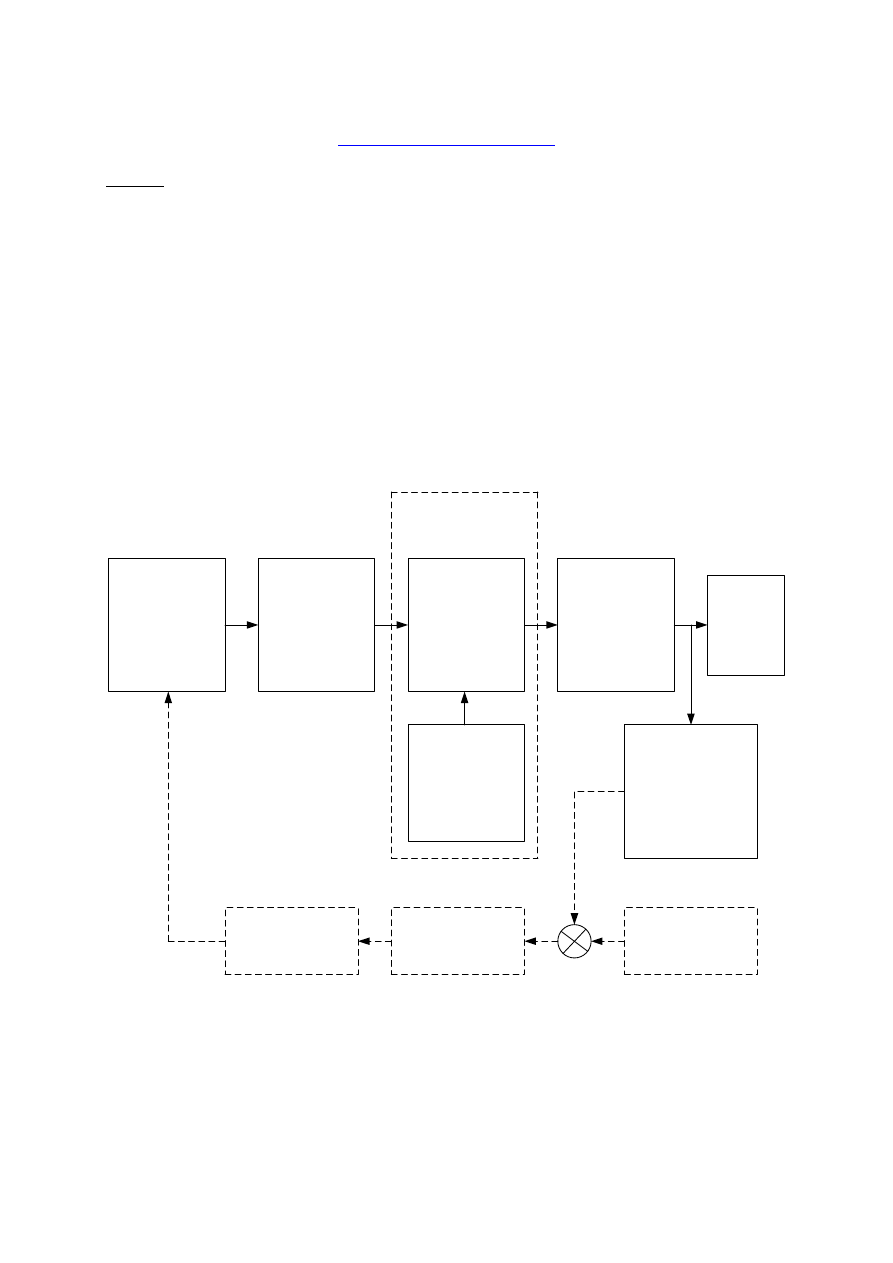
1

Dr hab. inż. Michał LISOWSKI, prof. P.Wr.

[e-mail]

Uwaga: poniższe materiały maja charakter autorski na prawach rękopisu. Ich udostępnianie
bez zgody autora, a także rozpowszechnianie jest prawnie zabronione.

Wykład 3

POMIAR JAKO PROCES PRZETWARZANIA SYGNAÓW

W algorytmie procesu pomiarowego został wyróżniony pomiar właściwy, który

składał się z:

• wyboru przetworników wielkości mierzonej na porównywaną,
• porównania z wzorcem,
• odczytu wyniku pomiaru.

Ten pomiar właściwy należy traktować jako proces przetwarzania sygnałów, którego

schemat pokazano na rys. 3.1.

Obiekt jako

źródło informacji

wielkości

mierzonej

Przetwornik

wielkości

mierzonej na

porównywaną

(czujnik)

Przyrząd

porównujący

Przetwornik

stanu

porównania na

wielkość

obserwowaną

(wskaźnik)

Obserwa-

tor

Wzorzec

wielkości

mierzonej

Przetwornik

pomiarowy

Urządzenie

zbierania danych

(komputer)

Zadajnik

Regulator

Urządzenie

wykonawcze

x

y

z

y

n

Sterowanie
procesem
technologicznym

Rys.3.1. Schemat procesu pomiarowego

W wyniku tego przetwarzania sygnał pomiarowy zmienia zwykle wielokrotnie

zarówno swój charakter fizyczny jak i swoją wartość. W konsekwencji powstają błędy
przetwarzania, czyli zniekształcenia informacji zawartych w sygnale. Przyczyną tego są
właściwości elementów przetworników pomiarowych, które:

2

1) gromadzą część energii w postaci kinetycznej (ruchome masy w układach

elektromechanicznych, indukcyjności w układach elektrycznych, bezwładności cieczy w
układach pneumatycznych i hydraulicznych),

2) gromadzą część energii w postaci potencjalnej (sprężystość w układach mechanicznych,

pojemność w układach elektrycznych, ściśliwość gazów w układach pneumatycznych),

3) powodują straty energetyczne sygnału pomiarowego (tarcie w układach mechanicznych,

rezystancja w układach elektrycznych, opory przepływu gazu i cieczy w układach
pneumatycznych i hydraulicznych).

Jeżeli wielkości mierzone są niezależne od czasu, czyli gdy nastąpiło już ustalenie się

sygnału, np. po włączeniu układu pomiarowego lub po zmianie sygnału pomiarowego, to
mamy doczynienie z pomiarami statycznymi. Natomiast gdy wielkość mierzona zmienia się
tak szybko, że sygnał wyjściowy przetwornika nie nadąża za sygnałem wejściowym mówimy
o pomiarach dynamicznych. Stad też i błędy przetwarzania sygnału dzielimy na:

• statyczne i
• dynamiczne.

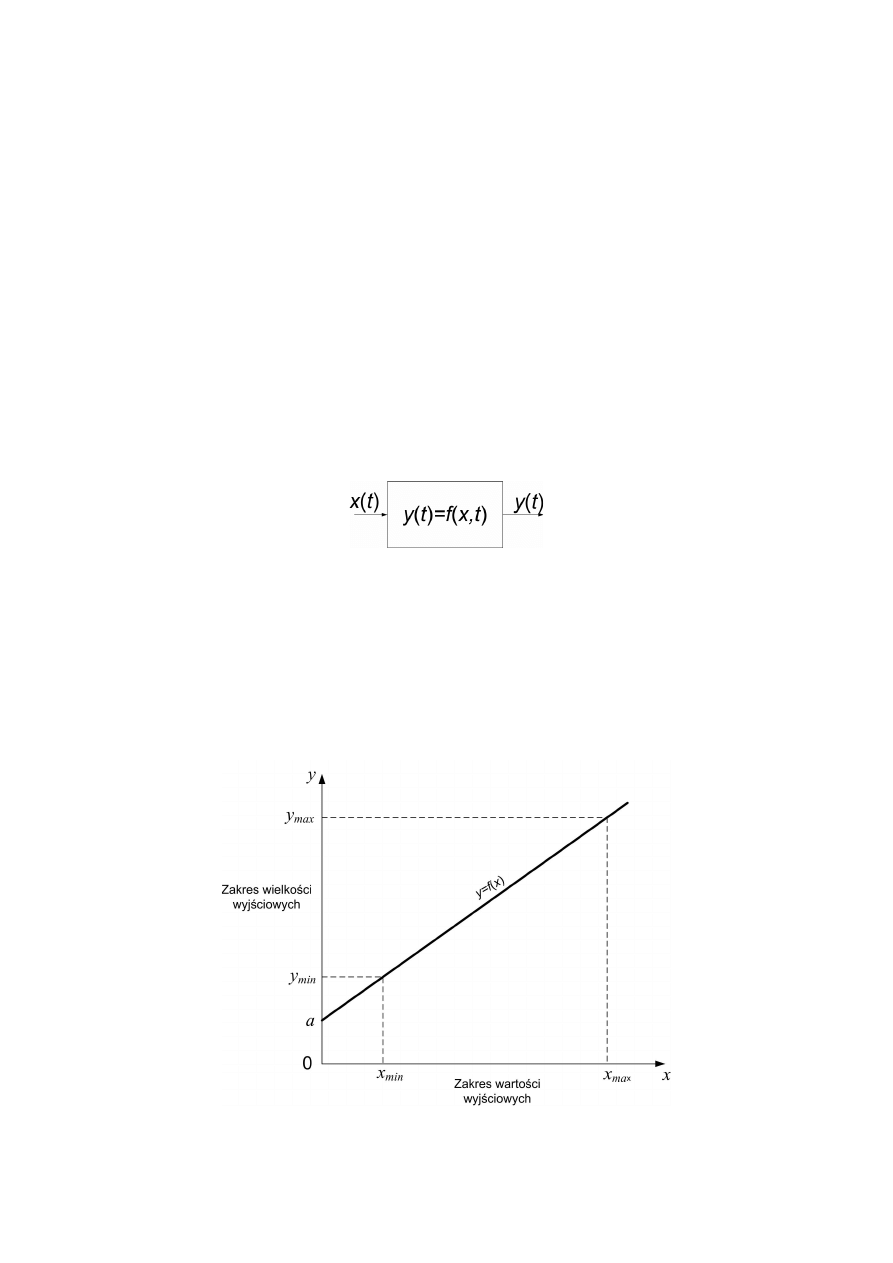
W warunkach dynamicznych w przetwarzaniu sygnałów należy uwzględnić czas i

przetwornik schematycznie przedstawia się w postaci pokazanej na rys. 3.2.

Rys. 3.2. Przetwornik pomiarowy w warunkach dynamicznych

Statyczne właściwości przetworników pomiarowych

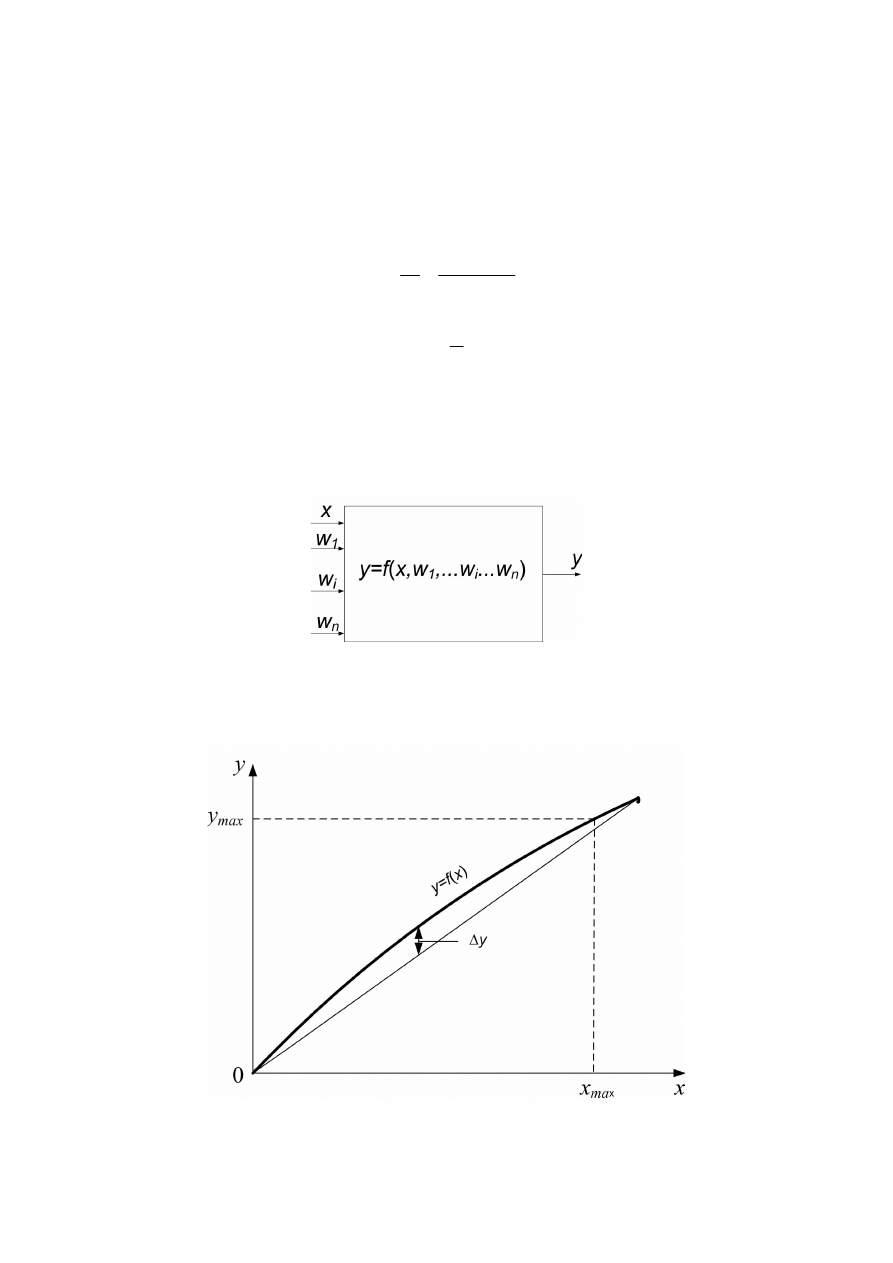
Charakterystyka przetwornika y = f(x) może mieć charakter:

• liniowy – przetwarzanie liniowe (rys. 3.3),
• nieliniowy – przetwarzanie nieliniowe.

Rys. 3.3. Charakterystyka przetwornika liniowego

3

Najczęściej stosuje się przetworniki o charakterystyce liniowej (rys. 3.3):

y = Sx + a ,

gdzie: a jest przesunięciem charakterystyki w stosunku do początku układu współrzędnych,

S – czułością przetwornika zdefiniowaną wzorem:

min

max

min

max

x

x

y

y

x

y

S

−

−

=

=

d

d

.

Odwrotność czułości jest stałą przetwarzania:

S

c

1

=

.

Najczęściej a = 0 oraz często x

min

= 0 i y

min

= 0. Wówczas x = cy.

W rzeczywistości sygnał wyjściowy jest funkcją nie tylko sygnału mierzonego x, ale

także wielu wielkości zakłócających w

1

÷

w

n

, czyli y = f(x, w

1

÷

w

n

). Schemat takiego

przetwornika pokazano na rys. 3.4.

Rys. 3. 4. Przetwornik rzeczywisty reagujący na sygnały zakłócające

Przetwornik może mieć charakterystykę odbiegającą od liniowej. Jego nieliniowość

przetwarzania charakteryzuje błąd przetwarzania ∆y (rys. 3.5).

Rys. 3.5. Nieliniowość przetwarzania

4

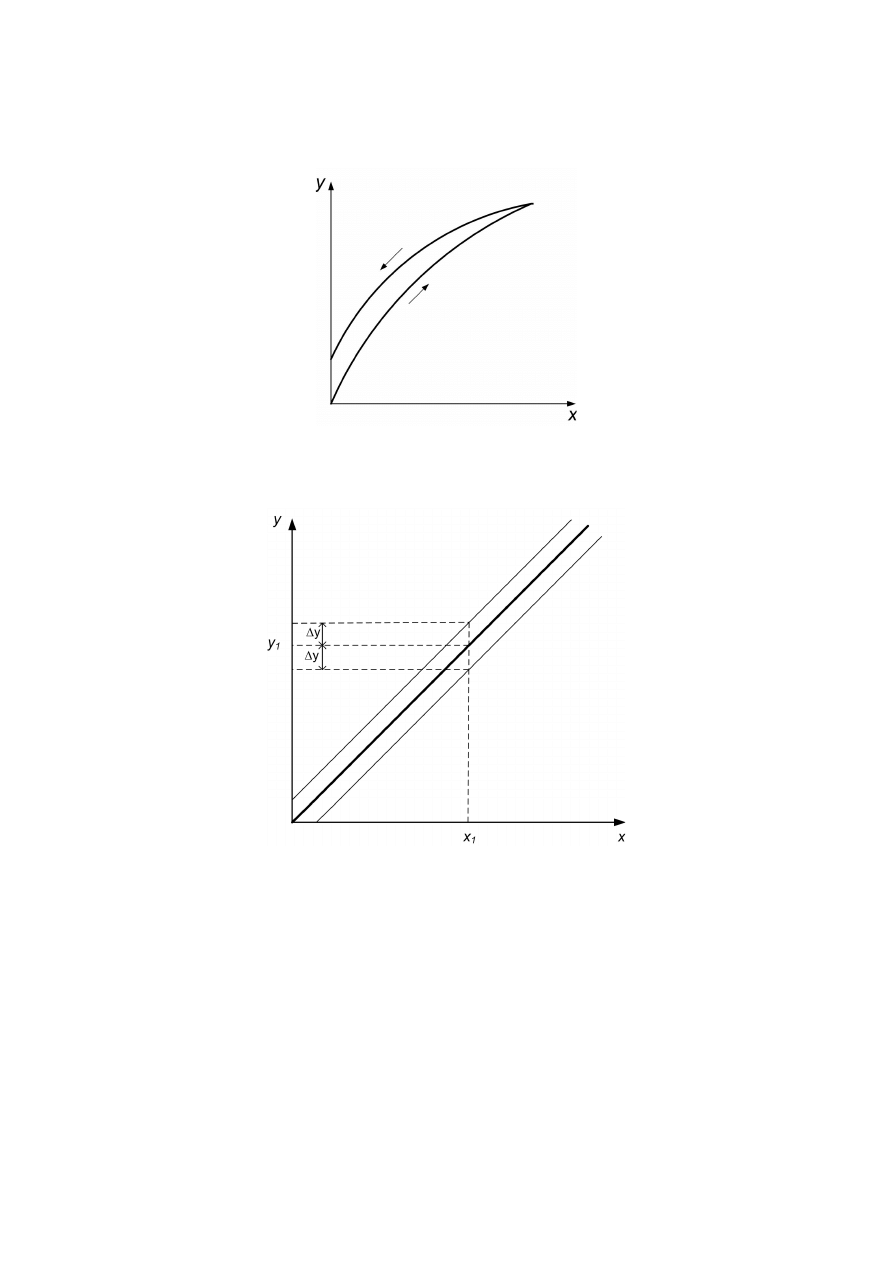
Przetwornik może mieć inną charakterystykę dla sygnały rosnącego i inną dla sygnału

malejącego, czyli mieć histerezę (rys. 3.6).

Rys. 3.6. Histereza przetwornika

Najważniejszym parametrem przetworników jest niedokładność przetwarzania (rys.

3.7).

Rys.3.7. Niedokładność przetwarzania

Jednej wartości sygnału wejściowego x

1

może odpowiadać pomiarowy wyjściowy sygnał y

1p

przedziału

y

y

y

y

y

w

∆

+

≤

≤

∆

−

1

1

1

.

METODY POMIAROWE

Metoda pomiarowa określa sposób realizacji pomiaru. Można je podzielić według:

1) sposobu przetwarzania sygnału,
2) sposobu uzyskiwania wyników,
3) sposobu porównania realizowanego w czasie procesu pomiarowego,

5

Ze względu na sposób przetwarzania sygnału metody pomiarowe dzielimy na:

1) bezpośredniego porównania,
2) pośredniego porównania,
3) różnicowe.

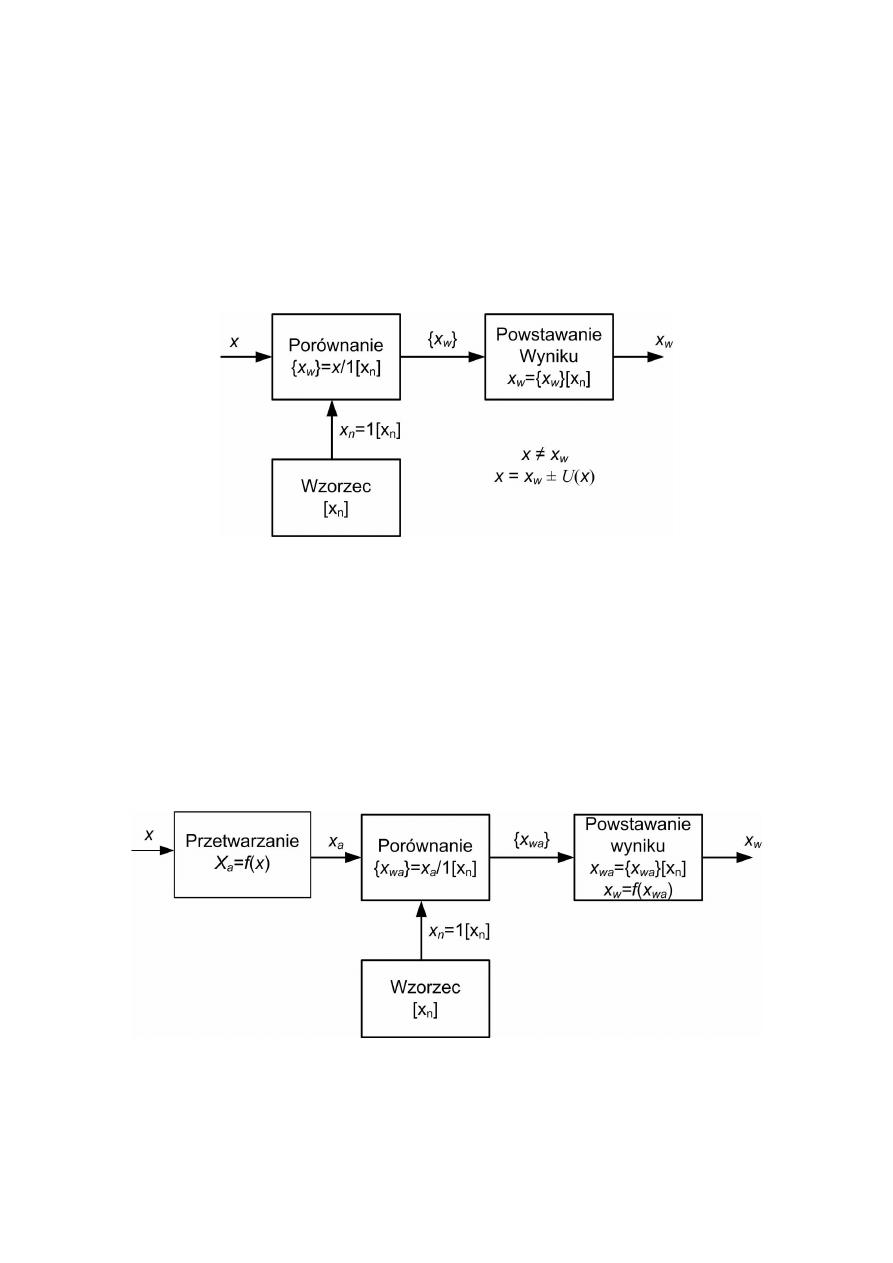
Metody bezpośredniego porównania

Łańcuch pomiarowy jest tu najkrótszy (rys. 3.8), co zapewnia największa dokładność

pomiarów. Przykładem może być pomiar długości przymiarem liniowym.

Rys. 3.8. Metoda bezpośredniego porównania

Otrzymany wynik pomiaru x

w

różni się od wartości rzeczywistej (prawdziwej) x, która

występuje w przedziale

( )

( )

x

U

x

x

x

U

x

w

w

+

≤

≤

−

.

Metody pośredniego porównania

Następuje tu przetworzenie wartości wielkości mierzonej na wartość innej wielkości
porównywanej z odpowiednim wzorcem jednostki miary (rys. 3.9). Tak realizowana jest
większość pomiarów.

Rys. 3.9. Metoda pośredniego przetwarzania

6

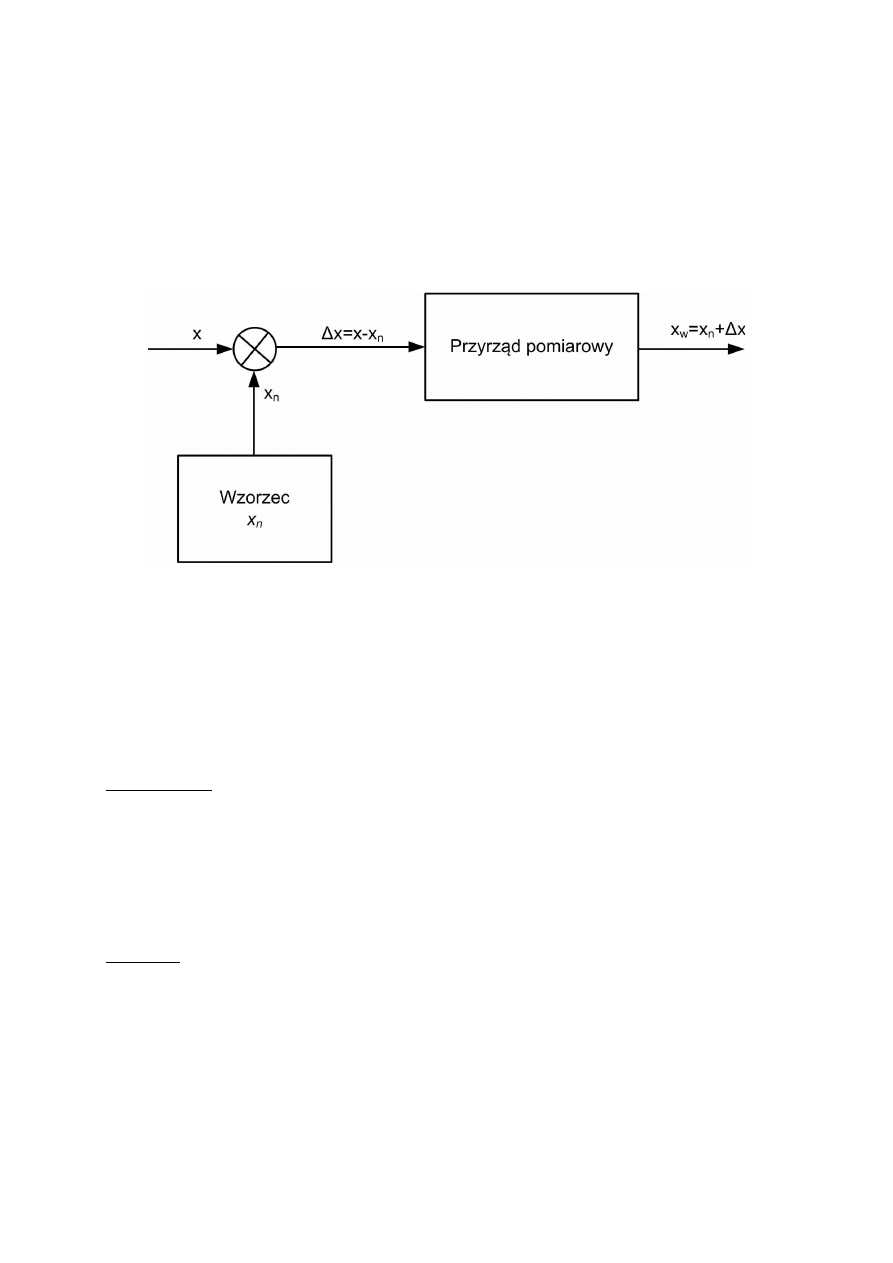
Metody różnicowe

W metodach bezpośredniego porównania teoretycznie wielkość mierzona x jest równa

wielkości wzorcowej x

n

i różnica tych wielkości jest równa 0. Tę metodę w bardzo

dokładnych pomiarach trudno jest zrealizować, gdyż wymaga zastosowania wzorca
regulowanego z taką precyzją aby wartość wielości wzorcowej była równa wartości wielkości
mierzonej. Z tego względu w pomiarach, w których wymaga się dużej dokładności,
najczęściej stosuje się metodę różnicową (rys. 3.10).

Rys. 3.10. Metoda różnicowa

Dokładność pomiaru metodą różnicową jest tym większa im mniejsza jest różnica ∆x.

Ze względu na sposobu uzyskiwania wyników metody pomiarowe dzielimy na:

1) proste (bezośrednie),
2) złożone (pośrednia).
W metodach prostych wynik pomiaru x

w

jest identyczny w sensie fizycznym z wielkością

mierzoną x i jest funkcją jednej wielkości (x ≅ x

w

).

Przykłady:

- pomiar masy wagą,

- pomiar napięcia woltomierzem.

W metodach złożonych (pośrednich) wynik pomiaru y jest funkcją wielu wielkości

mierzonych bezpośrednio. Oblicza się go ze złożonych funkcji:

(

)

wn

wi

w

w

w

x

x

x

x

f

y

y

...

...

,

2

1

=

≅

.

Przykład: Pomiar rezystancji metoda pośrednią przez pomiar prądu płynącego przez mierzony
rezystor i napięcia na tym rezystorze. Wynik pomiaru rezystancji oblicza się ze wzoru
R = U/I.

Ze względu na sposób porównania realizowanego w czasie procesu pomiarowego

metody pomiarowe dzielimy na:

1) zerowe,
2) wychyleniowe i cyfrowe,
3) koincydencyjne.

7

Metody zerowe

Metody te polegają na sprowadzeniu do zera (w rzeczywistości do progu nieczułości
detektora) różnicy między wartością mierzoną x i wzorcową x

n

. Jeżeli różnica

∆x = x – x

n

,

to

x

w

≅ x = x

n

.

Metody wychyleniowe i cyfrowe

Wartość wyniku uzyskuje się tu bezpośrednio ze wskazań przyrządów pomiarowych

analogowych (wychylenie wskazówki na skali przyrządu) i cyfrowych (wyświetlone cyfry na
polu cyfrowym).

Metody koincydencyjne

Pomiar polega tu na koincydencji pewnych wskazań lub sygnałów małej różnicy

między wartością mierzoną x i wartością wzorcową x

n

. Przykład: sposób pomiaru długości

suwmiarka z noniuszem.