II rok EiT
Szymikowski Mateusz
Pettke Radosław
Pietkiewicz Adam

Ćwiczenie nr4

Badanie parametrów charakteryzujących wiązkę

laserową (gaussowską)

Wstęp

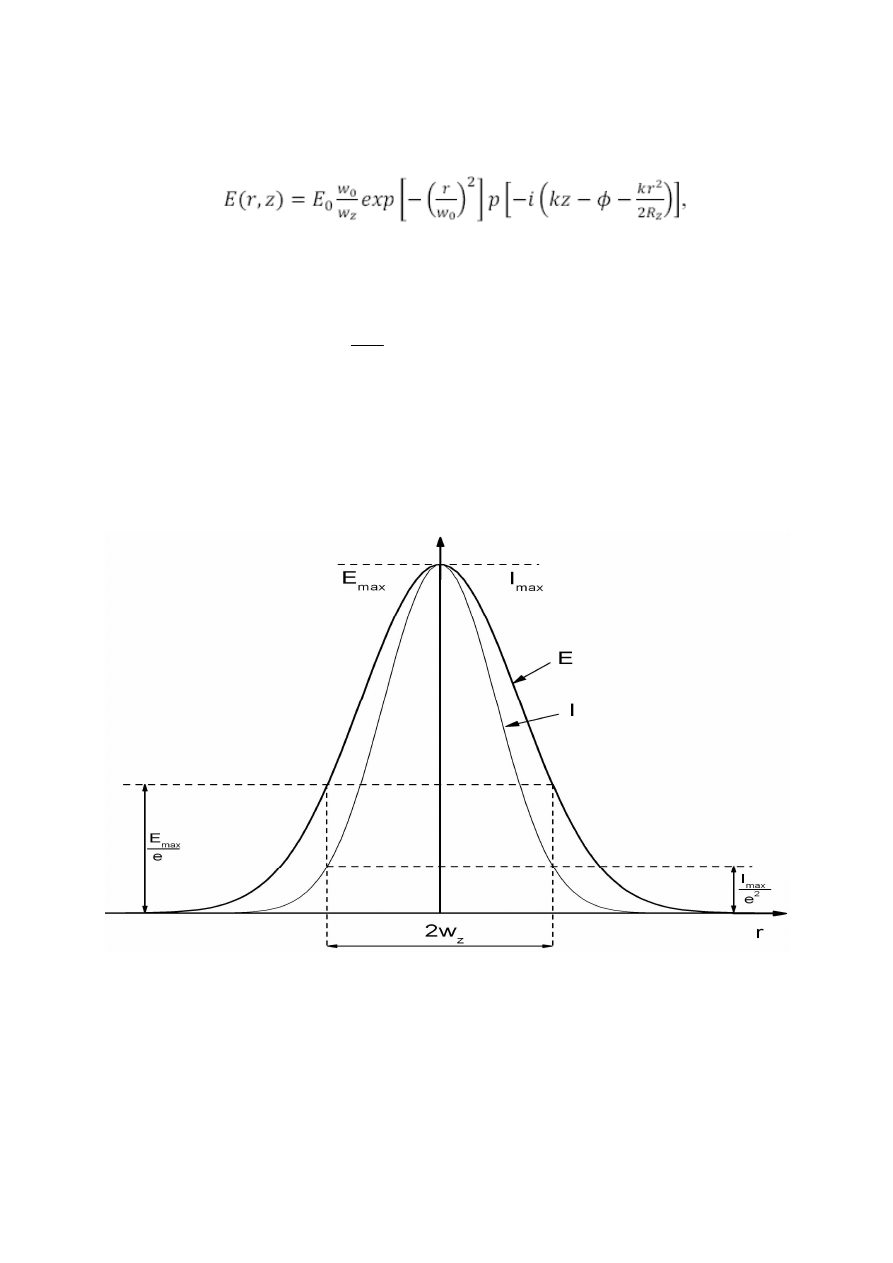
Wiązkę laserową dla modu podstawowego (TEM

00

) opisuje funkcja Gaussa. Wiązka ta jest

podstawowym rodzajem drgań generowanych przez laser i opisana jest równaniem :

Gdzie:
E(r,z) – amplituda wiązki w przekroju z w punkcie odległym o r od osi optycznej,
E

0

– wartość pola w z=0,

2w

0

– średnica wiązki laserowej w z=0 (tzw. przewężenie wiązki),

k – kołowa liczba falowa równa









2

k

λ- długość emitowanego promieniowania (dla lasera Nd:YAG używanego w ćwiczeniu λ=532nm),
2w

z

– średnica wiązki laserowej w płaszczyźnie odległej o z od przewężenia,

R

z

– promień krzywizny czoła fali w odległości z od przewężenia.

Zgodnie z definicją, przez średnicę wiązki laserowej w danym przekroju poprzecznym z rozumie
się średnicę okręgu utworzonego przez punkty, w których wartość amplitudy pola maleje e razy
względem jej wartości maksymalnej, lub odpowiednio intensywność wiązki zmaleje e

2

razy.

Rozkład amplitudy i natężenia wiązki laserowej w przekroju poprzecznym w odległości z od

przewężenia.

Zadania

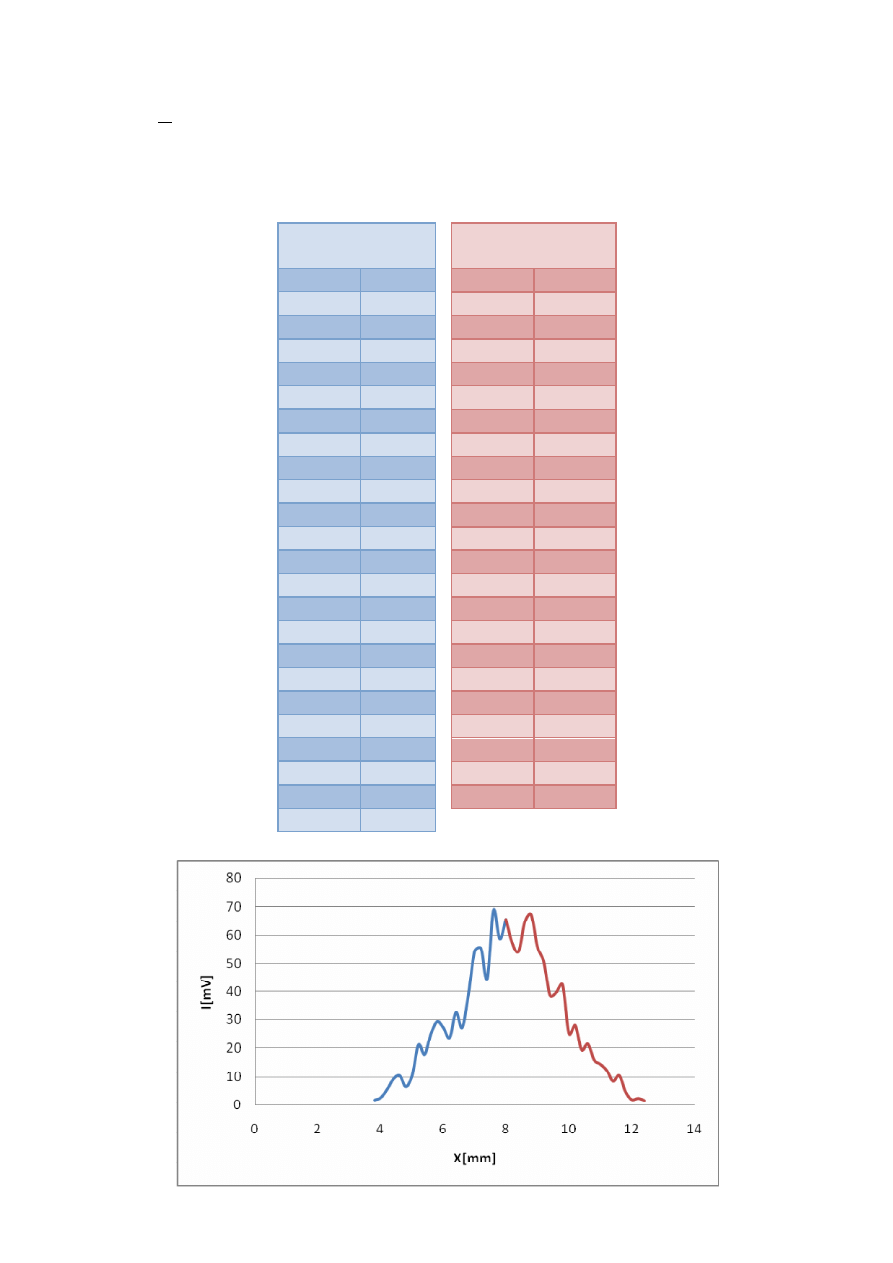
1.Wyznaczyć średnicę wiązki laserowej dla każdego profilu, mierząc jego szerokość na

poziomie natężenia maksymalnego. ∆

z = 10[cm]

a) z = 29[cm]

Inkrementacja

2mm

X[mm]

I[mV]

8

65,7

8,2

57,3

8,4

54,3

8,6

64,9

8,8

67,4

9

56

9,2

50,6

9,4

38,7

9,6

39,8

9,8

42,4

10

25,2

10,2

28,1

10,4

19,4

10,6

21,4

10,8

16

11

14,5

11,2

12,4

11,4

8,5

11,6

10,5

11,8

4,7

12

2

12,2

2,5

12,4

1,7

Dekrementacja

2mm

X[mm]

I[mV]

8

65,7

7,8

58,8

7,6

68,9

7,4

44,7

7,2

55,5

7

54,4

6,8

39,2

6,6

27,2

6,4

32,5

6,2

23,7

6

27,1

5,8

29,3

5,6

25

5,4

17,7

5,2

21

5

10,5

4,8

6,5

4,6

10,4

4,4

9,2

4,2

5,6

4

2,7

3,8

1,8

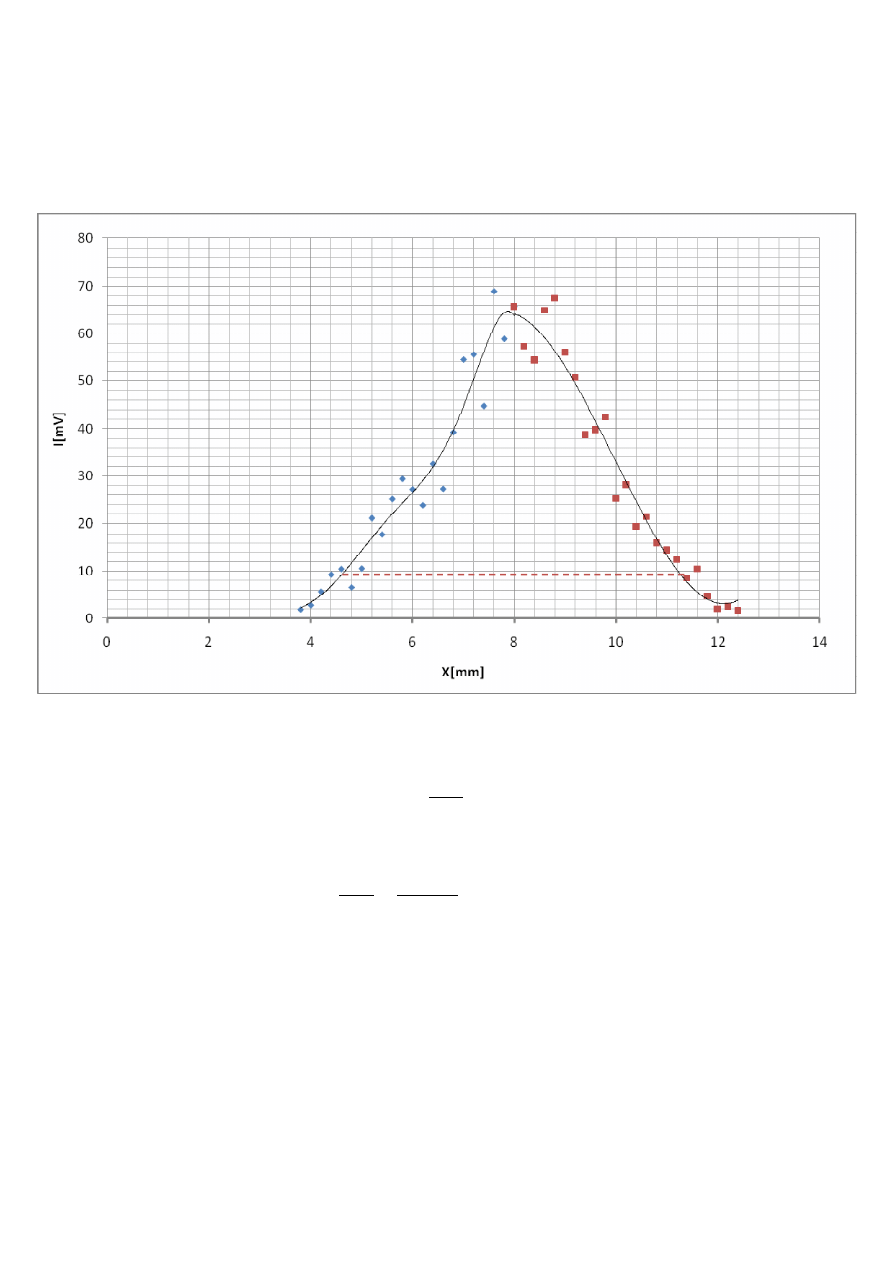
z = 29 [cm]

= 68,9[

]

=

68,9

≈ 9,32[mV]

Średnica wiązki laserowej dla z = 29[cm] wynosi około 6,8[mm

].

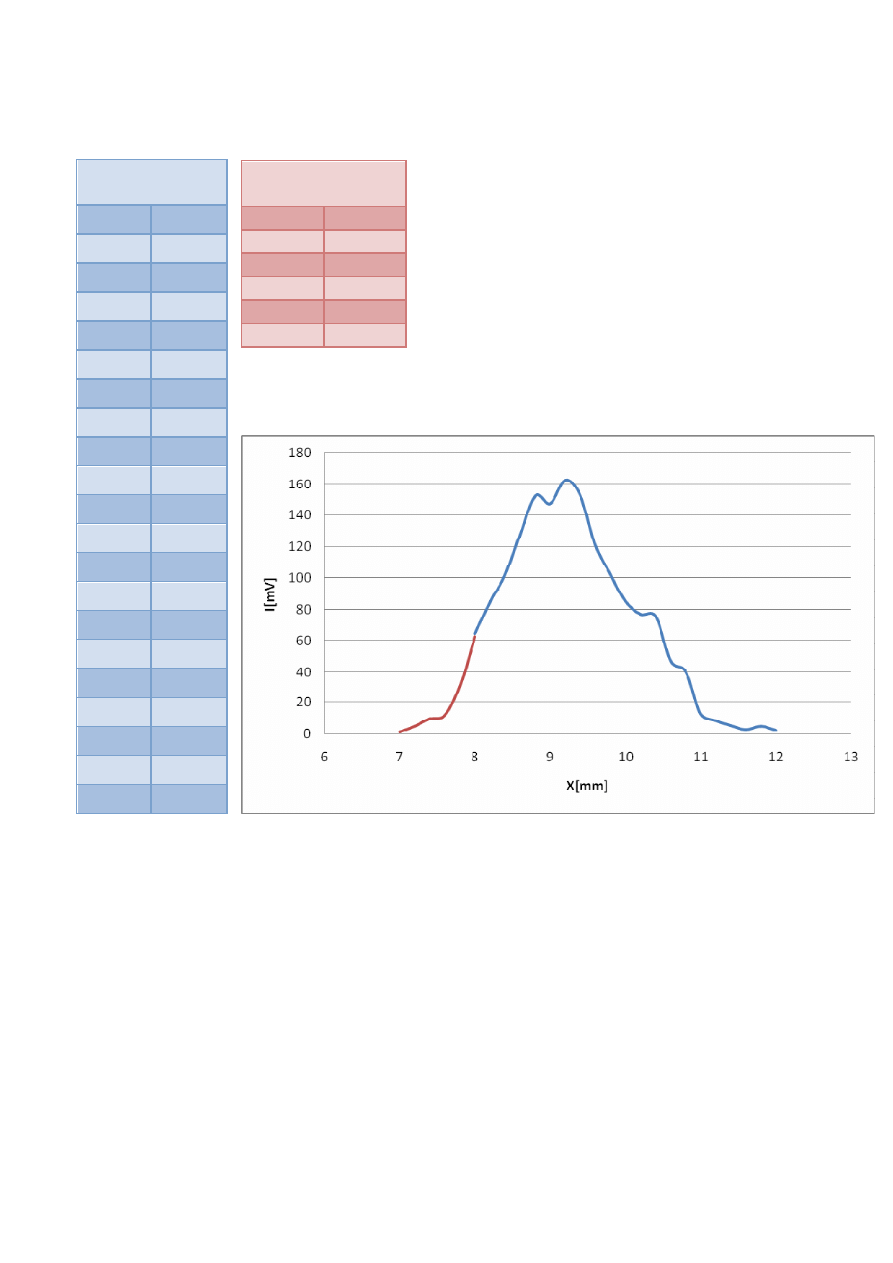
b) z - ∆z = 19[cm]

Inkrementacja

2mm

8

64,6

8,2

85,4

8,4

102,1

8,6

127,9

8,8

152,3

9

147,5

9,2

162,4

9,4

152,5

9,6

121,3

9,8

102,5

10

85,1

10,2

77,1

10,4

76

10,6

46,9

10,8

40,2

11

13,1

11,2

8,3

11,4

5,2

11,6

2,6

11,8

4,7

12

2

Dekrementacja

2mm

8

62,9

7,8

31,6

7,6

12,3

7,4

9,7

7,2

5

7

1,3

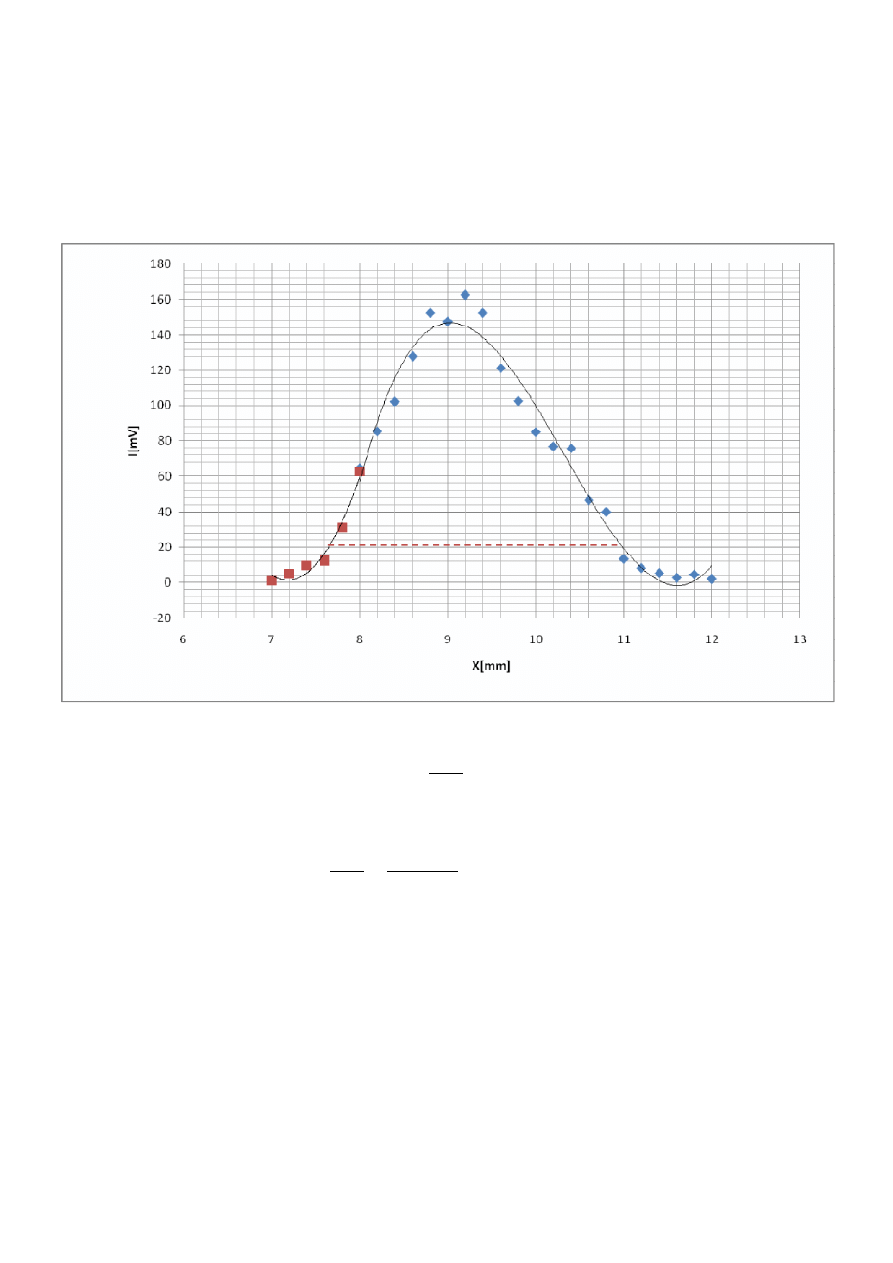
z - ∆z = 19[cm]

= 162,4[

]

=

162,4

≈ 21,98[mV]

Średnica wiązki laserowej dla z

-

∆z = 19[cm] wynosi około 3,3[mm

].

Dekrementacja

2mm

8

28,5

7,8

21,3

7,6

24

7,4

23,5

7,2

22,9

7

20,7

6,8

18,4

6,6

19,5

6,4

19,6

6,2

21,4

6

25,2

5,8

19,9

5,6

25,7

5,4

20,8

5,2

20,6

5

18,1

4,8

25,5

4,6

20,5

4,4

17,1

4,2

10,8

4

11,6

3,8

18,8

3,6

18,5

3,4

11,8

3,2

11,9

3

8,8

2,8

9,8

2,6

10,8

2,4

8,1

2,2

12,2

2

6,5

1,8

6,7

1,6

8,3

1,4

3,2

1,2

3,6

1

2,7

0,8

2,4

0,6

1,7

c) z + ∆z = 39[cm]

Inkrementacja

2mm

8

28,5

8,2

17,3

8,4

17,2

8,6

13,2

8,8

15,1

9

11,7

9,2

8,7

9,4

10,5

9,6

9,6

9,8

11,5

10

8,7

10,2

5,3

10,4

10,1

10,6

6,9

10,8

5,4

11

5

11,2

5,5

11,4

5,1

11,6

3,9

11,8

2

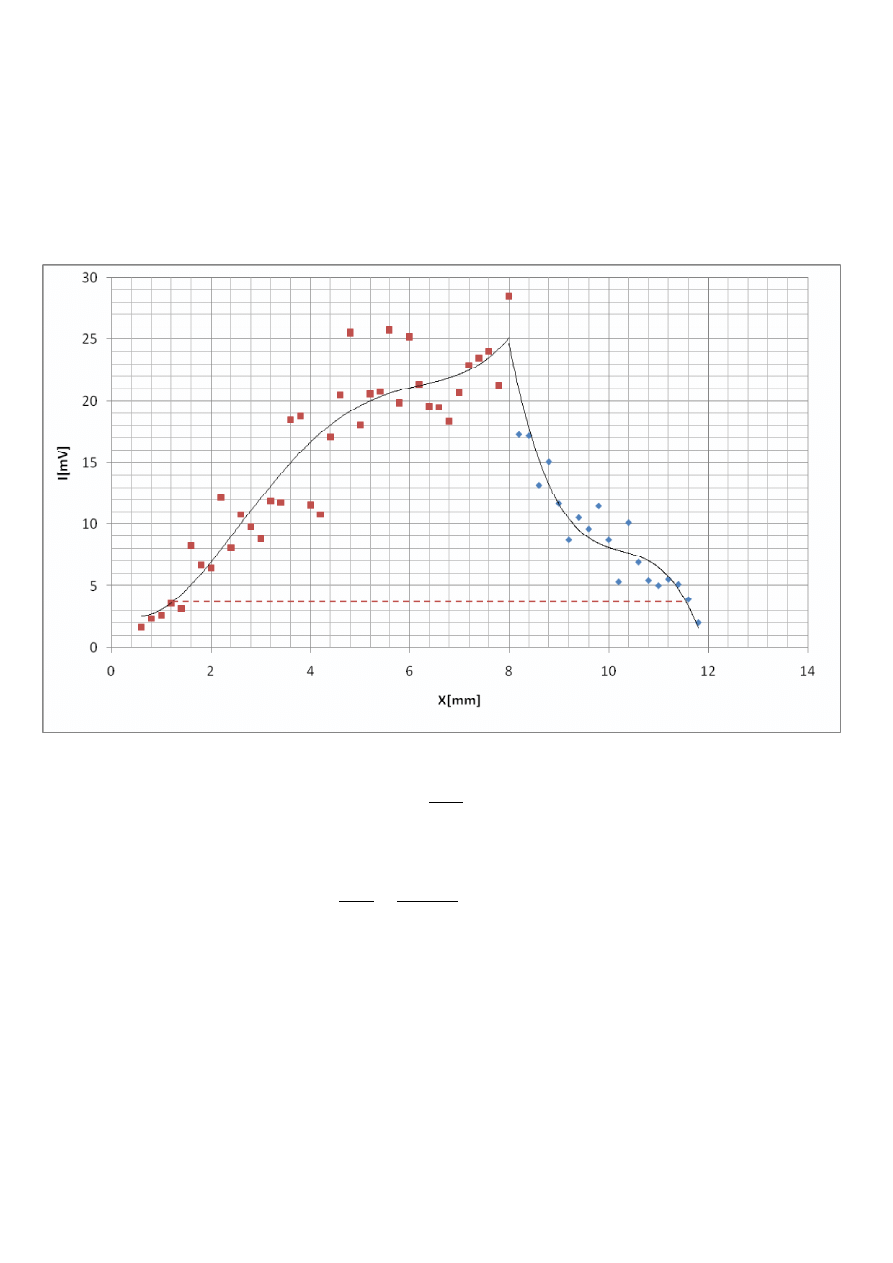
z + ∆z = 39[cm]

= 28,5[

]

=

28,5

≈ 3,86[mV]

Średnica wiązki laserowej dla z

+

∆z = 39[cm] wynosi około 10,4[mm

].

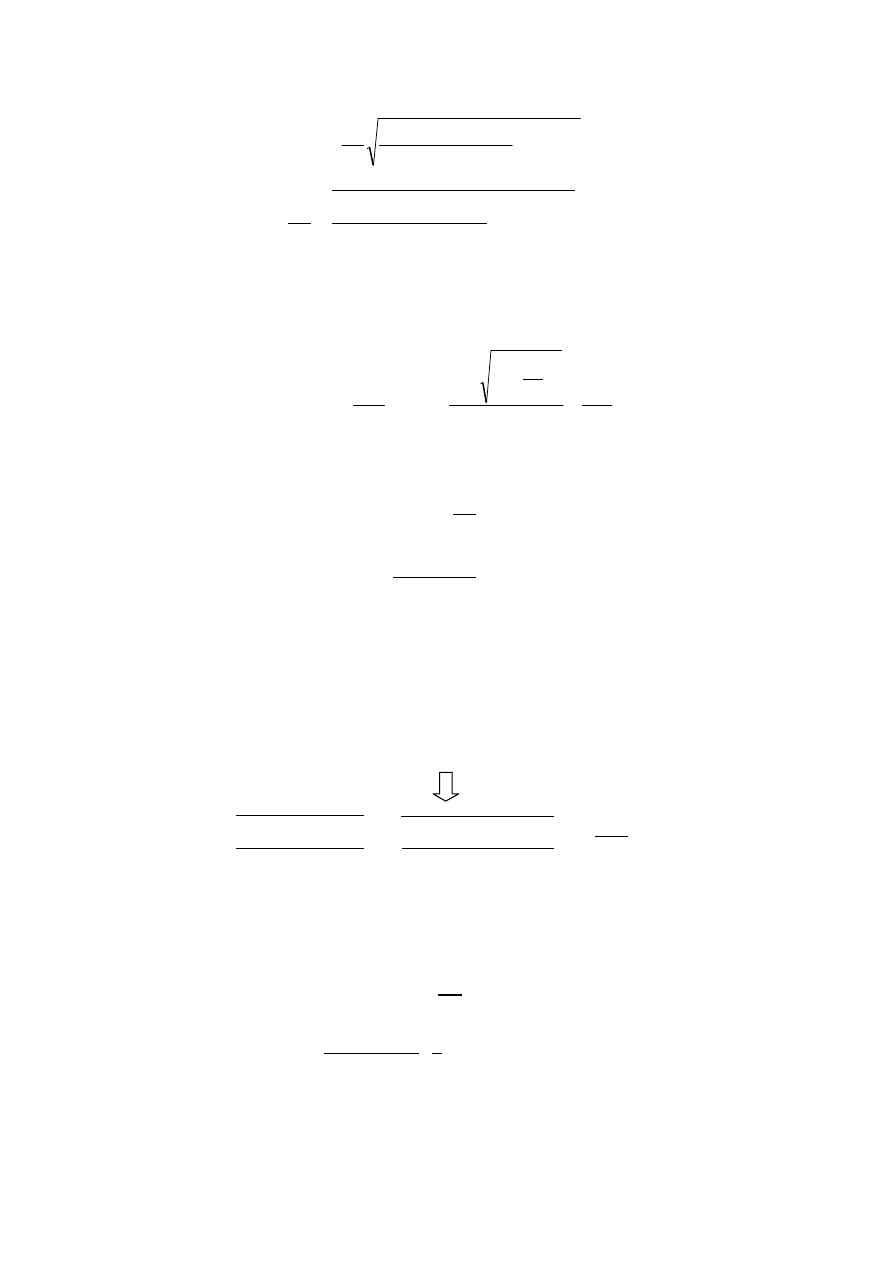
2. Obliczyć kąt rozbieżności wiązki laserowej.

Znając średnice wiązki laserowej dla różnych odległości możemy obliczyć kąt rozbieżności wiązki ze wzoru:

=

1

0,1

(0,021) + (0,007)

2

− (0,014) ≈ 0,07⁰

3. Obliczyć średnicę przewężenia wiązki laserowej.

0

2

0

2

2

1

2

2

lim

lim

w

z

D

z

w

z

w

z

z

z















































Po przekształceniu:





2

0



w

=

2 ⋅ 532

⋅ 0,07⁰

≈ 4,8

4. Obliczyć odległość płaszczyzny przewężenia od płaszczyzny wyjściowej (odległość z).

W celu obliczenia

z przekształcamy poniższy wzór:

(2

) = (2

) + ( ⋅ )

=

(2

) − (2

)

=

(0,014) − (10 )

0,0049

≈ 0,04 = 0,2[m]

5. Obliczyć parametr konfokalny.

=

D =

2π

532 ⋅ 10 m

⋅

1
4

⋅ 10

m = 0,2mm

2

2

2

)

2

(

2

)

2

(

)

2

(

1

z

z

z

w

w

w

z















6. Obliczyć promień krzywizny czoła fali w płaszczyźnie wyjściowej.

R = −z 1 +

π ⋅ w

λ ⋅ z

= −0,2 1 +

1
4

10

532 ⋅ 10

⋅ 0,2

≈ −0,2