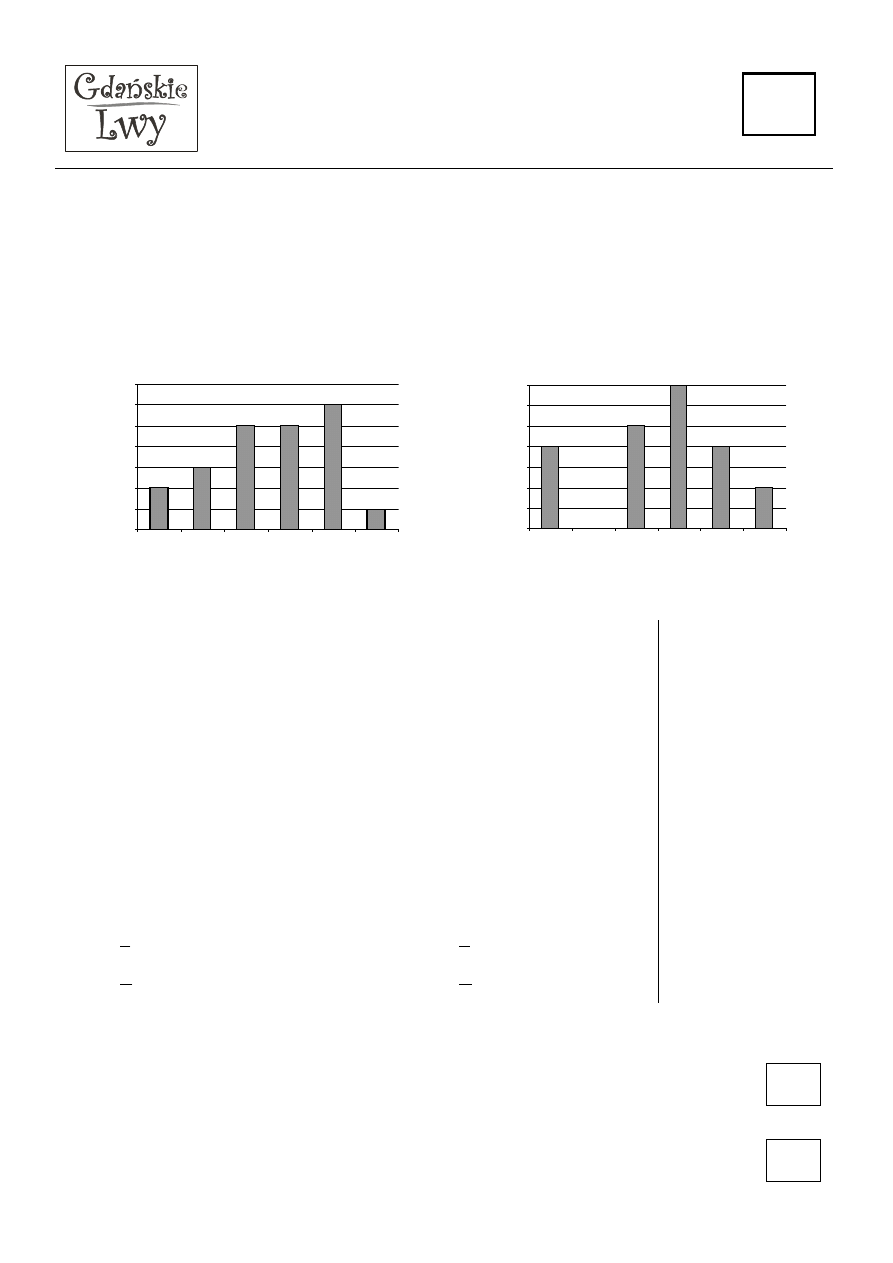
1

Matematyka – test dla uczniów klas piątych

szkół podstawowych w roku szkolnym 2008/2009

Etap międzyszkolny (60 minut)

[suma punktów]

Imię i nazwisko .................................................................................... Szkoła .............................................

Informacje do zadań od 1. do 4.

Na diagramach przedstawiono dane dotyczące wyników sprawdzianu przeprowadzonego w dwóch
klasach piątych pewnej szkoły podstawowej.

Klasa Va

0

1

2

3

4

5

6

7

1

2

3

4

5

6

ocena

li

c

z

b

a

u

c

z

n

ió

w

Klasa Vb

0

1

2

3

4

5

6

7

1

2

3

4

5

6

ocena

li

c

z

b

a

u

c

z

n

ió

w

Nazwy ocen: 6 – celujący, 5 – bardzo dobry, 4 – dobry, 3 – dostateczny, 2 – dopuszczający, 1 - niedostateczny

Podkreśl poprawne odpowiedzi w zadaniach od 1. do 3.

Brudnopis

1. W klasie Va ocenę bardzo dobrą otrzymało

a) 10 uczniów.

b) 6 uczniów.

c) 5 uczniów.

d) 4 uczniów.

2. Liczba uczniów klasy Vb, którzy otrzymali co najmniej ocenę

dopuszczającą to

a) 0.

b) 3.

c) 18.

d) 20.

3. W każdej z klas sprawdzian pisało 22 uczniów. W obydwu klasach łącznie

uczniowie, którzy otrzymali ocenę dobrą, stanowili

a)

11

3

wszystkich piszących.

b)

11

6

wszystkich piszących.

c)

22

5

wszystkich piszących.

d)

22

7

wszystkich piszących.

4. Wpisz w kratkę literę P, jeśli zdanie jest prawdziwe lub literę F jeśli zdanie jest fałszywe.

a) Najwyższą ocenę otrzymali uczniowie, którzy uzyskali maksymalną liczbę punktów.
Na podstawie diagramów nie można ustalić, ilu ich było, gdyż nie podano możliwej do

uzyskania liczby punktów.

b) W dniu sprawdzianu było nieobecnych dwóch uczniów klasy Va i trzech uczniów
klasy Vb. Zatem klasa Vb jest bardziej liczna niż klasa Va.

2

W zadaniach od 5. do 13. podkreśl poprawne odpowiedzi.

Brudnopis

5. Mateusz chciał kupić jak najdokładniejszą mapę Pomorza. W sklepie

dostępne były cztery różne mapy tego regionu. Mateusz powinien wybrać
mapę wykonaną w skali

a) 1 : 40 000.

b) 1 : 50 000.

c) 1 : 70 000.

d) 1 : 90 000.

6. Średnia odległość Ziemi od Słońca wynosi 15 ⋅ 10

7

km czyli

a) 0,15 mln km.

b) 1,5 mln km.

c) 15 mln km.

d) 150 mln km.

7. Tort urodzinowy podzielono na 12 równych części w sposób pokazany na

rysunku. Kąt między dwiema krawędziami jednego kawałka (zaznaczony

na rysunku łukiem) ma miarę

a) 20˚.

b) 30˚.

c) 45˚.

d) która zależy od wielkości tortu.

8. Kostka masła waży 250 g. W sklepie znajduje się 10 takich kostek, czyli

a) 0,25 kg masła.

b) 2,5 kg masła.

c) 25 kg masła.

d) 2500 kg masła.

9. Powierzchnia jeziora Hańcza wynosi 3,1 km

2

, czyli

a) 310 ha.

b) 31 ha.

c) 0,31 ha.

d) 0,031 ha.

10

.

Ewa ma dwa razy mniej pieniędzy niż Kuba. Gdy Kuba dał Ewie 18 zł, to

tym razem on miał dwa razy mniej pieniędzy niż Ewa. Razem mają

a) 36 zł.

b) 54 zł.

c) 64 zł.

d) inną kwotę niż podane.

11

.

Jedna puszka farby wystarcza na pomalowanie 15 m

2

powierzchni.

Najmniejsza liczba puszek, które należy kupić, aby móc pomalować
dwukrotnie ściany pokoju o łącznej powierzchni 47 m

2

to

a) 4.

b) 6.

c) 7.

d) 8.

12

.

Jeden z kątów przyległych ma miarę o 34˚ mniejszą od miary drugiego

kąta. Zatem

a) miara drugiego kąta to 146˚.

b) drugi z kątów jest kątem prostym.

c) jeden z tych kątów ma miarę równą 73˚.

d) każdy z tych kątów ma miarę mniejszą niż 100˚.

3

13

.

Uczestnicy koła plastycznego wykonali pięć żurawi origami. Każdy z nich

powstał poprzez zginanie kartki papieru w kształcie kwadratu o przekątnej
długości 20 cm. Na wykonanie wszystkich żurawi zużyto łącznie

Brudnopis

a) 200 cm

2

papieru.

b) 400 cm

2

papieru.

c) 1000 cm

2

papieru.

d) 2000 cm

2

papieru.

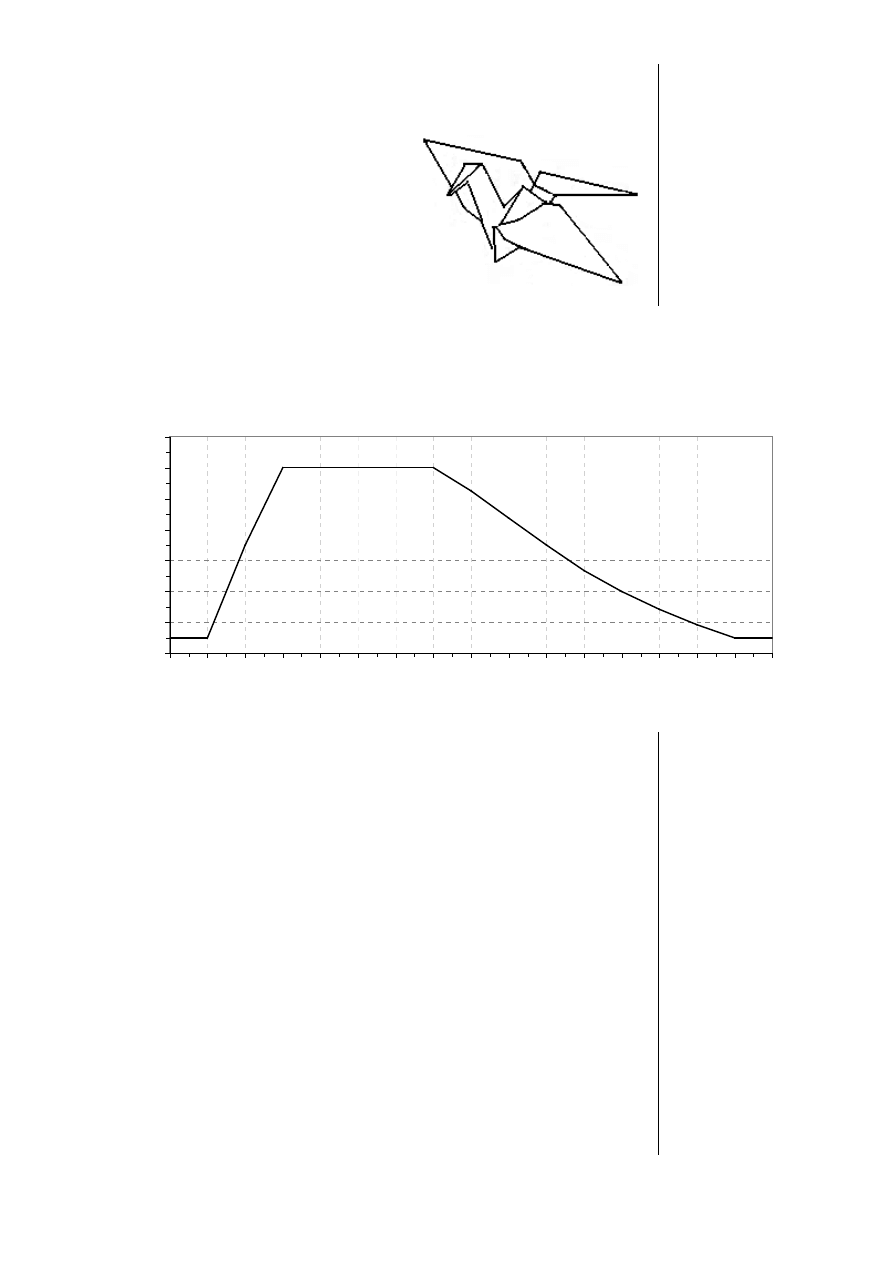
Na podstawie poniższego wykresu, podkreśl poprawne odpowiedzi w zadaniach od 14. do 17.

Wykres przedstawia zmiany temperatury piekarnika w godzinach od 11:50 do 14:30.

0

40

80

120

160

200

240

280

11:50 12:00 12:10 12:20 12:30 12:40 12:50 13:00 13:10 13:20 13:30 13:40 13:50 14:00 14:10 14:20 14:30

godzina

te

m

p

e

ra

tu

ra

[

o

C

]

14

.

O godzinie 12:10 temperatura w piekarniku wynosiła około

Brudnopis

a) 100˚C.

b) 120˚C.

c) 140˚C.

d) 160˚C.

15

.

Termometr na drzwiach piekarnika dwukrotnie wskazał 80˚C. Między

pierwszym i drugim wskazaniem tej temperatury upłynęła

a) mniej niż 1 h.

b) 1 h 5 min.

c) 1 h 35 min.

d) 1 h 45 min.

16

.

Przez pierwsze 20 min od momentu włączenia piekarnika temperatura

wzrosła o

a) 120˚C.

b) 140˚C.

c) 220˚C.

d) 240˚C.

17

.

Piekarnik wyłączono o godzinie

a) 12:20.

b) 13:00.

c) 14:20.

d) 14:30.

4

W zadaniach od 18. do 20. podkreśl poprawne odpowiedzi.

Brudnopis

18

.

Zegarek Kasi śpieszy się o 12 minut, a zegarek Wojtka późni o 3 minuty.

W momencie, gdy na zegarku Kasi była godzina 12:03, zegarek Wojtka
wskazywał godzinę

a) 11:48.

b) 11:54.

c) 12:12.

d) 12:15.

19

.

Konrad oczytał wskazanie wodomierza (patrz rysunek). Następnie nalał do

wanny 40 litrów wody. Wówczas wodomierz wskazywał

a) 134,505 m

3

.

b) 134,541 m

3

.

c) 134,901 m

3

.

d) 138,501 m

3

.

20

.

W szufladzie Piotrka znajduje się 6 skarpetek brązowych, 4 niebieskie

i 10 czarnych. Skarpetki różnią się między sobą tylko kolorem. W pokoju
Piotrka jest ciemno. Najmniejsza liczba skarpetek, które Piotrek powinien
wyjąć z szuflady, aby mieć pewność, że będą wśród nich dwie skarpetki
czarne, to

a) 2.

b) 10.

c) 12.

d) 20.

Rozwiąż zadanie 21.

21

.

Miejsca zamieszkania Bartka i Kamila są odległe o 12 km. Wyjeżdżając na wycieczkę rowerową,

chłopcy umówili się w połowie drogi między swoimi domami. Bartek jechał na spotkanie ze średnią
prędkością 18

h

km

. Choć Kamil wyjechał z domu 5 min później niż Bartek, na miejsce spotkania

obydwaj chłopcy przyjechali w tym samym momencie. Z jaką średnią prędkością jechał Kamil?

Obliczenia:

Odpowiedź: Kamil jechał ze średnią prędkością ......................

5

Wpisz w puste kratki liczby będące odpowiedziami do zadań od 22. do 23.

Brudnopis

22

.

Ala, Ola i Ula stoją w kolejce po bilety do kina. Między Alą i Ulą stoi

5 osób, przy czym Ula jest bliżej kasy niż Ala. Ola stoi tuż za Alą. Za Ulą
stoi 11 osób, a przed Olą 9 osób. Ile osób stoi w kolejce?

Informacja do zadania 23.

Palindrom – wyraz, liczba lub zdanie, które ma to samo znaczenie niezależnie
od tego, czy czytamy go od lewej do prawej strony, czy odwrotnie.
Przykłady liczb palindromicznych: 22, 56365, 1039301.

23

.

Maciek postanowił wypisać wszystkie trzycyfrowe liczby palindromiczne.

Ile liczb powinien zapisać Maciek?

Rozwiąż zadania od 24. do 25.

24

.

Ania i Zosia przygotowywały sztuczną biżuterię na szkolny festyn charytatywny. Każda z nich miała

wykonać taką samą liczbę naszyjników. Zrobienie jednego naszyjnika zajmuje Ani 6 minut, zaś Zosia
wykonuje taki sam naszyjnik w ciągu 8 minut. Gdy Ania zrobiła już umówioną liczbę naszyjników,
Zosi zostały jeszcze do zrobienia dwa naszyjniki. Ile naszyjników miała wykonać każda
z dziewczynek?

Obliczenia:

Odpowiedź: Każda z dziewczynek miała wykonać ......................................................

25

.

Marcin, Tomek i Paweł zbierają pieniądze na wspólne wakacje. Oszczędności Marcina stanowią

trzecią część oszczędności Tomka, zaś oszczędności Tomka – trzecią część oszczędności Pawła.
Paweł zgromadził o 96 zł więcej niż Marcin. Ile pieniędzy zaoszczędził Tomek?

Obliczenia:

Odpowiedź: Tomek zaoszczędził ......................

6

Wykonaj polecenie w zadaniu 26.

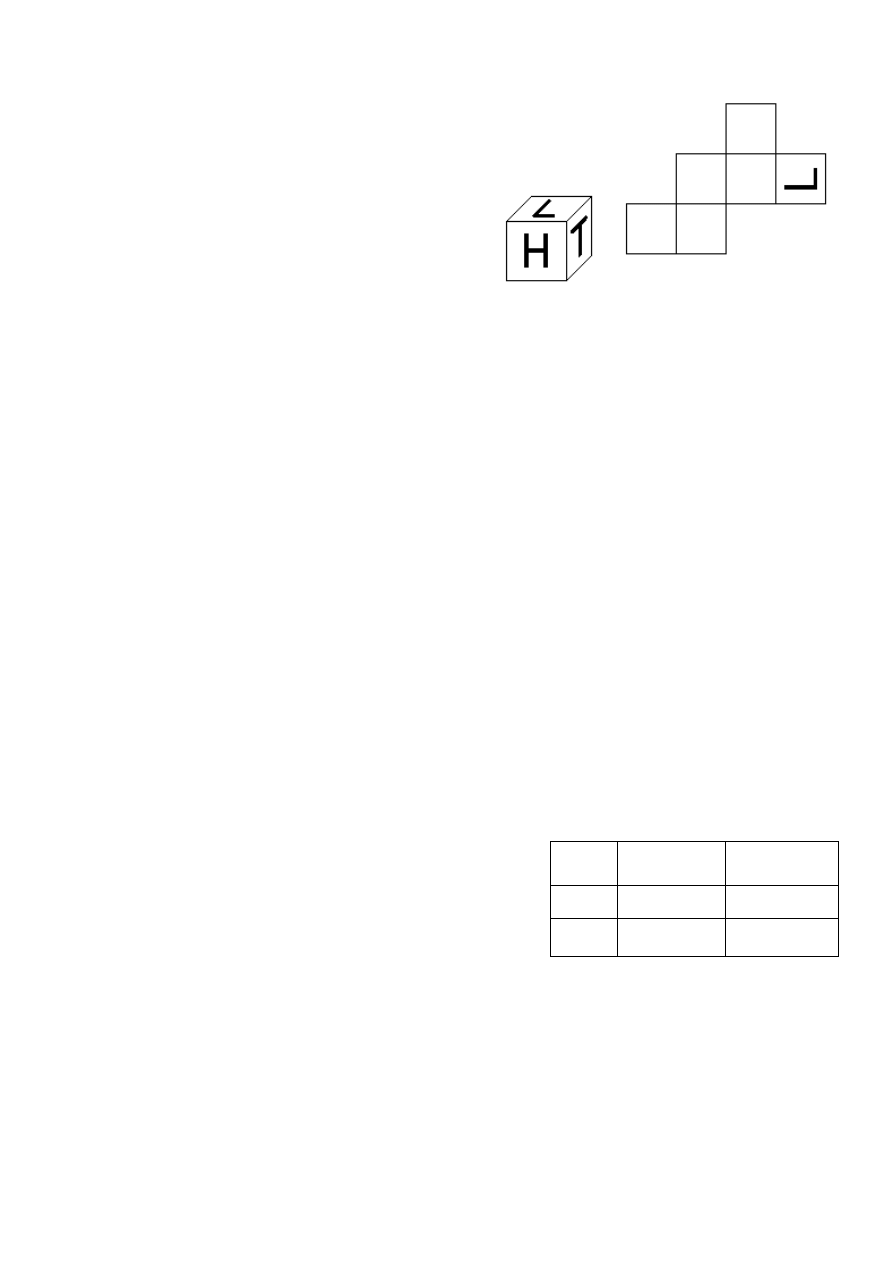
26

.

Na trzech widocznych ścianach sześcianu narysowano litery H, T, L.

Pozostałe ściany nie mają rysunków. Obok narysowano siatkę tego
sześcianu. Dorysuj, w odpowiednim miejscu i ułożeniu, brakujące
litery na siatce.

Rozwiąż zadania od 27. do 28.

27

.

Kacper, Wojtek i Olek wzięli udział w konkursie zorganizowanym przez klub osiedlowy „Barwa”.

Na specjalnie wydzielonym fragmencie muru malowali ilustracje do ulubionych książek. Zużyli
trzy puszki farby, które przyniósł Kacper i pięć takich samych puszek, które przyniósł Wojtek. Olek,
po dokonaniu obliczeń gwarantujących równy podział kosztów zakupu farb, oddał kolegom 40 zł do
podziału. Jak sprawiedliwie powinni podzielić miedzy siebie otrzymaną kwotę?

Obliczenia:

Odpowiedź: Kacper powinien otrzymać ......................, a Wojtek ......................

28

.

W klasie piątej jest 20 uczniów. Co miesiąc każdy z nich wrzucał do wspólnej skarbonki po jednej

monecie dwuzłotowej lub pięciozłotowej. Za zebrane pieniądze chcieli pojechać na wspólny piknik.
Po pięciu miesiącach Basia policzyła monety i chciała uzupełnić tabelkę, którą otrzymała
od nauczyciela (patrz poniżej). Wypełniając dane w tabeli pomyliła się i wpisała odwrotnie liczby
w kolumnie B. Otrzymana przez nią łączna kwota była o 78 zł niższa od rzeczywistej. Ile pieniędzy
zebrali uczniowie klasy piątej?

A

nominał

B

liczba monet

C

kwota

2 zł

Obliczenia:

5 zł

Odpowiedź: Uczniowie klasy piątej zebrali kwotę .....................