
Program produkcyjny
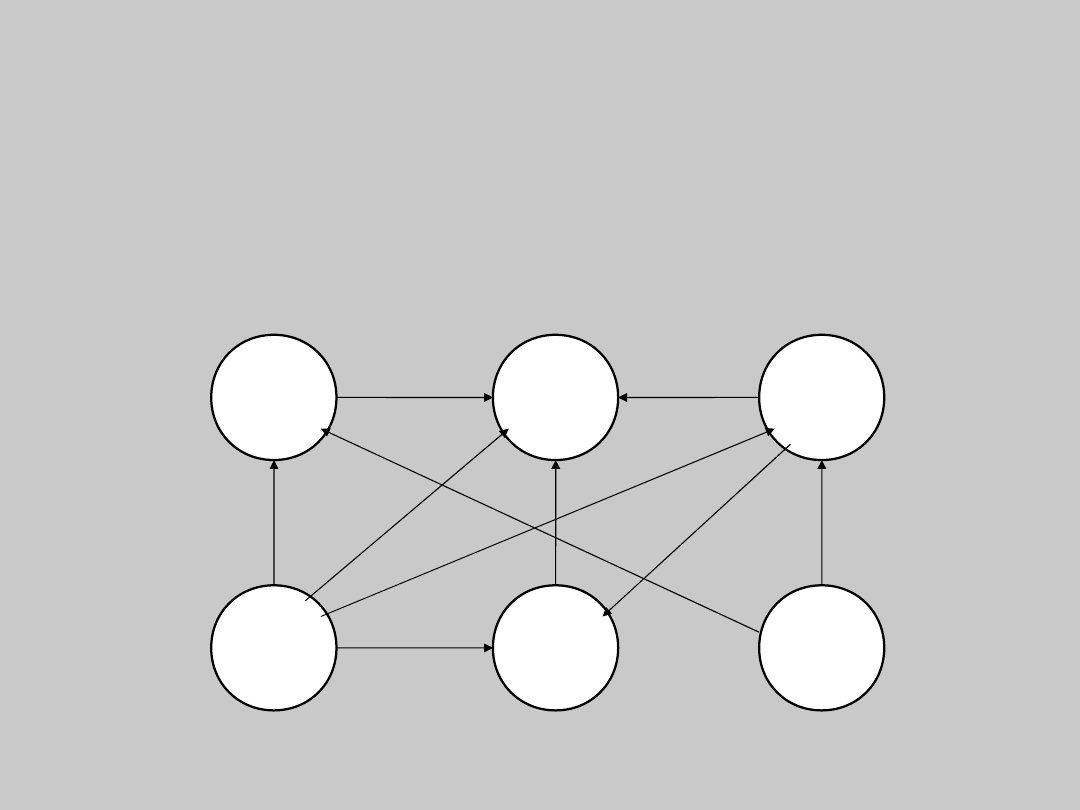
Metoda algebry macierzowej i teorii Gozinto
• Graf Gozinto wyrobu W1
W1
W2
W3
W6
W4
W5

• Graf Gozinto można przedstawić w ujęciu
matematycznym za pomocą macierzy kwadratowej Q
zwanej „macierzą bezpośrednich zapotrzebowań
elementów”
• Liczby n
ij
oznaczają ile i-tego
elementu wchodzi
bezpośrednio w skład jednego elementu j-tego
m
m
ij
n
Q
×
=

• na podstawie grafu Gozinto i macierzy Q tworzy
się macierz łącznego zapotrzebowania
elementów Y:
• z założenia przyjmuje się, że dla i=j elementy
macierzy przyjmują wartość 1
• można przyjąć również poniższy wzór:
• gdzie I oznacza macierz jednostkową
∑
⋅
=
k
kj
ik
ij
Y
Q
Y
(
)
I
Q
Y
Y
+
×
=

• Po przekształceniach:
(
)
1
−
−
=
Q
I
Y

• zakładając, że znany jest wektor programu
produkcyjnego wyrobów gotowych i wyrobów
niższych rzędów N:
• można wyznaczyć poszukiwane całkowite
zapotrzebowanie na wyroby:
ij
a
N
=
N
Y
X
×
=
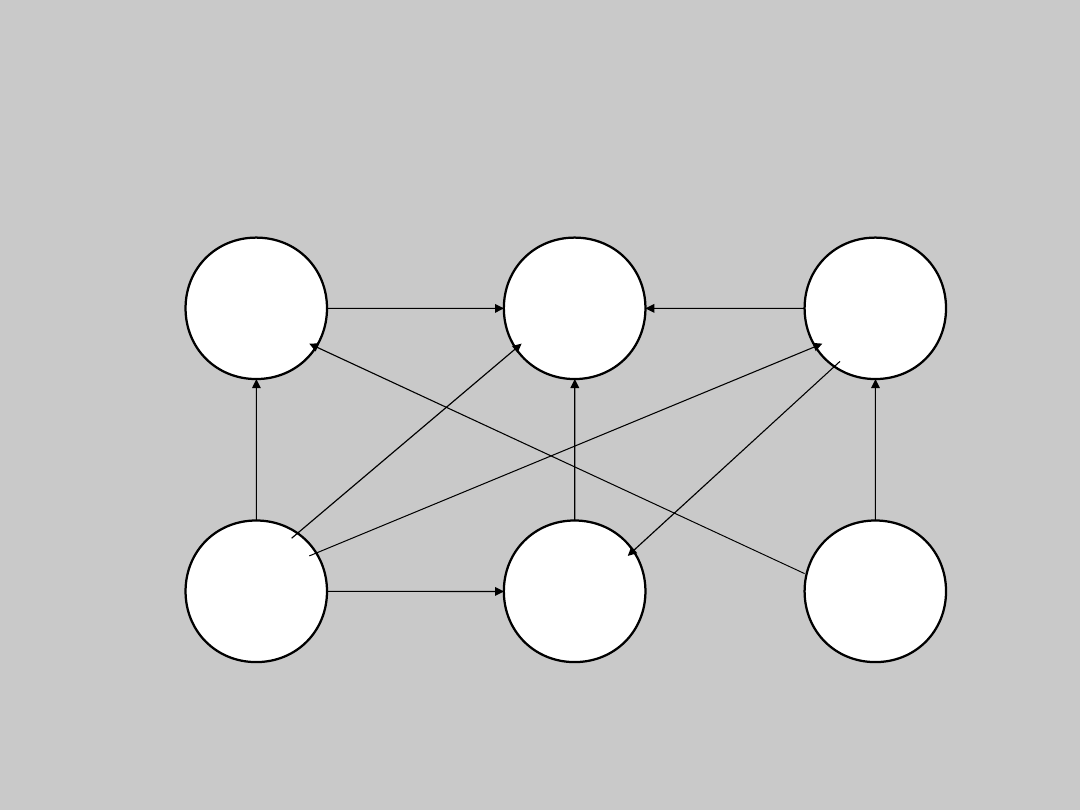
• Przykład wyznaczenia programu
produkcyjnego
W1
W2
W3
W6
W4
W5
5
3
3
1
2
5
4
2
4
1

• Założony program
produkcyjny wyrobu W1
oraz części zamiennych
W2-W6
• W1 – 400 szt
• W2 – 9 szt
• W3 – 76 szt
• W4 – 58 szt
• W5 – 44 szt
• W6 – 36 szt
=
36
44
58
76
9
400
N

• macierz bezpośrednich zapotrzebowań Q
=
0
0
0
2
3
0
0
0
1
5
5
1
0
0
0
0
0
4
0
0
4
0
0
2
0
0
0
0
0
3
0
0
0
0
0
0
Q

• macierz [I-Q]
[
]
−
=
−
0
0
0
2
3
0
0
0
1
5
5
1
0
0
0
0
0
4
0
0
4
0
0
2
0
0
0
0
0
3
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
Q
I

• zatem
−
−
−
−
−
−
−
−
−
−
=
−
1
0
0
2
3
0
0
1
1
5
5
1
0
0
1
0
0
4
0
0
4
1
0
2
0
0
0
0
1
3
0
0
0
0
0
1
]
[
Q
I

• Odwracanie macierzy [I-Q]
• Kol. 5 dodana do kol. 4 oraz kol. 1
• Kol. 6 pomnożona przez 2 i dodana do kol. 3:
−
−
−
−
−
−
−
−
−
−
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
2
3
0
0
1
1
5
5
1
0
0
1
0
0
4
0
0
4
1
0
2
0
0
0
0
1
3
0
0
0
0
0
1

• Kol. 5 pomnożona przez 5 i dodana do kol. 2 i 3:
−
−
−
−
−
−
−
1
0
0
2
0
0
0
1
1
0
0
1
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
3
0
0
1
0
5
5
0
0
0
1
0
0
4
0
0
4
1
0
2
0
0
0
0
1
3
0
0
0
0
0
1

• Odwracanie macierzy [I-Q]
• Kol. 6 pomnożona przez 3 i dodana do kol. 2
• Kol. 3 pomnożona przez 4 i dodana do kol. 4:
−
−
−
−
−
1
0
0
2
0
0
0
1
1
5
5
1
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
3
0
0
1
0
0
0
0
0
0
1
0
0
4
0
0
4
1
0
2
0
0
0
0
1
3
0
0
0
0
0
1

• Odwracanie macierzy [I-Q]
• Kol. 2 pomnożona przez 3 i dodana do kol. 1
−
−
−
1
0
8
2
3
0
0
1
21
5
5
1
0
0
1
0
0
0
0
0
4
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
4
0
0
0
1
0
2
0
0
0
0
1
3
0
0
0
0
0
1

• Odwracanie macierzy [I-Q]
• Kol. 3 pomnożona przez 2 i dodana do kol. 1
−
−
1
0
8
2
3
9
0
1
21
5
5
16
0
0
1
0
0
0
0
0
4
1
0
0
0
0
0
0
1
3
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
4
0
0
0
1
0
2
0
0
0
0
1
0
0
0
0
0
0
1

• Odwracanie macierzy [I-Q]
• Kol. 4 pomnożona przez 4 i dodana do kol. 1
−
1
0
8
2
3
13
0
1
21
5
5
26
0
0
1
0
0
0
0
0
4
1
0
2
0
0
0
0
1
3
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
4
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1

• macierz odwrotna [I-Q]
-1
1
0
8
2
3
45
0
1
21
5
5
110
0
0
1
0
0
4
0
0
4
1
0
18
0
0
0
0
1
3
0
0
0
0
0
1
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1

• macierz łącznego zapotrzebowania Y:
=
1
0
8
2
3
45
0
1
21
5
5
110
0
0
1
0
0
4
0
0
4
1
0
18
0
0
0
0
1
3
0
0
0
0
0
1
Y

• Program produkcyjny X = Y x N
=
×
=
18679
45687
1658
7508
1209
400
36
44
58
76
9
400
1
0
8
2
3
45
0
1
21
5
5
110
0
0
1
0
0
4
0
0
4
1
0
18
0
0
0
0
1
3
0
0
0
0
0
1
X
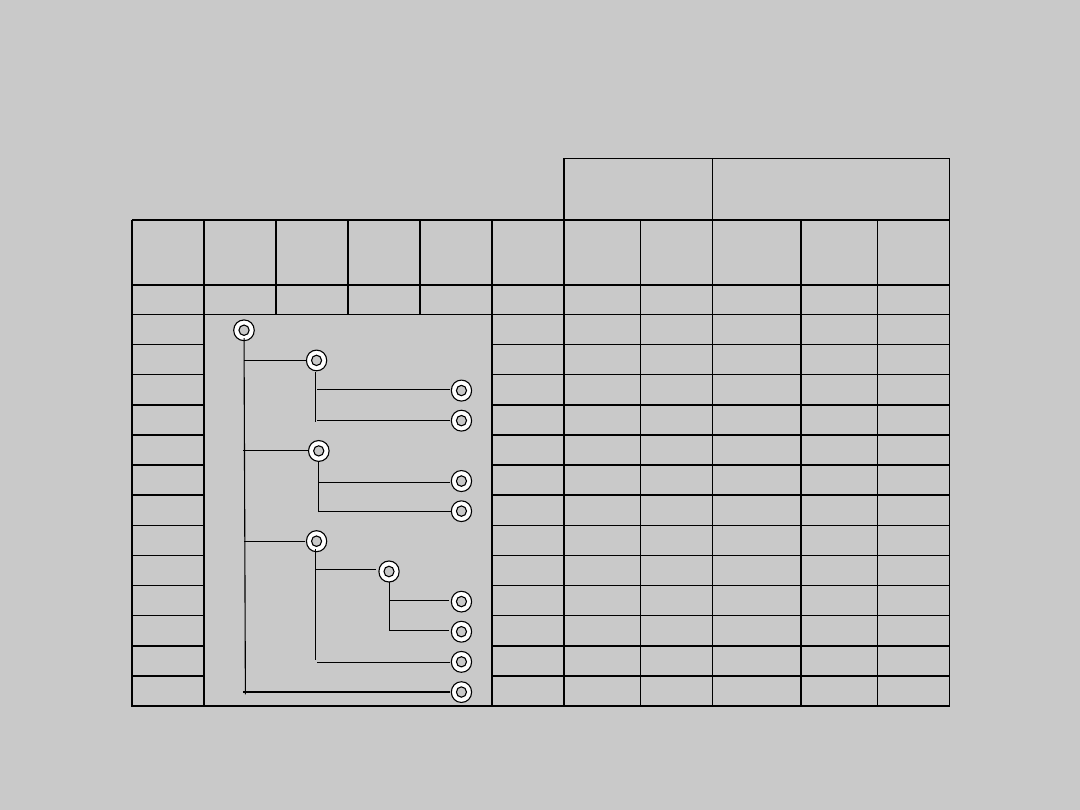
• metoda grafoanalityczna
Liczba sztuk na
Program produkcji
Lp
wyrób
gotowy
Zespół
I
Zespół
II
Detal
Symbol
wyrobu
zespół
nadrzęd
ny
wyrób
gotowy
podstawo
wy
części
zamien
ne
ogółem
1
2
3
4
5
6
7
8
9
10
11
1
W1
1
400
400
2
W2
3
3
1200
9
1209
3
W5
5
15
6000
45
6045
4
W6
3
9
3600
27
3627
5
W3
2
2
800
76
876
6
W5
5
10
4000
380
4380
7
W6
2
4
1600
152
1752
8
W4
4
4
1600
58
1658
9
W3
4
16
6400
232
6632
10
W5
5
80
32000
1160
33160
11
W6
2
32
12800
464+36
13300
12
W5
1
4
1600
58
1658
13
W5
1
1
400
44
444
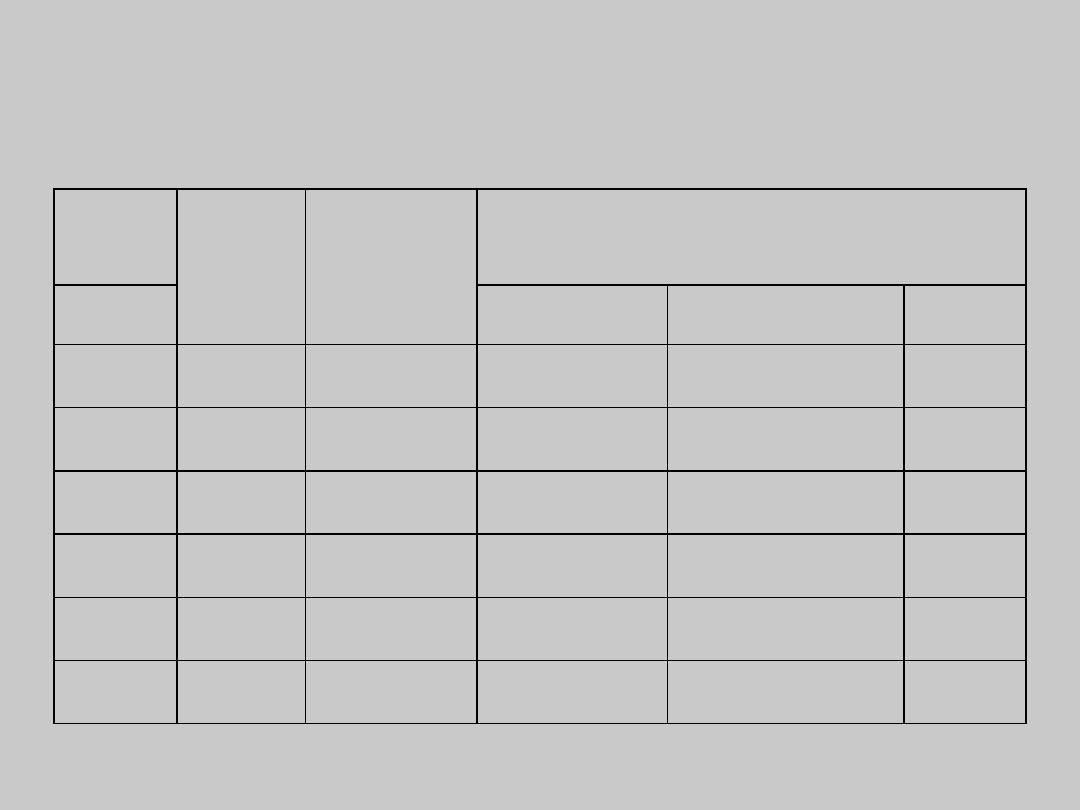
Program produkcyjny
Lp
Symbol
Liczba sztuk
Program produkcyjny
wyrobu
na wyrób
podstawowy
części zamienne
łącznie
1
W1
1
400
400
2
W2
3
1200
9
1209
3
W3
18
7200
308
7508
4
W4
4
1600
58
1658
5
W5
110
44000
1687
45687
6
W6
45
18000
679
18679
Document Outline
- Slajd 1
- Slajd 2
- Slajd 3
- Slajd 4
- Slajd 5
- Slajd 6
- Slajd 7
- Slajd 8
- Slajd 9
- Slajd 10
- Slajd 11
- Slajd 12
- Slajd 13
- Slajd 14
- Slajd 15
- Slajd 16
- Slajd 17
- Slajd 18
- Slajd 19
- Slajd 20
- Slajd 21
- Slajd 22
Wyszukiwarka
Podobne podstrony:
Program produkcji Plyty warstwowe
Program produkcyjny obliczenia
Karty Gotowe Program produkcji
projektowanie, projektowanie pyt, Program produkcji
PROGRAM PRODUKCJI HPL
program produkcyjny
program produkcji LFP
Program produkcyjny
Obliczenia wstępne do programu produkcyjnego
program produkcyjny
Optymalizacja programu produkcji betoniarni
1 roczny program produkcji czesci
Optymalizacja programu produkcji betoniarni
więcej podobnych podstron