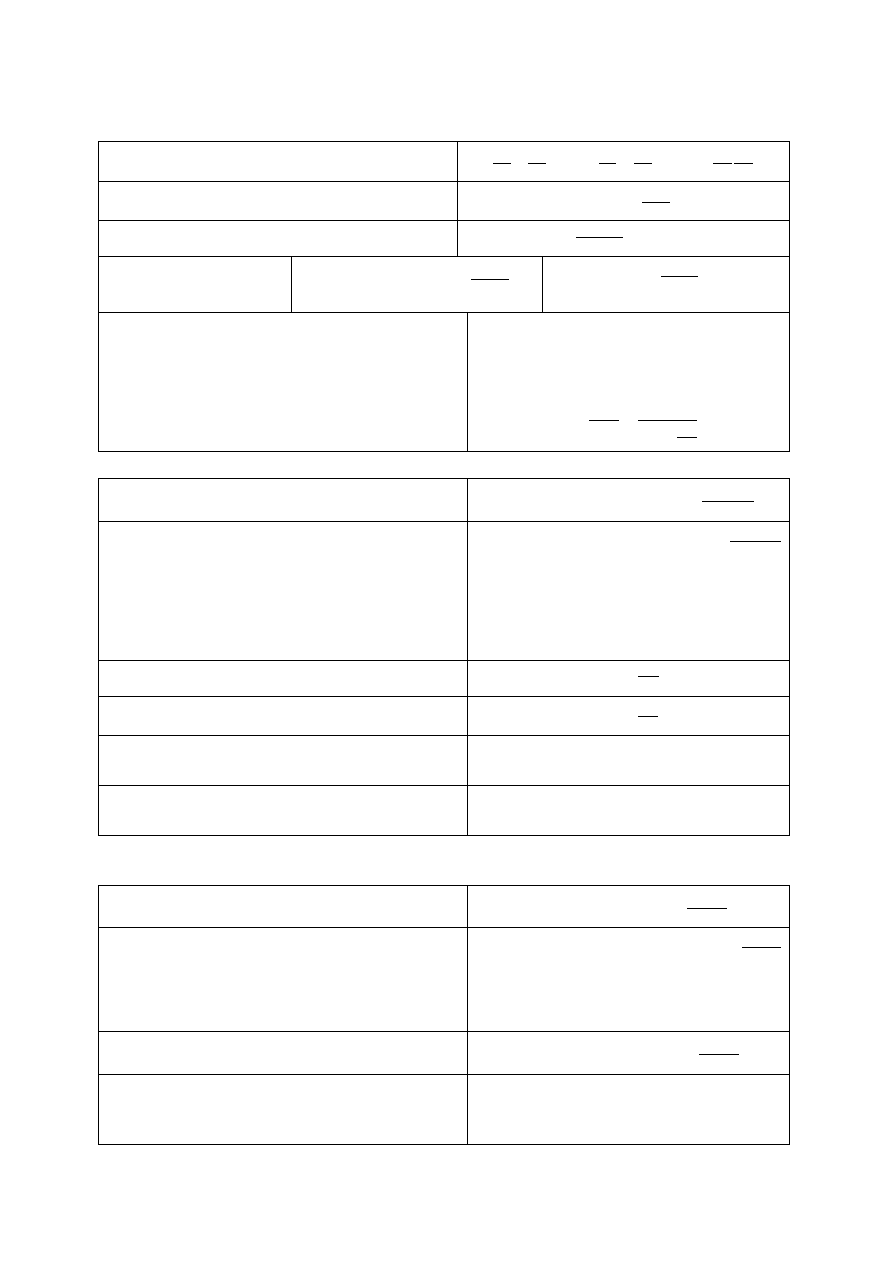
Równanie Bernouliego:

2 +

+ ℎ = 2 + + ℎ + 2

Równanie Darcy-Weisbacha:

−

= 2

Uwaga! Dla gazów równanie Darcy’ego-Weisbacha

może być stosowane gdy spełniony jest warunek:

−

≤ 0,03

Równanie Biel-Lummerta:

Gazociągi wysokiego i

średniego ciśnienia

−

= 8,635

,

=

0,05

,

Qn –obliczeniowy strumień gazu w war. norm., m

3

/h

Dw – średnica wewnętrzna rury, mm
L – długość rury, km
p1 – ciśnienie na początku rury, MPa
p2 – ciśnienie na końcu rury, MPa
Z – liczba gazowa zależna od gęstości względnej, -
d – gęstość względna

=

!

=

1,293 $%

&

Równanie Panhandle’a:

'( = 10

)

÷ 10

Gazociągi wysokiego i średniego ciśnienia

−

= 13,414 , -

, &.

, &.

), &.

Qn –obliczeniowy strumień gazu w war. norm., m

3

/h

Dw – średnica wewnętrznarury, mm
L – długość rury, km
p1 – ciśnienie na początku rury, bar
p2 – ciśnienie na końcu rury, bar
T – temperatura, K
d – gęstość względna, -
z – współczynnik ściśliwości, -

=

0,085

'(

, )/

Ciśnienie pseudozredukowane dla mieszanin

0

=

1

Temperatura pseudozredukowana dla mieszanin

-

0

=

-

-

1

Ciśnienie pseudokrytyczne dla mieszanin

1

= 2 3

4 14

45

Temperatura pseudokrytyczna dla mieszanin

-

1

= 2 3

4

-

14

45

Równanie Renouarda:

'( = 2 ∙ 10

)

÷ 2 ∙ 10

/

Gazociągi wysokiego i średniego ciśnienia

−

= 515,15

,

),

Qn –obliczeniowy strumień gazu w war. norm., m

3

/h

Dw – średnica wewnętrzna rury, mm
L – długość rury, km
p1 – ciśnienie na początku rury, MPa
p2 – ciśnienie na końcu rury, MPa
d – gęstość względna, -

=

0,05

'(

,

Równanie Renouarda: dla niskich ciśnień

−

= 2557,076

,

),

Qn –obliczeniowy strumień gazu w war. norm., m

3

/h

Dw – średnica wewnętrzna rury, mm
L – długość rury, m
p1 – ciśnienie na początku rury, kPa

= 0,21'(

8 ,

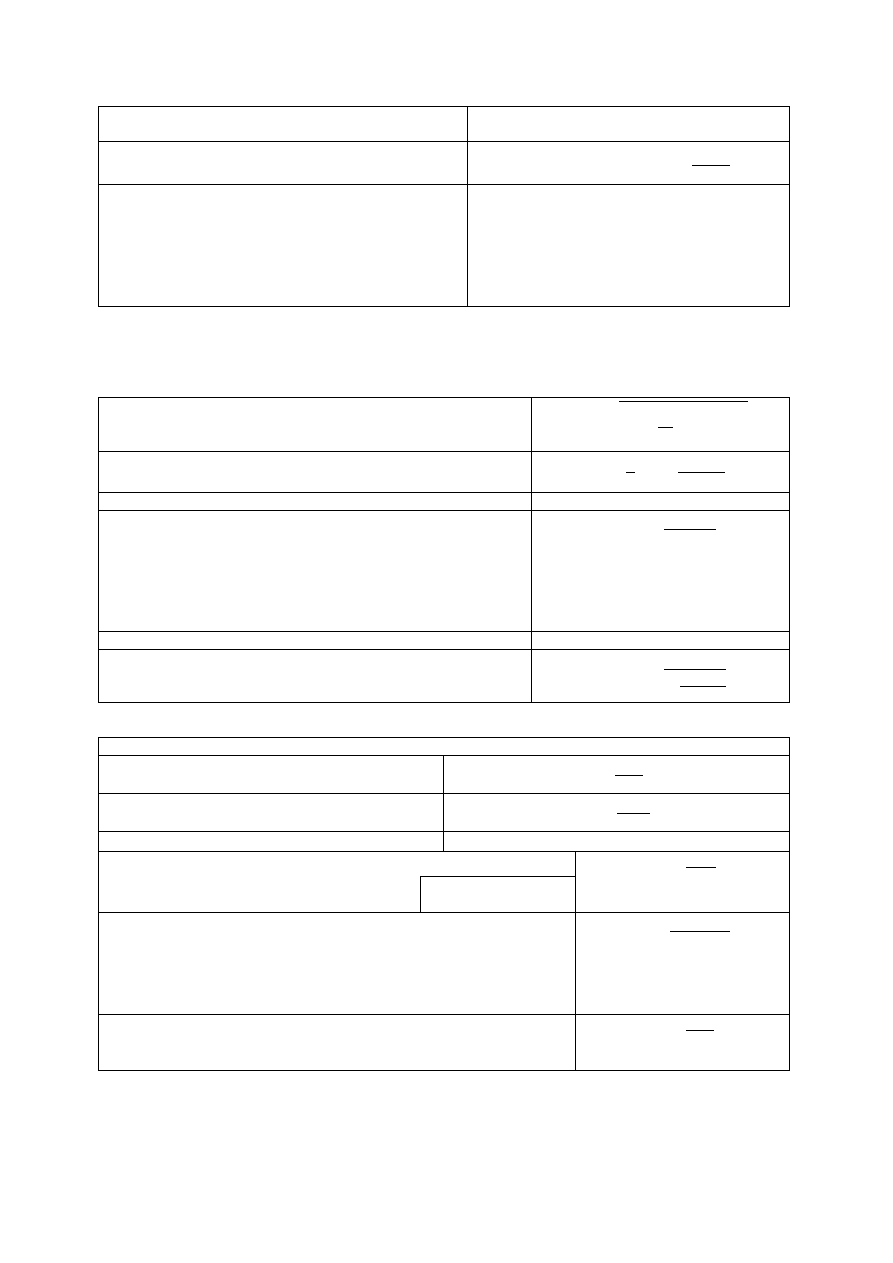
Spadek ciśnienia w gazociągu wysokiego i średniego ciśnienia

p

x

- ciśnienie w odległości Lx od początku gazociągu, Pa

9

= :

−

9

;

−

<

Średnie ciśnienie w gazociągu dla gazociągów wysokiego i
średniego ciśnienia

=0

=

2

3 > + + ?

Pojemność magazynowa rurociągu

V

g

-objętość gazociągu, m3

T

n

-temperatura normalna 273,15 K

T

śr

-temperatura średnia gazu, K

p

n

-ciśnienie normalne 101,325 kPa

p

sr

-cisnienie średnie gazu, Kpa

z

rz

-współ. ściśliwości w warunkach rzeczywistych

z

n

-współ, ściśliwości w warunkach normalnych ≈1

@

= A

@

ś0

- ,

-

=0

,

0C

Temperatura średnia gazu w gazociągu

T

0

-temp gruntu, K

T

1

- temp gazu na początku gazociągu, K

T

2

-temp gazu na końcu gazociągu, K

-

ś0

= - +

- − -

DE - − -

- − -

Nierównomierności czasowe maksymalnego poboru gazu

Maksymalny godzinowy pobór gazu:
n - liczba odbiorców gazu.

F

=

0 ś0

ℎ

0

E

Roczna liczba godzin użytkowania
(dla pokrycia szczytowego zapotrzebowania na gaz):

ℎ

0

=

8760

$

0

Roczny współczynnik nierównomierności czasowej:

$

0

= $

G

$

H

$

@

km - współczynnik nierównomierności miesięcznej w cyklu rocznym,

$

G

=

I

J

G/0

J

G/0

= 8,33%

a – maksymalny miesięczny pobór gazu, %
u m/r – średni udział miesięcy w ciągu roku:

$

G

= 1,25 ÷ 1,30

kd –współczynnik nierównomierności dobowej w cyklu
miesięcznym,
tw – średnia temperatura w pomieszczeniach mieszkalnych, °C
tmsr – średnia temperatura najzimniejszego miesiąca, °C
tdsr – średnia najzimniejszego dnia w miesiącu, °C

$

H

=

M − M

H=0

M − M

G=0

$

H

= 1,10 ÷ 1,15

kg - współczynnik nierównomierności godzinowej w cyklu dobowym,
c – maksymalny godzinowy pobór gazu, %
u

g/d

– średni udział godzin w ciągu dnia u

g/d

=4,17%

$

@

=

N

J

@/H

$

@

= 1,70 ÷ 1,80

p2 – ciśnienie na końcu rury, kPa
d – gęstość względna, -

Równanie Biel-Lummerta: dla niskich ciśnień

−

= 42,604

,

Qn –obliczeniowy strumień gazu w war. norm., m

3

/h

Dw – średnica wewnętrzna rury, mm
L – długość rury, m
p1 – ciśnienie na początku rury, kPa
p2 – ciśnienie na końcu rury, kPa
Z – liczba gazowa jako funkcja gęstości względnej gazu,-

= 0,21'(

8 ,

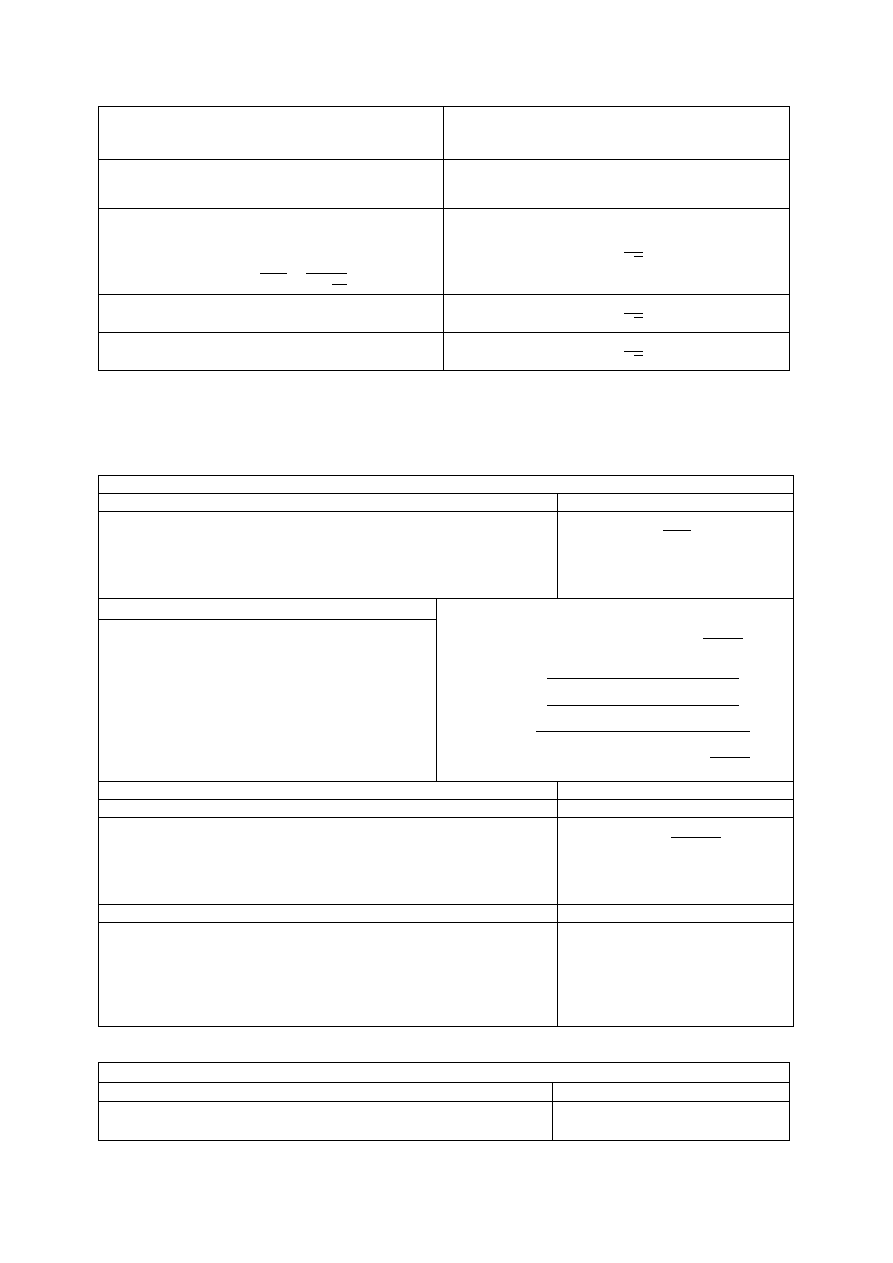
Ciepło spalania mieszaniny
H

si

-ciepło spalania i-tego składnika

n

i

-udział molowy/objętościowy i-tego składnika

O

=

= 2 O

=4

∙ E

4

45

Wartość opałowa mieszaniny
H

ii

-wartośc opałowa i-tego składnika

O

4

= 2 O

44

∙ E

4

45

Liczba Wobbego
Q-wartość kaloryczna odniesiona do jednostki
objętości gazu

P =

√

d-gęstość względna

=

R

R

STU

=

R

V

, .&

WX

YZ

Dolna Liczba Wobbego

P =

O

4

√

Górna Liczba Wobbego

P =

O

=

√

Obliczenia sieci dystrybucyjnych

Część zasilająca. Obciążenie obliczeniowe

Qrśr – średnie roczne zużycie gazu przez poje dyn. odbiorcę
n – liczba odbiorców gazu,
hp – liczba godzin przesyłu,
µ – współ spodziewanego wzrostu liczby odbiorców (1÷1,3),
Qprz – zużycie gazu przez odbiorców instytucjonalnych.

![\

=

0 ś0

ℎ

E +

0C

Wzór Renouarda (modyfikacja Osiadacza)

−

= 0,138166 ∙ 10

8

,

),

= :

0,138166 ∙ 10

8

∙ ∙ ∙

,

−

],^_

= :

− 0,138166 ∙ 10

8

,

),

p1 – ciśnienie na początku gazociągu, Pa
p2 – ciśnienie na końcu gazociągu, Pa
ρ- gęstość bezwględna, kg/m3
L – długość odcinka gazociągu, m
Q – obciążenie obliczeniowe, m3/h
D – średnica wewnętrzna gazociągu, m

Część rozdzielcza.

Wskaźnik jednostkowych strat ciśnienia:

∆p – spadek ciśnienia na całej długości gazociągu
- dla sieci niskiego ciśnienia: p1 – p2
- dla sieci niskiego ciśnienia: p1

2

-p2

2

L

max

– długość najdłuższej drogi zasilania,

1,1 – współczynnik uwzględniający opory miejscowe.

Δp

b

=

Δp

1,1L

def

Obciążenie obliczeniowe odcinka sieci rozdzielczej:

Qodc – obciążenie odcinkowe (maksymalne obciążenie sieci przez
użytkowników podłączonych na danym odcinku sieci rozdzielczej,
Qtr – obciążenie tranzytowe (maksymalne obciążenie sieci przez
wszystkich użytkowników podłączonych do sieci rozdzielczej za
rozważanym odcinkiem),
α – współczynnik redukcji obciążenia (0,5 ÷ 0,64).

![\

= g ∙

!H1

+

h0

Obciążenie odcinkowe i tranzytowe można wyznaczyć metodą Zajdy
Maksymalne obciążenie:

Q – średnie obciążenie przez daną kategorię odbiorców,
n – liczba punktów odbioru,

!H1

= E i + E i

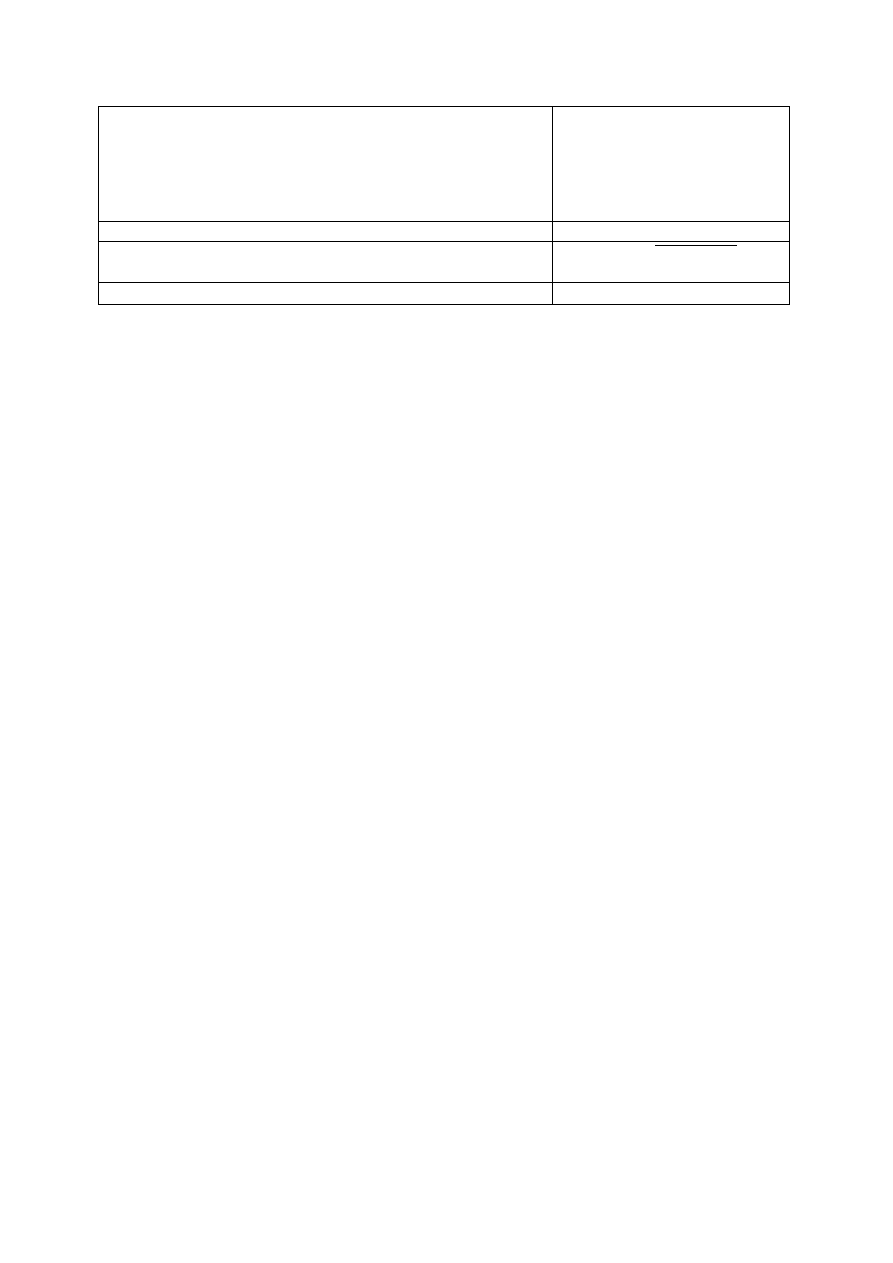
p – współczynnik jednoczesności poboru gazu w danej kategorii,
β – współczynnik korygujący zużycie gazu,
1 – odbiorcy zużywający gaz dla potrzeb komunalno-bytowych i
mali odbiorcy pozakomunalni,
2 – odbiorcy zużywający gaz do indywidualnego ogrzewania
pomieszczeń

h0

= E i + E i

Ciśnienia na końcu odcinka sieci rozdzielczej:

średniego ciśnienia

= j − ∙ ∆

l

niskiego ciśnienia

= − ∙ ∆

l