kwiecie
ń
, 2008 r.
Adam Szulc
Instytut Statystyki i Demografii
WYBRANE ZAGADNIENIA ESTYMACJI I WERYFIKACJI
JEDNORÓWNANIOWYCH MODELI REGRESJI
(w ramach wykładu: „Metody Statystyczne”)
I. JEDNORÓWNANIOWY MODEL EKONOMETRYCZNY: ............................................... 2
OGÓLNE ZASADY KONSTRUKCJI, ESTYMACJI I WERYFIKACJI ................................ 2
1. Definicja modelu regresji ................................................................................................. 2
2. Statystyczna analiza reszt modelu. ................................................................................. 4
3. Estymacja modelu liniowego za pomocą klasycznej metody najmniejszych kwadratów
(KMNK) ................................................................................................................................. 5
4. Ocena oszacowania modelu liniowego za pomocą klasycznej MNK ........................... 5
5. Postępowanie w sytuacjach wykraczających poza schemat klasycznej MNK .................. 7
II. WYBRANE METODY ESTYMACJI MODELI REGRESJI .............................................. 8
1. MNK z warunkami dodatkowymi .................................................................................. 8
2. Estymacja modeli ekonometrycznych za pomocą metody największej wiarygodności
(MNW) ................................................................................................................................... 8
3. Uwagi o estymacji modeli nieliniowych .......................................................................... 9
4. Estymacja za pomocą zmiennych instrumentalnych (MZI) ...................................... 10
5. Zmienne binarne w modelach regresji: regresja logitowa i probitowa ..................... 12
III. TESTY STATYSTYCZNE W MODELACH REGRESJI ................................................ 14
1. Testy warunków ograniczających modelu ................................................................... 14
2. Testy specyfikacji modelu .............................................................................................. 16
3. Test stabilności parametrów ......................................................................................... 17
4. Test homoskedastyczności reszt .................................................................................... 17
Dekalog ekonometrii stosowanej według Petera Kennedy’ego .................................. 18
Literatura podstawowa: .................................................................................................... 19
Literatura uzupełniająca: .................................................................................................. 19
ZADANIA ............................................................................................................................ 20
ZASADY ZALICZANIA ZAJĘĆ ....................................................................................... 24
ZADANIA Z OSTATNIEGO SPRAWDZIANU ................................................................ 25
2
WYBRANE ZAGADNIENIA ESTYMACJI I WERYFIKACJI
JEDNORÓWNANIOWYCH MODELI REGRESJI
Motto 1: KaŜdy ekonomista jest ekonometrykiem czy tego chce czy nie (Joseph Schumpeter)
Motto 2: Są trzy złote zasady ekonometrii: testować, testować i testować (David Hendry)
Motto 3: Dwóch rzeczy lepiej nie oglądać w czasie ich powstawania: parówek i oszacowań
modeli ekonometrycznych (Edward Leamer )
I. JEDNORÓWNANIOWY MODEL EKONOMETRYCZNY:
OGÓLNE ZASADY KONSTRUKCJI, ESTYMACJI I WERYFIKACJI
1. Definicja modelu regresji
Jednorównaniowy model regresji jest zdefiniowany następująco:
n)
1,2,...,
(i
)
x
,...,
x
,
x
(
g
y
i
ik
2
i
1
i
i
=
+
=
ε
(1.1)
gdzie:
y
i
- i-ta wartość zmiennej objaśnianej (zaleŜnej),
x
ij
- i-ta wartość j-tej zmiennej objaśniającej (niezaleŜnej; j=1,2,...k),
ε
i
- i-ta reszta (błąd) modelu (róŜnica między oszacowaną i empiryczną wartością y
i
),
n - liczba obserwacji,
k- liczba zmiennych objaśniających (jeŜeli w modelu występuje wyraz wolny to pozwalająca
oszacować odpowiedni parametr kolumna jedynek jest traktowana jako dodatkowa, k + 1-
sza zmienna).
Postać funkcji g określa typ modelu. W większości omawianych tu przypadków będzie to
funkcja liniowa. Model ma wtedy następującą postać:
n)
1,2,...,
(i
ε
ε
x
x
x
y
i
i
0
ik
k
...
2
i
2
1
i
1
i
=
+
=
+
=
+
+
+
+
a'
X
i
α
α
α
α
(1.2)
Alternatywna definicja modelu regresji jest następująca:
)]
x
,...,
x
,
x
(
[
E
)
x
,...,
x
,
x
(
g
ik
2
i
1
i
ik
2
i
1
i
=
=
X
|
Y
(1.3)
Funkcja regresji g oznacza w tym przypadku warunkową wartość oczekiwaną zmiennej
objaśnianej, pod warunkiem, Ŝe zmienne objaśniające przyjęły wartości określone przez (k-
wymiarowy) wektor X
1
. Aby modele zapisane za pomocą równań (1.1) i (1.3) były
równowaŜne, musi być spełniony warunek:
0
(
=
X)
|
ε
E
2
(1.4)
1
Wartość tej funkcji jest zwykle zwana (nieprecyzyjnie) wartością teoretyczną zmiennej Y.
2
Taki zapis (stosowany w dalszej części konspektu) jest równowaŜny zapisowi wektorowemu:
3
tzn. wartość oczekiwana reszty modelu dla dowolnego wektora zmiennych objaśniających X
jest równa zeru.
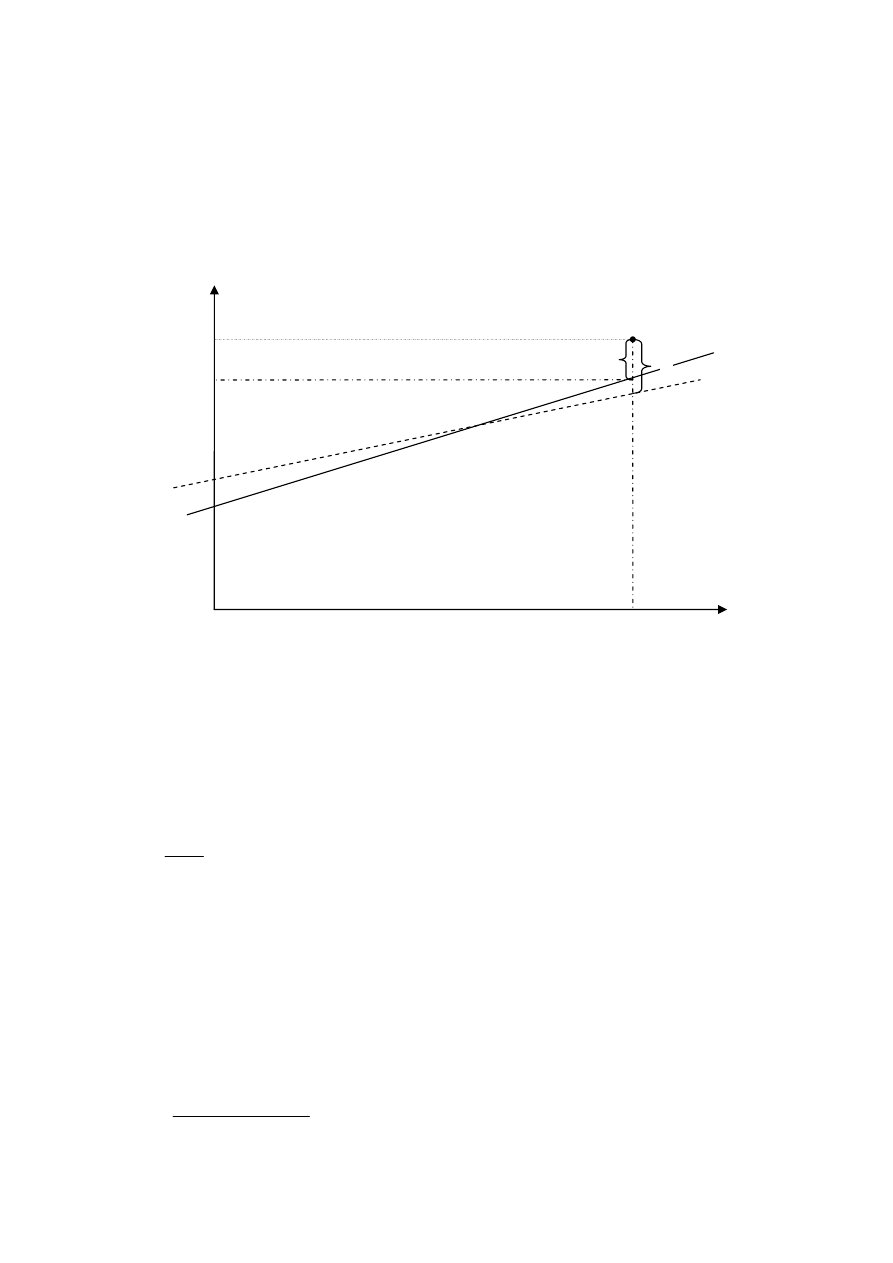
Rys. 1.1. ZałoŜenia modelu regresji liniowej z jedną zmienną objaśniającą
Rozpatrując najprostszy z moŜliwych model regresji czyli model liniowy z jedną zmienną
objaśniającą moŜna zilustrować istotę regresji ekonometrycznej za pomocą rysunku 1.1.
Przykładowo, dla zbioru gospodarstw domowych dane są indywidualne (czyli dostępne dla
kaŜdego gospodarstwa osobno) informacje o ich (łącznych) wydatkach na konsumpcję
(zmienna Y) i dochodach (zmienna X). Warunkowa wartość oczekiwana E(Y|X=x
i
) moŜe być
przedstawiona za pomocą prostej o równaniu: α
1
x
i1
+ α
0
. Zakłada się, Ŝe rzeczywista wartość
zmiennej Y jest wynikiem losowania przy ustalonej wartości zmiennej X. Wartości
parametrów funkcji regresji szacuje się na podstawie próby (losowej lub nielosowej
3
). Tak jak
wszystkie wyniki estymacji uzyskane za pomocą próby, róŜnią się one od rzeczywistych
=
=
=
=
0
.
.
.
0
0
)]
(
|
[
.
.
.
)]
(
|
[
)]
(
|
[
,...,
2
,
1
2
,...,
22
,
21
2
1
,...,
12
,
11
1
nk
n
n
n
k
k
x
x
x
E
x
x
x
E
x
x
x
E
X
X
X
ε
ε
ε
3
Nawet jeŜeli próba jest nielosowa, moŜna zastosować wnioskowanie statystyczne z uwagi na wyŜej
wymienione załoŜenie odnośnie losowości Y.
f(Y|X)
lub
f(Y,X)
x
1
x
2
. . . x
n
X
α
1
X+α
0
Y
(x
1
,y
1
)
(x
2
,y
2
)
(x
n
,y
n
)
N(α
1
x
n
+α
0
,σ
2
)
4
(czyli „obowiązujących” w populacji generalnej) wartości.
4
Charakter zaleŜności między
warunkową wartością oczekiwaną Y i zmienną X przesądzający o wyborze funkcji g jest (tak
jak kaŜdy model) przyjętym załoŜeniem na temat rzeczywistości. MoŜe ono być zatem
spełnione lub nie (dokładnie nie jest spełnione praktycznie nigdy). O tym czy przyjęcie danej
postaci jest słuszne moŜna się przekonać m. in. analizując rozkład reszt modelu ε.
2. Statystyczna analiza reszt modelu.
Występowanie w modelu reszt czyli róŜnic między teoretyczną i empiryczną wartością
modelu jest wynikiem m. in. faktu, iŜ na wartości Y mają wpływ nie tylko zmienne zawarte w
wektorze X. Inne przyczyny to błędy pomiaru wartości obu zmiennych (nie będą one
omawiane) oraz wybór niewłaściwej funkcji regresji. Znaczenie (często niedoceniane,
zwłaszcza w badaniach o charakterze aplikacyjnym) analizy reszt modelu wynika m. in. z
następujących przesłanek:
a/ Optymalną metodę szacowania parametrów modelu moŜna wybrać jedynie po
weryfikacji załoŜeń odnośnie rozkładu reszt.
b/ Oszacowanie „teoretycznych wartości” zmiennej objaśnianej oraz parametrów modelu
zawiera błędy losowe, które moŜna ocenić jedynie za pomocą analizy reszt.
c/ Jedynie za pomocą oceny rozkładu reszt moŜna stwierdzić czy przyjęcie określonej
postaci modelu jest uzasadnione.
Znajomość rozkładu reszt jest zatem konieczna zarówno na etapie modelowania jak i
weryfikacji.
ZałoŜenia odnośnie reszt jakie standardowo przyjmuje się w badaniu regresji opisują
równania 1.5 - 1.7.
0
(
(
=
=
ε)
X)
|
ε
E
E
(1.5)
Warunek ten oznacza, oprócz zerowej wartości oczekiwanej reszt, ich niezaleŜność od
wartości zmiennych objaśniających.
I
X)
|
εε'
2
(
σ
=
E
(1.6)
gdzie I jest macierzą diagonalną z wartościami 1 na przekątnej (zapis ′ oznacza transpozycje
wektora; w tym przypadku kolumna jest mnoŜona przez wiersz). Zapis ten oznacza
spełnianie dwóch warunków, które łącznie określa się jako sferyczność reszt: reszty nie są ze
sobą skorelowane, zaś ich warunkowa wariancja jest równa stałej σ
2
, niezaleŜnie od wartości
X. W przypadku spełniania pierwszego warunku mówimy o braku autokorelacji reszt, w
przypadku drugiego o homoskedastyczności reszt. Niespełnianie tych warunków określa się,
odpowiednio, mianem autokorelacji reszt oraz ich heteroskedastyczności.
)
,
0
(
:
(
I
X)
|
ε
σ
N
(1.7)
Warunek ten mówi, iŜ rozkład reszt jest dla danych wartości X normalny, z zerową wartością
oczekiwaną i wariancją σ
2
.
4
Jest to kolejny powód, dla którego „teoretyczne wartości” zmiennej objaśnianej uzyskane na podstawie
oszacowania modelu róŜnią się od rzeczywistych.
5
3. Estymacja modelu liniowego za pomocą klasycznej metody
najmniejszych kwadratów (KMNK)
ZałoŜenia omówione w poprzedniej części muszą być spełnione
5
, aby parametry liniowego
modelu (1.2) moŜna było oszacować za pomocą klasycznej metody najmniejszych kwadratów
(MNK). Wówczas wektor oszacowań parametrów modelu (uzyskany przez minimalizacje
sumy kwadratów reszt) ma postać następującego iloczynu macierzy:
Y
X'
)
XX'
a
1
(
-
=
(1.8)
Oszacowanie wariancji reszt oblicza się następująco:
1
2
−
−
=
k
n
s
e
e'
(1.9)
gdzie e jest wektorem empirycznych reszt modelu. Z kolei estymatory wariancji oszacowania
parametrów modelu (będących miarą błędu oszacowania) uzyskuje się za pomocą wzoru:
1
2
2
)
(
)
(
−
=
X
X'
a
s
S
(1.10)
JeŜeli wszystkie wymienione wcześniej załoŜenia (liniowość warunkowej wartości
oczekiwanej, załoŜenia 1.5 - 1.7 oraz odpowiedni rząd macierzy danych) są spełnione, to
uzyskane estymatory są nieobciąŜone, zgodne i najefektywniejsze (mają najmniejszą
wariancję ze wszystkich nieobciąŜonych estymatorów). Spełnianie powyŜszych załoŜeń nie
pozwala jeszcze stwierdzić, Ŝe oszacowany model spełnia stawiane przed nim wymagania
(np. pozwala wykorzystać oszacowania w prognozowaniu lub wyznaczaniu relacji
ekonomicznych między zmiennymi). Jest jednak warunkiem koniecznym dla poprawności
oszacowań uzyskanych za pomocą MNK.
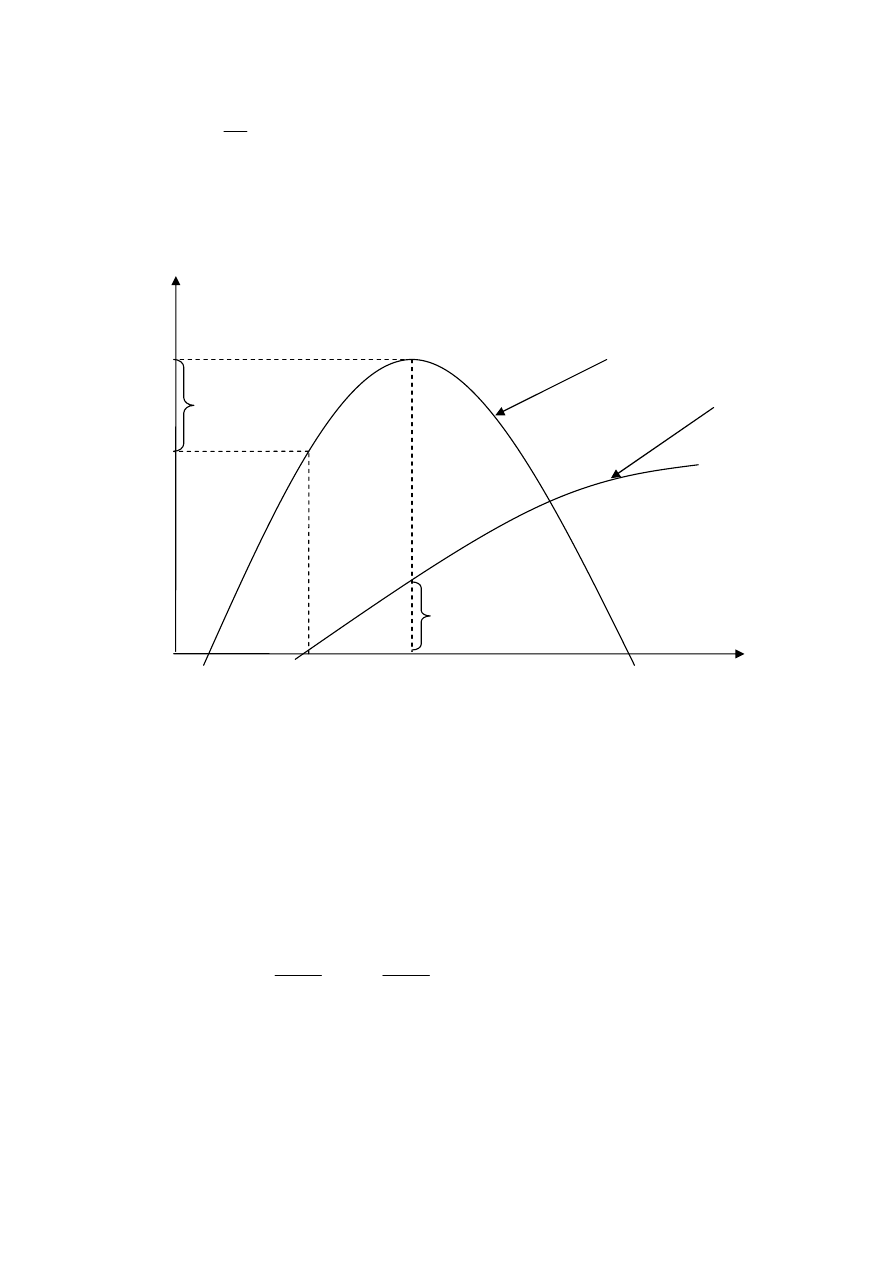
W przypadku, gdy w modelu występuje tylko jedna zmienna objaśniająca (k=2, a macierz X
ma wymiary n
x
2) wynik estymacji za pomocą klasycznej MNK moŜna zilustrować za
pomocą rysunku 1.2.
4. Ocena oszacowania modelu liniowego za pomocą klasycznej MNK
Miernikiem pozwalającym ocenić stopień dopasowania modelu do danych empirycznych jest
współczynnik determinacji:
∑
∑
∑
=
=
=
−
−
−
−
=
n
i
n
i
i
i
n
i
i
i
y
y
y
y
y
y
y
y
R
1
1
2
2
1
2
2
]
)
ˆ
ˆ
(
][
)
(
[
)]
ˆ
ˆ
)(
(
[
(1.11)
5
Oprócz warunków, jakie muszą spełniać reszty wymaga się równieŜ mi. in. aby wektor danych X był macierzą
o wymiarach n
x
k mającą rząd k.
6
Jest on równy kwadratowi współczynnika korelacji liniowej pomiędzy empirycznymi i
„teoretycznymi wartościami” zmiennej objaśnianej. R
2
przyjmuje wartości z przedziału [0,1].
JeŜeli spełnione są załoŜenia KMNK, to wyŜsze wartości oznaczają lepsze dopasowanie
modelu do danych empirycznych (i np. niŜszy błąd prognozy), choć nie istnieje Ŝadna stała
granica, poniŜej której oszacowanie naleŜałoby odrzucić. Jedynym warunkiem, który musi
być spełniony jest statystyczna istotność oszacowania tego parametru. MoŜna ją sprawdzić za
pomocą testu opisanego poniŜej (równanie 1.13 wraz z komentarzem).
Rys. 1.2. Model regresji w populacji generalnej i oszacowanie
Dwie kolejne metody oceny „jakości” oszacowania są testami statystycznymi pozwalającymi
ocenić czy parametry, których oszacowania uzyskano są istotnie róŜne od zera. Pierwszy z
testów pozwala ocenić w ten sposób oszacowanie kaŜdego parametru osobno. Statystyka
testowa dla j-tej zmiennej (j=1,2,...,k) ma postać:
)
(
j
j
a
S
a
t
=
(1.12)
gdzie mianownik jest błędem standardowym oszacowania j-tego parametru równania (1.2).
JeŜeli reszty mają rozkład normalny (spełniają warunek 1.7), to powyŜsza statystyka ma
rozkład t (Studenta) z (n-k-1) stopniami swobody. Hipoteza zerowa w tym teście mówi, Ŝe
wartość parametru w populacji generalnej jest równa zeru.
Kolejna statystyka testowa pozwala zweryfikować hipotezę mówiącą, Ŝe wszystkie oprócz
wyrazu wolnego parametry są równe zeru. Przy normalności rozkładu reszt statystyka ta,
zdefiniowana jak poniŜej ma rozkład F (Snedecora) z k i (n-k-1) stopniami swobody.
)
1
/(
)
1
(
/
2
2
−
−
−
=
k
n
R
k
R
F
(1.13)
ε
i
α
1
X+ α
0
Y
y
i
E(Y|X=x
i
)
x
i
X
a
1
X+ a
0
e
i
7
Współczynnik determinacji oraz statystyki zdefiniowane za pomocą równań (1.12) i (1.13)
stanowią najpopularniejsze narzędzia oceny „jakości” oszacowania modelu. Jak łatwo
zauwaŜyć, statystyka (1.13) stanowi takŜe test dla hipotezy mówiącej, Ŝe współczynnik
determinacji ma wartość zerową.
5. Postępowanie w sytuacjach wykraczających poza schemat klasycznej
MNK
ZałoŜenia odnośnie reszt modelu opisane za pomocą równań (1.5) - (1.7) w rzeczywistości są
spełniane dość rzadko. Przykładowo, warunek stałej i niezaleŜnej od wartości X wariancji jest
mało realistyczny, gdy model regresji opisuje zaleŜność wydatków konsumpcyjnych i
dochodów gospodarstw domowych (por. Rys. 1.1). ZróŜnicowanie wydatków
konsumpcyjnych z pewnością rośnie wraz z dochodem gospodarstw, jako Ŝe mogą one
wybierać między konsumpcją bieŜącą i oszczędzaniem czy inwestowaniem. Gospodarstwa
najmniej zamoŜne wydają, przeciętnie rzecz biorąc, niemal całość swoich dochodów na
zaspokojenie bieŜących potrzeb konsumpcyjnych. Zatem gospodarstwa o niskich dochodach
charakteryzują się stosunkowo niską wariancją wydatków. Z kolei warunek niezaleŜności
reszt między sobą jest bardzo trudny do spełnienia w przypadku modelowania szeregów
czasowych, zwłaszcza za pomocą tzw. modelu autoregresji. JeŜeli „teoretyczna wartość”
wyrazu szeregu czasowego w danym momencie zaleŜy od wartości wyznaczonych dla
okresów wcześniejszych, to trudno zakładać, Ŝe nie będzie od nich zaleŜna reszta modelu.
Stosunkowo najłatwiejsze do utrzymania jest załoŜenie o normalności rozkładu reszt,
zwłaszcza przy duŜej próbie.
Niespełnianie warunków (1.5 – 1.7) ma róŜnorakie konsekwencje. NajpowaŜniejsze skutki
niesie ze sobą skorelowanie reszt i zmiennych objaśniających. W tym przypadku uzyskane za
pomocą MNK estymatory parametrów modelu tracą nieobciąŜoność i zgodność. Metoda
postępowania w takim przypadku została opisana w § II.4. Niesferyczność reszt nie skutkuje
obciąŜonością estymatorów parametrów strukturalnych MNK, ale sprawia Ŝe tracą one
efektywność. ObciąŜone stają się natomiast estymatory wariancji oszacowań tych parametrów
(równanie 1.10). Ponadto w przypadku występowania autokorelacji reszt najczęściej ma
miejsce przeszacowanie wartości R
2
.
Częste w praktyce niespełnianie załoŜeń odnośnie rozkładu reszt nie jest jedynym
ograniczeniem dla praktycznej uŜyteczności modelu opisanego w Rozdziale I. TakŜe
załoŜenie liniowości warunkowej wartości oczekiwanej zmiennej objaśnianej często nie jest
spełnione. Wreszcie, w empirycznych zastosowaniach modeli regresji w analizie
ekonomicznej oszacowania nierzadko muszą spełniać określone zaleŜności w celu
zapewnienia zgodności z teoriami ekonomicznymi. Wszystkie te uwarunkowania zmuszają do
sięgnięcia po metody estymacji wykraczającej poza klasyczną MNK.
W kolejnych częściach zostały opisane zarówno wybrane metody estymacji modeli regresji
jak i testy pozwalające na wybór odpowiedniego modelu.
8
II. WYBRANE METODY ESTYMACJI MODELI REGRESJI
1. MNK z warunkami dodatkowymi
W wielu przypadkach teorie ekonomiczne wymagają, aby parametry modelu spełniały
określone warunki dodatkowe. Jednak uzyskane (dowolną metodą) na podstawie danych
empirycznych oszacowania często ich nie spełniają, w związku z czym warunki te trzeba na
uzyskane rozwiązania narzucić. Jednym z moŜliwych do zastosowania w takiej sytuacji
rozwiązań jest MNK z warunkami dodatkowymi. Uzyskane oszacowania stanowią wówczas
warunkowe minimum sumy kwadratów reszt. Zespół liniowych
6
warunków narzuconych na
wektor parametrów a zawsze moŜna przedstawić za pomocą układu równań:
r
'
a
R
=
~
(2.1)
gdzie R jest macierzą o wymiarach
)
1
(
+
×
k
m
, zaś r wektorem o wymiarach m
x
1 (m jest
liczbą warunków ograniczających). JeŜeli są spełnione wszystkie warunki pozwalające
zastosować klasyczną MNK, to wektor warunkowych oszacowań parametrów liniowego
modelu regresji moŜna przedstawić następująco:
)
(
]
)
(
[
)
(
~
1
1
1
r
-
Ra
R'
X
X'
R
R'
X
X'
-
a
a
−
−
−
=
(2.2)
gdzie a jest wektorem oszacowań uzyskanych za pomocą bezwarunkowej MNK (por.
równanie 1.8). Metody oszacowania wariancji reszt modelu oraz wariancji oszacowań
parametrów podaje A. Darnell (1994, str. 350-351).
W punkcie 1 rozdziału III omówione zostały dwa testy (Walda i ilorazu wiarygodności)
pozwalające ocenić czy narzucenie warunków dodatkowych jest uzasadnione przy danych
wektorach X i Y oraz danej postaci funkcji regresji.
2. Estymacja modeli ekonometrycznych za pomocą metody największej
wiarygodności (MNW)
Metoda największej wiarygodności jest znacznie bardziej uniwersalna i najczęściej
bardziej efektywna od metody najmniejszych kwadratów. MoŜna ją stosować równieŜ do
estymacji modeli nieliniowych, a takŜe w przypadku heteroskedastyczności lub autokorelacji
reszt
7
(por. równanie 1.6 z komentarzem). Estymatory uzyskane za pomocą tej metody są
zgodne i asymptotycznie najefektywniejsze. Mogą natomiast być one obciąŜone, co ma
istotne znaczenie w przypadku małych prób. Inną słabością tej metody jest mniejsza niŜ w
przypadku MNK odporność na niespełnianie załoŜenia o normalności rozkładu reszt.
Estymatory MNW parametrów w populacji generalnej uzyskuje się maksymalizując poniŜszą
funkcję wiarygodności:
6
Warunki nieliniowe nie będą tu omawiane.
7
Klasyczna MNK nie moŜe być stosowana w takim wypadku lecz moŜna skorzystać z estymatorów uzyskanych
za pomocą tzw. uogólnionej MNK (patrz: A. Darnell, 1994, str. 163-167)
9
∏
=
Θ
Θ
Θ
=
n
m
i
x
f
L
1
1
2
1
)
,...,
,
,
(
)
|
(
X
Θ
(2.3)
gdzie f jest funkcją gęstości prawdopodobieństwa dla zmiennej X, zaś Θ = [Θ
1
, Θ
2
, ... , Θ
m
]
wektorem szacowanych parametrów. Idea MNW polega na znalezieniu takich wartości
parametrów Θ, które maksymalizują prawdopodobieństwo lub gęstość prawdopodobieństwa
uzyskania próby X.
W praktyce duŜo wygodniej jest znaleźć maksimum dla funkcji będącej logarytmem L:
∑
=
Θ
Θ
Θ
=
n
i
m
i
x
f
L
1
2
1
,
)
,...,
,
(
ln
)
|
(
ln
X
Θ
(2.4)
W przypadku, gdy estymuje się liniowy model regresji z wieloma zmiennymi, estymator
uzyskany za pomocą MNW ma postać następującego wektora:
Y
Ω
X'
X
Ω
X'
a
ˆ
)
ˆ
(
ˆ
1
−
=
(2.5)
gdzie Ω
ˆ oznacza oszacowanie macierzy wariancji i kowariancji reszt. W przypadku
homoskedastyczności i braku autokorelacji reszt jest ona macierzą jednostkową (I w
równaniu 1.6) pomnoŜoną przez skalar. Łatwo zauwaŜyć, Ŝe powyŜsze równanie jest
wówczas identyczne z równaniem (1.8) czyli estymatory MNW stają się identyczne z
estymatorami uzyskanymi za pomocą MNK. W przypadku heteroskedastyczności lub
autokorelacji reszt niezbędne jest oszacowanie macierzy Ω
ˆ . Robi się to zakładając, Ŝe jej
elementy są określoną funkcją wartości zmiennych objaśnianych, następnie za pomocą MNW
znajdując parametry tej funkcji. Szczegóły tej i kilku innych metod szacowania Ω
ˆ
przedstawił W. Greene (str. 511-517 i 555-569). JeŜeli Ω
ˆ jest znana (w praktyce warunek ten
prawie nigdy nie jest spełniony) to oszacowanie a jest identyczne z oszacowaniem
uzyskanym za pomocą uogólnionej MNK.
Oszacowanie wariancji reszt modelu moŜna uzyskać następująco:
n
-
e
S
/
)
ˆ
(
ˆ
)
ˆ
(
)
(
ˆ
1
2
a
X
Y
Ω
'
a
X
Y
−
=
−
(2.6)
podczas gdy wariancję oszacowania parametrów modelu uzyskuje się za pomocą wzoru
1
2
2
)
ˆ
(
ˆ
)
ˆ
(
−
=
X
Ω
X'
a
s
S
(2.7)
Obydwa wyŜej wymienione estymatory są obciąŜone, ale zgodne, a tym samym nieobciąŜone
asymptotycznie.
3. Uwagi o estymacji modeli nieliniowych
Modele nieliniowe ze względu na parametry moŜna oszacować zarówno za pomocą MNW
jak i metody minimalizującej sumę kwadratów reszt, rozwijając funkcję nieliniową w
(liniową) sumę wyrazów szeregu Taylora. W tym drugim przypadku oszacowanie są z samej
10
istoty metody jedynie przybliŜeniami. Stosując MNW w przypadku wielu funkcji moŜna
wyznaczyć pochodne analitycznie, dzięki czemu uzyskuje się oszacowania dokładne. Biorąc
pod uwagę fakt, iŜ estymatory uzyskane tą metodą są zgodne i asymptotycznie
najefektywniejsze (co nie jest najczęściej spełnione w przypadku metod opartych na
minimalizacji sumy kwadratów reszt), naleŜałoby więc uznać jej wyŜszość nad MNK. Za
metodą MNK przemawiają jednak czasami względy praktyczne. Metoda MNW jest dostępna
tylko w niektórych pakietach statystyczno-ekonometrycznych, jest teŜ najczęściej znacznie
bardziej czasochłonna (choć wymaga teŜ znacznie mniej pamięci komputerowej).
W wielu przypadkach nieliniowe (ze względu na zmienne) modele moŜna oszacować, po
odpowiednich przekształceniach, metodami estymacji liniowej. Przykładowo, nieliniowy
model:
i
k
i
i
i
i
x
y
ε
α
α
∏
=
=
1
0
(2.8)
jest równowaŜny poniŜszemu modelowi logarytmicznemu:
i
k
1
i
i
i
0
i
ln
x
ln
ln
y
ln
ε
α
α
∑
=
+
+
=
(2.9)
który moŜe być oszacowany za pomocą metod liniowych (w miejsce wartości zmiennych Y i
X naleŜy podstawić ich logarytmy).
4. Estymacja za pomocą zmiennych instrumentalnych (MZI)
Estymatory uzyskane za pomocą zmiennych instrumentalnych pozwalają ograniczyć w
znacznym stopniu (negatywne) skutki liniowego skorelowania reszt modelu ze
zmiennymi objaśniającymi (por. równanie 1.5 wraz z komentarzem). W przypadku
występowania tej zaleŜności estymatory parametrów równania liniowego uzyskane za
pomocą klasycznej MNK tracą własność nie tylko nieobciąŜoności, ale i zgodności.
Przez zmienne instrumentalne (zwane teŜ instrumentami) naleŜy rozumieć dodatkowe
zmienne wykorzystane w estymacji odznaczające się dwiema własnościami: a/ są
nieskorelowane (w praktyce: słabo skorelowane) z resztami modelu, b/ są skorelowane z tymi
zmiennymi objaśniającymi w modelu pierwotnym, które są skorelowane z resztami (mówi
się, Ŝe te ostatnie zmienne są instrumentowane). Macierz zmiennych instrumentalnych
powinna zawierać co najmniej tyle zmiennych (kolumn), ile jest zmiennych objaśniających w
pierwotnym modelu skorelowanych z resztami oraz tzw. autoinstrumenty czyli te kolumny
macierzy X, które odpowiadają zmiennym nieskorelowanym z resztami. Postać estymatora
uzyskanego za pomocą zmiennych instrumentalnych jest następująca:
Y
'
W
X
'
W
a
ˆ
)
ˆ
(
1
−
=
)
(2.10)
gdzie
W
ˆ
oznacza macierz zawierającą (m. in.) zmienne instrumentalne
8
. Jedna z jej
moŜliwych postaci przedstawia równanie (2.13). JeŜeli są one nieskorelowane z resztami
8
Jeden ze sposobów konstrukcji tej macierzy został podany poniŜej.
11
pierwotnego modelu, to powyŜsze wyraŜenie jest asymptotycznie nieobciąŜonym
9
estymatorem parametrów modelu. Estymator wariancji reszt modelu ma postać:
I
k
n
s
−
=
e
'
e
)
)
)
2
(2.11)
gdzie e
)
jest wektorem reszt w zmodyfikowanym modelu, a k
I
stanowi liczbę zmiennych
instrumentalnych. Asymptotycznie nieobciąŜony estymator wariancji oszacowań parametrów
ma postać:
1
1
2
2
)
ˆ
(
ˆ
ˆ
)
ˆ
(
)
(
−
−
=
X
'
W
W
'
W
X
'
W
a
s
S
)
)
(2.12)
Wariancja ta jest tym mniejsza, im silniejsza jest korelacja między zmiennymi
instrumentowanymi i instrumentalnymi. Jest to jedno z kryteriów doboru zmiennych
instrumentalnych. Drugie kryterium stanowi, zgodnie z tym co zostało napisane powyŜej,
nieskorelowanie z resztami pierwotnego modelu czyli warunek konieczny dla nieobciąŜoności
a
)
. Nietrudno zgadnąć, Ŝe opierając się na kaŜdym z wymienionych kryteriów z osobna
uzyskalibyśmy dwa róŜne zestawy instrumentów. W praktyce znacznie bardziej istotne jest
skorelowanie instrumentów ze zmiennymi instrumentowanymi, co przekłada się na ich
efektywność. Z drugiej strony, jeŜeli jest ono silne, to są one równieŜ dość mocno
skorelowane z resztami. Zatem kaŜda dodatkowa zmienna instrumentalna zwiększa
obciąŜenie estymatorów. Skutecznym sposobem zwiększenia efektywności estymatorów bez
utraty informacji zawartej w potencjalnych instrumentach jest uŜycie ich kombinacji liniowej
zamiast pojedynczej zmiennej. Kombinację tę moŜna uzyskać np. szacując (za pomocą MNK)
model, w którym zmienna instrumentowana jest funkcją instrumentów i stosując to
oszacowanie jako zmienną instrumentalną
10
. MoŜna wykazać, Ŝe tak uzyskane estymatory
parametrów mają najniŜszą wariancję ze wszystkich estymatorów uzyskanych za pomocą
tych samych zmiennych instrumentalnych.
Macierz
Wˆ
uzyskuje się, niezaleŜnie od liczby zmiennych instrumentalnych i rodzaju
zastosowanej kombinacji, następująco:
X
W'
W)
W(W'
W
-1
=
ˆ
(2.13)
gdzie W jest macierzą uzyskaną poprzez zamianę w macierzy X zmiennych skorelowanych z
resztami przez instrumenty.
Metoda estymacji za pomocą zmiennych instrumentalnych, choć moŜe przynieść bardzo
korzystne skutki, nie powinna być stosowana pochopnie. PoniewaŜ istnienia liniowej
korelacji reszt i zmiennych objaśniających nie moŜna sprawdzić bezpośrednio
11
jej istnienie
moŜna jedynie podejrzewać na podstawie dociekań teoretycznych bądź doświadczenia
wynikającego z wcześniejszych estymacji z udziałem podobnych zmiennych. Formalne
uzasadnienie dla stosowania MZI stanowią wyniki testów ex post. Najpopularniejszy z nich
jest szczególnym przypadkiem testu Walda (por. punkt 1 w rozdziale III) i polega na ocenie
9
A więc równieŜ zgodnym, jeŜeli jego wariancja maleje do zera wraz ze wzrostem próby.
10
Jest to szczególny przypadek tzw. dwustopniowej (zwanej tez podwójną) metody najmniejszych kwadratów
(2MNK).
11
Korelacja liniowa uzyskanych za pomocą MNK reszt i dowolnej zmiennej objaśniającej w próbie zawsze
wynosi 0.
12
istotności róŜnicy pomiędzy oszacowaniami parametrów uzyskanych za pomocą MNK i MZI.
Jest on znany jako test Hausmana lub Durbina-Wu-Hausmana (DWH) i został opisany przez
Greene’a (str. 443-444) i Darnella (str. 132-135)
12
. Zalecane jest równieŜ sprawdzenie czy
instrumenty są dostatecznie mocno skorelowane ze zmiennymi instrumentowanymi. JeŜeli w
modelu jest instrumentowana jedna zmienna, to wystarczający jest test istotności R
2
po
oszacowaniu za pomocą MNK modelu w którym zmienną objaśnianą jest ta zmienna zaś
zmiennymi objaśniającymi instrumenty. W przypadku większej liczby zmiennych
instrumentowanych test tego typu moŜe okazać się niewystarczający (zwłaszcza w przypadku
silnego skorelowania pomiędzy nimi). Prostą procedurę postępowania w takiej sytuacji
przedstawił J. Shea (”Instrument relevance in multivariate linear models: a simple measure”,
Review of Economics and Statistics, 79, str. 348-52, 1997 r.).
5. Zmienne binarne w modelach regresji: regresja logitowa i probitowa
Zmienne binarne czyli przyjmujące tylko dwie wartości (najczęściej 0 i 1) są jedną z
najpopularniejszych metod modelowania ekonometrycznego. Ich uŜyteczność jest oczywista
w przypadku, gdy model regresji opisuje takie zjawiska jakościowe np. zaleŜność między
dochodem, a płcią. W najprostszym modelu tego typu zmienną objaśnianą byłby dochód,
zmienną objaśniającą zmienna przyjmująca wartość 1, gdy badana osoba jest kobietą i 0, gdy
męŜczyzną (lub odwrotnie). Model taki, a takŜe modele obejmujące większą liczbę binarnych
zmiennych objaśniających opisane poniŜej, moŜna oszacować tak samo jak modele ze
zmiennymi ciągłymi.
W wielu przypadkach konieczne jest, aby zmienne jakościowe wyznaczały więcej niŜ dwie
kategorie. Przykładem moŜe być model trendu z wahaniami okresowymi, np. kwartalnymi.
Zmienne binarne powinny przyjmować wartość 1, gdy obserwacja naleŜy do danego kwartału
i 0 w przeciwnym przypadku. Najprostszy model (zakładający stałość amplitudy wahań czyli
jej niezaleŜność od poziomu trendu) z kwartalnymi wahaniami miałby postać:
n)
1,2,...,
(i
=
+
=
+
+
+
+
i
i
i
i
i
x
x
x
t
y
ε
α
α
α
α
α
3
3
2
2
1
2
1
0
(2.14)
gdzie t oznacza czas, zaś zmienne x
1
, x
2
i x
3
przyjmują wartość 1 dla obserwacji naleŜących,
odpowiednio, do 1, 2 i 3 kwartału. W modelu został pominięty ostatni kwartał, któremu
odpowiadają zerowe wartości wszystkich wymienionych zmiennych. Pominięcie jednej
kategorii (jej wybór nie ma znaczenia) jest niezbędne, aby uniknąć liniowej zaleŜności
między zmiennymi.
W podanym przykładzie nie moŜna było z góry zakładać stałej (np. rosnącej) zaleŜności
między numerem kwartału, a siłą wahań okresowych. Zatem zastąpienie trzech zmiennych
binarnych jedną zmienną przyjmującą wartości 1, 2, 3 i 4 najczęściej nie upowaŜniałoby do
zastosowania liniowej estymacji parametrów. Nawet jednak w przypadku, gdy zaleŜność
między zmienną objaśnianą jest monotoniczna (np. między dochodem i poziomem
wykształcenia
13
lub między wydatkami na mieszkanie i liczbą osób w gospodarstwie
domowym) zastosowanie zmiennych binarnych moŜe być korzystne. Po pierwsze, uŜycie
12
Ten i podobne testy występują pod nazwą testów egzogeniczności (zaprzeczeniem egzogeniczności jest
endogeniczność).
13
MoŜna np. przyjąć, Ŝe wykształceniu podstawowemu odpowiada wartość zmiennej objaśniającej 1,
zawodowemu 2 itd. Inne rozwiązanie polega na zdefiniowaniu zmiennej jako liczby ukończonych lat nauki.
13
jednej zmiennej jest równowaŜne z mało realistycznym załoŜeniem, Ŝe np. „przyrost
wykształcenia” o jednostkę powoduje średnio stały (równy wartości odpowiedniego
parametru) przyrost zmiennej objaśniającej. Inny przykład uŜyteczności zmiennych binarnych
stanowią modele, w których pewne zmienne objaśniające mogą występować więcej niŜ raz,
co najczęściej powoduje stochastyczną współliniowość tych zmiennych
14
i obniŜa
efektywność estymatorów. W celu ograniczenia tego zjawiska niektóre zmienne moŜna co
najmniej raz zastąpić kilkoma zmiennymi binarnymi. Np. liczba osób moŜe być wyraŜona w
postaci kilku zmiennych binarnych, które przyjmują wartość 1 gdy gospodarstwo jest jedno,
dwu, trzy itd. osobowe. Jedyną, i niezbyt istotną, wadą takiego rozwiązania jest zwiększenie
liczby zmiennych objaśniających.
Sytuacje zmienia się, gdy binarna jest zmienna objaśniana. Zastosowanie MNK nie pozwala
uzyskać nieobciąŜonych czy zgodnych estymatorów (wartość oczekiwana reszt jest róŜna od
zera). W efekcie, zakres zmienności wartości teoretycznych zmiennej objaśnianej wykracza poza
przedział [0,1]. Tymczasem, wartości te naleŜałoby traktować jako wartość oczekiwaną
(„teoretyczną”) prawdopodobieństwa, Ŝe zmienna Y przyjmie wartość 1. Rozwiązaniem tego
problemu jest zastosowanie tzw. regresji logitowej lub probitowej. Polega ona na zastosowaniu
odpowiedniej rosnącej transformacji wartości teoretycznych zmiennej objaśnianej, dzięki której
przyjmuje ona wartości z przedziału [0,1]. Przykładowo, w przypadku regresji logitowej ma ona
postać:
)
exp(
1
)
exp(
)
exp(
1
)
exp(
ˆ
)
1
(
ˆ
...
2
2
1
0
...
2
2
1
0
α
X
α
X
i
i
+
=
+
=
=
=
+
+
+
+
+
+
+
+
ik
k
i
i
i
ik
k
i
i
i
i
i
x
x
x
x
x
x
P
y
P
α
α
α
α
α
α
α
α
(2.15)
Wobec powyŜszego, wartość oczekiwaną prawdopodobieństwa wylosowania próby Y czyli
odpowiadającą jej funkcję wiarygodności moŜna wyznaczyć następująco:
)]
(
1
[
)
(
)
|
(
0
1
α
X
α
X
Y
a
i
y
i
y
i
i
L
∏
∏
=
=
Λ
−
Λ
=
(2.16)
gdzie Λ jest transformacją logitową
15
występującą po prawej stronie równania (2.15).
Oszacowania parametrów modelu logitowego (i probitowego) wyznacza się za pomocą MNW,
znajdując wartości parametrów maksymalizujące powyŜszą funkcję (w praktyce: jej logarytm).
Szczegóły tej procedury przedstawił W. Greene (1997, str. 883)
16
. PoniewaŜ równanie (2.15)
moŜna równieŜ zapisać:
ik
k
i
i
i
i
i
x
x
x
P
P
α
α
α
α
+
+
+
+
=
−
...
2
2
1
0
)]
ˆ
1
/(
ˆ
ln[
(2.17)
to znak oszacowań parametrów modelu moŜna interpretować tak jak w przypadku zwykłego
modelu liniowego (jako Ŝe lewa strona równania jest rosnącą transformacją p
i
). Inna postać tego
samego równania pozwala zapisać iloraz dwóch prawdopodobieństw (ang.:”odds ratio”)
następująco:
14
Np. w modelach popytu ze zmiennymi demograficznymi liczba osób w gospodarstwie pojawia się przy kaŜdej
grupie wydatków.
15
W przypadku regresji probitowej transformacja P
i
jest dystrybuantą rozkładu normalnego standardowego.
Wprawdzie oszacowania parametrów tego typu modelu są róŜne od oszacowań modelu logitowego, ale ich
interpretacja jest identyczna. Bardzo zbliŜone są teŜ „wartości teoretyczne” prawdopodobieństw.
16
Podaje on układ równań nieliniowych, który rozwiązuje się w sposób numeryczny, nie moŜna więc podać
ogólnej postaci estymatorów parametrów.
14
)
exp(
)
0
(
)
1
(
α
X
i
=
=
=
Y
P
Y
P
(2.18)
Dodatnia wartość oszacowania oznacza pozytywny wpływ odpowiedniej zmiennej objaśniającej
na oszacowanie teoretycznej wartości prawdopodobieństwa, Ŝe Y przyjmie wartość 1.
Interpretacja wartości parametrów jest jednak bardziej skomplikowana. Nie moŜe być ona
traktowana, w odróŜnieniu od modeli liniowych, jako oszacowanie efektu marginalnego
względem x
i
. Z uwagi na nieliniowość modelu zmiana teoretycznej wartości
prawdopodobieństwa spowodowana zmianą i-tej zmiennej objaśniającej zaleŜy od wartości
zmiennych objaśniających X
i
(i-tego wiersza w macierzy danych). Dla j-tej zmiennej
objaśniającej efekt marginalny jej zmiany o jednostkę moŜna oszacować następująco:
j
j
a
x
Y
E
)]
(
1
)[
(
)
|
(
a
X
a
X
X
i
i
i
Λ
−
Λ
=
∂
∂
(2.19)
Wariancję oszacowań parametrów modelu logitowego moŜna oszacować za pomocą wzoru:
1
1
2
2
]
)
(
[
)
(
−
=
Λ
−
=
∑
n
i
i
y
S
'
X
X
a
X
a
i
i
i
(2.20)
III. TESTY STATYSTYCZNE W MODELACH REGRESJI
1. Testy warunków ograniczających modelu
W wielu przypadkach zgodność z teoriami ekonomicznymi wymaga, aby oszacowania
parametrów modelu spełniały pewne warunki. MoŜna to osiągnąć estymując model np. za
pomocą warunkowej MNK (por. rozdział II, cz.1). Regresja warunkowa moŜe być teŜ
wykorzystana jako test teorii ekonomicznych rozumianych jako przyjmowanie konkretnych
wartości przez parametry: jeŜeli oszacowania uzyskane za pomocą metod bezwarunkowych
są bliskie oszacowaniom warunkowym to moŜna uznać, Ŝe wyniki estymacji potwierdzają
teorię. W niniejszym paragrafie omówione zostaną dwa testy pozwalające stwierdzić, czy
róŜnice między oszacowaniami warunkowymi i bezwarunkowymi nakazują odrzucenie teorii.
Oba wykorzystują statystyki χ
2
przyjmujące tym większą wartość im większe występują
róŜnice (mówiąc w uproszczeniu), między oszacowaniami warunkowymi i bezwarunkowymi.
Ideę konstrukcji obu tych testów: ilorazu wiarygodności i Walda ilustruje rysunek 3.1.
Przedstawiony został na nim test dla jednego warunku h(Θ)=0 narzuconego na jeden parametr
Θ, jednak oba testy mogą być zastosowane równieŜ w przypadku wielu ograniczeń i wielu
parametrów.
Test ilorazu wiarygodności oparty jest na następującym załoŜeniu: jeŜeli warunek dodatkowy
(lub zespół warunków) jest prawdziwy, to narzucenie tego warunku nie powinno
spowodować duŜego spadku wartości funkcji wiarygodności. Statystyka zdefiniowana za
pomocą równania (3.1) przyjmuje tym większą wartość im większy jest ten spadek. JeŜeli jej
wartość przekroczy wartość krytyczną, to hipotezę mówiącą o spełnianiu warunku
(warunków) naleŜy odrzucić.
15
U
R
L
L
LR
ln
2
−
=
(3.1)
gdzie L
R
i L
U
są, odpowiednio, wartościami funkcji wiarygodności uzyskanymi dla modelu z
ograniczeniami i bez. PowyŜsza statystyka, przy prawdziwości hipotezy zerowej (h(Θ)=0) ma
asymptotyczny rozkład χ
2
o liczbie stopni swobody równej liczbie narzuconych ograniczeń.
Rys. 3.1. Test ilorazu wiarygodności i test Walda dla jednego warunku (na podstawie: Greene, str. 160)
Drugi z testów, zaproponowany przez Walda, zakłada, Ŝe jeŜeli warunek dodatkowy (lub
zespół warunków) jest prawdziwy, to uzyskane za pomocą estymacji warunkowej
oszacowania powinny je w przybliŜeniu spełniać. Statystyka testowa ma postać:
[
]
)]
ˆ
(
[
)]
ˆ
(
[
)]'
ˆ
(
[
1
2
Θ
Θ
Θ
h
h
S
h
W
−
=
(3.2)
gdzie:
'
Θ
Θ
Θ
Θ
Θ
Θ
∂
∂
∂
∂
=
ˆ
)
ˆ
(
h
)
ˆ
(
S
ˆ
)
ˆ
(
h
)]
ˆ
(
h
[
S
2
2
)
ˆ
(Θ
h
oznacza macierz testowanych warunków, której elementy obliczono podstawiając
oszacowania parametrów Θ.
)
ˆ
(
2
Θ
S
jest macierzą wariancji oszacowania parametrów Θ.
Statystyka Walda równieŜ ma asymptotyczny rozkład χ
2
o liczbie stopni swobody równej
liczbie narzuconych ograniczeń.
IW (LR)
Wald
ln L
U
ln L
R
ln L(Θ)
h(Θ)
0
R
Θ
ˆ
MNW
Θ
ˆ
Θ
16
Z teoretycznego punktu widzenia (np. oceniając moc testów) nie moŜna przyznać wyŜszości
Ŝadnej z powyŜszych metod. O wyborze winny więc decydować względy praktyczne. Wadą
testu ilorazu wiarygodności jest konieczność oszacowania dwóch modeli (z warunkami
dodatkowymi i bez). Wadą testu Walda jest konieczność wyznaczenia macierzy wariancji
oszacowań parametrów (co jednak najczęściej musi być zrobione z innych względów) i w
wielu przypadkach konieczność „ręcznego” wyznaczania wartości statystyki testowej.
2. Testy specyfikacji modelu
W licznych zastosowaniach liniowa postać modelu nie jest adekwatna i konieczny jest wybór
innej postaci funkcji regresji (g w równaniu 1.1). Teoria ekonomiczna bardzo rzadko pozwala
uzasadnić wybór jej konkretnej postaci, często więc naleŜy dokonać go posługując się metodą
prób i błędów lub poprzez obserwację rozkładu wartości empirycznych. PoniŜej zostały
przedstawione dwa testy (specyfikacji) pozwalające dokonać weryfikacji wyboru postaci
funkcji g.
Test RESET (Regression Equation Specification Error Test) zwany teŜ testem Ramsey’a
moŜe być wykorzystany do weryfikacji hipotezy o liniowości funkcji regresji (równania 1.2).
Aby wyznaczyć stosowną statystykę testową naleŜy oszacować model liniowy oraz model o
następującej postaci:
i
p
p
i
p
i
i
i
i
i
ik
k
i
i
i
ε
y
y
y
x
x
x
a
y
+
+
+
+
+
+
=
−
−
+
+
+
)
1
(
)
1
(
3
2
2
2
1
1
0
...
2
2
1
1
ˆ
...
ˆ
ˆ
β
β
β
α
α
α
(3.3)
gdzie
j
j
i
y
)
1
(
ˆ
−
(j=2,...,p) jest i-tą „teoretyczną wartością” zmiennej objaśnianej uzyskaną za
pomocą estymacji modelu liniowego (liniowej części równania 3.3). PoniŜsza statystyka
moŜe być uŜyta do konstrukcji testu.
)
1
/(
)
1
/(
]
[
−
−
−
−
=
k
n
URSS
p
URSS
RRSS
R
(3.4)
gdzie RRSS jest sumą kwadratów reszt modelu liniowego, zaś URSS sumą kwadratów reszt
modelu (3.3). JeŜeli hipoteza o liniowości jest prawdziwa, to R ma rozkład F z (p-1) i (n-k-1)
stopniami swobody. Gdy suma kwadratów reszt modelu liniowego jest znacznie większa od
sumy kwadratów reszt modelu nieliniowego, to statystyka R przekracza poziom krytyczny i
hipotezę o liniowości naleŜy odrzucić. Hipoteza alternatywna nie precyzuje postaci funkcji
regresji.
Kolejny test pozwala na specyfikacje postaci funkcji regresji w hipotezie zerowej i
alternatywnej, jest teŜ bardziej ogólny od testu RESET z uwagi na wielość potencjalnych
specyfikacji. Wykorzystuje on następującą transformację (Boxa i Coxa) zmiennej X:
=
≠
−
=
0
dla
ln(X)
0
dla
/
)
1
(
)
(
λ
λ
λ
λ
λ
X
X
(3.5)
UmoŜliwia ona zapis modelu regresji z jedną zmienną
17
za pomocą następującej
18
funkcji:
17
MoŜe on być uogólniony przez dodanie dowolnej liczby zmiennych objaśniających.
17
n)
1,2,...,
(i
0
)
(
1
1
)
(
=
+
+
=
i
i
i
ε
x
y
α
α
δ
λ
(3.6)
Model ten naleŜy oszacować za pomocą metody największej wiarygodności (szczegóły
przedstawił A. Darnell, 1994, str. 37) dwukrotnie: zakładając liniowość (wtedy λ=δ=1) oraz
przyjmując inne wartości λ i δ. Test liniowości jest w tym przypadku testem ilorazu
wiarygodności dla hipotezy zerowej: λ=δ=1. Test ten moŜna teŜ przeprowadzić takŜe dla
innych form funkcji regresji w hipotezie zerowej, choć w praktyce estymacja modelu, w
szczególności wariancji oszacowań jest dość trudna a czasami problematyczna. W przypadku
gdy test nie daje jednoznacznych wskazań odnośnie „właściwych” parametrów transformacji
Boxa-Coxa naleŜy przyjąć wartości oszacowań (parametrów strukturalnych i transformacji)
uzyskanych za pomocą metody największej wiarygodności.
3. Test stabilności parametrów
Omawiany test (Chowa) pozwala zweryfikować hipotezę o stałości relacji ekonomicznych w
modelach liniowych, objawiającej się niezmiennymi (w czasie lub przestrzeni) wartościami
parametrów w modelach. Niezmienność (w praktyce: przybliŜona) parametrów jest jednym z
zasadniczych warunków m. in. trafności prognoz. Stabilność parametrów bada się (ex post)
sprawdzając czy są one jednakowe w dwóch badanych podpróbach (np. w dwóch okresach
lub w dwóch regionach). Test Chowa wymaga trzech estymacji za pomocą MNK: dla całej
próby (Y,X) oraz dla dwóch podprób (Y
1
,X
1
) (Y
2
,X
2
). Pierwsza z nich (milcząco) zakłada, Ŝe
parametry są stałe dla całej badanej próby, jest więc estymacją z warunkami dodatkowymi (a
1
= a
2
). Dwie pozostałe są estymacjami bezwarunkowymi. JeŜeli hipoteza o stabilności
parametrów jest prawdziwa, to suma kwadratów reszt w estymacji warunkowej powinna być
równa sumie dwóch sum kwadratów reszt uzyskanych dla estymacji bezwarunkowych. JeŜeli
róŜnica między wyŜej wymienionymi sumami jest duŜa, to hipotezę o stabilności parametrów
naleŜy odrzucić. Statystyka testowa następującej postaci (por. objaśnienia do równania 3.4;
suma kwadratów reszt estymacji bezwarunkowej URSS jest sumą dwóch sum kwadratów
reszt uzyskanych za pomocą zastosowanej do kaŜdej podpróby oddzielnie MNK):
)
2
2
/(
)
1
/(
]
[
−
−
+
−
=
k
n
URSS
k
URSS
RRSS
Ch
(3.7)
ma rozkład F z (k+1) i (n-2k-2) stopniami swobody.
PowyŜszy test wymaga homoskedastyczności reszt. W przypadku niespełniania tego warunku
naleŜy go zmodyfikować stosując test Walda (szczegóły przedstawił A. Darnell, 1994, str.
51).
4. Test homoskedastyczności reszt
Występowanie heteroskedastyczności reszt nakazuje modyfikację metod estymacji wariancji
oszacowań parametrów i weryfikacji hipotez odnośnie parametrów modelu. Jej rozpoznanie
ma więc zasadnicze znaczenie w modelowaniu regresji. Przedstawiony poniŜej test
18
Przykładowo, model jest liniowy, gdy λ=δ=1 lub logarytmiczny, gdy λ=δ=0
18
wykorzystuje fakt, iŜ w przypadku homeskedastyczności reszt (co objawia się ich
niezaleŜnością od wartości zmiennych objaśniających) uporządkowanie (w dowolnej
kolejności) Ŝadnej ze zmiennych objaśniających nie powinno spowodować uporządkowania
reszt. Omówiony tu test zaproponowany przez S. Goldfelda i R. Quandta porównuje
wariancje reszt w dwóch podpróbach otrzymanych po uporządkowaniu badanej zmiennej
„podejrzanej” o skorelowanie z wariancją reszt. Wariancje te są wyznaczane poprzez
estymacje dwóch modeli, dla kaŜdej podpróby oddzielnie. JeŜeli powyŜsza zaleŜność nie ma
miejsca, to wariancje reszt w obydwu podpróbach nie powinny się istotnie róŜnić. W
przeciwnym przypadku hipotezę o homoskedastyczności reszt naleŜy odrzucić. Statystyka
testowa postaci (subskrypty 1 i 2 oznaczają numer próby):
)
1
/(
)
1
/(
2
2
1
1
1
−
−
−
−
=
k
n
k
n
GQ
2
'
'
e
e
e
e
(3.8)
ma rozkład F z (n
1
-k-1) i (n
2
-k-1) stopniami swobody (licznik powinien mieć wyŜsza wartość,
w przeciwnym przypadku naleŜy zamienić subskrypty). JeŜeli wartość krytyczna zostanie
przekroczona, to hipotezę zerową naleŜy odrzucić.
W wielu przypadkach moc testu moŜna zwiększyć, usuwając część obserwacji „środkowych”
(po uporządkowaniu). Tym samym jednak zmniejsza się liczbę stopni swobody, co z kolei
wpływa negatywnie na moc testu, tym bardziej, im mniejsza jest próba. Test Goldfelda i
Quandta wymaga, aby rozkład reszt był normalny.
Istnieje wiele innych testów heteroskedastyczności reszt. JeŜeli rozkład tych ostatnich nie jest
normalny, moŜna zastosować np. test White’a omówiony przez W. Greene’a (1997, str. 550-
551) i A. Darnella (1994, str. 438-440). Test ten jednak naleŜy stosować jedynie w przypadku
gdy mamy pewność, iŜ specyfikacja funkcji regresji jest poprawna. Inny test, zaproponowany
przez Breuscha i Pagana (Greene, 1997, str. 552-553), pozwala wykryć heteroskedastyczność
reszt dla wszystkich zmiennych objaśniających łącznie. W przypadku gdy w modelu
występuje więcej niŜ jedna zmienna objaśniająca, wykrycie zmiennej „odpowiedzialnej” za
heteroskedastyczność i tak wymaga testowania kaŜdej ze zmiennych osobno (np. za pomocą
testu Goldfelda-Quandta).
Dekalog ekonometrii stosowanej według Petera Kennedy’ego
1.
Będziesz uŜywać zdrowego rozsądku i teorii ekonomicznych.
2.
Będziesz zadawać właściwe pytania.
3.
Powinieneś znać kontekst (analizy - przyp. A. S.).
4.
Będziesz badać (“inspect”) dane.
5.
Nie będziesz oddawać czci skomplikowanej formie (”complexity”).
6.
Będziesz długo i uwaŜnie oglądać wyniki (estymacji - przyp. A. S.).
7.
Będziesz zwaŜać na koszty “przeszukiwania danych” (“data mining”).
8.
Będziesz zgadzać się na kompromisy.
9.
Nie będziesz mylić istotności z istotą
19
(zagadnienia - przyp. A. S.).
10.
Będziesz spowiadać się z odporności na załoŜenia (niedosłowne tłumaczenie ”Thou shalt
confess in the presence of sensitivity”).
19
W oryginale: ”significance” i ”substance”.
19
Literatura podstawowa:
William H. Greene, ”Econometric Analysis”, Prentice-Hall International, Inc. (róŜne
wydania; podawane tu numery stron pochodzą z wydania III z roku 1997)
Peter Kennedy, ”A Guide to Econometrics”, Blackwell Publishing (róŜne wydania)
G.S. Maddala (2006), “Ekonometria”, PWN.
Literatura uzupełniająca:
Wojciech W. Charemza i Derek F. Deadman (1997), „Nowa Ekonometria”, PWE.
Gregory C. Chow (1995), „Ekonometria”, PWN.
Adrian C. Darnell (1994), “A Dictionary of Econometrics”, Edward Elgar Publishing, Inc.
Fumio Hayashi (2000), ”Econometrics”, Princeton University Press (I rozdział i niektóre
zbiory danych dostępne na stronie
http://www.pup.princeton.edu
).
Dale J. Poirier (1995), ”Intermediate Statistics and Econometrics; A Comparative Approach”,
The MIT Press.
Aleksander Welfe „Ekonometria”, PWE (róŜne wydania)
Wybrane artykuły z Journal of Economic Perspectives, vol. 15, nr 4, 2001.
(z komputerów uczelnianych dostępne na stronie
www.jstor.org
)
Niezła strona polskojęzyczna Jerzego Mycielskiego
http://inflacja.icm.edu.pl/jmyc/
Cały obowiązujący zakres kursu moŜna znaleźć w niniejszym skrypcie zaś szczegółowe
wyjaśnienia w ksiąŜkach zaliczonych do literatury podstawowej. Literatura uzupełniająca
równieŜ opisuje te zagadnienia, ale Ŝadna z pozycji nie wyczerpuje zakresu w całości.
Przyjęta konwencja oznaczeń:
X, Y - zmienne
X, Y
- macierze (wektory) obserwacji
y
i
, x
ij
, x
i
- pojedyncze obserwacje
α ,Θ - wektory parametrów
α ,Θ - pojedyncze parametry
a
,
Θ
,
α ˆ
ˆ
- wektory oszacowań
i
i
,a
αˆ
- pojedyncze oszacowania
k - liczba zmiennych objaśniających w modelu (nie obejmuje wyrazu wolnego)
n - liczba obserwacji
wektor parametrów/oszacowań modelu jest kolumną
wektor obserwacji dla jednej zmiennej jest kolumną
wektor zmiennych dla jednej obserwacji jest wierszem
20
ZADANIA
20
1.* Dla gospodarstw domowych, których głowami są osoby powyŜej 40 roku Ŝycia
oszacowane zostały dwa modele, w których zmienną objaśnianą był m. in. dochód na osobę
(DOCH) wyraŜany w złotych miesięcznie. Zbiór zmiennych objaśniających był następujący:
•
WIEK - wiek głowy gospodarstwa,
•
PRAC - zmienna 0/1 przyjmująca wartość 1, gdy głowa gospodarstwa jest
pracownikiem (tylko drugi model)
•
EMEREN - zmienna 0/1 przyjmująca wartość 1, gdy głowa gospodarstwa jest
emerytem lub rencistą (tylko drugi model)
Próba liczyła ponad 20 000 obserwacji. Wyniki estymacji były następujące (w nawiasach
podane są statystyki t-Studenta):
I model
DOCH = -3,85*WIEK + 791 +
ε
(-13,3) (21,2)
R
2
= 0,008
II model:
DOCH = 1,50*WIEK + 88,2*PRAC - 104,2*EMEREN + 512,9 +
ε
(13,5) (9,0) (-9,2) (23,4)
R
2
= 0,025
W obydwu przypadkach R
2
okazał się istotnie większy od zera, zaś Ŝaden z testów nie
wykazał iŜ klasyczna MNK moŜe być niewłaściwa. W drugim modelu nie jest spełniona tzw.
„zasada koincydencji”. Czy niewłaściwy jest model czy teŜ powyŜsza zasada?
2. Które stwierdzenia są nieprawdziwe i dlaczego?
a/ W liniowym modelu z jedną zmienną kowariancja kwadratów reszt i zmiennej
objaśniającej nie róŜni się statystycznie od zera. Oznacza to homoskedastyczność reszt.
b/ Niska wartość R
2
w liniowym modelu z jedną zmienną dowodzi, Ŝe zaleŜność między
zmienną objaśnianą i objaśniającą jest nieliniowa lub statystycznie nieistotna.
c/ zmienne niezaleŜne muszą być losowe,
d/ JeŜeli model regresji liniowej został oszacowany za pomocą wszystkich obserwacji w
populacji generalnej (a = α), to R
2
= 1.
20
Gwiazdka oznacza, Ŝe zadanie jest nieco trudniejsze od pozostałych; „zal” oznacza, Ŝe
zadanie pochodzi z testów zaliczeniowych z poprzednich lat.
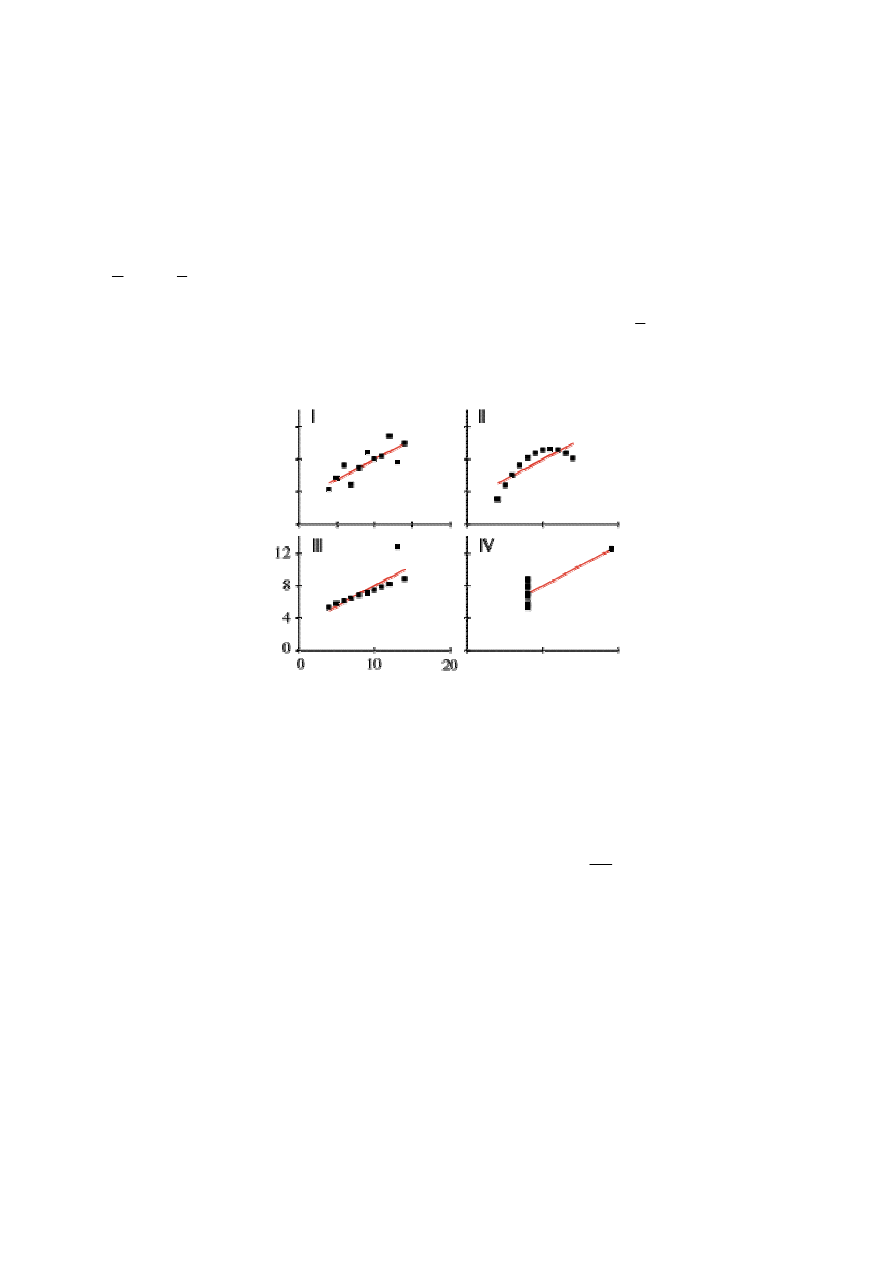
21
3. Za pomocą klasycznej MNK oszacowano dwa liniowe modele inflacji. W pierwszym z
modeli współczynnik determinacji okazał się większy niŜ w modelu drugim, natomiast
oszacowanie wariancji reszt było w nim mniejsze. Ponadto okazało się, Ŝe statystyka F
zdefiniowana za pomocą równania (1.13) tylko w przypadku drugiego oszacowania
przekracza wartość krytyczną przy poziomie istotności 0,05.
Które oszacowanie naleŜy uznać za lepsze?
4. Dane są 4 próby liczące po 11 elementów, dla których poniŜsze statystyki są jednakowe:
9
=
X
;
5
,
7
=
Y
;
10
)
(
2
=
X
D
;
73
,
3
)
(
2
=
Y
D
Oszacowanie modeli regresji za pomocą MNK dało równieŜ wiele jednakowych wyników:
3
5
,
0
ˆ
+
⋅
=
X
Y
;
188
,
0
)
(
=
a
S
;
667
,
0
2
=
R
;
∑
=
i
i
e
75
,
13
2
;
∑
=
−
i
i
Y
y
5
,
27
)
ˆ
ˆ
(
2
Graficzna ilustracja danych i funkcji regresji przedstawia się następująco:
Czy powyŜsze wyniki przekreślają sens posługiwania się modelami regresji?
(Przedstawiony zbiór danych znany jest jako kwartet Anscombe’a . Dane indywidualne moŜna
znaleźć np. tutaj: http://www2.sjsu.edu/faculty/gerstman/EpiInfo/cont-cont.htm.)
5.(zal.) Model wydatków konsumpcyjnych dla trzech grup wydatków (np. Ŝywność,
mieszkanie i ‘pozostałe’) ma postać:
i
i
l
l
l
l
l
il
P
X
p
p
p
w
ε
β
α
α
α
α
+
+
+
+
+
=
)
ln(
ln
ln
ln
3
3
2
2
1
1
gdzie w
il
oznacza udział (proporcję) wydatków na l-te dobro (l=1,2,3) w budŜecie i-tego
gospodarstwa (lub i-tej grupy gospodarstw), p
l
indeks cen l-tej grupy wydatków, X
i
sumę
wydatków i-tego gospodarstwa na głowę, P agregatowy indeks cen.
Od parametrów modelu wymaga się, aby spełniany był tzw. warunek jednorodności
zdefiniowany:
0
3
2
1
=
+
+
l
l
l
α
α
α
. Szacując model bez narzucenia warunków jednorodności
uzyskano oszacowania parametrów (w nawiasach podane są błędy standardowe oszacowań):
a
1
=1,8 (0,95) a
11
= 0,04 (0,008) a
12
=0,24 (0,009) a
13
= -0,1 (0,025) d
1
= 0,85 (0,72)
Zakładając (abstrakcyjnie!), Ŝe wszystkie elementy poza główną przekątną w macierzy
wariancji i kowariancji oszacowań parametrów (wzór 1.10) są równe zeru, naleŜy sprawdzić
przy poziomie istotności 0,01 hipotezę o jednorodności oszacowanego modelu.
Liczba obserwacji wynosi 5000.
22
6. W modelu występującym w zadaniu 5 zmienna X okazała się skorelowana z resztami
modelu? Jakie mogą być tego przyczyny? Jakie zmienne instrumentalne moŜna zastosować
do estymacji tego modelu.?
7.(zal.) Na podstawie danych indywidualnych z budŜetów gospodarstw domowych z 2002 r.
oszacowany został model wydatków na pieczywo
21
. Z uwagi na domniemane skorelowanie
reszt z dwiema pierwszymi zmiennymi (suma wydatków gospodarstwa i kwadrat tej sumy),
oszacowano model równieŜ za pomocą metody zmiennych instrumentalnych.
NaleŜy ustalić przyczynę skorelowania przynajmniej jednej ze zmiennych z resztami.
Jakie instrumenty mogą być uŜyte? (naleŜy wymienić co najmniej dwa, uzasadniając
odpowiedź).
Wyniki oszacowań przedstawia poniŜsza tabela.
Zmienna
MNK
MZI
oszacowanie
t
oszacowanie
t
wydatki
-0,222
-37,1
-0,274
-24,9
wydatki
2
0,014
32,5
0,018
21,9
miasto
-0,009
-32,8
-,007
-27,9
log_wiek
0,042
5,7
0,045
5,29
log_wiek
2
-0,005
-4,9
-0,005
5,1
wyraz wolny
0,797
37,1
0,975
25,3
R
2
0,61
0,59
NaleŜy teŜ ocenić prawdziwość poniŜszych stwierdzeń:
a/ Skoro t i R są (z jednym wyjątkiem) wyŜsze przy MNK, to naleŜy wykorzystać
oszacowania uzyskane tą metodą.
b/ Oszacowania uzyskane za pomocą MZI są nadal obciąŜone i niezgodne, poniewaŜ
pozostawione zostały zmienne skorelowane z resztami.
c/ Usunięcie pierwszych dwóch zmiennych pozwoli uzyskać za pomocą MNK nieobciąŜone
estymatory parametrów modelu.
8. (zal.). Za pomocą 54 obserwacji oszacowany został model o następującej ogólnej postaci:
i
i
i
i
e
b
x
a
x
a
y
+
+
+
=
)
(
2
)
(
1
δ
λ
gdzie zapis X
(λ)
oznacza transformację Boxa-Coxa. Dokonano następnie za pomocą testu
ilorazu wiarygodności weryfikacji dwóch hipotez:
H
0
: λ = 1 oraz H
0
: δ = 2 przy obustronnych hipotezach alternatywnych. Statystyki testowe
przyjęły wartości 0,64 oraz 0,9.
Posługując się tymi samymi danymi wykonano równieŜ test Chowa dla modelu:
0
1
ˆ
b
x
b
y
i
i
+
=
obliczając m. in. sumy kwadratów reszt RRSS i URRS. Którą (które) parę (pary) wartości
moŜna uznać za najbardziej prawdopodobne: a/ 190 i 175, b/ 190 i 180, c/ 225 i 185.
21
Zmienną objaśnianą jest udział wydatków na pieczywo w łącznej sumie wydatków gospodarstwa.
23
9*(zal.). Za pomocą 203 obserwacji oszacowano następujący model regresji:
i
2
i
2
1
i
1
0
i
ε
x
x
y
+
=
+
+
α
α
α
Dla p=2 wartość statystyki w teście Ramsey’a (RESET) wyniosła 3,89.
Za pomocą tej samej próby oszacowano równieŜ model:
i
2
2
i
4
2
i
3
2
1
i
2
1
i
1
0
i
x
x
x
x
y
µ
β
β
β
β
β
+
+
=
+
+
+
uzyskując m. in. wynik:
[
]
−
−
=
′
=
−
−
1
,
2
2
,
1
2
,
1
2
,
1
1
0
0
1
)
(
S
1
0
0
1
)]
(
h
[
S
1
2
1
2
b
b
gdzie
)
(
S
2
b jest macierzą wariancji i kowariancji oszacowań parametrów β
2
i β
4
. Które z
następujących par oszacowań parametrów β
2
i β
4
nie mogą (najprawdopodobniej) być
prawdziwymi oszacowaniami: b
2
=0,6 i b
4
=-1,2 oraz b
2
=1,8 i b
4
=-3,6. Odpowiedź naleŜy
uzasadnić.
10. Liniowy model wyjaśniający zmiany bezrobocia w Niemczech został oszacowany na
podstawie danych z landów wschodnich i zachodnich (osobno) oraz trzeci raz na podstawie
wszystkich danych łącznie. Liczba obserwacji wynosiła, odpowiednio: 22, 38 i 60. Modele
były identyczne i liczyły po 6 zmiennych objaśniających. Sumy kwadratów reszt w modelach
„wschodnim”, „zachodnim” i „połączonym” wynosiły odpowiednio: 90, 120 i 240.
Identyczny model został oszacowany dla Belgii trzykrotnie: dla Flandrii (28
obserwacji), dla Walonii (32 obserwacje) i dla całego kraju (60 obserwacji). Sumy kwadratów
reszt dla pierwszych dwóch estymacji wyniosły, odpowiednio, 75 i 95. Regionalne
zróŜnicowanie przyczyn bezrobocia jest znacznie wyŜsze w Niemczech niŜ w Belgii. Która z
trzech liczb: 280, 160 i 190 jest najbardziej prawdopodobna jako suma kwadratów reszt w
trzeciej estymacji modelu?
11. (zal.). Za pomocą 54 obserwacji oszacowany został model o następującej ogólnej postaci:
i
i
i
e
a
x
a
y
+
+
=
0
)
(
1
)
(
δ
λ
gdzie zapis Y
(λ)
oraz X
(δ)
oznacza transformację Boxa-Coxa. Dokonano następnie za pomocą
testu ilorazu wiarygodności weryfikacji dwóch hipotez:
H
0
: λ = 0 oraz H
0
: δ = 1 przy obustronnych hipotezach alternatywnych. Statystyka testowa
przyjęła wartość.
Posługując się tymi samymi danymi wykonano równieŜ test Chowa dla modelu:
0
1
ˆ
b
x
b
y
i
i
+
=
obliczając m. in. sumy kwadratów reszt RRSS i URRS. Którą (które) parę (pary) wartości
moŜna uznać za najbardziej prawdopodobne: a/ 190 i 175, b/ 190 i 180, c/ 225 i 185.
12
*
. Oszacowano dwa liniowe modele regresji z dwiema zmiennymi objaśniającymi (X
1
i X
2
)
za pomocą klasycznej MNK, uzyskując następujące informacje o wartościach zmiennej i
resztach:
24
Pierwsza estymacja:
X
1
1
1,2
1,6
2
2,1
2,2
2,3
2,9
3,1
ε
-0,1 -0,2 0,1
-0,2 -0,1 0,2
0,3
0,1
-0,1
Druga estymacja:
X
1
3,1
3,5
3,7
3,8
4
4,6
4,6
4,8
ε
0,3
-0,2 -0,2 0,3
-0,1 -0.1 0,2
-0,2
śaden z zastosowanych testów nie upowaŜnił do odrzucenia załoŜenia o normalności reszt.
Czy na tej podstawie moŜna wysnuć wniosek o homoskedastyczności reszt modelu
oszacowanego na podstawie całej próby (obejmującej 17 obserwacji)? Czy wniosek ten
zmieniłby się gdyby X
1
była jedyną zmienną objaśniającą?
ZADANIE DOMOWE
22
(nieobowiązkowe i, wbrew pozorom, trudne)
NaleŜy uzasadnić „przykazania” dekalogu Kennedy’ego (patrz: str. 18), odwołując się do
literatury i/lub własnych doświadczeń. MoŜna uŜywać negatywnych przykładów („do czego
prowadzi łamanie danego przykazania”). Za kaŜde przykazanie moŜna otrzymać 1 punkt (w
wyjątkowych przypadkach więcej) zaś końcowa ocena to liczba uzyskanych punktów minus
5, w przypadku gdy ocena jest nieujemna lub zero w przeciwnym przypadku.
Rozwiązania naleŜy złoŜyć w formie pisemnej podczas zajęć lub w Instytucie Statystyki i
Demografii (713F) do maja, godz. 15:00.
ZASADY ZALICZANIA ZAJĘĆ
Aktywność na ćwiczeniach będzie premiowana punktami (bez górnego limitu).
Do tej oceny będzie dodawana (ewentualna) ocena za zadanie domowe.
Dla osób, które chcą poprawić konto punktowe po zakończeniu zajęć przewidziane są dwa
sprawdziany (moŜna pisać tylko w jednym terminie). Końcowa ocena będzie sumą
wszystkich uzyskanych punktów, z dwoma ograniczeniami: a/ punkty za prace domową będą
dodane pod warunkiem uzyskania co najmniej 2 pkt. za sprawdzian lub 4 pkt. za aktywność,
b/ osoby, które uzyskały duŜo punktów za ćwiczenia i pracę domową
23
będą mogły
rozwiązywać tylko część zadań na sprawdzianie.
22
Zadanie naleŜy wykonać samodzielnie. W przypadku stwierdzenia jego podobieństwa do innych rozwiązań (w
szczególności rozwiązań przedstawionych przez inne osoby, ale nie tylko) ocena za pracę domową zostanie
obniŜona do zera.
23
Szczegóły będą podane później.
25
ZADANIA Z OSTATNIEGO SPRAWDZIANU
1. Eksperci Instytutu im. Doktora Kevorikiana twierdzą, Ŝe jeden wypalany dziennie papieros
zwiększa tętno średnio o 0,55 uderzenia na minutę. Na podstawie wyników badania 850 osób
oszacowano model, w którym zmienną objaśnianą było tętno a objaśniającą liczba
wypalanych dziennie papierosów. Wartość oszacowania parametru przy zmiennej
objaśniającej wyniosła 0,45, zaś wariancja tego oszacowania 0,0012.
Czy moŜna stwierdzić, Ŝe wyniki badania zaprzeczają przypuszczeniu ekspertów
Instytutu? Na pytanie naleŜy odpowiedzieć bez posługiwania się testem t-Studenta (wszystkie
inne testy są dozwolone). (4 pkt.)
Odpowiedź:
Hipotezę mówiącą, Ŝe oszacowanie parametru regresji wynosi 0,55 moŜna sprawdzić m. in.
za pomocą testu Walda. Jego statystyka testowa (wzór 3.2) przyjmuje wartość:
33
,
8
)'
55
,
0
45
,
0
(
0012
,
0
1
)
55
,
0
45
,
0
(
=
−
−
PoniewaŜ ma ona rozkład χ
2
z 1 stopniem swobody, to hipotezę zerową moŜna odrzucić
praktycznie przy dowolnym poziomie istotności. Ergo, eksperci Instytutu nie mają racji.
2. Tzw. translogarytmiczna funkcja pośredniej uŜyteczności danego gospodarstwa domowego
ma postać:
LIO
i
m
k
k
S
j
i
n
i
n
i
n
j
ij
i
i
i
p
LIO
S
LIO
LIO
d
X
LIO
d
p
X
LIO
d
p
X
LIO
d
p
X
v
γ
β
α
=
+
+
=
∑
∑
∑∑
=
=
=
=
1
1
1
1
0
exp
)
,
(
:
gdzie
)
,
(
ln
)
,
(
ln
2
1
)
,
(
ln
)
,
(
ln
P
P
P
P
P
P = [p
1
, p
2
, ... p
n
] jest wektorem cen, X sumą wydatków konsumpcyjnych gospodarstwa, LIO
liczbą osób zaś n oznacza liczbę (grup) dóbr (w omawianym modelu wynosi ona 5). Na
parametry funkcji zostały narzucone warunki:
∑
∑
∑
=
=
=
=
=
=
=
n
i
n
i
i
ij
i
1
1
n
1
i
;
0
n;
,
...
2,
1,
j
dla
0
;
1
γ
β
α
Wartości parametrów zostały oszacowane (za pomocą tzw. równości Roy’a) dwukrotnie: bez
narzuconych ograniczeń i z ograniczeniami. W pierwszym przypadku logarytm funkcji
wiarygodności wyniósł -1850. Jaką maksymalną wartość moŜe przyjąć logarytm funkcji
wiarygodności przy estymacji modelu z narzuconymi warunkami dodatkowymi, aby moŜna
było uznać, Ŝe nie są one spełniane „samorzutnie”.
(4 punkty).
Odpowiedź:
Odpowiedź na pytanie wymaga ustalenia przy jakiej wartości statystki w teście ilorazu
wiarygodności odrzucimy hipotezę zerową. Ma ona rozkład χ
2
z liczbą stopni swobody
równą liczbie testowanych warunków czyli 7 (1 + 5 +1). Przyjmując poziom istotności 0,05
ustalamy wartość krytyczną statystyki testowej na 14,1. Musimy zatem rozwiązać nierówność
(por wzór 3.1)
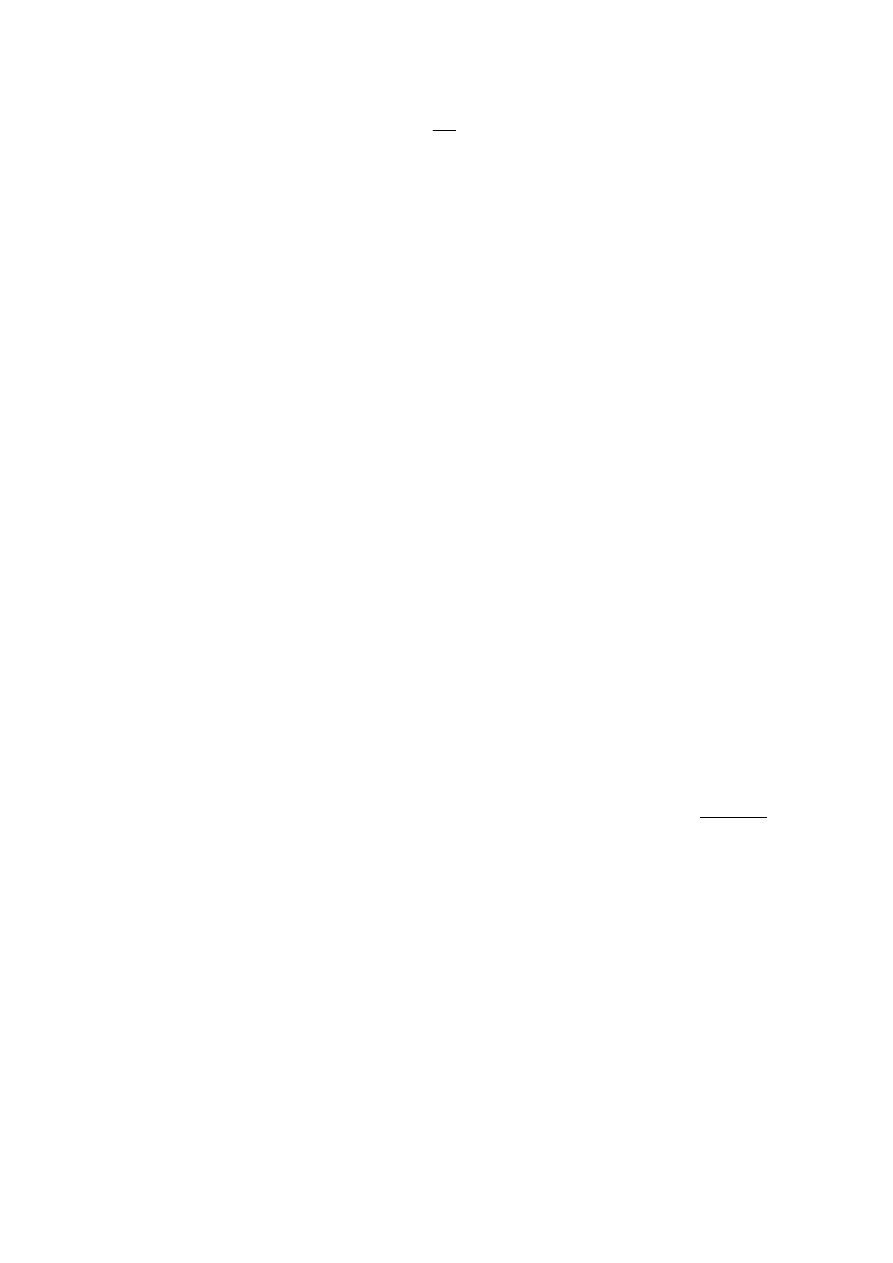
26
1
,
14
ln
2
>
−
U
R
L
L
PoniewaŜ ln L
U
=-1850, to ln L
R
>1857,05.
3. „Archimedes powiedział: dajcie mi punkt podparcia i dostatecznie długą dźwignię, a
podniosę Ziemię. Ekonomiści mają własną dźwignię Archimedesa: estymację metodą
zmiennych instrumentalnych” (Michael P. Murray, Journal of Economic Perspectives, nr 4,
2006).
Na czym polega podobieństwo między dźwignią Archimedesa i MZI?
(Wskazówka: nikomu nie udało się podnieść Ziemi metodą Archimedesa).
(1 pkt.)
Odpowiedź
Analogiczne ograniczenia w stosowaniu MZI to:
a/ nieuniknione skorelowanie instrumentów z resztami (skoro są skorelowane ze zmiennymi
instrumentowanymi), co odpowiada brakowi dostatecznie długiej dźwigni
b/ niemoŜność empirycznego sprawdzenia skorelowania zmiennych instrumentowanych z
resztami, co odpowiada brakowi punktu podparcia.
4. Proszę ocenić prawdziwość poniŜszych zdań, uzasadniając odpowiedź:
a/ JeŜeli statystyka testu Goldfelda-Quandta w modelu zaleŜności pomiędzy zmienną
instrumentowaną a (potencjalnymi) instrumentami przekroczyła wartość krytyczną, to
stosowanie metody zmiennych instrumentalnych nie jest wskazane.
b/ Odrzucenie hipotezy zerowej w teście Chowa nie pozwala za stosować testu RESET dla
tych samych danych i tego samego modelu.
c/ Przy duŜej próbie testem ilorazu wiarygodności moŜna zastąpić test F (1.13, str. 6 w
skrypcie) lecz testem F nie zawsze moŜna zastąpić test ilorazu wiarygodności.
d/ Usunięcie z modelu zmiennej objaśniającej skorelowanej z inną (pozostawioną) zmienną
objaśniającą moŜe skutkować niezgodnością estymatorów parametrów strukturalnych.
(4 punkty)
Odpowiedzi:
a/ NIE. Przekroczenie wartości krytycznej w teści G-Q wskazuje na skorelowanie wariancji
reszt z którąś ze zmiennych objaśniających, co nie świadczy o skorelowaniu samych reszt.
b/ NIE. Testy te mogą być do pewnego stopnia stosowane zamiennie jako testy liniowości.
c/ TAK. Test ilorazu wiarygodności słuŜy do testowania dowolnych hipotez o parametrach,
test F jedynie hipotezy mówiącej o ich zerowej wartości.
d/ TAK. Usunięta zmienna wchodzi w skład (nowych) reszt. Skoro pozostawiona jest z nią
skorelowana, to moŜe być równieŜ skorelowana z resztami.