Nauka o Materiałach

Wykład VIII

Odkształcenie   materiałów –
właściwości sprężyste

Jerzy Lis

Nauka o Materiałach

 

Treść wykładu:

1. Właściwości materiałów -wprowadzenie

2. Klasyfikacja reologiczna odkształcenia 

materiałów.

3. Statyczna próba rozciągania.

4. Odkształcenie sprężyste

4.1. Prawo Hooke’a - moduły sprężystości

4.2. Właściwości sprężyste układu dwu 

atomów

4.3. 0dkształcenie sprężyste kryształów

4.4. Właściwości sprężyste materiałów 

wielofazowych

4.5. Właściwości sprężyste materiałów 

porowatych

4.6. Metody pomiaru modułów sprężystości

4.7 Niesprężystość

Nauka o materiałach 

WŁAŚCIWOŚCI TWORZYW - WPROWADZENIE

•

O możliwości zastosowania danego materiału decydują jego 

właściwości użytkowe

•

Zachowanie się danego materiału w środowisku pracy to 

zaplanowana przez użytkownika (założona) odpowiedź na 

działające na niego czynniki (bodźce)

 

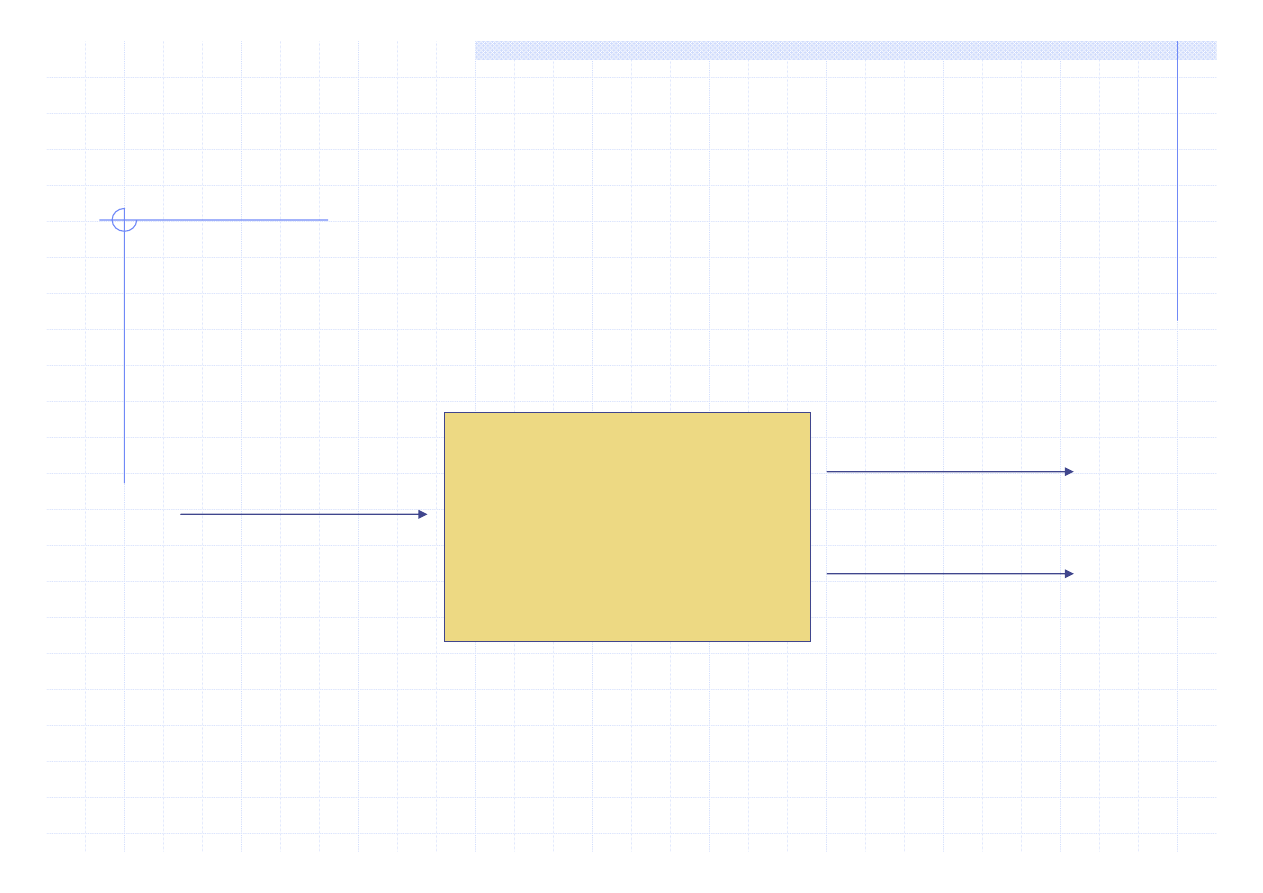
SCHEMAT ODDZIAŁYWANIA CZYNNIKÓW NA MATERIAŁ 

 

 

 

 

 

 

 

 

 

 

 

 

    MATERIAŁ

 

      Czynnik

 

          

odzew

   (właściwości)

    (Czas)

 

Nauka o materiałach 

WŁAŚCIWOŚCI TWORZYW - WPROWADZENIE

PODEJŚCIE INŻYNIERSKIE

Materiał traktowany jest jak „czarna skrzynka” - nie 

interesuje nas jego charakterystyka jedynie istniejące 

zależności funkcyjne

W wypadku parametrów ilościowych (mierzalnych)

odzew = funkcja ( czynników)

Sprowadza się tą zależność do możliwie najprostszych funkcji 

(modeli) matematycznych

np.:

zależność liniowa prawo 

Hooke’a

σ = Eε

Stałe w danym modelu charakterystyczne dla danego 

materiału określane w ściśle zdefiniowanych warunkach 

noszą nazwę stałych materiałowych

Nauka o materiałach 

WŁAŚCIWOŚCI TWORZYW - WPROWADZENIE

Podejście charakterystyczne dla nauki o materiałach  

 
 

 

 
 

 
 
 

 

 

Materiał nie jest traktowany jako „czarna skrzynka” lecz w 
myśl nauki o materiałach posiada swoją budowę wynikającą 

ze sposobu jego otrzymywania. 

 
Stałe w modelach (materiałowe) charakterystyczne dla 

materiału będą zależeć od jego budowy (sposobu 
otrzymywania) 

 

   MATERIAŁ:
- budowa 
 nano 
 mikro 
 makro 

      Czynnik 

     odzew 

(właściwości) 

    (Czas) 

Nauka o materiałach 

WŁAŚCIWOŚCI TWORZYW - WPROWADZENIE

Nauka o materiałach 

WŁAŚCIWOŚCI TWORZYW - WPROWADZENIE

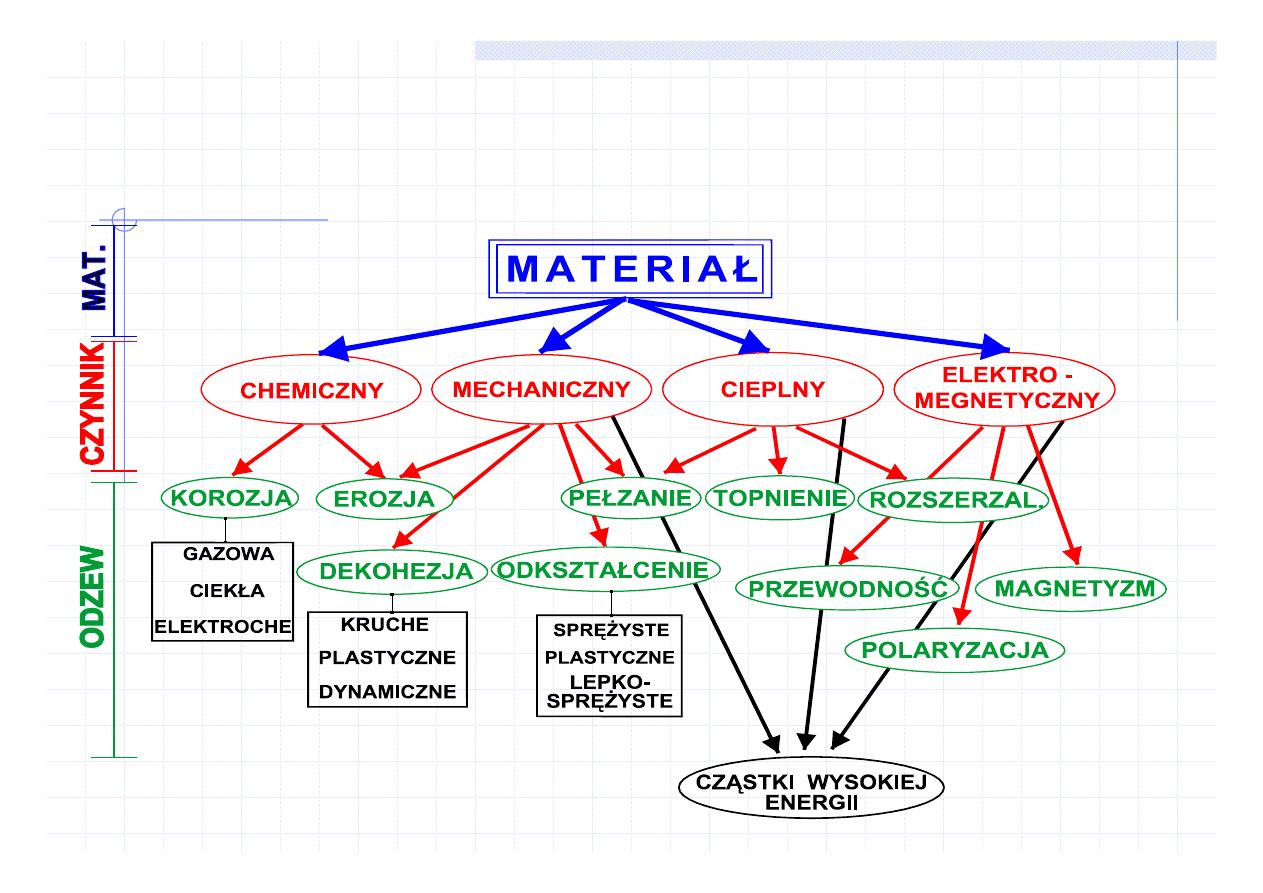
Podstawowym czynnikiem weryfikującym materiały 

inżynierskie jest działanie sił (naprężeń).

odkształcenie

naprężenie

MATERIAŁ

dekohezja

Naprężenia mogą zmienić wymiary (liniowe, kątowe) lub ciągłość 

materiału (dekohezja)

Nauka o materiałach 

MODELE ODKSZTAŁCENIA

Nauką opisującą nieniszczące odkształcanie  się ciał pod wpływem

działania sił jest reologia.

•

Reologia opiera się na modelach makroskopowych ciał 

poddawanych działaniu sił ścinania.

•

Modele te w sposób ogólny opisują zachowanie się ciał zarówno 

odkształcających się postaciowo (ciała sztywne i ciecze) jak i 

objętościowo (gazy)

•W klasyfikacji reologicznej (makroskopowej) jako najbardziej 

typowe można przyjąć trzy podstawowe modele zachowania się 

ciał:

* odkształcenie sprężyste

* odkształcenie plastyczne

* odkształcenie lepkościowe

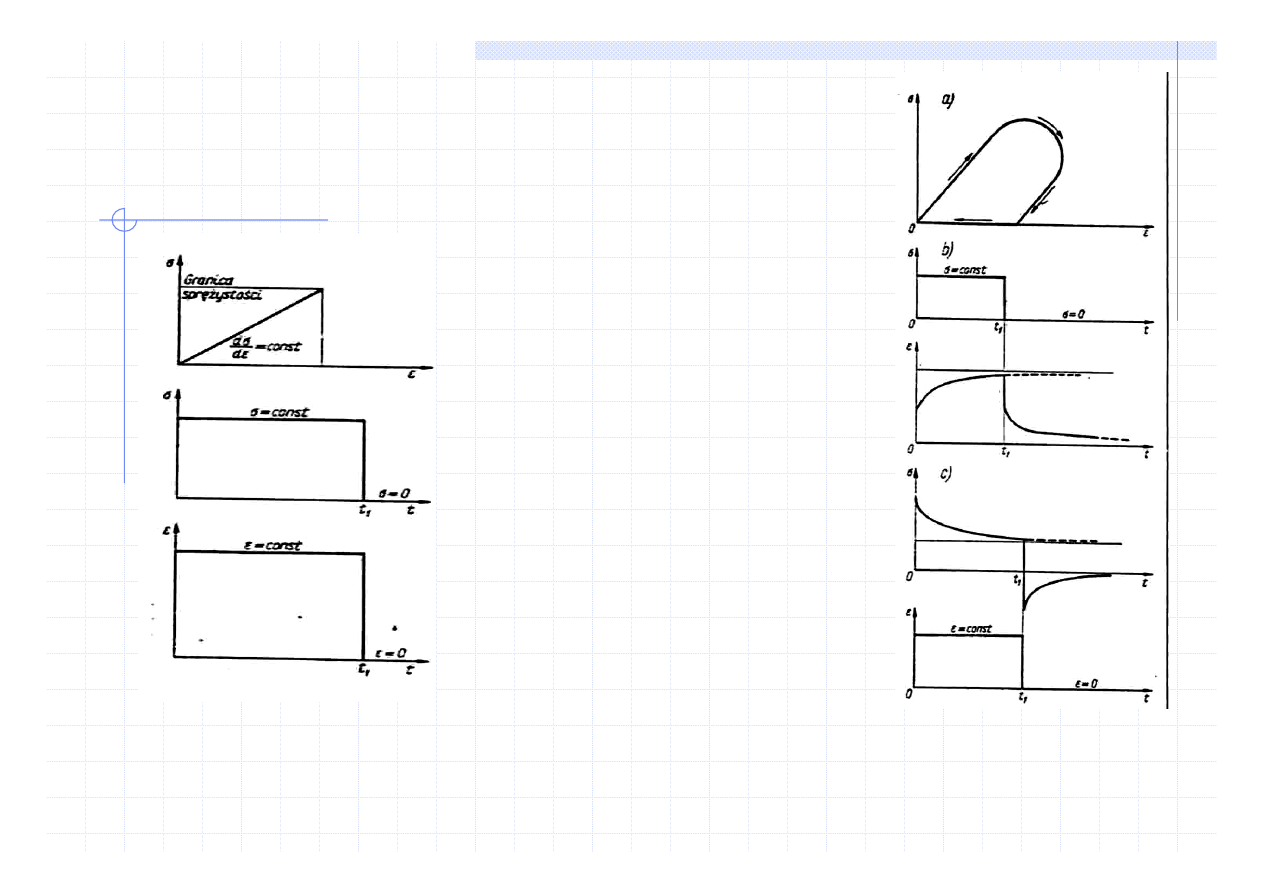
Nauka o materiałach 

MODELE ODKSZTAŁCENIA

Odkształcenie sprężyste

(odwracalne)

Ciało liniowo-sprężyste

Ciało o sprężystości opóźnionej

(Hooke’a)

(Kelvina)

σ = Eε

σ = Eε + ηdε/dt

ε(t) = σ

o

/E (1 - exp (- t/

τ))

τ - czas relaksacji

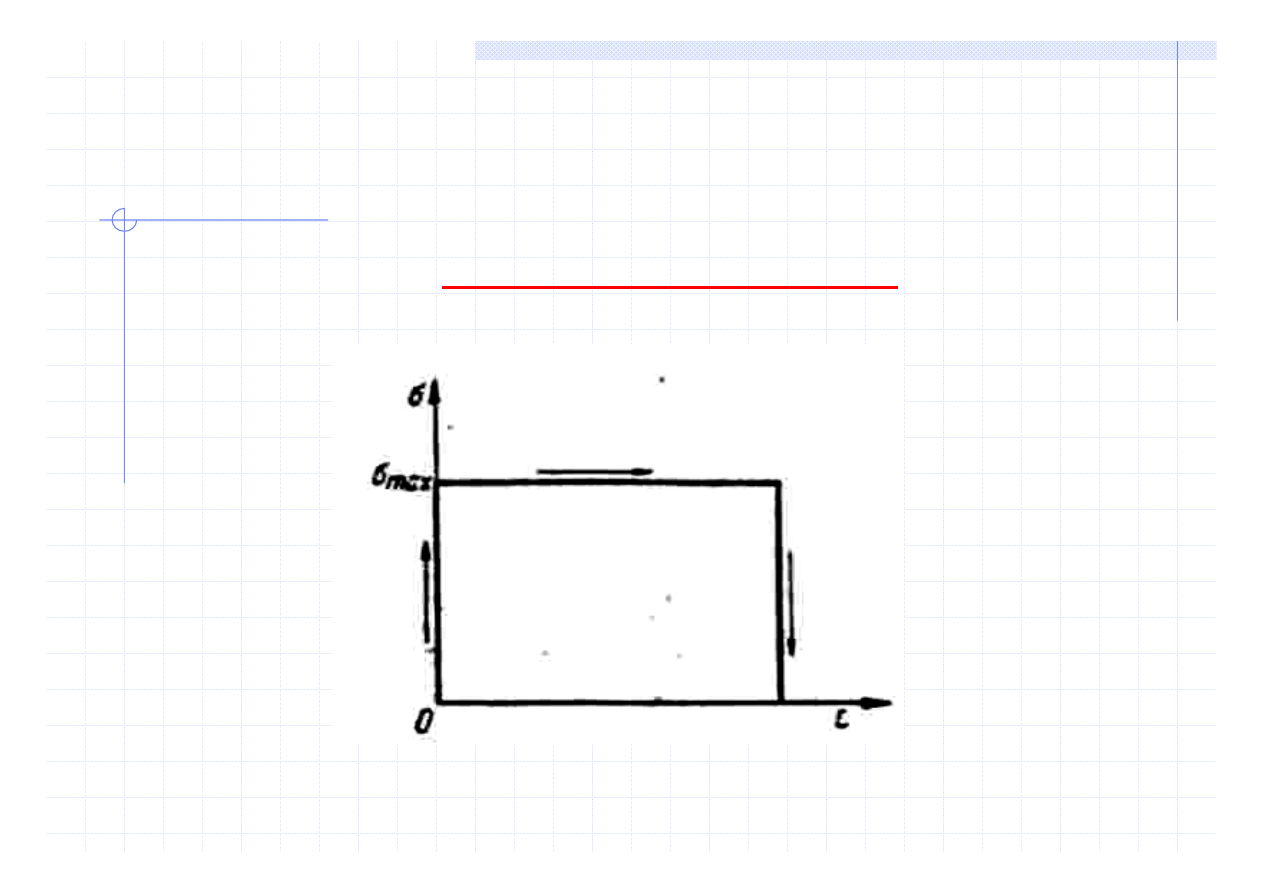
Nauka o materiałach 

MODELE ODKSZTAŁCENIA

Odkształcenie plastyczne

(nieodwracalne)

Ciało doskonale plastyczne

τ = τ

y

τ

y

- granica plastyczności

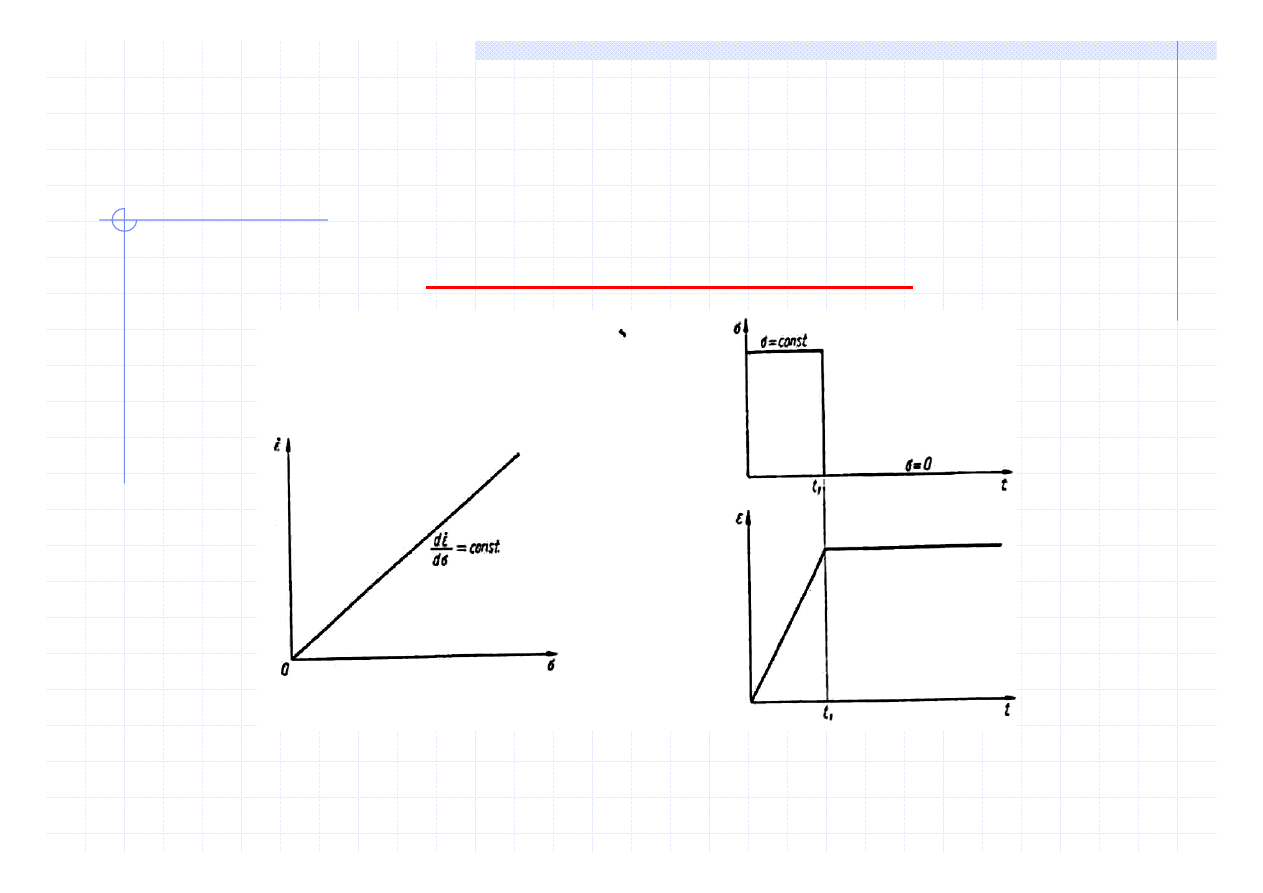
Nauka o materiałach 

MODELE ODKSZTAŁCENIA

Odkształcenie lepkościowe

Ciecz Newtona

σ = ηε

η - współczynnik lepkości

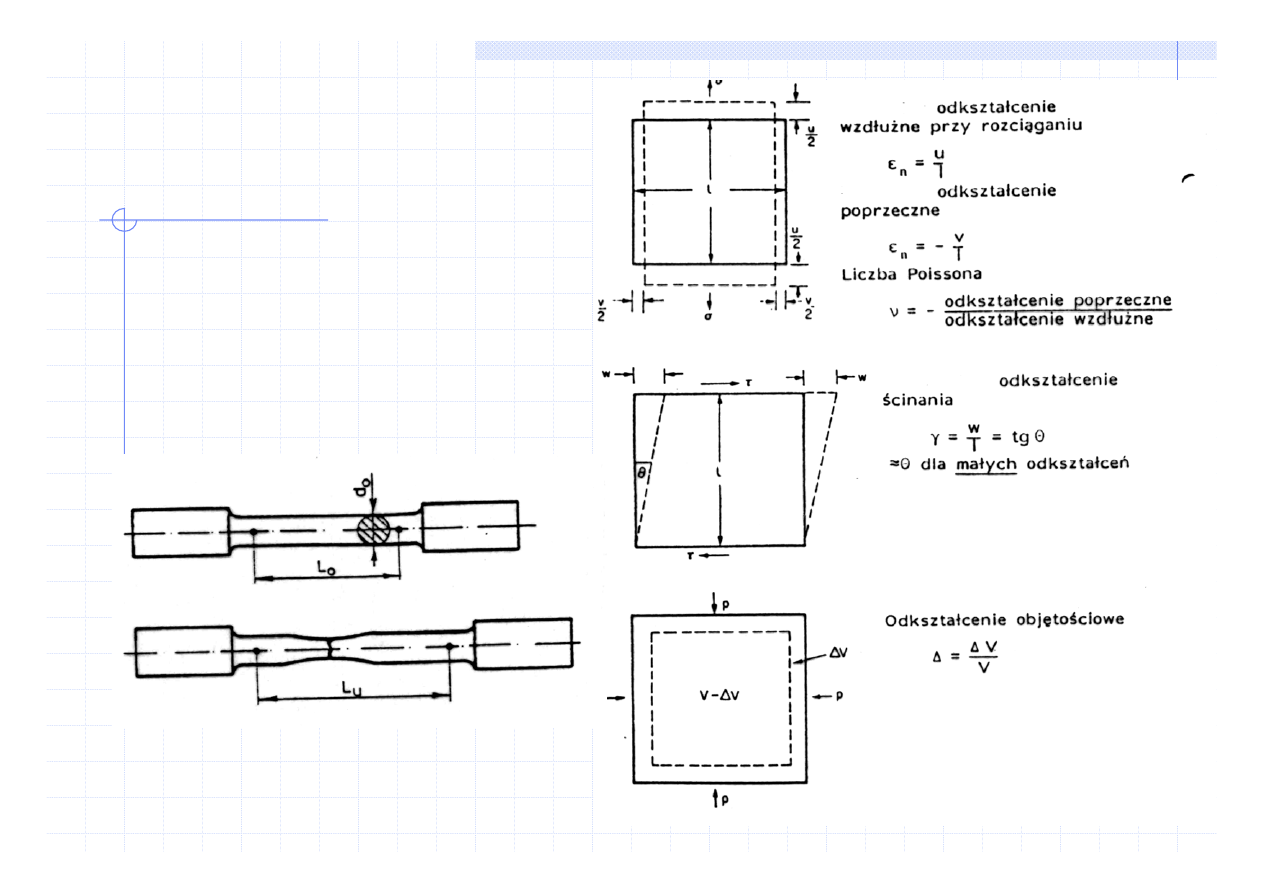
Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Zachowanie się materiałów pod 

wpływem naprężeń -

statyczna próba rozciągania 

(ściskania, zginania, ...)

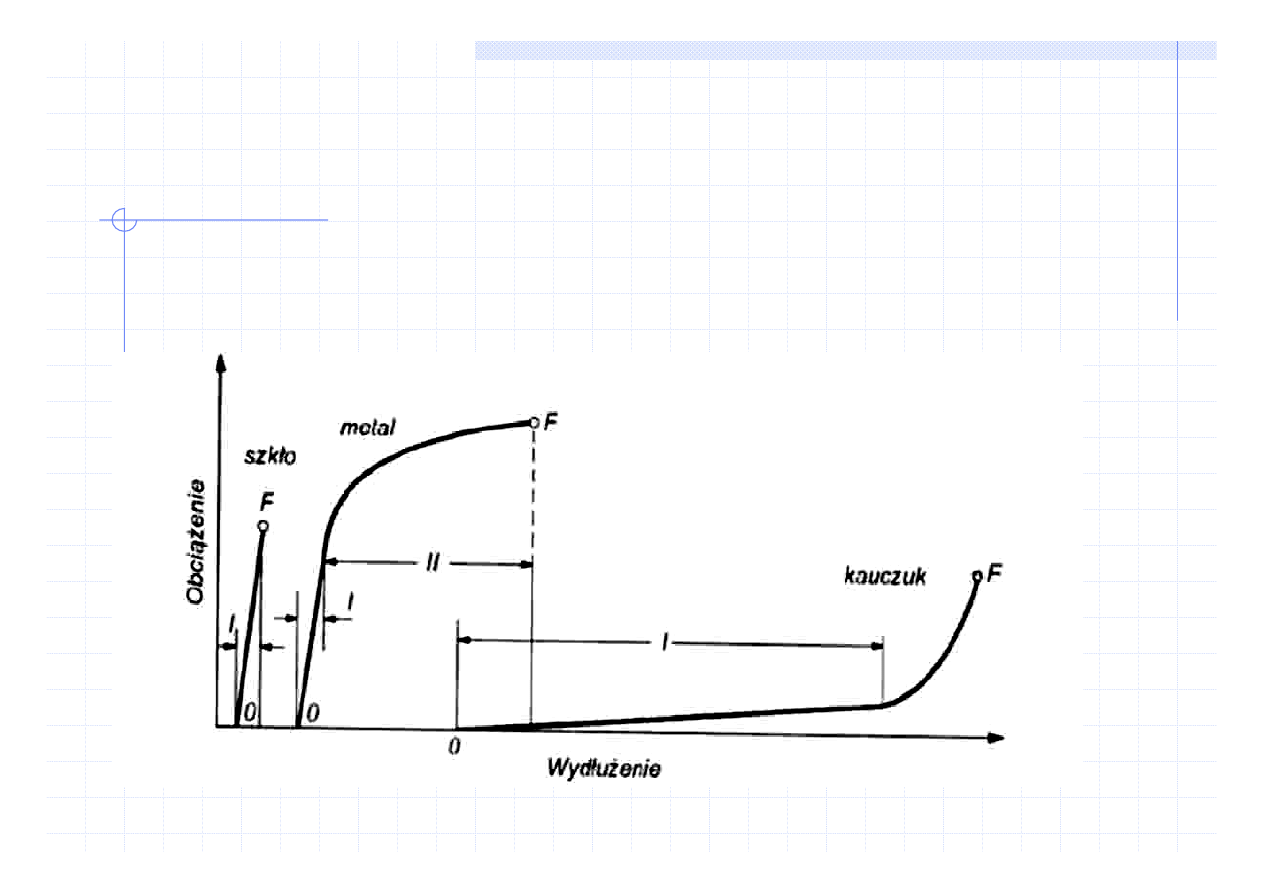
Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Rzeczywiste zachowanie się materiałów łączy ze sobą 

elementy zachowania modelowego sprężystego, 

plastycznego i lepkościowego

MATERIAŁY „KRUCHE”, „PLASTYCZNE”, „LEPKOSPRĘŻYSTE”

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Dla materiałów sztywnych w pierwszym etapie przy rosnących 

naprężeniach materiały zachowują się sprężyście tj. odkształcają

się nietrwale. 

W pewnym zakresie odkształcenie jest proporcjonalne do 

naprężenia.

Prawo Hooke’a

σ = E ε

τ = G γ

p = - K 

∆

E - moduł Younga

G - moduł sztywności (ścinania)

K - moduł ścisliwości (postaci)

ν- liczba Poissona

Moduły E, G, K i l. Poissona określają właściwości sprężyste 

materiałów.

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Pytania:

•od czego zależą moduły sprężystości 

materiałów?

* jak je można określić?

* jak je można zmieniać?

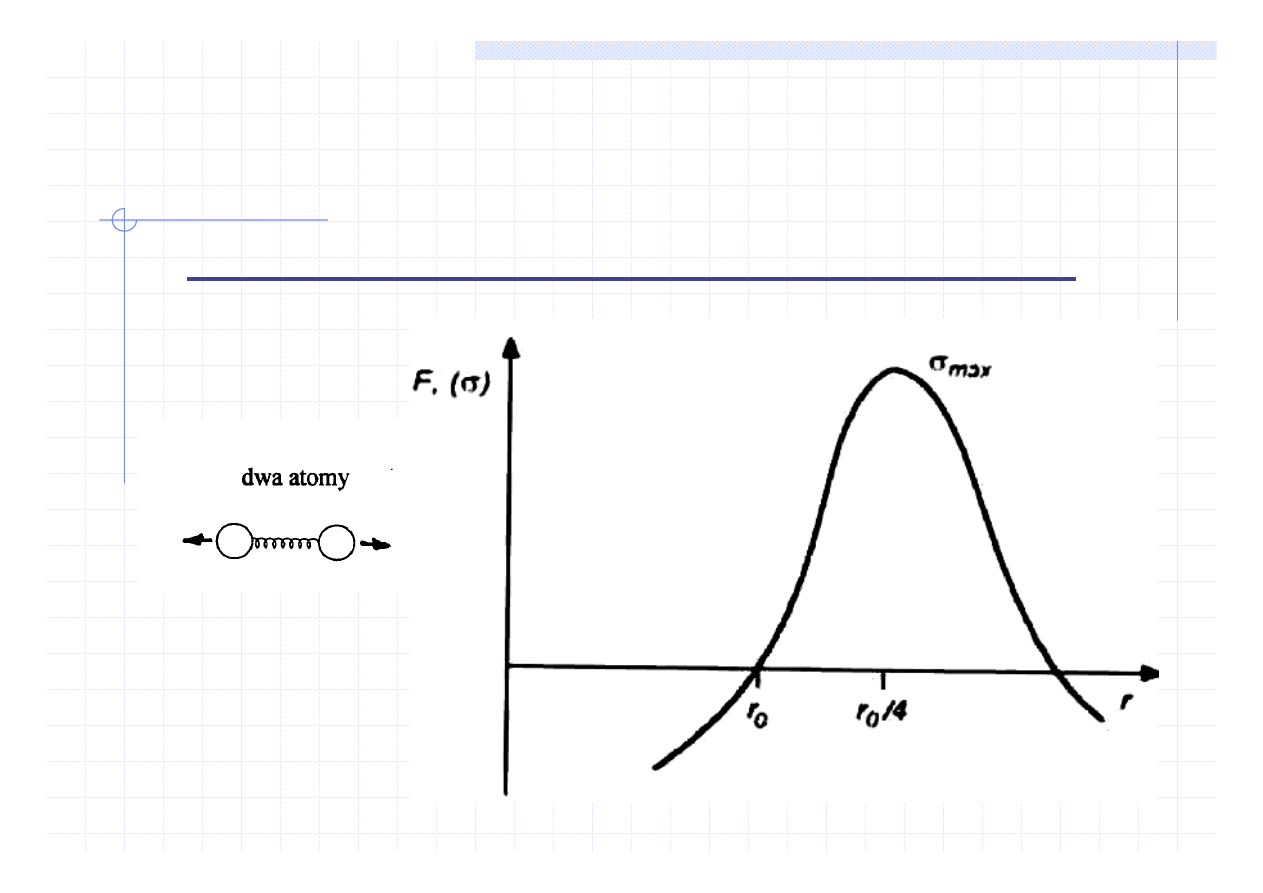
Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

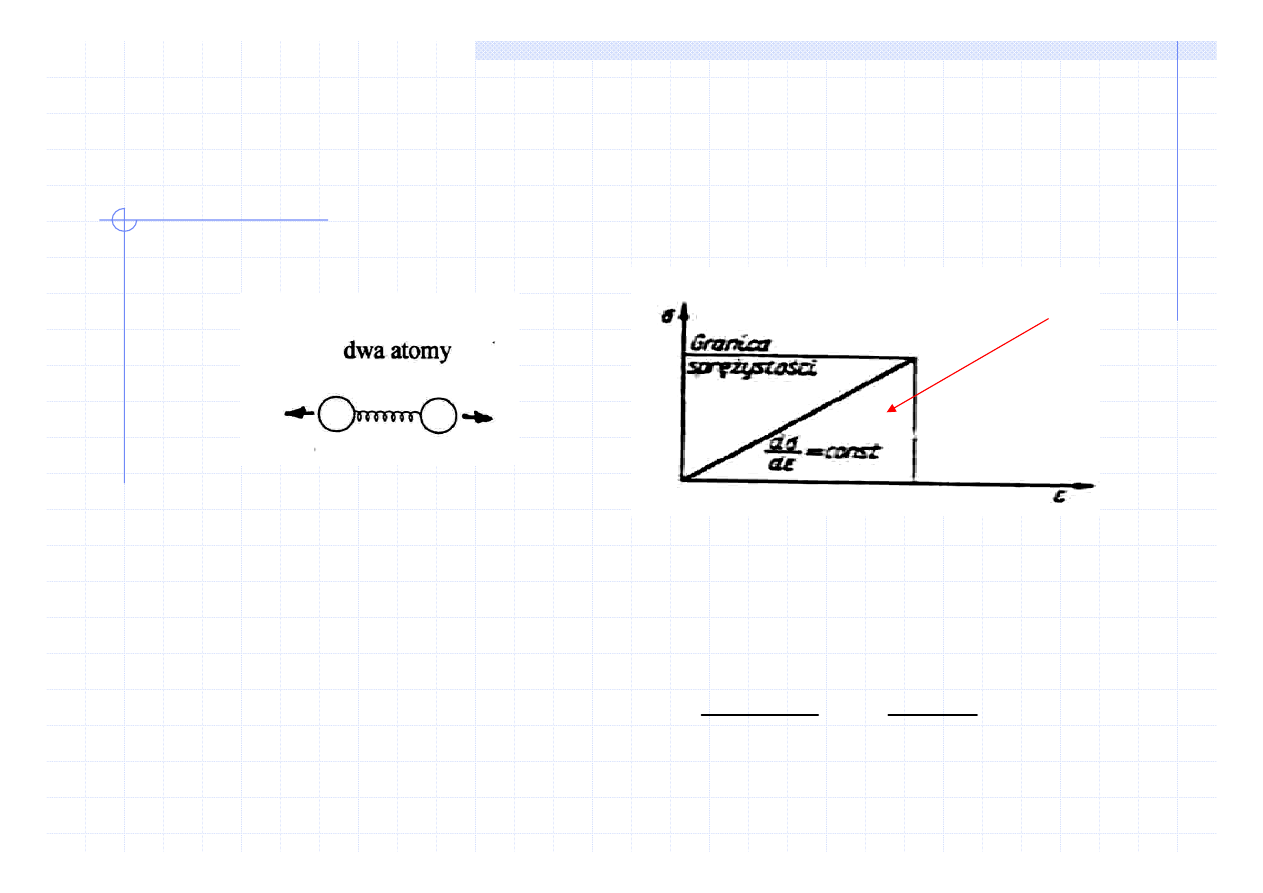
Odkształcenie sprężyste w układzie dwu atomów

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

ε

δ

δ

σ

ε

δ

δ

σ

ε

ε

δ

δ

σ

σ

ε

σ

d

r

F

r

d

r

F

r

d

r

dr

d

r

r

dr

r

F

r

d

r

F

r

F

a

F

o

r

r

o

o

r

r

o

o

o

o

r

r

o

o

=

=

=

⎟

⎠

⎞

⎜

⎝

⎛

=

=

=

∆

=

=

≈

=

∫

∫

1

)

(

1

)

(

1

~

0

0

2

2

W modelu rozważamy zależność 

naprężenia od odkształcenia dla dwu 

atomów odchylanych od położenia 

równowago przez siłę zewnętrzną.

Działania sił zewnętrznych wywołuje 

wewnętrzną przeciwnie skierowaną 

reakcję układu

Zakładamy układ izolowany w którym 

atomy są odchylany od położenia 

równowagi (r

o

) na niewielką odległość

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

C - stała sprężystości   ~ modułu sprężystości

Im większa siła wiązania  i im krótsze wiązanie tym 

większy moduł sprężystości materiału.

ε

σ

ε

δ

δ

σ

C

r

F

r

o

r

r

o

=

⎟

⎠

⎞

⎜

⎝

⎛

=

=

1

Nauka o materiałach 

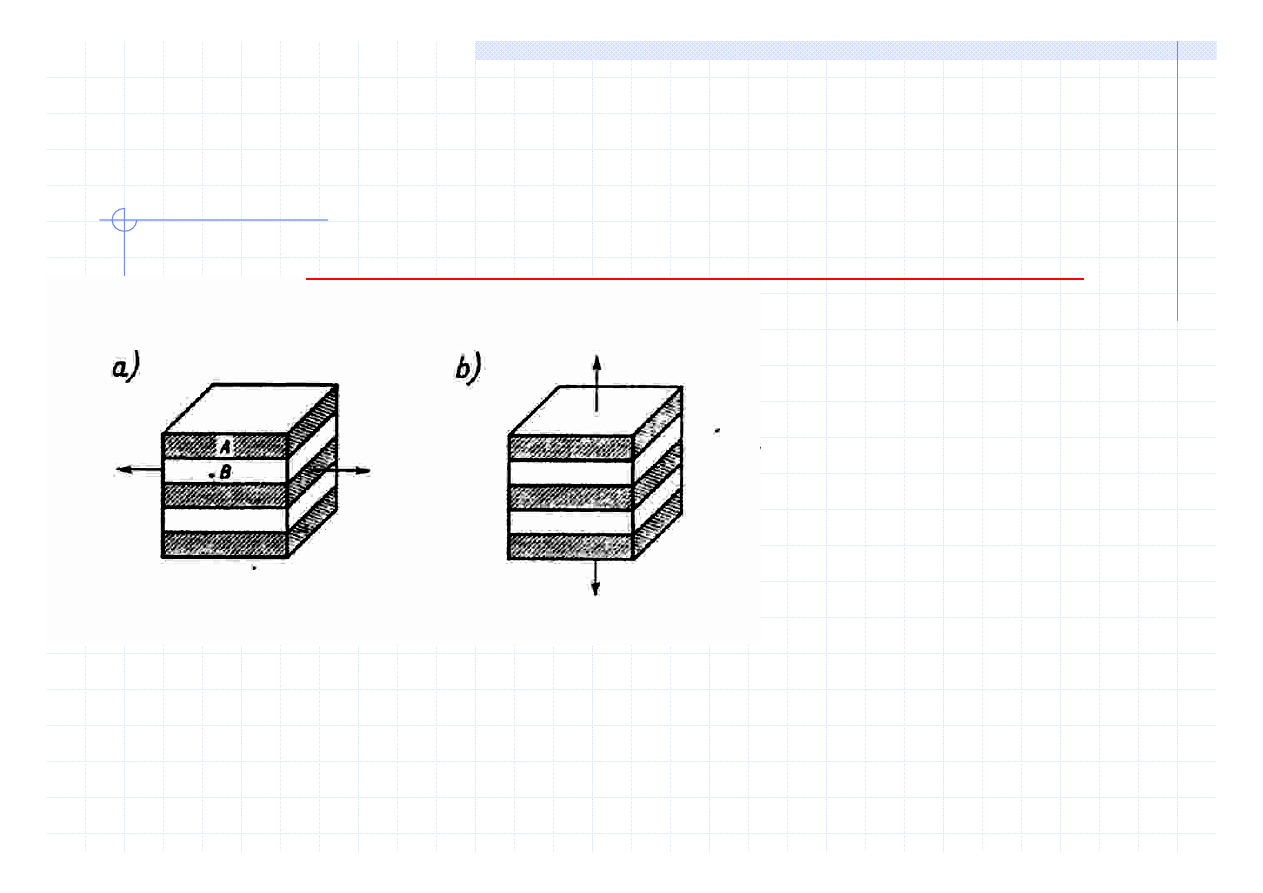
WŁAŚCIWOŚCI SPRĘŻYSTE

•Pełna macierz - 36 stałych sprężystości

•Wyższa symetria - redukcja stałych

* Materiał izotropowy  - 3 stałe : S

11

, S

12

, S

44

ε

1

= S

11

σ

1

+ S

12

σ

2

+ S

12

σ

3

ε

2 

= S

12

σ

1

+ S

11

σ

2

+ S1

2

σ

3

ε

11

= S

11

σ

1

+ S

12

σ

2

+ S

11

σ

3

ε

4

= S

44

σ

4

Przy czym

E = 1/ S

11

G = 1/S

44

ν = - S

12

/S

11

k

i

j

i

j

i

j

i

j

i

G

j

i

E

σ

σ

δε

δε

ν

δε

δσ

δε

δσ

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

=

=

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

=

=

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

=

6

,

5

,

4

......

3

,

2

,

1

......

Zależność między stałymi 

materiałowymi:

E=2G (1+

ν)

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

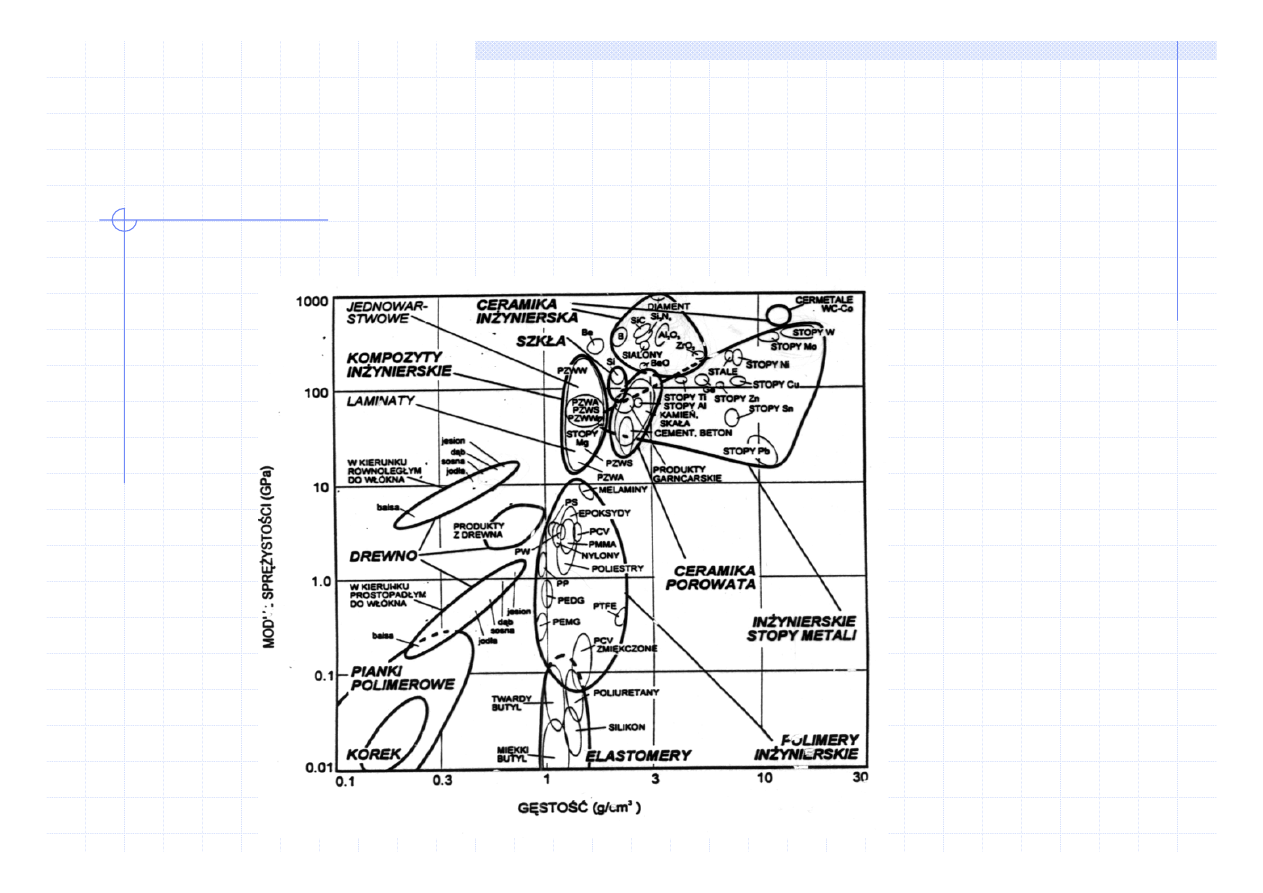
Porównanie wielkości E dla różnych materiałów

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Porównanie wielkości E dla różnych materiałów

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Energia odkształceń sprężystych

Energia 

równa się 

polu pod 

krzywą 

Gęstość energii( ilość na jednostkę objętości)  w [J/m

2

]

E

E

d

W

i

i

i

2

2

2

2

0

σ

ε

ε

ε

σ

ε

=

=

=

∫

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

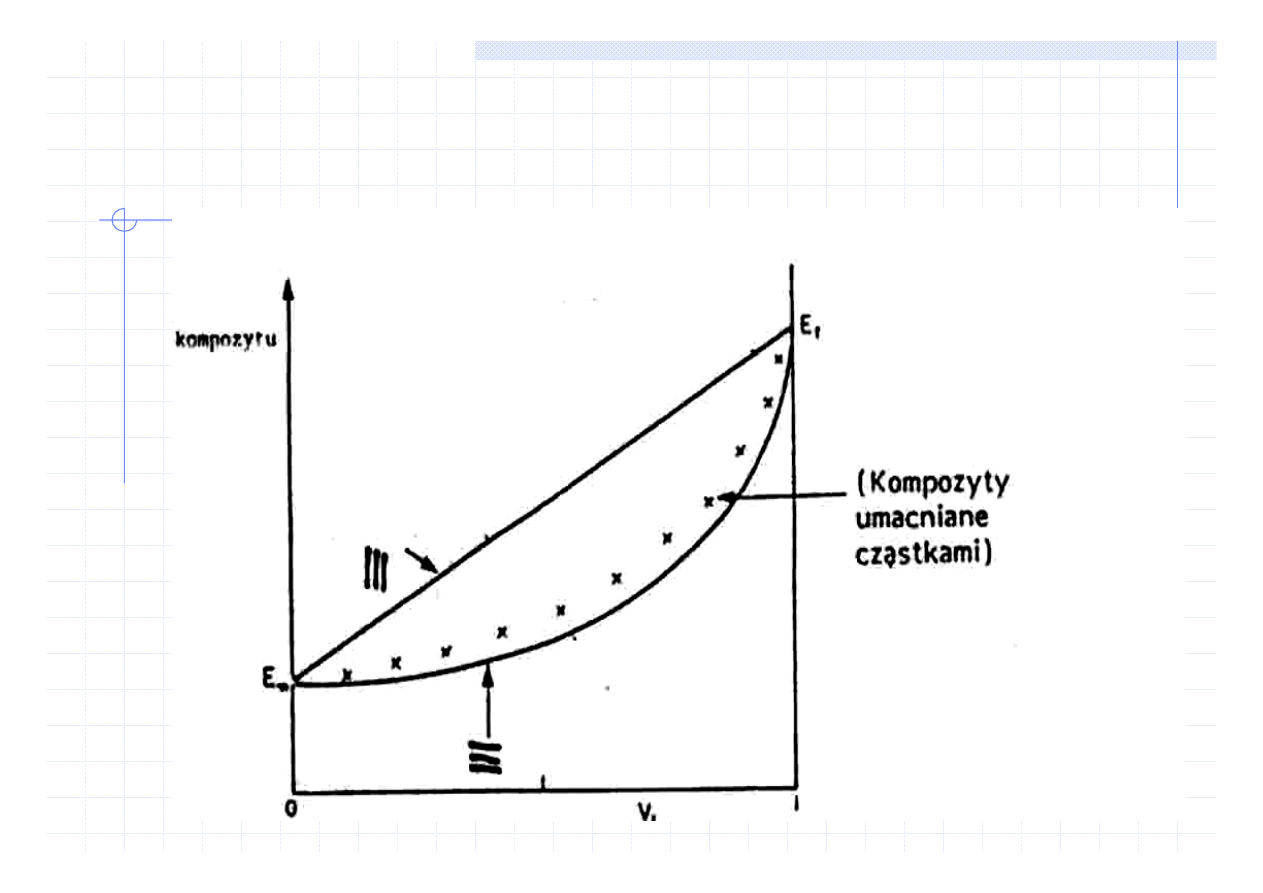
Właściwości sprężyste materiałów wielofazowych

Model równoległy

E = V

1

E

1

+ V

2

E

2

prawo mieszanin

Model szeregowy

1/E = V

1

/E

1

+ V

2

/E

2

Modele równoległy i szeregowy (uproszczone)
E – moduł Younga
V – udział objętościowy fazy

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Moduł Younga kompozytów

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

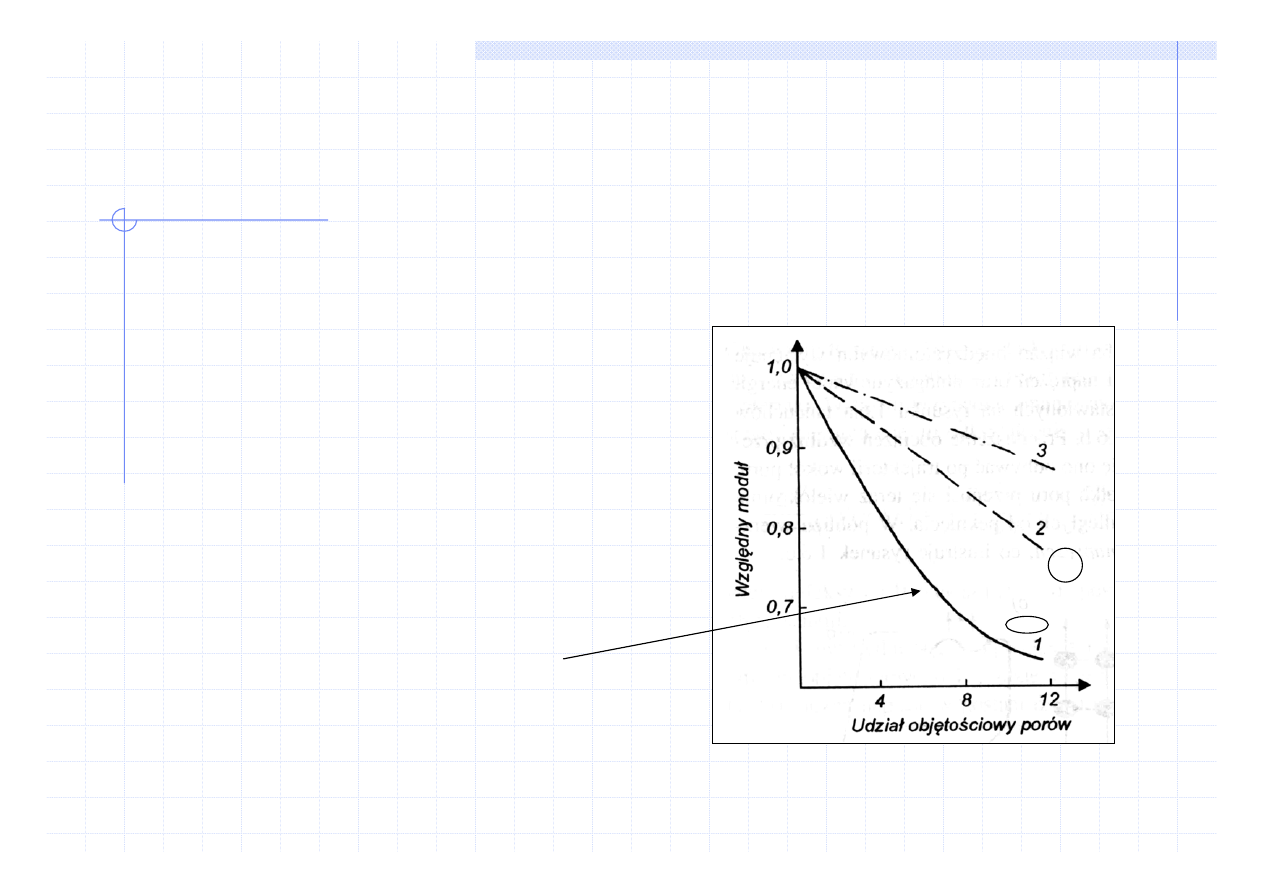
Właściwości sprężyste materiałów  porowatych

Fazę gazową w materiale  można traktować jak 

fazę o E=0
stąd

Z prawa mieszanin

E = E

o

(1- V

p

)

gdzie: 
V

p

- udział objętościowy porów

E

o

- moduł Younga materiału gęstego

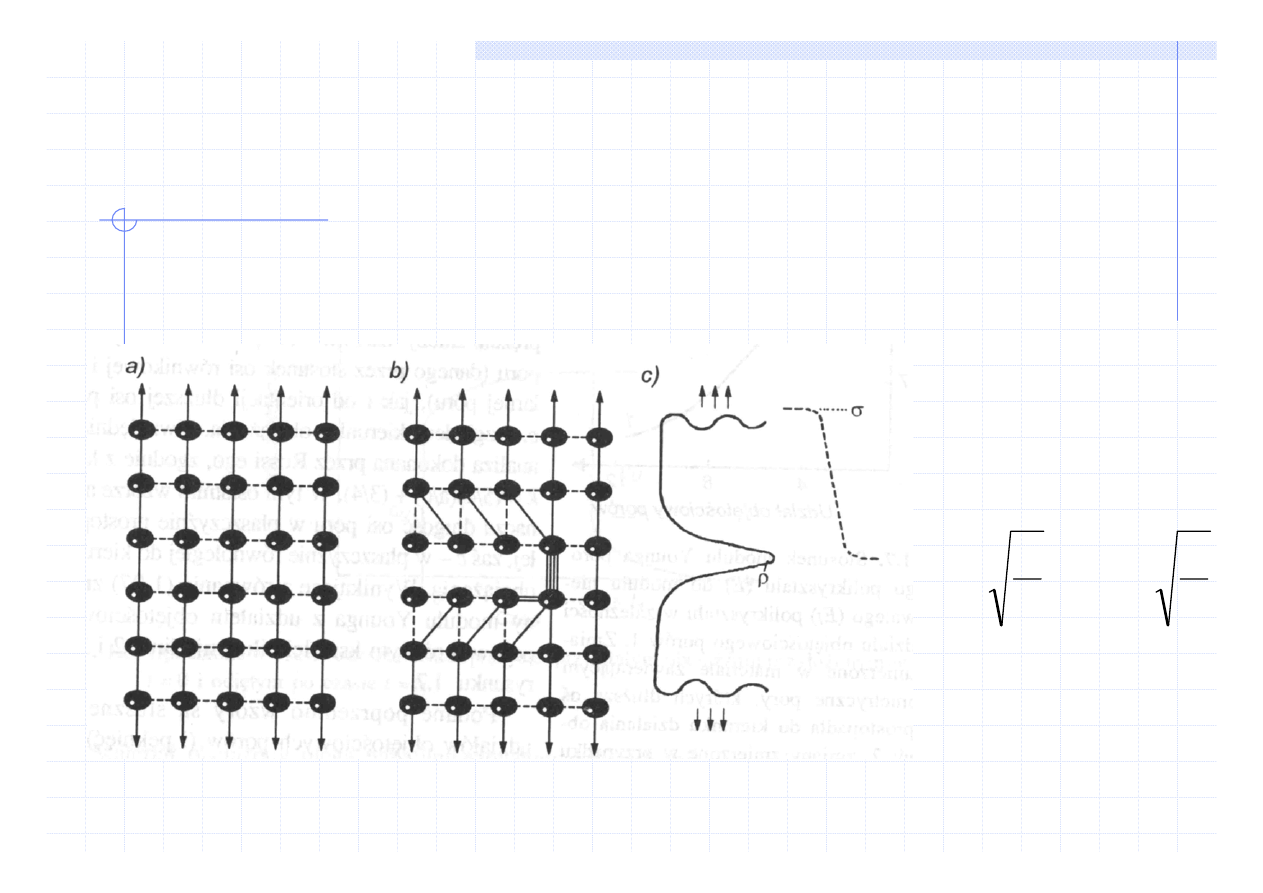
Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

W rzeczywistych materiałach następuje tzw. koncentracja 

naprężeń czyli 

naprężenie wewnątrz materiału jest większe niż 

przyłożone na zewnątrz

ρ

σ

ρ

σ

σ

c

c

z

z

2

2

1

≈

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Ogólnie 

σ

ρ

= k 

σ

z

k współczynnik koncentracji naprężeń

stąd 

E = E

o

(1- k V

p

)

Na przykład 
dla porów eliptycznych
wzór Rossi’ego
k = (5/4)(a/c) + 3/4

Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

METODY POMIARU MODUŁÓW SPRĘŻYSTOŚCI

STATYCZNE

DYNAMICZNE

moduł zrelaksowany

moduł niezrelaksowany

statyczne próby odkształcenie               pomiar szybkości fali mechanicznej

próbek materiałów                                penetrującej przez materiał

(rozciąganie)

(m. ultradźwiękowe)

(ściskanie)

(m. rezonansowe)

(zginanie) 
(skręcanie) 

Nauka o materiałach 

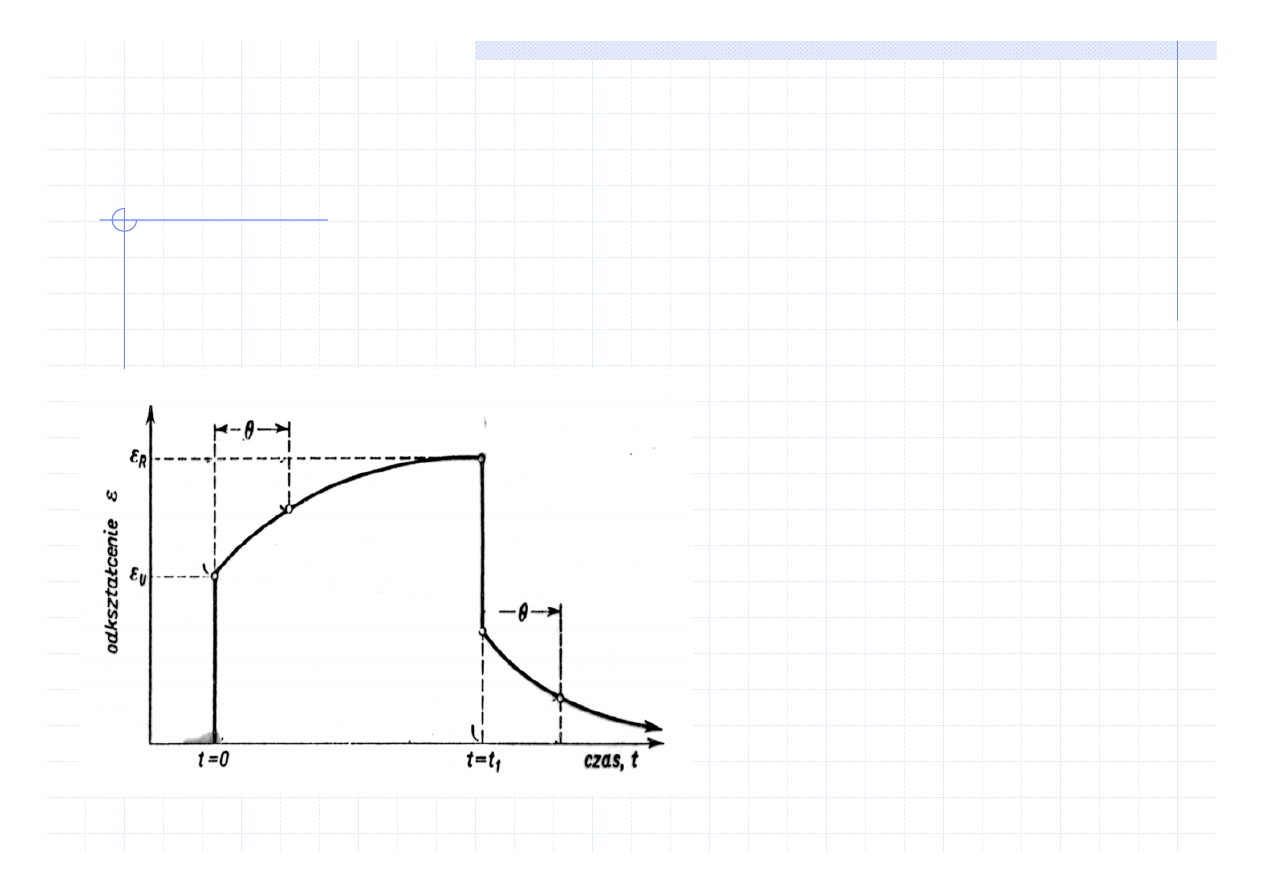
WŁAŚCIWOŚCI SPRĘŻYSTE

Zjawisko niesprężystości

Zjawisko zależności odkształcenia sprężystego od czasu nosi 

nazwę niesprężystości (sprężystości opóźnionej)

σ

o

=

const

ε = ε

o

+(

ε

U

-

ε

R

)exp(-t/

Θ)

gdzie:

ε

R

–

odkształcenie zrelaksowane

ε

U

–

odkształcenie niezrelaksowane

Θ -

czas relaksacji

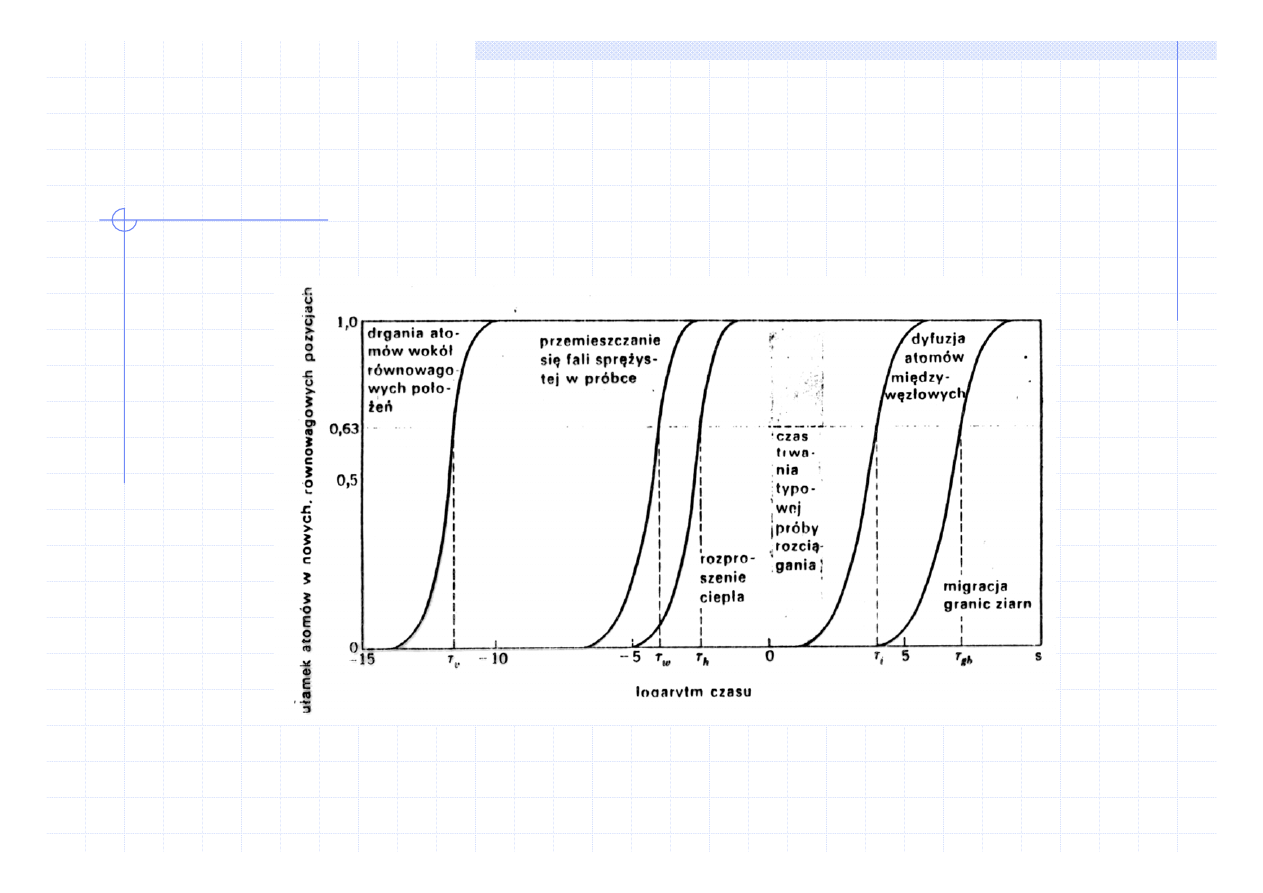
Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

Procesy relaksacyjne odkształcenia sprężystego  w materiałach

Jeżeli czas pomiaru właściwości sprężystych jest większy niż czas 

niezbędny dla zajścia danego procesu relaksacyjnego to proces ten nie 

będzie miał wpływu na pomiar 

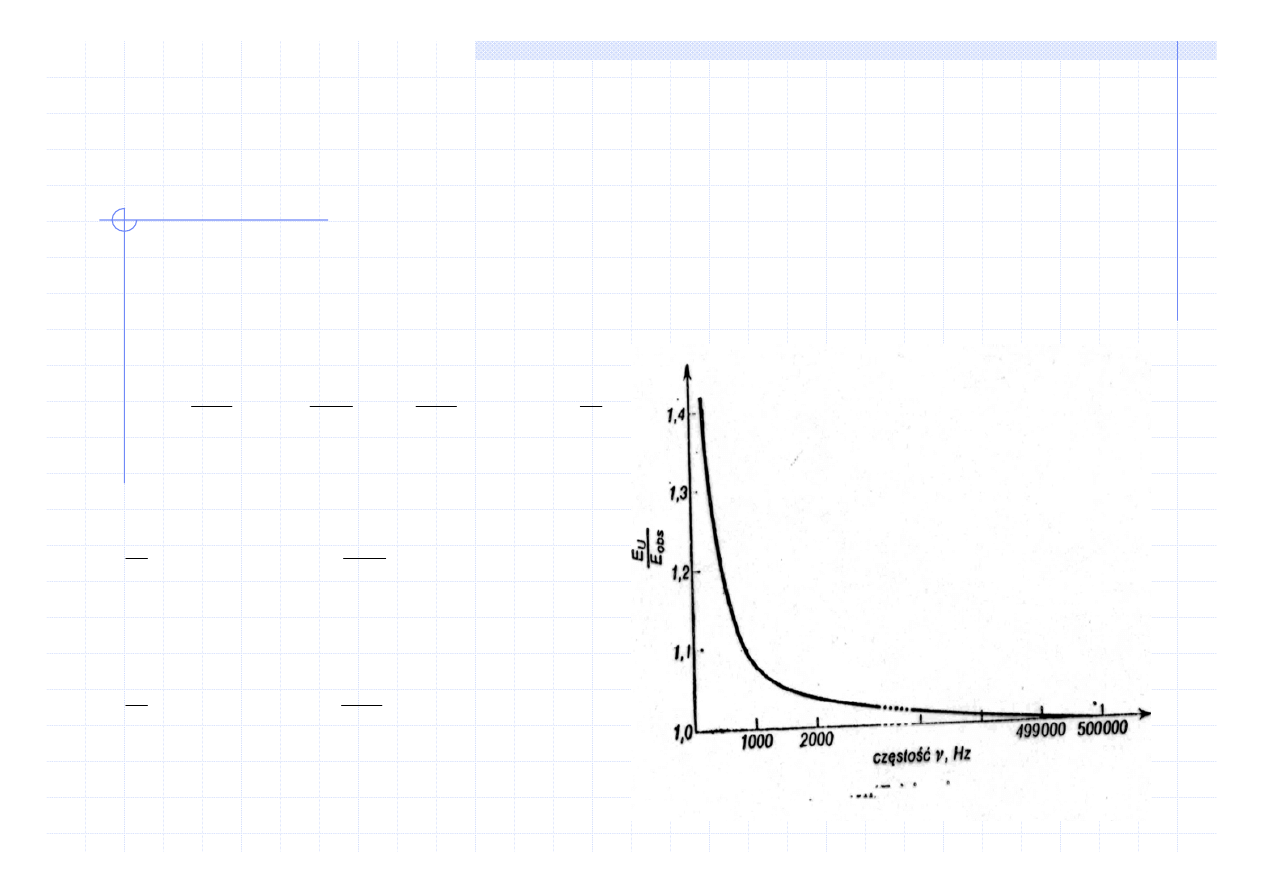
Nauka o materiałach 

WŁAŚCIWOŚCI SPRĘŻYSTE

E 

niezrelaksowany

≥ E

zrelaksowany

R

o

U

o

R

o

U

o

R

o

E

t

b

E

t

a

t

E

E

E

σ

ε

θ

σ

ε

θ

θ

σ

σ

σ

ε

≈

∞

→

≈

→

⎟

⎠

⎞

⎜

⎝

⎛−

⎥

⎦

⎤

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

.........

)

..........

0

)

exp

Nauka o Materiałach

Dziękuję 

do zobaczenia za 

tydzień