Materiał ćwiczeniowy z matematyki

Poziom podstawowy

Styczeń 2011

Klucz odpowiedzi do zadań zamkniętych

oraz

schemat oceniania

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okręgowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał ćwiczeniowy z matematyki - poziom podstawowy

2

KLUCZ ODPOWIEDZI DO ZADAŃ ZAMKNIĘTYCH

Nr zadania

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

Odpowiedź

A

D

C

B

D

C

A

A

D

B

A

B

A

B

C

C

A

A

B

B

B

D

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okręgowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał ćwiczeniowy z matematyki - poziom podstawowy

3

MODEL OCENIANIA ZADAŃ OTWARTYCH

Zadanie 23. (2 pkt)

Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego
na tym, że w drugim rzucie wypadnie parzysta liczba oczek.

I sposób rozwiązania

Oznaczamy: A – zdarzenie losowe polegające na wyrzuceniu w drugim rzucie parzystej
liczby oczek.
Obliczamy liczbę wszystkich zdarzeń elementarnych tego doświadczenia

36

=

Ω

.

Obliczamy liczbę zdarzeń elementarnych sprzyjających zdarzeniu losowemu A:

18

3

6

=

⋅

=

A

.

Obliczamy prawdopodobieństwo zdarzenia losowego A:

( )

2

1

36

18

=

=

A

P

.

Prawdopodobie

ń

stwo zdarzenia A jest równe

( )

2

1

=

A

P

.

II sposób rozwiązania

Oznaczamy: A – zdarzenie losowe polegaj

ą

ce na wyrzuceniu w drugim rzucie parzystej

liczby oczek.
Wypisujemy wszystkie mo

ż

liwe wyniki do

ś

wiadczenia i zaznaczamy zdarzenia elementarne

sprzyjaj

ą

ce zdarzaniu A.

(1, 1) (2, 1)

(3, 1)

(4, 1)

(5, 1)

(6, 1)

(1, 2)

(2, 2)

(3, 2)

(4, 2)

(5, 2)

(6, 2)

(1, 3)

(2, 3)

(3, 3)

(4, 3)

(5, 3)

(6, 3)

(1, 4)

(2, 4)

(3, 4 )

(4, 4)

(5, 4)

(6, 4)

(1, 5)

(2, 5)

(3, 5)

(4, 5)

(5, 5)

(6, 5)

(1, 6)

(2, 6)

(3, 6)

(4, 6)

(5, 6)

(6, 6)

Zliczamy liczb

ę

wszystkich zdarze

ń

elementarnych oraz zdarze

ń

sprzyjaj

ą

cych zdarzeniu A:

36

=

Ω

i

18

=

A

.

Obliczamy prawdopodobie

ń

stwo zdarzenia losowego A:

( )

2

1

36

18

=

=

A

P

.

Prawdopodobie

ń

stwo zdarzenia A jest równe

( )

2

1

=

A

P

.

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

4

Schemat oceniania

Zdający otrzymuje .................................................................................................................... 1 pkt

gdy:

•

poprawnie obliczy

36

=

Ω

i

18

=

A

i na tym poprzestanie lub dalej popełni bł

ą

d

albo

•

poprawnie wypisze wszystkie zdarzenia elementarne oraz poprawnie zaznaczy
wszystkie zdarzenia elementarne sprzyjaj

ą

ce zdarzeniu polegaj

ą

cemu na wyrzuceniu

w drugim rzucie parzystej liczby oczek i na tym poprzestanie lub dalej popełni bł

ą

d.

Zdający otrzymuje .................................................................................................................... 2 pkt

gdy poda prawdopodobie

ń

stwo zdarzenia losowego A:

( )

2

1

=

A

P

.

Uwaga

1.

Je

ż

eli zdaj

ą

cy bł

ę

dnie wyznaczy

Ω

(np.

6

=

Ω

) lub

A

(np.

3

=

A

), to

przyznajemy

0 punktów

za całe zadanie.

2.

Je

ż

eli zdaj

ą

cy wyznaczy

1

)

(

>

A

P

lub

0

)

(

<

A

P

, to przyznajemy

0 punktów

za całe

zadanie.

3.

Je

ż

eli zdaj

ą

cy popełni bł

ą

d rachunkowy przy obliczaniu

Ω

lub

A

i konsekwentnie

do popełnionego bł

ę

du rozwi

ąż

e zadanie, to przyznajemy

1 punkt

.

Zadanie 24. (2 pkt)

Rozwi

ąż

nierówno

ść

0

6

2

>

+

+

x

x

.

Rozwiązanie

Wyznaczamy wyró

ż

nik trójmianu kwadratowego

6

2

+

+

x

x

:

23

6

1

4

1

4

2

−

=

⋅

⋅

−

=

−

=

∆

ac

b

.

0

<

∆

, zatem trójmian kwadratowy

6

2

+

+

x

x

nie ma pierwiastków. Szkicujemy wykres

paraboli

6

2

+

+

=

x

x

y

i odczytujemy rozwi

ą

zanie.

R

x

∈

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

5

Schemat oceniania

Zdający otrzymuje .................................................................................................................... 1 pkt

gdy obliczy wyró

ż

nik trójmianu kwadratowego

23

−

=

∆

i zauwa

ż

y,

ż

e trójmian nie ma

pierwiastków.

Zdający otrzymuje .................................................................................................................... 2 pkt

gdy poda rozwi

ą

zanie nierówno

ś

ci:

R

x

∈

(lub inny równowa

ż

ny zapis).

Uwaga

1.

Przyznajemy

0 punktów

zdaj

ą

cemu, który rozwi

ą

zuje nierówno

ść

inn

ą

ni

ż

w tre

ś

ci

zadania.

2.

Je

ż

eli zdaj

ą

cy popełni bł

ą

d rachunkowy przy obliczaniu wyró

ż

nika trójmianu

kwadratowego i konsekwentnie do popełnionego bł

ę

du rozwi

ąż

e nierówno

ść

,

to przyznajemy

1 punkt

.

Zadanie 25. (2 pkt)

K

ą

t

α

jest k

ą

tem ostrym. Wiedz

ą

c,

ż

e

2

=

α

tg

, oblicz warto

ść

wyra

ż

enia

α

α

2

cos

sin

.

I sposób rozwiązania

Rysujemy trójk

ą

t prostok

ą

tny i wprowadzamy oznaczenia:

a – długo

ść

przyprostok

ą

tnej le

żą

cej przy k

ą

cie

α

,

2a – długo

ść

przyprostok

ą

tnej le

żą

cej naprzeciw k

ą

ta

α

,

c – długo

ść

przeciwprostok

ą

tnej.

2

2

=

=

a

a

tg

α

Z twierdzenia Pitagorasa otrzymujemy

( )

2

2

2

2

c

a

a

=

+

2

2

2

4

c

a

a

=

+

2

2

5

c

a

=

5

a

c

=

Z definicji funkcji trygonometrycznych k

ą

ta ostrego w trójk

ą

cie prostok

ą

tnym

otrzymujemy

5

5

2

5

2

5

2

2

sin

=

=

=

=

a

a

c

a

α

5

5

5

1

5

cos

=

=

=

=

a

a

c

a

α

a

c

2a

α

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

6

St

ą

d

5

2

5

1

5

5

2

5

5

5

5

2

cos

sin

2

2

=

=















=

α

α

.

II sposób rozwiązania











=

+

=

1

cos

sin

2

cos

sin

2

2

α

α

α

α

(

)







=

+

=

1

cos

cos

2

cos

2

sin

2

2

α

α

α

α

1

cos

cos

4

2

2

=

+

α

α

0

cos

5

1

cos

2

>

=

α

α

i

5

5

cos

=

α

St

ą

d

5

5

2

sin

=

α

.

Zatem

5

2

5

1

5

5

2

5

5

5

5

2

cos

sin

2

2

=

=















=

α

α













=













+

=

1

2

sin

sin

2

sin

cos

2

2

α

α

α

α

1

sin

4

1

sin

2

2

=

+

α

α

1

sin

4

5

2

=

α

0

sin

5

4

sin

2

>

=

α

α

i

5

5

2

sin

=

α

St

ą

d

5

5

2

5

5

2

cos

=

=

α

.

Zatem

5

2

5

1

5

5

2

5

5

5

5

2

cos

sin

2

2

=

=















=

α

α

.

III sposób rozwiązania

Dla

2

=

α

tg

odczytujemy z tablic trygonometrycznych:

°

≈

63

α

.

St

ą

d

891

,

0

63

sin

≈

°

oraz

454

,

0

63

cos

≈

°

.

Zatem

(

)

321

,

4

2062

,

0

891

,

0

454

,

0

891

,

0

63

cos

63

sin

2

2

≈

=

≈

°

°

.

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

7

Schemat oceniania I, II i III sposobu oceniania

Zdający otrzymuje ............................................................................................................1 pkt

gdy:

•

przekształci dane wyra

ż

enie do postaci wyra

ż

enia zawieraj

ą

cego tylko sin

α

i wykorzysta „jedynk

ę

trygonometryczn

ą

”, np.

2

sin

cos

α

α

=

,

1

sin

4

1

sin

2

2

=

+

α

α

i na tym poprzestanie lub dalej popełni bł

ą

d

albo

•

przekształci dane wyra

ż

enie do postaci wyra

ż

enia zawieraj

ą

cego tylko cos

α

i wykorzysta „jedynk

ę

trygonometryczn

ą

”, np.

α

α

cos

2

sin

=

,

1

cos

cos

4

2

2

=

+

α

α

i na tym poprzestanie lub dalej popełni bł

ą

d

albo

•

obliczy długo

ść

przeciwprostok

ą

tnej trójk

ą

ta prostok

ą

tnego o przyprostok

ą

tnych

długo

ś

ci 1 i 2 (lub ich wielokrotno

ś

ci) nawet z bł

ę

dem rachunkowym oraz zapisze

5

5

2

5

2

5

2

2

sin

=

=

=

=

a

a

c

a

α

i na tym zako

ń

czy

albo

•

obliczy długo

ść

przeciwprostok

ą

tnej trójk

ą

ta prostok

ą

tnego o przyprostok

ą

tnych

długo

ś

ci 1 i 2 (lub ich wielokrotno

ś

ci) z bł

ę

dem rachunkowym oraz zapisze

5

5

5

1

5

cos

=

=

=

=

a

a

c

a

α

i na tym zako

ń

czy

albo

•

narysuje trójk

ą

t prostok

ą

tny o przyprostok

ą

tnych długo

ś

ci 1 i 2 (lub ich

wielokrotno

ś

ci), obliczy długo

ść

przeciwprostok

ą

tnej i zaznaczy w tym trójk

ą

cie

poprawnie k

ą

t

α

albo

•

odczyta z tablic przybli

ż

on

ą

warto

ść

k

ą

ta

α

:

°

≈

63

α

(akceptujemy wynik

°

≈

64

α

)

i na tym zako

ń

czy lub dalej popełnia bł

ę

dy.

Zdający otrzymuje ............................................................................................................2 pkt

gdy:

•

obliczy warto

ść

α

α

2

cos

sin

:

5

2

5

1

5

5

2

5

5

5

5

2

cos

sin

2

2

=

=















=

α

α

albo

•

obliczy przybli

ż

on

ą

warto

ść

α

α

2

cos

sin

:

321

,

4

63

cos

63

sin

2

≈

°

°

.

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

8

Uwaga

1.

Je

ś

li zdaj

ą

cy przyjmie,

ż

e sin

5

α

=

i cos

12

α

=

, to otrzymuje

0 punktów

.

2.

Je

ś

li zdaj

ą

cy nie odrzuci odpowiedzi ujemnej, to otrzymuje

1 punkt

.

3.

Za rozwi

ą

zanie, w którym zdaj

ą

cy bł

ę

dnie zaznaczy k

ą

t

α

na rysunku i z tego korzysta

oceniamy na

0 punktów

.

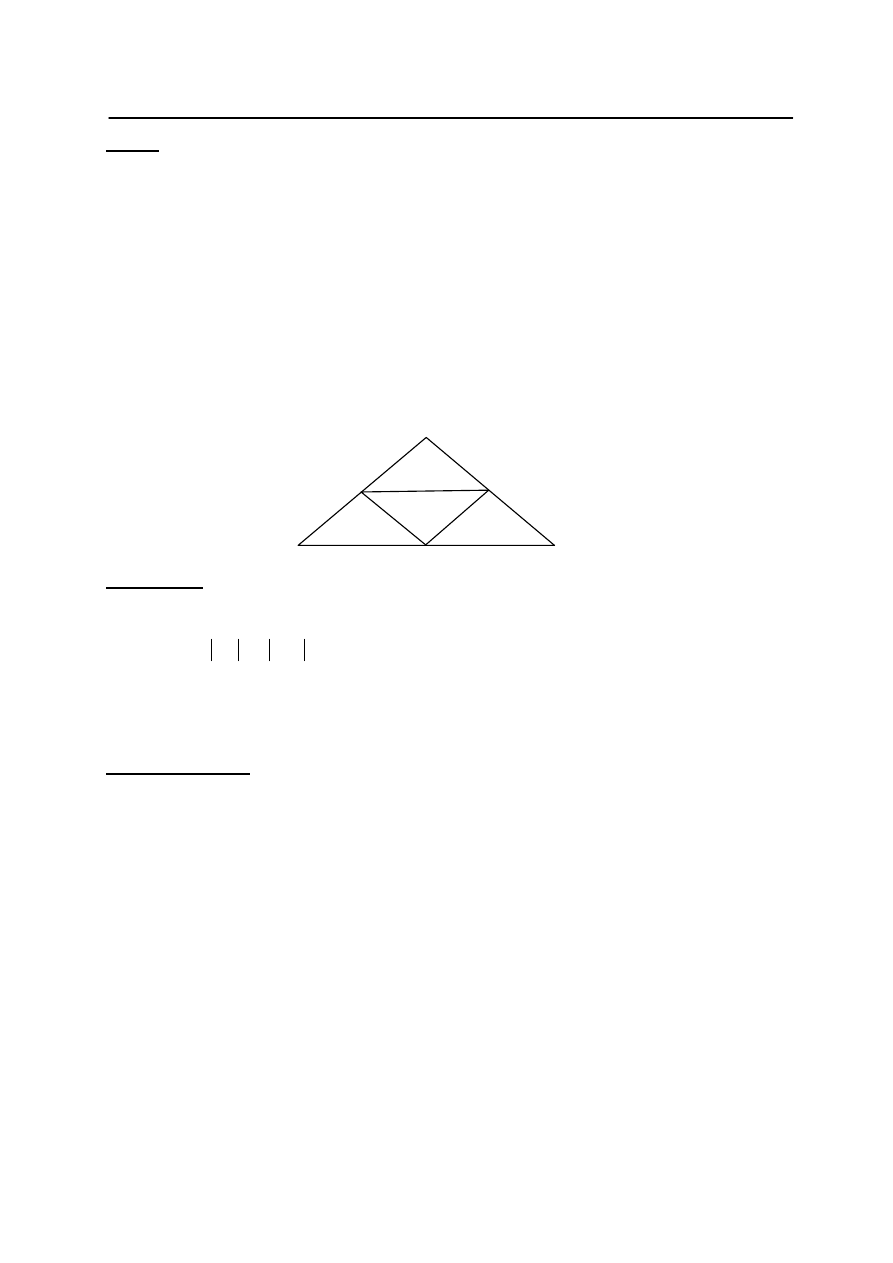
Zadanie 26. (2 pkt)

Punkty

A’, B’, C’ s

ą

ś

rodkami boków trójk

ą

ta

ABC. Pole trójk

ą

ta

A’B’C’ jest równe 4. Oblicz

pole trójk

ą

ta

ABC.

Rozwiązanie

Trójk

ą

ty

ABC i A’B’C’ s

ą

podobne (cecha

kkk). Poniewa

ż

odcinek

C’B’ ł

ą

czy

ś

rodki boków

AC i BC, to

'

'

2

B

C

AB

=

. Zatem skala podobie

ń

stwa przekształcaj

ą

cego trójk

ą

t

A’B’C’

na trójk

ą

t

ABC jest równa 2.

Obliczamy pole trójk

ą

ta

ABC

16

4

'

'

'

=

=

C

B

A

ABC

P

P

.

Schemat oceniania

Zdający otrzymuje .................................................................................................................... 1 pkt

gdy zauwa

ż

y podobie

ń

stwo trójk

ą

tów i wyznaczy skal

ę

podobie

ń

stwa: 2.

Zdający otrzymuje .................................................................................................................... 2 pkt

gdy poprawnie obliczy pole trójk

ą

ta

ABC:

16

=

ABC

P

.

A

B

C

A’

C’

B’

www.tomaszgrebski.pl

www.tomaszgrebski.pl

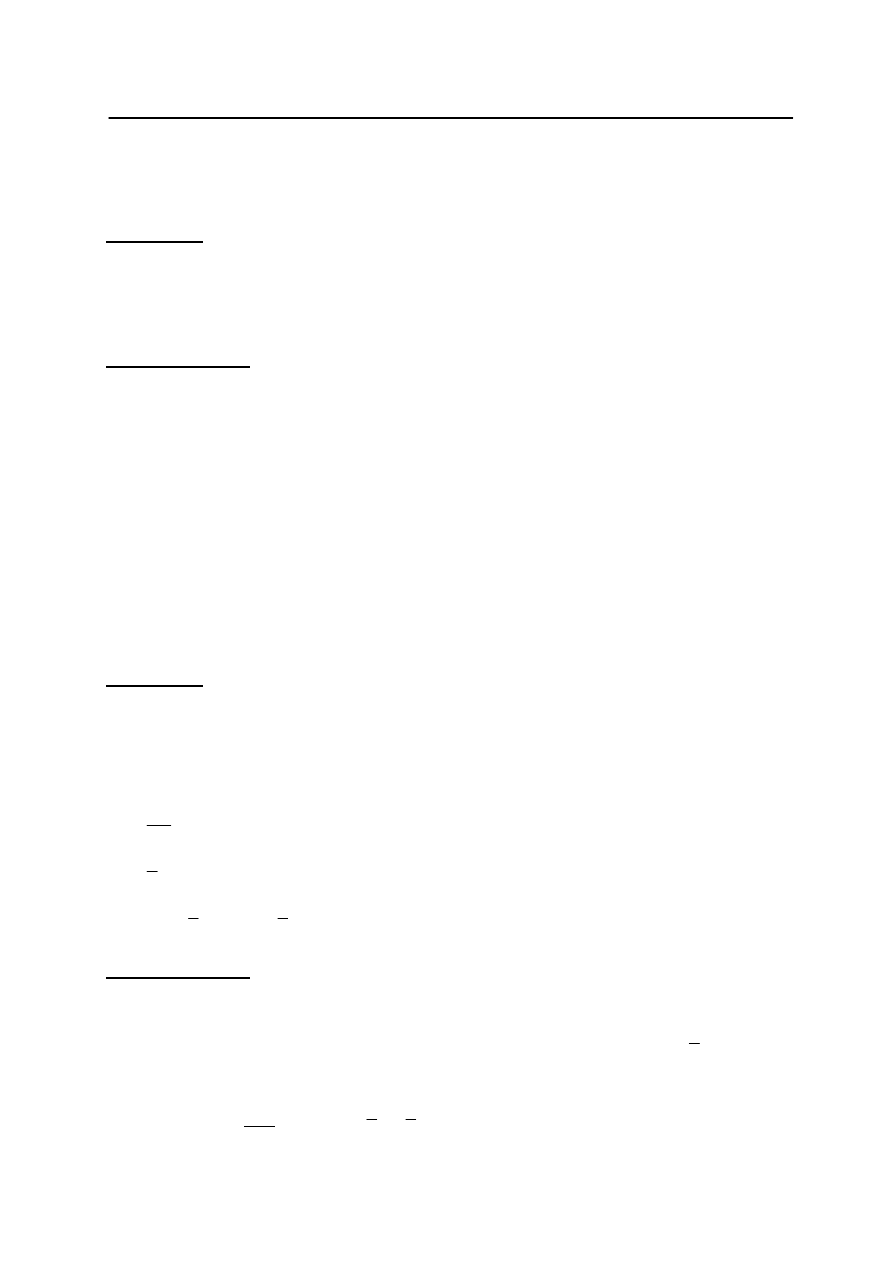
Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

9

Zadanie 27. (2 pkt)

Wyka

ż

,

ż

e ró

ż

nica kwadratów dwóch kolejnych liczb parzystych jest liczb

ą

podzieln

ą

przez 4.

Rozwiązanie

Wprowadzamy oznaczenia:

2n, 2n+2 – kolejne liczby parzyste

(

) ( )

(

)

1

2

4

4

8

4

4

8

4

2

2

2

2

2

2

2

+

=

+

=

−

+

+

=

−

+

n

n

n

n

n

n

n

Zatem ró

ż

nica

(

) ( )

(

)

1

2

4

2

2

2

2

2

+

=

−

+

n

n

n

jest liczb

ą

podzieln

ą

przez 4.

Schemat oceniania

Zdający otrzymuje .................................................................................................................... 1 pkt

gdy poprawnie zapisze ró

ż

nic

ę

kwadratów dwóch kolejnych liczb parzystych i poprawnie

zastosuje wzór skróconego mno

ż

enia:

(

) ( )

2

2

2

2

4

4

8

4

2

2

2

n

n

n

n

n

−

+

+

=

−

+

.

Zdający otrzymuje .................................................................................................................... 2 pkt

gdy wyka

ż

e,

ż

e ró

ż

nica kwadratów dwóch kolejnych liczb parzystych jest liczb

ą

podzieln

ą

przez 4:

(

) ( )

(

)

1

2

4

2

2

2

2

2

+

=

−

+

n

n

n

.

Zadanie 28. (2 pkt)

Proste o równaniach

1

9

−

−

=

x

y

i

5

2

+

=

x

a

y

s

ą

prostopadłe. Wyznacz liczb

ę

a.

Rozwiązanie

Proste o równaniach

1

9

−

−

=

x

y

i

5

2

+

=

x

a

y

s

ą

prostopadłe, zatem ich współczynniki

kierunkowe spełniaj

ą

warunek

1

2

1

−

=

⋅

a

a

.

Poniewa

ż

9

1

−

=

a

,

2

2

a

a

=

, to

2

2

1

9

a

a

a

⋅

−

=

⋅

.

St

ą

d

1

9

2

−

=

⋅

−

a

9

1

2

−

−

=

a

9

1

2

=

a

Zatem

3

1

=

a

lub

3

1

−

=

a

.

Schemat oceniania

Zdający otrzymuje .................................................................................................................... 1 pkt

gdy poprawnie zapisze warunek prostopadło

ś

ci prostych:

1

9

2

−

=

⋅

−

a

lub

9

1

2

=

a

.

Zdający otrzymuje .................................................................................................................... 2 pkt

gdy obliczy i poda obie warto

ś

ci

a:

3

1

,

3

1

−

.

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

10

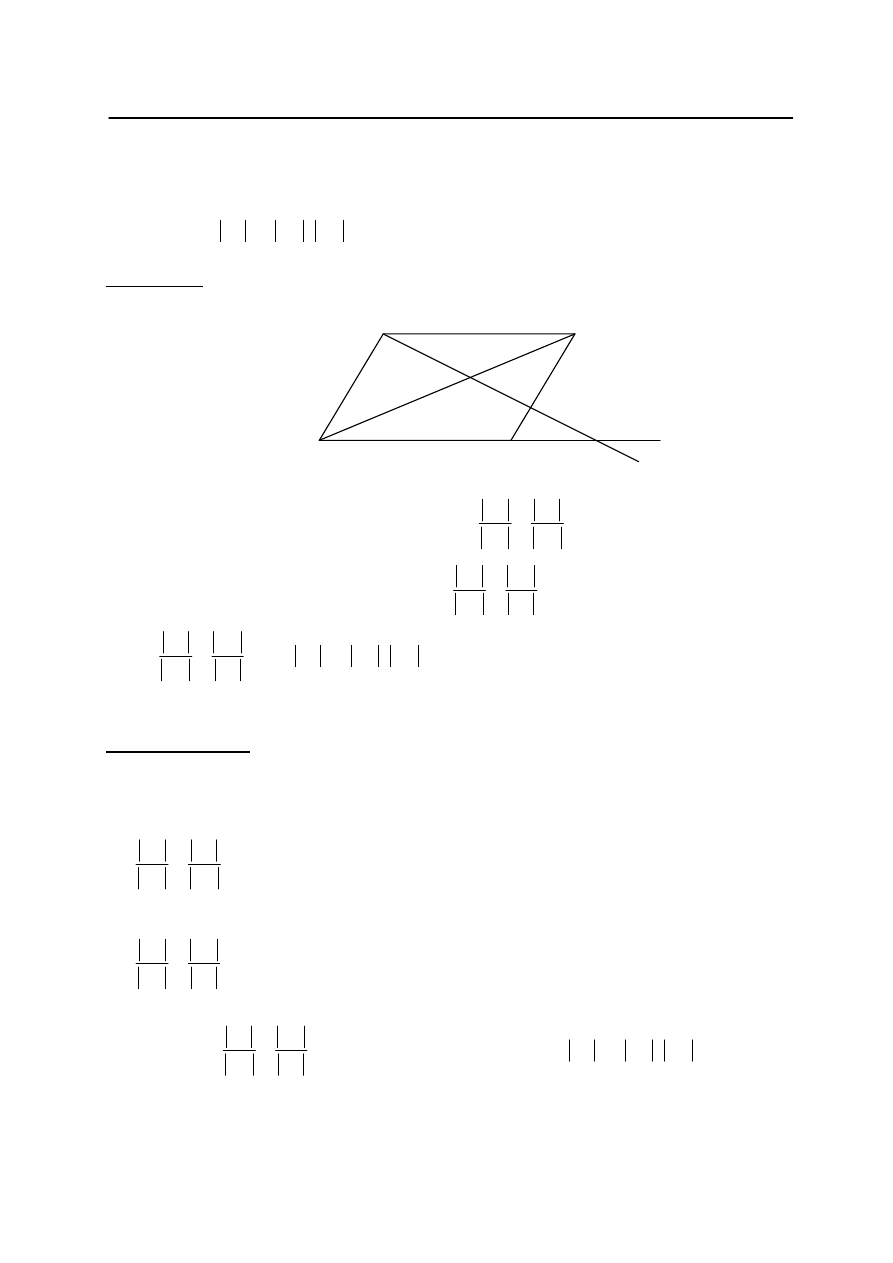
Zadanie 29. (2 pkt)

Prosta przechodz

ą

ca przez wierzchołek

A równoległoboku ABCD przecina jego przek

ą

tn

ą

BD

w punkcie

E i bok BC w punkcie F, a prost

ą

DC w punkcie G.

Udowodnij,

ż

e

EG

EF

EA

⋅

=

2

.

Rozwiązanie

Rysujemy równoległobok

ABCD i wprowadzamy oznaczenia

Trójk

ą

ty

AEB i DEG s

ą

podobne (cecha

kkk), wi

ę

c

EG

EA

ED

EB

=

.

Trójk

ą

ty

BEF i ADE równie

ż

s

ą

podobne, wi

ę

c

EA

EF

ED

EB

=

.

Zatem

EA

EF

EG

EA

=

. St

ą

d

EG

EF

EA

⋅

=

2

.

Schemat oceniania

Zdający otrzymuje .................................................................................................................... 1 pkt

gdy:

•

zauwa

ż

y podobie

ń

stwo trójk

ą

tów AEB i DEG i zapisze poprawny stosunek boków:

EG

EA

ED

EB

=

albo

•

zauwa

ż

y podobie

ń

stwo trójk

ą

tów BEF i ADE i zapisze poprawny stosunek boków:

EA

EF

ED

EB

=

Zdający otrzymuje .................................................................................................................... 2 pkt

gdy zapisze,

ż

e

EA

EF

EG

EA

=

i przekształci proporcj

ę

do postaci

EG

EF

EA

⋅

=

2

.

D

C

E

B

A

G

F

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

11

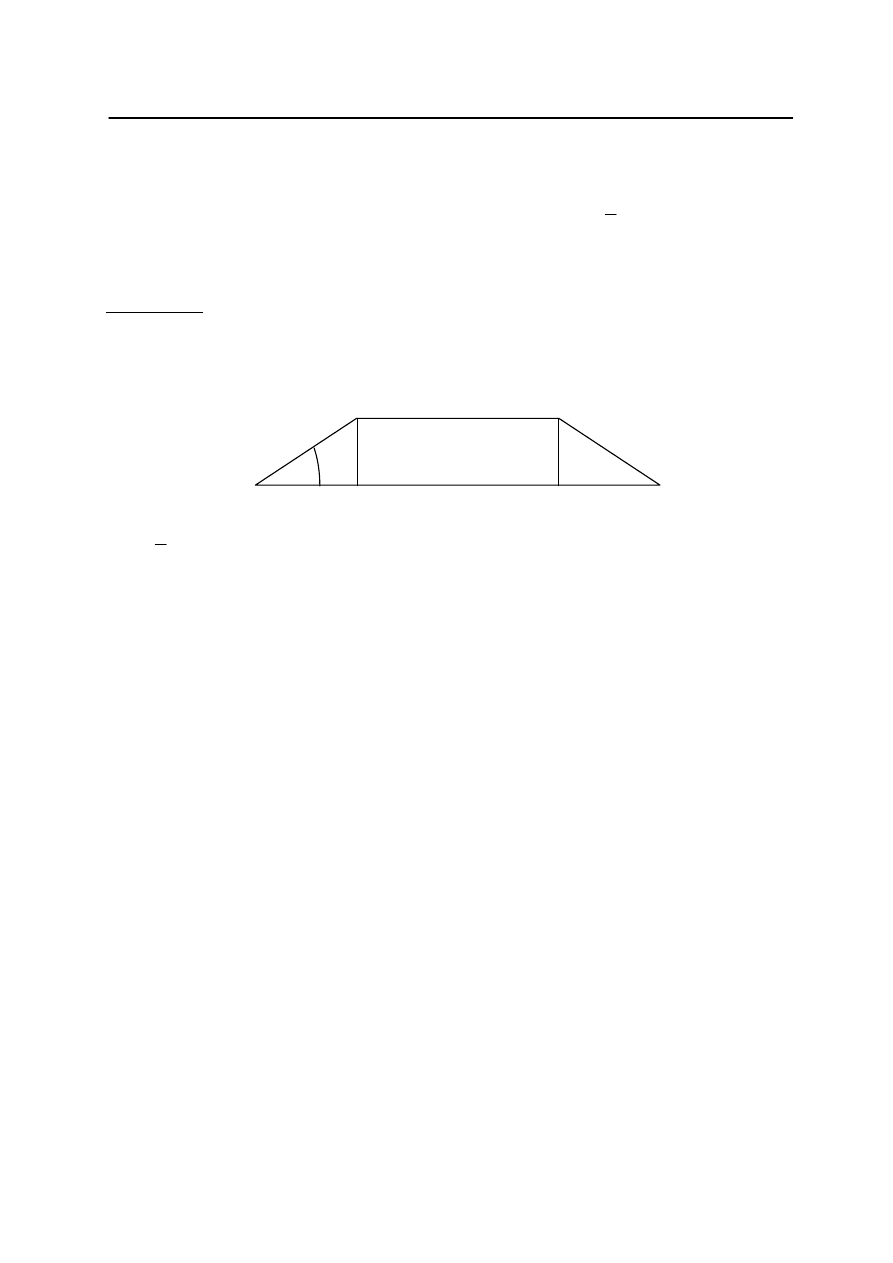
Zadanie 30. (4 pkt)

W trapezie równoramiennym

ABCD rami

ę

ma długo

ść

10. Obwód tego trapezu jest równy 40.

Wiedz

ą

c,

ż

e tangens k

ą

ta ostrego w trapezie

ABCD jest równy

4

3

, oblicz długo

ś

ci jego

podstaw.

Rozwiązanie

Rysujemy trapez i wprowadzamy oznaczenia
a, b – długo

ś

ci podstaw trapezu

d – długo

ść

ramienia trapezu

h – wysoko

ść

trapezu

4

3

=

α

tg

y

b

a

2

+

=

Obwód trapezu jest równy

40

2

=

+

+

d

b

a

. St

ą

d

20

=

+

b

a

.

Korzystaj

ą

c z twierdzenia Pitagorasa wyznaczamy długo

ść

odcinka

y.

( ) ( )

2

2

2

d

y

h

=

+

( ) ( )

2

2

2

4

3

d

x

x

=

+

2

2

2

10

16

9

=

+

x

x

25

:

/

100

25

2

=

x

4

2

=

x

2

=

x

St

ą

d

8

4

=

x

.

Zatem

16

4

2

+

=

⋅

+

=

b

x

b

a

.

20

=

+

b

a

20

16

=

+

+

b

b

16

20

2

−

=

b

St

ą

d

2

=

b

i

18

=

a

.

Podstawy trapezu

ABCD maj

ą

długo

ś

ci

18

=

a

i

2

=

b

.

a

b

d

y

h

y

α

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

12

Schemat oceniania

Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania .........................................................................................................................1 pkt

Zapisanie równania wynikaj

ą

cego z obwodu:

20

=

+

b

a

.

Rozwiązanie, w którym jest istotny postęp ......................................................................2 pkt

Obliczenie długo

ś

ci odcinka

y:

8

=

y

.

Pokonanie zasadniczych trudności zadania.....................................................................3 pkt

Obliczenie długo

ś

ci jednej z podstaw trapezu:

18

=

a

lub

2

=

b

.

Rozwiązanie pełne ..............................................................................................................4 pkt

Obliczenie długo

ś

ci obu podstaw trapezu:

18

=

a

i

2

=

b

.

Uwaga

1.

Je

ż

eli zdaj

ą

cy przyjmie,

ż

e

3

=

h

oraz

4

=

y

i konsekwentnie rozwi

ąż

e zadanie,

to za całe rozwi

ą

zanie przyznajemy

1 punkt

.

2.

Je

ż

eli zdaj

ą

cy popełni bł

ą

d rachunkowy i konsekwentnie do popełnionego bł

ę

du

rozwi

ąż

e zadanie, to przyznajemy

3 punkty

.

Zadanie 31. (6 pkt)

Trzy liczby tworz

ą

ci

ą

g arytmetyczny. Ich suma jest równa 15. Je

ż

eli pierwsz

ą

i trzeci

ą

liczb

ę

pozostawimy bez zmian, a drug

ą

pomniejszymy o jeden, to otrzymamy trzy kolejne wyrazy

ci

ą

gu geometrycznego. Oblicz wyrazy ci

ą

gu arytmetycznego.

I sposób rozwiązania

Ci

ą

g

(

)

r

a

r

a

a

2

,

,

1

1

1

+

+

– jest ci

ą

giem arytmetycznym.

Z tre

ś

ci zadania wynika,

ż

e

15

2

1

1

1

=

+

+

+

+

r

a

r

a

a

.

St

ą

d

15

3

3

1

=

+

r

a

.

5

1

=

+

r

a

Ci

ą

g

(

)

r

a

r

a

a

2

,

1

,

1

1

1

+

−

+

jest ci

ą

giem geometrycznym Zatem

(

)

(

)

r

a

a

r

a

2

1

1

1

2

1

+

=

−

+

.

Rozwi

ą

zujemy układ równa

ń

(

)

(

)







+

=

−

+

=

+

r

a

a

r

a

r

a

2

1

5

1

1

2

1

1

(

)

(

)







+

=

−

=

+

r

a

a

r

a

2

1

5

5

1

1

2

1

(

)

(

)







−

=

−

−

=

1

1

2

1

10

1

5

5

a

a

a

r

(

)







−

=

−

=

1

1

1

10

16

5

a

a

a

r







=

+

−

−

=

0

16

10

5

1

2

1

1

a

a

a

r

Rozwi

ą

zuj

ą

c równanie

0

16

10

1

2

1

=

+

−

a

a

otrzymujemy

2

1

=

a

lub

8

1

=

a

.

Zatem







=

=

3

2

1

r

a

lub







−

=

=

3

8

1

r

a

.

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

13

Obliczamy wyrazy ci

ą

gu arytmetycznego:











=

=

=

8

5

2

3

2

1

a

a

a

lub











=

=

=

2

5

8

3

2

1

a

a

a

.

II sposób rozwiązania

Ci

ą

g

(

)

c

b

a

,

,

– jest ci

ą

giem arytmetycznym.

Z tre

ś

ci zadania i własno

ś

ci ci

ą

gu arytmetycznego wynika,

ż

e

15

=

+

+

c

b

a

i

2

c

a

b

+

=

.

Ci

ą

g

(

)

c

b

a

,

1

,

−

jest ci

ą

giem geometrycznym. Zatem

( )

c

a

b

⋅

=

−

2

1

.

Rozwi

ą

zujemy układ równa

ń

(

)













⋅

=

−

+

=

=

+

+

c

a

b

c

a

b

c

b

a

2

1

2

15

(

)



















⋅

=

−

+

=

=

+

+

+

c

a

b

c

a

b

c

c

a

a

2

1

2

15

2

(

)













⋅

=

−

+

=

=

+

c

a

b

c

a

b

c

a

2

1

2

30

3

3

(

)













⋅

=

−

+

=

=

+

c

a

b

c

a

b

c

a

2

1

2

10

(

)













⋅

=

−

=

=

+

c

a

b

b

c

a

2

1

2

10

10

(

) (

)











⋅

−

=

−

=

−

=

c

c

b

c

a

10

1

5

5

10

2











−

=

=

−

=

2

10

16

5

10

c

c

b

c

a

Rozwi

ą

zuj

ą

c równanie

0

16

10

2

=

+

−

c

c

otrzymujemy

2

1

=

c

lub

8

2

=

c

.

Po podstawieniu otrzymujemy ci

ą

g arytmetyczny











=

=

=

2

5

8

c

b

a

lub











=

=

=

8

5

2

c

b

a

.

Schemat oceniania

Rozwiązanie, w którym postęp jest wprawdzie niewielki, ale konieczny na drodze
do całkowitego rozwiązania zadania ....................................................................................... 1 pkt

•

Wykorzystanie wzoru na n-ty wyraz ci

ą

gu arytmetycznego do zapisania wyrazów

ci

ą

gu:

,

1

a

r

a

+

1

,

r

a

2

1

+

i zapisanie warunku

5

1

=

+

r

a

.

albo

•

Wykorzystanie

własno

ś

ci

ci

ą

gu

arytmetycznego

oraz

zapisanie:

2

c

a

b

+

=

i

15

=

+

+

c

b

a

.

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

14

Rozwiązanie, w którym jest istotny postęp ............................................................................. 2 pkt

•

Zapisanie układu równa

ń

(

)

(

)

r

a

a

r

a

2

1

1

1

2

1

+

=

−

+

i

5

1

=

+

r

a

.

albo

•

Zapisanie układu równa

ń

(

)













⋅

=

−

+

=

=

+

+

c

a

b

c

a

b

c

b

a

2

1

2

15

.

Pokonanie zasadniczych trudności zadania ............................................................................ 4 pkt

Zapisanie i rozwi

ą

zanie równania z jedn

ą

niewiadom

ą

:

•

0

16

10

1

2

1

=

+

−

a

a

,

2

1

=

a

,

3

=

r

lub

8

1

=

a

,

3

−

=

r

,

albo

•

0

16

10

2

=

+

−

c

c

,.

2

1

=

c

lub

8

2

=

c

.

Uwaga

Je

ś

li zdaj

ą

cy obliczy tylko jedn

ą

warto

ść

, to otrzymuje

3 punkty

.

Rozwiązanie zadania do końca lecz z usterkami, które jednak nie przekreślają
poprawności rozwiązania (np. błędy rachunkowe) ................................................................ 5 pkt

Rozwiązanie pełne ..................................................................................................................... 6 pkt

Obliczenie wszystkich wyrazów ci

ą

gu: 2, 5, 8 lub 8, 5, 2.

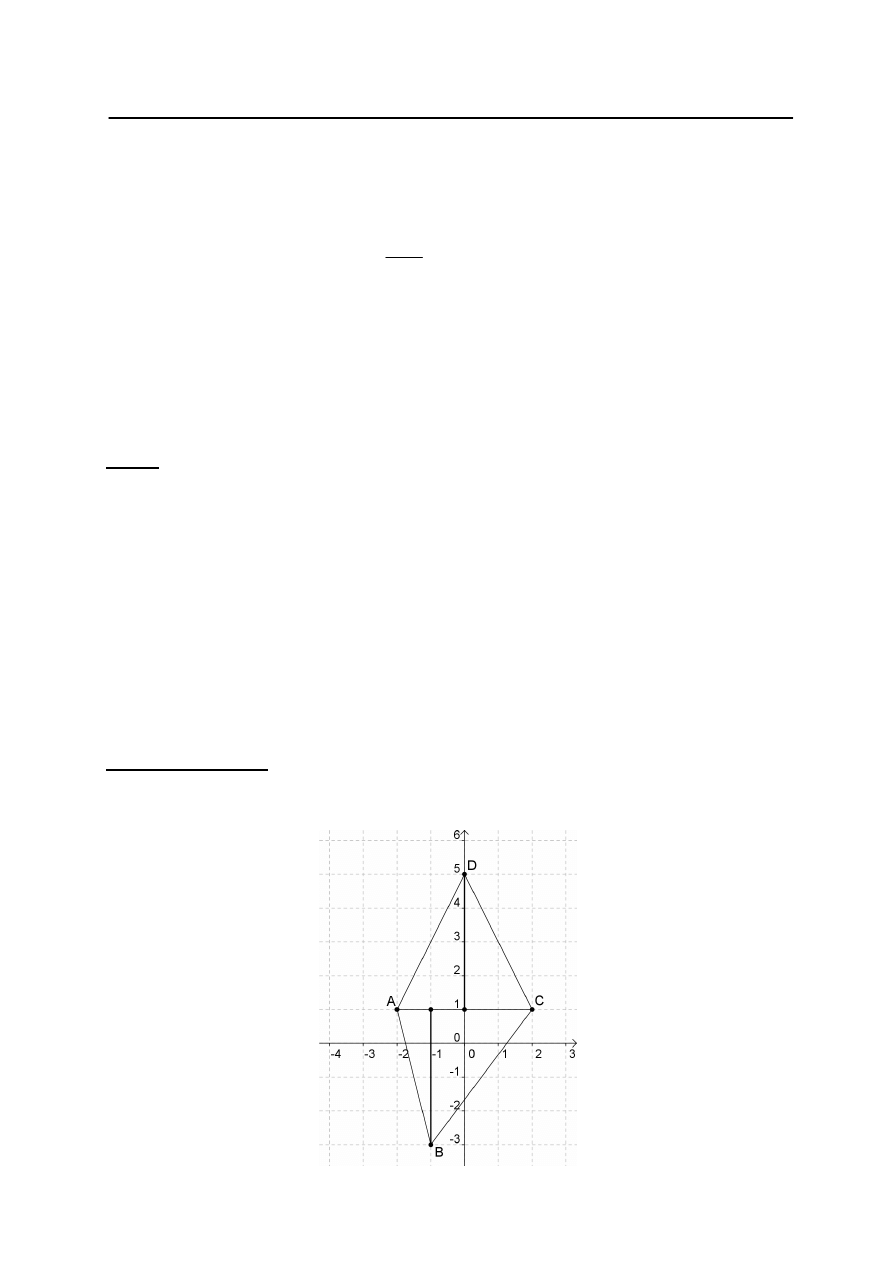
Zadanie 32. (4 pkt)

Oblicz pole czworok

ą

ta ABCD, którego wierzchołki maj

ą

współrz

ę

dne

(

)

1

,

2

−

=

A

,

(

)

3

,

1

−

−

=

B

,

( )

1

,

2

=

C

,

( )

5

,

0

=

D

.

I sposób rozwiązania

Zaznaczamy punkty

(

)

1

,

2

−

=

A

,

(

)

3

,

1

−

−

=

B

,

( )

1

,

2

=

C

,

( )

5

,

0

=

D

w układzie

współrz

ę

dnych i rysujemy czworok

ą

t ABCD.

h

1

h

2

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

15

Przek

ą

tna AC dzieli czworok

ą

t ABCD na dwa trójk

ą

ty: ACD i ABC. Wysoko

ść

w trójk

ą

cie

ACD jest równa

4

1

=

h

i jest jednocze

ś

nie odległo

ś

ci

ą

punktu D od prostej AC o równaniu

1

=

y

. Zatem pole trójk

ą

ta ACD jest równe

1

2

1

1

h

AC

P

⋅

=

.

Poniewa

ż

4

=

AC

i

4

1

=

h

, to

8

4

4

2

1

1

2

1

1

=

⋅

⋅

=

⋅

=

h

AC

P

.

Wysoko

ść

w trójk

ą

cie ABC jest równa

4

2

=

h

i jest jednocze

ś

nie odległo

ś

ci

ą

punktu B

od prostej AC o równaniu

1

=

y

. Zatem pole trójk

ą

ta ABC jest równe

2

2

1

2

h

AC

P

⋅

=

.

Poniewa

ż

4

=

AC

i

4

2

=

h

, to

8

4

4

2

1

2

2

1

2

=

⋅

⋅

=

⋅

=

h

AC

P

.

Pole czworok

ą

ta ABCD jest równe sumie pól trójk

ą

tów ACD i ABC.

Zatem

16

8

8

2

1

=

+

=

+

=

P

P

P

ABCD

.

Pole czworok

ą

ta ABCD jest równe 16.

II sposób rozwiązania

Zaznaczamy punkty

(

)

1

,

2

−

=

A

,

(

)

3

,

1

−

−

=

B

,

( )

1

,

2

=

C

,

( )

5

,

0

=

D

w układzie

współrz

ę

dnych i rysujemy czworok

ą

t ABCD.

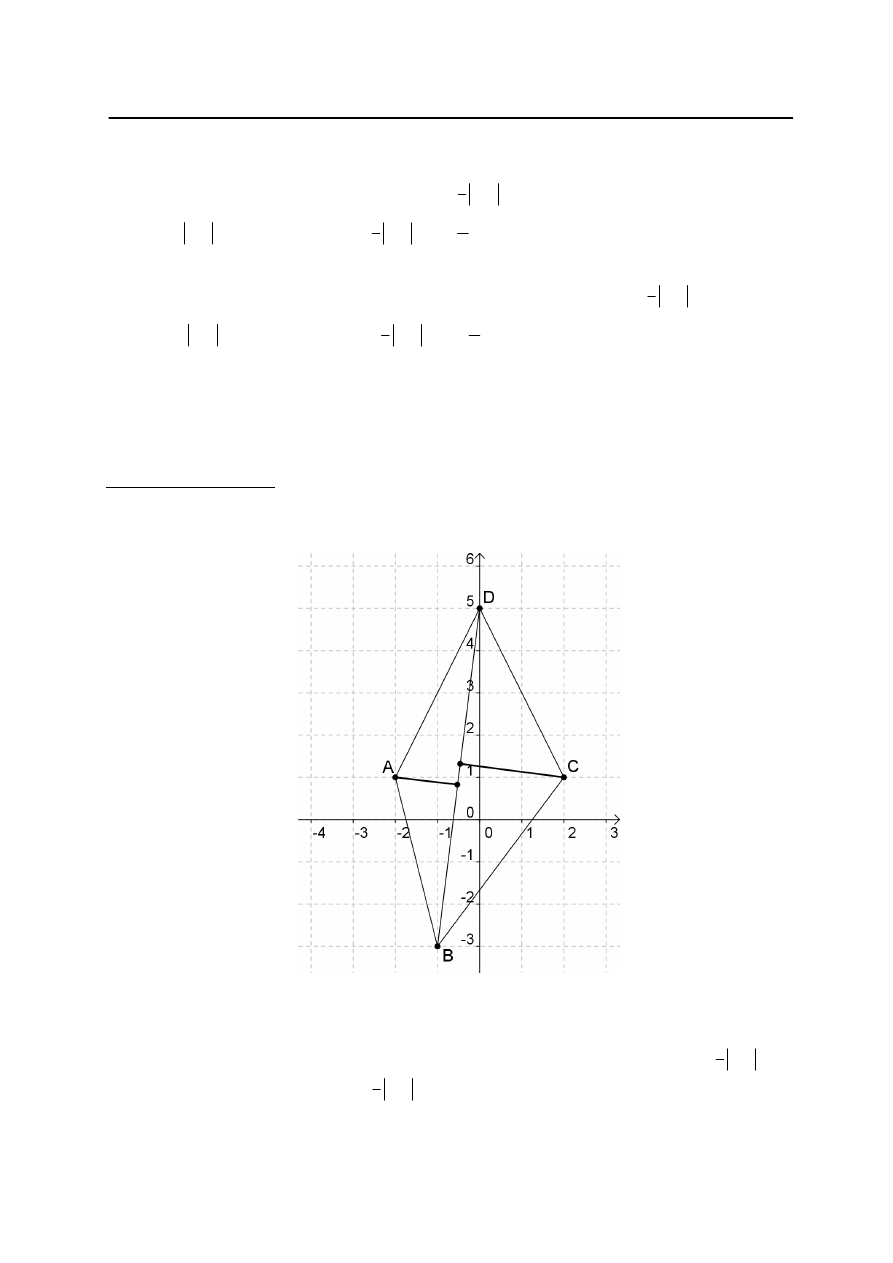
Przek

ą

tna BD dzieli czworok

ą

t ABCD na dwa trójk

ą

ty: ABD i BDC. Wysoko

ść

1

h

w trójk

ą

cie

ABD jest równa odległo

ś

ci punktu A od prostej BD, a wysoko

ść

2

h

w trójk

ą

cie BDC jest

równa odległo

ś

ci punktu C od prostej BD. Zatem pole trójk

ą

ta ABD jest równe

1

2

1

1

h

BD

P

⋅

=

,

a pole trójk

ą

ta BDC jest równe

2

2

1

2

h

BD

P

⋅

=

.

h

2

h

1

www.tomaszgrebski.pl

www.tomaszgrebski.pl

Okr

ę

gowa Komisja Egzaminacyjna w Poznaniu

Model oceniania

Materiał

ć

wiczeniowy z matematyki - poziom podstawowy

16

Wyznaczamy równanie prostej BD:

(

)

1

1

0

3

5

3

+

+

+

=

+

x

y

(

)

1

8

3

+

=

+

x

y

5

8

+

=

x

y

Posta

ć

ogólna równania prostej BD:

0

5

8

=

+

−

y

x

.

Obliczamy długo

ś

ci wysoko

ś

ci

1

h

i

2

h

, korzystaj

ą

c ze wzoru na odległo

ść

punktu od prostej.

( )

65

12

65

5

1

16

1

8

5

1

1

2

8

2

2

1

=

+

−

−

=

+

+

⋅

−

−

⋅

=

h

65

20

65

5

1

16

1

8

5

1

1

2

8

2

2

2

=

+

−

=

+

+

⋅

−

⋅

=

h

Obliczamy długo

ść

odcinka BD:

(

) (

)

65

64

1

3

5

1

0

2

2

=

+

=

+

+

+

=

BD

Pole czworok

ą

ta ABCD jest równe sumie pól trójk

ą

tów ABD i BDC.

Poniewa

ż

65

=

BD

i

65

12

1

=

h

, to

6

65

12

65

2

1

1

2

1

1

=

⋅

⋅

=

⋅

=

h

BD

P

.

Poniewa

ż

65

=

BD

i

65

20

2

=

h

, to

10

65

20

65

2

1

2

2

1

2

=

⋅

⋅

=

⋅

=

h

BD

P

.

Zatem

16

10

6

2

1

=

+

=

+

=

P

P

P

ABCD

.

Pole czworok

ą

ta ABCD jest równe 16.

Schemat oceniania

Rozwiązanie, w którym postęp jest niewielki, ale konieczny na drodze do pełnego
rozwiązania .........................................................................................................................1 pkt

Podział czworok

ą

ta na dwa trójk

ą

ty i wyznaczenie równania prostej AC:

1

=

y

lub prostej

BD:

5

8

+

=

x

y

.

Rozwiązanie, w którym jest istotny postęp ......................................................................2 pkt

Obliczenie odległo

ś

ci punktów B i D od prostej AC: 4

lub odległo

ś

ci punktów A i C od prostej BD:

65

12

i

65

20

.

Pokonanie zasadniczych trudności zadania.....................................................................3 pkt

Obliczenie pól trójk

ą

tów ACD i ABC:

8

2

1

=

=

P

P

lub pól trójk

ą

tów ABD i BDC:

6

1

=

P

i

10

2

=

P

.

Rozwiązanie pełne ..............................................................................................................4 pkt

Obliczenie pola powierzchni czworok

ą

ta ABDC: 16.

www.tomaszgrebski.pl

www.tomaszgrebski.pl