1

Podstawowe operacje arytmetyczne i logiczne dla liczb binarnych

1. Podstawowe operacje logiczne dla cyfr binarnych

Jeśli cyfry 0 i 1 potraktujemy tak, jak wartości logiczne „fałsz” i „prawda”, to działanie
elementów dwustanowych opisują operacje dwuelementowej algebry Boole’a.

Algebrę Boole’a definiują: dwuelementowy zbiór {0, 1} oraz trzy operacje: alternatywa (OR),
koniunkcja (AND) i negacja (NOT) wraz ze zbiorem aksjomatów i twierdzeń.

Zmienne należące do zbioru {0, 1} oraz ww. operacje nazywamy zmiennymi i operacjami
logicznymi.

Układy realizujące funkcje logiczne nazywamy funktorami logicznymi (powszechnie używa
się też określenia: bramki logiczne)

NEGACJA ( ang. NOT, pol. NIE, mat.

¬

)

Jest to zamiana wartości cyfry na przeciwną (tzn. 0 na 1 i 1 na 0).

¬

0 = 1

¬

1 = 0

Działanie podstawowych operacji logicznych często przedstawia się w postaci układów
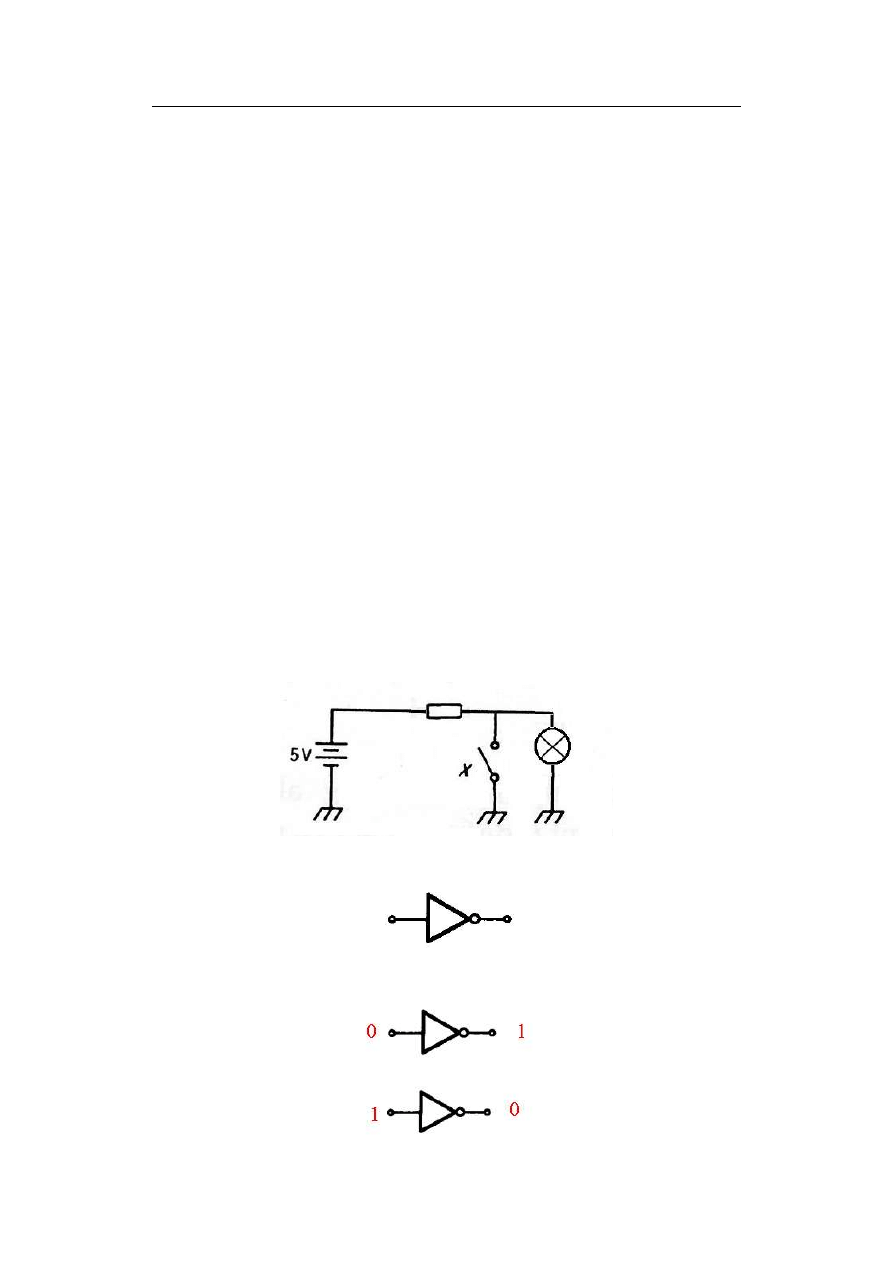
elektrycznych zawierających żarówki i wyłączniki. Przyjmując, że wyłącznik zwarty i
świecąca się żarówka reprezentują jedynkę, a wyłącznik rozwarty i zgaszona żarówka
reprezentują zero, działanie negacji realizuje przedstawiony niżej układ

Negacja jest operacją jednoargumentową.

Symbol graficzny funktora realizującego negację

Negacja jest najprostszym działaniem logicznym. Wynikiem jest liczba przeciwna do
wyjściowej.

Działanie funktora NOT

2

SUMA LOGICZNA ( ang. OR, pol. LUB, mat.

∨

)

Suma logiczna dwu cyfr binarnych jest równa 0 wtedy i tylko wtedy, gdy obydwie cyfry
są równe 0

0

∨

0 = 0

0

∨

1 = 1

1

∨

0 = 1

1

∨

1 = 1

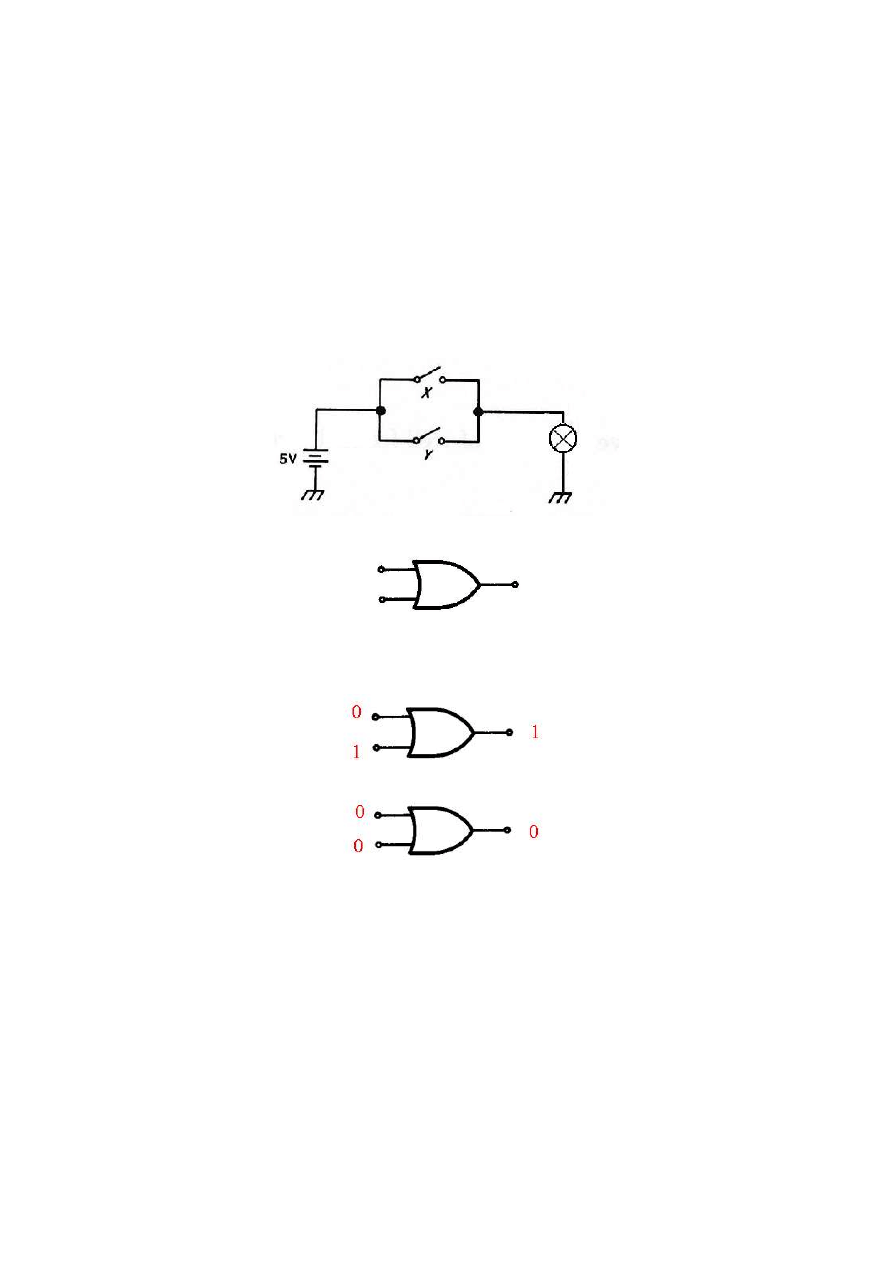
Sumę logiczną realizuje przedstawiony niżej układ

Symbol graficzny funktora OR

oraz przykłady działania tego funktora

ILOCZYN LOGICZNY ( ang. AND, pol. I, mat.

∧

)

Iloczyn logiczny dwu cyfr binarnych jest równy 1 wtedy i tylko wtedy, gdy obydwie
cyfry są równe 1

0

∧

0 = 0

0

∧

1 = 0

1

∧

0 = 0

1

∧

1 = 1

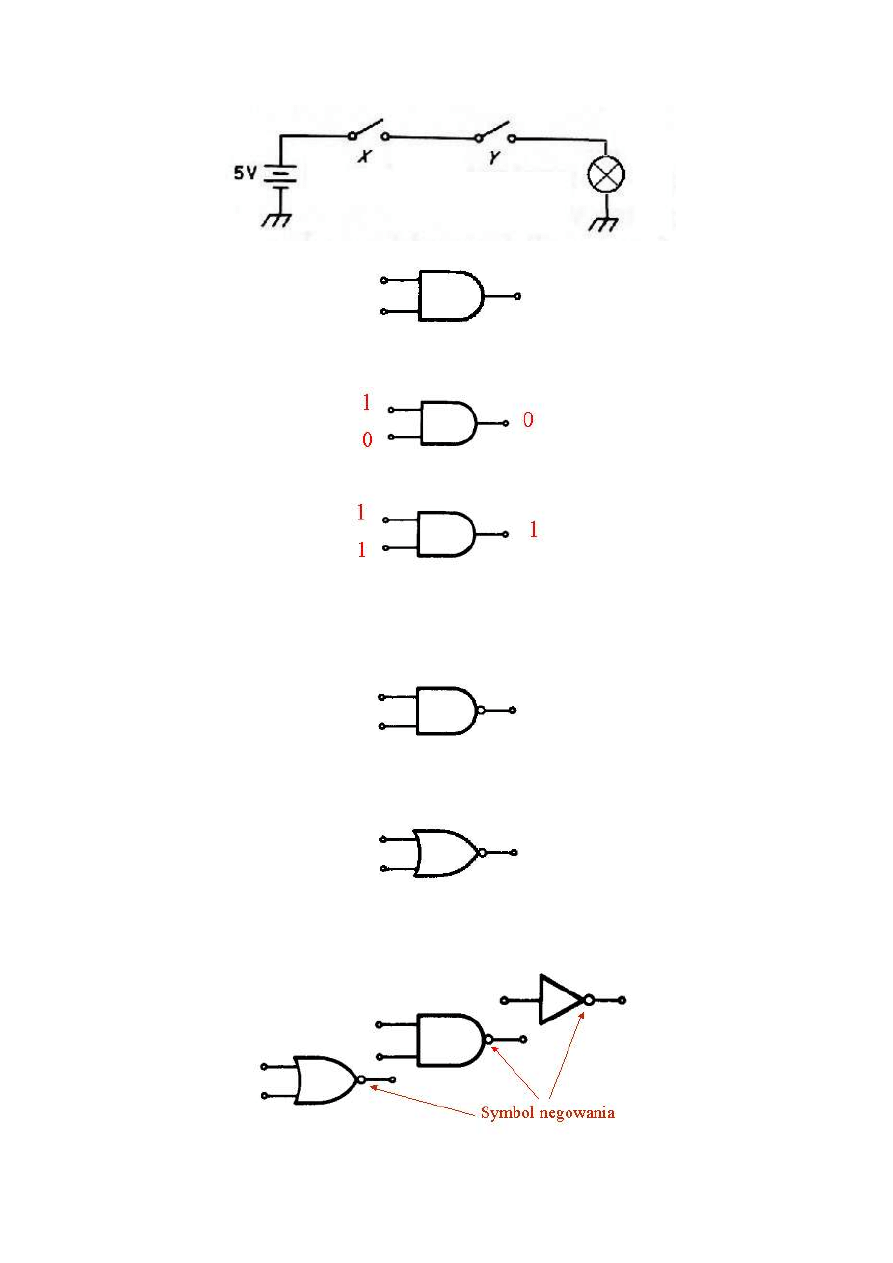
3

Iloczyn logiczny realizuje przedstawiony niżej układ

Symbol graficzny funktora AND

oraz przykłady działania tego funktora

Funktory NAND i NOR

NAND

≡

NOT AND

Symbol graficzny funktora NAND

NOR

≡

NOT OR

Symbol graficzny funktora NOR

4

ALTERNATYWA WYKLUCZAJĄCA

( ang. XOR, pol. ALBO, mat.

⊕

)

inaczej: różnica symetryczna, suma modulo 2

XOR

≡

eXclusive OR

Alternatywa wykluczająca dwu cyfr binarnych jest równa 0 wtedy i tylko wtedy, gdy
obydwie cyfry są jednakowe.

0

⊕

0 = 0

0

⊕

1 = 1

1

⊕

0 = 1

1

⊕

1 = 0

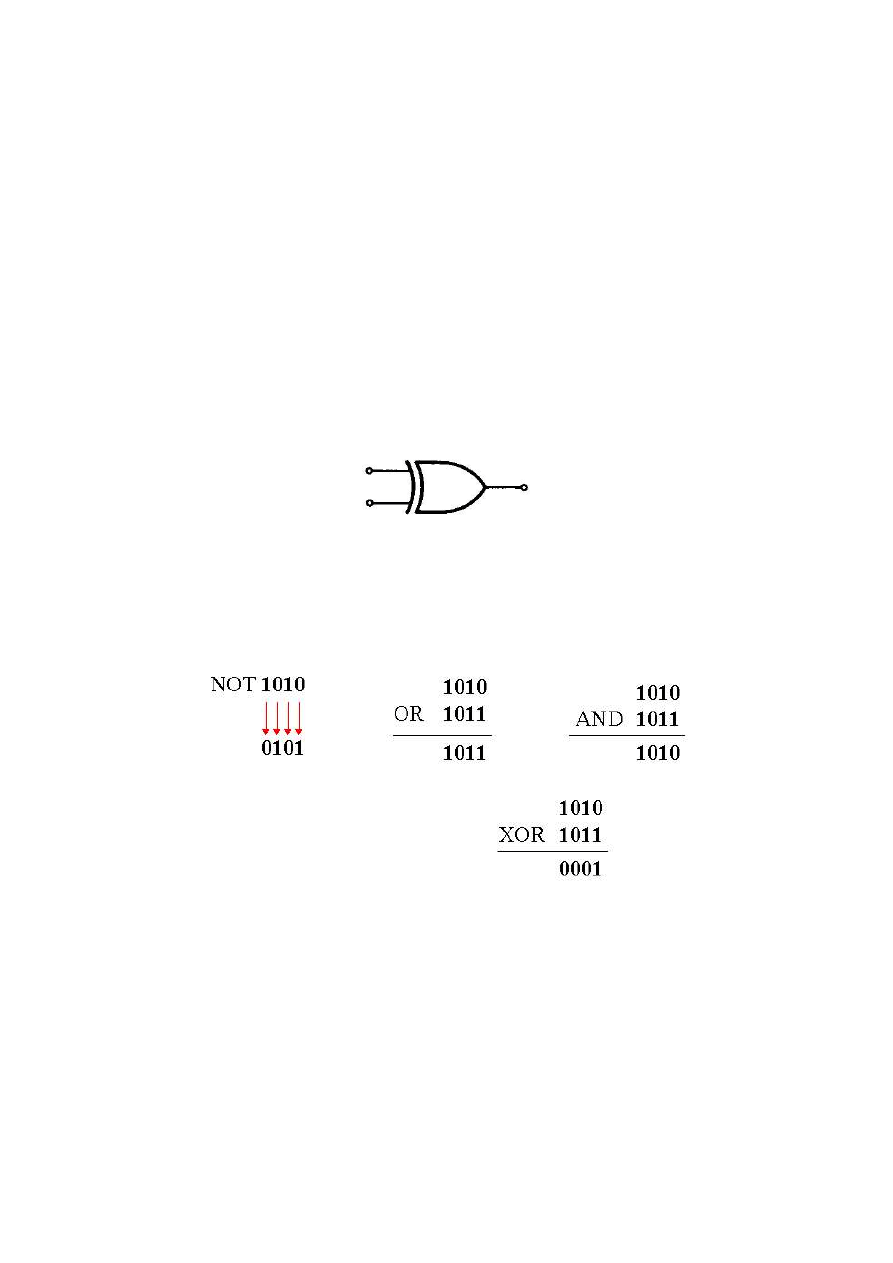
Symbol graficzny funktora XOR

2. Podstawowe operacje logiczne dla liczb binarnych

W operacjach logicznych liczba binarna jest traktowana jako zbiór pojedynczych cyfr.

Przykład:

3. Podstawowe operacje arytmetyczne dla liczb binarnych

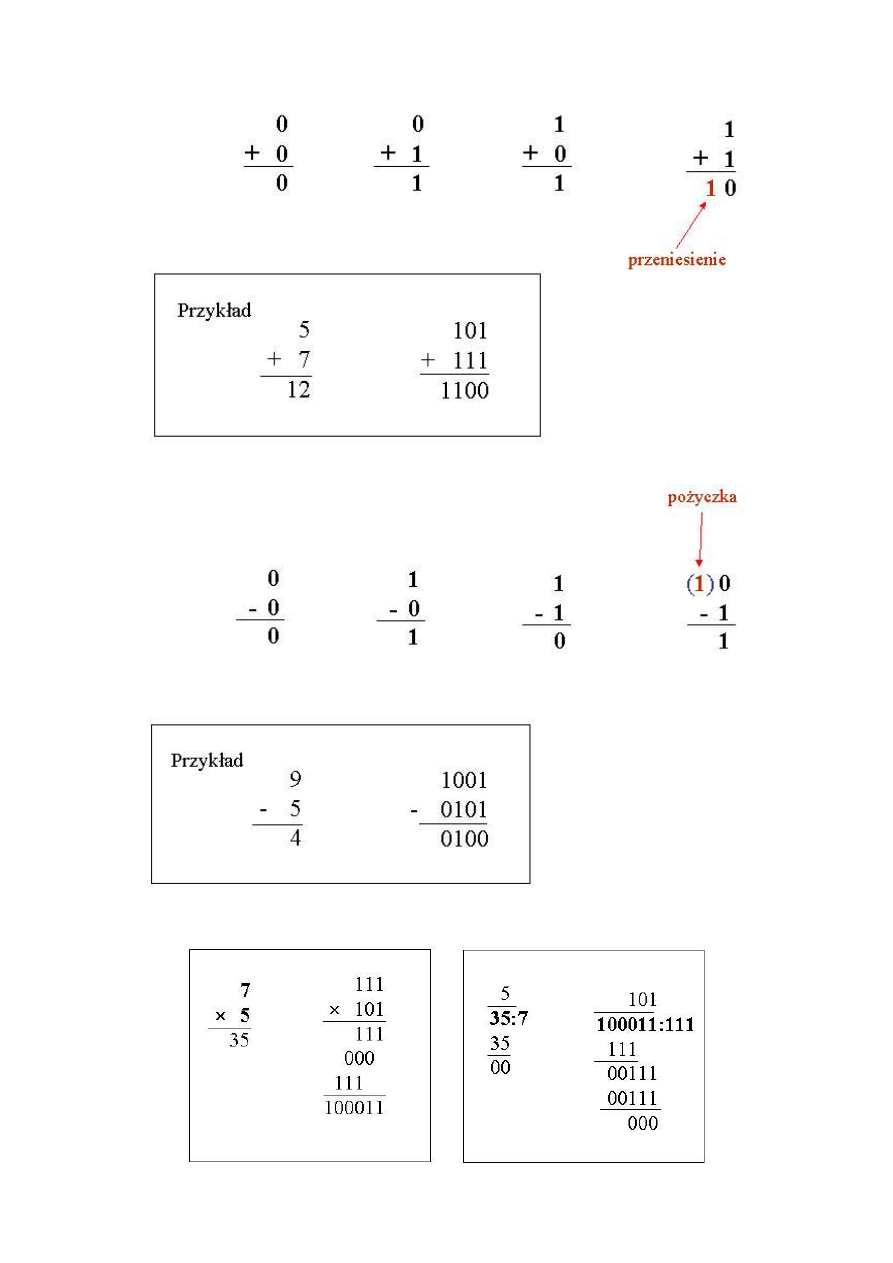
Dodawanie. Liczby dwójkowe dodajemy podobnie, jak dziesiętne. Gdy po dodaniu dwóch
cyfr uzyskuje się wartość niemożliwą do zapisania pojedynczą cyfrą, zachodzi tzw.
przeniesienie. Odejmujemy wtedy od wyniku podstawę systemu, a do następnej (starszej)
pozycji dodajemy 1.

W przypadku liczb dwójkowych przeniesienie wystąpi już wtedy, gdy wynik dodawania dwu
cyfr jest większy od 1

5

Reguły dodawania:

Odejmowanie. Reguły odejmowania:

Mnożenie i dzielenie. Przykłady

6

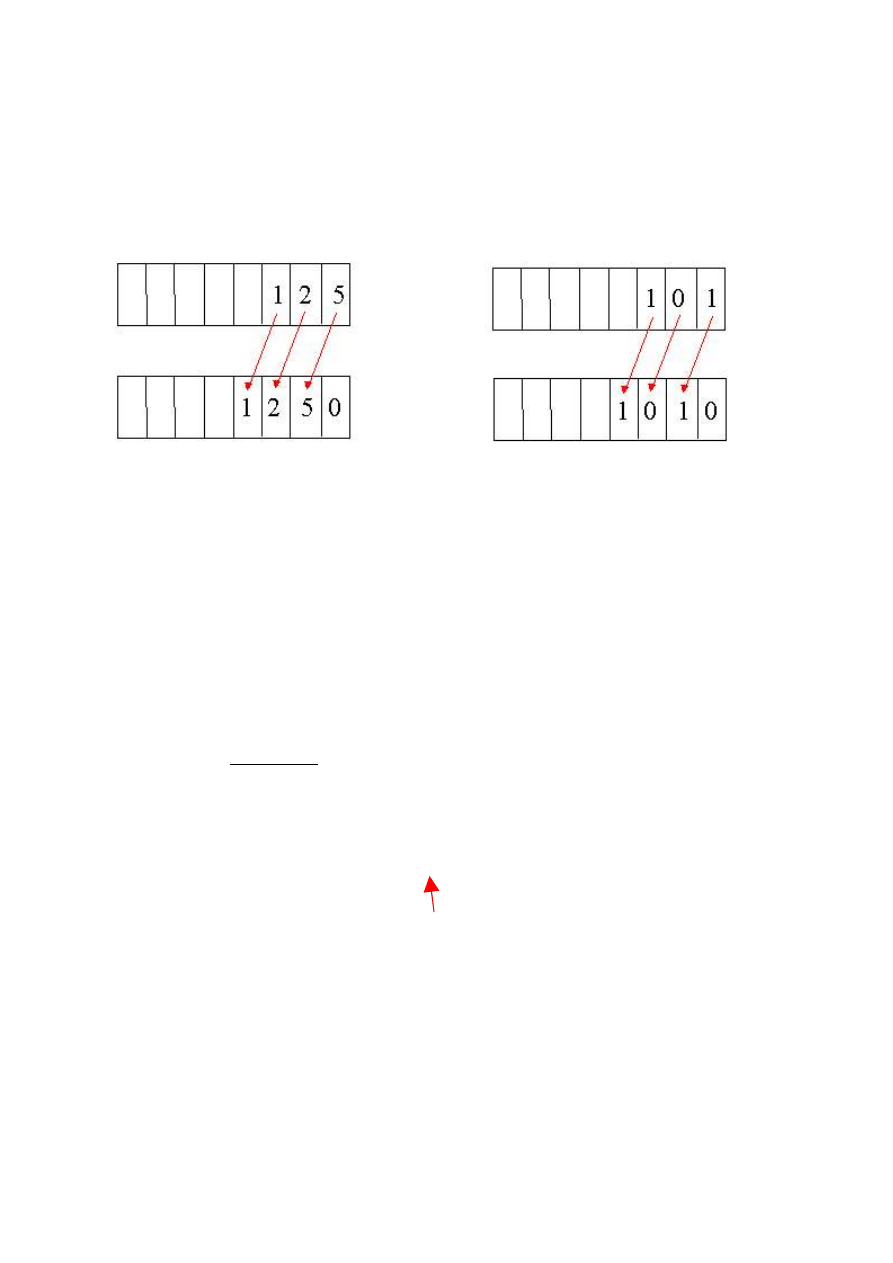
Mnożenie przez 2 w układzie binarnym

→

przesunięcie liczby o jedną pozycję w lewo i

dopisanie zera z prawej strony liczby

Dzielenie przez 2 w układzie binarnym

→

przesunięcie liczby o jedną pozycję w prawo i

odrzucenie ostatniej cyfry (jeśli liczba parzysta to tą cyfrą jest zero)

Przykład: mnożenie przez 10 w układzie dziesiętnym i przez 2 w dwójkowym

Podobnie mnożenie i dzielenie w układzie dwójkowym przez 4 i inne potęgi dwójki –
przesunięcie w lewo lub w prawo o odpowiednią liczbę pozycji.

4. Liczby ujemne

Przedstawiony wyżej system binarny, określany mianem naturalnego kodu binarnego (NKB
lub NB) pozwala na zapis tylko liczb dodatnich i zera. Aby możliwe było zapisywanie liczb
ujemnych, konieczna jest modyfikacja zapisu w taki sposób, żeby ciąg zer i jedynek zawierał
informacją zarówno o wartości bezwzględnej, jak i o znaku liczby.

4.1. System znak-moduł (ZM)

Pierwszy bit jest bitem znaku (nie przypisuje mu się wagi), 0 oznacza +, 1 oznacza -

np. dla liczb czterobitowych:

5

0101

-5 1101

bit znaku

Niestety, przyjęcie takiego systemu zapisu liczb komplikuje operacje binarnego dodawania i
odejmowania, które są wykonywane przez procesor.

Zero nie jest reprezentowane jednoznacznie, mamy bowiem np.

0000 +0
1000 -0

(podwójna reprezentacja zera)

7

4.2. System uzupełnieniowy do 2 (U2)

Znak liczby nie jest tu oddzielony od jej wartości , a „ujemność” liczby jest wbudowana w
metodę zapisu. Najstarsza waga jest ujemna, np. dla liczb czterobitowych mamy wagi:

-2

3

2

2

2

1

2

0

-8 4 2 1

czyli dla liczb czterobitowych:

0000 0
0001 1
......................
0111 7
1000 -8 (tzn. -8+0)
1001 -7 (tzn. -8+1)
1010 -6 (tzn. -8+2)
1011 -5 (tzn. -8+3)
......................
1111 -1 (tzn. -8+7)

Zalety:

- Każda liczba dodatnia zaczyna się od zera, a ujemna od jedynki
- Tylko jedno zero
- Łatwa zmiana znaku liczby
- Operacje arytmetyczne jak dla liczb NB

Wady:

- Porządek kodów nie jest zgodny z porządkiem liczb

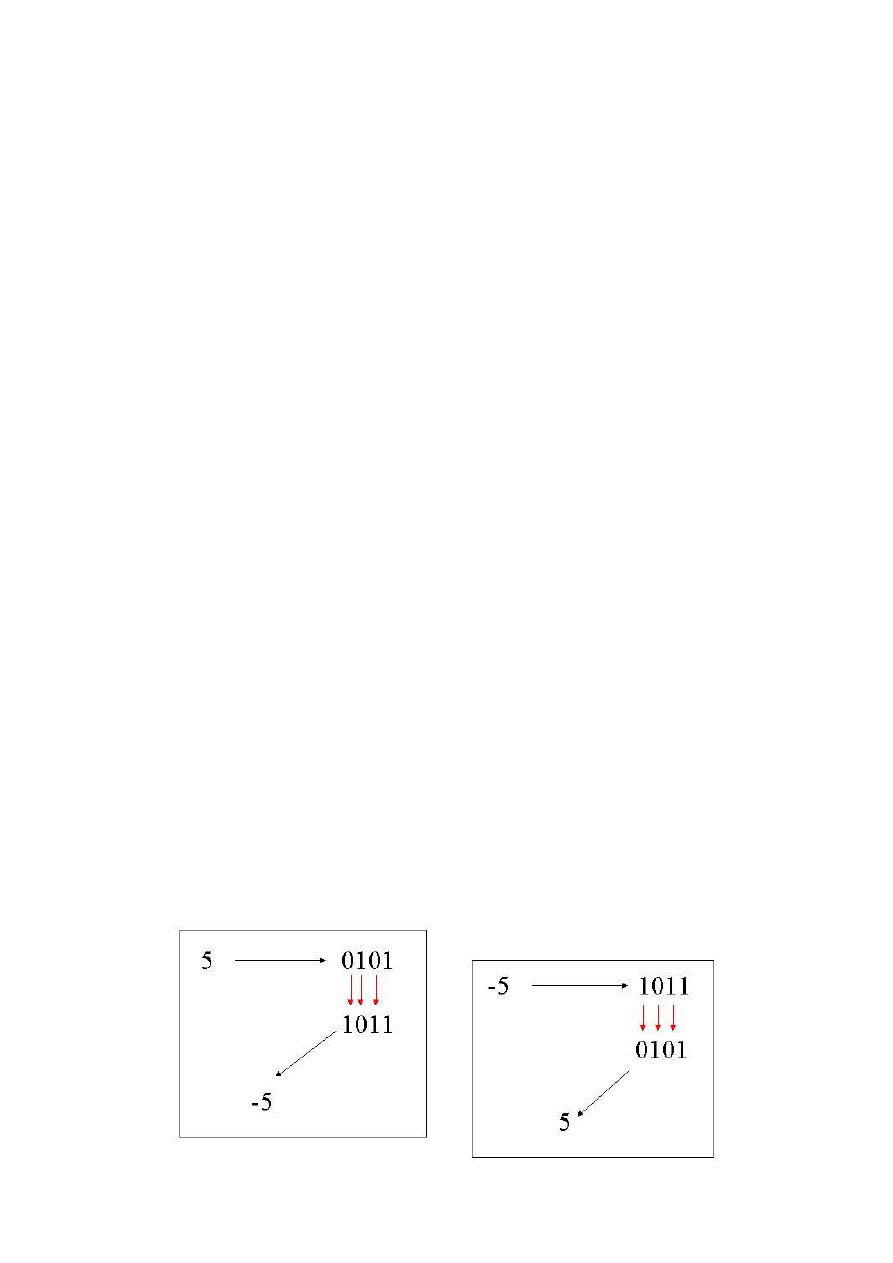
4.2.1. Zmiana znaku liczby w kodzie U2

Aby zmienić znak liczby, należy zamienić wszystkie cyfry na przeciwne, czyli 0 na 1 oraz 1
na 0 (w kierunku od lewej do prawej) za wyjątkiem najmniej znaczącej jedynki i zer za tą
jedynką.

Przykład dla liczb czterobitowych (zamiana 5 na –5 i odwrotnie)

8

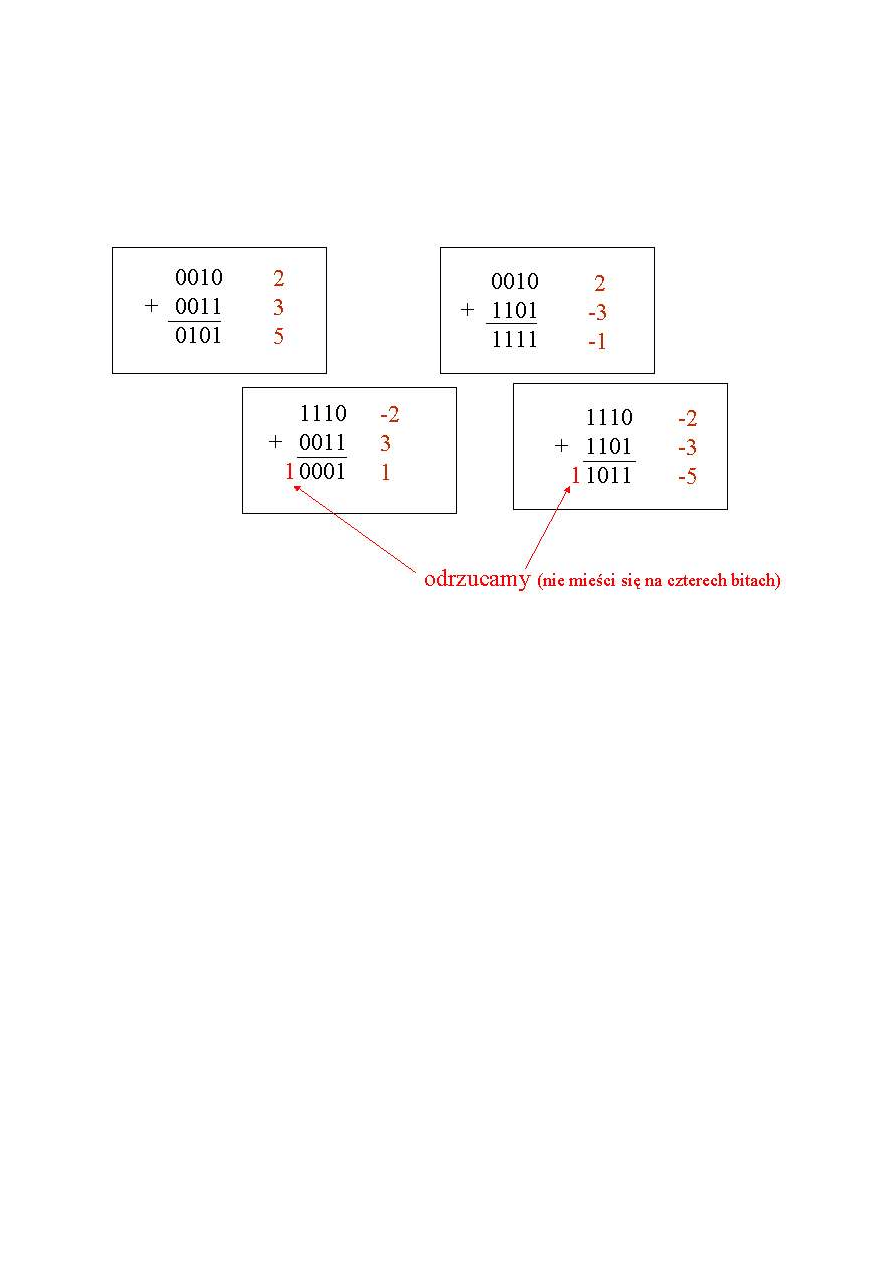
4.2.2. Dodawanie i odejmowanie liczb w kodzie U2

Dodawanie - tak samo, jak w kodzie naturalnym
Odejmowanie - dodanie z przeciwnym znakiem

Przykłady dla liczb czterobitowych

4.3. Kodowanie w systemie +N

System ten jest wykorzystywany w reprezentacjach zmiennopozycyjnych (np. IEEE754).
Porządek kodów jest zgodny z porządkiem liczb.

Przyjmuje się, że 00...000 reprezentuje liczbę najmniejszą, np. dla liczb k-bitowych

111...111 2

k-1

................
................
000...000 -2

k-1

+1

Dla liczb 8-bitowych

11111111-> 128
11111110 -> 127
................
10000000 -> 1
01111111 -> 0
................
00000001 -> -126
00000000 -> -127

9

Dla liczb k-bitowych N=2

k-1

- 1

Wartością liczby całkowitej jest

X

+N

= X

NB

– N

Przykład. Liczba 5 zapisana na 8 bitach w kodzie +N

5. Rozszerzenie nieskończone

Rozszerzenie nieskończone to rozszerzenie kodu liczby na większą liczbę pozycji z
zachowaniem oryginalnej wartości

Kod naturalny (NB)

→

wiodące zera są nieznaczące

Przykład:

5 zapisane na 4 pozycjach

0101

po rozszerzeniu na 8 pozycji

00000101

Kod U2

→

wiodące zera (dla liczb dodatnich) są nieznaczące

wiodące jedynki (dla liczb ujemnych) są nieznaczące

Przykład:

-5 zapisane na 4 pozycjach

1011

po rozszerzeniu na 8 pozycji

11111011

6. Cyfrowe układy arytmetyczne – przykład

Odpowiednie połączenie funktorów logicznych pozwala wykonywać operacje arytmetyczne.

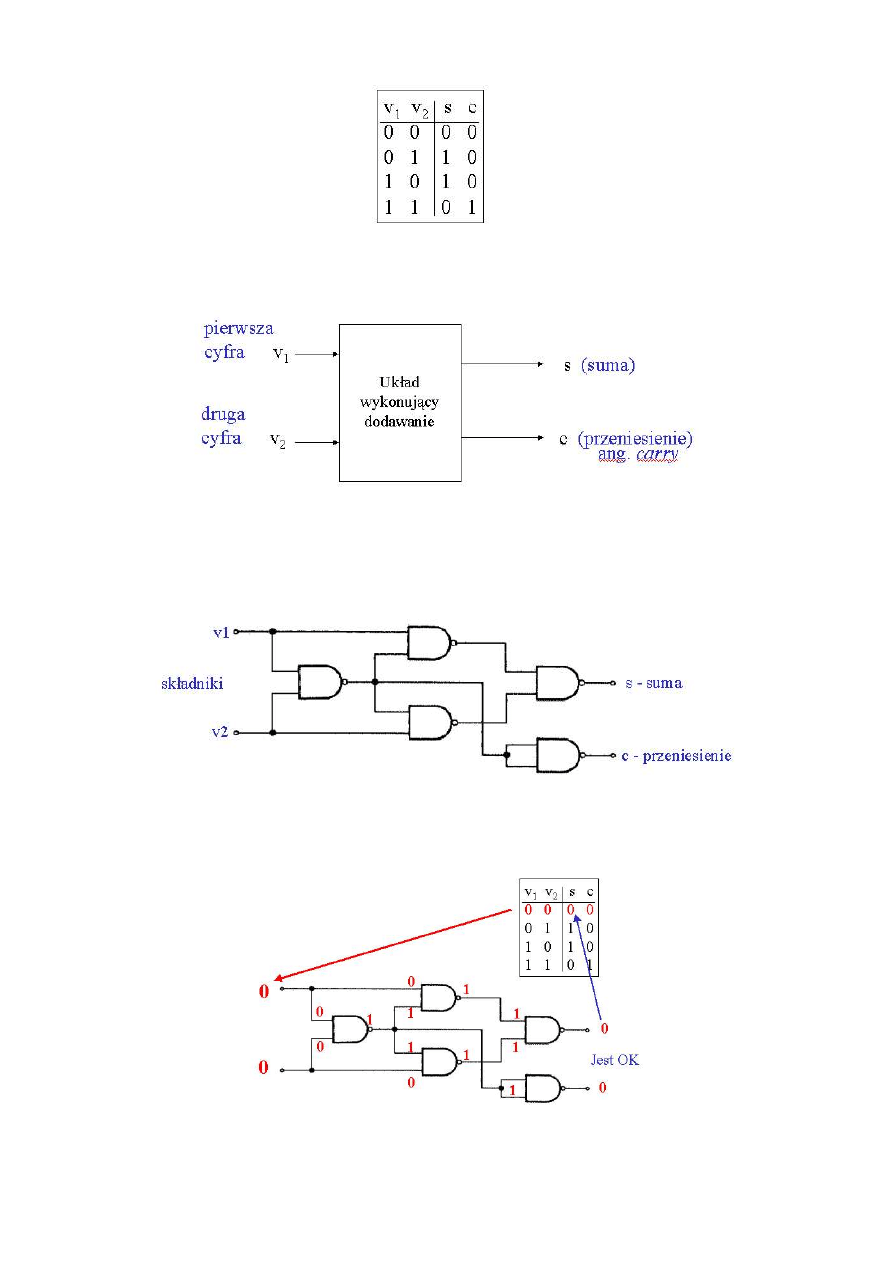
Reguły dodawania dwu cyfr binarnych w formie tabelki (v

1

, v

2

– dodawane cyfry, s – ich

suma, c – przeniesienie),

10

Urządzenie wykonujące dodawanie dwu cyfr binarnych zgodnie z ww. tabelką nazywa się
półsumatorem

Półsumator dodaje dwie cyfry dwójkowe (v

1

, v

2

), podając ich sumę (s) i przeniesienie (c).

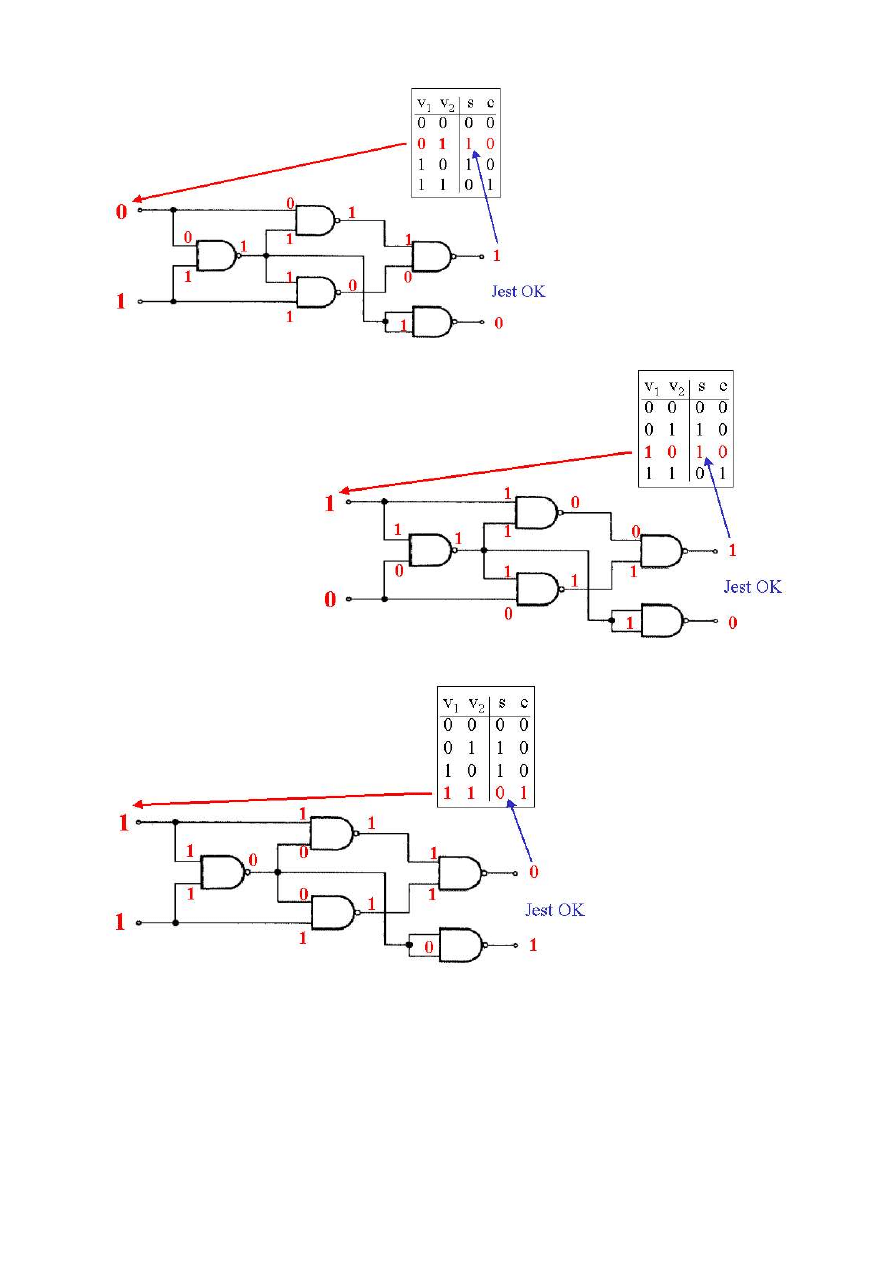
Przykład półsumatora zbudowanego z pięciu funktorów NAND

oraz sprawdzenie jego działania dla wszystkich możliwych wariantów danych wejściowych

11