E. Michlowicz: IMW – Modelowanie mechanizmu jazdy

1

WYKŁAD 5

MODELOWANIE MECHANIZMU JAZDY

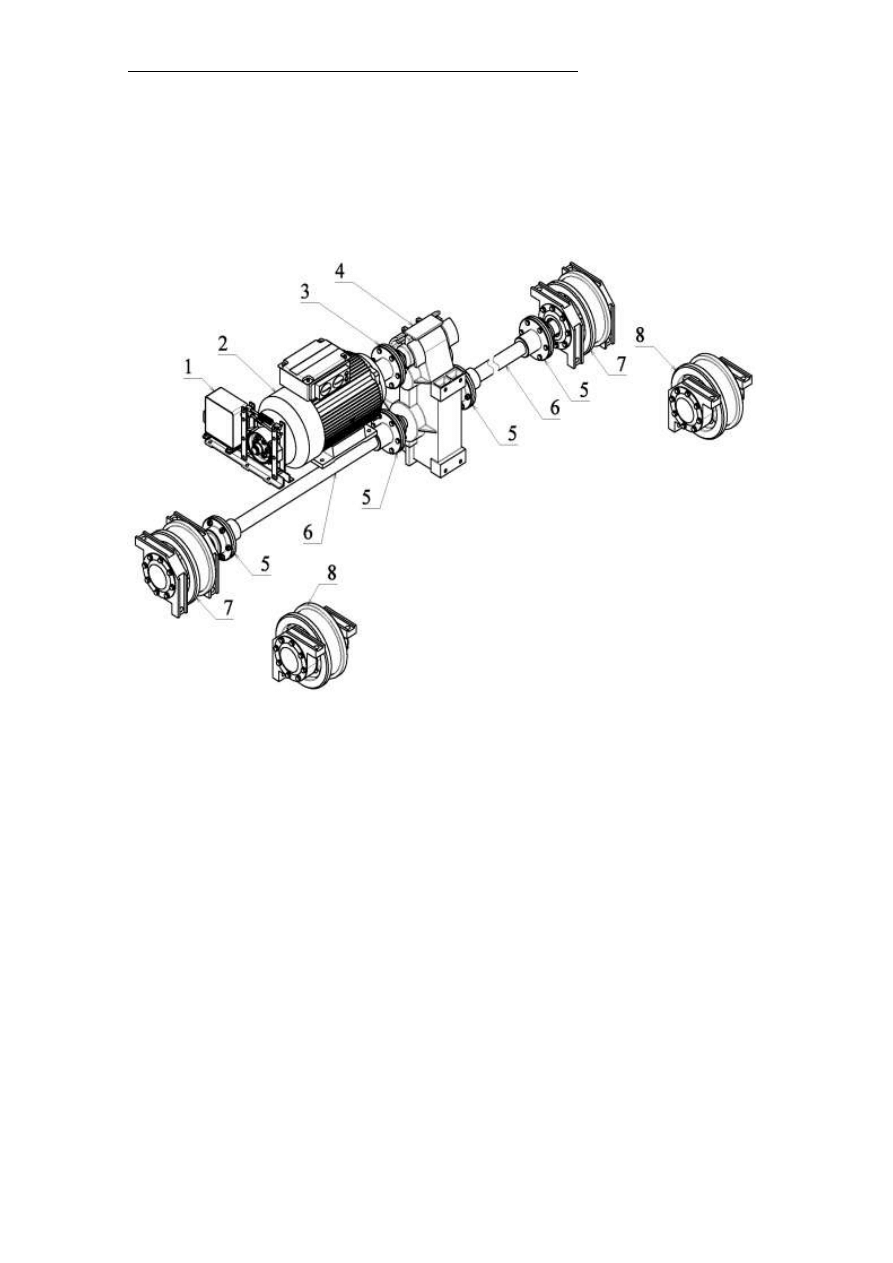
Mechanizm jazdy –

1 – hamulec,
2 – silnik,
3 – sprzęgło zębate dwustronne,
4 – przekładnia zębata,
5 - sprzęgło zębate dwustronne,
6 - sprzęgło zębate jednostronne,
7 – wał wolnobieżny,
8 – zestaw kołowy napędzany,
9 – zestaw kołowy nienapędzany.

1. Stany nieustalone w ruchu mechanizmu jazdy

Model mechanizmu jazdy najlepiej sprowadzić do modelu obrotowego,

ponieważ elementy układu poruszają się ruchem obrotowym zarówno od
strony napędowej (wał silnika, sprzęgło hamulcowe, koła zębate), jak i od
strony napędzanej (sprzęgła zębate, koła jezdne). Zobrazowane jest to na
rysunku 1.

E. Michlowicz: IMW – Modelowanie mechanizmu jazdy

2

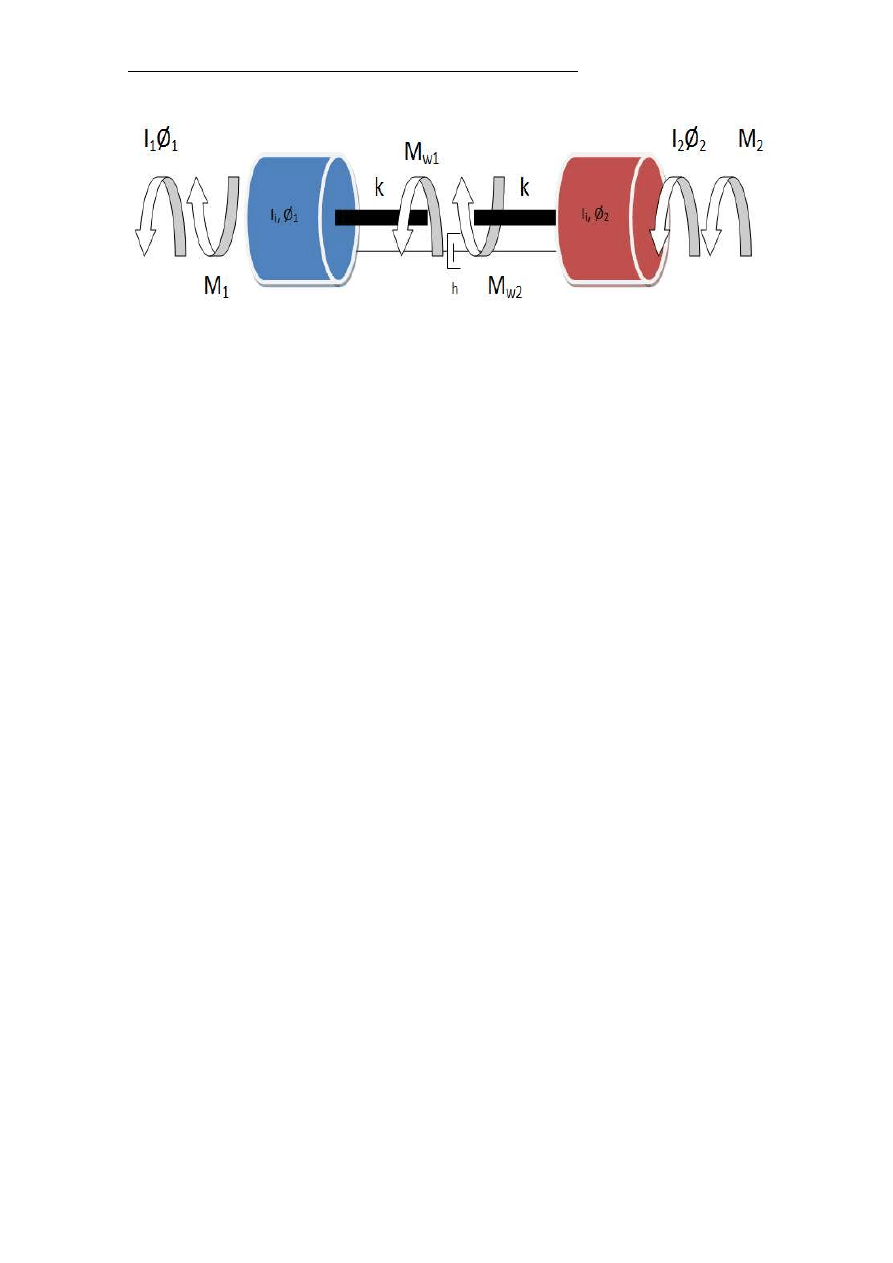
Rys. 1. Model matematyczny – mechanizmu jazdy

I

ZR1

– moment bezwładności zredukowany na wał wolnobieżny przekładni,

zastępujący moment bezwładności wirnika silnika ( I

S

), sprzęgła ( I

SP

), bębna

hamulca( I

H

), kół zębatych, sprzęgieł przy przekładni ( I

SP1

);

I

ZR2

– moment bezwładności zredukowany na wał wolnobieżny przekładni,

zastępujący moment bezwładności kół jezdnych ( I

K

), i sprzęgieł ( I

SP2

);

M

1

– moment siły na wale wolnoobrotowym przekładni, pochodzący od

momentu silnika ( M );
M

2

– moment siły na wale wolnoobrotowym przekładni, pochodzący od oporów

jazdy wózka ( W );
k – zastępczy współczynnik sztywności wolnoobrotowych wałów napędzających

koła jezdne;

h – zastępczy współczynnik tłumienia w wałach napędzających koła jezdne.

2. Równania ruchu

2.1. Rozruch

Mechanizm jazdy pokonuje siłę oporów jazdy W, która wynika z oporów

toczenia kół jezdnych wózka po szynach oraz oporów w łożyskach kół. Koła
jezdne obciążone są ciężarem masy m

2

, która obciąża mechanizm podnoszenia

oraz masy wózka m

w

. Zakładamy, że w fazie rozruchu bezwładność ładunku

zawieszonego na haku, a także jego wahania mają pomijalnie mały wpływ.

W mechanizmie jazdy podobnie jak w mechanizmie podnoszenia występują

trzy fazy ruchu. W fazie pierwszej występuje kasowanie luzów (głównie
międzyzębnych w przekładni zębatej).

W tej fazie ruchu masa m

1

obraca się bez oporu ze strony więzów.

Przebyta droga jest równa wielkości luzu w elementach więzów. Po niej
zaczyna się faza druga, którą jest napinanie więzów. Trwa ona do chwili
pokonania oporu momentu obciążenia przez moment skręcenia wału M

w

= k(φ

1

– φ

2

).

E. Michlowicz: IMW – Modelowanie mechanizmu jazdy

3

Ostatnia faza ruchu to ruch obu mas opisany układem równań:

(2.1)

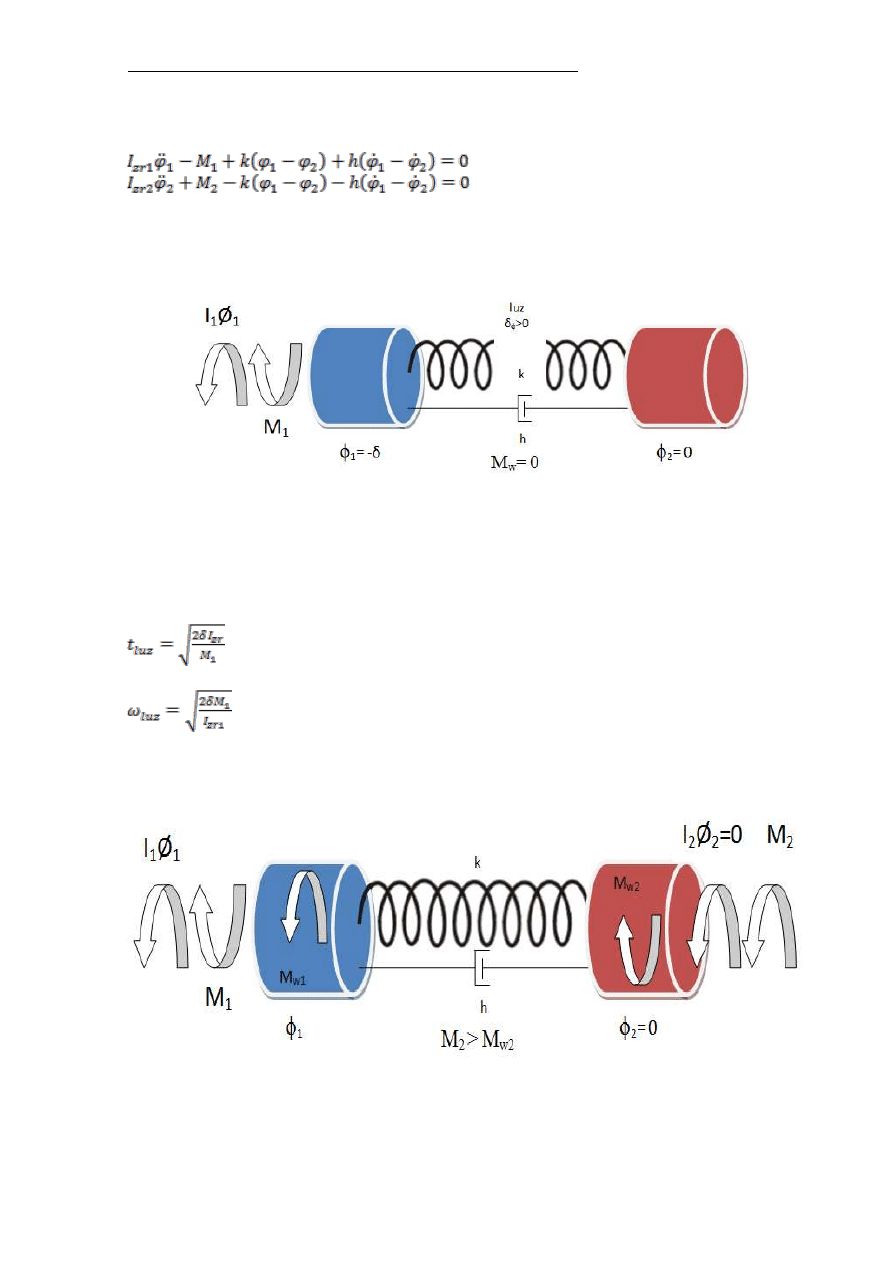
a) faza pierwsza

Rys. 2. Schemat sił działających w mechanizmie jazdy podczas rozruchu –

faza pierwsza

- kasowanie luzów (ω

1

=0, φ

1

=-δ, ω

2

=0, φ

2

=0 )

(2.2)

(2.3)

b) faza druga

Rys. 3. Schemat sił działających w mechanizmie jazdy podczas rozruchu –

faza druga

E. Michlowicz: IMW – Modelowanie mechanizmu jazdy

4

- napinanie więzów (φ

1

= , ω

1

= ω

luz

)

(2.4)

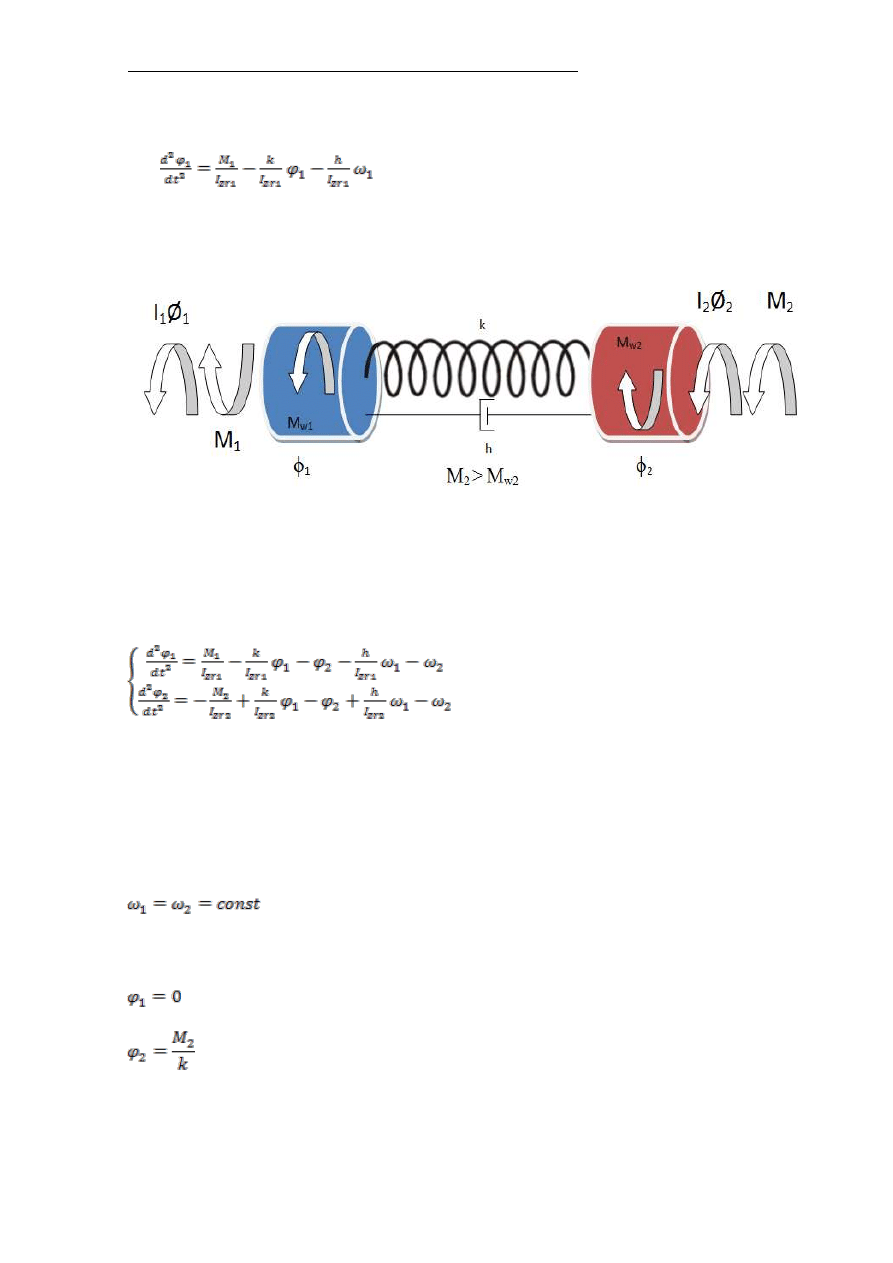
c) faza trzecia

Rys.4. Schemat sił działających w mechanizmie jazdy podczas rozruchu –

faza trzecia

- faza, w której obie masy są w ruchu (φ

1

= φ

1

(t

*

), ω

1

= ω(t

*

))

t

*

- czas napinania więzów

(2.5)

2.2. Hamowanie

W chwili rozpoczęcia hamowania ruch jest ustalony tj. prędkości obrotowe

obu końców wału napędowego są stałe i jednakowe:

a więź jest napięta momentem oporu jazdy:

W pierwszej fazie hamowania następuje kasowanie luzów. Aby proces

ten był łagodniejszy pomiędzy chwilą wyłączenia silnika i włączenia hamulca

E. Michlowicz: IMW – Modelowanie mechanizmu jazdy

5

stosuje się krótką przerwę, aby nastąpiło zwolnienie więzów. Pozwala to
uniknąć negatywnych skutków kasowania luzów przy pełnej wartości momentu
hamowania.

Druga faza zaczyna się od skasowania luzów, a koniec następuję w

momencie zatrzymania się masy m

1

. Występuje tu ruch opóźniony obu mas,

który można opisać układem równań różniczkowych.

Po zatrzymaniu masy m

1

rozpoczyna się faza trzecia, jest nią ruch masy

m

2

(kół wózka) hamowany oporami ruchu, w trakcie tej fazy następuje

zwolnienie więzów.

Pierwsza faza obie masy w ruchu (ω

1

= ω

2

= ω

nom

= const , φ

1

= 0, φ

2

= M

2

/k)

(2.6)

Druga faza jedna masa w ruchu (φ

2

= φ

2

(t

*

), ω

2

= ω

2

(t

*

))

t

*

- czas, po którym zatrzymała się masa 1

(2.7)

3. Parametry do identyfikacji

Z rozważań zawartych w punktach 1-2 wynika, że każdorazowo do
pełnego opisu równań ruch należy wyznaczyć sześć parametrów:

k – współczynnik sprężystości więzi (np. wału wolnoobrotowego),
h – współczynnik tłumienia więzi,
I

zr1

- moment bezwładności zredukowany na wał wolnoobrotowy –

od strony silnika,

I

zr2

– moment bezwładności zredukowany na wał – od strony kół

jezdnych wraz z przemieszczaną masą (wózek i ciężar),

M

1

lub M

h

– obciążenie czynne – od silnika lub hamulca,

M

2

– obciążenie bierne – od oporów jazdy (ciężar i wózek).

Ważne uwagi:

- przy redukcji sił lub momentów sił korzystamy z zasady zachowania
mocy w układzie (z uwzględnieniem odpowiedniej sprawności),

- przy redukcji mas lub momentów bezwładności korzystamy z zasady
zachowania energii badanego układu.