
C fr
C fr
C fr
C fr
Cyfrowe
Cyfrowe
Cyfrowe
Cyfrowe
yy
układy
układy
yy
układy
układy
układy
układy
k bi
j
k bi
j
układy
układy
k bi
j
k bi
j
kombinacyjne
kombinacyjne
kombinacyjne
kombinacyjne
6 marca 2011
Wojciech Kucewicz
2
yj
yj
yj
yj
Cyfrowe
Cyfrowe układy
układy kombinacyjne
kombinacyjne
Cyfrowe
Cyfrowe układy
układy kombinacyjne
kombinacyjne
X1
X1
X2
X2
X3
X3
Xn
Xn
Y1
Y1
Y2
Y2
Y3
Y3
Yn
Yn
Xn
Xn
Układy kombinacyjne charakteryzuje funkcja, która każdemu stanowi
Układy kombinacyjne charakteryzuje funkcja, która każdemu stanowi
wejściowemu X
wejściowemu X
ii
∈
∈
X
X jednoznacznie przyporządkowuje stan 0 lub 1 sygnału
jednoznacznie przyporządkowuje stan 0 lub 1 sygnału
jj
ii
j
p yp
j
yg
j
p yp
j
yg
wyjściowego
wyjściowego yy
ii
6 marca 2011
Wojciech Kucewicz
3

Tranzystor MOS
Tranzystor MOS
y
jako
y
jako
jako
przełącznik
jako
przełącznik
przełącznik
przełącznik
6 marca 2011
Wojciech Kucewicz
4
MOS jak przełącznik
MOS jak przełącznik
MOS jak przełącznik
MOS jak przełącznik
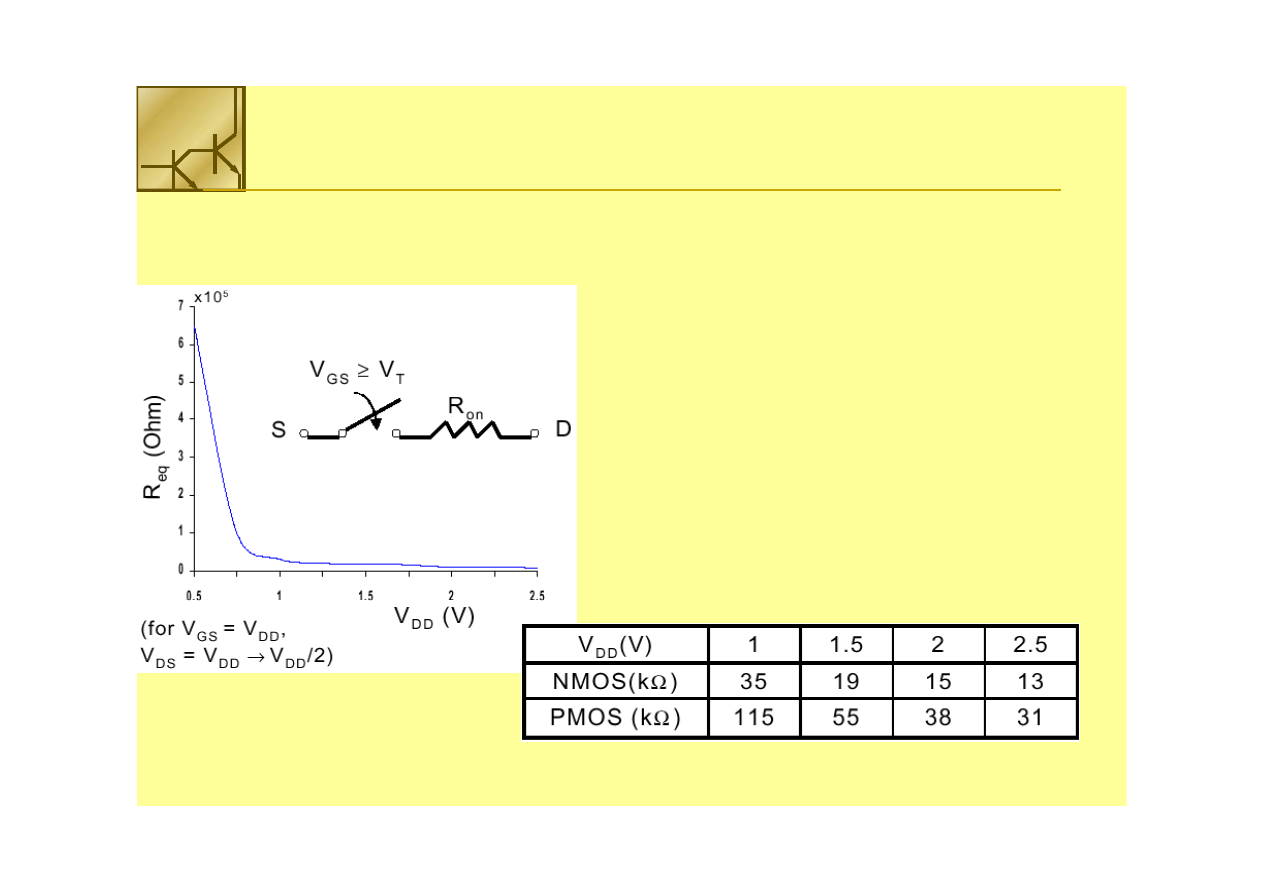
Tranzystor MOS może być traktowany jako przełącznik z nieskończoną
Tranzystor MOS może być traktowany jako przełącznik z nieskończoną
rezystancją w stanie wyłączonym i rezystancją
rezystancją w stanie wyłączonym i rezystancją RR
on
on
w stanie włączonym
w stanie włączonym
Rezystancja jest odwrotnie
Rezystancja jest odwrotnie
proporcjonalna do stosunku
proporcjonalna do stosunku W/L
W/L
((podwojenie
podwojenie W
W zmniejsza o połowę
zmniejsza o połowę RR
on
on
((p
j
p
j
j
p
ę
j
p
ę
on
on
))
Dla
DlaVV
DD
DD
>>V
>>V
T
T
++VV
DSat
DSat
/2, R
/2, R
on
on
nie zależy
nie zależy
od
od VV
DD
DD
od
od VV
DD
DD
Gdy
Gdy VV
DD
DD
obniży się do
obniży się do VV
T
T
,, RR
on
on
gwałtownie rośnie
gwałtownie rośnie
6 marca 2011
Wojciech Kucewicz
5
MOS transistor, 0.25um, W/L = 1.5, V
MOS transistor, 0.25um, W/L = 1.5, V
T
T
=
= --0.4V
0.4V
NMOS jak przełącznik
NMOS jak przełącznik
NMOS jak przełącznik
NMOS jak przełącznik
V
V
DD
DD
V
V
DD
DD
V
V
SS
SS
V
V
SS
SS
NMOS
NMOS
NMOS
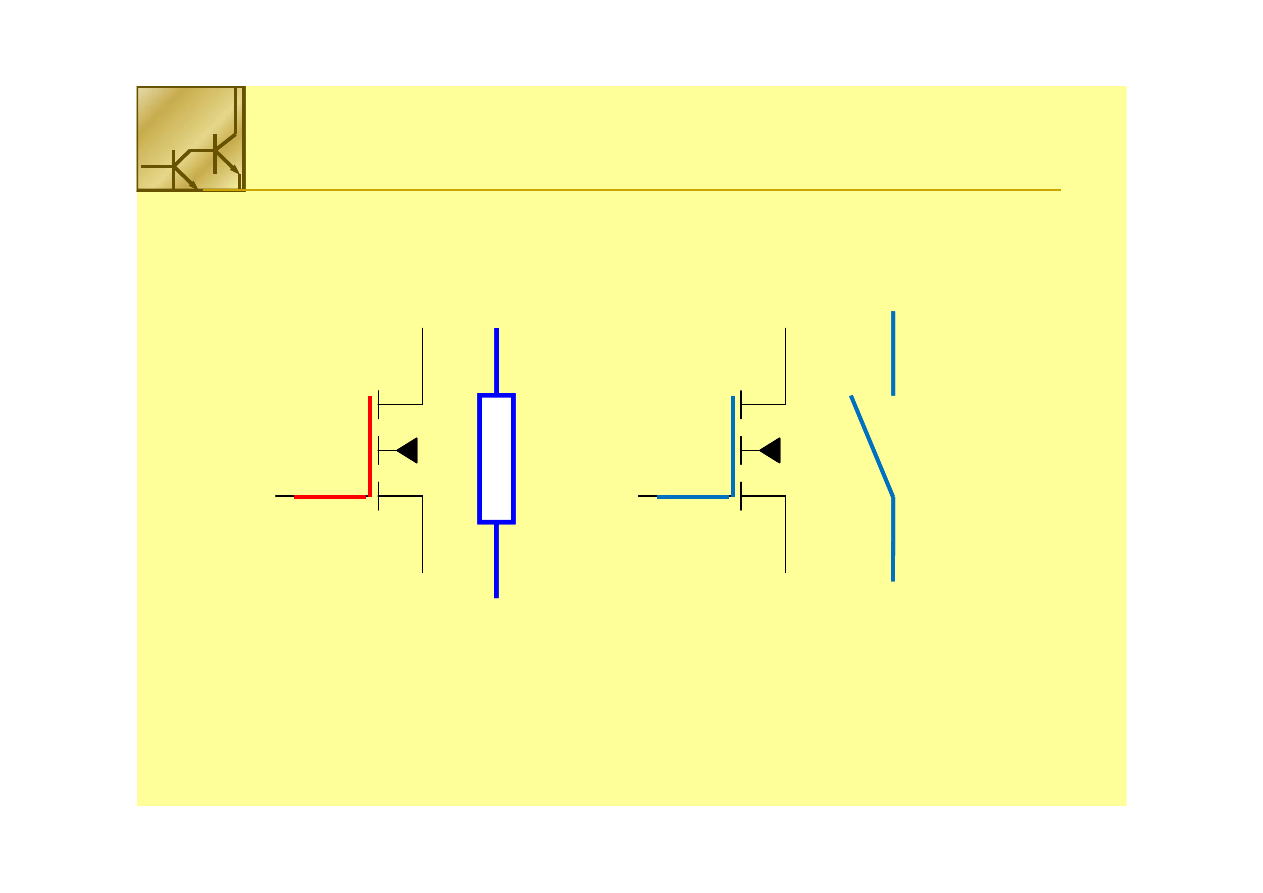
Tranzystor NMOS przewodzi, gdy na
bramkę przyłoży się wysokie napięcie
(> V
T
)
Tranzystor NMOS nie przewodzi, gdy
na bramkę przyłoży się niskie napięcie
(< V
T
)
6 marca 2011
Wojciech Kucewicz
6
NMOS jak przełącznik
NMOS jak przełącznik
NMOS jak przełącznik
NMOS jak przełącznik
Logiczny sygnał wejściowy
V
DS
Przełącznik
V
GS
Przełącznik
V
GS
Logiczny sygnał wyjściowy
V
sorce
Tranzystor
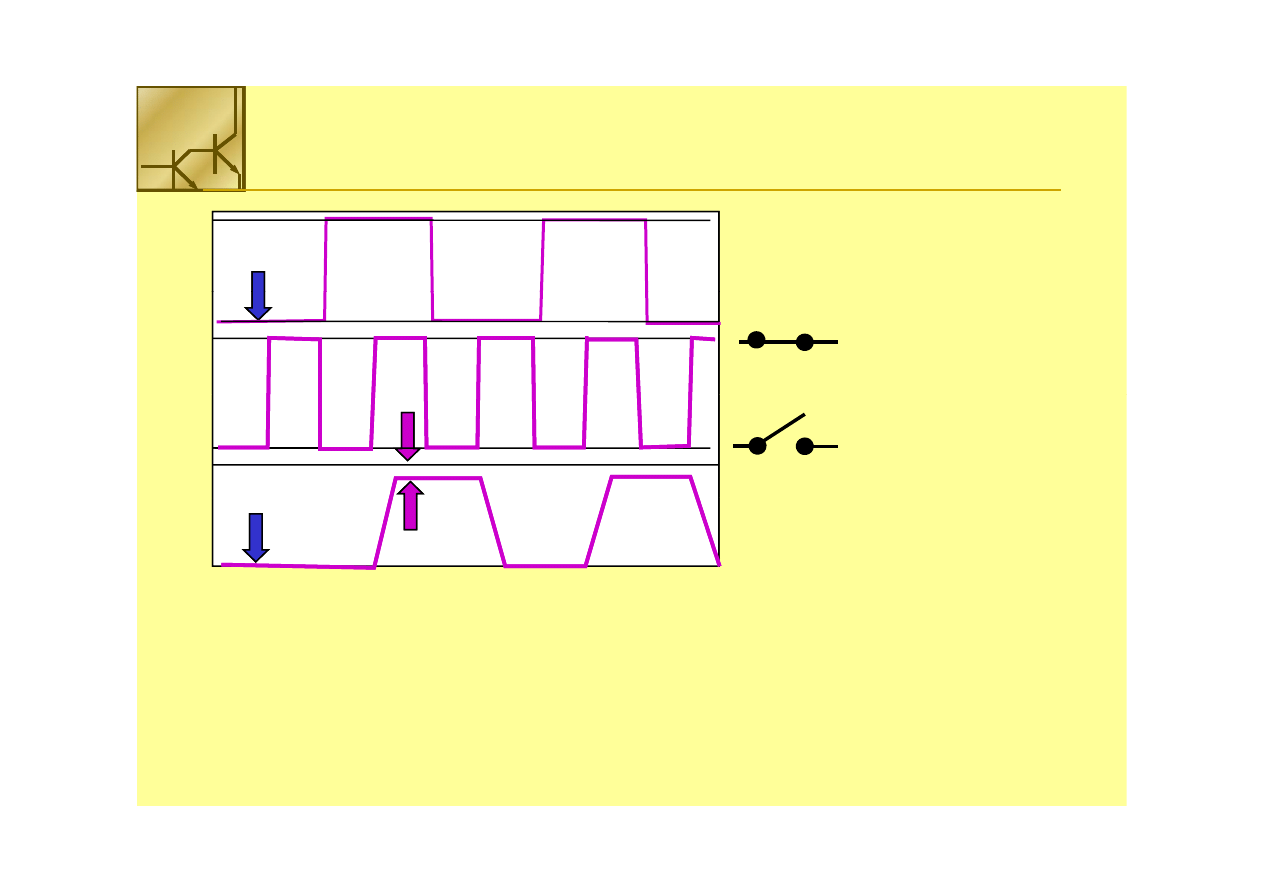
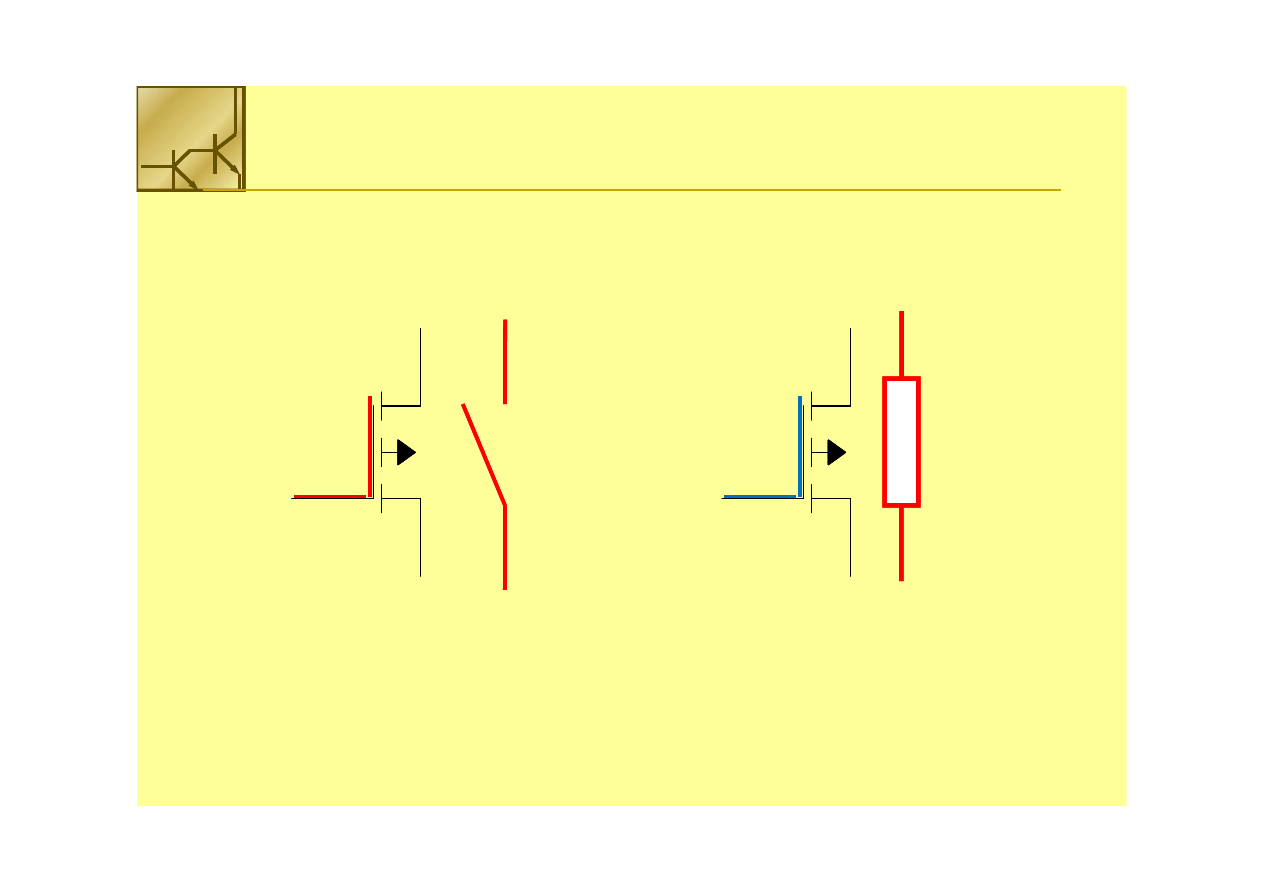
Tranzystor NMOS
NMOS dobrze
dobrze przewodzi
przewodzi niskie
niskie napięcie
napięcie ii gorzej
gorzej wysokie
wysokie
napięcie
napięcie ((V
V
DD
DD
--V
V
T
T
))
6 marca 2011
Wojciech Kucewicz
7
Tranzystor
Tranzystor NMOS
NMOS źle
źle przewodzi
przewodzi logiczną
logiczną jedynkę
jedynkę
PMOS jak przełącznik
PMOS jak przełącznik
PMOS jak przełącznik
PMOS jak przełącznik
V
V
DD
DD
V
V
DD
DD
V
V
SS
SS
V
V
SS
SS
PMOS
PMOS
PMOS
PMOS
PMOS
PMOS
Tranzystor PMOS nie przewodzi, gdy
na bramkę przyłoży się wysokie
napięcie
Tranzystor PMOS przewodzi, gdy na
bramkę przyłoży się niskie napięcie
6 marca 2011
Wojciech Kucewicz
8
PMOS jak przełącznik
PMOS jak przełącznik
PMOS jak przełącznik
PMOS jak przełącznik
Logiczny sygnał wejściowy
V
DS
Przełącznik
V
GS
Przełącznik
V
GS
Logiczny sygnał wyjściowy
V
sorce
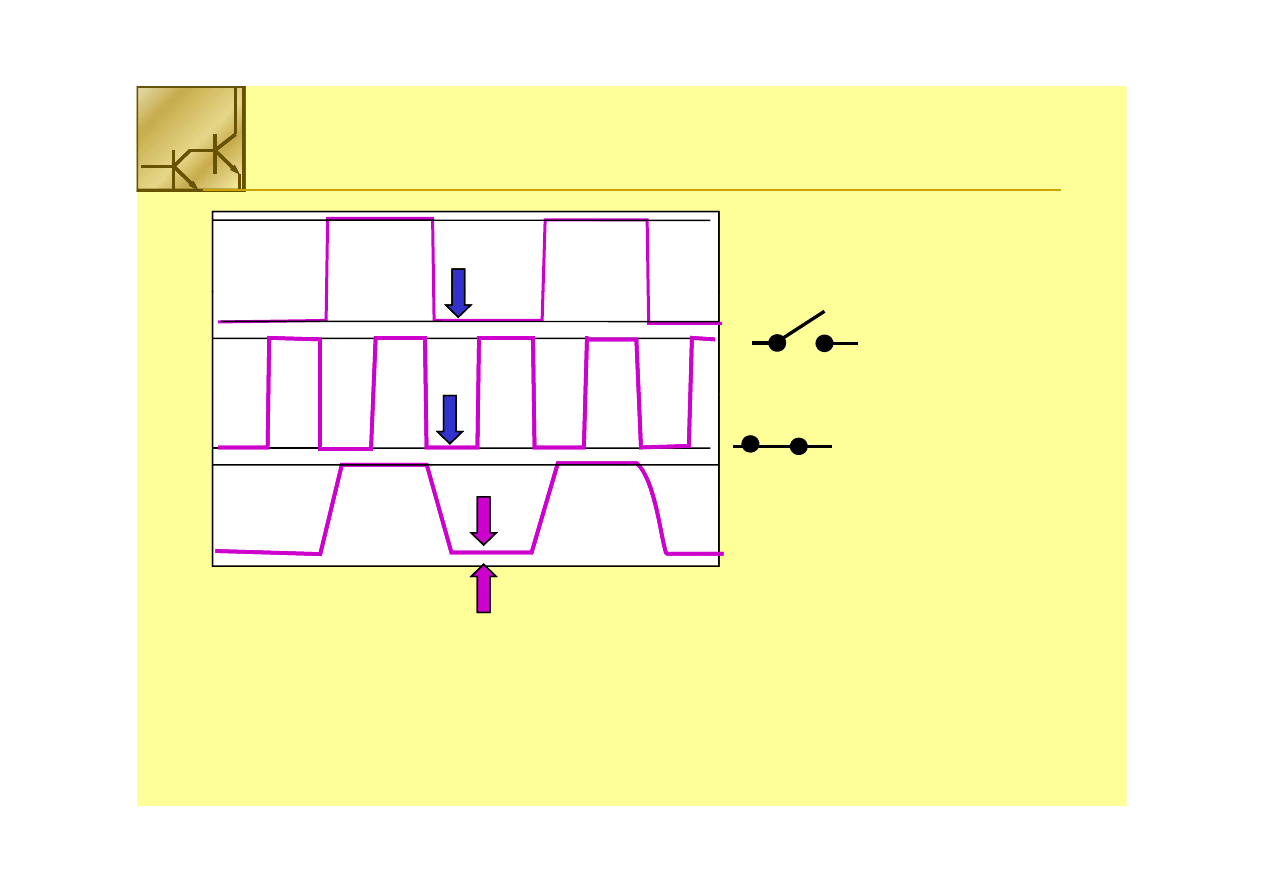
Tranzystor
Tranzystor PMOS
PMOS dobrze
dobrze przewodzi
przewodzi wysokie
wysokie napięcie
napięcie ii gorzej
gorzej niskie
niskie
napięcie
napięcie (V
(V
T
T
))
6 marca 2011
Wojciech Kucewicz
9
Tranzystor
Tranzystor PMOS
PMOS źle
źle przewodzi
przewodzi logiczne
logiczne zero
zero

Cyfrowe
Cyfrowe układy
układy kombinacyjne
kombinacyjne
Cyfrowe
Cyfrowe układy
układy kombinacyjne
kombinacyjne
Podstawowe bramki
Podstawowe bramki
Podstawowe bramki
Podstawowe bramki
Podstawowe bramki
Podstawowe bramki
Podstawowe bramki
Podstawowe bramki
6 marca 2011
Wojciech Kucewicz
10
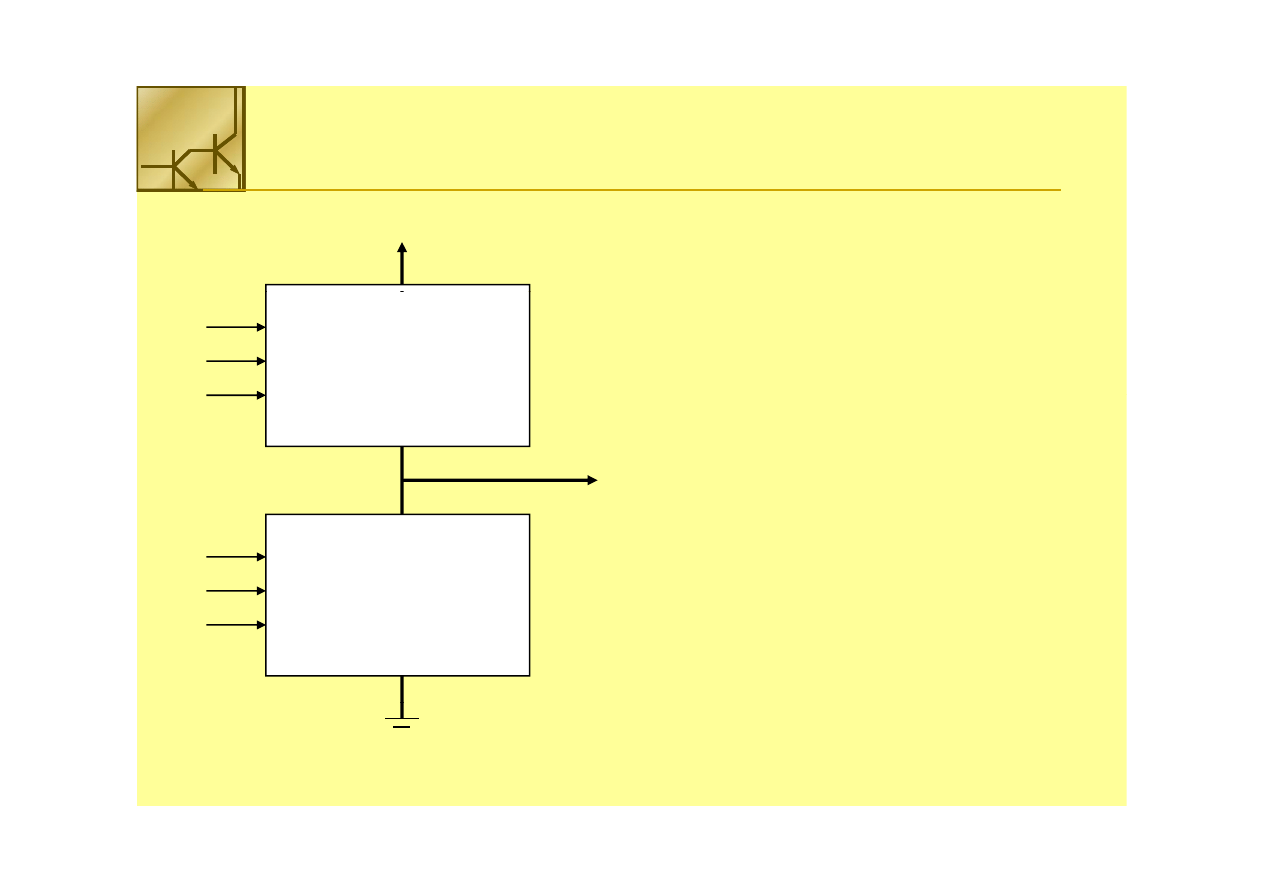
Bramka logiczna CMOS
Bramka logiczna CMOS
Bramka logiczna CMOS
Bramka logiczna CMOS
VV
DD
DD
Pull
Pull--up
up Network
Network
Constracted
Constracted
by PMOS
by PMOS
A
A
BB
CC
Układ logiczny łączący wysoki potencjał V
Układ logiczny łączący wysoki potencjał V
DD
DD
z
z
wyjściem buduje się z tranzystorów PMOS
wyjściem buduje się z tranzystorów PMOS
yy
CC
FF
out
out
Pull
Pull--down Network
down Network
Constracted
Constracted
A
A
BB
Układ logiczny łączący niski potencjał V
Układ logiczny łączący niski potencjał V
SS
SS
z
z
wyjściem buduje się z tranzystorów NMOS
wyjściem buduje się z tranzystorów NMOS
Constracted
Constracted
by NMOS
by NMOS
CC
yj
j
ę
y
yj
j
ę
y
6 marca 2011
Wojciech Kucewicz
11
VV
SS
SS
Inwerter
Inwerter CMOS
CMOS
Inwerter
Inwerter CMOS
CMOS
Inwerter
Inwerter CMOS
CMOS
Inwerter
Inwerter CMOS
CMOS
6 marca 2011
Wojciech Kucewicz
12
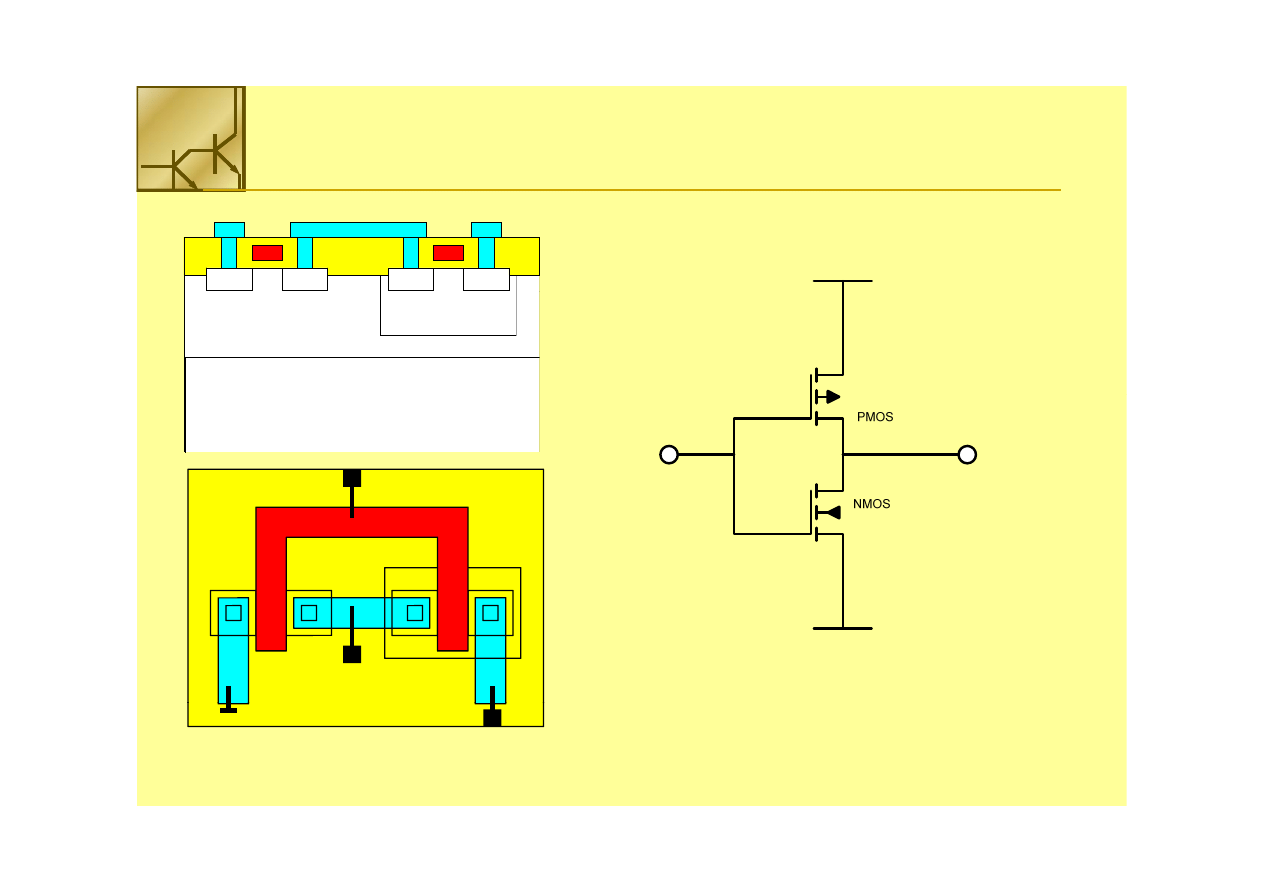
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
p+
p+
n+
n+
V
V
DD
DD
n
p
p
p
n+
V
IN
V
V
IN
IN
V
V
OUT
OUT
V
IN
V
OUT
V
V
V
V
SS
SS
6 marca 2011
Wojciech Kucewicz
13
OUT
V
SS
V
DD
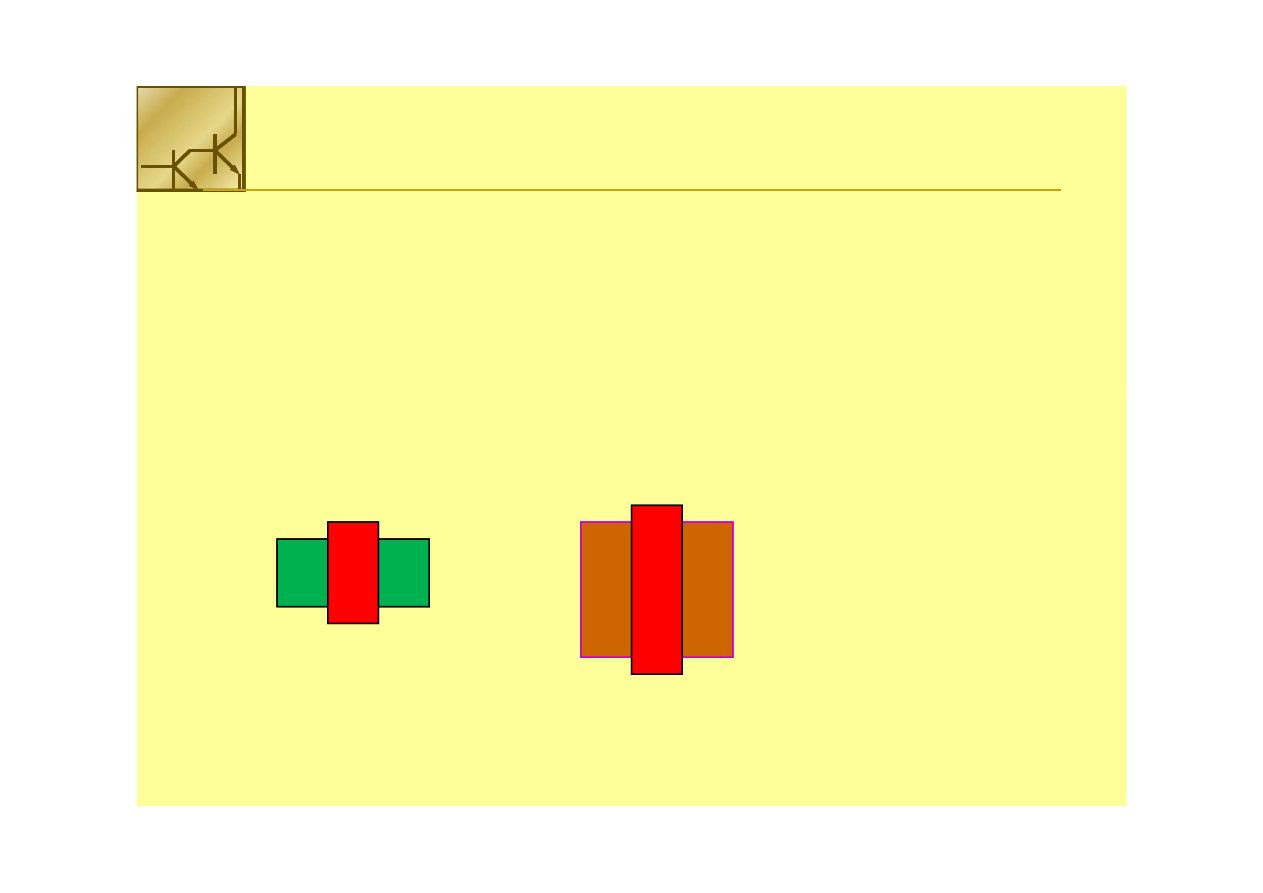
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Ab ić t ki
d d
t
t ó PMOS i NMOS k
ł
Ab ić t ki
d d
t
t ó PMOS i NMOS k
ł
Aby zapewnić taki sam prąd drenu tranzystorów PMOS i NMOS, kanał
Aby zapewnić taki sam prąd drenu tranzystorów PMOS i NMOS, kanał
tranzystora PMOS powinien być ok. dwukrotnie szerszy od kanału
tranzystora PMOS powinien być ok. dwukrotnie szerszy od kanału
tranzystora NMOS.
tranzystora NMOS.
Skompensuje to różnice ruchliwości nośników w obu tranzystorach.
Skompensuje to różnice ruchliwości nośników w obu tranzystorach.
S G D
S G D
NMOS
PMOS
6 marca 2011
Wojciech Kucewicz
14
PMOS
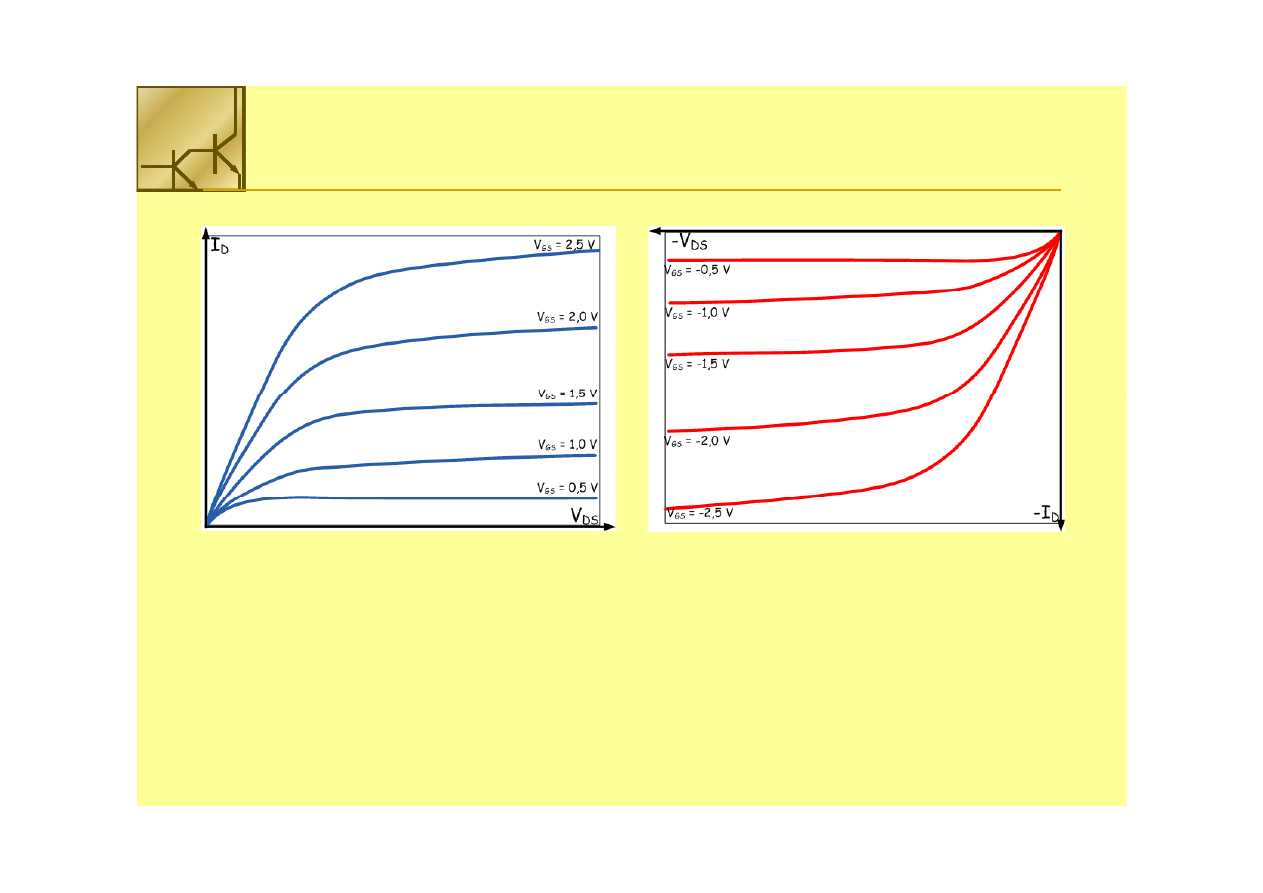
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
PMOS transistor, 0.25
PMOS transistor, 0.25μμm,
m,
N
NMOS transistor, 0.25
MOS transistor, 0.25μμm,
m,
,,
μμ
,,
LL
dd
= 0.25
= 0.25μμm, W/L =
m, W/L = 33, ,
VV
DD
DD
=
= --2.5V, V
2.5V, V
T
T
=
= --0.4V
0.4V
,,
μμ
,,
LL
dd
= 0.25
= 0.25μμm, W/L = 1.5,
m, W/L = 1.5,
VV
DD
DD
= 2.5V, V
= 2.5V, V
T
T
= 0.4V
= 0.4V
6 marca 2011
Wojciech Kucewicz
15
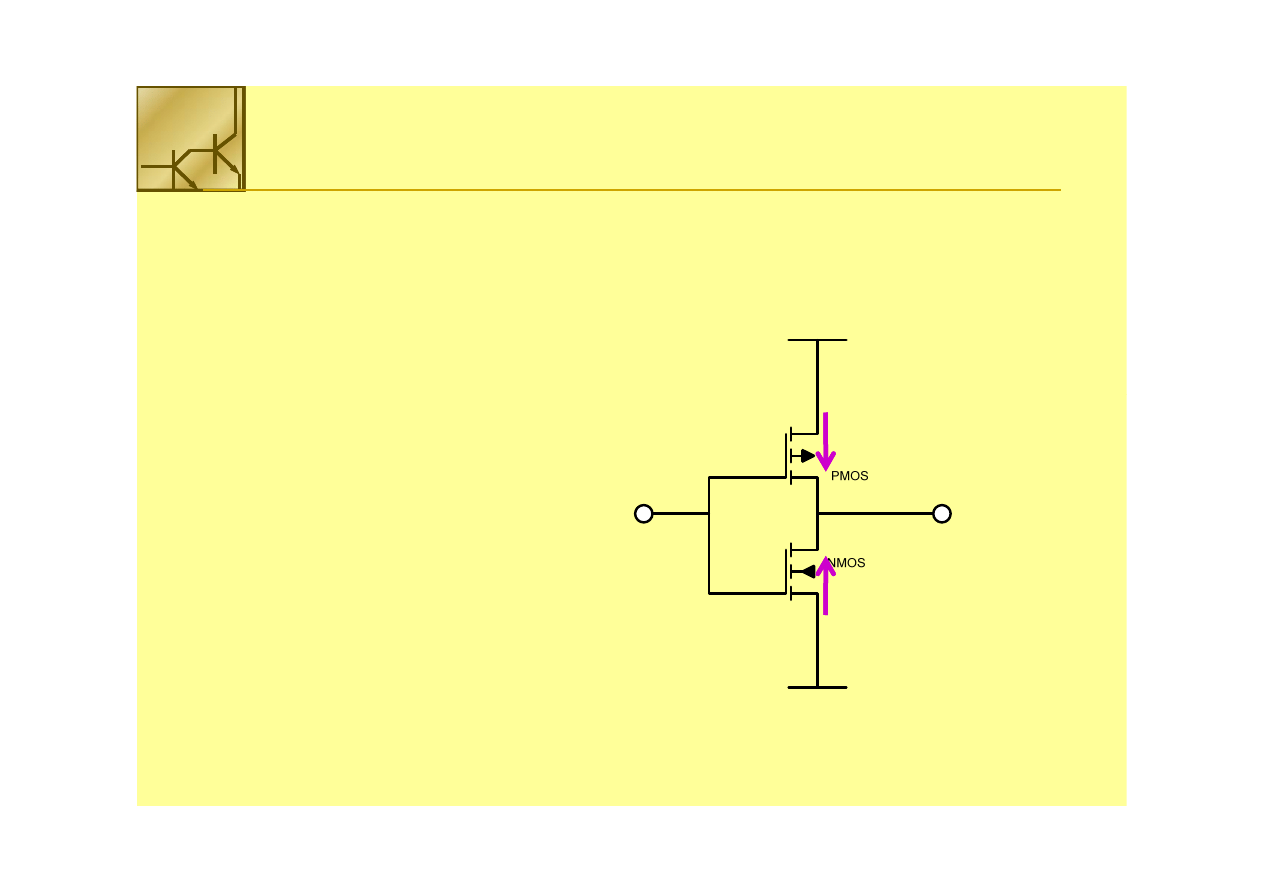
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Aby charakterystyki obu tranzystorów w inwerterze
narysować na wspólnym wykresie należy wprowadzić wspólne
zmienne V
IN
, V
OUT
, and I
D
II
D
D
= I
= I
D
D
V
V
DD
DD
II
Dn
Dn
= I
= I
D
D
VV
GSn
GSn
= V
= V
IN
IN
VV
DSn
DSn
= V
= V
OUT
OUT
II
Dp
Dp
S
S
II
Dp
Dp
=
= -- II
D
D
VV
GSp
GSp
= V
= V
IN
IN
-- VV
DD
DD
II
Dn
Dn
V
V
IN
IN
V
V
OUT
OUT
S
S
VV
DSp
DSp
= V
= V
OUT
OUT
-- VV
DD
DD
II
Dn
Dn
V
V
S
S
6 marca 2011
Wojciech Kucewicz
16
V
V
SS
SS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
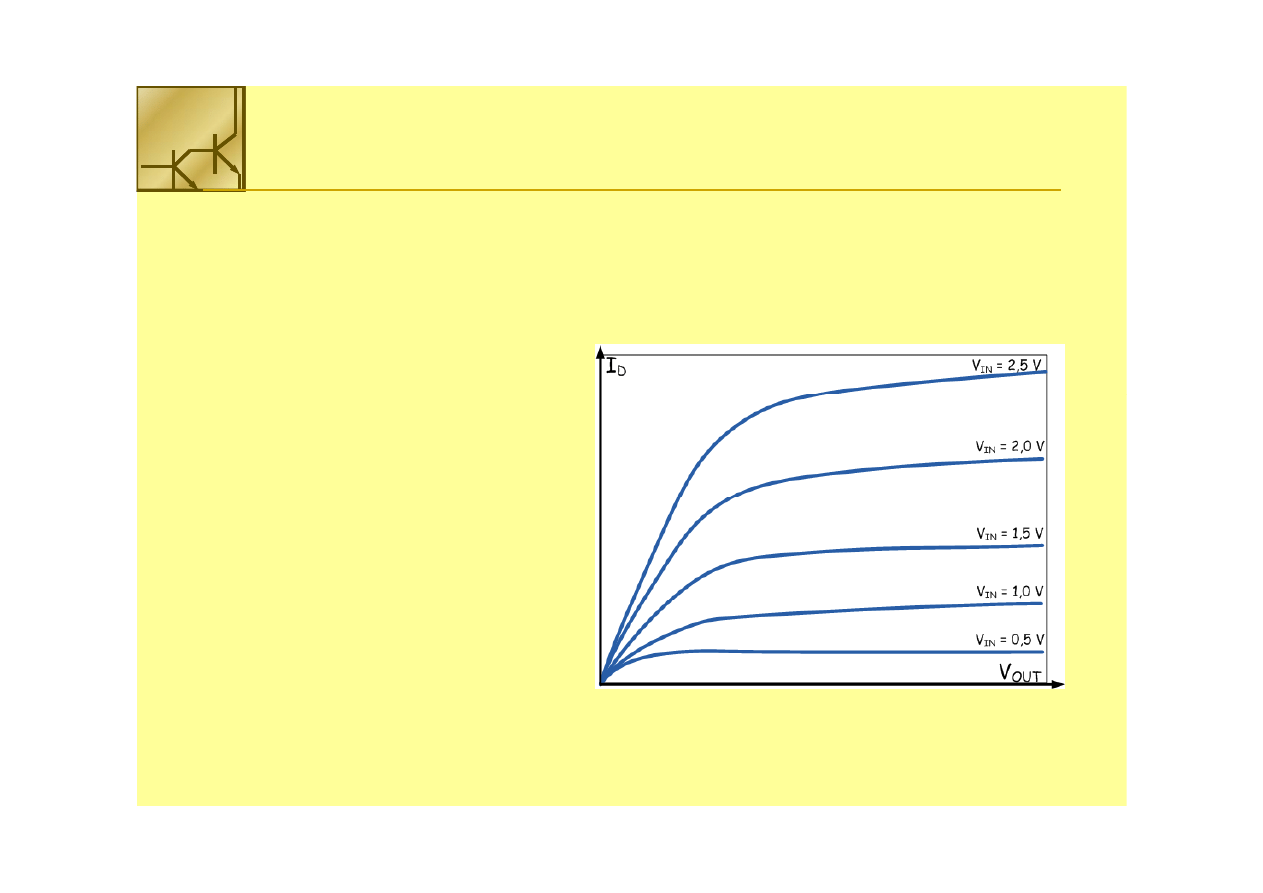
Aby charakterystyki obu tranzystorów w inwerterze
narysować na wspólnym wykresie należy wprowadzić wspólne
zmienne V
IN
, V
OUT
, and I
D
II
Dn
Dn
= I
= I
D
D
VV
GSn
GSn
= V
= V
IN
IN
VV
= V
= V
VV
DSn
DSn
= V
= V
OUT
OUT
6 marca 2011
Wojciech Kucewicz
17
Tranzystor NMOS
Tranzystor NMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
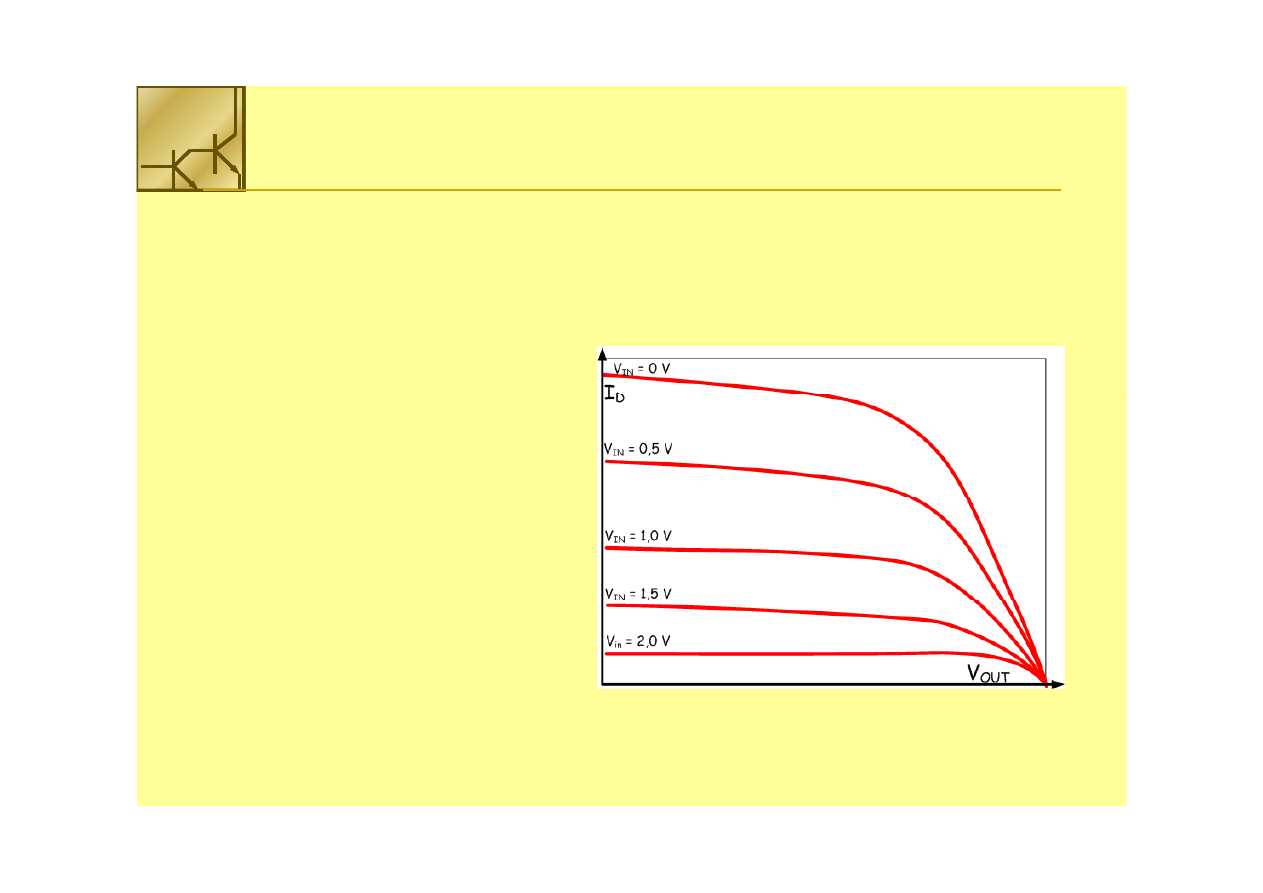
Aby charakterystyki obu tranzystorów w inwerterze
narysować na wspólnym wykresie należy wprowadzić wspólne
zmienne V
IN
, V
OUT
, and I
D
II
Dp
Dp
=
= -- II
D
D
VV
GSp
GSp
= V
= V
IN
IN
-- VV
DD
DD
VV
= V
= V
-- VV
VV
DSp
DSp
= V
= V
OUT
OUT
-- VV
DD
DD
6 marca 2011
Wojciech Kucewicz
18
Tranzystor PMOS
Tranzystor PMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
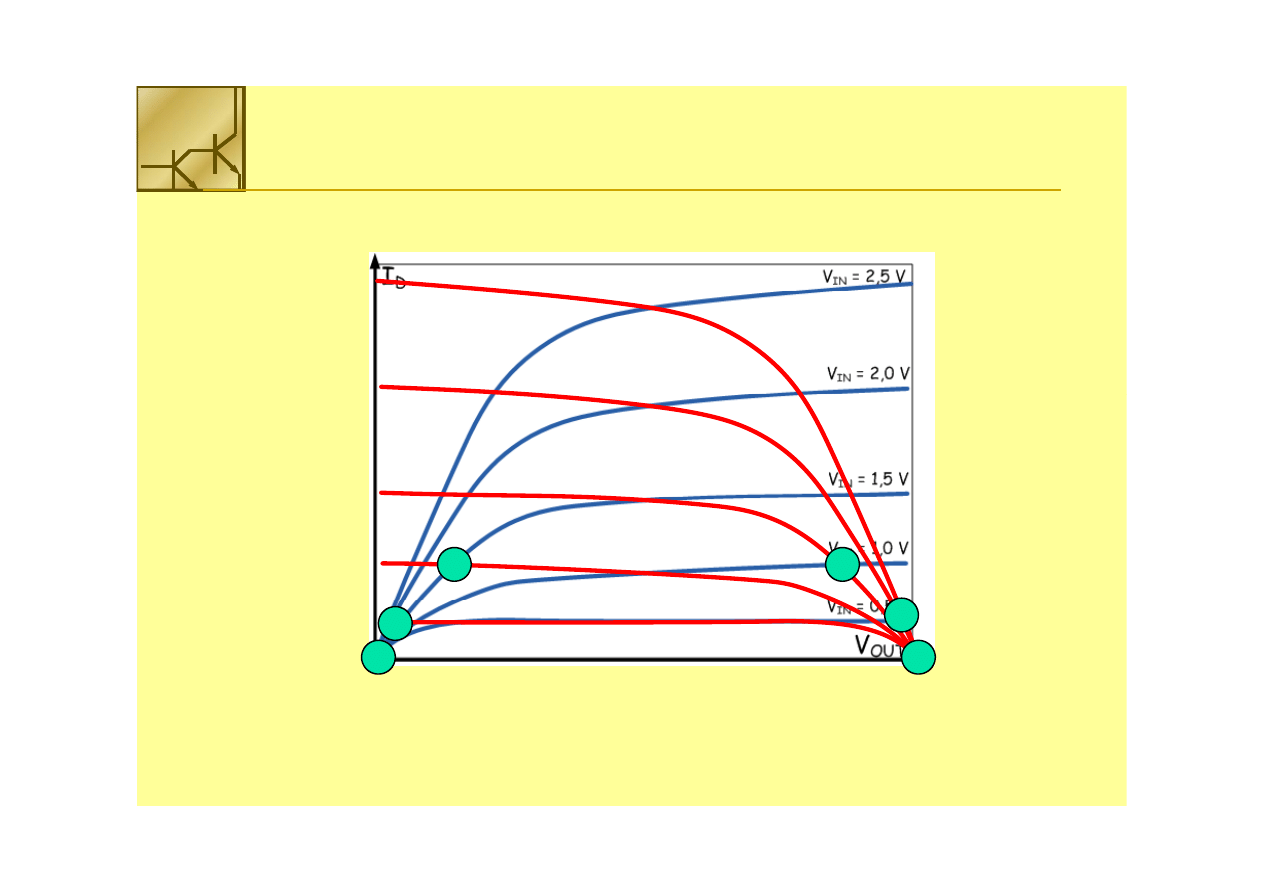
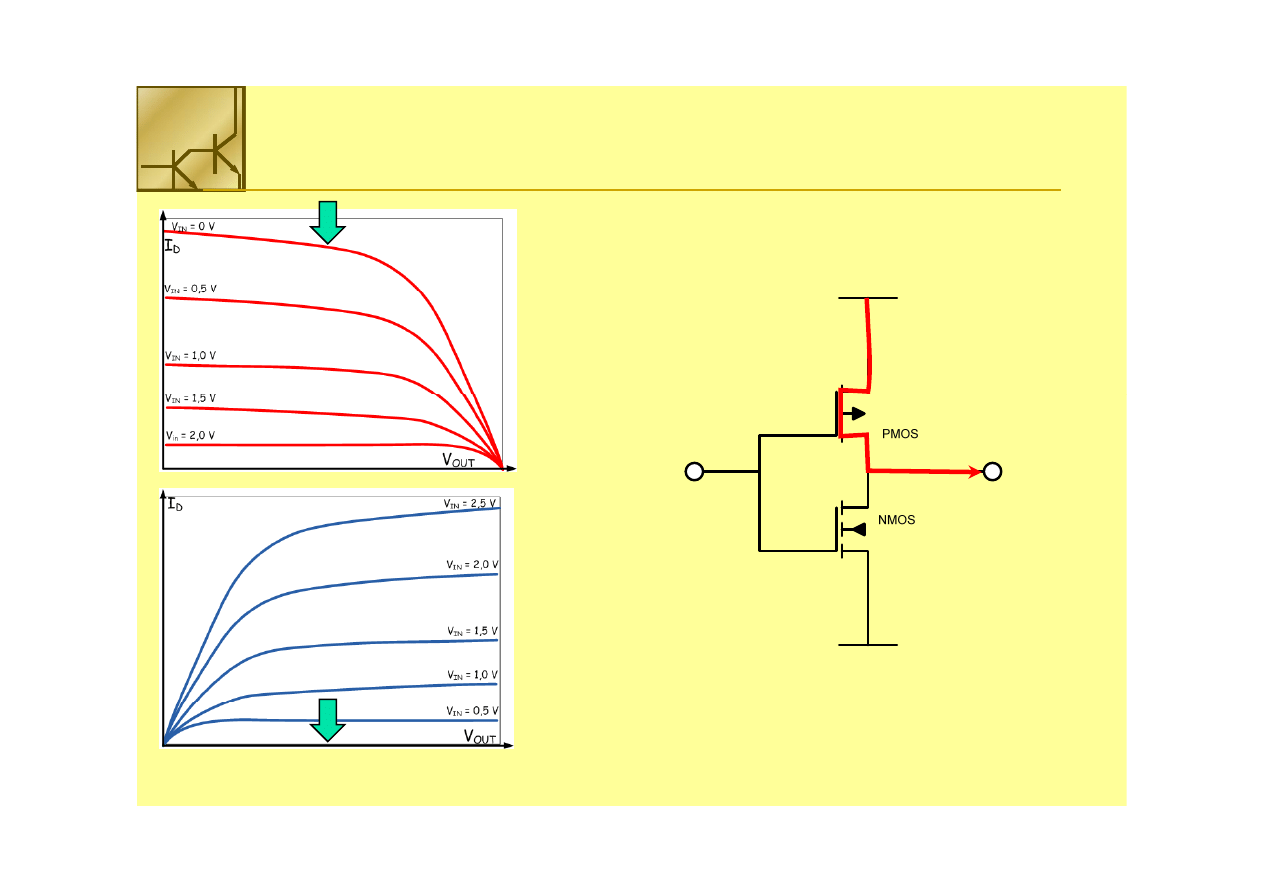
V
IN
= 0 V
V
IN
= 0,5 V
V
IN
= 1,0 V
V
IN
= 1,5 V
1,0
1,0
1,5
1,5
V
in
= 2,0 V
00
0,5
0,5
2,0
2,0
2,5
2,5
6 marca 2011
Wojciech Kucewicz
19
0.25
0.25μμm,
m,
W/
W/LL
nn
= 1.5, W/
= 1.5, W/LL
pp
= 4.5,
= 4.5,
VV
DD
DD
= 2.5V,
= 2.5V, VV
Tn
Tn
= 0.4V,
= 0.4V, VV
Tp
Tp
=
= --0.4V
0.4V
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
V
V
out
out
2,5 00
0,5
0,5
1,0
1,0
2,0
1,5
1,0
,
0,5
0
0,5 1,0 1,5 2,0 2,5 V
V
in
in
1,5
1,5
2,0
2,0
2,5
2,5
6 marca 2011
Wojciech Kucewicz
20
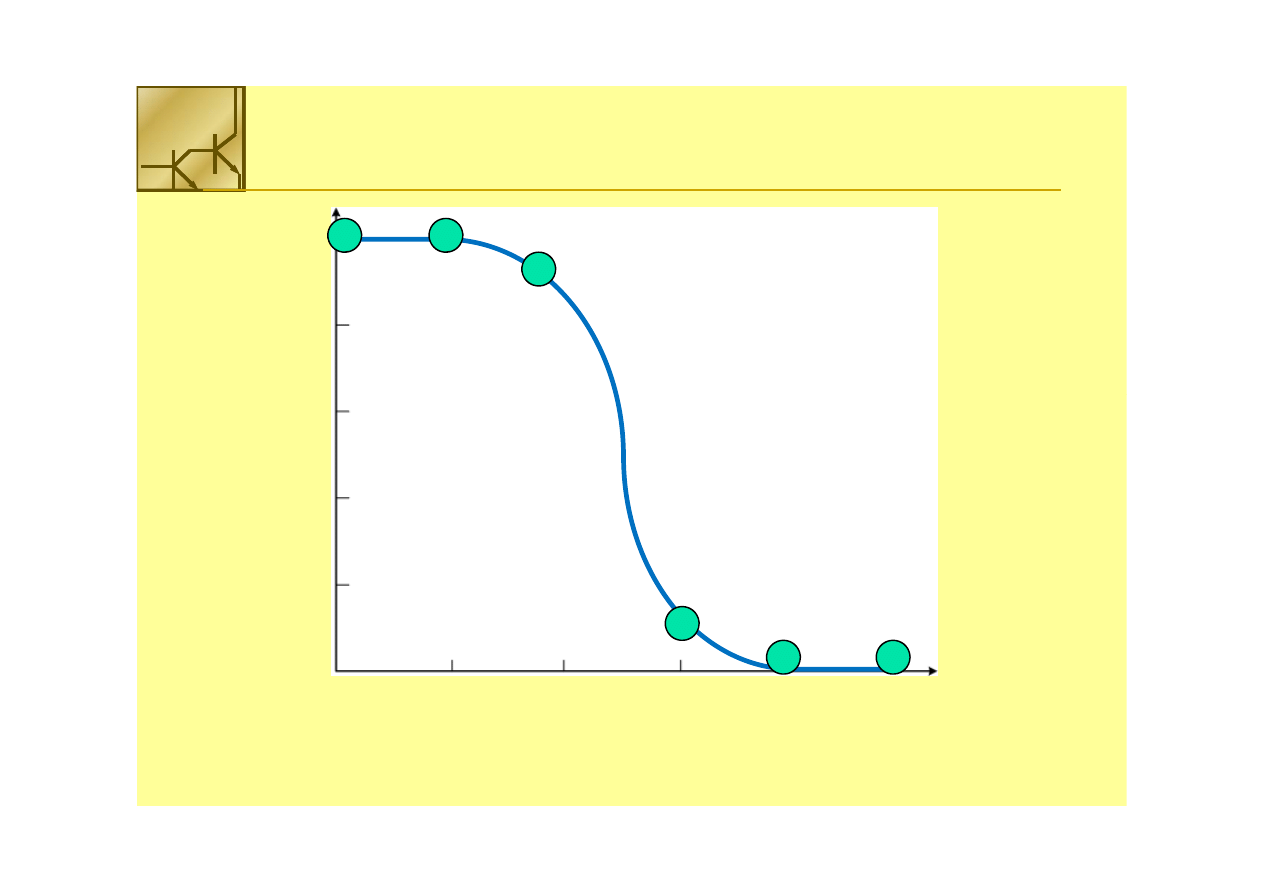
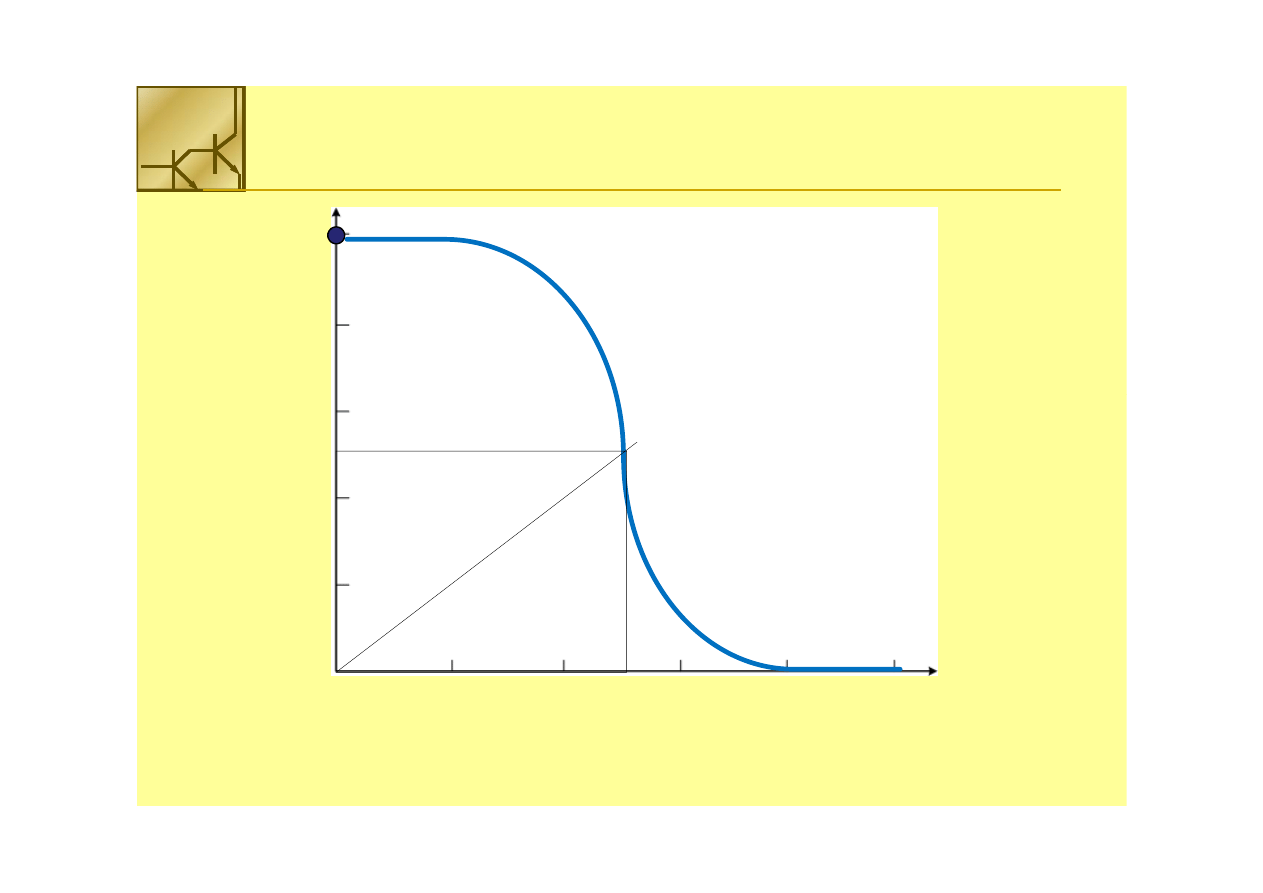
Charakterystyka przejściowa inwertera V
out
= f(V
in
)
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
V
V
DD
DD
V
V
IN
IN
V
V
OUT
OUT
VV
in
in
=
= VV
SS
SS
Î
Î
00
VV
out
out
=
= VV
DD
DD
Î
Î
11
V
V
SS
SS
6 marca 2011
Wojciech Kucewicz
21
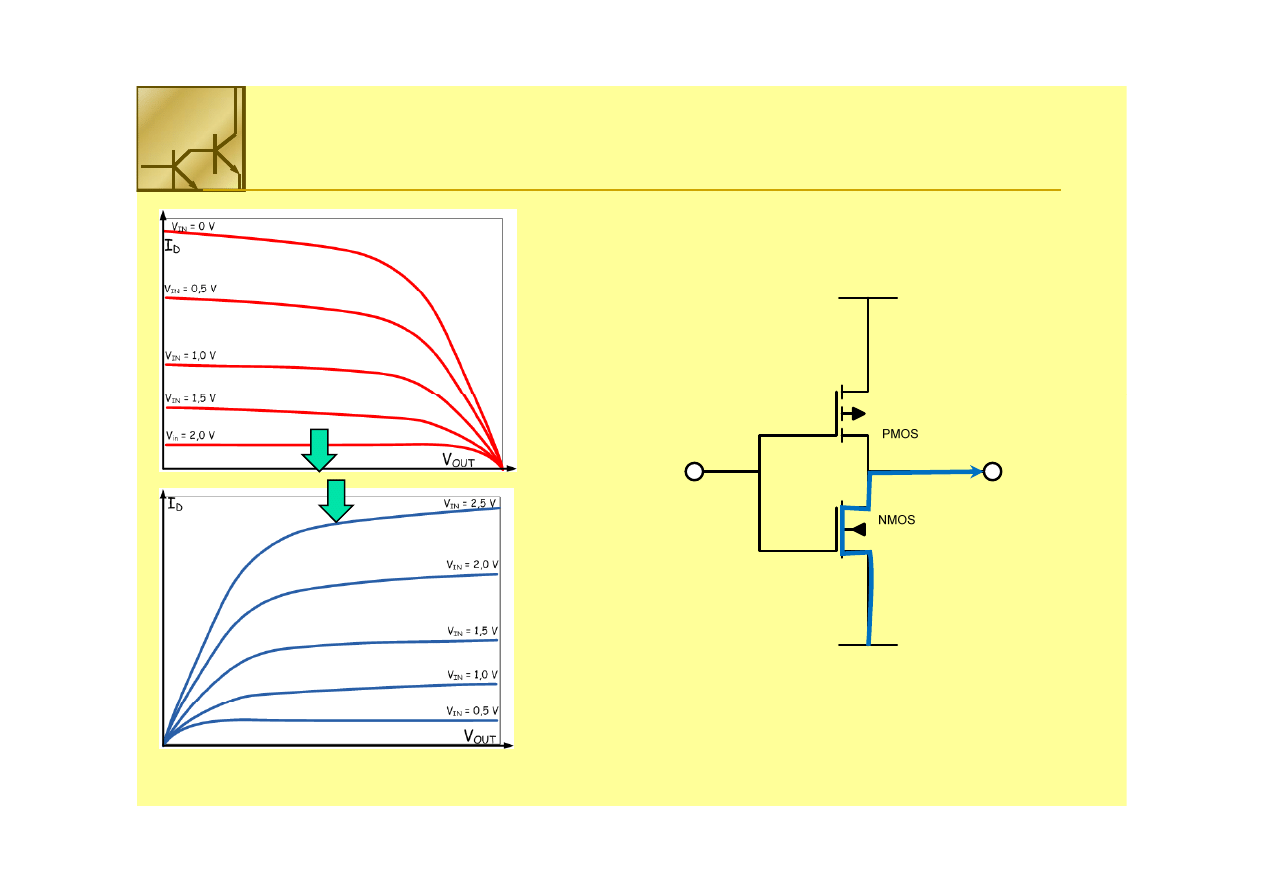
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
V
V
DD
DD
V
V
IN
IN
V
V
OUT
OUT
VV
in
in
=
= VV
DD
DD
Î
Î
11
VV
out
out
=
= VV
SS
SS
Î
Î
00
V
V
SS
SS
6 marca 2011
Wojciech Kucewicz
22

Próg
Próg
Próg
Próg
Próg
Próg
przełączania
przełączania
Próg
Próg
przełączania
przełączania
przełączania
przełączania
przełączania
przełączania
6 marca 2011
Wojciech Kucewicz
23
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
Inwerter CMOS
V
V
out
out
2,5
NMOS
NMOS off
off
PMO li
PMO li
NMOS
NMOS sat
sat
2,0
PMOS lin
PMOS lin
NMOS
NMOS sat
sat
PMOS lin
PMOS lin
1,5
1,0
Próg przełaczania V
m
NMOS
NMOS sat
sat
PMOS
PMOS sat
sat
,
0,5
NMOS lin
NMOS lin
PMOS
PMOS sat
sat
0
0,5 1,0 1,5 2,0 2,5 V
V
in
in
PMOS
PMOS sat
sat
NMOS lin
NMOS lin
PMOS
PMOS off
off
6 marca 2011
Wojciech Kucewicz
24
Inwerter przełącza się w momencie gdy napięcie wejściowe jest równe napięciu
wyjściowemu. W tym czasie oba tranzystory są w stanie nasycenia (przewodzą)
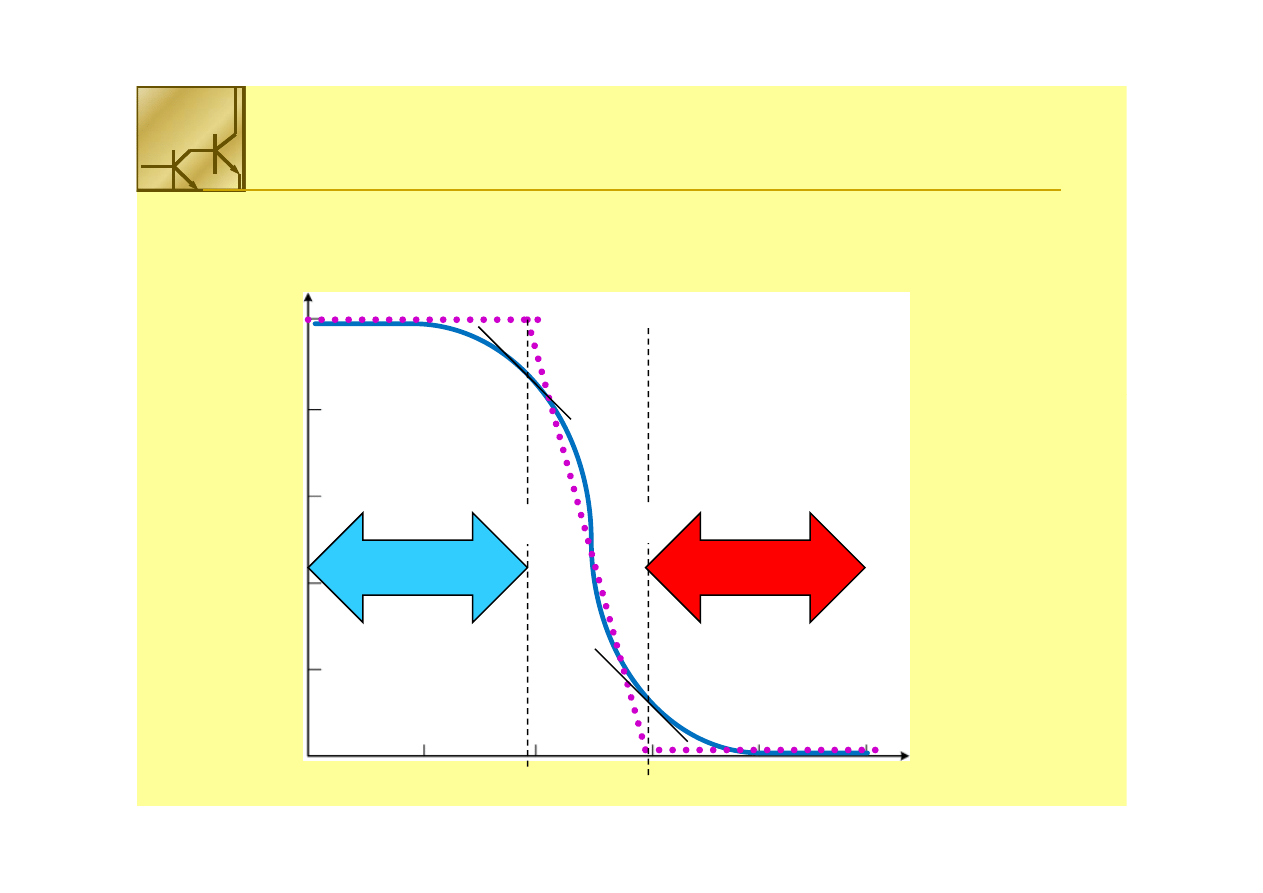
Margines szumów
Margines szumów
Margines szumów
Margines szumów
V
V
Górny próg dla napięcia niskiego V
IL
i dolny dla napięcia wysokiego V
IH
definiuje
się przy wzmocnieniu dV
out
/dV
in
= -1
Im większe wzmocnienie – tym większe marginesy szumów
V
V
out
out
2,5
2 0
2,0
1,5
,
1,0
VV
IL
IL
VV
IH
IH
00
11
0,5
Margines szumów dla
Margines szumów dla
napięcia niskiego
napięcia niskiego
wynosi
wynosi
NM
NM
LL
= V
= V
IL
IL
–– V
V
SS
SS
Margines szumów dla
Margines szumów dla
napięcia wysokiego
napięcia wysokiego
wynosi
wynosi
NM
NM
H
H
= V
= V
DD
DD
-- V
V
IH
IH
0
0,5 1,0 1,5 2,0 2,5 V
V
in
in
6 marca 2011
Wojciech Kucewicz
25
NM
NM
LL
V
V
IL
IL
V
V
SS
SS
NM
NM
H
H
V
V
DD
DD
V
V
IH
IH

Działanie
Działanie
Działanie
Działanie
Działanie
Działanie
dynamiczne
dynamiczne
Działanie
Działanie
dynamiczne
dynamiczne
dynamiczne
dynamiczne
dynamiczne
dynamiczne
6 marca 2011
Wojciech Kucewicz
26
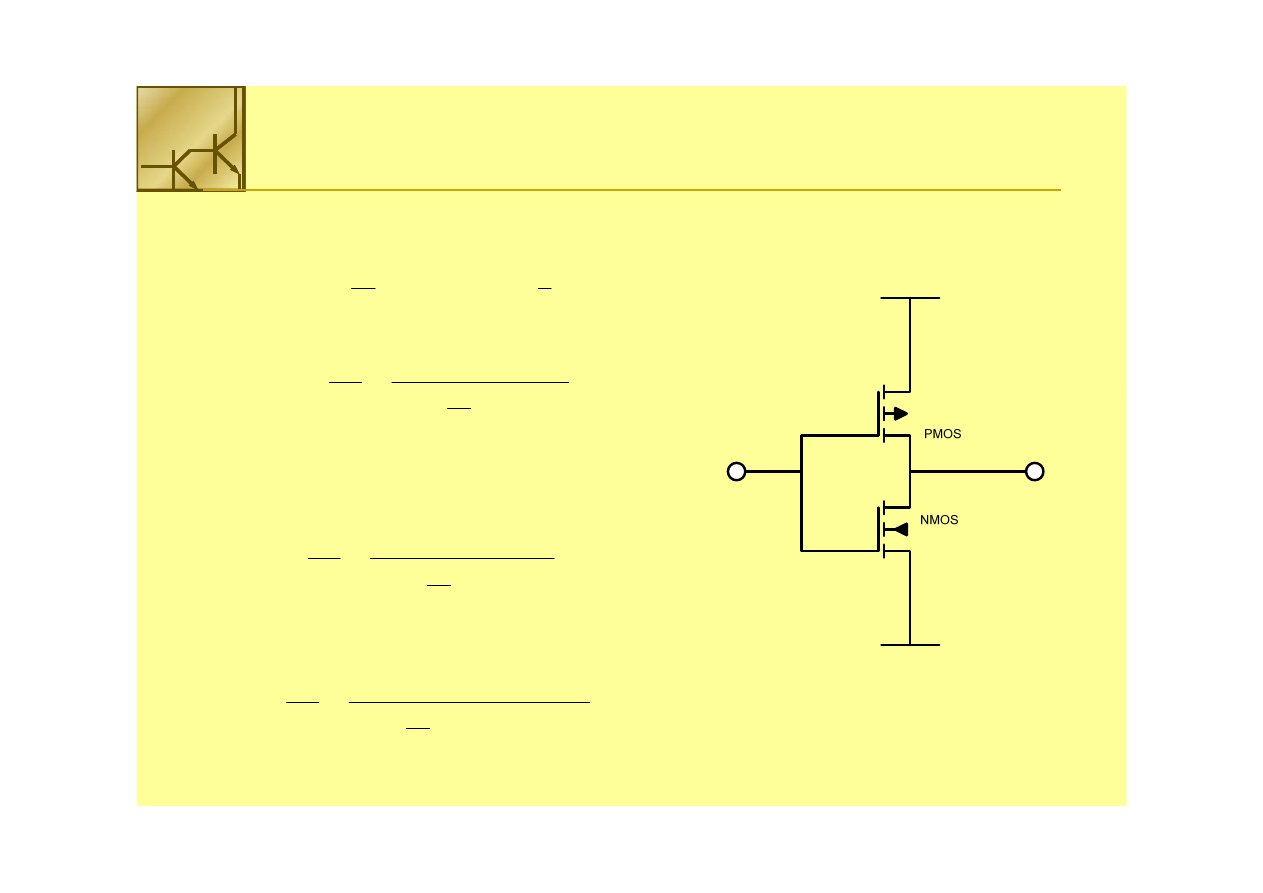
Działanie dynamiczne
Działanie dynamiczne
Działanie dynamiczne
Działanie dynamiczne
V
V
DD
DD
Tranzystor działający jako przełącznik może być traktowany jak rezystor:
(
)
DS
DS
T
GS
D
V
V
V
V
W
C
I
⎥
⎤
⎢
⎡
−
−
μ
=
1
2
(
)
(
)
DS
on
DS
DS
T
GS
ox
D
W
I
V
R
V
V
V
V
L
C
I
≈
=
⇓
⎥⎦
⎢⎣
μ
1
2
V
V
IN
IN
V
V
OUT
OUT
(
)
T
GS
ox
D
V
V
L
W
C
I
−
μ
Rezystancja tranzystora NMOS :
(
)
Tn
IN
ox
n
D
DS
NMOS
V
V
L
W
C
I
V
R
−
μ
≈
=
1
V
V
SS
SS
L
Rezystancja tranzystora PMOS :
DS
V
R
≈
=
1
6 marca 2011
Wojciech Kucewicz
27
(
)
Tp
IN
DD
ox
p
D
PMOS
V
V
V
L
W
C
I
R
+
−
μ
≈
=
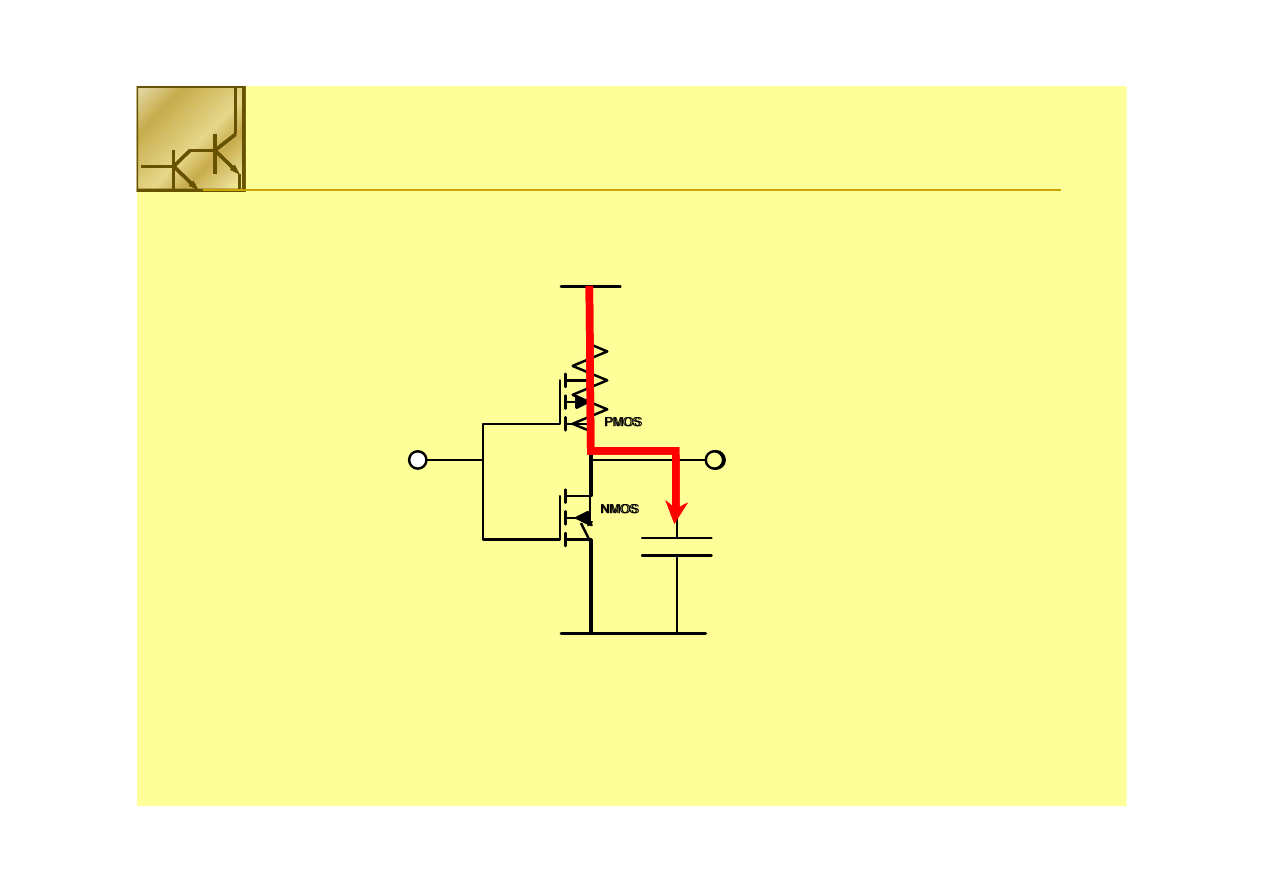
Działanie dynamiczne
Działanie dynamiczne
Działanie dynamiczne
Działanie dynamiczne
V
V
DD
DD
V
V
IN
IN
=0
=0
V
V
OUT
OUT
V
V
SS
SS
C
ł
i b
ki
t
0 1
l ż d
t
ji k
ł t
t
6 marca 2011
Wojciech Kucewicz
28
Czas przełączenia bramki ze stanu 0 na 1 zależy od rezystancji kanału tranzystora
PMOS i pojemności obciążenia
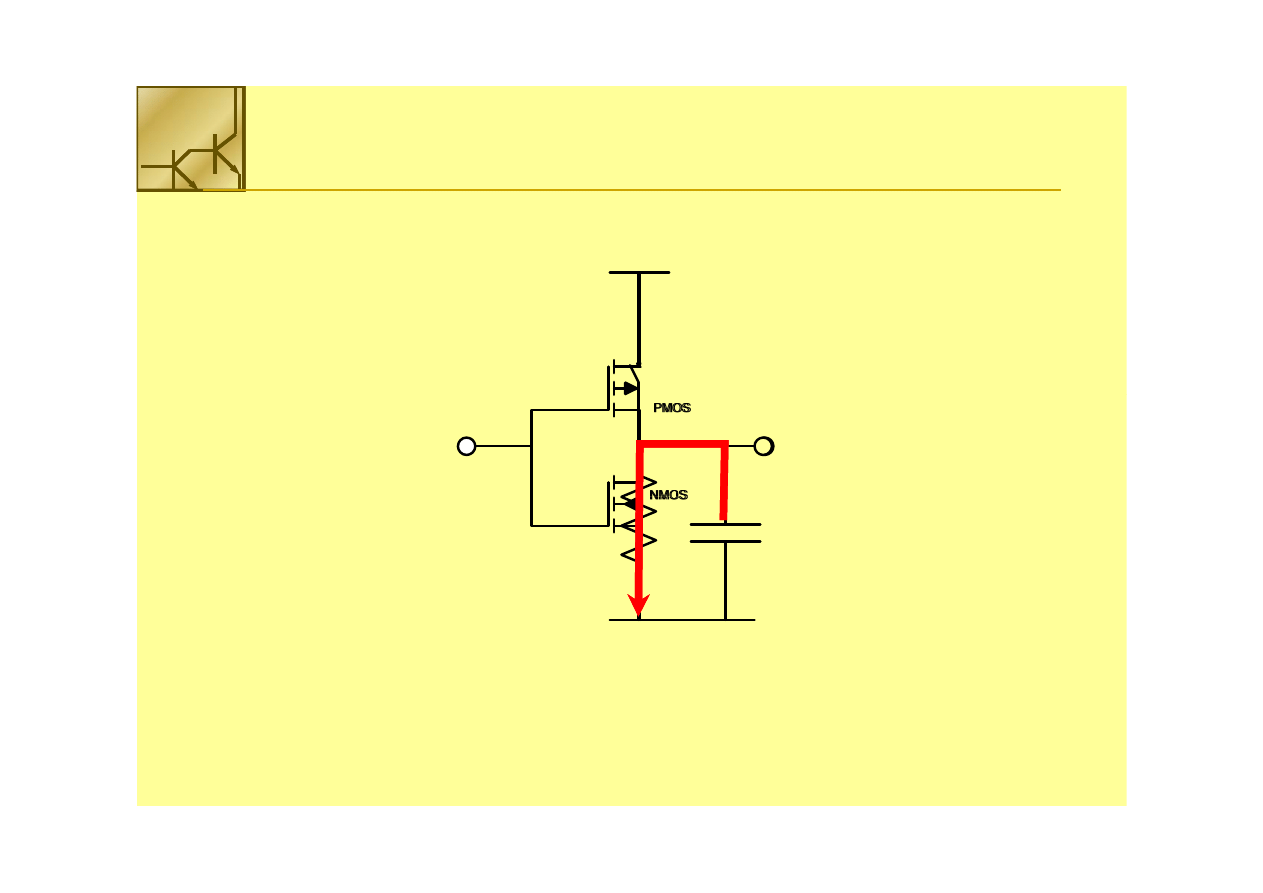
Działanie dynamiczne
Działanie dynamiczne
Działanie dynamiczne
Działanie dynamiczne
V
V
IN
IN
=1
=1
V
V
OUT
OUT
C
ł
i b
ki
t
1 0
l ż d
t
ji k
ł t
t
6 marca 2011
Wojciech Kucewicz
29
Czas przełączenia bramki ze stanu 1 na 0 zależy od rezystancji kanału tranzystora
NMOS i pojemności obciążenia

Pojemności
Pojemności
Pojemności
Pojemności
pasożytnicze
pasożytnicze
pasożytnicze
pasożytnicze
6 marca 2011
Wojciech Kucewicz
30
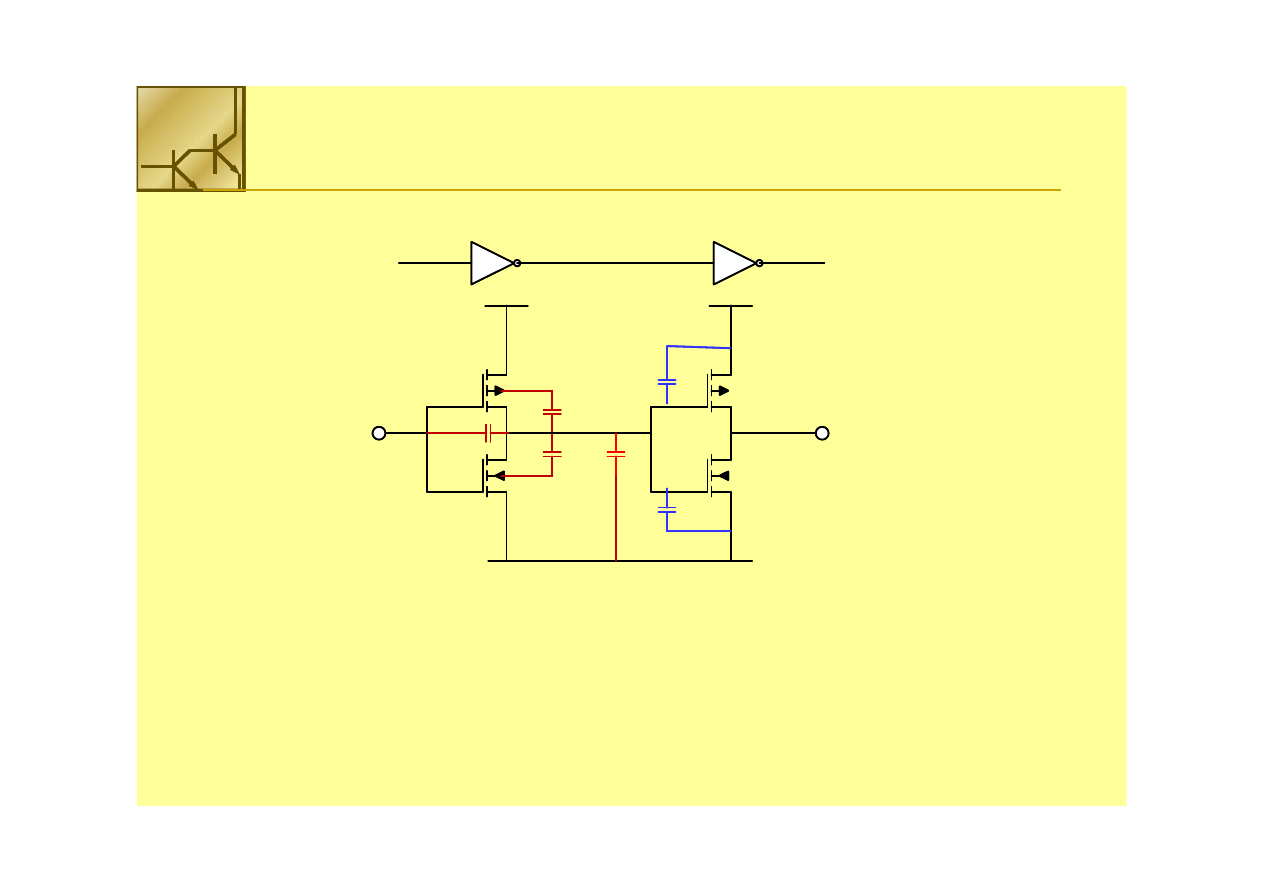
Źródła pojemności pasożytniczych
Źródła pojemności pasożytniczych
Źródła pojemności pasożytniczych
Źródła pojemności pasożytniczych
V
in
V
out
V
in
V
out
M2
M4
C
G4
M2
M4
C
G4
M1
M3
C
GD
C
DB2
C
DB1
C
W
V
in
V
out
M1
M3
C
GD
C
DB2
C
DB1
C
W
V
in
V
out
M1
M3
C
G2
M1
M3
C
G2
Pojemność doprowadzeń
Wewnętrzne pojemności bramki
6 marca 2011
Wojciech Kucewicz
31
Wewnętrzne pojemnośc ram
Pojemności dołączone z zewnątrz
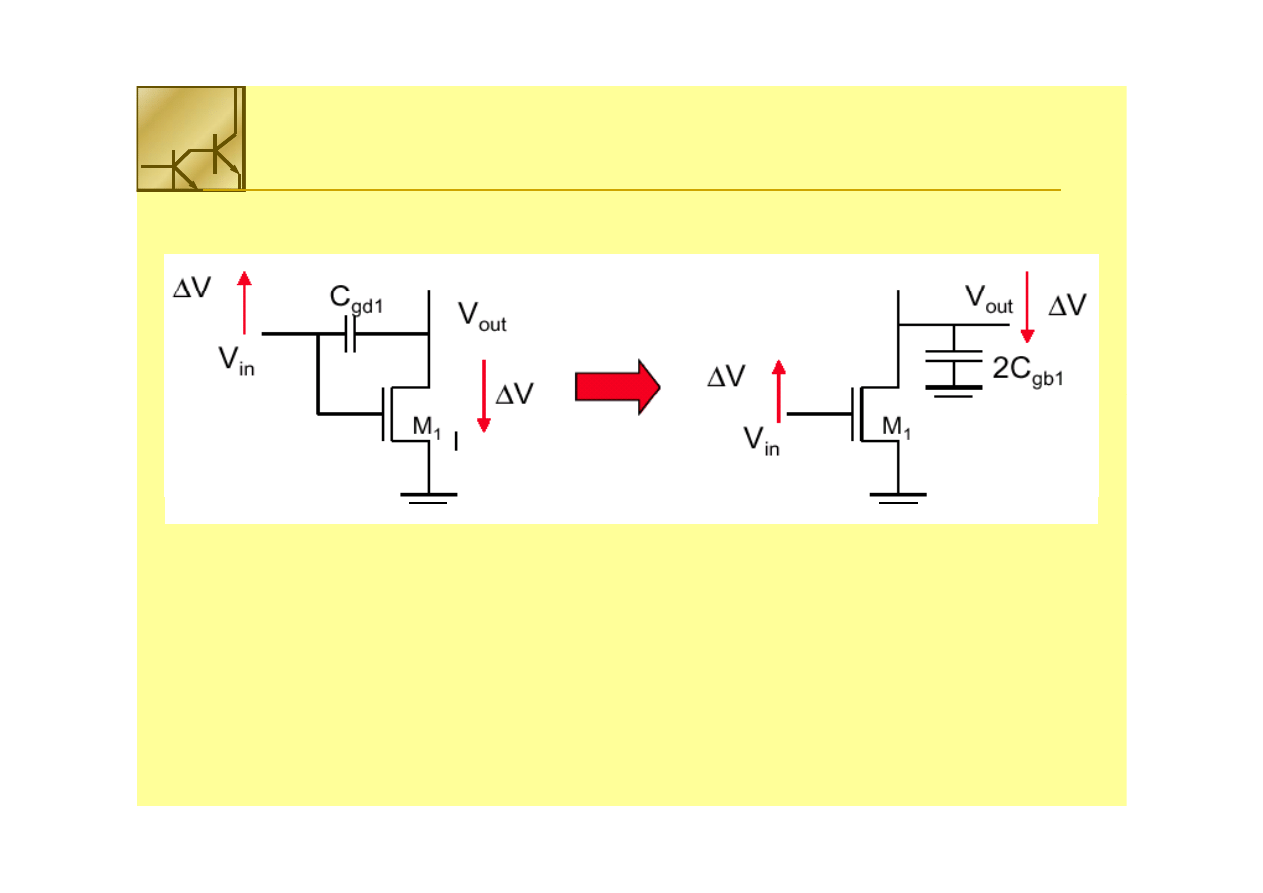
Efekt Millera
Efekt Millera
Efekt Millera
Efekt Millera
Kondensator na który przykładane jest identyczne napięcie
Kondensator na który przykładane jest identyczne napięcie
na obie okładki lecz przeciwnego znaku może być
na obie okładki lecz przeciwnego znaku może być
t i
k d
t
t ś i 2 i k
j
t i
k d
t
t ś i 2 i k
j
6 marca 2011
Wojciech Kucewicz
32
zastąpiony kondensatorem o wartości 2x większej
zastąpiony kondensatorem o wartości 2x większej
podłączonym do masy
podłączonym do masy
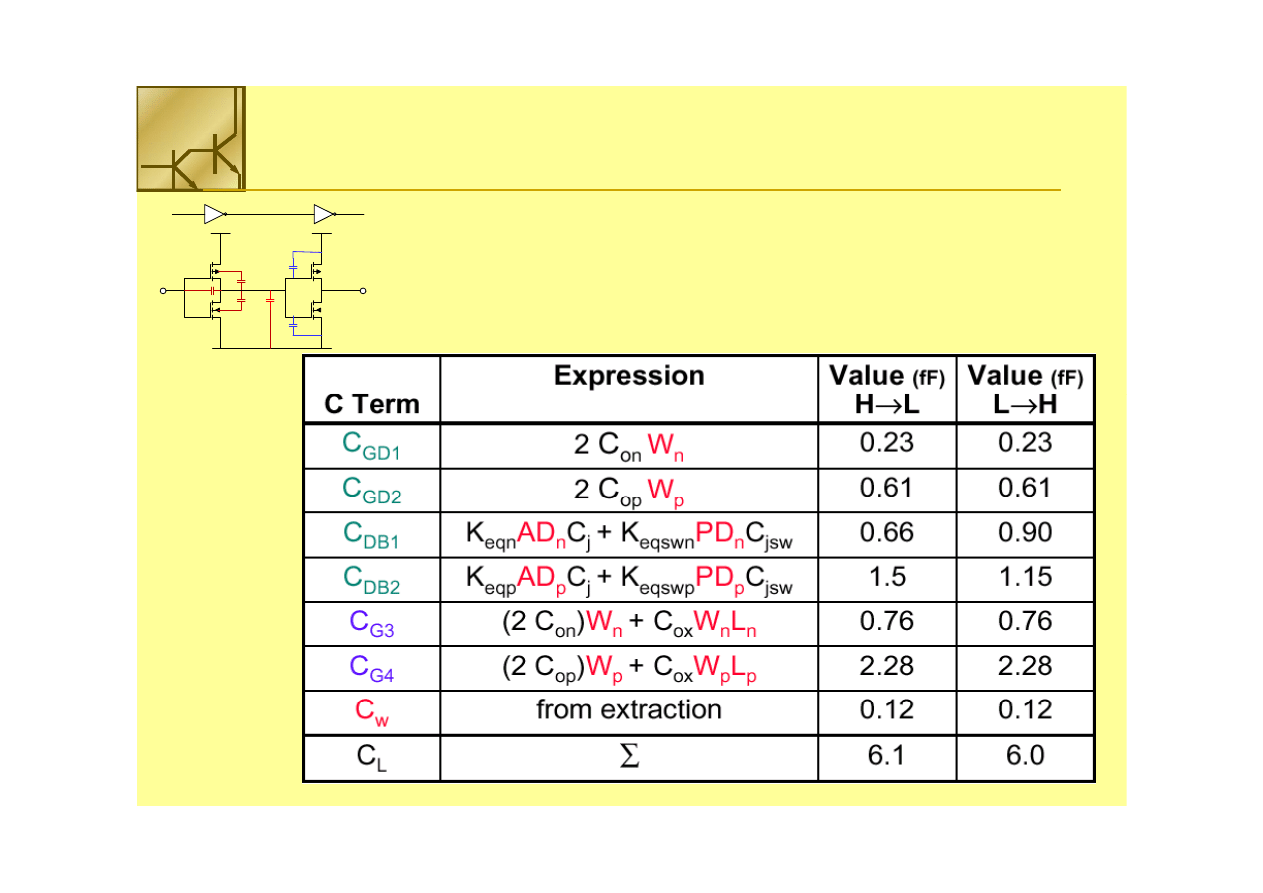
Capacitance Calculations
Capacitance Calculations
Capacitance Calculations
Capacitance Calculations
V
in
V
out
M2
M4
C
GD
C
DB2
C
G4
V
in
V
out
M1
M3
C
DB1
C
W
C
G2
6 marca 2011
Wojciech Kucewicz
33

Właściwości inwertera CMOS
Właściwości inwertera CMOS
Właściwości inwertera CMOS
Właściwości inwertera CMOS
Przełączanie w pełnym zakresie napięcia zasilania
Przełączanie w pełnym zakresie napięcia zasilania
Î
Î
duży margines szumów
duży margines szumów
Pozim
Pozim logiczny nie zależy od wymiarów tranzystorów
logiczny nie zależy od wymiarów tranzystorów
Î
Î
tranzystor
tranzystor może mieć minimalne wymiary
może mieć minimalne wymiary
Wyjście jest zawsze podłączone do
Wyjście jest zawsze podłączone do VV
DD
DD
lub
lub VV
SS
SS
((Gnd
Gnd))
Î
Î
nniska impedancja wyjściowa
iska impedancja wyjściowa
((rzędu
rzędu kkΩ
Ω
) )
nn ska mpedancja wyjśc owa
ska mpedancja wyjśc owa
((rzędu
rzędu kk ) )
Î
Î
mniejsza czułość na szum i zakłócenia
mniejsza czułość na szum i zakłócenia
6 marca 2011
Wojciech Kucewicz
34

Właściwości inwertera CMOS
Właściwości inwertera CMOS
Właściwości inwertera CMOS
Właściwości inwertera CMOS
Bardzo wysoka rezystancja wejściowa (bramka tranzystora
Bardzo wysoka rezystancja wejściowa (bramka tranzystora
Bardzo wysoka rezystancja wejściowa (bramka tranzystora
Bardzo wysoka rezystancja wejściowa (bramka tranzystora
MOS
MOS jest okładką kondensatora
jest okładką kondensatora) )
Î
Î
bliski zera prąd wejściowy
bliski zera prąd wejściowy
Î
Î
j d i
t
ż
j d i
t
ż t
t
i
t
t
i
t
ć
t
ć
Î
Î
jeden inwerter może
jeden inwerter może teroretycznie
teroretycznie sterować
sterować
nieskończoną ilość bramek
nieskończoną ilość bramek
B k b
ś d
ś
k
d
d l
l
B k b
ś d
ś
k
d
d l
l
Brak bezpośredniej ścieżki prądowej pomiędzy liniami zasilania
Brak bezpośredniej ścieżki prądowej pomiędzy liniami zasilania
Î
Î
brak strat mocy statycznej
brak strat mocy statycznej
Czas propagacji sygnału jest funkcją pojemności
Czas propagacji sygnału jest funkcją pojemności obciażenia
obciażenia i i
rezystancji kanału tranzystora
rezystancji kanału tranzystora
6 marca 2011
Wojciech Kucewicz
35

Czas propagacji
Czas propagacji
Czas propagacji
Czas propagacji
6 marca 2011
Wojciech Kucewicz
36
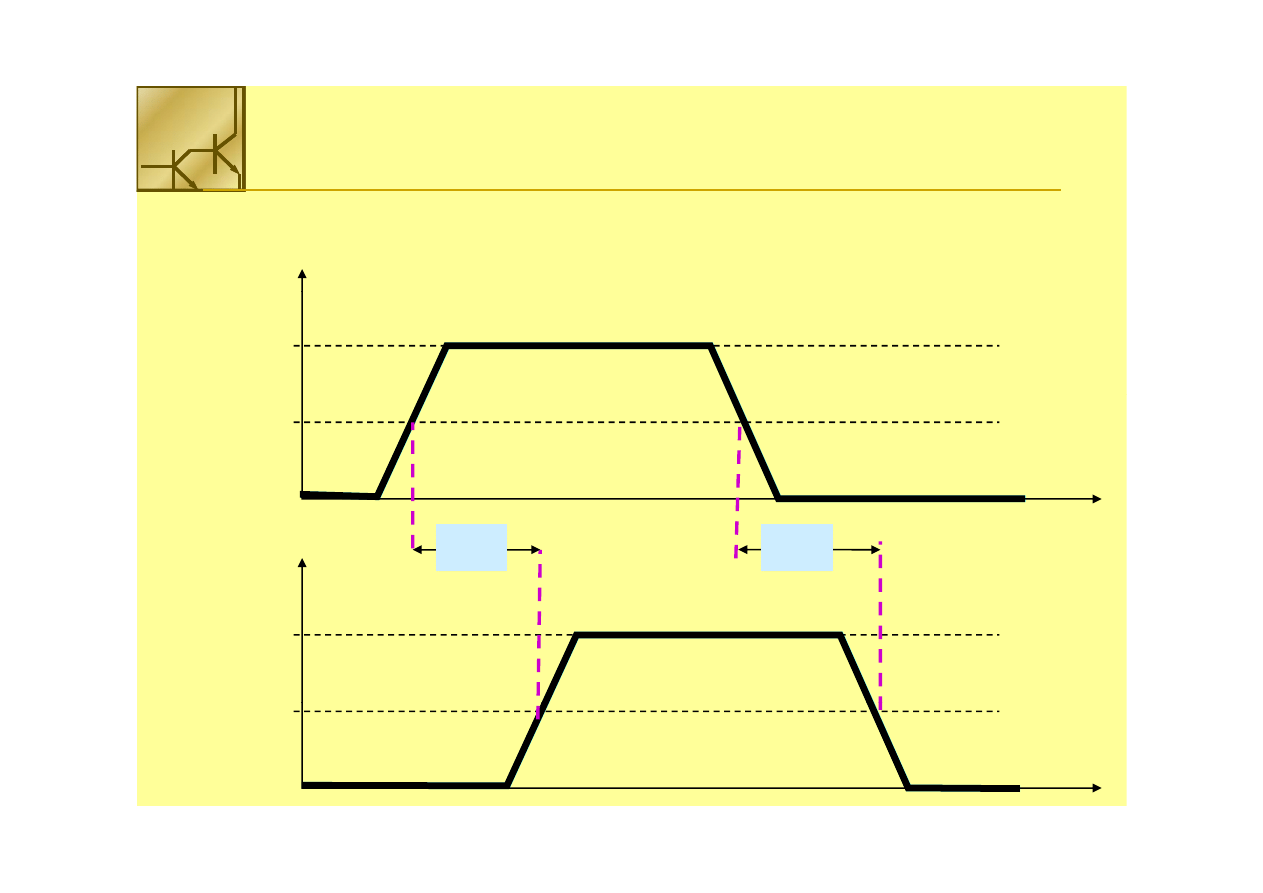
Czas propagacji
Czas propagacji
Czas propagacji
Czas propagacji
VV
in
in
Czas propagacji
Czas propagacji:: tplh, tphl
tplh, tphl
, , opóźnienie mierzone od
opóźnienie mierzone od
momentu, gdy sygnał wejściowy osiągnie 50% wartości
momentu, gdy sygnał wejściowy osiągnie 50% wartości
maksymalnej do czasu kiedy sygnał wyjściowy osiągnię 50
maksymalnej do czasu kiedy sygnał wyjściowy osiągnię 50
in
in
VV
max
max
maksymalnej, do czasu kiedy sygnał wyjściowy osiągnię 50
maksymalnej, do czasu kiedy sygnał wyjściowy osiągnię 50
% wartości maksymalnej. Generalnie
% wartości maksymalnej. Generalnie
tplh
tplh ≠≠ tphl
tphl
..
tt
VV
max
max
/2
/2
00
VV
out
out
tt
PLH
PLH
tt
PHL
PHL
VV
max
max
6 marca 2011
Wojciech Kucewicz
37
tt
VV
max
max
/2
/2
00
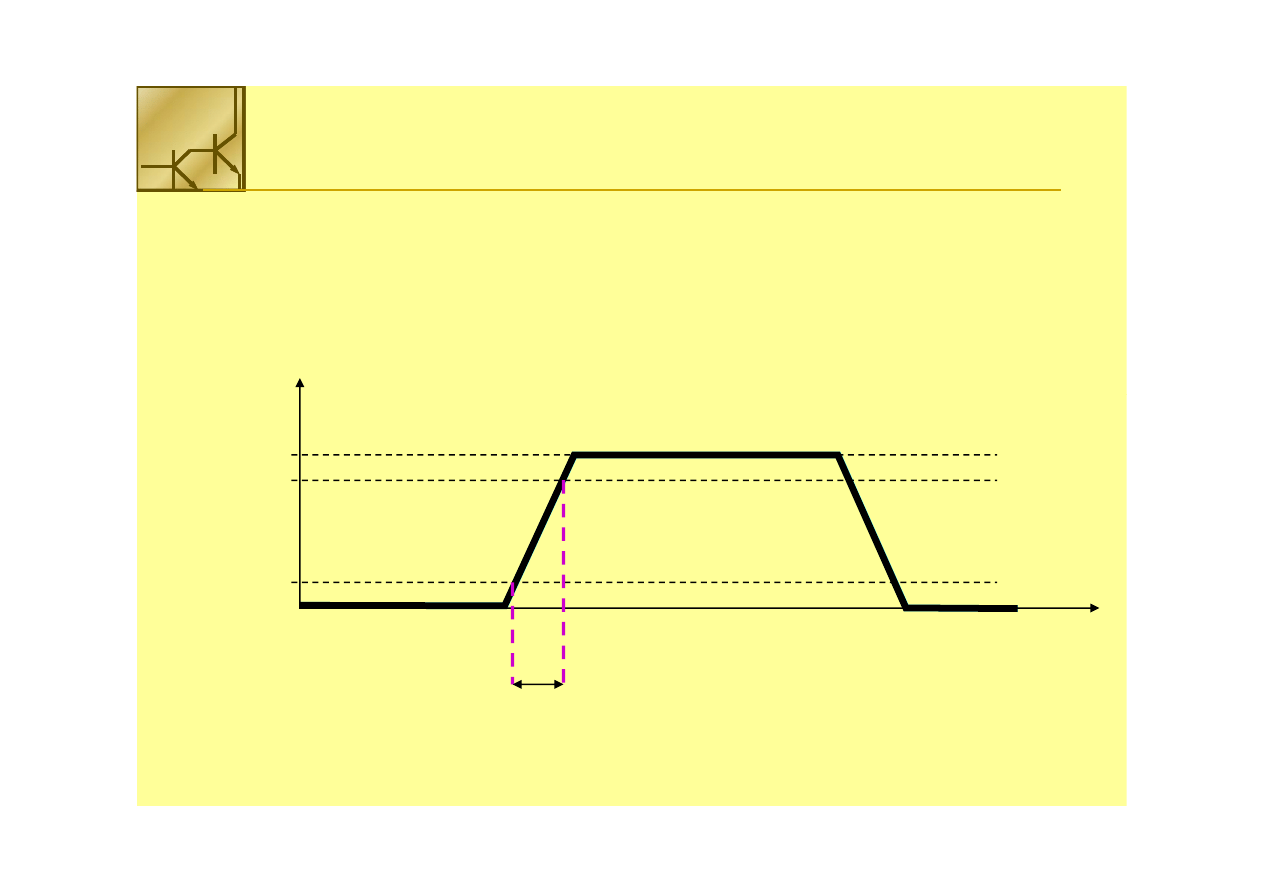
Czas propagacji
Czas propagacji
Czas propagacji
Czas propagacji
Czas narastania (
Czas narastania (Rise Time
Rise Time)):: tr
tr
, , czas potrzebny do wzrostu
czas potrzebny do wzrostu
sygnału od 10% do 90% jego wartości maksymalnej.
sygnału od 10% do 90% jego wartości maksymalnej.
VV
in
in
VV
in
in
VV
max
max
0,9 V
0,9 V
max
max
tt
,,
max
max
0,1 Vmax
0,1 Vmax
0000
tt
6 marca 2011
Wojciech Kucewicz
38
tt
rr
Czas propagacji
Czas propagacji
Czas propagacji
Czas propagacji
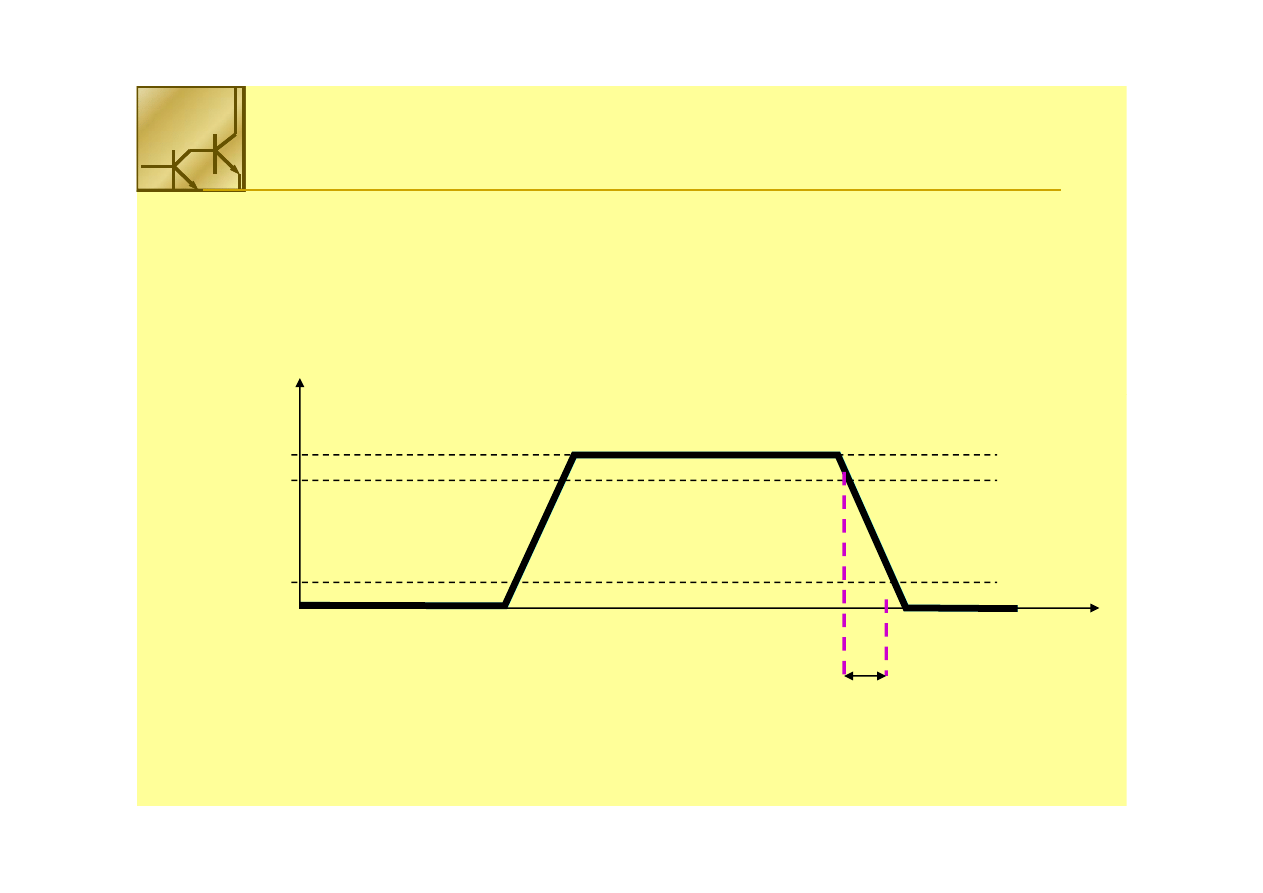
Czas opadania (
Czas opadania (Fall Time
Fall Time)): tf
: tf
, , czas potrzebny do spadku sygnału od
czas potrzebny do spadku sygnału od
90% do 10% jego wartości maksymalnej.
90% do 10% jego wartości maksymalnej.
VV
in
in
VV
in
in
VV
max
max
0,9 V
0,9 V
max
max
tt
,,
max
max
0,1 Vmax
0,1 Vmax
0000
tt
ff
6 marca 2011
Wojciech Kucewicz
39
ff
Czas propagacji w układach kombinacyjnych
Czas propagacji w układach kombinacyjnych
Czas propagacji w układach kombinacyjnych
Czas propagacji w układach kombinacyjnych
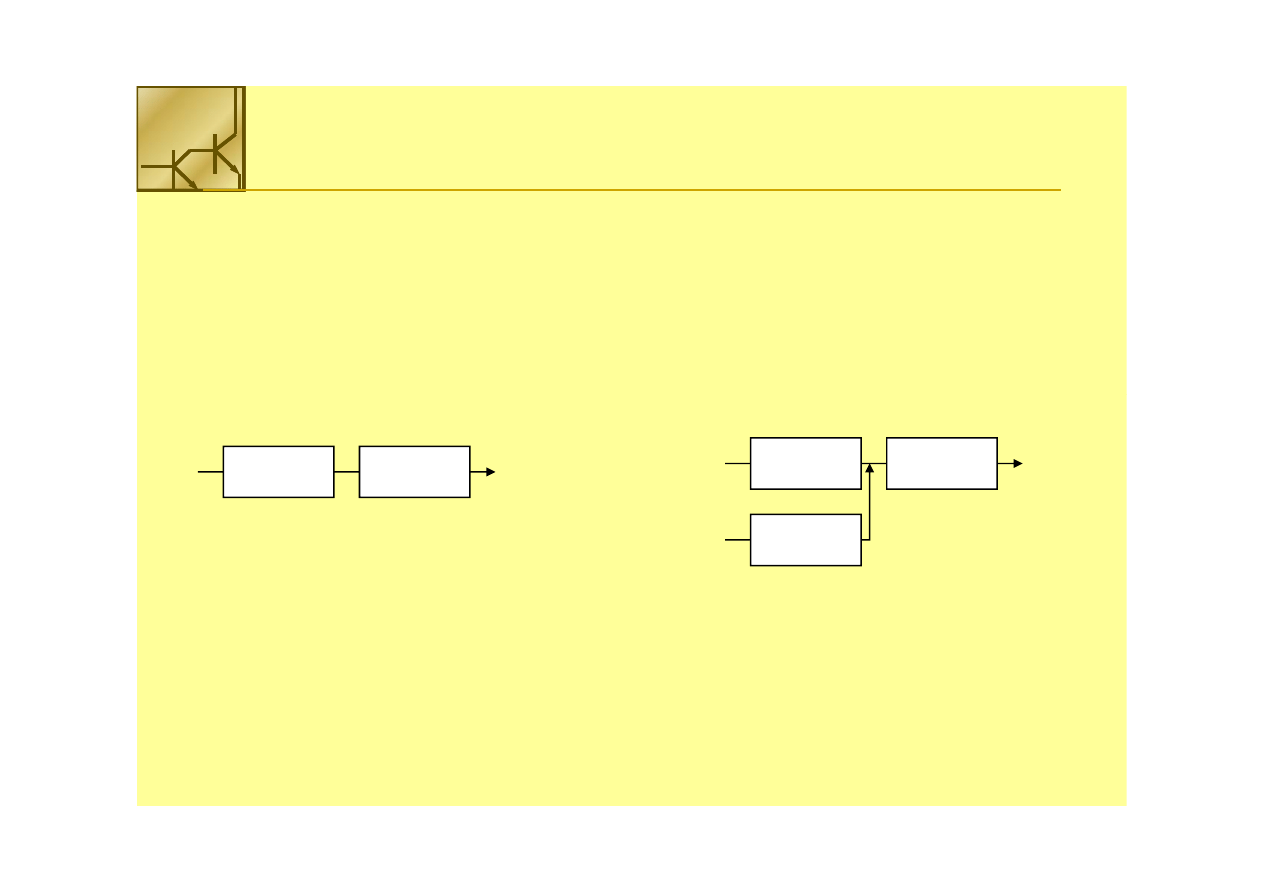
Czas propagacji sygnału w układzie wyznaczany jest to
Czas propagacji sygnału w układzie wyznaczany jest to
j i k
óź i i j ki
ż
t ić kł d i
j i k
óź i i j ki
ż
t ić kł d i
największe opóźnienie jakie może wystąpić w układzie
największe opóźnienie jakie może wystąpić w układzie
5
5 ns
ns
12 ns
12 ns
5 ns
5 ns
12 ns
12 ns
8 ns
8 ns
T
T
pp
= 5 ns + 12 ns = 17 ns
= 5 ns + 12 ns = 17 ns
T
T
pp
= 8 ns + 12 ns = 20 ns
= 8 ns + 12 ns = 20 ns
6 marca 2011
Wojciech Kucewicz
40
Czas propagacji w układach
Czas propagacji w układach
kombinacyjnych
kombinacyjnych
Czas propagacji w układach
Czas propagacji w układach
kombinacyjnych
kombinacyjnych
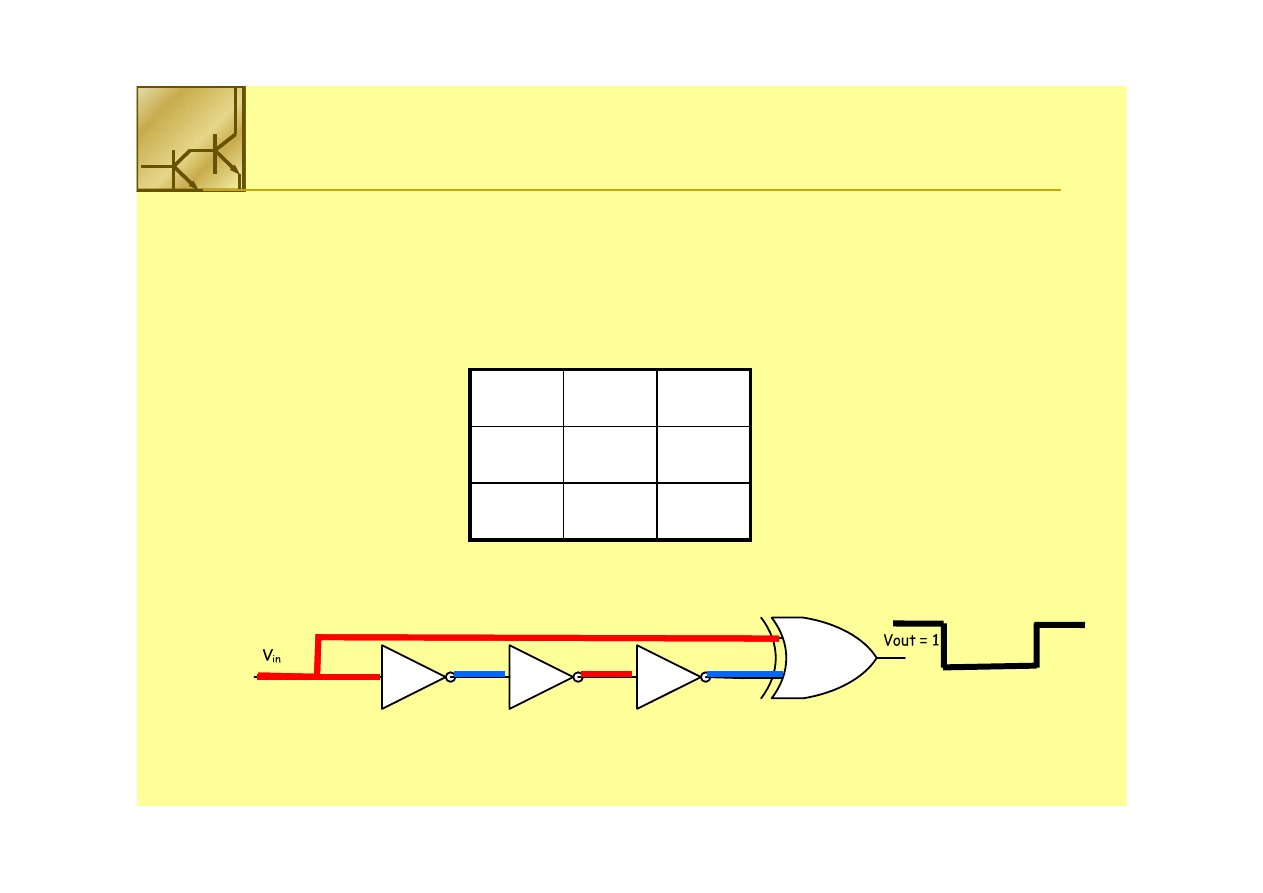
Zastosowanie bramek ze skończonym czasem
Zastosowanie bramek ze skończonym czasem propagacji
propagacji, ,
jj
tt
plh
plh
and
and tt
phl
phl
G t
G t
tt
tt
Gate
Gate
tt
PLH
PLH
tt
PHL
PHL
Invert
Invert
12
12
88
XOR
XOR
18
18
13
13
6 marca 2011
Wojciech Kucewicz
41
I1
I1
I2
I2
I3
I3
Czas propagacji w układach
Czas propagacji w układach
kombinacyjnych
kombinacyjnych
Czas propagacji w układach
Czas propagacji w układach
kombinacyjnych
kombinacyjnych
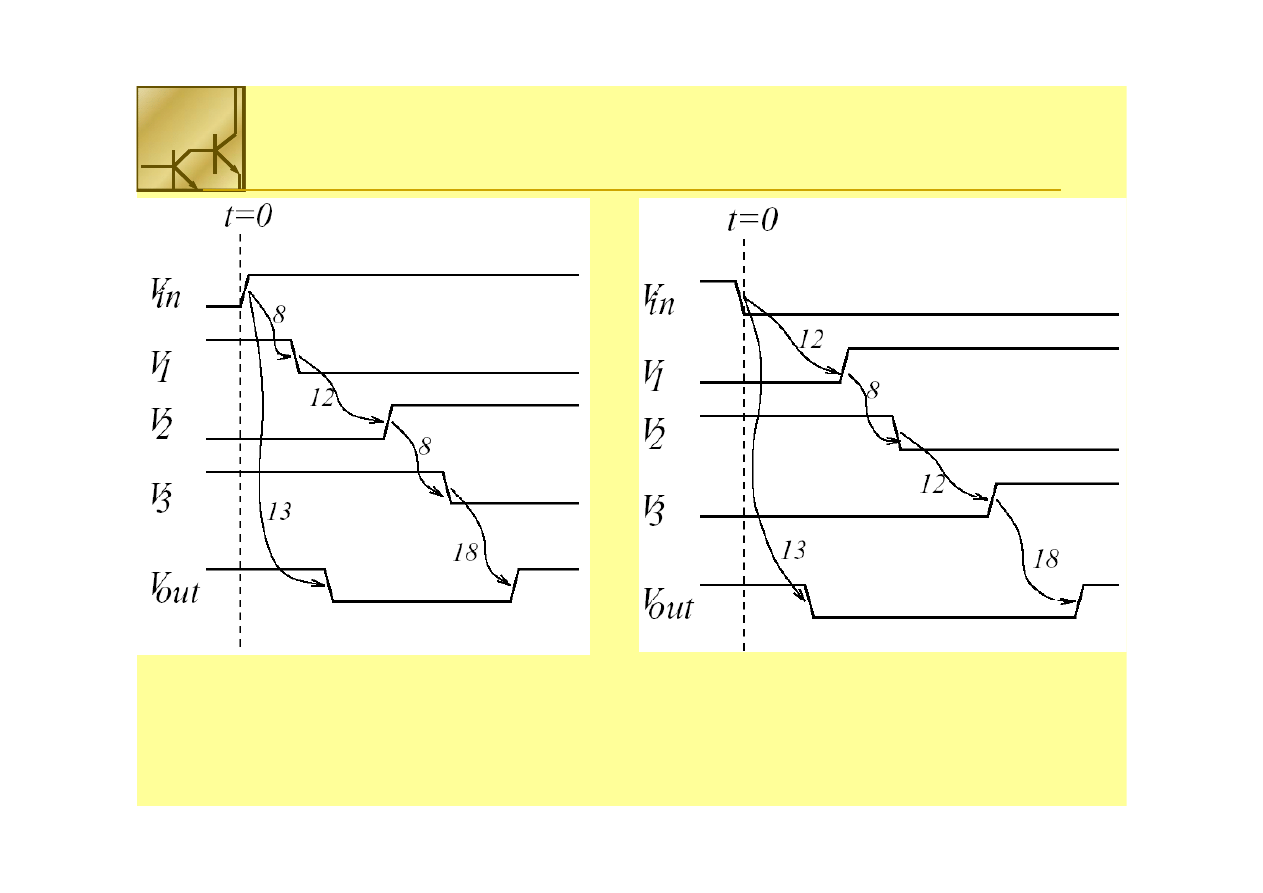
Przełączenie wejścia ze
Przełączenie wejścia ze
Przełączenie wejścia ze
Przełączenie wejścia ze
6 marca 2011
Wojciech Kucewicz
42
Przełączenie wejścia ze
Przełączenie wejścia ze
stanu niskiego do wysokiego
stanu niskiego do wysokiego
Przełączenie wejścia ze
Przełączenie wejścia ze
stanu wysokiego do niskiego
stanu wysokiego do niskiego

Straty mocy
Straty mocy
Straty mocy
Straty mocy
6 marca 2011
Wojciech Kucewicz
43
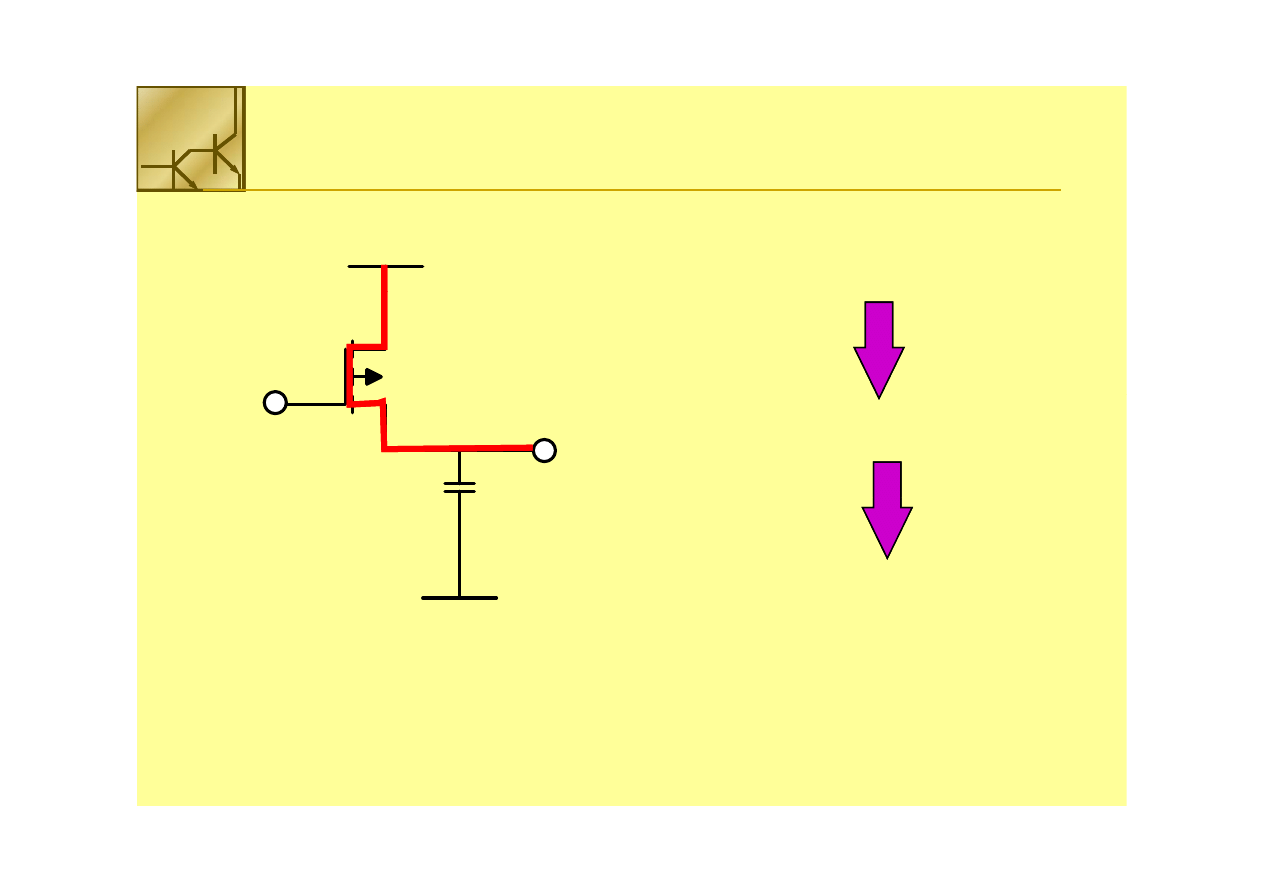
Dynamiczne straty mocy
Dynamiczne straty mocy
Dynamiczne straty mocy
Dynamiczne straty mocy
PP
dyn
dyn
= C
= C
L
L
••
VV
DD
DD
22
••
ff
PP
dyn
dyn
= C
= C
L
L
••
VV
DD
DD
22
••
ff
V
DD
dyn
dyn
L
L
DD
DD
dyn
dyn
L
L
DD
DD
Vin =0
PP
dyn
dyn
= 6fF • 2.5V
= 6fF • 2.5V
22
•• 500MHz = 20
500MHz = 20μμW
W
1M gates
1M gates
Vout = 1
V
SS
PP
tot
tot
= 20W
= 20W
PP
tot
tot
= 20W
= 20W
6 marca 2011
Wojciech Kucewicz
44
Każde przełączenie braki wymaga
przeładowania pojemności pasożytniczych
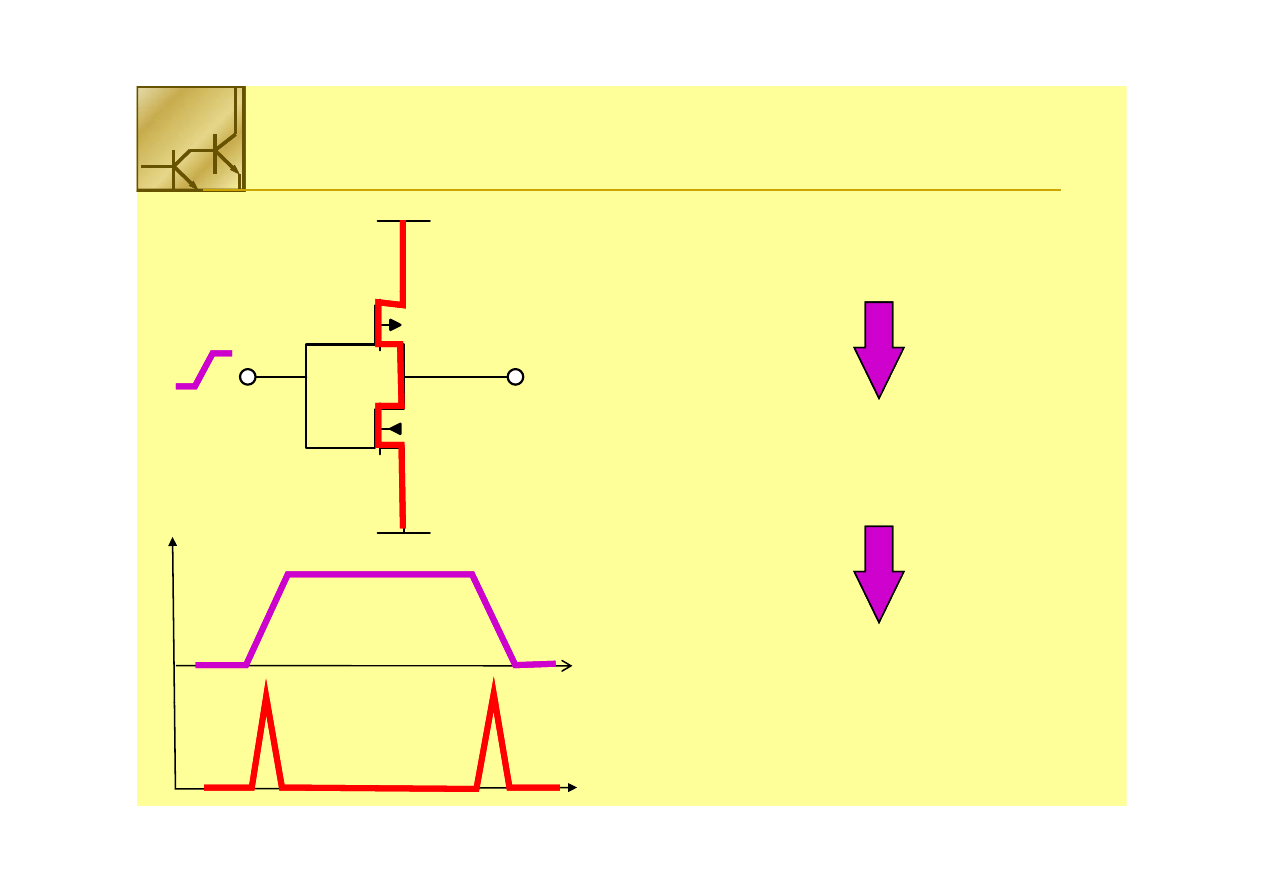
Straty mocy przy przełączaniu (
Straty mocy przy przełączaniu (direct
direct--
path
path))
Straty mocy przy przełączaniu (
Straty mocy przy przełączaniu (direct
direct--
path
path))
PP
dd
= t
= t
s
s
••
II
Peak
Peak
••
VV
DD
DD
••
ff
PP
dd
= t
= t
s
s
••
II
Peak
Peak
••
VV
DD
DD
••
ff
V
DD
PMOS
V
in
V
out
PP
dyn
dyn
= 100ps • 50
= 100ps • 50 μμA • 2.5V •
A • 2.5V • 500MHz
500MHz
= 6.25
= 6.25 μμW
W
NMOS
1M gates
1M gates
V
SS
V
V
in
in
PP
tot
tot
= 6.25 W
= 6.25 W
II
short
short
6 marca 2011
Wojciech Kucewicz
45
W momencie przełączania oba tranzystory:
PMOS i NMOS są przez moment jednocześnie
włączone
short
short
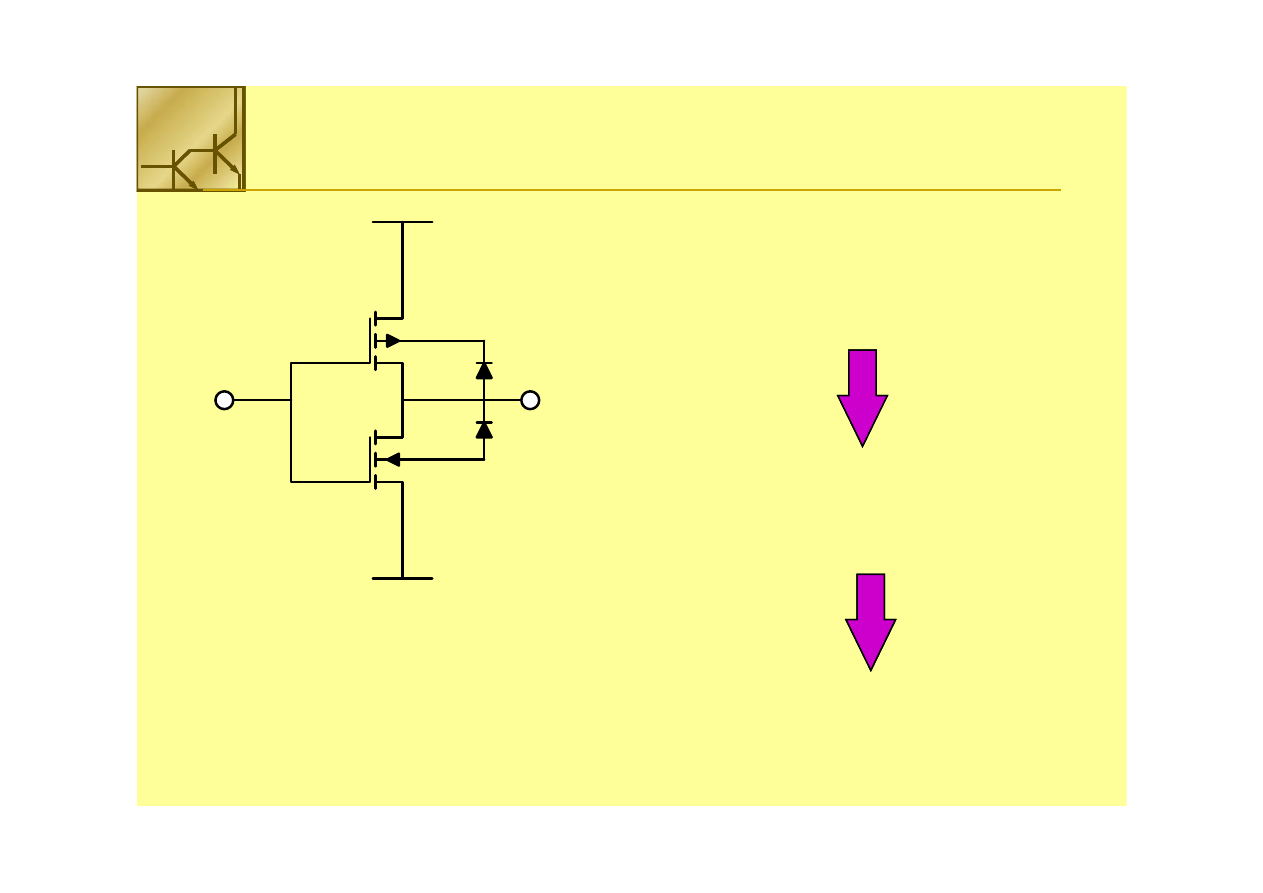
Statyczne straty mocy
Statyczne straty mocy
Statyczne straty mocy
Statyczne straty mocy
PP
I
I
VV
PP
I
I
VV
V
DD
PP
stat
stat
= I
= I
stat
stat
••
VV
DD
DD
PP
stat
stat
= I
= I
stat
stat
••
VV
DD
DD
PMOS
V
in
V
out
PP
stat
stat
= 10pA/
= 10pA/μμm
m
22
• 0.5
• 0.5 μμm
m
22
•• 2.5V
2.5V
NMOS
pp
= 125
= 125 pW
pW
V
SS
1M gates
1M gates
Źródło i dren są złączami p-n spolaryzowanymi zaporowo
6 marca 2011
Wojciech Kucewicz
46
PP
tot
tot
= 125
= 125 μμW
W

Podstawowe
Podstawowe
Podstawowe
Podstawowe
Bramki
Bramki
Bramki
Bramki
m
m
Logiczne
Logiczne
m
m
Logiczne
Logiczne
Logiczne
Logiczne
Logiczne
Logiczne
6 marca 2011
Wojciech Kucewicz
47

Bramka
Bramka
Bramka
Bramka
Bramka
Bramka
i j
i j
Bramka
Bramka
i j
i j
transmisyjna
transmisyjna
transmisyjna
transmisyjna
yj
yj
yj
yj
6 marca 2011
Wojciech Kucewicz
48
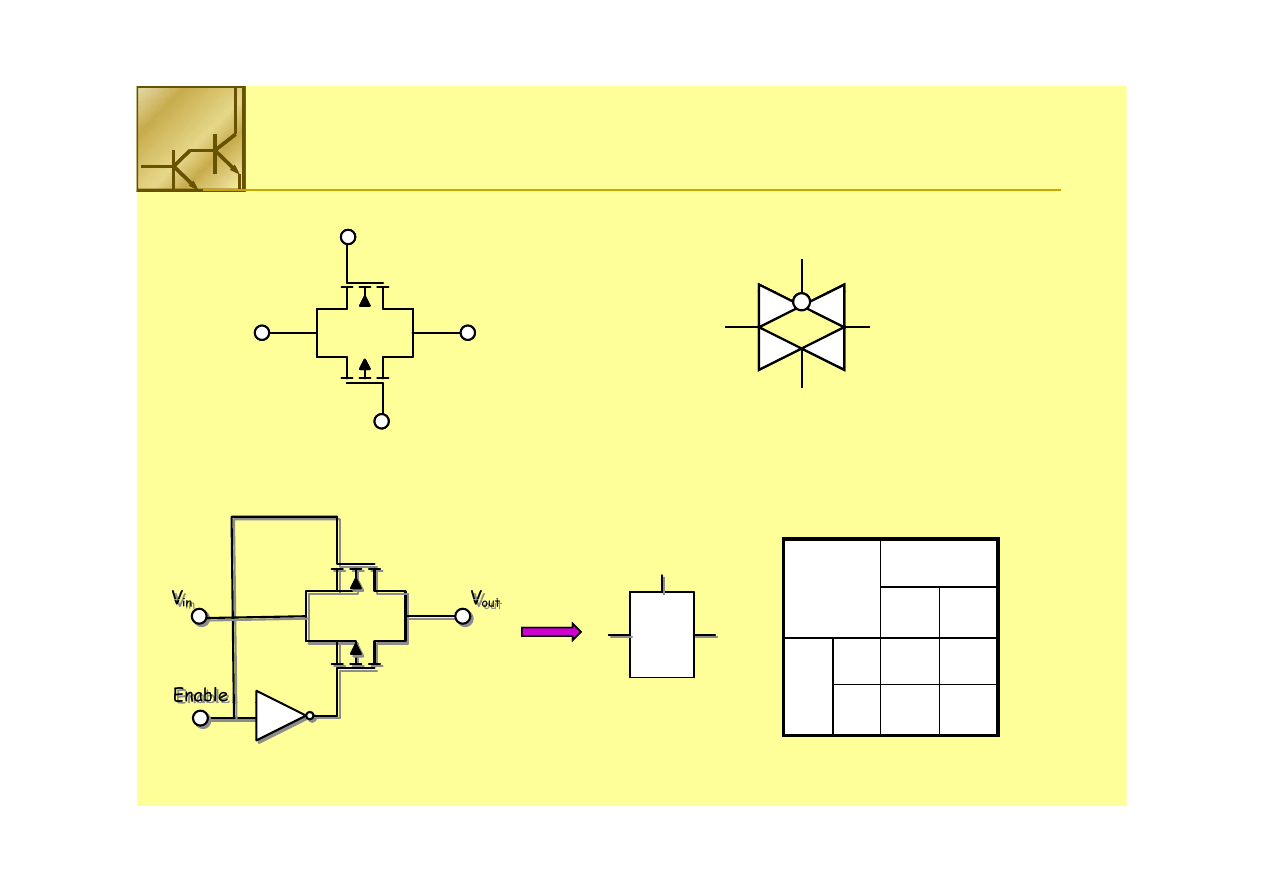
Bramka transmisyjna
Bramka transmisyjna
Bramka transmisyjna
Bramka transmisyjna
Enable
Enable
En’
En’
En’
En’
Input
Input
Ouput
Ouput
In
In
Out
Out
En
En
In
In
Out
Out
En
En
⇔
⇔
S D
S D
NotEnable
NotEnable
Bramka transmisyjna wykonana jest z 2 tranzystorów (NMOS i PMOS)
połączonych źródłami i drenami
Out
Out
Enable
Enable
połączonych źródłami i drenami .
En
En
00
11
In
In
00
xx
00
11
11
En
In Out
TG
En
In Out
TG
6 marca 2011
Wojciech Kucewicz
49
11
xx
11
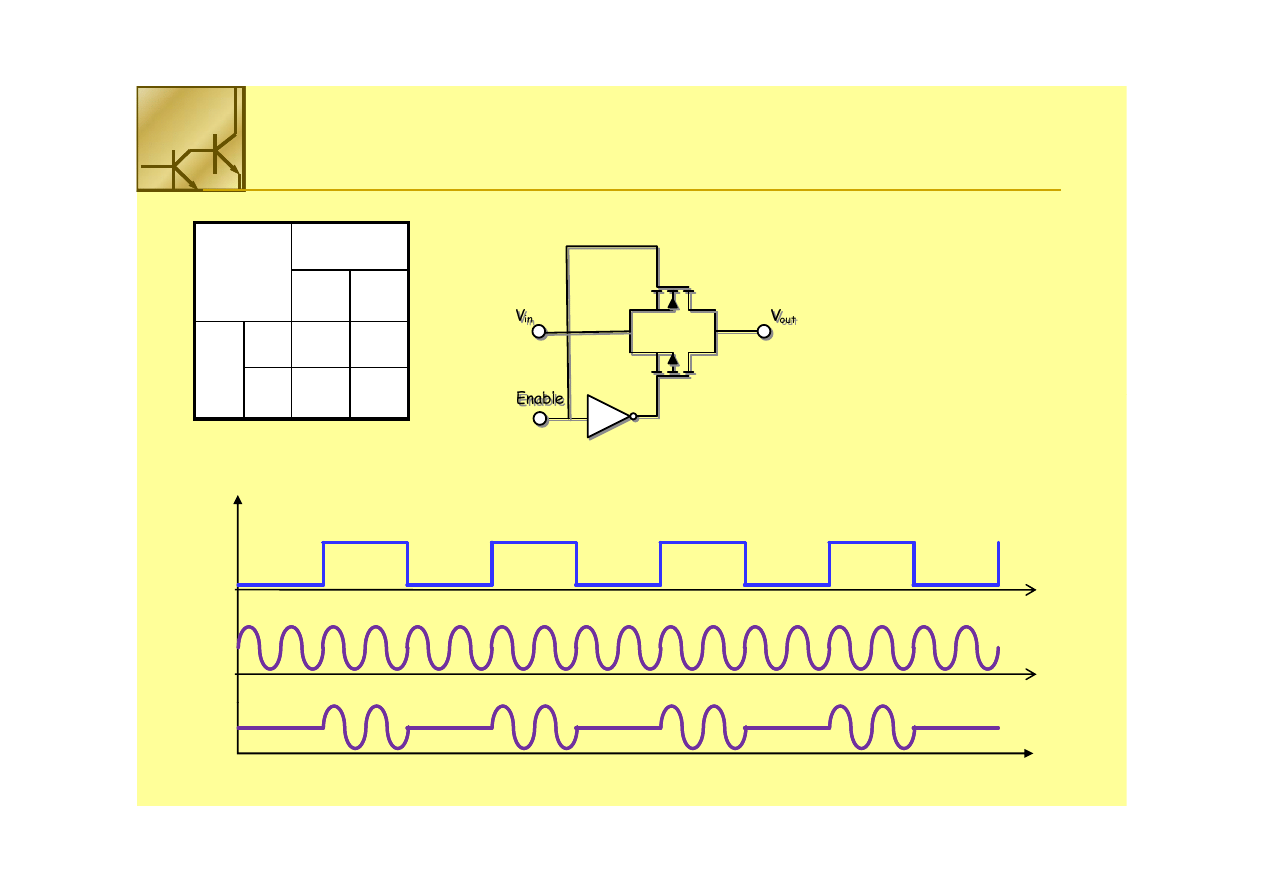
Bramka transmisyjna
Bramka transmisyjna
Bramka transmisyjna
Bramka transmisyjna
Out
Out
Enable
Enable
00
11
00
11
In
In
00
xx
00
11
xx
11
11
xx
11
Enable
Enable
V
V
in
in
V
V
6 marca 2011
Wojciech Kucewicz
50
V
V
out
out
t

Rejestr przesuwny
Rejestr przesuwny
Rejestr przesuwny
Rejestr przesuwny
j
p
y
j
p
y
j
p
y
j
p
y
6 marca 2011
Wojciech Kucewicz
51
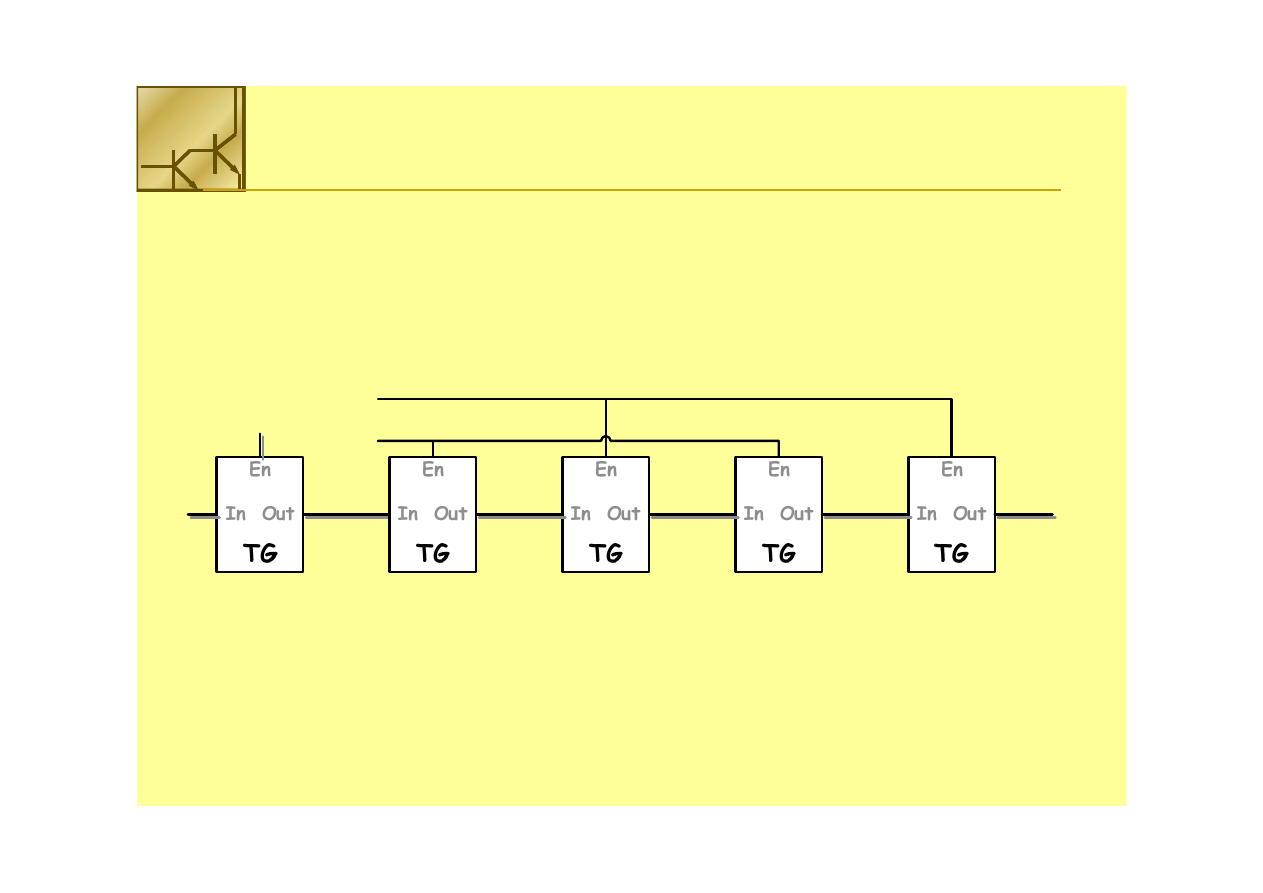
Rejestr przesuwny
Rejestr przesuwny
Rejestr przesuwny
Rejestr przesuwny
Łącząc bramki transmisyjne w szeregowo i przełączając je naprzemiennie
można utworzyć rejestr przesuwny.
n tΦ
O
O
O
O
1111
notΦ
Φ
O
O
11
O
O
11
11
1111
11
00
11
00
00000000
6 marca 2011
Wojciech Kucewicz
52

Inwerter
Inwerter
Inwerter
Inwerter
Inwerter
Inwerter
trójstanowy
trójstanowy
Inwerter
Inwerter
trójstanowy
trójstanowy
trójstanowy
trójstanowy
trójstanowy
trójstanowy
6 marca 2011
Wojciech Kucewicz
53
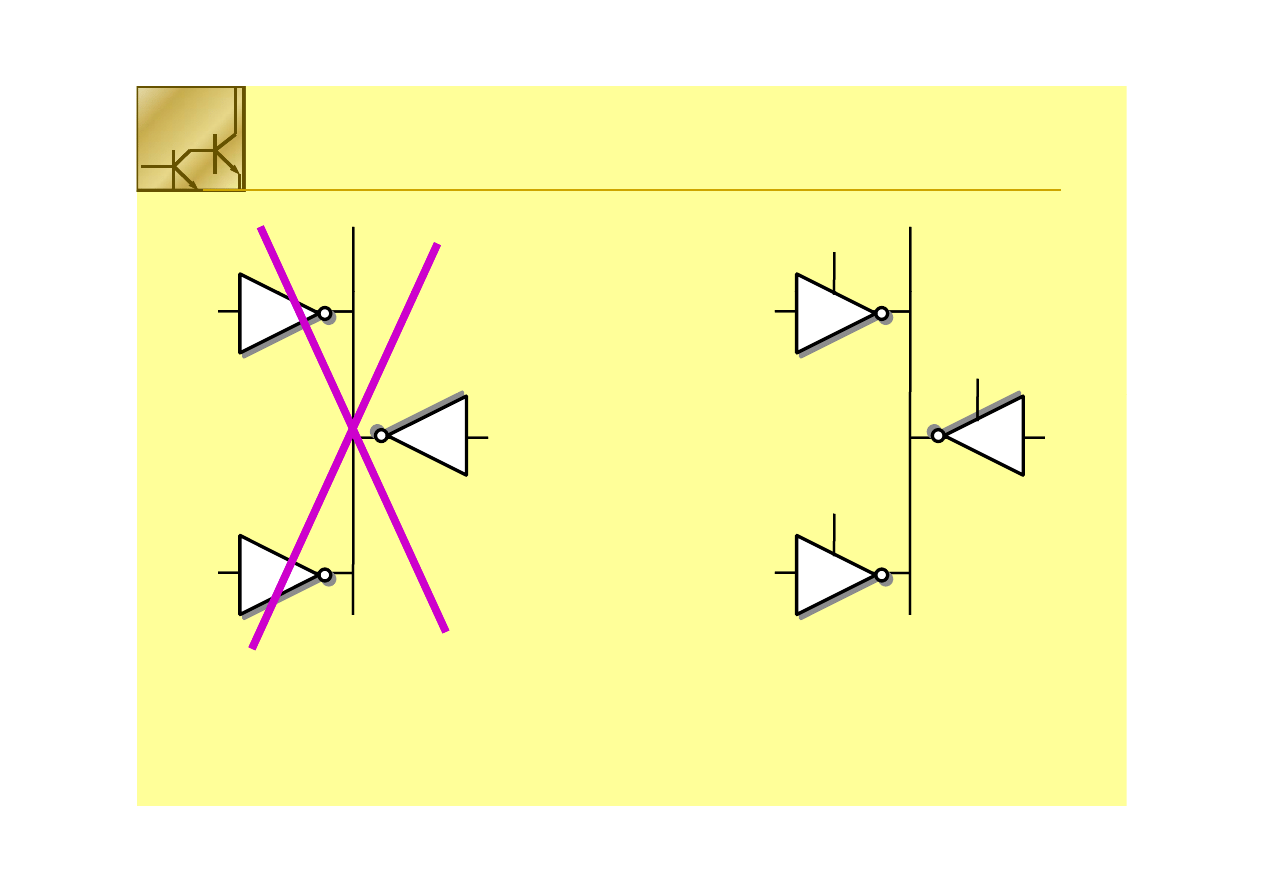
Inwerter trójstanowy
Inwerter trójstanowy
Inwerter trójstanowy
Inwerter trójstanowy
En
En
En
Jaki jest stan logiczny linii?
Jaki jest stan logiczny linii?
Jaki jest stan logiczny linii?
Jaki jest stan logiczny linii?
Wejście
Wejście Enable
Enable podłącza do linii tylko
podłącza do linii tylko
j d i
t ó d
j h ili
j d i
t ó d
j h ili
Wejście
Wejście Enable
Enable podłącza do linii tylko
podłącza do linii tylko
j d i
t ó d
j h ili
j d i
t ó d
j h ili
6 marca 2011
Wojciech Kucewicz
54
j
g
y
j
g
y
Konflikt logiczny
Konflikt logiczny
j
g
y
j
g
y
Konflikt logiczny
Konflikt logiczny
jeden z inwerterów w danej chwili
jeden z inwerterów w danej chwili
jeden z inwerterów w danej chwili
jeden z inwerterów w danej chwili
Jak to zrealizować?
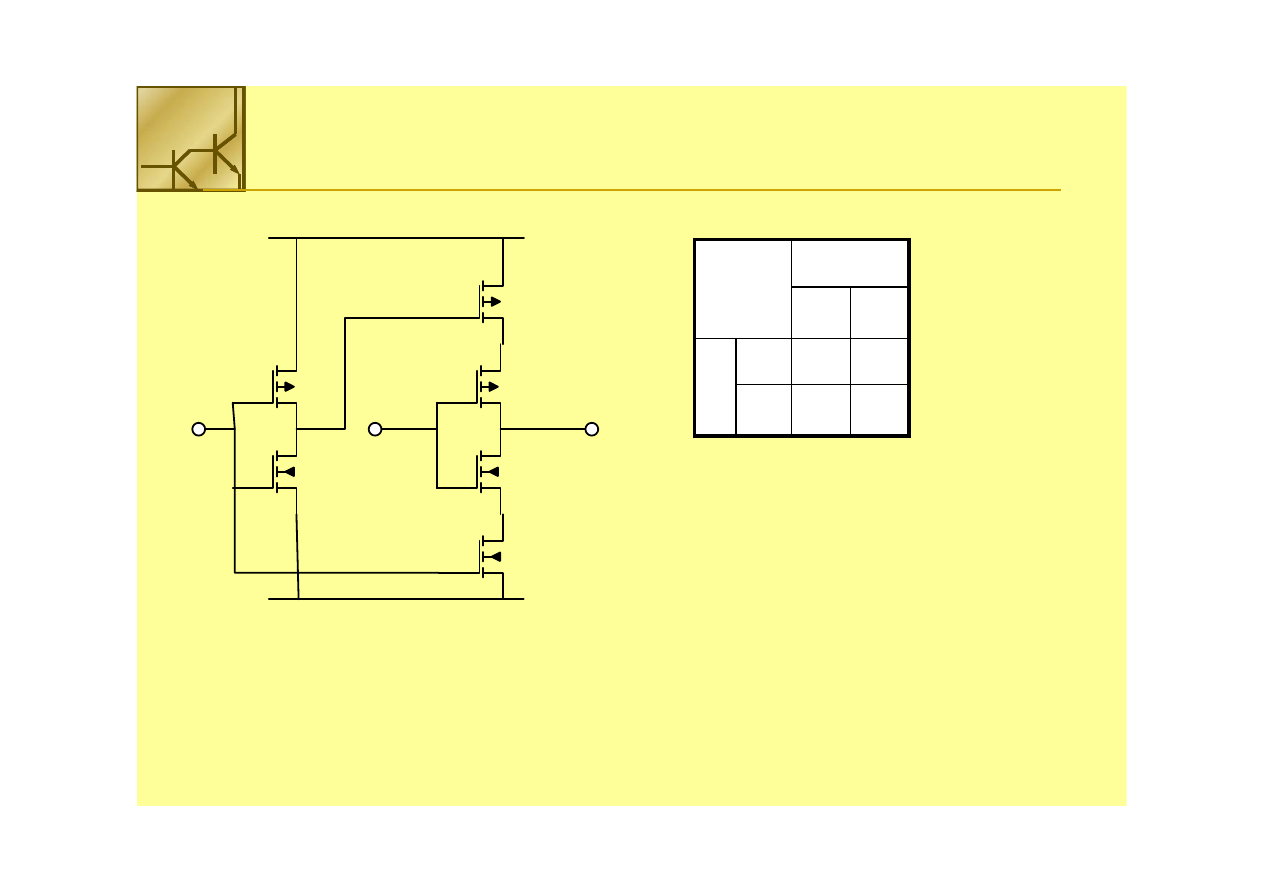
Inwerter trójstanowy
Inwerter trójstanowy
Inwerter trójstanowy
Inwerter trójstanowy
FF
Enable
Enable
V
DD
FF
00
11
InIn
00
xx
11
nn
11
xx
00
PMOS
NMOS
V
in
PMOS
NMOS
V
out
Enable
V
SS
6 marca 2011
Wojciech Kucewicz
55
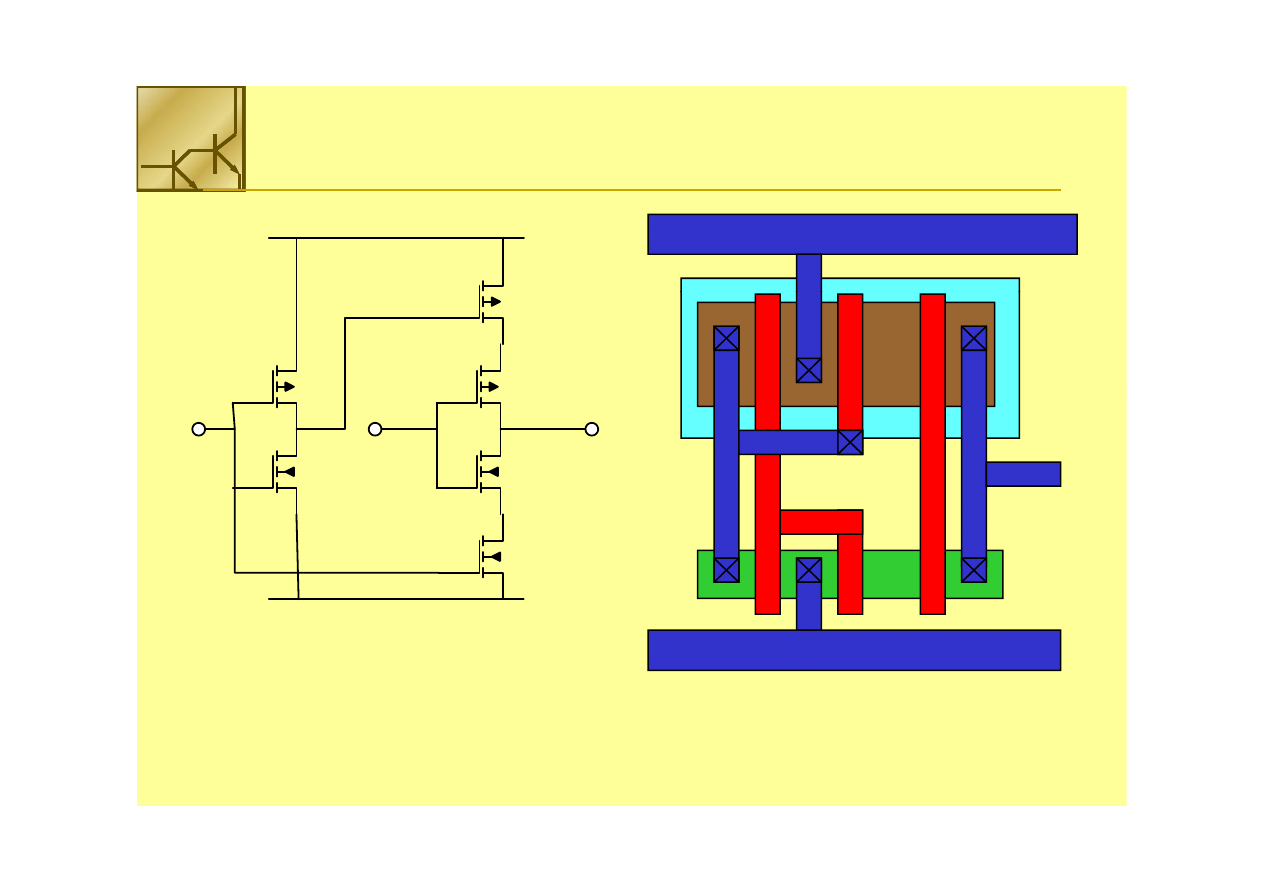
Inwerter trójstanowy
Inwerter trójstanowy
Inwerter trójstanowy
Inwerter trójstanowy
VV
DD
DD
V
DD
nablenableEnEn
FF
DataData
PMOS
NMOS
V
in
PMOS
NMOS
V
out
Enable
VV
SS
SS
V
SS
6 marca 2011
Wojciech Kucewicz
56

Bramki
Bramki
Bramki
NAND & NOR
Bramki
NAND & NOR
NAND & NOR
NAND & NOR
6 marca 2011
Wojciech Kucewicz
57
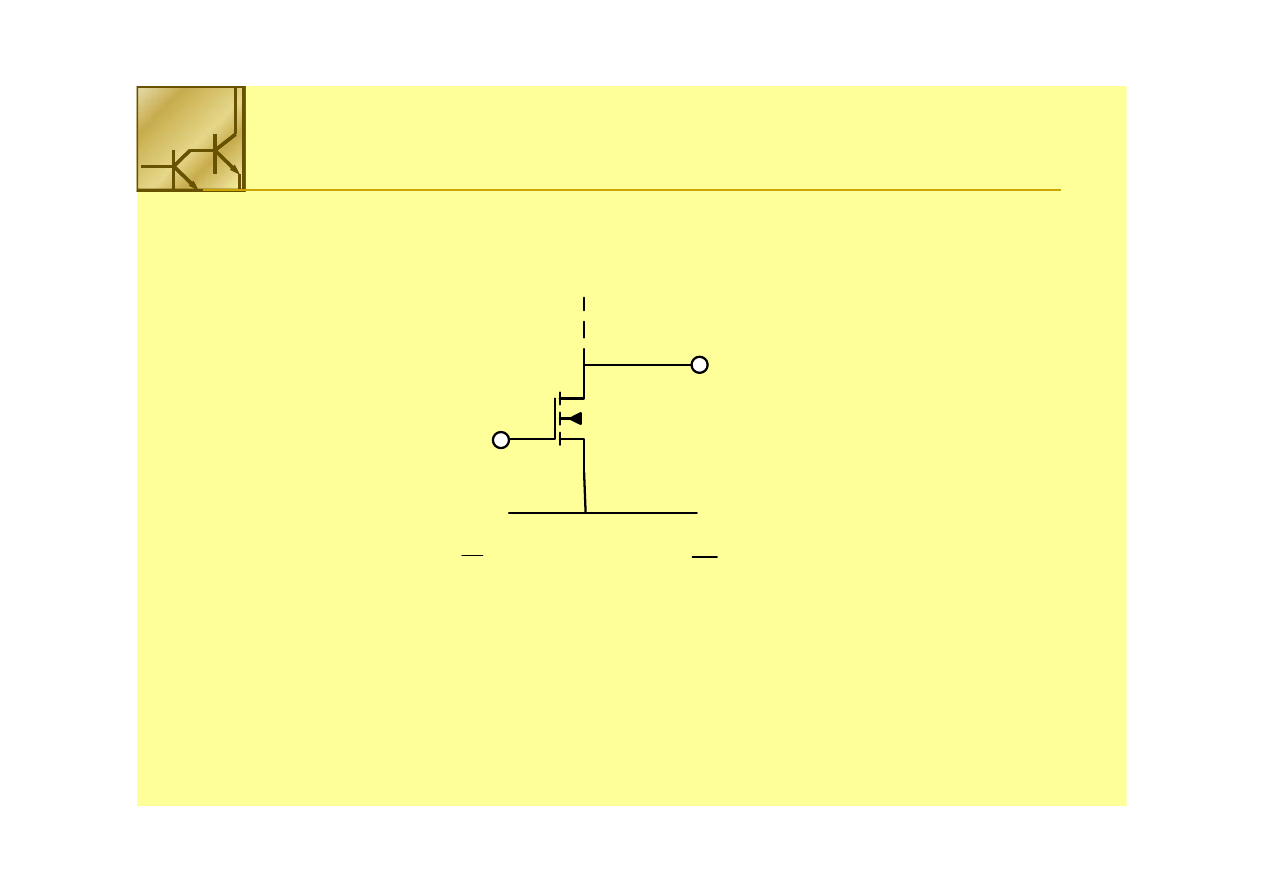
Logika NMOS
Logika NMOS
Logika NMOS
Logika NMOS
Tranzystory NMOS służą jako włączniki niskiego napięcia V
SS
.
Wysokie napięcie na bramce łączy wyjście z linią niskiego napięcia V
SS
.
F =V
SS
= 0
V
SS
NMOS
A =V
DD
= 1
V
SS
A
F
A
F
=
⇒
=
6 marca 2011
Wojciech Kucewicz
58
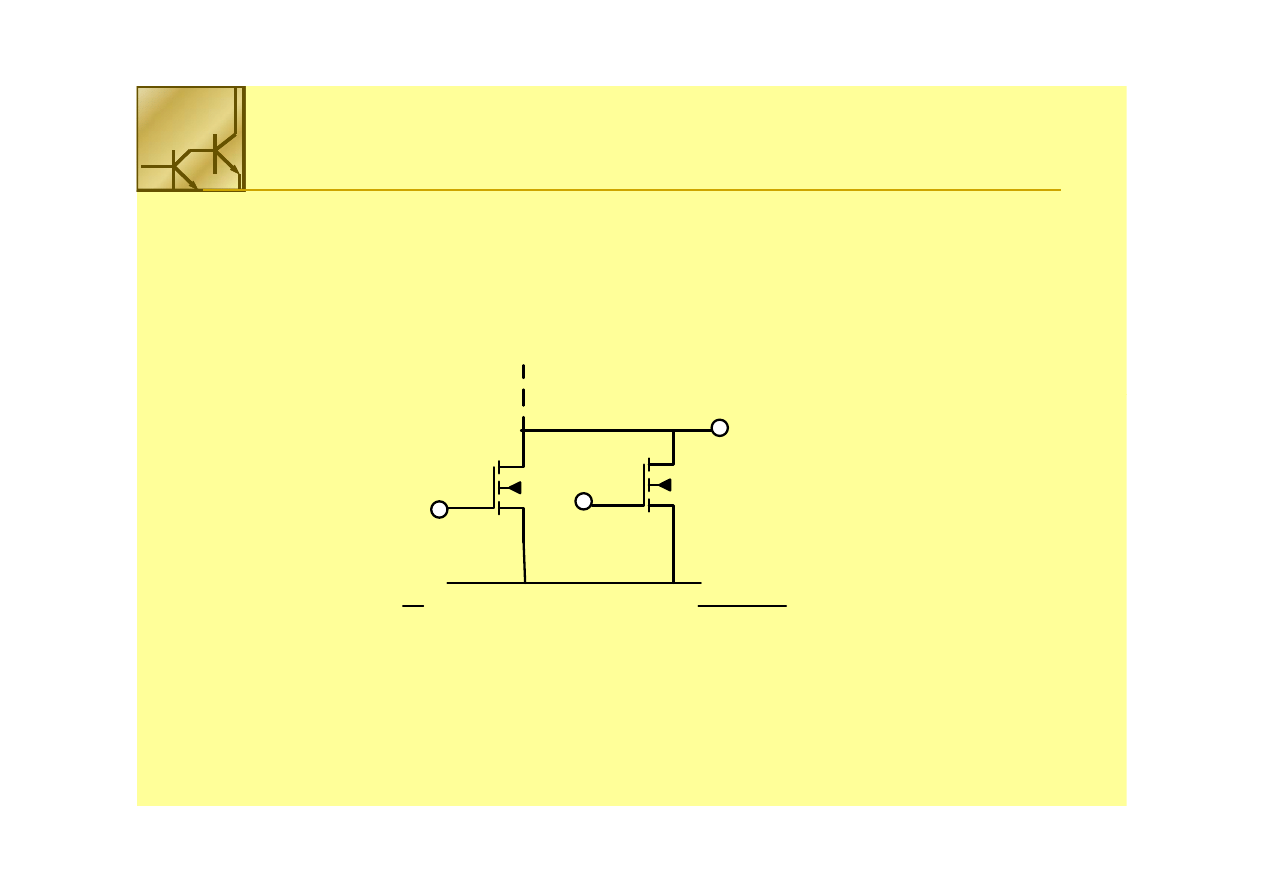
Logika NMOS
Logika NMOS
Logika NMOS
Logika NMOS
Połączenie równoległe tranzystorów NMOS realizuje funkcję logiczną zaprzeczenia
sumy. Wystarczy, że jeden z tranzystorów NMOS przewodzi (na bramce logiczna 1),
aby na wyjściu otrzymać logiczne 0.
y
yj
y
g
NMOS
F
A
B
V
SS
B
A
F
B
A
F
+
=
⇒
+
=
6 marca 2011
Wojciech Kucewicz
59
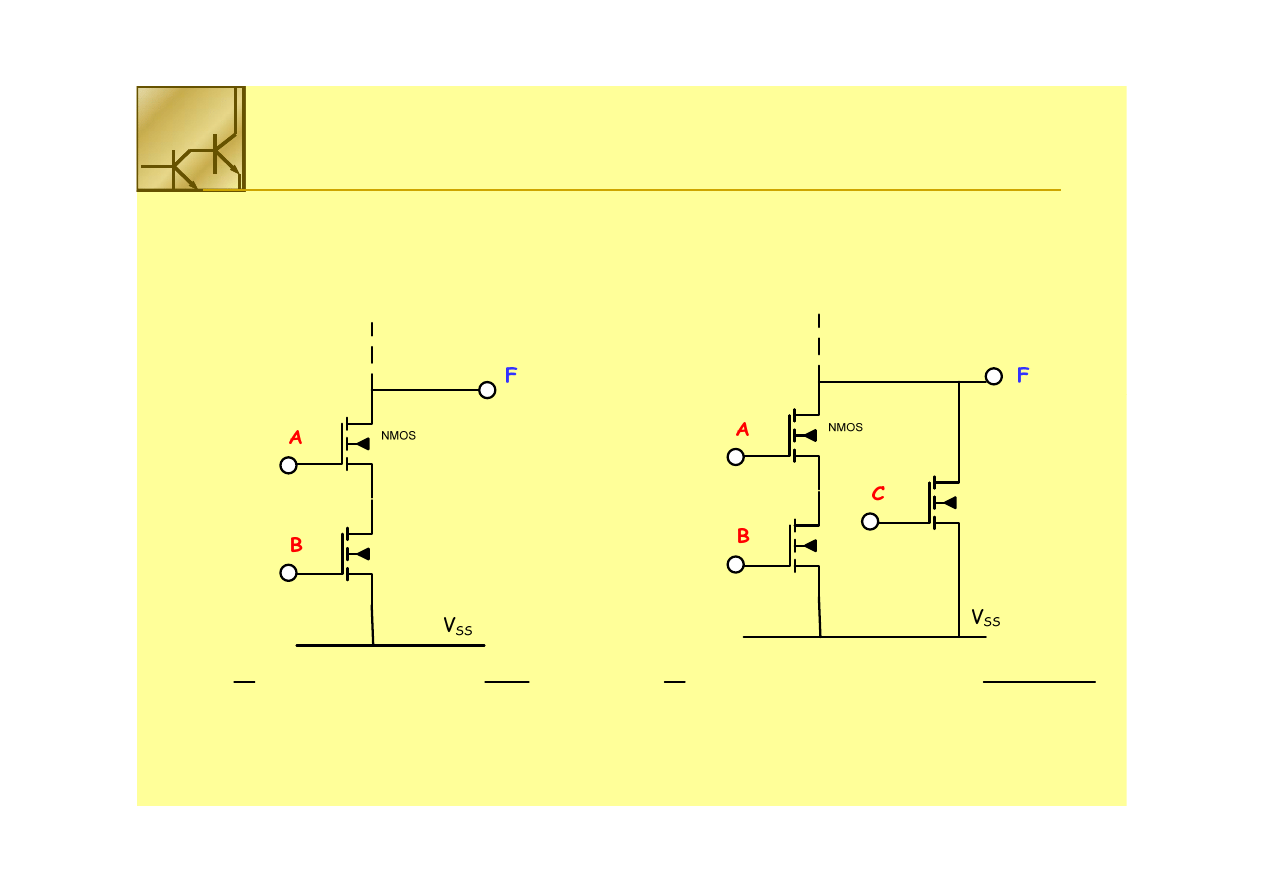
Logika NMOS
Logika NMOS
Logika NMOS
Logika NMOS
Połączenie szeregowe tranzystorów NMOS realizuje funkcję logiczną zaprzeczenia
iloczynu. Oba tranzystory NMOS muszą przewodzić (na bramkach logiczna 1), aby na
wyjściu otrzymać logiczne 0.
yj
y
g
AB
F
AB
F
=
⇒
=
C
AB
F
C
AB
F
+
=
⇒
+
=
6 marca 2011
Wojciech Kucewicz
60
AB
F
AB
F
=
⇒
=
C
AB
F
C
AB
F
+
=
⇒
+
=
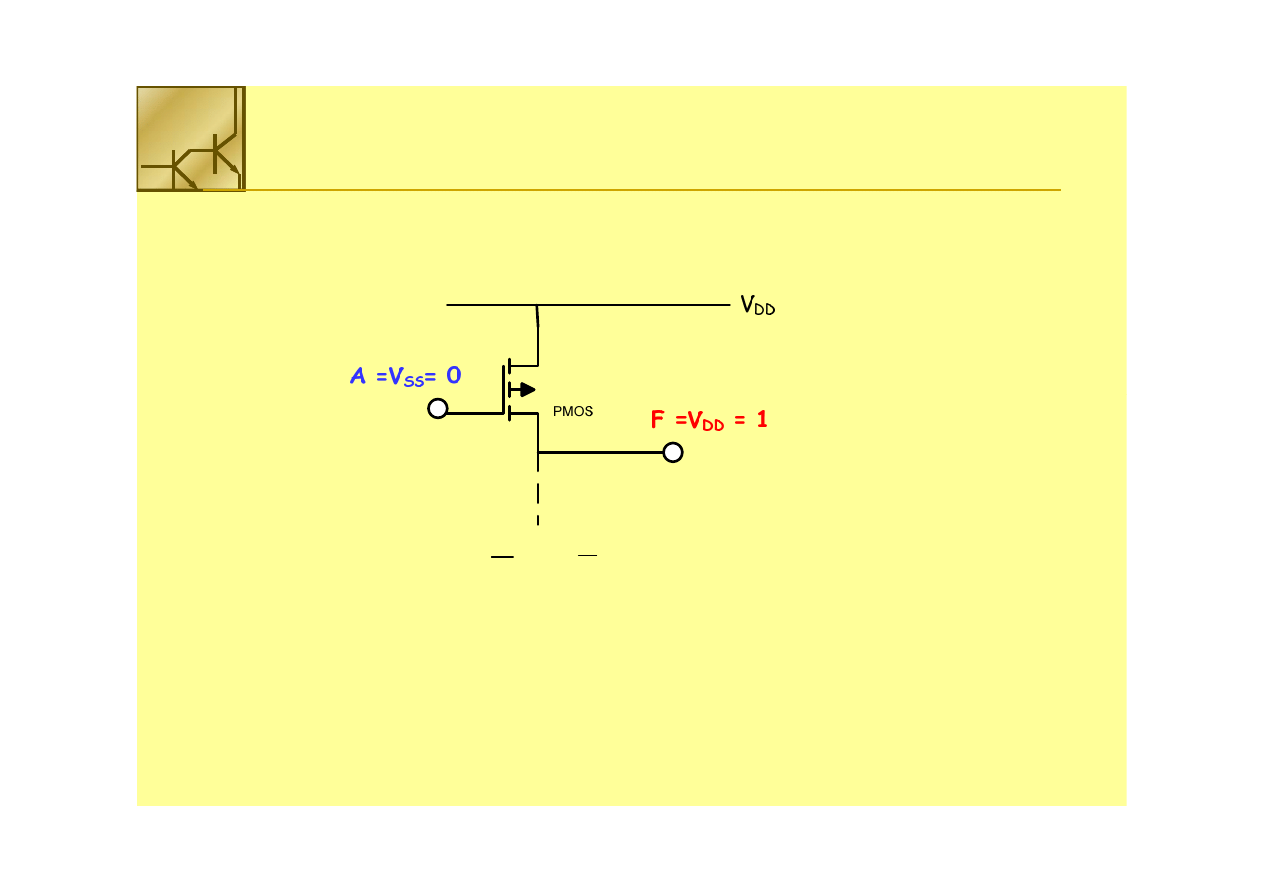
Logika PMOS
Logika PMOS
Logika PMOS
Logika PMOS
Tranzystory PMOS służą jako włączniki wysokiego napięcia V
DD
.
Niskie napięcie na bramce łączy wyjście z linią wysokiego napięcia V
DD
.
A
F
A
F
=
⇒
=
6 marca 2011
Wojciech Kucewicz
61
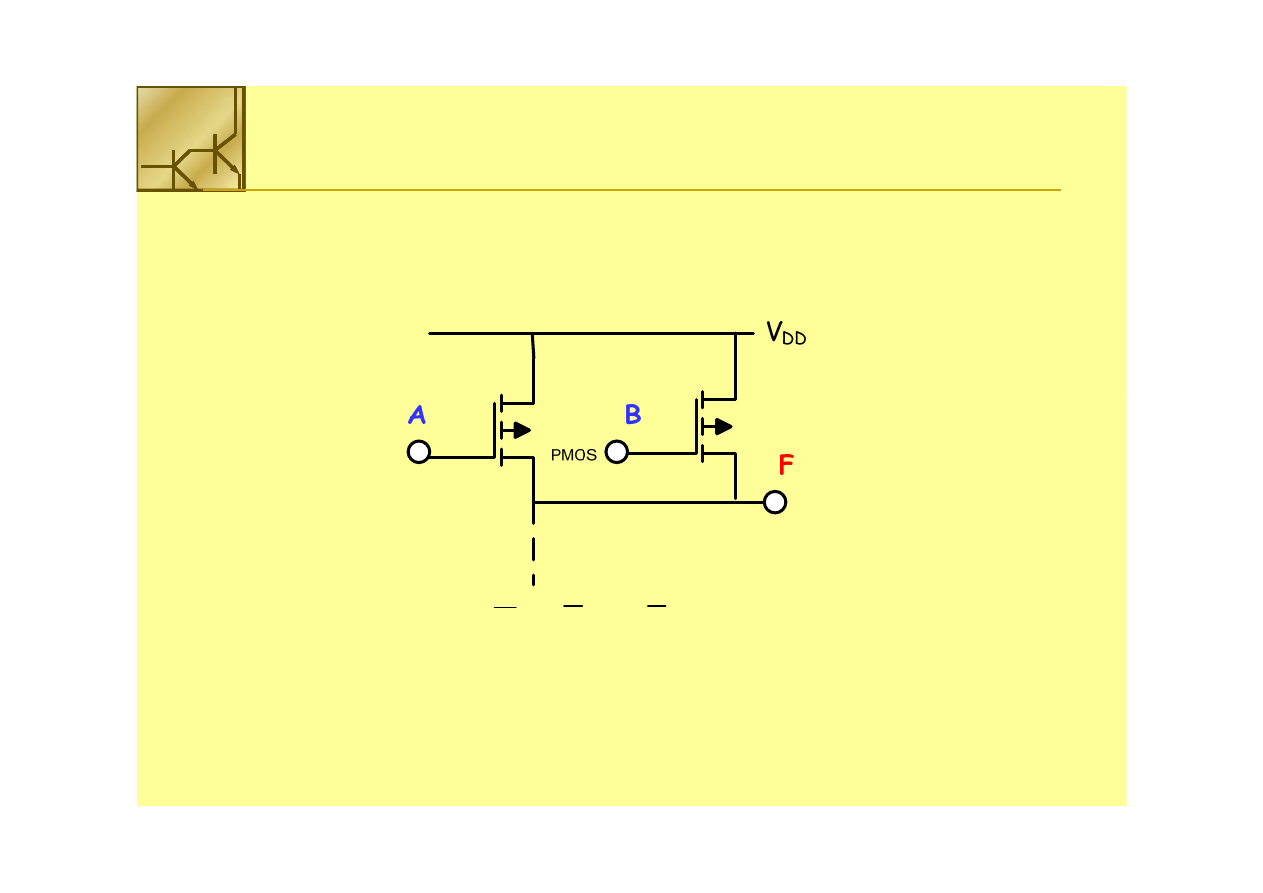
Logika PMOS
Logika PMOS
Logika PMOS
Logika PMOS
Połączenie równoległe tranzystorów PMOS realizuje funkcję logiczną sumę
zaprzeczeń. Wystarczy, że jeden z tranzystorów PMOS przewodzi (na bramce
logiczne 0), aby na wyjściu otrzymać logiczną 1.
g
)
y
yj
y
g
AB
F
B
A
F
=
⇒
+
=
6 marca 2011
Wojciech Kucewicz
62
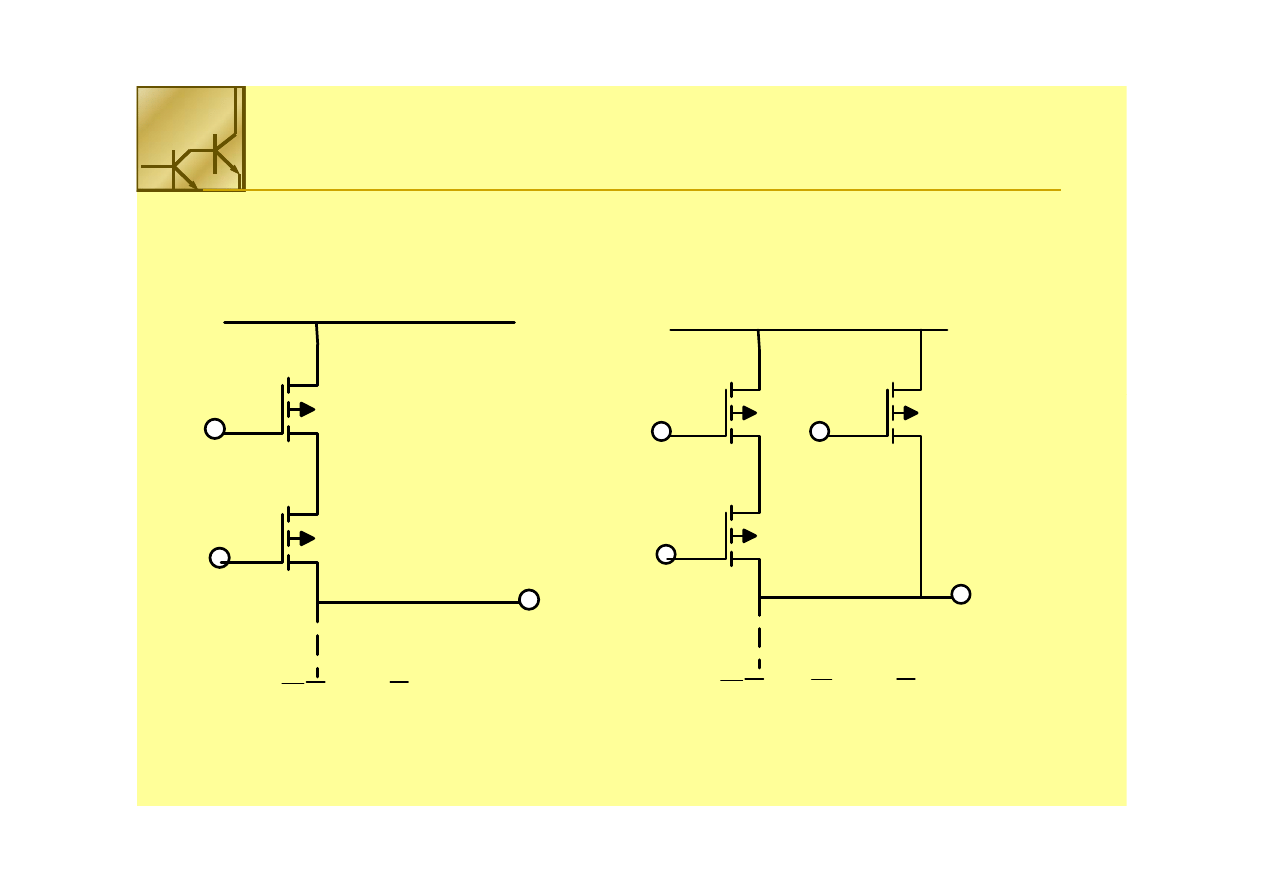
Logika PMOS
Logika PMOS
Logika PMOS
Logika PMOS
Połączenie szeregowe tranzystorów PMOS realizuje funkcję logiczną iloczynu
zaprzeczeń. Oba tranzystory PMOS muszą przewodzić (na bramkach logiczne 0), aby
na wyjściu otrzymać logiczną 1.
yj
y
g
V
DD
A
V
DD
A
C
PMOS
A
A
C
F
B
PMOS
F
B
B
A
F
B
A
F
+
=
⇒
=
C
)
B
A
(
F
C
B
A
F
+
=
⇒
+
=
6 marca 2011
Wojciech Kucewicz
63
B
A
F
B
A
F
+
=
⇒
=
C
)
B
A
(
F
C
B
A
F
+
=
⇒
+
=
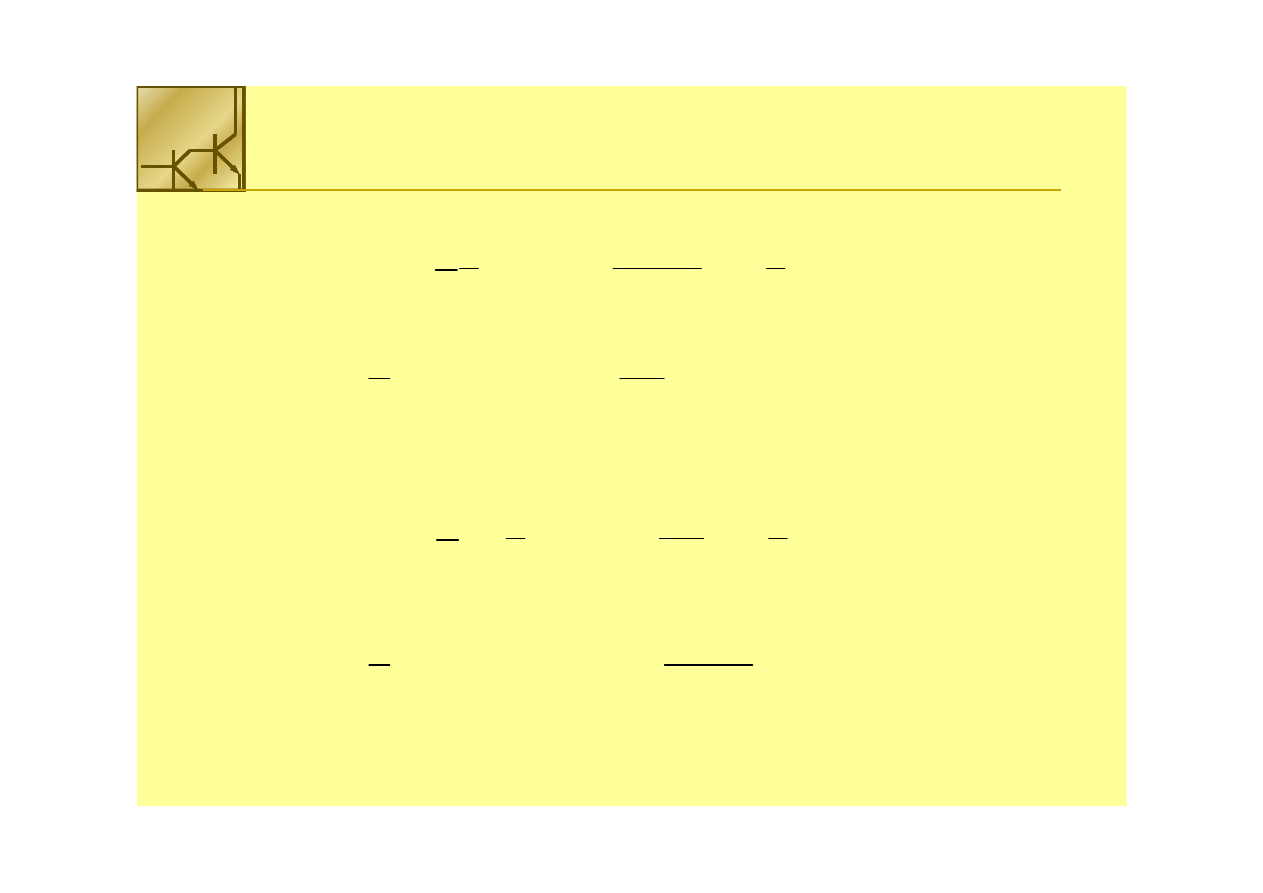
Logika PMOS
Logika PMOS
Logika PMOS
Logika PMOS
Połączenie szeregowe tranzystorów PMOS realizuje funkcję
B
A
F
B
A
F
B
A
F
+
=
⇒
+
=
⇒
=
B
A
F
B
A
F
B
A
F
+
=
⇒
+
=
⇒
=
Połączenie szeregowe tranzystorów NMOS realizuje funkcję
AB
F
AB
F
⇒
AB
F
AB
F
=
⇒
=
ó
ó
Połączenie równoległe tranzystorów PMOS realizuje funkcję
AB
F
AB
F
B
A
F
=
⇒
=
⇒
+
=
Połączenie równoległe tranzystorów NMOS realizuje funkcję
B
A
F
B
A
F
+
=
⇒
+
=
6 marca 2011
Wojciech Kucewicz
64

B
k NAND
B
k NAND
B
k NAND
B
k NAND
Bramka NAND
Bramka NAND
Bramka NAND
Bramka NAND
6 marca 2011
Wojciech Kucewicz
65
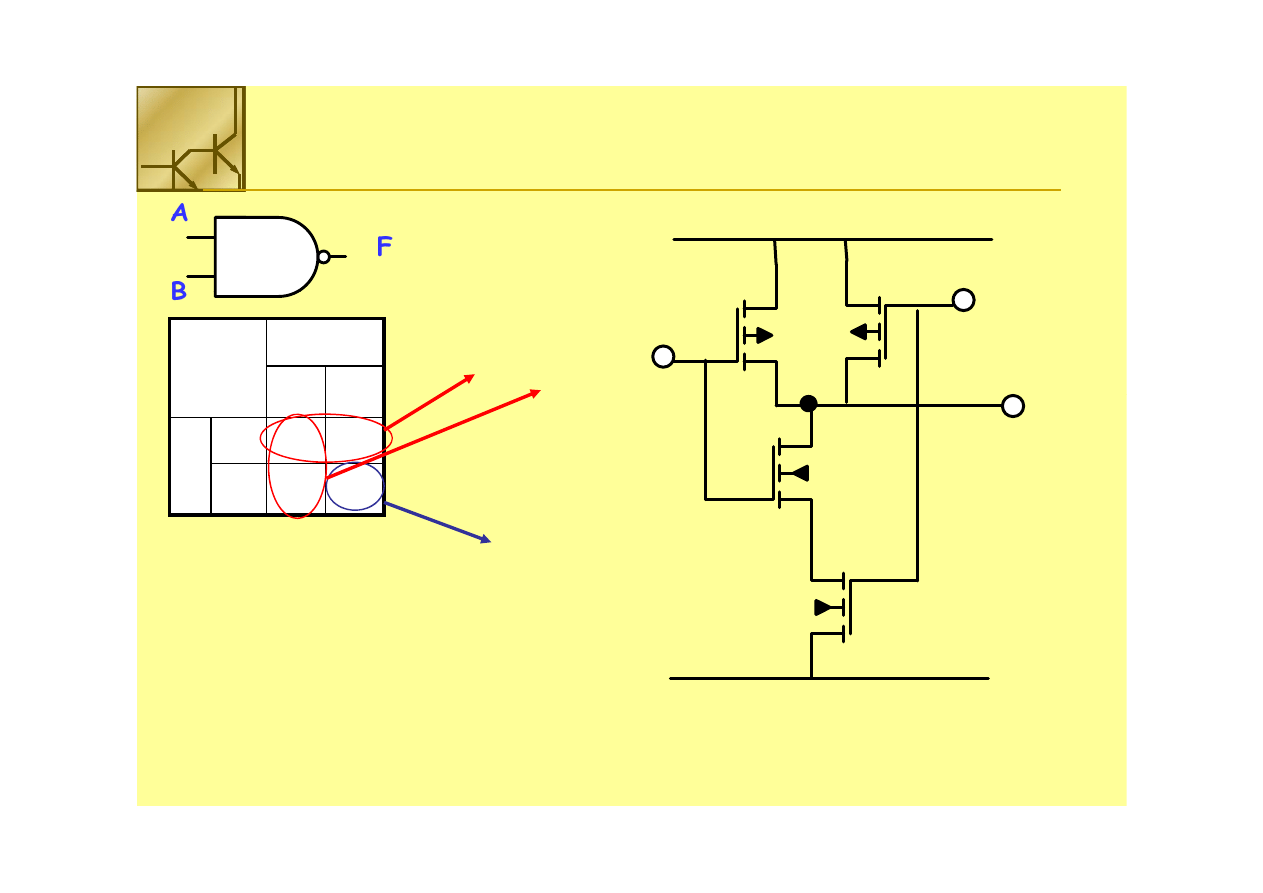
Bramka
Bramka NAND
NAND
Bramka
Bramka NAND
NAND
V
DD
B
FF
BB
00
11
F = A’ + B’
F = A’ + B’
PMOS
F
A
B
00
11
A
A
00
11
11
11
11
00
F’ = A • B
F’ = A • B
NMOS
V
SS
6 marca 2011
Wojciech Kucewicz
66
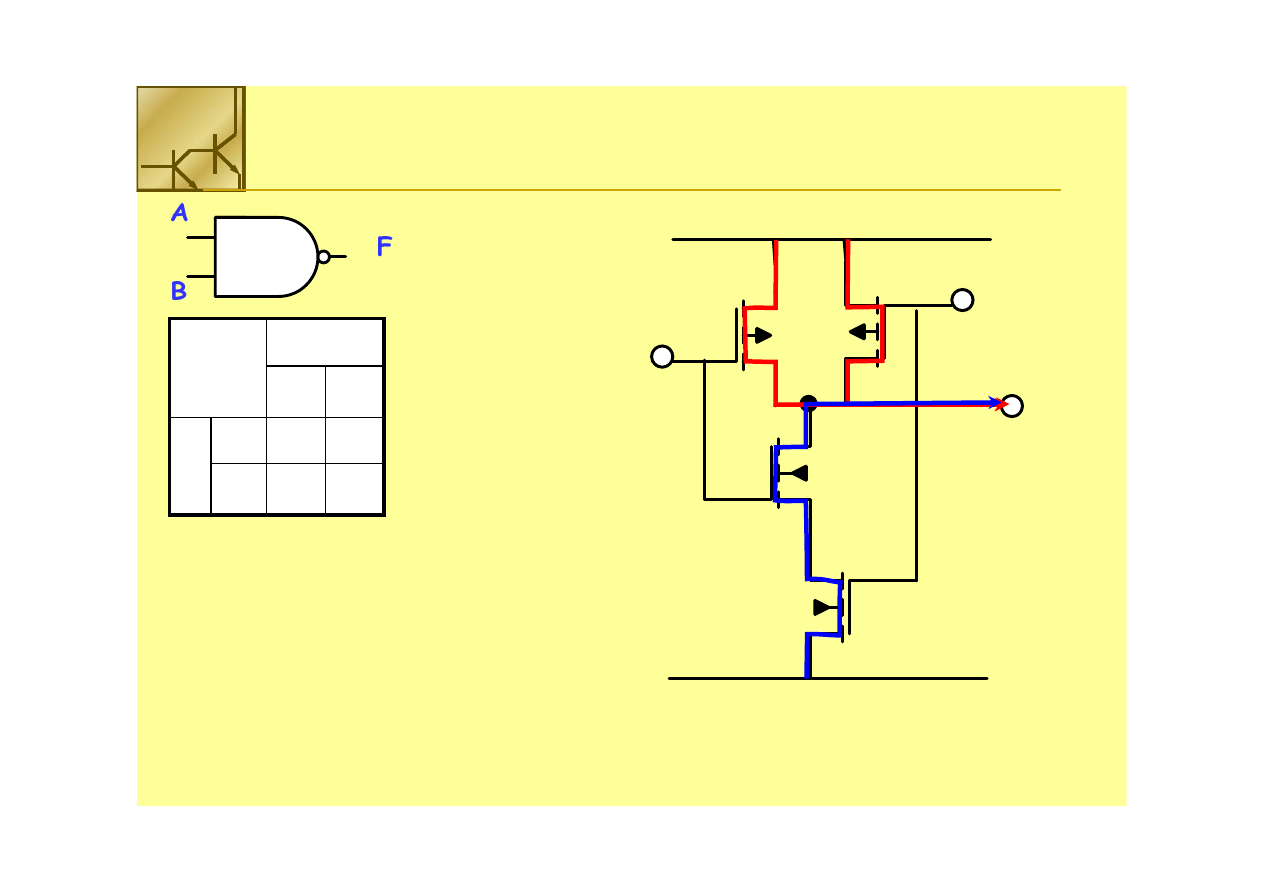
Bramka
Bramka NAND
NAND
Bramka
Bramka NAND
NAND
V
DD
B
FF
BB
00
11
PMOS
F
A
B
00
11
A
A
00
11
11
11
11
00
NMOS
V
SS
6 marca 2011
Wojciech Kucewicz
67
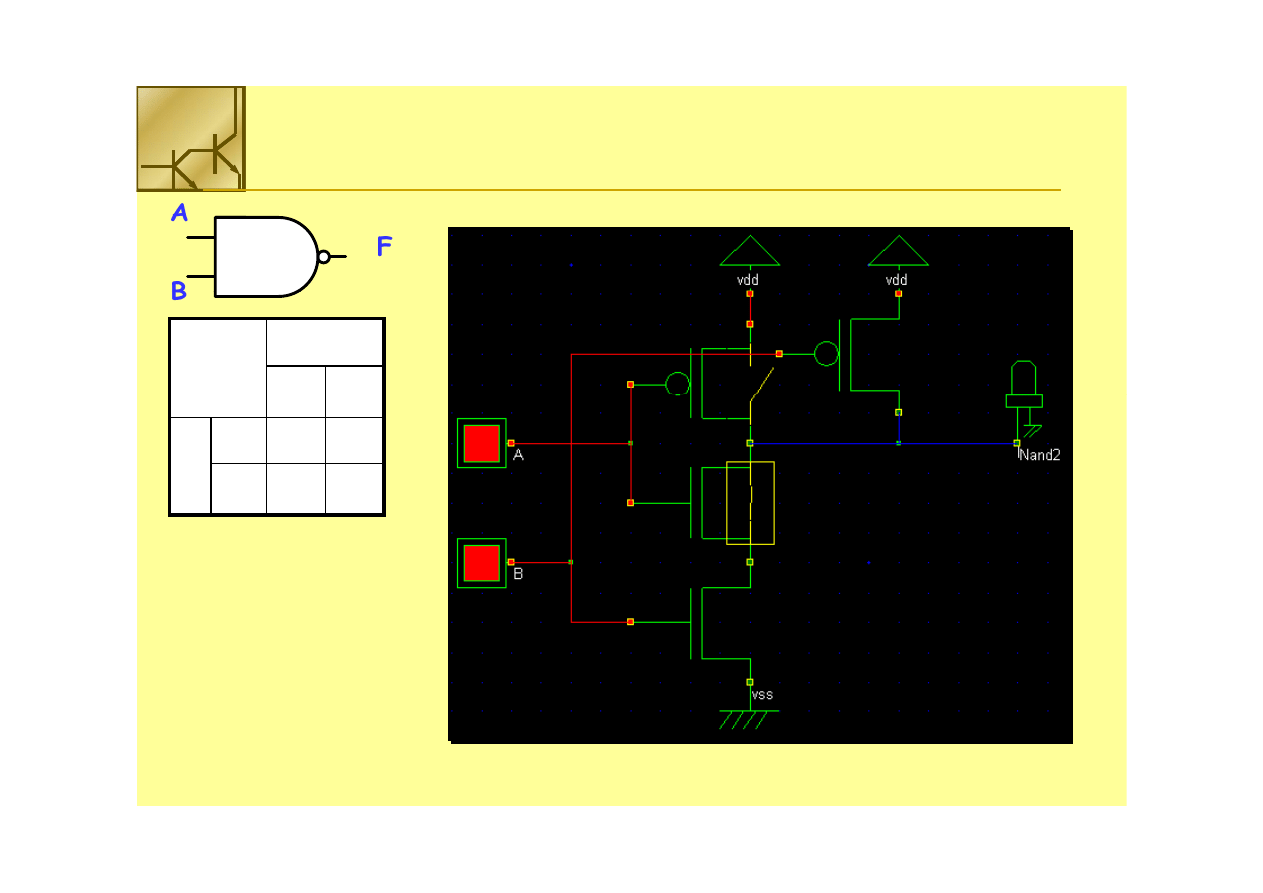
Bramka
Bramka NAND
NAND
Bramka
Bramka NAND
NAND
FF
BB
00
11
00
11
A
A
00
11
11
11
11
00
11
00
6 marca 2011
Wojciech Kucewicz
68
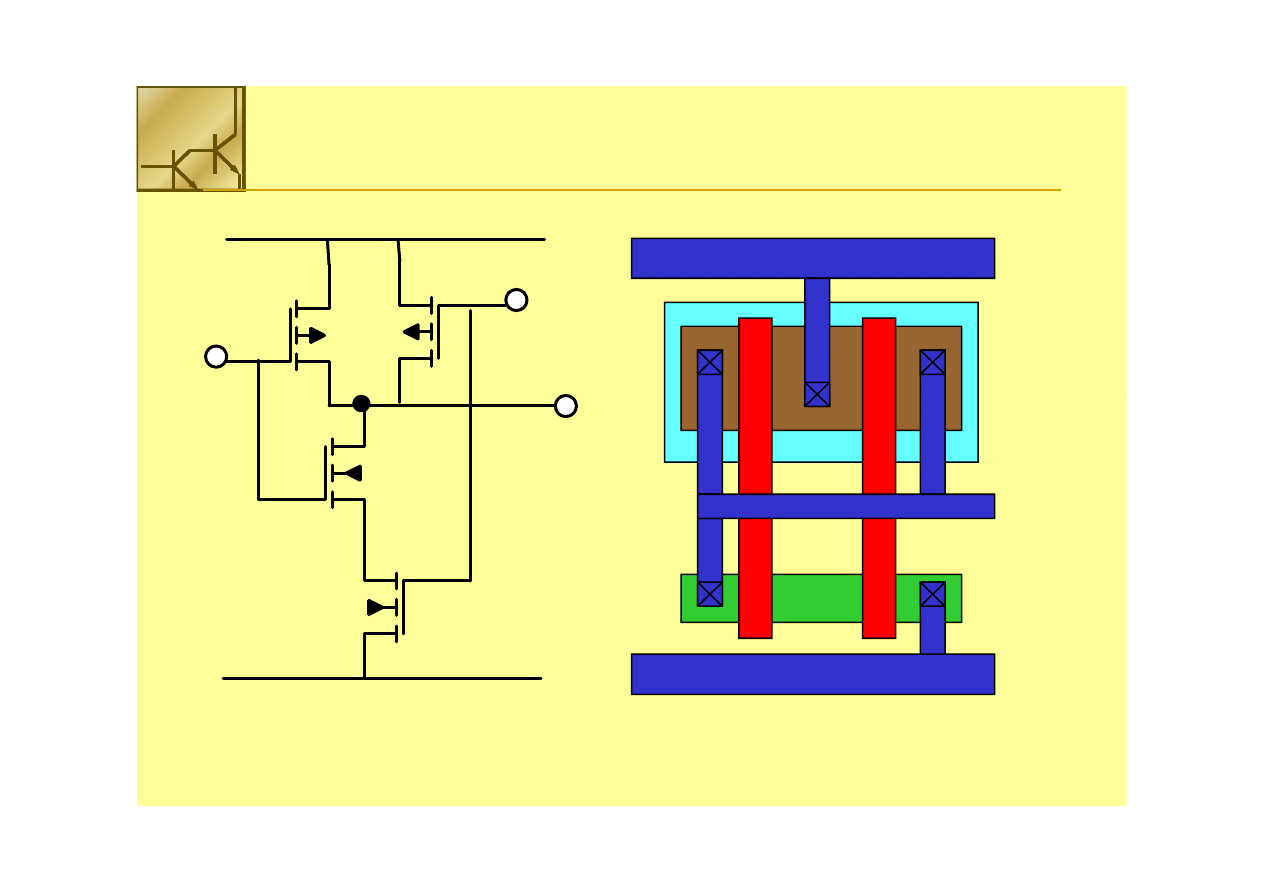
Bramka
Bramka NAND
NAND
Bramka
Bramka NAND
NAND
VV
DD
DD
V
DD
B
PMOS
F
A
B
A
A
BB
FF
NMOS
VV
SS
SS
V
SS
6 marca 2011
Wojciech Kucewicz
69

B
k NOR
B
k NOR
B
k NOR
B
k NOR
Bramka NOR
Bramka NOR
Bramka NOR
Bramka NOR
6 marca 2011
Wojciech Kucewicz
70
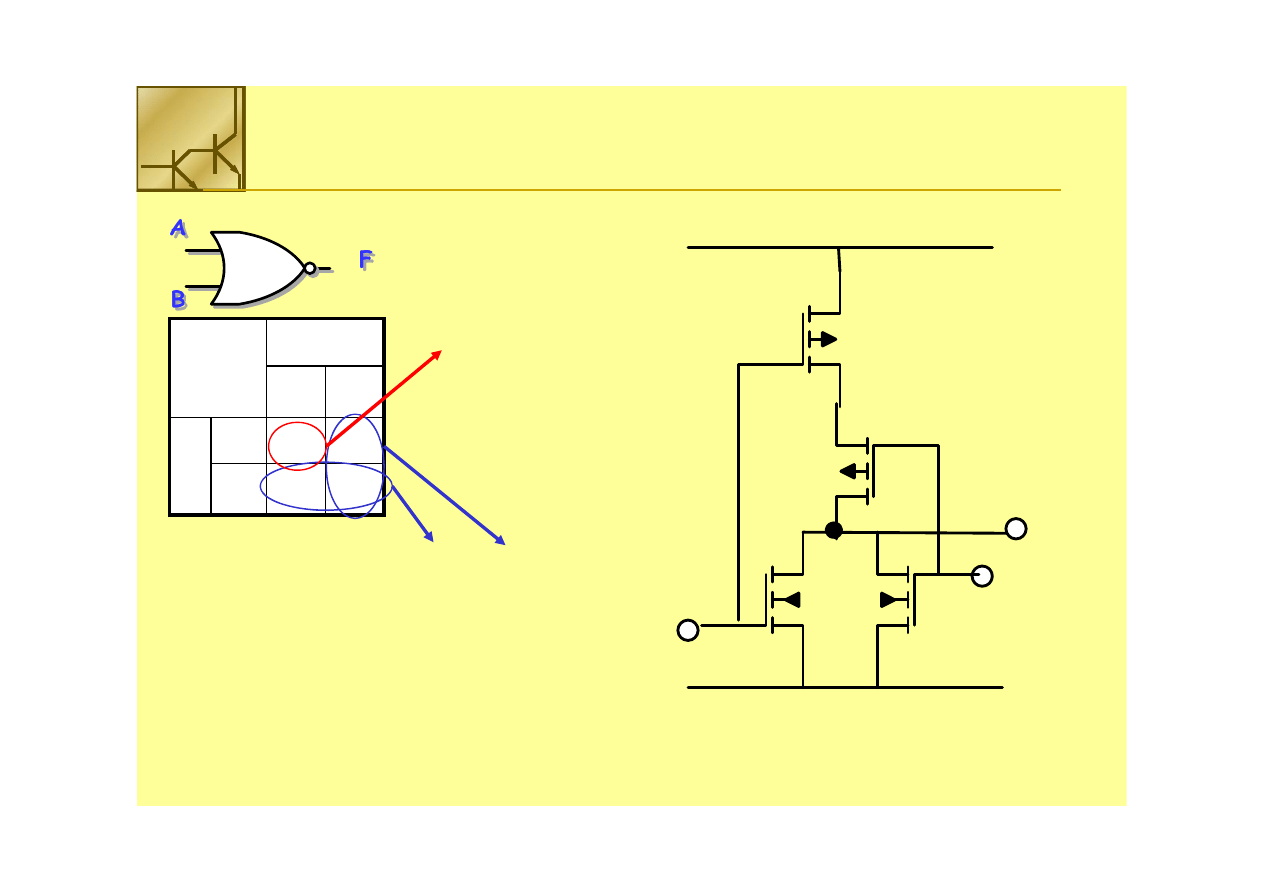
Bramka NOR
Bramka NOR
Bramka NOR
Bramka NOR
V
DD
FF
BB
00
11
F = A’ • B’
F = A’ • B’
00
11
A
A
00
11
00
11
00
00
PMOS
F
F’ = A + B
F’ = A + B
F
A
B
NMOS
A
B
V
SS
OS
6 marca 2011
Wojciech Kucewicz
71
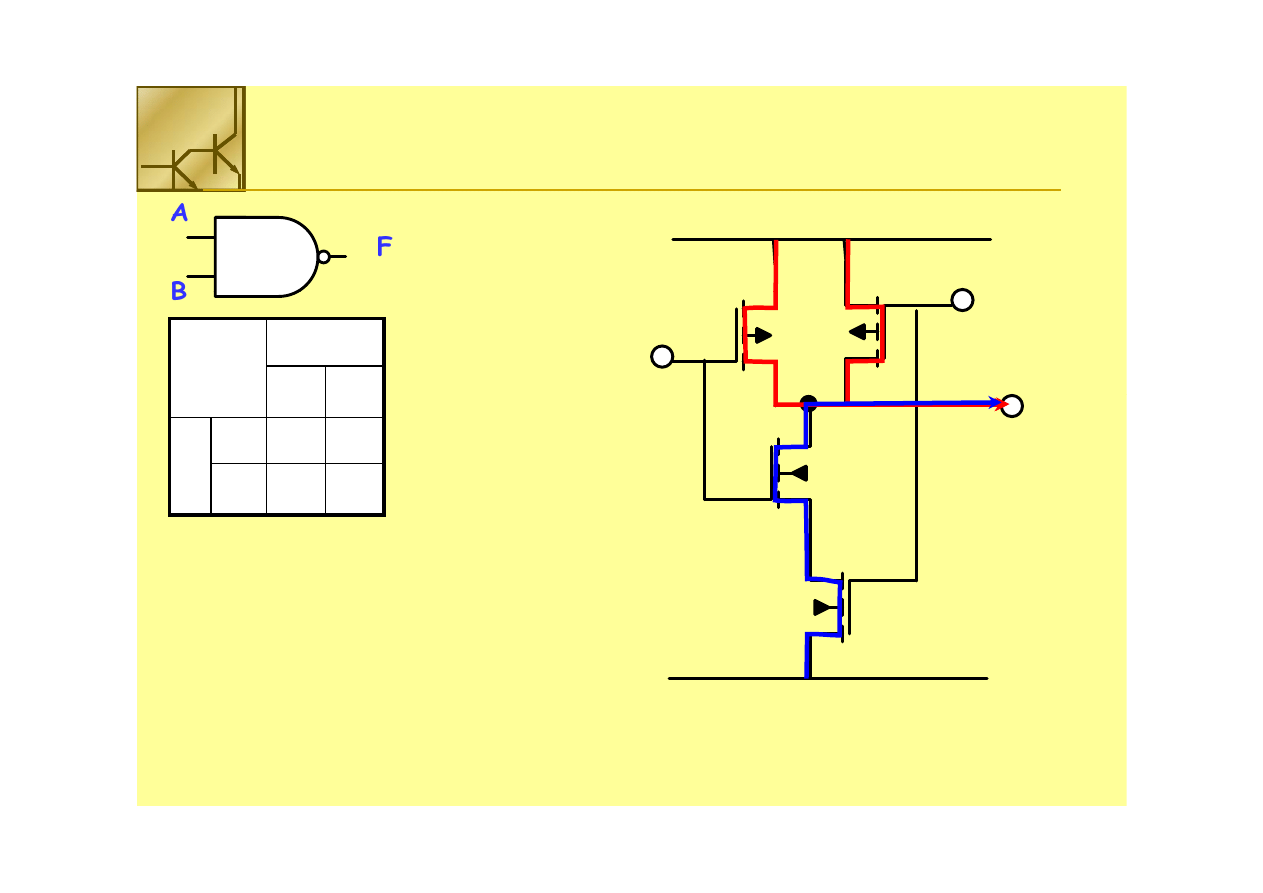
Bramka
Bramka NAND
NAND
Bramka
Bramka NAND
NAND
V
DD
B
FF
BB
00
11
PMOS
F
A
B
00
11
A
A
00
11
11
11
11
00
NMOS
V
SS
6 marca 2011
Wojciech Kucewicz
72
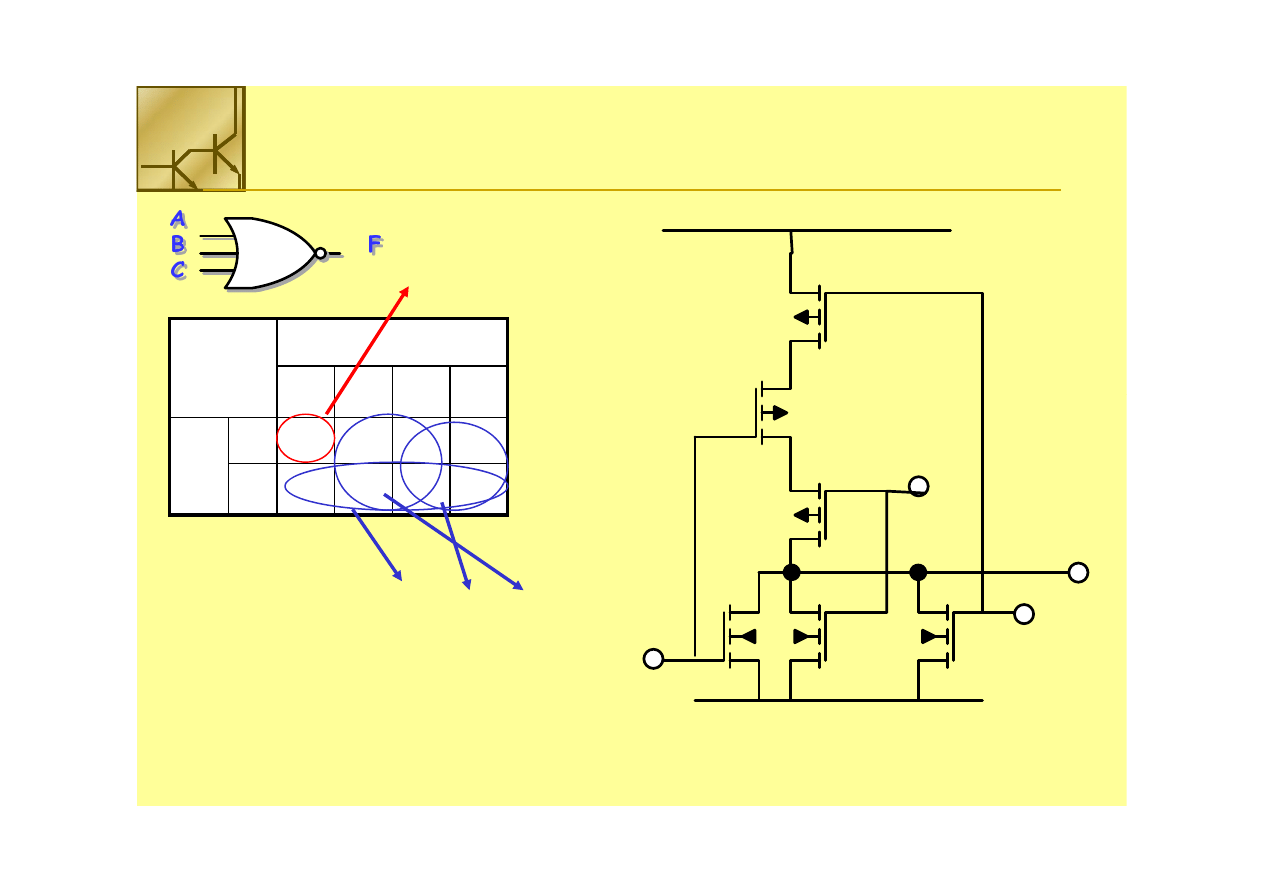
3 wejściowa bramka NOR
3 wejściowa bramka NOR
3 wejściowa bramka NOR
3 wejściowa bramka NOR
F=A’• B’• C’
F=A’• B’• C’
V
DD
FF
BC
BC
00
00
01
01
11
11
10
10
00
00
01
01
11
11
10
10
A
A
00
11
00
00
00
11
00
00
00
00
PMOS
B
F’ A B C
F’ A B C
F
F’=A + B + C
F’=A + B + C
A
V
SS
NMOS
C
6 marca 2011
Wojciech Kucewicz
73
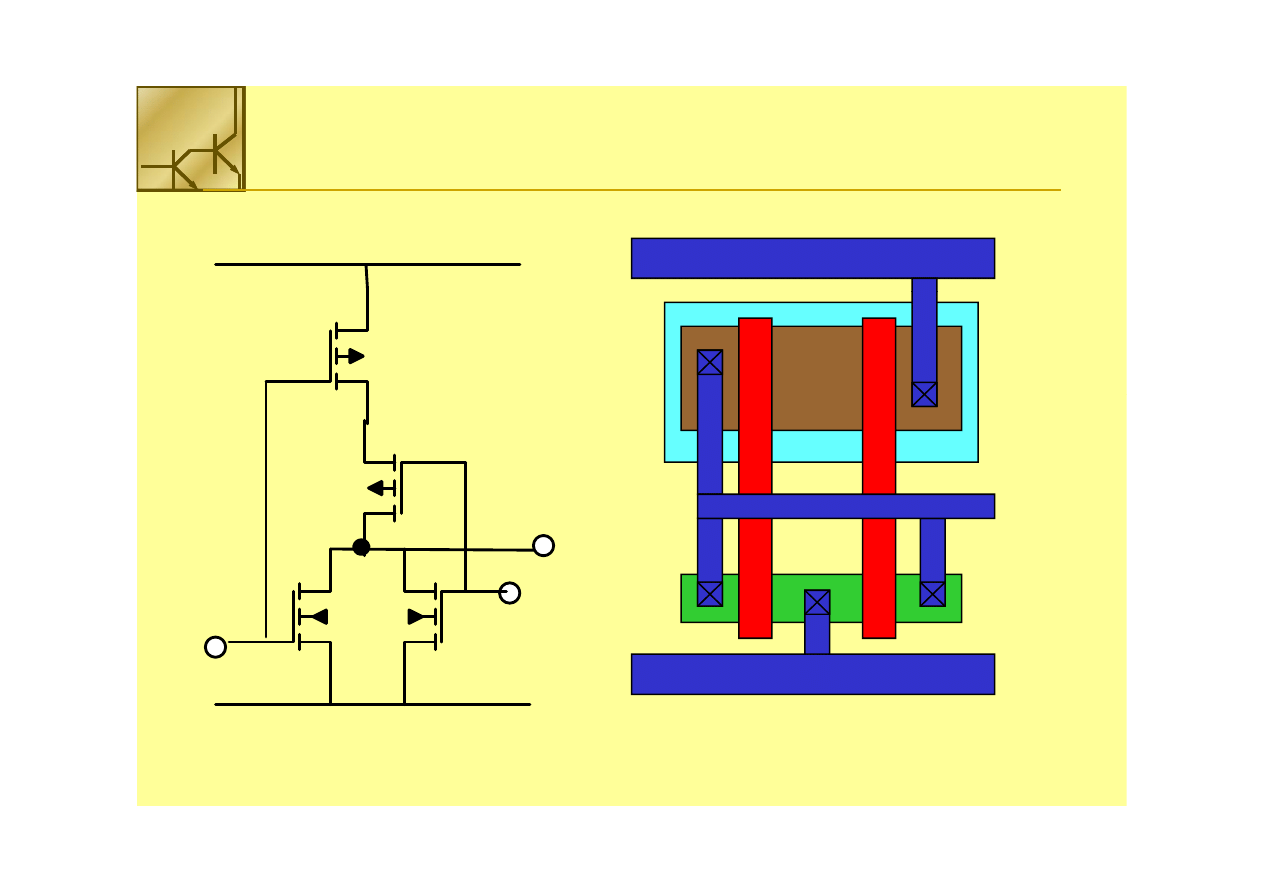
Bramka NOR
Bramka NOR
Bramka NOR
Bramka NOR
VV
DD
DD
V
DD
V
DD
A
A
BB
PMOS
FF
F
VV
SS
SS
A
B
V
SS
NMOS
6 marca 2011
Wojciech Kucewicz
74

B
k
B
k AND
AND
B
k
B
k AND
AND
Bramka
Bramka AND
AND
Bramka
Bramka AND
AND
6 marca 2011
Wojciech Kucewicz
75
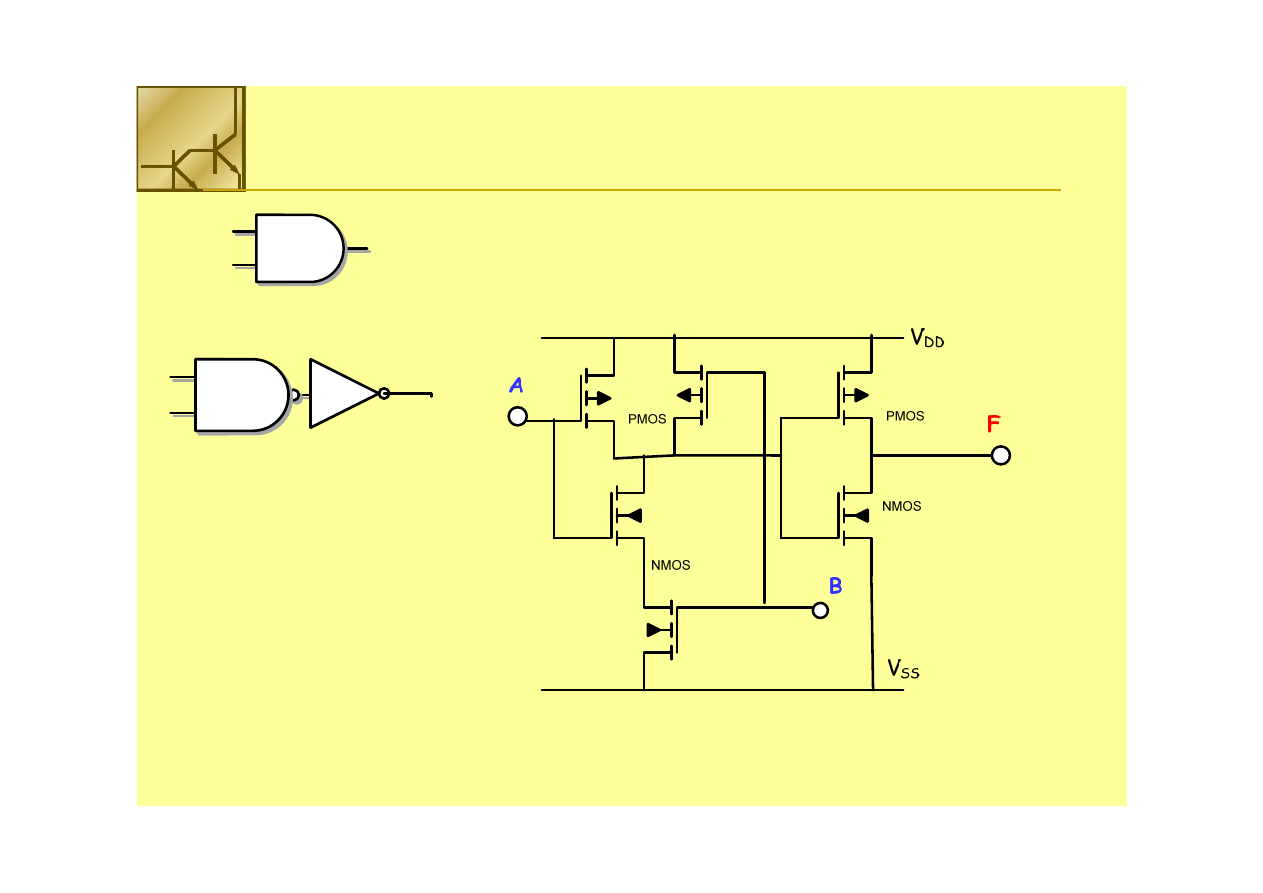
Bramka AND
Bramka AND
Bramka AND
Bramka AND
A
B
A
B
F
F
==
A
A
F
F
B
B
6 marca 2011
Wojciech Kucewicz
76

OR
OR
OR
OR
6 marca 2011
Wojciech Kucewicz
77
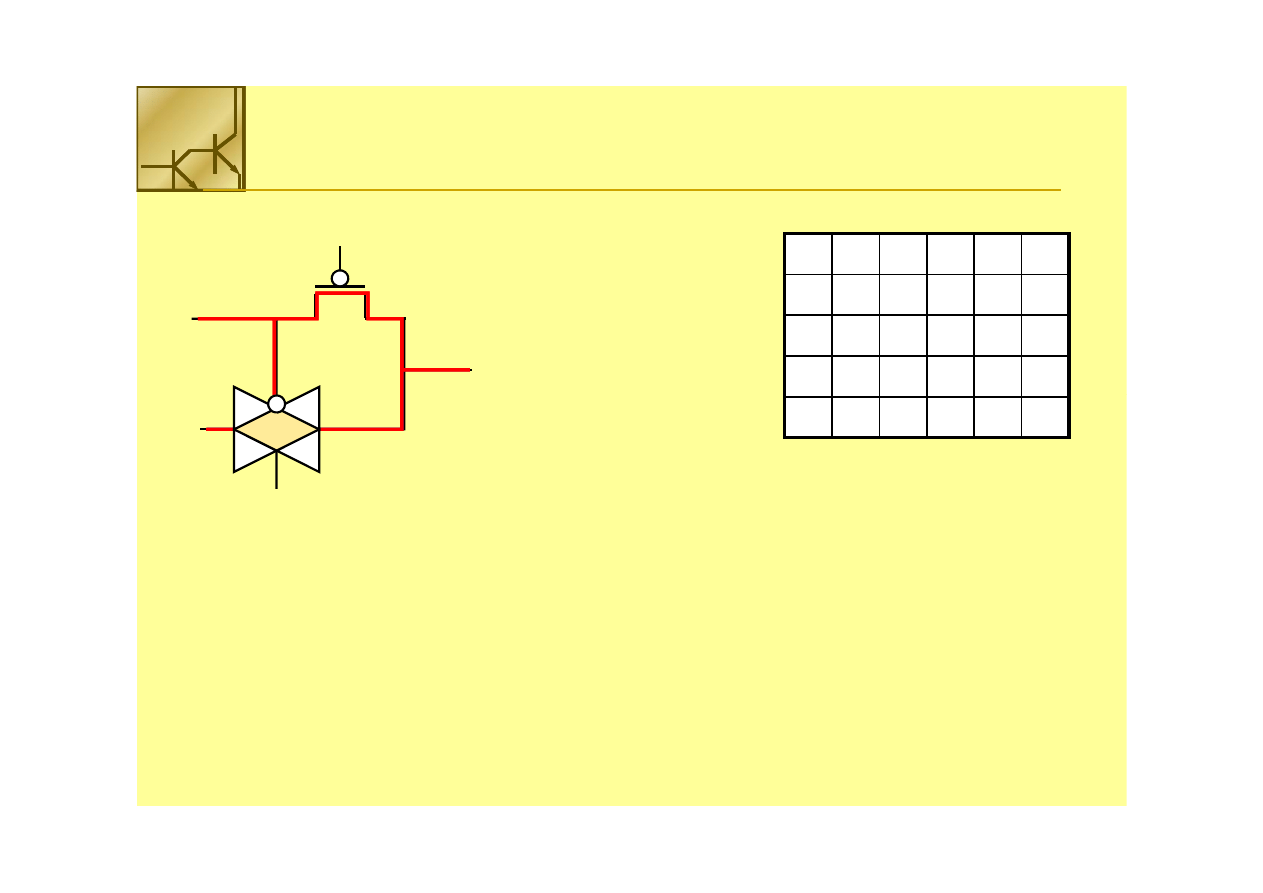
OR
OR
OR
OR
A
A
A’
A’
A
A
BB
A’
A’ A
A Î
Î
B
B Î
Î
A+B
A+B
00
00
11
X
X
BB
00
( ’)’
( ’)’
BB
F = A+B
F = A+B
A
A
00
00
11
X
X
BB
00
00
11
11
X
X
BB
11
11
00
00
A
A
X
X
11
A
A⋅⋅(A’)’
(A’)’
BB
A’
A’
11
11
00
A
A
X
X
11
BB⋅⋅A’
A’
A
A
Górna gałąź przewodzi przy A = 1 podczas, gdy dolna bramka transmisyjna przesyła
stan B na wyjście przy A = 0.
Ponieważ tranzystor PMOS przewodzi tylko wysokie napięcie odpowiadające logicznej
Pon eważ tranzystor PMOS przewodz tylko wysok e nap ęc e odpow adające log cznej
wartości A = 1, rozważanie przewodzenia logicznego 0 nie ma sensu.
Funkcja OR jest wynikiem formalnego zapisu funkcji realizowanych przez górne i
d ln r mi ukł du:
6 marca 2011
Wojciech Kucewicz
78
dolne ramię układu:
F =
F = A(
A(A
A’)’
’)’ +
+ A’B
A’B = A +
= A + A’B
A’B = A + B
= A + B
(Twierdzenie o absorbcji)

B
ki
B
ki
B
ki
B
ki
Bramki
Bramki
Bramki
Bramki
Bramki
Bramki
XOR i XNOR
XOR i XNOR
Bramki
Bramki
XOR i XNOR
XOR i XNOR
XOR i XNOR
XOR i XNOR
XOR i XNOR
XOR i XNOR
6 marca 2011
Wojciech Kucewicz
79
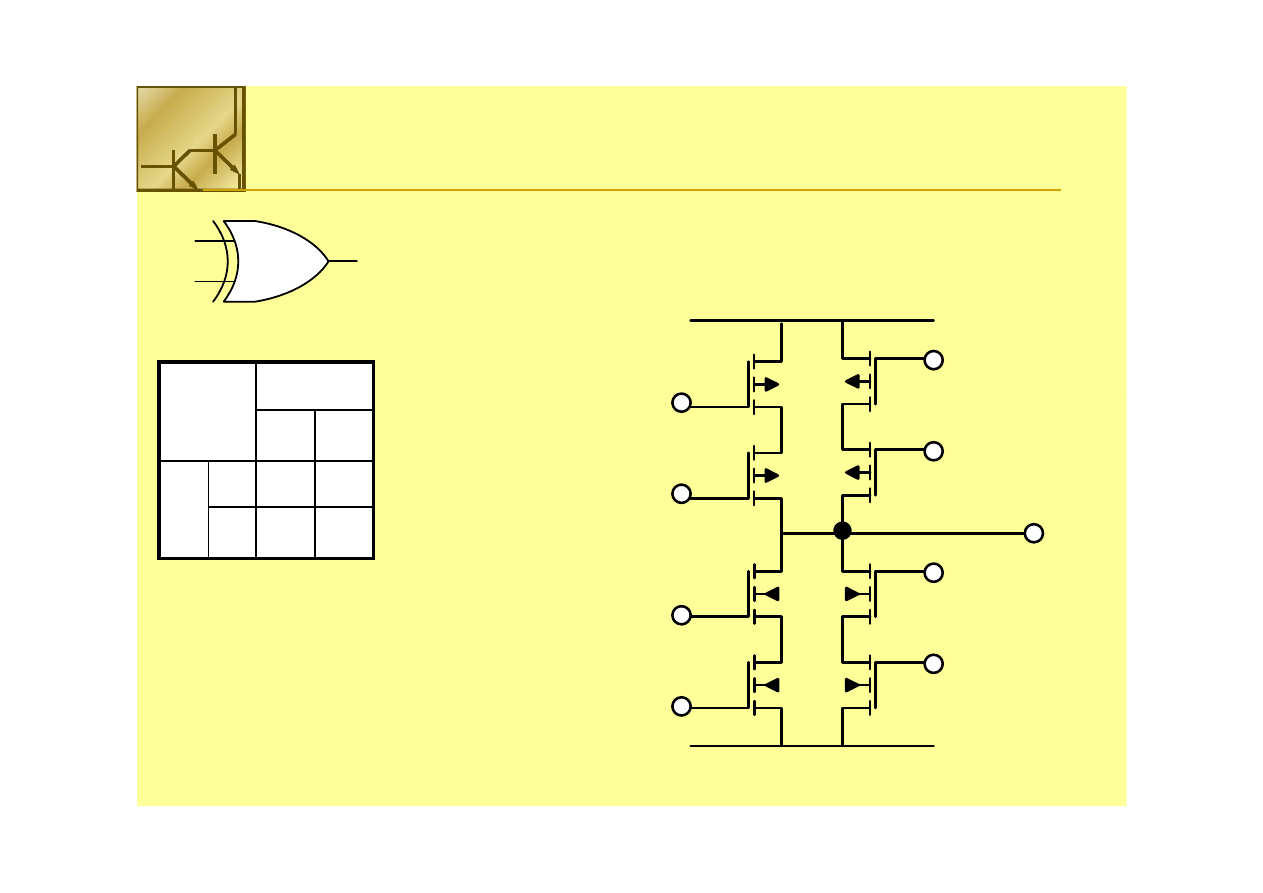
Bramka XOR
Bramka XOR
Bramka XOR
Bramka XOR
BB
V
DD
A’
A
FF
00
11
00
00
11
PMOS
F
A
B
B’
F =
F = A’B
A’B + AB’
+ AB’
A
A
11
11
00
XOR = F =A
XOR = F =A ⊕
⊕
B
B
NMOS
F
A
A’
F’ = AB +
F’ = AB + A’B
A’B’’
XOR = F =A
XOR = F =A ⊕
⊕
B
B
== A’B
A’B + AB’
+ AB’
A
B
B’
6 marca 2011
Wojciech Kucewicz
80
V
SS
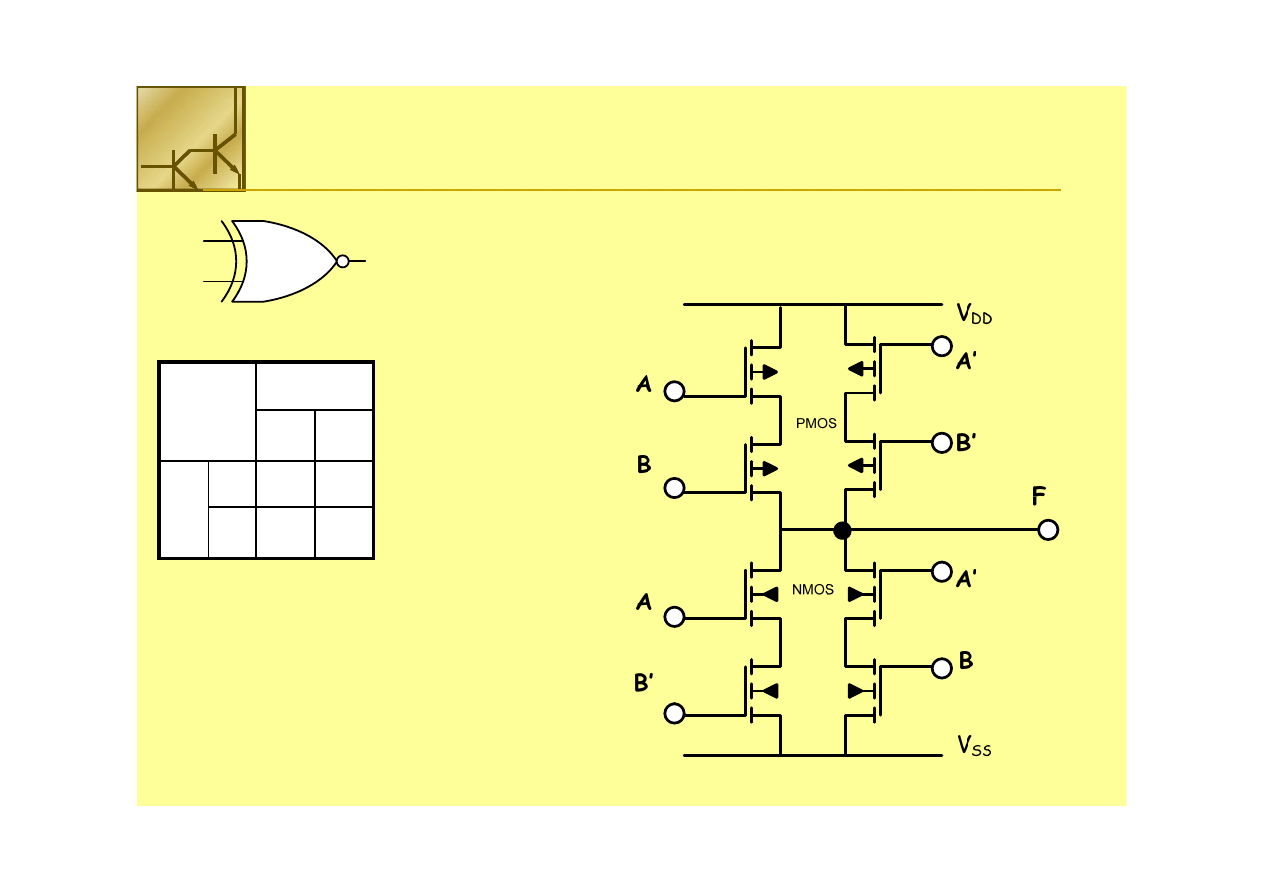
Bramka XNOR
Bramka XNOR
Bramka XNOR
Bramka XNOR
BB
FF
00
11
00
11
00
F = AB + A'B’
F = AB + A'B’
A
A
11
00
11
XNOR
XNOR = F
= F =(A
=(A ⊕
⊕
B)’
B)’
F’ = AB’ +
F’ = AB’ + A’B
A’B
XNOR
XNOR = F
= F =(A
=(A ⊕
⊕
B)
B)
== AB
AB +
+ A’B
A’B’’
6 marca 2011
Wojciech Kucewicz
81
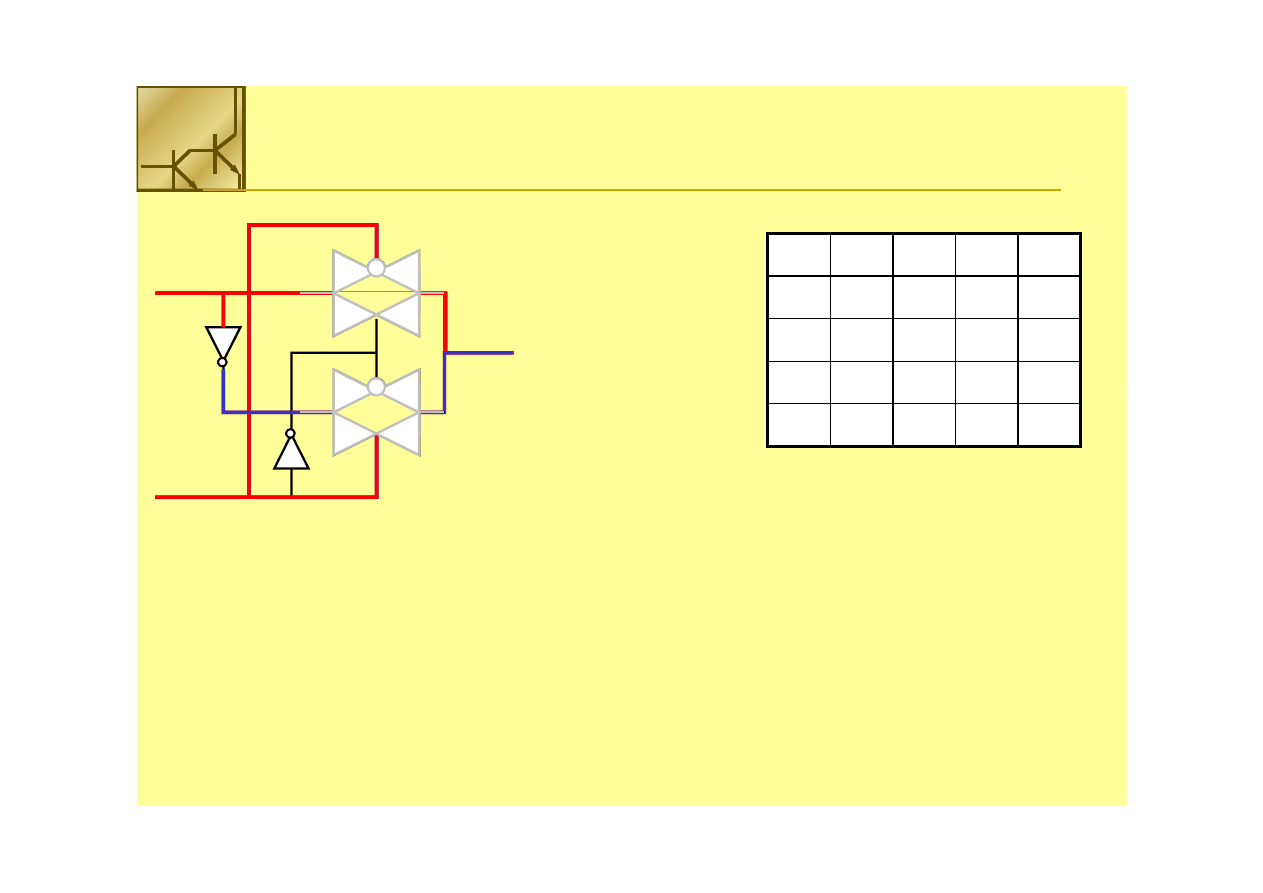
Bramka
Bramka
XOR
XOR
Bramka
Bramka
XOR
XOR
A
A
A
A
BB AB’
AB’ Î
Î
A’B
A’B Î
Î
A
A⊕
⊕
BB
00
00
A
A
X
X
00
AB’
AB’
A’
A’
B’
B’
00
00
A
A
X
X
00
00
11
X
X
A’
A’
11
11
00
A
A
X
X
11
F = A
F = A⊕
⊕
BB
BB
A
A
11
11
X
X
A’
A’
00
A’B
A’B
Układ multipleksera 2 na 1 z wejściami A i A’ oraz sygnałami sterującymi B i B’
Funkcja ekwiwalentna to:
Funkcja ekwiwalentna to:
F = A
F = A ⊕
⊕
B = A
B = A ⋅⋅ B’ + A’
B’ + A’ ⋅⋅ BB
6 marca 2011
Wojciech Kucewicz
82
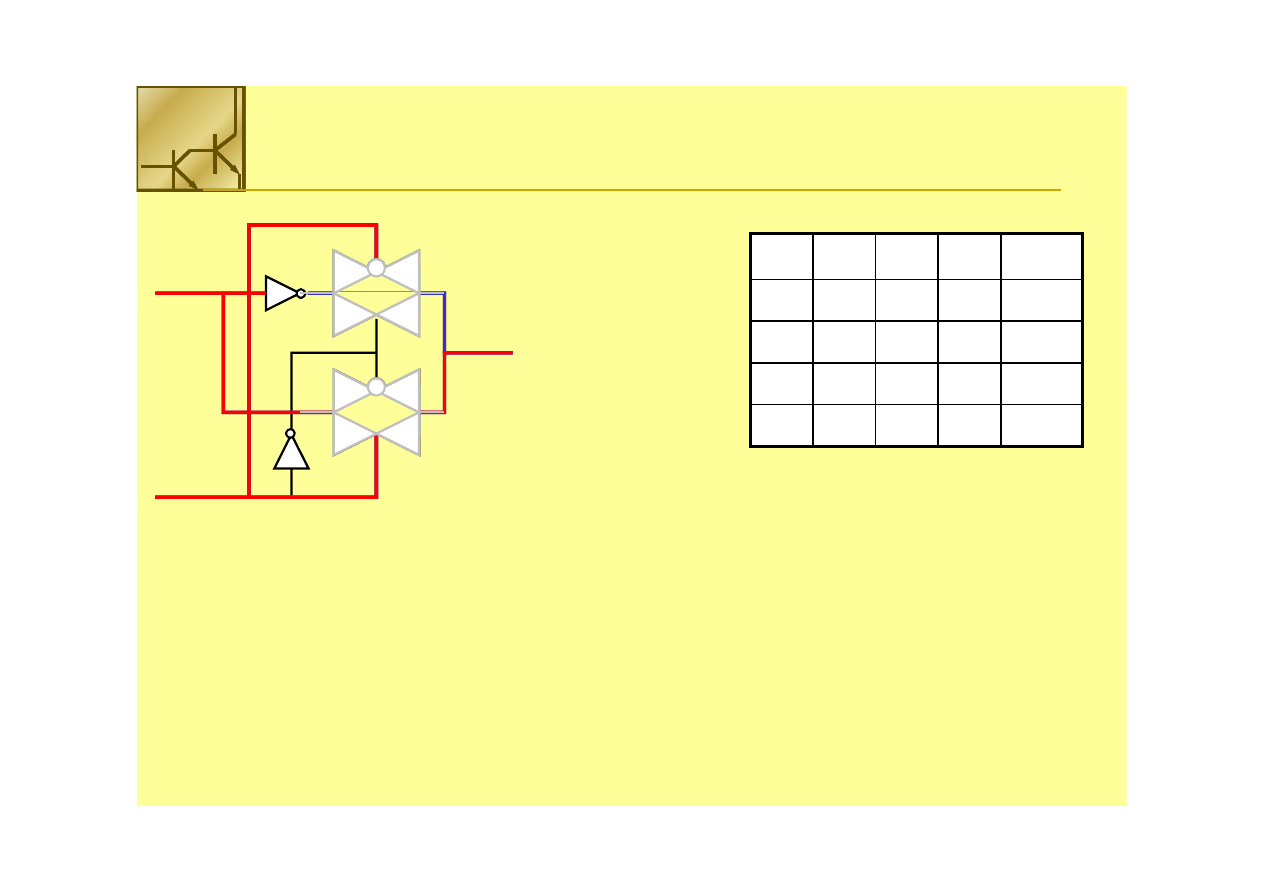
Bramka
Bramka
XNOR
XNOR
Bramka
Bramka
XNOR
XNOR
A’
A’
A
A
A
A
BB A’B’
A’B’Î
Î
AB
AB Î
Î
(A
(A⊕
⊕
B)’
B)’
00
00
’’
11
A’B’
A’B’
B’
B’
00
00
A’
A’
X
X
11
00
11
X
X
A
A
00
11
00
A’
A’
X
X
00
F = (A
F = (A⊕
⊕
B)’
B)’
BB
11
11
X
X
A
A
11
AB
AB
Układ multipleksera 2 na 1 z wejściami A i A’ oraz sygnałami sterującymi B i B’
Funkcja ekwiwalentna to:
Funkcja ekwiwalentna to:
F
F = (A
= (A ⊕
⊕
B)’ = A
B)’ = A ⋅⋅ B +A’
B +A’ ⋅⋅ B’
B’
6 marca 2011
Wojciech Kucewicz
83
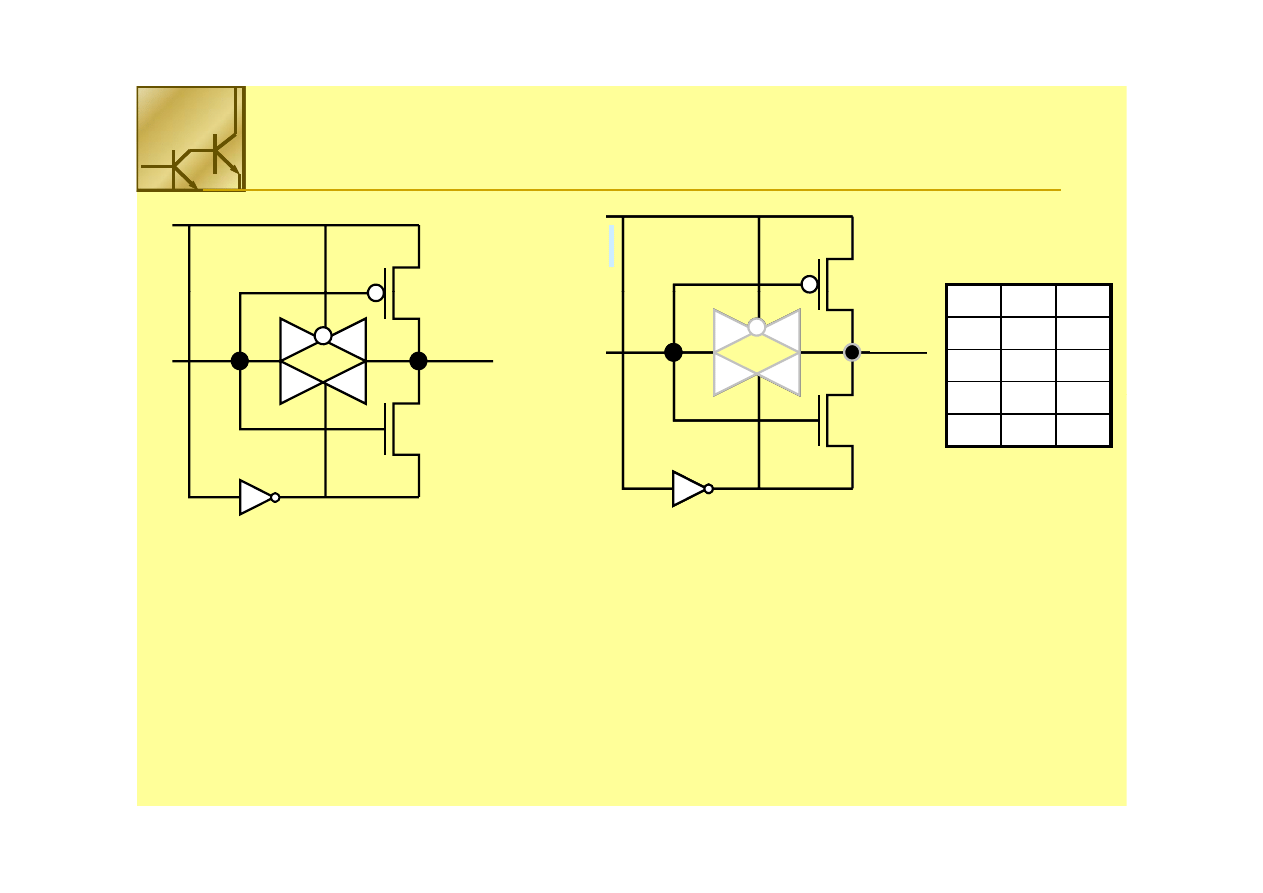
Bramka
Bramka
XOR
XOR
Bramka
Bramka
XOR
XOR
B
B
B = 0
B = 0
B = 1
B = 1
A
A
F = A
F = A⊕
⊕
BB
A
A
AB’
AB’
A
A
A
A⊕
⊕
BB
A
A
BB A
A⊕
⊕
BB
00
00
00
11
00
11
A
A
BB A
A⊕
⊕
BB
00
11
11
B’
B’
B’
B’
11
00
11
11
11
00
The transmission gate is switched into conduction when
B
=0, so that the output is
given by AB’. If B=1
,
then the transmission gate is OFF. In this case,
B=
1 is applied to
h
f PMOS d B’ 0 i
d h b
NMOS Si
h
the top of PMOS, and B’=0 is connected to the bottom on NMOS. Since these
correspond to respect voltage levels of and ground,
B
acts as a power supply voltage
for PMOS and NMOS, which form an inverter circuit with
A
as the input.
The output for this case is given by A’B , so that combing both possibilities gives
6 marca 2011
Wojciech Kucewicz
84
The output for this case is given by A B , so that combing both possibilities gives
F= A
F= A ⊕
⊕
B = A
B = A ⋅⋅ B’ +A’
B’ +A’ ⋅⋅ BB
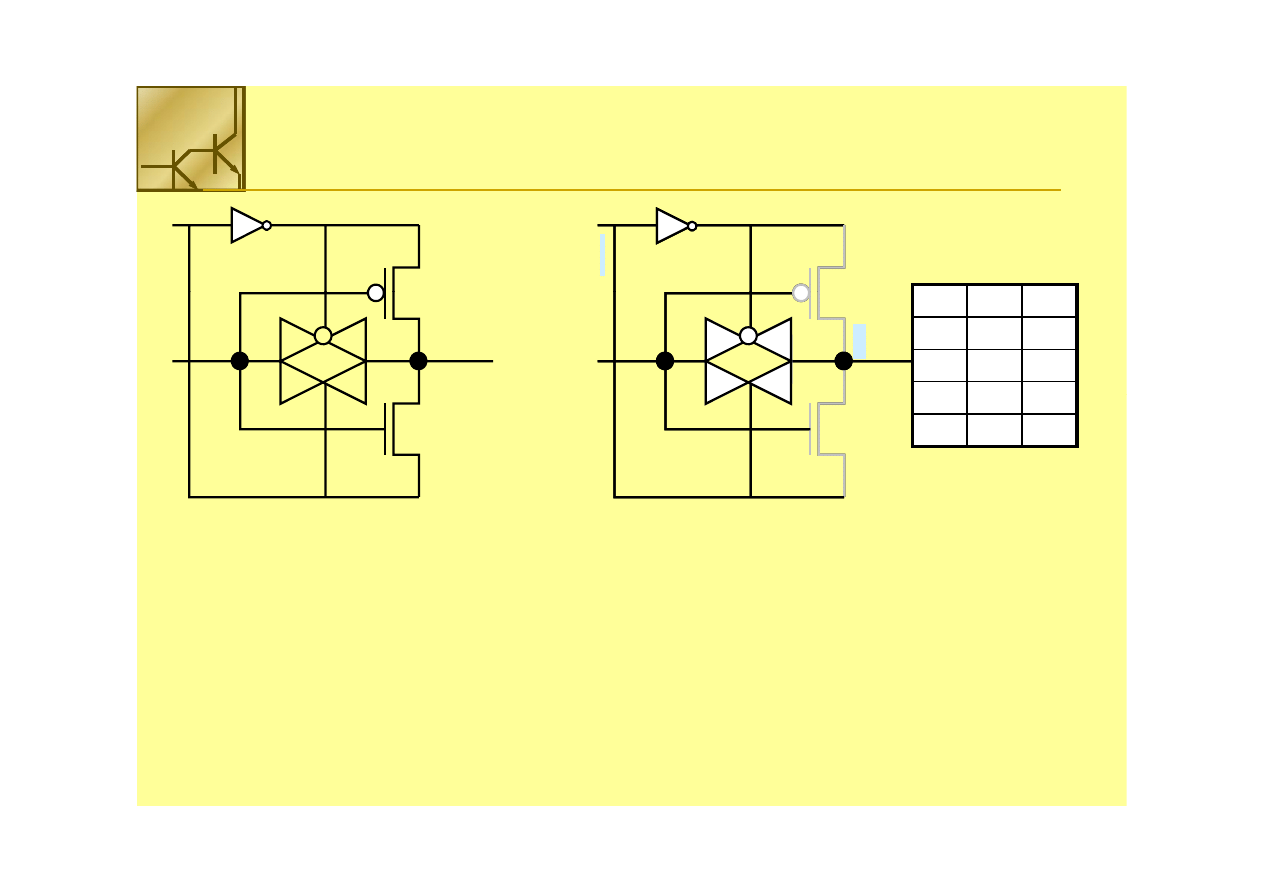
Bramka
Bramka
XNOR
XNOR
Bramka
Bramka
XNOR
XNOR
B
B
B = 0
B = 0
B’
B’
B = 1
B = 1
B’
B’
A
A
F = (A
F = (A⊕
⊕
B)’
B)’
A
A
A
A
A
A
BB A
A⊕
⊕
BB
00
00
11
11
00
00
A
A
BB A
A⊕
⊕
BB
00
11
00
11
00
00
11
11
11
The transmission gate is switched into conduction when
B
=1, so that the output is
given by AB If B=0
then the transmission gate is OFF In this case
B’=
1 is applied to
given by AB. If B=0
,
then the transmission gate is OFF. In this case,
B =
1 is applied to
the top of PMOS, and B=0 is connected to the bottom on NMOS. Since these
correspond to respect voltage levels of V
DD
and ground,
B
acts as a power supply
voltage for PMOS and NMOS, which form an inverter circuit with
A
as the input.
6 marca 2011
Wojciech Kucewicz
85
The output for this case is given by A’B’ , so that combing both possibilities gives
F= (A
F= (A ⊕
⊕
B)’ = A
B)’ = A ⋅⋅ B +A’
B +A’ ⋅⋅ B’
B’

Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
6 marca 2011
Wojciech Kucewicz
86
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
Jak zrealizować funkcję
Jak zrealizować funkcję??
F = (A • B) + (C • D)
F = (A • B) + (C • D)
Można to zrobić dwoma sposobami
Można to zrobić dwoma sposobami::
Można to zrobić dwoma sposobami
Można to zrobić dwoma sposobami
•• Projekt na poziomie bramek
Projekt na poziomie bramek
l m nt m k nst ukc jn m s p st b mki
l m nt m k nst ukc jn m s p st b mki
-- elementem konstrukcyjnym są proste bramki
elementem konstrukcyjnym są proste bramki
•• Projekt na poziomie tranzystorów
Projekt na poziomie tranzystorów
6 marca 2011
Wojciech Kucewicz
87
j
p
y
j
p
y
–– elementem konstrukcyjnym są tranzystory
elementem konstrukcyjnym są tranzystory
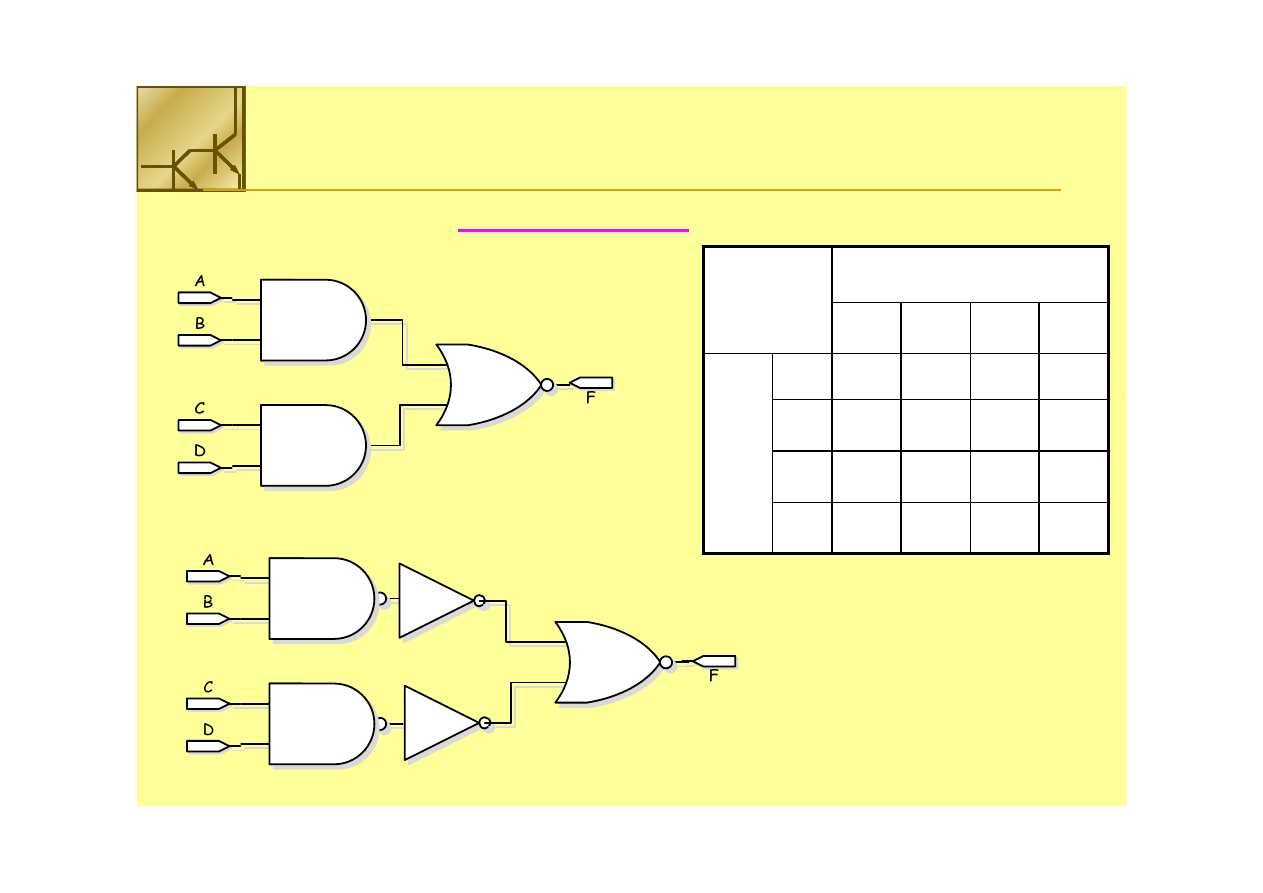
Projekt na poziomie bramek
Projekt na poziomie bramek
Projekt na poziomie bramek
Projekt na poziomie bramek
F = (A • B) + (C • D)
F = (A • B) + (C • D)
FF
CD
CD
FF
00
00
01
01
11
11
10
10
00
00
11
11
00
11
AB
AB
01
01
11
11
00
11
11
11
00
00
00
00
c
10
10
11
11
00
11
c
6 marca 2011
Wojciech Kucewicz
88
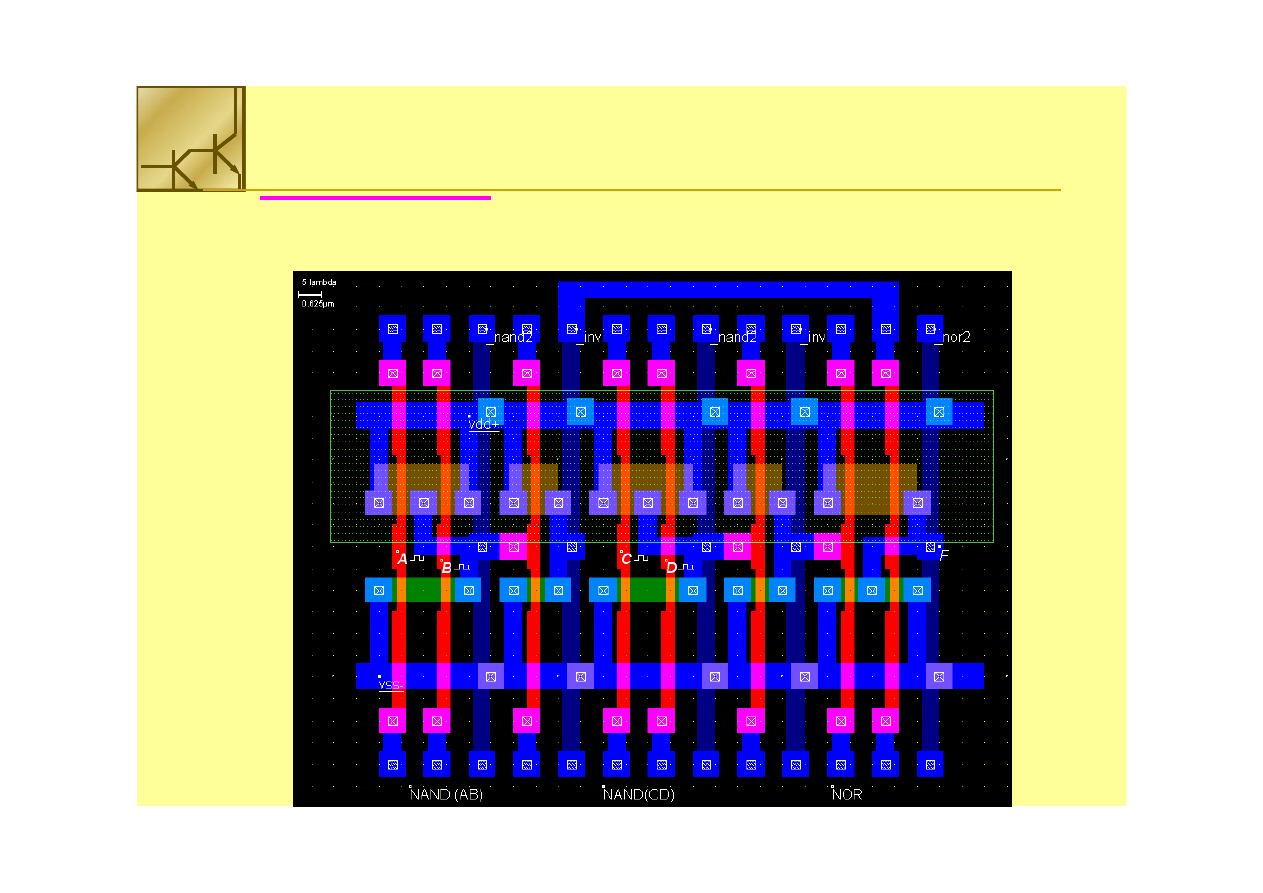
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
Circuit consists
Circuit consists 16 transistors
16 transistors
F = (A • B) + (C • D)
F = (A • B) + (C • D)
6 marca 2011
Wojciech Kucewicz
89
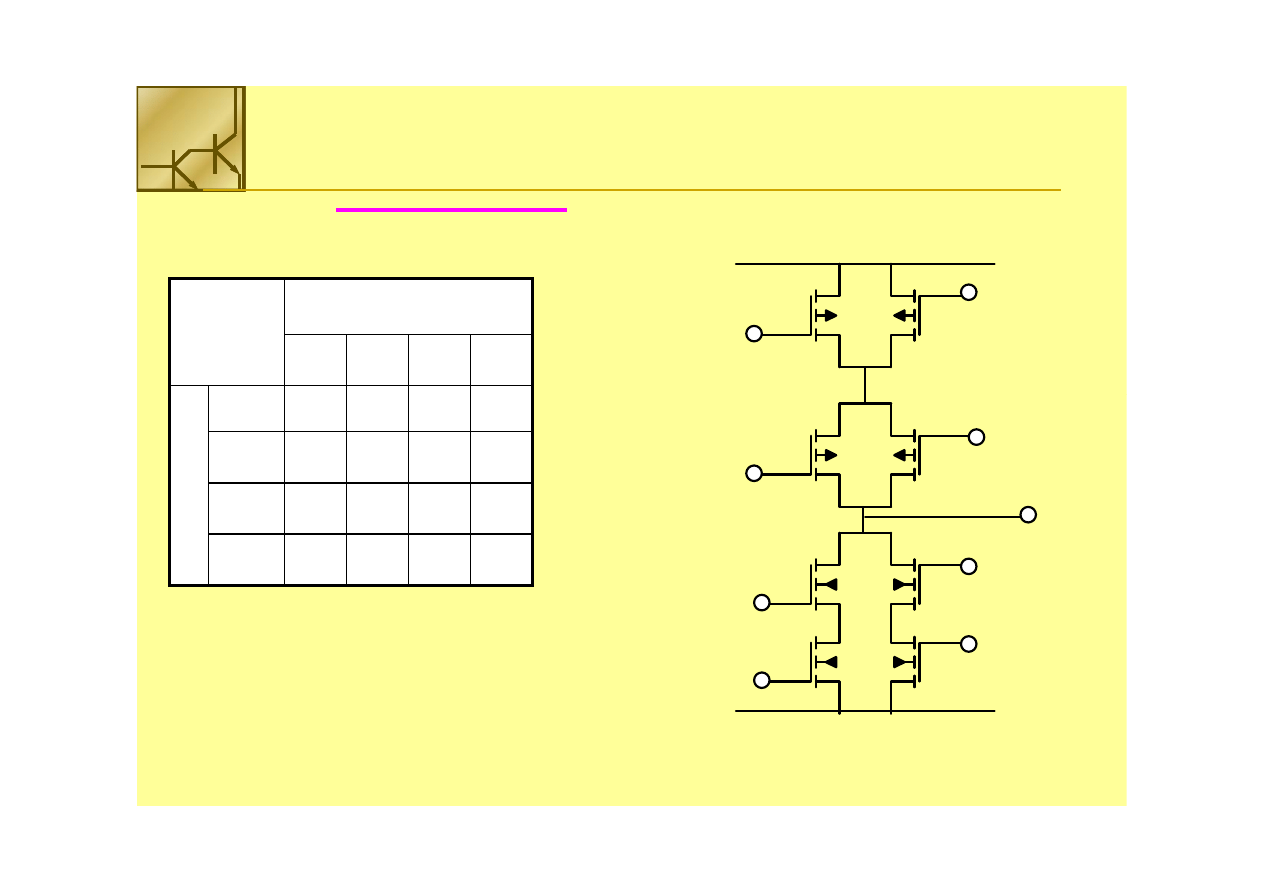
Bramki złożone
Bramki złożone
Bramki złożone
Bramki złożone
F
F = (A • B) + (C • D)
= (A • B) + (C • D)
PMOS
V
DD
FF
CD
CD
00
00
01
01
11
11
10
10
A
B
A
A
BB
0 0
0 0
11
11
00
11
0 1
0 1
11
11
00
11
F
C
D
BB
1 1
1 1
00
00
00
00
10
10
11
11
00
11
NMOS F’ AB CD
NMOS F’ AB CD
NMOS
A
C
NMOS: F’ = AB + CD
NMOS: F’ = AB + CD
PMOS: F =
PMOS: F = A’C’+A’D’+B’C’+B’D
A’C’+A’D’+B’C’+B’D’ =
’ =
= C’(
= C’(A’+B
A’+B’)+D’(
’)+D’(A’+B
A’+B’) = (
’) = (A’+B
A’+B’)(
’)(C’+D
C’+D’)’)
(AB
(AB)’ (
)’ (CD)’
CD)’ AB CD
AB CD
V
SS
B
D
6 marca 2011
Wojciech Kucewicz
90
Układ składa się 8 tranzystorów
Układ składa się 8 tranzystorów
=(AB
=(AB)’ (
)’ (CD)’=
CD)’=AB+CD
AB+CD
SS
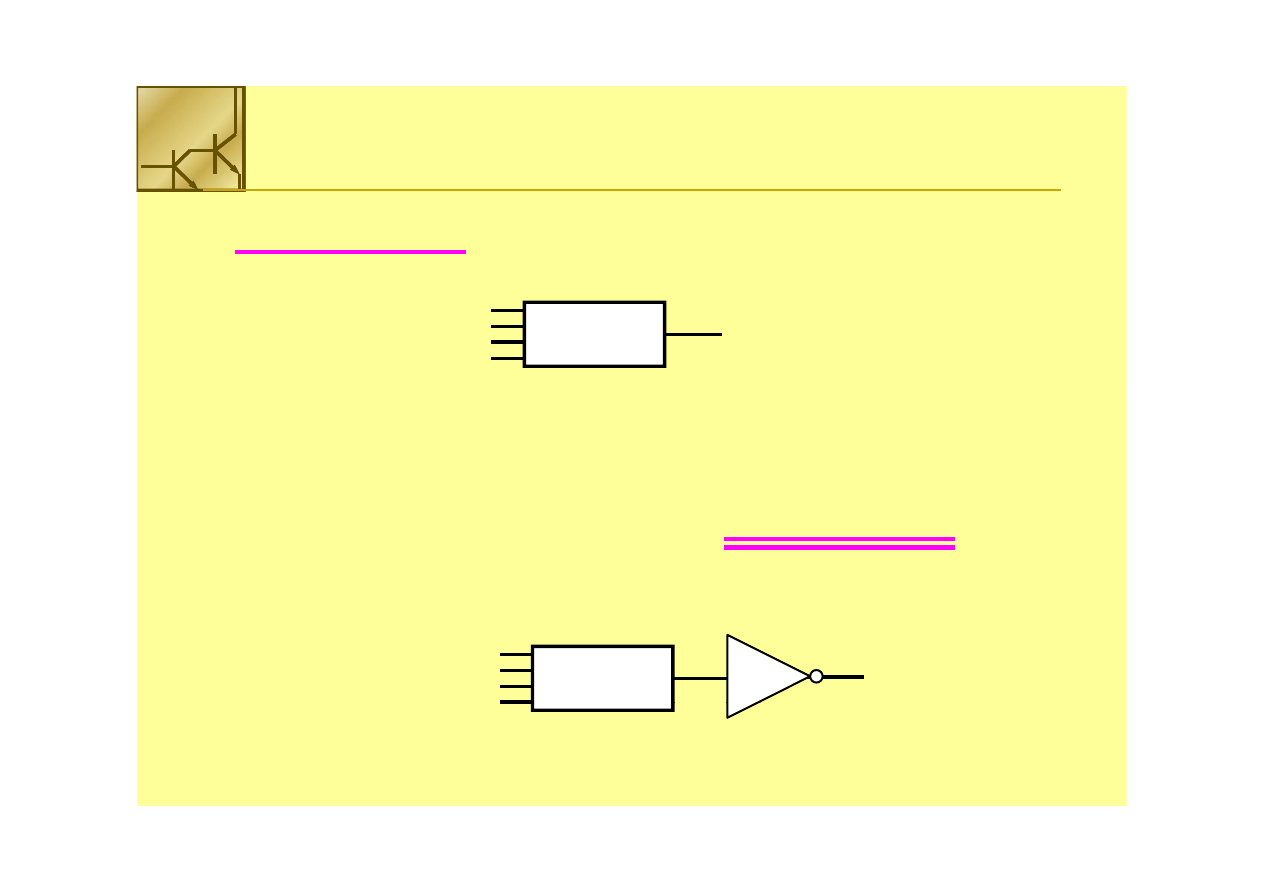
The Complex Gate
The Complex Gate
The Complex Gate
The Complex Gate
Najłatwiej jest projektować funkcje zaprzeczone:
Najłatwiej jest projektować funkcje zaprzeczone:
F = (A • B) + (C • D)
F = (A • B) + (C • D)
(
) (
)
(
) (
)
Function
Function
A
A
BB
CC
D
D
FF
Funkcje niezaprzeczone wymagają dodatkowego
Funkcje niezaprzeczone wymagają dodatkowego
inwertera:
inwertera:
F = (A • B) + (C • D) ==>
F = (A • B) + (C • D) ==> F
F = (A • B) + (C • D)
= (A • B) + (C • D)
Function
Function
A
A
BB
CC
FF
Not F
Not F
6 marca 2011
Wojciech Kucewicz
91
D
D
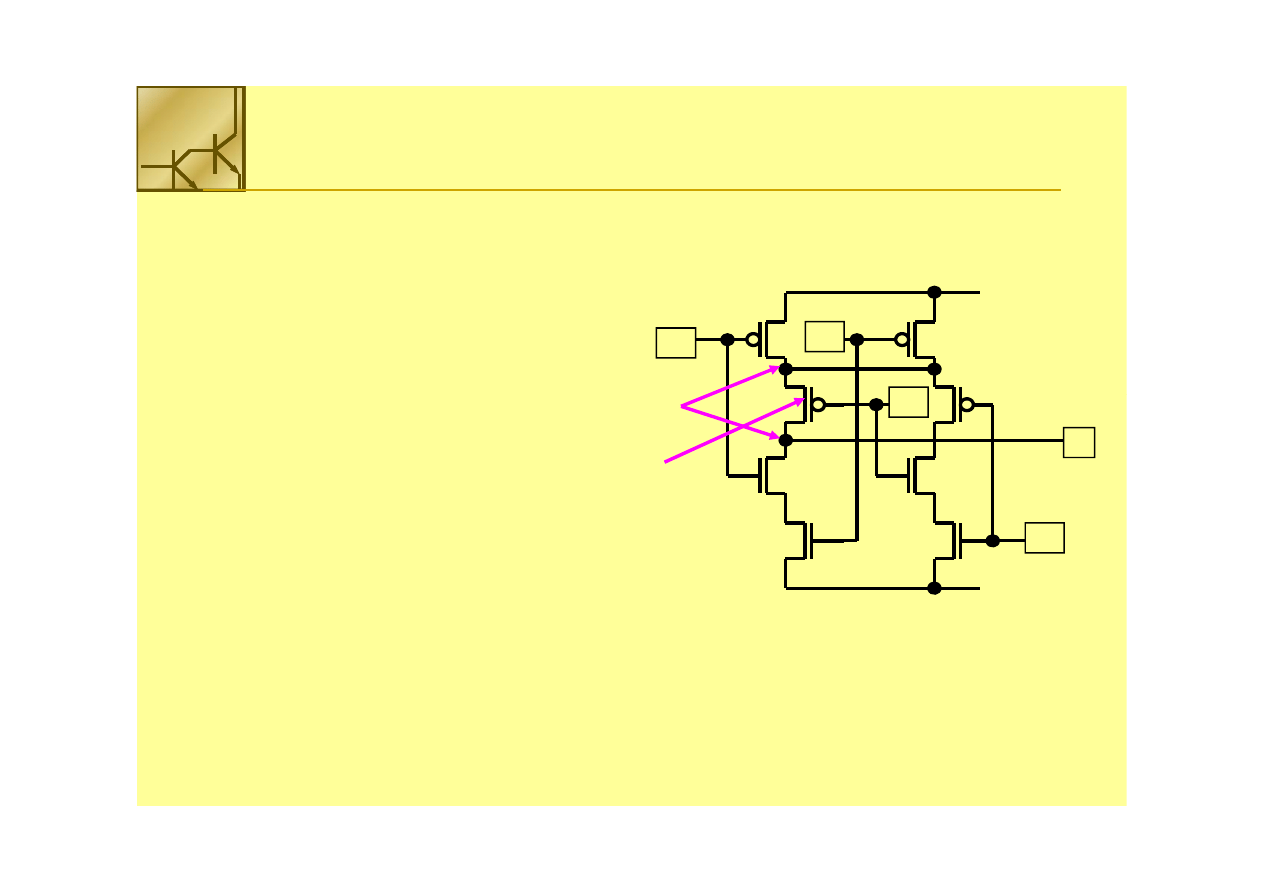
The Complex Gate
The Complex Gate
-- Euler Path
Euler Path
The Complex Gate
The Complex Gate
-- Euler Path
Euler Path
Euler graphs allow to find way of layout design without
Euler graphs allow to find way of layout design without
breaks
breaks
VV
DD
DD
A
A
PMOS
PMOS
BB
CC
N d
N d
FF
CC
Euler path consists:
Euler path consists:
Node
Node
Branch
Branch
VV
SS
SS
NMOS
NMOS
D
D
Euler path consists:
Euler path consists:
•• Nodes
Nodes
are source and drain connections
•• Branch
Branch
are transistors
Branches mirror the series parallel connection of the transistors in the circuit
SS
SS
Branches mirror the series-parallel connection of the transistors in the circuit.
Two graphs for nMOS and pMOS have to be created
6 marca 2011
Wojciech Kucewicz
92
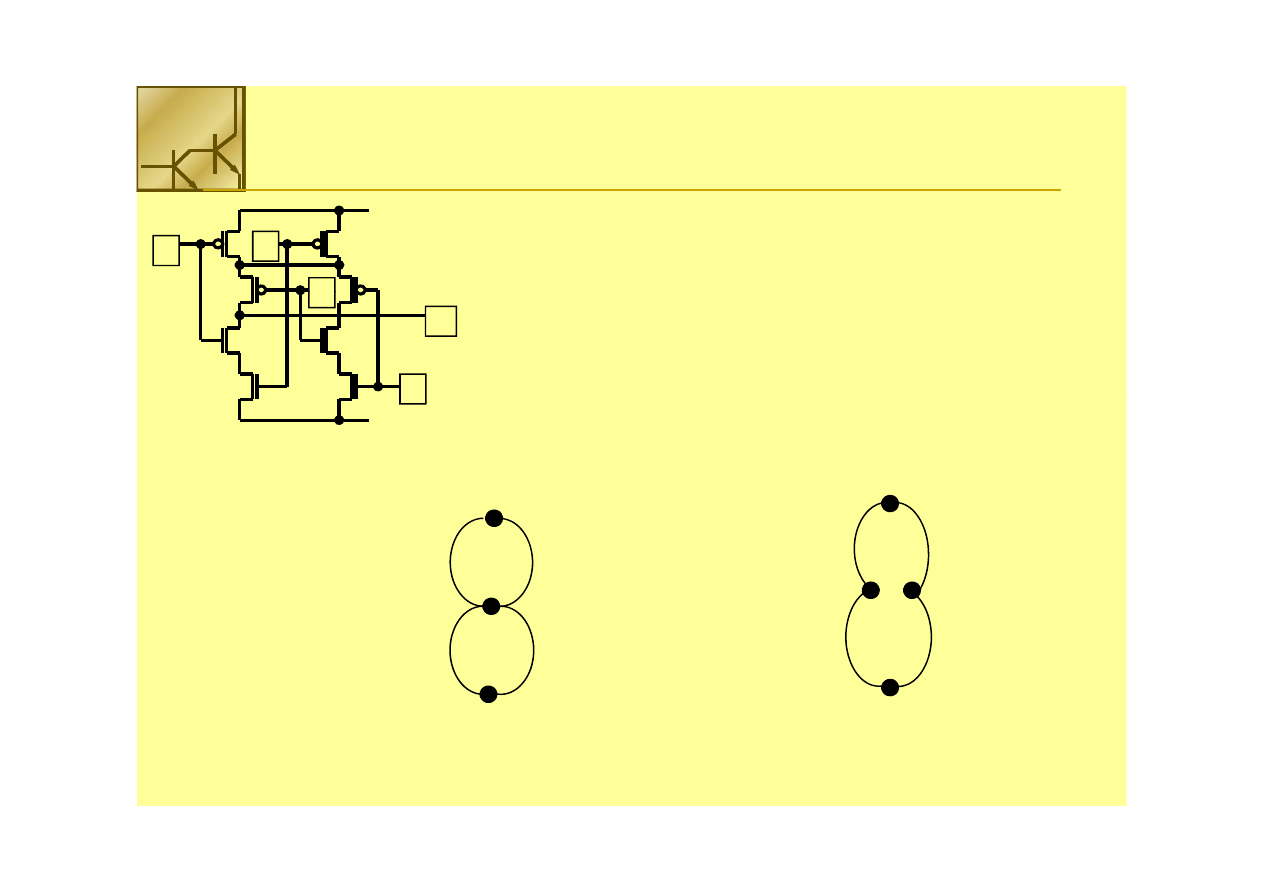
The Complex Gate
The Complex Gate
-- Euler Path
Euler Path
The Complex Gate
The Complex Gate
-- Euler Path
Euler Path
VV
DD
DD
A
A
PMOS
PMOS
BB
CC
Algorithm for Gate designed without
Algorithm for Gate designed without
breaks:
breaks:
••
Find all Euler paths that cover the graph
Find all Euler paths that cover the graph
FF
CC
D
D
••
Find all Euler paths that cover the graph
Find all Euler paths that cover the graph
•• Find a pMOS and nMOS Euler path that have identical labeling (ordering
Find a pMOS and nMOS Euler path that have identical labeling (ordering
of gate labels)
of gate labels)
•• If is not found
If is not found –– break the gate in minimum number of places to achieve
break the gate in minimum number of places to achieve
identical labeling in each piece of gate
identical labeling in each piece of gate
VV
SS
SS
NMOS
NMOS
NMOS L i
NMOS L i
VV
FF
PMOS
PMOS
Logic
Logic
NMOS Logic
NMOS Logic
VV
DD
DD
A
A
BB
A
A
CC
FF
Paths:
Paths:
ACDB
ACDB
ADCB
ADCB
Paths:
Paths:
ACDB
ACDB
ABDC
ABDC
VV
SS
SS
CC
D
D
BB
D
D
ADCB
ADCB
ABCD
ABCD
BDCA
BDCA
BCDA
BCDA
ABDC
ABDC
BACD
BACD
BDCA
BDCA
…………
…………
6 marca 2011
Wojciech Kucewicz
93
VV
SS
SS
FF
A
A →
→
C
C →
→
D
D →
→
BB
A
A →
→
C
C →
→
D
D →
→
BB
≡≡
…………
…………
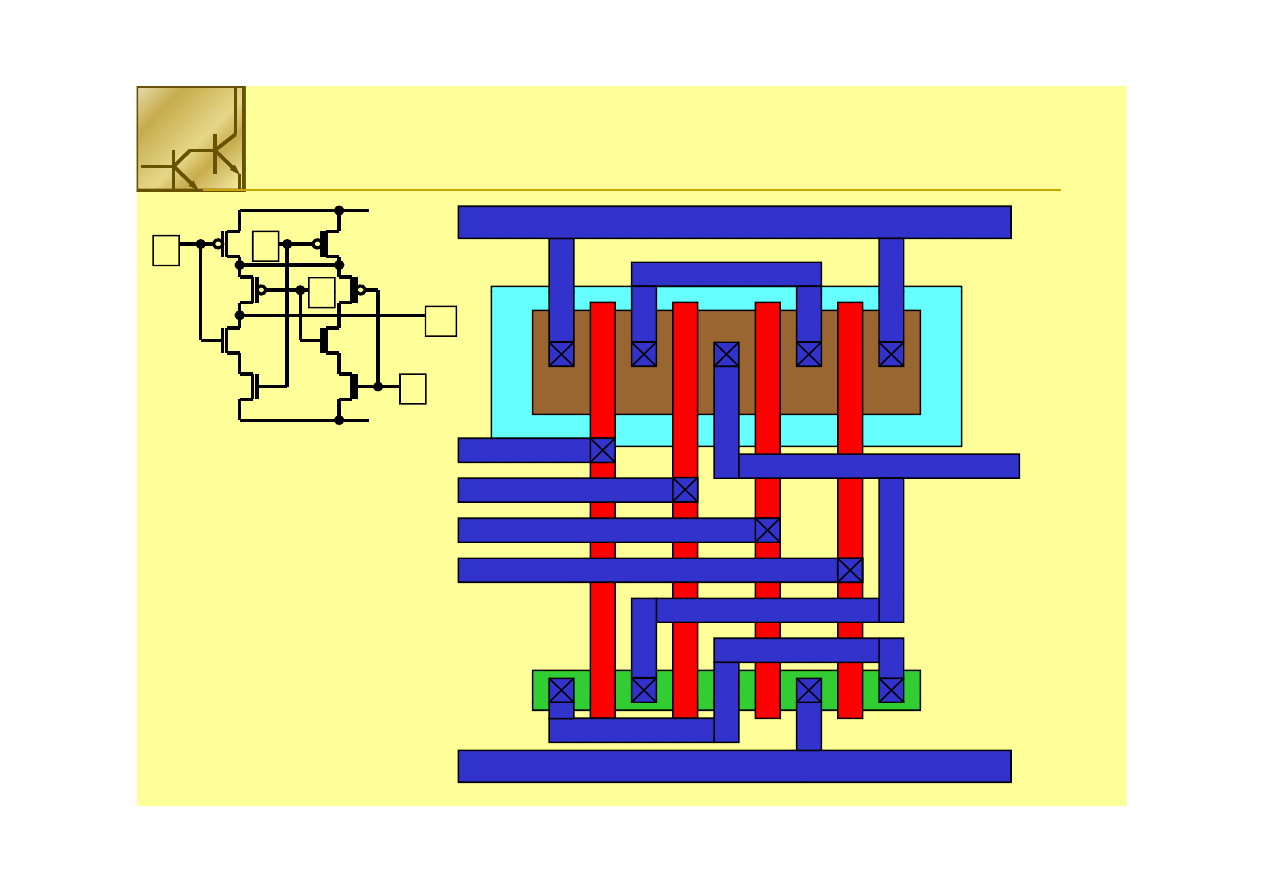
The Complex Gate
The Complex Gate
The Complex Gate
The Complex Gate
VV
DD
DD
A
A
PMOS
PMOS
BB
CC
VV
DD
DD
FF
CC
D
D
A C D B
A C D B
VV
SS
SS
NMOS
NMOS
A
A
FF
CC
BB
D
D
CC
6 marca 2011
Wojciech Kucewicz
94
VV
ss
ss

Cyfrowe układy kombinacyjne
Cyfrowe układy kombinacyjne
Cyfrowe układy kombinacyjne
Cyfrowe układy kombinacyjne
Multipleksery
Multipleksery
Multipleksery
Multipleksery
Multipleksery
Multipleksery
i d
lti l k
i d
lti l k
Multipleksery
Multipleksery
i d
lti l k
i d
lti l k
i demultipleksery
i demultipleksery
i demultipleksery
i demultipleksery
6 marca 2011
Wojciech Kucewicz
95
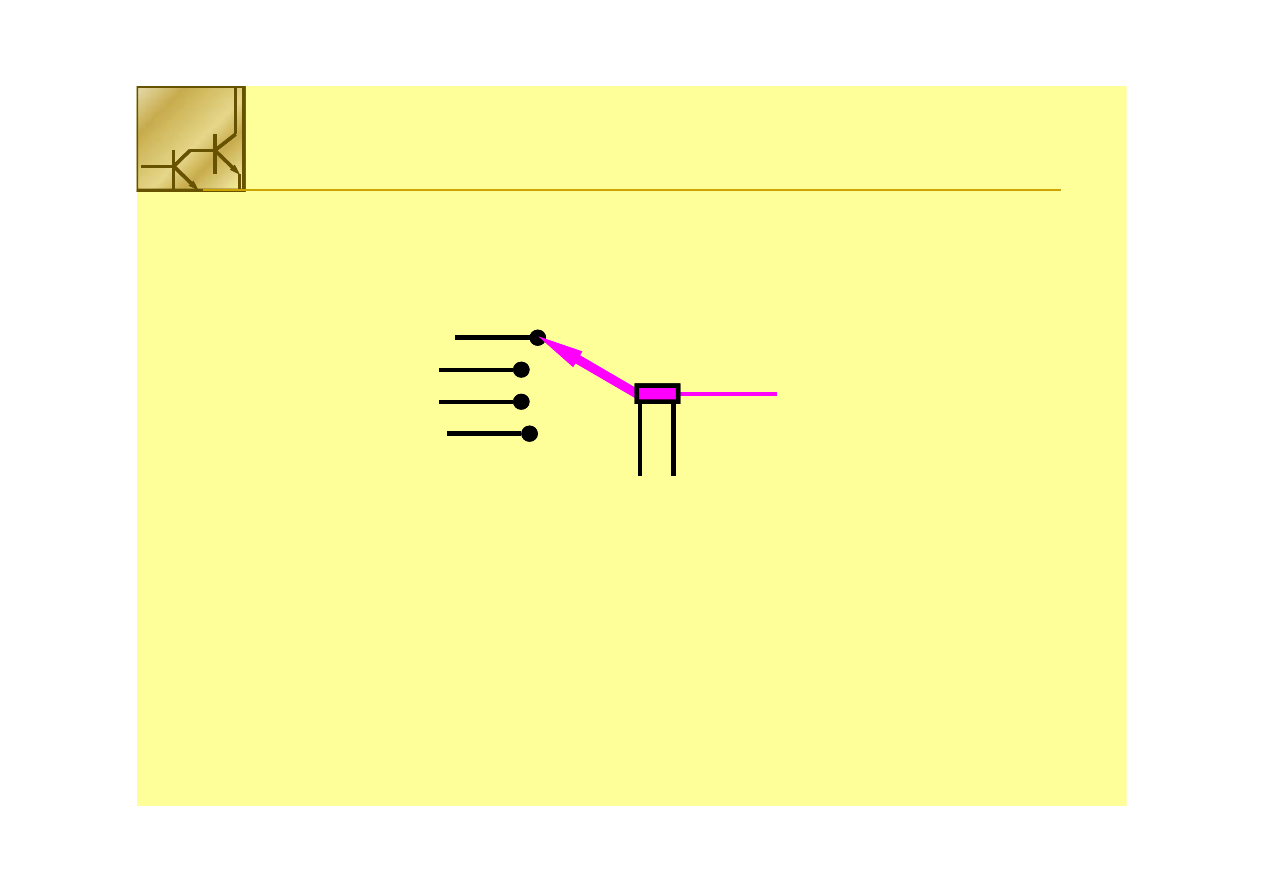
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Multiplekser umożliwiaj
Multiplekser umożliwiaj wybór i przesłanie na wyjście
wybór i przesłanie na wyjście sygnału
sygnału
jednego z N wejść
jednego z N wejść
j
g
j
j
g
j
D0
D0
D1
D1
D2
D2
Out
Out
D2
D2
D3
D3
S1
S1 S0
S0
Numer wejścia jest określany przez stan wejść adresowych (sterujących)
Numer wejścia jest określany przez stan wejść adresowych (sterujących)
S0 S1
S0 S1
S1
S1 S0
S0
S0, S1 ....
S0, S1 ....
Z uwagi na naturalny kod binarny stosowany do określenia adresu, liczba
Z uwagi na naturalny kod binarny stosowany do określenia adresu, liczba
wejść jest związana z liczbą wejść sterujących zależnością:
wejść jest związana z liczbą wejść sterujących zależnością:
N
N = 2
= 2
nn
6 marca 2011
Wojciech Kucewicz
96
j j
j
j y
j j
j
j y
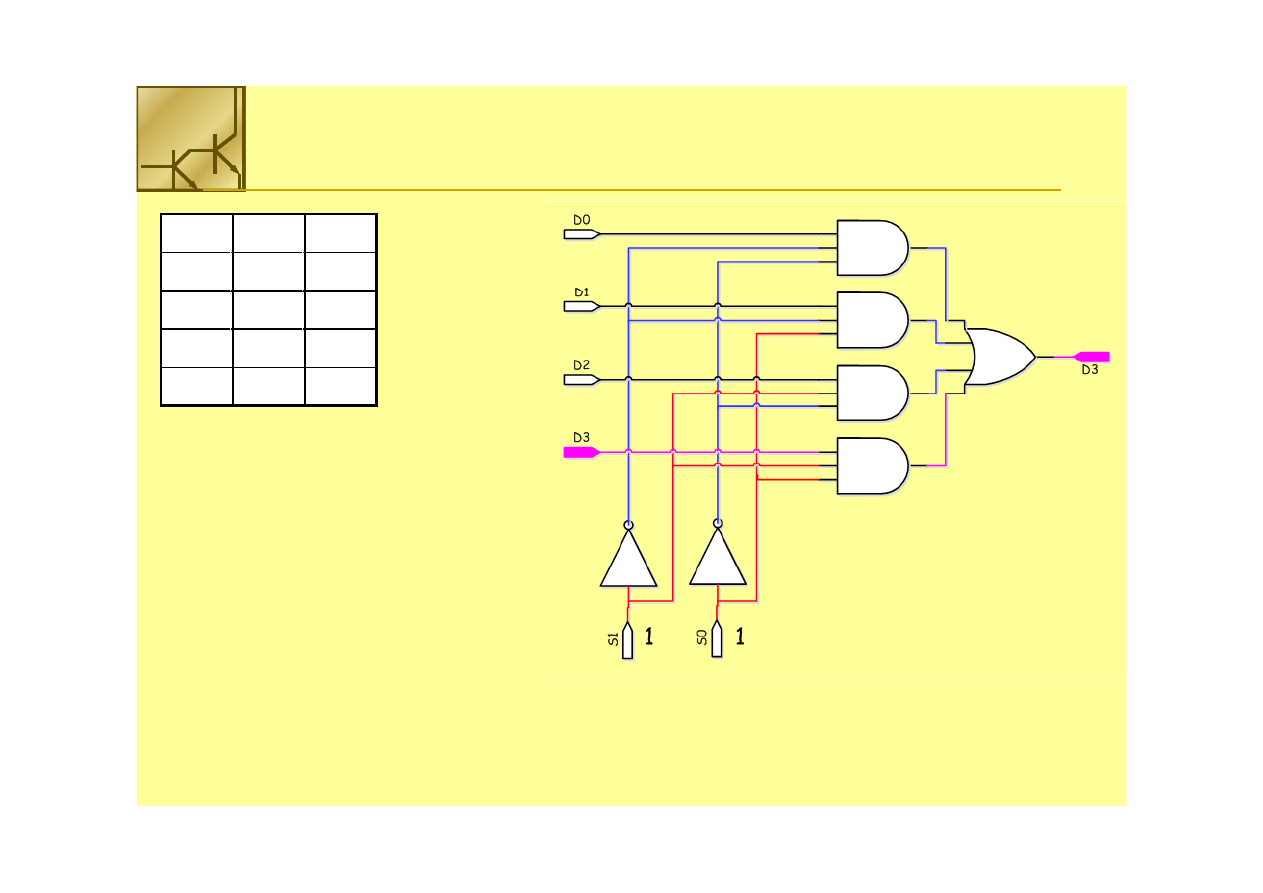
Multiplekser
Multiplekser
Multiplekser
Multiplekser
S1
S1
S0
S0
FF
00
00
D0
D0
00
11
D1
D1
11
00
D2
D2
11
11
D3
D3
11
11
D3
D3
Do zbudowania 2
Do zbudowania 2
nn
wejściowego multipleksera potrzebne
wejściowego multipleksera potrzebne jest
jest 22
nn
bramek AND (n+1)
bramek AND (n+1)--
6 marca 2011
Wojciech Kucewicz
97
j
g
p
p
j
g
p
p
jj
(
)
(
)
wejściowych oraz bramka OR
wejściowych oraz bramka OR 22
nn
--wejściowa
wejściowa
Multiplekser umożliwia zmianę formatu danych z równoległego na szeregowy.
Multiplekser umożliwia zmianę formatu danych z równoległego na szeregowy.
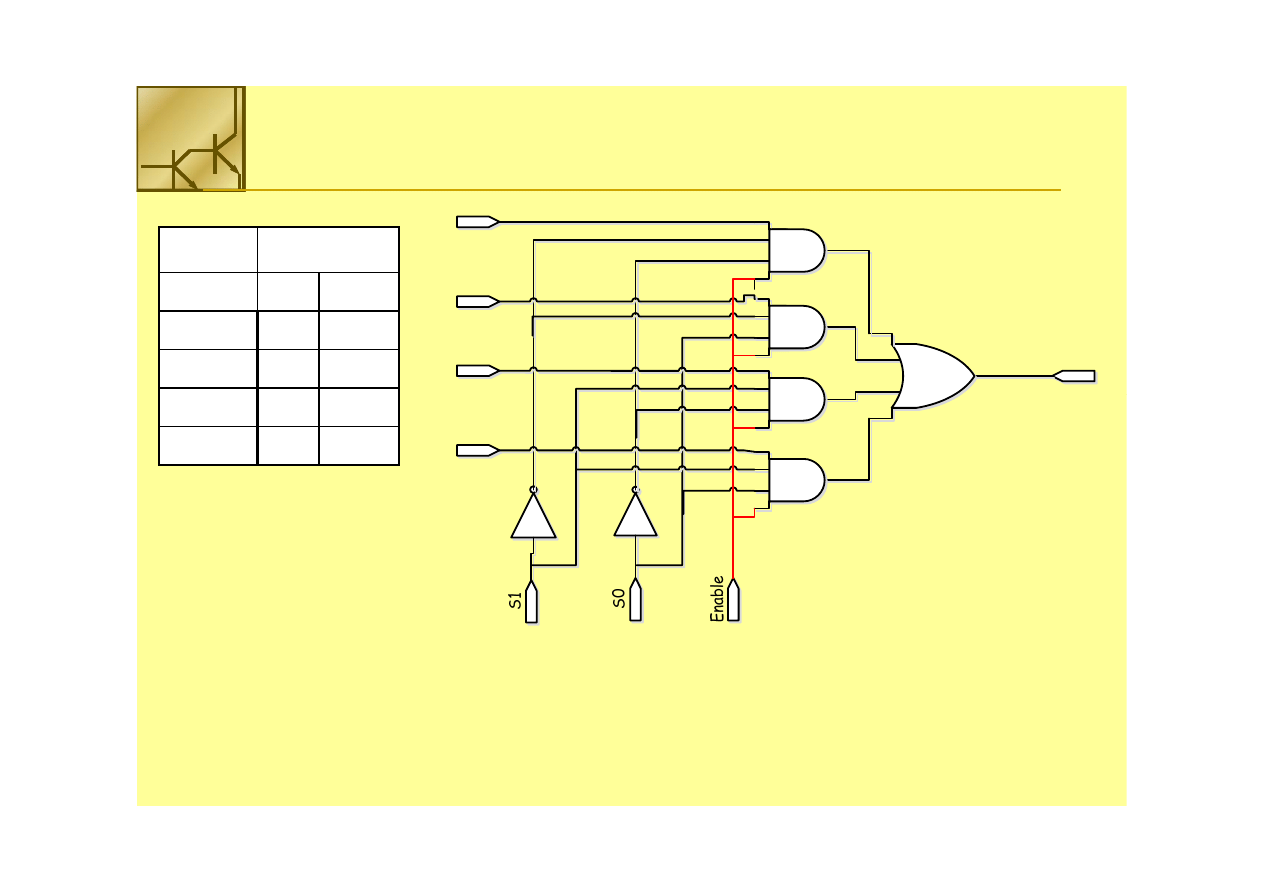
Multiplekser
Multiplekser
Multiplekser
Multiplekser
D0
D1
FF
Enable
Enable
S1 S0
S1 S0
00
11
D2
F
S1 S0
S1 S0
00
11
0
0 00
00
D0
D0
0 1
0 1
00
D1
D1
D3
F
1 0
1 0
00
D2
D2
1
1 11
00
D3
D3
b
b
1
Dodatkowe wejście
Dodatkowe wejście Enable
Enable pozwala zablokować stan wyjścia
pozwala zablokować stan wyjścia multipleksera.
multipleksera.
1
6 marca 2011
Wojciech Kucewicz
98
jj
p
yj
p
yj
pp
Sygnały z wejścia będą przesyłane do wyjścia tylko, gdy wejście
Sygnały z wejścia będą przesyłane do wyjścia tylko, gdy wejście Enable
Enable =1
=1
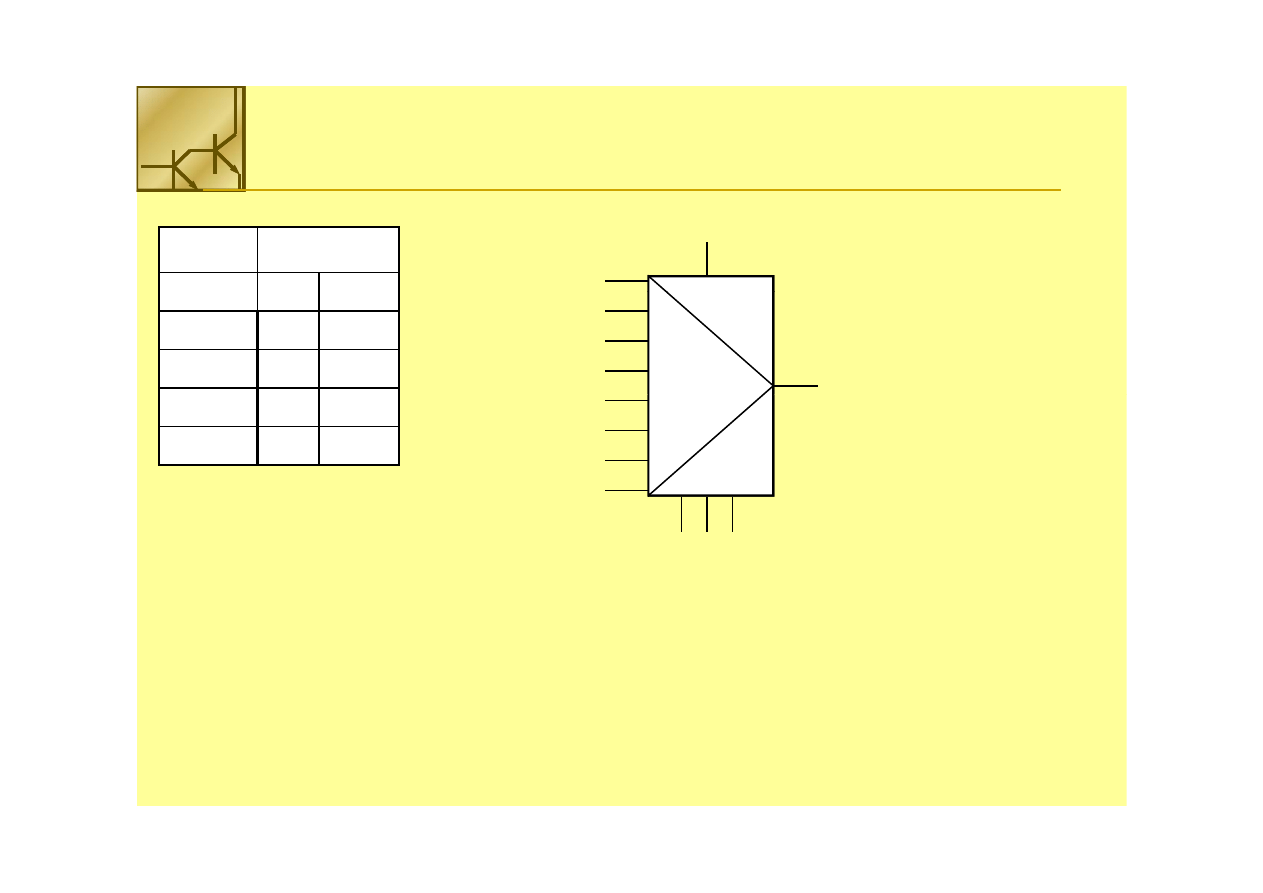
Multiplekser
Multiplekser
Multiplekser
Multiplekser
D0
D0
En
En
FF
Enable
Enable
S1 S0
S1 S0
00
11
D0
D0
D1
D1
..
..
..
FF
S1 S0
S1 S0
00
11
0
0 00
00
D0
D0
0 1
0 1
00
D1
D1
..
..
..
..
D8
D8
1 0
1 0
00
D2
D2
1
1 11
00
D3
D3
S1 S2 S3
S1 S2 S3
Funkcję multipleksera można opisać funkcją logiczną:
Funkcję multipleksera można opisać funkcją logiczną:
∑
−
=
⋅
⋅
=
1
N
0
k
k
k
En
D
S
Out
gdzie
gdzie S
S
kk
jest
jest mintermem
mintermem utworzonym z wektora adresu
utworzonym z wektora adresu
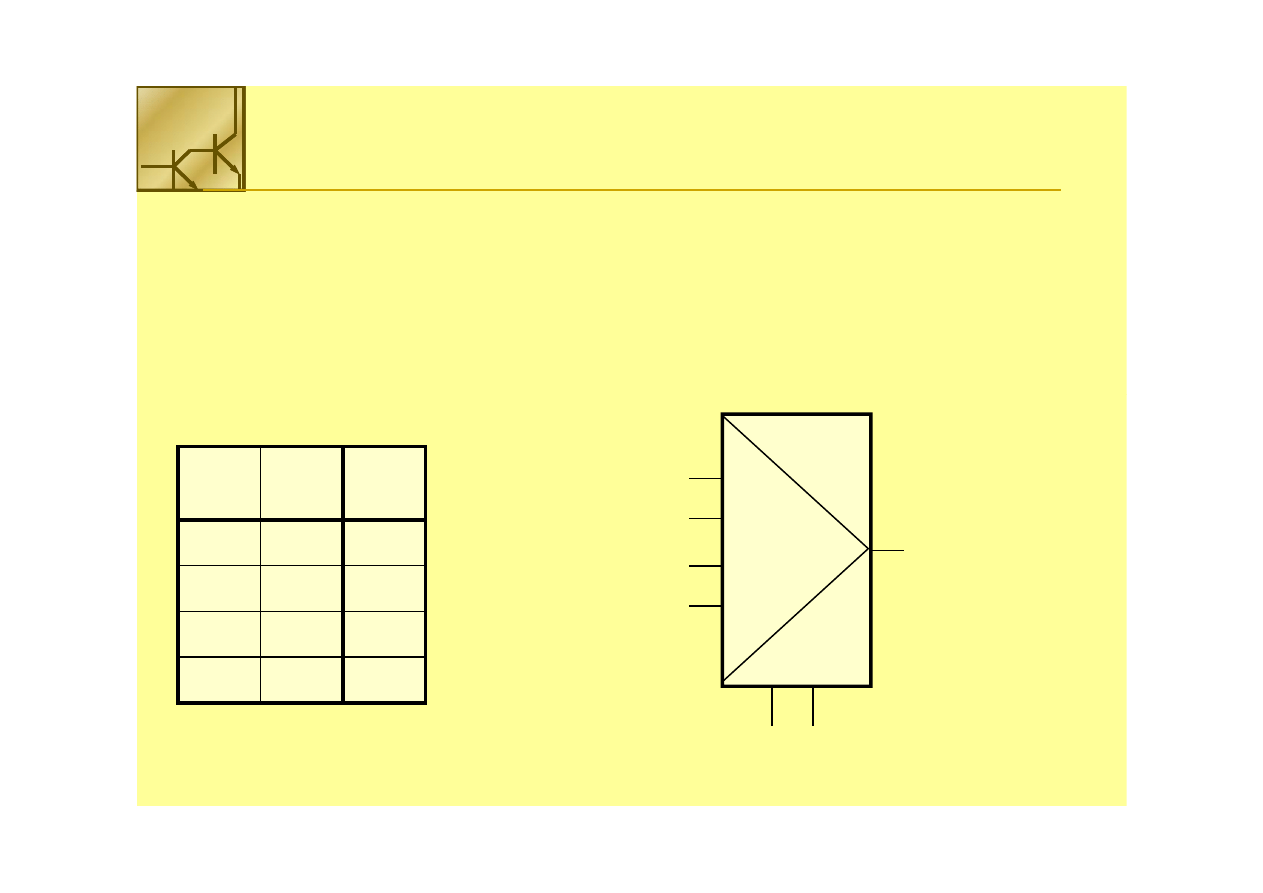
Multiplekser
Multiplekser
Multiplekser
Multiplekser
22
n
n
––wejściowy multiplekser może być użyty do realizacji dowolnej funkcji logicznej
wejściowy multiplekser może być użyty do realizacji dowolnej funkcji logicznej
o n
o n--zmiennych.
zmiennych.
R li j i j
b
ś d i dł
i d d
i d i h
jść
R li j i j
b
ś d i dł
i d d
i d i h
jść
Realizuje się ją poprzez bezpośrednie podłączenie do odpowiednich wejść
Realizuje się ją poprzez bezpośrednie podłączenie do odpowiednich wejść
multipleksera wartości logicznych „
multipleksera wartości logicznych „11”” lub „0”
lub „0”
S1
S1
S0
S0
FF
00
D0
D0
00
00
00
00
11
11
11
11
MultiplexerMultiplexer
D1
D1
D2
D2
FF
11
00
11
11
11
00
00
D3
D3
S1 S0
S1 S0
6 marca 2011
Wojciech Kucewicz
100
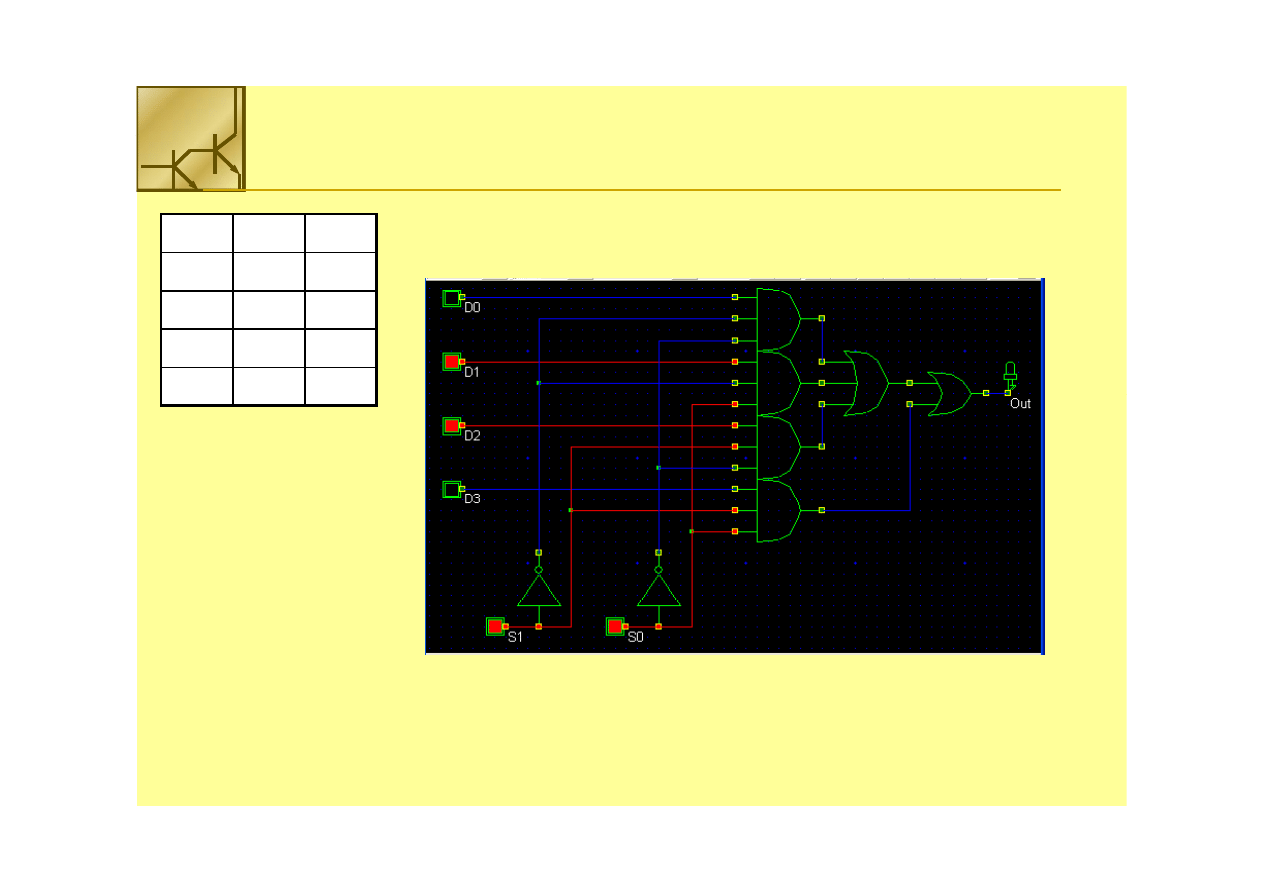
Multiplekser
Multiplekser
Multiplekser
Multiplekser
S1
S1
S0
S0
FF
00
00
D0
D0
00
11
D1
D1
11
00
D2
D2
11
11
D3
D3
D
D
6 marca 2011
Wojciech Kucewicz
101
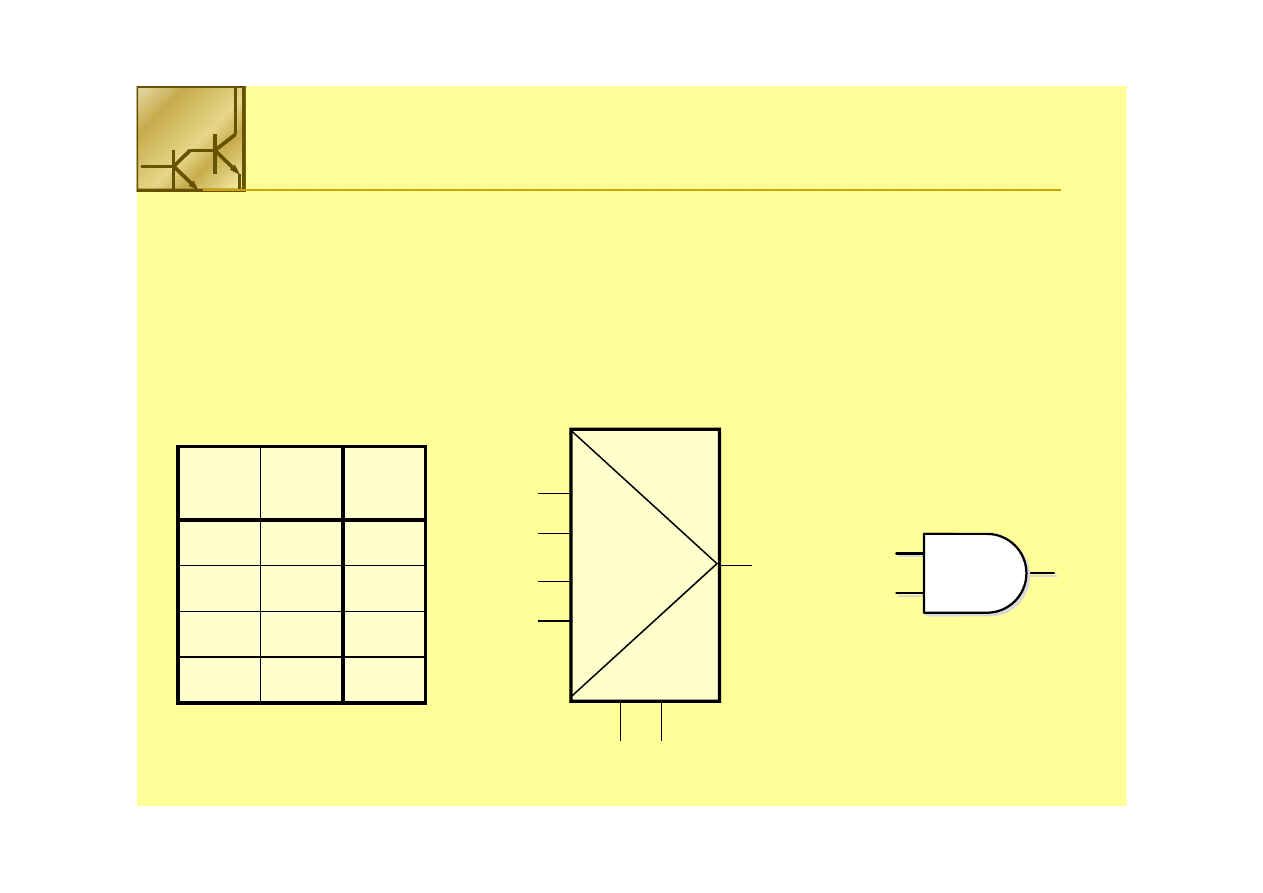
Multiplekser jako bramka AND
Multiplekser jako bramka AND
Multiplekser jako bramka AND
Multiplekser jako bramka AND
22
nn
––wejściowy multiplekser może być użyty do realizacji dowolnej funkcji logicznej
wejściowy multiplekser może być użyty do realizacji dowolnej funkcji logicznej
o n
o n--zmiennych.
zmiennych.
Realizuje się ją poprzez bezpośrednie podłączenie do odpowiednich wejść
Realizuje się ją poprzez bezpośrednie podłączenie do odpowiednich wejść
Real zuje s ę ją poprzez bezpośredn e podłączen e do odpow edn ch wejść
Real zuje s ę ją poprzez bezpośredn e podłączen e do odpow edn ch wejść
multipleksera wartości logicznych „
multipleksera wartości logicznych „11”” lub „0”
lub „0”
S1
S1
S0
S0
OUFT
OUFT
00
D0
D0
00
00
00
00
11
00
00
00
≡≡
D0
D0
D1
D1
D2
D2
FF
FF
S0
S0
S1
S1
11
00
00
11
11
11
11
D3
D3
S1 S0
S1 S0
S1
S1
6 marca 2011
Wojciech Kucewicz
102
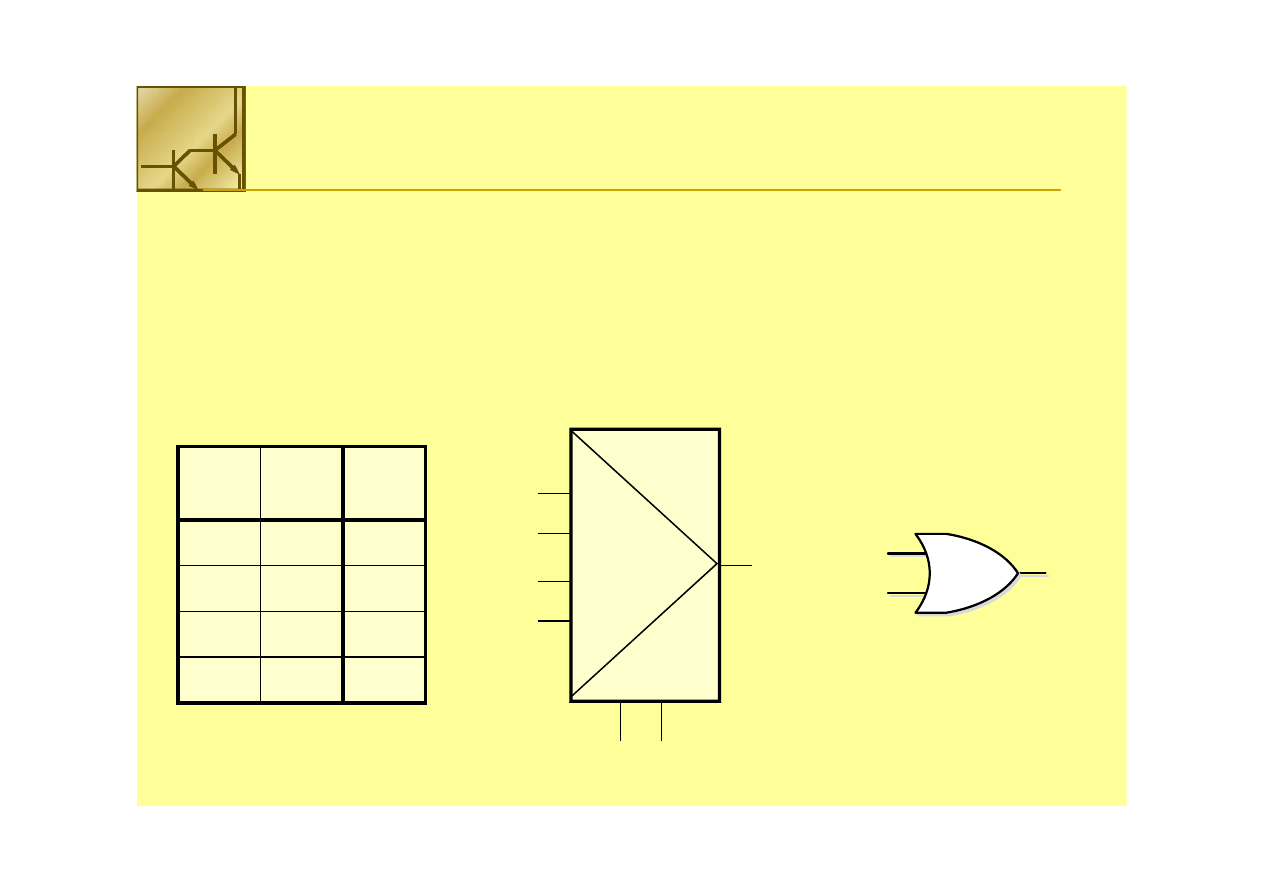
Multiplekser jako bramka OR
Multiplekser jako bramka OR
Multiplekser jako bramka OR
Multiplekser jako bramka OR
22
nn
––wejściowy multiplekser może być użyty do realizacji dowolnej funkcji logicznej
wejściowy multiplekser może być użyty do realizacji dowolnej funkcji logicznej
o
o nn--zmiennych
zmiennych. .
Realizuje się ją poprzez bezpośrednie podłączenie do odpowiednich wejść
Realizuje się ją poprzez bezpośrednie podłączenie do odpowiednich wejść
Real zuje s ę ją poprzez bezpośredn e podłączen e do odpow edn ch wejść
Real zuje s ę ją poprzez bezpośredn e podłączen e do odpow edn ch wejść
multipleksera wartości logicznych „
multipleksera wartości logicznych „11”” lub „0”
lub „0”
S1
S1
S0
S0
FF
00
D0
D0
00
00
00
00
11
11
11
11
≡≡
D0
D0
D1
D1
D2
D2
FF
FF
S0
S0
S1
S1
11
00
11
11
11
11
11
D3
D3
S1 S0
S1 S0
S1
S1
6 marca 2011
Wojciech Kucewicz
103
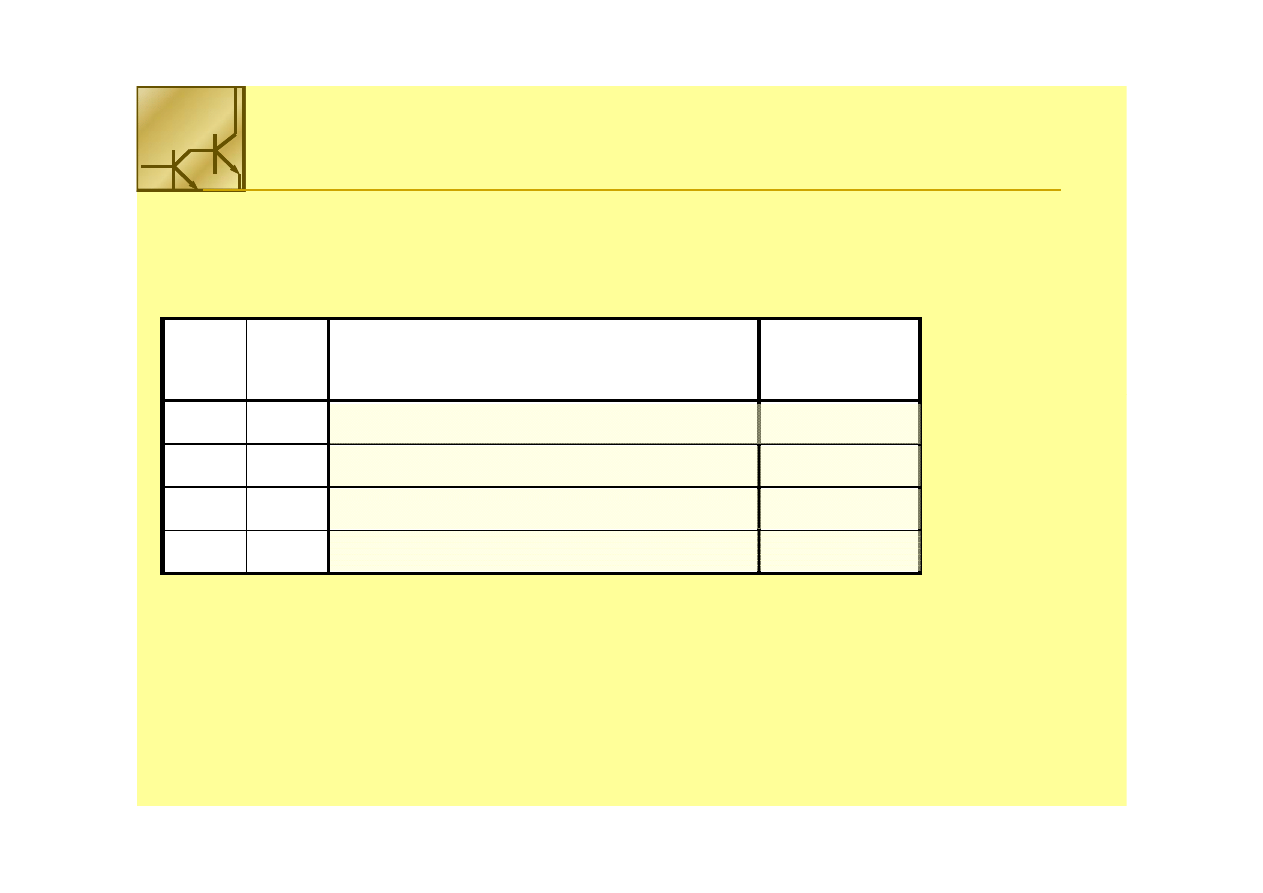
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Zastosowanie multipleksera 4 na 1 do realizacji funkcji 3 zmiennych
Zastosowanie multipleksera 4 na 1 do realizacji funkcji 3 zmiennych::
FF =
= x’
x’yy’’z + xyz
z + xyz’ +
’ + yz
yz
FF
FF
yy
yy
yy
S1=
S1=
yy
S0=
S0=
zz
= x’
= x’ ⋅⋅ 1
1 ⋅⋅ 0 + x
0 + x ⋅⋅ 0
0 ⋅⋅ 1 + 0
1 + 0 ⋅⋅ 00
00
= x’
= x’ ⋅⋅ 1
1 ⋅⋅ 1 + x
1 + x ⋅⋅ 0
0 ⋅⋅ 0 + 0
0 + 0 ⋅⋅ 11
x’
x’
00
00
00
11
= x’
= x’ ⋅⋅ 0
0 ⋅⋅ 1 + x
1 + x ⋅⋅ 1
1 ⋅⋅ 0 + 1
0 + 1 ⋅⋅ 11
11
= x’
= x’ ⋅⋅ 0
0 ⋅⋅ 0 + x
0 + x ⋅⋅ 1
1 ⋅⋅ 1 + 1
1 + 1 ⋅⋅ 00
xx
11
00
11
11
W ś l l k
D0 dł
d 0
Wejście multipleksera D0 podłączamy do 0,
D1 do x’,
D2 do x,
D3 do 1
6 marca 2011
Wojciech Kucewicz
104
D3 do 1
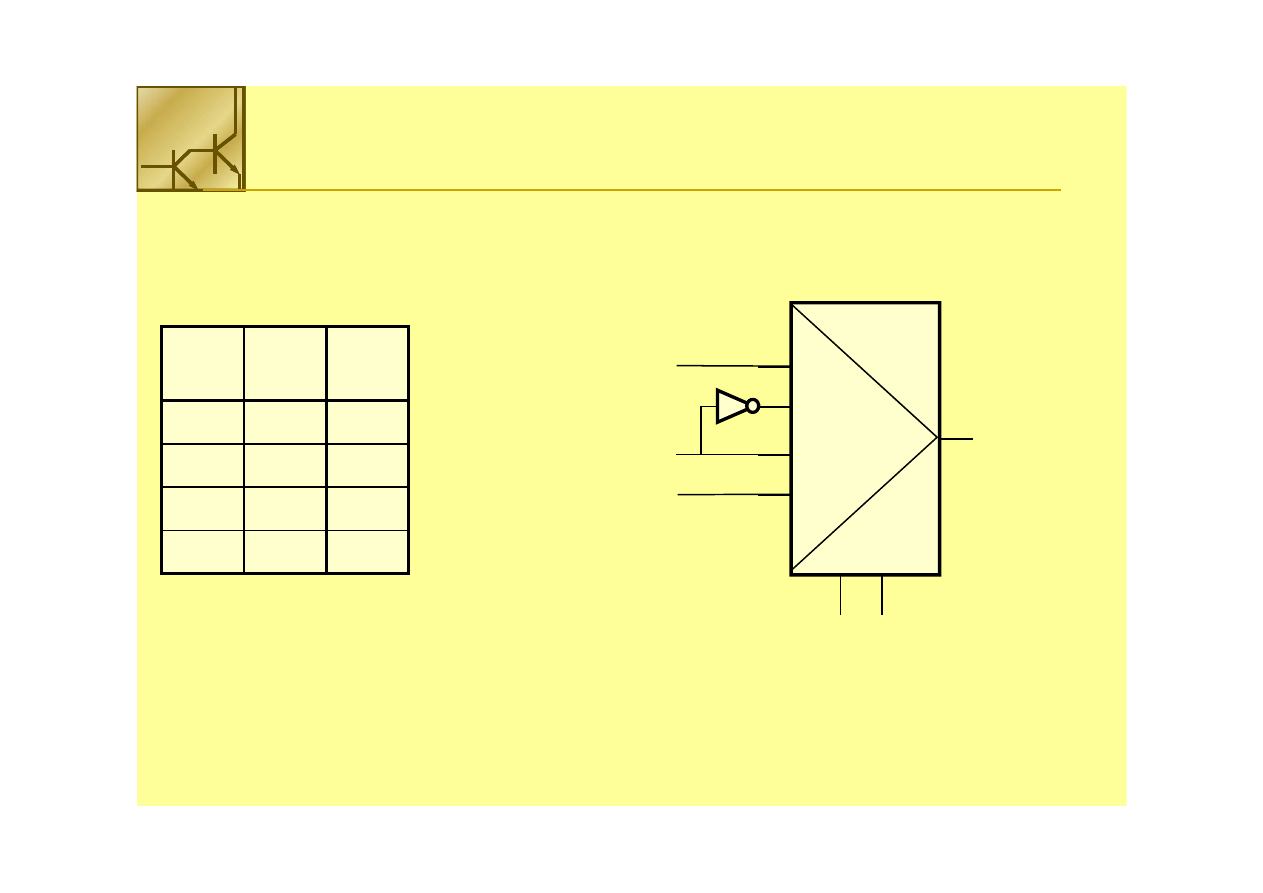
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Zastosowanie multipleksera 4 na 1 do realizacji funkcji 3 zmiennych
Zastosowanie multipleksera 4 na 1 do realizacji funkcji 3 zmiennych::
FF =
= x’
x’yy’’z + xyz
z + xyz’ +
’ + yz
yz
S1=
S1=
yy
S0=
S0=
zz
FF
00
yy
yy
yy
D0
D0
00
00
00
00
11
x’
x’
xx
FF
D1
D1
D2
D2
11
00
xx
11
11
11
1
1
D3
D3
S1 S0
S1 S0
y z
y z
ćć
6 marca 2011
Wojciech Kucewicz
105
Funkcję
Funkcję (n+1)
(n+1)--zmiennych
zmiennych można realizować przy pomocy multipleksera
można realizować przy pomocy multipleksera
22
nn
na
na 1
1 oraz inwertera
oraz inwertera
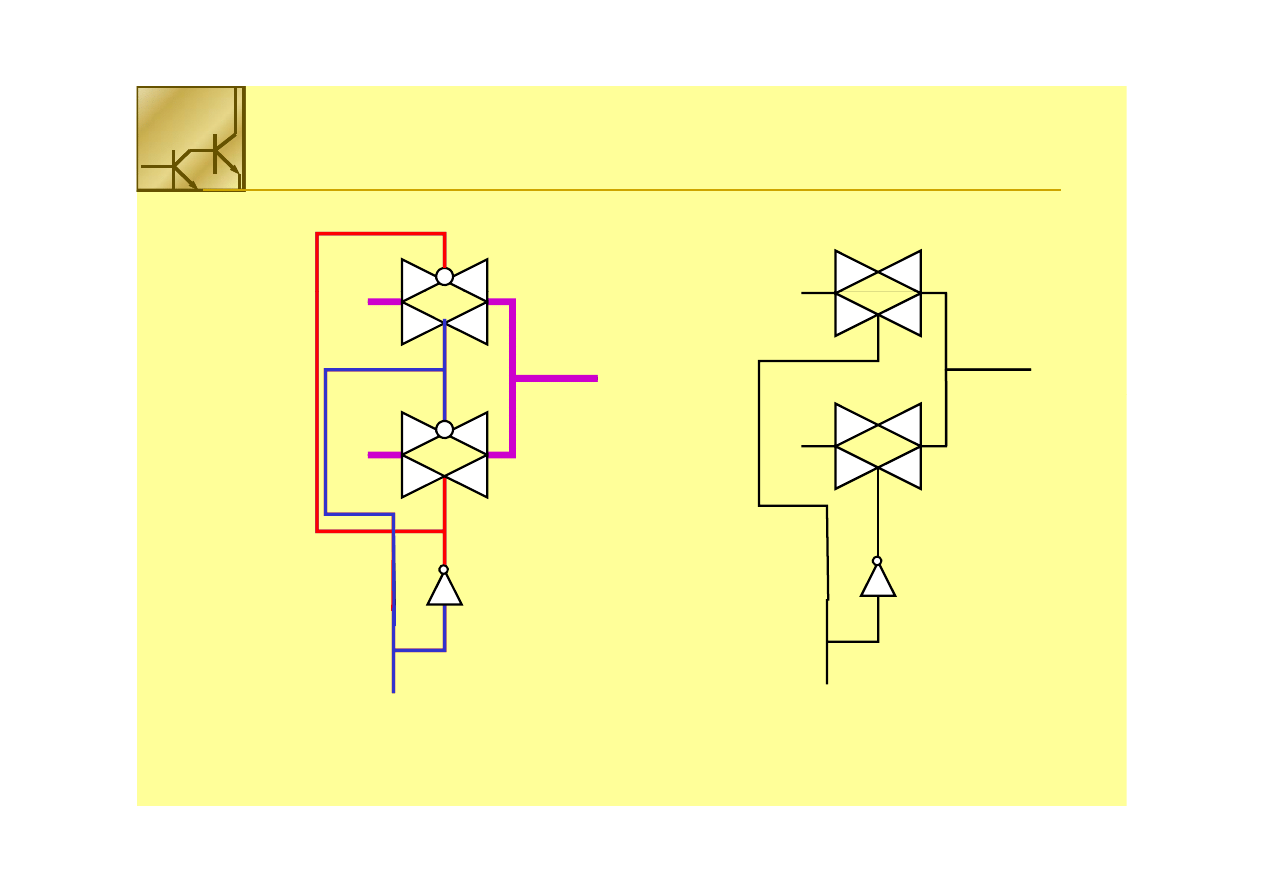
Multiplekser
Multiplekser
Multiplekser
Multiplekser
D0
D0
D0
D0
Out
Out
Out
Out
D1
D1
Out
Out
D1
D1
S
S
S
S
6 marca 2011
Wojciech Kucewicz
106
Multiplekser 2 na 1 można zbudować z 2 bramek transmisyjnych
Multiplekser 2 na 1 można zbudować z 2 bramek transmisyjnych
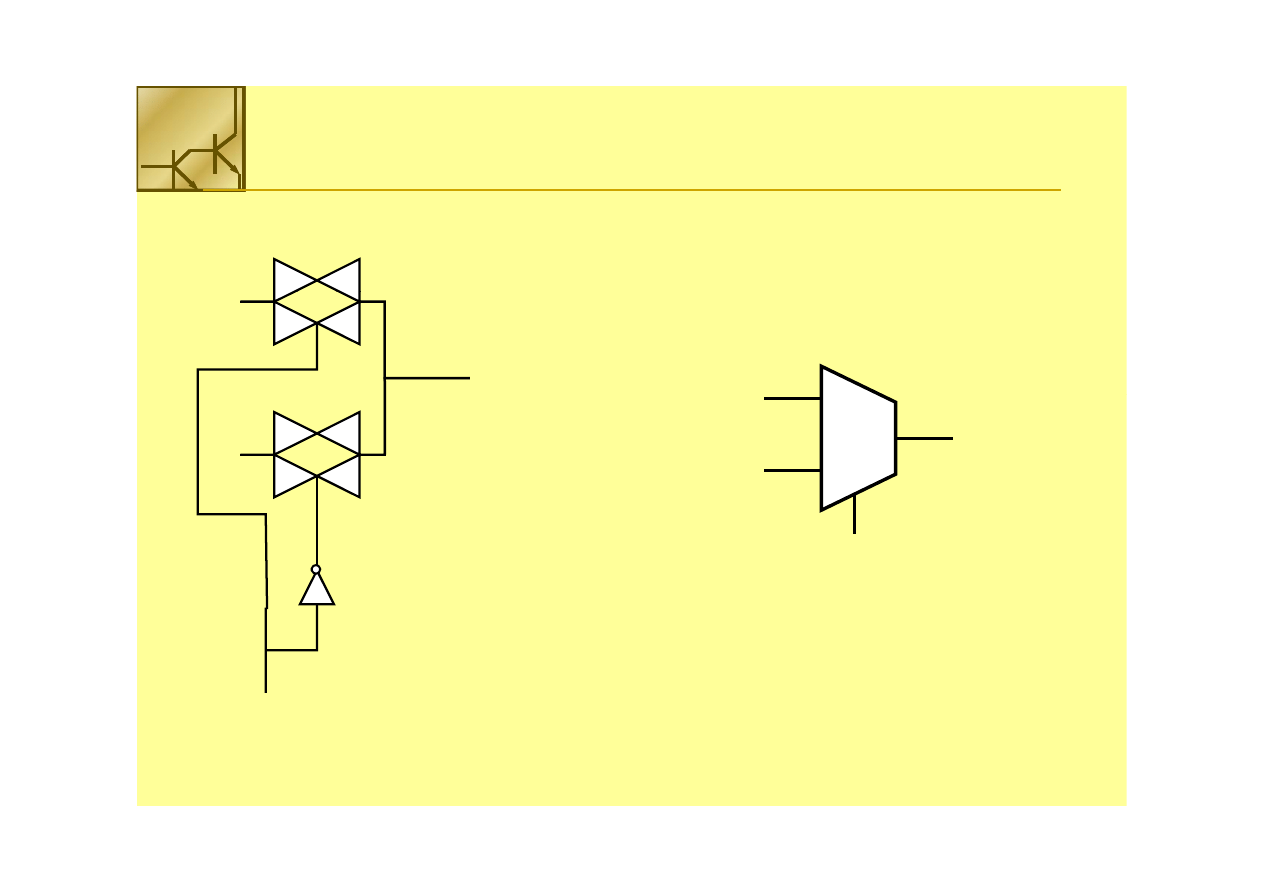
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Multiplexer
Multiplexer 22 na
na 11
D0
D0
FF
D0
D0
D1
D1
S
Sel
el
FF
==
==
D1
D1
Sel
Sel
6 marca 2011
Wojciech Kucewicz
107
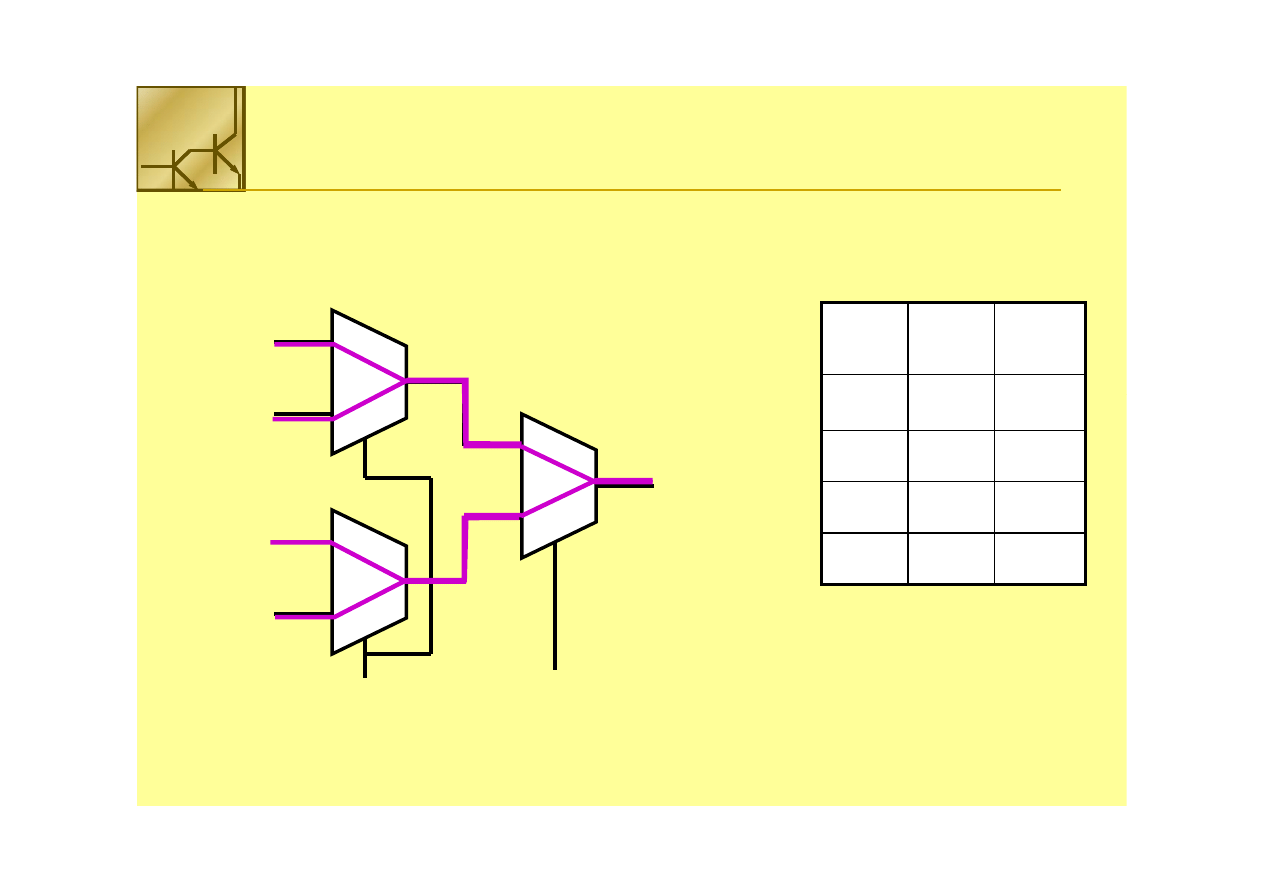
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Multiplekser 4 na 1 można zbudować z 2 multiplekserów
Multiplekser 4 na 1 można zbudować z 2 multiplekserów
2 na 1
2 na 1
M
UX
M
UX
D0
D0
Out
Out
A
A
S1
S1
S
S00
FF
00
00
A
A
MM
D1
D1
S
Sel
el
Out
Out
M
UX
M
UX
D0
D0
Out
Out
BB
FF
00
00
A
A
00
11
BB
11
00
M
UX
M
UX
D0
D0
D1
D1
Out
Out
MM
D1
D1
S
Sel
el
Out
Out
CC
D
D
11
00
CC
11
11
D
D
MM
D1
D1
S
Sel
el
D
D
S1
S1==
S
S0=
0=
0011
0011
6 marca 2011
Wojciech Kucewicz
108
S1
S1==
S
S0=
0=
0011
0011
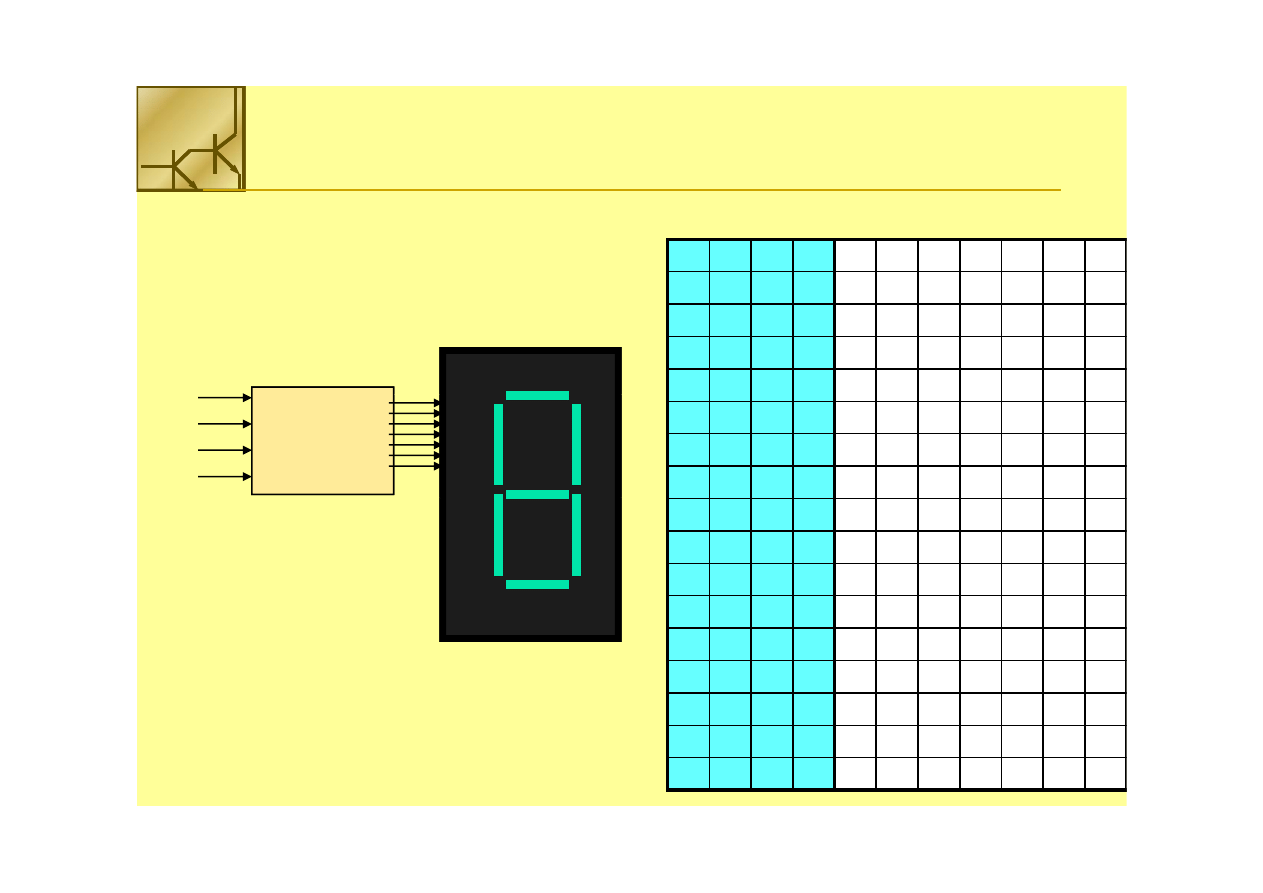
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Zbudować sterownik do wyświetlacza 7
Zbudować sterownik do wyświetlacza 7--segmentowego przy użyciu
segmentowego przy użyciu
multiplekserów
multiplekserów
xx
33
xx
22
xx
11
xx
00
aa
bb
cc
dd
ee
ff
gg
00
00
00
00
11
11
11
11
11
11
00
aa
00
00
00
00
11
11
11
11
11
11
00
00
00
00
11
00
11
11
00
00
00
00
00
00
11
00
11
11
00
11
11
00
11
00
00
11
11
11
11
11
11
00
00
11
Decoder
Decoder
BCD to 7 segm
BCD to 7 segm
xx
00
xx
11
xx
22
xx
33
bb
ff
aa
gg
00
11
00
00
00
11
11
00
00
11
11
00
11
00
11
11
00
11
11
00
11
11
00
11
11
00
11
00
11
11
11
11
11
cc
dd
ee
00
11
11
11
11
11
11
00
00
00
00
11
00
00
00
11
11
11
11
11
11
11
11
00
00
11
11
11
11
11
00
11
11
dd
11
00
11
00
xx
xx
xx
xx
xx
xx
xx
11
00
11
11
xx
xx
xx
xx
xx
xx
xx
11
11
00
00
xx
xx
xx
xx
xx
xx
xx
11
11
00
00
6 marca 2011
Wojciech Kucewicz
109
11
11
00
00
xx
xx
xx
xx
xx
xx
xx
11
11
11
00
xx
xx
xx
xx
xx
xx
xx
11
11
11
11
xx
xx
xx
xx
xx
xx
xx
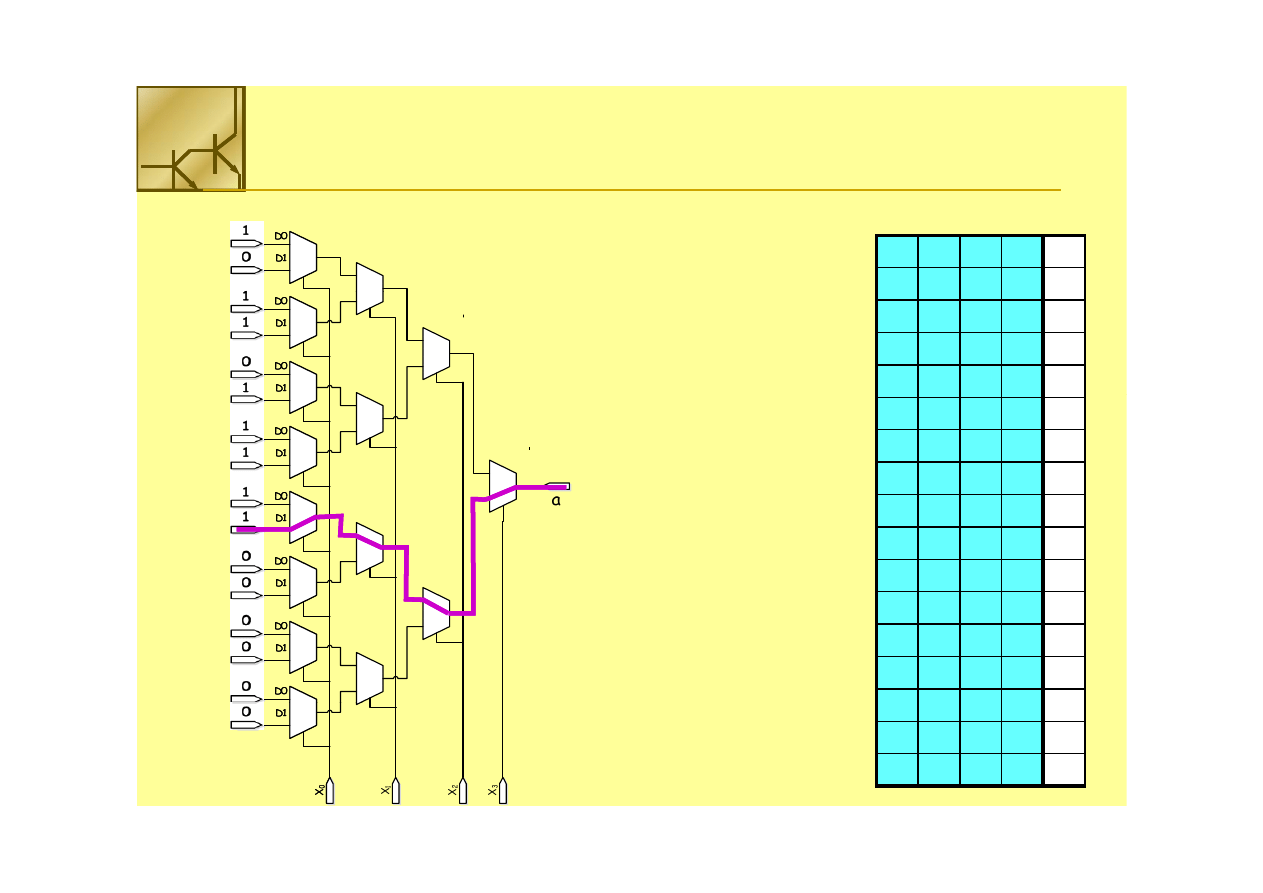
Multiplekser
Multiplekser
Multiplekser
Multiplekser
Budujemy multiplekser 16 do 1
Budujemy multiplekser 16 do 1
xx
33
xx
22
xx
11
xx
00
aa
00
00
00
00
11
00
00
00
11
00
00
00
11
00
11
00
00
11
11
11
00
11
00
00
00
00
11
00
11
11
00
11
11
00
11
00
11
11
11
11
11
00
00
00
11
11
00
00
11
11
11
00
11
00
xx
11
00
11
11
xx
11
11
00
00
xx
11
11
00
00
xx
6 marca 2011
Wojciech Kucewicz
110
11
11
00
00
xx
11
11
11
00
xx
11
11
11
11
xx
1 0 0
1
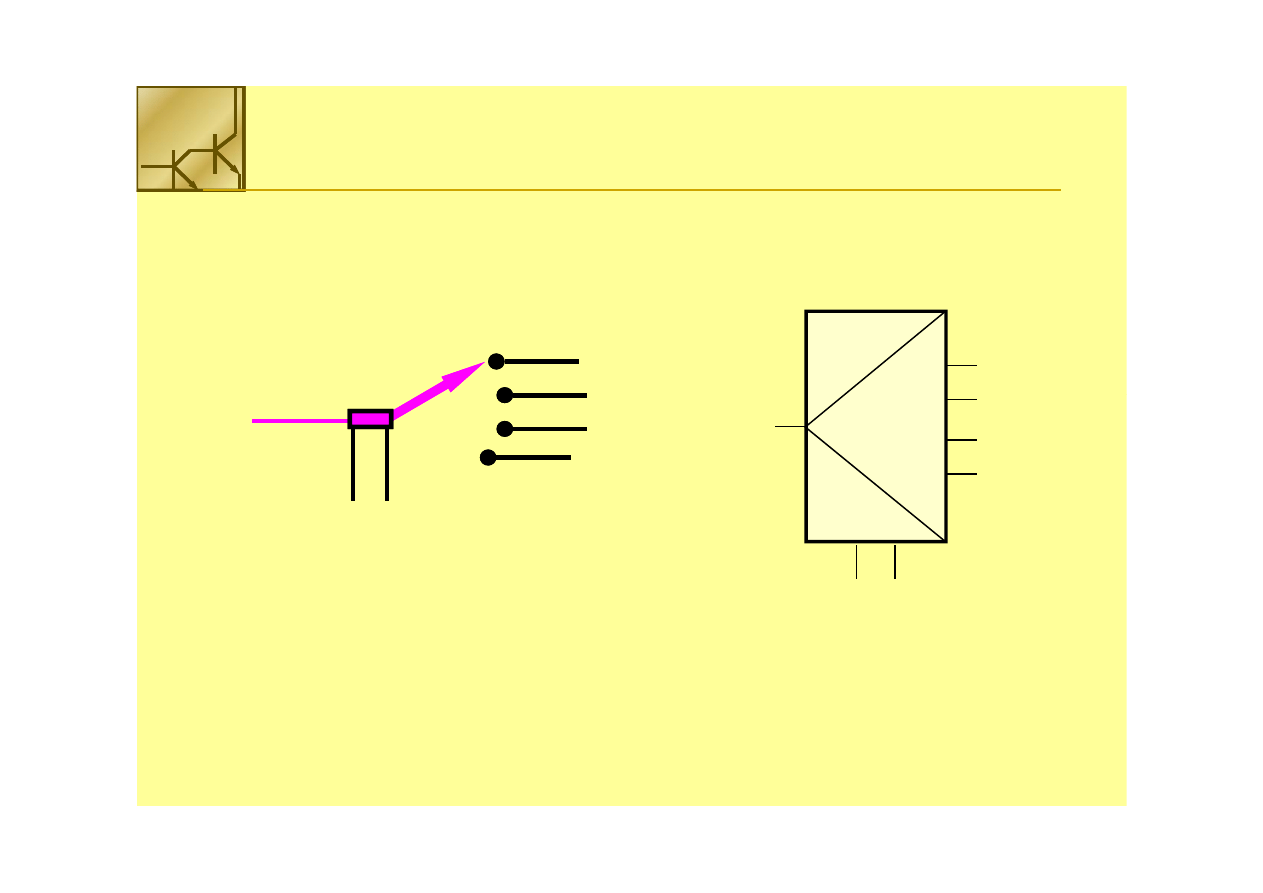
Demultiplekser
Demultiplekser
Demultiplekser
Demultiplekser
Demultiplekser umożliwia wybór
Demultiplekser umożliwia wybór i przesłanie
i przesłanie sygnału
sygnału
wejściowego na jedno z N wyjść
wejściowego na jedno z N wyjść
j
g
j
yj
j
g
j
yj
D0
D0
D1
D1
De
m
De
m
D0
D0
D1
D1
D1
D1
D2
D2
D3
D3
In
In
m
ultiplexer
m
ultiplexer
D1
D1
D2
D2
D3
D3
In
In
S1
S1 S0
S0
S1 S0
S1 S0
S1 S0
S1 S0
Numer wyjścia jest określany przez stan wejść adresowych (sterujących) S0, S1 ....
Numer wyjścia jest określany przez stan wejść adresowych (sterujących) S0, S1 ....
Z uwagi na naturalny kod binarny stosowany do określenia adresu, liczba wyjść jest
Z uwagi na naturalny kod binarny stosowany do określenia adresu, liczba wyjść jest
6 marca 2011
Wojciech Kucewicz
111
związana z liczbą wejść sterujących zależnością:
związana z liczbą wejść sterujących zależnością:
N = 2
N = 2
nn
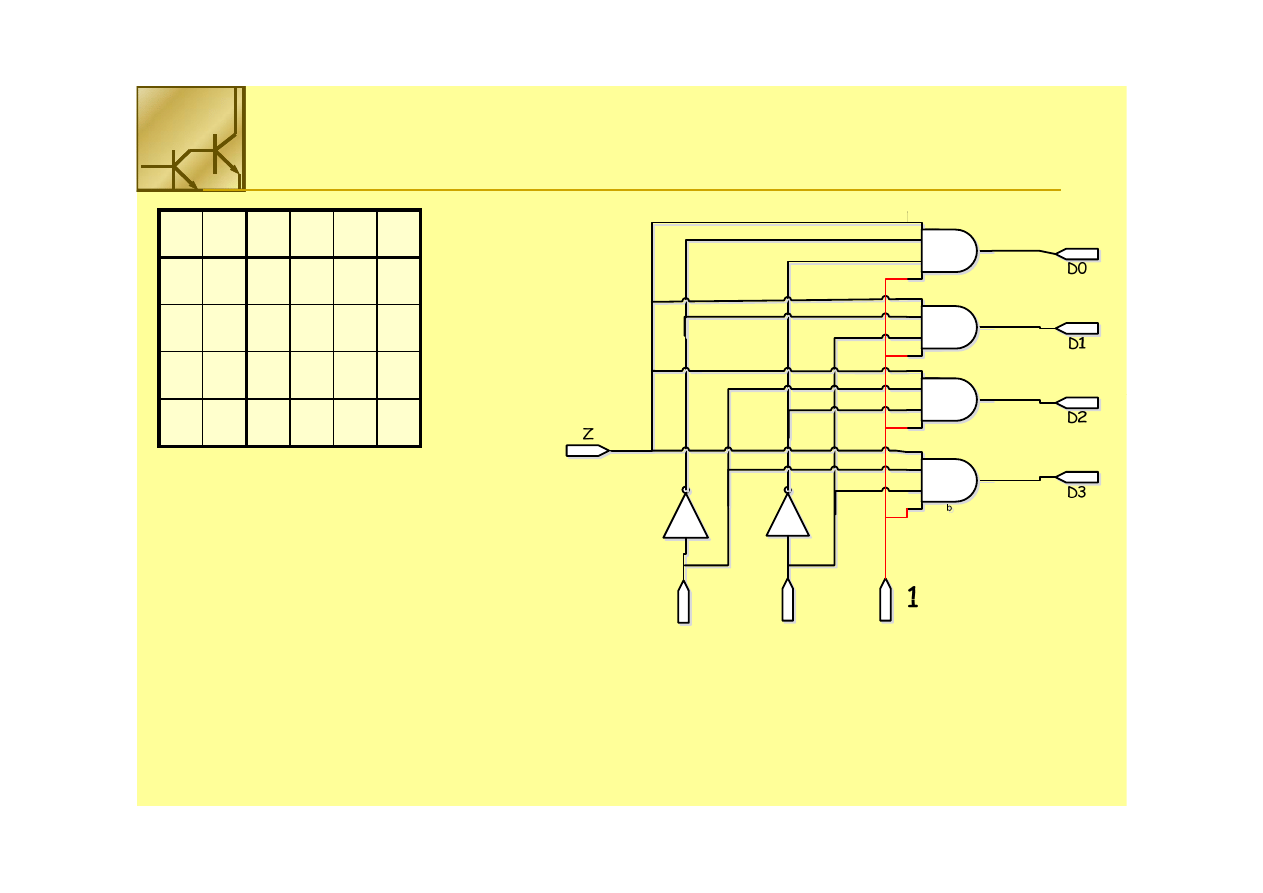
Demultiplekser
Demultiplekser
Demultiplekser
Demultiplekser
S1
S1 S0
S0 D3
D3 D2
D2 D1
D1 D0
D0
00
00
00
00
00
Z
Z
00
11
00
00
Z
Z
00
11
00
00
Z
Z
00
00
11
11
Z
Z
00
00
00
1
S
0
able
Aby uzyskać 2
Aby uzyskać 2
nn
wyjść należy zastosować n bramek AND (n+1)
wyjść należy zastosować n bramek AND (n+1) –– wejściowych
wejściowych
Demultiplekser umożliwia zmianę formatu danych z szeregowego na równoległy
Demultiplekser umożliwia zmianę formatu danych z szeregowego na równoległy
S
S
En
a
6 marca 2011
Wojciech Kucewicz
112
Demultiplekser umożliwia zmianę formatu danych z szeregowego na równoległy
Demultiplekser umożliwia zmianę formatu danych z szeregowego na równoległy
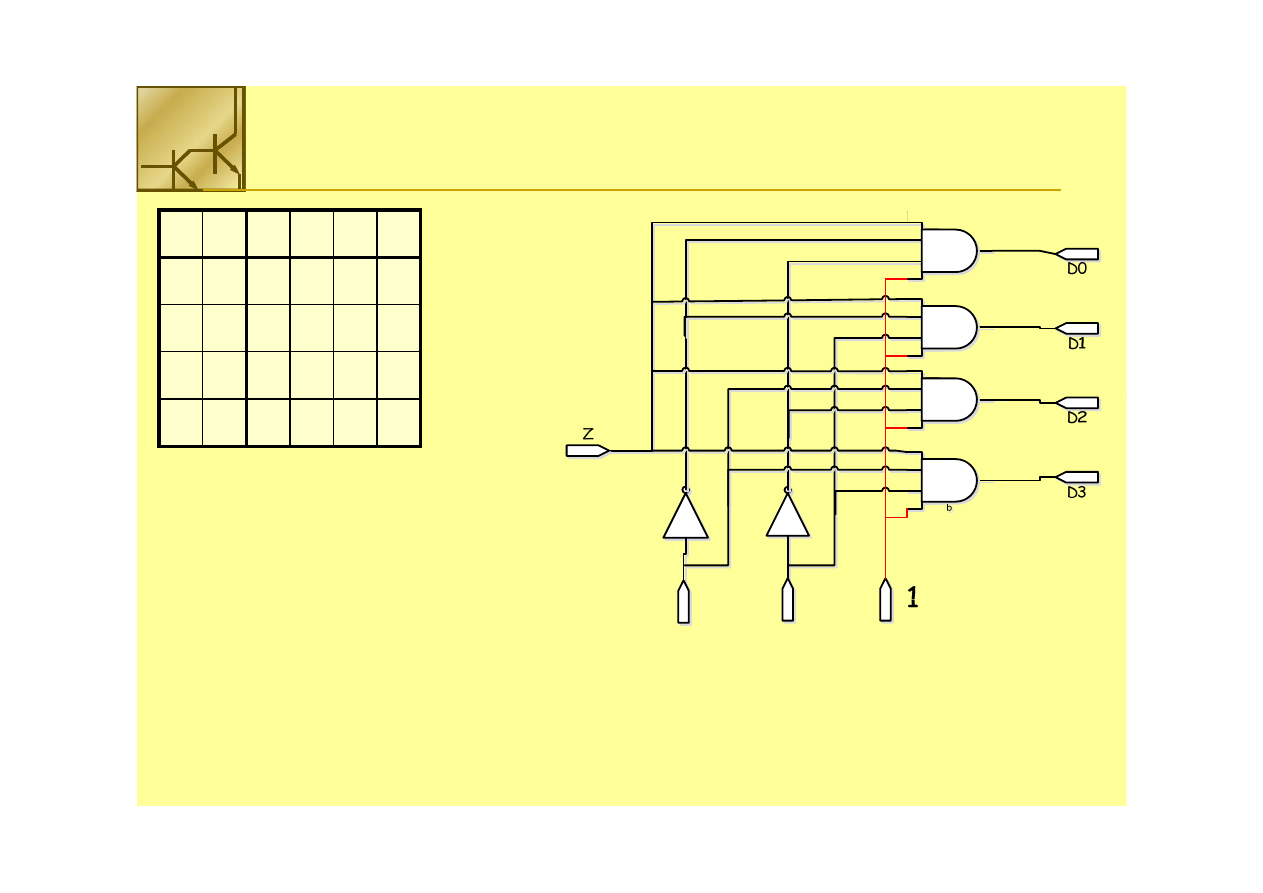
Demultiplekser
Demultiplekser
Demultiplekser
Demultiplekser
S1
S1 S0
S0 D3
D3 D2
D2 D1
D1 D0
D0
00
00
00
00
00
Z
Z
00
11
00
00
Z
Z
00
11
00
00
Z
Z
00
00
11
11
Z
Z
00
00
00
1
S
0
able
Funkcję demultipleksera można opisać funkcją logiczną:
Funkcję demultipleksera można opisać funkcją logiczną:
Z
S
D
k
k
⋅
=
S
S
En
a
6 marca 2011
Wojciech Kucewicz
113
Z
S
D
k
k
gdzie
gdzie S
S
kk
jest
jest mintermem
mintermem utworzonym z wektora adresu
utworzonym z wektora adresu
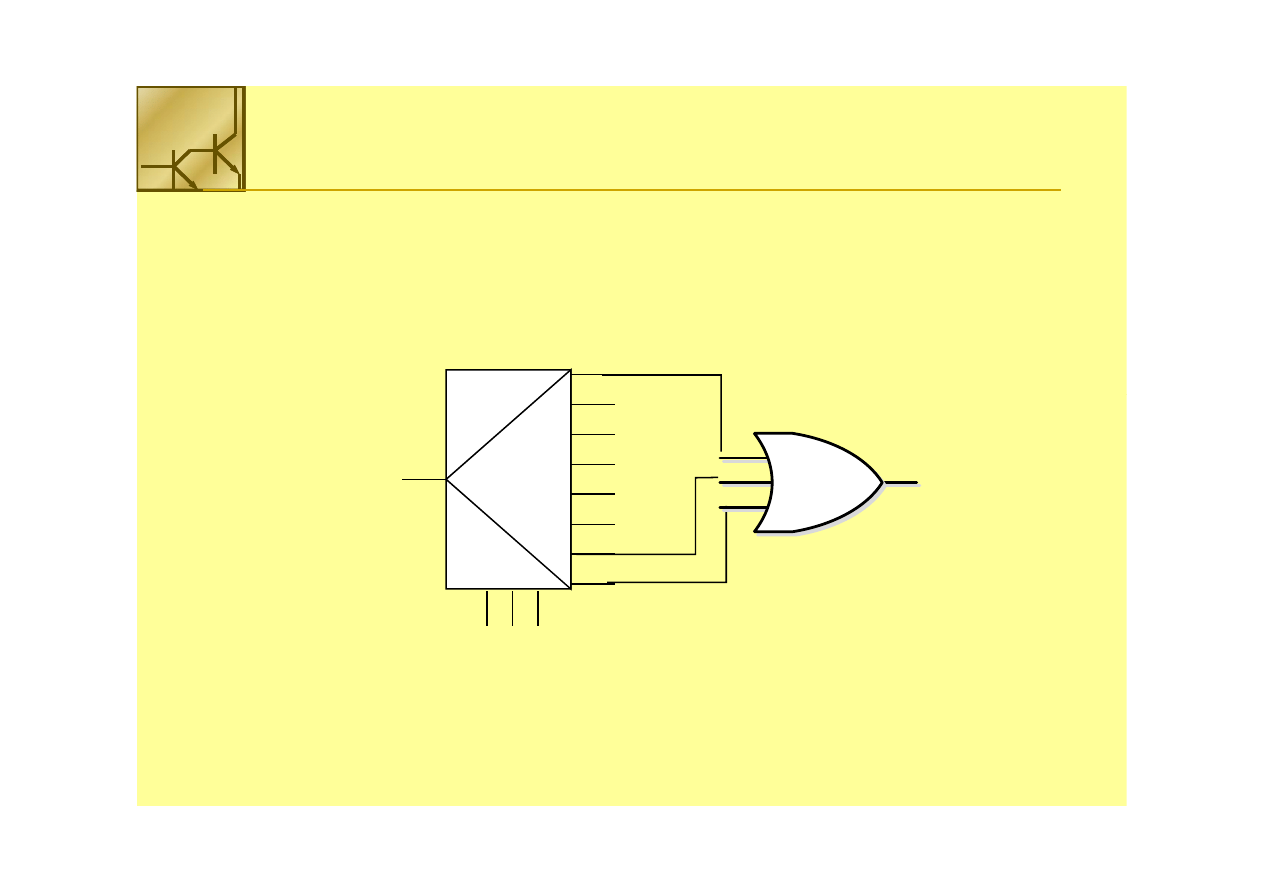
Demultiplekser
Demultiplekser
Demultiplekser
Demultiplekser
Po podaniu odpowiedniego sygnału na wejście demultipleksera na wyjściach są dostępne
Po podaniu odpowiedniego sygnału na wejście demultipleksera na wyjściach są dostępne
realizacje wszystkich
realizacje wszystkich mintermów
mintermów. Sumujemy przy pomocy bramki OR tylko te
. Sumujemy przy pomocy bramki OR tylko te
mintermy
mintermy, dla których funkcja przybiera wartość 1.
, dla których funkcja przybiera wartość 1.
a’b’c’
a’b’c’
a’b’c
a’b’c
11
a b c
a b c
a’bc’
a’bc’
a’bc
a’bc
ab’c’
ab’c’
ab’c
ab’c
abc’
abc’
abc
abc
a b c
a b c
6 marca 2011
Wojciech Kucewicz
114
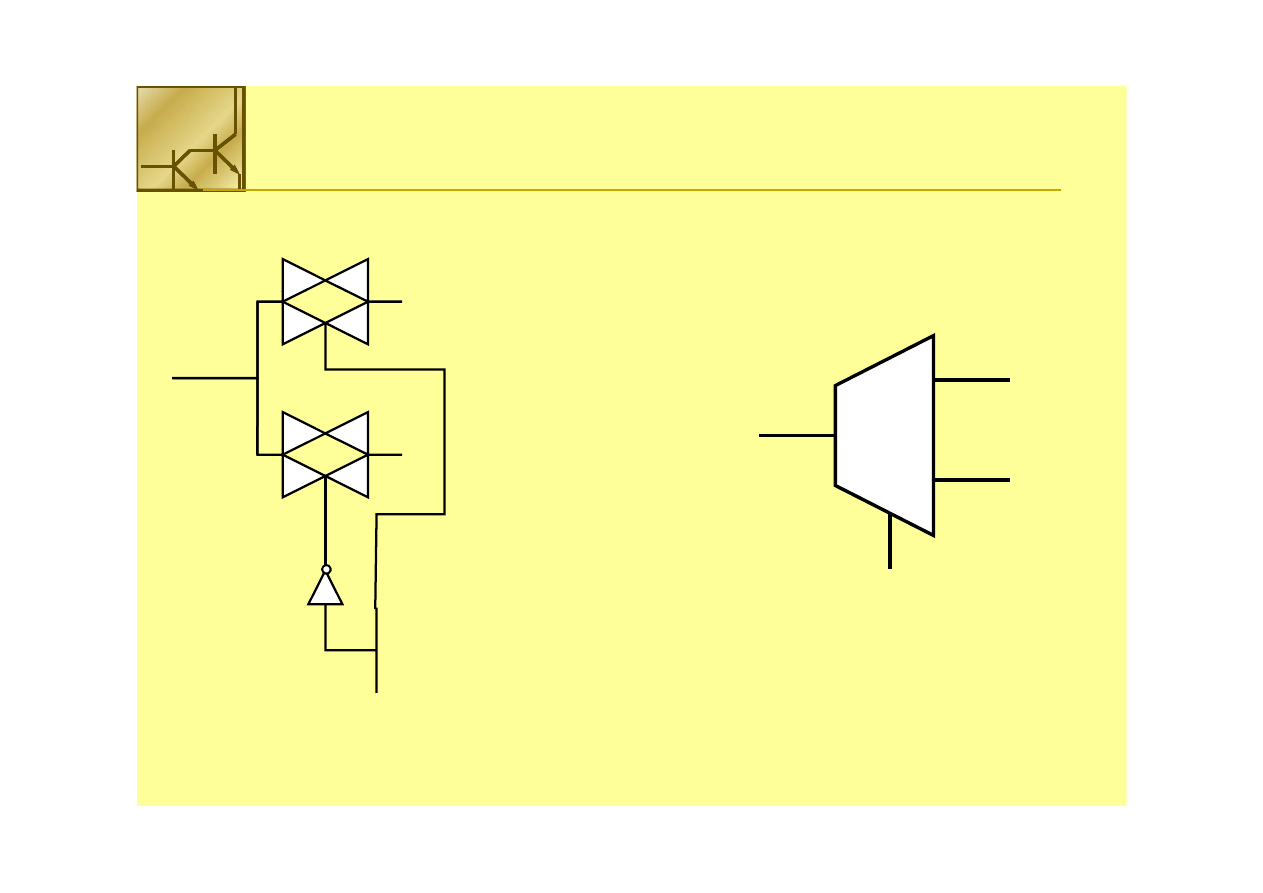
Demultiplekser
Demultiplekser
Demultiplekser
Demultiplekser
Dem
Demultiplexer
ultiplexer 11 to
to 22
D0
D0
D0
D0
In
In
DMUXDMUX
D1
D1
In
In
==
==
D1
D1
S
Sel
el
Sel
Sel
6 marca 2011
Wojciech Kucewicz
115
Podstawowym elementem demultipleksera może być bramka transmisyjna
Podstawowym elementem demultipleksera może być bramka transmisyjna

Kodery i
Kodery i
Kodery i
Kodery i
Kodery i
Kodery i
d k d
d k d
Kodery i
Kodery i
d k d
d k d
dekodery,
dekodery,
k
k dó
k
k dó
dekodery,
dekodery,
k
k dó
k
k dó
konwertery kodów
konwertery kodów
konwertery kodów
konwertery kodów
6 marca 2011
Wojciech Kucewicz
116
yy
Dekoder
Dekoder
Dekoder
Dekoder
Dekoder najczęściej służy do translacji słów kodu dwójkowego
Dekoder najczęściej służy do translacji słów kodu dwójkowego
na kod 1 z N
na kod 1 z N
Stan logiczny n wejść określa na którym z 2
Stan logiczny n wejść określa na którym z 2
nn
wyjść pojawi się
wyjść pojawi się
stan 1
stan 1
S
S
00
S
S
11
Decoder
Decoder
D0
D0
D1
D1
11
D2
D2
D3
D3
En
En
Dekoder dwubitowego słowa (X0, X1) na 1 z 4
Dekoder może posiadać wejście Enable
6 marca 2011
Wojciech Kucewicz
117
Dekoder może posiadać wejście Enable.
Jeżeli wejście Enable ma stan 1 to dekoder jest aktywny (na jednym z wyjść jest stan
1), a jeżeli 0 to dekoder jest nieaktywny ( na wszystkich wyjściach jest stan 0)
Dekoder 2
Dekoder 2--bitowy
bitowy
Dekoder 2
Dekoder 2--bitowy
bitowy
Tablicę prawdy dla dekodera 2
Tablicę prawdy dla dekodera 2--bitowego można zamienić na tablicę
bitowego można zamienić na tablicę Karnough
Karnough i i
wyznaczyć funkcję logiczną
wyznaczyć funkcję logiczną
S
S
11
S
S
00
En
En
D3
D3
D2
D2
D1
D1
D0
D0
00
00
11
00
00
00
11
x1 x0
En
0
1
x1 x0
En
0
1
x1 x0
En
0
1
S
1
S
0
En
0
1
00
11
11
00
00
11
00
11
00
11
00
11
00
00
11
11
11
11
00
00
00
0 0
00
11
0 1
00
00
1 1
00
00
0 0
00
00
0 1
00
11
1 1
00
00
0 0
00
00
0 1
00
00
1 1
00
00
0 0
00
00
0 1
00
00
1 1
00
11
11
11
11
11
00
00
00
xx
xx
00
00
00
00
00
1 0
00
00
D0 E S
D0 E S ’ S
’ S ’’
1 0
00
00
1 0
00
11
1 0
00
00
D0 = En S
D0 = En S
00
’ S
’ S
11
’’
D1 = En S
D1 = En S
00
S
S
11
’’
D2 En S
D2 En S ’ S
’ S
Wszystkie wyznaczone funkcje są mintermami
więc można je zrealizować przy pomocy
6 marca 2011
Wojciech Kucewicz
118
D2 = En S
D2 = En S
00
S
S
11
D3 = En S
D3 = En S
00
S
S
11
więc można je zrealizować przy pomocy
bramek AND
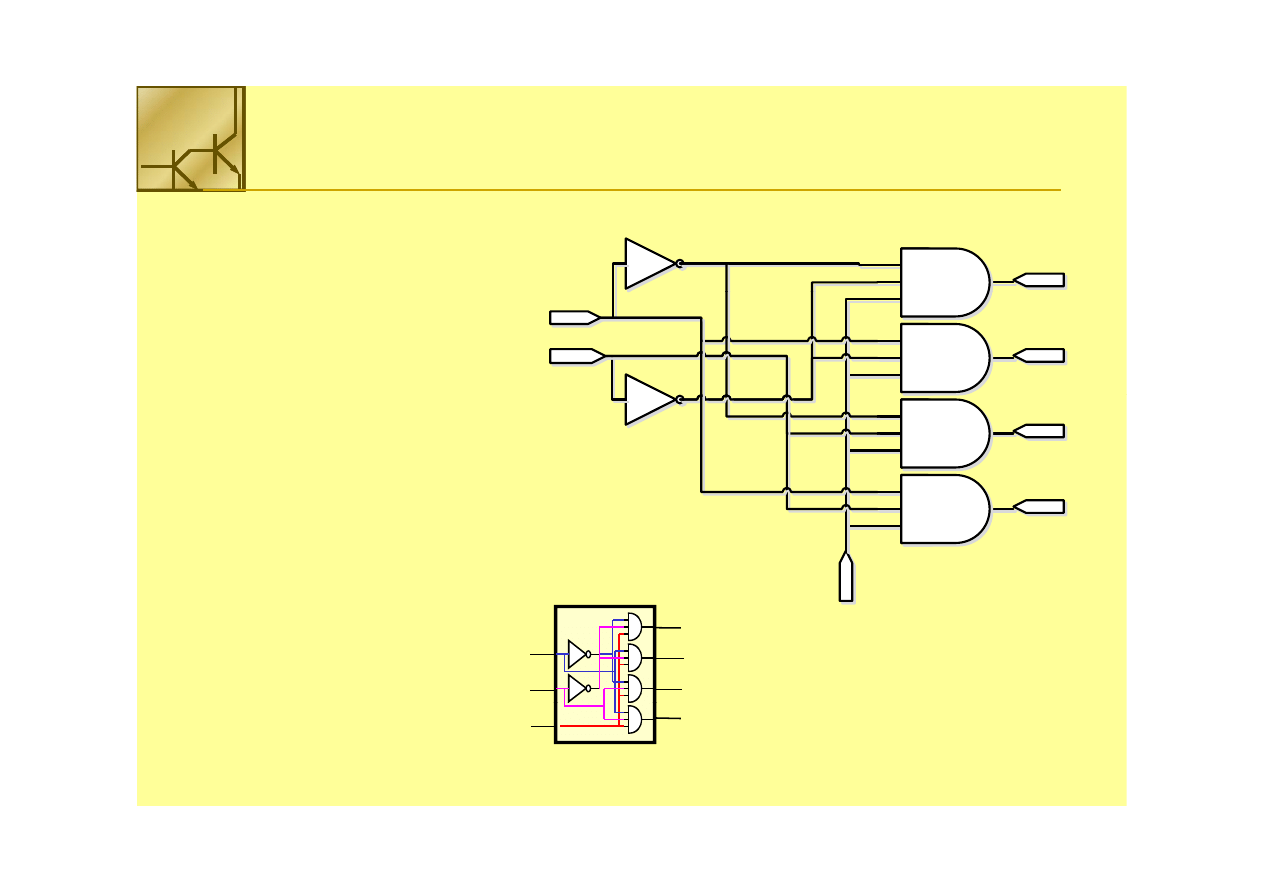
Dekoder
Dekoder
Dekoder
Dekoder
D
D
33
=
= EnS
EnS
00
S
S
11
D
D E S
E S ’S
’S
S0
D0
D
D
22
=
= EnS
EnS
00
’S
’S
11
D
D
11
=
= EnS
EnS
00
S
S
11
’ ’
D
D
00
=
= EnS
EnS
00
’S
’S
11
’ ’
b
b
S0
S1
D0
D1
00
00 11
b
b
b
b
D2
b
b
En
D3
Decode
r
Decode
r
E
S0
D0
D1
D2
S1
6 marca 2011
Wojciech Kucewicz
119
rr
En
D2
D3
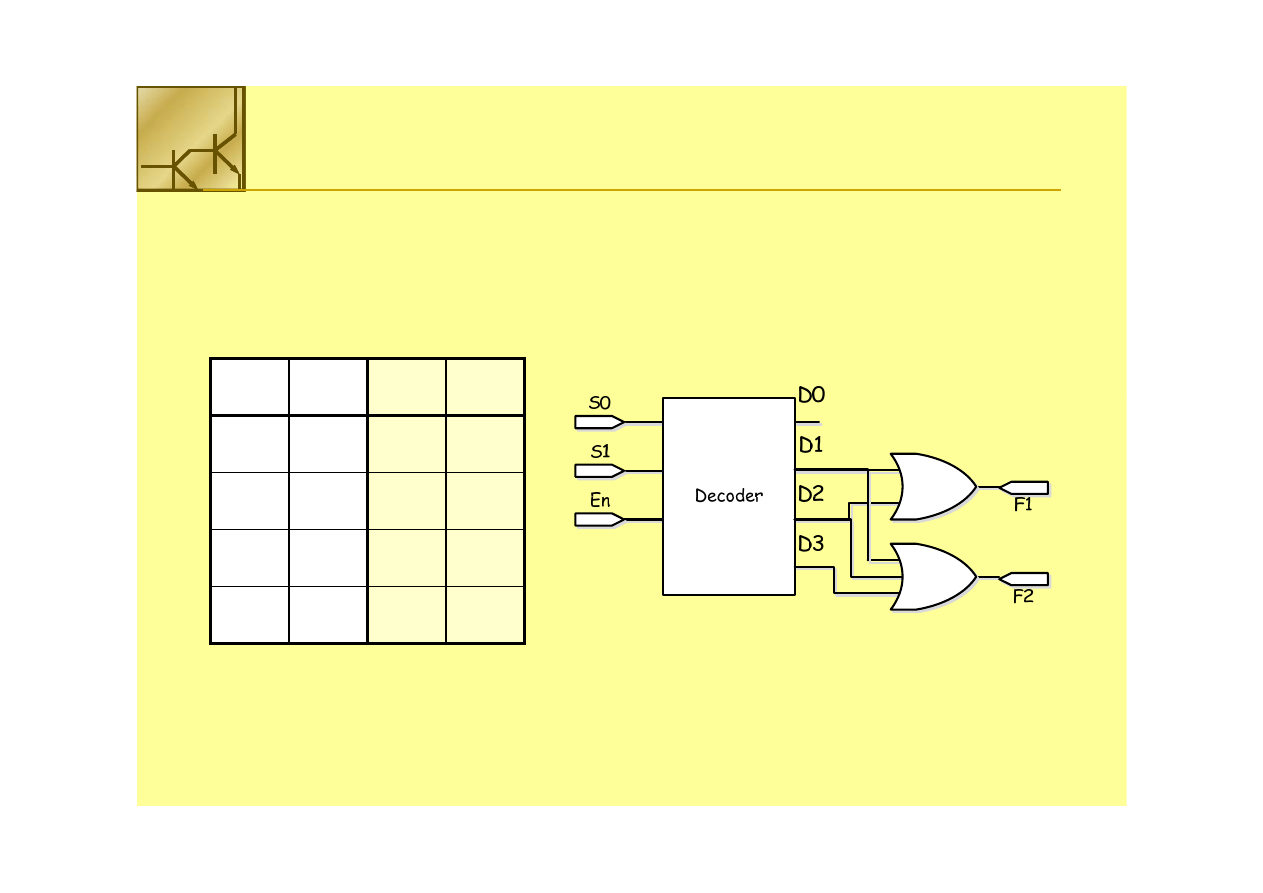
Dekoder
Dekoder
Dekoder
Dekoder
Dekoder może realizować funkcje logiczne.
Dekoder może realizować funkcje logiczne.
Ponieważ jego wyjścia są mintermami, należy zsumować te mintermy, dla których
Ponieważ jego wyjścia są mintermami, należy zsumować te mintermy, dla których
wartość funkcji wynosi 1
S
S
11
S
S
00
F1
F1
F2
F2
S
S
11
S
S
00
FF
FF
00
00
00
00
00
11
11
11
00
11
11
11
11
00
11
11
11
11
00
11
6 marca 2011
Wojciech Kucewicz
120
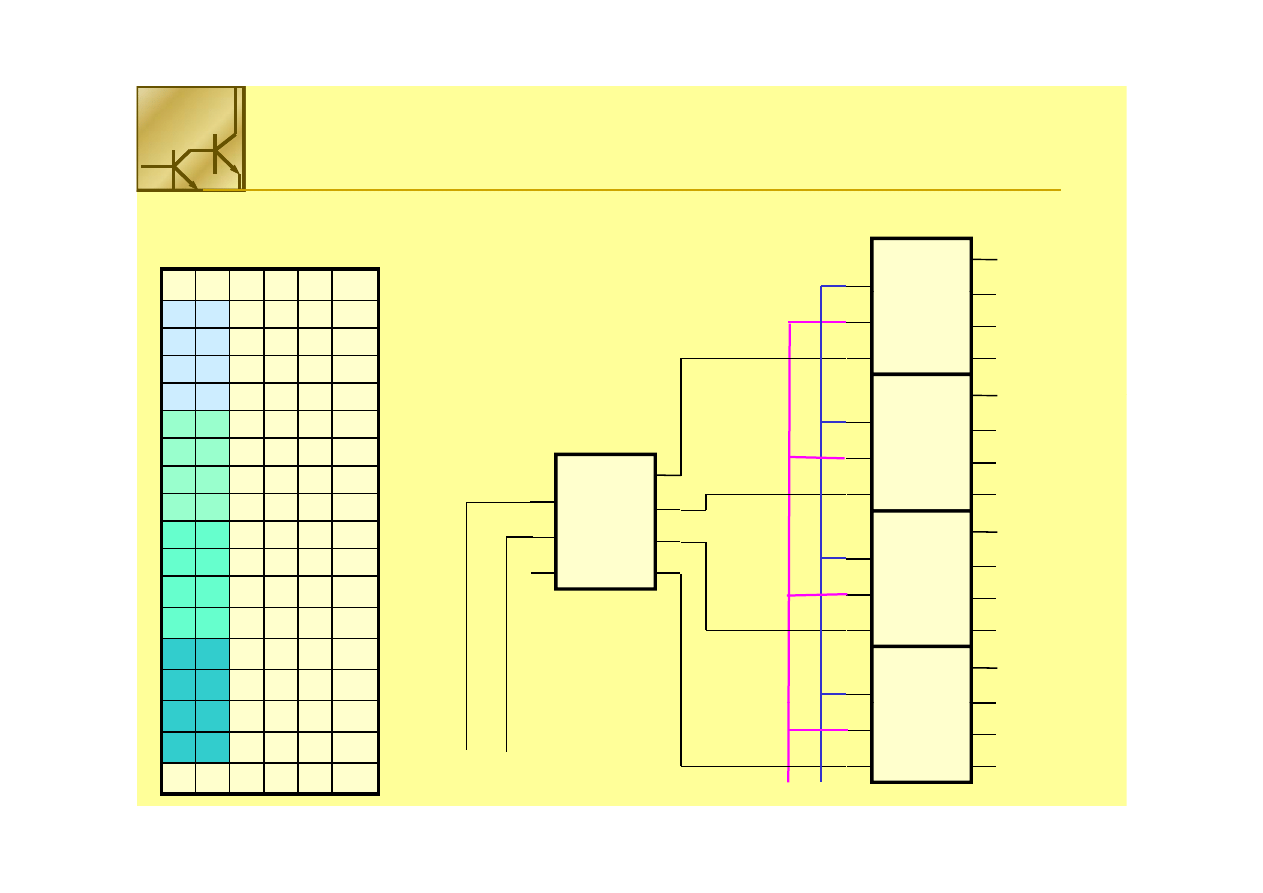
Dekoder 4
Dekoder 4--bitowy
bitowy
Dekoder 4
Dekoder 4--bitowy
bitowy
A
A
BB
CC
D
D
En
En
Out
Out
x0
D0
D1
m0
m0
m1
m1
Wielobitowy dekoder może być utworzony przez
Wielobitowy dekoder może być utworzony przez kaskodowe
kaskodowe połączenie dekoderów 2
połączenie dekoderów 2--
bitowych , gdzie jeden z dekoderów jest
bitowych , gdzie jeden z dekoderów jest
wykorzystany do włączania linii
wykorzystany do włączania linii enable
enable
00
00
00
00
11
m0
m0
00
00
00
11
11
m1
m1
00
00
11
00
11
m2
m2
00
00
11
11
11
33
En
D2
D3
x1
D0
m1
m1
m2
m2
m3
m3
m4
m4
x0
D0
D1
00
00
11
11
11
m3
m3
00
11
00
00
11
m4
m4
00
11
00
11
11
m5
m5
00
11
11
00
11
m6
m6
En
x0
D1
D2
D3
x1
m4
m4
m5
m5
m6
m6
m7
m7
En
x0
D1
D2
D3
x1
00
11
11
11
11
m7
m7
11
00
00
00
11
m8
m8
11
00
00
11
11
m9
m9
11
00
11
00
11
m10
m10
En
x0
D0
D1
D2
x1
m8
m8
m9
m9
m10
m10
11
00
11
11
11
m11
m11
11
11
00
00
11
m12
m12
11
11
00
11
11
m13
m13
En
D3
x1
x0
D0
D1
m10
m10
m11
m11
m12
m12
m13
m13
6 marca 2011
Wojciech Kucewicz
121
11
11
11
00
11
m14
m14
11
11
11
11
11
m15
m15
xx
xx
xx
xx
00
none
none
A
A
BB
En
D2
D3
x1
CC
D
D
m13
m13
m14
m14
m15
m15
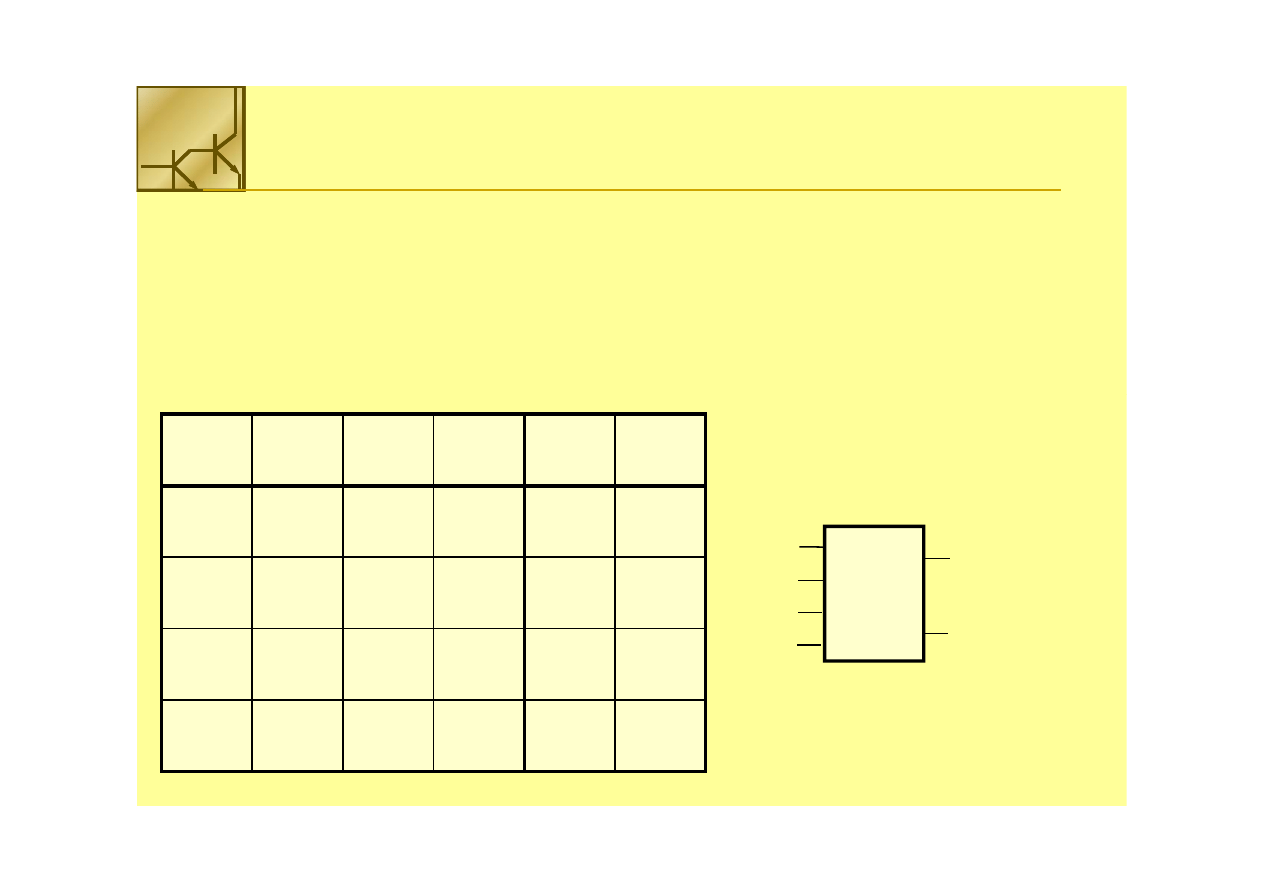
Koder
Koder
Koder
Koder
Koder działa odwrotnie niż dekoder
Koder działa odwrotnie niż dekoder t.zn
t.zn.
.
Kod 1 z 2
Kod 1 z 2
nn
zamienia na kod
zamienia na kod nn--bitowy
bitowy kod binarny
kod binarny
D3
D3
D2
D2
D1
D1
D0
D0
x1
x1
x0
x0
Encoder
Encoder
x0
D0
D1
00
00
00
11
00
00
00
00
11
00
00
11
Encoder
Encoder
D2
D3
x1
00
00
11
00
00
11
00
11
00
00
11
00
6 marca 2011
Wojciech Kucewicz
122
11
00
00
00
11
11
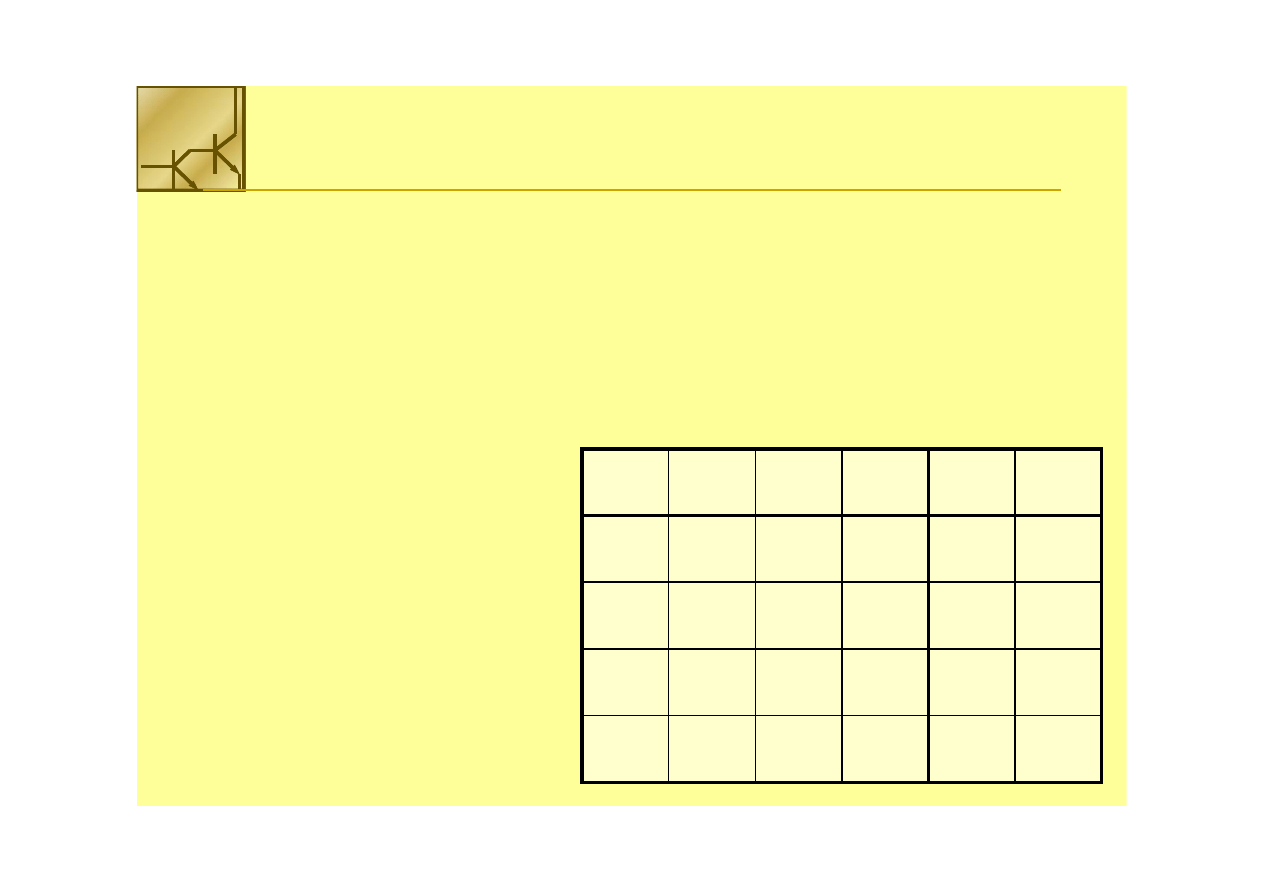
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
Przyjmijmy, że system składa się z 2
Przyjmijmy, że system składa się z 2
nn
urządzeń, które
urządzeń, które
wymagają obsługi. Przy pomocy kodera priorytetowego można
wymagają obsługi. Przy pomocy kodera priorytetowego można
ustalić kolejność obsługi urządzeń.
ustalić kolejność obsługi urządzeń.
D0
D0
D1
D1
D2
D2
D3
D3
x1
x1
x0
x0
Przykład:
Przykład:
11
X
X
X
X
X
X
00
00
Należy obsłużyć 4 urządzenia o
Należy obsłużyć 4 urządzenia o
różnym stopniu ważności
różnym stopniu ważności –– każde ma
każde ma
swój 2
swój 2--bitowy adres (x1x2).
bitowy adres (x1x2).
d
dł
d
ś D0
d
dł
d
ś D0
00
11
X
X
X
X
00
11
00
00
11
X
X
11
00
Urządzenie podłączone do wejścia D0
Urządzenie podłączone do wejścia D0
ma najwyższy priorytet obsługi, a
ma najwyższy priorytet obsługi, a
urządzenie podłączone do wejścia D3
urządzenie podłączone do wejścia D3
–– najniższy.
najniższy.
6 marca 2011
Wojciech Kucewicz
123
00
00
00
11
11
11
najniższy.
najniższy.
Zapisujemy to w tablicy prawdy
Zapisujemy to w tablicy prawdy
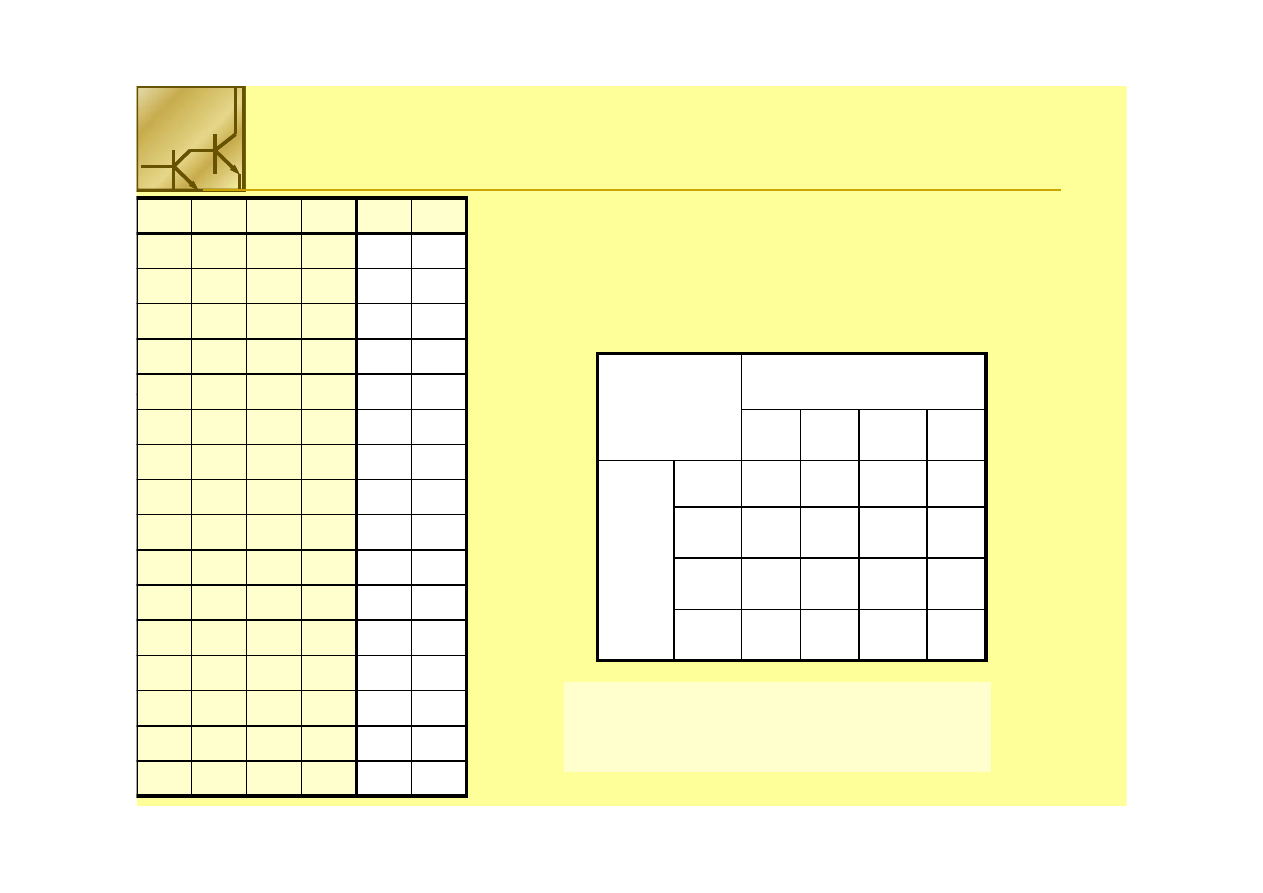
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
D
D
00
D
D
11
D
D
22
D
D
33
xx
11
xx
00
00
00
00
00
00
00
00
00
00
11
11
11
Budujemy tablicę prawdy dla wszystkich
możliwych kombinacji żądań obsługi w jednym
czasie.
00
00
00
11
11
11
00
00
11
00
11
00
00
00
11
11
11
00
00
11
00
00
00
11
Budujemy tablice Karnaugh dla stanu bitów adresu
urządzeń i wyznaczamy funkcję logiczną.
X1
X1
D3D2
D3D2
00
11
00
00
00
11
00
11
00
11
00
11
00
11
11
00
00
11
00
11
11
11
00
11
X1
X1
00
00
01
01
11
11
10
10
0 0
0 0
00
00
00
00
00
11
11
11
00
11
11
00
00
00
00
00
11
00
00
11
00
00
11
00
11
00
00
00
D1D0
D1D0
0 1
0 1
11
00
00
00
1 1
1 1
11
00
00
00
11
00
11
00
00
00
11
00
11
11
00
00
11
11
00
00
00
00
11
11
00
11
00
00
xx = D
= D ’D
’D ’D
’D +
+ D
D ’D
’D ’D
’D
xx = D
= D ’D
’D ’D
’D +
+ D
D ’D
’D ’D
’D
10
10
11
00
00
00
6 marca 2011
Wojciech Kucewicz
124
11
11
00
11
00
00
11
11
11
00
00
00
11
11
11
11
00
00
xx
11
= D
= D
00
D
D
11
D
D
33
+
+ D
D
00
D
D
11
D
D
2
2
= D
= D
00
’D
’D
11
’(D
’(D
33
+ D
+ D
22
))
xx
11
= D
= D
00
D
D
11
D
D
33
+
+ D
D
00
D
D
11
D
D
2
2
= D
= D
00
’D
’D
11
’(D
’(D
33
+ D
+ D
22
))
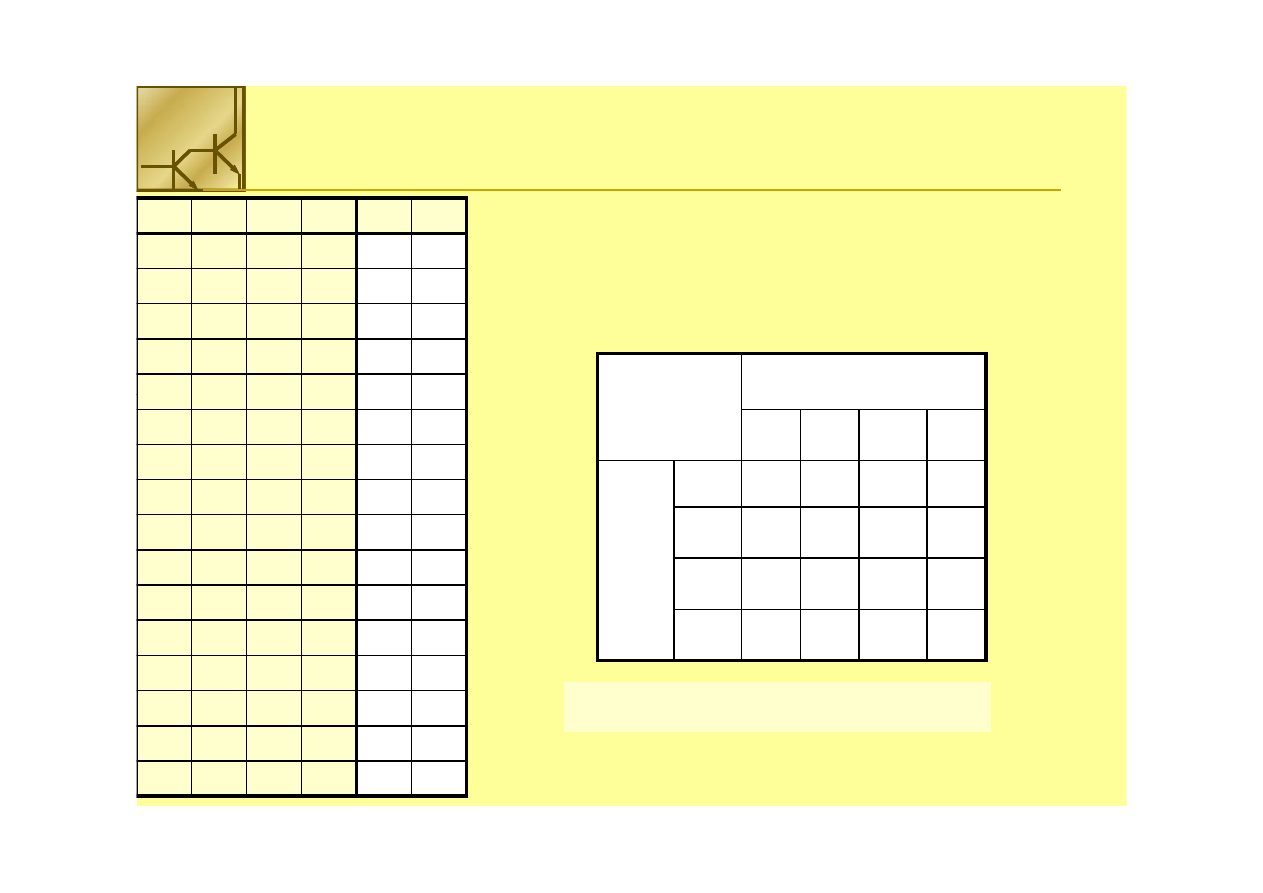
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
D
D
00
D
D
11
D
D
22
D
D
33
xx
11
xx
00
00
00
00
00
00
00
00
00
00
11
11
11
Budujemy tablicę prawdy dla wszystkich
możliwych kombinacji żądań obsługi w jednym
czasie.
00
00
00
11
11
11
00
00
11
00
11
00
00
00
11
11
11
00
00
11
00
00
00
11
Budujemy tablice Karnaugh dla stanu bitów adresu
urządzeń i wyznaczamy funkcję logiczną.
X0
X0
D0D1
D0D1
00
11
00
00
00
11
00
11
00
11
00
11
00
11
11
00
00
11
00
11
11
11
00
11
X0
X0
00
00
01
01
11
11
10
10
0 0
0 0
00
11
00
00
00
11
11
11
00
11
11
00
00
00
00
00
11
00
00
11
00
00
11
00
11
00
00
00
D2D3
D2D3
0 1
0 1
11
11
00
00
1 1
1 1
00
11
00
00
11
00
11
00
00
00
11
00
11
11
00
00
11
11
00
00
00
00
11
11
00
11
00
00
xx = D
= D ’D
’D ’D
’D + D
+ D ’D
’D
xx = D
= D ’D
’D ’D
’D + D
+ D ’D
’D
10
10
00
11
00
00
6 marca 2011
Wojciech Kucewicz
125
11
11
00
11
00
00
11
11
11
00
00
00
11
11
11
11
00
00
xx
00
= D
= D
00
D
D
22
D
D
33
+ D
+ D
00
D
D
11
xx
00
= D
= D
00
D
D
22
D
D
33
+ D
+ D
00
D
D
11
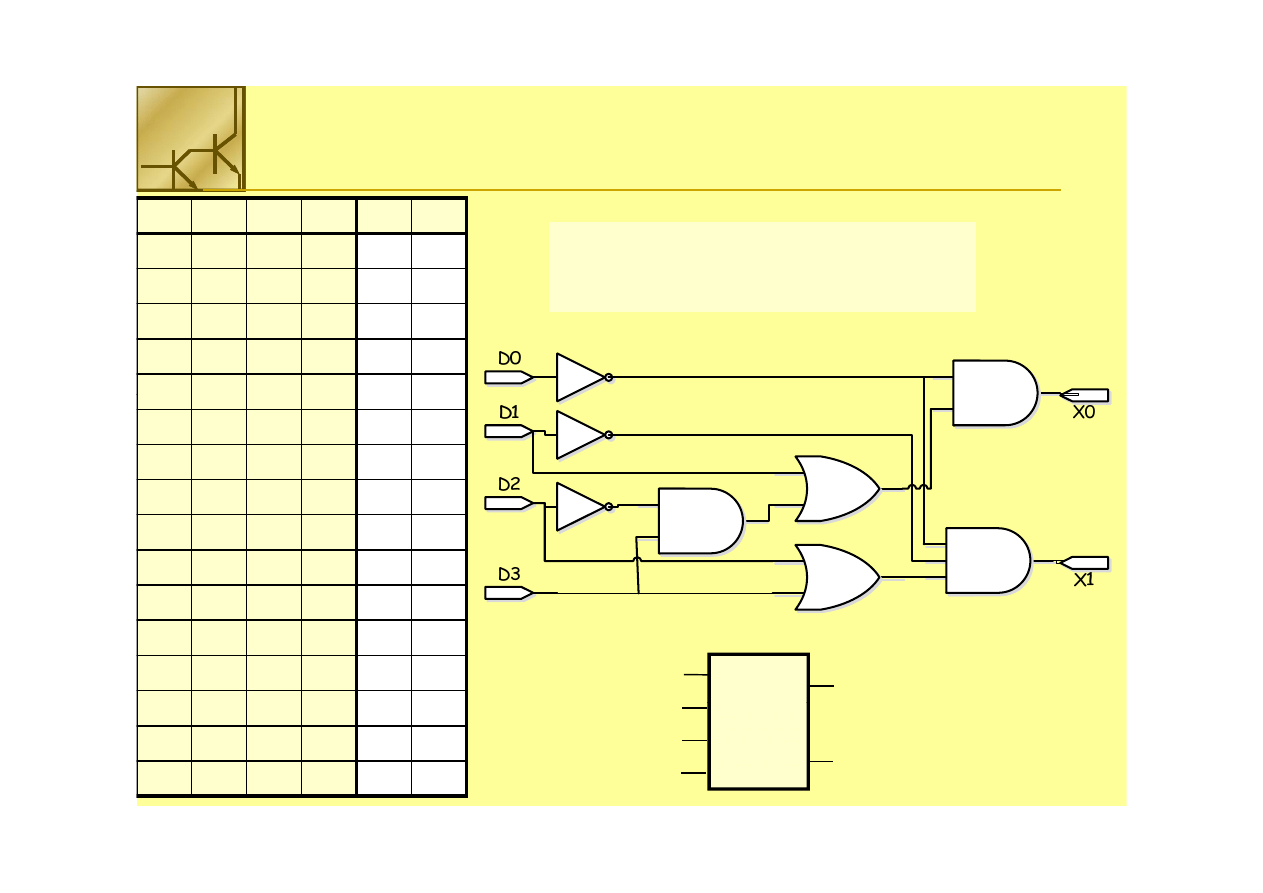
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
Koder priorytetowy
D
D
00
D
D
11
D
D
22
D
D
33
xx
11
xx
00
00
00
00
00
00
00
00
00
00
11
11
11
xx
11
= D
= D
00
’D
’D
11
’(D
’(D
33
+
+ D
D
22
))
xx
00
= D
= D
00
’(D
’(D
22
’D
’D
33
+
+ D
D
11
))
xx
11
= D
= D
00
’D
’D
11
’(D
’(D
33
+
+ D
D
22
))
xx
00
= D
= D
00
’(D
’(D
22
’D
’D
33
+
+ D
D
11
))
00
00
11
00
11
00
00
00
11
11
11
00
00
11
00
00
00
11
xx
00
= D
= D
00
(D
(D
22
D
D
33
+
+ D
D
11
))
xx
00
= D
= D
00
(D
(D
22
D
D
33
+
+ D
D
11
))
00
11
00
00
00
11
00
11
00
11
00
11
00
11
11
00
00
11
00
11
11
11
00
11
00
11
11
11
00
11
11
00
00
00
00
00
11
00
00
11
00
00
11
00
11
00
00
00
x0
D0
D1
11
00
11
00
00
00
11
00
11
11
00
00
11
11
00
00
00
00
11
11
00
11
00
00
6 marca 2011
Wojciech Kucewicz
126
Encoder
Encoder
D1
D2
D3
x1
11
11
00
11
00
00
11
11
11
00
00
00
11
11
11
11
00
00

Hazard
Hazard
Hazard
Hazard
Hazard
Hazard
Hazard
Hazard
6 marca 2011
Wojciech Kucewicz
127
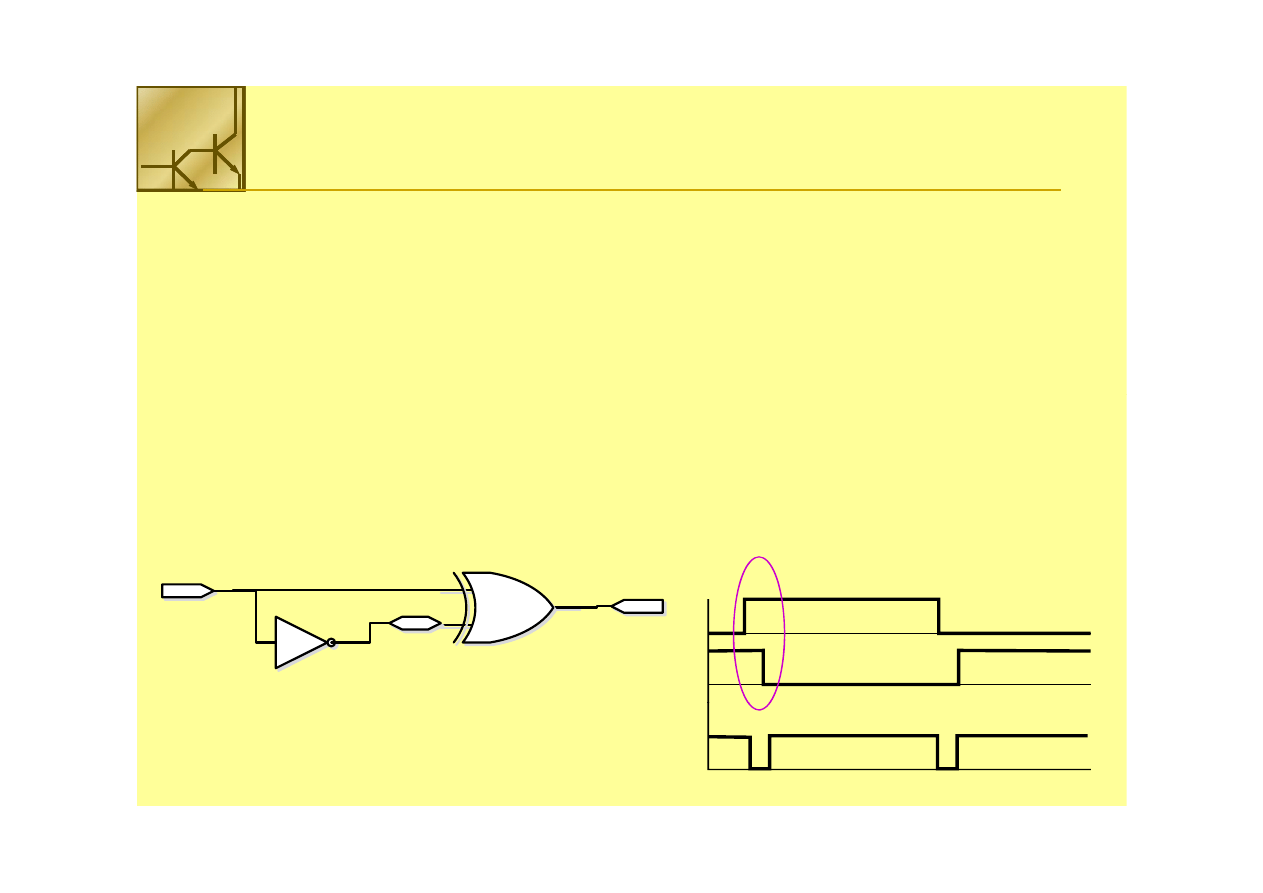
Hazard
Hazard
Hazard
Hazard
Hazardem nazywamy krótkie zakłócenie impulsowe na wyjściu
Hazardem nazywamy krótkie zakłócenie impulsowe na wyjściu
układu podczas procesów przejściowych
układu podczas procesów przejściowych
układu podczas procesów przejściowych.
układu podczas procesów przejściowych.
Zjawisko hazardu może wystąpić, gdy sygnał przesyłany jest dwoma
Zjawisko hazardu może wystąpić, gdy sygnał przesyłany jest dwoma
d
i
óż
h óź i i h d
i d j d j b
ki
d
i
óż
h óź i i h d
i d j d j b
ki
drogami o różnych opóźnieniach prowadzącymi do jednej bramki.
drogami o różnych opóźnieniach prowadzącymi do jednej bramki.
Na wyjściu bramki może powstać krótkotrwały impuls, wynikający z
Na wyjściu bramki może powstać krótkotrwały impuls, wynikający z
różnicy opóźnień.
różnicy opóźnień.
11
X
Y
X
X
YY
Z
Z
Y
F
6 marca 2011
Wojciech Kucewicz
128
Z
Z
HazardHazard
HazardHazard

Hazard
Hazard
Hazard
Hazard
Hazard funkcjonalny
Hazard funkcjonalny
powstaje na skutek jednoczesnej zmiany
powstaje na skutek jednoczesnej zmiany
Hazard funkcjonalny
Hazard funkcjonalny
-- powstaje na skutek jednoczesnej zmiany
powstaje na skutek jednoczesnej zmiany
dwóch lub więcej sygnałów wejściowych propagujących drogami o
dwóch lub więcej sygnałów wejściowych propagujących drogami o
różnych opóźnieniach (trudny do eliminacji)
różnych opóźnieniach (trudny do eliminacji)
Hazard logiczny
Hazard logiczny
–– pojedyncza zmiana sygnału na wejściu propaguje
pojedyncza zmiana sygnału na wejściu propaguje
drogami o różnych opóźnieniach (eliminowanie przez dodanie
drogami o różnych opóźnieniach (eliminowanie przez dodanie
d
h l
ó
kł d
)
d
h l
ó
kł d
)
nadmiarowych elementów w układzie).
nadmiarowych elementów w układzie).
Hazard krytyczny
Hazard krytyczny
-- występuje w układach asynchronicznych.
występuje w układach asynchronicznych.
6 marca 2011
Wojciech Kucewicz
129
Typy Hazardu
Typy Hazardu
Typy Hazardu
Typy Hazardu
Hazard statyczny polega na pojawieniu się na wyjściu układu impulsu związanego
Hazard statyczny polega na pojawieniu się na wyjściu układu impulsu związanego
z różnym opóźnieniem sygnałów wejściowych.
z różnym opóźnieniem sygnałów wejściowych.
Hazard statyczny „w jedynkach”
Hazard statyczny „w jedynkach”
Hazard statyczny „w zerach”
Hazard statyczny „w zerach”
6 marca 2011
Wojciech Kucewicz
130
y
y
y
y
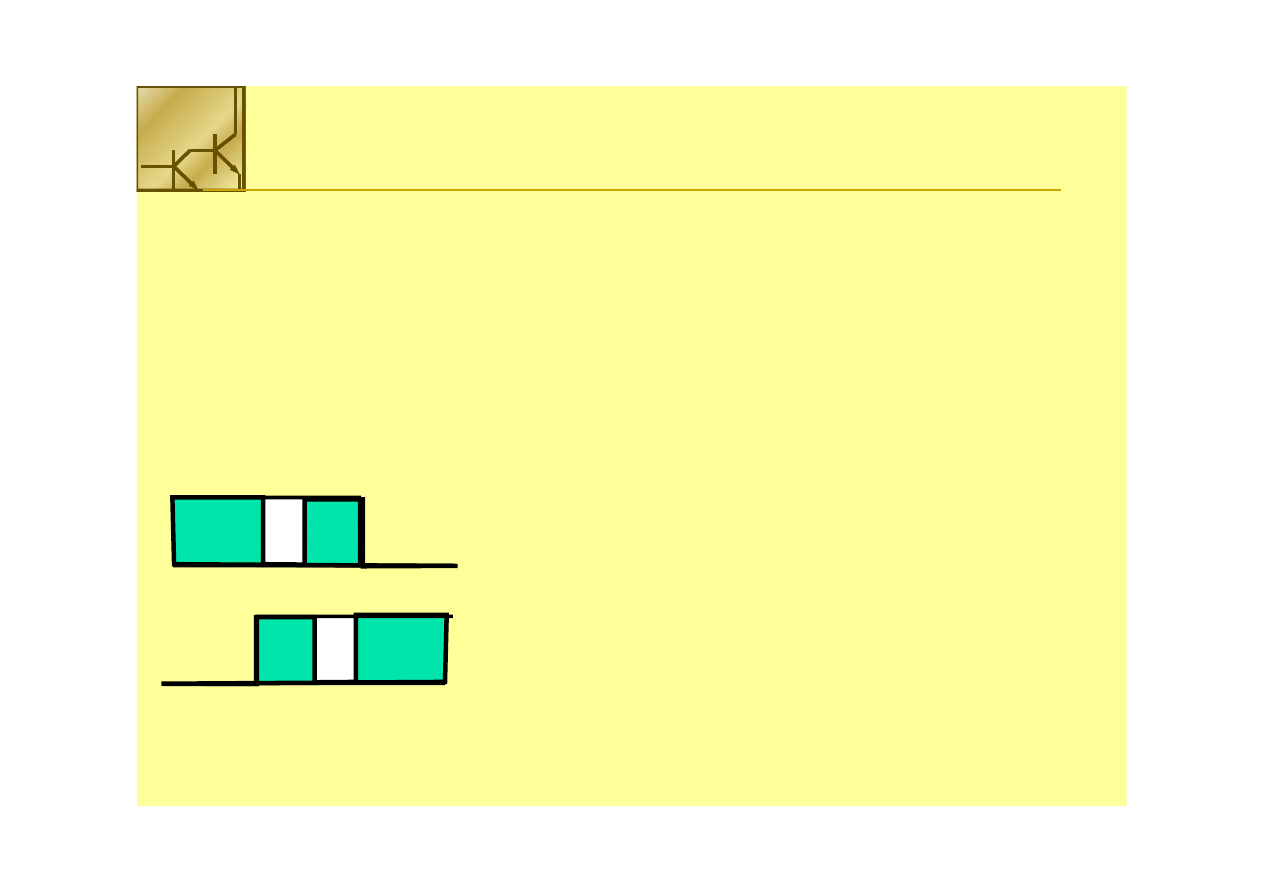
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny polega na pojawieniu się na wyjściu układu impulsu
Hazard dynamiczny polega na pojawieniu się na wyjściu układu impulsu
szpilkowego bezpośrednio po zmianie poziomów logicznych z 0 na 1 lub z 1 na 0.
szpilkowego bezpośrednio po zmianie poziomów logicznych z 0 na 1 lub z 1 na 0.
Hazard dynamiczny 1
Hazard dynamiczny 1 Î
Î
00
Hazard dynamiczny 0
Hazard dynamiczny 0 Î
Î
11
6 marca 2011
Wojciech Kucewicz
131
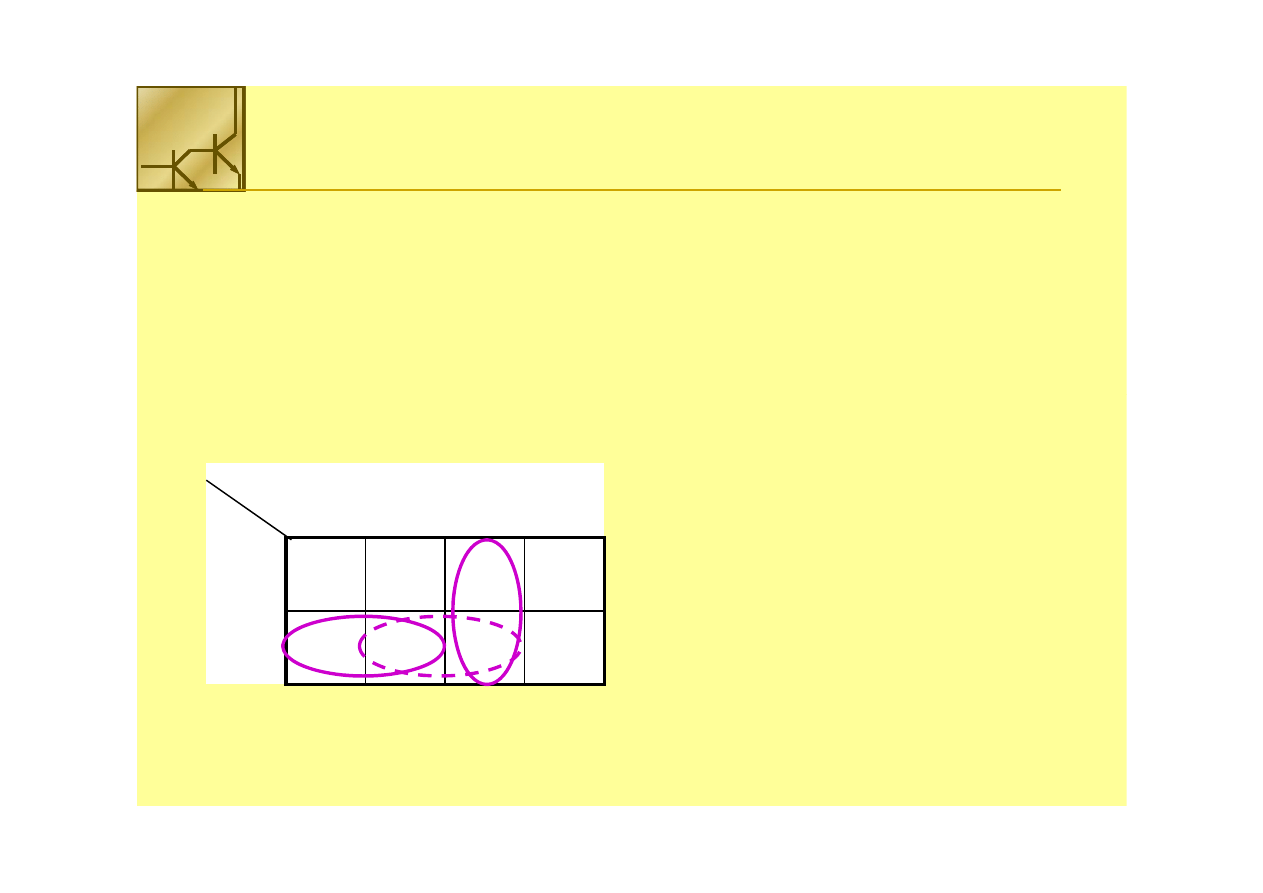
Hazard statyczny
Hazard statyczny
Hazard statyczny
Hazard statyczny
Hazard statyczny może wystąpić, gdy choćby jeden sygnał jest przesyłany dwoma
Hazard statyczny może wystąpić, gdy choćby jeden sygnał jest przesyłany dwoma
drogami o różnych opóźnieniach, prowadzącymi do jednej bramki. Możliwość
drogami o różnych opóźnieniach, prowadzącymi do jednej bramki. Możliwość
t i i h
d
ż k ć i t
t i i h
d
ż k ć i t K
h
K
h j ż li f
b l
k j t
j ż li f
b l
k j t
wystąpienia hazardu można wykryć na siatce
wystąpienia hazardu można wykryć na siatce Karnaugh
Karnaugh, jeżeli forma boolowska jest
, jeżeli forma boolowska jest
reprezentowana przez stykające się grupy, odpowiadające
reprezentowana przez stykające się grupy, odpowiadające implikantom
implikantom prostym.
prostym.
Stykanie się takich grup wskazuje na obecność hazardu. Aby uniknąć hazardu,
Stykanie się takich grup wskazuje na obecność hazardu. Aby uniknąć hazardu,
należy wprowadzić dodatkową bramkę reprezentującą dodatkowy
należy wprowadzić dodatkową bramkę reprezentującą dodatkowy implikant
implikant..
y p
ą
ę p
ją ą
y
y p
ą
ę p
ją ą
y
pp
xx
22
xx
11
00
00
01
01
11
11
10
10
F X
F X X
X X
X X’
X’
22 11
xx
00
00
00
01
01
11
11
10
10
00
00
00
11
00
F = X
F = X
22
X
X
11
+ X
+ X
00
X’
X’
22
F = X
F = X
22
X
X
11
+ X
+ X
00
X’
X’
22
+ X
+ X
00
X
X
11
11
11
11
11
00
F = X
F = X
22
X
X
11
+ X
+ X
00
X
X
22
+ X
+ X
00
X
X
11
6 marca 2011
Wojciech Kucewicz
132
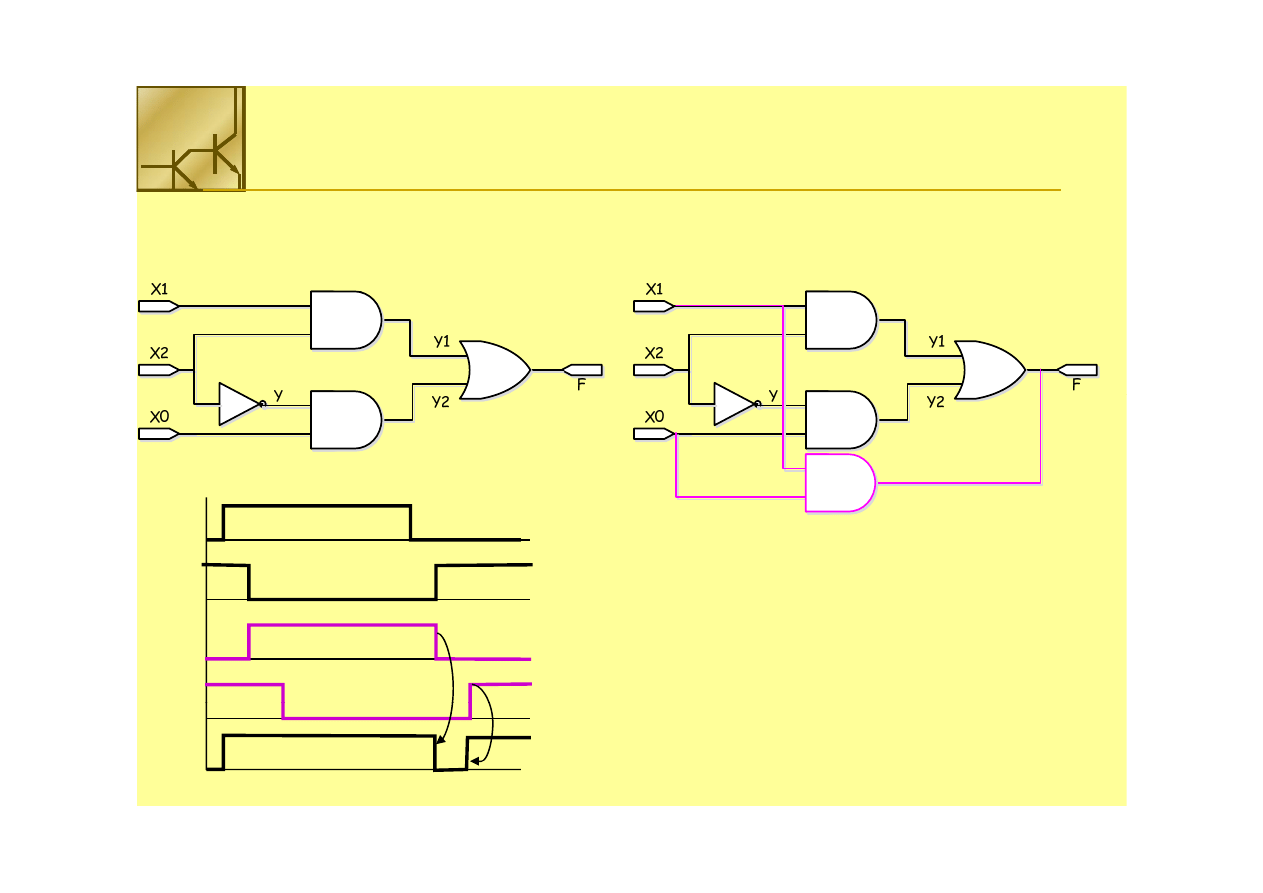
Hazard statyczny
Hazard statyczny
Hazard statyczny
Hazard statyczny
F = X
F = X
22
X
X
11
+ X
+ X
00
X’
X’
22
F = X
F = X
22
X
X
11
+ X
+ X
00
X’
X’
22
+ X
+ X
00
X
X
11
X
X
22
YY
YY
11
YY
22
Przy X
Przy X
00
= X
= X
11
= 1 impuls hazardu zostaje
= 1 impuls hazardu zostaje
wyeliminowany
wyeliminowany
6 marca 2011
Wojciech Kucewicz
133
22
FF
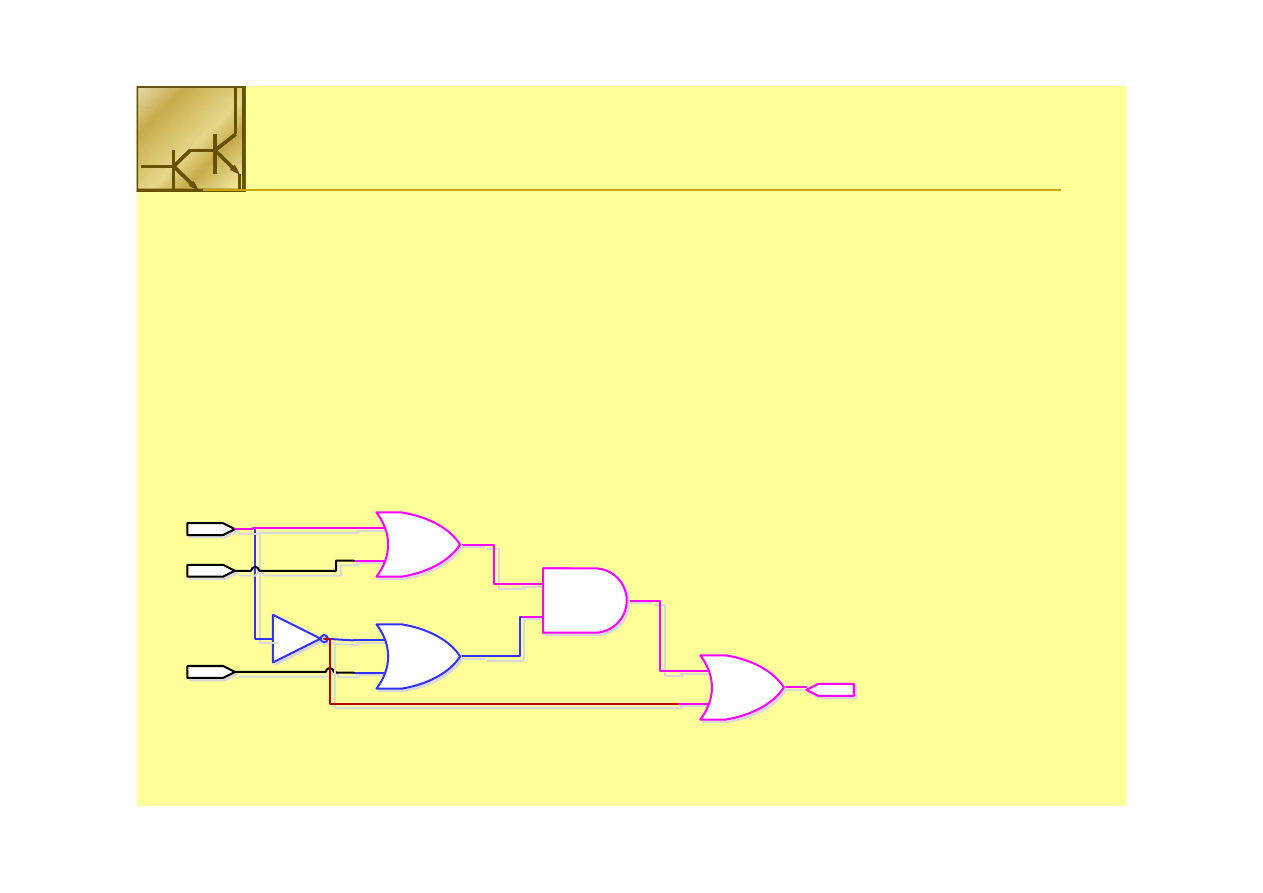
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
W układach wielopoziomowych można zaobserwować zjawisko hazardu dynamicznego.
W układach wielopoziomowych można zaobserwować zjawisko hazardu dynamicznego.
Polega ono na pojawieniu się na wyjściu układu impulsu szpilkowego bezpośrednio po
Polega ono na pojawieniu się na wyjściu układu impulsu szpilkowego bezpośrednio po
i i
i ó l i
h 0 1 l b 1 0 H
d d
i
ż
t ić d
i i
i ó l i
h 0 1 l b 1 0 H
d d
i
ż
t ić d
zmianie poziomów logicznych z 0 na 1 lub 1 na 0. Hazard dynamiczny może wystąpić, gdy
zmianie poziomów logicznych z 0 na 1 lub 1 na 0. Hazard dynamiczny może wystąpić, gdy
choćby
choćby jeden sygnał jest przesyłany do wyjścia trzema drogami o różnych opóźnieniach.
jeden sygnał jest przesyłany do wyjścia trzema drogami o różnych opóźnieniach.
X
X
11
Î
Î
YY
22
Î
Î
YY
44
Î
Î
FF
X
X
11
Î
Î
YY
11
Î
Î
YY
33
Î
Î
YY
44
Î
Î
FF
X
X
11
Î
Î
YY
11
Î
Î
FF
X1
X2
Y2
Y3
X0
F
Y1
Y3
Y4
6 marca 2011
Wojciech Kucewicz
134
F
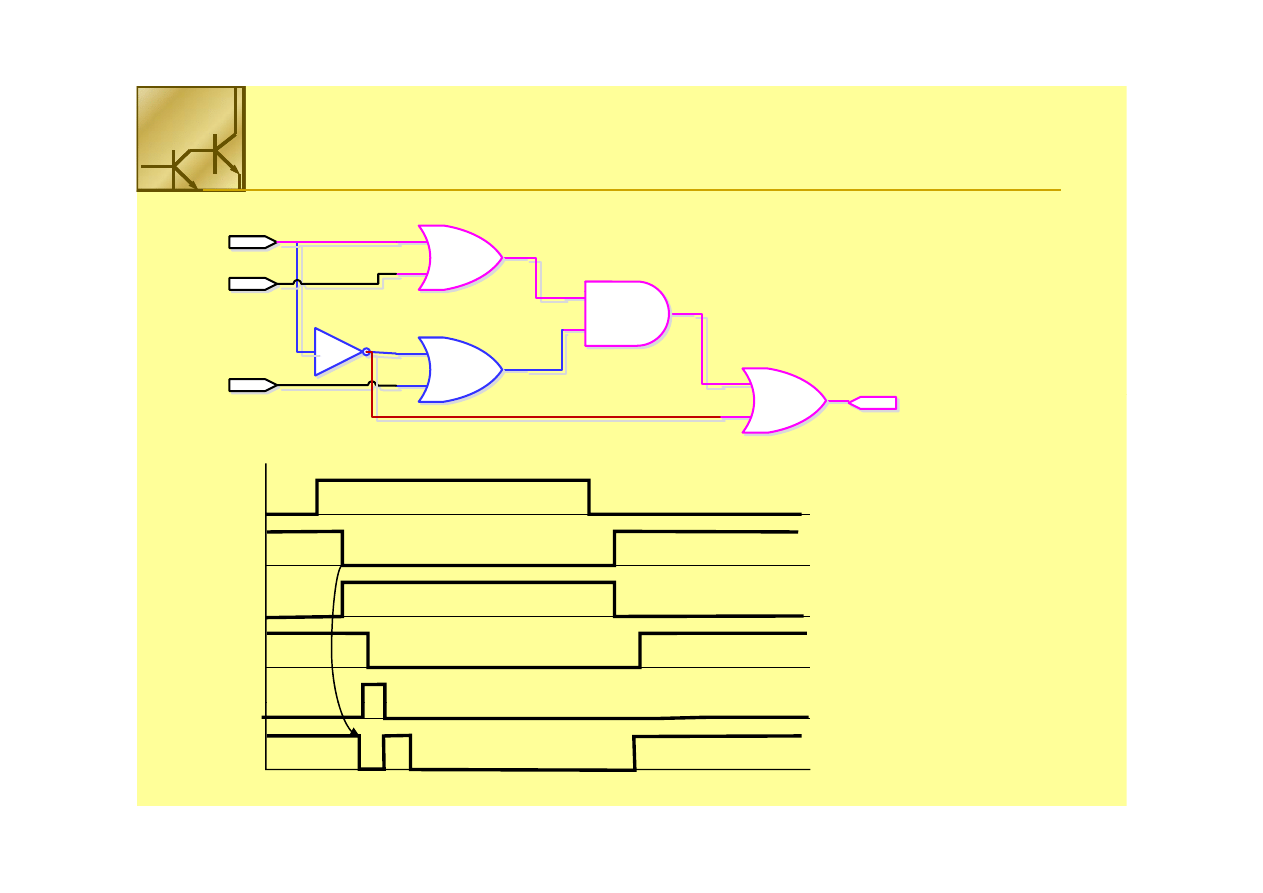
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
Hazard dynamiczny
X
X
11
X
X
22
= 0
= 0
X
X
11
Î
Î
YY
22
Î
Î
YY
44
Î
Î
FF
X
X
11
Î
Î
YY
11
Î
Î
YY
33
Î
Î
YY
44
Î
Î
FF
X1
X2
Y2
X
X
00
= 0
= 0
X
X
11
Î
Î
YY
11
Î
Î
YY
33
Î
Î
YY
44
Î
Î
FF
X
X
11
Î
Î
YY
11
Î
Î
FF
X0
Y1
Y3
Y4
X
X
11
F
YY
11
YY
2222
YY
33
YY
44
6 marca 2011
Wojciech Kucewicz
135
YY
44
FF
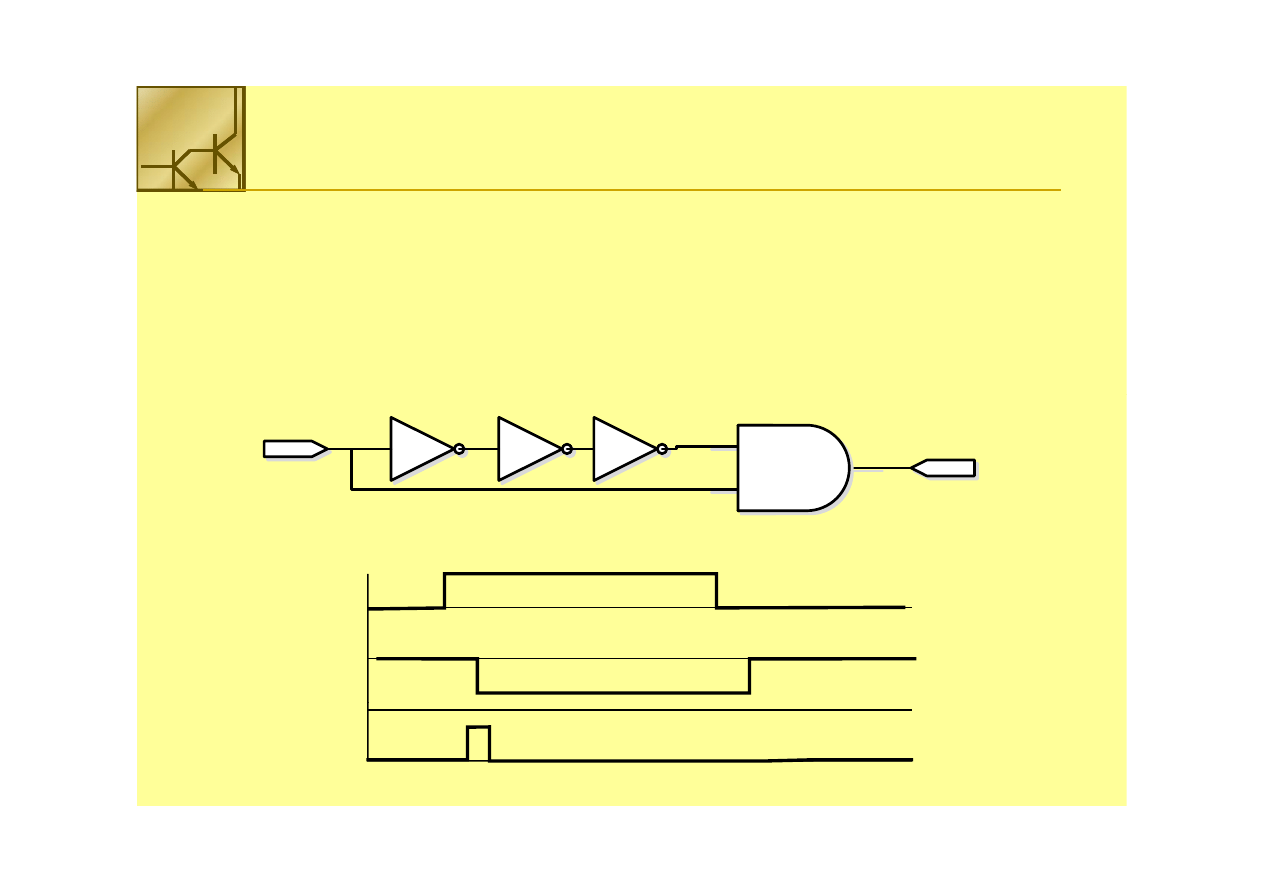
Hazard
Hazard
Hazard
Hazard
Układy generujące hazard są również celowo wykorzystywane w praktyce.
Układy generujące hazard są również celowo wykorzystywane w praktyce.
Są stosowane jako układy detektorów początku i końca impulsu wejściowego. Do
Są stosowane jako układy detektorów początku i końca impulsu wejściowego. Do
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
jednego z torów sygnału wejściowego przez połączenie kaskadowe dodatkowych
jednego z torów sygnału wejściowego przez połączenie kaskadowe dodatkowych
inwerterów lub bramek.
inwerterów lub bramek.
Sa
Sa to tzw. Układy logicznego różniczkowania.
to tzw. Układy logicznego różniczkowania.
X1
F
Y1
X
X
11
F
YY
11
6 marca 2011
Wojciech Kucewicz
136
FF
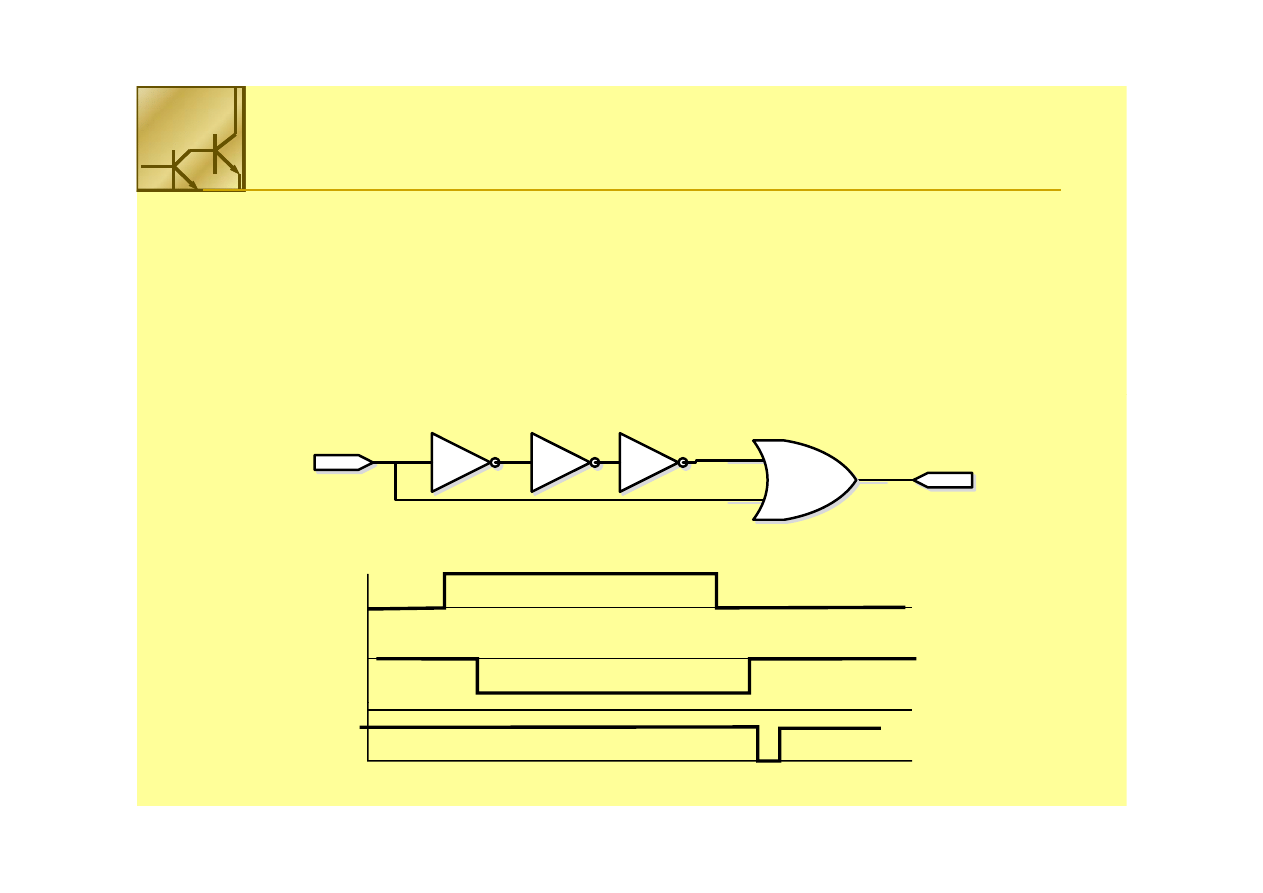
Hazard
Hazard
Hazard
Hazard
Układy
Układy generujące
generujące hazard są również celowo wykorzystywane w praktyce.
hazard są również celowo wykorzystywane w praktyce.
Są stosowane jako układy detektorów
Są stosowane jako układy detektorów początku
początku i końca impulsu wejściowego. Do
i końca impulsu wejściowego. Do
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
opóźnienie
y
p
yj
y
p
j
ę
ę
y
p
yj
y
p
j
ę
ę pp
jednego z torów sygnału wejściowego przez połączenie kaskadowe dodatkowych
jednego z torów sygnału wejściowego przez połączenie kaskadowe dodatkowych
inwerterów lub bramek.
inwerterów lub bramek.
Sa
Sa to tzw. Układy logicznego różniczkowania.
to tzw. Układy logicznego różniczkowania.
X1
F
Y1
X
X
11
F
YY
11
6 marca 2011
Wojciech Kucewicz
137
FF
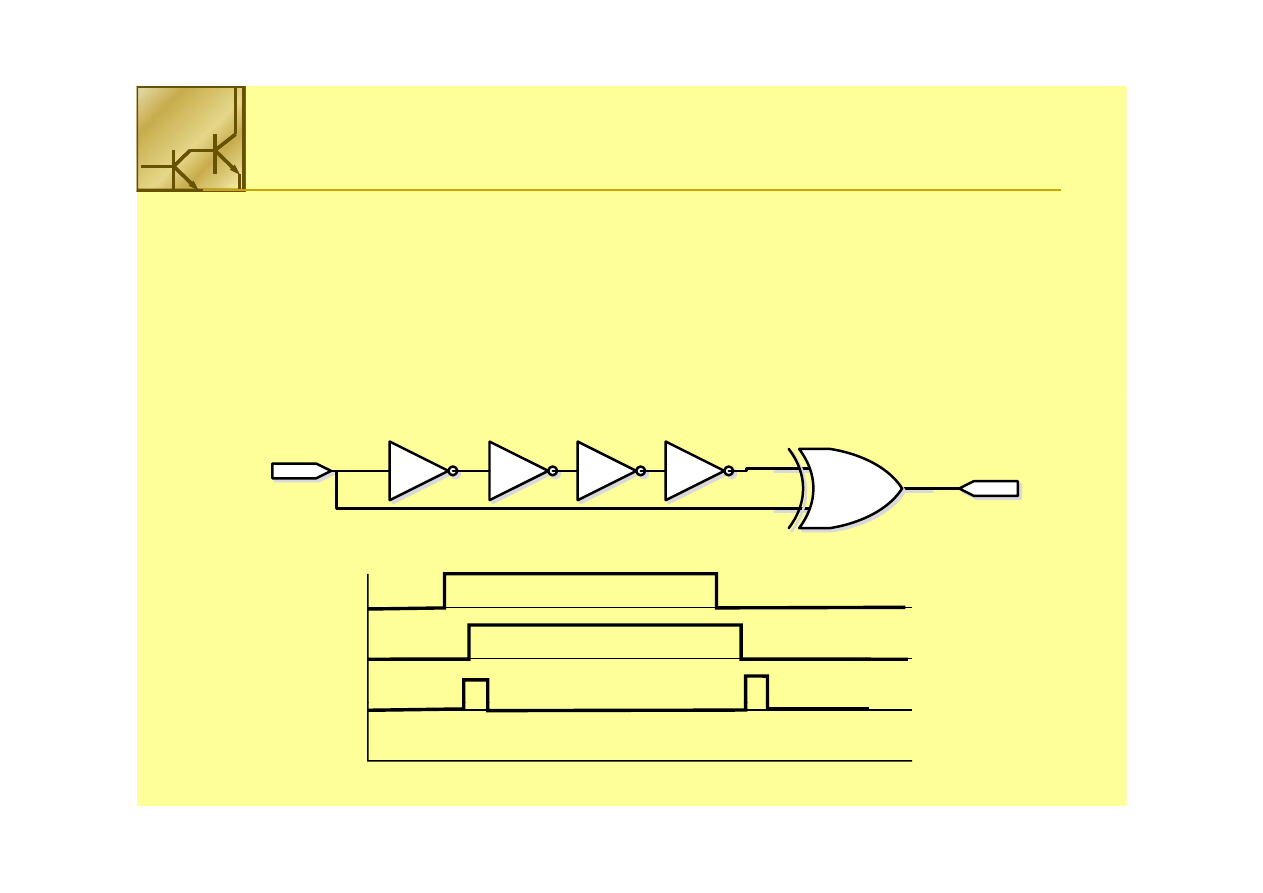
Hazard
Hazard
Hazard
Hazard
Układy generujące hazard są również celowo wykorzystywane w praktyce.
Układy generujące hazard są również celowo wykorzystywane w praktyce.
Są stosowane jako układy detektorów początku i końca impulsu wejściowego. Do
Są stosowane jako układy detektorów początku i końca impulsu wejściowego. Do
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
uzyskania impulsów wyjściowych o pożądanej szerokości zwiększa się opóźnienie
jednego z torów sygnału wejściowego przez połączenie kaskadowe dodatkowych
jednego z torów sygnału wejściowego przez połączenie kaskadowe dodatkowych
inwerterów lub bramek.
inwerterów lub bramek.
Sa
Sa to tzw. Układy logicznego różniczkowania.
to tzw. Układy logicznego różniczkowania.
X1
Y1
X
X
11
F
YY
11
6 marca 2011
Wojciech Kucewicz
138
FF
Wyszukiwarka
Podobne podstrony:
Cyfrowe układy kombinacyjne
Elektroniczne układy analogowe i cyfrowe, Układy kombinacyjne
elektronika cyfrowe układy kombinacyjne 3F2Z7LBV3UQWMPV3OADNTCQLCZHPW2DOT4WVVJQ
buchalski,logika układów cyfrowych, układy kombinacyjne kodery, multipleksy i?multipleksery (2)x
203 uklady kombinacyjne - kodery i dekodery, Politechnika Wrocławska - Materiały, logika ukladow cyf
Uklady kombinacyjne
Cyfrowe układy funkcjonalneB
układy kombinacyjne, Studia, semestr 4, Elektronika II, cw2
uklady kombinacyjne
Sprawozdanie - Uklady Kombinacyjne, Studia, semestr 4, Elektronika II, Elektr(lab)
Sprawozdanie Złożone układy kombinacyjne
multiplekserPP, Polibuda, IV semestr, SEM IV, Elektronika i Energoelektronika. Laboratorium, 10. Ukł
układy kombinacyjne, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, Elektryczny, Teo
Układy kombinacyjne oparte na elektronicznych układach TTL
Cyfrowe Układy Scalone Serii MCY74 N
MSE7Cyfrowe uklady kombinacyjne
więcej podobnych podstron