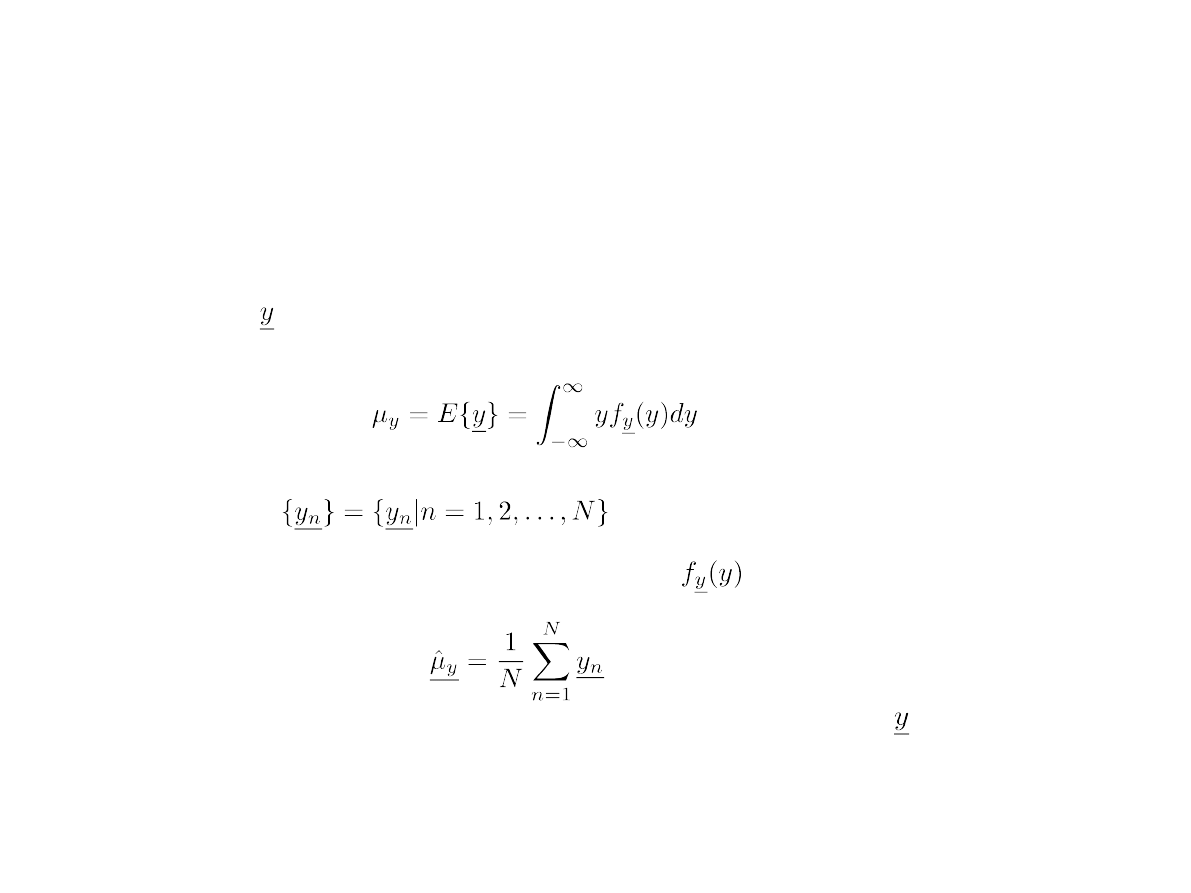
1

Metoda Monte Carlo

Podstawowa metoda Monte Carlo (MC)

Podstawowym zadaniem metody MC jest estymacja wartości oczekiwanej

pewnej zmiennej losowej. Wiele problemów można sprowadzić do tego typu

zagadnienia.

Założenia: jest zmienną losową o funkcji gęstości prawdopodobieństwa (fgp)

i wartości oczekiwanej:

Jeżeli

są niezależnymi zmiennymi losowymi o f.g.p. To ich średnia arytmetyczna

jest również zmienną losową:

będącą estymatorem wartości oczekiwanej zmiennej losowej

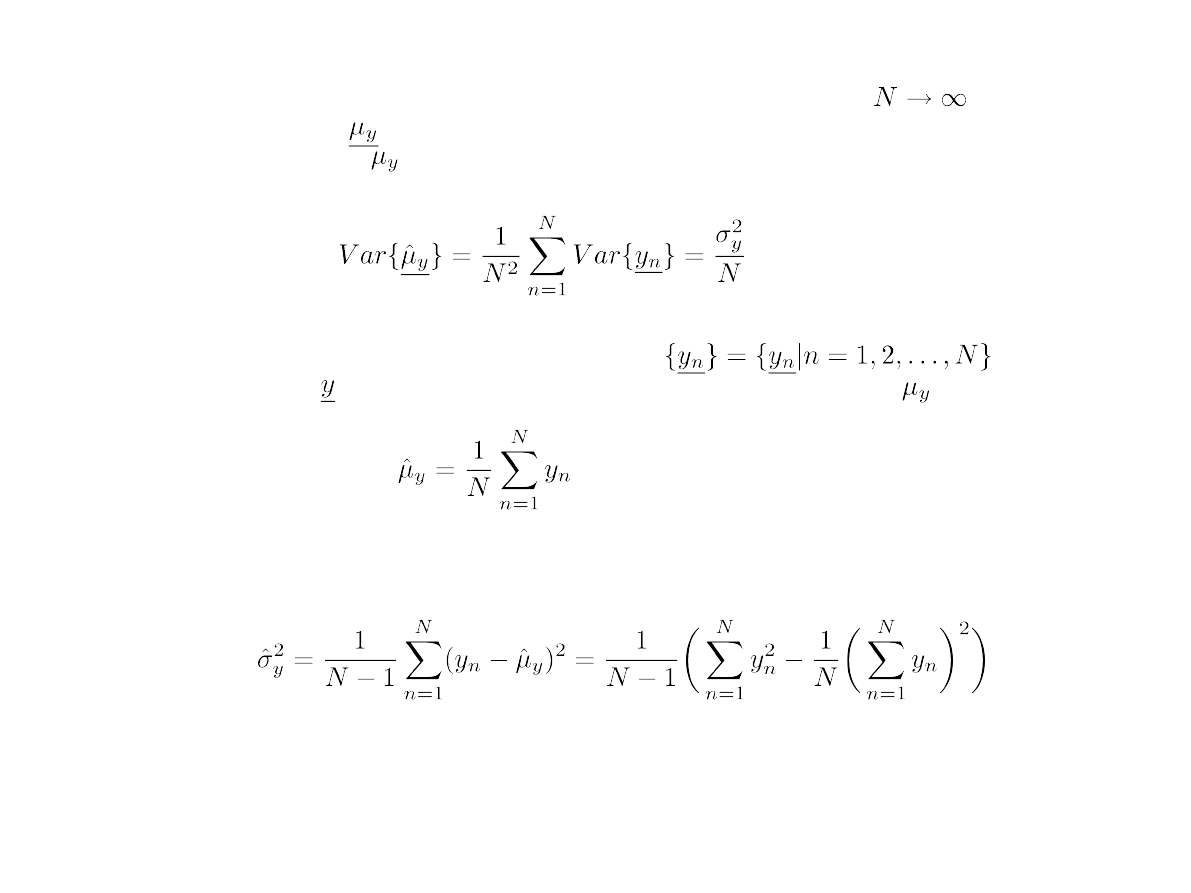
2

Metoda Monte Carlo

Zgodnie z założeniami centralnego twierdzenia granicznego przy

średnia arytmetyczna dąży do zmiennej losowej o rozkładzie normalnym

z wartością oczekiwaną i wariancją:

Mając do dyspozycji N niezależnych realizacji

zmiennej losowej o pewnej fgp, estymatę wartości oczekiwanej

wyznacza się ze wzoru:

a nieobciążoną estymatę wariancji tej zmiennej (nie wartości zmiennej)

przy pomocy wyrażenia:

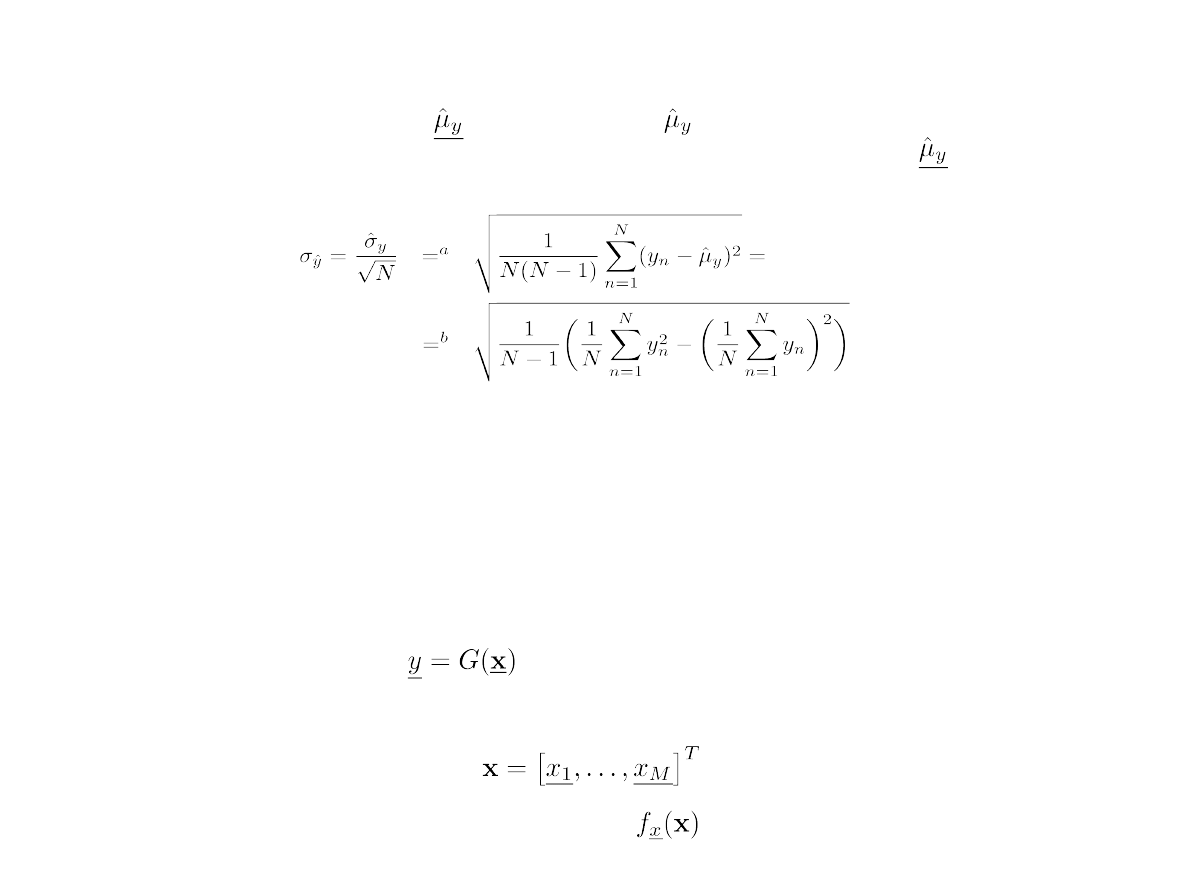
3

Metoda Monte Carlo

Realizacją zmiennej losowej jest estymata , dlatego za miarę dokladności

można przyjąć odchylenie standardowe estymatora zmiennej losowej

Obliczając wartość odchylenia standardowego zgodnie z (a) należy dwukrotnie

odwoływać się do wartości każdej próbki. W przypadku (b) odwołanie jest

jednokrotne ale błędy zaokrągleń przy sumowaniu mogą spowodować

pojawienie się wartości ujemnych pod pierwiastkiem.

Interesuje nas wyznaczenie (a raczej estymacja) wartości oczekiwanej

zmiennej losowej

ftóra jest funkcją wektora zmiennych (losowych):

o funkcji gęstości prawdopodobienstwa

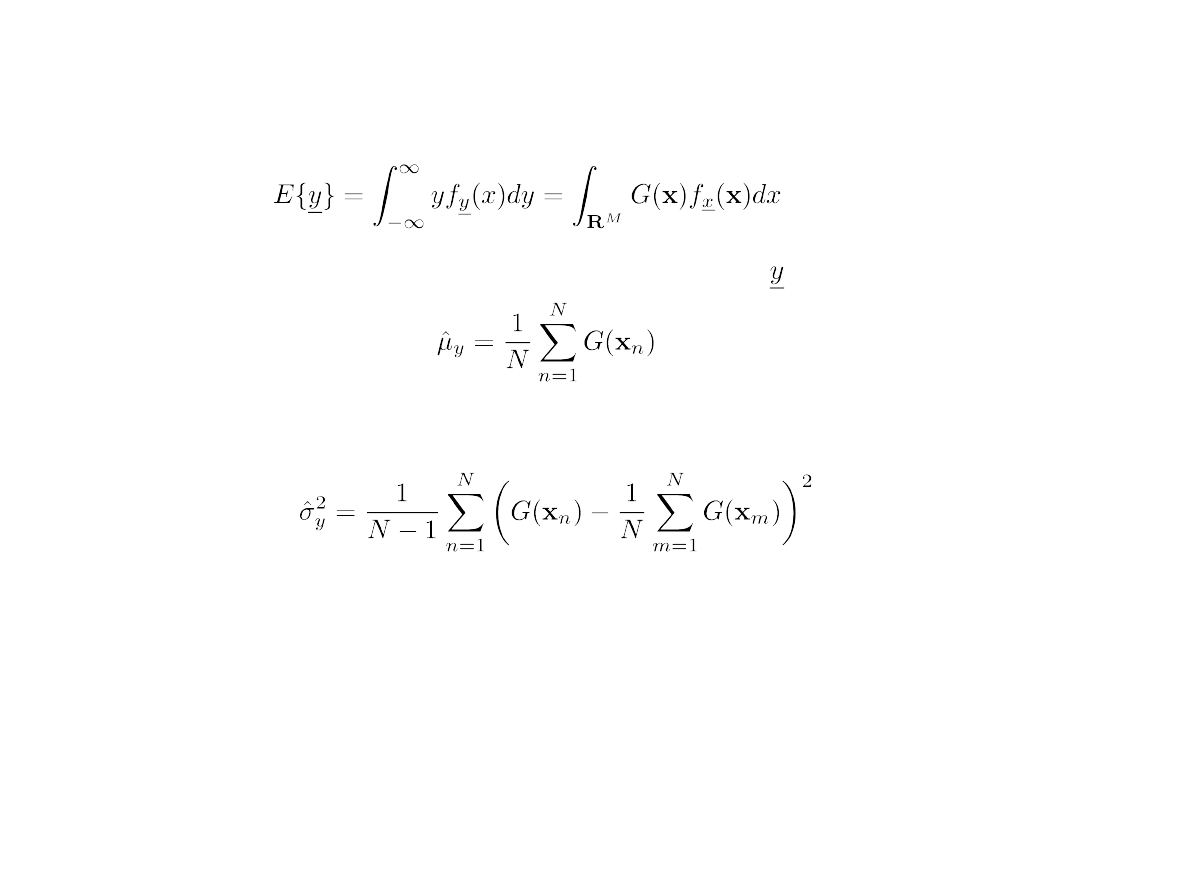
4

Metoda Monte Carlo

W metodzie MC wykorzystujemy przejście:

Estymację wartości oczekiwanej zmiennej losowej można wykonać

wg wzoru:

oraz wariancję tej zmiennej losowej:

Trzy powyższe wyrażenia są podstawą metody Monte Carlo przybliżonego

obliczania całek.

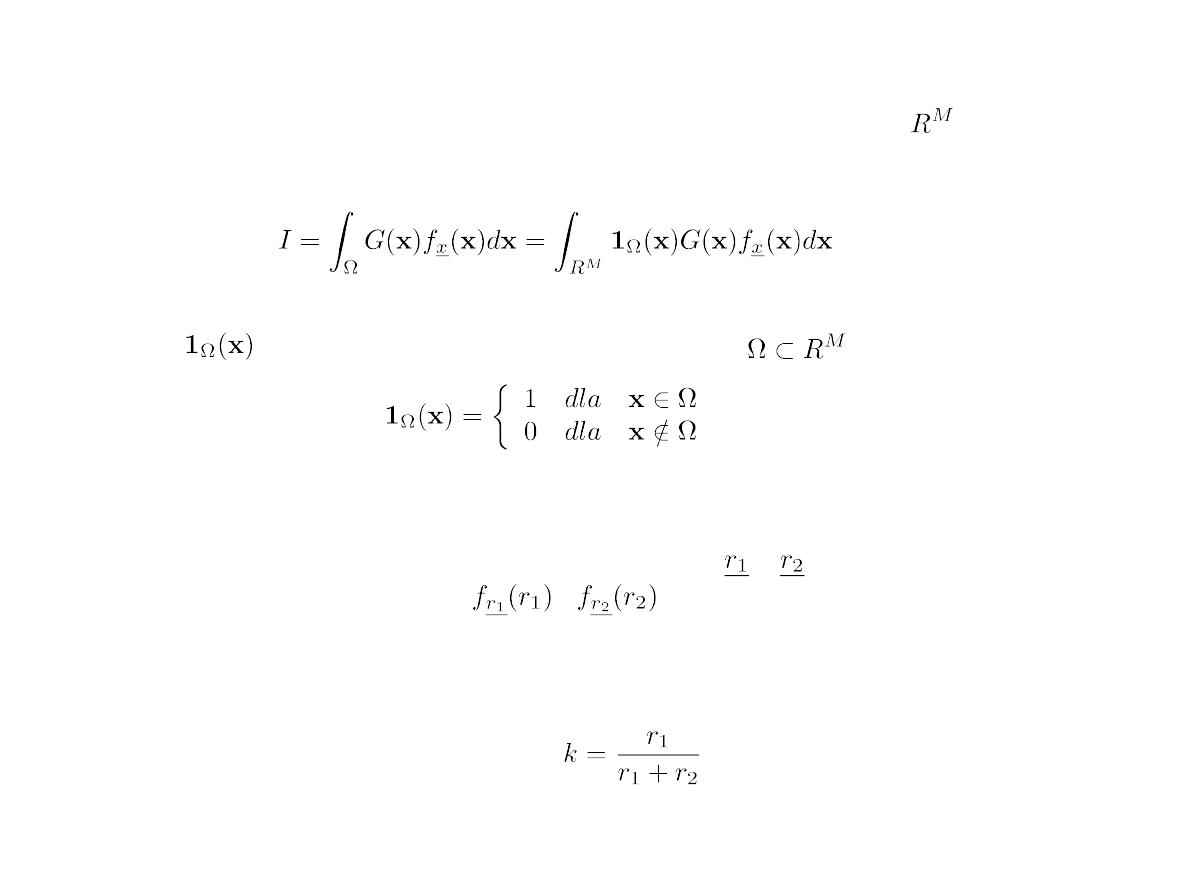
5

Metoda Monte Carlo

Zazwyczaj obszarem całkowania jest określony podzbiór przestrzeni .

W takim przypadku obliczaną całkę trzeba zapisać w nieco zmienionej postaci:

gdzie:

jest funkcją przynależności do zbioru

Przykład. Dzielnik napięcia powinien zapewniać tłumienie o wartości 0.5

z dokładnością 2%. Opory r

1

i r

2

mają rozrzuty produkcyjne które można

reprezentować za pomocą niezależnych zmiennych i o funkcjach

gęstości prawdopodobieństwa i . Wyznaczyć estymatę

uzysku produkcyjnego ´ , czyli średniego odsetka układów sprawnych.

Tłumienie napięciowe dzielnika:

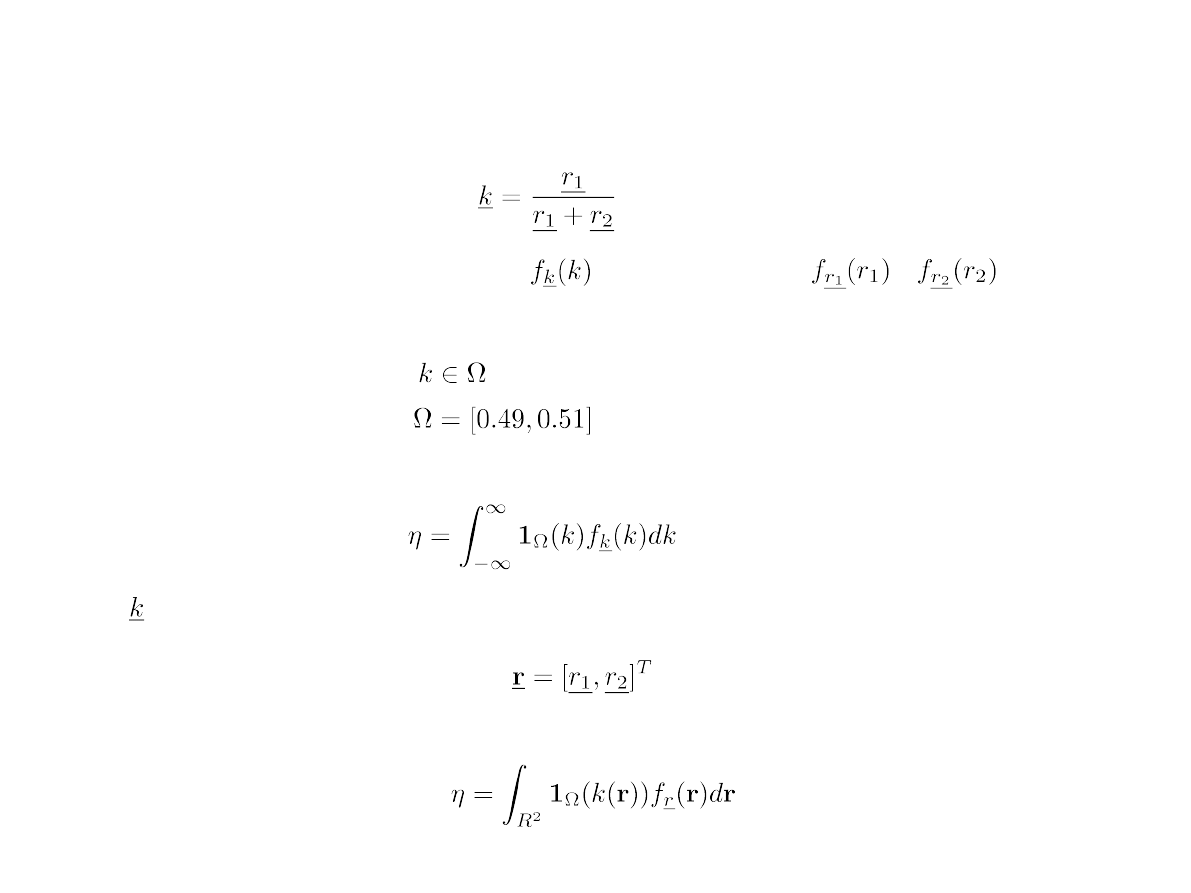
6

Metoda Monte Carlo

Tłumienie jest realizacją zmiennej losowej:

Rozkład tej zmiennej opisuje fgp zależna od fgp:

Warunkiem sprawności układu (jednej z wielu realizowanych możliwości)

jest :

Wykorzystujemy metodę MC do estymacji wartości oczekiwanej:

jest funkcją wektora losowego:

dlatego uzysk produkcyjny można wyrazić wzorem na średnią wartość

funkcji przynależności:

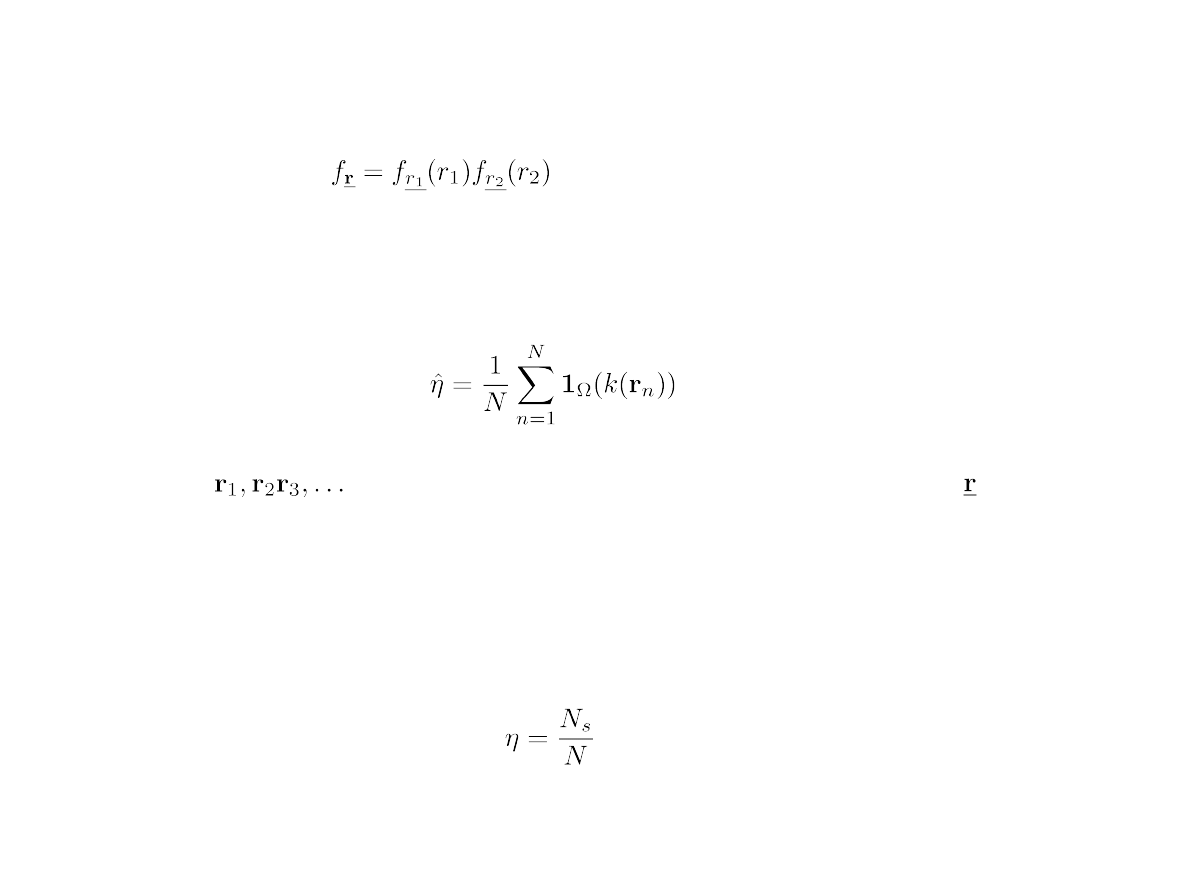
7

Metoda Monte Carlo

gdzie:

- iloczyn ze względu na niezależność

zmiennych losowych

Estymatę uzysku można obliczać jako średnią arytmetyczną:

gdzie:

Są niezależnymi realizacjiami wektora losowego

Algorytm wyznaczenia uzysku:

1)Wylosuj parę liczb: r

1

i r

2

, zwiększ N o 1

2)Jeśli obliczone k mieści się w obszarze ­ wówczas zwiększ N

s

o 1

3)Uzysk oblicz jako wartość ułamka

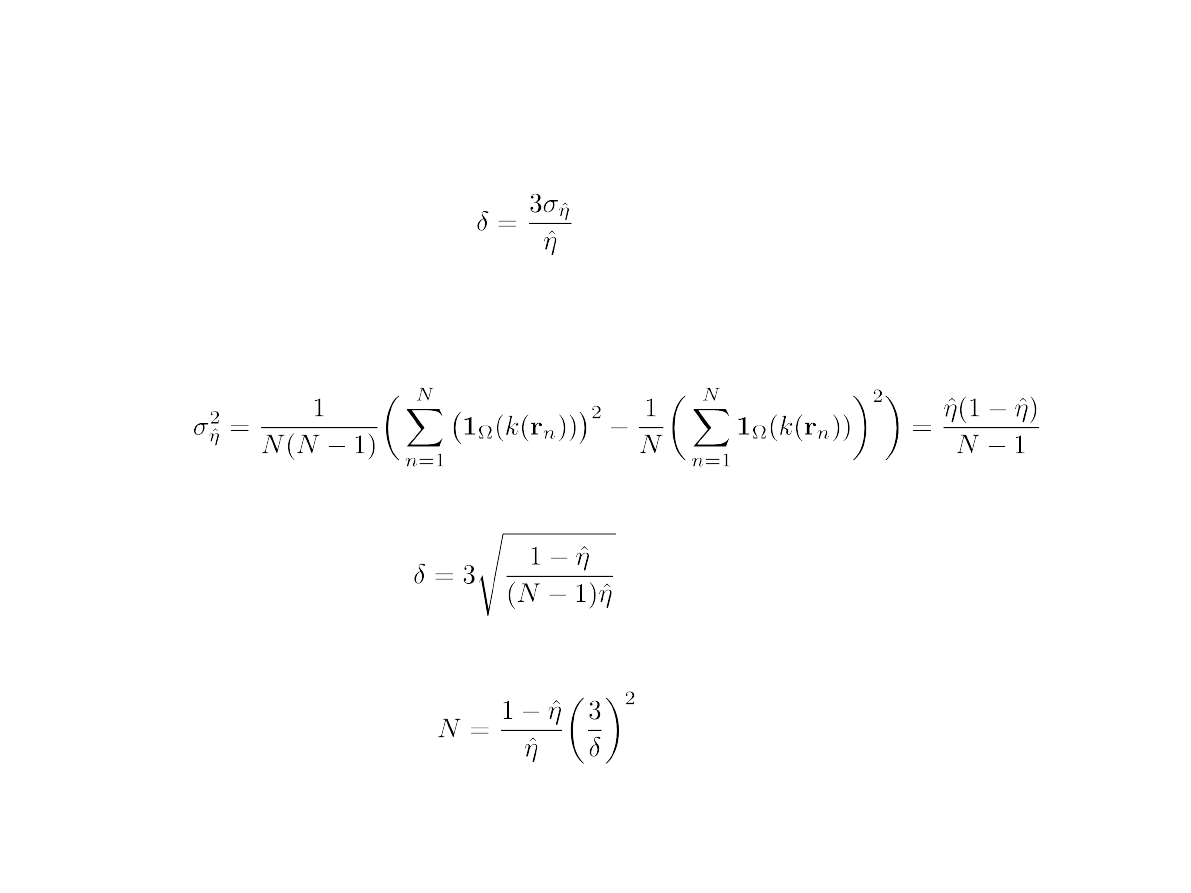
8

Metoda Monte Carlo

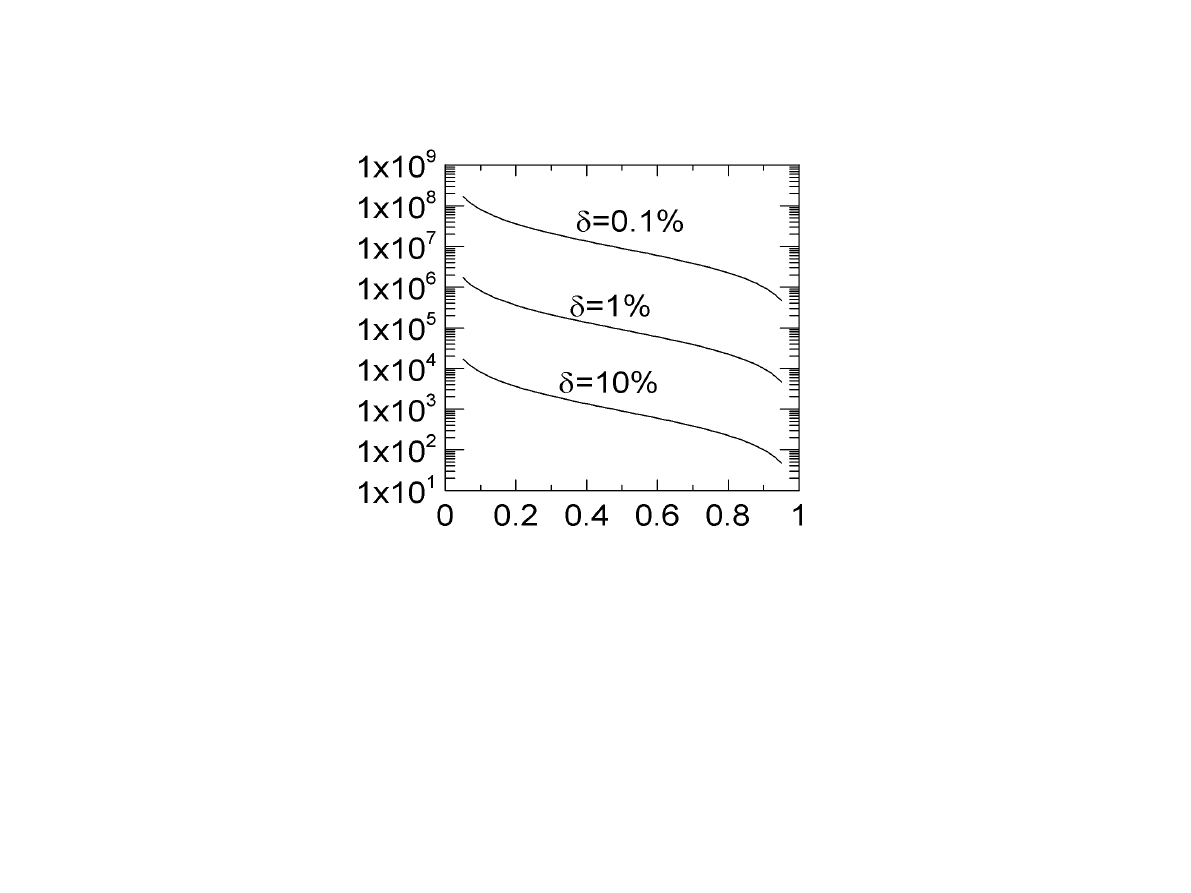
Przykład. Wyznaczyć minimalną liczbę N próbek wystarczającą do wyznaczenia

estymaty uzysku z trzysigmowym błędem względnym:

dla ± =0.1%,1%,10%.

Obliczamy wariancję estymatora:

Błąd względny:

Przekształcając go można otrzymać wyrażenie na minimalną liczbę próbek

potrzebną do uzyskania wymaganej dokładności:

9

Metoda Monte Carlo

Zależność minimalnej liczby próbek od założnego uzysku

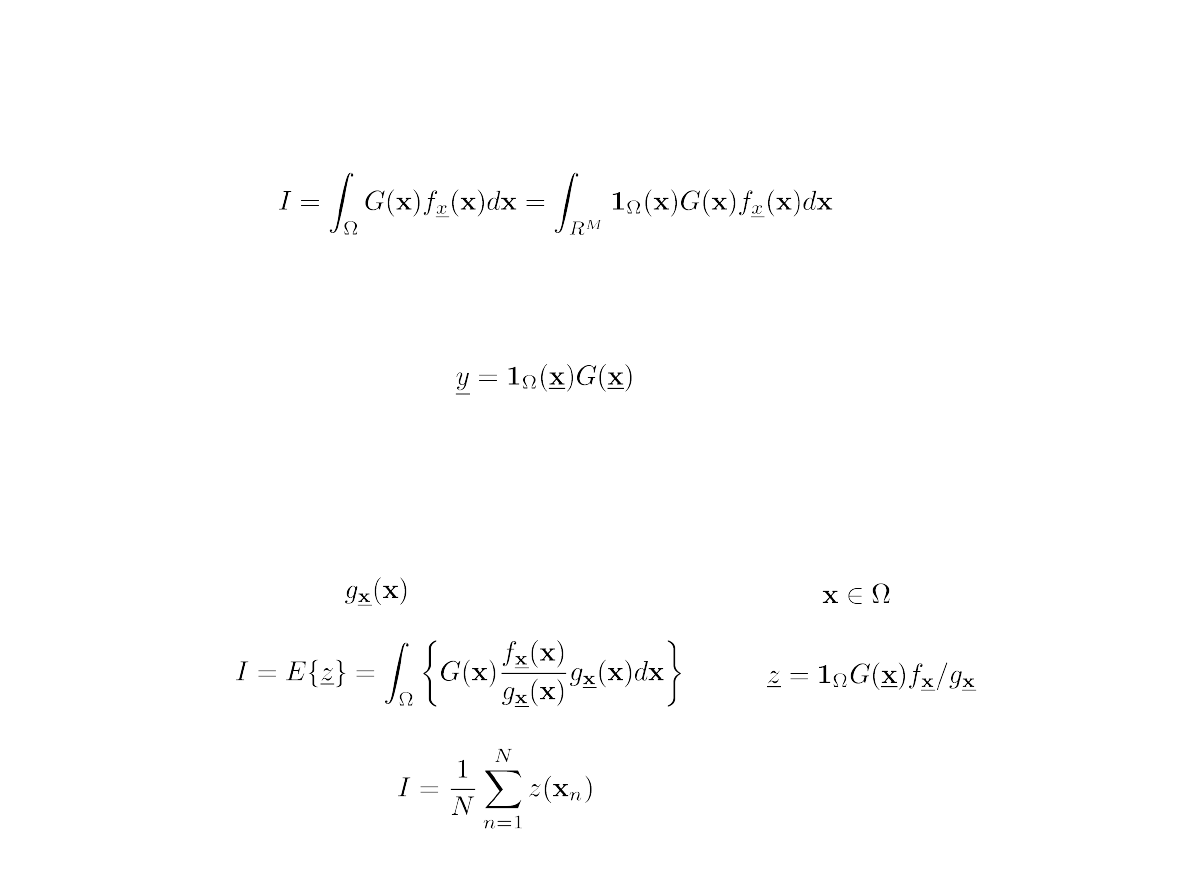
10

Metoda Monte Carlo

Metody zwiększania efektywności metody Monte Carlo.

Dokładność wyznaczenia całki metodą MC zależy od liczeby próbek N oraz

wariancji zmiennej losowej:

Wydajność metody można zwiększyć ustalając N i dokonując takiej transformacji

aby nowa zmienna losowa miała mniejszą wariancję.

1. Metoda losowania ważonego

Zakładamy że jest fgp dodatnio okresloną dla

Całkę estymujemy:

11

Metoda Monte Carlo

Zmienna losowa z ma taką samą wartość oczekiwaną jak zmienna losowa y oraz

wariancję zależną od fgp:

Wariancję etsymatora całki można zmniejszyć odpowiednio dobierając fgp

Najmniejszą wartość wariancja osiąga dla:

Jeżeli G(x) jest funkcją nieujemną, wówczas minimalna wariancja estymatora

ważonego jest równa 0. Należałoby jednak w takim przypadku znać wartość

całki w mianowniku. Zazwyczaj nie jest to możliwe, dlatego funkcję G(x)

zastępuje się inną G

1

(x), której całka może być łatwo obliczona. Minimalizacja

wariancji w takim przypadku zależy od jakości zastosowanego przybliżenia.

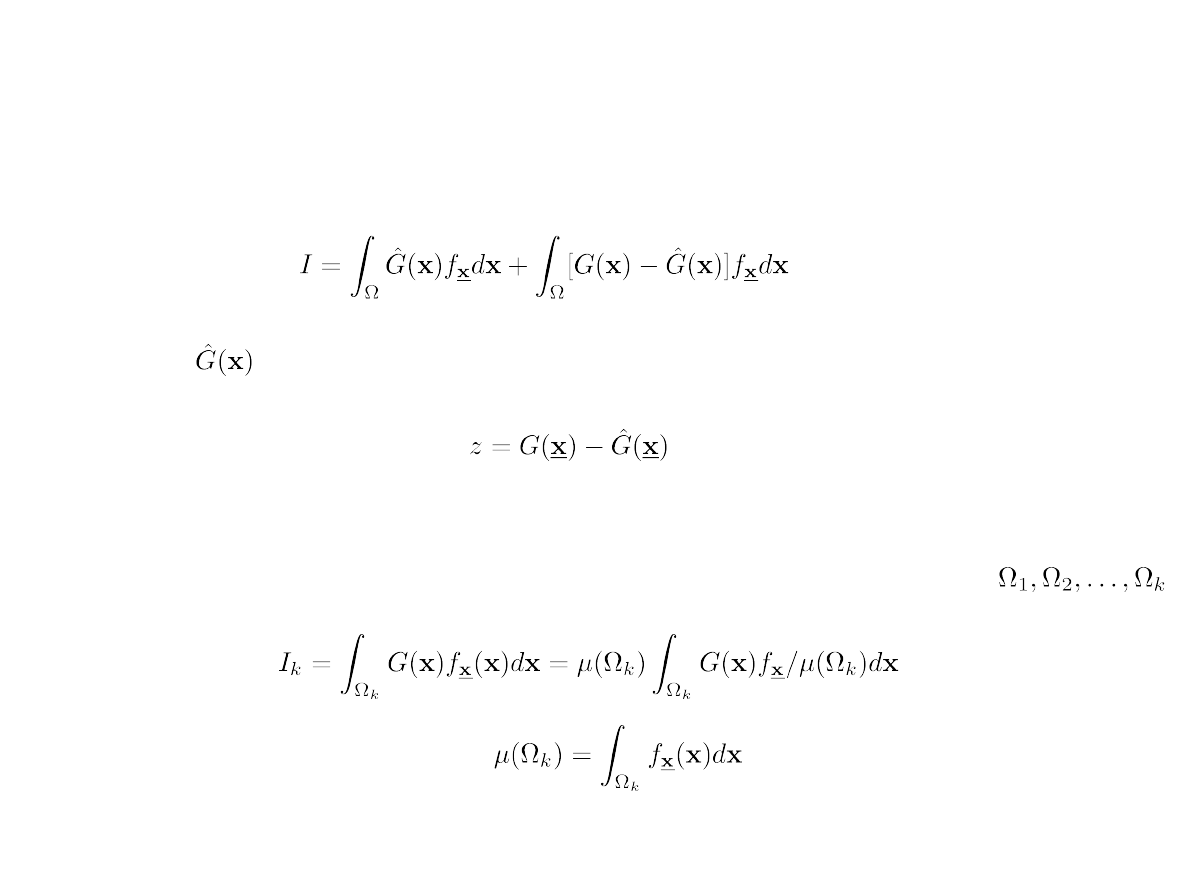
12

Metoda Monte Carlo

2. Metoda zmiennej kontrolnej.

Metoda polega na dekompozycji całki:

gdzie:

- jest aproksymacją funkcji G(x) umożliwiającą łatwe obliczenie

pierwszego wyrazu po prawej stronie analitycznie lub numerycznie.

Wariancja zmiennej losowej ma znacznie mniejszą wariancję

niż G(x).

3. Losowanie warstwowe

W metodzie tej obszar całkowania ­ dzieli się na K rozłącznych obszarów:

Całkę I oblicza się jako sumę takich całek:

gdzie: k=1,2,3,...,K

13

Metoda Monte Carlo

Całki I

k

można obliczać za pomocą podstawowej wersji metody MC:

Próbki są realizacjami wektora losowego o fgp:

4. Metoda obniżania krotności całki

Obniżenia krotności całki można dokonać gdy jest mozliwa dekompozycja

wektora oryginalnych zmiennych losowych:

oraz obszaru:

że zachodzi:

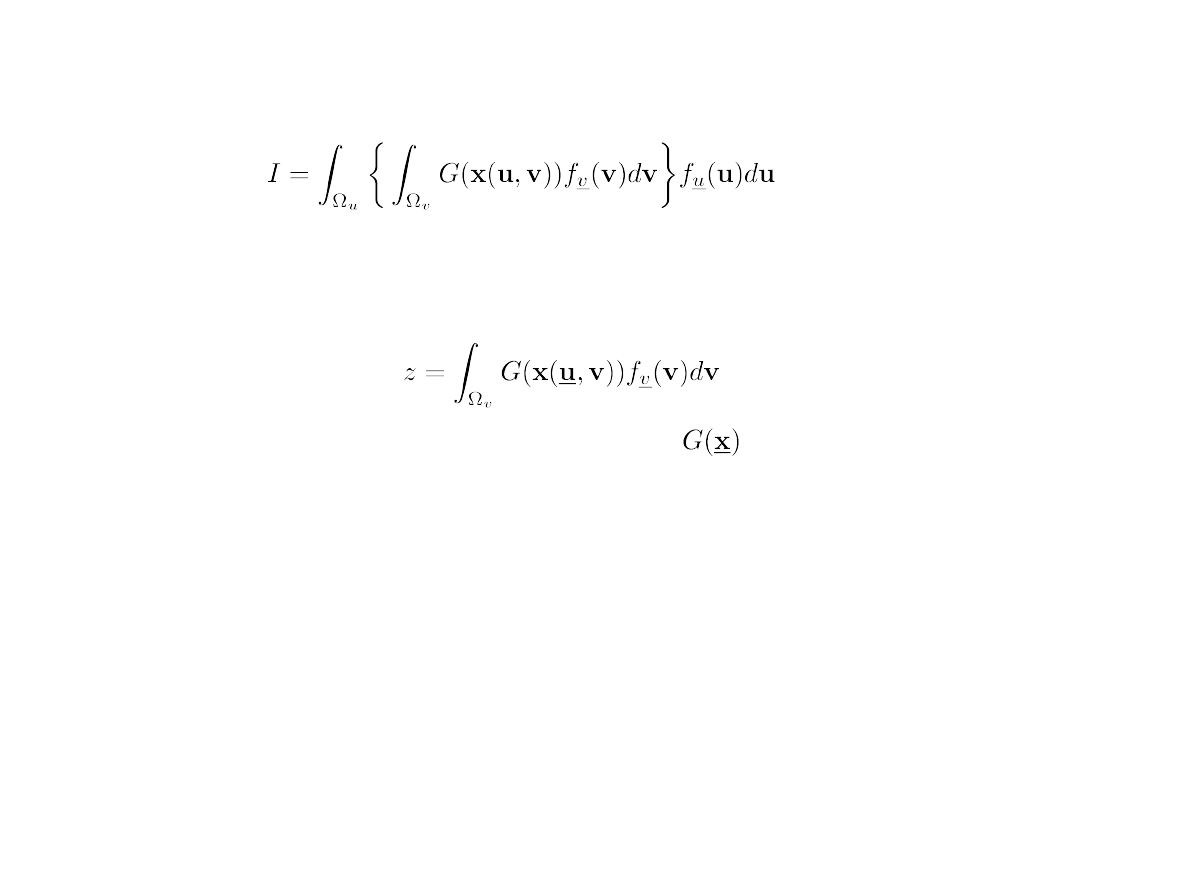
14

Metoda Monte Carlo

Zmienna losowa:

ma zazwyczaj mniejszą wariancję niż co pozwala dość łatwo

obliczyć całkę zewnętrzną. Metoda jest skuteczna jeśli potrafimy

dość dokładnie i szybko obliczyć całkę wewnętrzną (analitycznie

lub numerycznie).