Ilustracja metody

MONTE CARLO

obliczania

całek podwójnych

Często jest tak, iż wiemy, że istnieje całka oznaczona z funkcji

f

jednak nie potrafimy jej analitycznie policzyć. Konieczne jest

wtedy

zastosowanie

jakiejś

metody

numerycznej.

Metody całkowania oparte o użycie liczb losowych pojawiły się

w latach czterdziestych XX wieku. W Los Alamos w ramach

"Projektu Manhattan" (nad budową bomby jądrowej pracowali

wtedy m.in. John von Neumann, Stanisław Ulam, Richard

Feynman) potrzebne było obliczenie całek dotyczących

rozpraszania i absorpcji neutronów. Wykorzystana została

do

tego

metoda

Monte

Carlo.

Nazwa Monte Carlo, kasyna w Monaco, nawiązuje

do losowości gier hazardowych.

Projekt prezentuje zastosowanie metody Monte Carlo do

obliczania całek podwójnych. Zgodnie z Mocnym Prawem

Wielkich Liczb Kołmogorowa, całka dana jest wzorem:

Przybliżenie całki dla całek podwójnych wygląda następująco:

Gdzie x

k

i y

k

to odpowiednie losowe liczby

∫

∑



 →



−

∞

→

=

b

a

n

n

k

k

dx

x

f

X

f

n

a

b

)

(

)

(

1

∫∫

∑

=

−

≈

D

n

k

k

k

y

x

f

n

a

b

dxdy

y

x

f

1

2

)

,

(

)

(

)

,

(

k

k

u

a

b

a

x

)

(

−

+

=

k

k

v

a

b

a

y

)

(

−

+

=

Przykłady

całek

dxdy

y

x

D

∫∫

+

3

3

}

4

0

,

2

2

:

)

,

{(

2

x

y

x

y

x

D

−

≤

≤

−

≥

≥

=

dxdy

y

x

D

∫∫

+

3

3

dxdy

y

x

D

∫∫

+

3

3

Obliczenia analityczne

15

128

5

1

3

8

16

4

1

)

8

16

(

4

1

)

4

(

4

1

4

1

)

(

2

2

5

3

2

2

4

2

2

2

2

2

4

0

2

2

4

0

2

2

4

3

3

2

2

=













+

−

=

+

−

=

−

=













=

+

−

−

−

−

−

−

−

∫

∫

∫

∫

∫

x

x

x

dx

x

x

dx

x

dx

y

dy

y

x

dx

x

x

Metoda Monte Carlo

~obszar D zawarty jest w kwadracie
~n liczb u

i

i v

i

losujemy z rozkładu jednostajnego

I przekształcamy według wzorów.

~wykorzystując wylosowane liczby możemy przybliżyć całkę:

∑

∫∫

=

+

≈

+

n

k

k

k

D

y

x

n

dxdy

y

x

1

3

3

2

3

3

)

(

4

)

(

]

2

;

2

[

]

2

;

2

[

'

−

×

−

=

D

)

1

;

0

(

U

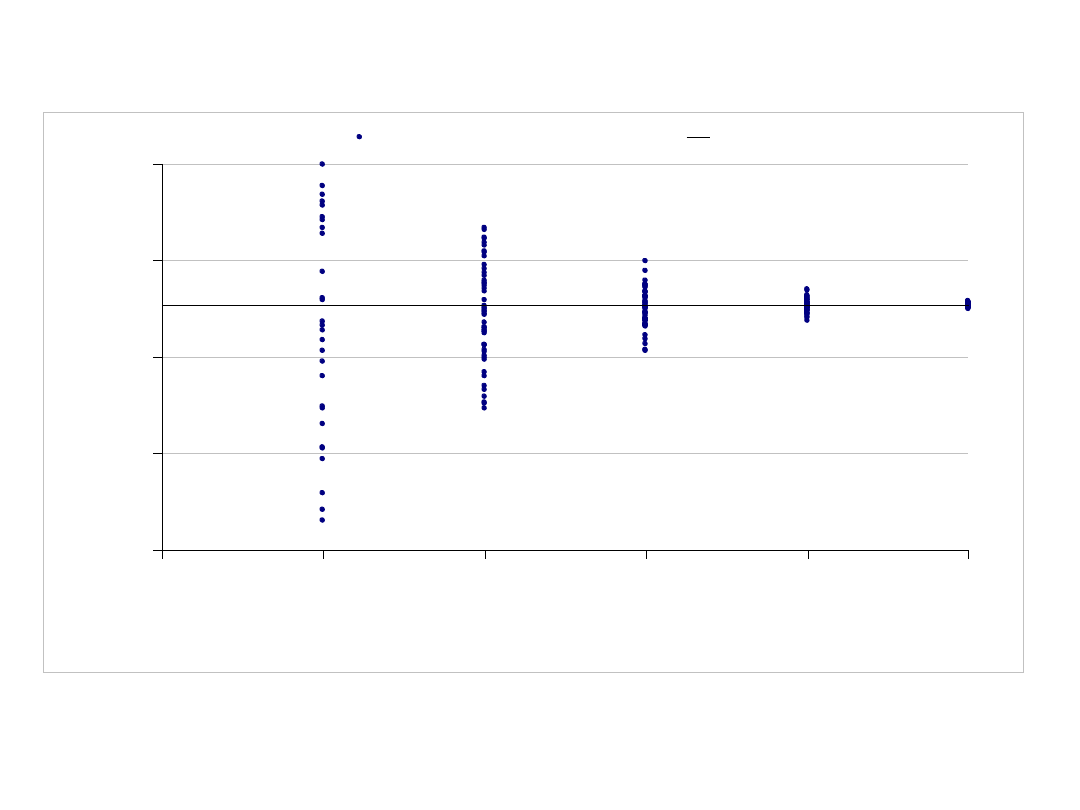
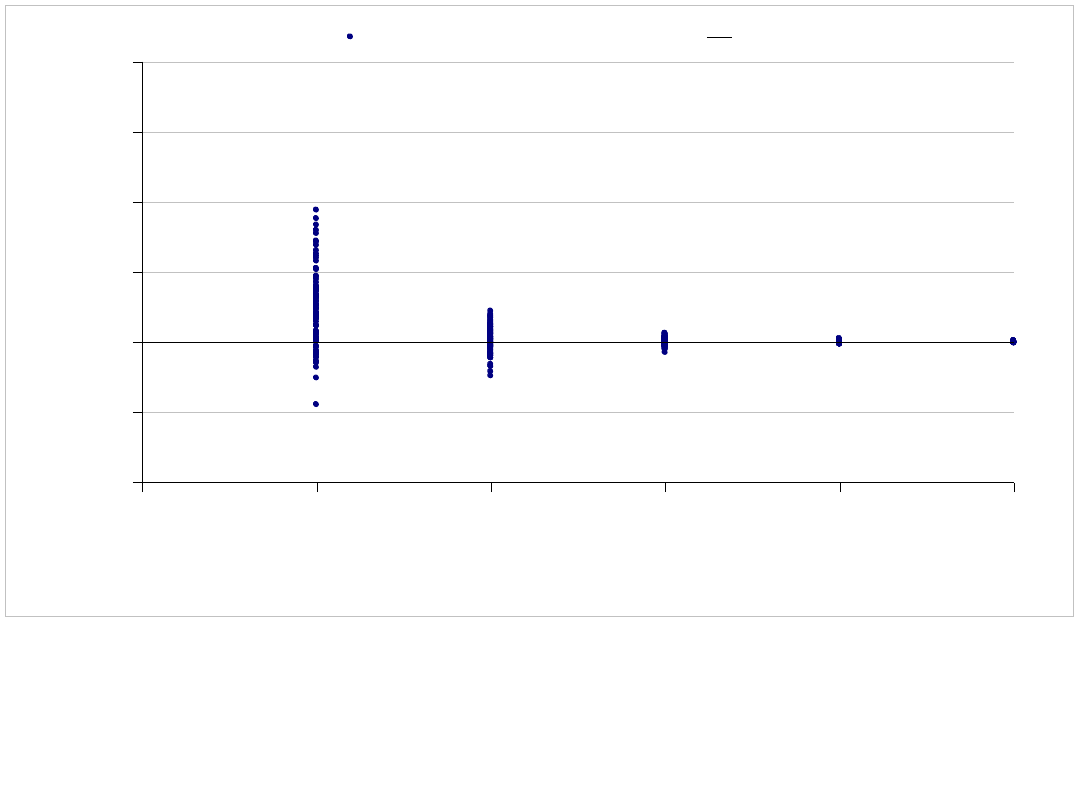
Stworzony został wykres przedstawiający rozkład wyników dla wykonanych 50 prób dla każdego n,

wyskalowany został półlogarytmicznie, pominięto ukazanie rozrzutu wartości dla n=1 i n=10 ze

względu na ich duże różnice

Wartość obliczona metodami standardowymi to 8,5(3) . Metodą Monte Carlo, dla 50 prób

przy n=1000000 uzyskujemy wartość średnią 8,535893, co stanowi bardzo dobre

przybliżenie rzeczywistej wartości całki.

y = 8,53333

6

7

8

9

10

10

100

1000

10000

100000

1000000

Ilosc prób Monte Carlo n

W

ar

to

sc

i u

zy

sk

an

e

Wyniki prób Monte Carlo

Wartość całki

dxdy

y

y

D

∫∫

)

sin(

dxdy

y

y

D

∫∫

)

sin(

}

,

0

:

)

,

{(

π

π

≤

≤

≤

≤

=

y

x

x

y

x

D

dxdy

y

y

D

∫∫

)

sin(

Obliczenia analityczne

∫ ∫

∫

∫∫

=









=

=

=

=

π

0

y

0

y

x

0

x

π

0

D

dy

y

sin(y)

x

dx

y

sin(y)

dy

dxdy

y

sin(y)

∫

=

−

−

=

=

π

π

0

2

)]

0

cos(

)

[cos(

)

sin( dy

y

Metoda Monte Carlo

~obszar D zawarty jest w kwadracie
~n liczb u

i

i v

i

losujemy z rozkładu jednostajnego

I przekształcamy według wzorów na x

i

i y

i

~wykorzystując wylosowane liczby możemy przybliżyć całkę:

]

;

0

[

]

;

0

[

'

π

π ×

=

D

)

1

;

0

(

U

∑

∫∫

=

≈

n

k

k

k

D

y

y

n

dxdy

y

y

1

2

)

sin(

4

)

sin(

π

y = 2

1

1,5

2

2,5

3

3,5

4

10

100

1000

10000

100000

1000000

Ilosc prób Monte Carlo n

W

ar

to

sc

i

uz

ys

ka

ne

Wyniki prób Monte Carlo

Wartość całki

Wykres przedstawiający rozkład wyników dla wykonanych
100 prób dla każdego n. Wartość obliczona metodami
standardowymi to 2 . Metodą Monte Carlo, dla 100 prób przy
n=1000000 uzyskujemy wartość średnią 1,99978.

∫∫

+

D

dxdy

y

x

)

(

2

2

∫∫

+

D

dxdy

y

x

)

(

2

2

( )

{

}

x

y

x

y

y

y

x

D

≤

+

≤

≥

=

2

2

,

0

:

,

∫∫

+

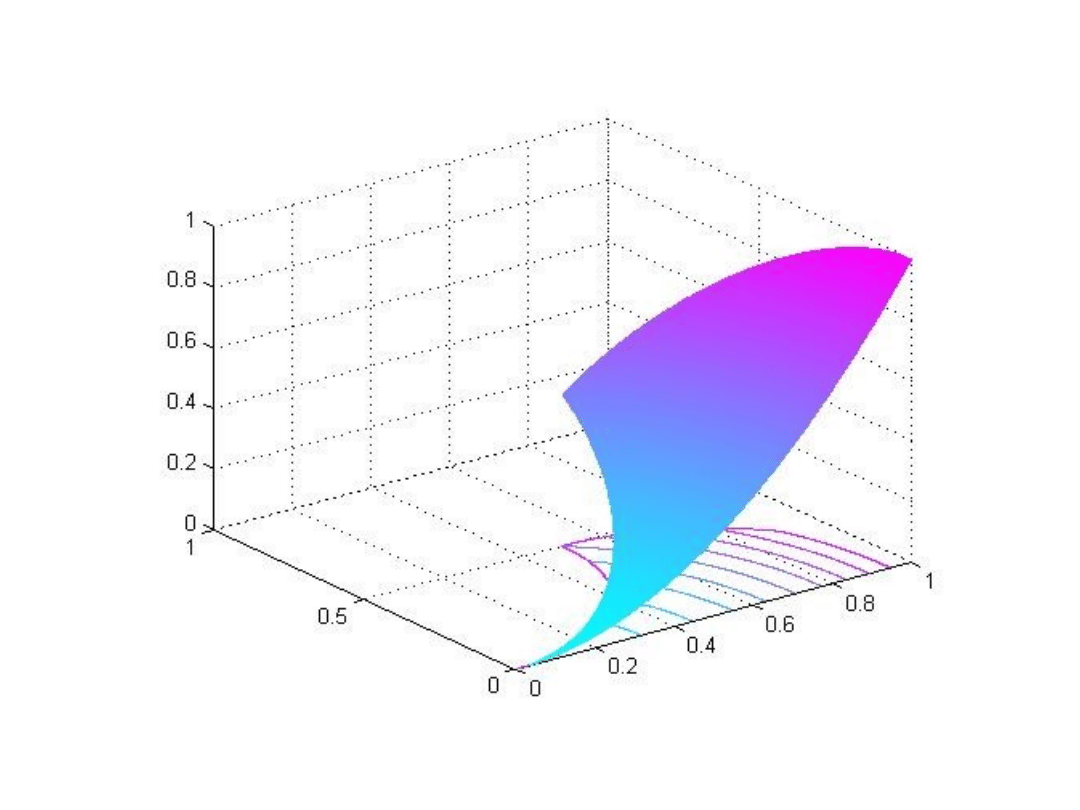
D

dxdy

y

x

)

(

2

2

Obliczenia analityczne

Aby obliczyć całkę analitycznie,
konieczne jest przejście na współrzędne biegunowe.
Obszar, po którym całkujemy, jest fragmentem koła

ϕ

ρ

ϕ

ϕ

ρ

ρ

ϕ

ρ

cos

sin

cos

sin

2

2

2

≤

≤

⇔

≤

≤

⇔

≤

+

≤

x

y

x

y

we współrzędnych biegunowych odpowiada on:

(

)













≤

≤

≤

≤

=

∆

ϕ

ρ

ϕ

π

ϕ

ϕ

ρ

cos

sin

,

4

0

:

,

(

)

)

8

1

sin

cos

(

4

1

sin

cos

4

1

4

1

)

(

4

0

4

0

4

4

cos

sin

4

4

0

4

0

cos

sin

2

2

2

2

=

=

−

=











=

=

=

+

=

=

=

=

∆

∫

∫

∫ ∫

∫∫

∫∫

π

ϕ

ϕ

π

ϕ

ρ

ϕ

ρ

π

π

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ρ

ϕ

ρ

ρ

ρ

ϕ

ϕ

ρ

ρ

ρ

d

d

d

d

d

d

dxdy

y

x

D

(

)

(

)

(

)

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

cos

sin

)

2

sin(

16

*

32

1

sin

cos

)

4

sin(

)

2

sin(

8

12

32

1

sin

)

4

sin(

)

2

sin(

8

12

32

1

cos

:

calki

zostaly

ane

wykorzyst

obliczenia

w

4

4

4

4

=

=

−

+

−

=

+

+

=

∫

∫

∫

d

d

d

Metoda Monte Carlo

~obszar D zawarty jest w kwadracie
~n liczb x

i

i y

i

losujemy bezpośrednio

z rozkładu jednostajnego

~wykorzystując wylosowane liczby możemy przybliżyć całkę:

∑

∫∫

=

+

≈

+

n

k

k

k

D

y

x

n

dxdy

y

x

1

2

2

2

2

)

(

1

)

(

]

1

;

0

[

]

1

;

0

[

'

×

=

D

)

1

;

0

(

U

y = 0,125

0

0,05

0,1

0,15

0,2

0,25

10

100

1000

10000

100000

1000000

Ilosc prób Monte Carlo n

W

art

os

ci

u

zy

sk

an

e

Wyniki prób Monte Carlo

Wartość całki

dxdy

e

D

y

x

∫∫

+

−

)

(

2

2

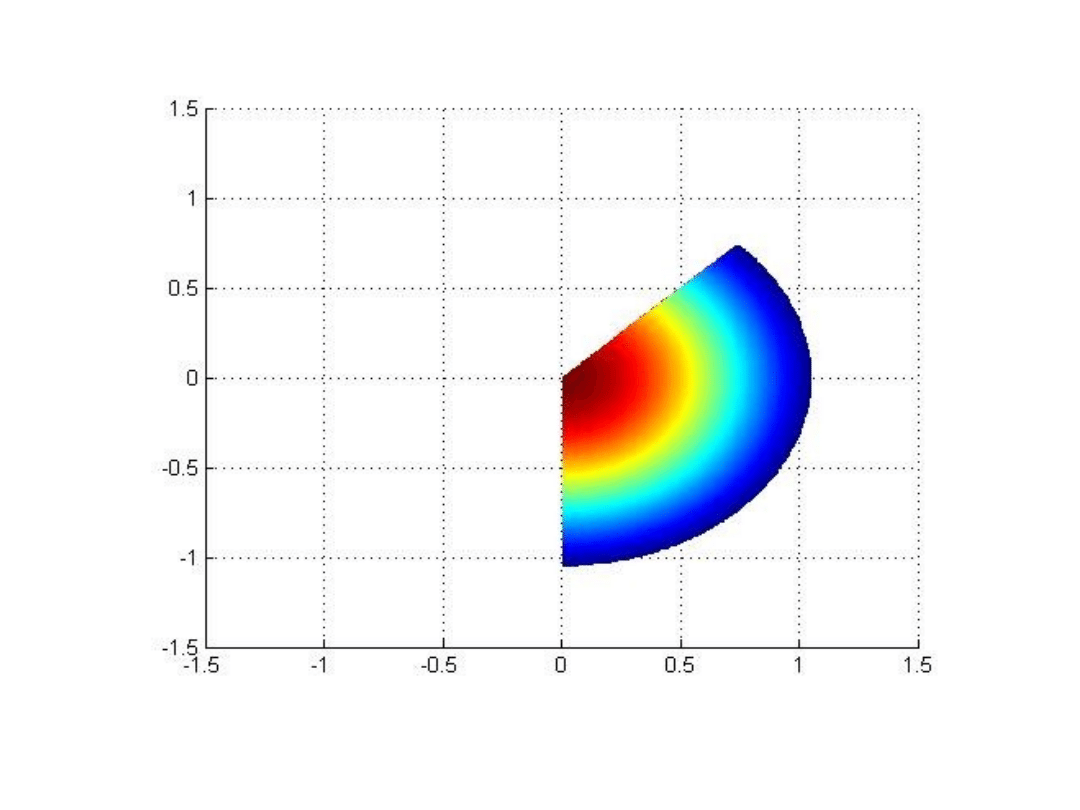
dxdy

e

D

y

x

∫∫

+

−

)

(

2

2

}

3

ln

,

,

0

:

)

,

{(

2

2

≤

+

≤

≥

=

y

x

x

y

x

y

x

D

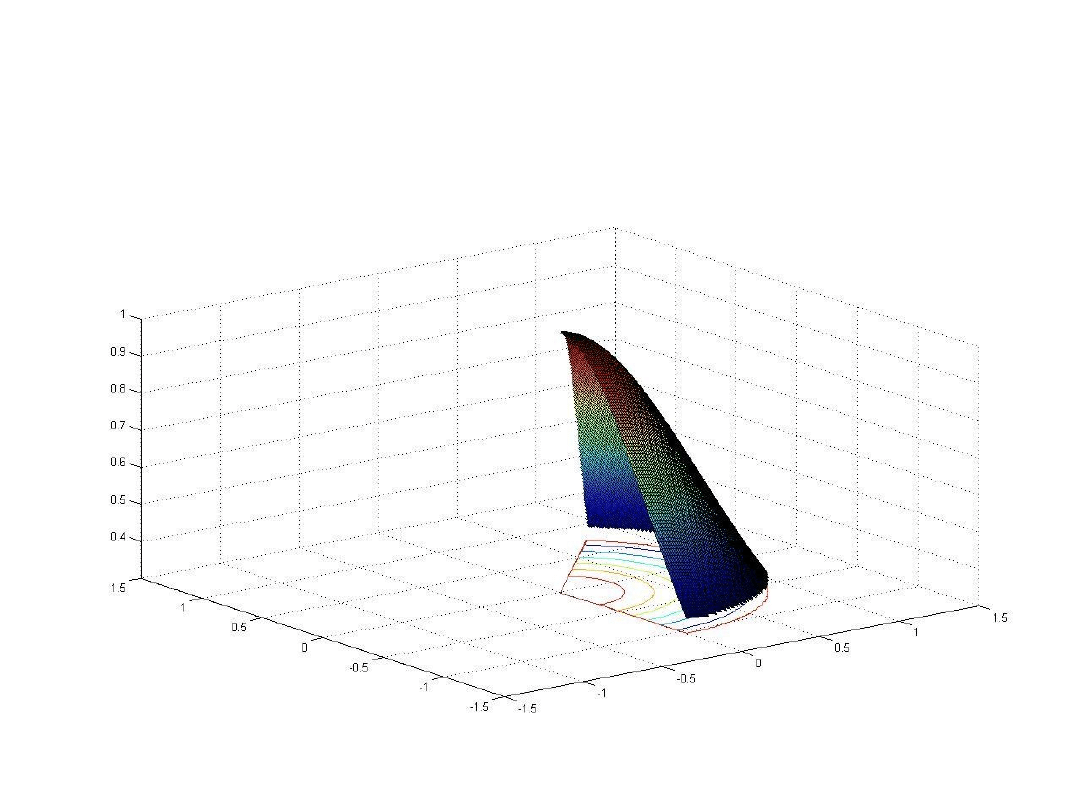
dxdy

e

D

y

x

∫∫

+

−

)

(

2

2

Obliczenia analityczne

dxdy

e

D

y

x

∫∫

+

−

)

(

2

2

}

3

ln

,

,

0

:

)

,

{(

2

2

≤

+

≤

≥

=

y

x

x

y

x

y

x

D

D we współrzędnych biegunowych odpowiada

}

3

ln

0

,

4

2

:

)

,

{(

≤

≤

≤

≤

−

=

∆

p

f

p

f

π

π

4

3

1

2

1

(

*

4

2

3

ln

2

2

2

2

2

4

2

0

4

2

4

2

3

ln

0

)

(

π

π

π

π

π

π

π

π

π

=

=

−

=

=

=

=

−

∫

∫

∫ ∫

∫∫

∫∫

−

−

−

−

−

∆

−

+

−

f

df

e

dp

pe

df

dfdp

e

dxdy

e

p

p

p

D

y

x

2

2

2

1

2

1

2

2

'

*

2

p

z

p

e

dz

e

pdp

dz

p

z

p

z

dp

pe

−

−

−

=

−

=





















−

=

−

=

−

=

=

∫

∫

Metoda Monte Carlo

~obszar D zawarty jest w kwadracie
~n liczb u

i

i v

i

losujemy z rozkładu jednostajnego

i przekształcamy według wzorów.

~wykorzystując wylosowane liczby możemy przybliżyć całkę:

∑

∫∫

=

+

−

+

−

≈

n

k

y

x

D

y

x

k

k

e

n

dxdy

e

1

)

(

2

)

(

2

2

2

2

3

ln

4

]

3

ln

;

3

ln

[

]

3

ln

;

3

ln

[

'

−

×

−

=

D

)

1

;

0

(

U

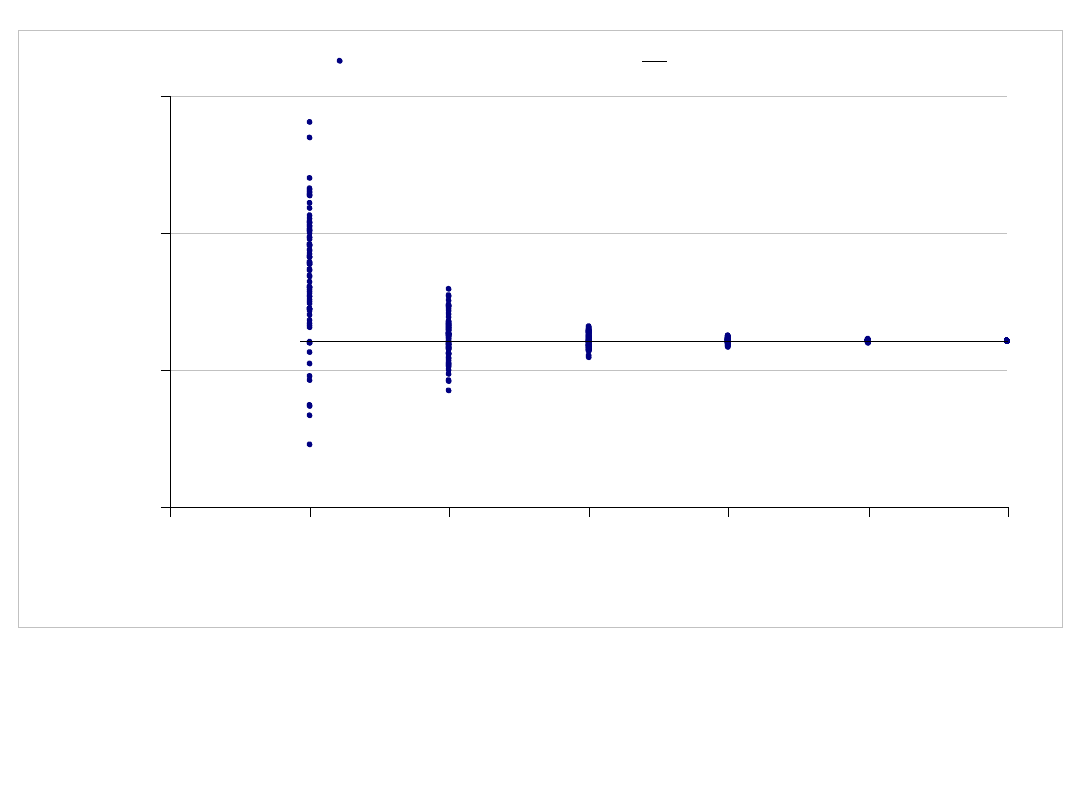
y = π/4

0,25

0,75

1,25

1,75

1

10

100

1000

10000

100000

1000000

Ilosc prób Monte Carlo n

W

art

os

ci

u

zy

sk

an

e

Wyniki prób Monte Carlo

Przewidywana wartość całki

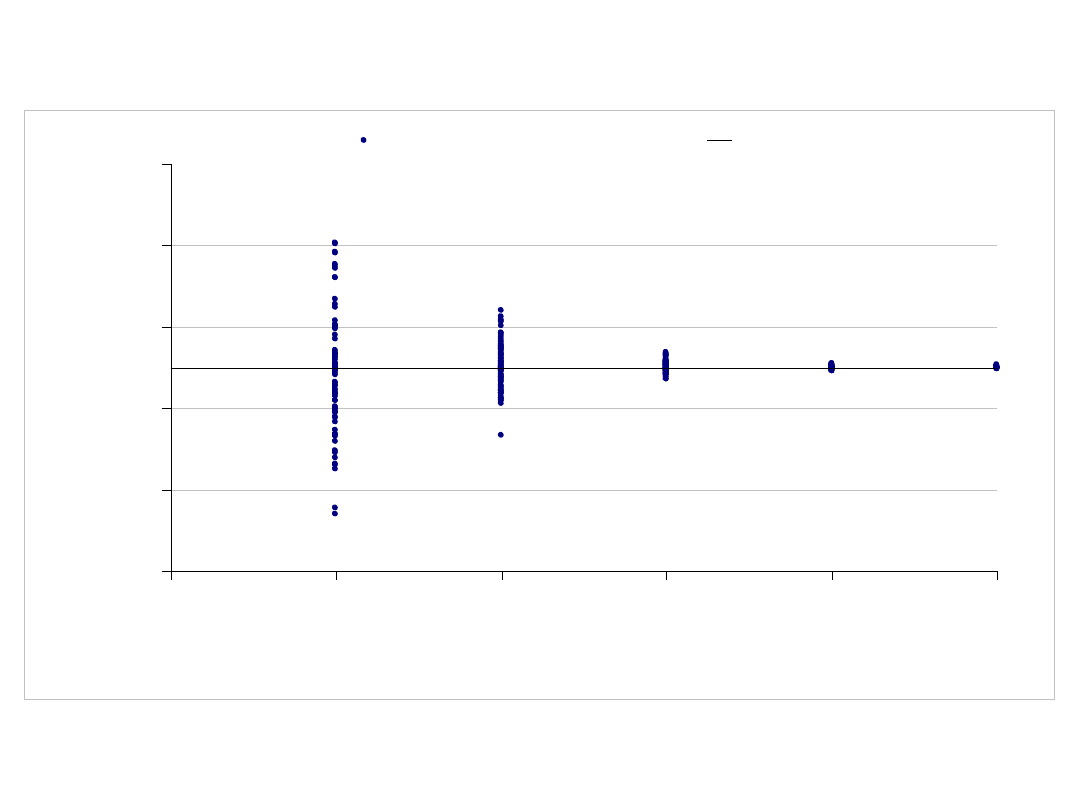
Wykres przedstawiający rozkład wyników dla wykonanych 80

prób dla każdego n

∫∫

D

)

sin(

10

dxdy

x

y

x

∫∫

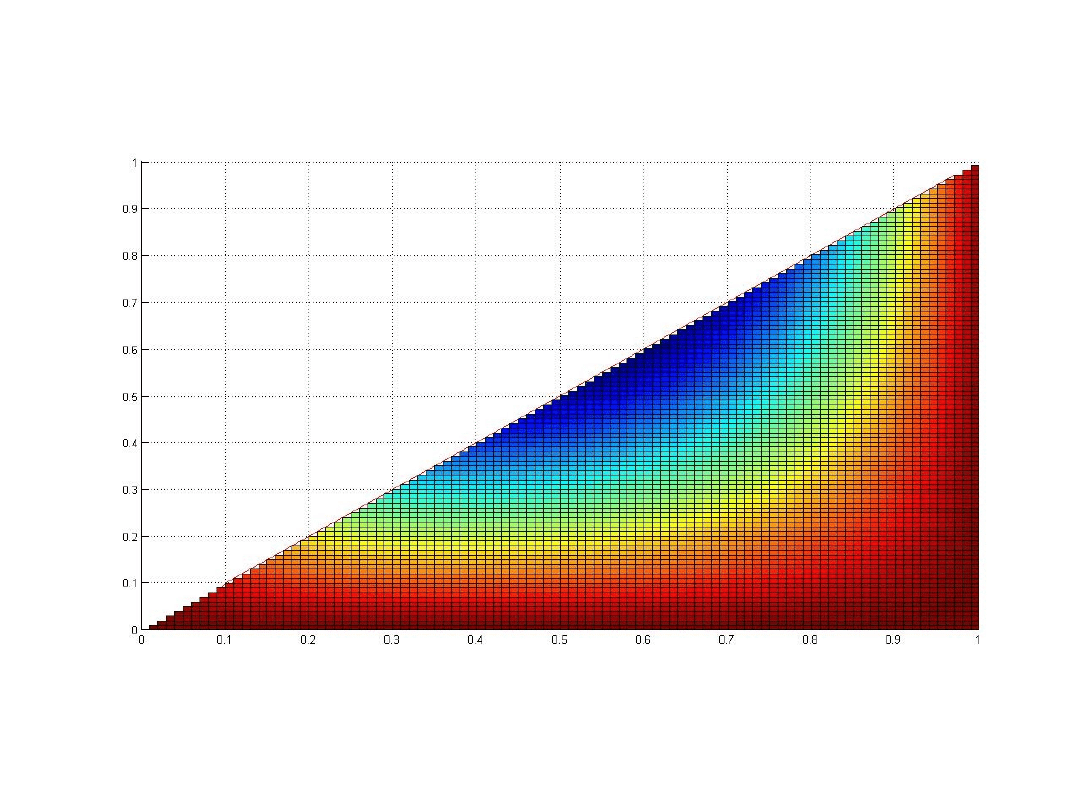
D

)

sin(

10

dxdy

x

y

x

}

0

;

1

0

:

)

,

{(

x

y

x

y

x

D

≤

≤

≤

≤

=

∫∫

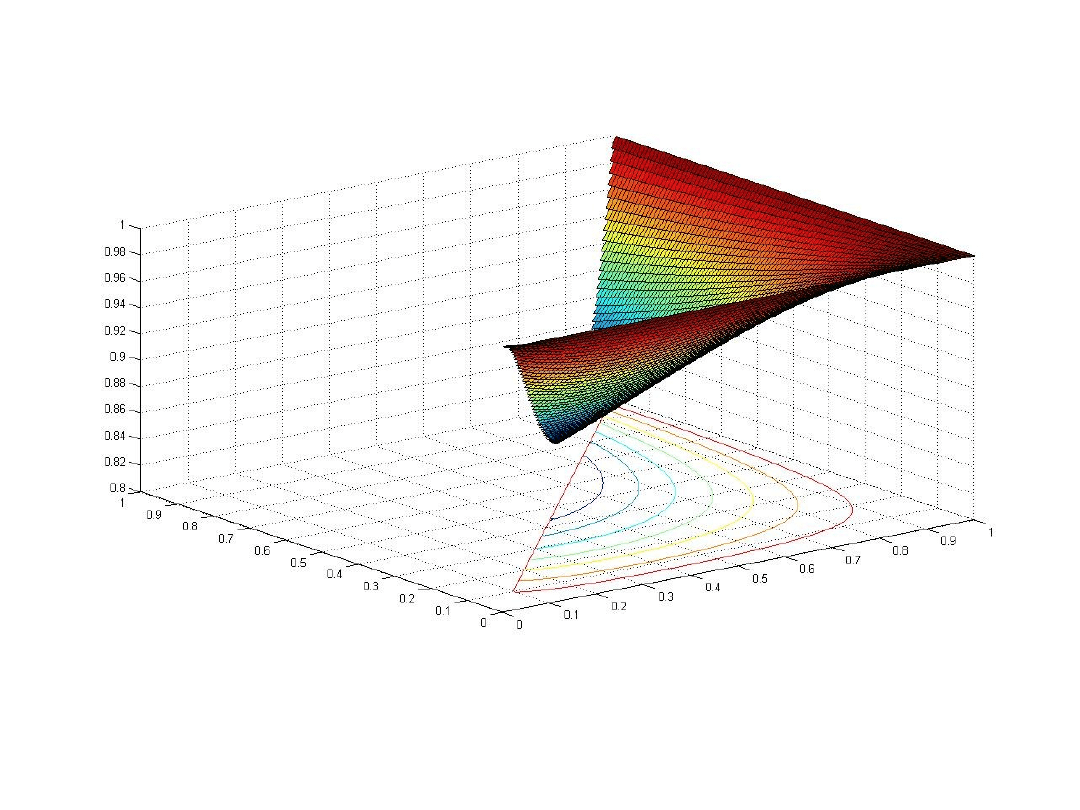
D

)

sin(

10

dxdy

x

y

x

Obliczenia analityczne

Całki tej nie da się wyrazić za pomocą funkcji
elementarnych. Tutaj z pomocą przychodzi metoda Monte
Carlo, dzięki której możemy poznać jej przybliżoną wartość.

Metoda Monte Carlo

~obszar D zawarty jest w kwadracie
~n liczb x

i

i y

i

losujemy bezpośrednio

z rozkładu jednostajnego

~wykorzystując wylosowane liczby możemy przybliżyć całkę:

∑

∫∫

=

≈

n

k

y

x

k

D

y

x

k

k

x

n

dxdy

x

1

)

sin(

)

sin(

10

10

]

1

;

0

[

]

1

;

0

[

'

×

=

D

)

1

;

0

(

U

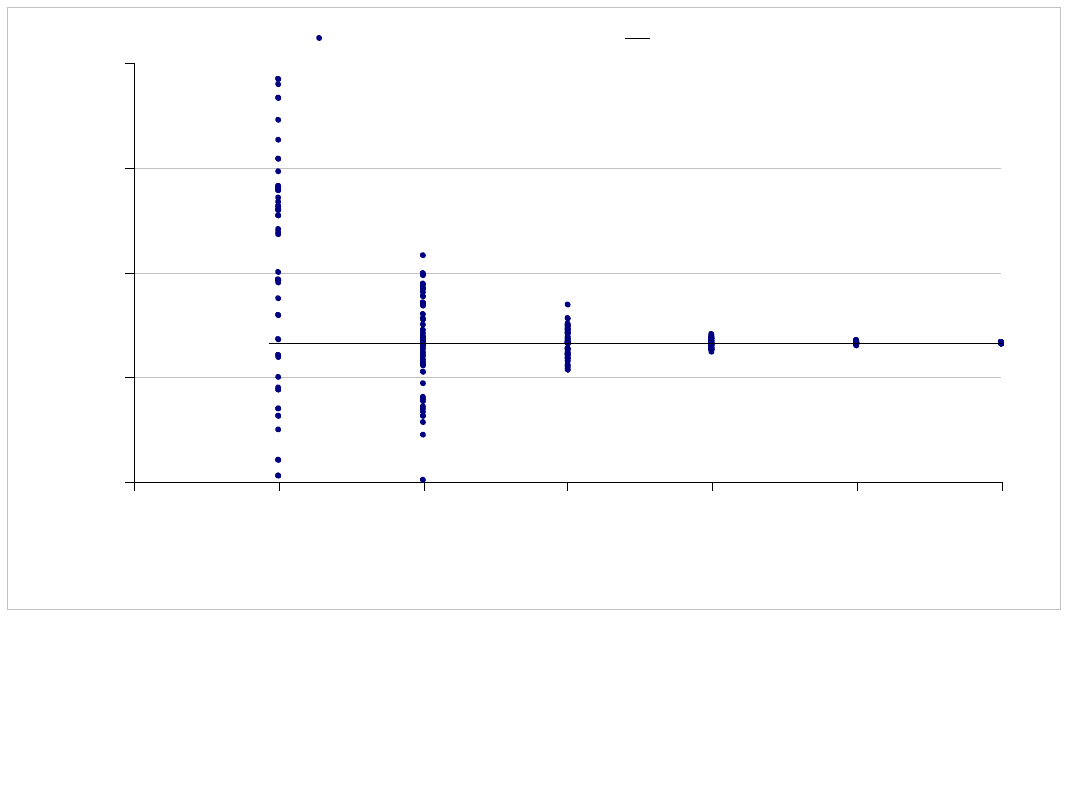
y = 1.31947

0

1

2

3

4

1

10

100

1000

10000

100000

1000000

Ilosc prób Monte Carlo n

W

ar

to

sc

i

uz

ys

ka

ne

Wyniki prób Monte Carlo

Przewidywana wartość całki

Autorzy projektu:

• Dorota Moskal

171695

• Mateusz Sawicki

171620

• Mariusz Orda

171665

• Michał Piórek

171677

• Mateusz Fuławka

171623

• Miłosz Karolonek

171595