
CHARAKTERYSTYKI CZASOWE UKŁADÓW DYNAMICZNYCH
Zadanie 1 Charakterystyki czasowe układów.
Problem:
Wyznaczyć odpowiedz skokową i impulsową całkującego z inercją
s
sT
k
s
G
)
1
(
)
(
+
=
(1)
s
sT
k
s
X
s
Y
s
G
)
1
(
)
(
)
(
)
(
+
=
=
(2)
s
1
;
1
=
= T
k
(3)
Odpowiedź skokową
wyznacza się ze wzoru:
( )
( )
{
}
)
(
1
s
X
s
G
L
t
h
−
=
( )
( )
=
−
s
s
G
L
t
h
1
gdzie:
s
X
1
)
(
=
jest skokiem
jednostkowym
Odpowiedź skokowa
+
=
−
)
1
(
1
)
(
1
sT
s
k
s
L
t
h
(4)
+
=
−
)
1
(
)
(
2
1
sT
s
k
L
t
h
(5)
Rozkładamy na ułamki proste
)
1
(
1
)
1
(
2
2
2
+
⋅
+
+
+
=
+
Ts
s
Ts
C
s
B
s
A
Ts
s
k
(6)
(7)
2
)
1
(
)
1
(
*
Cs
Ts
Bs
Ts
A
k
+
+
+
+
=
(8)
A
B
AT
s
C
B
s
k
+
+
+
+
=
)
(
)
(
2
(9)
=
=
+
=
+
k
A
B
AT
C
B
0
0
(10)
=
−
=
−
=
k
A
AT
B
B
C
+
+
−
=
−
1
)
(
2
1
Ts
kT
s
kT
s
k
L
t
h
(11)
T
t
kTe
kT
kt
t
h
−
+
−
=
)
(
(12)
−
−
=
−
T
t
e
T
t
k
t
h
1
)
(
(13)
Odpowiedź impulsowa:
+
=
−
)
1
(
)
(
1
sT
s
k
L
t
g
(14)
Rozkładamy na ułamki proste
)
1
(
1
)
1
(
+
⋅
+
+
=
+
Ts
s
Ts
B
s
A
Ts
s
k
(15)
g
(16)
Bs
Ts
A
k
+
+
=
)
1
(
L
g
=
A
B
AT
s
k
+
+
=
)
(
(17)
(18)
+
=
=
B
AT
k
A
0
(19)
=
−
=
B
kT
k
A
Odpowiedź impulsowa
wyznacza się ze wzoru:
( )
{
}
)
(
*
)
(
1
s
X
s
G
L
t
−
=
( )
{
}
( )
{
}
s
G
t
s
G
L
t
g
1
1
)
(
1
*
)
(
−
−
=
gdzie:
1
)
(
=
s
X
jest transformatą
impulsu Diraca (x(t)=
δ
(t))
1
)
1
(
+
−
+
=
+
Ts
kT
s
k
Ts
s
k
(20)
+
−
+
=
−
1
)
(
1
Ts
AT
s
k
L
t
g
(21)
T
t
kTe
k
t
g
−
−
=
)
(
(22)
)
1
(
)
(
T
t
Te
k
t
g
−
−
=
(23)
Odpowiedź liniowa
+
=
−
2
1
1
)
1
(
)
(
s
sT
s
k
L
t
y
(24)
+
=
−
)
1
(
)
(
3
1
sT
s
k
L
t
y
(25)
Rozkładamy na ułamki proste
)
1
(
1
)
1
(
3
2
3
3
+
⋅
+
+
+
+
=
+
Ts
s
Ts
D
s
C
s
B
s
A
Ts
s
k
(26)
(27)
A
s
B
AT
s
C
BT
s
CT
D
k
+
+
+
+
+
+
=
)
(
)
(
)
(
2
3
Odpowiedz liniową oblicza
się ze wzoru:
{
}
)
(
)
(
)
(
1
s
X
s
G
L
t
y
−
=
( )
=
−
2
1
)
(
s
s
aG
L
t
y
gdzie:
„a” jest to wartość stała,
prędkość narastania sygnału
a
s
s
X
*
1
)
(
2
=
(28)
=
+
=
+
=
+
=
0
0
0
CT
D
c
BT
B
AT
k
A
(28)
−
=
⇒
=
+
=
⇒
=
+
−
−
=
⇒
=
+
=
2
2
0
0
0
kT
D
kT
D
kT
C
C
kT
kT
B
B
kT
k
A
1
)
1
(
2
2
3
3
+
−
+
−
=
+
Ts
kT
s
kT
s
kT
s
kT
Ts
s
k
(30)
+
−
+
−
=
−
1
)
(
2
2
3
1
Ts
kT
s
kT
s
kT
s
kT
L
t
y
(31)
−
+
−
=
−
T
t
e
T
T
t
T
t
k
t
y
2
2
*
2
)
(
(32)
−
+
−
=
−
T
t
e
T
T
t
T
t
kT
t
y
1
2
)
(
2
2
2
(33)
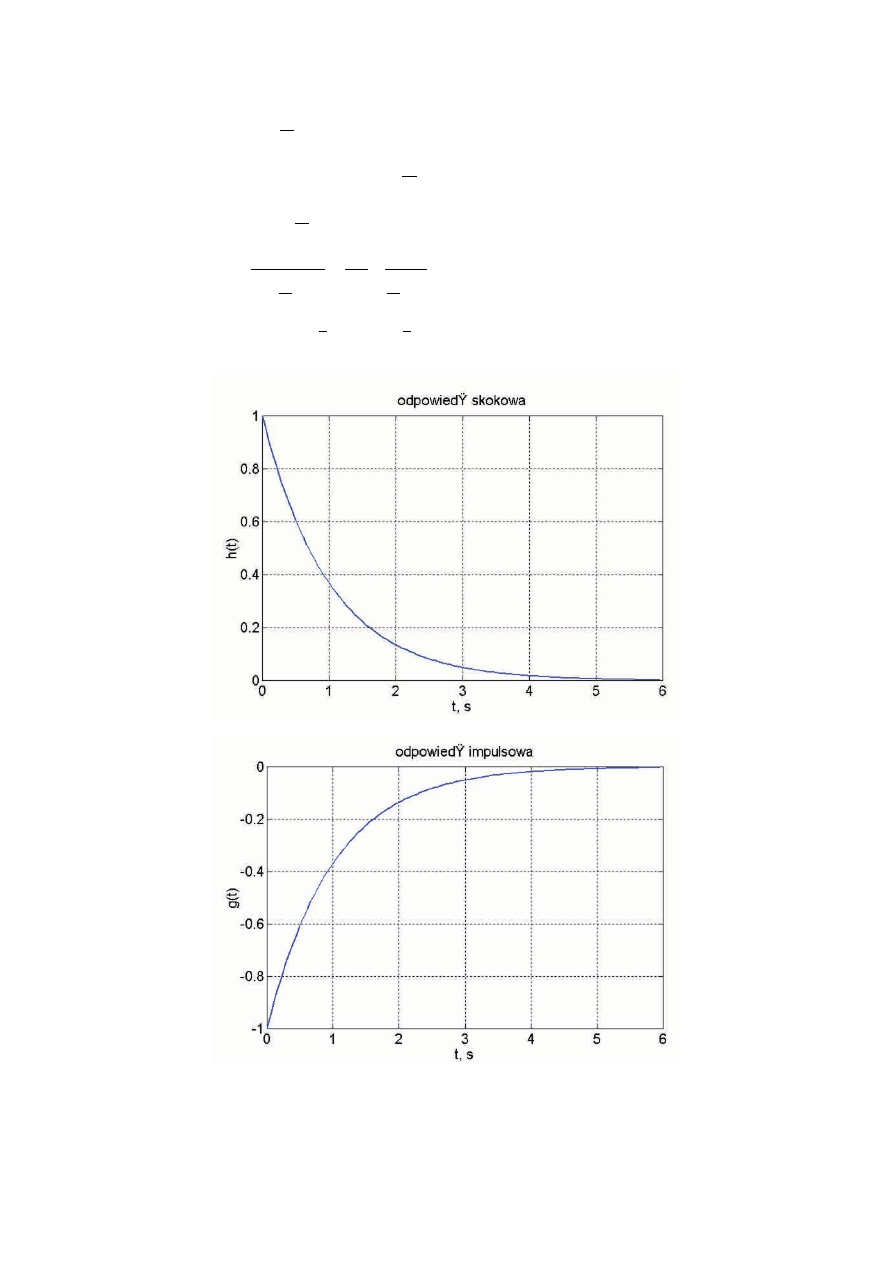
Rys. 1 Odpowiedz skokowa.
R
ys. 2 Odpowiedź impulsowa.
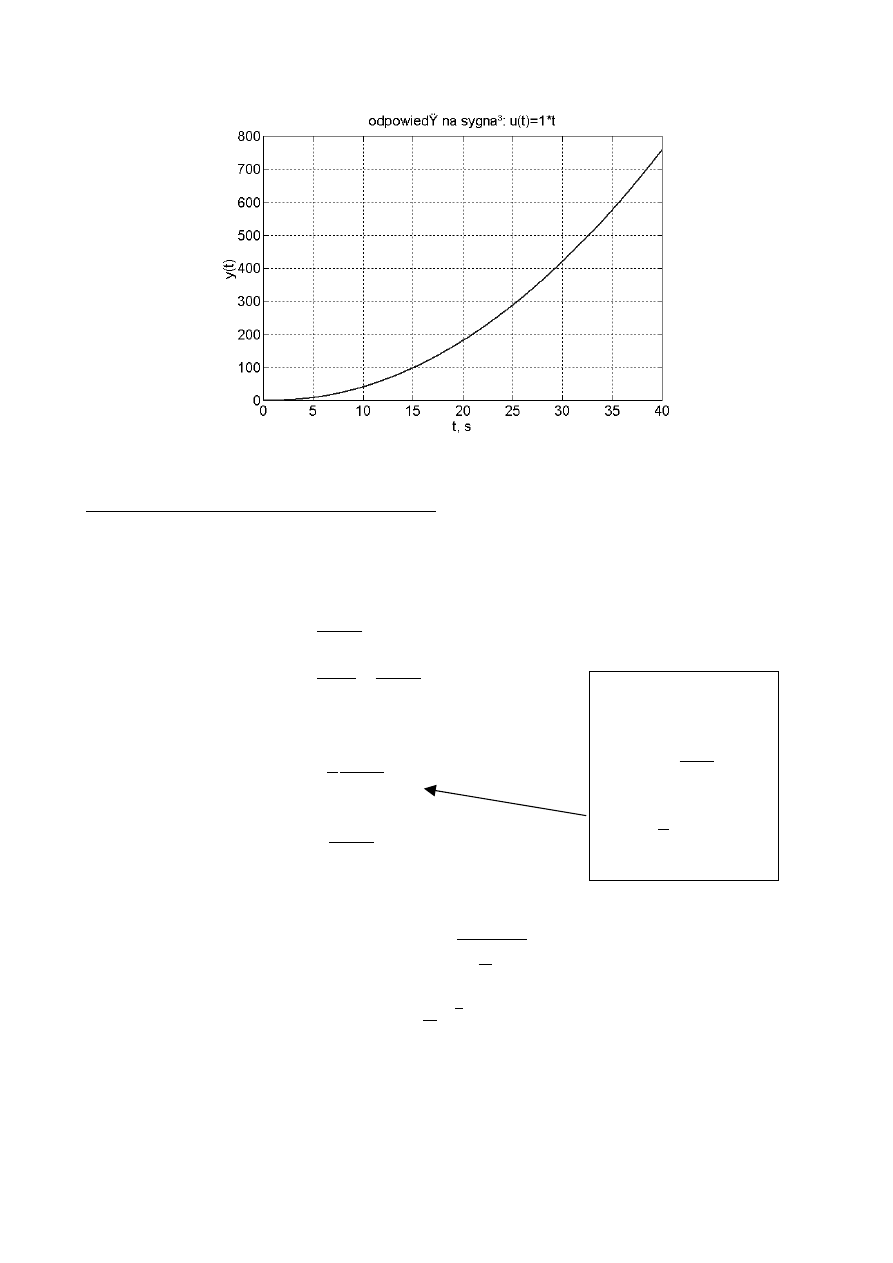
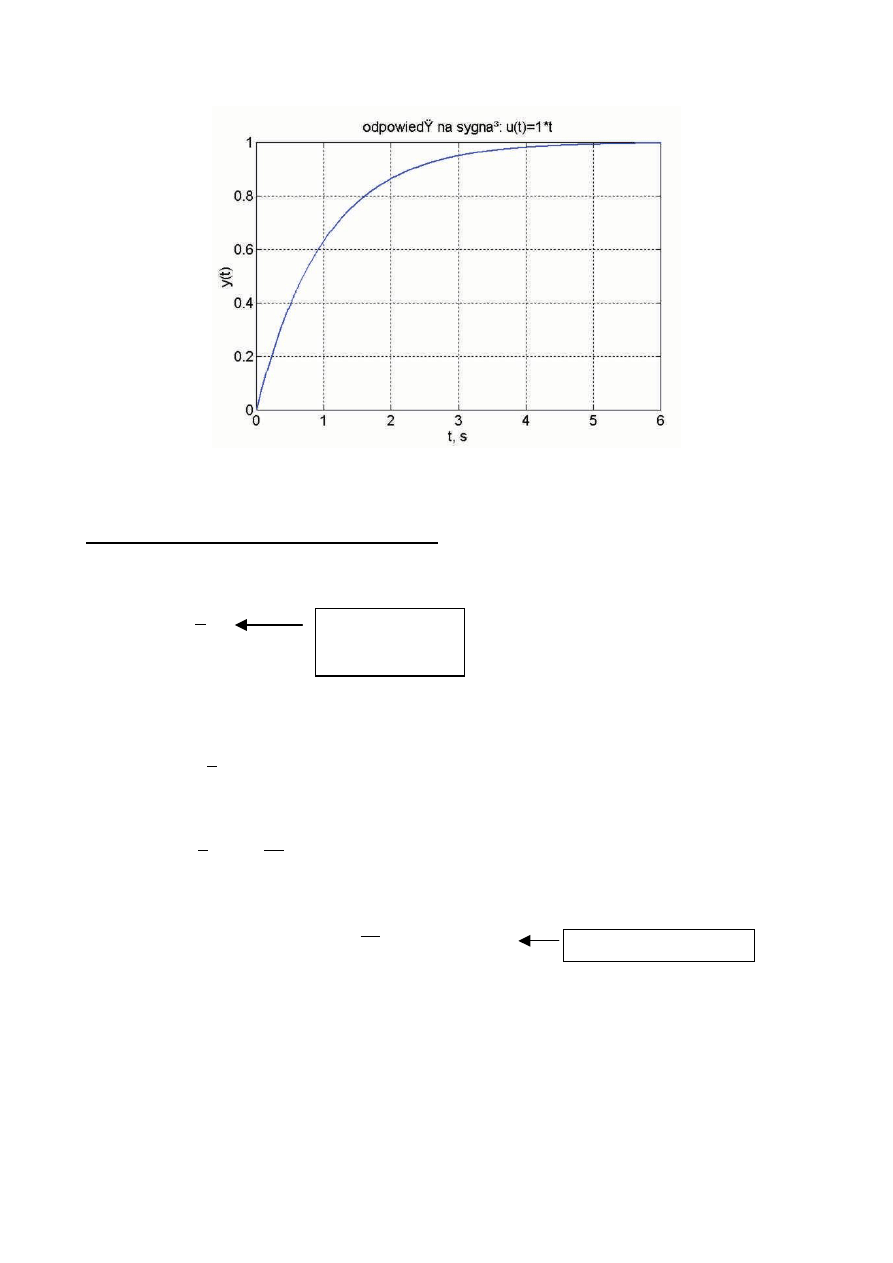
Rys. 3 Odpowiedź liniowa
Zadanie 2 Charakterystyki czasowe układów.
Problem:
Wyznaczyć odpowiedz skokową i impulsową obiektu różniczkowego z inercją (przy wyznaczeniu
odpowiedzi impulsowej rząd względny funkcji wymiernej , której orginał ma być wyznaczony wynosi zero ,
w związku z czym nie można bezpośrednio zastosować wzoru na transformatę odwrotną).
sT
sk
s
G
+
=
1
)
(
(1)
sT
sk
s
X
s
Y
s
G
+
=
=
1
)
(
)
(
)
(
(2)
1
;
1
=
= T
k
(3)
Odpowiedź skokowa
+
=
−
sT
sk
s
L
t
h
1
1
)
(
1
(4)
L
+
=
−
sT
k
L
t
h
1
)
(
1
(5)
Odpowiedź skokową
wyznacza się ze wzoru:
( )
( )
{
}
)
(
*
1
s
X
s
G
L
t
h
−
=
( )
( )
=
−
s
s
G
t
h
1
gdzie:
s
s
X
1
)
(
=
jest skokiem
jednostkowym
+
=
−
s
T
T
k
L
t
h
1
)
(
1
(6)
T
t
e
T
k
t
h
−
=
)
(
(7)
Odpowiedź impulsowa
+
=
−
sT
sk
L
t
g
1
)
(
1
(8)
+
−
+
=
−
sT
T
k
T
k
T
k
T
L
t
g
1
)
(
1
(9)
L
g
=
+
−
+
+
=
−
sT
T
k
sT
sT
T
k
L
t
g
1
1
1
)
(
1
(10)
+
−
=
−
sT
T
k
T
k
L
t
g
1
)
(
1
(11)
T
t
e
T
k
t
T
k
t
g
−
−
=
)
(
)
(
δ
(12)
)
)
(
(
)
(
T
t
e
t
T
k
t
g
−
−
=
δ
(13)
Odpowiedź liniowa
+
=
−
2
1
1
*
)
1
(
)
(
s
sT
sk
L
t
y
(14)
+
=
−
)
1
(
)
(
1
sT
s
k
L
t
y
(15)
+
=
−
)
1
(
)
(
1
s
T
sT
k
L
t
y
(16)
)
(t
δ
- impuls Diraca
natomiast
{ }
)
(
1
t
L
T
k
δ
=
−
{ }
T
t
e
L
sT
−
+
−
=
1
1
1
Odpowiedz liniowa oblicza się
ze wzoru
gdzie:
„a” jest to wartość stała, jest to
prędkość narastania sygnału
linowego
a
s
s
X
2
1
)
(
=
:
{
}
)
(
)
(
)
(
1
s
X
s
G
L
t
y
−
=
( )
=
−
2
1
)
(
s
s
aG
L
t
y
Odpowiedź impulsową
wyznacza się ze wzoru:
gdzie:
jest transformatą
impulsu Diraca
( )
{
}
)
(
*
)
(
1
s
X
s
G
L
t
g
−
=
( )
{
}
( )
{
}
s
G
t
s
G
L
t
g
1
1
)
(
1
*
)
(
−
−
=
1
)
(
=
s
X
Rozkładamy na ułamki proste
)
1
(
1
)
1
(
s
T
sT
s
T
B
sT
A
s
T
sT
k
+
⋅
+
+
=
+
(17)
BsT
s
T
A
k
+
+
=
)
1
(
(18)
T
A
s
BT
A
k
+
+
=
)
(
(19)
A
kT
T
A
k
=
⇒
=
(20)
T
A
B
A
BT
−
=
⇒
=
+
0
(21)
k
B
T
T
k
B
−
=
⇒
−
=
(22)
s
T
k
sT
kT
s
T
sT
k
+
−
=
+
1
)
1
(
(23)
)
1
(
)
(
T
t
T
t
e
k
ke
k
t
y
−
−
−
=
−
=
(24)
Rys. 1 Odpowiedź skokowa.
Rys. 2 Odpowiedź impulsowa.
Rys. 3 Odpowiedź liniowa
Zadanie 3 (charakterystyki czasowe układów)
Problem:
Obliczyć charakterystykę skokową i impulsową układu dynamicznego o transmitancji
s
s
G
5
)
(
=
Rozwiązanie:
Transformata wymuszenia skokowego
[ ]
.
1
)
(
s
t
L
=
1
Transformata odpowiedzi skokowej
.
5
)
(
1
)
(
2
s
s
G
s
s
H
=
=
Stosując odwrotne przekształcenie Laplace’a albo korzystając z tablicy transformat, łatwo znajdziemy
charakterystykę skokową
[
]
)
(
5
5
)
(
)
(
2
1
1
t
t
s
L
s
H
L
t
h
1
=
=
=
−
−
Transmitancja członu
całkującego
Patrz tablice transformat
dla t = 0[s]
h(t) = 0
dla t = 0,2[s]
h(t) = 1
dla t = 0,4[s]
h(t) = 2
dla t = 0,6[s]
h(t) = 3
dla t = 0,8[s]
h(t) = 4
dla t = 1[s]
h(t) = 5
Charakterystykę impulsową znajdziemy stosując wzór:
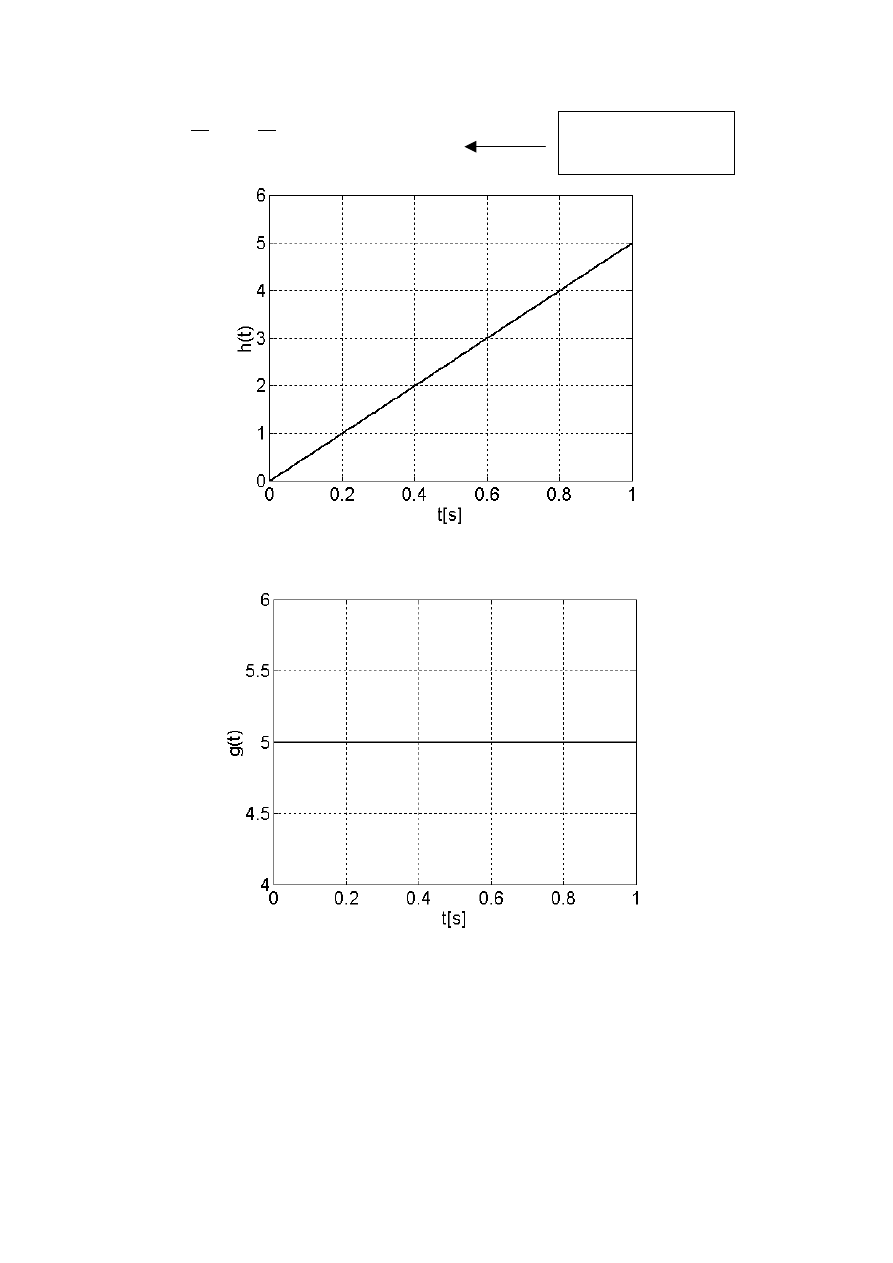
[
]
)
(
5
)
(
5
)
(
)
(
t
t
t
dt
d
t
h
dt
d
t
g
1
1
=
=
=
.
)
(
5
)
(
t
t
g
1
=
Charakterystyka impulsowa
jest pochodną odpowiedzi
skokowej.
Rys.5.1 Charakterystyka skokowa
Rys.5.2 Charakterystyka impulsowa
Zadanie 4 (charakterystyki czasowe układów)
Problem:
Obliczyć charakterystykę skokową i impulsową układu dynamicznego o transmitancji
)
2
3
)(
1
2
(
1
)
(
+
+
=
s
s
s
G
Rozwiązanie:
Transformata wymuszenia skokowego
[ ]
.
1
)
(
s
t
L
=
1
Transformata odpowiedzi skokowej
.
)
2
3
)(
1
2
(
1
)
(
1
)
(
+
+
=
=
s
s
s
s
G
s
s
H
Stosując odwrotne przekształcenie Laplace’a albo korzystając z tablicy transformat, łatwo znajdziemy
charakterystykę skokową
[
]
)
(
2
3
2
2
1
)
2
3
)(
1
2
(
1
)
(
)
(
3
2
2
1
1
1
t
e
e
s
s
s
L
s
H
L
t
h
t
t
1
−
−
=
+
+
=
=
−
−
−
−
dla t = 0[s]
h(t) = 0
dla t = 2[s]
h(t) = 0,160
dla t = 4[s]
h(t) = 0,334
dla t = 6[s]
h(t) = 0,428
dla t = 8[s]
h(t) = 0,471
dla t = 10[s]
h(t) = 0,488
dla t = 12[s]
h(t) = 0,496
Charakterystykę impulsową znajdziemy stosując wzór:
−
+
−
−
=
−
−
=
=
−
−
−
−
)
(
3
2
)
(
2
3
)
(
2
1
)
(
2
)
(
2
1
)
(
2
3
2
2
1
)
(
)
(
3
2
2
1
3
2
2
1
t
t
e
t
t
e
t
t
e
e
dt
d
t
h
dt
d
t
g
t
t
t
t
1
1
1
δ
δ
δ
.
dla t = 0[s]
g(t) = 0
dla t = 2[s]
g(t) = 0,104
dla t = 4[s]
g(t) = 0,066
dla t = 6[s]
g(t) = 0,031
Charakterystyka impulsowa
jest pochodną odpowiedzi
skokowej.
Transmitancja członu
inercyjnego II rzędu
b
a
e
b
e
a
b
a
ab
s
b
s
a
s
L
bt
at
≠
−
−
+
=
+
+
−
−
−
1
1
1
1
)
)(
(
1
1
Impuls Diraca
δ(t) jest
pochodna skoku
jednostkowego.
=
∞
≠
=
0
0
0
)
(
t
dla
t
dla
t
δ
dla t = 8[s]
g(t) = 0,013
dla t = 10[s]
g(t) = 0,005
dla t = 12[s]
g(t) = 0,002
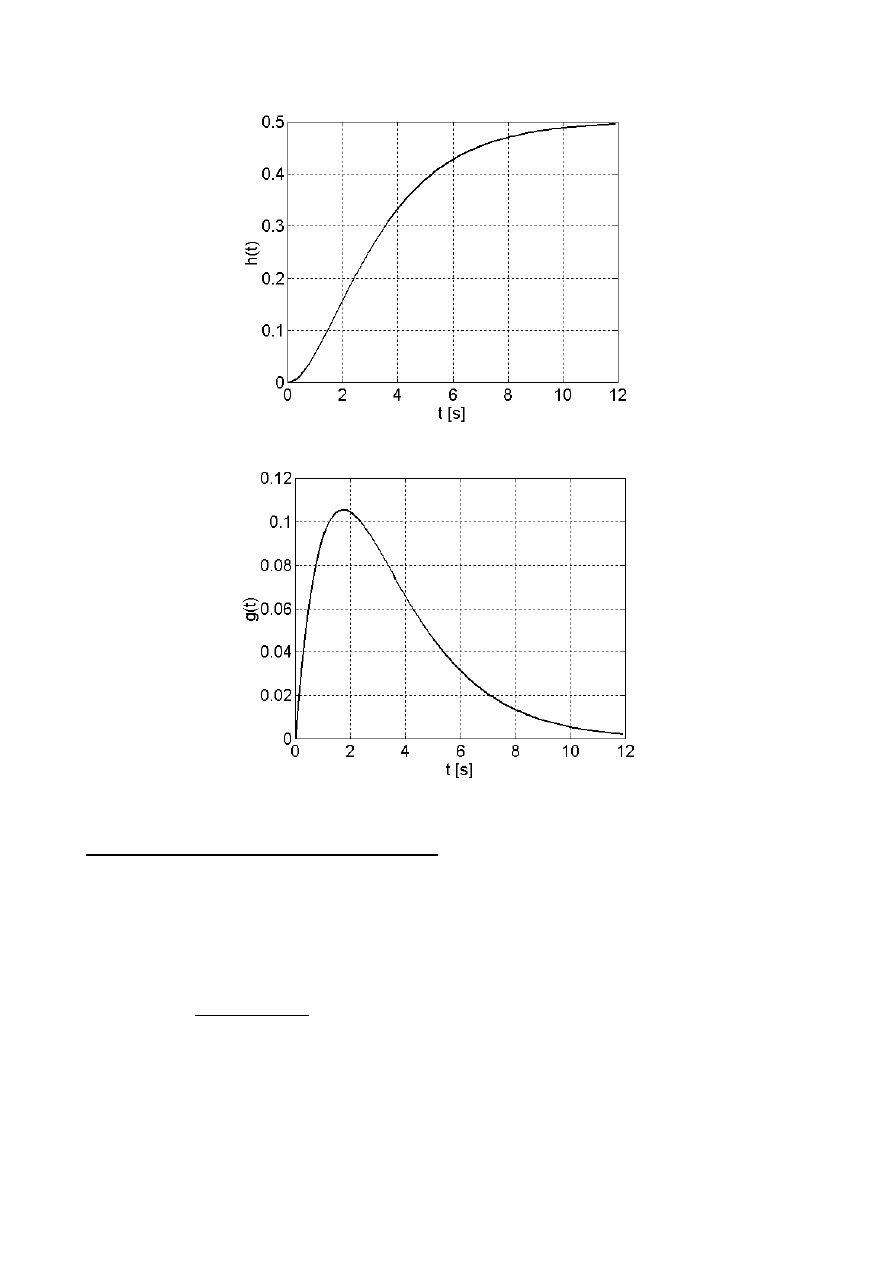
Rys.6.1 Charakterystyka skokowa
Rys.6.2 Charakterystyka impulsowa
Zadanie 5 (charakterystyki czasowe układów)
Problem:
Znaleźć zależność między parametrami charakterystyki czasowej elementu oscylacyjnego i
współczynnikami liczbowymi występującymi we wzorze na transmitancję operatorową.
1
2
1
)
(
2
2
+
+
=
Ts
s
T
s
F
ξ
.
Jak wyznaczyć k, T i
ξ na podstawie danej charakterystyki czasowej?

Rozwiązanie:
Równanie charakterystyki czasowej elementu oscylacyjnego dla wymuszenia skokowego x = x
0
1(t)
wynika z następujących przekształceń:
(
)
[
]
=
+
+
=
⋅
+
+
=
0
2
0
2
0
0
2
2
1
2
)
(
ϖ
δ
ξ
s
s
T
kx
s
x
Ts
s
T
k
s
Y
(
)
(
)
2
0
2
0
0
2
0
2
0
0
1
ϖ
δ
δ
ϖ
δ
ϖ
+
+
+
+
+
+
+
=
s
s
C
s
B
s
A
δ
0
+
ϖ
0
znajdujemy z warunku:
(
)
2
2
2
0
2
0
0
2
2
0
2
0
1
2
2
T
s
T
s
s
s
s
+
+
=
+
+
+
=
+
+
ξ
ϖ
δ
δ
ϖ
δ
T
ξ
δ
=
0
2
2
0
2
0
1
T
=
+
ϖ
δ
(
)
2
2
2
0
1
1
ξ
ϖ
−
=
T
Stałe A, B, C wynoszą
A = kx
0
2
0
0
0
0
1
ξ
ξ
ω
δ
−
−
=
−
=
kx
kx
B
0
kx
C
−
=
Równanie charakterystyki czasowej mając postać
⋅
−
⋅
−
−
=
⋅
−
⋅
−
t
e
t
e
kx
t
y
t
t
0
0
2
0
cos
sin
1
1
)
(
0
0
ϖ
ϖ
ξ
ξ
δ
δ
przekształcamy do postaci
+
−
−
=
−
)
sin(
1
1
)
(
0
2
0
0
ϕ
ω
ξ
δ
t
e
kx
t
y
t
kąt
ϕ
znajdujemy z warunku:
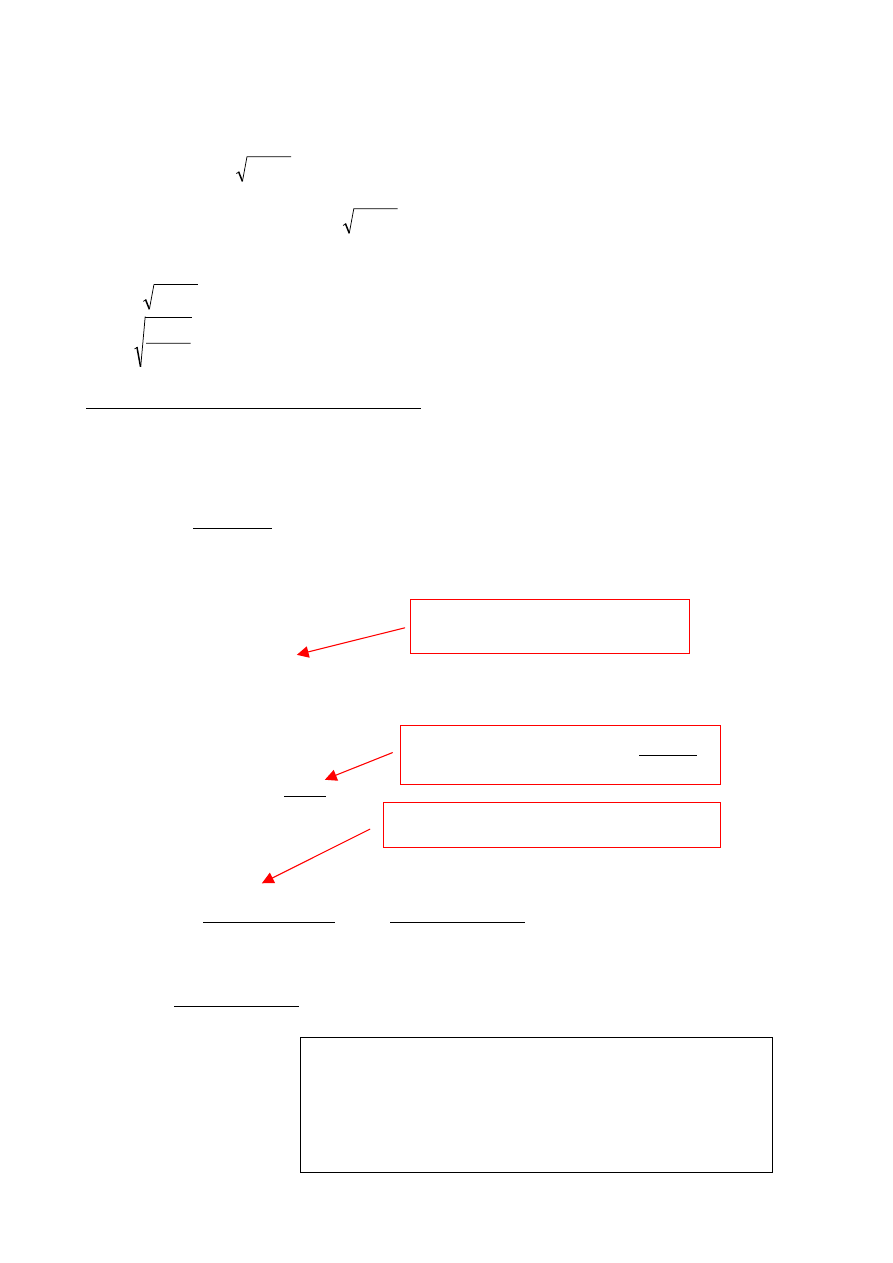
t
t
t
t
t
0
2
0
0
0
0
cos
1
sin
cos
sin
sin
cos
)
sin(
ϖ
ξ
ϖ
ξ
ϖ
ϕ
ϖ
ϕ
ϕ
ϖ
+
+
=
=
⋅
+
⋅
=
+
(
)
0
cos
1
sin
sin
)
(cos
0
2
0
=
⋅
−
−
+
−
t
t
ϖ
ξ
ϕ
ϖ
ξ
ϕ
ξ
ϕ
=
cos
1
≤
ξ
2
1
sin
ξ
ϕ
−
=
ξ
ξ
ϕ
2
1
−
=
tg
.
Zadanie 6 (
Charakterystyki czasowe układów)
Problem:
Wyznaczyć odpowiedź układu przy zerowych warunkach początkowych, jeżeli dana jest transformata G (s)
oraz sygnał wejściowy e(t).
( )
6
5
2
2
+
+
−
=
s
s
s
s
G
( )
)
(
1
)
sin(
5
t
t
t
e
=
Rozwiązanie:
Oznaczamy przez y (t) sygnał wejściowy.
Wykorzystując definicje transmitancji,
znajdujemy:
( )
( ) ( )
s
E
s
G
s
Y
⋅
=
( )
( ) ( )
{
s
E
s
G
L
t
y
1
−
=
}
(1)
Powstaje zależność
( )
{
}
1
5
)
sin(
5
2
1
+
=
=
−
s
t
L
s
E
(2)
Transformata Lapace’a
ω
ω
ω
+
=
−
2
1
)
(sin
s
t
L
Podstawiając równanie (2) oraz transmitancje od
definicji transmitancji otrzymujemy
Otrzymujemy równanie:
( )
(
)
(
)(
)
(
)
(
)(
)
(
)
(
)(
)(
)
+
−
+
=
−
−
+
−
=
−
+
+
−
=
−
−
−
1
1
2
5
1
2
2
2
5
1
6
5
2
5
1
2
1
2
2
1
s
s
s
L
s
s
s
s
L
s
s
s
s
L
t
y
(3)
Wykonujemy przekształcenia matematyczne
(
)(
2
1
2
x
x
x
x
a
c
bx
ax
−
−
=
+
+
)
przy czym x
1
i x
2
to pierwiastki rów. kwadratowego, po czym skracamy z licznik
z mianownikiem.
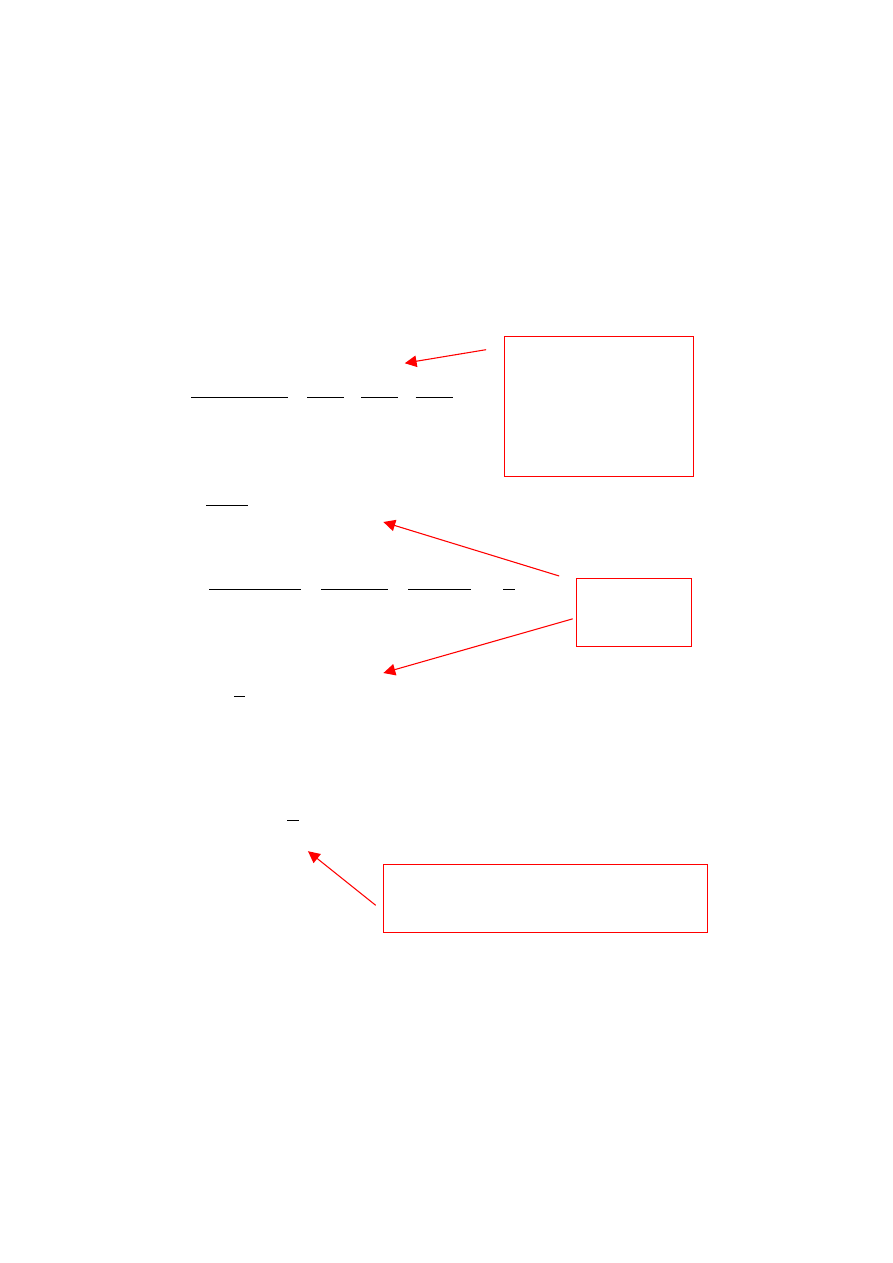
Równanie (4)
Rozkład funkcji na ułamki
proste w celu wykonania
odwrotnego
przekształcenia Lapace’a,
tabela z transformatami
została dodana do zadania
( ) ( )
(
)
j
s
k
j
s
k
s
k
s
s
s
Y
+
+
−
+
+
=
+
+
=
3
2
1
2
2
1
2
5
Równanie (5)
1
1
5
lim
2
2
1
=
+
=
−
→
s
k
s
Równanie (6)
(
)(
) (
)
(
)
(
)
j
j
j
j
j
s
s
j
s
2
1
2
1
1
2
2
5
2
2
5
2
5
lim
2
+
−
=
−
=
+
=
+
+
=
−
→
k
Postać
współczynników
rozkładu funkcji
Równanie (7)
(
)
j
k
k
2
1
2
1
*
3
2
−
−
=
=
Równanie (8)
( )
(
)
(
)
t
t
e
e
j
e
t
y
t
jt
t
sin
2
cos
2
1
2
1
Re
2
2
2
+
−
=
+
−
+
=
−
−
0
≥
t
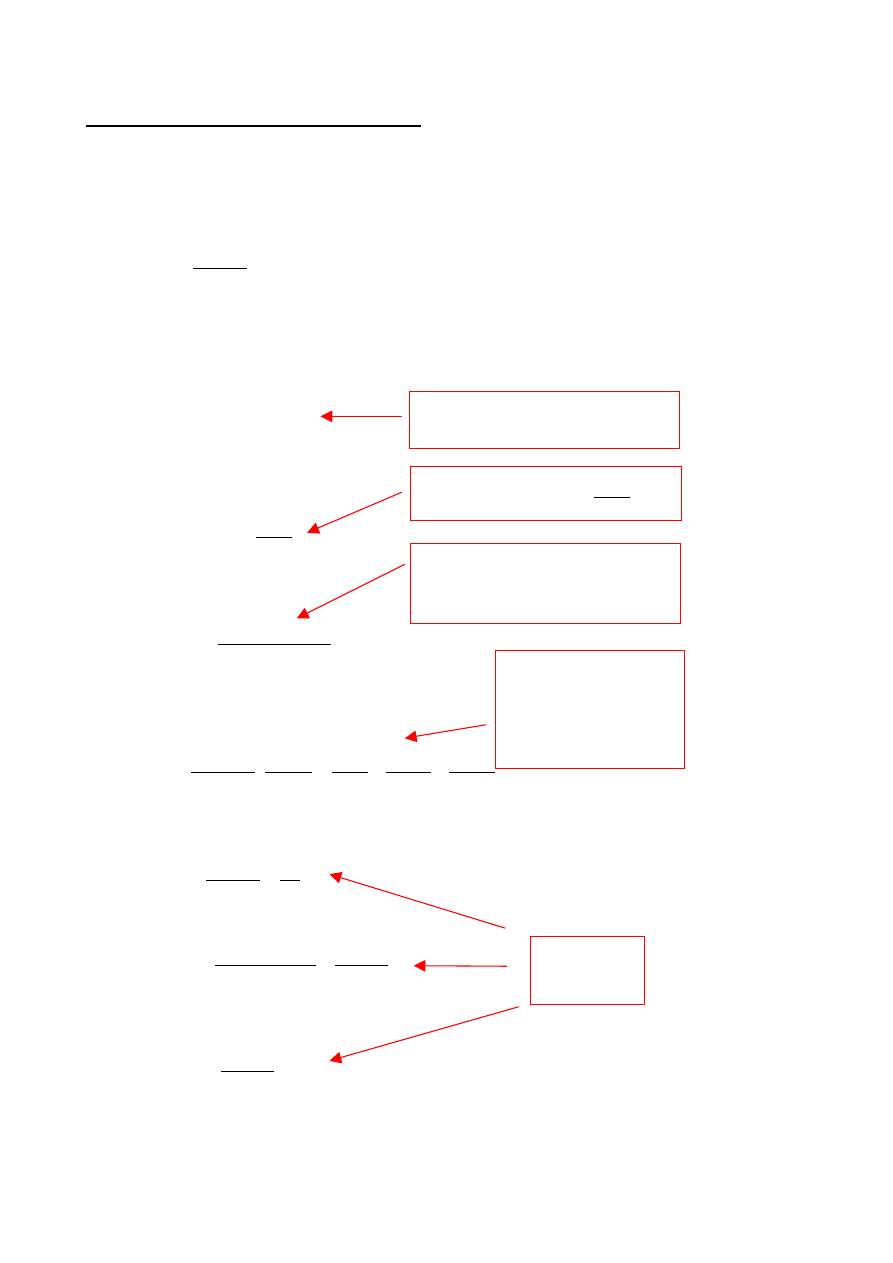
Odpowiedz układu przy zerowych warunkach
początkowych jest więc następująca, po
zastosowaniu transformaty Lapace’a
Zadanie 7 (
Charakterystyki czasowe układów)
Problem:
Wyznaczyć odpowiedź układu przy zerowych warunkach początkowych, jeżeli dana jest transformata G (s)
oraz sygnał wejściowy e(t).
( )
36
1
2
+
+
=
s
s
s
G
( )
( )
t
e
t
e
t
1
2
⋅
=
−
Rozwiązanie:
Oznaczamy przez y (t) sygnał wejściowy.
Równanie (1)
( )
( ) ( )
{
}
s
E
s
G
L
t
y
1
−
=
Powstaje zależność
Równanie (2)
( )
{ }
2
1
2
+
=
=
−
s
e
L
s
E
t
Równanie (3)
( )
(
)
(
)
+
⋅
+
+
=
−
2
36
1
2
1
s
s
s
L
t
y
Wykorzystując definicje transmitancji,
znajdujemy:
Transformata Lapace’a
2
1
−
=
s
e
at
Podstawiając równanie (2) oraz
transmitancje od definicji transmitancji
otrzymujemy
Równanie (4)
( )
(
)
(
)
6
6
2
2
1
36
1
3
2
1
2
j
s
k
j
s
k
s
k
s
s
s
s
Y
+
+
−
+
+
=
+
⋅
+
+
=
Rozkład funkcji na ułamki
proste w celu wykonania
odwrotnego
przekształcenia Lapace’a,
tabela z transformatami
została dodana do zadania
Równanie (5)
40
1
36
1
lim
2
2
1
=
+
+
=
−
→
s
s
k
s
Równanie (6)
Postać
współczynników
rozkładu funkcji
(
)(
)
240
19
3
6
2
1
lim
6
2
j
j
s
s
s
k
j
s
−
=
+
+
+
=
−
→
Równanie (7)
240
19
3
*
3
2
j
k
k
+
=
=
Równanie (8)

( )
+
+
−
=
+
+
−
=
−
−
t
t
e
e
j
e
t
y
t
j
t
6
sin
120
19
6
cos
40
1
40
1
240
19
3
Re
2
40
1
2
6
2
Odpowiedz układu przy zerowych warunkach
początkowych jest więc następująca, po
zastosowaniu transformaty Lapace’a
0
≥
t
Wyszukiwarka
Podobne podstrony:
Charakterystyki częstotliwościowe układów dynamicznych
L2 Badanie charakterystyk czasowych liniowych układów ciągłych
L2 Badanie charakterystyk czasowych liniowych układów ciągłych wartości elementów
CHARAKTERYSTYKI CZASOWE PODSTAWOWYCH OBIEKTÓW DYNAMICZNYCH
Charakterystyki czasowe podstawowych członów dynamicznych 7543789543
Charakterstyki czasowe podstawowych członów dynamicznych
Charakterstyki czasowe podstawowych członów dynamicznych 2
Charakterystyki czasowe JG
lab 1 pomiar charakter czasowych i cz stot
charakter czasowe nawigacja
2 Charakterystyki Czasowe
Identyfikacja Procesów Technologicznych, Identyfikacja charakterystyki statycznej obiektu dynamiczne
Identyfikacja Procesów Technologicznych, Identyfikacja charakterystyk statycznych obiektu dynamiczne
Narysować charakterystykę czasowo
03 ScilabControl, 2 ROK, 3ci SEMESTR, Modele ukladow dynamicznych, materialy na lab i cw
więcej podobnych podstron