Rozwiązywanie układów równań metodą Operacji elementarnych.

Dwa układy równań liniowych uważamy za równoważne wtedy i tylko wtedy jeżeli dowolne rozwiązanie jednego z nich
jest również rozwiązaniem drugiego układu. Operację elementarną na układzie równań nazywać będziemy, każde
przekształcenie układu równań w układ równoważny.
Rozróżniamy następujące operacje elementarne :
1. mnożenie dowolnego równania układu przez liczbę różną od zera,
2. Dodawanie do dowolnego równania układu liniowej kombinacji innych równań układu,
3. Przestawienie dwóch dowolnych równań układu,
4. Pominięcie dowolnego tożsamościowego równania układu.

Dokonując operacji elementarnej na układzie AX=B możemy go przekształcić w układ równoważny CX=D, gdzie macierz
C jest macierzą bazową.
Układ CX=D nazywamy postacią bazową układu AX=B.
Postać bazowa CX=D jest jednoznacznie wyznaczoną przez macierz blokową E=[ C

D ], którą otrzymujemy dokonując

operacji elementarnych na wierszach macierzy uzupełnionej (U) U=[ A

B]. Z postaci bazowej układu można natychmiast

odczytać rozwiązanie układu lub stwierdzić, że układ jest sprzeczny.
Jeżeli układ równań jest nieoznaczony (tzn. m < n) to wśród rozwiązań wyróżniamy tzw. Rozwiązanie bazowe.
Rozwiązaniem bazowym układu równań liniowych nazywamy takie rozwiązanie, w którym wszystkie zmienne niebazowe
są równe zeru.

x + y + z = 0
2x – y – z = - 3
4x – 5y – 3z = - 7

7

3

5

4

3

1

1

2

0

1

1

1

−

−

−

−

−

−

działamy na wierszach, musimy dojść do macierzy bazowej.

w1(-2) + w2
w1 (-4) + w3

7

7

9

0

3

3

3

0

0

1

1

1

−

−

−

−

−

−

w2

(-)

7

7

9

0

1

1

1

0

0

1

1

1

−

−

−

w2(-1) + w1
w2(9) + w3

2

2

0

0

1

1

1

0

1

0

0

1

−

w3 (

2

1

)

1

1

0

0

1

1

1

0

1

0

0

1

−

w3(-1) + w2

1

1

0

0

0

0

1

0

1

0

0

1

−

x = -1,

y = 0,

z = 1

Istnieje jedno rozwiązanie więc jest to układ oznaczony.

x + y + z + u = 0
-x + 2y – 2z + 3u = 0
2x + 3y + 3z + u = 0
3y – z + 4u = 1

1

4

1

3

0

0

1

3

3

2

0

3

2

2

1

0

1

1

1

1

−

−

−

w1 + w2; w1(-2) + w3

1

4

1

3

0

0

1

1

1

0

0

4

1

3

0

0

1

1

1

1

−

−

−

Układ sprzeczny ponieważ,

wyniki dwóch takich samych równań nie mogą mieć różnych wyników.

2x+3y+4z+ u=1
x+ y+ z+ u=0
-x+ 2z+3u=1
x+ 3y+6z+4u=2

2

4

6

3

1

1

3

2

0

1

0

1

1

1

1

1

1

4

3

2

−

zamieniamy miejscami w1 i w2

2

4

6

3

1

1

3

2

0

1

1

1

4

3

2

0

1

1

1

1

−

w1(-2) + w2
w1(1) + w3
w1(-1) + w4

2

3

5

2

0

1

4

3

1

0

1

1

2

1

0

0

1

1

1

1

−

w2(-1) + w1
w2(-1) + w3
w2(-2) + w4

0

5

1

0

0

0

5

1

0

0

1

1

2

1

0

1

2

1

0

1

−

−

−

w3 i w4 są równoważne, więc jeden z nich możemy usunąć (nie zmieni to układu)

0

5

1

0

0

1

1

2

1

0

1

2

1

0

1

−

−

−

w3(-2) + w2
w3 (1) + w1

0

5

1

0

0

1

11

0

1

0

1

7

0

0

1

−

−

niebazowe

Zmienne, które wchodzą w skład macierzy jednostkowej nazywamy zmiennymi bazowymi.

x + 7u = -1

x = -1 – 7u

y – 11u = 1

y = 1 + 11u

z + 5u = 0

z = -5u

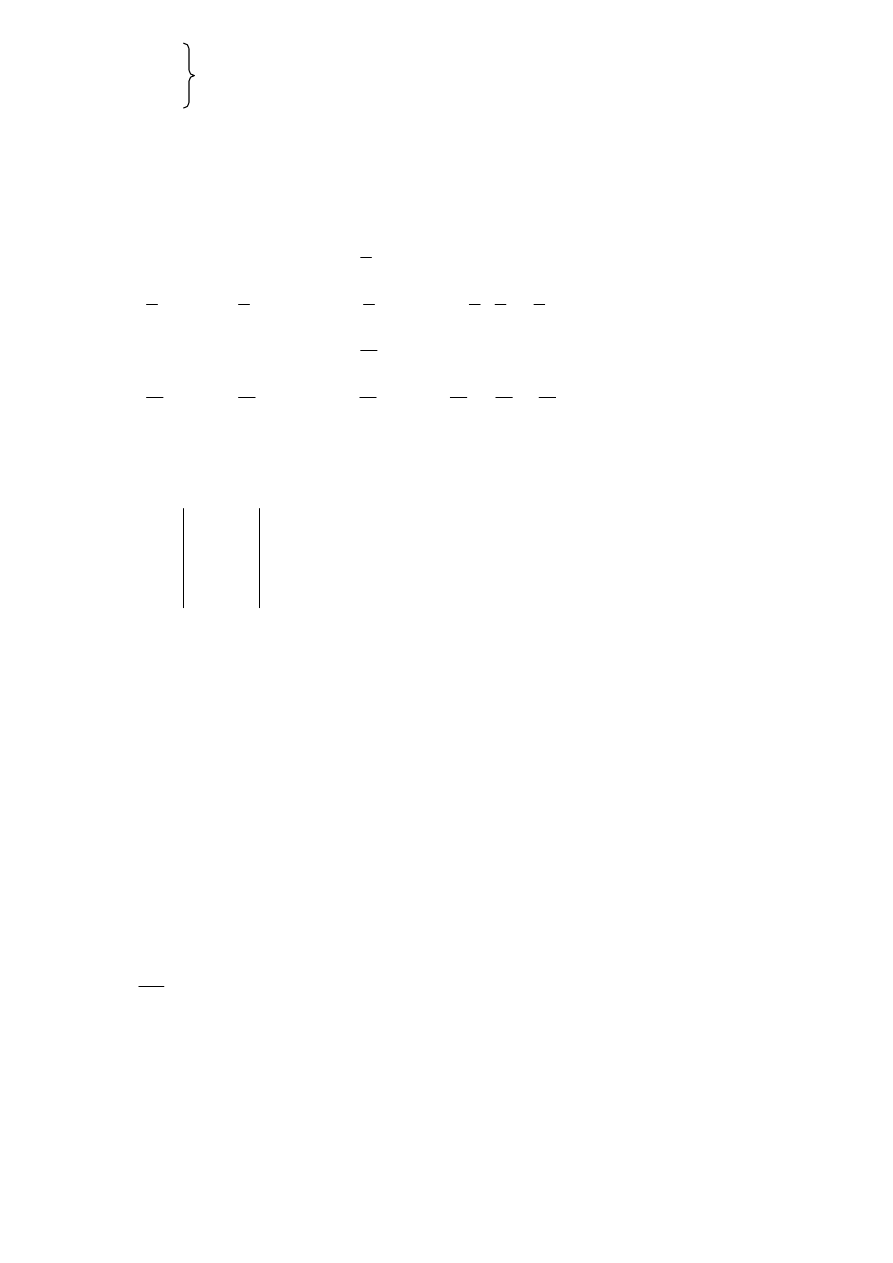
x=-1-7a
y=1+11a Rozwiązanie o g ó l n e
z=-5a
u=a

∈ R

Układ ma nieskończenie wiele rozwiązań więc jest układem nieoznaczonym.
Jeżeli za (a) podstawimy jakieś wartości to otrzymamy rozwiązanie szczegółowe.
Jeżeli za (a) podstawimy (0) zero, wtedy :

I.

x=-1, y=1, z=0 i oczywiście u=0

(-1, 1, 0, 0)

takie rozwiązanie nazywany rozwiązaniem bazowym (czyli przyrównujemy do zera)
Z układu możemy wyznaczyć więcej rozwiązań bazowych.

II.

Przyjmujemy,

że

x=0

czyli a=

7

1

−

więc :

y =

7

4

−

, z

=

7

5

,

u =

7

1

−

(

0,

7

4

−

,

7

5

,

7

1

−

)

III.

Przyjmujemy,

że

y=0

czyli a=

11

1

−

więc :

x =

11

4

−

, z

=

11

5

,

u =

11

1

−

(

11

4

−

, 0,

11

5

,

11

1

−

)

IV.

Przyjmujemy,

że

z=0

czyli

a=0

więc rozwiązanie jest takie samo jak w pierwszym (I) przypadku.

To znaczy, że mamy trzy różne rozwiązania bazowe.

3

6

5

1

0

0

2

4

3

0

1

0

1

2

1

0

0

1

b

w

w

b

w

w

b

w

w

v

u

z

y

x

Trzy zmienne bazowe i dwie zmienne niebazowe.
Przy wyznaczaniu wszystkich bazowych
x=b1-w1-w2
y=b2-w3-w4
z=b3-w5-w6
u=a

∈

R

możemy podstawić (0) zera za (a) i (b)

nie pytać się mnie co to znaczy

v=b

∈ R

Szczególny przypadek niejednorodnych układów równań – Układ Kramera.

Układ jest układem Kramera wtedy i tylko wtedy gdy :
1.

m = n

liczba równań jest taka sama jak liczba niewiadomych,

2. b

1

2

+... b

n

2

> 0

poszczególne muszą być różne od zera,

3.

R (A) = n

macierz (A) jest nieosobliwa (wyznacznik różny od zera)

Układ Kramera ma dokładnie jedno rozwiązanie, które można wyrazić wzorem :

x

k

=

w

w

k

,

dla

k = 1, ... , n

gdzie (w) jest wyznacznikiem macierzy (A), (w

k

) jest wyznacznikiem utworzonym z (w) przez zastąpienie k-tej kolumny,

kolumną wyrazów b

1

... b

n

Przykład :
x

1

+ x

2

+ x

3

= 0

2x

1

- x

2

- x

3

= -3

x

1

- x

2

+ x

3

= 0

R

k2(-1) + k3

R

= 1 + R

w1 + w2

1

1

1

1

1

2

1

1

1

−

−

−

2

1

1

0

1

2

0

1

1

−

−

1

2

1

1

−

= 1 + R

= 2 + R [3] = 2 + 1 =

0

3

1

1

3

W

1

-1 – 2 – 1 + 1 – 1 – 2 = -6

1

1

2

1

1

1

1

1

1

1

2

1

1

1

−

−

−

−

−

x=x1,

y=x2,

z=x3,

...

x

=

w

w

x

Wx =

=3+3 = 6

x1 = x =

1

1

3

1

1

0

1

1

0

1

1

3

1

1

0

−

−

−

−

−

−

−

w

w

x

=

6

6

−

=

-1

Wy =

= -3 + 3 = 0

x2 = y =

1

3

2

1

0

1

1

0

1

1

3

2

1

0

1

−

−

−

−

w

w

y

=

6

0

−

=

0

Wz =

= -3 –3 = -6

x1 = x =

1

1

3

1

1

0

1

1

0

1

1

3

1

1

0

−

−

−

−

−

−

−

w

w

x

=

6

6

=

1

Układ Kramera można rozwiązać przekształcając odpowiednio równanie macierzowe AX=B, mnożymy w tym celu
równanie macierzowe lewostronnie przez macierz odwrotną :

AX = B/A

-1

⇒

A

-1

⋅A⋅X = A

-1

⋅B

⇒

I

⋅X = A

-1

⋅B

⇒

X = A

-1

⋅B

Aby otrzymać rozwiązanie układu równań wystarczy znaleźć macierz odwrotną do macierzy (A) i pomnożyć ją
prawostronnie przez macierz (B)

A =

1

0

0

1

1

1

0

1

0

1

1

0

0

1

1

1

1

−

−

−

2

w1(-2)+w2, w1(-1)+w3

B =

0

3

0

−

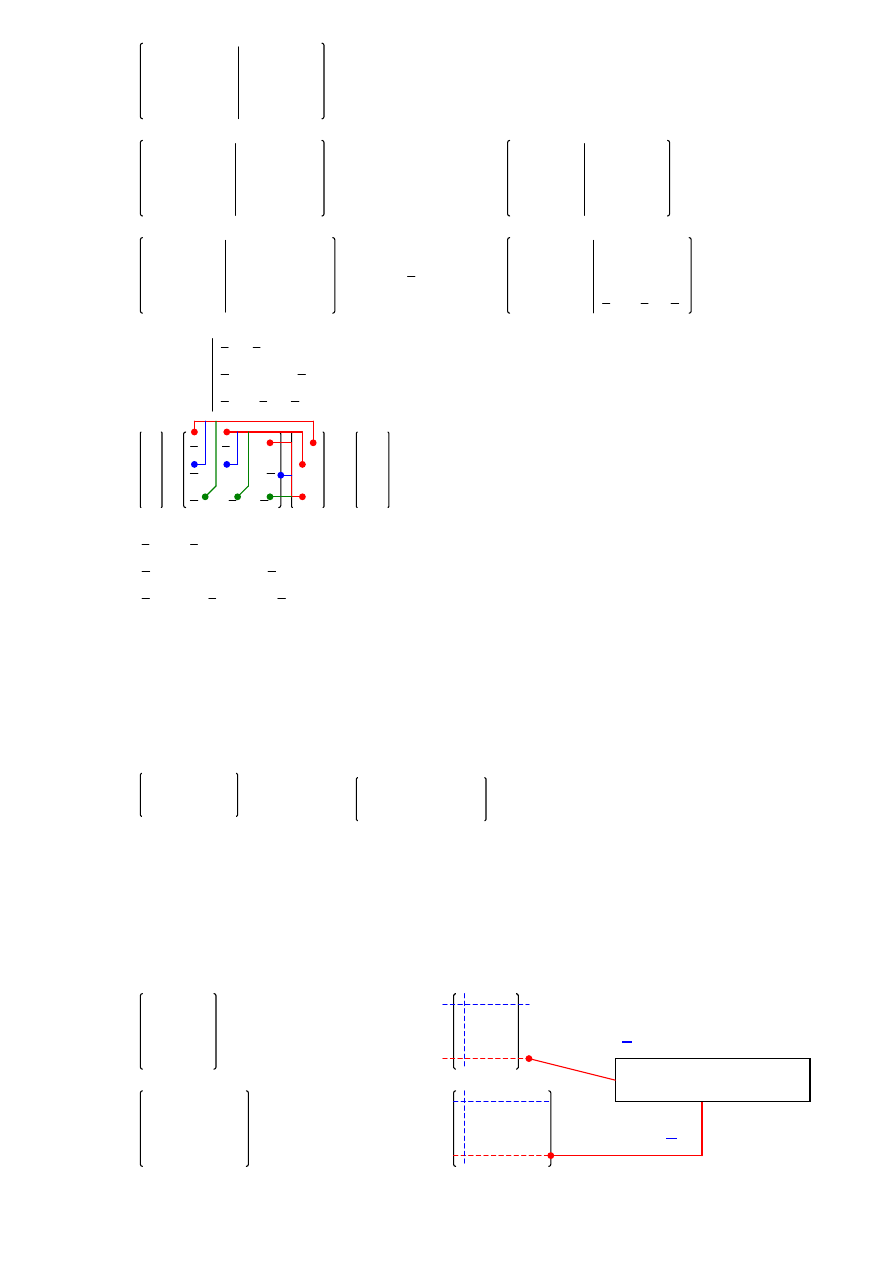
A =

1

0

1

0

1

2

0

0

0

w3(-1), w3(-1)+w2

0

2

0

3

3

1

1

1

1

−

−

−

−

−

A =

1

0

1

0

2

0

1

1

1

3

1

0

0

1

1

1

1

−

−

−

−

2

w2(-1)

A =

1

0

0

0

2

0

1

1

1

3

1

0

0

0

1

1

1

1

−

w2(-1)+w1,

w2(-2)+w3

A =

3

2

1

6

0

0

1

1

1

3

1

1

1

0

2

0

1

−

−

−

−

−

−

0

w3(-

6

1

)

A =

2

1

3

1

6

1

1

0

0

1

1

1

3

1

1

1

0

2

0

1

−

−

−

0

−

w3(2)+w1, w3(-3)+w2

A =

2

1

3

1

6

1

2

1

2

1

3

1

3

1

1

0

0

0

0

1

0

0

0

1

−

−

0

X =

=

3

2

1

x

x

x

2

1

3

1

6

1

2

1

2

1

3

1

3

1

0

0

−

−

=

0

3

0

−

1

0

1

−

x

1

=

3

1

⋅

0

+

3

1

⋅

(-3)

+ 0

⋅

0

= -1

x

2

=

2

1

⋅

0

+ 0

⋅

(-3)

+ (

2

1

−

)

⋅

0

= 0

x

3

=

6

1

⋅

0

+ (

3

1

−

)

⋅

(-3)

+

2

1

⋅

0

= 1

Ogólny przypadek niejednorodnych układów równań.
Układ równań możemy rozwiązać jeżeli nie jest sprzeczny.
Twierdzenie Kroneckera – Capelliego
Na to by układ nie był sprzeczny potrzeba i wystarcza, że rząd macierzy (A) jest równy rzędowi macierzy uzupełnionej
(czyli takiej z dodanymi wynikami równania).

R(A) = R(U)

A =

U =

mn

m

n

a

a

a

a

...

...

1

1

11

m

mn

m

n

n

b

a

a

b

a

a

...

...

1

1

11

Układ jest sprzeczny wtedy i tylko wtedy gdy R(A) jest różny od R(U), jeżeli układ nie jest sprzeczny to dokonując
pewnych przekształceń sprowadzamy go do postaci układu Kramera.
Z określenia układów jednorodnych wynika, że warunek R(A) = R(U) jest zawsze spełniony przez macierze (A) i (U). A
więc układ jednorodny nigdy nie jest sprzeczny.

x + y + z = 3
-2x + 2y + 3z = 3
-x + 3y + 4z = 6
1. Sprawdzamy rząd macierzy :

R =

w1(2)+w2, w1(1)+w3

R =

= 1 + R[ 4 5 ] =

4

3

1

3

2

2

1

1

1

−

−

5

4

0

5

4

0

1

1

1

2

2. Sprawdzamy rząd macierzy uzupełnionej :

R =

w1(2)+w2, w1(1)+w3

R =

= 1 + R[ 4 5 9 ] =

6

4

3

1

3

3

2

2

3

1

1

1

−

−

9

5

4

0

9

5

4

0

3

1

1

1

2

Skreślamy jedno, ponieważ są dwa
takie same (tożsamościowe)

Jeżeli rząd jest równy 2 to znaczy, że są dwa równania liniowo niezależne.

x + y = 3 – z
-2x + 2y = 3 – 3z

z = a

więc

x + y = 3 – a
-2x + 2y = 3 – 3a

W

2

2

1

1

−

= 2 – (-2) = 4

W

4

x =

w

w

x

Wx =

2

3

3

1

3

a

a

−

−

= 6 – 2a – 3 + 3a = 3 + a

x =

4

3

a

+

=

4

3

-

a

4

1

Wy =

a

a

3

3

2

3

1

−

−

−

= 3 – 3a + 6 – 2a = 9 – 5a

y =

w

w

y

=

4

5

9

a

−

=

4

9

-

a

4

5

z = a

∈ R

x+y+z+u=1
2x+3y–z–2u=1
3x–y+2z–3u=0
x–4y+3z–u=0

R(A) =

=

= 1+ R

=

1

3

4

1

3

2

1

3

2

1

3

2

1

1

1

1

−

−

−

−

−

−

4

0

7

2

5

0

3

1

1

0

4

3

1

1

1

1

−

−

−

−

−

−

4

7

2

5

3

1

1

4

3

−

−

−

−

−

−

w2(-3)+w1
w2(2)+w3

w1+w2
w1(-2)+w3
w1(-3)+w4

1 + R

1

= 2 + R [13 14] =

14

13

0

5

3

14

13

0

−

−

−

−

3

Macierz UZUPEŁNIONA

R =

=

= 1 + R

3

=

0

1

3

4

1

0

3

2

1

3

1

2

1

3

2

1

1

1

1

1

−

−

−

−

−

−

0

1

3

4

1

0

3

2

1

3

0

3

2

2

1

1

1

1

1

1

−

−

−

−

−

−

1

3

4

1

3

2

1

3

2

2

1

−

−

−

−

−

−

w1(-1)+w2

w1(-3)+w2
w1(-1)+w3

1 + R

= 2 + R

2

5

6

0

6

8

7

0

3

2

2

1

−

−

−

−

2

5

6

6

8

7

−

−

= 2 + R

2

5

6

0

7

11

−

−

= 3 + R[11 –7] =

4

W2(-3)+w1

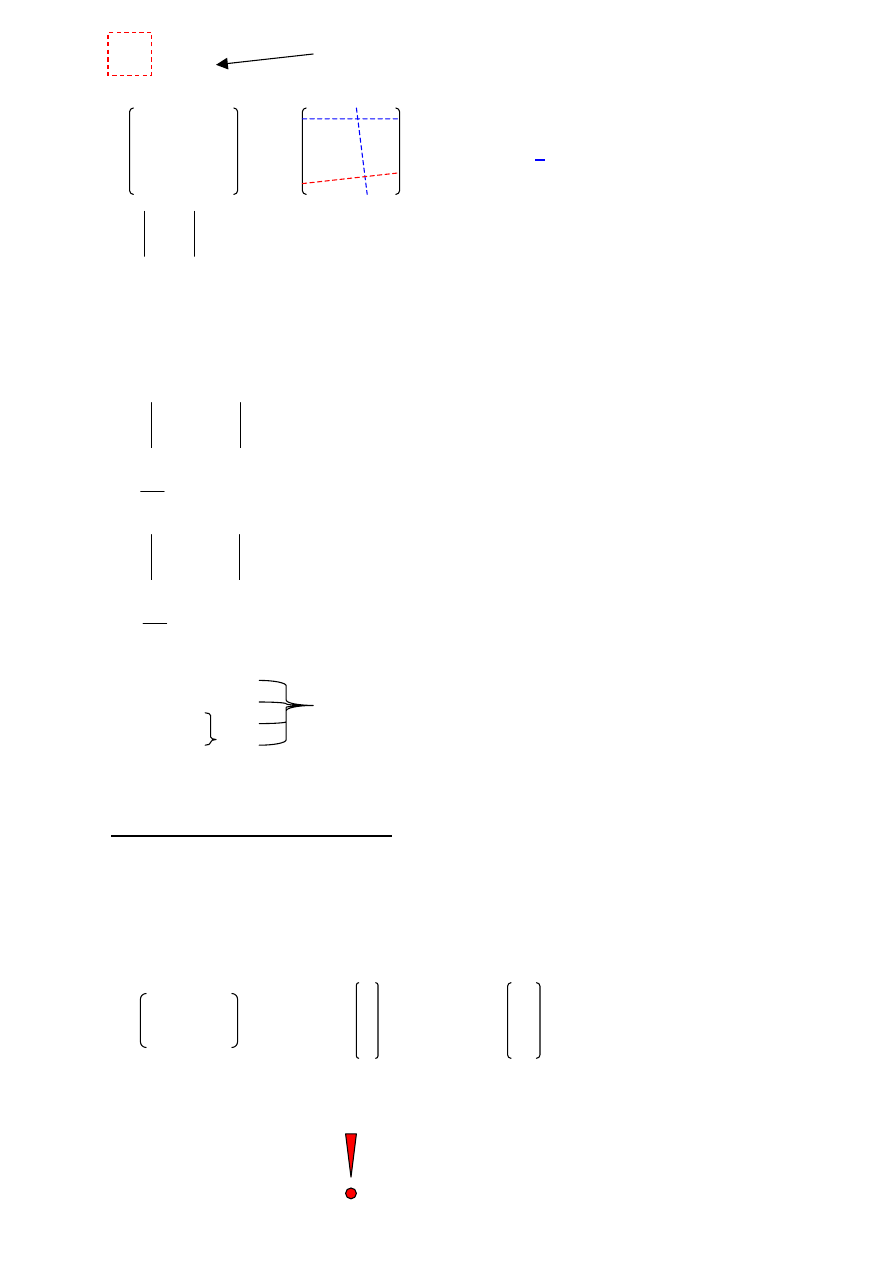
x + y + z + u=0
3x+4y–2z + u=0

Wszystkie zera to znaczy, że układ jest
jednorodny, więc nie jest sprzeczny
R(A) = R(U)

4x+5y– z +2u=0

R

= R

5

= 1 + R [5 6 3] =

2

1

5

4

1

2

4

3

1

1

1

1

−

−

3

0

6

5

3

0

6

1

1

1

1

2

w1+w3
w1(2)+

2

W =

4

3

1

1

= 4 – 3 = 1

x + y = –z – u
3x+4y= 2z – u

x + y = –a – b

gdzie : z = a

∈ R

3x+4y = 2a – b

u = b

∈ R

Wx =

4

2

1

b

a

b

a

−

−

−

= –4a – 4b – 2a + b = –6a – 3b

W

Wx

x

=

=

–6a – 3b

Wy =

b

a

b

a

−

−

−

2

3

1

= 2a – b + 3a + 3b = 5a + 2b

W

Wy

y

=

=

5a + 2b

x = –6a – 3b

y = 5a + 2b

każdy z każdym

z = a

u = b

∈ R

UKŁAD NIERÓWNOŚCI LINIOWEJ

Ogólna postać nierówności liniowej jest następująca :

I.

a

11

x

1

+ ... + a

1n

x

n

∆ b

1

a

m1

x

1

+ ... + a

mn

x

n

∆ b

m

Gdzie zamiast symbolu

∆ występuje jeden ze znaków <, ≤, >, ≥

Układ powyższy można zapisać w postaci macierzowej
A X

∆ B

mn

m

n

a

a

a

a

A

...

...

1

1

11

=

n

x

x

X

M

1

=

m

b

b

B

M

1

=

Rozwiązaniem układu nierówności nazywamy dowolny układ n-liczb spełniający wszystkie nierówności układu.
Układ nierówności jest sprzeczny jeżeli nie ma rozwiązania.
Metoda rozwiązywania układu nierówności o dowolnej liczbie niewiadomych.
Układ m-nierówności liniowych o n-niewiadomych

x

1

, x

2

, ... , x

n

postaci

II.

a

11

x

1

+ ... + a

1n

x

n

≤ b

1

a

21

x

1

+ ... + a

2n

x

n

≤ b

2

...

a

m1

x

1

+ ... + a

mn

x

n

≤ b

m

Weźmy teraz pod uwagę układ m-równań o (n + m) niewiadomych x

1

, x

2

, ... , x

n

; z

1

, z

2

, ... , z

m

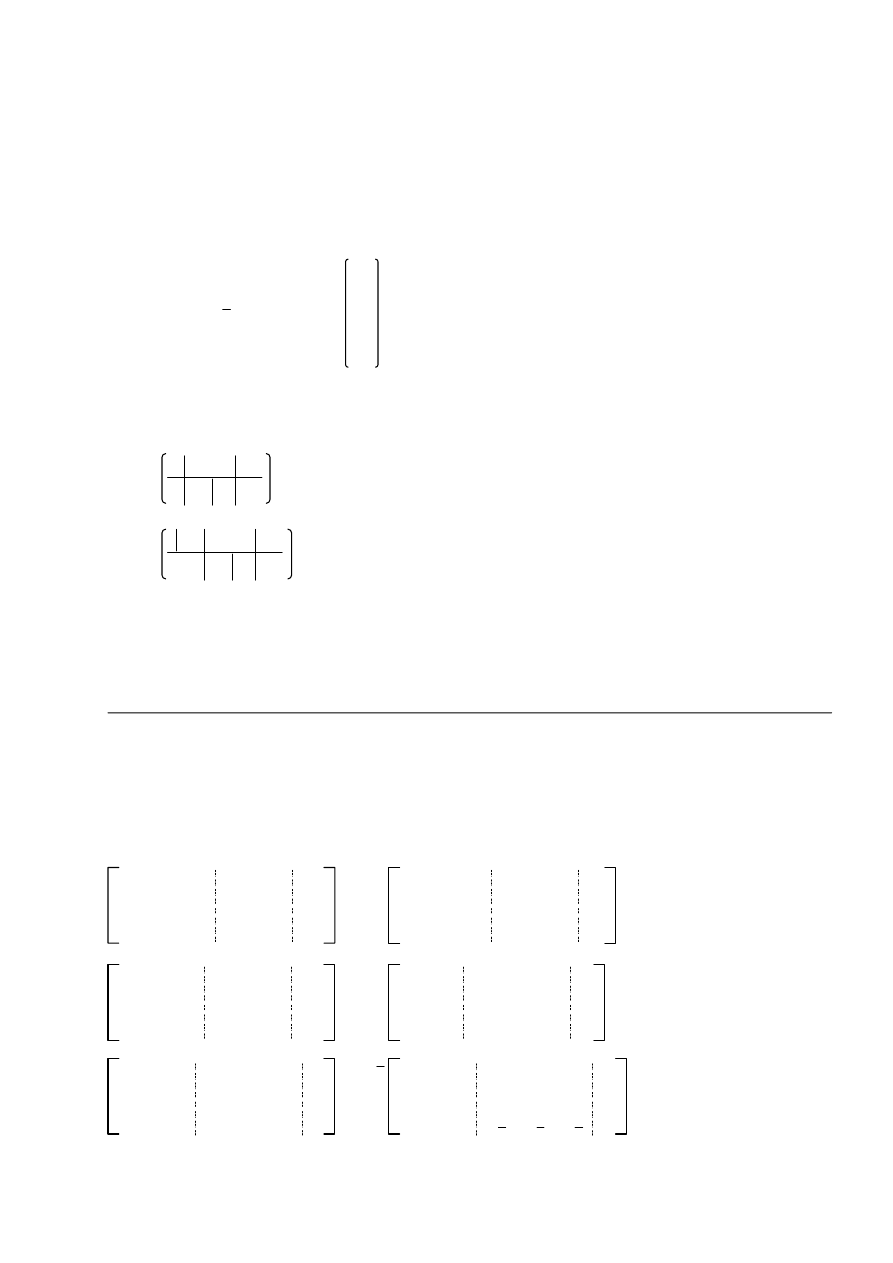
III.

a

11

x

1

+ a

12

x

2

... + a

1n

x

n

+ z

1

= b

1

a

21

x

1

+ a

22

x

2

... + a

2n

x

n

+ z

2

= b

2

...

a

m1

x

1

+ a

m2

x

2

... + a

mn

x

n

+z

m

= b

m

Okazuje się, że każdemu rozwiązaniu

,

...

układu nierówności ( II. ) odpowiada określone rozwiązanie

o

1

x

o

2

x

o

n

x

o

1

x

,

...

;

,

...

układu równań ( III. ) przy czym z

o

2

x

o

n

x

o

1

z

o

2

z

o

m

z

1

, z

2

, ... , z

m

≥ 0

Układy ( II. ) i ( III. ) możemy zapisać w postaci macierzowej.

IV.

A X ≤ B

V.

[ A

 I ] [

z

x

] = B

; z

≥ 0

m

z

z

z

z

M

2

1

=

Chcąc rozwiązać układ nierówności ( IV. ) rozwiązujemy odpowiadający mu układ równań ( V. )
Macierz uzupełnioną tego układu równań liniowych ma postać [ A

IB ]. Dokonując przekształceń elementarnych na

wierszach tych macierzy sprowadzamy ją do jednej z następujących postaci.
VI.

[ I

RC

1

]

VII.

2

'

2

1

1

0

C

I

R

C

R

I

VIII.

2

'

2

1

1

3

0

C

I

R

C

R

R

I

Z których otrzymujemy rozwiązania po skorzystaniu z poniższych twierdzeń :
1. Jeżeli macierz uzupełnioną układu równań (V.) sprowadzimy do postaci (VI.) to układ nierówności liniowych (IV.)

posiada rozwiązanie.

2. Jeżeli macierz uzupełnioną układu równań (V.) sprowadzimy do postaci (VI.) lub (VII.) to układ nierówności (IV.)

posiada rozwiązanie

⇔ gdy układ równań o macierzy uzupełnionej w postaci [ R

2

I’C

2

] posiada przynajmniej

jedno nieujemne rozwiązanie bazowe.

x

1

+ x

2

+ x

3

≥ 0

/

⋅(-1)

2x

1

– x

2

– x

3

≤ –3

x

1

– x

2

+ x

3

≥ 0

/

⋅(-1)

–x

1

– x

2

– x

3

≤ 0

⇒ –x

1

– x

2

– x

3

+ z

1

= 0

2x

1

– x

2

– x

3

≤ –3

⇒ 2x

1

– x

2

– x

3

+ z

2

= –3

–x

1

+ x

2

– x

3

≤ 0

⇒ –x

1

+ x

2

– x

3

+ z

3

= 0

0

1

0

0

1

1

1

3

0

1

0

1

1

2

0

0

0

1

1

1

1

−

−

−

−

−

−

−

−

=

0

1

0

1

0

2

0

3

0

1

2

3

3

0

0

0

0

1

1

1

1

−

−

−

−

−

w1(-1)
w1(-2)+w2
w1+w3

w2+w3

0

1

0

1

0

2

0

3

1

1

1

3

1

0

0

0

0

1

1

1

1

−

−

−

−

−

=

0

1

0

1

0

2

1

3

1

1

1

3

0

0

0

1

1

1

1

−

−

−

−

1

0

−

w2(-1)

w2(-1)+w1
w2(-2)+w3

0

3

2

1

6

0

0

3

1

1

1

3

1

0

3

1

1

0

2

0

1

−

−

−

−

−

−

=

1

1

0

0

3

1

1

1

3

3

1

1

0

2

0

1

2

1

3

1

6

1

−

−

−

−

−

−

1

0

−

−

)

(

3

6

1

−

w

w3(2)+w1
w3(-3)+w2

1

1

0

0

0

0

0

1

0

1

0

0

0

1

2

1

6

1

2

1

2

1

3

1

3

1

−

−

−

−

−

−

3

1

x

1

–

3

1

z

1

+

3

1

z

2

= – 1

x

2

–

2

1

z

1

+ +

2

1

z

3

= 0

x

3

–

6

1

z

1

–

3

1

z

2

–

2

1

z

3

= 1

x

1

= – 1 +

3

1

z

1

–

3

1

z

2

z

1

= a

≥ 0

x

2

=

2

1

z

1

–

2

1

z

3

z

2

= b

≥ 0

x

3

= 1 +

6

1

z

1

+

3

1

z

2

+

2

1

z

3

z

3

= c

≥ 0

x

1

= – 1 +

3

1

a –

3

1

b

x

2

=

2

1

a –

2

1

c

x

3

= 1 +

6

1

a +

3

1

b +

2

1

c

x

1

+ x

2

+ x

3

≥ 3

/

⋅(-1)

– x

1

– x

2

– x

3

≤ 3

x

1

+ 2x

2

+ 3x

3

≤ 8

x

1

+ 2x

2

+ 3x

3

≤ 8

Znaki nierówności muszą
mieć ten sam kierunek

x

2

+ 2x

3

≤ 5

x

2

+ 2x

3

≤ 5

– x

1

– x

2

– x

3

+ z

1

≤ 3

x

1

+ 2x

2

+ 3x

3

+ z

2

≤ 8

x

2

+ 2x

3

+ z

3

≤ 5

5

1

0

0

2

1

0

8

0

1

0

3

2

1

3

0

0

1

1

1

1

−

−

−

−

=

5

1

0

0

2

1

0

8

0

1

0

3

2

1

3

0

0

1

1

1

1

−

w1(-1)

w1(-1)+w2

5

1

0

0

2

1

0

8

0

1

1

2

1

0

3

0

0

1

1

1

1

−

=

0

1

1

1

0

0

0

5

0

1

1

2

1

0

2

0

1

2

1

0

1

−

−

−

−

−

−

w2(-1)+w1
w2(-1)+w3

Szukamy nieujemnych
rozwiązań tej macierzy

Jeżeli tej macierzy byśmy nie znaleźli to powiemy, że ten układ
nierówności jest sprzeczny

–z

1

– z

2

+ z

3

= 0

z

3

= z

1

+ z

2

z

3

= 0

( 0, 0, 0 )

x

1

– x

3

– 2z

1

– z

2

= -2

x

2

+ 2x

3

+z

1

+ z

2

= 5

x

1

= -2 + x

3

+2z

1

+z

2

x

2

= 5 – 2x

3

– z

1

– z

2

x

1

= – 2 + a

Układ nierówności może być :

-

sprzeczny (nie ma rozwiązania)

-

oznaczony (ma jedno rozwiązanie)

-

nieoznaczony (ma wiele rozwiązań)

x

2

= 5 – 2a – b

1

– b

2

z

1

= b

1

z

2

= b

2

≥ 0

z

3

= b

3

CIĄGI LICZBOWE I ICH GRANICE

Ciągiem nieskończonym lub po prostu ciągiem nazywamy odwzorowanie zbioru liczb naturalnych (y), jeżeli zbiór (y)
będzie zbiorem liczb rzeczywistych lub jego podzbiorem to będziemy mówić o ciągu liczbowym

a : N

→(y)

y = R, y

⊂ R

liczby

rzeczy

Funkcja czyli odwzorowanie, przyporządkowanie
pewnym liczbom pewne argumenty f : x(y)

a

n

– oznacza

n-ty wyraz ciągu

lub nazywa się go

wyrazem ogólnym ciągu

.

Pierwszy sposób określania ciągu
(a

n

), {a

n

} a

1

, a

2

, a

3

, a

4

, ... a

n

Drugi sposób określenia ciągu – Podanie wzoru
a

n

= 2n + 1,

n = 1, 2, 3, ...

Trzeci sposób określania ciągu – wypisujemy kilka początkowych argumentów, a następne wyrazy określamy za pomocą
wyrazów poprzedzających – sposób indukcyjny
a

1

= 1, a

n+1

= a

n

+1,

n = 1, 2, ...

Własności ciągu :
Jeżeli dla każdego (n) wyraz (a

n+1

> a

1

) to taki ciąg nazywamy rosnącym.

N

n

∈

∧

a

n+1

> a

n

-

rosnący

N

n

∈

∧

a

n+1

< a

n

- malejący

N

n

∈

∧

a

n+1

≥ a

n

- nie malejący

N

n

∈

∧

a

n+1

≤ a

n

- nie rosnący

A

∨

N

n

∈

∧

a

n

≤ A

- ciąg ograniczony z góry

A

∨

N

n

∈

∧

a

n

≥ A

- ciąg ograniczony z dołu

Badamy monotoniczność ciągu :

a

n

= 1 –

n

1

∧

a

N

n

∈

n+1

> a

1

a

n+1

– a

1

> 0

a

n+1

= 1 –

1

1

+

n

a

n+1

– a

1