Obliczanie granic ciągów liczbowych

Poniżej podamy sposób obliczania typowych granic ciągów liczbowych. Wszystkie rachunki
wykonamy za pomocą kalkulatora ClassPad 300 Plus.

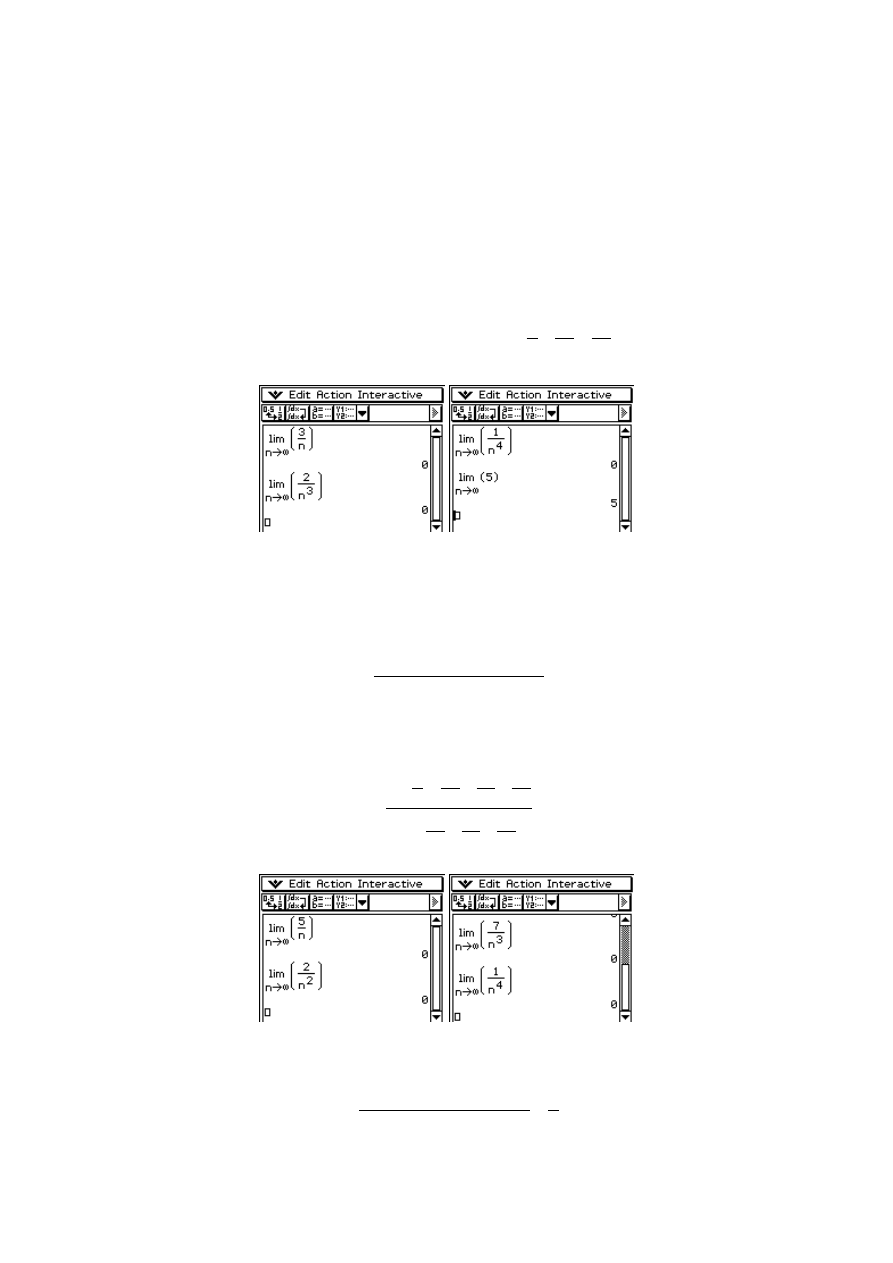
Przykład 1. Obliczyć granicę





1

2

3

5

lim

3

4











n

n

n

n

Jest to granica z wielomianu; wyciągamy największą potęgę przed nawias:







































4

3

4

3

4

1

2

3

5

lim

1

2

3

5

lim

n

n

n

n

n

n

n

n

n

Tak więc, wyrażenie w nawiasie dąży do 5, zaś wyrażenie przed nawiasem dąży do



, czyli



















1

2

3

5

lim

3

4

n

n

n

n

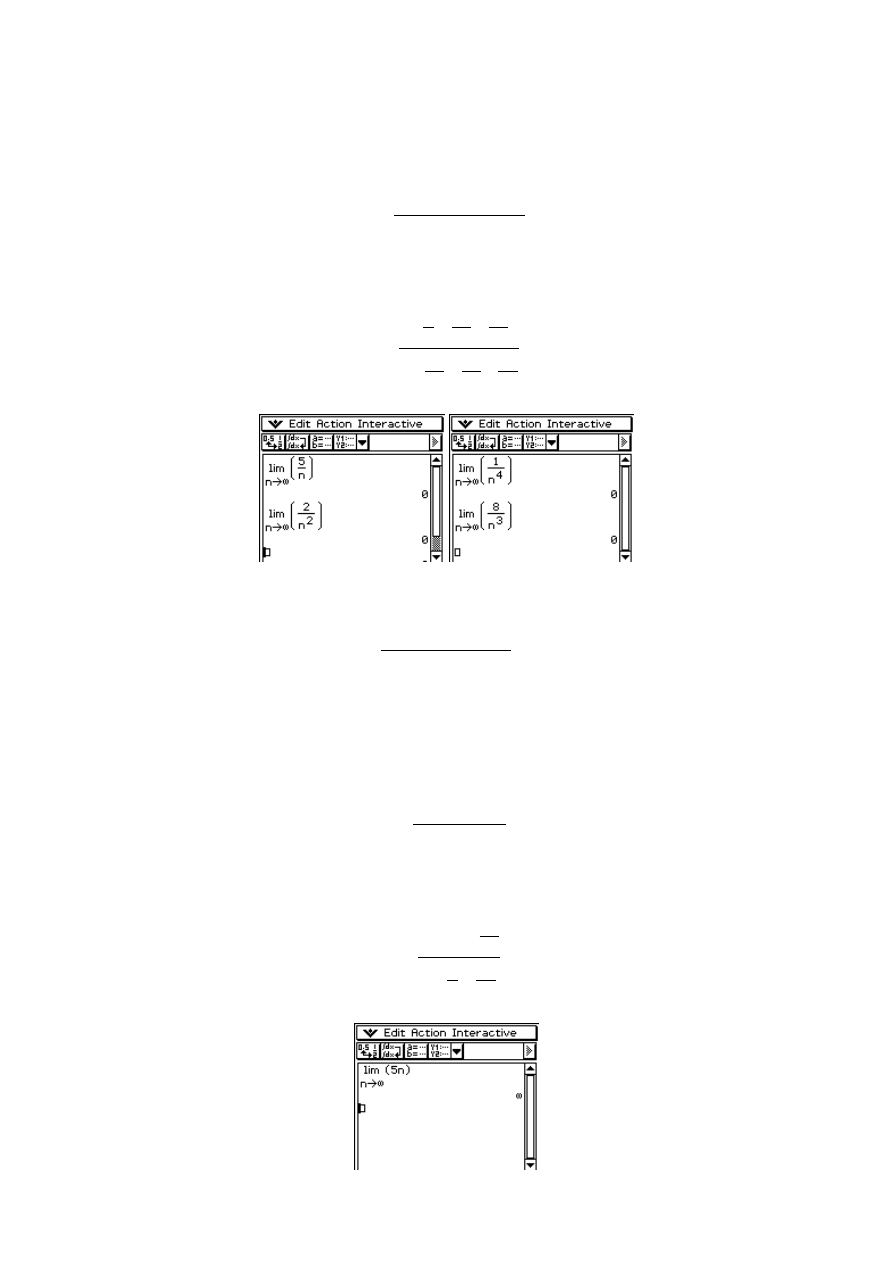
Przykład 2. Obliczyć granicę

11

8

2

3

1

7

2

5

2

lim

2

4

2

3

4



















n

n

n

n

n

n

n

n

W przypadku ilorazu dwóch wielomianów, dzielimy licznik i mianownik przez najwyższą potęgę
zmiennej z mianownika, czyli w tym przypadku przez

4

n

:

4

3

2

4

3

2

11

8

2

3

1

7

2

5

2

lim

n

n

n

n

n

n

n

n



















Tak więc, wszystkie składniki licznika za wyjątkiem 2 i wszystkie składniki z mianownika za
wyjątkiem 3 dążą do zera, czyli

3

2

11

8

2

3

1

7

2

5

2

lim

2

4

2

3

4





















n

n

n

n

n

n

n

n

Uwaga.

Łatwo zauważyć, że jeżeli licznik i mianownik są wielomianami tego samego stopnia,

to granica jest ilorazem współczynników przy najwyższych potęgach wielomianu z licznika i
wielomianu z mianownika.

Przykład 3. Obliczyć granicę

2

8

2

3

1

2

5

lim

2

4

2

3

















n

n

n

n

n

n

W przypadku ilorazu dwóch wielomianów, dzielimy licznik i mianownik przez najwyższą potęgę
zmiennej z mianownika, czyli w tym przypadku przez

4

n

:

4

3

2

4

2

2

8

2

3

1

2

5

lim

n

n

n

n

n

n

n

















Tak więc, wszystkie składniki licznika i wszystkie składniki z mianownika za wyjątkiem 3 dążą do
zera, czyli

0

2

8

2

3

1

2

5

lim

2

4

2

3



















n

n

n

n

n

n

Uwaga.

Łatwo zauważyć, że jeżeli licznik jest wielomianem stopnia niższego niż mianownik,

to granica jest zawsze równa zero.

Przykład 4. Obliczyć granicę

2

8

3

1

2

5

lim

2

2

3













n

n

n

n

n

W przypadku ilorazu dwóch wielomianów, dzielimy licznik i mianownik przez najwyższą potęgę
zmiennej z mianownika, czyli w tym przypadku przez

2

n

:

2

2

2

8

3

1

2

5

lim

n

n

n

n

n













Tak więc, licznik dąży do



i wszystkie składniki z mianownika za wyjątkiem 3 dążą do zera, czyli

















2

8

3

1

2

5

lim

2

2

3

n

n

n

n

n

Uwaga.

Łatwo zauważyć, że jeżeli licznik jest wielomianem stopnia wyższego niż mianownik,

to granica jest zawsze równa



ze znakiem plus lub minus, który zależy od znaku ilorazu

współczynników przy najwyższych potęgach licznika i mianownika.



















2

8

3

1

2

5

lim

2

2

3

n

n

n

n

n



















2

8

3

1

2

5

lim

2

2

3

n

n

n

n

n





















2

8

3

1

2

5

lim

2

2

3

n

n

n

n

n

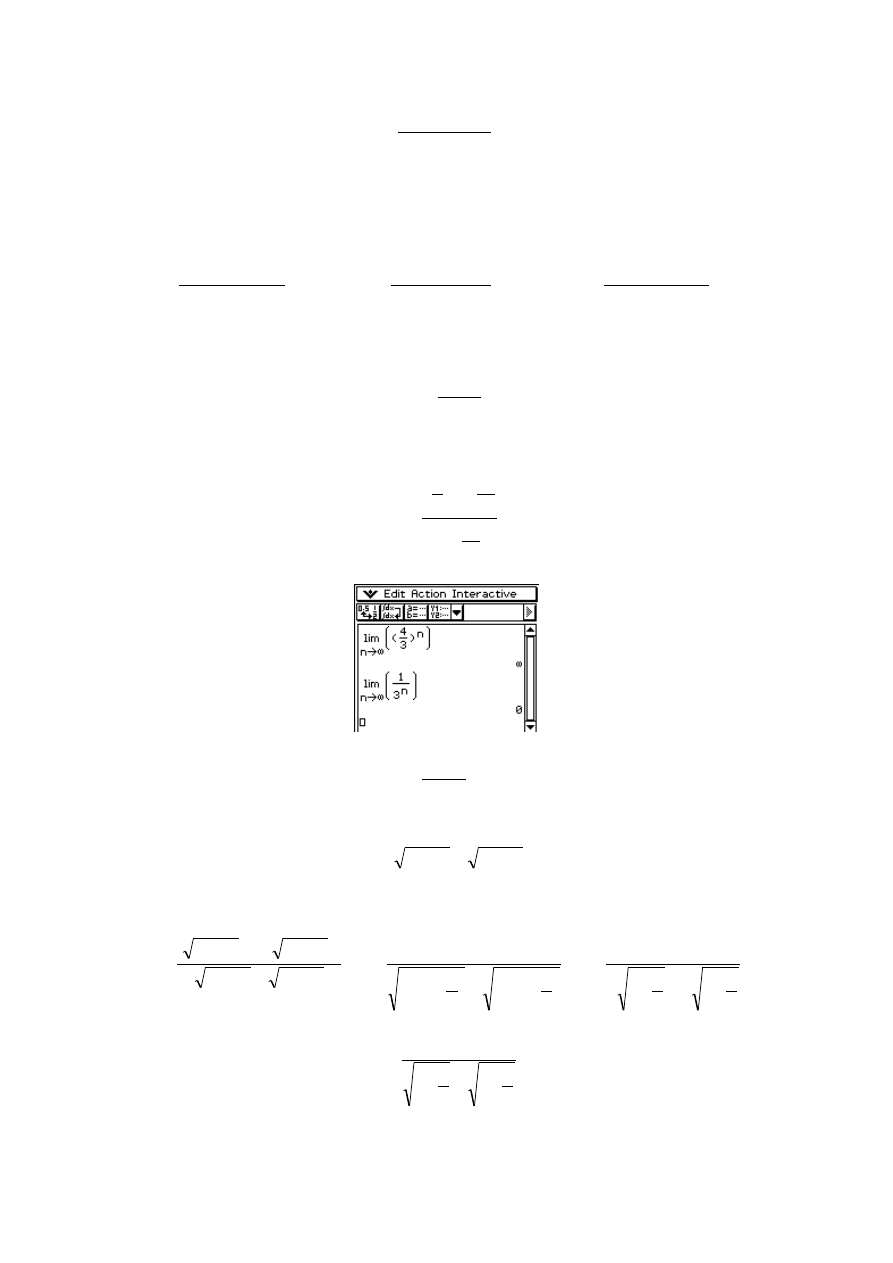
Przykład 5. Obliczyć granicę

4

3

3

4

lim









n

n

n

Licznik i mianownik są funkcjami wykładniczymi, dzielimy każdy składnik przez

n

3

:

n

n

n

n

3

4

1

3

3

3

4

lim

































4

3

3

4

lim

n

n

n

Przykład 6. Obliczyć granicę





n

n

n

n

n











2

2

lim

Korzystamy ze wzoru skróconego mnożenia:

2

2

)

)(

(

b

a

b

a

b

a









, zatem



 



n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

n

1

1

1

1

2

lim

)

1

1

(

)

1

1

(

2

lim

lim

2

2

2

2

2

2

2

2









































Po skróceniu przez n dostajemy

n

n

n

1

1

1

1

2

lim











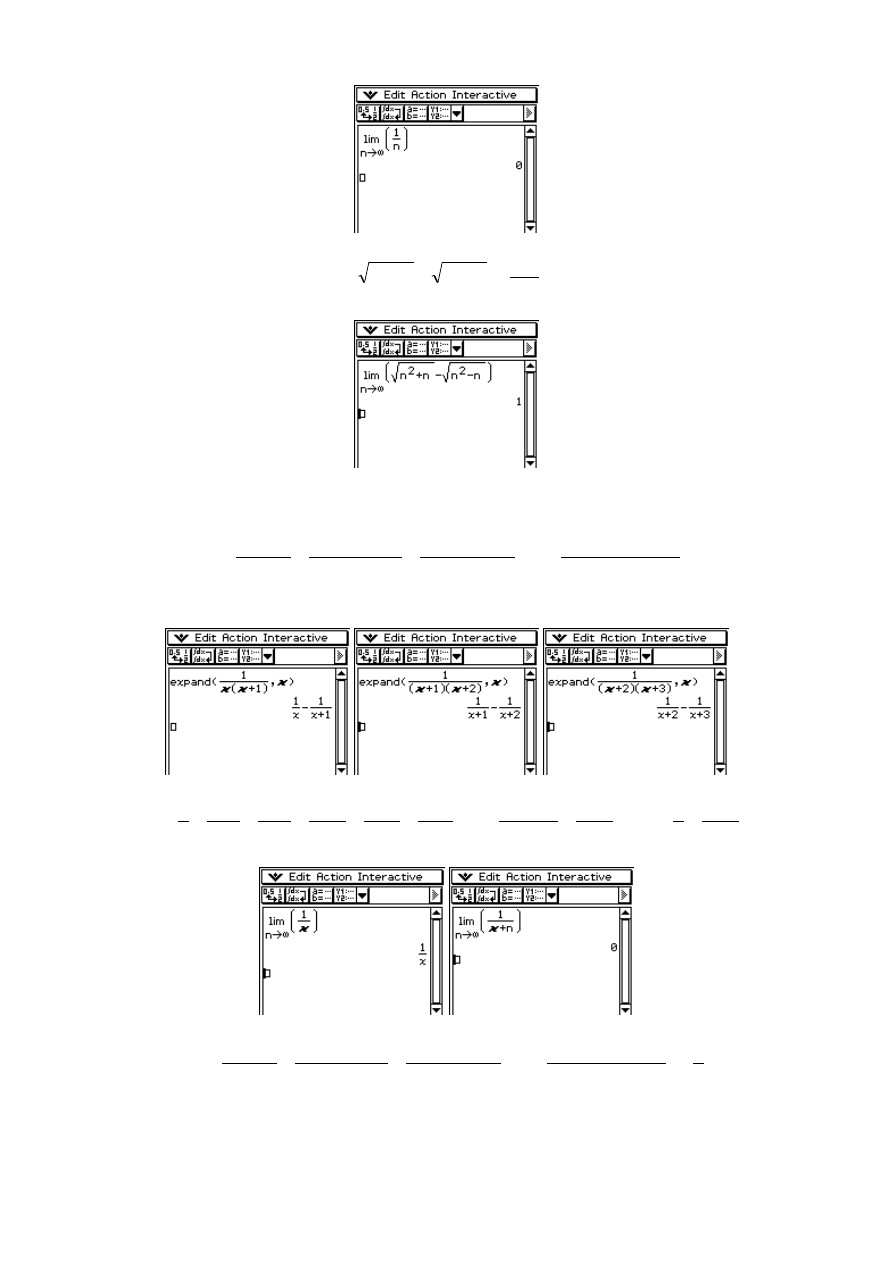
czyli ostatecznie





1

1

1

2

lim

2

2

















n

n

n

n

n

Sprawdźmy:

Przykład 7. Obliczyć granicę przy x różnym od zera









































)

)(

1

(

1

...

)

3

)(

2

(

1

)

2

)(

1

(

1

)

1

(

1

lim

n

x

n

x

x

x

x

x

x

x

n

Zauważmy, że

zatem







































































n

x

x

n

x

n

x

x

x

x

x

x

x

n

n

1

1

lim

1

1

1

...

3

1

2

1

2

1

1

1

1

1

1

lim

Ostatecznie

x

n

x

n

x

x

x

x

x

x

x

n

1

)

)(

1

(

1

...

)

3

)(

2

(

1

)

2

)(

1

(

1

)

1

(

1

lim









































