Ćwiczenie 6

„Badanie wyładowań elektrycznych w układach

izolacyjnych”

opracował Mariusz Benesz

1. Cel i zakres ćwiczenia

Celem ćwiczenia jest zapoznanie się z warunkami powstawania, mechanizmami rozwoju

i formami wyładowań elektrycznych w układach izolacyjnych. Zakres ćwiczenia obejmuje
obserwacje powstawania i rozwoju wyładowań oraz pomiar napięcia początkowego
wyładowań niezupełnych U

0

i napięcia przeskoku U

P

w powietrznych układach izolacyjnych

typu wsporczego i przepustowego.

2. Wprowadzenie

Wytrzymałość elektryczną

1

układów izolacyjnych obniżają wszelkiego rodzaju procesy

jonizacji, efektem których jest wzrost koncentracji cząsteczek naładowanych przechodzących
w rożne formy wyładowań elektrycznych. Wyładowania elektryczne można podzielić na:

- wyładowania zupełne, powodujące zwarcie elektrod układu izolacyjnego,
- wyładowania niezupełne, nie powodujące zwarcia elektrod układu izolacyjnego

i o zasięgu ograniczonym do pewnej przestrzeni wokół elektrod.

Układy izolacyjne, ze względu na rozkład pola elektrycznego oraz zjawiska zachodzące

na powierzchniach granicznych między poszczególnymi dielektrykami wchodzącymi w skład
danego układu izolacyjnego, można podzielić na dwa zasadnicze typy:

- układ izolacyjny typu wsporczego, charakteryzującego się obecnością wyłącznie

składowej stycznej natężenia pola elektrycznego,

- układ izolacyjny typu przepustowego, charakteryzującego się przewagą składowej

normalnej natężenia pola elektrycznego.

Występujące wyładowania elektryczne na powierzchniach granicznych dielektryków

w układzie izolacyjnym typu wsporczego noszą nazwę wyładowań powierzchniowych, zaś
wyładowania elektryczne występujące na powierzchniach granicznych dielektryków

w układzie izolacyjnym typu przepustowego noszą nazwę wyładowań ślizgowych.

1

Wytrzymałość elektryczna – graniczna wartość natężenia pola elektrycznego, przy którym układ izolacyjny

traci swoje właściwości izolacyjne.

6 – 1

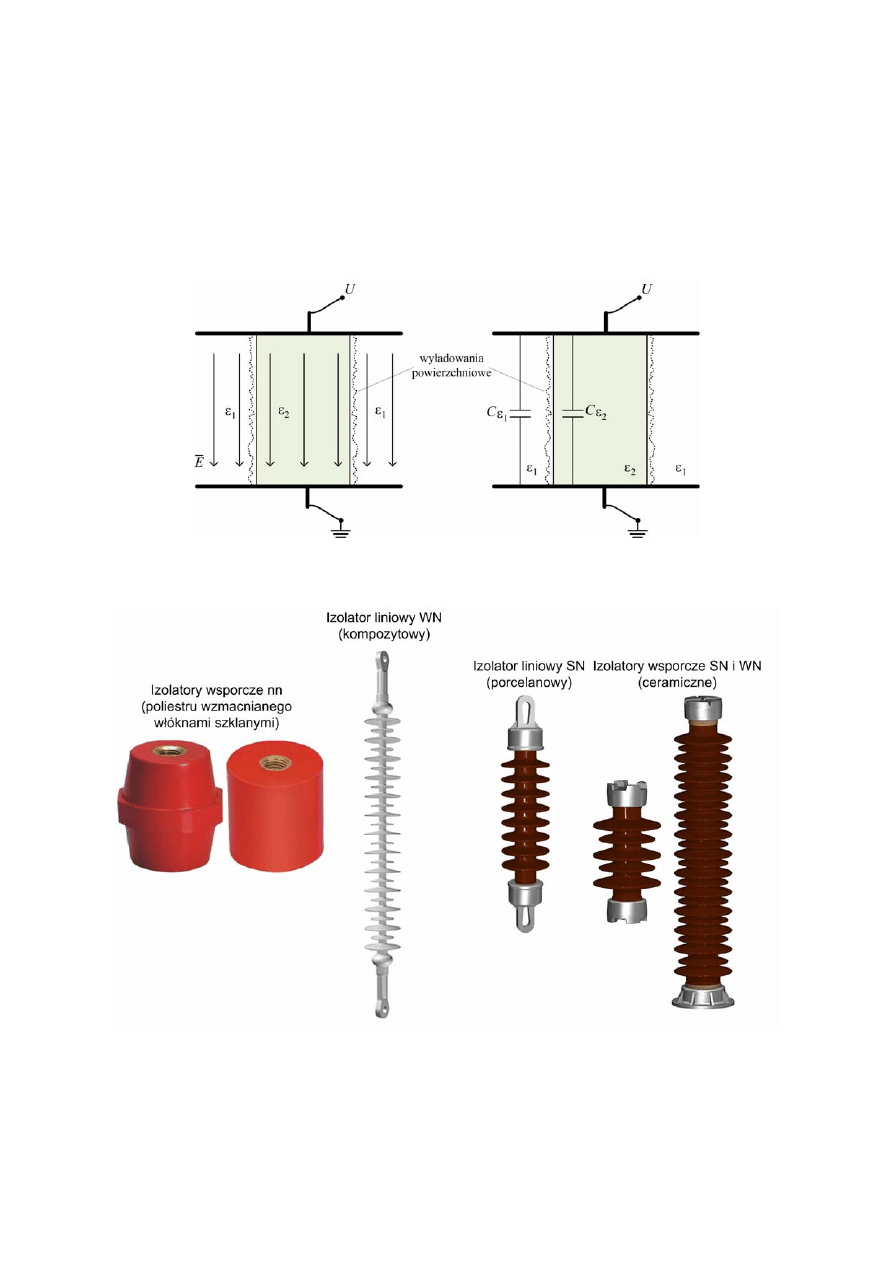
2.1. Wyładowania powierzchniowe
Wyładowania powierzchniowe w układach izolacyjnych występują w sytuacjach, kiedy

mamy do czynienia z równoległym rozkładem pola elektrycznego w stosunku do powierzchni
granicznych między dielektrykami wchodzącymi w skład danego układu.

Typowym układem, w którym występują tego typu wyładowania elektryczne to izolator

wsporczy, czyli układ, w którym materiał izolacyjny (np. w formie walca) stanowi przerwę
izolacyjną pomiędzy równoległymi elektrodami (rys. 6.1).

Rys. 6.1. Układ izolacyjny typu wsporczego

a) rozkład pola elektrycznego, b) warunki zapoczątkowania wyładowania powierzchniowego

Rys. 6.2. Rzeczywiste układy izolacyjne typu wsporczego [8,9]

Tego typu układy izolacyjne mogą mieć jednostajny rozkład natężenia pola elektrycznego,

jeżeli elektrody są płaskie i równolegle zamocowane a powierzchnia kontaktu dielektryka
z elektroda jest znacznie mniejsza niż powierzchnia samych elektrod (rysunek 6.1a). W takim

6 – 2

przypadku występujące w układzie uwarstwienie dielektryków nie wpływa na rozkład pola
i jest on jednostajny. Do odkształcenia pola elektrycznego i obniżenia wartość napięcia
przeskoku może dojść w wyniku [1, 3]:

- występowania wyładowań niezupełnych w wszelkiego rodzaju szczelinach czy

wgłębieniach w dielektryku,

- zmiany przewodności po powierzchni dielektryka spowodowane np. obecnością

warstwy zabrudzeniowej na powierzchni dielektryka.

W rzeczywistych układach izolacyjnych, gdzie mamy do czynienia z ograniczonymi

wymiarami geometrycznymi, rozkład pola jest dość często silnie niejednostajny i opis
występujących na powierzchniach granicznych wyładowań jest utrudniony. Przykłady
rzeczywistych układów izolacyjnych typu wsporczego przedstawiono na rysunku 6.2.

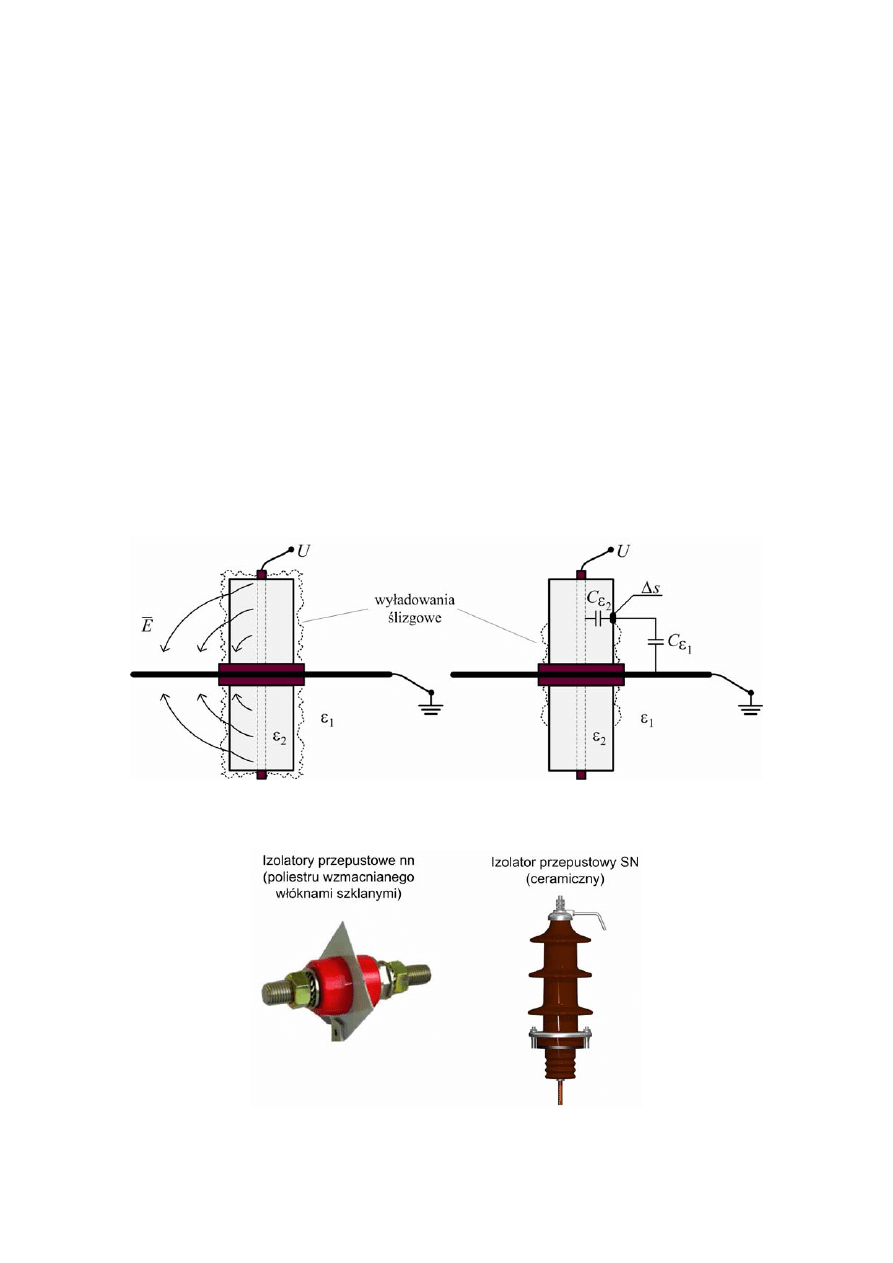
2.2. Wyładowania ślizgowe
Wyładowania ślizgowe w układach izolacyjnych występują w tzw. układach ukośnych,

w których wektor natężenia pola elektrycznego zmienia kierunek na powierzchniach
granicznych między dielektrykami wchodzącymi w skład danego układu.

Typowym układem, w którym występują tego typu wyładowania elektryczne to izolator

przepustowy, czyli walec izolacyjny, zamocowany w zewnętrznym kołnierzu (zwykle
uziemionym) i zawierającym wewnątrz szynę przewodzącą (rys. 6.3).

Rys. 6.3. Układ izolacyjny typu przepustowego

a) rozkład pola elektrycznego, b) warunki zapoczątkowania wyładowania ślizgowego

Rys. 6.4. Rzeczywiste układy izolacyjne typu przepustowego [8,9]

6 – 3

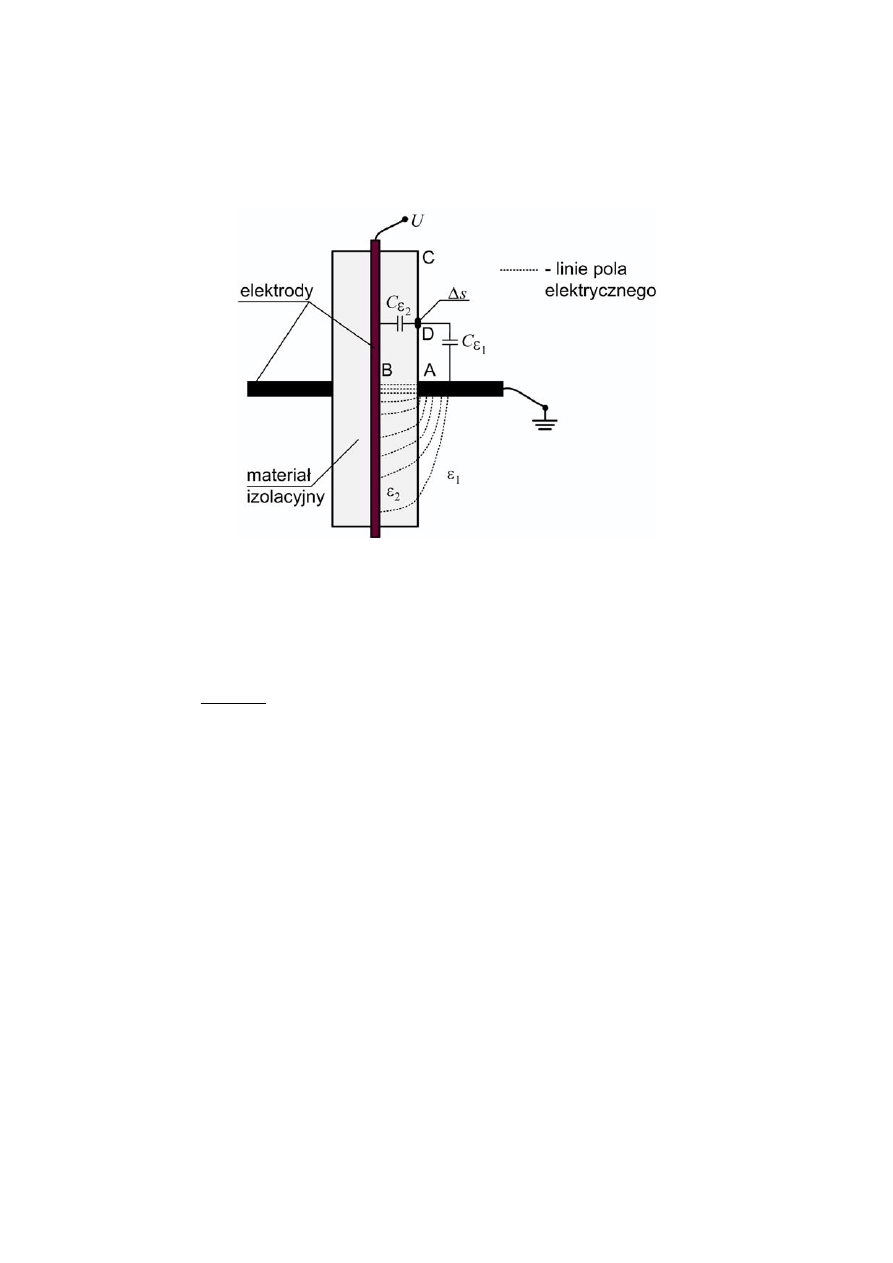
Na rysunku 6.5 przedstawiono elektryczne warunki rozwoju wyładowań ślizgowych.

W takim układzie obok warstwy dielektryka stałego, która jest narażona na przebicie (droga
AB), mamy do czynienia z dielektrykiem gazowym (powietrzem), w którym może dojść do
wyładowań powierzchniowych (droga ADC).

Rys. 6.5. Mechanizm rozwoju wyładowań ślizgowych

Rozpatrując elementarną powierzchnię graniczną

Δs (np. w punkcie D) mamy do

czynienia z pojemnościowym dzielnikiem napięcia (rys. 6.5), przy czym znaczna część
przyłożonego do układu napięcia przypada na pojemność związana z otaczającym
dielektrykiem (powietrzem):

2

ε

1

ε

2

ε

1

ε

C

C

C

U

U

+

⋅

=

[kV]

(6.1)

gdzie:

-

C

ε1

: pojemność elementarnej powierzchni granicznej względem elektrody uziemionej,

-

C

ε2

:

pojemność elementarnej powierzchni granicznej względem elektrody do, której
przyłożono napięcie

U,

-

U

ε1

: napięcie związane z pojemnością

C

ε1

.

Przy zwiększeniu napięcia

U powyżej napięcia początkowego, niejednostajność rozkładu

napięcia jest powodem pojawienia się wyładowań świetlących w pobliżu elektrody
uziemionej. Pojawiające się smugi świetlne rozszerzają się i łączą w iskry ślizgowe, które
poruszają się z głośnym trzaskiem. Przy dalszym zwiększaniu napięcia iskry wydłużają się
i docierają do przeciwnej elektrody – mamy do czynienia z zupełnym przeskokiem iskrowym.
Należy tutaj zaznaczyć, że składowa normalna wektora natężenia pola elektrycznego wokół
układu izolacyjnego typu przepustowego odpowiada za powstanie wyładowania, zaś za
rozwój i rozprzestrzenianie wyładowania (iskier ślizgowych) odpowiada składowa styczna.

W normalnych warunkach eksploatacyjnych nie powinno się dopuścić do sytuacji,

w których mogą wystąpić wyładowania powierzchniowe czy ślizgowe. By do tego nie
dopuścić stosowane są różne środki zapobiegawcze, mające na celu:

- podwyższenie napięcia początkowego wyładowań przez zmniejszenie jednostkowej

pojemności powierzchniowej

C

0

, uzyskiwane m.in. poprzez zwiększenie grubości lub

6 – 4

wysokości dielektryka albo poprzez dobór odpowiednich materiałów dielektrycznych
(zmniejszenie różnic między przenikalnościami elektrycznymi),

- zmniejszenie nierównomierności rozkładu pola elektrycznego stosując sterowanie pola

metodą pojemnościową lub rezystancyjną, uzyskiwane m.in. poprzez stosowanie pokryć
przewodzących (lakierów) lub ekranów w dielektryku.

2.3. Napięcie początkowe U

0

i napięcie przeskoku U

P

w układach

izolacyjnych typu wsporczego i przepustowego

Zarówno w układach izolacyjnych typu wsporczego, jak i przepustowego napięcie

początkowe wyładowań niezupełnych zależy głównie od kształtu elektrod (stopnia
nierównomierności pola elektrycznego), a napięcie przeskoku

U

P

– od drogi przeskoku

wzdłuż powierzchni dielektryka. Nie ma prostej zależności pozwalającej na wyznaczenie tych
wielkości. Jedynie można się posłużyć wzorami empirycznym, które pozwalają z mniejszym
czy większym przybliżeniem wyliczyć wyżej wymienione wartości.

Wartość skuteczną napięcie początkowego

U

0

wyładowania niezupełnego można wyliczyć

np. ze wzoru Toeplera

2

[4]:

4

44

,

0

0

0

10

36

,

1

−

⋅

=

C

U

[kV]

(6.2)

gdzie:

- C

0

: jednostkowa pojemność powierzchniowa [F/cm

2

] układu izolacyjnego, przy czym

dla układu izolacyjnego typu wsporczego

3

:

h

C

w

ε

ε

0

0

⋅

=

[F/cm

2

],

(6.3)

a dla układu izolacyjnego typu przepustowego:

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⋅

=

r

R

R

C

w

ln

ε

ε

0

0

[F/cm

2

]

(6.4)

gdzie:

-

ε

0

: przenikalność elektryczna próżni

ε

0

= 8,85·10

-14

[F/cm],

-

ε

w

: względna przenikalność elektryczna dielektryka [-],

- h :

wysokość dielektryka [cm],

- R, r : promień wewnętrzny i zewnętrzny dielektryka [cm].
Wartość skuteczną napięcie przeskoku U

P

wyładowania zupełnego można wyliczyć np. na

podstawie następującego równania

4

[7]:

14

36

,

3

+

⋅

=

h

U

P

[kV]

(6.5)

gdzie:

- h: odległość między elektrodami [cm].

2

Uwaga: równanie słuszne dla C

0

≥ 0,25·10

-12

[F/cm

2

].

3

Uwaga: równania dotyczą układów izolacyjnych jednowarstwowych.

4

Uwaga: równanie słuszne dla odległości między elektrodami h > 8 cm, a większe dokładności otrzymuje się

przy h > 30 cm.

6 – 5

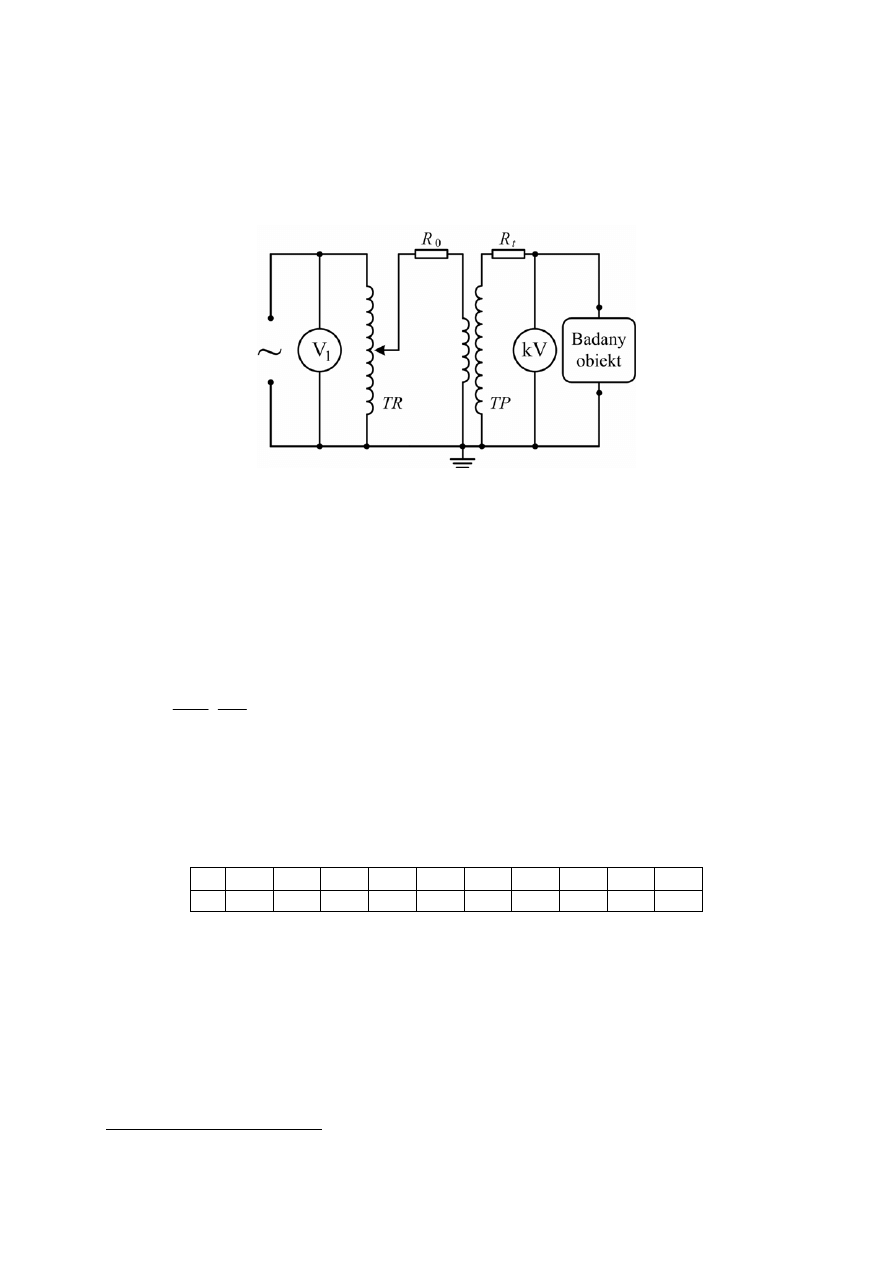
3. Program ćwiczenia

Badania przeprowadza się w układzie pomiarowym, którego schemat został

przedstawiony na rysunku 6.6.

Rys. 6.6. Schemat układu pomiarowego

R

0

– rezystor ograniczający prąd zwarcia, R

t

– rezystor tłumiący drgania,

TR – transformator regulacyjny, TP – transformator probierczy.

Badając poszczególne układy izolacyjne wykonuje się pomiary napięć (początkowego

i przeskoku) w warunkach laboratoryjnych, które są określone przez następujące parametry:
temperaturę t [°C], ciśnienie p [hPa] oraz wilgotność względną w [%]. Chcąc następnie
porównać te wielkości z wielkościami napięć wyliczonych na podstawie równań (6.2) i (6.5)
należy uwzględnić przy wielkościach wyliczonych współczynnik korekcyjny k, który zależy
od gęstości względnej powierza

δ

w

, określonej równaniem:

T

p

w

293

1013

δ

⋅

=

[-]

(6.6)

gdzie:

- p : ciśnienie otoczenia, w którym dokonano pomiaru [hPa],
- T : temperatura otoczenia, w którym dokonano pomiaru [°K].

Wartość współczynnika korekcyjnego k w funkcji gęstości względnej zestawiono w tabeli 6.1.

Tabela 6.1. Wartości współczynnika korekcyjnego k

5

[5]

ρ

w

0,70 0,75 0,80 0,85 0,90 0,95 1,00 1,05 1,10 1,15

k 0,72 0,77 0,82 0,86 0,91 0,95 1,00 1,05 1,09 1,13

3.1. Badanie wyładowań powierzchniowych
Przed przystąpieniem do pomiarów należy zaznajomić się z budową modelu izolatora

wsporczego oraz zmierzyć potrzebne wymiary geometryczne, by na podstawie wzorów
empirycznych móc porównać wielkości zmierzone z wyliczonymi. Wyniki pomiarów
i obliczeń zestawić w tabeli 6.2, jak również przedstawić w formie odpowiednich wykresów.

5

Uwaga: przy odczytywaniu współczynnika k dla pośrednich wartości

δ

w

dokonać aproksymacji liniowej.

6 – 6

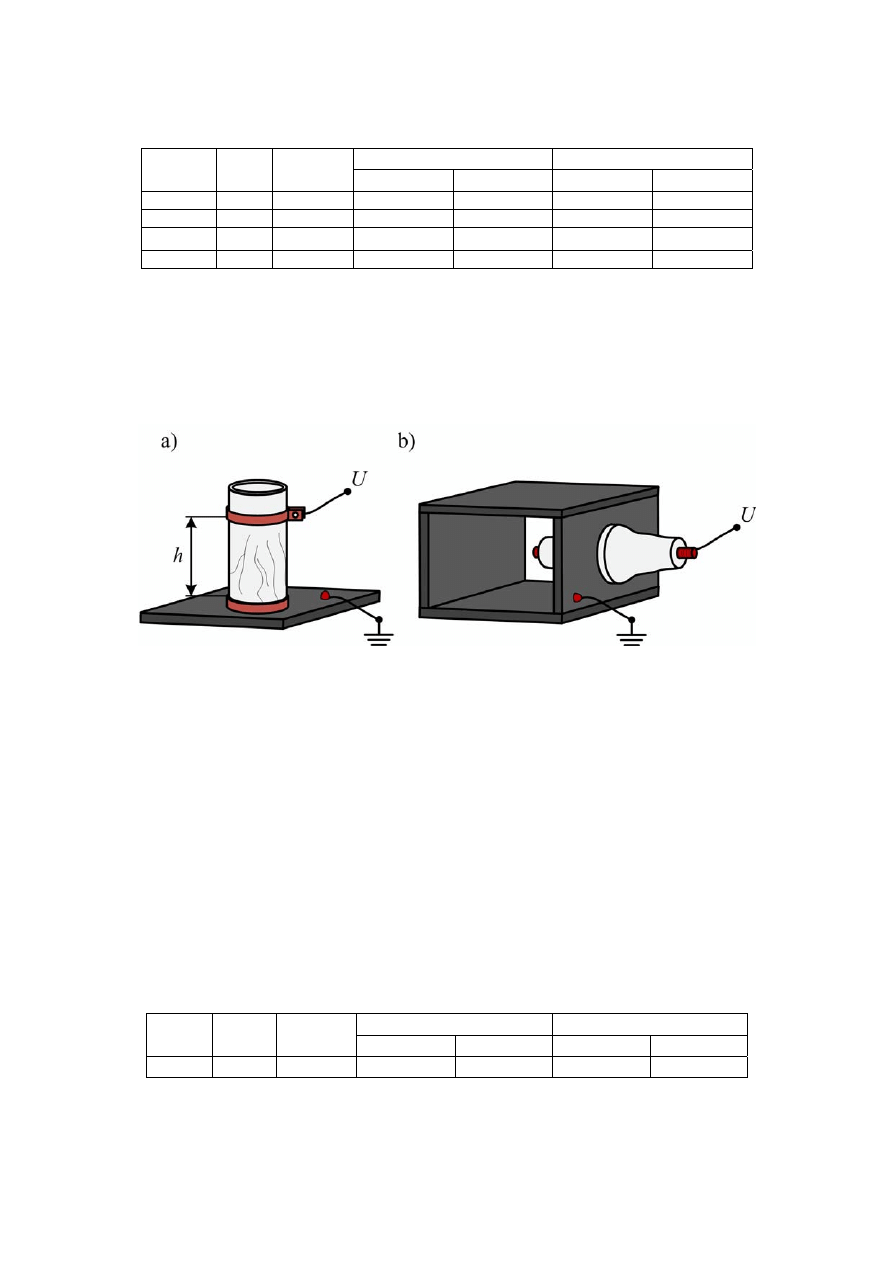
Tabela 6.2 Wyniki pomiarów i obliczeń napięć przy badaniu wyładowań powierzchniowych

na modelu izolatora wsporczego

U

0

[kV]

U

P

[kV]

Lp.

h

[mm]

C

0

[pF/cm

2

] zmierzone wyliczone zmierzone wyliczone

1

6

2

8

M

M

8

20

h – wysokość izolatora, C

0

– jednostkowa pojemność powierzchniowa, U

0

– napięcie początkowe

wyładowań niezupełnych, U

P

– napięcie przeskoku.

Mechanizm rozwoju wyładowań powierzchniowych zaobserwować na modelu izolatora

wsporczego, którego szkic został przedstawiony na rysunku 6.7a. Model ten posiada regulację
odległości między stopą a kołpakiem izolatora, przy czym regulacja ta odbywa się przez
poluzowanie śruby dociskowej.

Rys. 6.7. Model badanego izolatora: a) wsporczego, b) przepustowego

Obok obserwacji mechanizmu rozwoju wyładowań powierzchniowych, badania tego typu

wyładowań obejmują również pomiar napięcia początkowego wyładowań niezupełnych U

0

oraz pomiar napięcia przeskoku U

P

przy różnych wysokościach izolatora. Pomiarów tych

napięć dokonać należy dla wysokości izolatora w zakresie od 6 do 20 cm, przy zmianie co
2 cm. Neonówka, wchodząca w skład układu pomiarowego, jest zastosowana jako wskaźnik
napięcia początkowego wyładowań niezupełnych U

0

i wpinana tylko w czasie pomiaru U

0

.

3.2. Badanie wyładowań ślizgowych
Przed przystąpieniem do pomiarów należy zaznajomić się z budową modelu izolatora

wsporczego oraz zmierzyć potrzebne wymiary geometryczne by na podstawie wzorów
empirycznych móc porównać wielkości zmierzone z wyliczonymi. Wyniki pomiarów
i obliczeń zestawić w tabeli 6.3

Tabela 6.3 Wyniki pomiarów i obliczeń napięć przy badaniu wyładowań powierzchniowych

na modelu izolatora przepustowego

U

0

[kV]

U

P

[kV]

r

[mm]

R

[mm]

C

0

[pF/cm

2

] zmierzone wyliczone zmierzone wyliczone

r, R – promień wewnętrzny i zewnętrzny izolatora, C

0

– jednostkowa pojemność

powierzchniowa, U

0

– napięcie początkowe wyładowań niezupełnych, U

P

– napięcie przeskoku.

6 – 7

Mechanizm rozwoju wyładowań ślizgowych zaobserwować na modelu izolatora

przepustowego, którego szkic został przedstawiony na rysunku 6.7b.

Obok obserwacji mechanizmu rozwoju wyładowań ślizgowych, badania tego typu

wyładowań obejmują również pomiar napięcia początkowego wyładowań niezupełnych U

0

oraz pomiar napięcia przeskoku U

P

. Neonówka, wchodząca w skład układu pomiarowego,

jest zastosowana jako wskaźnik napięcia początkowego wyładowań niezupełnych U

0

i wpinana tylko w czasie pomiaru U

0

.

3.3. Wyznaczenie zależności U

0

=f(g)

Wyznaczenie zależności U

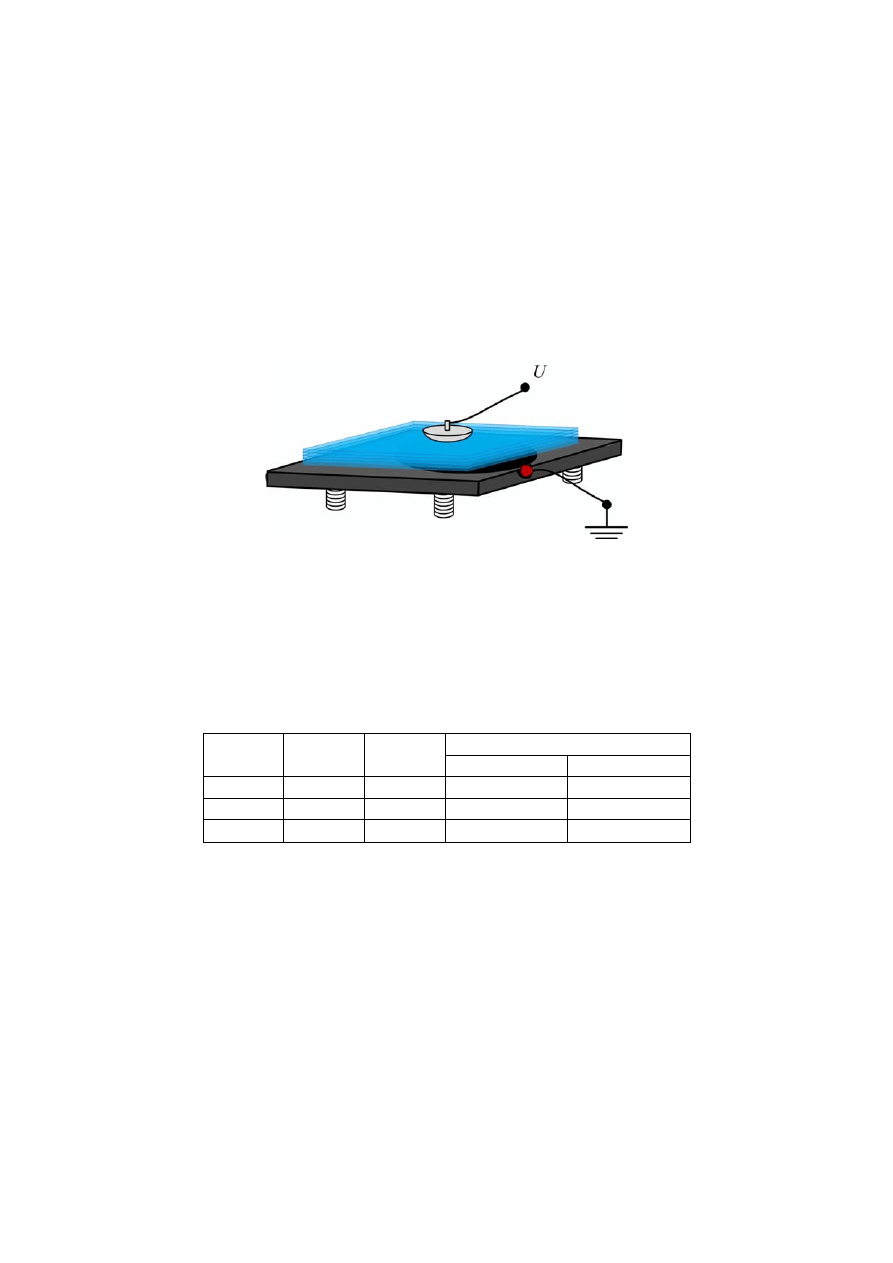
0

w funkcji grubości warstwy izolacji g wykonać dla płaskiego

układu izolacyjnego, którego szkic przedstawiono na rysunku 6.8.

Rys. 6.8. Model badanego płaskiego układu izolacyjnego

Pomiarów dokonać dla kilku warstw materiału izolacyjnego (płyt szklanych). Zmierzyć

potrzebne wymiary geometryczne, by na podstawie wzorów empirycznych móc porównać
wielkości zmierzone z wyliczonymi. Jako wskaźnik napięcia początkowego wyładowań
niezupełnych U

0

zastosować neonówkę. Wyniki pomiarów i obliczeń zestawić w tabeli 6.4

jak również przedstawić w formie odpowiednich wykresów.

Tabela 6.4 Wyniki pomiarów i obliczeń napięć przy wyznaczaniu zależności U

0

= f(g)

U

0

[kV]

Lp.

g

[mm]

C

0

[pF/cm

2

]

zmierzone wyliczone

1

2

M

g – grubość materiału izolacyjnego, C

0

– jednostkowa pojemność

powierzchniowa, U

0

– napięcie początkowe wyładowań niezupełnych.

3.4. Badanie izolatorów liniowych i stacyjnych
Dla wskazanych przez prowadzącego izolatorów liniowego i stacyjnego zaobserwować

mechanizm rozwoju wyładowań i wyznaczyć napięcie początkowe wyładowań niezupełnych
U

0

i napięcie przeskoku U

P

w warunkach: na sucho i na mokro. Zmierzyć potrzebne wymiary

geometryczne, by na podstawie wzorów empirycznych móc porównać wielkości zmierzone
z wyliczonymi. Wyniki pomiarów i obliczeń zestawić w tabeli 6.5.

6 – 8

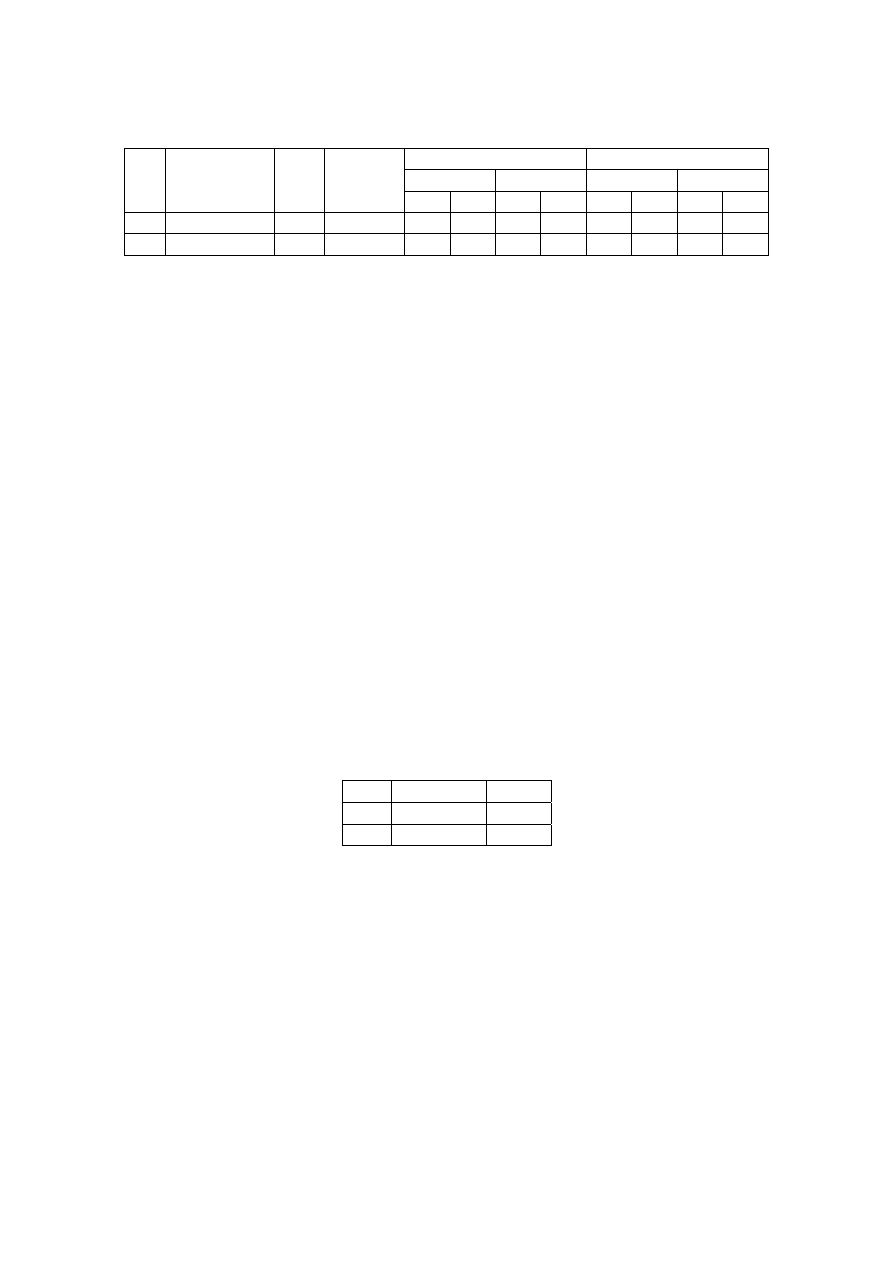
Tabela 6.5 Wyniki pomiarów i obliczeń napięć przy badaniu izolatorów liniowych

i stacyjnych

Badania na sucho

Badania na mokro

U

0

[kV]

U

P

[kV]

U

0

[kV]

U

P

[kV]

Lp.

Typ

i oznaczenie

izolatora

h

[cm]

C

0

[pF/cm

2

]

Z W Z W Z W Z W

1

2

h – odległość między okuciami izolatora, C

0

– jednostkowa pojemność powierzchniowa, U

0

– napięcie

początkowe wyładowań niezupełnych, Z – wartości zmierzone, W – wartości wyliczone.

4. Sprawozdanie

Sprawozdanie powinno zawierać:

- krótki wstęp teoretyczny obejmujący najważniejsze zagadnienia związane z wyko-

nywanym ćwiczeniem,

- schemat układu probierczego,
- warunki otoczenia przeprowadzanych pomiarów,
- charakterystykę badanych obiektów (krótki opis, staranne rysunki),
- wyniki pomiarów i obliczeń dotyczących układu izolacyjnego typu wsporczego

i przepustowego,

- wyznaczenie napięcia U

0

i U

P

na poszczególnych izolatorach liniowym i wsporczym

na podstawie wzorów empirycznych i porównanie ich z wartościami zmierzonymi,

- wyznaczenie napięcia początkowego wyładowań ślizgowych U

0

dla układu

izolacyjnego cylindrycznego i płaskiego na podstawie wzorów empirycznych
i porównanie ich z wartościami zmierzonymi,

- wykresy

zależności U

P

= f (h) i U

0

= f (g),

- wnioski (zebrane w kilku spójnych zdaniach, ewentualnie wypunktowanych).

Przy obliczeniach przyjąć następujące wartości względnej przenikalności elektrycznej

materiałów izolacyjnych:

Lp. Materiał

ε

w

[-]

1

porcelana

4 ÷ 5

2 szkło 7

5. Zagadnienia do samodzielnego opracowania

5.1. Kryterium, podział i charakterystyka wyładowań w układach izolacyjnych WN.
5.2. Mechanizm rozwoju wyładowań w układach izolacyjnych WN.
5.3. Sposoby ograniczania powstawania wyładowań w układach izolacyjnych WN.
5.4. Obliczyć napięcie początkowe U

0

wyładowań ślizgowych dla układu

przedstawionego na rysunku 6.9a, jeżeli grubość warstwy masy kablowej g = 2 mm,
a jej względna przenikalność elektryczna

ε

w

= 3.

5.5. Obliczyć napięcie początkowe U

0

wyładowań ślizgowych dla układu

przedstawionego na rysunku 6.9b, jeżeli grubość płyty szklanej a = 3 mm, a jej
względna przenikalność elektryczna

ε

w

= 7. Jakie można wysunąć wnioski

porównując otrzymane wyniki z wynikami z zadania 5.4?

6 – 9

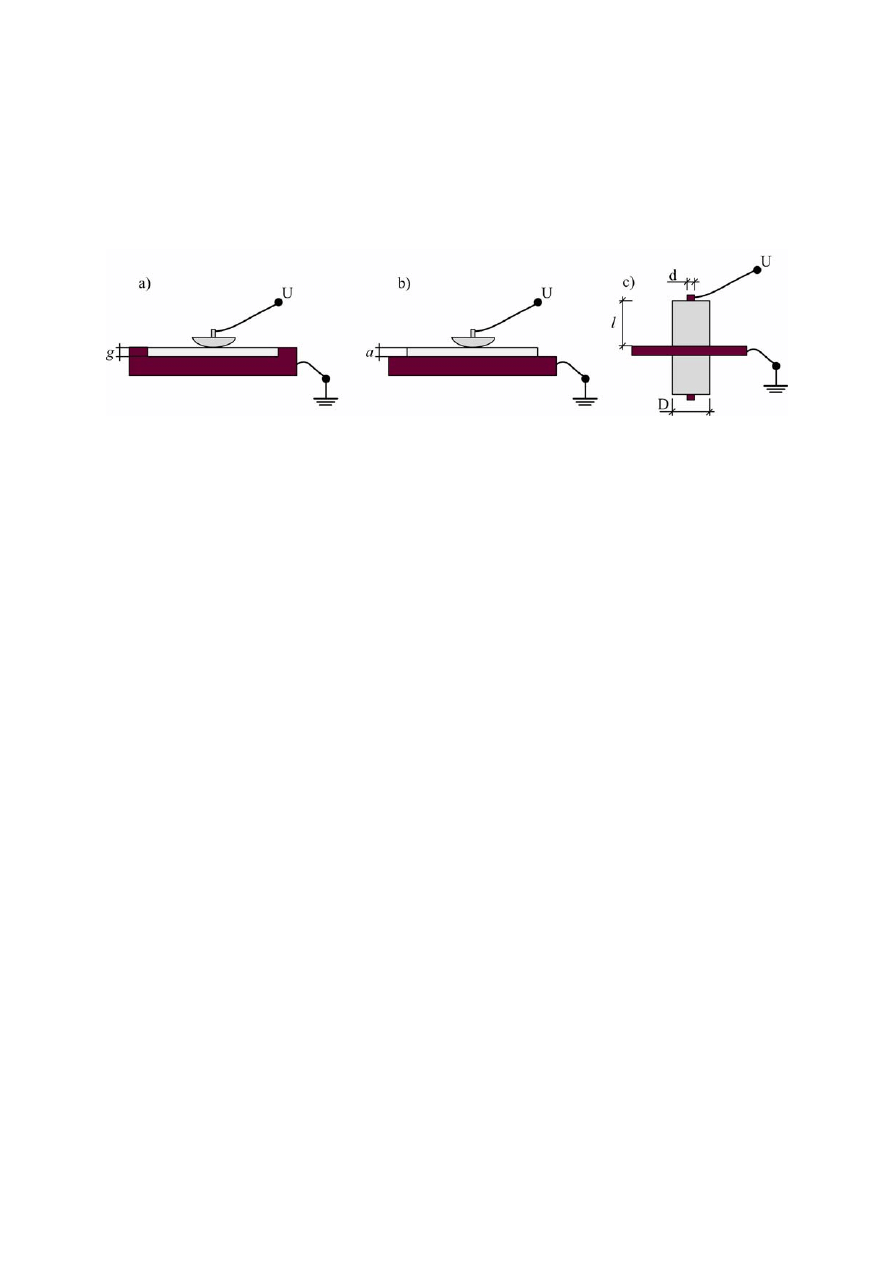
5.6. Obliczyć napięcie początkowe U

0

wyładowań powierzchniowych oraz napięcie

przeskoku U

P

dla układu przedstawionego na rysunku 6.9c, jeżeli długość izolatora

l = 20 cm, średnica sworznia (metalowej szyny) d = 3 cm, grubość warstwy
porcelany g = 7 cm i względna przenikalność elektryczna porcelany

ε

w

= 5. Czy

w tym układzie U

0

< U

P

? Jak zmieni się sytuacja, jeżeli długość izolatora

zwiększymy o 50 %?

Rys. 6.9. Układy do zagadnień 5.4 – 5.6

6. Literatura

1. Flisowski Z. „Technika Wysokich Napięć”, Wydawnictwo Naukowo – Techniczne,

Warszawa 1996.

2. Florkowska B. „Podstawy metod badań układów izolacyjnych wysokiego napięcia”,

Skrypt AGH nr 1245, Kraków 1992.

3. Florkowska B. „Technika Wysokich Napięć”, Skrypt AGH nr 1294, Kraków 1991.
4. Florkowska B. „Wytrzymałość elektryczna gazowych układów izolacyjnych

wysokiego napięcia”, Wydawnictwo Naukowo – Dydaktyczne AGH, Kraków 2003.

5. Kosztaluk R. „Technika badań wysokonapięciowych T1 i T2”, Wydawnictwo

Naukowo – Techniczne, Warszawa 1985.

6. Norma PN-81/E-05001 „Urządzenia elektroenergetyczne wysokiego napięcia.

Znamionowe napięcia probiercze ”.

7. Szpor St., Dzierżek H., Winiarski W. „Technika wysokich napięć”, Wydawnictwo

Naukowo – Techniczne, Warszawa 1978.

8. www.ces.com.pl – strona internetowa Centrum Elektroniki Stosowanej „CEZ” Sp.

z o.o., stan na marzec 2009r.

9. www.zapel.com.pl – strona internetowa Zakładu Porcelany Elektrotechnicznej

„ZAPEL S.A.”, stan na marzec 2009r.

6 – 10