>
restart:
Rozwiązywanie układów równań nieliniowych
Metoda graficzna
>
with(plots):
Warning, the name changecoords has been redefined
Układ dwóch równań
>
f[1]:=x[1]*sinh(x[1]*x[2])-1/2;
:=
f
1
−
x
1
(
)
sinh x
1
x
2
1
2
>
f[2]:=(x[1]^2+x[2]^2)^2-2*(x[1]^2-x[1]*x[2]^5)-9/10;
:=
f
2
−
+
−
(
)
+
x
1
2
x
2
2
2
2 x
1
2
2 x
1
x
2
5
9
10
>
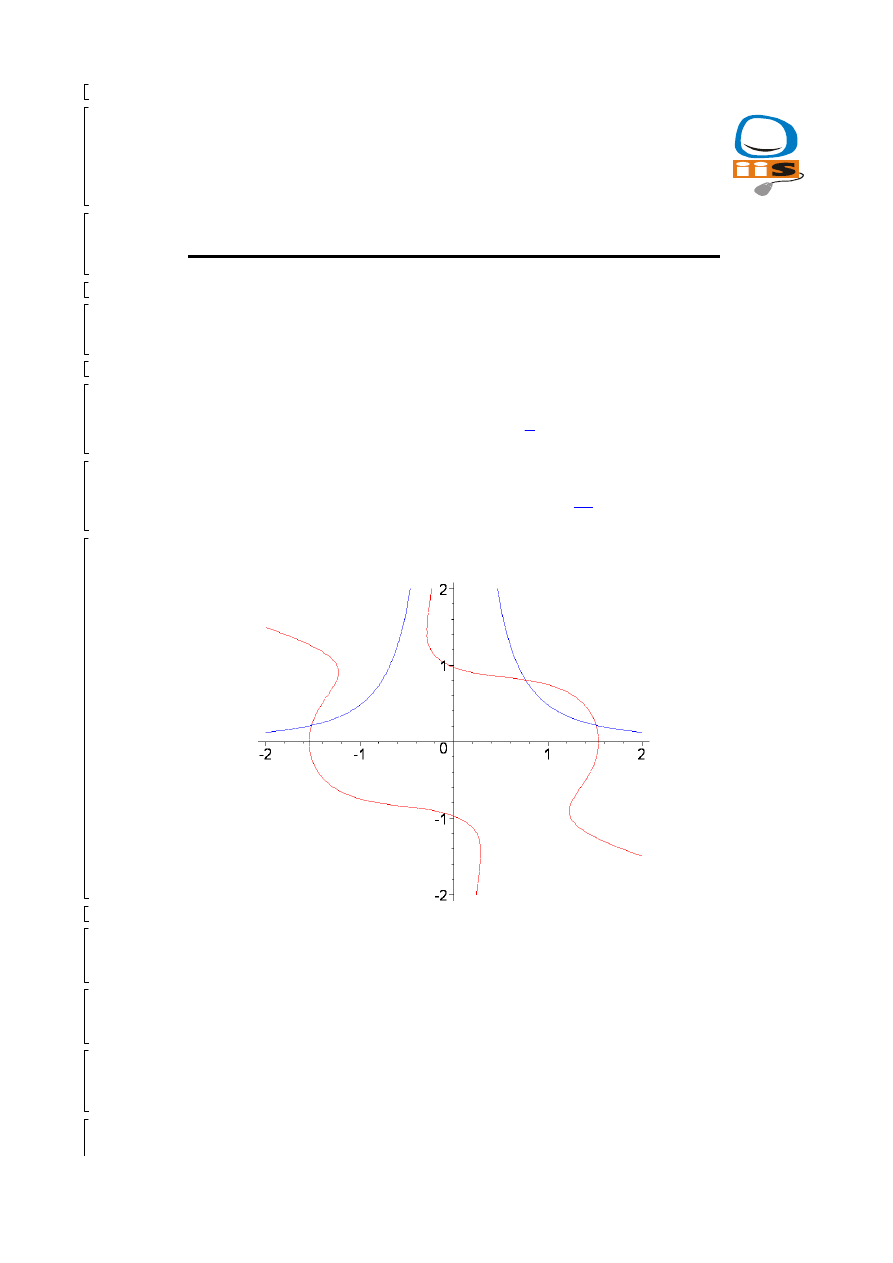
implicitplot([f[1]=0,f[2]=0],x[1]=-2..2,x[2]=-2..2,color=[blue,r
ed],numpoints=2000);
Układ trzech równań
>
f[1]:=x[1]^2-x[2]^2+x[3]^2-1;
:=
f
1
− + −
x
1
2
x
2
2
x
3
2
1
>
f[2]:=(x[1]-2)^2+(x[2]-2)^2+(x[3]-2)^2-36;
:=
f
2
+
+
−
(
)
−
x
1
2
2
(
)
−
x
2
2
2
(
)
−
x
3
2
2
36
>
f[3]:=x[2]-exp(-x[1]*x[3]);
:=
f
3
−
x
2
e
(
)
−x
1
x
3
>
implicitplot3d([f[1]=0,f[2]=0,f[3]=0],x[1]=-5..8,x[2]=-5..8,x[3]
=-5..8,color=[blue,green,red],orientation=[65,135],numpoints=500
0);
>
Metoda Newtona-Raphsona
>
Układ dwóch równań
>
with(LinearAlgebra):
>
n:=2;
:=
n
2
>
eps:=10.^(2-Digits);
:=
eps
0.1000000000 10
-7
>
f:=Vector(n):A:=Matrix(n):
>
f[1]:=x[1]*sinh(x[1]*x[2])-1/2;
f[2]:=(x[1]^2+x[2]^2)^2-2*(x[1]^2-x[1]*x[2]^5)-9/10;
:=
f
1
−
x
1
(
)
sinh x
1
x
2
1
2
:=
f
2
−
+
−
(
)
+
x
1
2
x
2
2
2
2 x
1
2
2 x
1
x
2
5
9
10
>
for i to n do
for j to n do
A[i,j]:=diff(f[i],x[j]):
end do:
end do:
>
A;
+
(
)
sinh x
1
x
2
x
1
(
)
cosh x
1
x
2
x
2
x
1
2
(
)
cosh x
1
x
2
−
+
4 (
)
+
x
1
2
x
2
2
x
1
4 x
1
2 x
2
5
+
4 (
)
+
x
1
2
x
2
2
x
2
10 x
1
x
2
4
>
w:=abs(f[1])<eps and abs(f[2])<eps;
w
<
−
x
1
(
)
sinh x
1
x
2
1
2
0.1000000000 10
-7
and
:=
<
−
+
−
(
)
+
x
1
2
x
2
2
2
2 x
1
2
2 x
1
x
2
5
9
10
0.1000000000 10
-7
>
x:=Vector([1.,1.]);
:=
x
1.
1.
>
i:=0;
:=
i
0
>
while not w do
x:=x-A^(-1).f:
i:=i+1:
end do:
>
x;i;
0.761370793108574806
0.810172721149395758
5
>
f;
0.
0.14 10
-8
>
Paktyczne implementacje metody Newtona-Raphsona
>
1. Liniowy ukad równań ze względu na elementy wektora h
( )
( )
( )
(
)
(
)
k
k
k
⋅
= −
A x
h
f x
)
(
)
(
)
1
(
k
k
k
h
x
x
+
=
+
>
>
x:=Vector([1.,1.]);
:=
x
1.
1.
>
i:=0;
:=
i
0
>
while not w do
h:=eval(LinearSolve(A,-f)):
x:=x+h:
i:=i+1:
end do:
>
x;i;
0.7613707930
0.8101727213
5
>
h;
0.2377202314 10
-6
-0.3330045624 10
-6
>
f[1];f[2];
0.
0.22 10
-8
>
1. Iteracja ze stałą macierzą B
)
(
)
(
)
(
)
1
(
k
k
k
x
f
B
x
x
⋅
−
=
+
>
x:=Vector([1.,1.]);
:=
x
1.
1.
>
B:=A^(-1);
:=
B
0.453736644776852105
-0.0388973461080574582
-0.151245548258950702
0.0685213375915747076
>
i:=0;
:=
i
0
>
while not w do
x:=x-B.f:
i:=i+1:
end do:
>
x;i;
0.761370792799353380
0.810172722281518598
35
>
f[1];f[2];
0.5 10
-9
0.82 10
-8
>
Rozwiązanie Maple'a
>
x:='x';
:=
x
x
>
sys:={f[1],f[2]};
:=
sys
{
}
,
−
+
−
(
)
+
x
1
2
x
2
2
2
2 x
1
2
2 x
1
x
2
5
9
10
−
x
1
(
)
sinh x
1
x
2
1
2
>
niew:={x[1],x[2]};
:=
niew
{
}
,
x
1
x
2
>
fsolve(sys,niew); # Maple wybiera pierwiastek
{
}
,
=
x
1
-1.516486440
=
x
2
0.2136586364
>
fsolve(sys,{x[1]=0..1,x[2]=0..1}); # my wybieramy pierwiastek
{
}
,
=
x
1
0.7613707931
=
x
2
0.8101727211
>
>