
Rozwiązywanie numeryczne równań nieliniowych
Wybrane metody znajdowania miejsc zerowych
funkcji jednej zmiennej
1. Metoda połowienia przedziału (bisekcji)
2. Metoda iteracji prostej
3. Metoda Newtona (stycznych)
4. Metoda Halley’a

Metoda połowienia przedziału (bisekcji)
Sz: pierwiastek f(x) = 0 z dokładnością eps
a
x
b
)
(x
f
×
×
2
x
1
x
2
1
b
a
x
+
=
0
)
(
1
<
x
f
0
)
(
2
>
x
f
n
n
n
x
eps
x
x
→
<
−
−1
jeżeli
- przybliżona wartość pierwiastka
Z:
f(x) – funkcja ciągła w przedziale domkniętym [a, b]
0
)
(
)
(
<
⋅ b
f
a
f
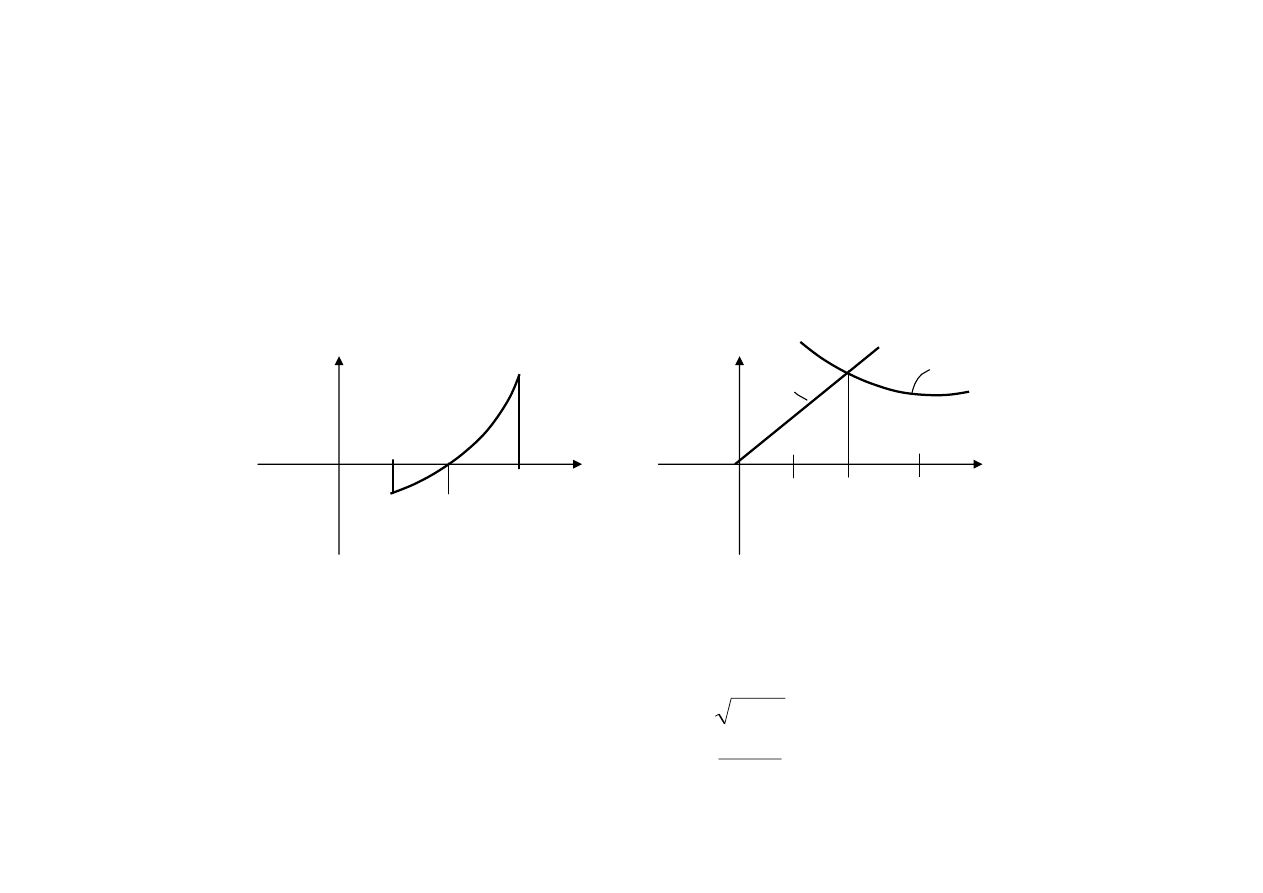
Metoda iteracji prostej
)
(
0
)
(
x
g
x
x
f
=
→
=
a
x
b
)
(x
f
∗
x
→
a
x
b
)
(x
g
∗
x
x
Zamiana równania f(x) = 0 na x = g(x) nie zawsze jest procesem jednoznacznym !
−
=
+
=
−
=
→
=
−
−
1
5
5
5
0
5
2
3
3
3
x
x
x
x
x
x
x
x
Sz: pierwiastek f(x) = 0 z dokładnością eps
Z: f(x) – funkcja ciągła w przedziale domkniętym [a, b]
0
)
(
)
(
<
⋅ b
f
a
f

Zbieżność metody iteracji prostej
*
*
k
k
k
k
x
x
x
x
x
x
∆ =
− →
=
−∆
1
1
1
1
*
*
( )
k
k
k
k
k
x
x
x
x
x
x
g x
+
+
+
+
∆
=
−
→
=
−∆
=
( )
( *)
( *) ...
k
k
g x
g x
x g x
′
=
− ∆
+
1
*
( *)
( *)
k
k
x
x
g x
x g x
+
′
−∆
=
− ∆
1
( *)
k
k
x
g x
x
+
′
∆
=
∆
− zbieżność liniowa
*
( *)
x
g x
=
( *)
1
g x
′
<
− warunek zbieżności

n
n
n
x
eps
x
x
→
<
−
−1
jeżeli
- przybliżona wartość pierwiastka
Metoda Newtona (stycznych)
a
x
b
)
(x
f
1
x
=
2
x
3
x
x = b – pierwsze przybliżenie
Z: f(x) – funkcja ciągła w przedziale domkniętym [a, b]
0
)
(
)
(
<
⋅ b
f
a
f
Sz: pierwiastek f(x) = 0 z dokładnością eps
k
k
k
h
x
x
+
=
+1
n
n
n
x
eps
x
f
x
f
→
<
−
⋅
0
)
(
)
(
jeżeli
- przybliżona wartość pierwiastka
Warunki zakończenia obliczeń:

Wzór iteracyjny metody Newtona (stycznych)
)
(
)
(
1
k
k
k
k
x
f
x
f
x
x
′
−
=
+
)
(
)
(
)
(
2
)
(
)
(
2
2
1
k
k
k
k
k
k
k
x
f
x
f
x
f
x
f
x
f
x
x
′′
−
′
′
−
=
+
Wzór iteracyjny metody metoda Halley’a
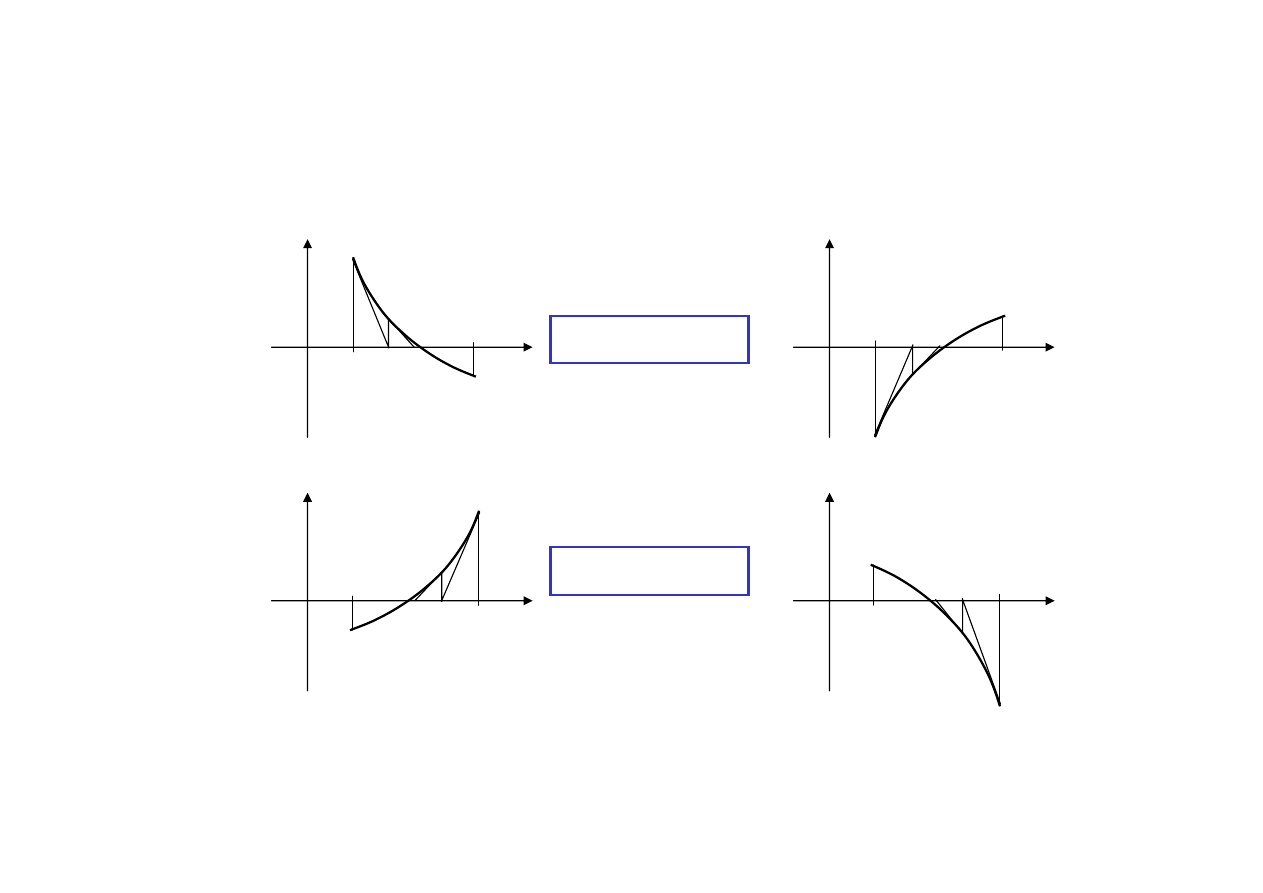
Możliwe przypadki
0
)
(
0
)
(
>
′′
>
a
f
a
f
0
)
(
0
)
(
<
′′
<
a
f
a
f
a
x
b
)
(x
f
a
x
b
)
(x
f
0
)
(
0
)
(
>
′′
>
b
f
b
f
0
)
(
0
)
(
<
′′
<
b
f
b
f
a
x
b
)
(x
f
a
x
b
)
(x
f
0
)
(
)
(
>
′′
⋅
a
f
a
f
0
)
(
)
(
>
′′
⋅
b
f
b
f
a - pierwsze przybliżenie
b - pierwsze przybliżenie
Z: nie zmienia znaku w przedziale [a,b]
)
(x
f ′′
Wyszukiwarka
Podobne podstrony:
2008 Metody obliczeniowe 12 D 2008 11 28 20 53 30
2008 Metody obliczeniowe 13 D 2008 11 28 20 56 53
metody obliczeniowep1 10
2008 Metody obliczeniowe 07 D 2008 10 29 19 28 1
2008 Metody obliczeniowe 06 D 2008 10 22 20 13 23
2008 Metody obliczeniowe 02 D 2008 10 1 21 28 5
2008 Metody obliczeniowe 08 D 2008 11 11 21 31 58
2008 Metody obliczeniowe 09 D 2008 11 11 21 32 51
fluoromethcathinone a new substance of abuse forensic sci intl 185 10 20 2009 j forsciint 2008 11 01
2008 Metody obliczeniowe 03 D 2008 10 1 22 5 47
2008 Metody obliczeniowe 08 D 2008 11 11 21 31 58
więcej podobnych podstron