Instytut Technologii Maszyn i Automatyzacji
Instrukcja Zakładu Metrologii i Badań Jakości
Nr 5
Podstawy Metrologii
BŁAĘDY POMIARÓW
WYZNACZENIE BŁĘDÓW POMIARU I NIEPEWNOŚCI POMIAROWEJ
DLA BEZPOŚREDNIEJ (RÓŻNICOWEJ)
METODY POMIARU
Opracował
dr inż. Stanisław Fita
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
2
1.PODSTAWOWE POJĘCIA METROLOGII I ICH OKREŚLENIA
Każda dziedzina wiedzy, nauki, lub techniki tworzy zbiór pojęć na własne potrzeby.
Często czerpie je z nauk pokrewnych lub z systemów pojęciowych innych krajów Jednak
żadna dziedzina wiedzy nie rozporządza jednym, jedynym uniwersalnym systemem pojęć
Metrologia warsztatowa (miernictwo warsztatowe) jest częścią metrologii - dziedziny
wiedzy o pomiarach - obejmującej wszystkie zagadnienia zarówno teoretyczne, jak i
praktyczne, odnoszące się do pomiarów niezależnie od ich dokładności. Słownictwo metrologii
warsztatowej ma zatem swe źródło w słownictwie metrologii. Metrologia jest nauką
interdyscyplinarną i korzysta z kolei z systemów pojęć takich nauk, jak fizyka i matematyka.
Podstawowe nazwy i określenia pojęć metrologii zawarte są w Polskiej Normie, której
słownictwo opiera się na międzynarodowym słowniku metrologii.
1.1 WIELKOŚĆ I WARTOŚĆ
Otaczające nas ciała i zjawiska można opisać (scharakteryzować) pewnym zbiorem
cech. Cechy te dzieli się na niemierzalne, to jest takie, które da się opisać tylko jakościowo,
np.: smak, zapach i mierzalne, które można opisać nie tylko jakościowo, ale i ilościowo, np.:
długość, masę, czas itp. Taka właśnie, właściwość zjawiska lub ciała, którą można wyznaczyć
jakościowo i ilościowo jest wielkością. Wielkość poddana mierzeniu jest nazywana wielkością
mierzoną. Natomiast wielkość nie będącą przedmiotem pomiaru, ale wpływającą na wartość
wielkości mierzonej lub wskazania przyrządu pomiarowego, lub wartość wzorca miary,
odtwarzającego wielkość jest wielkością wpływową. Na przykład, podczas dokładnych
pomiarów długości, wielkością wpływową jest temperatura.
Stan danej wielkości wyrażony iloczynem liczby i jednostki miary jest wartością
wielkości określonej (krótko - wartością), np.: 5 m, 12 kg. W podanych przykładach liczby są
wartościami liczbowymi wielkości a litery oznaczeniem jednostki miary. Jednostka miary jest to
wartość danej wielkości, której wartość liczbową umownie przyjęto równą jedności. Wartość
liczbowa wielkości zaś, liczbą oderwaną w wyrażeniu wartości określonej wielkości. Wartość
liczbowa zależy więc od przyjętej jednostki miary.
Wartość rozpatrywanej wielkości wyznacza się podczas pomiaru, a pomiar to czynności
doświadczalne mające na celu wyznaczenie wartości wielkości. W definicji tej nie mówi się o
tym, że czynności te trzeba najpierw zaplanować w oparciu o określoną teoretyczną, dobrać
sprzęt pomiarowy a dopiero wtedy je wykonać. Po wykonaniu pomiaru otrzymuje się jedną lub
więcej wartości odczytanych ze wskazań przyrządu pomiarowego. Wartość wielkości
mierzonej otrzymana w czasie pomiaru jest wynikiem pomiaru. Tak uzyskany wynik, jest
najczęściej surowym wynikiem pomiaru, ponieważ nie uwzględnia poprawek i nie ma
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
3
wyznaczonej niepewności pomiaru.
Wynik pomiaru uzyskany jako odczyt wskazania przyrządu zawsze różni się od
wartości prawdziwej, nazywanej wartością rzeczywistą, czyli wartością charakteryzującą
wielkość określoną jednoznacznie w warunkach istniejących w chwili, w której wartość ta jest
badana. Rzeczywista wartość wielkości jest więc wartością idealną, teoretyczną, najczęściej
nieznaną. Jest to pojecie abstrakcyjne, umowne.
Dlatego też wartość rzeczywistą zastępuje się wartością poprawną. Wartość poprawna
wielkości jest to wartość, którą się uważa w takim stopniu przybliżoną do wartości rzeczywistej
tej wielkości, że różnica miedzy tymi wartościami może być pominięta z punktu widzenia celu,
do którego wartość przybliżona jest potrzebna.
Poprawna wartość wielkości wyznacza się przeważnie za pomocą metod i przyrządów
o dokładności odpowiedniej dla każdego poszczególnego przypadku. Na przykład, licznik
energii elektrycznej, dla którego graniczne błędy dopuszczalne wynoszą
±2%, sprawdza się
licznikiem kontrolnym, którego błąd wskazań w tym zakresie nie przekracza
±1%. Licznik
kontrolny wskazuje wówczas wartości poprawne energii elektrycznej do celów legalizacji.
2 POJĘCIE BŁĘDU
Wynik każdego pomiaru, jak to już stwierdzono powyżej, różni się od wartości wielkości
mierzonej. Przyczyn powstania różnic jest wiele i niemal każdy człon łańcucha pomiarowego i
otoczenie może wywierać większy lub mniejszy wpływ niezgodność wyniku pomiaru z
wartością wielkości mierzonej, nazywaną błędem pomiaru. Pierwszą z przyczyn tej
niezgodności może być nieokreśloność obiektu pomiaru, dalej sposób odbioru sygnału
pomiarowego, błędy przetworników, błędy komparatora, błędy wzorca, niedoskonałość
urządzenia wskazującego, błędy obserwacji wskazania, błędy obliczeń i utrwalania wyniku i
wreszcie wpływ otoczenia (w postaci zakłóceń) na wszystkie wymienione człony.
Upraszczając, można przypisać przyczyny powstawania błędów obiektowi pomiarów,
przyrządowi pomiarowemu, obserwatorowi i otoczeniu.
Wartość wielkości mierzonej , wymieniona w definicji, jest wartością porównawczą
może być równa:
− wartości rzeczywistej (prawdziwej),
− wartości poprawnej,
− średniej arytmetycznej wyników serii pomiarów.
Wspomniana niezgodność może być wyrażona w postaci różnicy wyniku pomiaru i
jednej z powyższych wartości. W pierwszym przypadku będzie to błąd rzeczywisty, dalej błąd
poprawy i błąd pozorny.
Na przykład błąd poprawny wynosi:
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
4
p
x
x
x
−
=
∆
gdzie:
∆x – wartość bezwzględna błędu poprawnego,
x – wynik pomiary (surowy)
x
p
– wartość poprawna wielkości mierzonej.
W niektórych przypadkach, na przykład kiedy trzeba porównać błąd pomiaru różnych
wielkości, wygodniejszą formą przedstawiania błędy jest jego wartość względna:
[ ]
%
100
x
x
x
p
p
⋅
−
=
δ
Pierwszy sposób podawania błędu stosuje się, między innymi w pomiarach wielkości
geometrycznych a drugi w pomiarach wielkości elektrycznych. Wartość błędu bezwzględnego
podaje się w jednostkach mierzonej wielkości, natomiast błąd względny jest wyrażany jako
ułamek dziesiętny lub – najczęściej – w procentach.
3. KLASYFIKACJA BŁĘDÓW
Błąd i jego składowe mogą być klasyfikowane według różnych kryteriów. Jednym z nich
(już wymienianym), jest przyczyna lub źródło powstawania błędu. Z metrologicznego punktu
widzenia najważniejszym kryterium jest charakter błędu. Wyróżnia się wtedy: błąd
systematyczny, błąd przypadkowy
i błąd nadmierny (gruby).
3.1 BŁĄD SYSTEMATYCZNY
Błąd systematyczny to błąd, który przy wielu pomiarach tej samej wartości pewnej
wielkości, wykonywanych w tych samych warunkach, pozostaje stały co do wartości
bezwzględnej jak i co do znaku, lub zmienia się według określonego prawa wraz ze zmianą
warunków.
Przykładem błędu stałego może być błąd powstały podczas ważenia za pomocą
odważnika o masie przyjętej jako równej jego masie nominalnej 1 kg, podczas gdy jego masa
poprawna wynosi 1,010 kg.
Błąd systematyczny zmienny, może zmieniać się w sposób ciągły, lub okresowy. Na
przykład, podczas pomiarów odchyłek średnicy serii wałków za pomocą czujnika
zamocowanego w statywie, na skutek promieniowania cieplnego mierzącego, następuje
stopniowe nagrzewanie się kolumny statywu i jej wydłużanie się. Błąd będzie więc narastał
wraz ze wzrostem temperatury kolumny. Błąd zmieniający się w sposób okresowy występuje,
na przykład, w przypadku niewspółśrodkowego położenia osi podziałki i wskazówki.
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
5
3.2 BŁĄD PRZYPADKOWY
Jest to błąd zmieniający się w sposób nieprzewidziany zarówno co do wartości
bezwzględnej, jak i co do znaku, podczas wykonywania dużej liczby pomiarów tej samej
wartości pewnej wielkości w warunkach praktycznie niezmiennych (za pomocą tego samego
narzędzia pomiarowego i przez tego samego obserwatora w jednakowych warunkach
otoczenia). Przyczynami tego błędu może być rozrzut wskazań przyrządu pomiarowego,
spowodowany odkształcaniem się jego elementów, tarciem, niestarannym odczytywaniem
wskazań przez obserwatora, lub krótkotrwałymi niezauważalnymi zmianami wielkości
wpływowych.
3.3 BŁĄD NADMIERNY
Błąd wynikający nieprawidłowego wykonania pomiaru. Może on wynikać z fałszywie
odczytanego wskazania, czyli omyłki, z użycia uszkodzonego przyrządu, lub niewłaściwego
jego zastosowania. Częstą pomyłką, jest odczytywanie wskazania przyrządu
wielozakresowego z niewłaściwej podziałki. Zdarza się, że zapomina się dodać grubość
szczęk podczas pomiaru średnicy otworu suwmiarką jednostronną.
Błąd systematyczny pomiaru bezpośredniego
Błędy systematyczne są znane co do wartości bezwzględnej jak i co do znaku. Można
więc je usunąć z wyniku pomiaru za pomocą poprawki, którą można wyznaczyć teoretycznie
lub doświadczalnie:
X
P
∆
−
=
Poprawiony wynik pomiaru będzie miał postać:
P
X
X
p
+
=
Należy jednak pamiętać, że poprawkę wyznacza się również z pewnym błędem, który
jeśli nie może być pominięty, powinien być uwzględniony w oszacowaniu błędów
przypadkowych. Ustalenie przyczyn i źródeł powstawania błędów systematycznych należy do
zadania obserwatora (pomiarowca). Poprawnie zaplanowany, przygotowany i wykonany
pomiar nie powinien być obarczony błędami systematycznymi. Chyba, że warunki pomiaru, lub
zastosowana metoda pomiaru nie pozwala na ich uniknięcie.
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
6
Błędy przypadkowe w pomiarach pośrednich
Wyniki pomiarów obarczone błędami przypadkowymi (błędy przypadkowe) można, dla
odpowiednio dużej liczby pomiarów (n > 30), uważać za zmienną losową o rozkładzie
normalnym, ponieważ:
− błędy są zdarzeniami niezależnymi,
− każdorazowo może pojawić się błąd tylko o jednej wartości,
− błędy o małych wartościach zdarzają się częściej niż duże,
− błędy o jednakowych wartościach i przeciwnych znakach są jednakowo
prawdopodobne,
− błąd równy zeru jest najbardziej prawdopodobny.
Wpływ błędów przypadkowych na wynik pomiaru można wyznaczyć w oparciu
o rachunek prawdopodobieństwa. W tym celu należy wykonać serię pomiarów; zgodnie
z wcześniej przytoczoną definicją. Otrzymuje się w rezultacie n wyników:
X
1
, X
2
, X
3
, ..., X
i
, ..., X
n
Rozrzut ich wartości jest spowodowany błędami przypadkowymi. Następnie liczy się
średnią arytmetyczną tych wyników z zależności:
∑
=
⋅
=
+
+
+
+
+
=
n
1
i
i
n
i
3
2
1
X
n
1
n
X
X
X
X
X
X
K
K
Poszczególne wyniki pomiarów można opisać zależnościami:
n
i
3
2
1
p
s
r
n
p
s
r
i
p
s
r
3
p
s
r
2
p
s
r
1
X
X
X
X
X
X
X
X
X
X
∆
+
∆
+
=
∆
+
∆
+
=
∆
+
∆
+
=
∆
+
∆
+
=
∆
+
∆
+
=
M
M
gdzie:
X
r
–
wartość rzeczywista (prawdziwa),
i
p
∆ – wartość błędów przypadkowych,
s
∆ – wartość błędów systematycznych
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
7
Po wstawieniu do zależności wyników pomiarów, uzyskuje się:
∑
∑
=
=
∆
+
∆
+
=
∆
+
∆
⋅
+
⋅
=
n
1
i
p
s
r
n
1
i
p
s
r
i
i
n
1
X
n
n
X
n
X
Gdy liczba pomiarów dąży do nieskończoności i błędy systematyczne są równe zeru,
średnia arytmetyczna odpowiada wartości rzeczywistej mierzonej wielkości a suma błędów
przypadkowych staje się równa zeru.
W praktyce liczba wykonywanych pomiarów jest niewielka (n = 3
÷ 20), ponieważ
przedłużanie ciągu pomiarowego absorbuje dużo czasu i trudno jest utrzymać takie same
warunki pomiaru. Wtedy najczęściej zakłada się, że błędy pomiaru podporządkowane są
rozkładowi normalnemu i wyznacza odchylenie średnie kwadratowe serii n pomiarów od
wartości średniej, ze wzoru:
(
)
1
n
X
X
s
n
1
i
2
i
−
−
=
∑
=
Otrzymana z wyników pomiarów wartość średnia X różni się od wartości rzeczywistej X
r
mierzonej wielkości. Miarą tej rozbieżności jest odchylenie kwadratowe średniej arytmetycznej:
(
)
(
)
1
n
n
X
X
n
s
s
n
1
i
2
i
+
−
=
=
∑
=
Granice błędu przypadkowego
∆
p
na odpowiednim poziomie ufności można wyznaczyć jako
iloczyn odchylenia średniego kwadratowego s przez odpowiednią wartość parametru t, dla
przyjętego poziomu ufności. Na przykład: dla t = 1, poziom ufności wynosi P = 0,68, dla t = 2 –
P = 0,95, dla t = 3 – P = 0,997. Niepewność pojedynczego wyniku pomiaru obarczonego tylko
błędem przypadkowym wynosi:
ts
p
±
=
∆
a wartości średniej –
s
t
± . Wynik serii pomiarów może być zapisany w postaci:
n
s
t
X
s
t
X
X
±
=
⋅
±
=
y-
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
8
Gdy liczba pomiarów w serii jest niewielka, wartości s i s są obliczane tylko w przybliżeniu i
nie odpowiadają ściśle parametrom rozkładu normalnego, słusznego dla dużej liczby wyników
pomiaru. Dla małych prób dostatecznie dobrym przybliżeniem opisu zmiennych losowych,
jakimi są wyniki pomiarów, jest rozkład t-Studenta .
4. PODSTAWOWE ZASADY RACHUNKU BŁĘDÓW
1. Najlepszym przybliżeniem serii n pomiarów (X,. X
:
. ... X„) wielkości fizycznej X jest średnia
arytmetyczna:
∑
=
=
n
1
i
i
X
n
1
X
2. Błąd bezwzględny i - tego pomiaru wielkości fizycznej X jest równy
X
X
X
i
i
−
=
∆
3. Błędem względnym
δ wartości zmierzonej X, nazywamy stosunek błędu bezwzględnego ∆X
i
do wartości średniej :
X
X
X
i
i
∆
=
δ
Błąd względny wyrażony w procentach nazywamy błędem procentowym.
4. Średni błąd kwadratowy
x
S pojedynczego pomiaru skończonej serii n pomiarów wielkości
fizycznej X wynosi:
(
)
1
n
x
x
S
n
1
i
2
i
x
−
−
=
∑
=
5. Średni błąd kwadratowy
X
S wartości średniej X skończonej serii n pomiarów wielkości
fizycznej X wynosi:
(
)
(
)
( )
(
)
1
n
n
X
1
n
n
x
x
S
n
1
i
2
i
n
1
i
2
i
x
−
∆
=
−
−
=
∑
∑
=
=
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
6 Wartości błędów zaokrąglamy zawsze w górę. Najpierw błędy zaokrąglamy z dokładnością
do jednej cyfry znaczącej. Jeżeli wstępne zaokrąglenie powoduje wzrost wartości błędu o
więcej niż 10%, zaokrąglamy go z dokładnością do dwóch cyfr znaczących.
7. Wyniki pomiarów zaokrąglamy z dokładnością do miejsca, na którym występuje ostatnia
cyfra znacząca błędu.
8. Wynik pomiaru zapisujemy w postaci
∆
±
X
,
gdzie X jest najlepszym przybliżeniem
wartości mierzonej, a
∆ jest wartością błędu bezwzględnego pomiaru wielkości X. Zapisując
wynik pomiaru należy podać jednostki układu SI w jakich wielkość została zmierzona
9. Klasa przyrządu pomiarowego „kl” jest to wyrażony w procentach stosunek maksymalnego
błędu bezwzględnego
∆X
max
do zakresu pomiarowego Z.
%
100
Z
X
kl
max
⋅
∆
=
10. Prawo przenoszenia niezależnych błędów przypadkowych dla wielkości złożonej
(
)
n
2
1
x
,
,
x
,
x
f
y
K
=
ma postać.
2
pm
m
2
2
p
2
2
1
p
1
p
X
f
X
f
X
f
y
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∆
∂
∂
+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∆
∂
∂
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∆
∂
∂
=
∆
K
gdzie
(
m
,
,
2
,
1
i
X
f
i
L
=
∂
∂
)
oznacza wartość pochodnej cząstkowej funkcji
,
a
∆
(
)
m
2
1
X
,
,
X
,
X
f
y
K
=
mi
jest wartością przypadkowego błędu pomiaru i – tej wielkości X.
11. Prawo przenoszenia błędów systematycznych (skorelowanych) dla wielkości złożonej
(
)
n
2
1
x
,
,
x
,
x
f
y
K
=
ma postać:
sm
m
2
s
2
1
s
1
s
X
f
X
f
X
f
y
∆
∂
∂
+
+
∆
∂
∂
+
∆
∂
∂
=
∆
K
Opracował: dr inż. Stanisław FITA
9
12. Jeżeli wielkość mierzona jest wyrażona w postaci iloczynu dowolnych potęg wielkości
mierzonych bezpośrednio
, obliczyć korzystając z metody pochodnej
m
n
1
2
k
1
X
X
cX
y
K
⋅
=
logarytmicznej:
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
10
n
n
2
2
1
1
X
X
m
X
X
l
X
X
k
y
y
∆
+
+
∆
+
∆
=
∆
K
13. Jeżeli zmierzono wartości (X
i
,Y
i
), i = 1, 2, ..., n dwóch różnych wielkości fizycznych X i Y, o
których wiadomo, że są związane ze sobą zależnością liniową, to najlepszym przybliżeniem
współczynników X i B w równaniu y = Ax + B jest:
Γ
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
∑
∑
∑
=
=
=
1
y
x
y
x
n
A
n
1
i
i
n
1
i
i
n
1
i
i
i
Γ
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
=
∑
∑
∑
∑
=
=
=
=
1
y
x
x
y
X
B
n
1
i
i
i
n
1
i
i
n
1
i
i
n
1
i
2
i
gdzie:
2
n
1
i
i
1
1
i
2
i
x
x
n
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
Γ
∑
∑
=
=
Wartości A i B są obarczone błędami:
Γ
σ
=
∆
∑
=
n
1
i
2
i
y
x
A
,
Γ
σ
=
∆
n
B
y
gdzie:
(
)
2
n
B
Ax
y
n
1
i
2
i
i
y
−
−
−
=
σ
∑
=
OBLICZANIE BŁĘDÓW PRZYPADKOWYCH NA PODSTAWIE ROZKŁADU T-STUDENTA
Gdy liczba pomiarów jest niewielka, wartości s i s są obliczane tylko w przybliżeniu i nie
odpowiadają ściśle parametrom rozkładu normalnego słusznego dla dużej liczby wyników
pomiarów. Dla małych prób dostatecznie dobrym przybliżeniem opisu zmiennych losowych,
jakimi są wyniki pomiarów, jest rozkład t-Studenta. Jest to funkcja matematyczna zależna od
liczby pomiarów n użytych do obliczania odchylenia średniego kwadratowego s. Przykładowe,
zaokrąglone wartości współczynników t i
n
t
rozkładu Studenta dla różnych liczb pomiarów n i
różnych poziomów ufności p, podano w tabeli. Korzystając z rozkładu Studenta można
wyznaczyć:
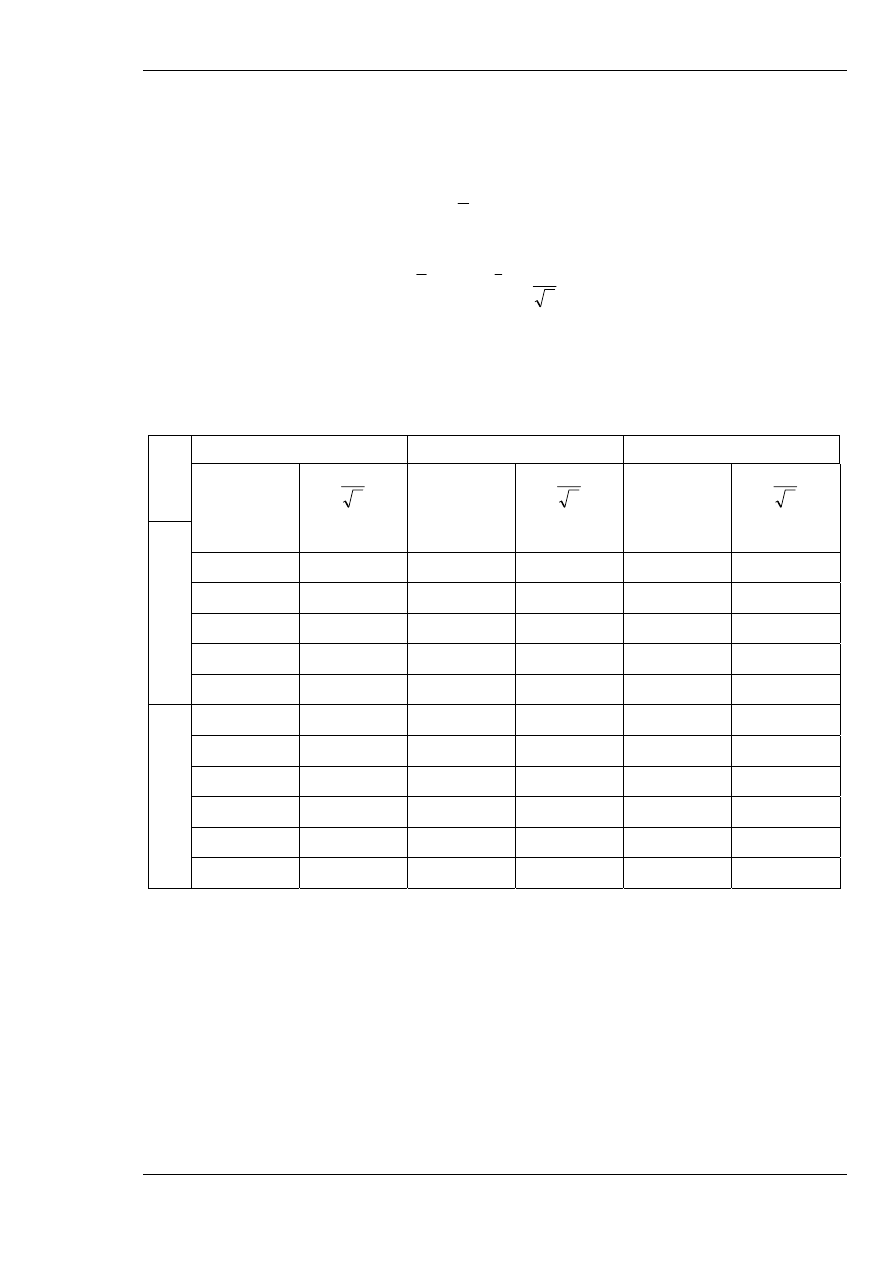
Instytut Technologii Maszyn i Automatyzacji
Zakład Metrologii i Badań Jakości
Opracował: dr inż. Stanisław FITA
11
− błąd przypadkowy pojedynczego pomiaru X:
s
t
p
,
n
p
⋅
±
=
∆
− błąd przypadkowy średniej X :
s
n
t
s
t
p
,
n
p
,
n
p
⋅
±
=
⋅
±
=
∆
Współczynniki t rozkładu Studenta
p = 0,68
P = 0,95
p = 0,997
n
t
n
t
t
n
t
t
n
t
1
1,8
1,3
12,7
9,0
233
166
3
1,32
0,76
4,3
2,5
19,2
11,1
4
1,20
0,60
3,2
1,6
9,2
4,6
5
1,15
0,51
2,8
1,24
6,6
3,0
6
1,11
0,45
2,6
1,05
5,5
2,3
7
1,08
0,38
2,7
0,84
4,5
1,6
10
1,06
0,34
2,3
0,72
4,1
1,29
20
1,03
0,23
2,1
0,47
3, 4
0,77
30
1,02
0,19
2,0
0,37
3,3
0,60
50
1,01
0,14
2,0
0,28
3,16
0,45
100
1,00
0,10
2,0
0,20
3,1
0,31
200
1,00
0,07
1,97
0,14
3,04
0,22