Instytut Technologii Maszyn i Automatyzacji

Instrukcja Zakładu Metrologii i Badań Jakości

Nr 1

Podstawy Metrologii

METODY POMIAROWE

POMIARY POŚREDNIE, BEZPOŚREDNIE I POŚREDNIE

PRZYRZĄDAMI NONIUSZOWYMI I CZUJNIKOWYMI

Opracował

dr inż. Stanisław Fita

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

Opracował: dr inż. Stanisław FITA

2

1. Pomiar a sprawdzanie.

Według normy pomiar są to czynności doświadczalne mające na celu wyznaczenie

wartości wielkości. Definicja ta jest bardzo ogólna i nie mówi jak należy go realizować Z tego

punktu widzenia, bardziej szczegółowe jest stwierdzenie, że:

mierzenie polega na porównaniu cechy o nieznanym stanie ze znanymi stanami tej samej

cechy, aż do ustalenia takiego stanu o znanej mierze, który jest równoważny stanowi

mierzonemu; jako miarę cechy przyjmuje się miarę równoważnej jej cechy wzorcowej. Dążenie

do matematycznego sformalizowania tej definicji doprowadziło do zapisu, że:

mierzenie jest eksperymentem prowadzącym do wyznaczenia liczb modelujących

konkretne cechy przedmiotów i zdarzeń (J. Jaworski).

Opis sposobu pomiaru obejmuje, oprócz czynności ściśle pomiarowych, również takie, jak:

przygotowanie mierzonych przedmiotów i przyrządów pomiarowych, wzajemne ustawienie

przedmiotu i przyrządu, konserwację przedmiotów i przyrządów po pomiarach oraz obliczenia

i zapisanie wyniku pomiaru. Niekiedy rozróżnia się pomiar oraz mierzenie i przypisuje temu

ostatniemu terminowi czynności ściśle pomiarowe (R. Kolman).

W przypadku stosowania sprawdzianów mówi się o sprawdzaniu, które polega na

stwierdzeniu czy wartość mierzonej wielkości mieści się w przewidzianych granicach. Na przykład

czy średnica wałka mieści między wymiarami granicznymi. Niekiedy uważa się, że sprawdzanie

jest pojęciem szerszym od mierzenia. Aby sprawdzić poprawność wykonania, na przykład wałka,

trzeba zmierzyć jego wymiary, odchyłki kształtu, chropowatość powierzchni, twardość itp. Jest to

raczej kontrola wykonania, niż sprawdzanie.

2. Metody pomiarowe. Klasyfikacja.

Metody pomiarowe klasyfikuje się według różnych kryteriów. Najczęściej dzieli się je

ze względu na sposób:

– uzyskania wyniku pomiaru,

– porównania dokonywanego w trakcie procesu pomiarowego,

– przetwarzania

sygnału pomiarowego.

W pomiarach warsztatowych można jeszcze podzielić pomiary z uwagi na wykorzystywaną bazę

pomiarową na odniesieniowe i bezodniesieniowe, oraz z uwagi na sposób odbierania sygnału

pomiarowego na stykowe i bezstykowe. Należy jednak pamiętać, że klasyfikacja ta nie jest

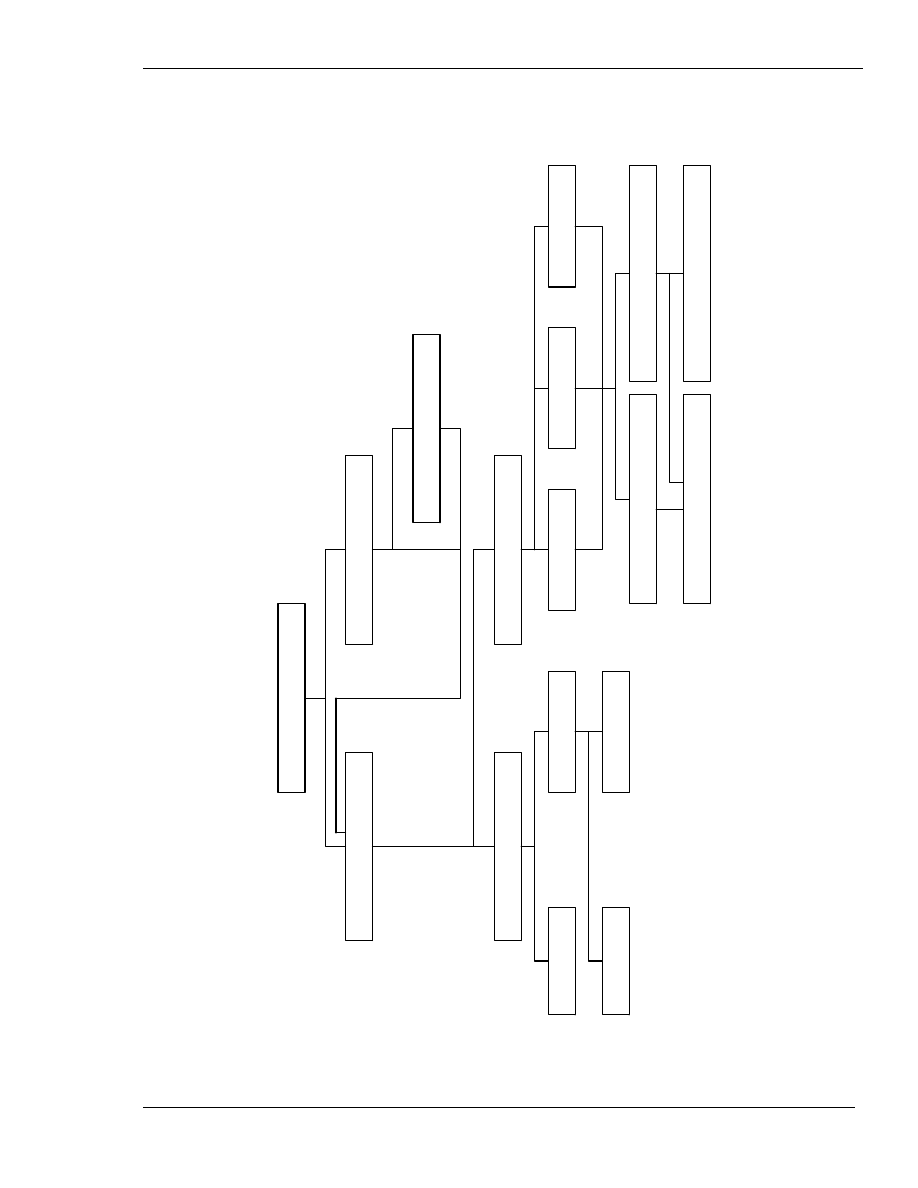
Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

Opracował: dr inż. Stanisław FITA

3

Meto

dy pomia

row

e

Metod

a

bezw

zgl

ę

dna

Po

średnie

Be

zp

o

śre

dnie

Met

ody zer

o

w

e

Me

tody w

ychy

łow

e

K

lasyczn

a

Ró

żnicow

a

P

o

rów

naw

cza

Ró

żnicow

a

Komp

ensacyjn

a

Komparacyjn

a

Pod

staw

ienia

R

ó

w

now

aż

enie r

ę

cz

ne

Równ

o

w

a

żenie auto

m

atyczne

Ró

wn

o

w

aż

enie ci

ąg

łe

R

ó

w

now

a

żenie prog

ramow

e

R

ys. 1. Klasyfikacj

a

metod pomiarow

ych

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

nie jest sztywna, a jedynie umowna, ponieważ ten sam pomiar można zakwalifikować

(w niektórych przypadkach) do różnych metod, nawet dla tego samego kryterium.

Ze względu na sposób otrzymania wyniku wyróżnia się metodę pomiarową bezpośrednią,

pośrednią i złożoną.

Metoda pomiarowa bezpośrednia - metoda, dzięki której wartość wielkości mierzonej

otrzymuje się bezpośrednio, bez potrzeby wykonywania dodatkowych obliczeń opartych na

zależności funkcyjnej mierzonej wielkości od innych wielkości. Równanie tej metody ma postać:

X

c

Y

⋅

=

gdzie:

Y – surowy wynik pomiaru,

c –

stała przyrządu (zwykle c = 1)

X –

wartość odczytana.

Metoda pomiarowa pozostaje bezpośrednia nawet wówczas, gdy trzeba wykonania

pomiarów uzupełniających dla określenia wartości wielkości wpływowych, w celu wprowadzenia

odpowiednich poprawek (np. poprawki na temperaturę). Metodą tą realizowane są na przykład

pomiary masy wagą uchylna, pomiary długości przymiarem kreskowym czy też mikrometrem.

Metoda pomiarowa pośrednia polega na tym, że wartość wielkości mierzonej otrzymuje się

pośrednio z pomiarów bezpośrednich innych wielkości związanym odpowiednio (znaną

zależnością) z wielkością mierzoną. Wynik pomiaru jest wtedy funkcją wielkości mierzonych:

(

)

n

3

2

1

X

,

X

,

X

,

X

f

Y

K

=

gdzie:

X

1

, X

2

, X

3

,

…X

n

– surowe wyniki pomiarów wielkości mierzonych bezpośrednio.

Przykładem realizacji tej metody jest pomiar gęstości ciała na podstawie pomiarów jego

masy i objętości, a w pomiarach długości, pomiar średnicy wałka na podstawie pomiaru

długości cięciwy i jej strzałki.

Metoda polegająca na bezpośrednim wyznaczaniu wartości pewnej liczby wielkości albo

na pośrednim wyznaczaniu wartości tych wielkości grupowanych w różnych kombinacjach, co

wymaga rozwiązań odpowiednich układów równań, jest metodą złożoną. Ogólnie może to być

następujący układów równań:

(

)

(

)

(

)

⎪

⎪
⎭

⎪

⎪
⎬

⎫

=

=

=

0

Y

,

Y

,

Y

,

Y

X

,

X

,

X

,

X

f

0

Y

,

Y

,

Y

,

Y

X

,

X

,

X

,

X

f

0

Y

,

Y

,

Y

,

Y

X

,

X

,

X

,

X

f

n

3

2

1

n

3

2

1

n

n

3

2

1

n

3

2

1

2

n

3

2

1

n

3

2

1

1

K

K

M

K

K

K

K

Opracował: dr inż. Stanisław FITA

4

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

Opracował: dr inż. Stanisław FITA

5

Metoda ta jest wykorzystywana na przykład do pomiaru masy poszczególnych odważników

kompletu, gdy znana jest masa jednego z nich i gdy są znane wyniki porównań mas różnych

możliwych kombinacji odważników. W pomiarach długości i kąta metodę tę stosuje się,

na przykład do wyznaczania odchyłki kąta prostego trzech kątowników, przez wzajemne

porównanie par tych kątowników ustawianych na płycie pomiarowej.

Sposób porównywania bardziej różnicuje metody pomiarowe niż sposób otrzymania

wyniku. I tak, norma wyróżnia metodę podstawową i kilka odmian metod porównawczych. Można

też spotkać inny podział metod porównawczych (Z. Orzeszkowski). Metody porównawcze dzieli

się na trzy grupy, a mianowicie: metody bezpośredniego porównania, metody różnicowe i metody

pośredniego porównania oraz wyodrębnia z metody zerowej metodę kompensacyjną i metodę

komparacyjną.

Zgodnie z wcześniej wymienioną normą, poszczególne metody definiuje się następująco:

Metoda pomiarowa podstawowa polega na pomiarach wielkości podstawowych wymienionych

w definicji wielkości. Metoda ta jest też czasem nazywana metodą bezwzględną. Przykładem

metody podstawowej jest pomiar wartości ciśnienia za pomocą manometru obciążnikowo-

tłokowego. W metodzie tej za podstawę przyjmuje się definicję ciśnienia jako stosunku siły

normalnej do pola przekroju, na które działa siła. Jest to wiec metoda pośrednia. Natomiast

w pomiarach wielkości podstawowych będzie to metoda bezpośrednia.

Metoda pomiarowa porównawcza polega na porównaniu wartości wielkości mierzonej

z inna wartością tej samej wielkości lub też ze znaną wartością innej wielkości jako funkcji

wielkości mierzonej. Pomiarem porównawczym, zgodnie z definicją, jest pomiar objętości cieczy

za pomocą wzorca pojemności, a także pomiar ciśnienia za pomocą manometru. Niekiedy uważa

się, że tylko w porównywaniu dwóch wielkości tego samego rodzaju ma się do czynienia z metodą

porównawczą.

Metoda pomiarowa bezpośredniego porównania polega na porównani całkowitej wartości

wielkości mierzonej z wartością znaną tej samej wielkości, która w postaci wzorca wchodzi

bezpośrednio do pomiaru. Pomiary długości za pomocą przymiaru kreskowego, objętości cieczy

za pomocą pojemnika, masy za pomocą wagi przez zrównoważenie mierzonej masy ciała

odpowiednią sumą mas odważników są przykładami metody bezpośredniego porównania. Należy

dodać, że przykłady pierwszy i trzeci są ilustracją metody podstawowej, ponieważ długość i masa

są wielkościami podstawowymi.

Odmianami metody bezpośredniego porównania są metody podstawiania i przestawiania.

Pierwsza z nich polega na zastąpieniu wartości wielkości mierzonej wartości A znaną tej samej

wielkości, wybraną w ten sposób, aby skutki wywołane przez te wartości były takie same.

Przykładem takiego pomiaru jest wyznaczanie masy za pomocą wagi i odważników metodą

Bordy. Druga z metod polega na zrównoważeniu wartości wielkości mierzonej najpierw ze znaną

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

Opracował: dr inż. Stanisław FITA

6

wartością A tej samej wielkości, następnie na podstawieniu wielkości mierzonej na miejsce A

i ponownym zrównoważeniu jej za pomocą wartości B tej samej wielkości. Jeżeli pozycja

wskazówki pokazującej równowagę jest jednakowa w obu przypadkach, to wartość wielkości

mierzonej jest równa pierwiastkowi kwadratowemu z iloczynu A i B. Metodę tę stosuje się do

wyznaczania masy za pomocą wagi i odważników kontrolnych metodą podwójnego ważenia

Gaussa.

Jedną z częściej stosowanych jest metoda pomiarowa różnicowa. Polega ona na

porównaniu wartości wielkości mierzonej z niewiele różniącą się od niej znaną wartością tej samej

wielkości i pomiarze różnicy tych wartości. Metodą tą mierzy się odchyłkę A od wymiaru

nominalnego N średnicy D wałka; wymiar nominalny jest wtedy wartością znaną, odtwarzaną

przez stos płytek, a średnica D wartością wielkości mierzonej.

Metoda pomiarowa zerowa jest odmianą metody różnicowej. Polega na sprowadzeniu do

zera różnicy miedzy wartością wielkości mierzonej a wartości a znaną tej samej wielkości z nią

porównywaną. Porównanie ze sobą wartości pewnej wielkości może być zastąpione przez

porównanie odpowiadających im wartości innej wielkości. Jeżeli do pomiaru odchyłki średnicy

wałka tak dobierze się wysokość stosu płytek, że wskazanie czujnika - gdy pod jego końcówką

znajduje się stos płytek a potem wałek - będzie takie same, to metoda różnicowa stanie się

metodą zerową.

W pomiarach elektrycznych oraz pomiarach wielkości nieelektrycznych metodami

elektrycznymi stosuje się dwie odmiany metody zerowej, a mianowicie metodę kompensacyjną

i metodę komparacyjną.

Metoda kompensacyjna charakteryzuje się tym, że wielkości mierzonej przeciwstawia się

wzorcową wielkość kompensującą tego samego rodzaju o znanej wartości, która kompensuje

fizyczne działanie wielkości mierzonej na detektor. W stanie równowagi fizycznej działanie

wielkości mierzonej i kompensującej są jednakowe i przeciwnie skierowane, dlatego następuje

pełna kompensacja ich działania. Fizyczne działanie wielkości można kompensować tylko wtedy,

gdy jej sygnał jest nośnikiem energii Jako przykład realizacji tej metody podaje się wagę

równoramienną, w której następuje kompensacja momentów.

Jeżeli jedną lub obie porównywane wielkości przetworzy się tak, aby reprezentowały

wielkości jednakowe, będące nośnikami energii, a następnie je skompensuje, to taka metoda

pomiaru nazywa się komparacyjną.

leszcze jedną odmianą metody różnicowej jest metoda koincydencyjna. Polega ona na

wyznaczaniu przez obserwację koincydencji pewnych wskazów lub sygnałów małej różnicy

między wartością wielkości mierzonej i z nią porównywanej znanej wartości tej samej wielkości

Metodą tą mierzy się czas; obserwuje się koincydencję wzorcowych sygnałów czasu z sygnałami

zegara porównawczego. Podobny jest pomiar ułamkowych części milimetra za pomocą noniusza

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

suwmiarki.

Również często jest stosowana metoda pomiarowa wychyleniowa. Jest to metoda

porównawcza, polegająca na wyznaczaniu wartości wielkości mierzonej na podstawie wychylenia

wskazówki urządzenia wskazującego lub ogólniej - na podstawie zmiany wzajemnego położenia

wskazówki i podziałki Jest ona stosowana podczas pomiaru ciśnienia za pomocą manometru

z elementem sprężystym, pomiaru masy za pomocą wagi uchylnej, a także napięcia

woltomierzem z analogowym urządzeniem wskazującym W każdym z tych przykładów występuje

niezgodność rodzaju wielkości mierzonej i wzorcowej cała wartość wielkości mierzonej jest wtedy

przetwarzana w przyrządzie na wielkość tego samego rodzaju co wzorcowa, a następnie

porównania. Zwykle metoda wychyleniowa polega na wywołaniu momentu siły, zależnego od

wartości wielkości mierzonej. Moment ten jest równoważony przez przeciwnie skierowany moment

wytworzony elementem sprężystym, którego odkształcenia powodują ruch części ruchomej

urządzenia wskazującego Wychylenie tej części wskazuje wartość wielkości mierzonej na

podziałce wywzorcowanej w jednostkach wielkości mierzonej.

Ze względu na sposób przetwarzania sygnału pomiarowego rozróżnia się metodę

analogową i cyfrową. W metodzie analogowej wartość wielkości mierzonej, która zmienia się

w sposób ciągły, odpowiada również wielkość wyjściowa (wskazanie) o ciągłych wartościach.

W metodzie cyfrowej ciągłym przedziałom wartości wielkości mierzonej są przyporządkowane

nieciągłe (dyskretne) przydziały wartości wielkości wyjściowej To znaczy, że wartości wyjściowe

mają formę cyfrową, która składa się z całkowitej liczby kwantów

Jeśli odbiorca wyniku jest obserwator, to stosowany jest dziesiętny system zapisu cyfr, jeśli

maszyna cyfrowa - system kodowany dwójkowo. Gdy w układzie pomiarowym tylko urządzenie

wskazujące pracuje cyfrowo, a proces pomiarowy przebiega analogowo, wówczas metoda taka

nie może być uważana za w pełni cyfrową.

Ze względu na sposób określenia wyniku rozróżnia się następujące rodzaje pomiarów:

Pomiary bezpośrednie

, w których wynik y otrzymuje się wprost ze wskazania" narzędzia

pomiarowego, jako wartość x mierzonej wielkości, co można przedstawić za pomocą

następującego związku:

x

y

=

Przykładem pomiaru bezpośredniego jest określenie długości przedmiotu przez porównanie

z przymiarem kreskowym.

Pomiary pośrednie

, w których wynik y oblicza się z zależności:

(

)

n

2

1

x

,

x

,

x

f

y

K

=

Opracował: dr inż. Stanisław FITA

7

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

Opracował: dr inż. Stanisław FITA

8

jaką jest związany z wartościami x

1

, x

2

,

…x

n

wielkości mierzonych bezpośrednio. Np. pomiar taki

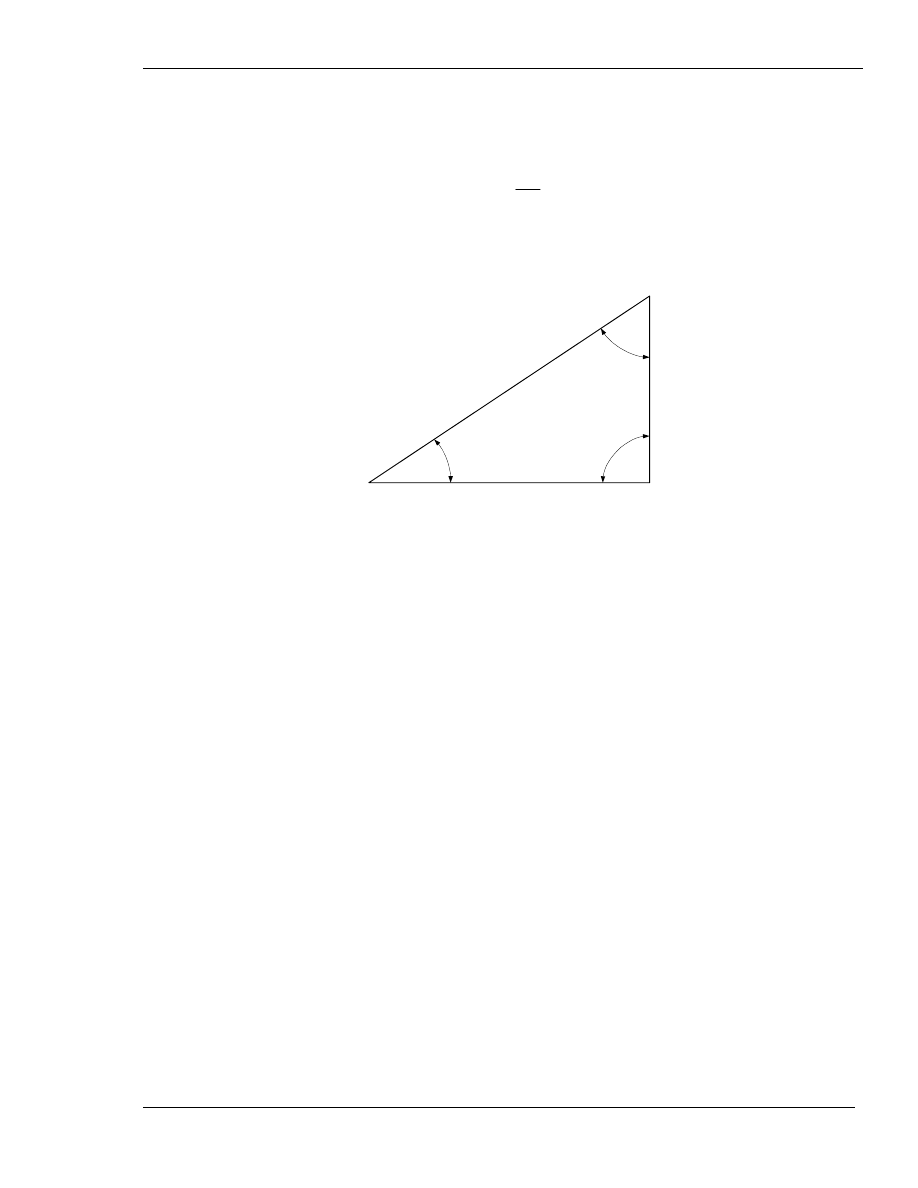
ma miejsce, gdy kąt

α (rys. 2) określamy z zależności:

AB

BC

tg

arc

mierząc długość boków AB i BC w trójkącie prostokątnym ABC.

A

C

B

β

γ

α

Rys. 2.

Pomiary złożone (uwikłane)

, w których m wyników y

i

i n wartości x

j

bezpośrednio lub

pośrednio mierzonych wielkości są związane zespołem m równań:

(

)

n

2

1

i

i

x

,

x

,

x

f

y

K

=

Wyniki y

i

otrzymuje się, rozwiązując równania. Przykładem tego rodzaju pomiarów może być

wzorcowanie galwanometru połączonego z termoparą, dla której zależność wskazania E od

temperatury

θ gorącego końca termopary określa związek:

(

) (

)

2

0

0

B

A

E

θ

−

θ

+

θ

−

θ

=

gdzie:

θ

0

– temperatura zimnych końców termopary

A i B

– stale układu pomiarowego.

Stałe A i B określa się z otrzymanych dwóch wskazań E

1

i E

2

galwanometru, jeśli gorący

koniec termopary osiąga kolejno dwie znane wartości

θ

1

i

θ

2

temperatury. Podstawiając

wymienione wartości do wzoru, otrzymujemy zespół dwóch równań, których rozwiązanie określa

stałe A i B. Mając te stałe możemy ustalić zależność wskazań E galwanometru od temperatury

θ

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

gorącego końca termopary.

Zasadę, na której oparty jest sposób przeprowadzenia pomiaru, nazywamy metodą

pomiarową

. Rozróżnia się następujące ważniejsze metody pomiarowe:

Metoda bezpośredniego porównania

polega na porównaniu całkowitej wartości

mierzonej wielkości z wartością znaną tej samej wielkości, która w postaci wzorca wchodzi

bezpośrednio do pomiaru. Przykładem jest pomiar długości, za pomocą przymiaru kreskowego

lub. pomiar objętości cieczy za pomocą pojemnika.

Metoda przez podstawienia

polega na zastąpieniu wartości wielkości mierzonej

wartością znaną tej wielkości, wybraną w ten sposób, aby skutki wywołane przez te dwie wartości

były takie same. Jako przykład może służyć metoda podstawieniowa Bordy pomiaru masy

polegająca na tym, że wstępnie zrównoważoną na wadze mierzoną masę zastępuje się

odważnikami doprowadzającymi wagę do poprzedniego wskazania. Odważniki zastępujące masę

określają jej miarę.

Metoda przez przestawienie

jest odmianą metody bezpośredniego porównania i polega

na zrównoważeniu wartości x wielkości mierzonej najpierw znaną wartością a

1

tej wielkości,

następnie na podstawieniu wielkości mierzonej na miejsce a

1

i ponownym zrównoważeniu jej ze

znaną wartością a

2

tej samej wielkości. Jeżeli wskazania przyrządu pomiarowego są jednakowe w

obu przypadkach, to wartość wielkości mierzonej jest równa:

2

1

a

a

x

=

Na tej zasadzie oparta jest np. metoda podwójnego ważenia Gaussa stosowana do pomiaru masy

za pomocą wagi i odważników.

Metoda różnicowa

jest metodą porównawczą polegającą na porównaniu wartości

wielkości mierzonej z niewiele różniącą się od niej znaną wartością tej samej wielkości' i pomiarze

różnicy tych wartości. Przykładem tej metody może być pomiar za pomocą czujnika różnicy

długości przedmiotu mierzonego i płytki wzorcowej.

Metoda zerowa

jest metodą różnicową, w której różnicę wartości wielkości mierzonej i

znanej wartości tej samej wielkości z nią porównywanej sprowadza się do zera. Przykładem może

być pomiar oporu elektrycznego za pomocą mostka Wheatstone'a i wskaźnika równowagi.

Metoda koincydencyjna polega na zaobserwowaniu zgodności wskazań lub sygnałów

odpowiadających wartości wielkości mierzonej i z nią porównywanej znanej wartości wielkości

tego samego rodzaju. Przykładem tej metody jest pomiar długości za pomocą suwmiarki, w

którym zetknięciu szczęk suwmiarki z przedmiotem mierzonym w miejscach określających jego

długość odpowiada wskazanie noniusza na podziałce suwmiarki.

Opracował: dr inż. Stanisław FITA

9

Wartością nominalną wzorca miary

jest wartość podana na nim, którą on powinien

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

Opracował: dr inż. Stanisław FITA

10

odtwarzać.

Wskazaniem narzędzia pomiarowego

jest wartość wielkości mierzonej wskazana przez

to narzędzie. Pojęcie wskazania odnosi się również do wzorców miar, w przypadku których jest.

ono równoważne wartości nominalnej wzorca.

Stałą narzędzia pomiarowego

nazywa się współczynnik, przez który należy pomnożyć

wskazanie tego narzędzia w celu otrzymania wyniku pomiaru. Jeśli narzędzie wskazuje

bezpośrednio wartość wielkości mierzonej, to jego stała jest równa jedności. Jeśli wskazania

narzędzia pomiarowego wyrażone są w innej jednostce niż jednostka miary, wielkości mierzonej,

to jego stała jest liczbą mianowaną. Natomiast jeśli wskazania narzędzia pomiarowego są

wyrażone w jednostce wielkości mierzonej, to jego stała jest liczbą oderwaną. Narzędzie

wielozakresowe z jedną podziałką ma wiele stałych odpowiadających poszczególnym zakresom

pomiarowym.

Obserwacja wskazania narzędzia pomiarowego

polega na systematycznym śledzeniu

jego wskazań. Odczytanie wskazania narzędzia pomiarowego polega na liczbowym określaniu

wartości tego wskazania.

Doświadczenie

polega na zebraniu spostrzeżeń na podstawie zaobserwowanych .faktów.

Eksperyment

jest zabiegiem wywołującym efekt w określonych warunkach.

Wartość wielkości mierzonej, otrzymana z przeprowadzonego pomiaru nazywa się

wynikiem pomiaru

. Wynik pomiaru jest surowy, gdy nie zawiera poprawek lub gdy nie jest

określona jego niedokładność. Wynik pomiaru jest poprawiony, gdy uwzględnia poprawki

wynikające z systematycznych błędów pomiaru.

Powtarzalność pomiarów

jest stopniem zgodności kolejnych ich wyników otrzymanych

przy pomiarze tej samej wartości wielkości w niezmienionych warunkach i przez tego samego

obserwatora.

Odtwarzalność pomiaru

jest stopniem zgodności wyników pomiarów tej samej wartości

wielkości otrzymanych bądź w rożnych warunkach, bądź za pomocą różnych narzędzi

pomiarowych, różnych metod bądź też przez różnych obserwatorów.

Adaptacyjność

pomiaru polega na samoczynnym dostosowaniu się sposobu i narzędzia

pomiarowego do zmieniających się warunków lub powstałych w czasie pomiaru wymagań.

3. Ilość informacji w wyniku pomiaru.

W naukach przyrodniczych i w technice głównym źródłem informacji są wyniki pomiarów

charakteryzujące stany i procesy zachodzące w świecie materialnym. Idealizując rzeczywiście

zachodzące fakty, można założyć, że dostarczana przez pomiary informacja może napływać

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

w sposób ciągły, tj. określać procesy, które charakteryzują się wielkościami przyjmującymi

dowolne wartości w danym zakresie. Jednak wielkości fizyczne mają charakter ziarnisty, tzn.,

że mogą zmieniać się tylko z określonym stopniowaniem, gdyż fakty w świecie materialnym

zachodzą tylko skokami i mogą być notowane tylko ze skończoną dokładnością. Gdyby, jakieś

zjawisko zmieniało się w sposób ciągły w określonym zakresie, to w tym zakresie

charakteryzowałoby się nieskończenie wielu wartościami, zatem pełne poznanie zjawiska

wymagałoby nieskończonej ilości informacji. Takie założenie prowadzi do sprzeczności. Na

przykład założenie ciągłości energii prowadzi do niedorzecznego wniosku, że całka energii widma

promieniowania ma wartość nieskończenie wielką. Zmusiło to Plancka do stworzenia teorii

kwantów zakładającej, że materia może promieniować energię jedynie skończonymi porcjami

zwanymi kwantami, które są proporcjonalne do częstotliwości promieniowania. Ciągłe krzywe

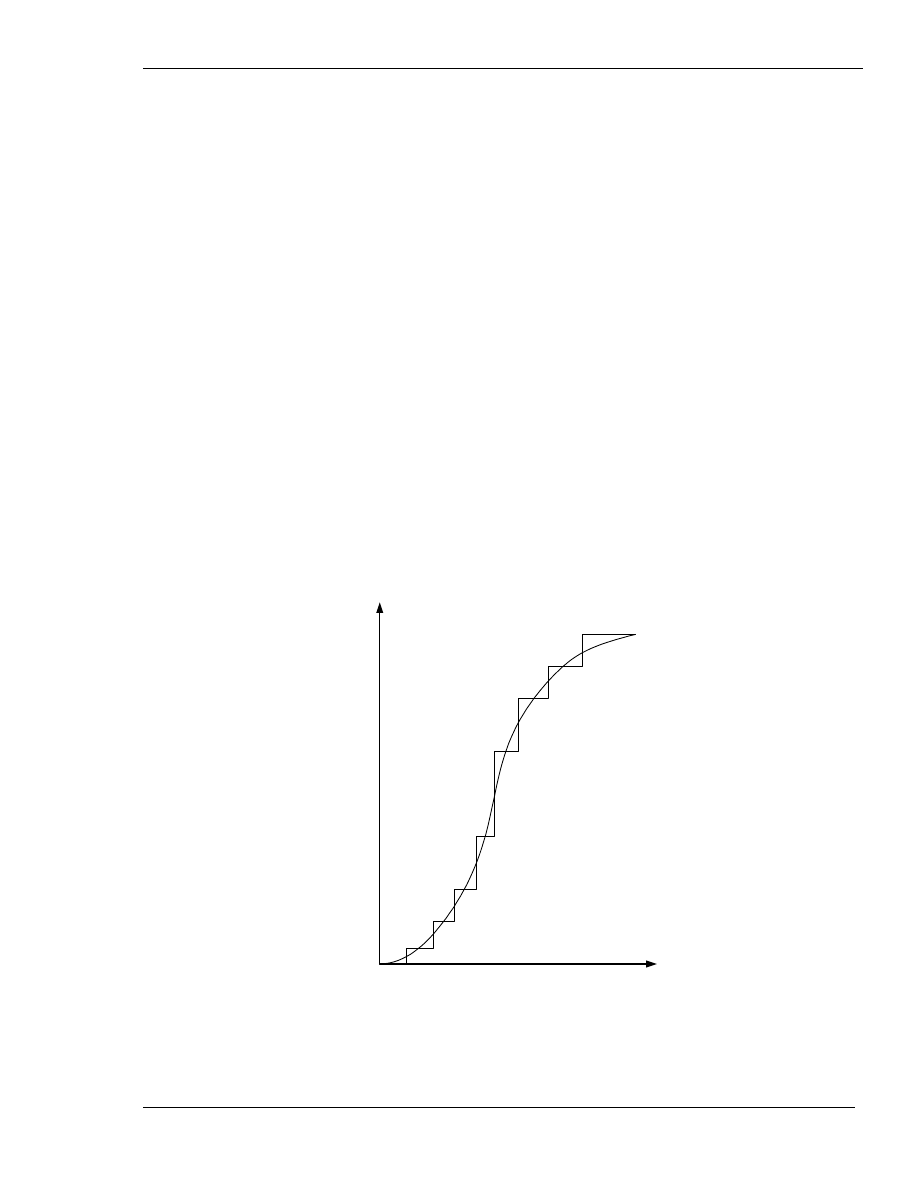
matematyczne, za pomocą których przedstawia się zależności między wielkościami fizycznymi,

stanowią, dogodną idealizację, lecz w ściślejszym ujęciu, powinny to być krzywe schodkowe. Np.

zależność natężenia I prądu anodowego (rys. 3) od napięcia V siatki w triodzie przedstawia się

zwykle w postaci linii ciągłej w kształcie litery S. Prąd ten, jak wiadomo, jest strumieniem

elektronów, może zatem zmieniać się tylko skokami. Zatem krzywa zależności I do V powinna być

schodkową linią łamaną, której idealizacją z dostateczną dokładnością w praktyce może być linia

ciągła.

I

V

Pr

ą

d an

odow

y

Napięcie na siatce w triodzie

Rys. 3.

Wyniki pomiarów mają również charakter ziarnisty, gdyż wyrażają się jako wielokrotności

najmniejszej części jednostki, jaka może być notowana przy pomiarze. Ponadto, na skutek

Opracował: dr inż. Stanisław FITA

11

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

niedoskonałości narzędzi pomiarowych, zakłócających wpływów zewnętrznych, ograniczonej

wrażliwości obserwatora i nieokreśloności, jaką zawsze jest obarczona wielkość mierzona, żaden

wynik pomiaru nie może być nieskończenie dokładny. Dwie wielkości uznane za jednakowe przy

zastosowaniu do ich porównania określonej dokładności pomiaru mogą okazać się niejednakowe

przy zastosowaniu dokładności większej. Podobnie wartość wielkości uważana za stałą przestaje

nią być, gdy dokładniejsze pomiary wykrywają dotychczas nieuchwytne jej zmiany.

Informację zawartą w wyniku pomiaru można traktować, jako odpowiedź na pytanie, jaką

miarę należy przypisać wielkości mierzonej. Przyjęto określać ilość informacji liczbą

elementarnych odpowiedzi „tak" lub „nie", jakich wymaga uzyskanie tej informacji. Wtedy

jednostką ilości informacji jest tzw. bit (BInary uniT), czyli jednostka dwójkowa, to jest ilość

informacji równoważna jednej odpowiedzi elementarnej na pytanie elementarne. Zatem b bitów

odpowiada informacji wymagającej postawienia b pytań elementarnych, aby odpowiedzieć, który

z N = 2

b

teoretycznie możliwych przypadków zachodzi, przy czym:

N

log

b

2

=

Najskuteczniejszym sposobem poszukiwania wymagającej wielu pytań elementarnych

pożądanej informacji jest kolejny podział tych pytań na dwie grupy, zapewniające w każdej grupie

największą swobodę wyboru, który wtedy składa się z szeregu tzw. dychotomi, czyli kolejnych

podziałów na dwie części. Na przykład gdy wiadomo, że liczba całkowita x znajduje się

w przedziale zamkniętym od 1 do 16, to jej określenie wymaga odpowiedzi na cztery pytania

elementarne, gdyż

4

16

log

b

2

=

=

b. Stosując zasadę dychotomi, pytania te mogą być kolejno

następujące:

1) Czy x jest większe od 8?

Nie

2) Czy x jest większe od 4?

Tak

3) Czy x jest większe od 6?

Tak

4) Czy x jest równe 8?

Nie

Zatem x = 7. Ilość uzyskanej w ten sposób informacji wynosi 4 bity, gdyż jej uzyskanie

w najbardziej niesprzyjających warunkach wymaga odpowiedzi na cztery pytania elementarne

dotyczące szesnastu przypadków możliwych.

Odpowiedź na pytanie, jaka jest miara danej wielkości jest pełna tylko wtedy, gdy

jednocześnie z wartością tej miary podaje się obarczającą ją niedokładność określenia. Dlatego

ilość informacji zawartą w wyniku pomiaru wielkości x, można ocenić, znając jego niedokładność

±

∆x, to jest stopniowanie 2∆x, z jakim została zmierzona ta wielkość za pomocą zastosowanych

środków pomiaru (rys. 4).'

Opracował: dr inż. Stanisław FITA

12

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

0

x

1

2

∆x

+

∆x

-

∆x

x

Rys. 4.

Przed wykonaniem pomiaru nie wiadomo, w którym z przedziałów

(

x

x

,

x

x

)

∆

+

∆

−

znajduje się

wartość x wielkości mierzonej. Powstaje zatem potencjalne zagadnienie, który z N

0

teoretycznie

możliwych przypadków zachodzi, przy czym:

x

2

x

N

0

∆

=

N

0

określa tzw. liczbę kwantowania wielkości mierzonej, czyli liczbę przedziałów lub stopni

(kwantów), w których wartość tej wielkości a priori może się znajdować. Znalezienie wartości

mierzonej ma więc charakter probabilistyczny, gdyż polega na ustaleniu jedynie z dużym

prawdopodobieństwem, w którym z określonych niedokładnością pomiaru przedziałów znajduję

się poszukiwana wartość wielkości.

Po przeprowadzeniu pomiaru powinno się mieć pewność, że wartość zmierzonej wielkości

znajduje się w określonym przedziale

(

)

x

x

,

x

x

∆

+

∆

−

. Przedział ten stanowi miarę niepewności,

wewnątrz którego nie można mówić o bliższym określaniu wartości x. Ilość I informacji zawarta w

wyniku pomiaru jest równa różnicy b

0

bitów, jakich wymaga usunięcie nieokreśloności, co do

wartości wielkości x przed pomiarem przy N

0

przypadkach możliwych i liczby b

1

bitów

charakteryzujących nieokreśloność po pomiarze przy N

1

< N

0

przypadkach możliwych. Zatem:

1

0

2

1

0

N

N

log

b

b

I

=

−

=

Ponieważ w przybliżeniu

0

0

N

1

p

=

jest prawdopodobieństwem przed pomiarem i

1

1

N

1

p

=

jest

prawdopodobieństwem po pomiarze, z jakim można przypuszczać, że wielkość x ma wartość x

1

,

Opracował: dr inż. Stanisław FITA

13

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

zatem powyższy wzór można napisać w postaci:

0

1

2

p

p

log

I

=

Jeśli na skutek uzyskanej informacji mamy. pewność, że zmierzona wielkość znajduje się

w przedziale

(

, to p

1

= 1, czyli N

1

= 1, zatem wzór przybiera postać:

)

x

x

,

x

x

∆

+

∆

−

0

2

N

log

I

=

gdzie N

0

jest liczbą .przedziałów lub stopni (kwantów), w których wielkość x mogłaby a priori się

znajdować, biorąc pod uwagę niedokładność pomiaru.

Po przejściu na logarytmy dziesiętne, otrzymamy:

0

N

lg

3219

,

3

I

=

Na przykład, gdy zmierzona długość x = 1000 mm i niedokładność pomiaru wynosi

∆x = ±0,1 mm,

to N

0

= 5000, zatem ilość uzyskanej informacji jest równa I = 12,3 bitów.

Niedokładność pomiaru wyrażona w jednostce wielkości mierzonej i podana w postaci

granic ±

∆x nazywa się niedokładnością bezwzględną, którą określają zwykle liczby mianowane,

np. ±0,1 mm. Niedokładność względną

δ pomiaru określa stosunek wartości 2∆x; kwantowania

wielkości mierzonej do znalezionej wartości x tej wielkości:

0

N

1

x

x

2

=

∆

=

δ

Niedokładność względna jest równa odwrotności liczby kwantowania N

0

wielkości mierzonej i

wyraża się liczbą oderwaną.

Istnieje możliwość zmniejszenia niedokładności pomiaru za pomocą dwóch urządzeń

pomiarowych, z których jedno kwantuje wielkość mierzoną w przedziałach dużych, natomiast

drugie ocenia wartość wielkości wewnątrz każdego z poprzednio kwantowanych przedziałów.

W ogólnym ujęciu jeśli przyrząd pomiarowy składa się z m takich kolejnych urządzeń, przy czym

niedokładność względna pomiaru za pomocą i-tego urządzenia jest równa

δ

i

, to niedokładność

względna całego przyrządu pomiarowego wynosi:

Opracował: dr inż. Stanisław FITA

14

i

m

1

i

δ

Π

=

δ

=

Instytut Technologii Maszyn i Automatyzacji

Zakład Metrologii i Badań Jakości

przy czym każde z urządzeń powinno zapewniać uzyskanie wymaganej dokładności oceny

uzyskiwanej za pomocą urządzenia ostatniego.

Na przykład, gdy. w suwmiarce zakres pomiarowy 140 mm ulega kwantowaniu co 1 mm i

w każdym przedziale milimetrowym tego zakresu ocena mierzonej długości może być dokonana

z niedokładnością bezwzględną w granicach ±0,1 mm za pomocą noniusza, to

δ

1

= 1 : 140 i

δ

2

=

0,2 : 1. Zatem niedokładność względna suwmiarki wynosi:

3

2

1

10

43

,

1

−

⋅

=

δ

δ

=

δ

w odniesieniu do wymiaru 140 mm.

Podobnie w maszynie do pomiarów długości zakres pomiarowy 3 m jest kwantowany co

100 mm za pomocą wzorca kreskowego i każdy stumilimetrowy przedział tego zakresu może być

kwantowany co 1 mm za pomocą wzorca z podziałką milimetrową i mikroskopu. Następnie w

każdym milimetrowym przedziale mierzoną długość można ocenić z niedokładnością

bezwzględną nie przekraczającą ±1,5

µ

m za pomocą urządzenia mikrometrycznego. Wtedy

δ

1

=

0,1 : 3,

δ

2

= 1 : 100 i

δ

3

= 0,003 :1. Zatem niedokładność względna maszyny pomiarowej jest

równa:

6

3

2

1

10

−

=

δ

δ

δ

=

δ

Jeśli niedokładność względna pomiaru wynosi

δ, to ze wzorów można określić ilość

informacji, jaką zawiera wynik pomiaru. Ilość ta wyrażona w bitach jest równa

δ

−

=

δ

=

lg

3219

,

3

1

lg

3219

,

3

I

W ten sposób niedokładność pomiaru jest ściśle związana z ilością zawartej w jego wyniku

informacji.. Teoria informacji zaczyna w coraz większym stopniu znajdować zastosowanie w

metrologii i niewątpliwie w najbliższej przyszłości stanie się jedną z głównych podstaw

teoretycznych w zakresie dokładnych pomiarów.

Opracował: dr inż. Stanisław FITA

15