13. Zjawiska transportu w gazach
Wybór i opracowanie zadań.13.1-13.11.Bogumiła Strzelecka
13.1. Ile razy zmieni się współczynnik dyfuzji gazu dwuatomowego, jeżeli w wyniku :
a) izotermicznego,
b) adiabatycznego
rozprężania gazu jego ciśnienie zmniejszyło się dwukrotnie?
13.2. Współczynnik dyfuzji tlenu w warunkach normalnych jest równy 1,41
⋅10
-4
m
2
/s.
Znaleźć współczynnik dyfuzji tego gazu w temperaturze 50
o
C, jeżeli gaz ogrzewano przy
stałej objętości.
13.3. Współczynnik przewodnictwa cieplnego gazu trójatomowego jest równy 1,45
⋅10
-2
W/m
⋅K, a współczynnik dyfuzji w tych samych warunkach wynosi 10
-5
m
2
/s. Znaleźć liczbę
cząsteczek gazu w 1m
3
w tych warunkach.
13.4. Znaleźć współczynnik przewodnictwa cieplnego chloru, jeżeli wiadomo, że
współczynnik lepkości dynamicznej tego gazu w danych warunkach jest równy 1,29
⋅10
-5
N
⋅s/m
2
.
13.5. W jakiej temperaturze współczynnik lepkości dynamicznej azotu jest równy
współczynnikowi lepkości dynamicznej wodoru w temperaturze 19
o
C? Średnica atomu azot
wynosi 3,1
⋅10
-10
m, a średnica atomu wodoru – 2,3
⋅10
-10
m.
13.6. Obliczyć ilość ciepła przewodzonego przez ścianę mieszkania w zimie w czasie t., jeżeli
przewodnictwo cieplne ściany wynosi
χ, grubość ściany jest równa d, zaś jej powierzchnia S.
Temperatura w mieszkaniu wynosi T
1
, a na zewnątrz T
2
< T
1
. Ile należy spalić węgla w celu
wyrównania ubytku ciepła przez przewodnictwo, zakładając, że tylko
η część ciepła
dostarczonego przez spalanie węgla idzie na wyrównanie tego braku. Ze spalenia 1 kg węgla
uzyskujemy r [J] ciepła.
13.7. Naczynie szklane o powierzchni S i grubości ścianek d, zawierające mieszaninę wody z
lodem w równowadze termicznej, postawiono w pokoju o temperaturze T
1
. Wiedząc, że
przez
jednostkę powierzchni szkła, przy gradiencie temperatur
∆T/d, w każdej sekundzie
dopływa ilość ciepła
χ, obliczyć ile lodu ulegnie stopieniu w tym naczyniu w czasie τ. Ciepło
topnienia lodu jest równe l.
13.8. Ściana drewniana ma grubość d. Jaką grubość powinien mieć mur z cegieł, aby miał
taką samą przewodność cieplną jak ta ściana z drewna. Współczynnik przewodnictwa
cieplnego drewna wynosi
χ
1
a cegły -
χ
2
.
13.9. Dwie płytki – miedziana i żelazna, z których każda ma grubość 1 cm, dokładnie
przylegają do siebie. Temperatura zewnętrznej powierzchni płytki miedzianej jest równa 373
K, a temperatura zewnętrznej powierzchni płytki żelaznej jest równa 273 K. Znaleźć
temperaturę płaszczyzny zetknięcia płytek jeżeli współczynniki przewodnictwa cieplnego są
równe
χ
1
= 390 W/m
⋅K (miedź), χ
2
= 62 W/m
⋅K (żelazo).
13.10. Piec elektryczny o mocy P =2kW i powierzchni S = 0,25 m
2
pokryty jest ogniotrwałym
materiałem o grubości d =10 cm. Współczynnik przewodnictwa cieplnego tego materiału jest
równy
χ = 0,8W/m⋅K. Jaka jest temperatura zewnętrznej powierzchni pieca, jeżeli temperatura
jego wewnętrznej powierzchni jest równa t =1200
o
C?
13.11. Zamknięty termos styropianowy zawierający masę m cieczy o temperaturze T
o
wstawiono do pieca o stałej temperaturze T
1
> T
w
(T
w
– temperatura wrzenia cieczy).
Ogrzewana powierzchnia termosu wynosi S, zaś grubość ścianek naczynia d. Współczynnik
przewodnictwa cieplnego styropianu jest równy
χ, zaś ciepło właściwe wody wynosi c. Po
jakim czasie ciecz w naczyniu zagotuje się?
Rozwiązania:
13.1.R.
Współczynnik dyfuzji wyraża się wzorem:
λ
⋅
= v
D
3
1
,
v – wartość średniej prędkości arytmetycznej cząsteczek gazu, λ - średnia droga swobodna
cząsteczek.
m
kT
v
⋅
=
π
8
, gdzie k – stała Boltzmanna, T – temperatura, m – masa cząsteczki;
V
n
d
2
2
1
⋅
=
π
λ
, gdzie d –średnica czynna cząsteczki, n – liczba cząsteczek, V – objętość.
Podstawiając powyższe zależności do wyrażenia opisującego współczynnik dyfuzji i
uwzględniając, że :
kT
p
V
n = otrzymujemy zależność:
(1)
p
d
kT
m
kT
D
2
2
8
3
1
⋅
⋅
⋅
=
π
π
a) w przemianie izotermicznej T = const, możemy więc napisać, że D ~
p
1
Wówczas
2
2
1
1
2
=
=
p
p
D
D
b) Przy przemianie adiabatycznej możemy napisać D ~
p
T
3
Wówczas
(2)
2
1
3
1
3
2
1
2
p
p
T
T
D
D
⋅
=
.
Korzystając z równania adiabaty otrzymujemy zależność:
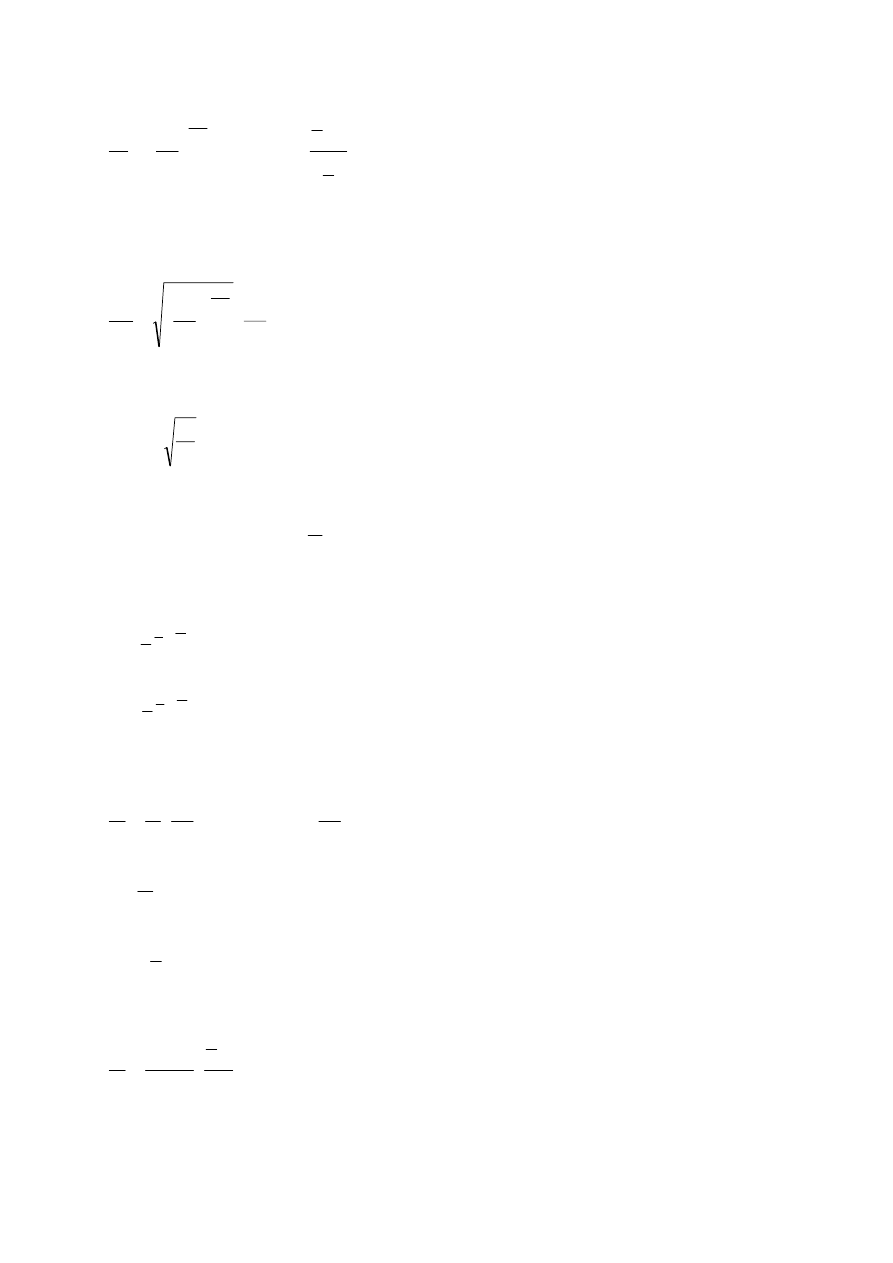
χ
χ 1
1
2
1
2
−
=
p
p
T
T
, gdzie
2
1
2
i
i +
=
χ
, i – liczba stopni swobody dla gazu dwuatomowego jest
równa 5.
Podstawiając powyższe zależności do równania (2) otrzymujemy :
49
,
1
2
1
1
3
1
2
1
2
=
⋅
=
−
p
p
p
p
D
D
χ
χ
13.2. O.
0
0
T
T
D
D
=
13.3.R.
Należy obliczyć wielkość:
V
n
.
Korzystamy z następujących zależności:
v
c
v
⋅
⋅
⋅
=
ρ
λ
χ
3
1
- współczynnik przewodnictwa cieplnego;
λ
⋅
= v
D
3
1
- współczynnik dyfuzji.
Obliczamy:
µ
χ
v
C
V
m
D
⋅
=
, ponieważ
µ
v
V
C
c
=
.
A
N
m
n
⋅
=
µ
, gdzie
µ jest masą 1 mola gazu, N
A
- stała Avogadro,
zaś
R
i
C
V
2
=
, gdzie R – uniwersalna stała gazowa, i – liczba stopni swobody (dla gazu
trójatomowego wynosi 7) , otrzymujemy zależność
µ
µ
χ
R
i
N
V
n
D
A
2
⋅
⋅
⋅
=
.
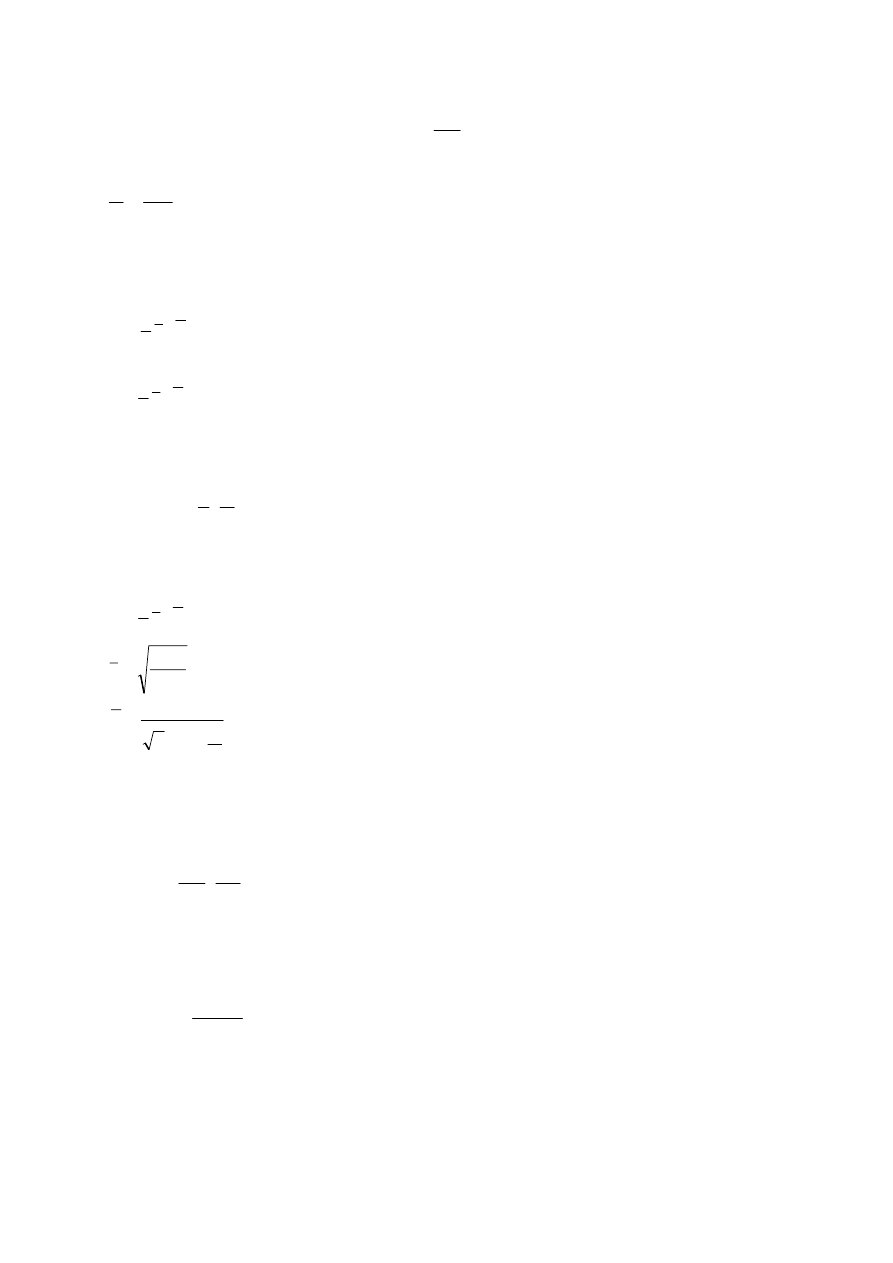
Po przekształceniach oraz uwzględniając, że
K
J
k
N
R
A
/
10
38
,
1
23
−
⋅
=
=
otrzymujemy:
3
23
10
5
,
3
2
−
⋅
=
=
m
Dki
V
n
χ
.
13.4.R.
v
c
v
⋅
⋅
⋅
=
ρ
λ
χ
3
1
-współczynnik przewodnictwa cieplnego;
ρ
λ
η
⋅
= v
3
1
⋅ - współczynnik lepkości dynamicznej.
Uwzględniając powyższe zależności otrzymujemy:
K
m
W
R
i
c
V
⋅
⋅
=
⋅
⋅
=
⋅
=
−
/
10
77
,
3
2
3
η
µ
η
χ
13.5.R.
ρ
λ
η
⋅
= v
3
1
⋅ - współczynnik lepkości dynamicznej
µ
π ⋅
=
RT
v
8
, gdzie k – stała Boltzmanna, T – temperatura, m – masa cząsteczki;
V
n
d
2
2
1
⋅
=
π
λ
, gdzie d –średnica czynna cząsteczki, n – liczba cząsteczek, V – objętość
Uwzględniając powyższe zależności oraz pamiętając, że
H
N
η
η =
otrzymujemy
C
d
d
T
T
o
H
N
H
N
H
N
204
4
4
≅
⋅
⋅
=
µ
µ
13.6.R.
Ilość ciepła przewodzonego przez ściany mieszkania:
d
T
T
t
S
Q
2
1
−
⋅
⋅
= χ
Ilość ciepła uzyskana ze spalenia m masy węgla:
r
m
Q
⋅
=
1
.
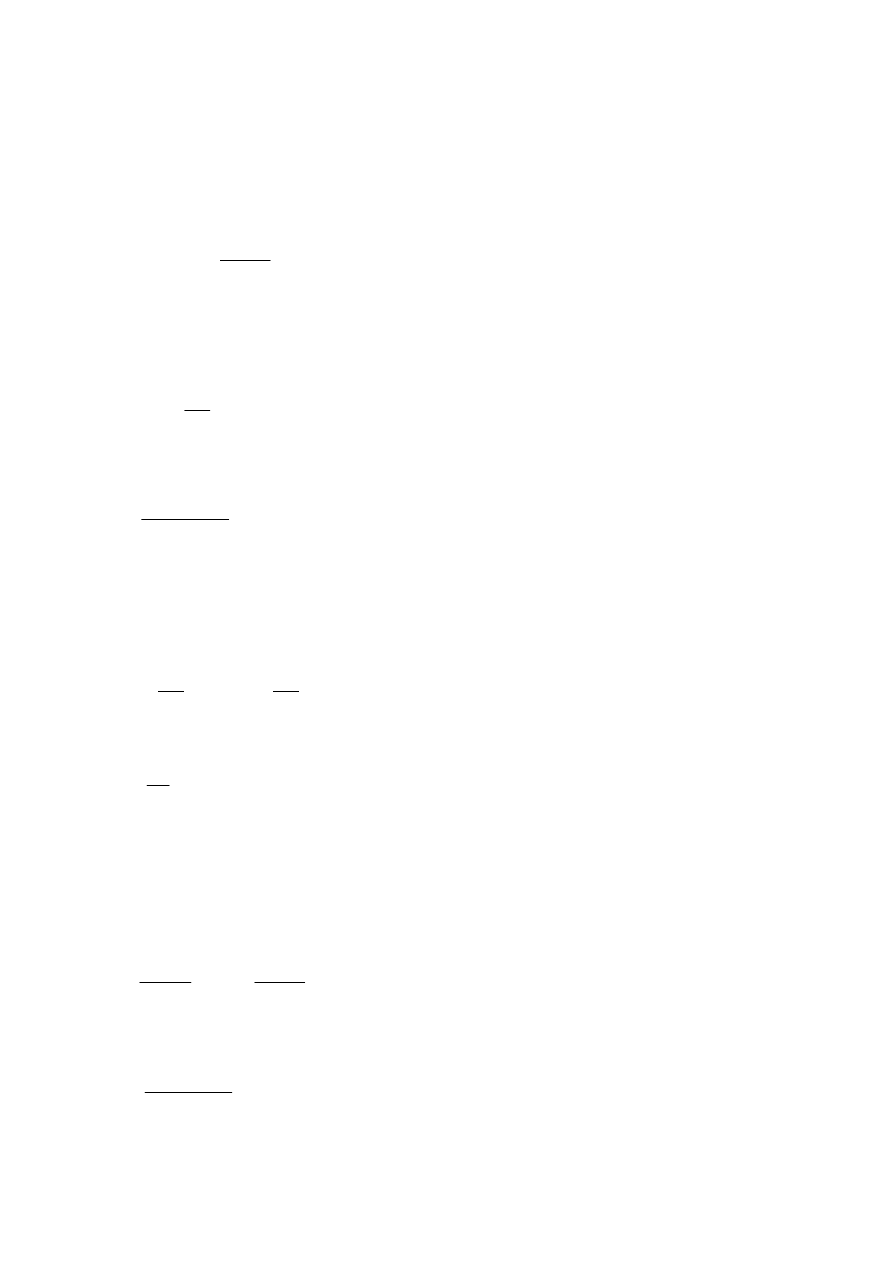
Część uzyskanego ze spalenia węgla ciepła wyrównuje straty ciepła:
Q
Q
=
1
η
Po przekształceniach otrzymujemy:
r
d
T
T
t
S
m
⋅
−
⋅
⋅
⋅
⋅
=
2
1
χ
η
13.7.R.
Ilość ciepła przewodzonego przez ścianki naczynia
τ
χ
⋅
∆
⋅
⋅
=
d
T
S
Q
Masa lodu stopiona przez to ciepło wynosi:
l
d
T
S
m
⋅
⋅
∆
⋅
⋅
=
τ
χ
13.8.R.
Ilość ciepła przewodzona przez ścianę z drewna w czasie
τ musi byś równa ilości ciepła
przewodzonego przez mur z cegieł w tym samym przedziale czasu:
τ
χ
τ
χ
⋅
∆
⋅
⋅
=
⋅
∆
⋅
⋅
x
d
T
S
d
T
S
2
1
Stąd:
d
d
x
1
2
χ
χ
=
13.9.R.
Ilość ciepła przewodzonego przez płytkę z miedzi musi być równa ilości ciepła
przewodzonego przez płytkę z żelaza:
τ
χ
τ
χ
d
T
T
S
d
T
T
S
x
s
1
2
2
1
−
=
−
Po przekształceniach otrzymujemy:
K
T
T
T
x
3
.
339
2
1
2
2
1
1
=
+
+
=
χ
χ
χ
χ
13.10.R.
Ciepło wytwarzane przez piec:
τ
⋅
= P
Q
Ciepło przenoszone przez warstwę:
τ
χ
⋅
−
⋅
⋅
=
d
T
T
S
Q
x
Porównując powyższe równania i przekształcając otrzymujemy:
K
S
d
P
T
T
x
473
=
⋅
⋅
−
=
χ
13.11.R.
Ciepło, które przepłynie do naczynia w czasie dt :
,
dt
d
T
S
dQ
∆
⋅
⋅
= χ
gdzie:
∆
, a T
T
T
T
−
=
1
jest temperaturą, jaką osiągnie woda
pobierając ciepło dQ w czasie dt.
Ciepło pobrane przez wodę zmieni jej temperaturę o dT:
c
m
dQ
dT
⋅
=
.
Porównując powyższe równania otrzymujemy:
(
)
dt
T
T
c
m
d
S
dT
⋅
−
⋅
⋅
⋅
=
1
χ
.
Woda w naczyniu zagotuje się gdy temperatura T osiągnie wartość temperatury wrzenia dla
wody T
w
.
Przekształcając powyższe równanie, całkujemy je obustronnie
∫
∫
⋅
⋅
⋅
=
−
τ
χ
0
1
dt
c
m
d
S
T
T
dT
w
o
T
T
i otrzymujemy wzór na czas, po którym ciecz w termosie zagotuje się:
w
T
T
T
T
S
c
m
d
−
−
⋅
⋅
⋅
=
1
0
1
ln
χ
τ
.