Fizyka O gólna: Wyk ³ad II

1

Prawa Zachowania

Zasady zachowania odgrywaj¹ w fizyce szczególn¹ rolê.

Oprócz zasad zachowania dobrze poznanych w szkole:
C

zasady zachowania pêdu

C

zasady zachowania momentu pêdu

C

zasady zachowania energii

istnieje wiele innych zasad zachowania jak np.
<

zasada zachowania ³adunku

<

zasady zachowania masy

<

zasady zachowania liczby barionowej

(tj. liczby protonów, neutronów i innych tzw. cz¹stek
ciê¿kich)

oraz bardziej egzotyczne
<

zasady zachowania dziwnoœci

<

zasady zachowania parzystoœci

i inne

Zasady te s¹ ogólniejsze ni¿ np. prawa Newtona.

Wynikaj¹ z symetrii otaczaj¹cego nas œwiata.

(twierdzenie Noether 1918 r)

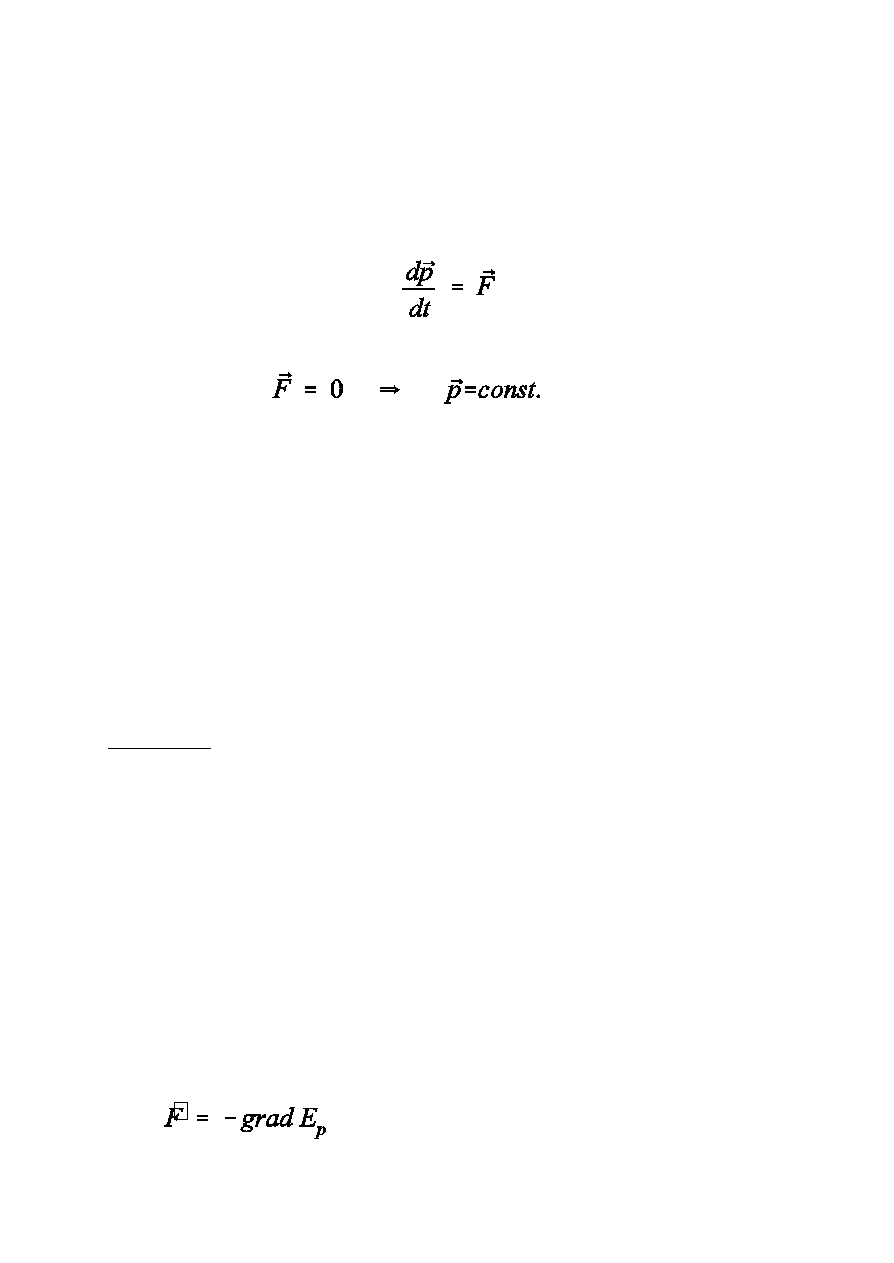
Fizyka O gólna: Wyk ³ad II

2

Zasada zachowania pêdu

II zasada dynamiki Newtona dla ruchu postêpowego zawiera
zasadê zachowania pêdu:

Wniosek:

Komentarz:
Zasada dynamiki Newtona jest równaniem wektorowym. Jest
wiêc równowa¿na 3 równaniom skalarnym. St¹d jeœli w uk³adzie
wspó³rzêdnych kartezjañskich Fx … 0 a pozosta³e sk³adowe si³y

znikaj¹ to zasada zachowania pêdu spe³niona jest w kierunku osi
Oy i Oz ale nie w kierunku Ox.

Zasada zachowania pêdu wynika z jednorodnoœci przestrzeni

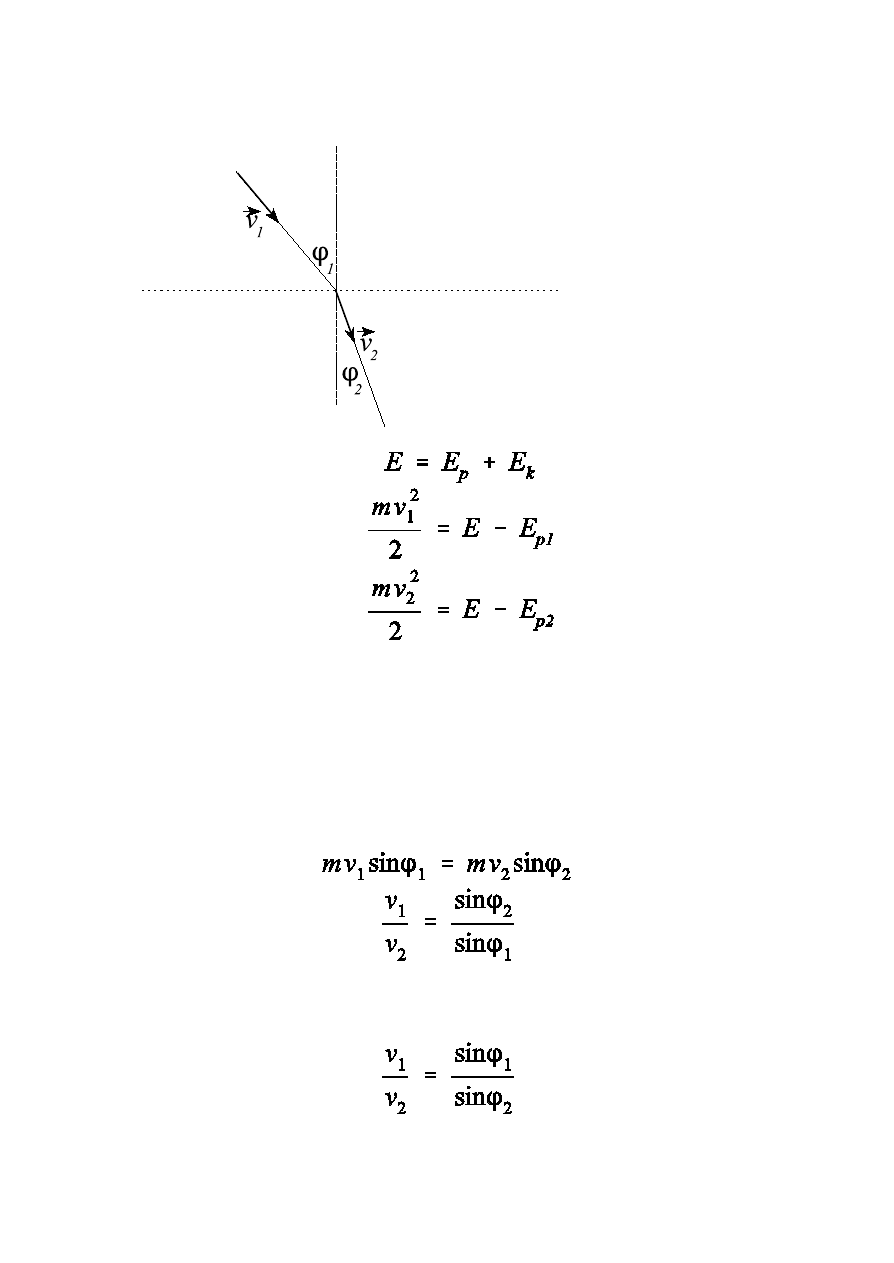
Przyk³ad:
Dana jest cz¹stka o masie m i energii mechanicznej E.
Cz¹stka ta przekracza granicê pomiêdzy dwoma oœrodkami
padaj¹c na ni¹ pod k¹tem n1. Pod jakim k¹tem opuœci ona

granicê pomiêdzy oœrodkami jeœli wiadomo, ¿e w oœrodku, z
którego nadlatuje ma energiê potencjaln¹ Ep1 zaœ w oœrodku, do

którego przechodzi ma energiê Ep2 ?

Wskazówki:
<

energia mechaniczna jest to suma energii kinetycznej i
energii potencjalnej

<

oba oœrodki s¹ zachowawcze st¹d energia mechaniczna jest
zachowana

<

Fizyka O gólna: Wyk ³ad II

3

Si³a dzia³a tylko wzd³u¿ kierunku prostopad³ego do granicy
oœrodków (w tym kierunku wystêpuje gradient energii
potencjalnej).
St¹d wzd³u¿ tej granicy spe³niona jest zasada zachowania pêdu:

Dla porównania prawo Sneliusa dla œwiat³a:

Fizyka O gólna: Wyk ³ad II

4

Zasada zachowania momentu pêdu

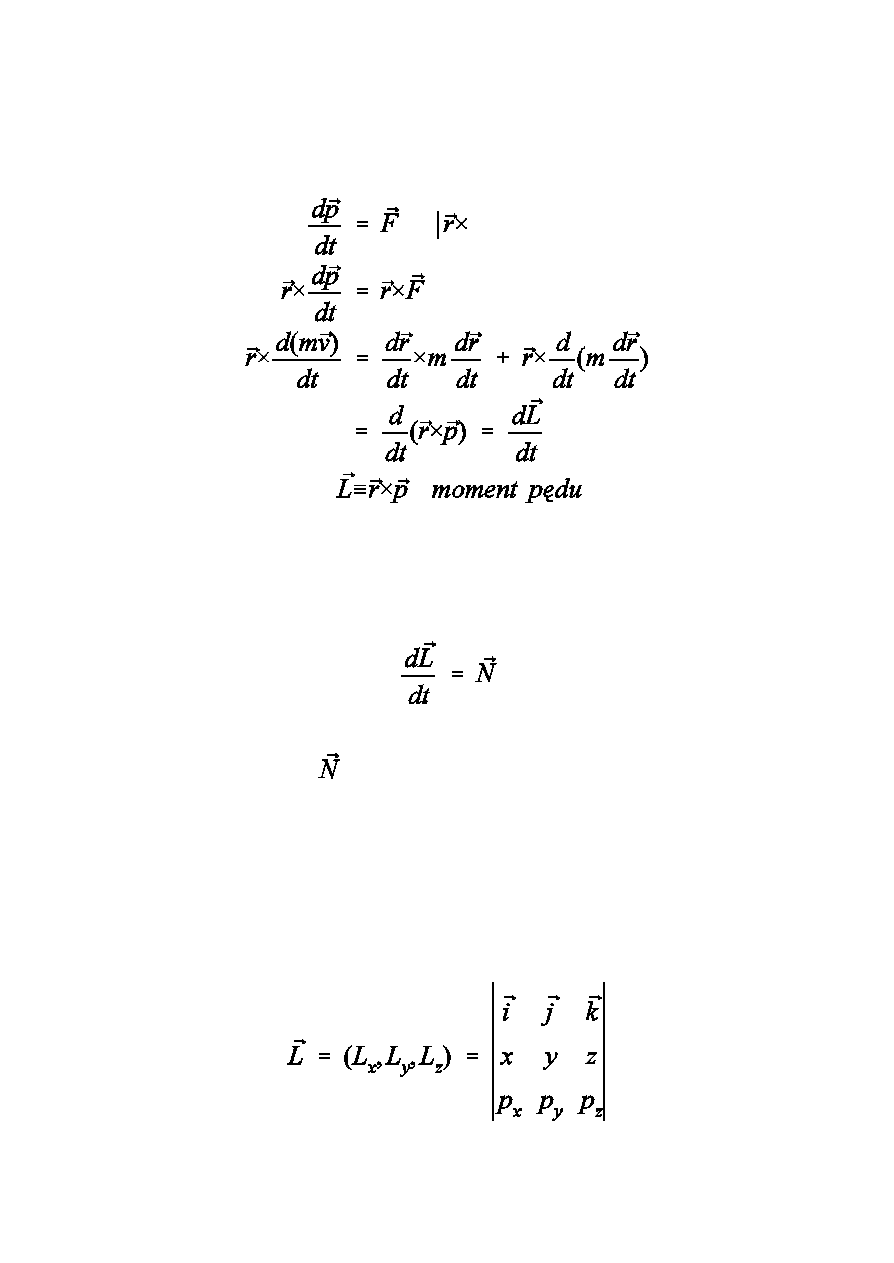
Wyjdziemy z II zasady dynamiki Newtona

Otrzymaliœmy II zasadê dynamiki Newtona dla ruchu
obrotowego

Gdy moment si³y znika moment pedu jest sta³y. Zasada
dynamiki Newtona wyra¿a wiêc zasadê zachowania. Ta ostatnia
ma zakres zastosowania o wiele szerszy: obowi¹zuje równie¿
tam gdzie si³y nie s¹ newtonowskie oraz w mechanice
kwantowej.
Prosty sposób na obliczenie momentu pêdu we wspó³rzêdnych
kartezjañskich:

Fizyka O gólna: Wyk ³ad II

5

Zasada zachowania momentu pêdu wi¹¿e siê z izotropowoœci¹
przestrzeni:

uk³ad odoizolowany nie zmienia swoich w³asnoœæi po
obróceniu o dowolny k¹t.

przyk³ad si³a centralna
Definicja si³a jest centralna gdy

czyli gdy

wtedy:

a wiêc

Przyk³ady si³ centralnych
si³a grawitacyjna

si³a elektrostatyczna

F(r) < 0 oznacza si³ê przyci¹gaj¹c¹

Przyk³ad: cz¹stka swobodna tj. gdy

zgodnie z II zasad¹ dynamiki Newtona.

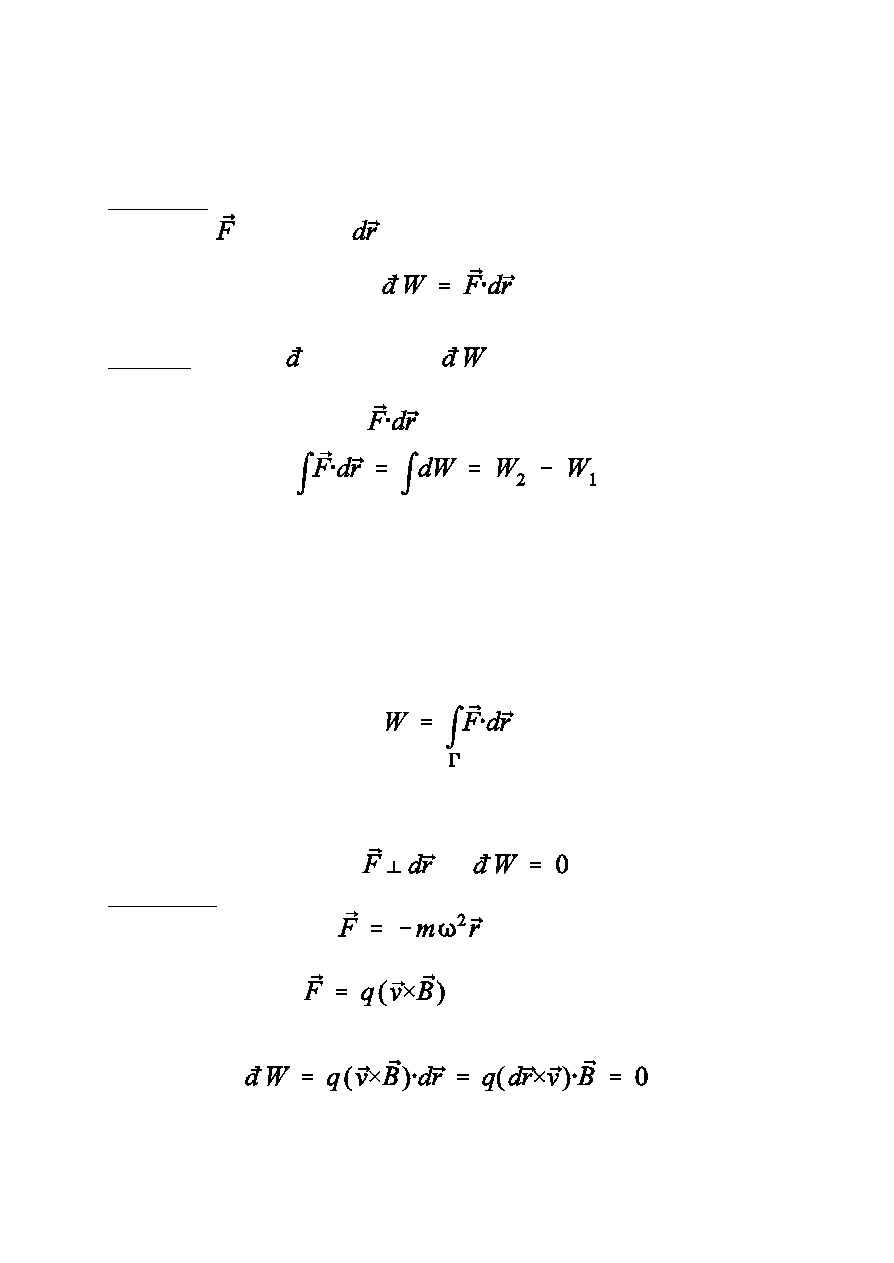
Fizyka O gólna: Wyk ³ad II

6

Praca, moc, energia

Definicja:
Praca si³y na drodze

jest równa

Uwaga: symbol

oznacza, ¿e

nie jest ró¿niczk¹ (zupe³n¹)

pracy W.
Symbol dW oznacza³by

jest ró¿niczk¹ a w konsekwencji

gdzie W1, W2 s¹ wartosciami pracy na krañcach drogi

pokonanej przez dane cia³o.

Poniewa¿ praca nie jest zwyczajn¹ ró¿niczk¹ wiêc na ogó³ praca
zalezy od drogi ' po jakiej zosta³a wykonana.

Wniosek

Gdy si³a

to

.

Przyk³ady
<

sila doœrodkowa

nie wykonuje pracy w ruchu

po okrêgu

<

si³a Lorenza
dowód:

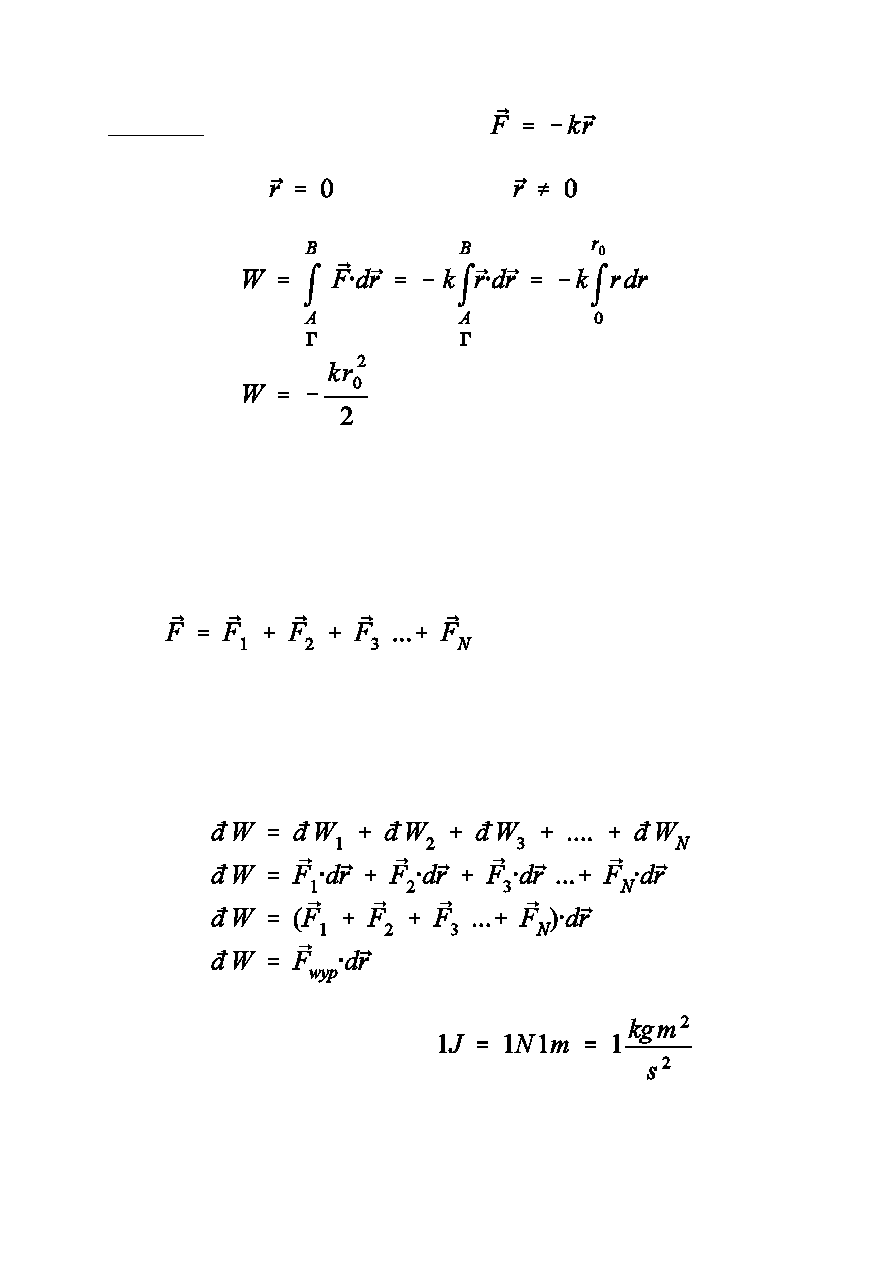
Fizyka O gólna: Wyk ³ad II

7

Przyk³ad

praca si³y sprê¿ystej

k jest sta³¹ sprê¿ystoœci.

od punktu A (

) do punktu B (

)

Praca jest ujemna: trzeba j¹ wykonaæ aby ruch siê odby³

Addytywnoœæ - wa¿na w³asnoœæ pracy

Jeœli

gdzie poszczególne sk³adowe si³y s¹ niezale¿ne

to

Jednostk¹ pracy jest d¿ul

Fizyka O gólna: Wyk ³ad II

8

Moc

moc chwilowa

Podzieliliœmy infinityzymalnie ma³y przyrost pracy przez czas
potrzebny do wykonania infinityzymalnie ma³ego przesuniêcia.

Jednostk¹ mocy jest wat

Definiuje siê te¿ moc œredni¹

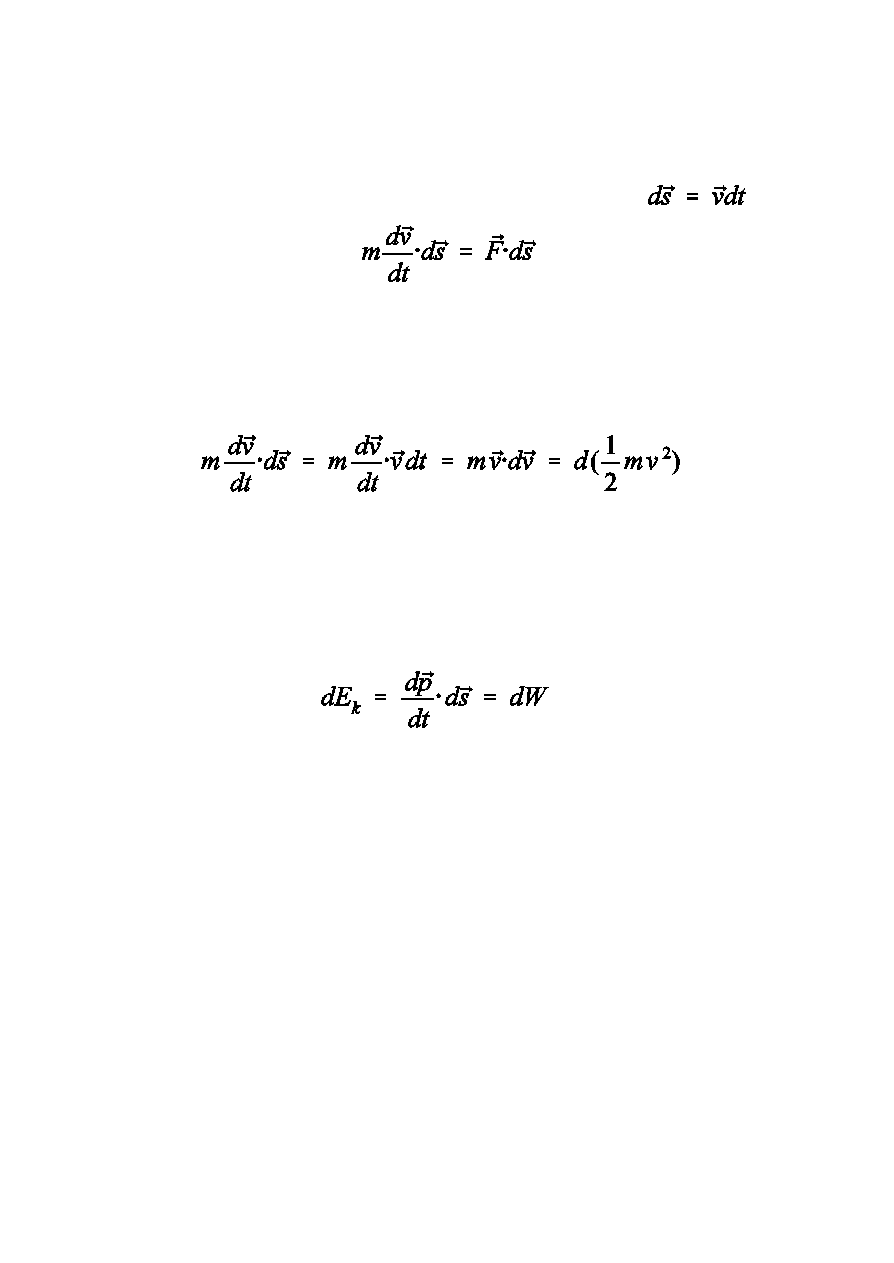
Fizyka O gólna: Wyk ³ad II

9

Energia Kinetyczna

Pomno¿ymy obie strony II prawa Newtona przez

Interesuje nas wielkoœæ po lewej stronie znaku równoœci:

Wielkoœæ w nawiasie nazywamy energi¹ kinetyczn¹
St¹d

Przyrost energii kinetycznej okazuje siê równy pracy
wykonanej na uk³adzie.

Jednostka energii kinetycznej jest te¿ d¿ul ale bywa u¿ywana
elektronowolt

1 eV = 1,602189 10-19 J

Fizyka O gólna: Wyk ³ad II

10

Rozpatrzmy ruch badanego cia³a pomiêdzy punktami A i B toru
'

Wnioski
#

jest to sposób na pomiar pracy bez potrzeby znajomoœci
toru '

#

moc chwilowa wyra¿a wia¿e siê z szybkosci¹ zmian energii
kinetycznej

Energia potencjalna

Na ogó³ si³a

.

Czêsto mamy do czynienia z si³¹ niezale¿n¹ jawnie od czasu

przy czym zarówno po³o¿enia jak i prêdkoœci s¹ funkcjami czasu
i s¹ poszukiwane.

Wtedy:
zawodzi proste ca³kowanie po czasie funkcji

:

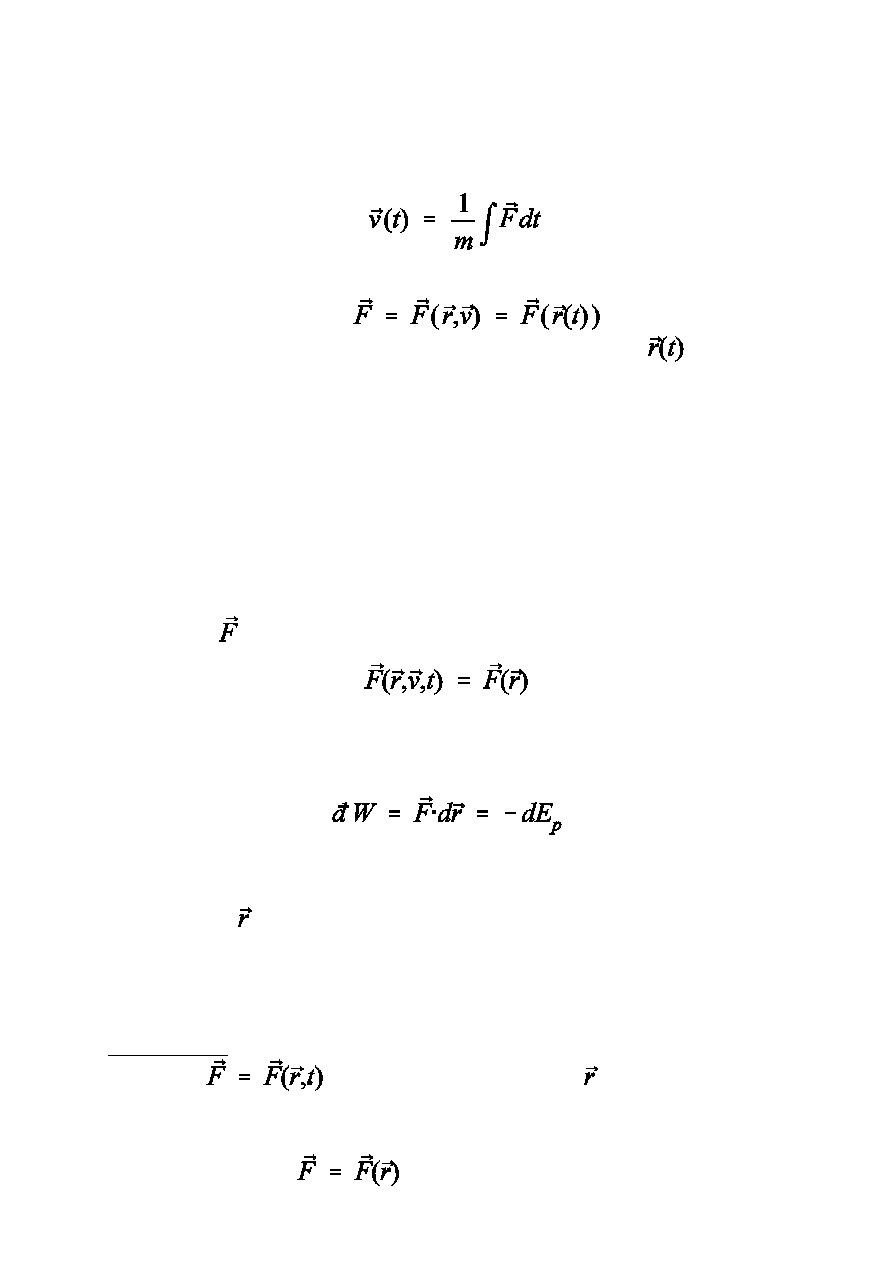
Fizyka O gólna: Wyk ³ad II

11

jeœli chcemy znaleŸæ prêdkoœæ z równania ruchu Newtona
tj. z

to nawet jeœli funkcja

tylko to i tak nie

mo¿emy wykonaæ calkowania bez jawnej postaci

.

Szukamy wiêc takiego sposobu rozwi¹zania zagadnienia
ruchu aby ca³kowaæ po dr a nie po dt.

Istnieje obszerna klasa si³:

si³y zachowawcze

dla których nie jest potrzebna znajomoœæ kszta³tu toru aby móc
wyznaczyæ pracê.

Definicja: jest si³¹ zachowawcz¹ je¿eli

tak¹, ¿e

gdzie Ep jest jednoznaczn¹ funkcj¹ skalarn¹ promienia

wodz¹cego , która jest ci¹g³a wraz z pochodnymi i niezale¿na
od czasu.

Ep nazywamy potencja³em si³y

lub energi¹ potencjaln¹

Komentarz

Si³a

mo¿e mieæ potencja³ V( ,t) (jest wtedy si³¹

niestacjonanrn¹).
Jednak¿e nazwa energia potencjalna zarezerwowana jest dla
wê¿szej klasy si³

, które s¹ zachowawcze.

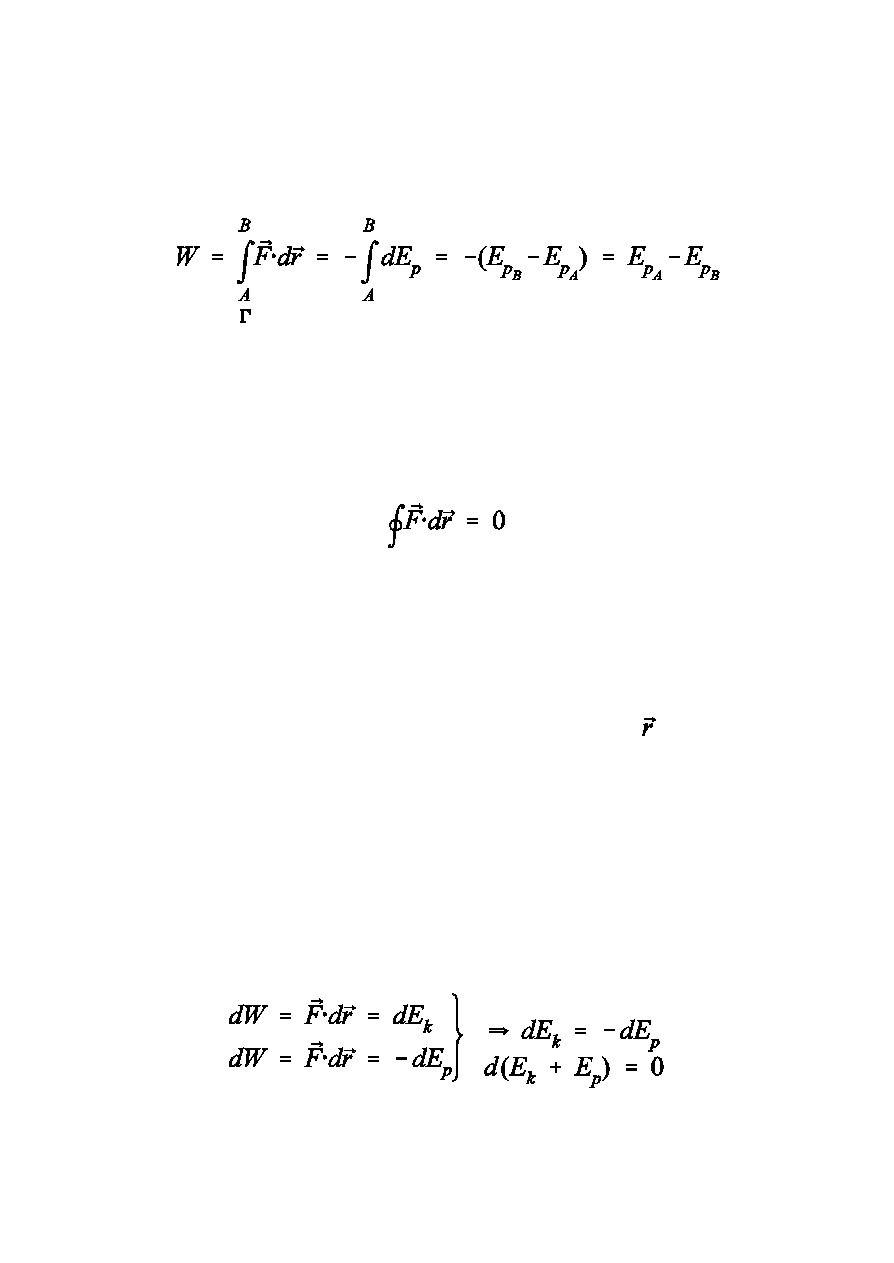
Fizyka O gólna: Wyk ³ad II

12

Konsekwencje definicji energii potencjalnej:
#

Niech Ep istnieje.

Wtedy

Praca si³y zachowawczej pomiêdzy dwoma punktami A i B
nie zale¿y od wyboru drogi pomiedzy tymi punktami.

#

cyrkulacja si³y zachowawczej znika

<

to wyra¿enie mo¿e s³u¿yæ jako definicja si³y
zachowawczej

<

w analizie wektorowej dowodzi siê, ¿e znikanie
cyrkulacji danego wektora jest równoznaczne z
istnieniem zwi¹zanej z nim funkcji Ep( ).

#

Energia potencjalna okreœlona jest z dok³adnoœci¹ do
pewnej sta³ej addytywnej, która zale¿y od wyboru punktu
odniesienia.

Zasada zachowania energii

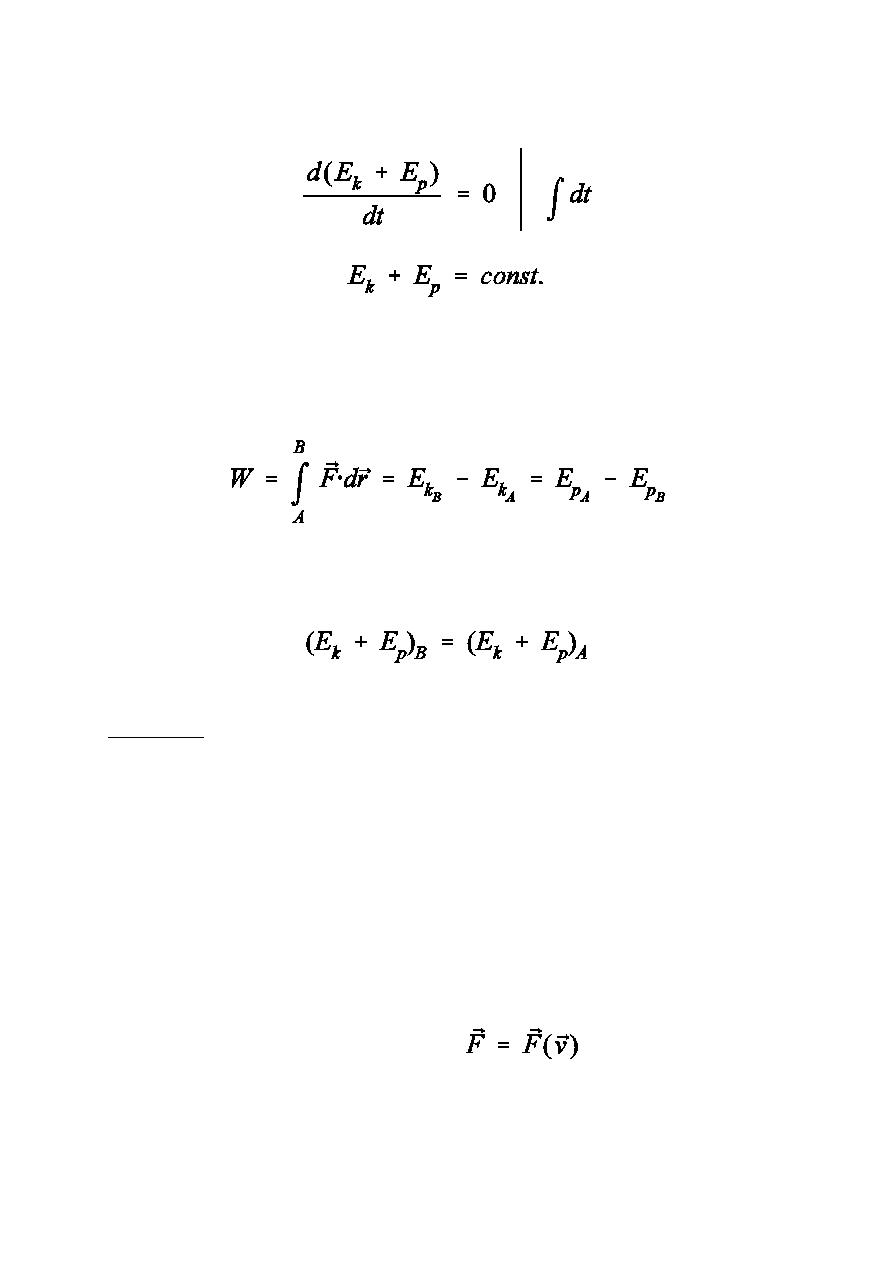
Dla si³ zachowawczych

Fizyka O gólna: Wyk ³ad II

13

Inaczej

Ta sama zasada w postaci ca³kowej:

Porz¹dkuj¹c otrzymuje siê

Wniosek

Energia mechaniczna Ek + Ep = E

pozostaje sta³a podczas ruchu pod wp³ywem si³
zachowawczych.

Zasada zachowania energii mechanicznej wynika z
jednorodnoœci czasu.

Zasada zachowania dla si³ niezachowawczych

Na ogó³ si³y niezachowawcze

i s¹ przeciwnie

skierowane do kierunku prêdkosci.

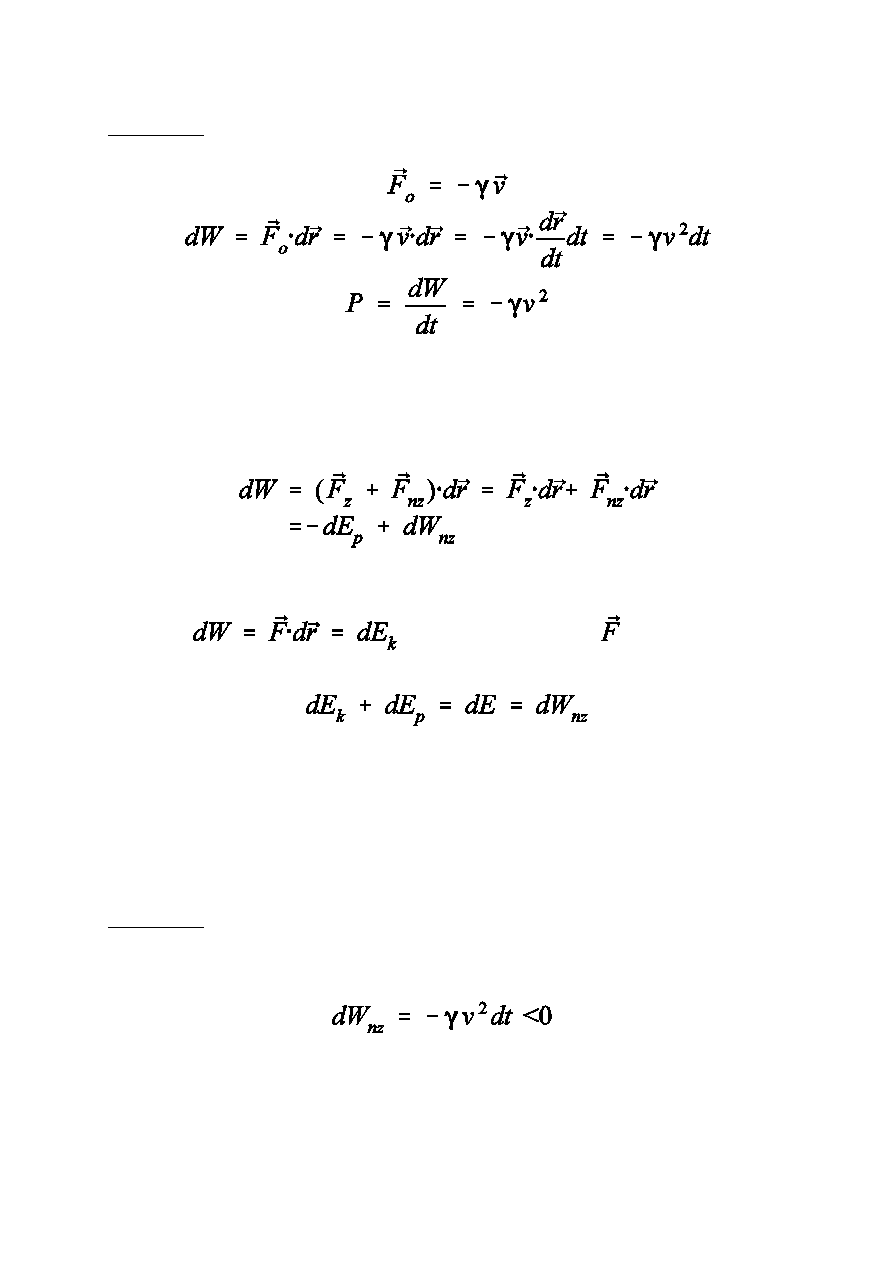
Fizyka O gólna: Wyk ³ad II

14

Przyk³ad si³a tarcia lepkiego

Gdy na punkt materialny dzia³a jednoczeœnie si³y zachowawcze
i niezachowawcze:

ale
zawsze

dla dowolnej si³y

dlatego

Zasada zachowania energii:
Zmiana energii mechanicznej jest równa pracy si³
niezachowawczych.

Przyk³ad
Wy¿ej wymieniona si³a oporu jest si³¹ niezachowawcz¹ st¹d