Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej. (413)
OPIS TEORETYCZNY.
Udowodniono, e wiat o mo na traktowa zarówno jako zbiór cz stek (fotonów) wylatuj cych ze ród a
wiat a i poruszaj cych si po liniach prostych (korpuskularna teoria wiat a wyja niaj ca np. bardzo
dobrze zjawisko fotoelektryczne czy efekt Comptona), jak te jako fal z wszystkimi charakterystycznymi
dla niej w asno ciami (np. dyfrakcja, interferencja, polaryzacja).
W tym drugim uj ciu wiat o jest fal elektromagnetyczn , poprzeczn , rozchodz
si w przestrzeni z
bardzo du predko ci . Natrafiaj c na przeszkod , wiat o ulega ugi ciu czyli
dyfrakcji
i zmienia
kierunek rozchodzenia si .
Zjawisko to mo na wyjasni np. w oparciu o
zasad Huygensa.
Otó w wypadku natrafienia na
przeszkod , czo a niektórych cz stkowych fal kulistych nie mog rozchodzi si swobodnie w niektórych
kierunkach. Zatem powsta a w wyniku
interferencji
fal cz stkowych powierzchnia styczna do tych fal
(czo o fali wypadkowej) tak e zmieni swój kszta t Zatem kierunek rozchodzenia si fali tak e ulegnie
zmianie.
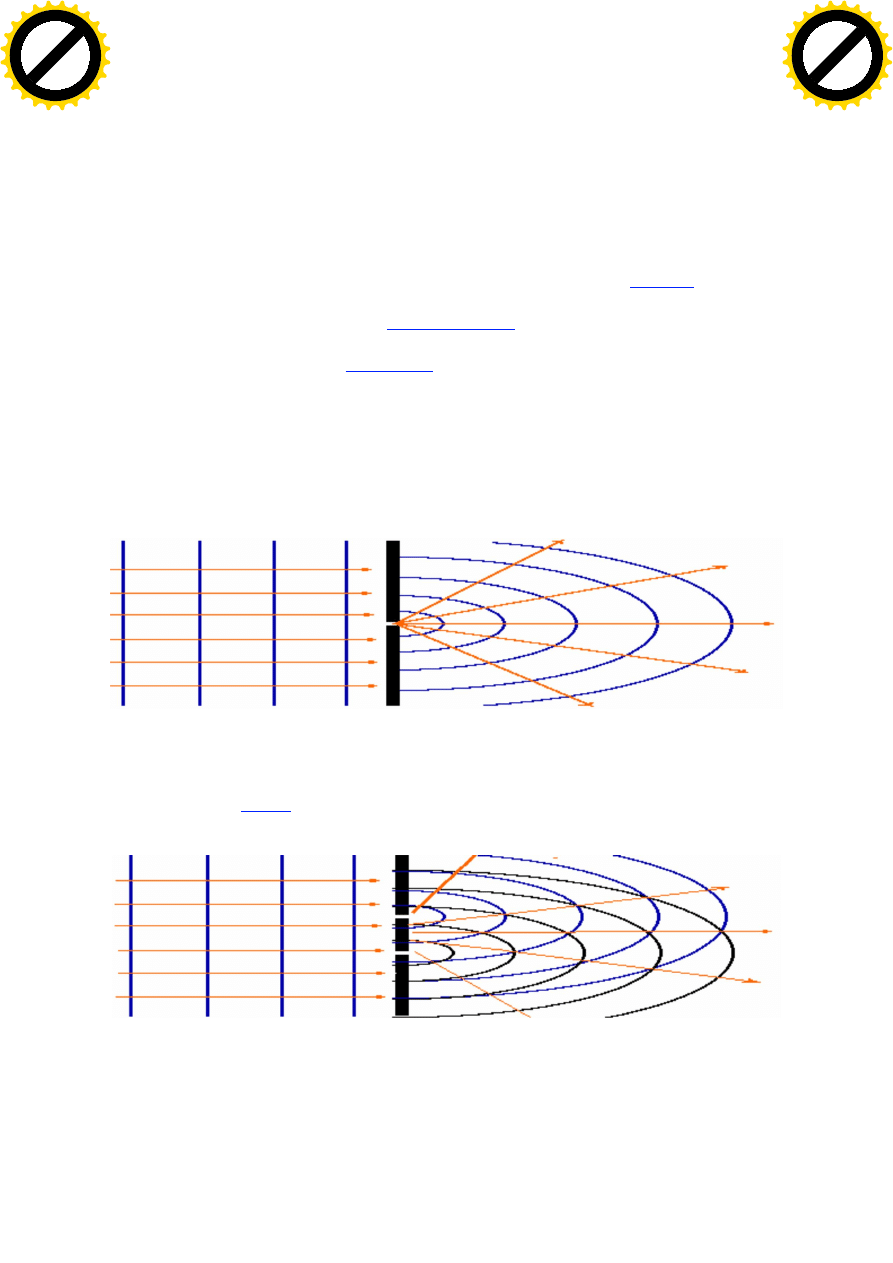
Zjawisko dyfrakcji i interferencji szczególnie wyra nie mo na zaobserwowa przy przej ciu wiat a przez
uk ad w skich szczelin. Po przej ciu przez jedn , w sk szczelin , wiat o rozchodz ce si prostoliniowo
(fala p aska), zmienia si w fal kulist , rozchodz
si we wszystkich kierunkach.
Je li szczeliny b
dwie, sytuacja zmieni si , gdy wi zki wiat a wychodz ce z ró nych szczelin b
si
spotyka , a poniewa s
spójne
, interferuj ze sob .
Je li za szczelinami ustawimy ekran, zaobserwujemy na nim szereg jasnych punkcików - pr ków
interferencyjnych. Powstan one w tych miejscach, w których wi zki wychodz ce z ró nych szczelin
spotkaj si w zgodnej fazie.
Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej
1 z 6
2009-11-16 17:31
Okre lenie po
enia tych punktów jest proste. W fali padaj cej
powierzchnia falowa
dochodzi
równocze nie do obu szczelin wi c wychodz ce ze szczelin wi zki s w tej samej fazie. Zatem na ekranie
fale spotkaj si w zgodnej fazie wtedy, gdy przeb
t sam drog optyczn (k=0) albo gdy przebyte
przez nie drogi b
ró ni si o ca kowit wielokrotno d ugo ci fali
(k=0,1,2...).
Taki uk ad szczelin mo na potraktowa jako przybli ony model siatki dyfrakcyjnej. Rzeczywista siatka
dyfrakcyjna sk ada si z wielu szczelin. Cz sto przypada ich kilkaset na jeden milimetr szeroko ci siatki.
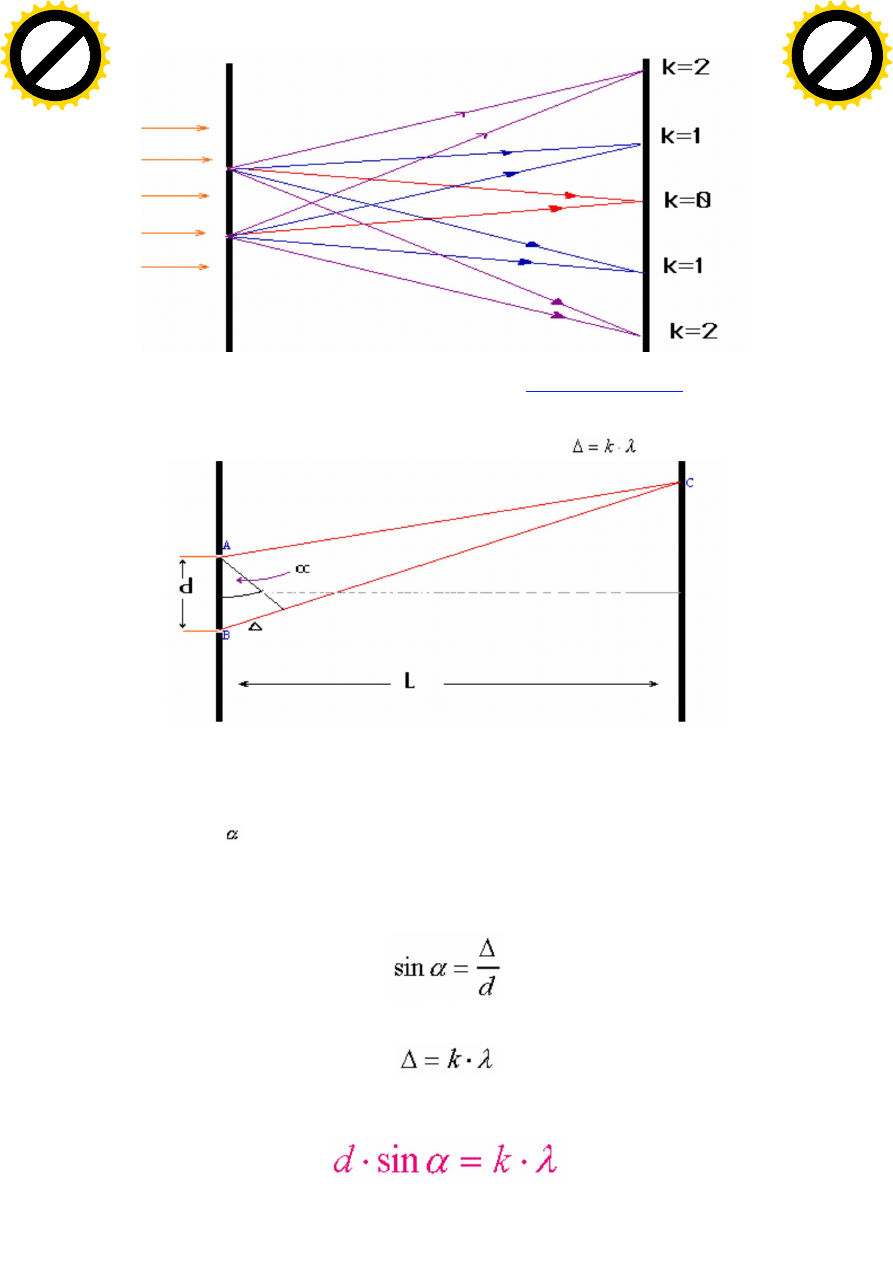
Odleg
mi dzy s siednimi szczelinami (na rysunku oznaczona jako d ) nazywana jest sta siatki. Z
rysunku wida , e k t
, pod którym zaobserwujemy wzmocnienie interferencyjne (jasny pr ek) i k t B
w trójk cie ABC s równe. (Uwaga. Na rysunku nie jest zachowana skala. W rzeczywisto ci odleg
mi dzy szczelinami d= AB << L (L to odleg
mi dzy szczelinami a ekranem), dzi ki czemu obie wi zki
wychodz jakby -w tej skali- z tego samego punktu).
Z zale no ci geometrycznych wida
e:
oraz
Otrzymujemy st d tzw równanie siatki dyfrakcyjnej:
Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej
2 z 6
2009-11-16 17:31

enie pr ków na ekranie okre la zale no :
Kojarz c powy sze wzory otrzymujemy zale no , w oparciu o któr mo na do wiadczalnie wyznaczy
ugo fali wiat a:
Bardzo eleganck ilustracj zjawiska interferecji mo esz obejrze je li dysponujesz komputerem w miar
szybkim i z co najmniej 12MB RAM.
Skocz tutaj
METODA POMIAROWA.
Do do wiadczenia nale y u
ród a wiat a monochromatycznego. W naszym przypadku b dzie to
miniaturowy laser pó przewodnikowy, wysy aj cy wiat o czerwone. Laser o wietla bezpo rednio siatk
dyfrakcyjn równoleg wi zk promieni, a pr ki interferencyjne obserwujemy na ekranie, na tle skali
milimetrowej.
rodkowy pr ek, zwany pr kiem zerowym (odpowiada k=0),s
y za punkt odniesienia do pomiaru
odleg
ci x dla pr ków wy szych rz dów. Dla siatki, któr dysponujemy na pracowni (sta a siatki d=
0,005mm czyli 200 szczelin/mm) i dla wiat a danej d ugo ci mo emy zaobserwowa maksymalnie pr ki
trzeciego rz du (k=3).
CEL WICZENIA.
Celem wiczenia jest wyznaczenie d ugo ci fali wiat a monochromatycznego, poprzez pomiar ugi cia
wiat a na transmisyjnej siatce dyfrakcyjnej o znanej sta ej siatki.
WYKONANIE WICZENIA.
czamy laser i ustawiamy laser i siatk w statywie w taki sposób, aby na ekranie by y widoczne pr ki
interferencyjne na tle skali. Nale y zadba o to, aby siatka i ekran by y ustawione równolegle wzgl dem
siebie. (Laser jest na sta e zamocowany tak, aby wiat o pada o na siatk prostopadle. Wa ne!) Mierzymy
odleg
od siatki do ekranu oraz odleg
ci od pr ka zerowego do pr ków I, II i III rz du. Pomiary
przeprowadzamy zarówno dla pr ków le cych z lewej jak i z prawej strony pr ka centralnego, notuj c
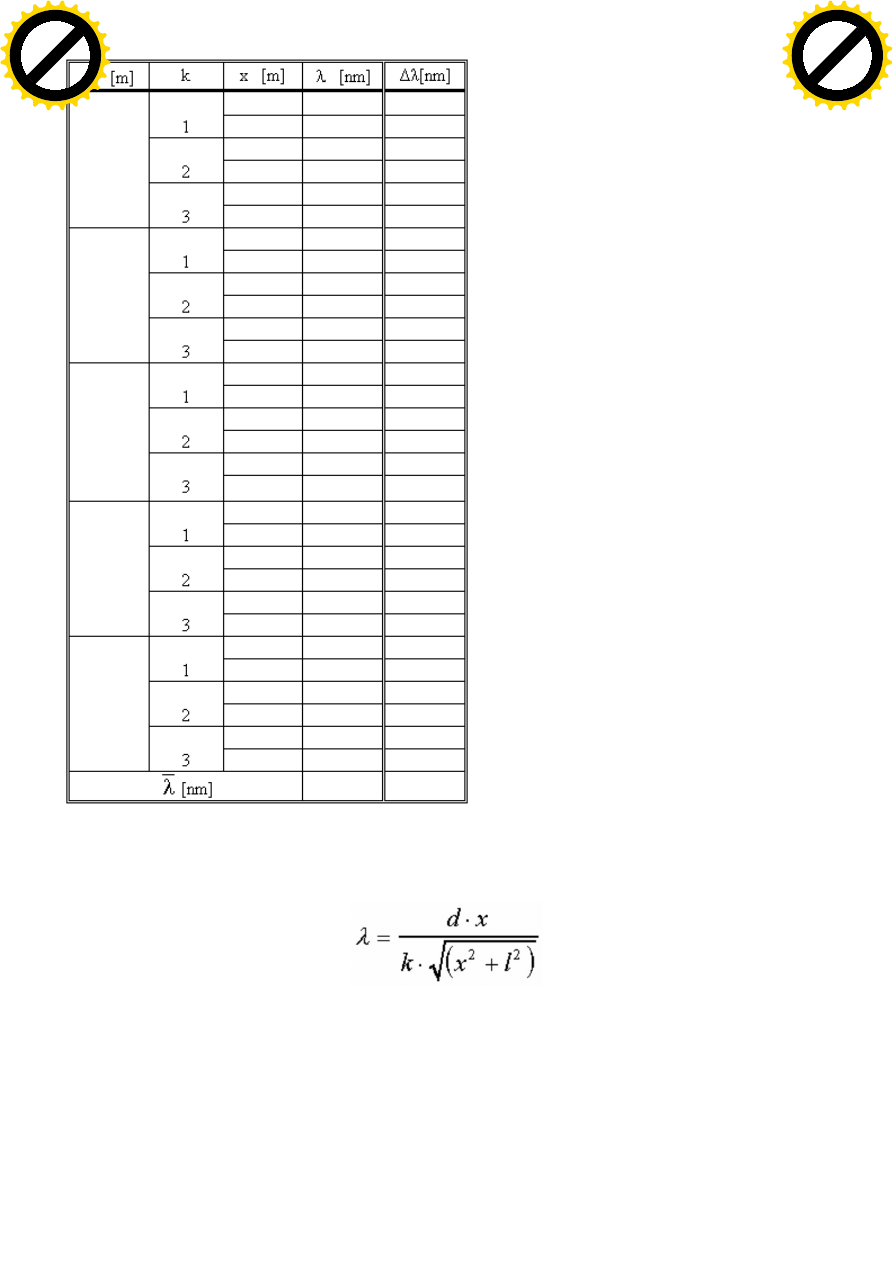
za ka dym razem rz d pr ka. Podobne pomiary powtarzamy dla czterech innych odleg
ci mi dzy siatk
a ekranem. Wyniki umieszczamy w tabeli:
Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej
3 z 6
2009-11-16 17:31
OPRACOWANIE WYNIKÓW POMIARÓW.
Nale y obliczy d ugo ci fali wynikaj cych z pomiarów poszczególnych pr ków ze wzoru :
Nastepnie znale warto
redni d ugo ci fali oraz okre li niepewno pomiaru Ka dy pomiar d ugo ci
fali w tym wiczeniu przeprowadzany jest z inn dok adno ci i dlatego, aby pomiary bardziej dok adne
mia y wi kszy wp yw na wyniki ni pomiary mniej dok adne nale y jako redni d ugo fali przyj tzw.
redni arytmetyczn wa on . Jako wag danego pomiaru nale y przyj
wielko odwrotnie
proporcjonaln do kwadratu b du pomiaru, czyli wyra enie typu
Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej
4 z 6
2009-11-16 17:31
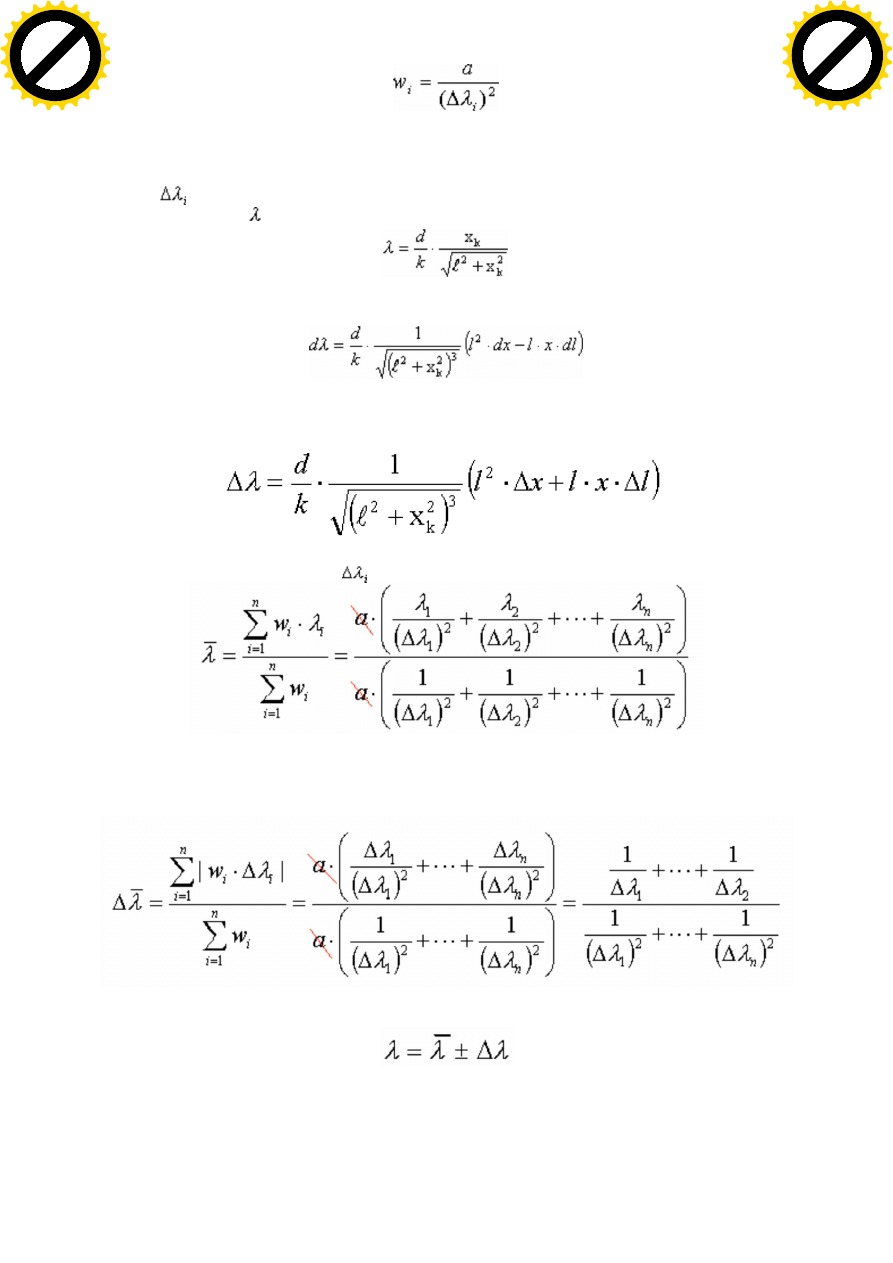
Sta a "a" jest tu zupe nie dowolna i wygodnie jest w tym wypadku przyj j jako a=10
-9
, poniewa
ugo fali wyra
b dziemy w nanometrach.
Niepewno ci
obliczamy jako b dy maksymalne pomiarów po rednich metod ró niczki zupe nej:
- obliczamy pochodn d z funkcji
wynosi ona:
- zamieniamy "-" na "+" i ostatecznie wi c niepewno
Po obliczeniu wszystkich niepewno ci
obliczamy redni wa on d ugo fali wg wzoru :
A nast pnie b d maksymalny redniej wa onej:
Wynik przedstawi w postaci:
UWAGA
Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej
5 z 6
2009-11-16 17:31

Mo na tu tak e
ci gn
pe
posta instrukcji stanowiskowej
zapisan w formacie WORD-a
Powrót do
Strony tytu owej
Pomiar d ugo ci fali wiat a za pomoc siatki dyfrakcyjnej
6 z 6
2009-11-16 17:31
Wyszukiwarka
Podobne podstrony:
Wyznaczanie długości fali światła za pomocą siatki dyfrakcyjnej, Monika Wojakowska
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
przew met termistor, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjnej
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
przew met termistor, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjnej
dyfrakcja pomiar dlugosci fali Nieznany
Lab 24, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatk
CW 79, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siatki
MOJALAB, Labolatoria fizyka-sprawozdania, !!!LABORKI - sprawozdania, Lab, !!!LABORKI - sprawozdania,
fizy2 sprawozdanie15 wersja2, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali ś
Pomiar dlugosci fali swietlnej, Nazwisko i Imie :
POPRAWA, MIBM WIP PW, fizyka 2, laborki fiza(2), 24-Wyznaczanie długości fali światła za pomocą siat
pomiar długości fali metodą intrferencji, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo,
więcej podobnych podstron