ZAGADNIENIA DO PRZYGOTOWANIA DLA KLASY III A i III B LO

1. Rachunek prawdopodobieństwa

1. Reguła mnożenia
2. Permutacje
3. Wariacje bez powtórzeń
4. Wariacje z powtórzeniami
5. Zadania z kombinatoryki
6. Zdarzenia losowe
7. Prawdopodobieństwo klasyczne

8. Własności prawdopodobieństwa

Przykłady zadań:

1. Ile jest liczb naturalnych trzycyfrowych parzystych , których wszystkie cyfry są mniejsze od 7?
2. Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo, że suma oczek jest nie mniejsza od 4.
3. W urnie jest 6 kul czarnych i 4 białe. Losujemy bez zwracania 3 kule. Oblicz prawdopodobieństwo, że wylosowano dokładnie 2 kule
czarne.
4. Spośród liczb naturalnych od 1 do 13 wybieramy kolejno trzy liczby bez zwracania. Oblicz prawdopodobieństwo zdarzeń:
a) pierwsza z wylosowanych liczb będzie nieparzysta
b) ostatnią z wylosowanych liczb będzie liczba 13
5. Z liczb 1, 2, 3, 4, 5 tworzymy kody pięciocyfrowe o różnych cyfrach. Jakie jest prawdopodobieństwo wylosowania ze wszystkich
kodów takiego, w którym liczby 4 i 5 będą obok siebie.
6. Z talii 52 kart wylosowano jedna kartę. Oblicz prawdopodobieństwo, że wylosowano kiera lub damę.

7. A i B są zdarzeniami losowymi takimi, że:

).

(

.

6

,

0

)

(

,

5

,

0

)

(

8

,

0

)

'

(

B

A

P

Oblicz

B

A

P

B

P

i

A

P

2. Statystyka

1. Średnia arytmetyczna
2. Mediana i dominanta
3. Odchylenie standardowe
4. Średnia ważona

Przykłady zadań:

1.W poniższej tabeli przedstawiono wyniki sondażu przeprowadzonego w grupie uczniów, dotyczącego czasu przeznaczonego dziennie
na przygotowanie zadań domowych.
Czas w
godzinach

1

2

3

4

Liczba
uczniów

5

10

15

10

Oblicz średnią arytmetyczną, medianę i dominantę oraz odchylenie standardowe czasu przeznaczonego dziennie na przygot. zad. dom..
2. Nauczyciel ustala ocenę semestralną, licząc średnią ważoną następujących liczb: średniej ocen ze sprawdzianów (z wagą 0,3), średniej
ocen z klasówek (z wagą 0,5), średniej za pracę na lekcji (z wagą 0,2) i za zadania domowe (z wagą 0,1). Oblicz ocenę semestralną
ucznia z następujących ocen: sprawdziany: 2,3,5,1, klasówki: 1,4,2,5, praca na lekcji: 3,5,5, zadania domowe: 1,1,3,5. Wynik zaokrąglij
do liczby całkowitej.
3. Do podanej serii wyników 7, 6, 4, 1, 14, 7, 120, 23 dopisz jeden wynik, tak aby średnia arytmetyczna wzrosła o 2.

3. Stereometria

1. Proste i płaszczyzny w przestrzeni
2. Graniastosłupy
3. Odcinki w graniastosłupach
4. Objętość graniastosłupa
5. Ostrosłupy
6. Objętość ostrosłupa
7. Kąt między prostą a płaszczyzną
8. Kąt dwuścienny

Przykłady zadań:

1. Oblicz pole powierzchni całkowitej graniastosłupa prawidłowego trójkątnego, w którym przekątna ściany bocznej o długości 6cm jest
nachylona do płaszczyzny podstawy pod kątem 60°.

2. Podstawą graniastosłupa prostego jest kwadrat o boku długości 3

2

. Wysokość graniastosłupa jest równa 5

2

. Oblicz długość

przekątnej graniastosłupa i jego objętość.

3. W ostrosłupie prawidłowym trójkątnym długość krawędzi bocznej jest równa 8, a kąt między krawędzią boczną i wysokością
ostrosłupa ma miarę 60°. Oblicz objętość tego ostrosłupa.
4. Wysokość ściany bocznej ostrosłupa prawidłowego czworokątnego tworzy z podstawą kąt 60°. Oblicz sinus kąta, jaki z podstawą
tego ostrosłupa tworzy jego krawędź boczna.

ZAGADNIENIA DO PRZYGOTOWANIA DLA KLASY II A LO

1. Wielomiany

1. Stopień i współczynniki wielomianu
2. Dodawanie i odejmowanie wielomianów
3. Mnożenie wielomianów
4. Wzory skróconego mnożenia
5. Rozkład wielomianu na czynniki
6. Równania wielomianowe
7. Dzielenie wielomianów
8. Równość wielomianów
9. Twierdzenie Bézouta

10. Pierwiastki wielokrotne
11. Wykres wielomianu
12. Nierówności wielomianowe

Przykłady zadań:

1. Dane są wielomiany W(x) = 4x

3

+ 2x

2

– 3x – 4 F(x) = -x

2

+ 5x – 6. Wyznacz wielomian: G(x) = -3W(x) + 2F(x)

2. Określ stopień wielomianu: W(x) = (x-1)(x+1)

2

(x-3)

3. Wyznacz współczynniki wielomianu:

n

x

mx

x

x

W

2

3

)

(

, jeżeli

9

)

2

(

5

)

1

(

W

i

W

4. Dobierz współczynniki a i b tak, aby wielomiany: W(x) = (3a – 1)x

3

+ (2b – a)x

2

+(a + b)x – 4 oraz F(x) = 2x

3

– 5x

2

– x – 4 były

równe.
5. Rozłóż wielomian na czynniki i wyznacz jego pierwiastki. Określ ich krotność:

a) W(x) = x

4

– 2x

3

– x

2

+ 2x

b) W(x) = (x

2

– 6x + 8)(x

2

– 4)(x

2

– 4x + 4)

6. Nie wykonując dzielenia sprawdź, czy wielomian w jest podzielny przez dwumian q. Zapisz i uzasadnij wniosek.

1

)

(

;

1

3

3

2

)

(

2

3

4

x

x

q

x

x

x

x

x

w

7. Rozwiąż równania: a) 5x

3

– 4x

2

+ 45x – 36 = 0;

b) 2x

3

+ 9x

2

+ 10x + 3 = 0

8. Rozwiąż nierówność, określ krotność pierwiastków i stopień wielomianu: -2x² (x-1)² (x² -6x – 7) ≥ 0

2. Funkcje wymierne

1. Proporcjonalność odwrotna

2. Wykres funkcji

x

a

x

f

)

(

3. Przesunięcie wykresu funkcji

x

a

x

f

)

(

wzdłuż osi OX i wzdłuż osi OY

4. Przesunięcie wykresu funkcji

x

a

x

f

)

(

o wektor

5. Funkcja homograficzna
6. Przekształcenia wykresu funkcji
7. Wyrażenia wymierne
8. Mnożenie i dzielenie wyrażeń wymiernych
9. Dodawanie i odejmowanie wyrażeń wymiernych

10. Równania wymierne
11. Wyrażenia wymierne – zastosowania
12. Nierówności wymierne
13. Funkcje wymierne
14. Równania i nierówności z wartością bezwzględną

Przykłady zadań:

1. Podaj dziedzinę wyrażenia i doprowadź je do najprostszej postaci.

a)

6

3

4

2

2

x

x

x

x

b)

x

x

x

x

)

3

(

)

2

)(

9

(

2

2. Wyznacz dziedzinę, zbiór wartości funkcji f, miejsce zerowe oraz f(0) i narysuj jej wykres: f(x) =

2

4

3

x

x

3. Wykonaj działania, odpowiedź podaj w najprostszej postaci:

a)

x

x

x

2

1

+

x

x

x

2

1

; b)

x

x

x

4

9

2

2

:

4

9

6

2

x

x

x

4. Rozwiąż równanie i nierówność:

a)

1

2

2

1

x

x

x

x

; b)

0

3

2

1

2

x

x

x

x

5. Rozwiąż równanie i nierówność:

a)

8

2

x

; b)

2

3

x

;

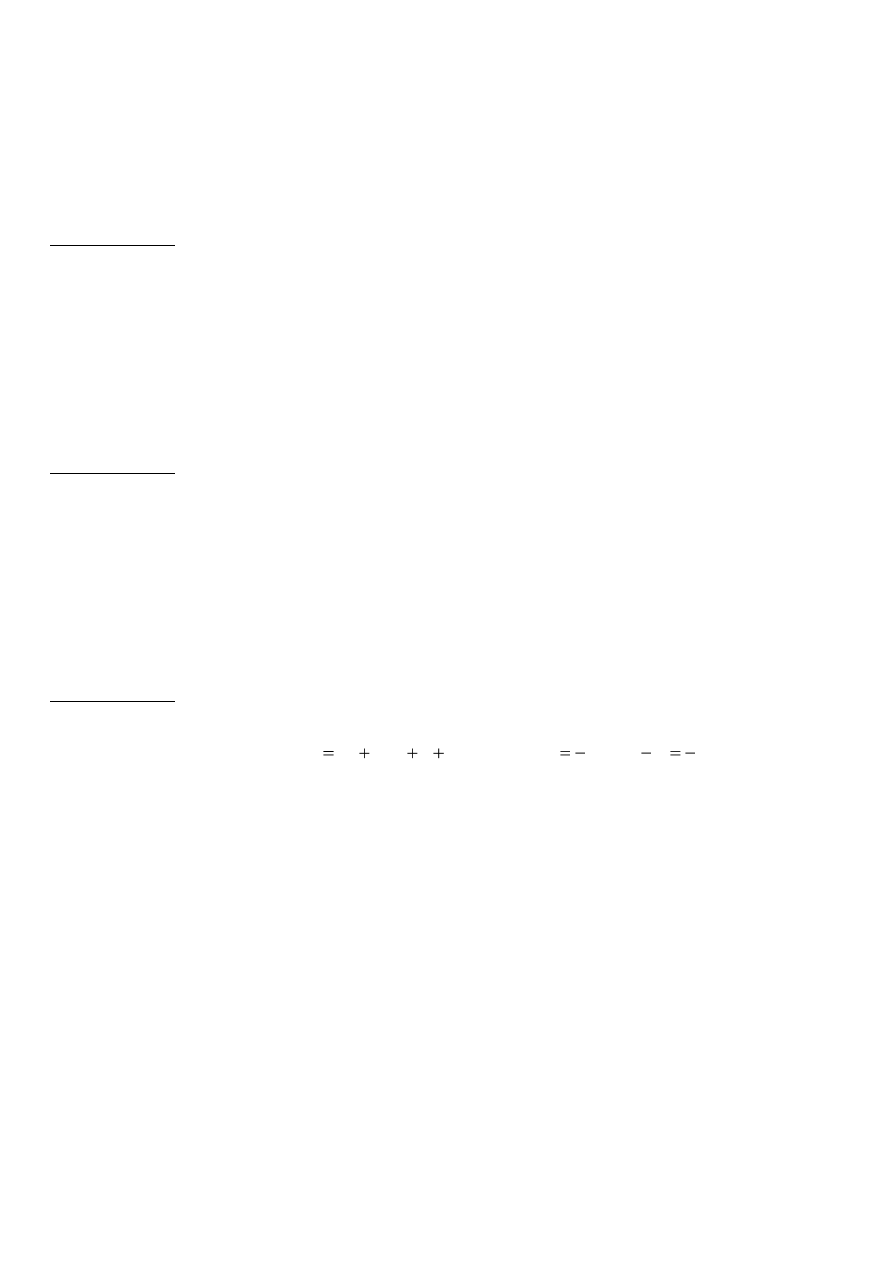
ZAGADNIENIA DO PRZYGOTOWANIA DLA KLASY II B LO

1. Funkcja kwadratowa

1. Wykres funkcji f (x) = ax

2

2. Przesunięcie wykresu funkcji f (x) = ax

2

wzdłuż osi OX i OY

3. Postać kanoniczna i postać ogólna funkcji kwadratowej
4. Rozwiązywanie równań kwadratowych przez rozkład na czynniki
5. Rozwiązywanie równań kwadratowych za pomocą wzorów
6. Postać iloczynowa funkcji kwadratowej

7. Nierówności kwadratowe

8. Funkcja kwadratowa – zastosowania

Przykłady zadań:

1. Wyznacz największą i najmniejszą wartość funkcji f(x) = -x² + 2x + 4 w przedziale < -1;2 >
2. Rozwiąż równania i nierówności: a) 3x² + 2x +1 = 3x + 4x² - 3; b) -3x² + x – 4 ≤ 0 ; c) x² - 3x +2 > 0
3. Przedstaw trójmian kwadratowy f(x) = x² + 2x – 8
a) w postaci iloczynowej; b) w postaci kanonicznej; c) sporządź wykres funkcji
4. Funkcja kwadratowa przyjmuje najmniejszą wartość równą -1, a do jej wykresu należą punkty (1; 3) i (5; 3). Wyznacz wzór tej
funkcji.
2. Trygonometria

1. Trójkąty prostokątne
2. Funkcje trygonometryczne kąta ostrego
3. Trygonometria – zastosowania
4. Rozwiązywanie trójkątów prostokątnych
5. Związki między funkcjami trygonometrycznymi

Przykłady zadań:

1. Rozwiąż trójkąt prostokątny, jeżeli przeciwprostokątna ma długość 5 cm, a jeden z kątów 37º.
2. Jaki kąt z powierzchnią ziemi tworzą promienie słoneczne, jeżeli drzewo o wysokości 20 m rzuca cień długości 17 m.
3. Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego, jeżeli: a) sin α = 0,8; b) tg α = 2
4. Przedstaw w prostszej postaci: a) ( 1 – cos α )( 1 + cos α )
b) cos α ctg ( 90 – α )

3. Wielomiany

1. Stopień i współczynniki wielomianu
2. Dodawanie i odejmowanie wielomianów
3. Mnożenie wielomianów
4. Wzory skróconego mnożenia
5. Rozkład wielomianu na czynniki (1)
6. Równania wielomianowe

Przykłady zadań:

1. Dane są wielomiany W(x) = 4x

3

+ 2x

2

– 3x – 4 F(x) = -x

2

+ 5x – 6. Wyznacz wielomian: G(x) = -3W(x) + 2F(x)

2. Określ stopień wielomianu: W(x) = (x-1)(x+1)

2

(x-3)

3. Wyznacz współczynniki wielomianu:

n

x

mx

x

x

W

2

3

)

(

,

jeżeli

9

)

2

(

5

)

1

(

W

i

W

4. Rozłóż wielomian na czynniki nierozkładalne:

a) W(x) = x

4

– 2x

3

– x

2

+ 2x

b) W(x) = (x

2

– 6x + 8)(x

2

– 4)(x

2

– 4x + 4)

5. Rozwiąż równania: a) x

3

– 3x

2

- 4x + 12 = 0

;

b) x

5

-2x

4

- 15x

3

=0

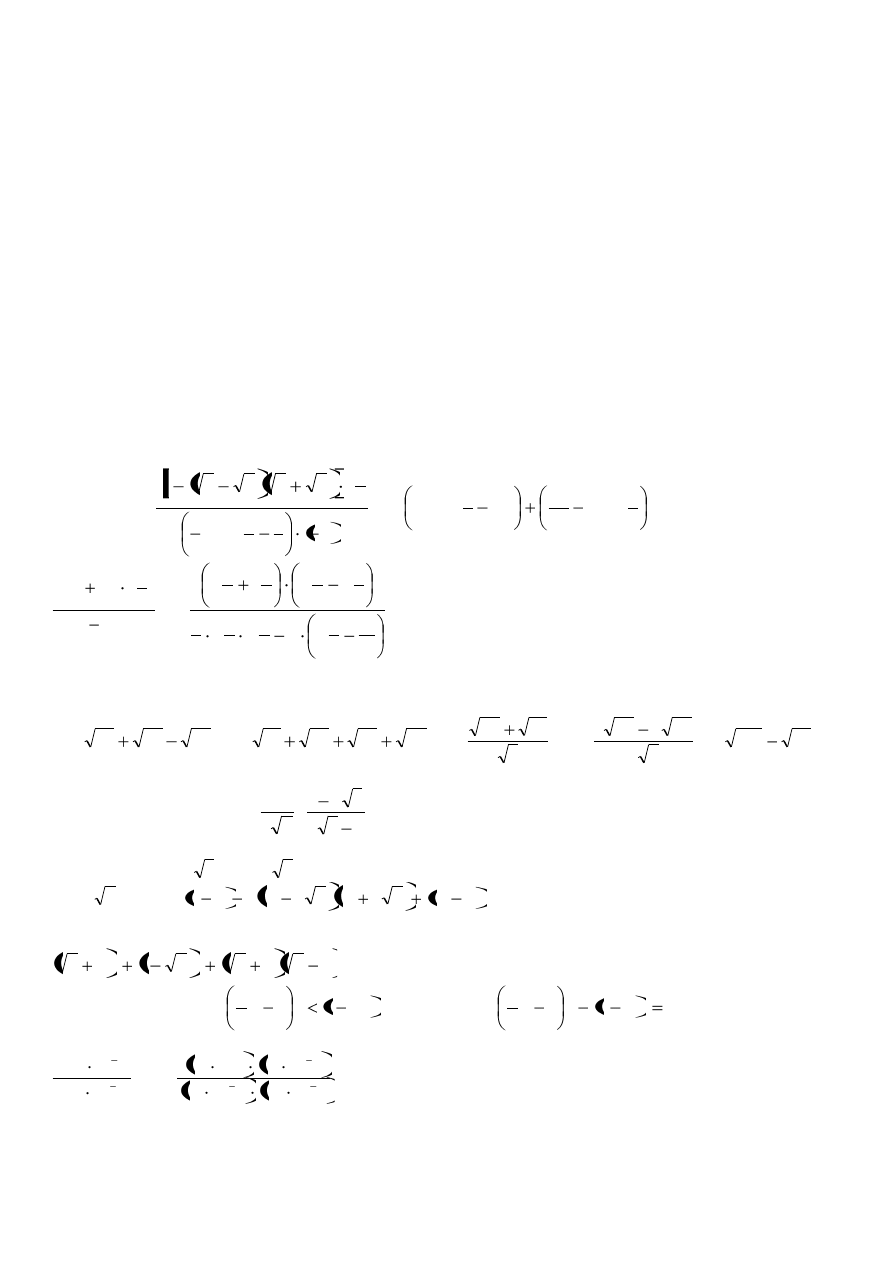
ZAGADNIENIA DO OPRACOWANIA W KLASIE I B LO

MATEMATYKA – SEMESTR I

1. Świat liczb rzeczywistych

 Działania w zbiorze liczb wymiernych i niewymiernych
 Pierwiastek kwadratowy i sześcienny (własności, działania)
 Przekształcenia algebraiczne (wzory skróconego mnożenia – kwadraty)
 Działania na potęgach (potęga o wykładniku całkowitym)
 Notacja wykładnicza
 Przybliżenia; błąd bezwzględny i względny
 Zastosowanie procentów w zadaniach

2. Zbiory

 Działania na zbiorach (suma, iloczyn, różnica)
 Przedziały liczbowe i działania na przedziałach liczbowych
 Wartość bezwzględna i jej własności
 Równania i nierówności z wartością bezwzględną

==============================================================================

PRZYKŁADOWE ZADANIA DO ROZWIĄZANIA

Zad. 1. Oblicz: a)

3

2

1

3

1

5

2

5

:

3

2

1

1

2

7

2

7

7

; b)

5

3

1

:

2

,

0

40

17

5

,

0

3

1

1

:

76

,

0

;

c)

4

,

8

:

1

,

2

5

,

2

3

1

1

8

,

1

6

,

3

2

; d)

5

11

2

1

2

2

3

2

2

4

3

3

5

1

5

1

2

3

2

2

2

1

1

4

1

2

Zad.2
Uprość wyrażenie:

;

5

2

45

4

20

3

)

;

3

12

27

)

;

27

72

75

18

)

;

72

50

32

)

d

c

b

a

e)

3

3

54

128

Zad. 3.

Usuń niewymierność z mianownika:

2

5

6

;

2

3

5

3

2

1

Zad. 4. Zapisz wyrażenie w najprostszej postaci i oblicz jego wartość:

a) dla a= - 0,5 : ( 2

3

+ 3a )( 2

3

- 3a ) – 5( 4 – a )² + 2( 2 – a )

b) dla a=

2

:

2

4

3

2

2

2

2

2

2

2

2

a

a

a

a

Zad. 5. Sprowadź wyrażenie do najprostszej postaci:

5

2

5

2

2

1

3

2

2

2

Zad. 6. Rozwiąż nierówność:

2

2

2

1

3

3

2

9

x

x

oraz równanie: 4

0

2

3

2

1

2

2

x

x

Zad.7. Oblicz i wynik przedstaw w notacji wykładniczej:

a)

13

24

10

500

10

5

,

24

; b)

4

7

5

8

10

8

,

4

10

7

,

1

10

1

,

5

10

2

,

1

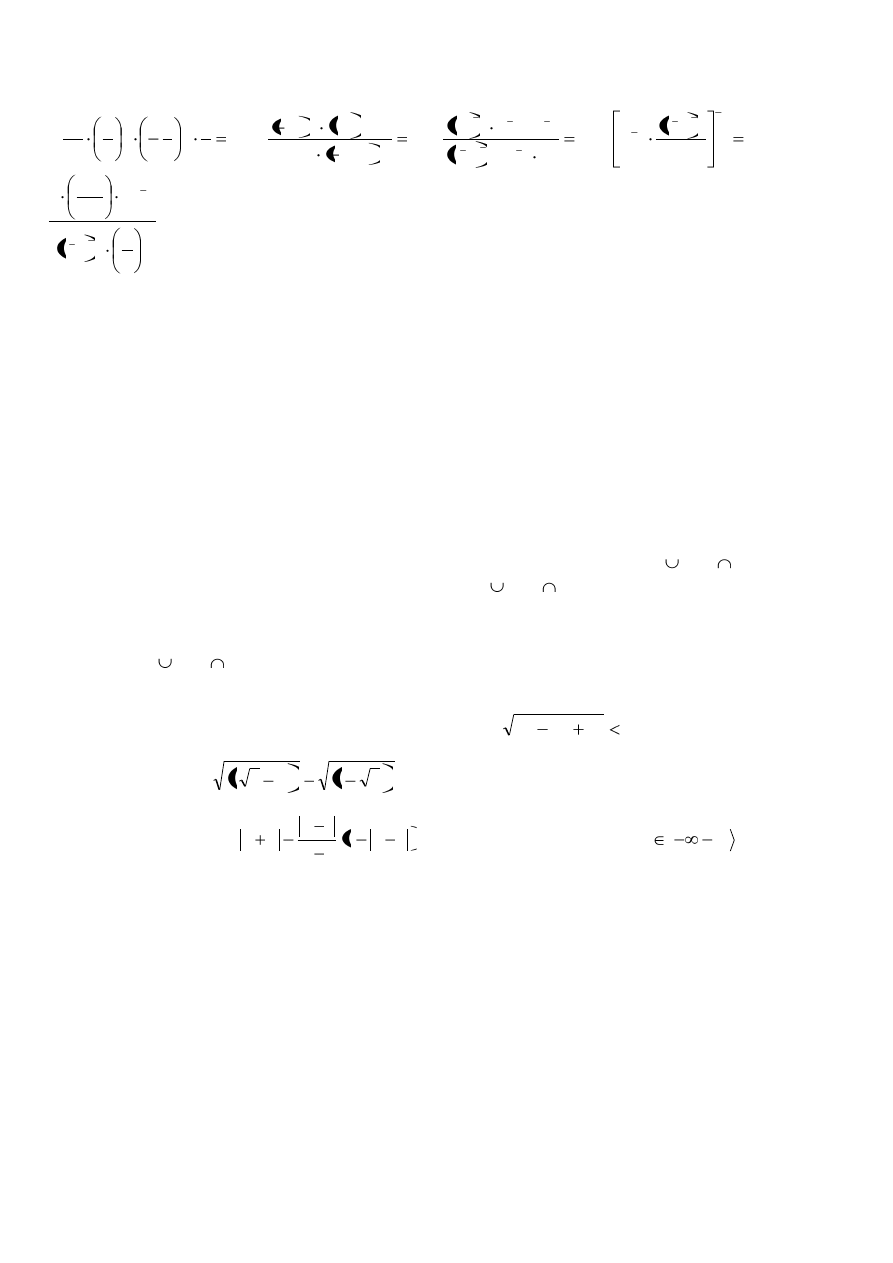
Zad.8.
Zapisz w postaci jednej potęgi:

3

2

5

3

6

2

6

5

2

4

2

5

3

3

5

3

44

4

3

)

:

:

)

128

1024

64

:

2

2

)

3

1

3

1

9

1

27

1

)

a

a

a

d

a

a

a

a

a

a

c

b

a

e)

5

2

3

2

3

2

1

4

64

16

1

8

Zad.9.
Dana jest liczba x. Podaj jej przybliżenie do części setnych i oblicz błąd względny i bezwzględny z dokładnością do 0,01%

a) x = 19,2391
b) x = 315, 781
c) x = 4,9999

Zad. 10.
Pan Tomaszewski zarabiał 1250 zł, dostał podwyżkę i obecnie zarabia 1500 zł. O ile procent podwyższono mu pensję?
Zad. 11.
Cenę pewnego towaru najpierw zwiększono o 8%, a potem zmniejszono o 25%. Teraz towar ten kosztuje 1215 zł. Jaka była cena
początkowa?
Zad. 12.
Wartość samochodu równą 24 000 zł najpierw obniżono o 15%, następnie podwyższono o 15% . Oblicz końcową cenę towaru. O ile
procent zmieniła się cena?
Zad. 13.
Cenę towaru podniesiono o 20% a następnie obniżono o 20% po tych zmianach towar kosztuje o 24 zł mniej niż na początku. Wyznacz
cenę początkową.
Zad. 14. Dane są zbiory: A = { x : x є N i x < 9 } oraz B ={ x : x є C i -1 ≤ x < 6 }. Wyznacz zbiory:

A

B

A

B

A

,

,

\

.

\

,

A

B

B

Zad. 15. Dane są zbiory: A = < -8 ; -2 >, B = ( -5 ; 3 ). Wyznacz zbiory:

A

B

A

B

A

,

,

\

.

\

,

A

B

B

Zad. 16. Dane są zbiory:

a) A = { x : x є C i -5 ≤x < 6 } oraz B ={ x : x є N i x <11 }
b) A = ( -5 ; 8> oraz B = (4; 10>

Wyznacz zbiory:

A

B

A

B

A

,

,

\

.

\

,

A

B

B

Zad. 17. Rozwiąż równania i nierówności:

a) | x – 6 | = 4 , b) | x - 3 | < 1 , c) | 3x + 2 | = 1 , d) | 7 + x | ≥ 3 , e)

2

16

8

2

x

x

.

Zad. 18. Określ znak liczby:

2

2

5

3

6

5

2

Zad. 19. Doprowadź wyrażenie

3

2

1

1

2

3

x

x

x

x

do najprostszej postaci, wiedząc, że

2

;

(

x

.