„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
5
ZALECENIA FRANCUSKIE
Opierają się na normie NF P 94-200 i obejmują:
a) analizę stateczności wewnętrznej - sprawdzenie sił rozciągających
oraz sił kotwiących zbrojenie w gruncie,
b) analizę stateczności zewnętrznej - ze względu na poślizg wzdłuż
podstawy oraz nośności podłoża,
c) analizę stateczności ogólnej.
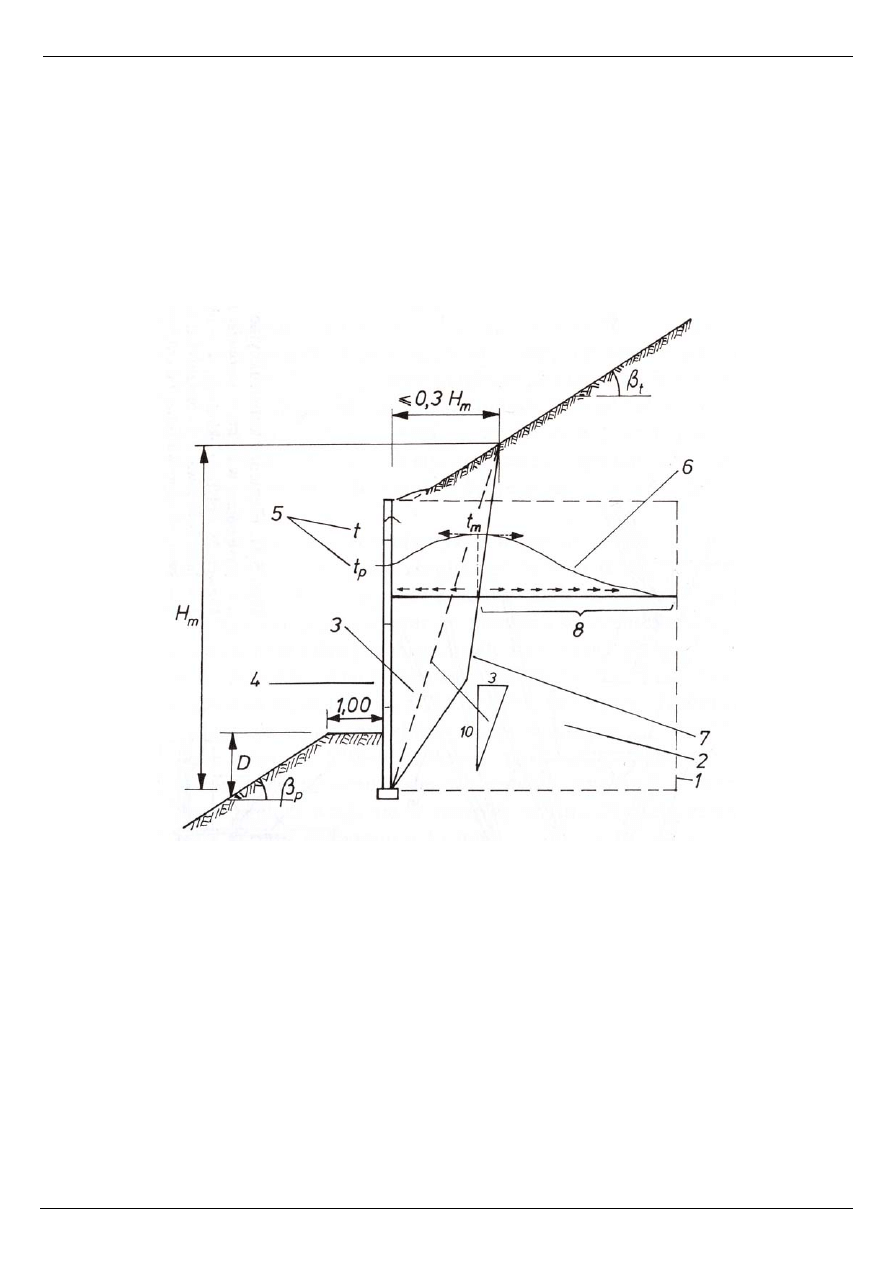
LEGENDA:
1 – masyw gruntu zbrojonego 5 – siły rozciągające w zbrojeniu (tp, tm)
2 – strefa kotwienia zbrojenia 6 – rozkład siły rozciąg. wzdłuż zbrojenia
3 – strefa aktywna gruntu zbrojonego 7 – linia maksymalnych rozciągań
4 – obudowa czoła konstrukcji 8 – odcinek kotwienia zbrojenia
Rys. 1. Schemat obliczeniowy konstrukcji z gruntu zbrojonego.
„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
6
Sprawdzenie stateczności wewnętrznej
Sprawdzenie to wykonuje się w celu stwierdzenia:
→ czy naprężenia rozciągające w zbrojeniu masywu gruntowego będą
w zakresie dopuszczalnym oraz,
→ czy opory kotwienia zbrojenia będą odpowiednio większe, niż siły
wyciągające zbrojenie z gruntu.
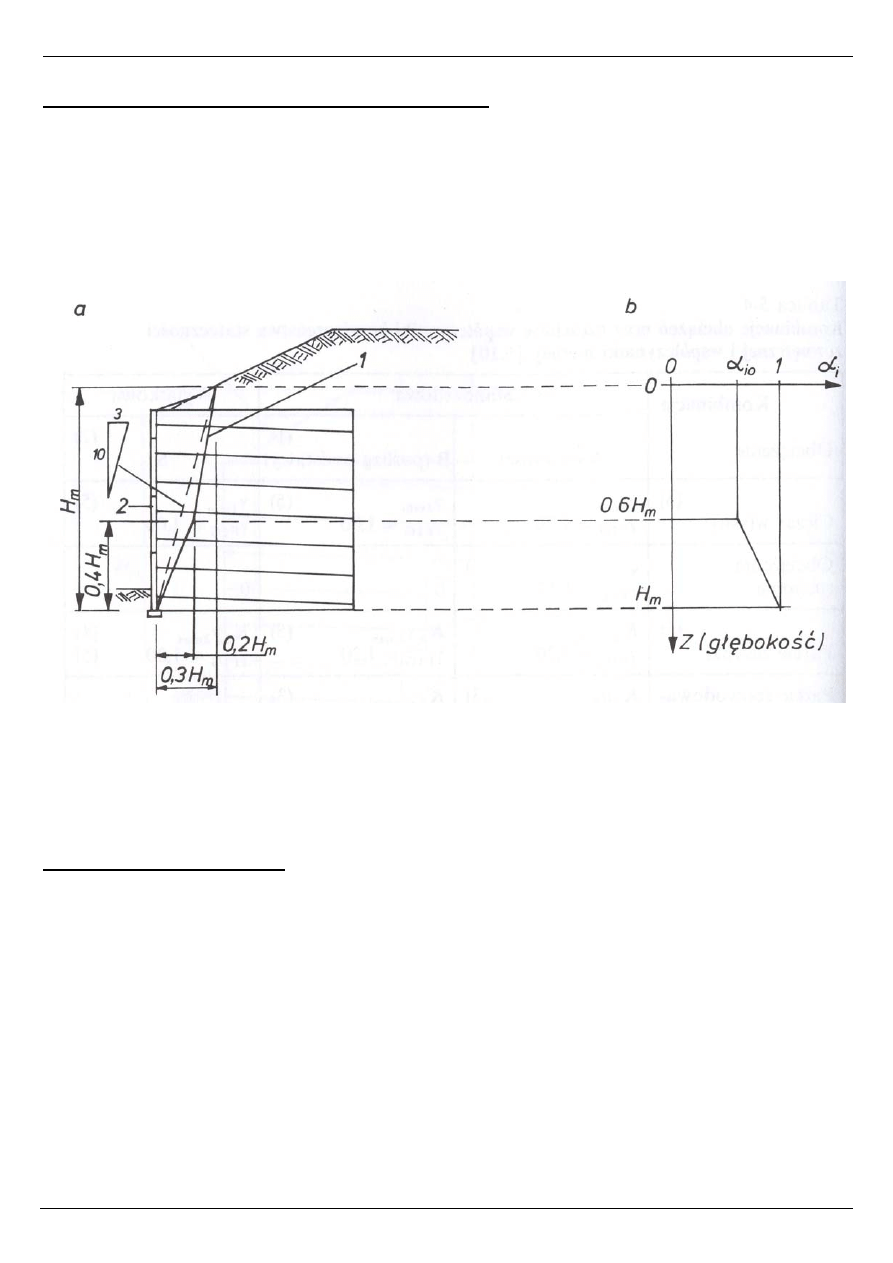
Rys. 2. Schemat do obliczeń stateczności wewnętrznej konstrukcji z gruntu
zbrojonego: a) położenie linii maksymalnych rozciągań (1),
b) zmiana współczynnika
i
α
z głębokością,
Sposób postępowania:
Na początku określa się maksymalną siłę rozciągającą w zbrojeniu
(na 1 m wzdłuż obudowy) ze wzoru:
a
h
m
h
t
⋅
=
σ
[kN/m]
gdzie:
a
h ─ rozstaw warstw zbrojenia w pionie [m],
h
σ
─ maksymalne naprężenie poziome w analizowanej warstwie
zbrojenia spowodowane ciężarem jej nadkładu [kPa] wyznaczane
ze wzoru:
qh
v
h
K
σ
σ
σ
+
⋅
=
[kPa]

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
7
Przy czym
K
jest współczynnikiem zależnym od głębokości (z) położenia
warstwy zbrojenia w masywie gruntowym, wg wzoru:
-
]
)
1
(
6
,
1
[
1
)
(
o
o
a
z
z
z
z
z
K
K
+
−
⋅
⋅
Ω
⋅
=
, jeżeli
o
z
z
<
-
1
)
(
Ω
⋅
=
a
z
K
K
, jeżeli
o
z
z
≥
gdzie:
o
z = 6 m,
a
K ─ współczynnik parcia czynnego dla masywu gruntu zbrojonego:
)
2
4
(
1
2
k
a
tg
K
ϕ
π
−
=
[ - ]
k
1
ϕ
─ kąt tarcia wewnętrznego gruntu zasypowego (masyw zbrojony).
1
Ω ─ współczynnik kształtu, dla zbrojenia arkuszowego:
5
,
1
1
=
Ω
.
Sposób określania naprężeń pionowych w poziomie (z) polega na
obliczeniu wypadkowych obciążeń powyżej analizowanej warstwy
i rozłożeniu ich zgodnie z zasadą Meyerhofa na szerokości
)
2
)
(
(
x
e
z
L
−
.
W przypadku konstrukcji z pionową obudową, naprężenia pionowe określa
się ze wzoru:
vq
x
v
v
e
z
L
z
R
z
σ
σ
+
−
=
2
)
(
)
(
)
(
[kPa]
gdzie:
)
(z
R
v
─ wypadkowa obciążeń w poziomie (z) [kN/m],
)
(z
L
─ długość elementu zbrojącego w poziomie (z) [m],
vq
σ
─ naprężenie pionowe od obciążenia naziomu konstrukcji z gruntu
zbrojonego, z uwzględnieniem rozłożenia tego obciążenia [kPa],
)
(
)
(
z
R
z
M
e
v
x
=
[m]
gdzie:
)
(z
M
─ moment wywracający w poziomie (z), w środku warstwy
zbrojenia, który jest wypadkowym wszystkich momentów
powodowanych przez obciążenia przyłożone powyżej poziomu
(z), z uwzględnieniem ich rozłożenia [kNm/m].

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
8
Naprężenia rozciągające przy obudowie oblicza się wg wzoru:
∑
⋅
+
⋅
=
a
hq
vi
i
p
h
K
t
)
(
σ
σ
α
[kN/m]
gdzie:
vi
σ
─ naprężenie pionowe odpowiadające; [kPa].
i
α
─ współczynnik zależny od podatności obudowy i głębokości;
w
przypadku pionowych obudów wynosi:
-
=
0
i
α
0,75 dla bardzo odkształcalnych obudów (metalowych
i z geosyntetyków),
-
=
0
i
α
0,85 dla umiarkowanie odkształcalnych obudów
(z prefabrykatów betonowych),
-
=
0
i
α
1,00 dla sztywnych obudów (z betonowych płyt o długości
równej wysokości konstrukcji),
W każdej warstwie zbrojenia mobilizuje się tarcie (opór kotwienia), którego
wartość charakterystyczną oblicza się ze wzoru:
v
a
f
bL
N
r
σ
μ
⋅
⋅
⋅
=
*
2
[kN/m]
gdzie:
N ─ liczba elementów zbrojących na 1 m wzdłuż obudowy, przy czym
w przypadku zbrojenia powłokowego N = 1;
2 - liczba 2 uwzględnia występowanie tarcia na dolnej i górnej
powierzchni zbrojenia,
b
─ szerokość elementu zbrojenia, która w przypadku zbrojenia
powłokowego równa jest 1 m,
a
L ─ długość kotwienia zbrojenia w analizowanej warstwie (poza klinem
odłamu – patrz rys) [m],
v
σ
─ średnie pionowe naprężenie wywierane na analizowaną warstwę
zbrojenia [kPa]
*
μ
─ współczynnik rzeczywistego tarcia w analizowanej warstwie, w
przypadku zbrojenia powłokowego:
*
μ
=
k
tg
1
ϕ

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
9
Każdej warstwie zbrojącej powinno się zapewnić bezpieczeństwo przed
zerwaniem poprzez spełnienie następujących nierówności:
mt
ck
m
F
r
t
γ
γ
≤
⋅
3
mt
ak
p
F
r
t
γ
γ
≤
⋅
3
gdzie:
p
m
t
t ,
─ rozciąganie zbrojenia,
ck
r
─ wytrzymałość charakterystyczna warstwy odpowiada
wytrzymałości długoterminowej (uwzględniającej pełzanie)
zbrojenia (zgodnie z zaleceniami producenta) [kN/m],
ak
r
─ wytrzymałość charakterystyczna warstwy zbrojenia w połączeniu
z obudową [kN/m], (odpowiada charakterystycznej wytrzymałości
warstwy zbrojenia podzielonej przez częściowy współczynnik
bezpieczeństwa zależny od sposobu połączenia zbrojenia z
obudową, wynoszący 1,05
÷1,3),
mt
γ
─ częściowy współczynnik bezpieczeństwa ze względu na zerwanie
warstwy zbrojącej, przyjmowany 1,50 dla konstrukcji
standardowych oraz 1,65 dla szczególnych.
W każdej warstwie zbrojenia musi zostać spełniona nierówność
zapewniająca bezpieczne kotwienie:
mf
f
m
F
r
t
γ
γ
≤
⋅
3
gdzie:
m
F
t
,
3
γ
─ jak wyżej,
f
r
─ charakterystyczna wartość tarcia,
mf
γ
─ częściowy współczynnik bezpieczeństwa kotwienia zbrojenia
przyjmowany 1,20 w przypadku konstrukcji standardowych oraz
1,30 w przypadku konstrukcji szczególnych.

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
10
Sprawdzenie stateczności zewnętrznej
Najczęstsze kombinacje obciążeń uwzględniane podczas sprawdzania
stateczności zewnętrznej konstrukcji z gruntu zbrojonego oraz częściowe
współczynniki bezpieczeństwa γ
m
zalecane przez francuską normę
NF P 94-200 zestawiono w tabeli.
Tab. Kombinacje obciążeń, częściowe współczynniki bezpieczeństwa
Kombinacja
Obciążenie
Standardowa
A (nośność)
B
(poślizg w podstawie)
Ciężar własny
γ
1max
γ
F1G
= 1,20
γ
1min
γ
F1G
= 1,00
Obciążenia ruchome
γ
F1q
= 1,33
0
Parcie zasypki
γ
F1G
= 1,20
γ
F1G
= 1,20
Parcie spowodowane
obciążeniem
ruchomym
γ
F1q
= 1,33
γ
F1q
= 1,33
Współczynnik metody γ
F3
= 1,125
γ
F3
= 1,00
Stateczność ze względu na poślizg
Stateczność konstrukcji na przesunięcie w wyniku poślizgu wzdłuż
podstawy będzie zapewniona, gdy zostaną spełnione następujące warunki:
)
/
/
(
1
1
3
mc
k
m
k
F
h
c
L
tg
R
R
γ
γ
ϕ
γ
ϕ
υ
⋅
+
⋅
≤
⋅
)
/
/
(
3
mc
fk
m
fk
F
h
c
L
tg
R
R
γ
γ
ϕ
γ
ϕ
υ
⋅
+
⋅
≤
⋅
gdzie:
v
h
R
R ,
─ składowa pozioma i pionowa wypadkowego obciążenia w
podstawie konstrukcji, [kN/m wzdłuż obudowy],
k
k
c
1
1
,
ϕ
─ charakterystyczne wartości kąta tarcia wewnętrznego i
spójności gruntu w masywie zbrojonym [stopnie, kPa],

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
11
fk
fk
c
,
ϕ
─ charakterystyczne wartości kąta tarcia wewnętrznego i
spójności gruntu podłoża [stopnie, kPa],
L
─ długość warstw zbrojenia gruntu [m],
3
F
γ
─ współczynnik metody [-],
ϕ
γ
m
─ częściowy współczynnik bezpieczeństwa stosowany do
tangensa kąta tarcia wewnętrznego; w przypadku
standardowej kombinacji obciążeń równy 1,20, a w przypadku
kombinacji wyjątkowej 1,10 [-],
mc
γ
─ częściowy współczynnik bezpieczeństwa sze względu na
spójność; w przypadku standardowej kombinacji obciążeń
równy 1,65, a w przypadku kombinacji wyjątkowej 1,50 [-].
Nośność podłoża
Podłoże gruntowe pod konstrukcją zbrojoną można uznać za nośne,
jeżeli spełniona zostanie następująca nierówność:
mq
fu
ref
q
q
γ
≤
gdzie:
fu
q ─ nośność graniczna podłoża [kPa],
mq
γ
─ częściowy współczynnik bezpieczeństwa nośności podłoża
masywu zbrojonego, przyjmowany 1,50 [-],
ref
q ─ obciążenie podłoża masywem zbrojonym [kPa] wg wzoru:
v
b
v
F
ref
R
M
L
R
q
2
3
−
⋅
=
γ
[kPa]
gdzie:
3
,
,
F
v
L
R
γ
─ jak wyżej,
b
M
─ moment wypadkowy w środku podstawy konstrukcji z gruntu
zbrojonego [kNm/m], z pominięciem współczynnika metody
3
F
γ
.
„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
12
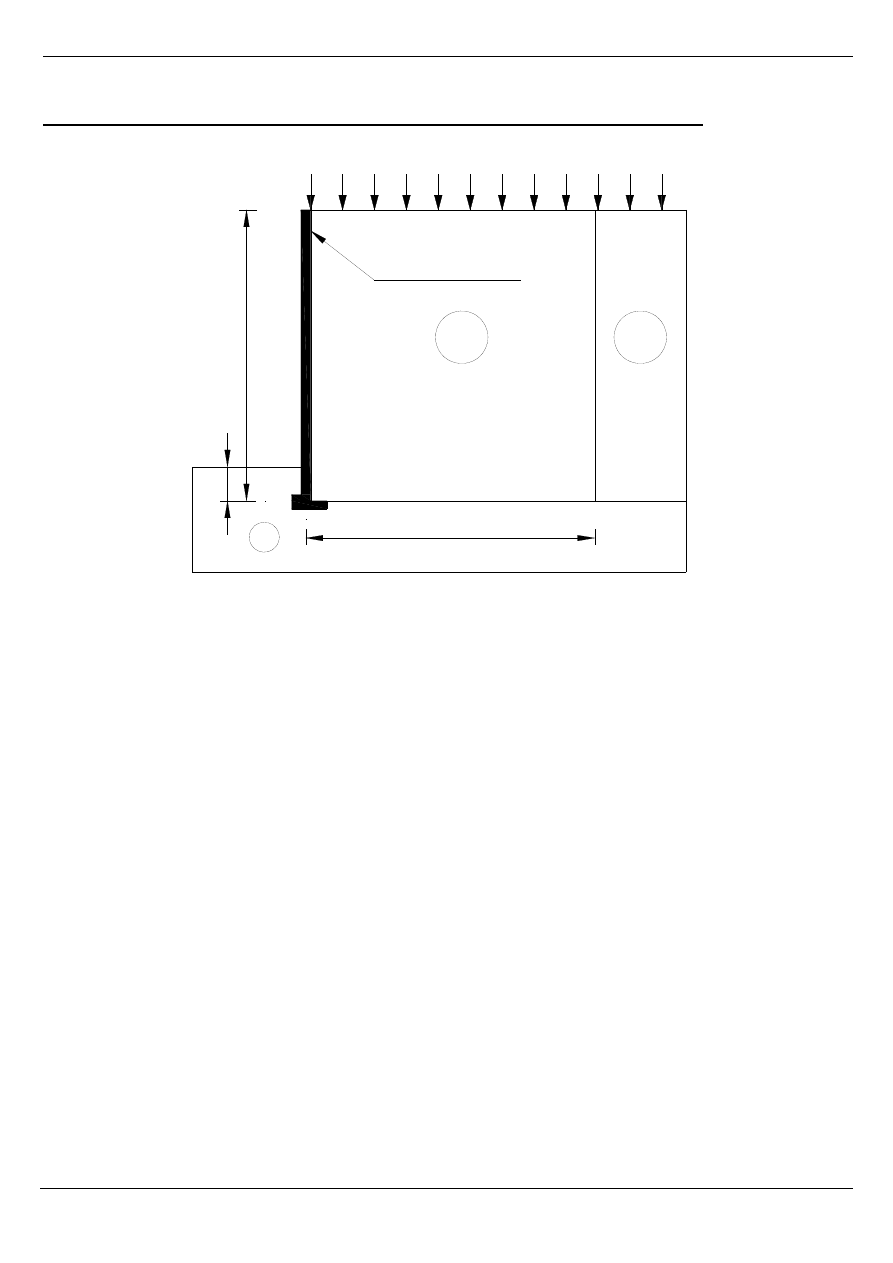
PRZYKŁAD OBLICZENIOWY wg wytycznych francuskich
Pd
Ps
0,
7m
q = 15 kPa
L [m]
H = 6m
Pd
Obudowa z bloczków
betonowych
Parametry geotechniczne gruntów:
─ zasyp Ps:
70
,
0
=
D
I
,
3
/
64
,
18
m
kN
w
=
γ
,
o
w
2
,
34
=
φ
,
0
=
w
c
;
─ grunt rodzimy za konstrukcją Pd:
60
,
0
=
D
I
,
3
/
17
,
17
m
kN
b
=
γ
,
o
b
31
=
φ
,
0
=
b
c
;
─ podłoże Pd:
50
,
0
=
D
I
,
3
/
17
,
17
m
kN
f
=
γ
,
o
f
4
,
30
=
φ
,
0
=
f
c
;
Przyjęto zbrojenie geosiatką Tensar oraz obudowę z bloczków betonowych.
UWAGA:
Przykładowa konstrukcja ma pionowe lico i nie występują grunty
spoiste … w Państwa dane do projektu są bardziej skomplikowane …

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
13
Stateczność zewnętrzna
Współczynnik parcia czynnego
a
K
:
320
,
0
)
2
31
45
(
2
=
−
= tg
K
a
Wartość parcia zatem jest równa:
m
kN
H
q
K
H
E
a
a
/
74
,
127
)
2
17
,
17
6
15
(
320
,
0
6
)
2
(
=
⋅
+
⋅
⋅
=
⋅
+
⋅
⋅
=
γ
Przyjęto minimalną długość zbrojenia
H
L
⋅
≥ 6
,
0
, zatem
m
L
6
,
3
=
.
Składowe wypadkowego obciążenia w podstawie konstrukcji:
m
kN
E
R
a
G
F
h
/
29
,
153
74
,
127
2
,
1
1
=
⋅
=
⋅
=
γ
m
kN
H
L
L
q
R
w
v
/
62
,
456
64
,
18
6
6
,
3
6
,
3
15
=
⋅
⋅
+
⋅
=
⋅
⋅
+
⋅
=
γ
Stateczność konstrukcji ze względu na poślizg wzdłuż podstawy
Sprawdzenie warunku stateczności na poślizg:
─ dla masywu
(
)
m
kN
tg
m
kN
/
6
,
258
2
,
1
2
,
34
62
,
456
/
29
,
153
0
,
1
29
,
153
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
≤
=
⋅
─ dla podłoża
m
kN
tg
m
kN
/
35
,
223
2
,
1
)
4
,
30
(
62
,
456
/
29
,
153
0
,
1
29
,
153
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
≤
=
⋅
Warunki stateczności na przesuw spełnione
„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
14
Nośność podłoża
mq
fu
ref
q
q
γ
≤
m
kN
R
v
/
95
,
547
62
,
456
2
,
1
=
⋅
=
0
=
R
e
(
)
(
)
m
e
e
e
e
z
e
a
a
a
a
h
23
,
2
32
,
0
6
17
,
17
15
32
,
0
15
32
,
0
6
17
,
17
15
32
,
0
15
2
3
6
2
3
2
1
2
1
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
+
+
⋅
⋅
⋅
+
+
⋅
⋅
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
⋅
=
m
kNm
e
R
e
R
M
h
h
R
v
B
/
14
,
341
23
,
2
29
,
153
0
95
,
547
−
=
⋅
−
⋅
=
⋅
−
⋅
=
Obciążenie podłoża masywem gruntu zbrojonego:
kPa
R
M
L
R
q
v
b
v
F
ref
69
,
232
95
,
547
14
,
341
2
6
,
3
95
,
547
125
,
1
2
3
=
⋅
−
⋅
=
−
⋅
=
γ
Nośność graniczna podłoża określana według wzoru:
B
B
D
D
c
fu
N
L
N
D
N
c
q
⋅
⋅
+
⋅
⋅
+
⋅
=
γ
γ
min
26
,
19
)
2
4
,
30
45
(
)
2
45
(
2
4
,
30
2
=
+
⋅
=
+
⋅
=
⋅
⋅
tg
e
tg
e
N
tg
tg
D
π
φ
π
φ
12
,
31
4
,
30
1
26
,
19
1
=
−
=
−
=
tg
tg
N
N
D
C
φ
03
,
8
4
,
30
)
1
26
,
19
(
75
,
0
)
1
(
75
,
0
=
⋅
−
⋅
=
⋅
−
⋅
=
tg
tg
N
N
D
B
φ
kPa
q
fu
06
,
728
03
,
8
6
,
3
17
,
17
26
,
19
7
,
0
17
,
17
12
,
31
0
=
⋅
⋅
+
⋅
⋅
+
⋅
=
kPa
kPa
37
,
485
5
,
1
06
,
728
69
,
232
=
≤
Warunek nośności spełniony
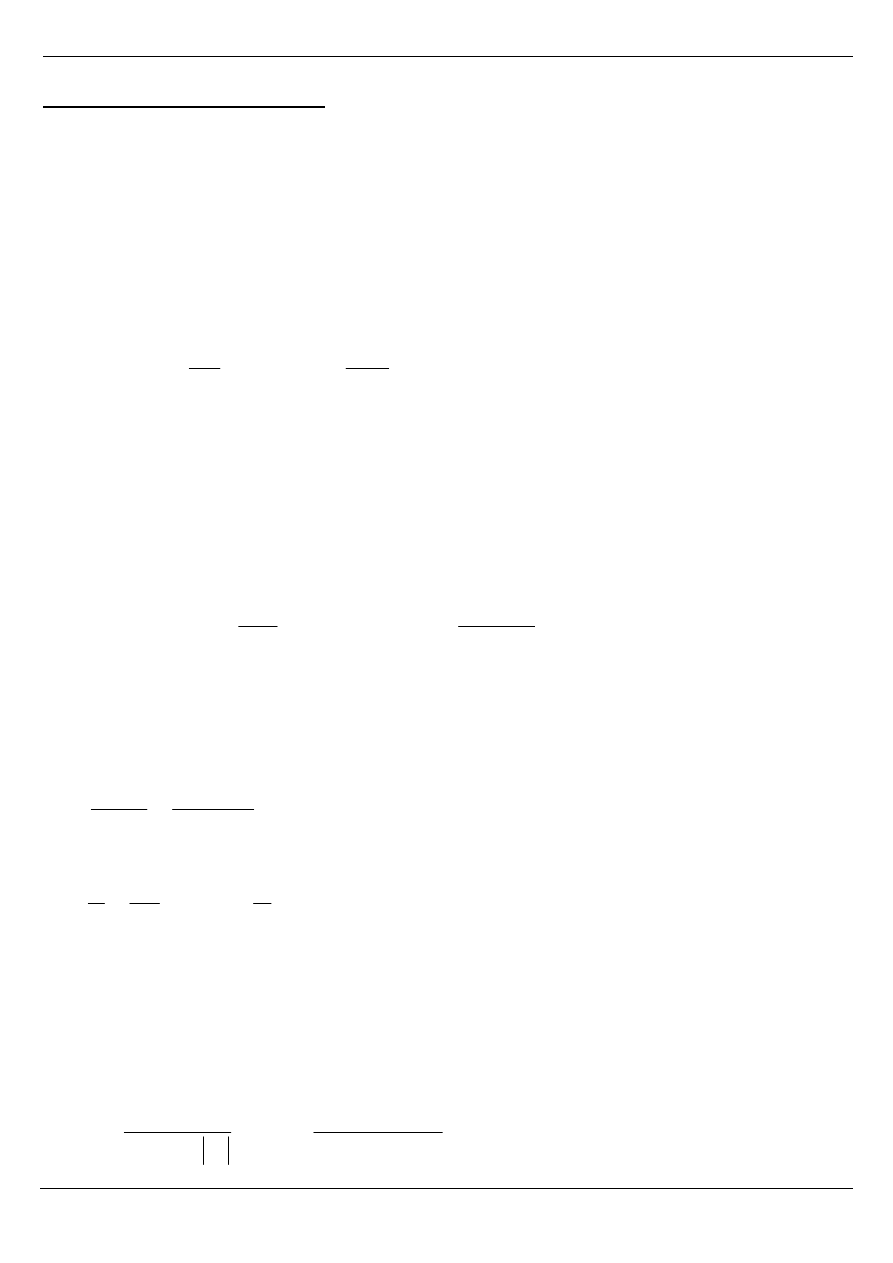
„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
15
Stateczność wewnętrzna
Przykład obliczeń dla 9-tej warstwy zbrojenia.
Przy rozstawie
m
h
a
5
,
0
=
dla 9-tej warstwy zbrojenia, zagłębienie
o
z
m
z
=
= 6
Stąd współczynnik parcia
1
Ω
⋅
=
a
K
K
280
,
0
2
2
,
34
45
2
45
2
1
2
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
tg
tg
K
k
a
φ
420
,
0
5
,
1
280
,
0
=
⋅
=
K
Wypadkowa obciążeń w poziomie z:
m
kN
L
z
z
R
v
/
62
,
402
6
,
3
6
64
,
18
)
(
=
⋅
⋅
=
⋅
⋅
=
γ
Wypadkowa parcia w poziomie z:
m
kN
z
q
K
z
z
E
a
a
/
29
,
119
2
64
,
18
6
15
280
,
0
6
2
)
(
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
⋅
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
+
⋅
⋅
=
γ
Moment wywracający w poziomie z:
m
kNm
e
E
e
R
z
M
h
a
R
v
/
81
,
263
21
,
2
29
,
119
0
31
,
201
)
(
−
=
⋅
−
⋅
=
⋅
−
⋅
=
m
z
R
z
M
e
v
x
655
,
0
62
,
402
81
,
263
)
(
)
(
−
=
−
=
=
Dla
344
,
0
67
,
1
6
,
3
6
=
∞
=
=
=
η
B
L
i
L
z
Stąd wypadkowa od obciążeń zewnętrznych w poziomie z:
kPa
q
vq
17
,
5
15
344
,
0
=
⋅
=
⋅
=
η
σ
Naprężenia pionowe zatem są równe:
kPa
e
z
L
z
R
z
vq
x
v
v
02
,
181
17
,
5
655
,
0
2
6
,
3
62
,
402
2
)
(
)
(
)
(
=
+
⋅
−
=
+
−
=
σ
σ

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
16
Maksymalne naprężenie poziome:
kPa
K
qh
v
h
12
,
76
02
,
181
420
,
0
=
⋅
=
+
⋅
=
σ
σ
σ
Zatem maksymalne rozciągania zbrojeniu wynoszą:
kPa
h
t
a
h
m
06
,
38
5
,
0
12
,
76
=
⋅
=
⋅
=
σ
Dla obudowy betonowej
85
,
0
=
io
α
, dla
0
,
1
0
,
6
=
⇒
=
=
i
m
H
z
α
Naprężenia rozciągające przy obudowie wynoszą więc:
(
)
kPa
h
K
t
a
hq
vi
i
p
06
,
38
5
,
0
02
,
181
0
,
1
420
,
0
)
(
=
⋅
⋅
⋅
=
⋅
+
⋅
=
∑
σ
σ
α
Współczynnik rzeczywistego tarcia:
68
,
0
2
,
34
*
=
= tg
μ
Długość kotwienia zbrojenia w analizowanej warstwie (poza klinem odłamu)
wg uproszczonego schematu;
m
z
H
L
L
a
6
,
3
)
6
6
(
*
3
,
0
6
,
3
)
(
*
3
,
0
=
−
−
=
−
−
=
Wartość charakterystyczna zmobilizowanego tarcia:
kPa
bL
N
r
v
a
f
75
,
885
02
,
181
68
,
0
6
,
3
1
2
1
2
*
=
⋅
⋅
⋅
⋅
⋅
=
⋅
⋅
⋅
=
σ
μ
Sprawdzenie bezpieczeństwa ze względu na zerwanie
Wytrzymałość charakterystyczna warstwy odpowiadająca wytrzymałości
długoterminowej (uwzględniającej pełzanie) zbrojenia geosyntetycznego
(zgodnie z zaleceniami producenta) dla geosiatki RE160:
m
kN
P
r
c
ck
/
4
,
69
=
=
Wytrzymałość charakterystyczna zbrojenia w połączeniu z obudową:
m
kN
F
r
ml
k
ak
/
1
,
66
05
,
1
4
,
69
=
=
=
γ

„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
17
Warunki bezpieczeństwa:
mt
ck
m
F
r
t
γ
γ
≤
⋅
3
kPa
kPa
26
,
46
5
,
1
4
,
69
82
,
42
06
,
38
125
,
1
=
≤
=
⋅
mt
ak
p
F
r
t
γ
γ
≤
⋅
3
kPa
kPa
06
,
44
5
,
1
1
,
66
82
,
42
06
,
38
125
,
1
=
≤
=
⋅
Warunki bezpieczeństwa za zerwanie spełnione
Sprawdzenie oporu kotwienia:
mf
f
m
F
r
t
γ
γ
≤
⋅
3
kPa
kPa
12
,
738
2
,
1
75
,
885
82
,
42
06
,
38
125
,
1
=
≤
=
⋅
Warunek spełniony
W wyniku obliczeń (tab.) przyjęto rozkład zbrojenia z georusztu
Tensar 160RE o układzie jak na rysunku.
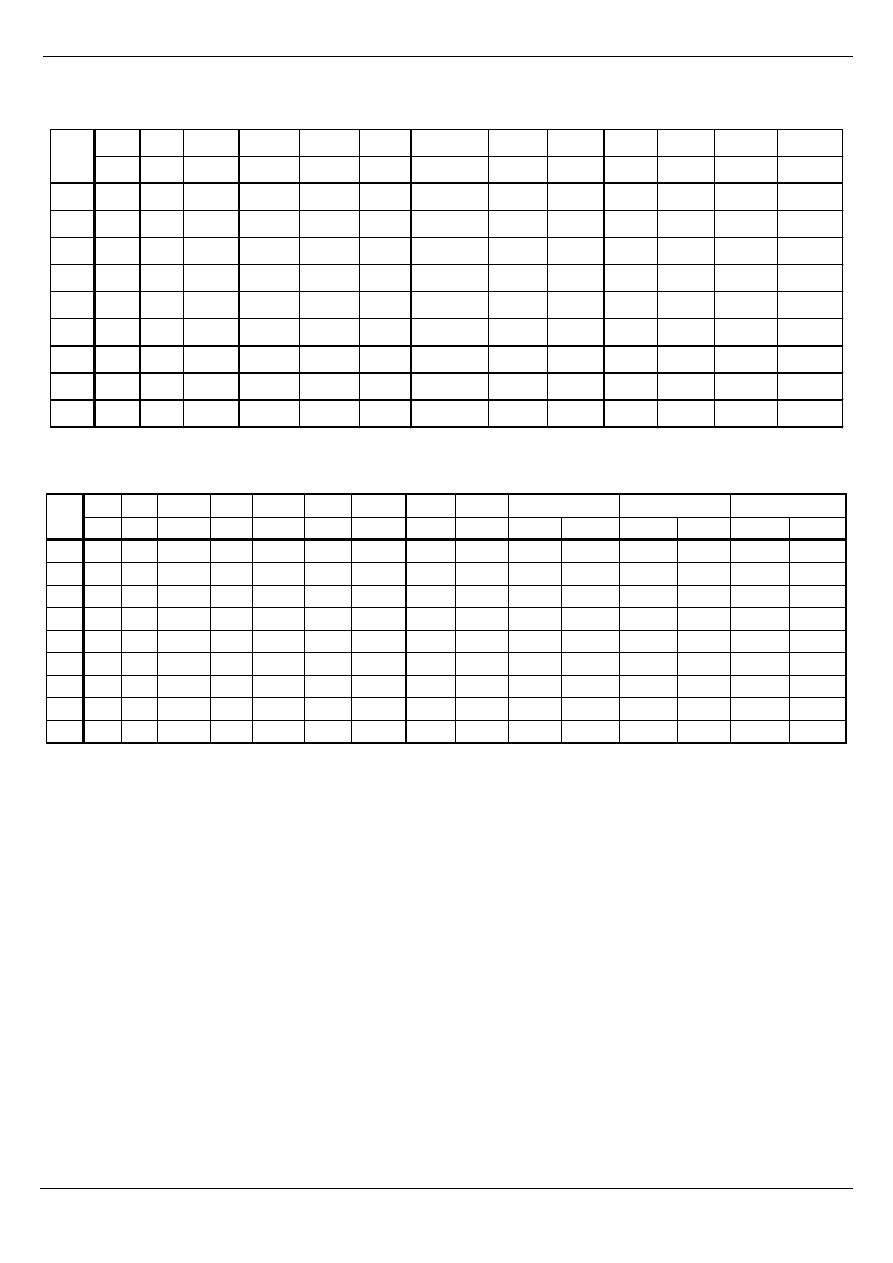
„Geosyntetyki
w
budownictwie”
dr
inż. Angelika Duszyńska
Cz. 1: Zalecenia FRANCUSKIE
18
Tab. Zestawienie wyników obliczeń stateczności wewnętrznej wg zaleceń francuskich
h
a
z
K
R
v
E
a
e
h
M
z
ex
z/L
>
>
v q
>
v
>
h
[m]
[m]
-
[kN/m] [kN/m] [m] [kNm/mb]
[m]
-
-
[kPa]
[kPa]
[kPa]
1
1
1,0 0,631 67,10
6,82
0,44
-2,97
-0,044 0,278 0,819 12,28 31,39
19,80
2
1
2,0 0,589 134,21 18,86
0,82
-15,38
-0,115 0,556 0,674 10,10 49,92
29,39
3
1
3,0 0,547 201,31 36,13
1,17
-42,44
-0,211 0,833 0,558 8,38
71,71
39,20
4
0,5
3,5 0,526 234,86 46,72
1,35
-63,10
-0,269 0,972 0,510 7,66
84,34
44,33
5
0,5
4,0 0,505 268,42 58,62
1,52
-89,38
-0,333 1,111 0,468 7,02
98,51
49,71
6
0,5
4,5 0,484 301,97 71,83
1,70
-121,94 -0,404 1,250 0,431 6,46
114,60 55,42
7
0,5
5,0 0,463 335,52 86,35
1,87
-161,43 -0,481 1,389 0,398 5,97
133,17 61,60
8
0,5
5,5 0,442 369,07 102,16 2,04
-208,50 -0,565 1,528 0,369 5,54
154,96 68,42
9
0,5
6,0 0,421 402,62 119,29 2,21
-263,81 -0,655 1,667 0,344 5,17
181,02 76,12
Nr
w arst
i0
= 0,85
*= 0,680
F3
= 1,125
ml
= 1,05
mt
= 1,5
mf
= 1,2
h
a
z
t
m
t
p
L
a
r
f
r
ck
r
ak
[m]
[m] [kN/m]
-
[kN/m]
m
[kN/m] [kN/m] [kN/m] [kN/m] [kN/m]
[kN/m] [kN/m] [kN/m]
[kN/m]
1
1
1,0
19,80
0,85
16,83
2,10
89,61
69,40
66,10
22,28
46,27
18,94
44,06
22,28
74,67
2
1
2,0
29,39
0,85
24,98
2,40
162,84 69,40
66,10
33,06
46,27
28,10
44,06
33,06
135,70
3
1
3,0
39,20
0,85
33,32
2,70
263,18 69,40
66,10
44,10
46,27
37,49
44,06
44,10
219,31
4
0,5
3,5
22,17
0,85
18,84
2,85
326,71 69,40
66,10
24,94
46,27
21,20
44,06
24,94
272,26
5
0,5
4,0
24,85
0,88
21,75
3,00
401,66 69,40
66,10
27,96
46,27
24,47
44,06
27,96
334,72
6
0,5
4,5
27,71
0,91
25,11
3,15
490,67 69,40
66,10
31,17
46,27
28,25
44,06
31,17
408,89
7
0,5
5,0
30,80
0,94
28,88
3,30
597,32 69,40
66,10
34,65
46,27
32,48
44,06
34,65
497,77
8
0,5
5,5
34,21
0,97
33,14
3,45
726,63 69,40
66,10
38,49
46,27
37,28
44,06
38,49
605,52
9
0,5
6,0
38,06
1,00
38,06
3,60
885,75 69,40
66,10
42,82
46,27
42,82
44,06
42,82
738,12
Nr
w arst
F3*
t
m
< r
ck
/
mt
F3*
t
p
< r
ak
/
mt
F3*
t
m
< r
f
/
mf
Wyszukiwarka
Podobne podstrony:
Folie wyklad2 Krakow id 286699 Nieznany
Folie wyklad5 Krakow id 179153 Nieznany
FOLIE MOD IIIa id 179134 Nieznany
Folie wyklad2 Krakow id 179150 Nieznany
cnbop pib Wytyczne id 117882 Nieznany
Folie wyklad3 Krakow v2 id 1791 Nieznany
prasa Wytyczne 2010 PRC id 3851 Nieznany
Folie wewnATMtrzne id 179146 Nieznany
prasa Wytyczne 2010 ERC id 3851 Nieznany
Folie DEKALOG id 179126 Nieznany
Folie id 179108 Nieznany
Finansowanie hz folie id 172344 Nieznany
folie 2 id 179109 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
więcej podobnych podstron