Wprowadzenie do MATLABa

opracowała

dr Beata Bylina

Spis treści:

1. Interfejs graficzny MATLABa. Korzystanie z pomocy.
2. Wprowadzenie do obliczeń numerycznych w MATLABie.
3. Podstawy programowania w MATLABie.
4. Octave – darmowy klon Matlaba.

1. Interfejs graficzny MATLABa. Korzystanie z pomocy

MATLAB jest to środowisko oraz język programowania przeznaczone do obliczeń

numerycznych. System MATLAB składa się z 5 głównych części:

•

Środowisko MATLAB jest to zestaw narzędzi, z którymi pracuje użytkownik lub
programista. Umożliwia zarządzanie zmiennymi oraz importowanie i eksportowanie
danych.

•

Biblioteka funkcji matematycznych jest to zbiór algorytmów obliczeniowych,
obejmujących zarówno funkcje elementarne, jak i bardziej skomplikowane.

•

System Handle Graphics zawiera polecenia wysokiego poziomu, służące do 2- i 3-
wymiarowej wizualizacji danych, przetwarzania obrazu, animacji i grafiki prezentacyjnej.
Biblioteka funkcji graficznych zawiera również komendy niskiego poziomu, które
umożliwiają całkowite dostosowanie grafiki do potrzeb użytkownika oraz budowanie
graficznego interfejsu użytkownika (ang. Graphical User Interface), wykorzystywanego w
aplikacjach.

•

Język MATLAB jest to język programowania wysokiego poziomu, opartym na
wykorzystaniu operacji na macierzach i tablicach.

•

Programowy interfejs aplikacji (API) jest to biblioteka, która pozwala na pisanie
programów w języku C lub Fortran. Programy te mogą współdziałać z MATLABem.

•

Simulink program towarzyszący MATLABowi, jest interaktywnym systemem, służącym do
symulacji nieliniowych systemów dynamicznych.

System MATLAB pracuje w trybie interpretacji poleceń podawanych z klawiatury lub

zapisanych w pliku tekstowym. Praca w trybie bezpośrednim (interaktywnym) umożliwia
prowadzenie dialogu między użytkownikiem a programem MATLAB na zasadzie pytanie-
odpowiedz. Po wydaniu polecenia i naciśnięciu klawisza ENTER MATLAB natychmiast wyświetla
jego wynik. Umieszczenie po poleceniu średnika spowoduje wykonanie obliczeń, ale bez zwracania
wyniku. Polecenie powinno się mieścić w jednym wierszu. Kilka poleceń w jednym wierszu
oddzielone są od siebie przecinkami lub średnikami. Pracując pod systemem Windows klikamy
ikonę odpowiadającą programowi MATLAB. Po uruchomieniu programu MATLAB powita on
użytkownika znakiem zachęty >>. Każdą komendę zatwierdzamy przez naciśnięcie klawisza
ENTER. Aby, przywołać polecenia, które zostały wcześniej wpisane należy użyć klawisza strzałki
w górę. TAB pozwala uzupełnić nazwy funkcji i zmiennych.

Środowisko MATLAB'a składa się z pulpitu, okna graficznego i okna edytora. Dwa ostatnie

1

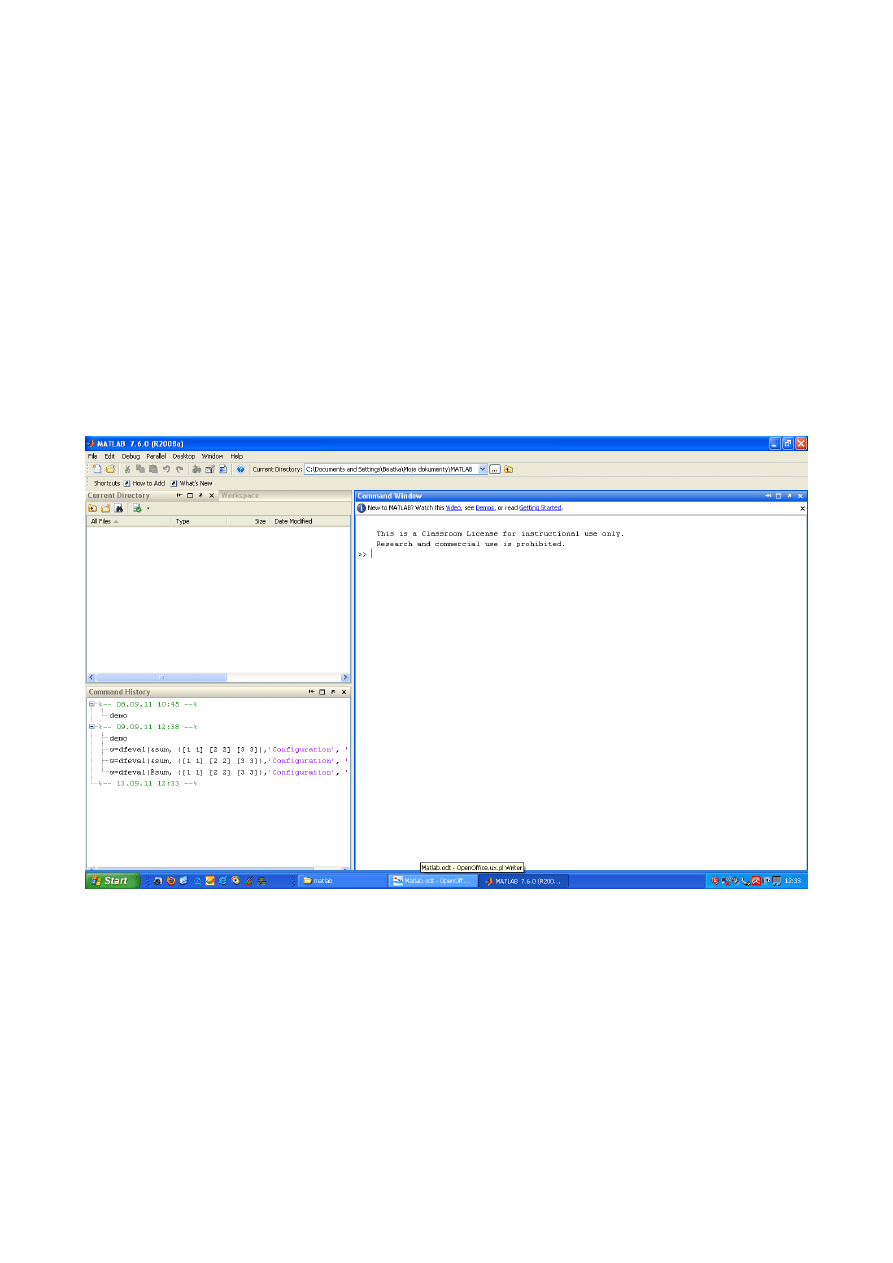
pojawiają się tylko wtedy jeśli są wywołane przez specjalne polecenia. Na rys 1. przedstawiono
zrzut ekranu z pulpitu MATLAB'a przy ustawieniach domyślnych. Okna wchodzące w skład pulpitu
MATLAB'a:

1. Command Window (Okno poleceń) w tym oknie wyświetlany jest znak gotowości

MATLAB'a jako >>, po tym znaku wpisujemy wszystkie polecenia. Każdą komendę
zatwierdzamy przez naciśnięcie klawisza ENTER.

2. Current Folder/Directory (Okno bieżącego katalogu) w tym oknie zawarte są wszystkie

pliki w bieżącym katalogu. Za pomocą specjalnych opcji (klikając prawy klawiszem myszy
na nazwę pliku) można np. uruchamiać m-pliki, zmieniać ich nazwę itp.

3. Workspace (Okno przestrzeni roboczej) w ty oknie znajdują się informację o wszystkich

utworzonych zmiennych. Zmienne te można poddawać różnym operacjom (klikając prawy
klawiszem myszy na nazwę zmiennej) np. zmieniać nazwę zmiennej.

4. Command History (Okno historii poleceń) w tym oknie znajdują się wszystkie polecenia

wpisane przez użytkownika. Polecenia te można wybierać i uruchamiać dwukrotnym
kliknięciem. Można też z tych poleceń tworzyć np. skrypty wykorzystując menu podręczne.

Wszystkie okna można pozamykać. W menu Desktop można ustawić okna na pulpicie.

Rys 1. Zrzut ekranu z pulpitu MATLAB'a wraz z domyślnymi oknami.

Podczas pracy z systemem przydatne są polecenia znane z systemów operacyjnych:

who

- lista aktualnych zmiennych w przestrzeni roboczej;

whos

– lista aktualnych zmiennych w przestrzeni roboczej wraz z rozmiarem;

clear

– czyści przestrzeń roboczą;

clear all

– usuwa wszystkie zmienne i funkcje z przestrzeni roboczej;

computer

– wyświetla informacje o typie komputera;

clc

– czyści okno Command Window;

clock

– wyświetla godzinę i datę jako wektor;

date

– wyświetla datę w postaci łańcucha;

2

ver

– wyświetla informacje na temat licencji i wersji MATLAB'a;

exit

– wyjście z systemu;

Pomoc w programie MATLAB jest dostępna zarówno przez menu główne jak również z linii

poleceń. Polecenie

help nazwa_funkcji,

umożliwia otrzymanie informacji o funkcji podanej jako

parametr w poleceniu

help.

Na serwerze

http://www.mathworks.com

znajdują się materiały w

języku angielskim na tema MATLAB'a. Wpisując polecenie

demo

mamy dostęp do samouczków

MATLAB'a w formie video lub m-plików.

1. Potraktuj MATLAB jak kalkulator i oblicz:

a. [68–(10–4)+8]:(–2)
b. (17–2):3–4+(–2)
c. (5998+38/56)(5998+38/56)(5998+38/56)

2. Znajdź informacje w pomocy na temat podstawowych funkcji trygonometrycznych.
3. Znajdź w pomocy przykłady dotyczące funkcji wykładniczej

exp

().

4. Sprawdź aktualną godzinę.
5. Wyświetl informacje na temat licencji i wersji MATLAB'a, a także na temat dostępnych

toolboxów.

2. Wprowadzenie do obliczeń numerycznych w MATLABie

Program umożliwia definiowanie zmiennych. Nazwa zmiennej to ciąg liter i cyfr oraz

znaków specjalnych, nazwy zmiennych muszą zaczynać się od litery. W nazwach zmiennych nie
może się pojawić znak %, ponieważ oznacza on komentarz w MATLABie, rozróżniane są duże i
małe litery. W MATLABie nie należy zmiennych deklarować, ani określać ich rozmiaru. W
MATLABie znak = oznacza przypisanie wartość wyrażenia z prawej strony pod zmienną
znajdującą się po lewej stronie. Przykłady nazw zmiennych: a, A, list1, Ala_ma_kota,
StalaGrawitacji.

Wszelkie wprowadzane i deklarowane dane (liczby, tekst) MATLAB traktuje jako macierz -
pojedyncza liczba jest traktowana jako macierz o wymiarze 1x1. Typy danych w MATLABie:

•

double - macierz pełna. Liczby są reprezentowane w formacie zmiennoprzecinkowym w
podwójnej precyzji. W MATLABie wykonujemy operacje arytmetyczne tylko na liczbach
typu double.

•

char - typ tekstowy jakim jest dowolny napis. Formalnie jest to tak samo jak w języku C 8-
bitowy typ całkowity (zakres 0 - 255). Dana liczba reprezentuje odpowiadający jej kod
ASCII.

•

sparse - macierz rzadka. Elementy zerowe macierzy nie są zapamiętywane w pamięci
komputera.

•

struct - struktura. Tak jak w każdym języku programowania struktura jest typem danych

3

ZADANIA DO SAMODZIELNEGO WYKONANIA – ZESTAW 1

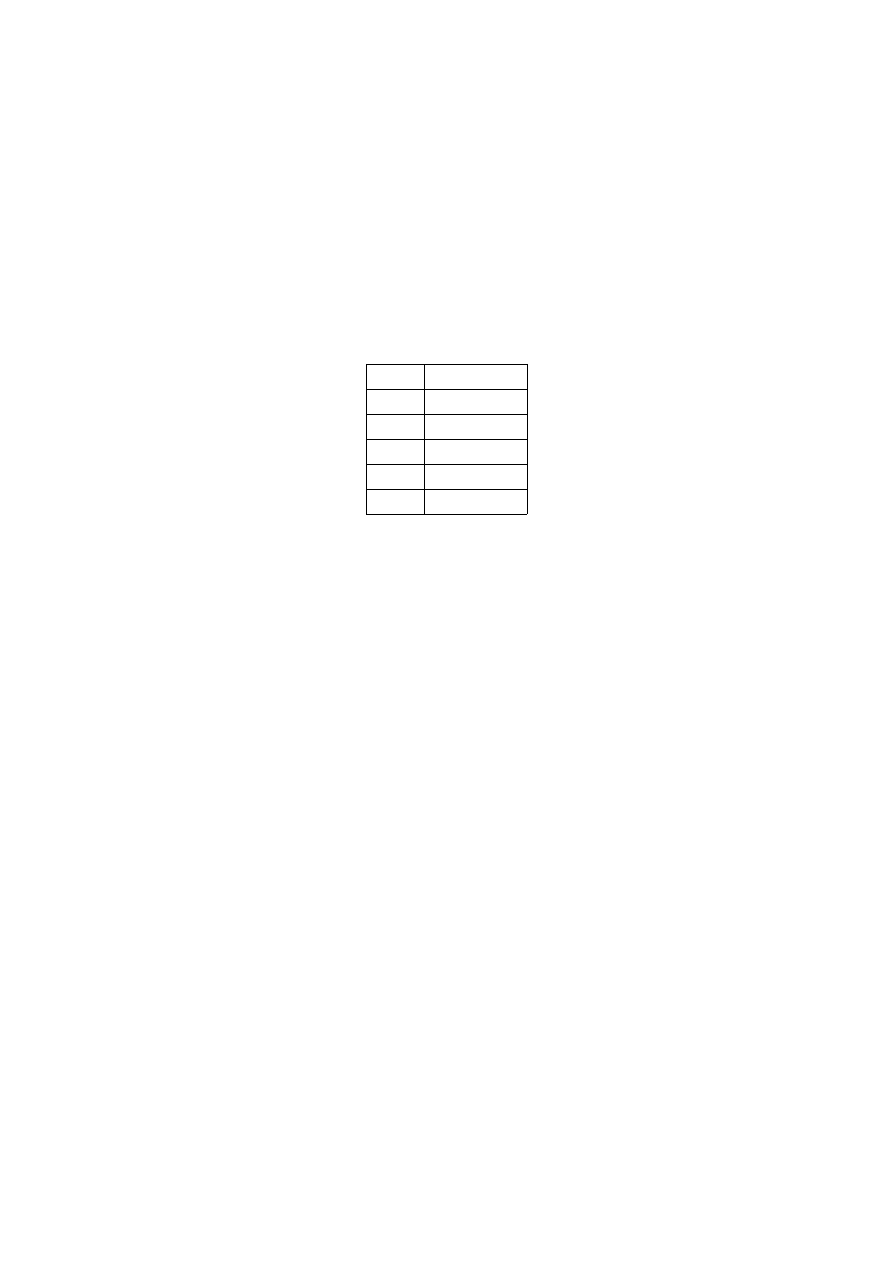
zawierającym w swoich polach dane różnych typów.

•

cell - tablica komórkowa (blokowa) - pojedynczymi elementami takiej macierzy mogą być
nie tylko liczby, ale i dowolne dane z powyższych typów. W macierzy komórkowej możemy
przechować kilka macierzy o różnym wymiarze, tekst i strukturę jednocześnie.

•

uint8 - 8-bitowy typ całkowity (zakres 0 - 255) przeznaczony do zapisywania w pamięci
obrazów graficznych. Na tym typie danych nie można wykonywać żadnych operacji
arytmetycznych.

Charakterystyczne dla języka programowania MATLAB jest automatyczne rozpoznawanie typów
zmiennych - nie występuje deklaracja typu (przykładowo w języku C przed użyciem zmiennej abc
konieczna jest linia - "double abc;"). MATLAB rozpoznaje typ zmiennej przy jej pierwszym użyciu,
należy tylko odpowiednio ją wywołać.

Tabela 1. Przykłady wywołania typów danych w MATLABie.

Typ

Wywołanie

double a=1 (a=[1])
char

a='napis'

sparse a=sparse(1)
struct a.składnik=1
cell

a={1}

Wyrażenia skalarne to liczby rzeczywiste lub zespolone. Dla wyrażeń skalarnych zdefiniowano pięć
podstawowych operatorów: +, -, *, /, ^ (potęgowanie) oraz = = jako operator porównania
wykorzystywany w operacjach logicznych. System wykonuje polecenia natychmiast po naciśnięciu
klawisza ENTER jeśli nie kończyło się ono średnikiem.
Zmienna

ans

zwiera wynik ostatnio wykonanej operacji i zmienia się ona zawsze po wykonaniu

kolejnej operacji.

4

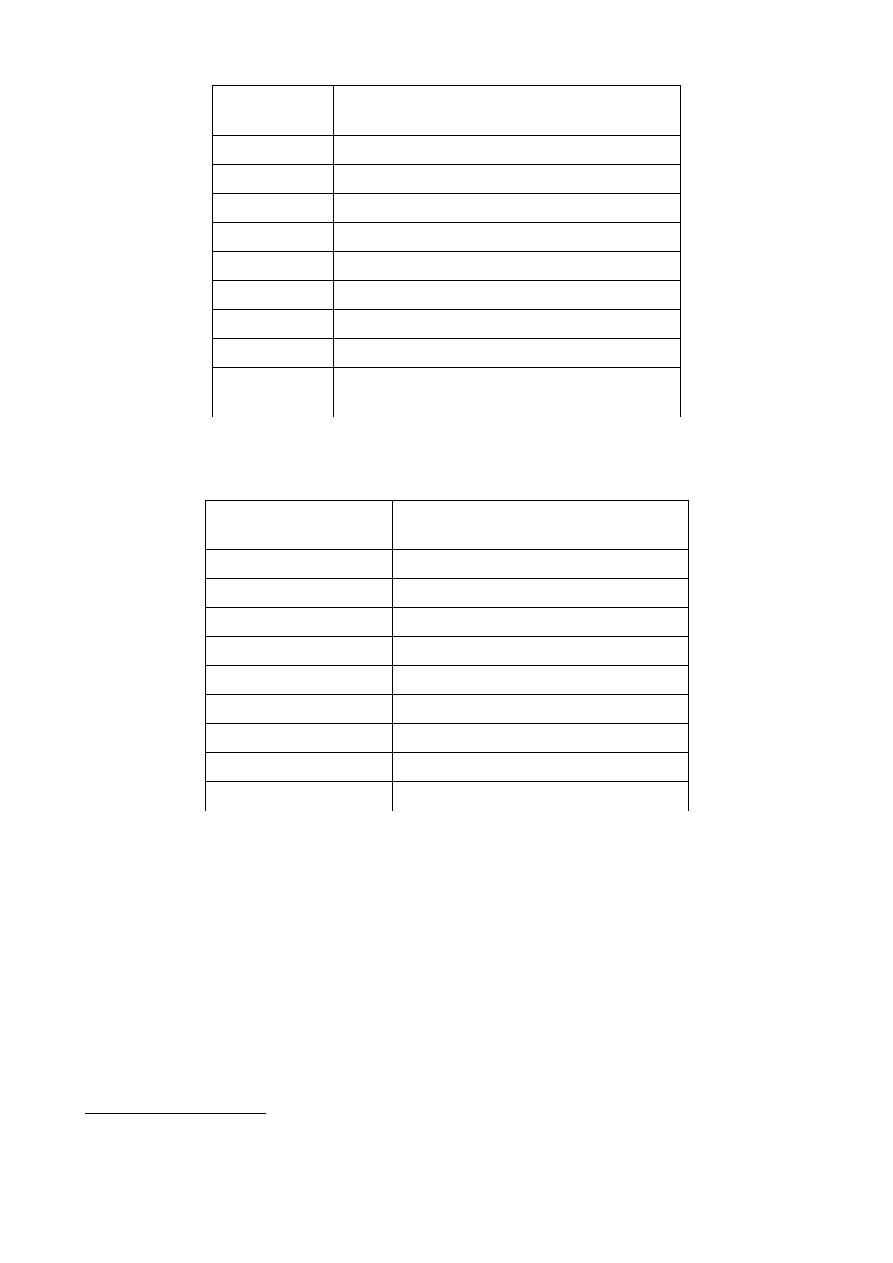
Stała w

MATLABie

Opis

i, j

jednostka urojona, z liczb zespolonych

pi

liczba 

exp(1)

podstawa logarytmu naturalnego

inf

nieskończoność

nan

wielkość nie jest liczbą

eps

najmniejsza liczba taka, że 11

logical(0)

FAŁSZ (stała boolowska)

logical(1)

PRAWDA (stała boolowska)

ans

Standardowa zmienna przypisywana do
wyrażenia nieskojarzonego

W MATLABie zdefiniowane są pewne funkcje matematyczne. Funkcje bez litery m na końcu są
funkcjami, które przekształcają każdy element macierzy wejściowej z osobna.

Funkcje matematyczne

w MATLABie

Opis

abs()

Wartość bezwzględna

exp(), expm()

1

Funkcja wykładnicza o podstawie e

log(), logm()

Logarytm naturalny

log10()

Logarytm o podstawie 10

sin()

Sinus

sqrt(), sqrtm()

Pierwiastek kwadratowy

tan()

Tangens

mod()

Reszta z dzielenia argumentów x i y

factorial()

silnia

1 Obliczana jest exponenta macierz wykorzystując aproksymację Padego.

5

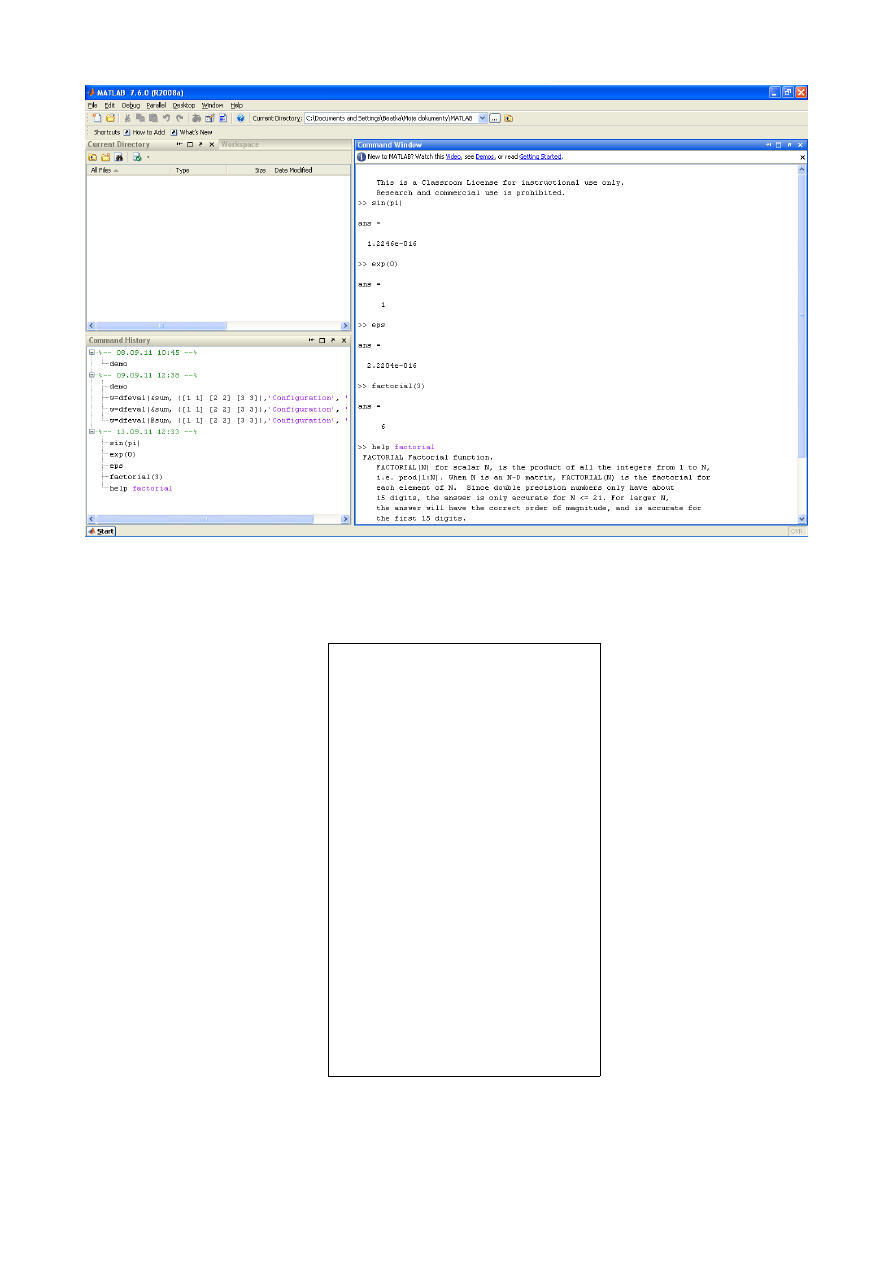
Rys 2. Zrzut ekranu z pulpitu MATLAB'a i praca interaktywną z wykorzystaniem funkcji
matematycznych

Rys 3. Fragment kodu przedstawiający deklarowanie zmiennych

oraz użycie podstawowych operatorów arytmetycznych.

6

>> 5+3

ans =
8
>> x = 5; y = 3;
>> x + y
ans =
8
>> a = [2 3]; b = [1 6];
>> a / b
ans =
0.5405
>> a ./ b
ans =
2.0000 0.5000

1. Zmiennej a nadaj wartość 8, zmiennej b nadaj wartość 34,4. Oblicz: a+b, a–b, a*b, a/b,

3*(a+b).

2. Oblicz: 27!, log(1024), (2+3i)*(3-2i), |14-15|.
3. Sprawdź w MATLABie poprawność obliczeń:

sin



6

=

0,5

3,87⋅10

5

−

72,86

3

2−



2

=

370,255

4. Oblicz wartość zmiennej: y=

2



∣

x∣−4

−

6

x

2

−

5x

dla x=8,167 oraz x=−8,167 .

5. Oblicz:

a.



e

12

−

1

e

8

b. sin 0.001
c. cos 

d. 23

33



123−ln 2

Wektory w MATLABie są zdefiniowane jako uporządkowany ciąg liczb, którego elementy

są rozpoznawane przez indeksy. Indeksy mają wartości w zbiorze liczb naturalnych (są
indeksowane od jedynki). Do poszczególnych elementów wiersza odwołujemy się wykorzystując
nawiasy okrągłe, np.

b(3)=4,

gdzie

b(3)

oznacza odwołanie się do 3-ciego elementu wektora

b.

Wektory w MATLABie to macierze o jednej kolumnie lub jednym wierszu.

Sposoby tworzenia

wektorów:

•

Wypisanie wszystkich elementów wektora

: wierszowego

a=[1 2 3 4]

i kolumnowego

b=[1;

2; 3; 4]

•

Zdefiniowanie elementów wektora wierszowego jako ciągu arytmetycznego

wykorzystując

polecenie

w=pocz:k:kon

, gdzie

pocz

oznacza wartość pierwszego elementu wektora,

k

oznacza o ile wartość każdego elementu wektora zostanie powiększona,

kon

oznacza

wartość końcową wektora, np.

a=10:1:15, a=[10 11 12 13 14 15]

•

Zdefiniowane

n -elementowego wektora wierszowego z równomiernie rozłożonymi liczbami

w przedziale 〈 x

1,

x

n

〉 wykorzystując polecenie

linspace(x_1, x_n, n)

. Polecenie

b=linspace(-5, 5, 3)

tworzy wektor 3 elementowy o wartościach

b=[-5, 0, 5]

.

Podstawowym typem danych w MATLABie są macierze. Elementami macierzy mogą być:

•

liczby rzeczywiste

•

liczby zespolone

•

wielomiany.

Macierze zapisujemy w nawiasach kwadratowych [], elementy w wierszu oddzielamy spacjami lub

7

ZADANIA DO SAMODZIELNEGO WYKONANIA – ZESTAW 2

przecinkami, zaś poszczególne wiersze oddzielamy od siebie średnikami. Do poszczególnych
elementów macierz odwołujemy się wykorzystując nawiasy okrągłe i wpisując odpowiednio wiersz
i kolumnę po przecinku, np. B

(3, 4)=-43,

gdzie

B(3,4)

oznacza odwołanie się do elementu w 3-cim

wierszu i 4-tej kolumnie macierzy B

.

Wykorzystując operator zakresu czyli dwukropek : możemy

odwołać się do całego wiersza, np.

B(2, :)

lub do całej kolumny

B(:, 2)

lub do jej dowolnej

podmacierzy przez wskazanie zakresu indeksów, np.

B(2:3,1:2)

. Praktycznym obiektem jest

macierz pusta, którą definiujemy poleceniem

C=[]

.

Sposoby tworzenia macierzy:

•

Wypisanie wszystkich elementów macierzy,

np.

A=[ 1 2 3; 4 5 6]

oznacza macierz

zawierającą dwa wiersze i trzy kolumny postaci:

A=

[

1 2 3
4 5 6

]

•

Wykorzystanie gotowych poleceń do generowania macierzy specjalnych

na przykład

macierz składającej się z samych jedynek lub zer, np. A=ones(4) tworzy macierz o
wymiarze 4 o wszystkich elementach równych 1.

•

Przez dołączanie lub usuwanie wiersza lub kolumny do istniejących macierzy

. Polecenie

A=[A u] powoduje dołączenie kolumny do macierzy A, oczywiście wektor kolumnowy
musi mieć tyle elementów ile macierz A wierszy. Dowolny wiersz można usunąć z macierzy
przekształcając ją na wektor zerowy, np. A(2, :)=[] usuwa drugi wiersz macierzy A.

•

Generowanie macierzy losowej

, np. poleceniem A=rand(3, 4) powoduje utworzenia

macierzy losowej składającej się z 3 wierszy i 4 kolumn.

•

Otrzymywanie macierzy z zewnętrznych plików.

W tabeli przedstawiono polecenia działające na wektorach i macierzach:

Polecenia w

MATLBie

Opis

fft(A)

Obliczanie szybkiej transformaty Fouriera

lenght(A)

Wyznaczanie liczbę elementów wektora

max(A)

Wyznaczanie wartości elementu maksymalnego w wektorze

min(A)

Wyznaczanie wartości elementu minimalnego w wektorze

mean(A)

Wyznaczanie wartości średniej wektora

size(A)

Wyznaczanie wymiaru wektora

sum(A)

Sumowanie wszystkich elementów wektora

prod(A)

Wyznaczanie iloczynu wszystkich elementów wektora

det(A)

Obliczanie wyznacznika macierzy

inv(A)

Odwracanie macierzy

rank(A)

Wyznaczanie rzędu macierzy

norm(A)

Wyznaczanie normy macierzy

2

trace(A)

Wyznaczanie śladu macierzy

eig(A)

Wyznaczanie wartości i wektorów własnych macierzy

2 Polecenie

norm()

może być wywołany w różny sposób, szczegółów należy szukać w pomocy programu.

8

W MATLABie istnieją polecenia wspomagające definiowanie macierzy specjalnych. Argumentami
tych poleceń są liczba wierszy n i liczba kolumn m.

Polecenia o tworzenia

macierzy specjalnych w

MATLABie

Opis

eye()

Tworzy macierz z 1 na głównej przekątnej

ones()

Tworzy macierz o wszystkich elementach równych 1

rand()

Tworzy macierz z liczbami pseudolosowymi o rozkładzie
jednostajnym <0, 1>

randn()

Tworzy macierz z liczbami pseudolosowymi o rozkładzie
normalnym

tril()

W danej macierzy wypełnia zerami wszystkie elementy znajdujące
się nad główną przekątną

triu()

W danej macierzy wypełnia zerami wszystkie elementy znajdujące
się pod główną przekątną

zeros()

Tworzy macierz o wszystkich elementach równych 0

magic()

Tworzy macierz kwadratową obrazującą magiczny kwadrat

3

Przykłady operacji na macierzach:
1. Utworzenie macierzy A przez wypisanie wszystkich jej elementów:
>> A=[1 2 3; 4 5 6; 7 8 9]
A =
1 2 3
4 5 6
7 8 9
2. Obliczenie wyznacznika utworzonej macierzy:
>> det(A)
ans =
0
3. Próba obliczenia macierzy odwrotnej:
>> inv(A)
Warning: Matrix is close to singular or badly scaled.
Results may be inaccurate. RCOND = 1.541976e-018.
ans =
1.0e+016 *

-0.4504 0.9007 -0.4504
0.9007 -1.8014 0.9007
-0.4504 0.9007 -0.4504
4. Utworzenie wektora wierszowego:
>> b=[1 2 3]

3 Kwadrat magiczny – tablica składająca się z n wierszy i n kolumn (n>2), w którą wpisano n

2

różnych dodatnich

liczb naturalnych w ten sposób, że suma liczb w każdym wierszu, w każdej kolumnie i w każdej przekątnej jest taka
sama (tzw. suma magiczna).

9

b =
1 2 3
5. Próba obliczenia iloczynu wcześniej utworzonej macierzy A i wektora wierszowego b:
>> A*b

??? Error using ==> mtimes
Inner matrix dimensions must agree.

6. Obliczenie iloczynu wcześniej utworzonej macierzy A i transpozycji wektora wierszowego b:
>> A*b'
ans =
14
32
50
7. Utworzenie macierzy jednostkowej o wymiarze 3:
>> eye(3)
ans =
1 0 0
0 1 0
0 0 1
8. Utworzenie macierzy diagonalnej o rozmiarze 5, która na przekątnej ma liczby 3:
>> 3*eye(5)
ans =
3 0 0 0 0
0 3 0 0 0
0 0 3 0 0
0 0 0 3 0
0 0 0 0 3
9. Utworzenie macierzy kwadratowej złożonej z samych 1 o wymiarze 3:
>> B=ones(3)
B =
1 1 1
1 1 1
1 1 1
10. Zsumowanie macierzy A i B.
>> A+B
ans =
2 3 4
5 6 7
8 9 10
11. Oblicz 3AB-B
>>3*A*B-B
ans =
17 17 17
44 44 44
71 71 71

W MATLABie za pomocą operatorów wykonuje się dwa rodzaje operacji na wektorach i
macierzach: operacje macierzowe i operacje tablicowe. Operacje macierzowe określane są regułami
algebry liniowej i możemy macierze: dodawać, odejmować, mnożyć, potęgować, transponować, a
także dzielić prawostronnie A/B jest równoznaczne z obliczeniem A/ B ⇔ A∗B

−

1

oraz dzielić

10

lewostronnie A ∖ B= A

−

1

∗

B .

Operacje tablicowe są to operacje wykonywane na elementach macierzy. Ważnym operatorem jest
kropka ., która oznacza zastosowanie operatora do każdego elementu wektora lub macierzy.
Mnożenie, dzielenie i potęgowanie elementu przez element pomiędzy dwiema macierzami lub
wektorami o tych samych rozmiarach wykonuje się poprzez wstawienie stosownego operatora
arytmetycznego, poprzedzonego kropką.
.

Operator arytmetyczny

tablicowy

Opis

.*

Mnożenie elementu przez element

./

Dzielenie elementu przez element

A./ B ⇔ Ai , j/ B i , j

.\

Lewostronne dzielenie elementu przez element

A. ∖ B⇔ Bi , j/ Ai , j

.^

Potęgowanie elementu przez element

.'

Transpozycja sprzężona

Przykłady działań tablicowych
>> A=[1 2; 3 4]
A =
1 2
3 4
>> B=zeros(2)
B =
0 0
0 0
>> B(1,1)=2
B =
2 0
0 0
>> B(2,2)=1
B =
2 0
0 1
>> A*B
ans =
2 2
6 4
>> A.*B
ans =
2 0
0 4
>> A^2
ans =
7 10
15 22
>> A.^2
ans =

11

1 4
9 16
>> A/B
ans =
0.5000 2.0000
1.5000 4.0000
>> A./B
ans =
0.5000 Inf
Inf 4.0000
>> A.\B
ans =
2.0000 0
0 0.2500

W MATLABie możemy rozwiązywać układ równań liniowych postaci Ax=b , gdzie A jest
macierzą, b jest wektorem kolumnowym używając lewostronnego mnożenia macierzowego

x= A∖ b .

Przykład rozwiązywania układu równań liniowych.
Rozwiąż układ równań postaci:

x y=2
x− y =4

Rozwiązanie w MATLABie:
>> A=[1 1; 1 -1] % tworzymy macierz współczynników układu równań liniowych
A =
1 1
1 -1
>> b=[2 ; 4] % tworzymy wektor wyrazów wolnych
b =
2
4
>> x=A\b %wykorzystując operacje dzielenia lewostronnego obliczamy wektor x
x =
3
-1
>> A*x==b %sprawdzamy czy otrzymane rozwiązanie jest prawidłowe przez porównanie
ans =
1
1

Operatory relacji i operatory logiczne
Działania w postaci operatorów relacji dają wynik w postaci macierzy lub wektora o wartościach
zero lub jeden. Argumentami relacji mogą być macierze. Wymiary porównywanych macierzy
muszą być takie same. W wyrażeniach logicznych o argumentach macierzowych każdy element
macierzy równy zero jest traktowany jak FALSE, a element o wartościach równych jeden jak
TRUE.

12

Operator relacji

Opis

<

Mniejsze niż

<=

Mniejsze lub równe

>

Większe niż

>=

Większe lub równe

~=

nierówne

%= =

równe

Operator logiczny

Opis

&

Logiczne AND (koniunkcja)

|

Logiczne OR (alternatywa)

~

Logiczne dopełnienie NOT (negacja)

xor

Wykluczające OR (alternatywa wykluczająca)

Przykład działania operatorów relacji i logicznych:
Jeżeli w=[1, 2,3] oraz v=[1,−2, 9] oblicz w≥v , w∧v , w∨v .

>> w=[1 2 3]
w =
1 2 3
>> v=[1 -2 9]
v =
1 -2 9
>> w>=v
ans =
1 1 0
>> w&v
ans =
1 1 1
>> w|v
ans =
1 1 1

ZADANIA DO SAMODZIELNEGO WYKONANIA

1. Utwórz wektor t o 10 elementach 1, 2, 3, …, 10 (spróbuj utworzyć taki wektor kilkoma

sposobami). Następnie oblicz:

•

x=tsin t

13

ZADANIA DO SAMODZIELNEGO WYKONANIA – ZESTAW 3

•

y=

1−2t

2t

•

y=



t e

t

2. Równanie linii prostej ma postać y=axb , gdzie a ,b∈R są odpowiednio

współczynnikiem kierunkowym i wyrazem wolnym. Dla a=−2 i b=1 oblicz
wykorzystując własności wektorów współrzędne y dla następujących wartości
współrzędnych x :

x=0,0.1 , 0.2 , 0.3 , 0.4 , 0.5 ,0.6 , 0.7 ,0.8 , 0.9 , 1.0

3. Utwórz wektor o pięciu elementach równomiernie rozłożonych pomiędzy 0 i 2. Następnie

oblicz sumę wszystkich elementów tego wektora.

4. Niech dane będą macierze: A=

[

1 2 3
4 5 6
7 8 9

]

B=

[

1

12 −3

0

9

1

−

3 −2

0

]

.Wykonaj operacje:

2A+3B, A-2B, A*B, B*A.

5. Wyznacz rząd macierzy podanych w poprzednim zadaniu.
6. Znajdź wartości własne, wektory macierzy z zadania pierwszego.
7. Dla macierzy z zadania 4 znajdź macierz odwrotną i transponowaną.

8. Sprawdź, czy układ równań ma rozwiązanie:

2x4y−4z=0

−

2x− yz =10

x y z=8

9. Wyciągnij z macierzy A pierwszy i ostatni wiersz. Oblicz iloczyn skalarny tak otrzymanych

wektorów.

10. Przestaw 3 i 4 wiersz macierzy A oraz 1 i 2 kolumnę.
11. Utwórz macierz o elementach losowych o rozmiarze 5. Oblicz sumę oraz iloczyn

wszystkich elementów tej macierzy.

12. Dla

a

= 1,1;

b

= 6,25;

c

=

3



3 ,

d

=  oblicz:

a

2



ab−b , sin c , ab/c , e

2



log a ,



abcd

13. Utwórz

wektory:

v=[1, 2,3, 4,5, 6, 7] w=[10, 11,12, 13, 14,15, 16,17] oblicz

2vw , v./w , w.∗v , w.

2

14. Utwórz poniższe macierze, korzystając z funkcji generujących

zeros

,

eye

,

ones:

D=

{

0 0 0
0 0 0

}

,

E=

{

5 0 0
0 5 0
0 0 5

}

, F =

{

3 3
3 3

}

15. Utwórz macierz G, wykorzystaj do jej utworzenia macierze 2x2 :

14

G=

{

2 6 0 0

0

0

3 9 0 0

0

0

0 0 1 2

0

0

0 0 3 4

0

0

0 0 0 0 −5 5
0 0 0 0

5

3

}

Wykresy
Matlab umożliwia tworzenie wykresów dwu- i trójwymiarowych. Opisy wszystkich dostępnych
funkcji grafiki są dostępne poprzez polecenie help plot.

Podstawowe funkcje służące do rysowania wykresów w Matlabie:

•

plot(x, y)

– rysuje wykres na podstawie wartości elementów dwóch wektorów,

•

loglog(x, y)

– rysuje wykres ze skalą logarytmiczna na obu osiach,

•

polt3(x, y, z)

– rysuje wykres na podstawie wartości elementów trzech wektorów,

•

ezplot(‘funkcja’, [xmin xmax])

– rysuje wykres funkcji jednej zmiennej w określonym

przedziale,

•

mesh(z)

– rysuje siatkę wartości macierzy ,

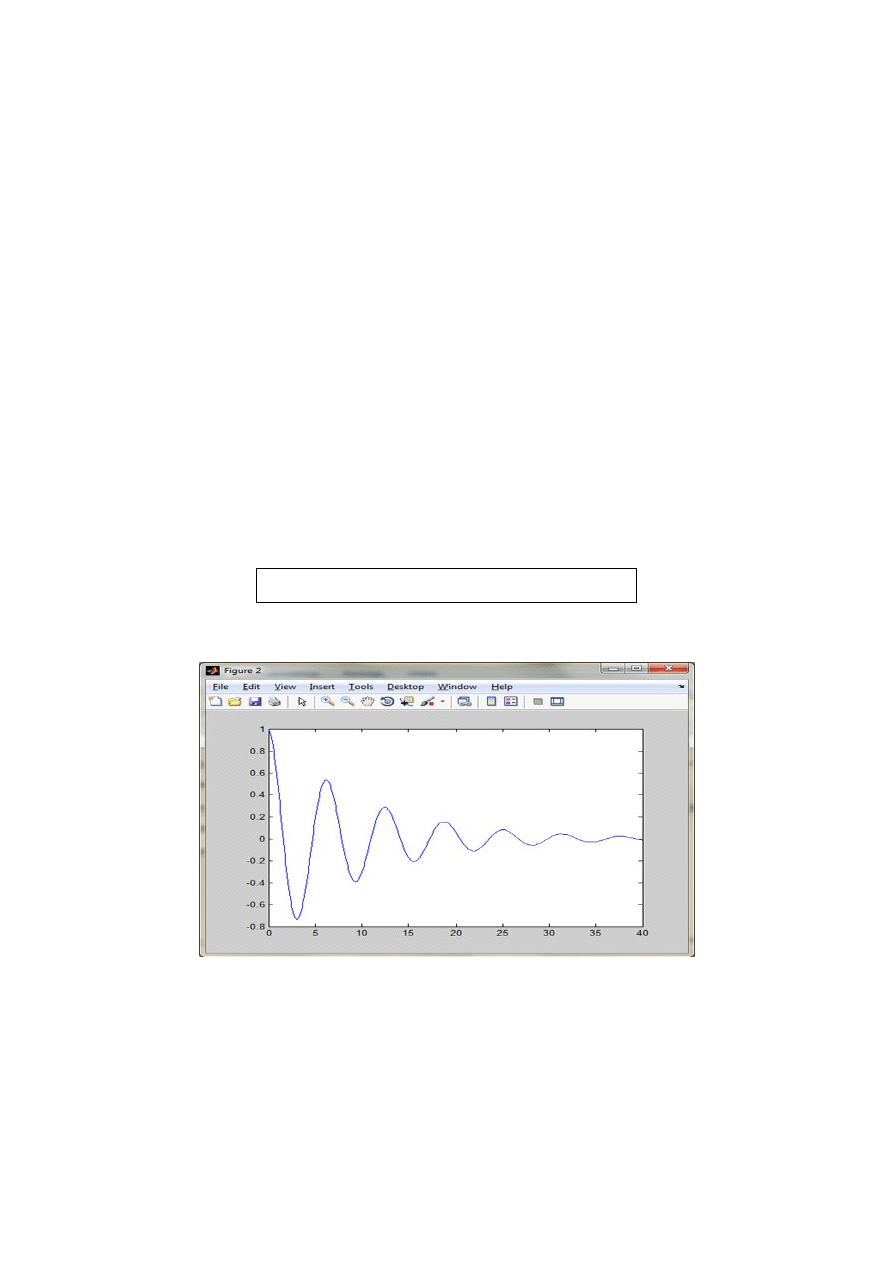
Rys 4. Fragment kodu umożliwiający narysować wykres funkcji w przedziale od 0 do 40.

Rys 5. Wykres funkcji w przedziale od 0 do 40.

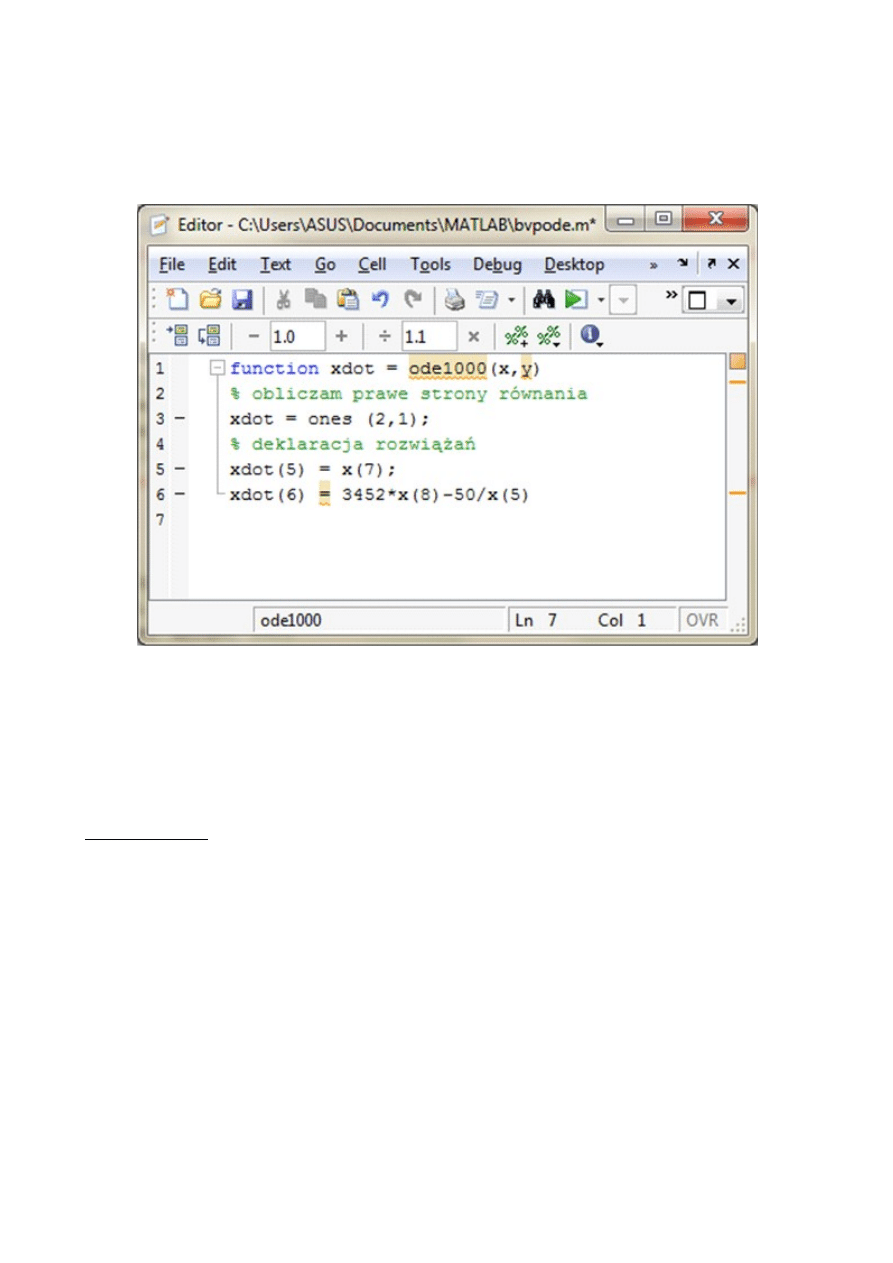
3. Podstawy programowania w MATLABie

MATLAB jest językiem programowania, który umożliwia pisanie programów

komputerowych zwanych inaczej skryptami. Skrypty można budować ze wszystkich dostępnych
funkcji bibliotecznych oraz funkcji zdefiniowanych przez użytkownika. W MATLABie mam kilka
instrukcji sterujących przepływem danych:

15

fplot('exp(-x/10).*cos(x)',[0 40])

•

instrukcje proste

•

instrukcje warunkowe

•

instrukcje pętli

Rys.6. Okno edytora tekstowego z przykładowym pilikiem.

Skrypt to ciąg poleceń, komentarzy, wywołań funkcji, zapisanych w odrębnym pliku dyskowym
realizującym określony przez użytkownika algorytm. Skrypty umieszczamy w m-plikach
skryptowych, które nie maja argumentów, operują na danych z przestrzeni roboczej, każdy taki
skrypt ma rozszerzenie .m. Plik skryptowy jest uruchamiany przez wpisanie jego nazwy bez
rozszerzenia m.
Cechy skryptów:

•

Plik skryptu jest M-plikiem , tzn. że ma rozszerzenie .m.

•

Plik taki jest uruchamiany przez wpisanie jego nazwy (bez rozszerzenia .m) w wierszu
poleceń. Jest to równoznaczne z wpisywaniem wszystkich komend zawartych kolejno w
wierszu poleceń.

•

Pliki skryptów działają na zmiennych globalnych, czyli zmiennych już istniejących w
przestrzeni roboczej.

•

Nazwy skryptów muszą zaczynać się od litery, pozostałe znaki mogą być cyframi i znakami
podkreślenia.

W trakcie pisania skryptów lub funkcji przydatnych jest kilka poleceń:

•

disp

('łańcuch') – wyświetla tekst lub tablice;

•

inpu

t('łańcuch') – polecenie wyświetla zawartość łańcucha i oczekuje na wprowadzenie

16

danych z klawiatury;

•

return

– zwraca sterowanie funkcji wywołującej;

Przykład skryptu:

Listing 1. Treść pierwszego skryptu, zapisanego w pliku pierwszyskrypt.m.

Funkcje definiowane bezpośrednio ograniczają się do prostych wyrażeń matematyczne, polega na
bezpośrednim włączeniu kodu funkcji w program interpretowany lub umieszczeniu go w skrypcie.
Funkcje bezpośrednie definiujemy przy użyciu polecenia

inline()

. Tak zdefiniowaną funkcję

możemy wywołać z linii komend lub z wnętrza skryptu. Ogólna wersja polecenia

inline()

w

MATLABie jest następująca:

f=

inline

('wzor', 'arg1', …, 'argn')

Przykład

Napisz funkcję definiowaną bezpośrednio funkcje obliczania wartości

y  x =

sin x 

cos x

. Oblicz

wartość y 0 , y  .

>> y=inline('sin(x)/cos(x)', 'x')
y =
Inline function:
y(x) = sin(x)/cos(x)
>> y(0)
ans =
0
>> y(pi)
ans =
-1.2246e-016

Funkcje definiujemy w oddzielnym pliku dyskowym (tzw. M-plik funkcyjnym), którego nazwa
powinna być zgodna z identyfikatorem funkcji i mieć rozszerzenie m. M-pliki funkcyjne działają na
zmiennych lokalnych i globalnych. Komunikują się z przestrzenią roboczą przez parametry
formalne i zmienne globalne. Ogólna wersja funkcji zewnętrznej w MATLABie jest następująca:

Function [

p_wyn_1

,

p_wyn_2

, …,

p_wyn_n

] = Nazwa_funkcji (

p_we_1, p_we_2, …, p_we_n

)

Ciąg_Instrukcji;

end

17

disp(

'To mój pierwszy skrypt'

);

disp(

'Najpierw zdefiniuje zmienne x i y'

);

x=12.12; disp(x);
y=13.13; disp(y);

z=input(

'Podaj liczbe rzeczywista '

,

's'

);

if

(z>=x)&(z<=y)

disp(

'nalezy do przedzialu <x, y>'

)

else

disp(

'nie nalezy'

)

end

Przykłady wierszy definicji funkcji:

function [param1, param2, param3] = nazwa_funkcji_1 (par_we1, par_we2);

function [param1] = nazwa_funkcji_2 (par_we1, par_we2);

function param1 = nazwa_funkcji_3 (par_we1);

function [] = nazwa_funkcji_4 (par_we);

function nazwa_funkcji_5 (par_we);

Do przerywania pracy funkcji i powrót do programu nadrzędnego z zachowaniem argumentów
wyjściowych funkcji służy instrukcja

return

.

Cechy funkcji zdefiniowanych przez użytkownika:

•

Plik funkcji jest m-plikiem.

•

Zmienne funkcji mają charakter lokalny, są wymazane z przestrzeni roboczej po wykonaniu
funkcji.

•

Plik funkcji rozpoczyna się wierszem definicji, w którym zawarta jest lista danych
wejściowych i wyników (oddzielane przecinkami).

•

Nazwa funkcji musi być zgodna z nazwą pliku (bez rozszerzenia .m).

•

Po wierszu definicji funkcji powinien być komentarz rozpoczynający się od znaku %.
Wszystkie wiersze komentarzy następujące bezpośrednio za wierszem definicji wyświetlane
są po wpisaniu polecenia

help

dla danej funkcji

.

Przykład funkcji:

Listing 2. Przykład funkcji o nazwie pole_kwadratu, która dla zadanej wartość a parametru

wejściowego oblicza pole w zmiennej p. Funkcja ta zapisana jest w pliku o nazwie

pole_kwadratu.m.

Wywołanie funkcji pole_kwadratu dla liczby 5 może mieć postać:
>>pole_kwadratu(5)
lub
>>pole=pole_kwadratu(5)

Funkcja na liście wejściowej
Kiedy funkcja ma zostać wskazana na liście wejściowej innej funkcji, wówczas przekazywana
nazwa musi mieć postać łańcucha znakowego. Na przykład wbudowana funkcja

fzero

znajduje

miejsce zerowe dla funkcji użytkownika z jedną zmienną. Składnia wywołania to

fzero(f, x),

gdzie

f

jest nazwą funkcji czyli jej uchwytem, zaś

x

to przybliżenie początkowe. Funkcje f można

zakodować i przekazać jej nazwę poprzez listę wejściową

fzero

kilkoma sposobami, które

przedstawimy w dalszej części wykorzystując funkcję:

f  x =x

2



2x5

•

Przy użyciu funkcji inline. Funkcja f  x  zostanie zdefiniowana przy użyciu inline i
przekazywać jej funkcje w sposób następujący:

fr = inline('x^2+2x+5');
r0=fzero(fr, 3);

•

Przy użyciu pliku funkcji . Funkcja f  x  zostanie zakodowana w pliku WartFun.m. I
wywołać funkcję

fzero.

r0=fzero('WartFun',3);

18

function

[p]=pole_kwadratu(a)

% function [p]=pole_kwadratu(a)
% obliczam dla zadanego parametru pole kwadratu

p=a*a;

•

Przy użyciu uchwytu funkcji. Uchwyt funkcji jest zmienną tworzoną przez użytkownika
przy użyciu symbolu @.

f1=@WartFun % tworzy uchwyt funkcji f1 dla 'WartFun'
r1=fzero(f1, 3)
lub
r1=fzero(@WartFun,3)

Wśród instrukcji prostych wyróżniamy: instrukcje puste, instrukcje przypisania, sekwencje

kilku instrukcji. Instrukcja pusta składa się tylko ze znaku średnika lub pustej linii w skrypcie i
powoduje przekazanie sterowania do następnej linii. Instrukcja przypisania była już wcześniej
wspomniana i powoduje przypisanie wartości zmiennej za pomocą znaku =. Sekwencja kilku
instrukcji (nie koniecznie prostych) to zapisanie kilku instrukcji w jednej linii oddzielonych
znakami ;(średnik) lub ,(przecinek).

Za pomocą instrukcji warunkowych możemy sterować przebiegiem procesu obliczeń w zależności
od spełnienia lub niespełnienia pewnych warunków logicznych. Ogólna wersja instrukcji
warunkowej w MATLABie jest następująca:

If

warunek_logiczny

instrukcja_1

else

instrukcja2

end

Każdą instrukcje warunkową kończymy poleceniem

end

. W miejsce instrukcja_1 i instrukcja_2

można wstawić dowolną instrukcje na przykład instrukcję

if

i otrzymujemy w ten sposób instrukcje

zagnieżdżoną.

Przykład 1 instrukcji if:

Przykład 2 instrukcji if:

19

function

[max]=sz_ObliczMax(a,b)

%oblicza maximum z dwóch liczb rzeczywistych a i b

if

a>b

max=a;

else

max=b;

end

;

Przykład 3 instrukcji if … elseif:
Napisz skrypt, w którym pobierasz od użytkownika znak. Sprawdzasz czy znak jest małą literą i czy
jest samogłoską czy spółgłoską. Wykorzystaj następujące funkcje:

isempty

(A) – jeśli macierz jest pusta funkcja przyjmuje wartość TRUE.

any

(A) – jeśli jakikolwiek element wektora jest niezerowy funkcja przyjmuje wartość TRUE.

Rozwiązanie w pliku sz_skrypt2.m.

Inną instrukcją warunkową w MATLABie jest polecenie

swich

…

case

zwana też instrukcją

wariantowego wyboru. Ogólna wersja instrukcji

swich

w MATLABie jest następująca:

swich

Identyfikator

case

Wartość_Identyfikatora_1

Ciąg_Instrukcji_1

case

Wartość_Identyfikatora_2

Ciąg_Instrukcji_2
.
.
.

case

Wartość_Identyfikatora_n

Ciąg_Instrukcji_n

otherwise

Inny_Ciąg_Instrukcji

20

function

[O, P]= sz_oblicztrojkat(a,b,c)

% function [O, P]= sz_oblicztrojkat(a,b,c)
% Obliczanie pola i obwodu trójkata dla trzech zadanych liczb opisujacych

% dlugosc bokow tojkata

if

(a+b>c) & (a+c >b) & (b+c>a)

O=a+b+c;

% wzor Herona na pole trojkata P=sqrt(O/2*(O/2-a)*(O/2-b)*(O/2-c))

P=(a+b+c)/2;

%polowa obwodu trojkata

P=sqrt(P*(P-a)*(P-b)*(P-c));

else

O=0; P=0;

return

end

zn=input(

'Wprowadz z klawiatury znak malej litery-->'

,

's'

);

if

(isempty(zn)) disp(

'koniec'

),

return

,

end

;

disp([

'wpisano znak: "'

,zn,

'"'

]);

sam=[

'a'

'e'

'i'

'o'

'u'

'y'

];

if

any(zn==sam)

wyn=[

'jest samogloska'

];

elseif

(

'a'

<=zn)&(zn<=

'z'

)

wyn=[

'jest spólgloska'

];

else

wyn=[

'nie jest mala litera'

];

end

;

disp(wyn)

end

Zmienna Identyfikator może przyjmować wartości liczbowe lub łańcuchowe. W zależności od tego
czy Identyfikator przyjmuje wartości liczbowe czy łańcuchowe to takie wartości automatycznie
przyjmują Wartość_Identyfikatora_1, Wartość_Identyfikatora_2, …, Wartość_Identyfikatora_n.

Listing. Przykład skryptu z instrukcją swich, gdzie zmienna kolor przyjmuje wartości

łańcuchowe (plik sz_skrypt1.m).

Przykład instrukcji swich
Napisz skrypt, w który wygenerujesz liczbę naturalną n z zakresu <1, 20>. Jeśli n=10 i n=20 to
liczba jest wyświetlana na ekran, w innym przypadku pisany jest komentarz, że nie jest to ani liczba
10 ani liczba 20.

Rozwiązanie w pliku skrypt_swich.m.

Instrukcja definiująca pętle pozwala użytkownikowi powtarzać grupę instrukcji. Pętla typu

for

pozwala powtarzać pojedynczą instrukcję lub cały blok instrukcji tyle razy aż wartość indeksu
będzie równa koniec. Ogólna wersja pętli

for

w MATLABie jest następująca:

for

Index=pocz:krok:koniec

Ciąg_Instrukcji;

end

Liczba pocz odpowiada wartości początkowej zmiennej Index, zaś koniec odpowiada wartości
kończącej obliczenia. Liczba krok określa przyrost zmiennej index w jednym kroku iteracyjnym.
Jeśli wartość zmiennej krok=1 wtedy w pętli

for

może pojawić się konstrukcja Index=pocz:koniec.

21

n=round(20*rand(1,1));

switch

n

case

1

disp(1);

case

2

disp(2);

otherwise

disp(

'To nie jest ani liczba 10 ani liczba 20'

);

end

kolor=input(

'kolor='

,

's'

);

switch

kolor

case

'czerwony'

c=[1 0 0];

case

'zielony'

c=[0 1 0];

case

'niebieski'

c=[0 0 1];

otherwise

error(

'bledny wybór koloru'

)

end

;

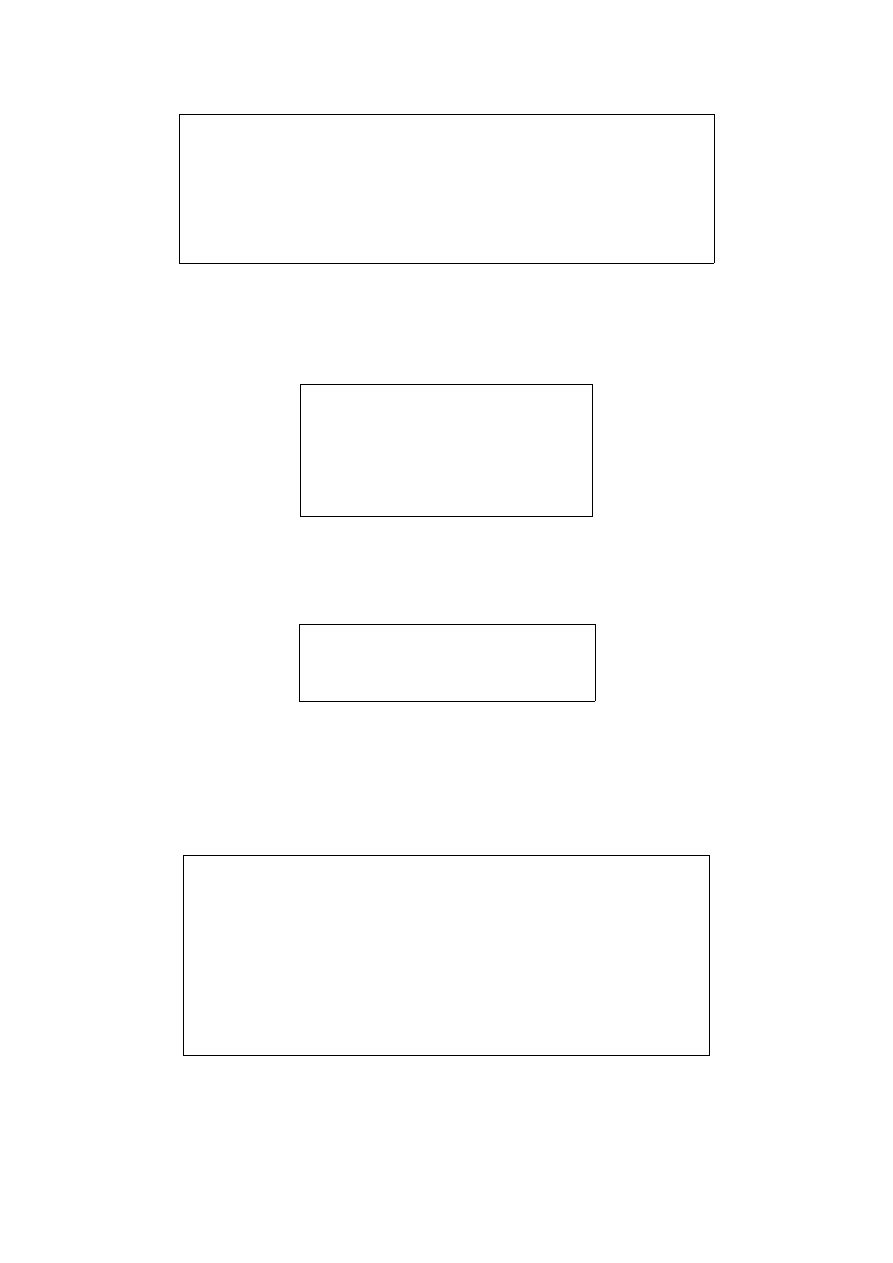
Przykład 1 instrukcji for:

Przykład 2 instrukcji for:
Napisz skrypt, w który wygenerujesz n liczb z zakresu <1, 30>, obliczysz ich sumę oraz średnią
arytmetyczną, a wynik wyświetlisz na ekranie monitora.
Rozwiązanie w pliku s_for.m.

Inną instrukcja pętli pozwala powtarzać grupę grupę instrukcji do momentu, aż warunek logiczny
zostanie spełniony jest pętla

while

. Ogólna wersja pętli

while

w MATLABie jest następująca:

while

Wyrażenie_logiczne

Ciąg_Instrukcji;

end

Przykład pętli while
Napisz algorytm, który wypisuje w odwrotnej kolejności cyfry liczby dodatniej i całkowitej.
Przydatne funkcje:

rem

(x,y) – reszta z dzielenia x przez y;

fix

(A) – zakrągla do najmniejszej liczby całkowitej;

int2str

() - konwersja liczby całkowitej na string;

22

function

[m]=sz_TworzMacierz(n)

% Funkacja tworzy macierz o zadanym wzorze na jej elementy

for

i=1:n

for

j=1:n

m(i,j)=i+j-2;

end

end

suma=0;

for

i=1:n

liczba=round(30*rand(1,1));

suma=suma+liczba;

end

disp(suma)
disp(suma/n)

function

[]=sz_WypiszOdwrotna(l)

% function []=WypiszOdwrotna(l)

% Funkcja wypisuje na ekranie liczbê odwrotna do liczby l

x=l; i=0;

while

x>0;

i=i+1;
y(i)=rem(x,10);

x=fix(x/10);

end

;

disp(int2str(y));

1. Napisz skrypt, który wyświetla Twoje imię i nazwisko oraz odpowiedni tekst powitalny.
2. Napisz skrypt, który prosi użytkownika o podanie dwóch liczb całkowitych nieujemnych a

następnie oblicza i wyświetla w oknie konsoli pole i obwód prostokąta.

3. Napisz skrypt, który pobiera od użytkownika wartość zmiennej a typy rzeczywistego, jeśli

wartość zmiennej jest dodatnia oblicza pole powierzchni całkowitej i objętość sześcianu o
boku dł. a. Wynik wyświetla na ekranie.

4. Napisz skrypt, który pobiera od użytkownika liczby rzeczywiste a i b i rozwiązuje równanie

liniowe ax+b=0.

5. Napisz skrypt, który pobiera od użytkownika liczby rzeczywiste a, b, c i rozwiązuje

równanie kwadratowe ax^2+bx+c=0.

6. Napisz skrypt, który pobiera 9 rzeczywistych liczb, a11, a12, a13, a21, a22, a23, a31, a32,

a33 będącymi wpółczynnikami macierzy 3x3 i oblicza wyznacznik tej macierzy.

7. Napisz skrypt, który oblicza średnią arytmetyczną dziesięciu liczb wprowadzanych przez

użytkownika.

8. Napisz funkcje, która obliczy k-ty wyraz ciągu danego wzorem a_n=3*n-1
9. Napisz skrypt, który wczyta jednowymiarową, ośmioelementową tablicę liczb

rzeczywistych, wyświetli wprowadzone liczby, a następnie policzy i wyświetli ich średnią
arytmetyczną.

10. Napisz skrypt, który pobiera od użytkownika n-elementową tablicę liczb rzeczywistych

(najpierw pobierz liczbę n potem kolejne elementy tablicy) w podwójnej precyzji i
wyznacza:

a) minimalną wartość
b) maksymalną wartość
c) sumę wszystkich wartości
d) iloczyn wszystkich wartości

11. Napisz funkcję obliczającą (z twierdzenia Pitagorasa) długość wektora na płaszczyźnie XY

gdy dane są współrzędne jego początku (xp,yp) oraz końca (xk,yk). Zastosuj tę funkcję do
obliczenia:

a) długości wektora o współrzędnych początku: (5,47; 14,5) i współrzędnych końca:
(24,8;

55,66)

b) odległości między dwoma wierzchołkami gór jeśli wiadomo, że wysokości tych
gór wynoszą 327m oraz 1024m, a odległość w poziomie miedzy nimi (na mapie)
wynosi

2

km.

c) minimalnej długości linii energetycznej D (bez uwzględniania zwisu) gdy
wierzchołki czterech słupów leżą w jednej płaszczyźnie pionowej a ich wpółrzędne
są: (0,0); (200, 180); (400,230); (600,150)

Dzięki poleceniu

diary()

można zapisać każdą interaktywną sesje obliczeniową (to znaczy historię

poleceń i ich wyniki) na dysku w pliku ASCII, który może być oglądany w dowolnym edytorze
tekstu.

diary on

otwarcie pliku do zapisu bez podania nazwy, system MATLABa tworzy plik o nazwie

diary umieszczony w aktualnym folderze.

diary off

zamkniecie pliku.

23

ZADANIA DO SAMODZIELNEGO WYKONANIA – ZESTAW 4

diary

('nazwa_pliku') otwarcie pliku do zapisu.

Zakończenie sesji z MATLABem powoduje utratę zmiennych. Do zapisywania do pliku
zewnętrznego i odczytywania z pliku wartości niektórych lub wszystkich zmiennych służą
polecenia

save

i

load

.

save

'nazwa_pliku' [ 'zm_1', 'zm_2', …, 'zm_n']

load

'nazwa_pliku' ['zm_1', 'zm_2', …, 'zm_n']

W poleceniu

save

i

load

można używać nawiasów okragłych wtedy mają one postać:

save

('nazwa_pliku' [, 'zm_1', 'zm_2', …, 'zm_n'])

load

('nazwa_pliku' [, 'zm_1', 'zm_2', …, 'zm_n'] )

Nawiasy kwadratowe oznaczają, że polecenie

save

i

load

wypisania zmiennych oznaczają, że będą

zapisane wszystkie zmienne z przestrzeni roboczej i polecenia przyjmują postać:

save

'nazwa_pliku'

load

'nazwa_pliku'

Plik w który zapisujemy zmienne ma rozszerzenie mat i jest plikiem binarnym, chyba że zmienimy
to używając odpowiednich opcji.

Przykład
>> save plik.mat B %spowoduje zachowanie zmiennej B w pliku binarnym o nazwie plik.mat.
>>save('nazwa_pliku.mat', 'B', '-ASCII') %spowoduje zachowanie zmiennej B w pliku tekstowym
o nazwa_pliku.mat.

1. Przy użyciu pliku Q.mat wywołaj funkcję sz_euler.m.

4. Octave – darmowy klon MATLABa

Scilab

4

- niekomercyjny system programowania wysokiego poziomu obliczeń naukowych.

System ten jest rozwijany przez INRIA (Institut National de Recherche en Informtique et
Automatique). Scilab to środowisko ułatwiające wykonywanie obliczeń numerycznych, między
innymi:

•

metody dotyczące algebry liniowej,

•

aproksymację i interpolację,

•

rozwiązywanie równań różniczkowych,

•

analizę i przetwarzanie danych,

4

www.scilabsoft.inria.fr

– domowa strona Scilaba

24

ZADANIE DO SAMODZIELNEGO WYKONANIA – ZESTAW 4

•

metody elementów skończonych,

•

metody teorii grafów i wiele innych

Octave – to interaktywny system operacyjny do obliczeń numerycznych i grafiki. Stanowi

on odpowiednik Matlaba będąc z nim w dużym stopniu zgodny. Octave jest językiem
programowania, co oznacza, że jego użytkowanie sprowadza się do wytworzenia kodu programu,
który ma zostać zinterpretowany. Prace nad Octave rozpoczęły się w 1988 roku. Pierwsza wersja
alpha ukazała się 4 stycznia 1993 roku. Wersja 1.0 została wydana 17 lutego 1994 roku. Najnowsza
stabilna wersja środowiska nosi numer 3.2.4. (z dnia 28.01.2010 roku). W tej chwili Octave
rozprowadzany jest w postaci binarnej wraz z wieloma dystrybucjami Linuxa, dostępna jest także
wersja na Microsoft Windows. Octave został pierwotnie stworzony jako program do projektowania
reaktorów chemicznych. Obecnie jest rozwijany pod przewodnictwem dr. Johna W. Eatona i
udostępniany na zasadach GNU General Public Licence (Powszechnej Licencji Publicznej GNU –
licencji wolnego i otwartego oprogramowania).

Istnieją dwie metody pracy w Octave. Pierwsza z nich polega na przygotowaniu wcześniej

w dowolnym edytorze tekstowym programu (skryptu) i przekazaniu go do wykonania. Programy
takie napisane są czystym tekstem i zapisane w plikach z rozszerzeniem .m. Druga metoda, tzw.
interaktywna polega na wpisaniu metod w wierszu poleceń interpretatora. Edytor wbudowany w
Octave jest edytorem wierszowym. Specyfika pracy z takim edytorem polega na tym, że edycji
może zostać poddany tylko bieżący wiersz. Wiersze powyżej są tylko napisami i ich edycja nie jest
możliwa. Po wierszu poleceń można się poruszać swobodnie jak w każdym innym edytorze.
Natomiast klawiszami „w górę”, „w dół” można w wierszu poleceń przewijać listę historii, która
umożliwia dostęp do wcześniej wykonanych poleceń. Edytor można opuścić wydając polecenie
quit, exit lub naciskając kombinacje klawiszy Ctr+D.

Octave rozróżnia wielkość liter. Komendy zakończone średnikiem nie zostają wyświetlone na
ekranie. Pomoc jest dostępna w programie po wpisaniu polecenia help, które skutkuje
wyświetleniem listy dostępnych tematów pomocy. Możemy również precyzyjnie określić
interesujące nas zagadnienie np.:

Rys. 4.2.1 Fragment kodu przedstawiający definiowanie polecenia help.

zostanie wyświetlona pomoc do funkcji plot rysującej wykresy (Rys. 4.2.1).

GNU Octave pozwala na operowanie na liczbach rzeczywistych i zespolonych. Dostępne są
wszystkie standardowe operacje arytmetyczne, takie jak dodawanie, odejmowanie, potęgowanie. Ta
ostatnia operacja może być reprezentowana jako ** (dwie gwiazdki) lub ^ (daszek) (Rys. 4.3.1).

Rys. 4.3.1 Fragment kodu przedstawiający wykorzystanie operatorów matematycznych.

Liczby zespolone są wbudowanym typem danych. Reprezentowane są jako sumy postaci a+bi,
gdzie i to jednostka urojona, która w Octave jest reprezentowana jako jedna z liter i, I, j, J (Rys.
4.3.2). Wszystkie działania określone na liczbach rzeczywistych są określone także dla liczb
zespolonych. Przykładowo

25

Rys. 4.3.2 Fragment kodu ukazujący reprezentacje liczb zespolonych.

Octave daje dużą swobodę, jeżeli chodzi o operowanie na wektorach i macierzach. Do ich
reprezentacji służy podstawowa w tym programie struktura danych, czyli tablica. Najprostszym
sposobem utworzenia nowego wektora jest wymienienie wszystkich jego elementów (Rys. 4.3.3.).

Rys. 4.3.3 Fragment kodu przedstawiający zadeklarowanie wektora wierszowego.

Otrzymujemy w ten sposób wektor wierszowy. Aby otrzymać wektor kolumnowy, konieczne jest
wykonanie operacji transponowania. Jest ona reprezentowana za pomocą apostrofu ‘ (Rys. 4.3.4).

Rys. 4.3.4 Fragment kodu przedstawia operację transponowania, która prowadzi do powstania wektora

kolumnowego.

Podobnie możemy zdefiniować macierz, oddzielając kolejne wiersze średnikami (Rys. 4.3.5).

Rys. 4.3.5 Fragment kodu ukazujący zadeklarowanie macierzy 3 na 3.

Niektóre macierze mogą być zbudowane poprzez wywołanie funkcji GNU Octave. Przekładem są
macierze złożone z samych zer lub z samych jedynek. aby uzyskać macierz o wymiarach 3 na 3
(Rys. 4.3.6), wypełniona zerami wystarczy wpisać:

Rys. 4.3.6 Fragment kodu przedstawiający użycie funkcji zeros w celu stworzenia macierzy wypełnionej

zerami.

Analogicznie funkcja ones wypełnia macierz o zadanych rozmiarach jedynkami. Funkcje te są
przydatne w sytuacji, gdy chcemy najpierw zbudować macierz o zadanym kształcie, którą w
kolejnych krokach wypełniamy w określony sposób.
Bardzo przydatnym mechanizmem GNU Octave są zakresy (Rys. 4.3.7). Zakres jest wygodnym
sposobem zapisania wektora wierszowego, którego elementy są równomiernie rozłożone. Do
zakresu służy operator : (dwukropek).

26

Rys. 4.3.7 Fragment kodu przedstawiający wykorzystanie zakresów do stworzenia wektorów.

W tym wypadku zakres r1 to wektor liczb od 1 do 10, r2 to wektor zawierający co drugą liczbę
całkowitą z przedziału od 1 do 20. Dodawanie zakresów, podobnie jak dodawanie wektorów, polega
na dodawaniu elementu po elemencie.
Podobnie jak operacja dodawania, także i inne operacje arytmetyczne są zdefiniowane dla zakresów
i tablic. Jeżeli przed operatorem potęgowania (^) dodamy kropkę, to potęgowanie zostanie
zastosowane do każdego z elementów tablicy z osobna (Rys.4.3.8). Jest to prosty sposób na
uzyskanie np. wszystkich sześcianów liczb z zakresu od 1 do 10.

Rys. 4.3.8 Fragment kodu przedstawiający użycie operatora .^.

Napisy w Octave mogą być reprezentowane jako ciąg znaków ograniczonych bądź cudzysłowami –
„napis”, bądź apostrofami – ‘napis’. Ponieważ apostrof jest używany także do transponowania
macierzy bezpieczniej jest używać cudzysłowów.

Instrukcja warunkowa if pozwala na wykonanie bloku kodu, jeżeli spełniony zostanie zadany
warunek. W poniższym przykładzie (Rys. 4.4.1) wybierany jest jeden z dwóch warunków (x>5
bądź x<5)

Rys. 4.4.1 Fragment kodu przedstawiający wykorzystanie instrukcji warunkowej if.

Znaki > oznaczają kontynuacje wpisywanej komendy po naciśnięciu klawisza ENTER. Program
sygnalizuje w ten sposób oczekiwanie na zakończenie rozpoczętej konstrukcji, takiej jak instrukcja
if, bądź zamknięcie nawiasów. Jeżeli chcemy rozróżnić pomiędzy większą ilością możliwości, to
możemy zastosować konstrukcje if-elseif tak jak w poniższym przykładzie (Rys. 4.4.2).

Rys. 4.4.2 Fragment kodu przedstawiający wykorzystanie instrukcji warunkowej if-elseif.

Komenda endif oznacza zamkniecie konstrukcji.
Drugim sposobem warunkowego wykonania komend jest instrukcja switch. Pozwala ona na
wyszczególnienie co ma być wykonane w zależności od tego, do jakiego zbioru należy zmienna. W

27

poniższym przykładzie zmienna test ma wartość 2, wykonane zostanie przypisanie x=0 (Rys. 4.4.3).

Rys. 4.4.3 Fragment kodu przedstawiający wykorzystanie instrukcji warunkowej switch.

Do poruszania się po tablicach służy pętla for. Jeśli chcemy, by program wypisał kwadraty liczb od
1 do 10 używamy polecenia:

Rys. 4.4.4 Fragment kodu przedstawiający wykorzystanie pętli for.

znaki > oznaczają, iż program czeka na wprowadzenie komendy endfor, która oznacza zamknięcie
pętli for.
Jeżeli chcemy wykonywać jakiś zestaw poleceń tylko dla danych spełniających określony warunek
korzystamy z pętli while.

Rys. 4.4.5 Fragment kodu przedstawiający wykorzystanie pętli while.

Równanie kwadratowe ma postać

0

3

2

2

1

=

+

+

a

x

a

x

a

, gdzie

3

2

1

,

,

a

a

a

to liczby rzeczywiste.

Współczynniki

3

2

1

,

,

a

a

a

będziemy przechowywać w trójwymiarowej tablicy A, np.

2

1

=

a

,

6

2

=

a

,

1

3

=

a

.

Rys. 4.5.1 Fragment kodu przedstawiający utworzenie tablicy współczynników - A.

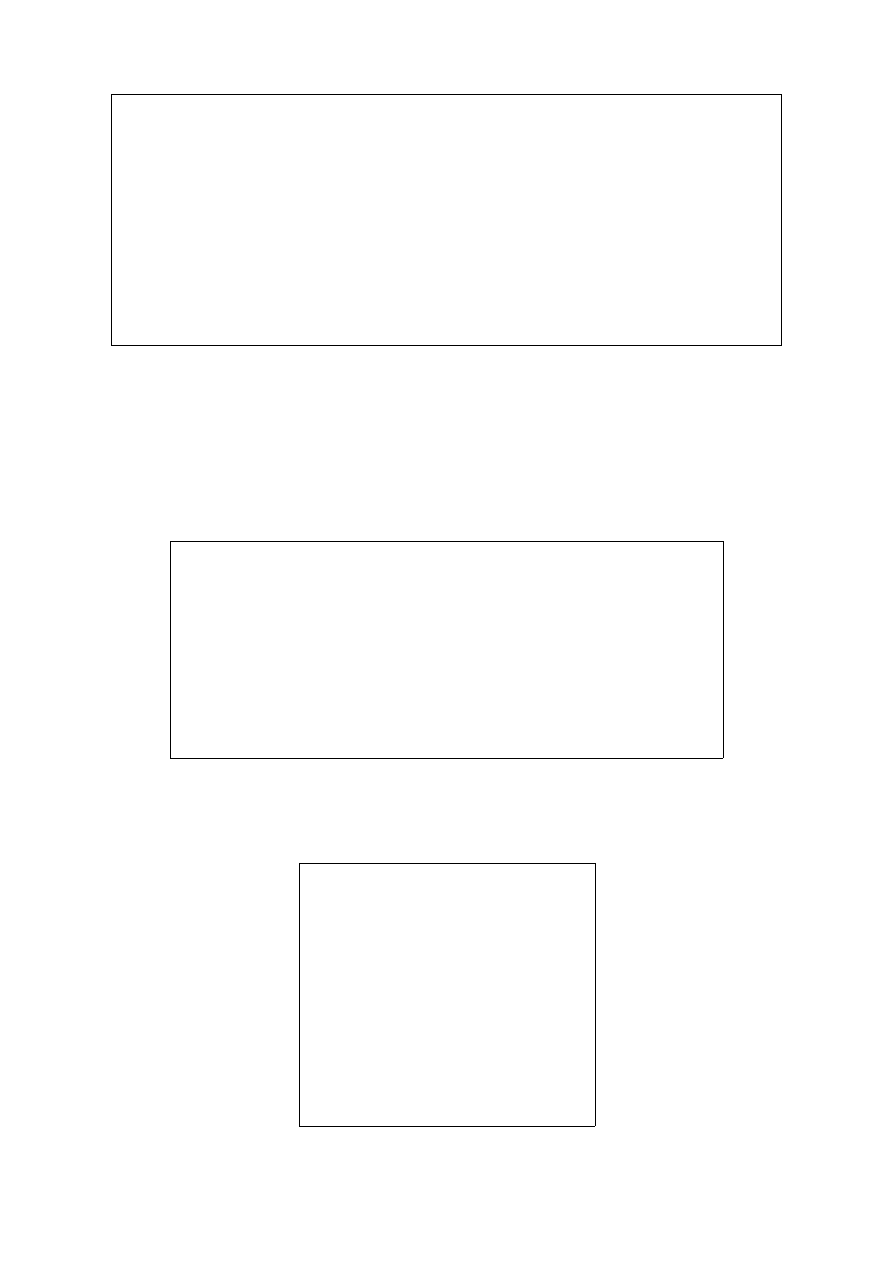
Definiujemy funkcję, która będzie reprezentowała nasz wielomian:

Rys. 4.5.2 Fragment kodu przedstawiający zdefiniowanie funkcji reprezentującej wielomian.

Funkcje pozwalają na zdefiniowanie nowego polecenia równoważnego grupie komend. Definicja
funkcji rozpoczyna się słowem kluczowym function (Rys. 4.5.2). Po nim następuje
wyszczególnienie, gdzie będzie przechowywana wartość zwracana – w powyższym przykładzie
wartość zwracaną reprezentuje zmienna y. Dalej następuje nazwa funkcji wraz z jej argumentami.
W tym przypadku mamy dwa argumenty: x – reprezentujący argument funkcji kwadratowej oraz a
reprezentujący tablicę współczynników. Ciało funkcji zawiera komendy, które zostaną wykonane
podczas wywoływania funkcji. Nasza funkcja zawiera jedno przypisanie, które zapisuje wartość

28

obliczeń w zmiennej y. Przy potęgowaniu zmiennej wykorzystany został operator .^. Pozwala nam
to przekazać tablicę jako pierwszy argument funkcji kwadratowej, co jest przydatne przy
korzystaniu z funkcji plot. Np.

Rys. 4.5.3 Fragment kodu przedstawiający ukazanie wartości elementu A.

zatem, aby obliczyć wartość funkcji

( )

1

6

2

2

+

+

=

x

x

x

f

wystarczy napisać:

Rys. 4.5.4 Fragment kodu przedstawiający wykorzystanie funkcji kwadratowa(2,A) w celu obliczenia

wartości funkcji.

Octave zarówno w środowisku Linux jak i Microsoft Windows do generowania wykresów
wykorzystuje środowisko Gnuplot. W związku z tym dziedziczy zarówno jego ograniczenia jak i
możliwości.
Do generowania wykresów dwuwymiarowych w Octave można użyć wielu funkcji. Najczęściej
wykresy liniowe można uzyskać przy pomocy polecenia plot(x,y). Np.:

Rys. 4.6.1 Fragment kodu przedstawiający wykorzystanie funkcji plot służącej do rysowania wykresów.

Octave jest narzędziem do obliczeń numerycznych. Program nie zawiera wbudowanego pakietu do
obliczeń symbolicznych. Obliczenia te możemy wykonywać po zainstalowaniu odpowiedniego
pakietu. Ma on jednak ograniczenia, na przykład nie zawiera polecenia do symbolicznego
obliczania całek. GNU Octave jest programem kompatybilnym z programem Matlab. Całkowanie
symboliczne w Matlabie wykonujemy za pomocą polecenia – int.
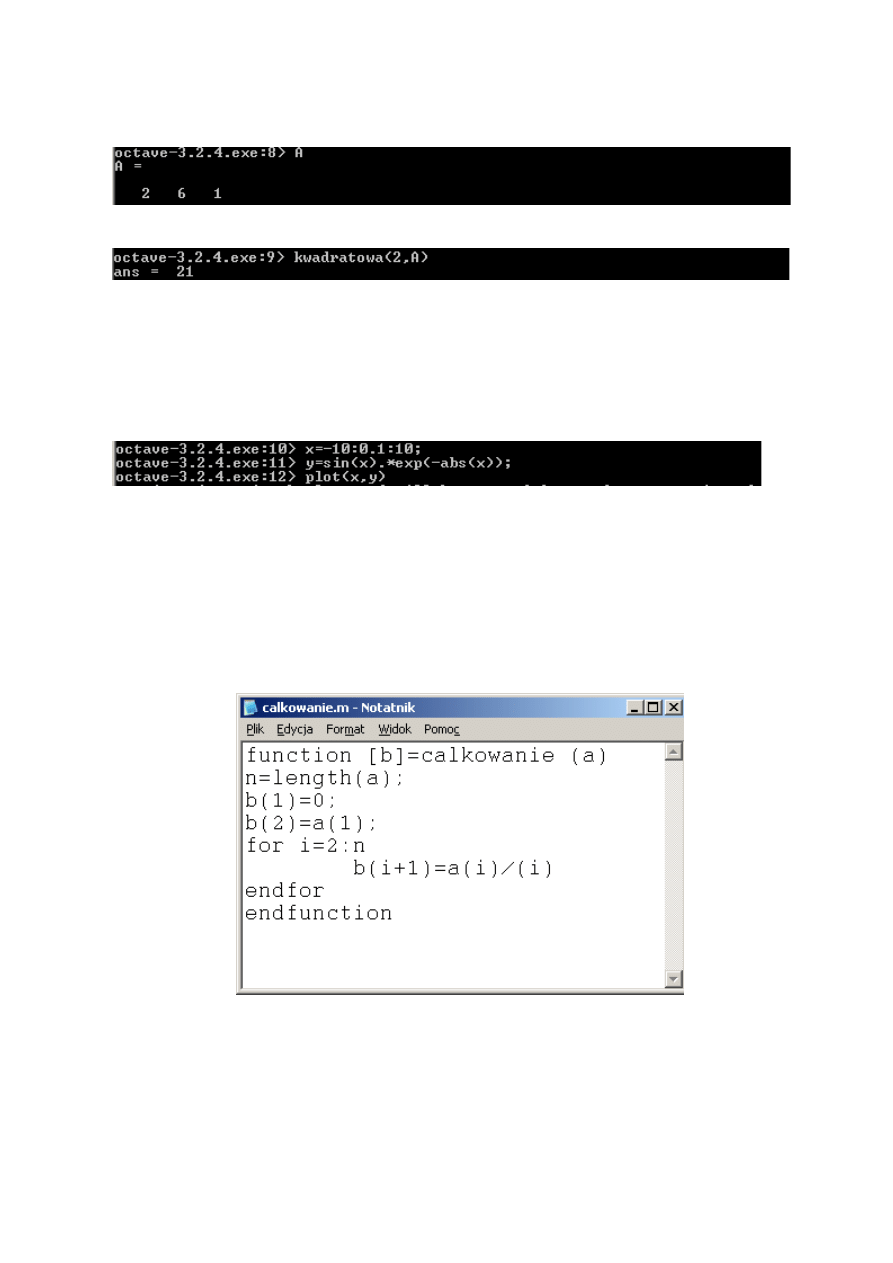
Poniżej przedstawiony został kod funkcji umożliwiającej obliczanie współczynników znajdujących
się przy odpowiednich potęgach x, podczas całkowania symbolicznego wielomianu postaci

n

n

x

a

x

a

x

a

a

+

+

+

+



2

2

1

0

(Rys. 4.7.1).

Rys. 4.7.1 Skrypt zawierający funkcję wykorzystywaną do wyliczania współczynników

n

a

a

a

,

,

,

1

0



wielomianu n-tego stopnia.

Parametrem wejściowym powyższej funkcji jest wektor złożony z współczynników

n

a

a

a

,

,

,

1

0



.

W wyniku otrzymujemy wektor złożony z wartości współczynników wielomianu wyliczonych
podczas całkowania wielomianu wejściowego. Pierwszą pozycję wektora wyjściowego zajmuje
zawsze 0 (zero). Miejsce to odpowiada za wyraz wolny wielomianu powstałego w skutek

29

całkowania wielomianu początkowego.
Przykład 4.7.1
Obliczyć

∫

xdx .

Korzystając z funkcji przedstawionej powyżej otrzymujemy

Rys. 4.7.2 Fragment kodu zawierający instrukcje otwarcia pliku z funkcją wyliczającą współczynniki

wielomianu oraz wykorzystanie jej do obliczenia całki

∫

xdx .

C

x

C

x

xdx

+

=

+

=

∫

2

2

2

1

2

Jest to zgodne z obliczeniami przedstawionymi na Rys. 4.7.2. Dwa pierwsze miejsca w wektorze
wynikowym zajmują zera ponieważ w wielomianie wyjściowym nie mamy pierwszej i zerowej
potęgi x.

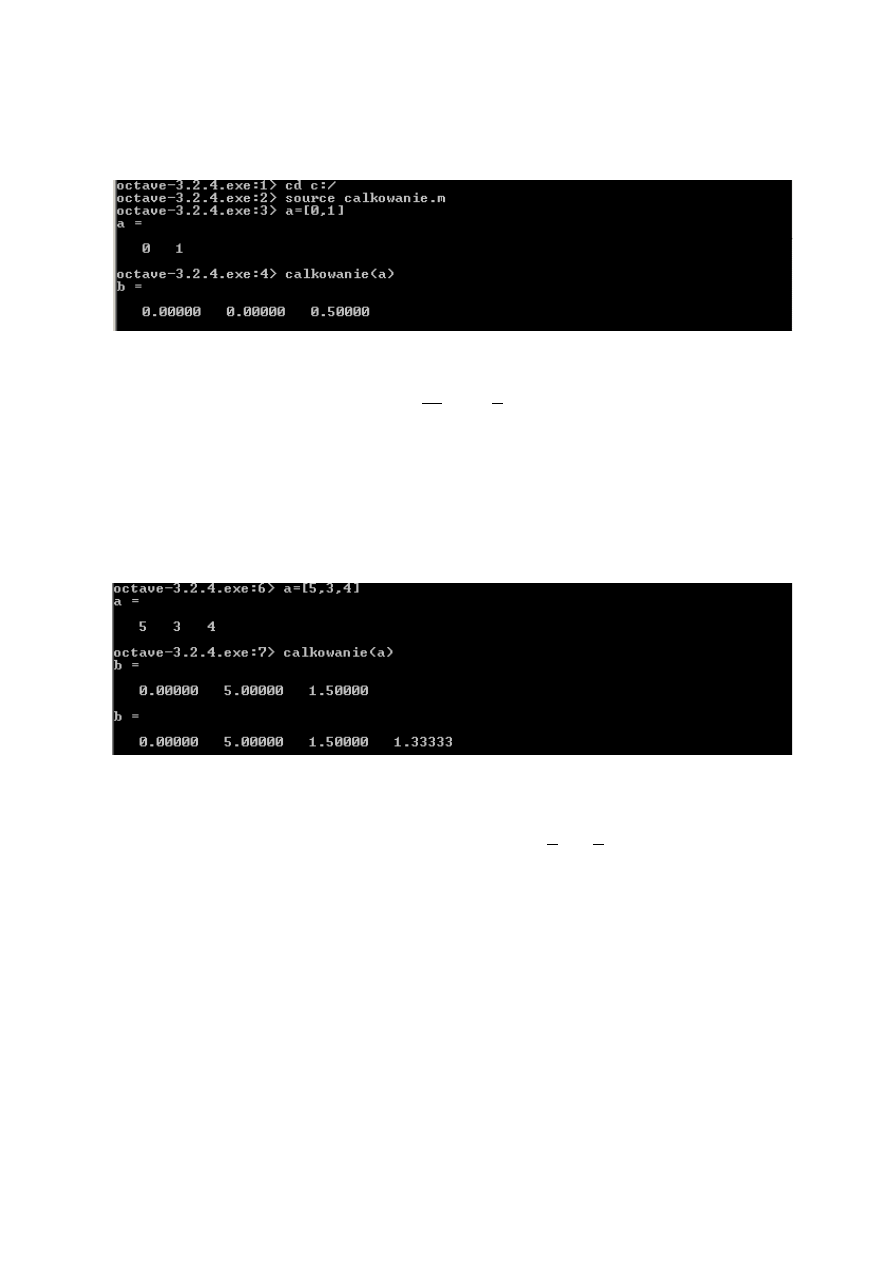
Przykład 4.7.2
Obliczyć

∫

+

+

dx

x

x

5

3

4

2

.

Wykorzystujemy funkcję przedstawiona na Rys. 4.7.1.

Rys. 4.7.3 Fragment kodu przedstawiający wykorzystanie funkcji calkowanie(a) do wyliczenia

współczynników wielomianu podczas całkowania

∫

+

+

dx

x

x

5

3

4

2

.

Sprawdzenie:

C

x

x

x

dx

xdx

dx

x

dx

x

x

+

+

+

=

+

+

=

+

+

∫

∫

∫

∫

5

2

3

3

4

5

3

4

5

3

4

2

3

2

2

.

Przykład 4.7.3
Obliczyć

∫

+

+

+

dx

x

x

x

1

5

2

2

3

.

30

Rys. 4.7.4 Fragment kodu przedstawiający wykorzystanie funkcji calkowanie(a) wyliczającej współczynniki

wielomianu powstałego w skutek całkowania

∫

+

+

+

dx

x

x

x

1

5

2

2

3

.

Sprawdzenie:

C

x

x

x

x

dx

xdx

dx

x

dx

x

dx

x

x

x

+

+

+

+

=

+

+

+

=

+

+

+

∫

∫

∫

∫

∫

2

3

4

2

3

2

3

2

1

3

5

4

2

1

5

2

1

5

2

.

Octave posiada kilka wbudowanych funkcji do numerycznego obliczania całek.
1. quad – całkowanie przy pomocy kwadratury Gaussa

v = quad (f, a, b),

v = quad(fun, a, b, tol),

v = quad(fun, a, b, tol, sing),

[v ,ier, nfun, err] = quad(…).

Pierwszym argumentem jest nazwa funkcji, uchwyt funkcji lub nazwa funkcji wbudowanej. Musi
mieć ona postać y=f(x), gdzie y i x są skalarami. Drugi i trzeci argument to odpowiednio dolna i
górna granica całkowania funkcji f (jedna lub obie mogą być nieskończone). Opcjonalny argument
tol jest wektorem określającym pożądana dokładność wyników. Pierwszym elementem wektora jest
błąd bezwzględny, a drugi elementem jest pożądany błąd względny. Gdy wybieramy tylko błąd
względny, ustawiamy błąd bezwzględny na zero. Argument sing jest wektorem wartości, w którym
całka jest rozumiana jako całka pojedyncza.
W wyniku otrzymujemy zmienne v oraz ier zawierające odpowiednio wynik całkowania oraz
całkowity kod błędu (zero oznacza udane całkowanie). nfun zwraca liczbę ocen funkcji podczas
całkowania. Natomiast err zawiera oszacowanie błędu rozwiązania.
Przy użyciu quad_options możemy ustawić inne parametry opcjonalne dla funkcji quad.

quad_options(opt, val)

Gdy funkcja ta wywoływana jest z dwoma parametrami, pozwala na ustawienie opcji parametrów
funkcji quad. Natomiast, jeśli bierzemy pod uwagę jeden parametr zwraca ona wartość
odpowiedniej opcji. Jeśli argumenty nie są dostarczone nazwy wszystkich dostępnych opcji i ich
aktualne wartości są wyświetlane.
Dostępne opcje:

- „absolute tolerance” (błąd bezwzględny) - może być zerowa;
- „relative tolerance” (nieujemna błąd względny) – jeśli błąd bezwzględny wynosi zero, błąd
względny musi być większy lub równy max(50*eps,0.5e-28);
- „single precision absolute tolerance” (błąd bezwzględny dla pojedynczej precyzji) - może
być zerowa;
- „single precision relative tolerance” (nieujemna błąd względny dla pojedynczej precyzji) -
jeśli błąd bezwzględny wynosi zero, błąd względny musi być większy lub równy
max(50*eps,0.5e-28).

Przykład 4.7.4

31

Obliczyć całkę

∫

π

0

sin xdx

x

.

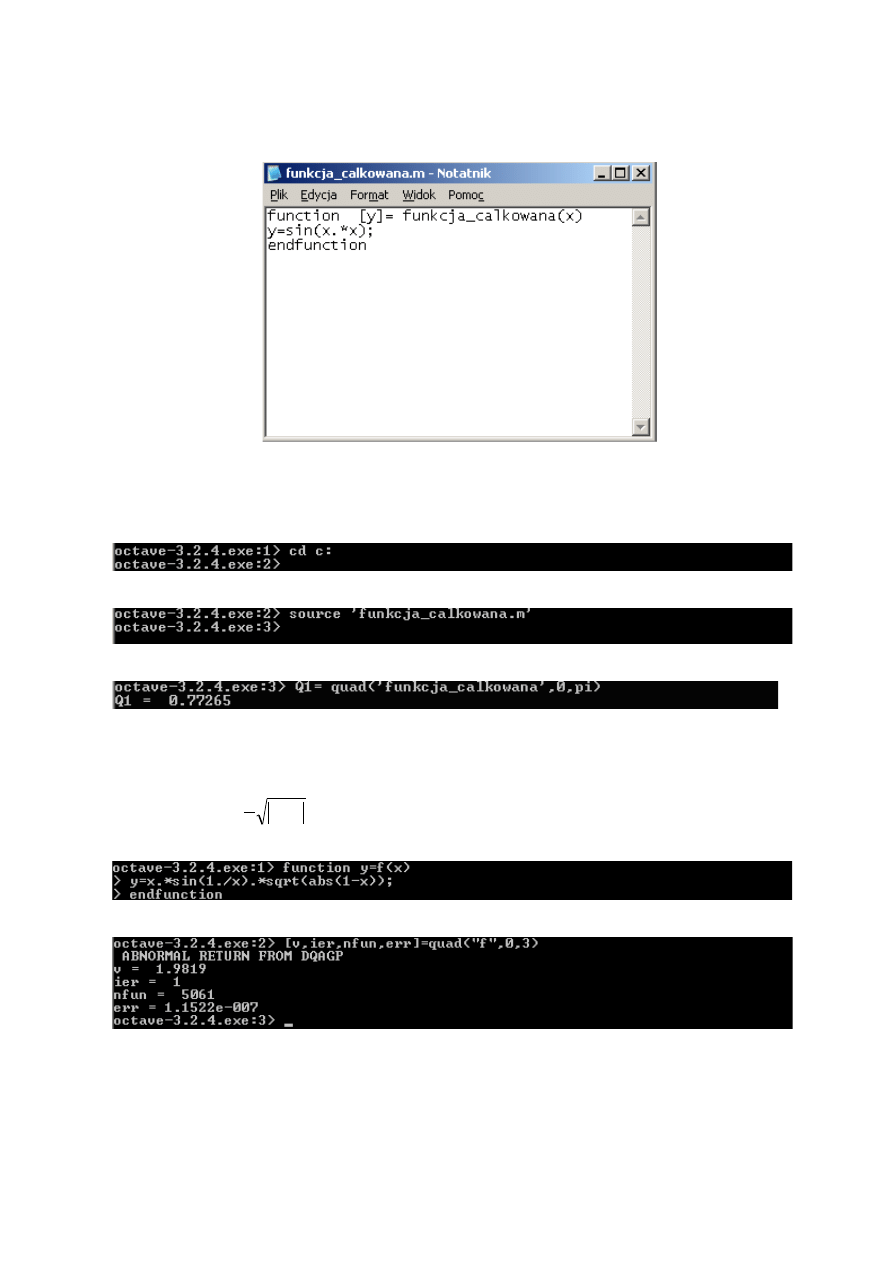
Tworzymy skrypt zawierający funkcje podcałkową na przykład funkcja_calkowana.m (Rys. 4.7.5)

Rys. 4.7.5 Skrypt przedstawiający funkcje podcałkową

x

x sin

.

Następnie przechodzimy w oknie poleceń Octave do katalogu w którym zapisaliśmy plik z naszą
funkcją (Rys. 4.7.6).

Rys. 4.7.6 Fragment kodu przedstawiający przejście do katalogu c.

Otwieramy plik funkcja_calkowana.m (Rys. 4.7.7).

Rys. 4.7.7 Fragment kodu przedstawiający otwarcie pliku z kodem funkcji (Rys. 4.7.5).

Wywołujemy funkcję quad z zadanymi parametrami (Rys. 4.7.8)

Rys. 4.7.8 Fragment kodu przedstawiający wywołanie funkcji służących do całkowania numerycznego

(quad).

Przykład 4.7.5

Obliczyć całkę

dx

x

x

x

−

∫

1

1

sin

3

0

.

Określamy funkcję (Rys. 4.7.9)

Rys. 4.7.9 Fragment kodu zawierający określenie funkcji podcałkowej z Przykładu 4.7.5.

Wywołujemy funkcję quad w zadanych granicach:

Rys. 4.7.10 Fragment kodu przedstawiający wywołanie funkcji quad.

Mimo że funkcja quad zwraca niezerową wartość ier wynik jest dość dokładny.

2. quadl – całkowanie przy pomocy adaptacyjnej reguły Gaussa - Lobatto

q = quadl(f, a, b),

32

q = quadl(f, a, b, tol),

q = quadl(f, a, b, tol, trace),

q = quadl(f, a, b, tol trace, p1, p2, …).

Funkcja quadl(f, a, b) przybliża całkę precyzyjnie. Pierwszy argument – f, jest albo uchwytem
funkcji, funkcją wbudowaną, lub łańcuchem zawierającym nazwę funkcji do oszacowania (nazwa
skryptu). Funkcja f musi zwracać wektor wartości wyjściowych dla danego wektora wartości
wejściowych. Argument tol określa błąd względny. Natomiast argument trace zwraca węzły
kwadratury. Dodatkowe argumentu p1, p2, … przekazywane są bezpośrednio do f. Aby skorzystać z
wartości domyślnych dla tol i trace można pola te pozostawić puste.

Przykład 4.7.6

Obliczyć całkę

∫

π

0

sin xdx

x

.

Postępujemy jak w Przykładzie 4.7.5

Rys. 4.7.11 Fragment kodu przedstawiający wywołanie funkcji wbudowanej quadl z różnymi parametrami

opcjonalnymi (tol =1, trace=1) dla funkcji podcałkowej z Przykładu 4.7.5.

Argument opcjonalny trace zwrócił węzły kwadratury(Rys.4.7.11), co jest przydatne podczas
rysowania wykresów.

3. quadgk – całkowanie przy pomocy kwadratury Gaussa – Kronroda

q = quadgk(f, a, b, abstol, trace),

q = quadgk(f, a, b, prop, val,…),

[q, err] = quadgk(…).

Funkcja f może być zdefiniowana jako uchwyt funkcji, funkcja wbudowana, lub ciąg znaków
zawierający nazwę funkcji (skryptu). Granice całkowania a, b, mogą być skończone lub
nieskończone i zawierać osobliwości na końcach przedziału.

Przykład 4.7.7

Obliczyć

(

)

∫

∞

+

0

1

1

dx

x

x

.

Rys. 4.7.12 Fragment kodu przedstawiający wywołanie funkcji quadgk dla funkcji podcałkowej z Przykładu

4.7.7.

Rys. 4.7.13 Fragment kodu przedstawiający wykorzystanie funkcji quadgk przy argumencie abstol=e.

Błąd bezwzględny może być przekazywana jako czwarty argument (Rys. 4.7.13).

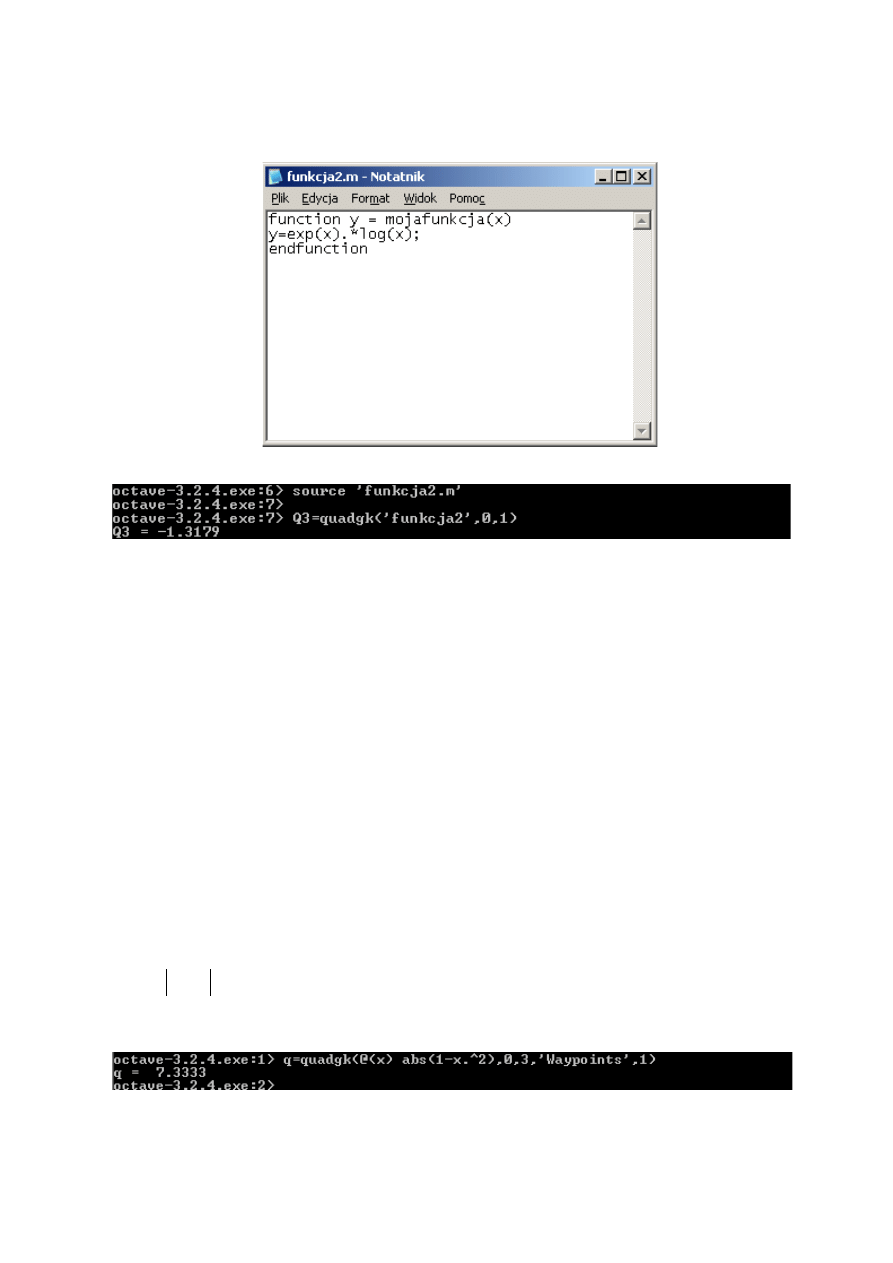
Przykład 4.7.8

33

Obliczyć całkę

( )

x

x

e

log

1

0

∫

.

Tworzymy skrypt

Rys. 4.7.14 Skrypt zawierający wzór funkcji podcałkowej z Przykładu 4.7.5.

Następnie

Rys. 4.7.15 Fragment kodu przedstawiający otwarcie pliku z funkcją podcałkową (Przykład 4.7.8) oraz

użycie funkcjo quadgk w celu obliczenia całki

( )

x

x

e

log

1

0

∫

.

Pewne właściwości funkcji quadgk mogą być przekazywane jako para par, val:

- AbsTol (błąd bezwzględny) – domyślnie 1e-10;
- RelTol (błąd względny) – domyślnie 1e-5;
- MaxIntervalCount – funkcja quadgk początkowo dzieli przedział całkowania na 10
podprzedziałów. Jeśli podprzedziały te zawierają niedopuszczalne błędy dzielone są na dalsze
podprzedziały. Jeżeli liczba podrzedziałów przekracza, w dowolnym momencie, 650
podrzedziałów wtedy sygnalizowana jest słaba zbieżność i bieżący wynik całkowania nie
zostaje zwracany. MaxIntervalCount wykorzystywana jest do zmiany liczby podprzedziałów;
- WayPoints – jeśli pierwsza pochodna funkcji podcałkowej jest nieciągła, wtedy za pomocą
WayPoints możemy oznaczyć punkty nieciągłości. Spowoduje to, że końce podprzedziałów
przedziału całkowania pokryją się z punktami nieciągłości funkcji podcałkowej. Prowadzi to do
znacznej poprawy oszacowania błędu kwadratury oraz zwiększa szybkość obliczeń.
- Trace – jeśli zwraca wartość logiczną true wtedy funkcja quadgk drukuje informacje o
zbieżności kwadratury.

Przykład 4.7.9

Obliczyć

dx

x

∫

−

3

0

2

1

.

Punktem nieciągłości w tym przypadku jest

1

=

x

.

Zatem

Rys. 4.7.16 Fragment kodu przedstawiający wykorzystanie właściwości funkcji quadgk (WayPoints).

34

4. quadv – całkowanie przy pomocy wzoru Simpsona

q = quadv(f, a, b),

q=quadv(f, a, b, tol),

q=quadv(f, a, b, tol, trace),

q =quadv(f, a, b, tol, trace, p1, p2,…),

[q,fcnt] = quadv(…).

Algorytm używany przez funkcję quagv obejmuje podział przedziału całkowania na podprzedziały i
zastosowanie na każdym z nich wzoru Simpsona. Argument tol oznacza błąd kwadratury,
domyślnie wynosi on 1e-6. Dodatkowe argumenty p1, p2, … przekazywane są bezpośrednio do
funkcji f. Aby skorzystać z wartości domyślnych dla tol i trace pozostawiamy te miejsca puste.

5. quadcc – całkowanie przy pomocy kwadratury Clenshawa – Curtisa

[int, err, nr_points] = quadcc(f, a, b, tol),

[int, err,nr_points] = quadcc(f, a, b, tol, sing).

Dwie dodatkowe zmienne err oraz nr_point zwracają odpowiednio błąd kwadratury oraz liczbę
węzłów w których całki dobrze oszacowano. Należy pamiętać, że funkcja quadcc jest ogólnym
algorytmem kwadratury i może być mniej skuteczna niż metody takie jak quadgk lub trapz.

6. trapz – całkowanie przy pomocy wzoru trapezów

z = trapz(y),

z = trapz(x, y),

z = trapz(…, dim).

Zakłada się, że argument x jest wektorem o współrzędnych równomiernie rozmieszczonych.
Funkcja trapz(x,y) oblicza całkę względem argumentu x. Natomiast argument opcjonalny dim jest
wymiarem.

Przykład 4.7.10

Obliczyć

∫

π

0

sin xdx .

Rys. 4.7.17 Fragment kodu przedstawiający wykorzystanie funkcji trapz(X,Y) przy wcześniejszym ustaleniu

parametrów X i Y.

7. cumtrapz – całkowanie przy pomocy złożonego wzoru trapezów

z = cumtrapz(x),

z= cumtrapz(x, y),

z = cumtrazp(…, dim).

Zakłada się, że argument x jest wektorem o współrzędnych równomiernie rozmieszczonych.
Funkcja cumtrapz(x,y) oblicza całki względem argumentu x. Natomiast argument opcjonalny dim
jest wymiarem.

Przykład 4.7.11

Obliczyć

∫

3

1

2

dx

x

.

35

Rys. 4.7.18 Fragment kodu przedstawiający wywołanie funkcji cumtrapz dla wcześniej ustalonych wartości

argumentu x.

8. dblquad - obliczanie całek podwójnych

q = dblquad(f, xa, xb, ya, yb, tol, quadf,…)

Argumenty 2-4 oznaczają kolejno dolną i górna granice całkowania zmiennej x oraz dolną i górną
granice całkowania zmiennej y. Funkcja f musi zawierać wektor x oraz stałą (skalar) – y, zwraca
wektor o takiej samej długości jak wektor x.

Przykład 4.7.12

Obliczyć

∫ ∫

+

π π

π

0

2

cos

sin

ydxdy

x

x

y

.

.

Rys.

4.7.19 Fragment kodu przedstawiający obliczenie całki podwójnej

∫ ∫

+

π π

π

0

2

cos

sin

ydxdy

x

x

y

przy wcześniejszym

zdefiniowaniu funkcji podcałkowej.

Przykład 4.7.13

Obliczyć

∫ ∫

1

0

1

0

)

sin(

dxdy

xy

xy

π

.

Rys. 4.7.20 Fragment kodu przedstawiający obliczenie całki podwójnej z Przykładu 4.7.11 przy użyciu

uchwytu funkcji @.

9. triplequad – obliczanie całek potrójnych

q= triplequad(f, xa, xb, ya, yb, za, zb, tol, quadf, …)

Argumenty xa, xb, ya, yb, za, zb oznaczają odpowiednio dolną i górną granice całkowania x, dolną i
górną granice całkowania y oraz dolną i górną granice całkowania z.

Przykład 4.7.14

Obliczyć

∫ ∫ ∫

1

0

1

0

1

0

xyzdxdydz .

36

Rys. 4.7.21 Fragment kodu przedstawiający użycie funkcji triplequad w celu obliczenia całki potrójnej z

Przykładu 4.7.14.

W zależności od tego jaką wersje programu GNU Octave posiadamy mamy do dyspozycji niektóre
z wyżej wymienionych funkcji do całkowania numerycznego. Powyższe przykłady zostały
wykonane na wersji 3.2.4. Wersja ta nie zawiera wbudowanych funkcji quadv oraz quadcc.

Literatura:

1. Cyprian T. Lachowicz: Matlab, Scilab, Maxima. Opis i przykłady zastosowań. Politechnika

Opolska. Opole 2005.

2. Dokumentacja Octave:

www.octave.org

3. Rudra Pratap, Matlab7 dla naukowców i inżynierów, Wydawnictwo Naukowe PWN 2008.

37