geometria i garsc dowodow id 18 Nieznany

POLITECHNIKA ÓDZKA

Wydzia Fizyki Technicznej, Informatyki i Matematyki Stosowanej

Kierunek: Matematyka

Specjalno´s´c:Matematyka Finansowa i Ubezpieczeniowa

Aleksandra Wojtas

nr albumu: 110492

Szczególne linie, punkty i okregi zwiazane z trójkatem

Praca magisterska napisana w Instytucie Matematyki

pod kierunkiem prof. Jana Kubarskiego

ód´z, czerwiec 2007

Przedmowa

Tematem mojej pracy magisterskiej sa szczególne punkty, linie i okregi zwiazane

z trójkatem. Sposród wszystkich istniejacych (a sa ich setki jak podkresla w swojej

600 stronicowej encyklopedii specjalnych punktów trojkata Clark Kimberling, "En-

cyclopedia of Triangle Centers - ETC", [10]) wybra am te, które moim zdaniem sa

najbardziej znane oraz których w asno´sci uzna am za najbardziej ciekawe i godne

zaprezentowania. Za cel mojej pracy postawi am sobie zebranie i opisanie podsta-

wowych twierdze´n o punktach, liniach i okregach zwiazanych z trójkatem.

O ile by o to mozliwe stara am sie kazde z nich poprzedzi´c krótkim komentarzem

o jego twórcy lub osobie, która je udowodni a (informacje bibliogra czne: [14],

[11], [12]), a takze przedstawi´c dowód. W pracy pojawiaja sie równiez uzupe -

nienia o twierdzenia pomocnicze bad´z lematy wraz z dowodami.

W przedmowie przedstawie nie tylko strukture pracy, ale podziele sie takze

osobistymi re eksjami jakie mia am przy jej pisaniu. Prace podzieli am na sze´s´c

g ównych rozdzia ów.

W pierwszym z nich prezentuje podstawowe wiadomo´sci o trójkacie, na których

opieram sie w dalszej cze´sci pracy, szczególne w dowodach twierdze´n. Sa tam

miedzy innymi twierdzenie Pitagorasa, sinusów oraz cosinusów, a takze przyk a-

dowe zadanie na zastosowanie jednego z nich dla trójkata równobocznego. W roz-

dziale tym wprowadzam oznaczenia cech podobie´nstwa, którymi pos uguje sie

w ca ej pracy.

Drugi rozdzia to prezentacja najbardziej znanych punktów charakterystycznych

trójkata. Sa nimi ortocentr, ´srodek ciezko´sci oraz ´srodki okregów wpisanego i opi-

sanego na trójkacie. Kazde z przedstawionych twierdze´n popieram przeprowa-

dzonym przez siebie dowodem. Opisy bibliogra czne odnosza sie do literatury,

w której pó´zniej znalaz am dowody tych twierdze´n. W wiekszo´sci okaza y sie one

zblizone do prezentowanych przeze mnie pomys ów. Ponadto w rozdziale tym sfor-

mu owa am lemat o odcinku aczacym ´srodki dwóch boków trójkata. Poczatkowo

zrobi am to z my´sla o dowodzie istnienia ´srodka ciezko´sci, jednak w toku pisania

pracy okaza o sie, ze ma on o wiele wiecej zastosowa´n i cytuje go przy kolejnych

dowodach. Do podstawowych twierdze´n doda am twierdzenia o podziale pola na

równe cze´sci z wykorzystaniem punktów charakterystycznych (´srodka ciezko´sci

oraz ´srodkowych boków trójkata). Co prawda uzupe niajac moja prace o odno´sniki

bibliogra czne zauwazy am, ze twierdzenia te nie pojawiaja sie zbyt czesto w li-

teraturze, jednak mi wydawa y sie ciekawe i warte opisania. Kazde z nich zosa o

przeze mnie udowodnione.

Rozdzia ten wzbogaci am notka biogra czna o Leonahrdzie Eulerze przy okazji

wprowadzania de nicji prostej Eulera. Cytuje tu równiez twierdzenie zaczerpnie-

te z ksiazki Zetela o zalezno´sciach miedzy po ozeniem punktów charakterysty-

cznych. W tym przypadku dowód opar am o zamieszczony w ksiazce, jednak

bardzo znacznie go poszerzy am. Zainspirowana tym twierdzeniem siegne am po

iii

trójkat ortyczny i równiez dla niego wykaza am zalezno´sci po ozenia szczególnych

punktów.

Trzeci rozdzia mojej pracy zawiera informacje o okregach zwiazanych z trójkatem.

Na poczatek prezentuje czesto pomijane w literaturze okregi dopisane do trójkata.

Umie´sci am tu twierdzenie o dwusiecznych katów zewnetrznych. Poczatkowo sfor-

mu owa am i udowodni am je sama, gdyz uwaza am, ze jest ono niezbedne w po-

kazaniu po ozenia ´srodka okregu dopisanego. Pó´zniej znalaz am je w literaturze,

ale bez dowodu. Szczególna uwage w tym rozdziale po´swieci am okregowi dziewie-

ciu punktów oraz jego w asno´sciom. Przeprowadzi am szczególowy dowód istnie-

nia tego okregu oraz po ozenia jego ´srodka i d ugo´sci promienia. W dowodach

umie´sci am wiele rysunków, aby by y czytelne i atwo by o ´sledzi´c mój tok rozu-

mowania. Rozdzia ten zawiera równiez sformuowany przeze mnie lemat (wraz

z dowodem), który jest szczególnym przypadkiem lematu z rozdzia u 1.

Kolejny rozdzia po´swieci am prostym zwiazanym z trójkatem, zwanym prostymi

Cevy. Dwa najwazniejsze twierdzenia tego rozdzia u to twierdzenie Menelaosa

i Cevy, które zaczerpne am z ksiazki S. I. Zetela [17]. W literaturze spotka am

dwie wersje tych dowodów - wektorowa i bezwektorowa. Zdecydowa am sie na te

druga. Kazdy z dowodów przeprowadzi am dla warunku koniecznego i wystarcza-

jacego, ponadto dzielac je na podpunkty w zalezno´sci od po ozenia punktu prze-

ciecia prostych Cevy. Dowód drugiego z nich jest poprawiony w odniesieniu do

ksiazki Zetela, gdyz znalaz am tam b ad, polegajacy na wyciagnieciu b ednego

wniosku z zapisanej proporcji. Na zko´nczenie tego rozdzia u pracy da am twierdze-

nie dotyczace prostych Cevy - twierdzenie Van Aubela. Dowód jest zblizony do za-

wartego w ksiazce Zetela, jednak podzieli am go na wiecej przypadków i zrobi am

bardziej szczegó owo.

Piaty rozdzia to prezentacja charakterystycznych punktów trójkata, które nie zosta y

wymienione w rozdziale drugim, z uwagi na to, ze do dowodów potrzebne by y

twierdzenia zawarte w rozdziale czwartym. Sa to twierdzenie o punkcie Gergonne'a,

Nagela oraz twierdzenie Napoleona. Pierwsze z nich udowodni am z wykorzy-

staniem twierdzenia Cevy, co w znaczny sposób u atwi o mi wykazanie przecina-

nia sie trzech prostych w jednym punkcie. Idee dowodu twierdzenia Nagela zaczer-

pne am z ksiazki Zetela, jednak kilkuzdaniowy dowód zmieni am na niemal dwu-

stronicowy, gdyz ten zawarty w literaturze by moim zdaniem zbyt skrótowy i nie

zawiera wyja´snie´n podstawowych obserwacji. Dodatkowym wk adem w ten, jak

i w kolejny rozdzia jest próba odnalezienia rzeczywistych autorów twierdze´n.

W rozdziale 5 próbowa am odnale´z´c korzenie twierdzenia Napoleona i przekona´c

sie czy ówczesny w adca Francji by rzeczywi´scie wybitnym matematykiem.

Poszukujac materia ów do mojej pracy natkne am sie na przynajmniej cztery sposoby

dowodów twierdzenia kryjacego sie pod ta nazwa. W swojej pracy umie´sci am

tylko jeden z nich, wnikliwie przeze mnie przeanalizowany, nieco rozszerzony

i opisany.

Szósty rozdzia pracy to zebrane twierdzenia zwiazane z okregiem opisanym na

Przedmowa

trójkacie. Zawar am je na ko´ncu pracy, gdyz dopiero w tym miejscu moge skorzy-

sta´c ze wszystkich niezbednych twierdze´n potrzebnych do dowodów. Jednak jak

okaza o sie w trakcie pisania, to nie ich dowody sprawi y mi najwieksza tru-

dno´s´c, a odnalezienie faktycznego autora twierdzenia Simsona. Opisane losy tego

twierdzenia zajmuja obszerny wstep do tego rozdzia u. Na zako´nczenie prezentuje

kilka rysunków, które w miare przejrzysty sposób przedstawiaja omawiane

w pracy punkty linie i okregi zwiazane z trójkatem. Te, jak i wszystkie inne rysunki

zosta y wykonane przeze mnie w programie do rysowania CABRI, dostepnym w

internecie bez licencji.

Spis Tre´sci

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

vii

Wstep

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1 Wiadomo´sci wstepne

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

1.1 Podstawowe wiadomo´sci o trójkacie. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.2 Podobie´nstwo trójkatów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.3 Przydatne twierdzenia do obliczania d ugo´sci boków . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.3.1 Twierdzenie Pitagorasa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.3.2 Wzór cosinusów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.3.3 Wzór sinusów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

2 Najbardziej znane punkty charakterystyczne

. . . . . . . . . . . . . . . . . . . . . . . . . .

2.1 ´Srodek ciezko´sci . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

2.2 ´Srodek okregu opisanego . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

2.3 Ortocent . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

2.4 ´Srodek okregu wpisanego . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

2.5 Prosta Eulera . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

3 Najpopularniejsze okregi zwiazane z trójkatem

. . . . . . . . . . . . . . . . . . . . . . .

3.1 Okregi dopisane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

vii

Spis Tre´sci

viii

3.2 Okrag dzieweciu punktów . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

4 Proste Cevy

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

4.1 Twierdzenie Menelaosa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

4.2 Twierdzenie Cevy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

4.3 W asno´s´c prostych Cevy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

5 Szczególne punkty trójkata

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

5.1 Punkt Gergonne'a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59

5.2 Punkt Nagela. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

5.3 Twierdzenie Napoleona . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65

6 Twierdzenia zwiazane z okregiem opisanym na trójkacie

. . . . . . . . . . . .

6.1 Twierdzenie Simsona . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

6.2 Twierdzenie Lemoine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

6.3 Twierdzenie Salmona . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

7 Dodatki

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Bibliogra a

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

Wstep

Geometria, czyli nauka o gurach geometrycznych i zalezno´sciach miedzy nimi

powsta a juz w Starozytno´sci. Na poczatku by a ona pojmowana czysto praktycznie, na

potrzeby zmierzenia konkretnych przedmiotów czy odleg o´sci. Dopiero ok. IV wieku

p.n.e. zaczeto formuowa´c pierwsze twierdzenia, a takze podejmowa´c próby ich udowodnie-

nia.

Przedmiotem mojej pracy jest geometria trójkata, czyli jeden z dzia ów szeroko rozu-

mianej geometrii euklidesowej. Ograniczenie moich rozwaza´n do jednej gury geome-

trycznej, jej w a´sciwo´sci, szczególnych powiaza´n z okregami oraz liniami by o w a´sciwie

konieczne, ze wzgledu na to, ze kazdy trójkat posiada mnóstwo charakterystycznych pun-

któw oraz zwiazków z innymi gurami.

"Trójkat zawiera wiecej cudów na centymetr kwadratowy niz jakakolwiek inna dziedzina

matematyki." (C. Kimberling)

Jak zaobserwowa am piszac te prace rozwój geometrii mozna podzieli´c na trzy prze o-

mowe etapy. Pierwszy z nich nich przypada na Starozytno´s´c. Wówczas geometria, jak

i inne dziedziny nauki przezywa y wielki rozwój. Wówczas nie tylko powsta o najs yn-

niejsze twierdzenie dotyczace trójkatów - Pitagorasa, ale równiez twierdzenie Talesa

z Miletu, które pomog o w wielu obliczeniach. Jednak najwiekszym sukcesem ówczesnych

czasów by o matematyczne dzie o Euklidesa pt. "Elementy". Nie do´s´c, ze zawiera o ono

wszystkie aksjomaty dotyczace ówczesnej geometrii, to jeszcze porzadkowa o i zbiera o

matematyczna wiedze starozytno´sci.

Wstep

Drugi etap rozwoju geometrii przypisa abym na okres O´swiecenia. Wówczas pono-

wnie zaczeto interesowa´c sie geometria i bada´c szczególne w a´sciwo´sci trójkatów. Wtedy

w a´snie po raz pierwszy sformuowano i udowodniono szereg twierdze´n jakie umie´sci am

w pracy m.in. Twierdzenie Georgonne'a, Lemonie, Salmona.

Trzecia i ostatnia fala rozwoju geometrii rozpocze a sie moim zdaniem pod koniec

XX wieku, wraz z rozwojem technik informatycznych. Nowoczesne programy kompu-

terowe umozliwiaja prowadzenie bardzo dok adnych oblicze´n, za´s rozwój Internetu umozli-

wia publikowanie efektów pracy i szeroki do nich dostep. Ostatnim z odkrytych pun-

któw szczególnych trójkata, do którego uda o mi sie dotrze´c jest punkt Bailey'a, nazwany

tak na cze´s´c Profesora Bailey'a z Universytetu Evansville. Jest to przyk ad wspania ego

po aczenia wcze´sniejszych odkry´c ze wspó czesno´scia, gdyz wykazano, ze punkt Bayley'a

lezy na prostej Eulera [10].

Zatem wida´c, ze geometria trójkata nie jest dziedzina martwa i nadal sie rozwija.

W Internecie, i nie tylko mozemy ´sledzi´c dalsze jej losy i spodziewa´c sie , ze w ciagu

najblizszych lat lista szczególnych punktów trójkata z Encyklopedii Kinberlinga [10] wyd uzy

sie o kolejne pozycje.

Rozdzia 1

Wiadomo´sci wstepne

1.1 Podstawowe wiadomo´sci o trójkacie

De nicja 1

[14, str. 287] Trójkatem nazywamy wielokat o trzech bokach (inaczej,

domknieta cze´s´c p aszczyzny ograniczona amana zwyczajna zamknieta o trzech bokach).

De nicja 2 [14, str. 133] amana, której dwa kolejne odcinki nie leza na jednej prostej

oraz zaden punkt nie nalezy do wiecej jak dwóch odcinków nazywamy amana zwyczajna.

Jak wida´c z de nicji pierwsza wyjatkowa cecha jaka posiada trójkat w porównaniu

z innymi wielokatami, jest to, ze jest on zawsze gura wypuk a. Do jego zbudowania

potrzeba dok adnie trzech dowolnych odcinków spe niajacych nierówno´s´c trójkata.

De nicja 3 (nierówno´s´c trójkata) [16, str. 38] Suma d ugo´sci kazdych dwóch boków

trójkata jest zawsze wieksza od d ugo´sci trzeciego boku.

1.1 Podstawowe wiadomo´sci o trójkacie

W kazdym trójkacie jeden dowolnie wybrany bok nazywamy podstawa, a dwa po-

zosta e ramionami. W zalezno´sci od d ugo´sci boków trójkaty mozemy podzieli´c na:

róznoboczne - wszystkie boki róznej d ugo´sci,

równoramienne - dwa boki tej samej d ugo´sci,

równoboczne - wszystkie boki równej d ugo´sci.

Za´s dokonujac klasy kacji ze wzgledu na katy mamy:

rozwartokatne -posiadaja kat rozwarty,

prostokatne - posiadaja kat prosty,

ostrokatne - posiadaja wszystkie katy ostre.

Trójkat nie ma ´srodka symetrii, moze za´s mie´c o´s symetrii - dwie je´sli jest to trójkat

równoboczny, jedna, gdy równoramienny lub wcale w przypadku trójkata róznobocznego.

Kazdy trójkat posiada trzy wysoko´sci (odcinki opadajace z wierzcho ków pod katem

prostym na przeciwleg e podstawy lub ich przed uzenia) oraz trzy ´srodkowe (odcinki opada-

jace z wierzcho ków na ´srodek przeciwleg ego boku). W dowolny trójkat mozna wpisa´c

okrag (tak, aby mia dok adnie po jednym punkcie wspólnym z kazdym bokiem) oraz

mozna na nim opisa´c okrag (tak, aby przechodzi dok adnie przez trzy jego wierzcho ki).

1.3 Przydatne twierdzenia do obliczania d ugo´sci boków

1.2 Podobie ´nstwo trójkatów

Powiemy, ze dwa trójkaty sa do siebie podobne, jezeli spe niony jest przynajmniej jeden

z nastepujacych warunków [16, str. 40]:

bok - bok - bok (bbb) - D ugo´sci odpowiednich boków jednego trójkata sa

proporcjonalne do d ugo´sci boków drugiego.

bok - kat - bok (bkb) - D ugo´sci dwóch boków jednego trójkata sa proporcjonalne

do d ugo´sci dwóch boków drugiego, a katy zawarte miedzy nimi w obu trójkatach sa

takie same.

kat - kat - kat (kkk) - Miary katów jednego trójkata sa równe odpowiednim miarom

drugiego.

Powyzsze warunki sa równowazne.

Z podobie´nstwa trójkatów bede wielokrotnie korzysta´c przy dowodzeniu twierdze´n,

wówczas bede sie odwo ywa´c do przyjetych tu oznacze´n.

1.3 Przydatne twierdzenia do obliczania d ugo´sci boków

1.3.1 Twierdzenie Pitagorasa

Jednym z najbardziej znanych twierdze´n dotyczacych trójkata prostokatnego jest twierdze-

nie Pitagorasa. Cho´c w nazwie pojawia sie nazwisko s ynnego greckiego matematyka

i lozofa, to nie mozemy by´c pewni czy s usznie przypisuje sie jemu autorstwo tego

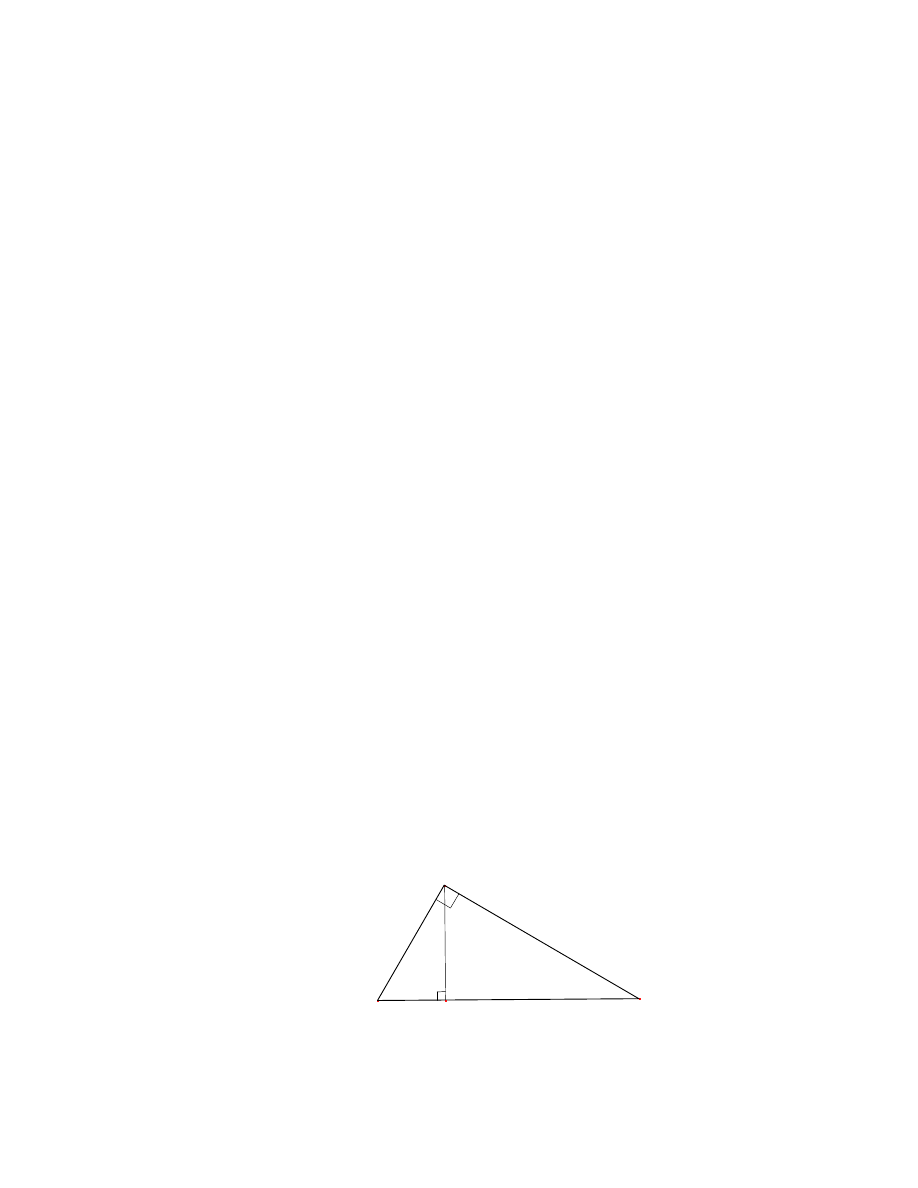
1.3 Przydatne twierdzenia do obliczania d ugo´sci boków

twierdzenia. Nie pozostawi on po sobie zadnych prac, które mog yby ´swiadczy´c, ze to

w a´snie on jako pierwszy sformuowa czy udowodni to twierdzenie. Hipotez jest kilka.

Jedne z nich mówia, ze to nie mistrz, a jeden z jego uczniów odkry to twierdzenie. Inne

za´s mówia, ze nawet je´sli to Pitagoras sformuowa je pierwszy, to nie by jego autorem,

gdyz by o ono znane jeszcze przed jego narodzinami w starozytnych Chinach, Indiach, czy

Babilonii.

Twierdzenie 1

(Pitagorasa) [16, str. 46] W dowolnym trójkacie prostokatnym suma

kwadratów d ugo´sci przyprostokatnych jest równa kwadratowi d ugo´sci przeciwprostoka-

tnej.

Szacuje sie, ze istnieje ponad 100 sposobów na udowodnienie tego twierdzenia,

przedstawie jednak tylko jeden z nich, opierajacy sie na podobie´nstwie trójkatów.

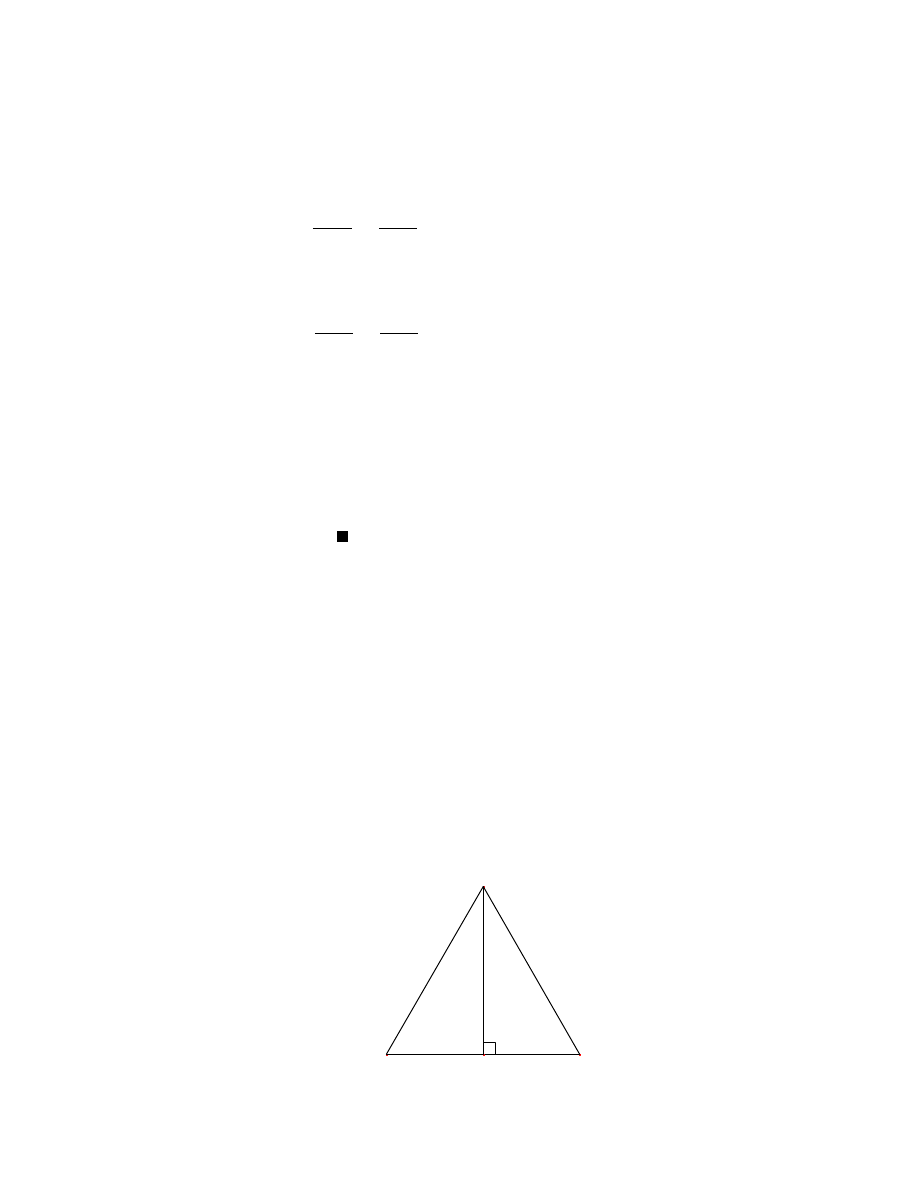
Dowód:

[16, str. 46] We´zmy dowolny trójkat prostokatny 4ABC i wykre´slmy w nim

wysoko´s´c opadajaca na przeciwprostokatna, jak na rysunku:

1.3 Przydatne twierdzenia do obliczania d ugo´sci boków

Zauwazmy, ze z podobie´nstwa trójkatów 4ABC i 4BDC (kkk) mamy:

jBDj

jBCj

jBCj
jABj

, skad jBCj

jBDj jABj ,

(1.1)

za´s z podobie´nstwa trójkatów 4ABC i 4ADC (kkk):

jADj

jACj

jACj
jABj

, skad jACj

jADj jABj .

(1.2)

Dodajac do siebie stronami równo´sci (1.1) i (1.2) otrzymamy:

jBCj

jACj

jBDj jABj + jADj jABj = jABj (jBDj + jADj) = jABj jABj ,

jABj

jBCj

jACj

co naleza o udowodni´c.

Przedstawie teraz krótkie zadanie na zastosowanie twierdzena Pitagorasa, którego

wynik wykorzystam w dalszej cze´sci mojej pracy.

Zadanie: Wyra´z d ugo´s´c wysoko´sci trójkata równobocznego w zalezno´sci od d u-

go´sci boku a.

Niech dany bedzie trójkat równoboczny o boku a. Narysujmy jedna z jego wysoko´sci

i oznaczmy jej d ugo´s´c przez h.

1.3 Przydatne twierdzenia do obliczania d ugo´sci boków

Oczywi´scie wysoko´s´c opada na podstawe pod katem prostym, dzielac ja na po owy (bo

trójkat jest równoboczny). Zatem stosujac twierdzenie Pitagorasa mamy:

1
2

= a

1
4

3
4

h =

1.3.2 Wzór cosinusów

Twierdzenie cosinusów czesto zwane jest uogólnieniem twierdzenia Pitagorasa, gdyz mozna

je stosowa´c dla dowolnego trójkata, niekoniecznie prostokatnego.

Twierdzenie 2 (cosinusów) [15, str. 21], [13, str. 60] Niech a, b, c beda d ugo´sciami boków

dowolnego trójkata, za´s niech bedzie miara kata zawartego miedzy bokami o d ugo´sciach

i b. Wówczas prawdziwa jest równo´s´c:

= a

+ b

2ab cos

(1.3)

Uwaga: Zauwazmy, ze je´sli zastosujemy to twierdzenie do trójkata prostokatnego, to wó-

wczas = 90 . Poniewaz cos90 = 0, to z (1.3 )otrzymamy:

= a

+ b

czyli twierdzenie Pitagorasa.

1.3 Przydatne twierdzenia do obliczania d ugo´sci boków

1.3.3 Wzór sinusów

Twierdzenie 3 (sinusów) [15, str. 24] Niech a, b, c beda d ugo´sciami boków dowo-

lnego trójkata, za´s , , miarami katów lezacymi odpowiednio naprzeciwko tych boków.

Wówczas prawdziwy jest wzór:

sin

(W dowolnym trójkacie stosunki d ugo´sci boków, do sinusów katów lezacych naprzeciwko

nich sa sta e.)

Rozdzia 2

Najbardziej znane punkty charakterystyczne

Jak juz wspomnia am we wstepie mojej pracy, punktów o szczególnych w a´sciwo-

´sciach, w dowolnym trójkacie mozemy zidenty kowa´c ponad tysiac. W tym rozdziale

chcia abym przedstawi´c kilka najpopularniejszych, które mozemy odnale´z´c w kazdym

trójkacie, posiadajac zaledwie podstawowa wiedze z dziedziny geometrii euklidesowej.

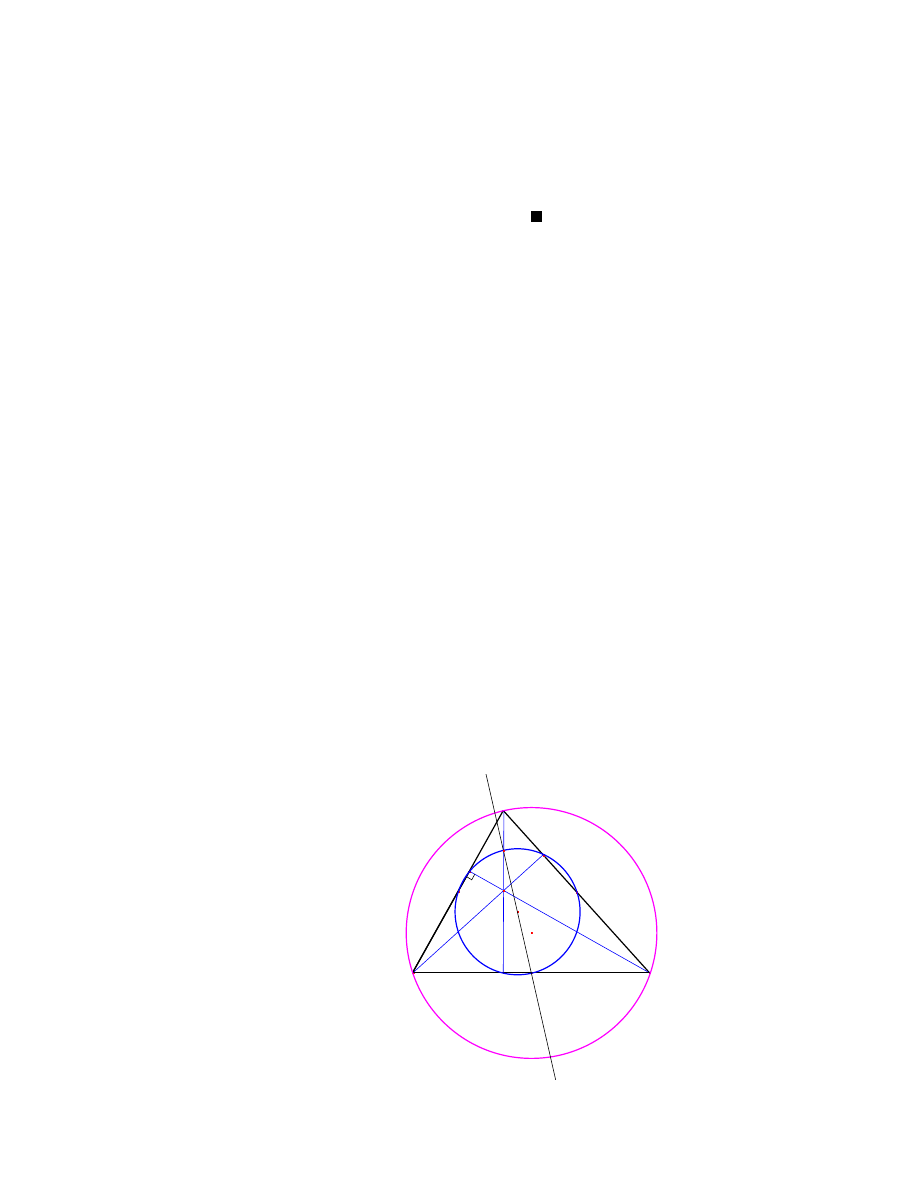
W rozdziale tym przedstawie m. in. ´srodek ciezko´sci, ortocent i ´srodek okregu opisanego,

które jak odkry Euler leza (wraz z ´srodkiem okregu dziewieciu punktów) na jednej prostej,

zwanej prosta Eulera.

2.1 ´Srodek ciezko´sci

Lemat 1 [9, str. 163] Odcinek aczacy ´srodki dwóch boków trójkata jest równy co do

d ugo´sci po owie trzeciego boku i jest do niego równoleg y.

Dowód:

[9, str.163] We´zmy dowolny trójkat 4ABC. ´Srodki boków AC i BC

oznaczmy odpowiednio przez K i L.

jKCj =

1
2

jACj

jLCj =

1
2

jBCj

2.1 ´Srodek ciezko´sci

Zauwazmy, ze kat przy wierzcho ku C jest jednakowy dla trójkatów 4ABC i 4KLC.

Ponadto ich ramiona sa proporcjonalne, bo z za ozenia mamy, ze:

jKCj

jACj

1
2

jLCj

jBCj

1
2

Stad i z drugiej cechy podobie´nstwa trójkatów (bkb) otrzymujemy, ze trójkaty 4ABC

i 4KLC sa podobne, za´s skala ich podobie´nstwa jest równa k =

1
2

. Zatem pozosta e boki

trójkatów AB i KL sa równiez proporcjonalne i zachodzi:

jKLj =

1
2

jABj :

Pokazemy teraz, ze odcinki AB i KL sa równoleg e. Z podobie´nstwa trójkatów 4ABC

i 4KLC widzimy, ze prawdziwa jest proporcja:

jKCj

jKLj

jACj
jABj

Zatem na mocy twierdzenia odwrotnego do twierdzenia Talesa otrzymujemy, ze odcinki

i AB sa równoleg e.

Twierdzenie 4

(o ´srodkowych) [15, str. 47], [13, str. 53], [7, str. 39] ´Srodkowe

trójkata przecinaja sie w jednym punkcie, zwanym ´srodkiem ciezko´sci trójkata. ´Srodek

ciezko´sci dzieli kazda z ´srodkowych w stosunku 2 : 1, przy czym d uzszy odcinek aczy

´srodek ciezko´sci z wierzcho kiem trójkata.

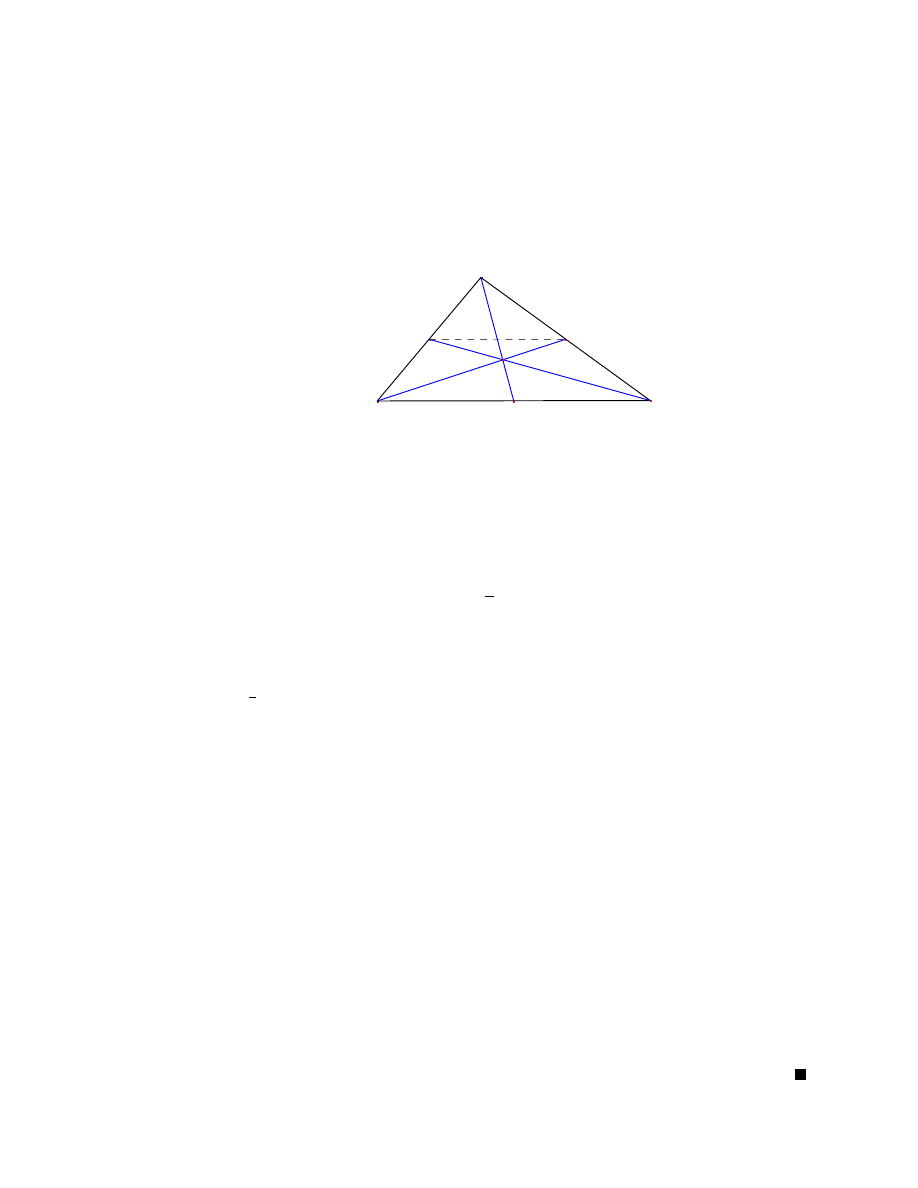
2.1 ´Srodek ciezko´sci

Dowód:

[15, str. 47] Niech dany bedzie dowolny trójkat 4ABC oraz jego ´srodkowe

, BB

i CC

. Oznaczmy punkt przeciecia ´srodkowych AA

i BB

przez O.

Z lematu 1 mamy, ze odcinki AB i A

sa do siebie równoleg e oraz

jAA

j =

1
2

jABj :

Zauwazmy, ze trójkaty 4ABO i 4AB

sa do siebie podobne (kkk), a skala ich podobie´nstwa

wynosi k =

1
2

. Zatem mamy:

j = jBOj ,

j = jAOj

czyli ´srodkowe trójkata przecinaja sie w stosunku 2 : 1. Przeprowadzajac analogiczne

rozumowanie dla ´srodkowych AA

oraz CC

dochodzimy do wniosku, ze:

j = jCOj ,

j = jAOj ,

a zatem punkt O jest punktem przeciecia wszystkich trzech ´srodkowych trójkata 4ABC.

2.1 ´Srodek ciezko´sci

Twierdzenie 5 [5, str. 8] ´Srodkowe trójkata dziela go na sze´s´c mniejszych trójkatów

o równych polach.

Dowód:

Niech dany bedzie dowolny trójkat 4ABC oraz jego ´srodkowe AQ, BR

i CP . Oznaczmy punkt przeciecia ´srodkowych przez O.

Oczywi´scie pola trójkatów 4AP O i 4P BO, 4BQO i 4QCO, a takze 4CRO i 4ARO

sa równe, poniewaz ich podstawy oraz wysoko´sci sa równej d ugo´sci. Zauwazmy pona-

dto, ze z tego samego powodu równe sa pola trójkatów 4AP C i 4P BC, które mozemy

wyrazi´c poprzez odpowiednie sumy pól wcze´sniej wymienionych trójkatów. Tak wiec:

4AP C

= P

4AP O

+ P

4ARO

+ P

4CRO

= P

4AP O

+ 2P

4ARO

4P BC

= P

4P BO

+ P

4BQO

+ P

4QCO

= P

4P BO

+ 2P

4BQO

Natomiast z równo´sci tych pól mamy dalej:

4AP O

+ 2P

4ARO

= P

4P BO

+ 2P

4BQO

2.1 ´Srodek ciezko´sci

Wykorzystujac równo´s´c pól trójkatów 4AP O i 4P BO oraz dzielac powyzsza równo´s´c

przez 2 dostajemy:

4ARO

= P

4BQO

Postepujac analogicznie dla trójkatów 4BQA i 4QCA pokazaliby´smy, ze:

4ARO

= P

4AP O

a dalej z przechodnio´sci okaza o by sie, ze wszystkie pola sa sobie równe.

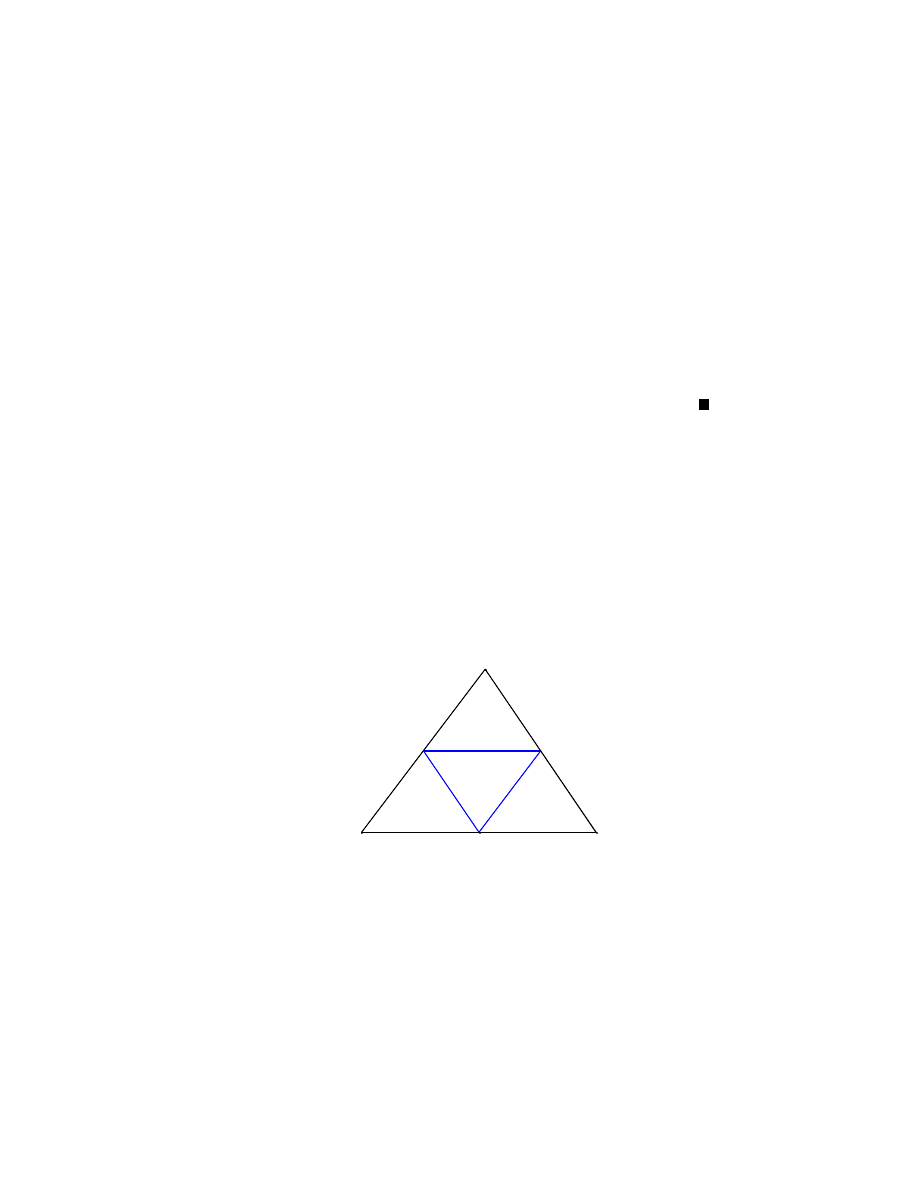
Twierdzenie 6

Odcinki aczace ´srodki boków dowolnego trójkata dziela go na cztery

mniejsze trójkaty o równych polach.

Dowód:

We´zmy dowolny trójkat 4ABC oraz ´srodki jego boków P , Q, R. Po aczmy

je odcinkami, tak aby powsta trójkat 4P QR.

Na mocy lematu 1 dostajemy nastepujace równo´sci:

jAP j = jP Bj = jRQj

jBQj = jQCj = jRP j

jCRj = jRAj = jP Qj ,

2.2 ´Srodek okregu opisanego

czyli odcinki P Q, QR i RP podzieli y trójkat 4ABC na cztery trójkaty podobne (bbb),

a wiec o takich samych polach.

2.2 ´Srodek okregu opisanego

´Srodek okregu opisanego na dowolnym trójkacie pokrywa sie z punktem przeciecia symetral-

nych jego boków.

Twierdzenie 7

(o symetralnych) [15, str. 30], [13, str. 55], [16, str. 114], [7, str. 39]

Symetralne boków dowolnego trójkata przecinaja sie w jednym punkcie.

Dowód:

[15, str. 30] We´zmy dowolny trójkat 4ABC. Narysujmy symetralne boków

i BC, a punkt ich przeciecia oznaczmy przez S.

2.3 Ortocent

Narysujmy odcinki aczace punkt S z wierzcho kami trójkata 4ABC. Zauwazmy, ze

w trójkatach 4ASB i 4BSC symetralna boku pe ni role wysoko´sci i dzieli podstawy tych

trójkatów na po owy. Wynika stad, ze sa to trójkaty równoramienne, zatem:

jASj = jBSj

oraz

jBSj = jCSj .

Z przechodnio´sci dostajemy jako wniosek, iz:

jASj = jCSj .

´Swiadczy to o tym, ze trójkat 4ASC jest równiez równoramienny, a zatem jego wysoko´s´c

poprowadzona z wierzcho ka S dzieli podstawe AC na po owy, a w zwiazku z tym musi

zawiera´c sie w symetralnej boku AC. Pokazali´smy wiec, ze wszystkie symetralne boków

trójkata 4ABC przecinaja sie w jednym punkcie.

2.3 Ortocent

Twierdzenie 8 [13, str. 54], [9, str. 164], [8, str. 84] W dowolnym trójkacie wysoko´sci,

lub ich przed uzenia przecinaja sie w jednym punkcie.

Dowód:

[9, str. 165] Zauwazmy, ze w przypadku trójkata prostokatnego twierdzenie

to wynika w sposób oczywisty. Dwie wysoko´sci pokrywaja sie z bokami, a trzecia musi

2.3 Ortocent

zawsze wychodzi´c z ich wspólnego wierzcho ka.

Rozwazmy zatem przypadek gdy trójkat jest ostrokatny lub rozwartokatny. Poniewaz

dowód wyglada analogicznie, to przeprowadze go dla przypadku trójkata ostrokatnego.

We´zmy dowolny trójkat ostrokatny 4ABC i narysujmy jego wysoko´sci.

Nastepnie poprowad´zmy przez wierzcho ki trójkata 4ABC proste równoleg e do przeci-

wleg ych podstaw. Punkty przeciecia narysowanych prostych oznaczmy odpowiednio A

, C

(jak na rysunku). Po krótkiej analizie katów tak otrzymanych trójkatów zauwazamy,

2.4 ´Srodek okregu wpisanego

ze trójkaty: 4ABC, 4AB

, 4CA

, 4ABC

sa do siebie przystajace. Stad wynika

równo´s´c nastepujacych odcinków:

j = jCA

j = jBC

j = jAB

j :

(2.4)

Poniewaz rysowane przez nas proste by y rónoleg e do boków, to obserwujemy, ze wysoko´sci

trójkata 4ABC sa prostopad e do odcinków A

, B

, C

. Z tego oraz równo´sci (2.4)

wynika, ze proste zawierajace wysoko´sci trójkata 4ABC sa jednocze´snie symetralnymi

boków trójkata 4A

. Na podstawie twierdzenia o symetralnych wiemy, ze musza

one przecina´c sie w jednym punkcie. Zatem pokazali´smy, ze wysoko´sci trójkata 4ABC

przecinaja sie w jednym punkcie.

De nicja 4 [13, str. 55], [7, str. 39] Punkt przeciecia prostych zawierajacych wysoko´sci

trójkata nazywamy jego ´srodkiem ortycznym, ortocentrem lub ortocentrum.

Uwaga: Jezeli bedziemy rozwaza´c trójkat ostrokatny, to ortocent bedzie zawsze leza

wewnatrz trójkata. Na zewnatrz gdy bedzie to trójkat rozwartokatny. Za´s w przypadku

trójkata prostokatnego ortocent pokryje sie z wierzcho kiem przy kacie prostym tego trójkata.

2.4 ´Srodek okregu wpisanego

´Srodek okregu wpisanego w dowolny trójkat pokrywa sie z punktem przeciecia dwusie-

cznych jego katów wewnetrznych.

2.4 ´Srodek okregu wpisanego

Twierdzenie 9 (o dwusiecznych katów wewnetrznych) [9, str.116], [7, str.39], [5, str.10]

Dwusieczne katów wewnetrznych trójkata przecinaja sie w jednym punkcie.

Dowód:

Niech dany bedzie dowolny trójkat 4ABC, dwusieczna kata ^A przecinajaca

bok BC w punkcie Q oraz dwusieczna kata

^B przecinajaca bok AC w punkcie R.

Oznaczmy punkt przeciecia prostych AQ i BR przez W . Poniewaz W lezy na dwusiecznej

kata

^A, to jest on jednakowo odleg y od boków AC i AB trójkata 4ABC. Analogicznie,

poniewaz W lezy na dwusiecznej kata

^B, to jest on jednakowo odleg y od boków AB

i BC. A zatem punkt W znajduje sie w równej odleg o´sci od boków BC i AC, zatem lezy

na dwusiecznej kata

^C. Stad wniosek, ze dwusieczne wszystkich katów wewnetrznych

trójkata przecinaja sie w jednym punkcie.

Uwaga [16, str. 47]: Poniewaz w trójkacie równobocznym wysoko´sci pokrywaja sie

z symetralnymi boków, dwusiecznymi katów zewnetrznych oraz ´srodkowymi, to ortocent

pokrywa sie ze ´srodkiem okregu opisanego, wpisanego, a takze z ´srodkiem ciezko´sci.

2.5 Prosta Eulera

Lehonard Euler by wybitnym szwajcarskim matematykiem (1707-1783), który dokona

waznych odkry´c niemal w kazdej dziedzinie matematyki, w tym równiez geometrii. Urodzi

sie w Bazyleii i tam tez pobiera pierwsze lekcje matematyki od samego Johanna Bernoul-

liego. Tytu magistra zdoby w wieku zaledwie 16 lat, a majac 20 zosta zaproszony do

Akademii w Sankt Petersburgu, gdzie przebywa do roku 1741. Sciezka jego naukowej

kariery prowadzi dalej przez Berlin, gdzie pracowa do 1766 roku. Ostatnie lata swojego

zycia spedzi w Rosji, dokad z Berlina sprowadzi a go po latach Katarzyna Wielka. O tym,

ze Euler by genialnym matematykiem moze ´swiadczy´c liczba wydanych przez niego prac

naukowych - za jego zycia opublikowano 473 z nich, a krótko po jego ´smierci kolejne 200.

acznie opublikowano ich az 734. Co wiecej nalezy wspomnie´c, ze Euler tworzy swoje

matematyczne dzie a mimo upo´sledzenia. W wieku 28 lat straci wzrok na jedno oko,

a w 1766 roku o´slep zupe nie.

Przedstawie teraz twierdzenie odkryte przez Eulera, dotyczace szczególnej prostej w trójka-

cie, na cze´s´c autora, zwana prosta Eulera.

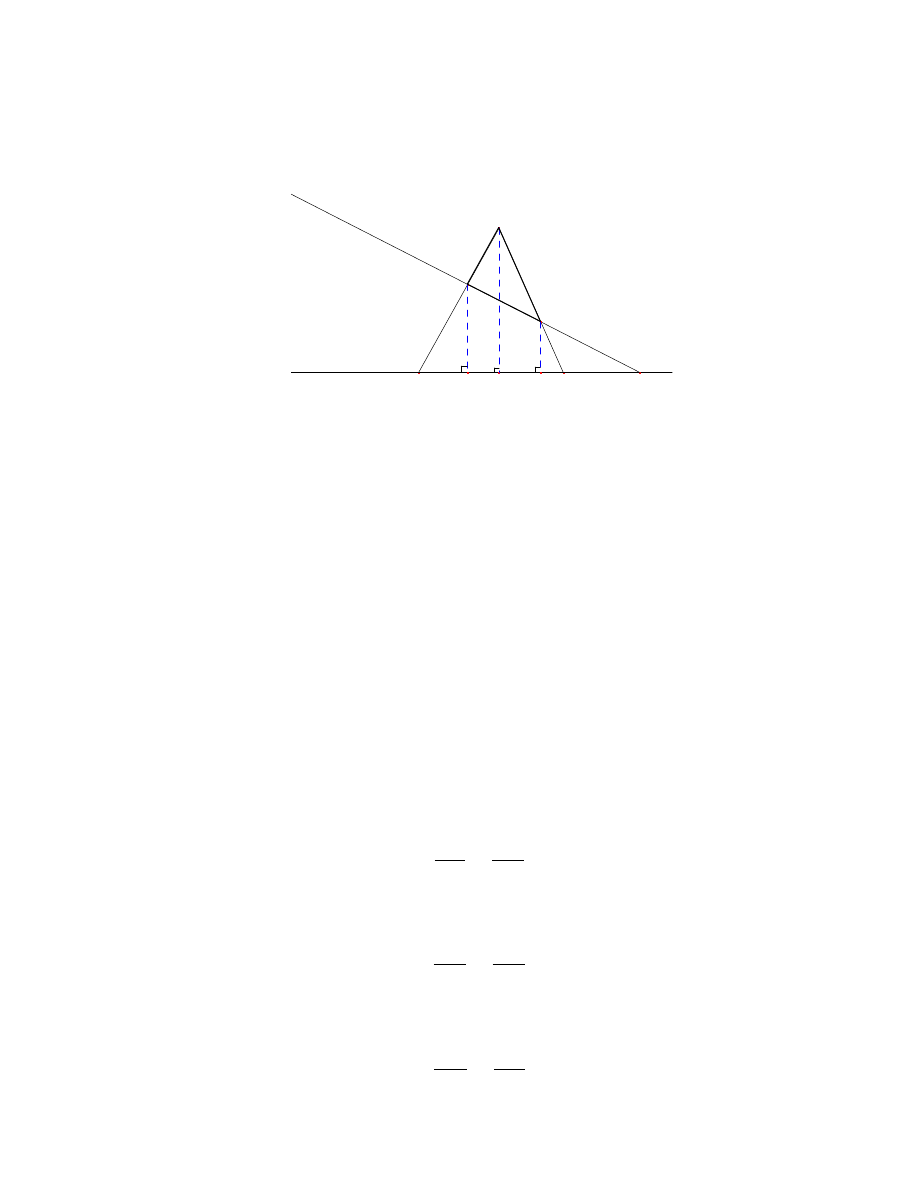
De nicja 5 [17, str. 54] W dowolnym trójkacie prosta przechodzaca przez ortocentr, ´srodek

ciezko´sci oraz ´srodek okregu opisanego na tym trójkace nazywamy prosta Eulera.

Twierdzenie 10

(prosta Eulera) [5, str. 19] W dowolnym trójkacie jego ortocentr,

´srodek ciezko´sci oraz ´srodek okregu opisanego na tym trójkace sa wspó liniowe, przy czym

2.5 Prosta Eulera

odleg o´s´c ortocentru od ´srodka ciezko´sci jest dwa razy wieksza niz ´srodka ciezko´sci od

´srodka okregu opisanego.

Dowód:

[5, str. 18-19] We´zmy dowolny trójkat 4ABC. Wyznaczmy punkty ´srodkowe

jego boków i nazwijmy je odpowiednio P , Q, R. Nastepnie po aczmy je odcinkami.

Zauwazmy, ze tak powsta y trójkat 4P QR jest podobny (bbb) do trójkata 4ABC w skali

k =

1
2

, poniewaz na mocy lematu 1 d ugo´sci jego boków sa równe po owie d ugo´sci boków

trójkata 4ABC. Narysujmy teraz ´srodkowe w trójkacie 4ABC - AQ, BR, CP .

Z twierdzenia 4 wiemy, ze przecinaja sie one w punkcie O, zwanym ´srodkiem ciezko´sci.

Dorysujmy teraz symetralne boków trójkata 4ABC. Z twierdzenia 7 mamy, ze przecinaja

2.5 Prosta Eulera

sie one w punkcie S.

Zauwazmy, ze zawieraja one wysoko´sci trójkata 4P QR (gdyz jego boki sa równoleg e

do boków trójkata 4ABC, a symetralne jako prostopad e do boków trójkata 4ABC, sa

równiez prostopad e do boków trójkata 4P QR). Stad punkt S jest ortocentrum trójkata

4P QR. Nanie´smy teraz na rysunek wysoko´sci trójkata 4ABC.

2.5 Prosta Eulera

Na mocy twierdzenia 8 wysoko´sci przecinaja sie w punkcie H. Po aczmy teraz odcinkami

punkty H i O oraz O i S i przyjrzyjmy sie powsta ym trójkatom 4CHO i 4P SO,

Poniewaz trójkaty 4ABC i 4P QR sa podobne w skali k =

1
2

, to:

1
2

jCHj = jP Sj .

Z twierdzenia 4 wynika, ze:

1
2

jCOj = jP Oj .

Zauwazmy, ze ´srodkowa boku AB jest równoleg a do wysoko´sci opadajacej z wierzcho ka

na ten bok. Te dwa odcinki równoleg e po aczone sa odcinkiem CP , stad

^HCO = ^OPS

jako naprzemianleg e wewnetrzne. Z powyzszych rozwaza´n wynika wiec prosty wniosek,

ze trójkaty 4CHO i 4P SO sa podobne (bkb), a wiec ich boki sa proporcjonalne, a katy

równe. Zatem:

1
2

jHOj = jSOj

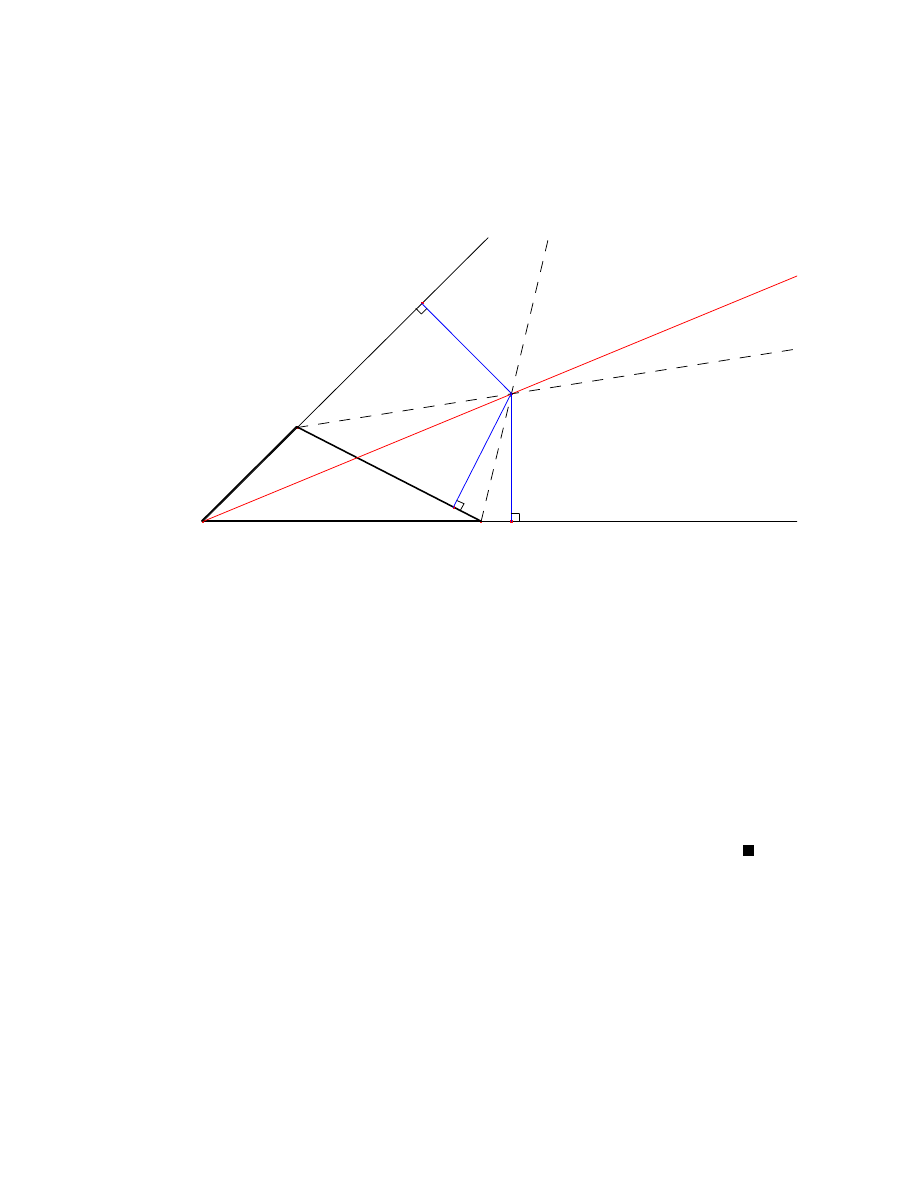
2.5 Prosta Eulera

oraz punkty H, O i S sa wspó liniowe.

De nicja 6 [5, str. 9] Trójkatem ortycznym nazywamy trójkat zwiazany z dowolnym

trójkatem, tak ze jego wierzcho ki sa spodkami wysoko´sci tego trójkata.

Twierdzenie 11 [5, str. 17] Jezeli mamy dowolny trójkat 4ABC i zwiazany z nim trójkat

ortyczny 4P QR, to ortocent trójkata 4ABC pokrywa sie z ´srodkiem okregu wpisanego

w trójkat 4P QR.

Dowód:

[4] Aby udowodni´c to twierdzenie nalezy pokaza´c, ze wysoko´sci trójkata

4ABC pokrywaja sie z dwusiecznymi trójkata 4P QR. We´zmy dowolny trójkat 4ABC

i narysujmy w nim wysoko´sci. Ich spodki oznaczmy przez P , Q R i po aczmy tak, aby

utworzy y trójkat ortyczny.

2.5 Prosta Eulera

Zauwazmy, ze trójkaty 4BQH i 4ARH sa do siebie podobne (kkk), gdyz oba sa prosto-

katne, a jeden z ich katów jest równej miary, jako wierzcho kowy, stad:

^RAH = ^QBH .

Przyjrzyjmy sie teraz czworokatowi ARHP . Zauwazmy, ze jego dwa przeciwleg e katy

^ARH oraz ^HPA sa sobie równe i maja po 90 . Poniewaz suma katów w czworoka-

cie wypuk ym wynosi 360 , to suma dwóch pozosta ych jego katów musi wynosi´c 180 .

Zatem warunek konieczny aby opisa´c na tym czworokacie okrag jest spe niony. Gdy juz

opiszemy okrag obserwujemy, ze katy

^RAH i ^RPH, sa równe jako wpisane

w okrag oparte na tym samym uku RH. Przeprowadzajac analogiczne rozumowanie dla

czworokata BQHP , okazuje sie, ze równiez katy

^QBH i ^QPH sa równe jako wpisane

w okrag oparte na tym samym uku HQ: A zatem, poniewaz równe by y katy

^RAH

^QBH, to z przechodnio´sci równo´sci dostajemy, ze:

^RPH = ^QPH .

Pokazali´smy wiec, ze wysoko´s´c CP trójkata 4ABC jest jednocze´snie dwusieczna kata

^RPQ trójkata 4PQR. Analogicznie udowodniliby´smy, ze wszystkie wysoko´sci trójkata

4ABC pokrywaja sie z dwusiecznymi trójkata 4P QR, a zatem ortocent pokrywa sie

z ´srodkiem okregu wpisanego.

Rozdzia 3

Najpopularniejsze okregi zwiazane z

trójkatem

Z pewno´scia gdyby zorganizowa´c plebiscyt na najpopularniejsze okregi majace zwiazek

z trójkatem zwyciezy yby wpisany i opisany. A juz ma o kto wymieni by okregi dopisane,

których istnienie wynika przeciez intuicyjne.

okrag wpisany

okrag opisany

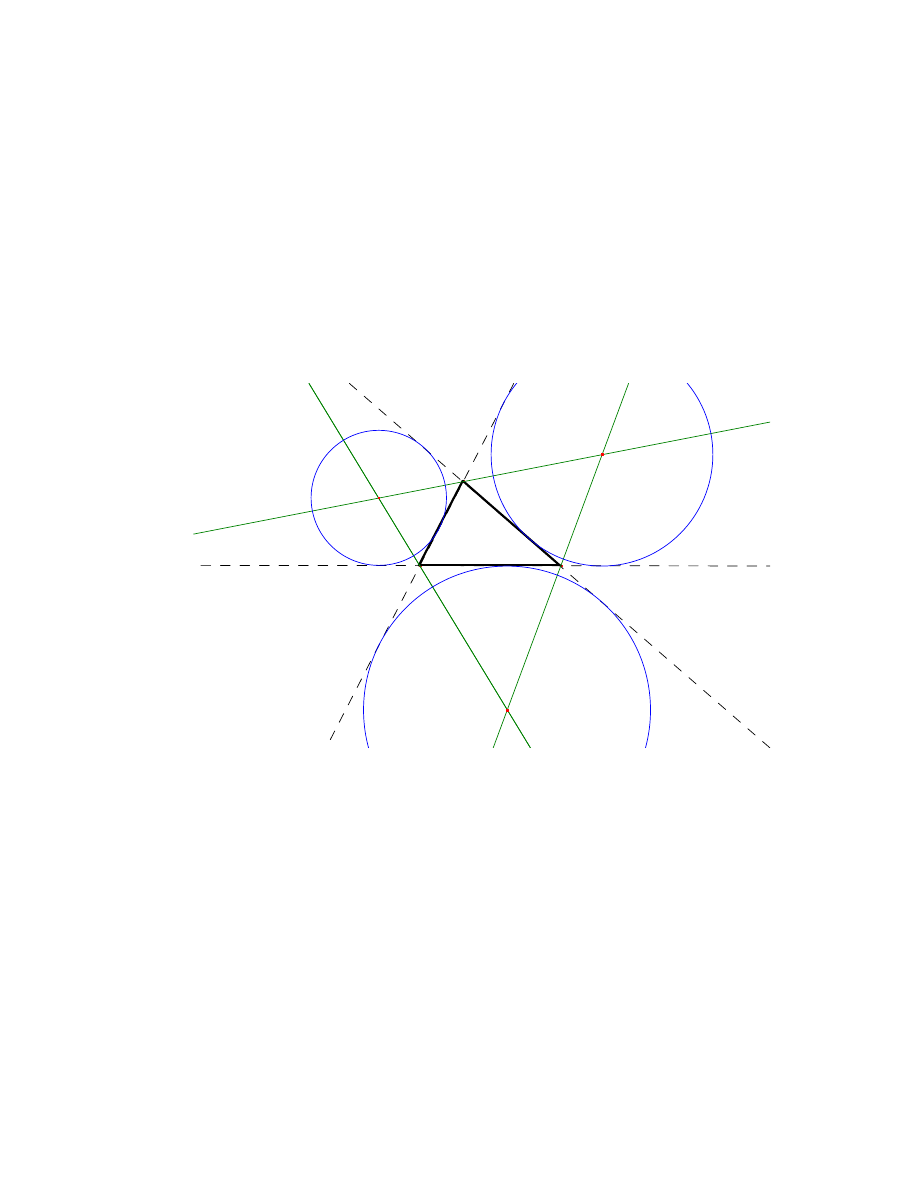
3.1 Okregi dopisane

De nicja 7 [6, str. 11], [5, str. 12] Okregiem dopisanym do trójkata nazywamy okrag

styczny do jednego z boków tego trójkata oraz do przed uze´n pozosta ych.

okregi dopisane

´Srodek okregu dopisanego lezy w punkcie przeciecia dwusiecznych katów zewnetrznych

i kata wewnetrznego. Istnienia tego punktu dowodzi nastepujace twierdzenie, które zosta o

udowodnione przeze mnie w ramach uzupe nienia zgromadzonych materia ów.

Twierdzenie 12 [8, str. 86] Dwusieczne katów zewnetrznych przy dwóch wierzcho kach

dowolnego trójkata przecinaja sie w punkcie nalezacym do dwusiecznej kata wewnetrznego

przy trzecim jego wierzcho ku.

3.2 Okrag dzieweciu punktów

Dowód:

We´zmy dowolny 4ABC. Narysujmy dwusieczne katów zewnetrznych przy

wierzcho kach B i C. Oznaczmy punkt ich przeciecia przez D.

Zauwazmy, ze z tego, iz punkt D lezy na dwysiecznej kata

^C wynika, ze jest równo

oddalony od prostych AC i BC. Za´s z po ozenia na dwusiecznej kata

^B, ze jest tak samo

odleg y od prostych AB i BC. A zatem wynika, ze punkt D jest w jednakowej odleg o´sci

od prostych zawierajacych boki AC i AB trójkata 4ABC. Stad i z w asno´sci dwusiecznej

mamy, ze punkt D lezy na dwusiecznej kata wewnetrznego

^A trójkata 4ABC.

3.2 Okrag dzieweciu punktów

Poczatkowo odkryty i opublikowany w 1765r. w Petersburgu przez Eulera, nastepnie

zapomniany i znów w 1822r. wy oniony na ´swiat o dzienne przez niemieckiego Pro-

fesora Matematyki Karla Feuerbacha - okrag zawierajacy dziewie´c szczególnych punk-

3.2 Okrag dzieweciu punktów

tów trójkata - ´srodki boków, spodki wysoko´sci oraz po owy odcinków utworzonych przez

wierzcho ki i ortocentrum. Ze wzgledu na te w a´snie dziewie´c szczególnych punktów,

okrag ten popularnie zwany jest okregiem dziewieciu punktów. (Jednakze okazuje sie, ze

nie sa to jedyne charakterystyczne punkty trójkata przez które przechodzi.) W literaturze

okrag ten spotykamy równiez pod nazwa okregu Feuerbacha.

Wykaze teraz, ze istotnie zawiera on wymienione punkty.

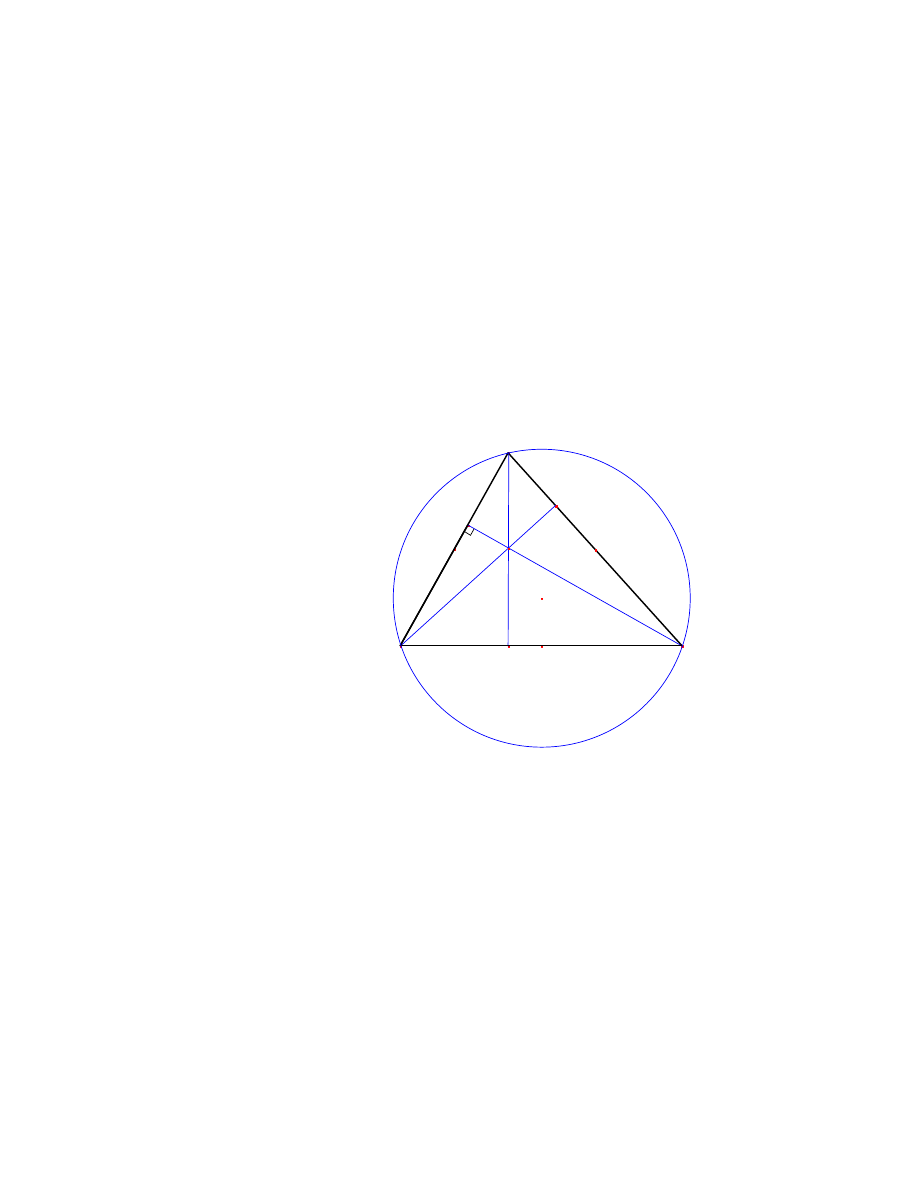
Lemat 2 W dowolnym trójkacie prostokatnym d ugo´s´c odcinka aczacego wierzcho ek przy

kacie prostym z ´srodkiem przeciwprostokatnej jest równa po owie jej d ugo´sci.

Dowód:

We´zmy dowolny trójkat prostokatny 4ABC. Oznaczmy ´srodki jego boków

, BC i CA odpowiednio przez P , Q, R.

Na mocy lematu 1 mamy, ze odcinek aczacy ´srodki dwóch boków jest równoleg y do

trzeciego i co do d ugo´sci równy jego po owie. Zatem:

jRQj = jAP j = jP Bj ,

3.2 Okrag dzieweciu punktów

jCRj = jRAj = jQP j .

Narysujmy odcinek AQ. Zauwazmy, ze trójkaty 4AQP i 4BP Q sa do siebie podobne

(bkb), stad jAQj = jQBj.

De nicja 8 (punkty Eulera) [17, str. 52] W dowolnym trójkacie punkty lezace na jego

wysoko´sciach i dzielace odleg o´s´c od ortocentru do wierzcho ka na pó nazywamy pun-

ktami Eulera.

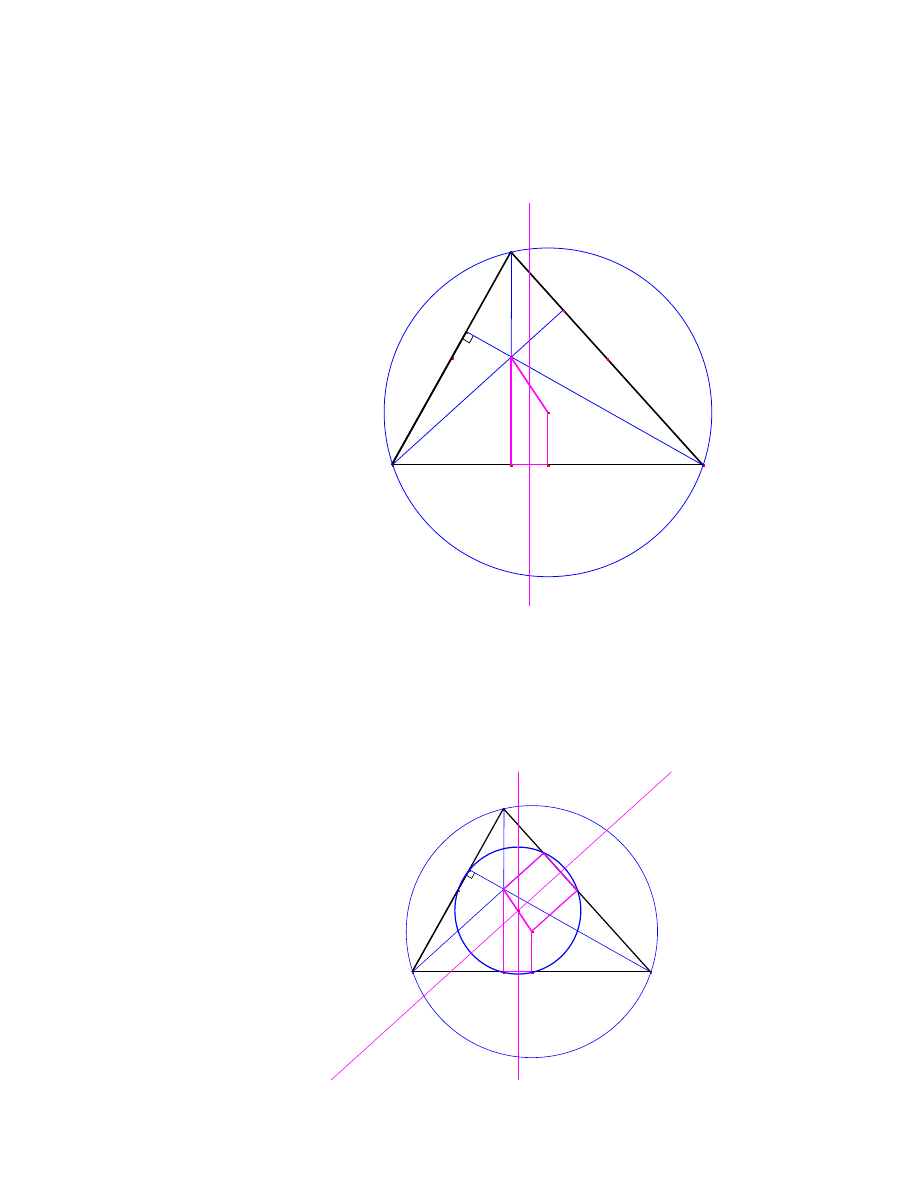
Twierdzenie 13 (okrag dziewieciu punktów) [17, str. 52], [5, str. 20] W dowolnym trójka-

cie ´srodki jego boków, spodki wysoko´sci i punkty Eulera leza na jednym okregu zwanym

okregiem dziewieciu punktów.

Dowód:

[17, str. 52-53] We´zmy dowolny trójkat 4ABC. ´Srodki jego boków

oznaczmy odpowiednio przez P , Q, R , za´s spodki wysoko´sci przez A

, B

, C

, jak na

rysunku:

3.2 Okrag dzieweciu punktów

Oczywi´scie na kazdym trójkacie mozemy opisa´c okrag, zatem równiez na trójkacie 4P QR.

Stosujac lemat 2 do trójkata 4ABB

otrzymujemy, ze:

R =

1
2

Za´s z lematu 1, dla trójkata 4ABC mamy:

QP =

1
2

oraz P R k AC.

Przyrównujac do siebie te dwa równania otrzymamy równo´s´c:

R = QP

Stad zauwazamy, ze czworokat B

QRP

jest trapezem równoramiennym, a zatem okrag

przechodzacy przez punkty P , Q, R przechodzi równiez przez punkt B

, gdyz na tym

trapezie mozemy opisa´c okrag. W analogiczny sposób mozemy udowodni´c, ze do tego

okregu naleza punkty A

i C

. Oznaczmy teraz przez D, E i F punkty ´srodkowe odcinków

, BH i CH. Pokazemy teraz, ze punkt F równiez nalezy do rozwazanego okregu.

Stosujac lemat 1 dla trójkata 4BHC, otrzymujemy, ze F P k HB.

3.2 Okrag dzieweciu punktów

Odcinek HB zawiera sie w wysoko´sci BB

, zatem jest prostopad y do odcinka AC.

W odcinku AC zawiera sie za´s odcinek QB

, równoleg y do RP , co pokaza am w pier-

wszej cze´sci dowodu. Stad otrzymujemy, ze RP ? F P . Analogicznie, stosujac lemat 1

dla trójkata 4AHC, otrzymujemy, ze QF k AH.

Odcinek AH zawiera sie w wysoko´sci AA

, zatem jest prostopad y do odcinka BC. Za´s

odcinek BC, równoleg y do QR. Stad otrzymujemy, ze F Q ? QR. Pokazali´smy za-

tem, ze w czworokacie F QRP , katy lezace naprzeciwko siebie

^Q i ^P maja po 90 .

Poniewaz czworokat F QRP jest wypuk y, to suma jego katów musi wynosi´c 360 , zatem

suma katów

^F i ^R wynosi 180 , stad na tym czworokacie mozna opisa´c okrag i jest

nim rozwazany przez nas okrag opisany na trójkacie 4P QR (bo przez dowolne 3 punkty

moze przechodzi´c tylko jeden okrag).

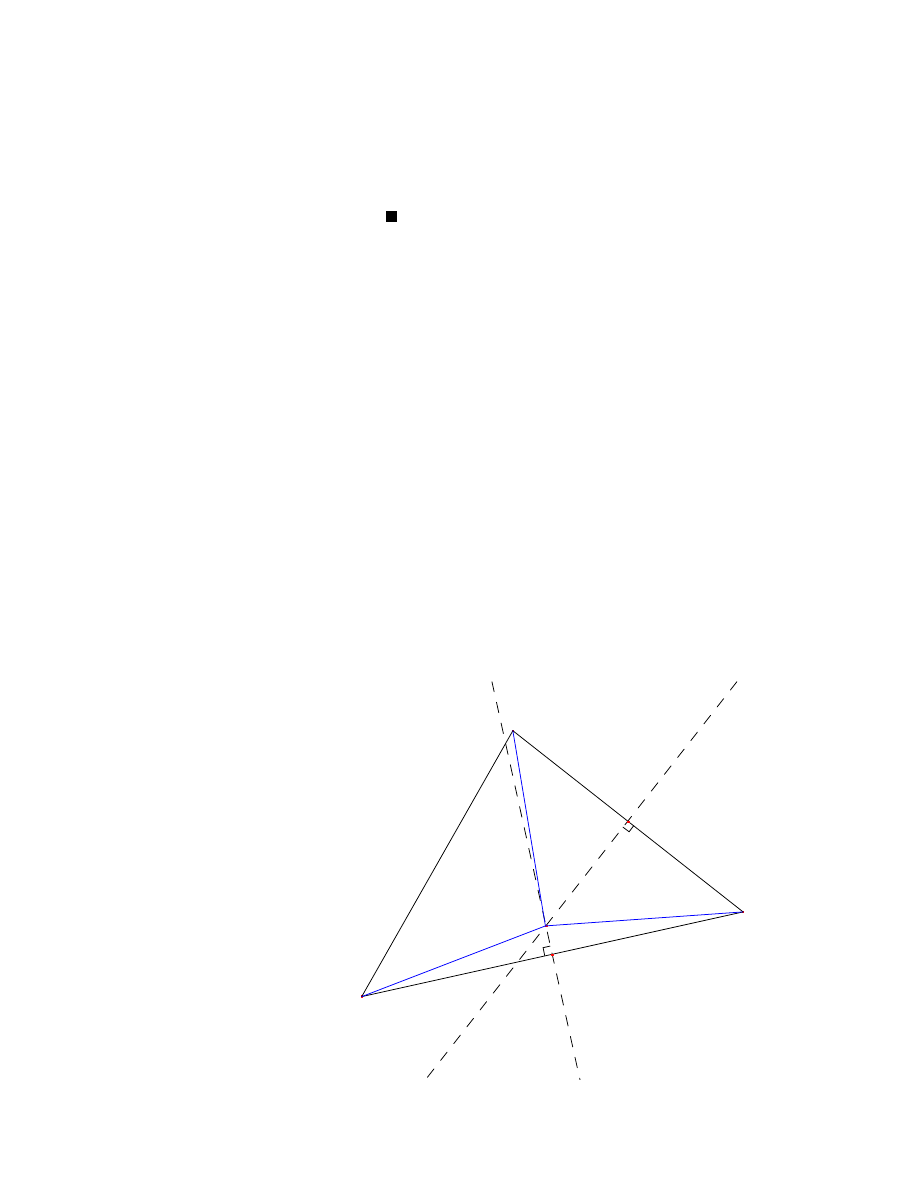
Twierdzenie 14 [17, str. 52] ´Srodek okregu dziewieciu punktów dla dowolnego trójkata

lezy w po owie odcinka aczacego ortocentr oraz ´srodek okregu opisanego.

3.2 Okrag dzieweciu punktów

Dowód:

[17, str. 53] We´zmy dowolny trójkat 4ABC, o punktach ´srodkowych boków

, Q, R oraz wysoko´sciach AA

, BB

, CC

, przecinajacych sie w punkcie H. Oznaczmy

ponadto ´srodek okregu opisanego na nim przez S.

Chcemy znale´z´c ´srodek okregu dziewieciu punktów dla trójkata 4ABC. Aby to zrobi´c

wystarczy wskaza´c punkt przeciecia dwóch symatralnych dowolnych cieciw tego okregu.

Zauwazmy, ze omawiany okrag przechodzi przez punkty C

i R nalezace do boku AB.

Rozwazmy wiec cieciwe C

. Odcinki C

oraz SR sa do niej prostopad e, stad równole-

3.2 Okrag dzieweciu punktów

g e do siebie.

Rozwazmy trapez C

RSH

i narysujmy symetralna jego boku C

. Jest ona równiez

równoleg a do podstaw trapezu, a po´srednio z lematu 1 o ´srodkach boków trójkata dzieli

odcinek HS na pó . Postepujac analogicznie dla punktów A

dostajemy podobny wniosek.

3.2 Okrag dzieweciu punktów

Stad ´srodek okregu dziewieciu punktów lezy w po owie odcinka HS, czyli odleg o´sci

miedzy ortocentrum, a ´srodkiem okregu opisanego.

Wniosek: Okrag opisany na trójkacie ortycznym pokrywa sie z okregiem dziewieciu

punktów dla trójkata pierwotnego. Inaczej, ´srodek okregu opisanego trójkata ortycznego

lezy w po owie odcinka utworzonego przez ortocent i ´srodek okregu opisanego pierwot-

nego trójkata.

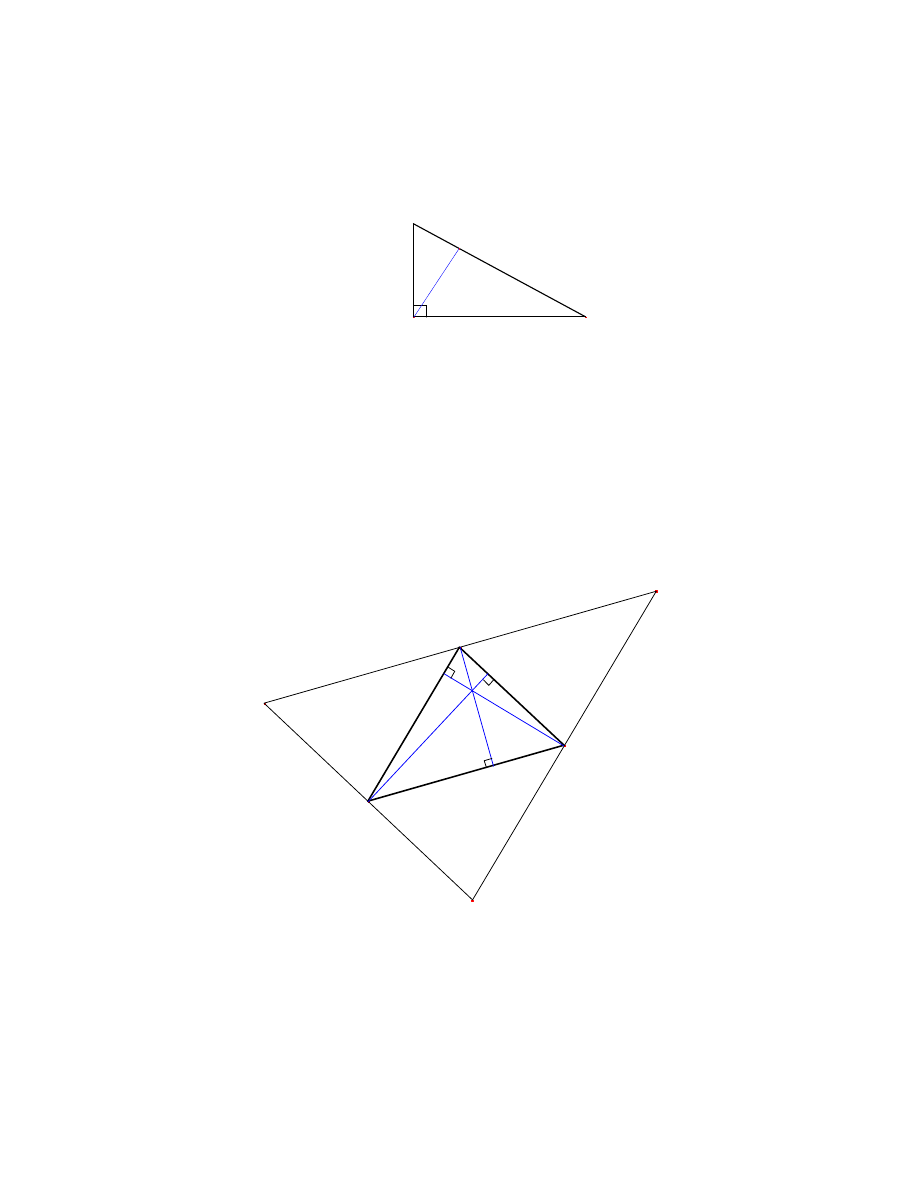
Twierdzenie 15 [17, str. 53] D ugo´s´c promienia okregu dziewieciu punktów jest równa

po owie d ugo´sci promienia okregu opisanego na nim.

Dowód:

[17, str. 53] We´zmy dowolny trójkat 4ABC oraz zwiazany z nim okrag

dziewieciu punktów o ´srodku w punkcie D, a takze okrag na nim opisany o ´srodku S:

Naszkicujmy wysoko´sci tego trójkata AA

, BB

, CC

oraz oznaczmy ´srodki jego boków

przez P , Q, R.

3.2 Okrag dzieweciu punktów

Poprowadzmy z punktu P prosta przechodzaca przez punkt D. Zauwazmy, ze przetnie ona

wysoko´s´c CC

w punkcie F. Z w asno´sci okregu dziewieciu punktów wynika, ze punkt F

jest punktem Eulera, czyli dzieli odcinek CH na pó , stad:

HF = F C

Po aczmy teraz odcinkami punkty H i S oraz S i P .

Zauwazmy, ze powsta e w ten sposób trójkaty 4P SD i 4F HD sa do siebie podobne

(bkb) - katy

^FDH i ^PDS równe jako wierzcho kowe, FD i DP sa promieniami tego

samego okregu, za´s HD = DS z twierdzenia 14. Wnioskiem z tej obserwacji jest równo´s´c

odcinków P S i HF . Poniewaz zarówno wysoko´s´c CC

, jak i odcinek P S sa prostopad e

do podstawy AB, to odcinki CF i SP do siebie równoleg e. Nastepnie aczac punkty P ,

3.2 Okrag dzieweciu punktów

, C i F otrzymamy równoleg obok, w którym m.in. odcinki P F i SC sa równe.

Zauwazmy, ze P F jest ´srednica okregu dziewieciu punktów, za´s SC jest promieniem

okregu opisanego na trójkacie 4ABC. Zatem d ugo´s´c promienia okregu dziewieciu punk-

tów jest równa po owie d ugo´sci promienia okregu opisanego na tym samym trójkacie.

Mozna równiez udowodni´c nastepujace twierdzenia zwiazane z okregiem dziewieciu

punktów:

3.2 Okrag dzieweciu punktów

Twierdzenie 16 (Feuerbacha) [17, str. 58] Okrag dziewieciu punktów jest styczny do

okregów dopisanych do trójkata, a takze posiada dok adnie jeden punkt wspólny z okregiem

wpisanym. Punkt ten nosi nazwe punktu Feuerbacha.

Twierdzenie 17 (Hamiltona) [17, str. 57] Okrag dziewieciu punktów danego trójkata

jest równiez okregiem dziewieciu punktów dla trzech trójkatów, których dwa wierzcho ki

pokrywaja sie z wierzcho kami danego, a trzeci jest jego ortocentrum.

Rozdzia 4

Proste Cevy

De nicja 9 [1] Dla dowolnego trójkata prostymi Cevy nazywamy proste przechodzace

przez jego wierzcho ki i przecinajace sie w jednym punkcie.

W geometrii trójkata bardzo czesto w dowodach róznych twierdze´n wykorzystujemy

pomocniczo twierdzenia dotyczace prostych Cevy. Dzieje sie tak, poniewaz na ich pod-

stawie atwo wykaza´c równoleg o´s´c prostych lub tez fakt, ze przecinaja sie w jednym

punkcie. Ponadto okazuje sie, ze wiekszo´s´c prostych aczacych wierzcho ki trójkata, ze

szczególnymi punktami na jego bokach, to w a´snie proste Cevy. Zauwazmy, ze spo´sród

wymienionych do tej pory prostych, do prostych Cevy mozemy zaliczy´c:

proste zawierajace wysoko´sci,

´srodkowe,

proste zawierajace dwusieczne katów.

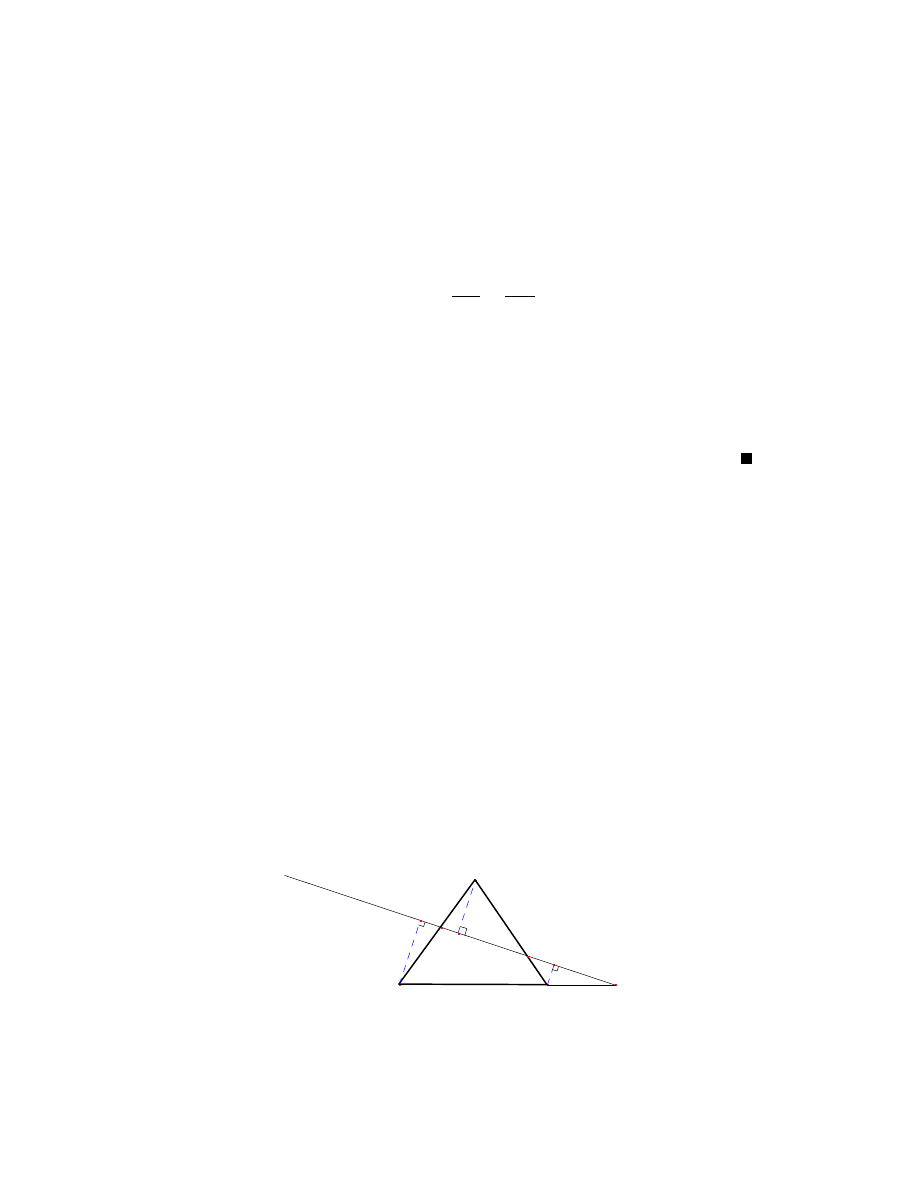
4.1 Twierdzenie Menelaosa

Jednym z najbardziej znanych twierdze´n zwiazanych z trójkatem jest twierdzenie Menelaosa.

Zosta o ono pierwotnie sformuowane przez Menelaosa z Aleksandrii (70-130r.) w trzecim

4.1 Twierdzenie Menelaosa

tomie jego traktatu pt.: "Sfery". Oryginalnie dotyczy o trójkata sferycznego, jednak obe-

cnie pod ta nazwa rozumiemy nastepujace twierdzenie:

Twierdzenie 18 (Menelaosa) [2], [5, str. 66] Niech dany bedzie dowolny trójkat 4ABC

oraz punkty P , Q, R rózne od A, B, C nalezace odpowiednio do prostych AB, BC i CA.

Punkty te sa wspó liniowe wtedy i tylko wtedy gdy zachodzi równo´s´c:

CR
BP

= 1

Zanim przystapie do udowodnienia tego twierdzenia sformuuje i udowodnie lemat pomo-

cniczy:

Lemat 3 Jezeli na prostej AB umie´scimy punkty X i Y , i zachodzi ponizszy stosunek

d ugo´sci odcinków

a przy tym punkty X, Y leza oba poza odcinkiem AB, albo sie w nim zawieraja, to

X = Y

Dowód:

Za ózmy, ze na prostej AB po ozone sa punkty X i Y , i zachodzi stosunek

(4.5)

atwo zauwazy´c, ze punkty A, B, X, Y musza by´c rózne od siebie, bo je´sli by tak nie

by o, to kazda z d ugo´sci odcinków wymienionych w proporcji musia aby wynosi´c zero.

Wówczas wszystkie cztery punkty leza yby w tym samym miejscu i nie mia o by sensu

4.1 Twierdzenie Menelaosa

mówienie o ich po ozeniach wzgledem odcinka AB. Je´sli za ozymy, ze punkty te sa rózne,

to mozemy rozwazy´c trzy mozliwo´sci ich wzajemnego po ozenia:

a) Punkty X, Y zawieraja sie w odcinku AB:

b) Punkty X, Y leza oba poza odcinkiem AB, z jednej strony odcinka.

c) Punkty X, Y leza oba poza odcinkiem AB, po róznych stronach odcinka AB.

Ad a)

Zauwazmy, ze d ugo´s´c odcinka AB mozemy wyrazi´c poprzez sume:

AB = AX + BX

Mozemy to równanie podzieli´c stronami przez d ugo´s´c odcinka BX, stad:

BX
BX

+ 1

(4.6)

Analogicznie wykorzystujac podzia odcinka AB punktem Y , i dzielac stronami przez BY

otrzymaliby´smy:

(4.7)

4.1 Twierdzenie Menelaosa

Wykorzystujac przyjete za ozenie (4.5) oraz (4.6) i (4.7) otrzymujemy, ze:

1 =

a stad po krótkich przekszta ceniach:

BX = BY

co implikuje:

X = Y

Ad b)

Zauwazmy, ze prawdziwe sa równo´sci:

AX = AB + BX

oraz AY = AB + BY

Dzielac je stronami odpowiednio przez BX i BY dostaniemy:

BX
BX

oraz

BY
BY

a to po skorzystaniu z przyjetego za ozenia (4.5) da nam, ze:

+ 1 =

+ 1

BX = BY

4.1 Twierdzenie Menelaosa

co daje w efekcie iz:

X = Y

Ad c)

Dla tego przypadku mozemy napisa´c:

BX = AX + AB

Dzielac stronami przez BX otrzymamy:

1 =

(4.8)

= 1

A takze:

AY = AB + BY

co po podzieleniu przez BY da nam:

+ 1

(4.9)

Dalej z (4.8) mamy:

1 =

(4:5)

(4:9)

+ 1 +

4.1 Twierdzenie Menelaosa

a stad:

0 =

Tak by´c nie moze, bo przeciez punkty A i B nie pokrywaja sie. Zatem przy powyzszych

za ozeniach lematu przypadek po ozenia punktów z podpunktu c jest sprzeczny.

Dowód:

(twierdzenia Menelaosa) [2] "=)" We´zmy dowolny trójkat 4ABC oraz trzy

wspó liniowe punkty P , Q, R lezace odpowiednio na prostych AB, BC i CA. Pokazemy,

ze zachodzi powyzsza równo´s´c. Zauwazmy, ze mozliwe sa tylko dwa przypadki po ozenia

prostej P QR wobec trójkata 4ABC. Prosta ta moze przecina´c dwa boki trójkata (rys. 1)

lub tez znajdowa´c sie poza nim (rys. 2). Jednak w obu przypadkach dowód jest identyczny.

rys. 1

4.1 Twierdzenie Menelaosa

rys. 2

Poprowad´zmy z wierzcho ków trójkata 4ABC odcinki prostopad e do prostej P QR. Otrzy-

mane w ten sposób punkty oznaczmy A

, B

, C

. Zauwazmy, ze powsta e w ten sposób

trójkaty sa do siebie podobne (kkk), tzn:

4AA

R =

4CC

Q =

4BB

P =

4AA

Mozemy wiec napisa´c odpowiednie proporcje:

z tego, ze 4AA

R =

4CC

mamy:

z tego, ze 4CC

Q =

4BB

mamy:

za´s z tego, ze 4BB

P =

4AA

mamy:

4.1 Twierdzenie Menelaosa

Przekszta cajac otrzymane równo´sci otrzymamy:

CR
AR

BQ
CQ

Nastepnie wymnazajac je stronami przez siebie dostajemy:

CR
AR

BQ
CQ

CR
AR

BQ
CQ

= 1

"(=" Za ózmy teraz, ze spe nione sa za ozenia twierdzenia oraz zachodzi równo´s´c:

CR
AR

BQ
CQ

= 1

Pokazemy, ze punkty P , Q, R sa wspó liniowe. Oznaczmy punkt przeciecia sie prostych

oraz RQ przez X, jak ilustruje rysunek:

a) gdy prosta RQ przecina boki trójkata 4ABC :

rys.1a

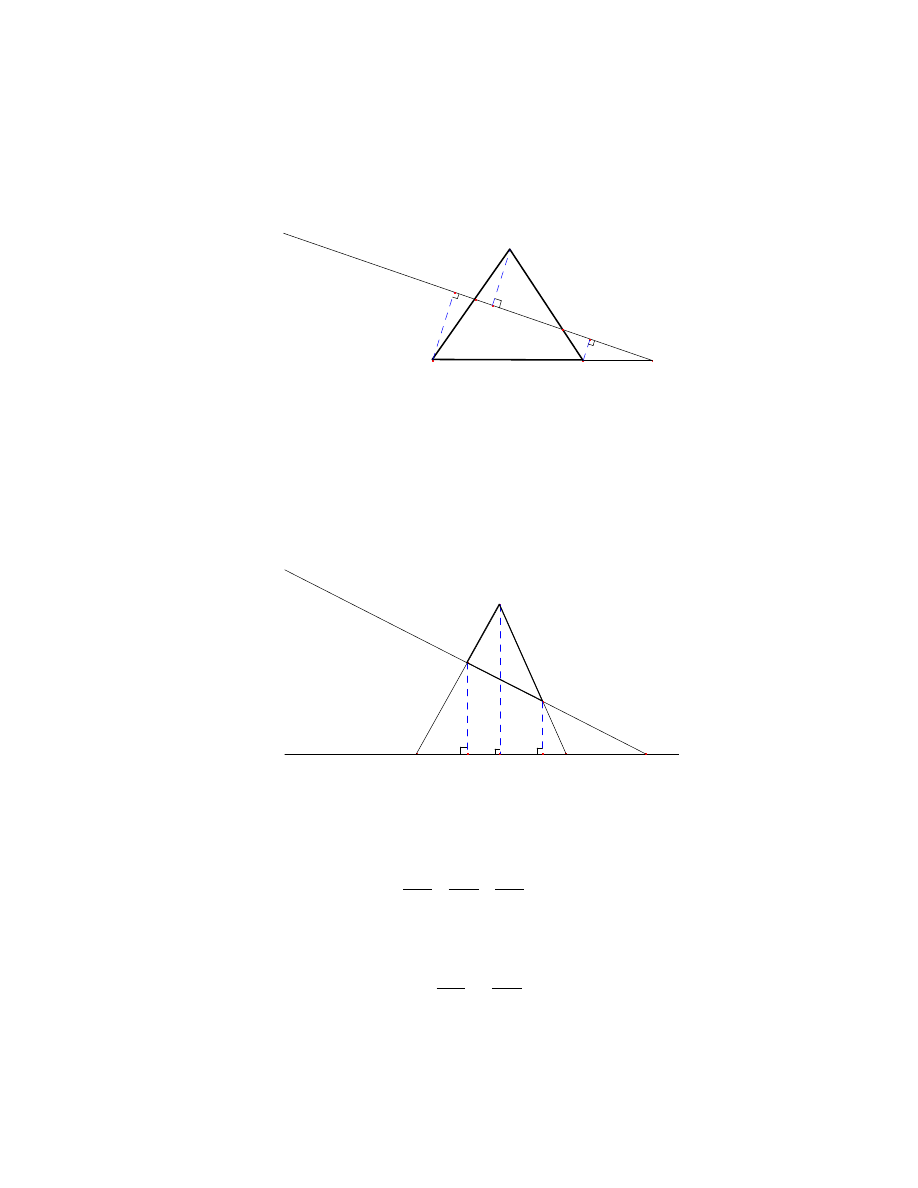
4.1 Twierdzenie Menelaosa

rys. 1b

b) gdy prosta RQ lezy poza trójkatem 4ABC :

rys. 2

(4.10)

Przeprowadzajac analogiczne rozumowanie jak w pierwszej cze´sci dowodu otrzymamy, ze:

= 1

Stad oraz z za ozenia dostajemy:

z wyzej przyjetych za oze´n wiemy, ze pynkty A, B, P i X sa wspó liniowe.

Jak wida´c mozliwe sa tylko dwa przypadki po ozenia punktu przeciecia X. Moze leze´c

4.2 Twierdzenie Cevy

on wewnatrz boku AB (rys. 1b), lub na zewnatrz (rys. 1a i rys. 2). Zauwazmy, ze

aby zachodzi a przyjeta przez nas w za ozeniu równo´s´c w odniesieniu do rozrysowanych

przypadków, punkt P musi znajdowa´c sie wewnatrz odcinka AB dla rys 1a, a na zewnatrz

dla pozosta ych. Stad mamty wniosek, ze punkty P i X musza oba znajdowa´c sie wewnatrz

lub na zewnatrz boku AB:

Stad oraz z otrzymanej proporcji, a takze lematu 3 mozemy wnioskowa´c, ze punkty

i X pokrywaja sie. W ten sposób wykazali´smy, ze punkty P , Q, R sa wspó liniowe.

4.2 Twierdzenie Cevy

Zadziwiajacym moze wydawa´c sie fakt, ze identyczna równo´s´c jak w twierdzeniu Menela-

osa wystepuje równiez w twierdzeniu Cevy. Cho´c za ozenia obu sa identyczne, to dotycza

one zupe nie innych w asno´sci.

Zyjacy znacznie pó´zniej od Menelaosa, w oski matematyk Giovanni Ceva (1648-1736), na

którego cze´s´c proste przechodzace przez wierzcho ki trójkata i przecinajace sie w jednym

punkcie nazywamy cewianami, odkry , ze prawdziwe jest:

Twierdzenie 19 (Cevy) [17, str. 11-13], [5, str. 4] Niech dany bedzie trójkat 4ABC

oraz punkty P , Q, R rózne od A, B, C nalezace odpowiednio do prostych AB, BC i CA.

Proste AQ, BR oraz CP przecinaja sie w jednym punkcie (lub sa do siebie równoleg e)

wtedy i tylko wtedy gdy zachodzi równo´s´c:

CR
BP

= 1

4.2 Twierdzenie Cevy

Dowód:

[17, str. 11-12], [1], [5, str. 4-5] "=)" We´zmy dowolny trójkat 4ABC oraz

punkty P , Q, R rózne od A, B, C po ozone odpowiednio na prostych AQ, BR oraz CP

tak, aby odcinki AQ, BR, CP :

1. przecina y sie w jednym punkcie S,

2. by y do siebie równoleg e.

Dowód przeprowadzimy osobno dla dwóch przypadków.

Ad 1. Dla uproszczenia dowodu narysujmy prosta KL przechodzaca przez punkt C

i równoleg a do AB tak, aby punkty K i L by y odpowiednio punktami przeciecia

z prostymi BR oraz AQ.

Zauwazmy, ze powsta e w ten sposób trójkaty sa do siebie podobne (kkk), skad mozemy

napisa´c nastepujace proporcje:

z tego, ze 4KCR = 4ABR mamy:

CR
AR

;

(4.11)

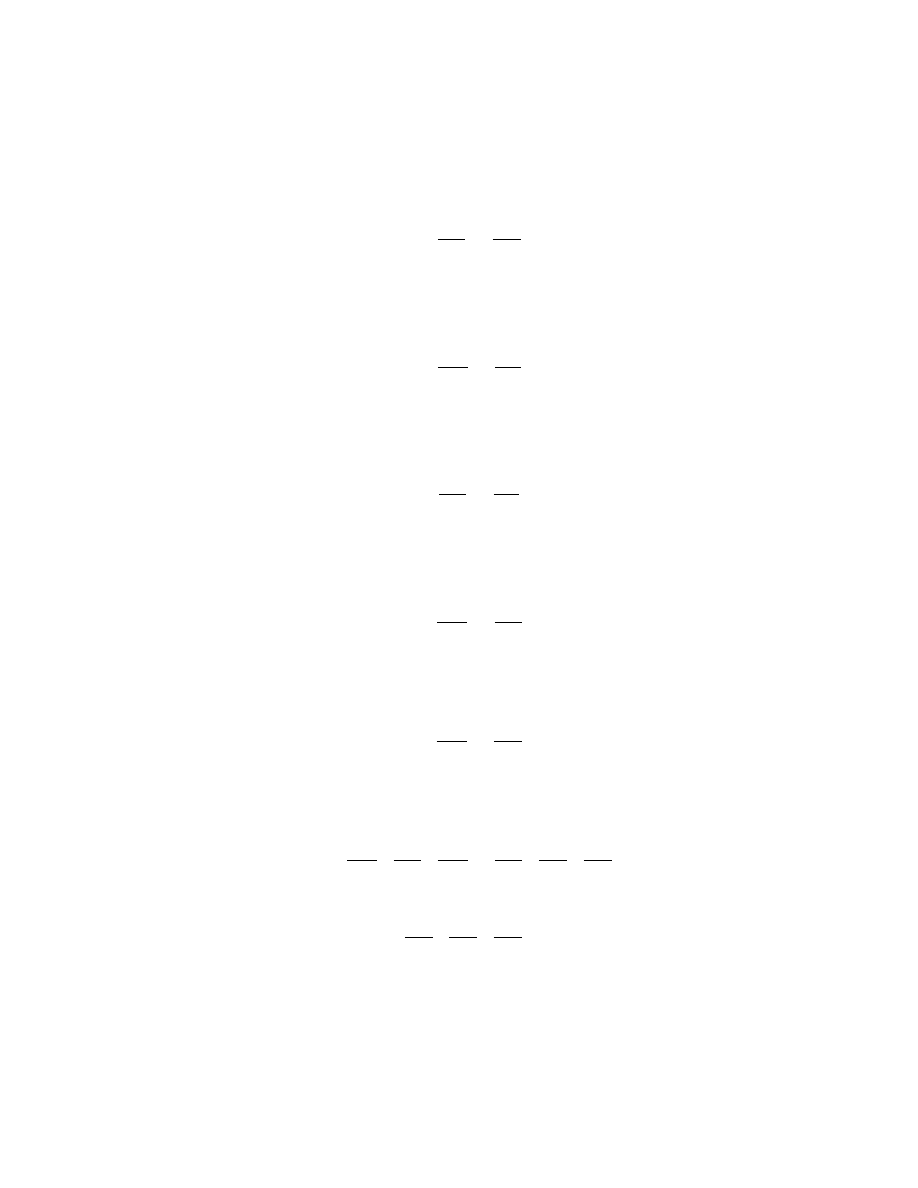
4.2 Twierdzenie Cevy

z tego, ze 4CLQ = 4ABQ mamy:

BQ
CQ

;

(4.12)

z tego, ze 4KCS = 4P BS mamy:

CS
SP

;

(4.13)

z tego, ze 4CLS = 4AP S mamy:

CS
SP

(4.14)

Przyrównuja´c równo´s´ci (4.13) i (4.14) otrzymujemy:

a po przekszta ceniach:

(4.15)

Wymnazajac stronami (4.11), (4.12) oraz (4.15) dostajemy:

CR
AR

BQ
CQ

;

CR
BP

= 1

co ko´nczy dowód w przypadku 1.

Ad 2. Dla uproszczenia dowodu narysujmy prosta KL przechodzaca przez punkt C

i równoleg a do AB tak, aby punkty K i L by y odpowiednio punktami przeciecia

4.2 Twierdzenie Cevy

z prostymi BR oraz AQ.

Zauwazmy, ze powsta e w ten sposób trójkaty sa do siebie podobne (kkk), skad mozemy

napisa´c nastepujace proporcje:

z tego, ze 4KCQ = 4ABQ mamy:

BQ
AB

;

(4.16)

z tego, ze 4CLR = 4ABR mamy:

AR
AB

(4.17)

Przekszta cajac równo´sci (4.16) i (4.17) otrzymujemy odpowiednio:

AB =

KC BQ

;

AB =

CL AR

;

4.2 Twierdzenie Cevy

stad:

KC BQ

CL AR

;

BQ CR

CQ AR

(4.18)

Zauwazmy ponadto, ze:

;

a stad po przekszta ceniu otrzymujemy:

P B

(4.19)

Wymnazajac teraz stronami (4.18) i (4.19) dostajemy:

BQ CR AP
CQ AR P B

;

CR
BP

= 1

co ko´nczy dowód w przypadku 2.

"(=" We´zmy dowolny trójkat 4ABC oraz punkty P , Q, R rózne od A, B, C po ozone

odpowiednio na prostych AQ, BR oraz CP oraz za ózmy, ze zachodzi równo´s´c:

CR
BP

= 1:

Pokazemy, ze proste AQ, BR oraz CP przecinaja sie w jednym punkcie (lub sa do siebie

równoleg e). W przypadku gdy chcemy pokaza´c, ze AQ, BR oraz CP przecinaja sie

w jednym punkcie zak adamy, ze proste AQ, BR przecinaja sie w punkcie S, przez który

nie przechodzi prosta CP . Gdy rozwazamy przypadek, w którym proste sa równoleg e

rezygnujemy z tego za ozenia na rzecz równoleg o´sci prostych AQ i BR. Poprowadzmy

teraz prosta CS, a punkt jej przeciecia z bokiem AB oznaczmy przez X. Na mocy pier-

4.3 W asno´s´c prostych Cevy

wszej cze´sci twierdzenia prawdziwa jest równo´s´c:

= 1:

Stad i za ozenia otrzymujemy, ze:

;

zatem na mocy lematu 3 punkty X oraz P pokrywaja sie.

4.3 W asno´s´c prostych Cevy

Twierdzenie 20 (van Aubela) [17, str. 22] Dla dowolnego trójkata 4ABC, jezeli proste

Cevy przecinaja sie w punkcie K, to prawdziwa jest równo´s´c

jAKj
jQKj

jARj
jCRj

jAP j

jBP j

Dowód:

[17, str. 22-25] Niech bedzie dany dowolny trójkat 4ABC oraz trzy proste

Cevy przecinajace sie w punkcie K. Rozpatrzmy dwa przypadki:

1. Punkt K lezy wewnatrz trójkata 4ABC.

2. Punkt K lezy poza trójkatem 4ABC.

4.3 W asno´s´c prostych Cevy

Ad 1.

Oznaczmy punkty przeciecia boków trójkata z prostymi Cevy odpowiednio przez P , Q, R.

Poprowadzmy prosta MN równoleg a do BC przechodzaca przez punkt A. Zauwazmy, ze

powsta e w ten sposób trójkaty 4NAR i 4BCR, 4AMP i 4CBP , 4MNK i 4BCK

oraz 4AMK i 4CQK sa do siebie podobne (kkk). W trójkatach 4NAR i 4BCR

katy przy wierzcho ku R sa jednakowej miary, jako katy wierzcho kowe, za´s

^N = ^B,

^A = ^C jako naprzemianleg e wewnetrzne. Korzystajac z tego mozemy wyciagna´c

nastepujace wnioski:

z tego, ze 4NAR = 4BCR mamy:

jANj

jARj

jCBj
jCRj

;

(4.20)

z tego, ze 4AMP = 4CBP mamy:

jAP j

jBP j

jAMj

jCBj

;

(4.21)

z tego, ze 4MNK = 4BCK mamy:

jMNj

jCBj

jMNj

jCKj

;

(4.22)

4.3 W asno´s´c prostych Cevy

z tego, ze 4AMK = 4BQK mamy:

jMKj

jCKj

jAKj
jQKj

(4.23)

Zauwazmy, ze z (4.22) i (4.23) mozemy napisa´c:

jMNj

jCBj

jAKj
jQKj

(4.24)

Ponadto, poniewaz punkt A lezy pomiedzy punktami M i N mamy:

jMNj = jANj + jAMj:

(4.25)

Przekszta cajac równo´s´c (4.20) otrzymujemy:

jANj =

jARj jCBj

jCRj

;

(4.26)

za´s z równo´sci (4.21) dostajemy, ze:

jAMj =

jAP j jCBj

jBP j

(4.27)

Z (4.24) mozemy dalej zapisa´c:

jAKj
jQKj

jMNj

jCBj

(4:25)

jAMj + jANj

jCBj

jAMj

jCBj

jANj

jCBj

(4:26);(4:27)

jARj jCBj

jCRj

jCBj

jAP j jCBj

jBP j

jCBj

jARj jCBj
jCRj jCBj

jAP j jCBj

jBP j jCBj

jARj
jCRj

jAP j

jBP j

4.3 W asno´s´c prostych Cevy

co naleza o udowodni´c.

Ad2.

Oznaczmy punkty przeciecia boków trójkata 4ABC oraz ich przed uze´n z prostymi Cevy

odpowiednio przez P , Q, R. Poprowad´zmy prosta MN równoleg a do BC; przechodzaca

przez punkt A. Zauwazmy, ze powsta e w ten sposób trójkaty sa do siebie parami przysta-

jace (4MAR i 4BCR, 4ANP i 4BCP , 4MNK i 4BCK oraz 4MAK i 4BQK).

Korzystajac z tego mozemy zapisa´c nastepujace równo´sci:

z tego , ze 4MAR = 4BCR mamy:

AR
CR

;

(4.28)

z tego, ze 4ANP = 4BCP mamy:

;

(4.29)

z tego, ze 4MNK = 4BCK mamy:

M N

M K

;

(4.30)

4.3 W asno´s´c prostych Cevy

z tego, ze 4MAK = 4BQK mamy:

M K

AK
QK

(4.31)

Z (4.30) i (4.31) otrzymujemy, ze:

AK
QK

M N

Oczywi´scie MN = AM + AN, za´s przekszta cajac proporcje (4.28) i (4.29) otrzymu-

jemy:

AM =

BC AR

;

(4.32)

AN =

BC AP

(4.33)

Podsumowujac mamy:

AK
QK

M N

AM + AN

(4:32);(4:33)

BC AR

BC AP

BC AR
CR BC

BC AP

BP BC

AR
CR

;

co naleza o udowodni´c.

Rozdzia 5

Szczególne punkty trójkata

5.1 Punkt Gergonne'a

Okazuje sie, ze cztery wyzej wymienione szczególne punkty, powsta e w skutek przeciecia

prostych Cevy, to jeszcze nie wszystkie charakterystyczne, powstajace w ten sposób.

Do zbioru szczególnych punktów trójkata nalezy m. in punkt Gergonne'a, którego

nazwa pochodzi od francuskiego matematyka Josepha Diaza Gergonne'a (1771-1859) [12].

Pierwsze wykszta cenie w dziedzinie matematyki uzyska on w Collegu w Nancy, a pó´zniej

od prywatnych korepetytorów, co w ówczesnych czasach by o bardzo popularnym sposo-

bem zdobywania wiedzy. Jego edukacja zosta a przerwana przez Rewolucje Francuska,

w której bra czynny udzia , jako kapitan Gwardii Narodowej. Gdy we Francji nasta juz

pokój, Gergonne podrózowa po Europie, a do Francji powróci w 1793 roku, gdzie w

Nimes dosta stanowisko matematyka Politechniki École. Poniewaz Gergonne boryka sie

z problemem wydawania swoich prac, w roku 1810 zacza sam wydawa´c magazyn matem-

atyczny pod tytu em: "Annales de mathématiques pures et appliquées" ("Roczniki matem-

atyki czystej i stosowanej"). Georgonne interesowa sie szczególnie geometria, stad tez by

to temat najcze´sciej pojawiajacy sie na amach jego rocznika. Na przestrzeni 21 lat jego

wydawania swoje prace publikowa y w nim takie matematyczne s awy jak cho´cby Pon-

celet czy Steiner. Zapoznajac sie z biogra a tego matematyka natra am na jeden

z jego cytatów, który wydaje mi sie bardzo inspirujacy, dlatego postanowi am go w a´snie

5.1 Punkt Gergonne'a

tu zacytowa´c:

"Dopóki nie da sie w kilku s owach wyt umaczy´c danej teorii dowolnemu napotkanemu

przechodniowi, dopóty nie mozna odczuwa´c satysfakcji z wypowiedzenia w niej

ostatniego s owa."

Twierdzenie 21 (punkt Gergonne'a) [17, str. 14] Proste aczace wierzcho ki trójkata

z punktami styczno´sci okregu wpisanego w ten trójkat przecinaja sie w jednym punkcie.

Punkt ten nazywamy punktem Gergonne'a.

Dowód:

[17, str. 14] We´zmy dowolny trójkat 4ABC oraz wpisany w niego okrag

o ´srodku W . Punkty styczno´sci okregu z bokami AB, BC, CA oznaczmy odpowiednio P ,

, R.

Pokazemy, ze proste AQ, BR i CP przecinaja sie w jednym punkcie. Zauwazmy, ze prosta

jest dwusieczna kata

^RAP, to:

j^RAW j = j^W AP j .

5.1 Punkt Gergonne'a

Odcinki RW oraz W P sa sobie równe jako promienie okregu wpisanego oraz:

?RA,

W P

?AP:

Z tych obserwacji wynika wniosek, ze trójkaty 4AW R i 4AW P sa podobne (bbb) za-

tem:

jARj = jAP j :

(5.34)

Przeprowadzajac analogiczne rozumowanie dla pozosta ych trójkatów otrzymujemy, ze:

jBP j = jBQj ;

(5.35)

jCQj = jCRj :

(5.36)

Mnozac stronami równo´sci (5.34), (5.35), (5.36) otrzymujemy:

AR BP CQ = AP BQ CR

za´s dzielac stronami przez (AR CQ BP ) mamy:

AP CR BQ
AR CQ BP

= 1:

Zauwazmy, ze równo´s´c ta jest identyczna z równo´scia z twierdzenia Cewy, a to ´swiadczy

o tym, ze proste AQ, BR i CP przecinaja sie w jednym punkcie.

5.2 Punkt Nagela

Twierdzenie, które przedstawie ponizej pochodzi od niemieckiego geometry Chri-

stiana Heinricha von Nagela (1803-82) [11]. Po uko´nczeniu studiów teologicznych w 1825

roku zacza on uczeszcza´c na wyk ady z matematyki na Uniwersytecie Tübingen w Niem-

czech. Po roku zosta on nauczycielem matematyki oraz nauk przyrodniczych w jednym

z liceów i nadal kontynuowa swoja nauke. W roku 1830 uzyska tytu doktora mate-

matyki, a w pracy awansowa na stanowisko profesora. W 1940 roku wyda ksiazke o idei

nauczania w szko ach ´srdnich. By a to pierwsza z jego sze´sciu ksiazek, które opublikowa .

Z punktu widzenia mojej pracy najwazniejsza z nich to "Rozwój Wspó czesnej Geometrii

Trójkata". Zawar w niej nie tylko twierdzenie i dowód dotyczace punktu Nagela, ale

równiez punktu Gergonne'a. Zanim odszed na emeryture w 1875 roku zosta wyrózniony

tytu em Rektora uczelni w Ulmie, a takze Honorowego Obywatela tego miasta.

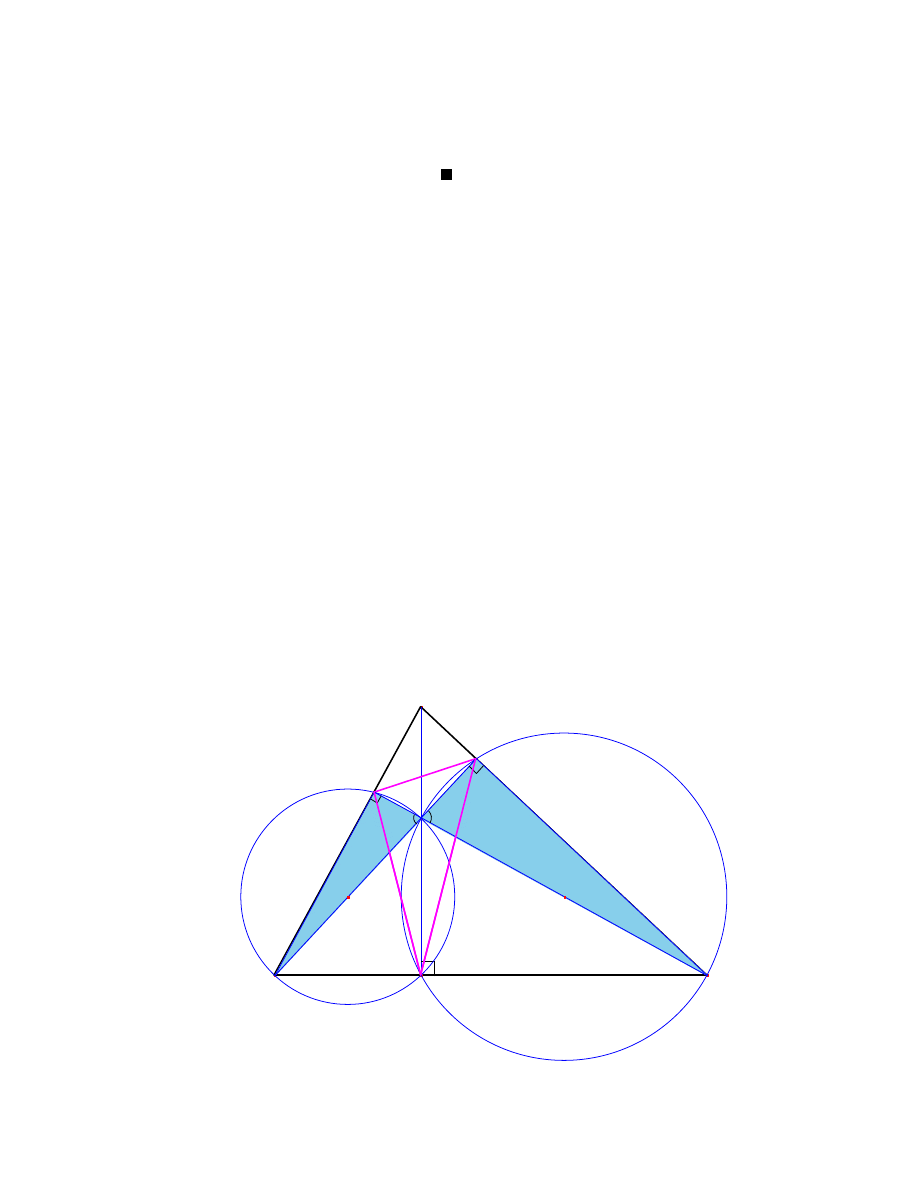
Twierdzenie 22

(punkt Nagela) [17, str. 20] Proste aczace wierzcho ki dowolnego

trójkata z punktami styczno´sci odpowiednich okregów dopisanych przecinaja sie w jednym

punkcie zwanym punktem Nagela.

5.2 Punkt Nagela

Dowód:

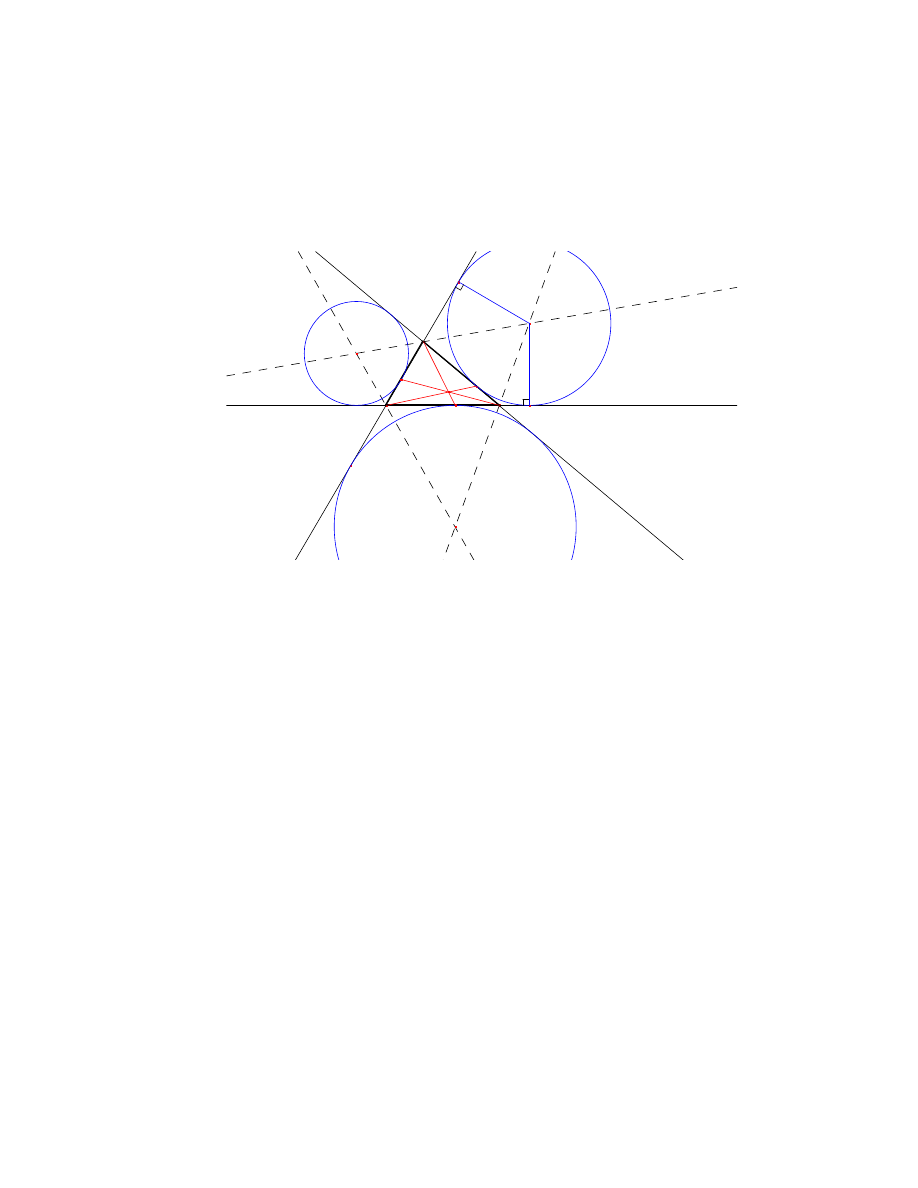
[17, str. 20-21] We´zmy dowolny trójkat 4ABC i narysujmy okregi dopisane

do niego. Punkty styczno´sci z trójkatem 4ABC oznaczmy odpowiednio Q, R, P .

W dalszej cze´sci dowodu bedziemy rozwaza´c okrag styczny bezpo´srednio do boku BC,

o ´srodku w punkcie S

. Przyjmijmy dalej oznaczenia:

- punkt styczno´sci rozwazanego okregu z prosta AC,

- punkt styczno´sci rozwazanego okregu z prosta AB.

Zauwazmy, ze poniewaz ´srodek okregu S

lezy na dwusiecznej kata

^A, a punkty X i Y

sa punktami jego styczno´sci z ramionami kata, to:

AX = AY:

(5.37)

Obserwujemy równiez, ze:

= CQ;

(5.38)

BX = BQ;

5.2 Punkt Nagela

zatem oznaczajac obwód trójkata 4ABC przez 2p mozemy zapisa´c:

2p = AB +BC +AC = AB +BQ+CQ+AC

(5:38)

= AB +BX +CY +AC = AX +AY

Dalej z (5.37) mamy:

AX = AY = p

Stad wniosek, ze punkt Q i wierzcho ek A podzieli y obwód na po owe. Przeprowadzajac

analogiczne rozwazania dla pozosta ych punktów styczno´sci okregów dopisanych mozemy

uogólni´c, ze punkty styczno´sci wraz z przeciwleg ymi wierzcho kami trójkata dziela ob-

wód na pó . Korzystajac dalej z tego wniosku mozemy zapisa´c nastepujace równo´sci:

CQ = p

AR = p

BP = p

(5.39)

AP = p

BP = p

RC = p

(5.40)

Mnozac stronami równo´sci z (5.39) otrzymujemy:

CQ AR RC = (p

AC) (p

AB) (p

BC)

(5.41)

za´s z (5.40):

AP BP RC = (p

AC) (p

AB) (p

BC)

(5.42)

Nastepnie dzielac stronami (5.42) przez (5.41) mamy:

AP BP RC
CQ AR BP

= 1

Z twierdzenia Cevy wynika, ze skoro spe niona jest powyzsza równo´s´c, to proste AQ, BR,

musza przecina´c sie w jednym punkcie.

5.3 Twierdzenie Napoleona

Kolejne twierdzenie, które przedstawie nosi nazwe twierdzenia Napoleona. Zamieszczam

je w a´snie w rozdziale dotyczacym szczególnych punktów trójkata, gdyz dotyczy ´srodków

ortycznych trójkatów równobocznych zwiazanych z dowolnym trójkatem.

Napoleon Bonaparte [5], [11] by znany ówczesnym ze swoich matematycznych

zainteresowa´n. Szczególnie pasjonowa a go geometria. Jednakze najprawdopodobniej nie

osiagna on zadnych znaczacych wyników w tej dziedzinie. Istnieje anegdota, ze zanim

og osi siebie w adca Francji zaangazowa sie w matematyczne dysputy z Lagrangem

i Laplacem. Jednakze wiedza Napoleona w dziedzinie matematyki musia a nie by´c

osza amiajaca, gdyz Laplace powiedzia mu wprost, ze ostatnia rzecza, która by od niego

pragna sa lekcje geometrii. Niemniej jednak ta szczera opinia nie zniecheci a Napoleona

do niego i mianowa go dowódca inzynierii swojego wojska. Z powyzszych przyczyn

watpliwym wydaje sie fakt, ze to w a´snie Napoleon udowodni czy cho´cby sformuowa

twierdzenie sygnowane jego nazwiskiem. Podobne jak i watpliwa by a jego znajomo´s´c

angielskiego aby sformuowa , przypisywany mu palindrom "Able was I ere I saw Elba".

Twierdzenie 23

(Napoleona) [5, str. 63], [3] Jezeli na bokach dowolnego trójkata

skonstruujemy na zewnatrz trójkaty równoboczne, to trójkat powsta y przez po aczenie ich

´srodków ortycznych jest równoboczny.

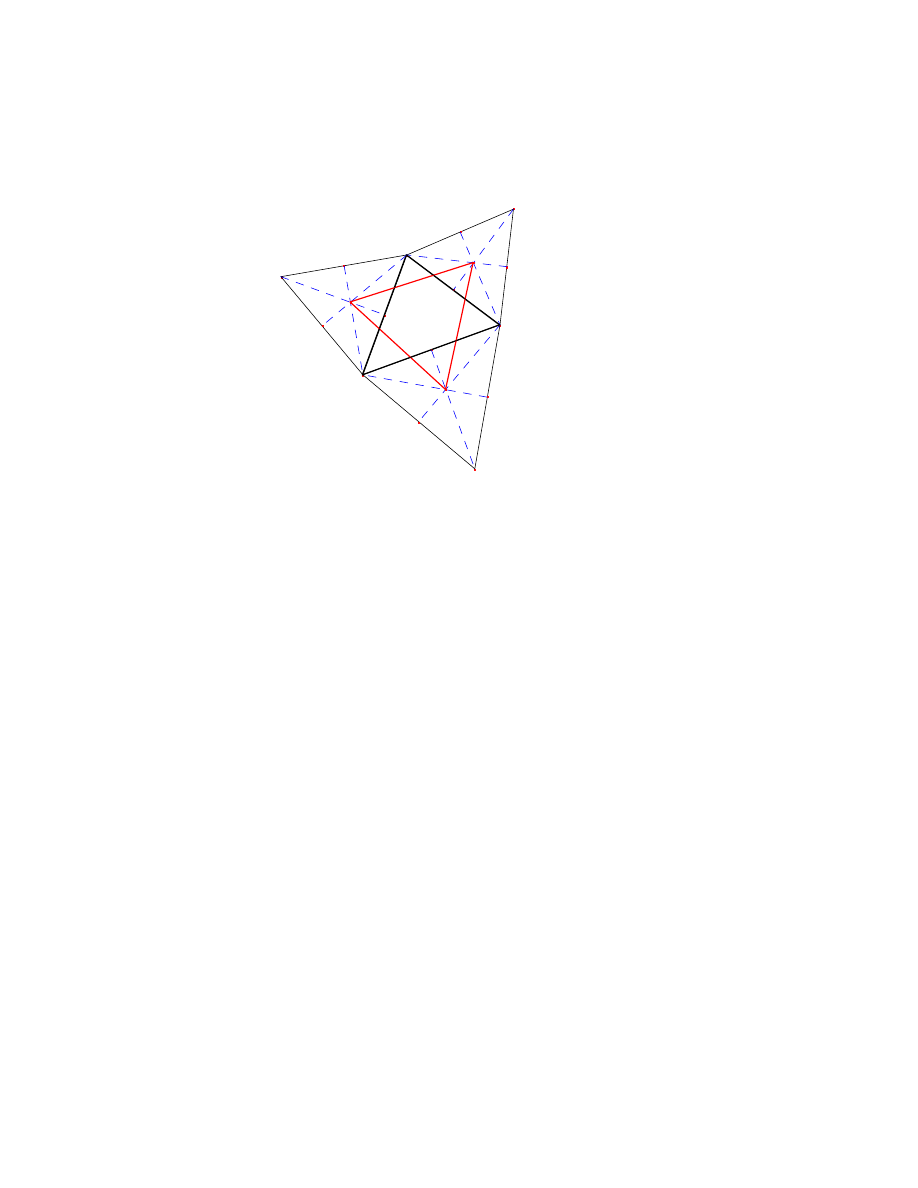
5.3 Twierdzenie Napoleona

Dowód:

[3] We´zmy dowolny trójkat 4ABC.

Budujemy na jego bokach trójkaty równoboczne 4ACB

, 4CBA

oraz 4ABC

Nastepnie konstruujemy wysoko´sci tych trójkatów, a powsta e w ten sposób ´srodki orty-

czne oznaczamy odpowiednio D, E i F . Bedziemy chcieli pokaza´c, ze trójkat 4DEF jest

równoboczny. Dla uproszczenia dowodu przyjmijmy nastepujace oznaczenia. Niech:

DC = DA = s;

EC = EB = t;

F B = F A = u;

DE = x;

EF = y;

F D = z;

AB = c;

BC = a;

CA = b;

5.3 Twierdzenie Napoleona

^ACB = ^C;

^CBA = ^B;

^BAC = ^A:

Poniewaz trójkaty 4ACB

, 4CBA

, 4ABC

sa równoboczne, to na mocy zadania przed-

stawionego w rozdziale 1 ich wysoko´sci wyraza sie wzorami:

4ACB

4CBA

4ABC

Na poczatek we´zmy pod uwage trójkat 4ACB

. Poniewaz jest on równoboczny, to jego

wysoko´sci pokrywaja sie z ´srodkowymi, a co za tym idzie ´srodek ortyczny jest punktem

przeciecia ´srodkowych. Jak wiemy z odpowiedniego twierdzenia punkt ten dzieli ´srodkowe

w stosunku 2 : 1 czyli:

s =

2
3

4ACB

2
3

b =

(5.43)

Przeprowadzajac analogiczne rozumowanie dla pozosta ych trójkatów równobocznych

dostajemy:

t =

(5.44)

u =

Poniewaz w trójkace równobocznym wysoko´sci pokrywaja sie równiez z dwusiecznymi

katów wewnetrznych, które wynosza w nim 60 , to mozemy napisa´c, ze:

j^DCAj = j^ECBj = j^EBCj = j^CF Bj = j^CF Aj = j^CADj = 30 .

5.3 Twierdzenie Napoleona

Rozwazmy teraz trójkat 4DCE. Stosujac prawo cosinusów mamy:

= s

+ t

2st cos(30 +

j^Cj + 30 );

= s

+ t

2st cos(

j^Cj + 60 ):

(5.45)

Podstawiajac do (5.45) równo´sci z (5.43) i (5.44) otrzymamy:

a cos(

j^Cj + 60 );

3
9

cos(

j^Cj + 60 ) / 3;

= b

+ a

2ab cos(

j^Cj + 60 ):

(5.46)

Wykorzystujac w (5.46) wzór na cosinus sumy katów mamy dalej:

= b

+ a

2ab [cos

j^Cj cos 60

sin

j^Cj sin 60 ] ;

= b

+ a

2ab

1
2

cos

j^Cj

sin

j^Cj

;

= b

+ a

ab cos

j^Cj +

3ab sin

j^Cj:

(5.47)

Napiszemy teraz posta´c twierdzenia cosinusów dla trójkata 4ABC:

= a

+ b

2ab cos

j^Cj;

stad:

cos

j^Cj =

2ab

(5.48)

Dla tego trójkata mamy tez (po´srednio) z twierdzenia sinusów, ze:

4ABC

1
2

ab sin

j^cj;

5.3 Twierdzenie Napoleona

zatem:

sin

j^Cj =

4ABC

(5.49)

Podstawiajac (5.48) i (5.49) do (5.47) otrzymujemy:

= b

+ a

2ab

3ab

4ABC

;

= b

+ a

+ 2

3 P

4ABC

;

1
2

+ b

+ c

+ 2

3 P

4ABC

(5.50)

Zauwazmy, ze przeprowadzajac analogiczne rozumowanie jak powyzej dla trójkatów

4EBF i 4F AD dostaliby´smy, ze:

1
2

+ b

+ c

+ 2

3 P

4ABC

;

(5.51)

1
2

+ b

+ c

+ 2

3 P

4ABC

(5.52)

Przyrównujac do siebie (5.50), (5.51) i (5.52) mamy:

= 3y

= 3z

;

a poniewaz d ugo´sci boków musza by´c dodatnie to:

x = y = z

a zatem 4DEF jest równoboczny.

Rozdzia 6

Twierdzenia zwiazane z okregiem opisanym na

trójkacie

W rozdziale tym chcia abym zaprezentowa´c kilka twierdze´n zwiazanych z okregiem

opisanym na trójkacie. Pierwsze z nich, to tzw. twierdzenie Simsona. Jednak cho´c w´sród

matematyków odnajdujemy Szkota, Roberta Simsona (1687-1768) [12], którego przez lata

kojarzono z tym w a´snie twierdzeniem okazuje sie, ze nie on jest jego autorem. Sim-

son zajmowa sie geometria trójkata, jednak w´sród jego notatek nie znaleziono ani s owa,

które mog o by potwierdza´c, ze próbowa je udowodni´c czy cho´cby sformuowa´c jego tre´s´c.

Powstaje wiec pytanie komu rzeczywi´scie zawdzieczamy to twierdzenie i dlaczego nosi

ono nazwe Simsona. Okazuje sie, ze zosta o ono napisane w 1797 roku przez Williama

Wallace'a, równiez szkockiego matematyka, zyjacego w latach 1768-1843. Jak atwo za-

uwazy´c, Wallace nie móg by´c uczniem Simsona. Mozna by sie domy´sla´c, ze by´c moze

zainspirowany jego pracami stworzy je i zadedykowa swojemu rodakowi. Jednak fakty

okazuja sie by´c inne, a dzieki temu, ze nie tylko mnie, ale równiez J.S. Mackaya (pier-

wszego prezesa Edinburgh Math Society) zainteresowa o to pytanie, wiemy jak by o na-

prawde. Francuski matematyk, zajmujacy sie geometria François Joseph Servois (1768-

1847) odniós sie do twierdzenia autorstwa Wallacea s owami "le theoreme suivant, qui

est, je crois, de Simson", co po polsku oznacza "nastepujace twierdzenie, które jest, jak

mniemam, Simsona". Nastepnie Jean Victor Poncelet (1788-1867) powo ujac sie na jego

s owa, równiez przypisa autorstwo Simsonowi. I tak b ad by powielany, a nazwisko przy

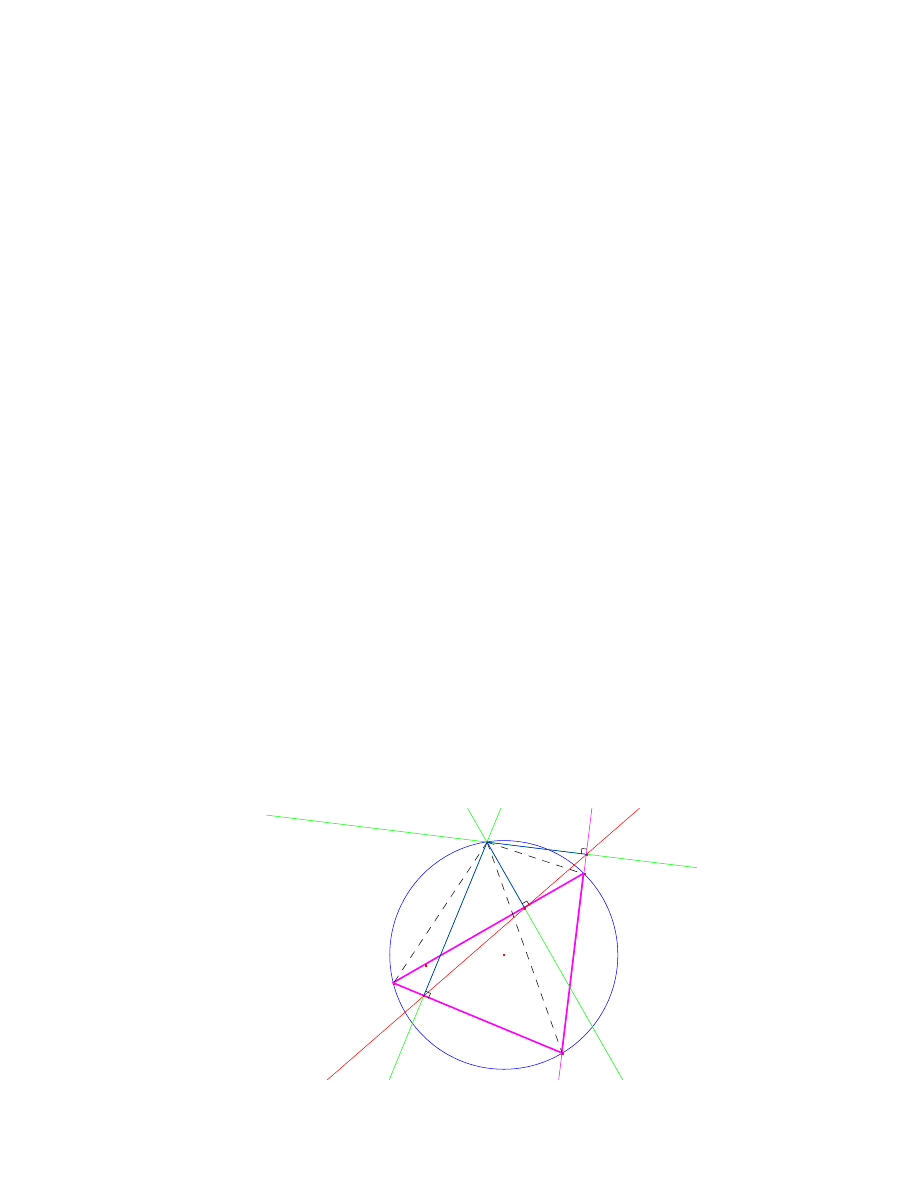
6.1 Twierdzenie Simsona

tym twierdzeniu utrwalane, az do wnikliwej analizy J.S. Mackaya, który pokaza jak by o

w rzeczywisto´sci.

6.1 Twierdzenie Simsona

Dzi´s twierdzenie oraz prosta Simsona spotykane sa równiez pod nazwa twierdzenia i prostej

Wallace'a. A oto i one:

Twierdzenie 24 (Simsona) [17, str. 49] Spodki prostopad ych opuszczonych z dowolnego

punktu okregu na boki trójkata wpisanego w ten okrag leza na jednej prostej zwanej prosta

Simsona.

Dowód:

[5, str. 40-41], [17, str. 49-50] We´zmy dowolny trójkat 4ABC wpisany

w okrag o ´srodku S. Wybierzmy na tym okregu dowolny punkt X i poprowadzmy

z niego proste prostopad e do boków trójkata 4ABC lub ich przed uze´n. Spodki tych

prostopad ych oznaczmy odpowiednio przez P , Q i R. Narysujmy równiez odcinki aczace

punkt X z wierzcho kami A, B, C.

6.1 Twierdzenie Simsona

Zauwazmy, ze katy

^CXB i ^CAB maja równa miare, jako wpisane, oparte na tym

samym uku CB. Oznaczmy ja przez

^ . Podobnie jak ^XAC i ^XBC oparte na uku

, których miare bedziemy dalej oznacza´c przez

^ . Przyjrzyjmy sie teraz trójkatom

prostokatnym 4AP X i 4BQX. Oznaczmy:

^CXQ = ^ ;

^PXA = ^ .

Sumy katów w tych trójkatach mozemy zapisa´c odpowiednio:

w 4BQX :

^ + ^ + ^ + 90 = 180 ;

w 4AP X :

^ + ^ + ^ + 90 = 180 ;

stad:

^ = ^ .

Zauwazmy dalej, ze trójkaty 4QXC i 4AP X sa podobne (kkk), zatem prawdziwa jest

proporcja:

XC
XA

(6.53)

Katy

^XCA i ^XBA maja identyczna miare, bo sa oparte na tym samym uku XA

i bedziemy ja oznacza´c przez

^ . Chcac zapisa´c sumy katów dla trójkatów 4XRC

i 4XP B mamy:

w 4XRC :

90 +

^ + ^ = 180 ;

6.2 Twierdzenie Lemoine

w 4XP B :

90 +

^ + ^PXB = 180 ;

stad obserwujemy, ze:

^PXB = ^ .

Zatem trójkaty 4XRC i 4XP B sa podobne (kkk), a co za tym idzie prawdziwa jest

proporcja:

P B
RC

XB
XC

(6.54)

Zauwazmy równiez, ze podobne sa trójkaty 4XAR i 4XQB (kkk), stad:

(6.55)

Wymnazajac stronami (6.53), (6.54), (6.55) otrzymamy:

P B
RC

XC
XA

XB
XC

= 1

czyli:

P B
RC

= 1:

A dalej na podstawie twierdzenia Menelaosa mozemy stwierdzi´c, ze punkty P , Q, R sa

wspó liniowe.

6.2 Twierdzenie Lemoine

Kolejne twierdzenie zwiazane z okregiem opisanym na trójkacie nosi nazwe za-

czerpnieta od nazwiska francuskiego matematyka Emile'a Michel'a Hyacinthe'a Lemoine

(1840-1912) [12], [11] . W roku 1860 uko´nczy on Politechnike w Paryzu i rozpocza prace

6.2 Twierdzenie Lemoine

jako inzynier, ale nadal jako hobby zajmowa sie geometria. Co ciekawe, nie tylko mate-

matyka, ale równiez muzyka by a jego pasja - by on za ozycielem i cz onkiem muzycznego

zespo u "La Trompette" (Trabki) Jednakze wbrew pozorom twierdzenie to nie zosta o

odkryte po raz pierwszy przez Lemoine, a tylko nazwane w 1884 r. przez J. Neuberga

na jego cze´s´c. Jednak i on nie by pierwszym odkrywca, gdyz twierdzenie to pojawi o

sie wcze´sniej w pracach L.Huilier'a w 1809 oraz Grebego w 1847. Ta niespotykana ilo´s´c

"odkrywców" jak na jedno twierdzenie spowodowa a, ze po dzi´s dzie´n spotykane jest ono

oraz punkt, którego dotyczy pod róznymi nazwami - we Francji jako punkt Lemoine,

w Niemczech jako punkt Grabego, oraz jako punkt L.Huilier'a-Lemoine'-Grebego.

Twierdzenie 25

(Lemoine) [17, srt. 49] Iloczyn odleg o´sci dowolnego punktu okregu

opisanego na trójkacie od wierzcho ka trójkata wpisanego i od boku przeciwleg ego do

tego wierzcho ka jest dla dowolnego punktu wielko´scia sta a.

Dowód:

[17, str. 50] We´zmy dowolny trójkat 4ABC wpisany w okrag o ´srodku S.

Wybierzmy na tym okregu dowolny punkt X i poprowadzmy z niego proste prostopad e

do boków trójkata 4ABC lub ich przed uze´n. Spodki tych prostopad ych oznaczmy

odpowiednio przez P , Q i R. Narysujmy równiez odcinki aczace punkt X z wierz-

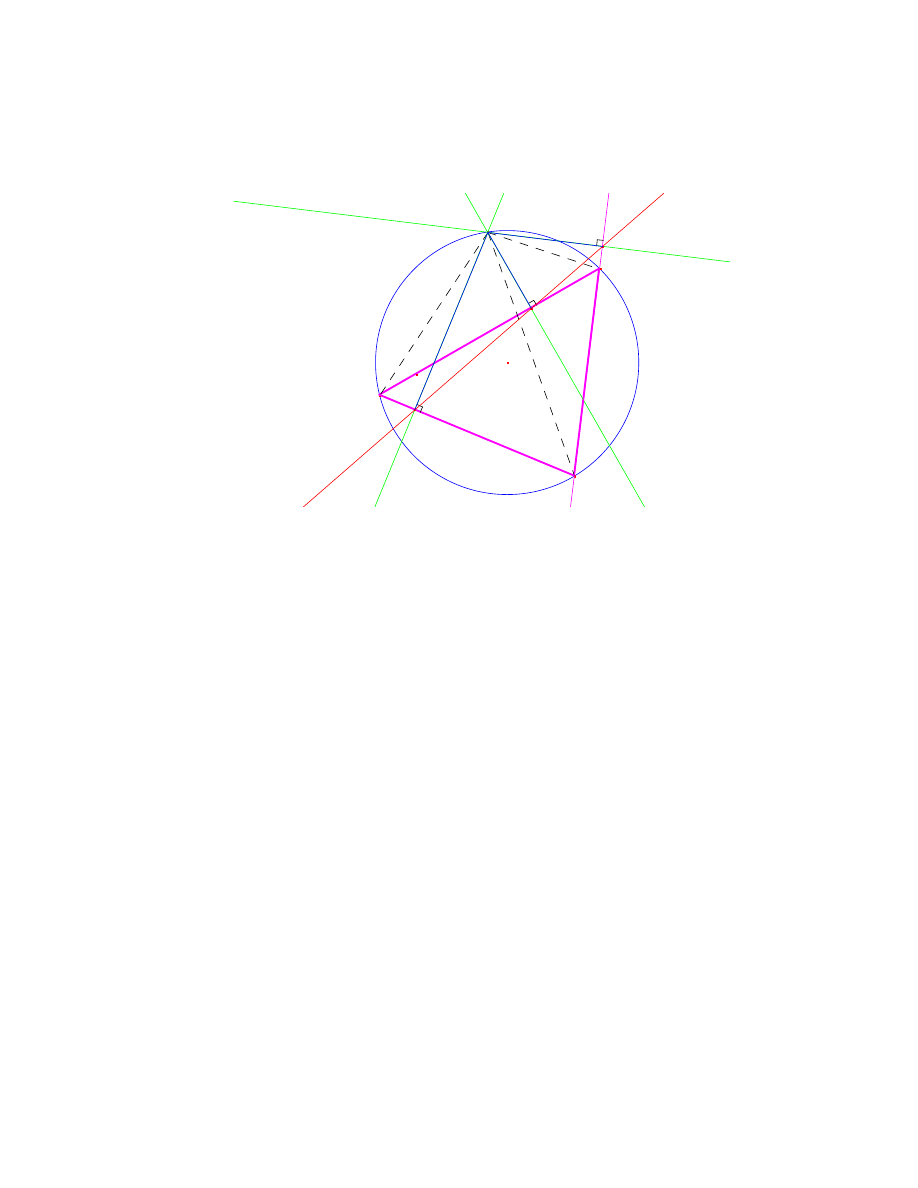
6.2 Twierdzenie Lemoine

cho kami A, B, C.

Zauwazmy, ze katy

^CXB i ^CAB maja równa miare, jako wpisane, oparte na tym

samym uku CB. Oznaczmy ja przez

^ . Podobnie jak ^XAC i ^XBC oparte na uku

, których miare bedziemy dalej oznacza´c przez

^ . Przyjrzyjmy sie teraz trójkatom

prostokatnym 4AP X i 4BQX. Oznaczmy:

^CXQ = ^ ;

^PXA = ^ .

Sumy katów w tych trójkatach mozemy zapisa´c odpowiednio:

w 4BQX :

^ + ^ + ^ + 90 = 180 ;

w 4AP X :

^ + ^ + ^ + 90 = 180 ;

stad:

^ = ^ .

6.2 Twierdzenie Lemoine

Zauwazmy dalej, ze trójkaty 4QXC i 4AP X sa podobne (kkk), zatem prawdziwa jest

proporcja:

XQ
XP

XC
XA

skad XQ XA = XP XC.

(6.56)

Katy

^XCA i ^XBA maja identyczna miare, bo sa oparte na tym samym uku XA

i bedziemy ja oznacza´c przez

^ . Chcac zapisa´c sumy katów dla trójkatów 4XRC

i 4XP B mamy:

w 4XRC :

90 +

^ + ^ = 180 ;

w 4XP B :

90 +

^ + ^PXB = 180 ;

stad obserwujemy, ze:

^PXB = ^ .

Zatem trójkaty 4XRC i 4XP B sa podobne (kkk), a co za tym idzie prawdziwa jest

proporcja:

XP
XR

XB
XC

skad XP XC = XR XB .

(6.57)

Zauwazmy równiez, ze podobne sa trójkaty 4XAR i 4XQB (kkk), stad:

XR
XQ

skad XR XB = XQ XA .

(6.58)

Z przechodnio´sci relacji równo´sci oraz (6.56), (6.57), (6.58) otrzymujemy:

XA XQ = XB XR = XC XP

co naleza o pokaza´c.

6.3 Twierdzenie Salmona

Twierdzenie, które za chwile przedstawie przypisywane jest irlandzkiemu matem-

atykowi i teologowi zarazem - Georgowi Salmonowi (1819-1904) [12], w swojej m odo´sci

studiowa on matematyke w Dublinie oraz Trinity, gdzie zdobywa liczne stypendia i wy-

róznienia. Podczas jednego z wyjazdów na stypendia zacza interesowa´c sie duchowa

sfera zycia. Zainteresowania te poch one y go tak bardzo, ze zaniecha bada´n w dziedzinie

matematyki, a gdy w roku 1862 zaproponowano mu stanowisko profesora uczelni w Tri-

nity, postawiono mu warunek - albo matematyka, albo teologia. Salmon bez wahania

wybra teologie. Jednak najprawdopodobniej jego decyzja nie by a spowodowana nieche-

cia do matematyki, a mozliwo´scia sprawdzenia sie jako teolog, gdyz ko´sció Irlandii przezy-

wa wówczas kryzys. Niemniej jednak równiez jako teolog Salmon zajmowa sie matem-

atyka, ale juz dla w asnej przyjemno´sci i podczas gdy jego teologiczne dysputy sz y do

druku, matematyczne notatki zostawa y w prywatnych notesach.

Twierdzenie 26 (Salmona) [17, str. 50] Jezeli z punktu lezacego na okregu poprowadzimy

3 dowolne cieciwy i na kazdej z nich jako na ´srednicy zbudujemy dowolny okrag, to te okregi

przecinaja sie parami w trzech punktach lezacych na jednej prostej.

Dowód:

[17, str. 50-51] Oznaczmy ko´nce trzech dowolnych cieciw wychodzacych

z wybranego punktu X przez A, B, C. Wówczas punkty te utworza trójkat 4ABC

wpisany w okrag. Z punktu X poprowadzimy odcinki prostopad e do boków trójkata

4ABC, a punkty ich przeciecia z bokami lub ich przed uzeniami oznaczymy przez P ,

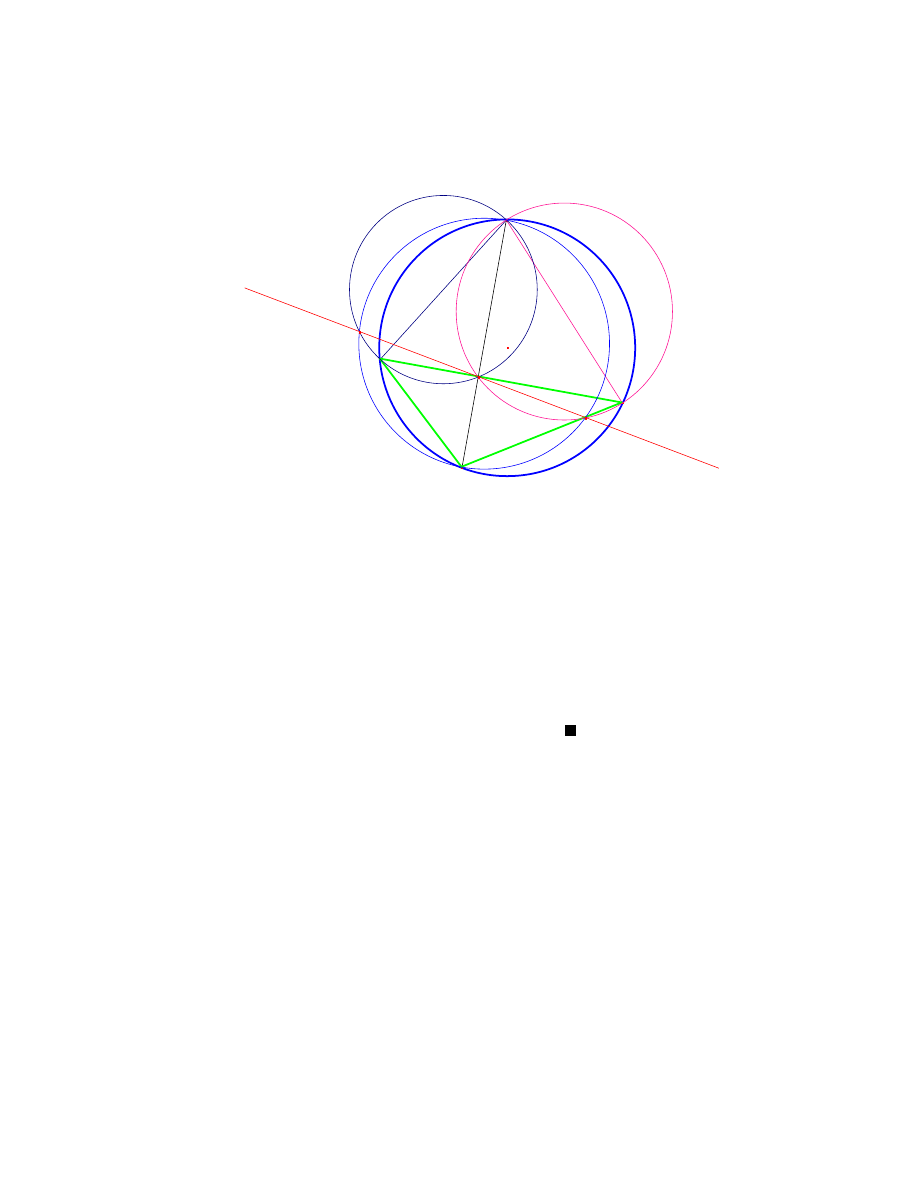
6.3 Twierdzenie Salmona

, R.

Zgodnie z twierdzeniem Simsona punkty P , Q, R beda leza y na jednej prostej. Pokazemy

teraz, ze punkty te sa równiez punktami przeciecia okregów skonstruowanych na cieciwach

, XB, XC. Zauwazmy, ze kat

^XPA jest prosty jako wpisany w okrag o ´srednicy

i oparty na niej, a takze jako wpisany w okrag o ´srednicy XB i równiez na niej oparty.

Stad punkt P jest punktem przeciecia tych dwóch okregów. Analogicznie wykazemy dla

punktów R i Q, ze sa one punktami przeciecia okregów.

Rozdzia 7

Dodatki

SZCZEGÓLNE OKREGI ZWIAZANE Z TRÓJKATEM

Okr gi dopisane

Okr g opisany

Okr g wpisany

Okr g dziewi ciu punktów

7 Dodatki

SZCZEGÓLNE PUNKTY ZWIAZANE Z TRÓJKATEM

rodek okr gu wpisanego

rodek okr gu dopisanego

rodki boków

spodki wysoko ci

ortocentr

rodek okr gu opisanego

rodek ci

ko ci

punkt Gergonne'a

punkt Nagela

rodek okr gu dziewi ciu punktów

7 Dodatki

SZCZEGÓLNE PROSTE ZWIAZANE Z TRÓJKATEM

prosta Eulera

prosta Simsona

przyk adowe proste Cevy
(symetralne boków)

Bibliogra a

[1] A. Bogomolny, Ceva's Theorem: A Matter of Appreciation, X.1999,

http://www.cut-the-knot.org/Generalization/CevaPlus.shtml

[2] A. Bogomolny, The Menelaus Theorem, XI. 1999,

http://www.cut-the-knot.org/Generalization/Menelaus.shtml

[3] S. Brodie, Napoleon's Theorem, http://www.cut-the-knot.org/proofs/napoleon.shtml

[4] A. Brombacher, An exploration of triangles and points of concurrency,

http://jwilson.coe.uga.edu/EMT668/EMT668.Student.Folders/BrombacherAarnout/write-
up%203.aarnout/WRITEUP3AARNOUT.htmlW.

[5] H. S. M. Coxeter, Geometry Revisited, The Mathematical Association of America,

New York 1967

[6] H. S. M. Coxter, Introduction to Geometry, John Wiley & Sons INC.

[7] R. Doman, Wyk ady z Geometrii Elementarnej, Wydawnictwo Naukowe, Pozna´n 2001

[8] R. Fenn, Geometry, Springer, London 2003

[9] W.Janowski, Geometria dla klasy I Liceum Ogólnokszta cacego i Technikum,

Pa´nstwowe Zak ady Wydawnictw Szkolnych, Warszawa 1969

[10] C. Kimberling, Encyclopedia of Triangle Centers - ETC,

http://faculty.evansville.edu/ck6/encyclopedia/

[11] C. Kimberling, Triangle Geometers, http://faculty.evansville.edu/ck6/bstud/tg.html

[12] J O'Connor, E. F Robertson, Biographies,

http://turnbull.mcs.st-and.ac.uk/~history/Biographies/

[13] J. R. Silvester, Geometry Ancient and Modern, Oxford University Press

[14] W. Waliszewski redaktor naczelny, Encyklopedia Szkolna Matematyka,

Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1989

[15] D. Zakrzewska, M. Zakrzewski, Jak rozwiazywa´c zadania - Geometria, Quadrivium,

Wroc aw 1996

Bibliogra a

[16] A. Zalewska, E. Stachowski, Z Pitagorasem do liceum - Teoria,

O cyna Wydawniczo-Poligra czna i Reklamowo-Handlowa "ADAM", Warszawa 1995

[17] S. I. Zetel, Geometria Trójkata, Pa´nstwowe Zak ady Wydawnictw Szkolnych,

Warszawa 1964

Wyszukiwarka

Podobne podstrony:
geometria kolo szyna id 189562 Nieznany
funkcje transporterow ABC id 18 Nieznany
Kilka dowodow id 550212 Nieznany
Gamo P23 CO2 ilmapistooli id 18 Nieznany
Funkcja blony otrzewnowej id 18 Nieznany
geometria 113,5x66cm id 189441 Nieznany
geometria i garść dowodów
lekcja 18 id 265103 Nieznany
18 04 2013 WBC(LEUKOCYTY)id 176 Nieznany (2)
Grishkova kompetenciya 18 id 19 Nieznany
house geometric shapes id 20624 Nieznany
c4 18 12 2010 id 97240 Nieznany
A, TEST 18 id 49152 Nieznany (2)
EATON 18 wylacznik ppoz id 1496 Nieznany
ZZWK egzamin 18 06 2012 id 5944 Nieznany
GEOMETRIA PDF id 189573 Nieznany
GEOMETRIA 2 id 189404 Nieznany
7 18 id 44737 Nieznany (2)

więcej podobnych podstron