GEOMETRIA WYKREŚLNA - PODSTAWOWE KONSTRUKCJE

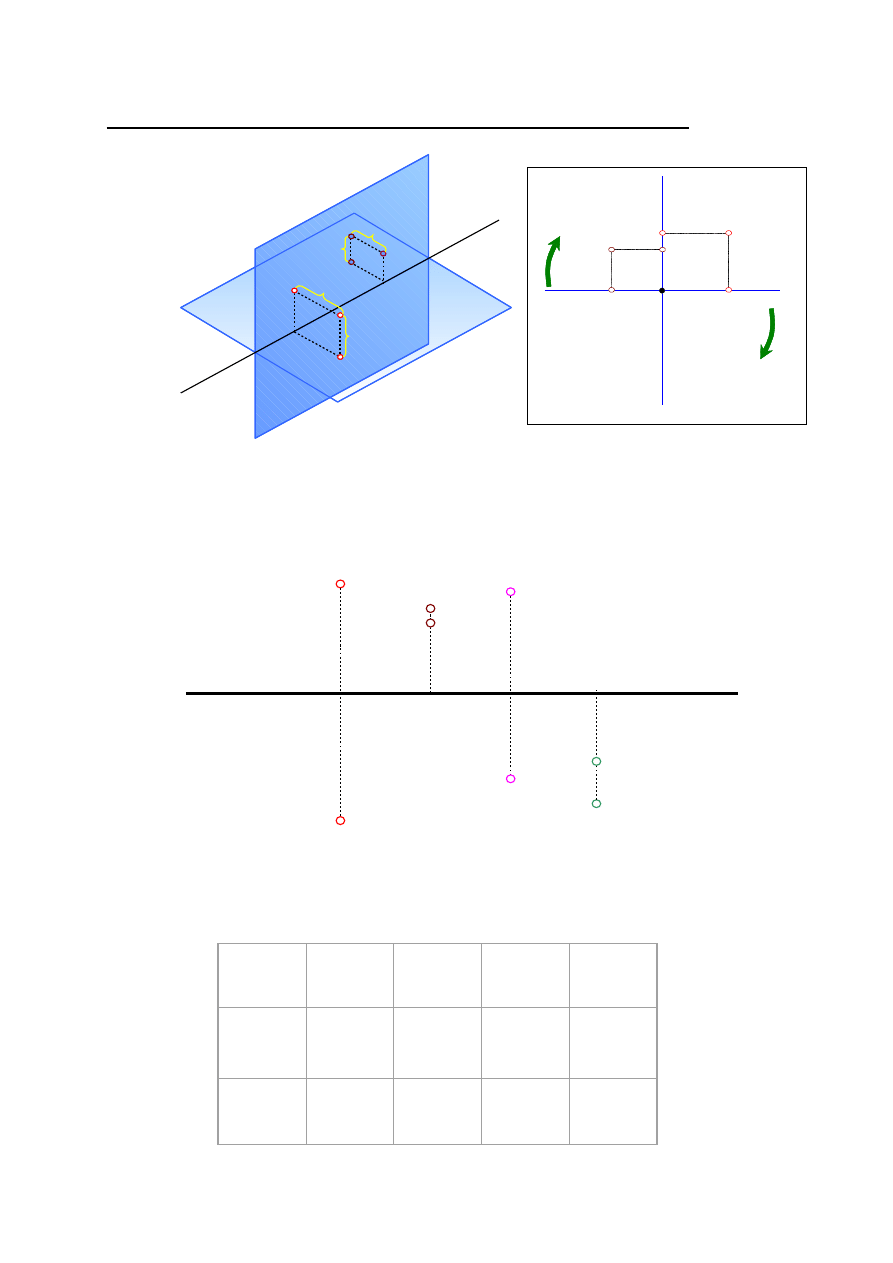
Rzuty punktów w różnych częściach przestrzeni

π

2

π

1

−π

1

−π

2

Oś rzutowania

x

A

A”

A’

B”

B

B’

g

g

w

w

I

II

III

IV

π

2

w – wysokość
g - głębokość

π

2

,−π

1

x

A’

A”

B’

B”

−π

2

, π

1

C’

C”

D’

D”

ćwiartki

→

I II III IV

1

I

II

III

IV

w

+

+

-

-

g

+

-

-

+

I

II

III

IV

w

+

+

-

-

g

+

-

-

+

II

II

II

III

III

IV

IV

w

w

+

+

+

+

--

--

gg

+

+

--

--

+

+

π

1

− π

1

− π

2

π

2

I

II

III

IV

A

A”

A’

B

B”

B’

x





π

1

−π

1

−π

2

π

2

H

p

”

V

p

’

p’

p”

H

p

x

V

p

I

II

III

IV

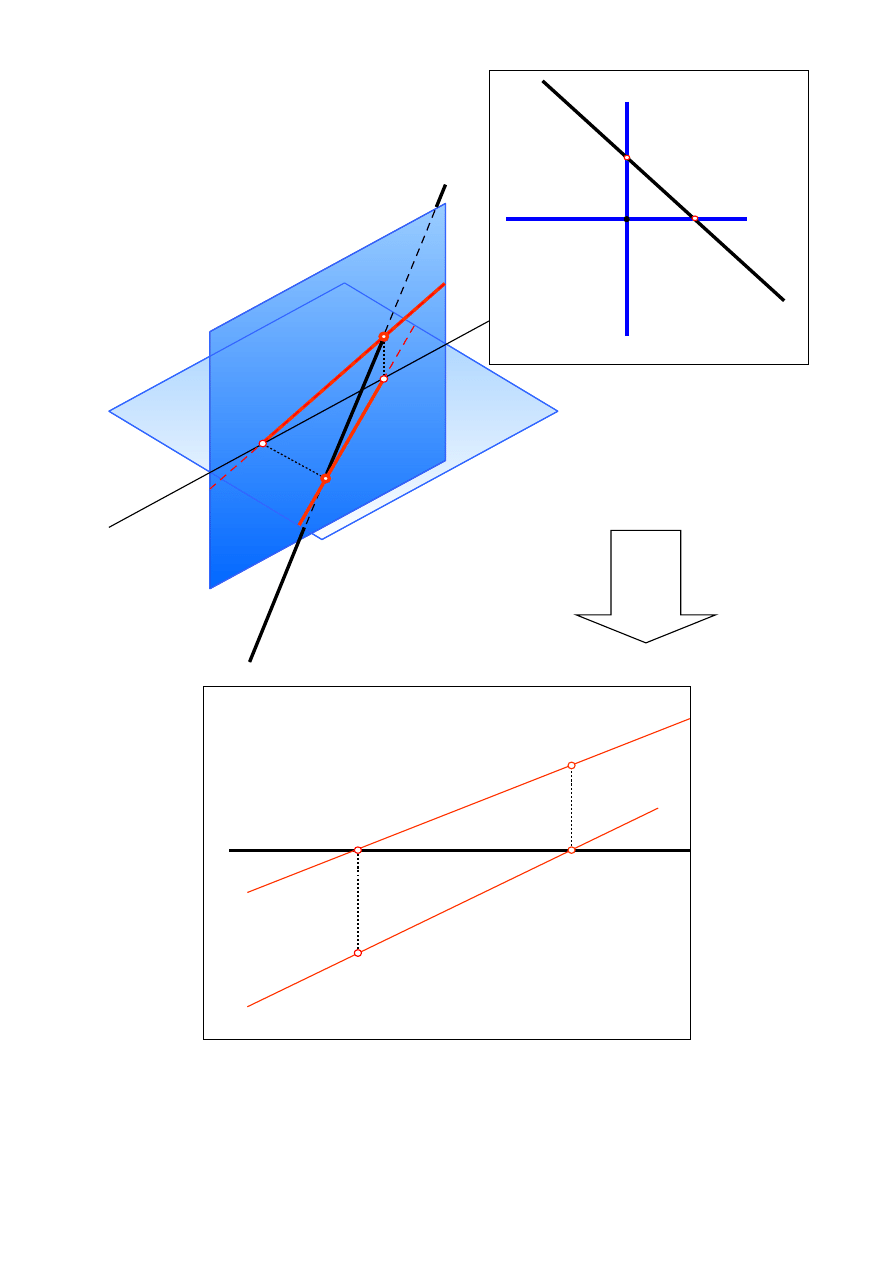
Położenie prostej p w przestrzeni

p

π

1

−π

1

−π

2

π

2

I

II

III

IV

V

p

H

p

x

p

2

π

2

,−π

1

x

H

p

p”

-

π

2

, π

1

H

p

”

V

p

’

V

p

p’

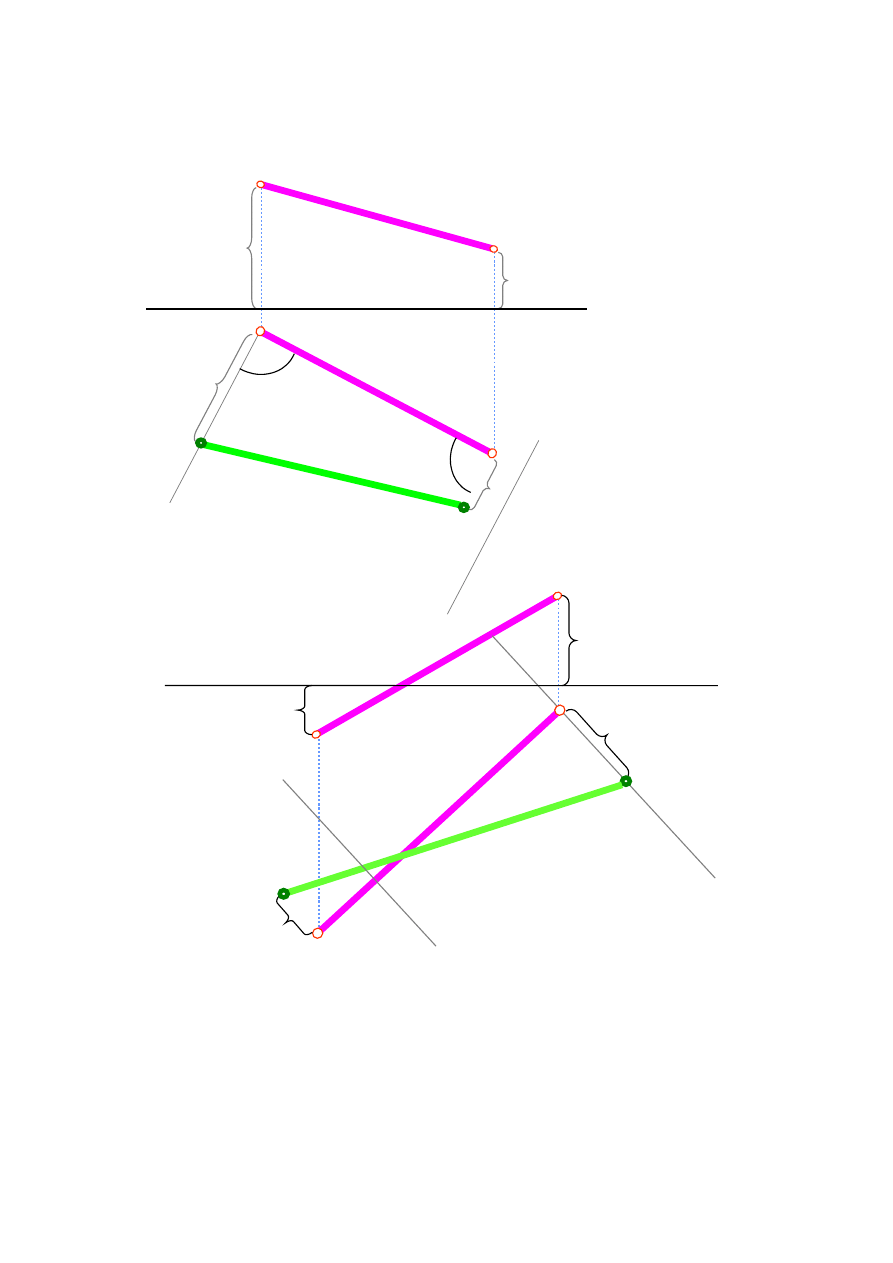
Konstrukcja kładu odcinka – wyznaczanie rzeczywistej długości odcinka.

x

A’

B’

B”

A”

wysokość

punktu A

wysokość

punktu B

A

x

B

x

rzeczywista długość

odcinka

.

3

x

C’

D’

D”

C”

wysokość

punktu C

(ujemna)

wysokość

punktu D

(dodatnia)

rzeczywista długość

odcinka

wysokość

punktu D

wysokość

punktu C

C

x

D”

D

x

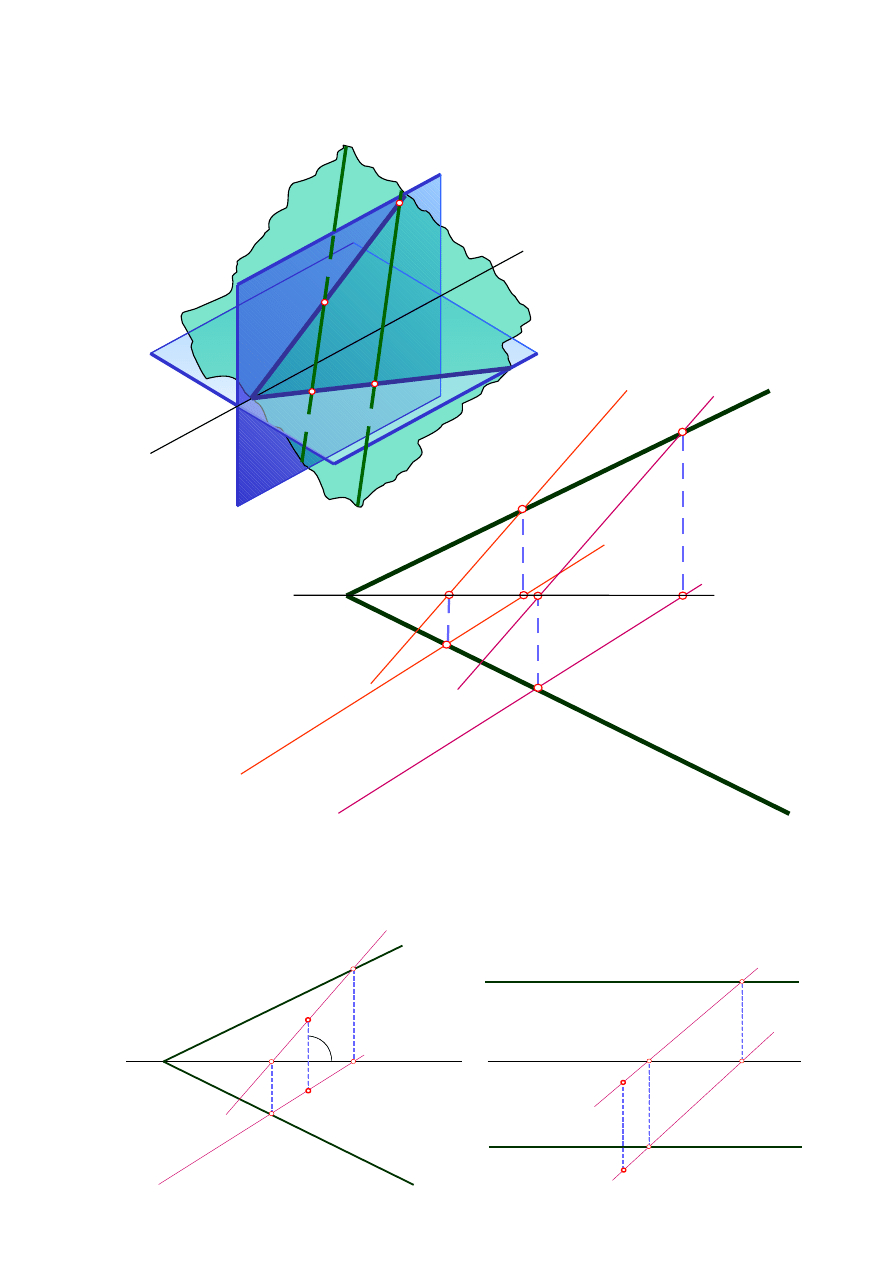
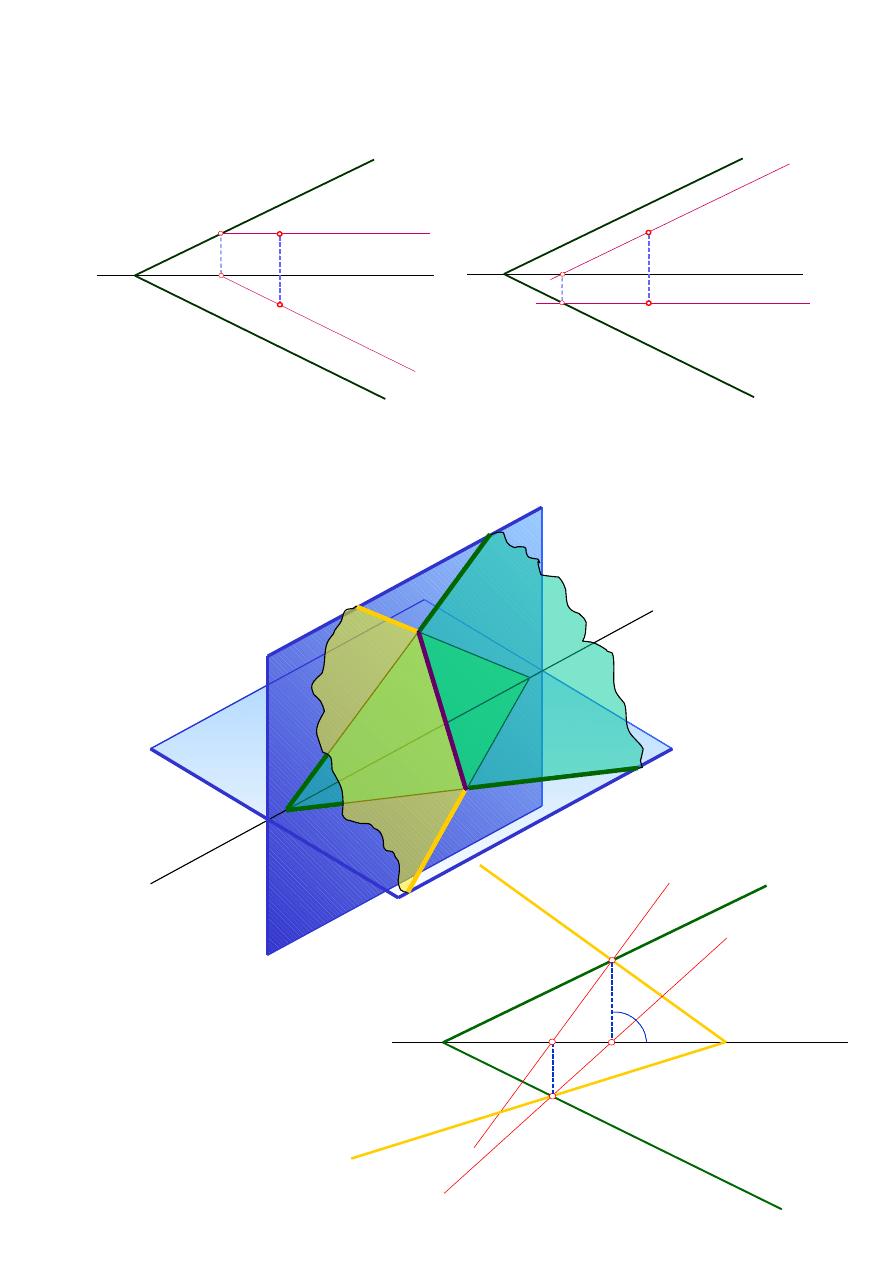
Obraz prostych a i b znajdujących się na płaszczyźnie

α

Określanie przynależności punktu do płaszczyzny:

1. Przy pomocy prostej dowolnej leżącej na płaszczyźnie
2. Przy pomocy prostej poziomej leżącej na płaszczyźnie
3. Przy pomocy prostej czołowej leżącej na płaszczyźnie.

1)

4

π

1

−π

1

−π

2

x

II

III

IV

π

2

α

I

h

α

v

α

a

V

a

V

b

H

a

H

b

D
”

b

x

v

α

h

α

X

α

H

a

”

H

b

”

H

b

’=H

b

H

a

’=H

a

V

a

’

V

a

”=V

a

V

b

’

V

b

”=V

b

a”

b”

a’

D”

b’

x

v

α

h

α

X

α

H

b

”

H

b

’=H

b

V

b

’

V

b

”=V

b

a”

a’

A”

A’

. .

x

v

α

h

α

A”

d”

V

d

V

d

’

H

d

H

d

”

d’

A’

2)

3)

Krawędź płaszczyzn

α

i

β

5

x

v

α

h

α

X

α

A”

A’

b”

b’

V

b

V

b

’

x

v

α

h

α

X

α

A”

A’

c”

c’

H

c

H

c

”

−π

1

−π

2

x

II

III

IV

π

2

π

1

α

β

I

h

β

v

β

h

α

v

α

D
”

k

x

v

α

h

α

v

β

h

β

V

k

H

k

V

k

’

H

k

”

k”

k’

. .

x

v

α

h

α

v

α

h

α

X

α

p’

p”

h

ε

=

v

ε

V

k

H

k

H

k

”

V

k

’

M’

M”

k’

=k”

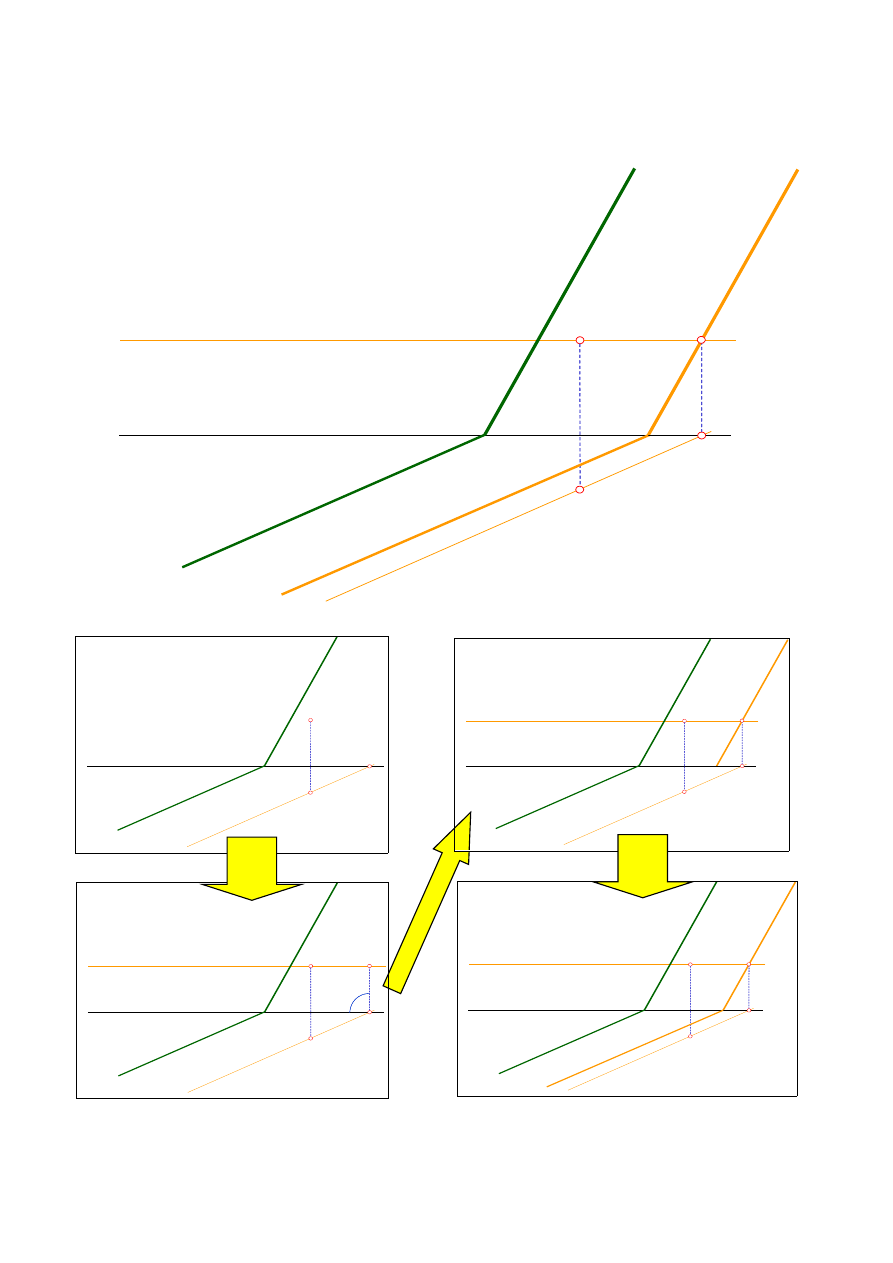
Prosta p przebijająca płaszczyznę

α

w punkcie M.

Wyznaczanie punktu przebicia
płaszczyzny

α

prostą p

1.

Wyznaczenie płaszczyzny rzutującej

ε

(płaszczyzna zawiera prostą p)

2.

Wyznaczenie krawędzi między płaszczyznami

α

i

ε

3.

Miejsce przecięcia rzutu k’ krawędzi z rzutem p’ prostej wyznacza rzut M’ punktu

4.

Wyznaczenie drugiego rzutu M” punktu na rzucie prostej p”

H

p

α

h

α

v

α

X

α

π

1

−π

1

−π

2

x

II

III

IV

π

2

I

M

p

6

x

v

α

h

α

A’

A”

a’

V

a

’

Dana jest płaszczyzna

α

i punkt A nie leżący na niej. Przeprowadzić

płaszczyznę

β

przechodzącą przez A i równoległą do

α

.

7

x

v

α

h

α

A’

A”

h

β

v

β

a’

a”

V

a

V

a

’

X

β

x

v

α

h

α

A’

A”

a’

a”

V

a

V

a

’

. .

x

v

α

h

α

A’

A”

v

β

a’

a”

V

a

V

a

’

X

β

x

v

α

h

α

A’

A”

h

β

v

β

a’

a”

V

a

V

a

’

X

β

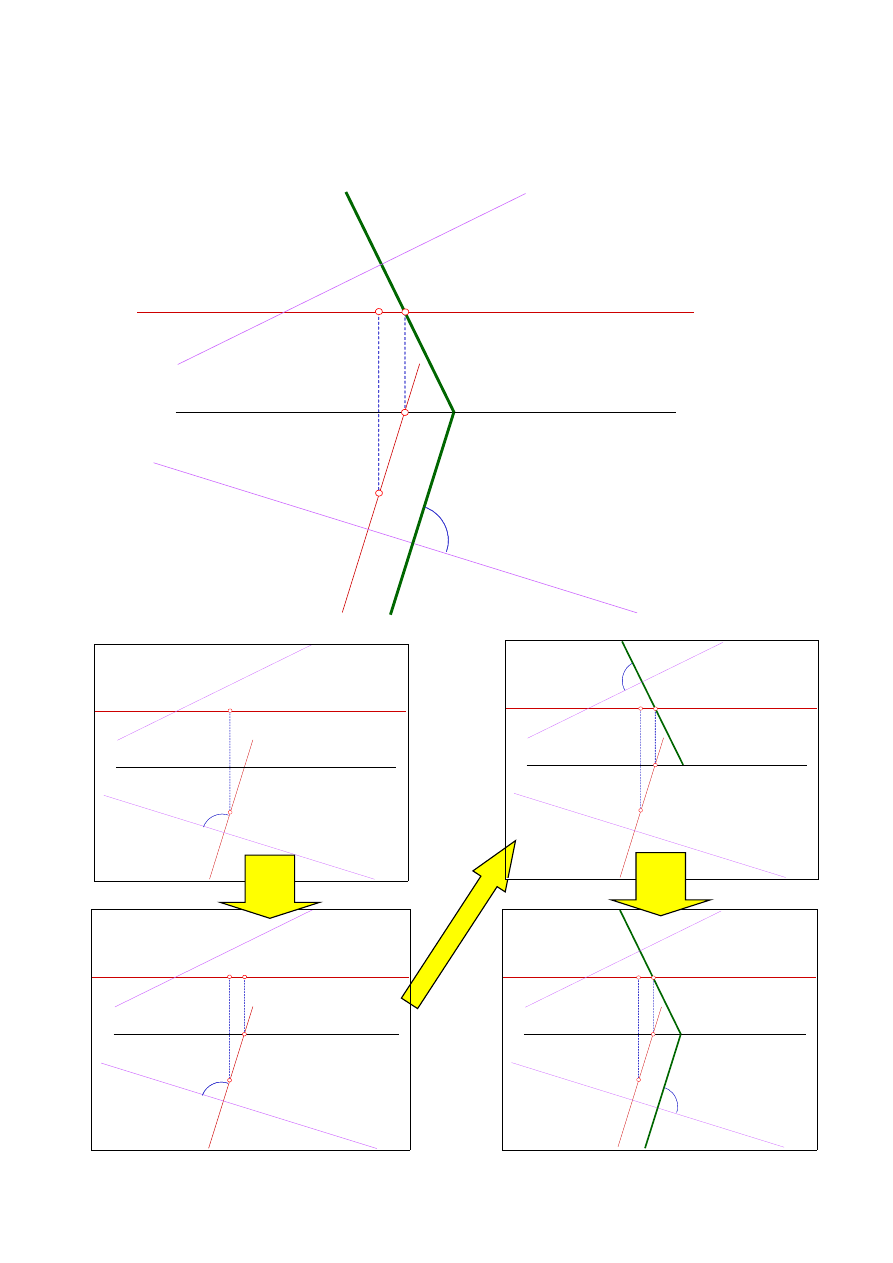
Dana jest prosta p i punkt A. Przeprowadzić płaszczyznę

α

przechodzącą

przez A i prostopadłą do p.

8

x

p”

p’

A”

A’

m”

m’

. .

x

p”

p’

A”

A’

m”

m’

V

m

’

V

m

. .

x

p”

p’

A”

A’

v

α

X

α

m”

m’

V

m

’

V

m

..

V

m

’

x

p”

p’

A”

A’

v

α

h

α

X

α

m”

m’

V

m

. .

V

m

’

x

p”

p’

A”

A’

v

α

h

α

X

α

m”

m’

V

m

. .

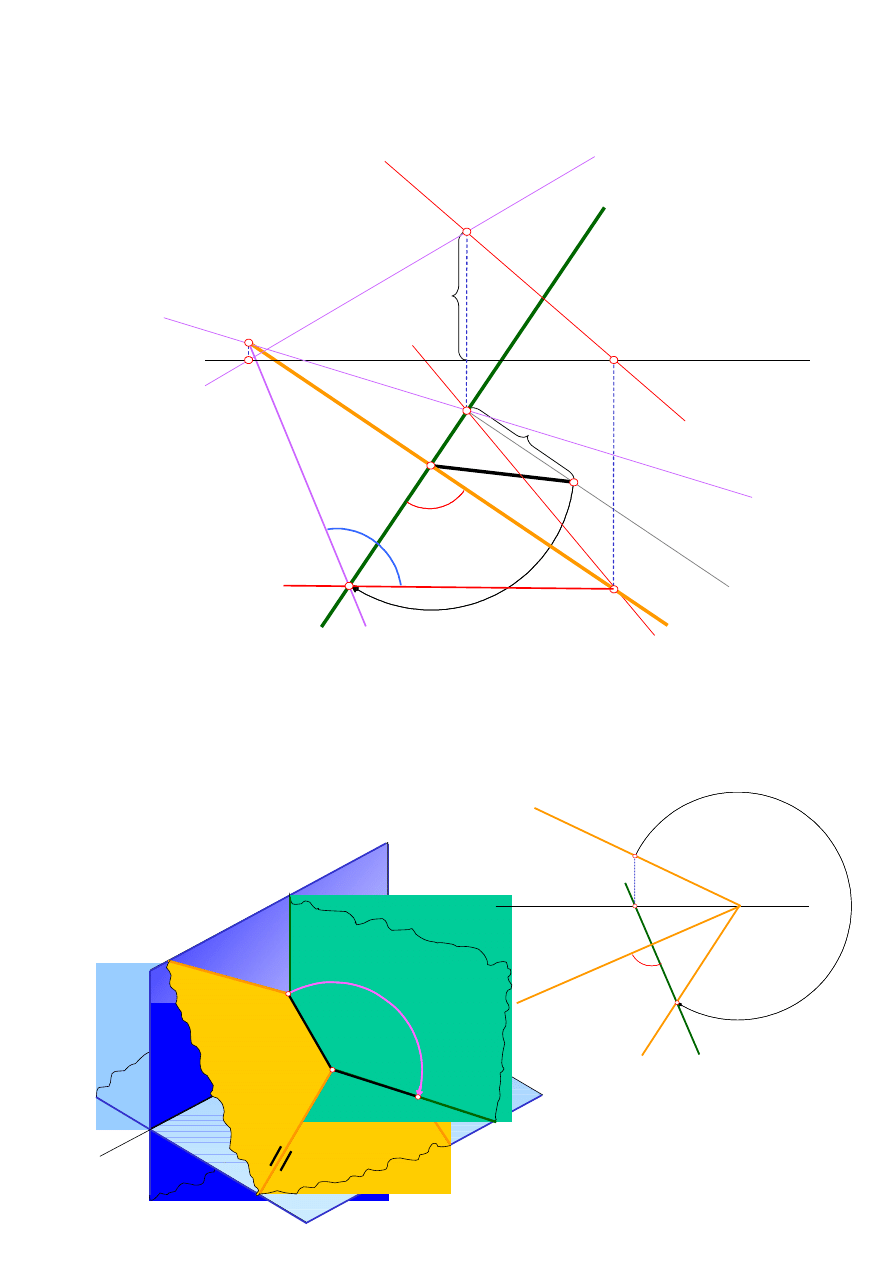
Dane są proste a i b. Wyznaczyć rzeczywisty kąt między tymi prostymi.

1.

Wyznaczenie rzutów punktu przecięcia prostych (M’ i M”)

2.

Wyznaczenie śladu h

α

płaszczyzny na której leżą proste a i b

3.

Wyznaczenie h

ω

(prostopadle do h

α

)

4.

Wyznaczenie M

x

5.

Wyznaczenie M

o

6.

Kąt między prostymi a

o

i b

o

jest rozwiązaniem zadania

Konstrukcja kładu płaszczyzny

KŁAD PŁASZCZYZNY
(

α

o

)pozwala na wyznaczenie

rzeczywistych wymiarów elementów
znajdujących się na płaszczyźnie

α

.

9

π

1

III

II

IV

I

π

2

α

ο

α

ο

ωω

α

1=1”

v

α

h

α

1

o

S

r

v

ω

v

α

ο

r

x

..

x

v

α

h

α

h

ω

1”

1’

1

o

X

α

v

α

ο

=X

α

o

x

a’

M”

M’

b’

a”

b”

H

a

”

H

b

”

H

b

= H

b

o

H

a

=H

a

o

h

α

M

x

S

o

..

r

x

h

ω

M

o

φ

a

o

b

o

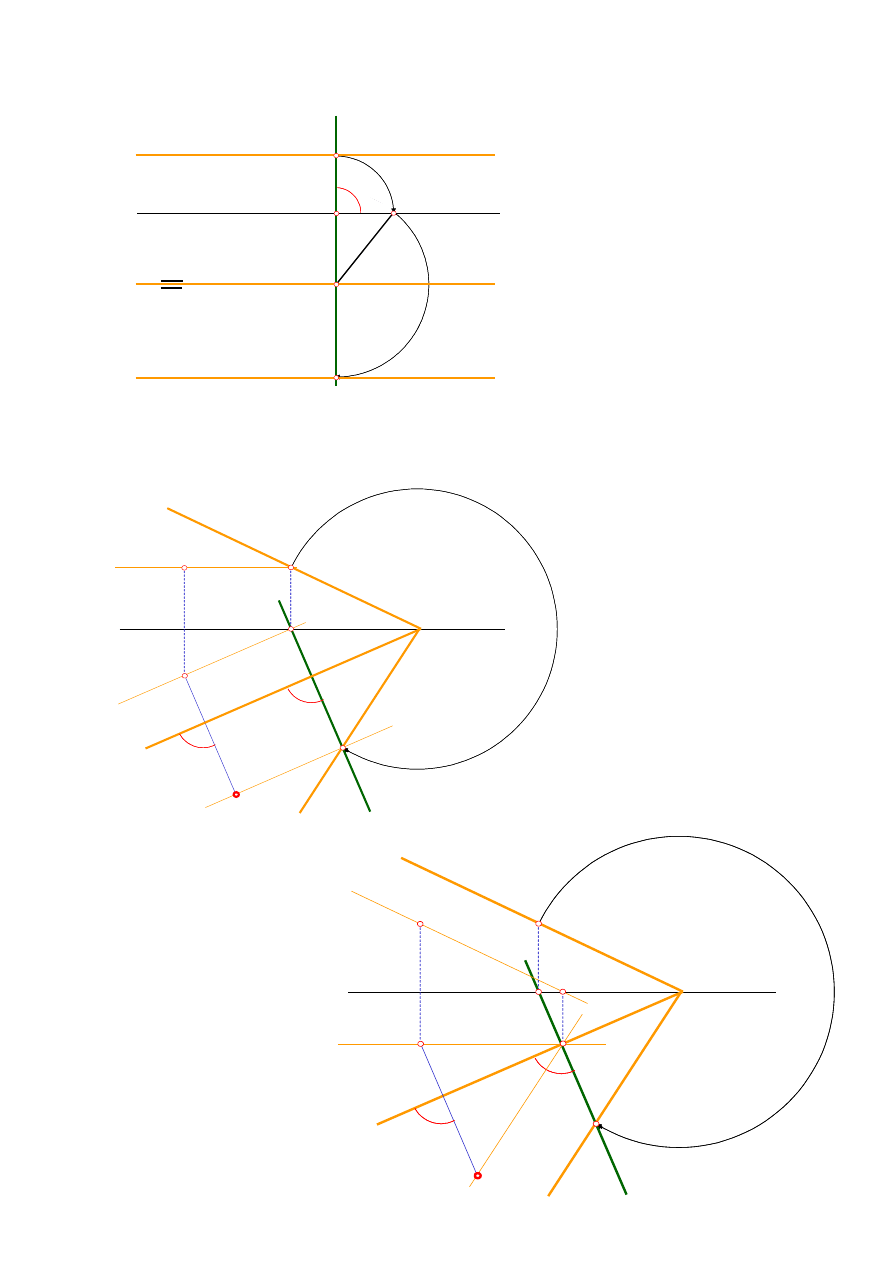
Kład płaszczyzny

α

równoległej do osi x

Konstrukcja do wyznaczania punktu A

o

na kładzie płaszczyzny

Przy użyciu prostej poziomej

Przy użyciu prostej czołowej

10

1’

. .

x

v

α

h

α

h

ω

1”

1

x

1

o

v

α

ο

r

v

ω

S

..

x

v

α

h

α

h

ω

V

a

X

α

v

α

ο

=X

α

o

A’

A”

V

a

’

a’

a”

V

a

o

A

o

a

o

..

..

x

v

α

h

α

h

ω

1”

1’

1

o

X

α

v

α

ο

=X

α

o

A’

A”

b”

b’

H

b

”

H

b

b

o

A

o

..