PŁASKA GEOMETRIA MAS

Środek ciężkości figury płaskiej

Momentami statycznymi M

x

i M

y

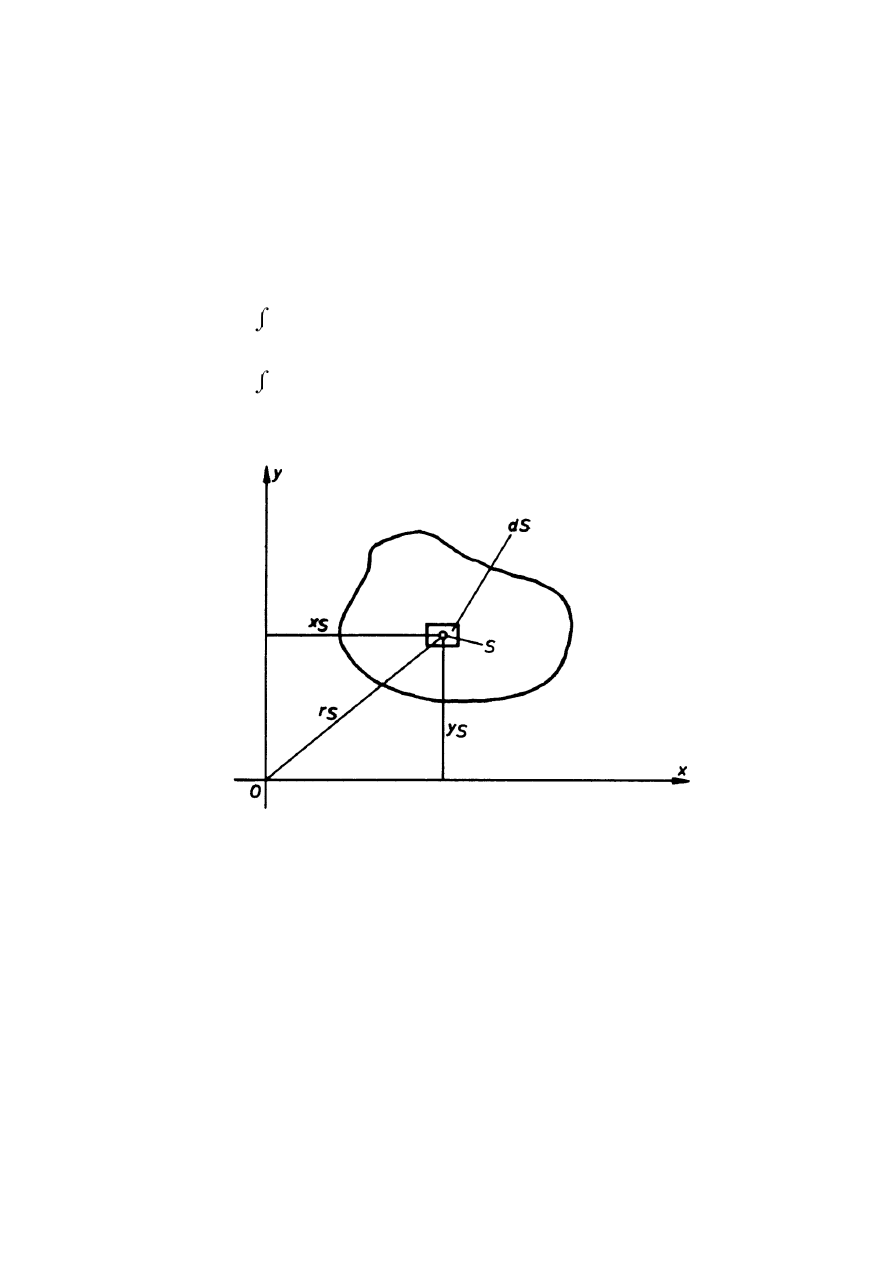
figury płaskiej względem osi x lub y (rys. 7.1)

nazywamy granicę algebraicznej sumy iloczynów elementarnych pól dS przez ich odległości

od osi, gdy elementarne pola dS dążą do zera, tzn.:

M

x

=

S

y dS

M

y

=

S

x dS

(7.1)

Rys. 7.1.

Punkt S, którego położenie jest określone za pomocą promienia wektora r, nazywamy

środkiem masy układu (środkiem ciężkości).

Jeśli znane jest położenie środka ciężkości figury płaskiej, to wtedy momenty statyczne

można określić wprost:

M

x

= S y

S

,

M

y

= S x

S,

(7.2)

gdzie:

S – pole figury płaskiej,

x

S

, y

S

– współrzędne jej środka ciężkości w przyjętym układzie osi x, y.

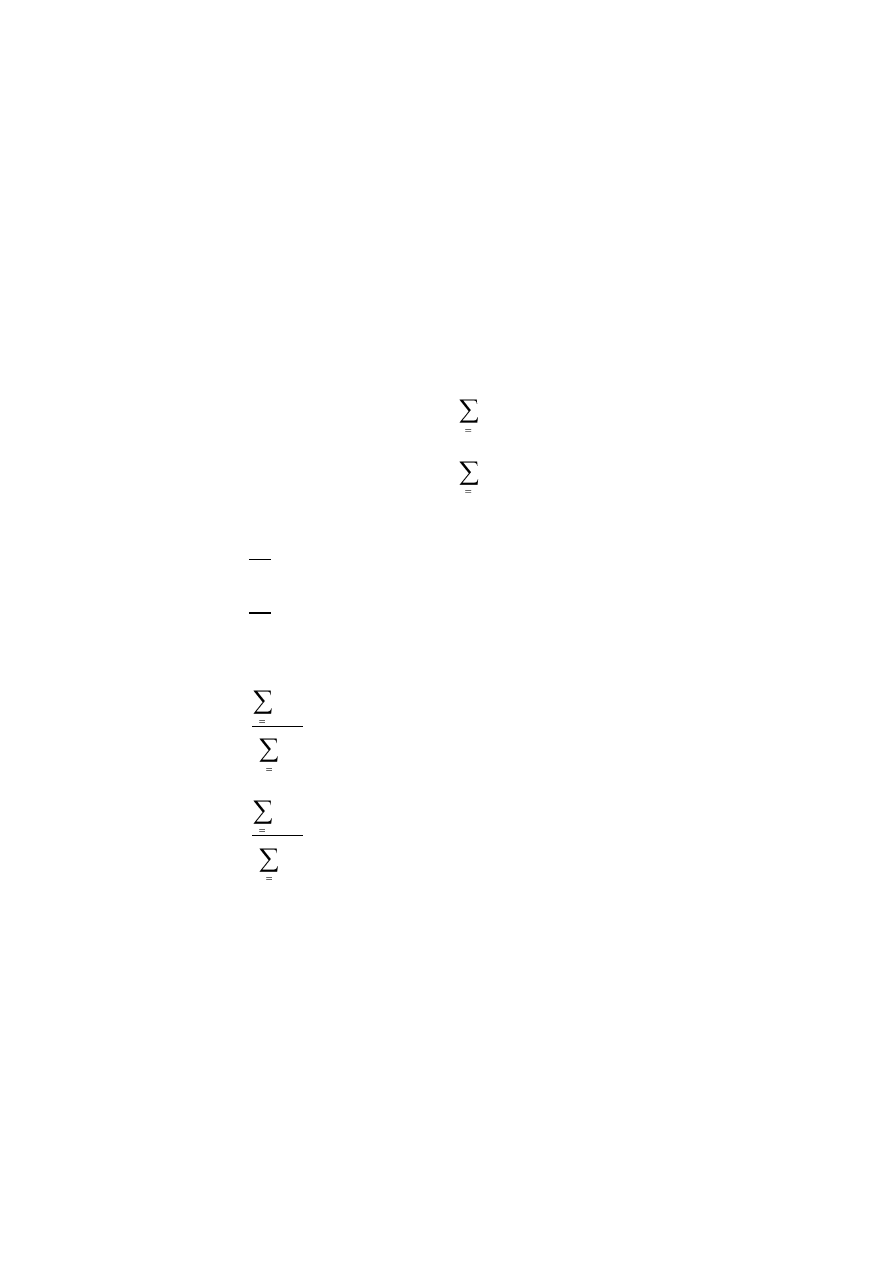
Współrzędne x

S

, y

S

mogą być dodatnie lub ujemne. Wobec tego i momenty statyczne

mogą przyjmować dodatnie lub ujemne wartości. Dla każdej osi przechodzącej przez środek

ciężkości (tzw. osi ciężkości) współrzędne są równe zeru. Wynika stąd wniosek, że momenty

statyczne obliczane względem osi ciężkości są równe zeru.

Do obliczenia momentu statycznego figury złożonej, której środka ciężkości nie

potrafimy wyznaczyć w sposób bezpośredni, zmuszeni jesteśmy podzielić tę figurę na figury

elementarne (o znanym położeniu środków ciężkości) i wtedy moment statyczny całej figury

względem danej osi będzie równy sumie momentów poszczególnych elementów względem

tej osi:

M

x

= S

1

y

1

+ S

2

y

2

+ … + S

n

y

n

=

n

i

i

i

y

S

1

M

y

= S

1

x

1

+ S

2

x

2

+ … + S

n

x

n

=

n

i

i

i

x

S

1

(7.3)

Współrzędne środka ciężkości figury płaskiej można wyznaczyć z (7.2):

x

S

=

M

y

S

y

S

=

M

x

S

(7.4)

Dla figur złożonych otrzymamy z przekształcenia wzoru (7.3):

x

S

=

n

i

i

n

i

i

i

S

x

S

1

1

,

y

S

=

n

i

i

n

i

i

i

S

y

S

1

1

.

(7.5)

Równania (7.5) pozwalają wyznaczyć współrzędne środka ciężkości figury płaskiej, gdy

znane są pola powierzchni i współrzędne środków ciężkości poszczególnych figur.

Przy wyznaczaniu środków ciężkości pomocne są pewne twierdzenia, a mianowicie:

- środek ciężkości układu płaskiego leży w płaszczyźnie tego układu,

- środek ciężkości linii prostej leży na tej linii,

- środek ciężkości dwóch punktów materialnych leży na prostej łączącej te punkty i dzieli

odległość obu punktów na odcinki o długościach odwrotnie proporcjonalnych do ich mas,

- środek ciężkości układu mającego środek symetrii leży w tym środku,

- jeżeli układ ma oś symetrii, środek ciężkości leży na niej,

- jeżeli układ ma dwie lub więcej osi symetrii, środek ciężkości leży na przecięciu się tych

osi,

- rzut środka ciężkości figury płaskiej na dowolną płaszczyznę jest środkiem ciężkości

rzutu tej figury na daną płaszczyznę.

Moment statyczny figury płaskiej względem dowolnego punktu O jest sumą wektorową

momentów statycznych poszczególnych elementów układu względem O.

Moment statyczny dowolnej figury płaskiej względem dowolnej prostej L równa się

wektorowej sumie momentów statycznych poszczególnych figur elementarnych względem tej

prostej L.

Wynikają stąd pewne własności środka ciężkości, których znajomość ułatwia

rozwiązywanie szeregu zagadnień, a mianowicie:

- jeśli moment statyczny dowolnej figury płaskiej względem pewnego punktu jest równy

zeru, to punkt ten jest środkiem ciężkości. Podobnie możemy powiedzieć, że jeśli moment

statyczny figury płaskiej względem pewnej prostej jest równy zeru, to wtedy ta prosta

przechodzi przez środek ciężkości,

- jeśli figura płaska posiada oś symetrii, to moment statyczny figury względem tej osi jest

równy zeru,

- jeśli figurę płaską podzielimy na elementy o polach powierzchni S

1

, S

2

,... S

n

o znanych

środkach ciężkości, to środek ciężkości całej figury płaskiej jest równocześnie środkiem

ciężkości poszczególnych figur (S

1

, S

2

,... S

n

) względem ich środków.

Momenty bezwładności i dewiacji (zboczenia) figury płaskiej

Oprócz momentów statycznych, które są momentami stopnia pierwszego, istnieją

momenty stopnia drugiego, którymi są momenty bezwładności oraz momenty dewiacji

(zboczenia). Mają one szczególne znaczenie w wytrzymałości materiałów.

Osiowym momentem bezwładności figury płaskiej względem dowolnej osi leżącej w

płaszczyźnie figury (rys. 7.1) nazywamy granicę algebraicznej sumy, dla całej powierzchni S

figury płaskiej, iloczynów elementarnych pól dS przez kwadrat ich odległości od danej osi,

gdy elementarne pola dążą do zera, tzn.:

J

x

=

S

y

2

dS

J

y

=

S

x

2

dS

(7.6)

Momenty te są zawsze dodatnie i można je traktować jako swego rodzaju miarę rozproszenia

przekroju wokół danej osi: im bardziej pole figury płaskiej jest skupione wokół osi, tym

moment bezwładności względem niej jest mniejszy.

Biegunowym momentem bezwładności figury płaskiej nazywamy granicę algebraicznej

sumy, dla całej powierzchni S figury płaskiej, iloczynów elementarnych pól dS przez kwadrat

odległości od początku układu współrzędnych (rys. 7.1), gdy elementarne pola dążą do zera.

Wykorzystując związek geometryczny występujący między współrzędnymi (x, y) a

odległością biegunową r (rys. 7.1), biegunowy moment bezwładności możemy określić jako

sumę osiowych momentów bezwładności, gdyż:

r

2

= x

2

+ y

2

J

0

=

S

r

2

dS =

S

(x

2

+ y

2

) dS = J

x

+ J

y

(7.7)

Moment ten jest swego rodzaju miarą rozproszenia pola figury płaskiej wokół początku

układu współrzędnych.

Z podanych zależności wynika:

- moment bezwładności względem osi jest równy sumie momentów bezwładności

względem dwóch płaszczyzn wzajemnie prostopadłych, przecinających się wzdłuż tej osi,

- biegunowy moment bezwładności J

0

jest równy sumie momentów bezwładności

względem dwu wzajemnie prostopadłych osi, przecinających się w punkcie O (dla układu

płaskiego).

Miarą momentu bezwładności jest [m

4

].

Momentem dewiacji (zboczenia) figury płaskiej o powierzchni S nazywamy granicę

algebraicznej sumy iloczynów elementarnych powierzchni dS → 0 przez ich współrzędne x i

y. Sumowanie to odbywa się po całej powierzchni S figury płaskiej, tzn.:

J

xy

=

S

xy dS

(7.8)

Moment dewiacji J

xy

danej figury płaskiej równa się zeru, jeśli choć jedna z osi,

względem których został wyznaczony, jest osią symetrii rozpatrywanej figury. J

xy

może

przyjmować wartości dodatnie, ujemne lub zero.

Między momentami bezwładności względem układów osi równoległych, z których

jeden jest układem osi środkowych: x

S

, y

S

(rys. 7.2), zachodzą następujące związki (tzw.

wzory Steinera):

J

x

= J

xS

+ a

2

S,

J

y

= J

yS

+ b

2

S,

(7.9)

J

xy

= J

xSyS

+ a b S,

gdzie:

a, b – współrzędne środka ciężkości w układzie xy (rys. 7.2),

x

S

, y

S

– osie przechodzące przez środek ciężkości figury płaskiej,

x, y – osie równoległe do x

S

, y

S

.

Twierdzenie Steinera, które zostało zapisane za pomocą wzorów (7.9) wyraża się

następująco:

Rys. 7.2.

Moment bezwładności względem dowolnej osi x, równoległej do osi x

S

, przechodzącej

przez środek ciężkości figury płaskiej, jest równy momentowi bezwładności tej figury

względem osi x

S

,

powiększony o iloczyn pola powierzchni i kwadrat odległości pomiędzy

osiami.

Z twierdzenia Steinera wynika, że momenty bezwładności względem osi

przechodzących przez środek ciężkości są najmniejsze. Płaszczyzny takie lub osie nazywa się

płaszczyznami lub osiami środkowymi.

Moment bezwładności względem płaszczyzny, osi lub punktu można wyrazić jako

iloczyn masy ciała przez kwadrat pewnej odległości noszącej nazwę promienia bezwładności,

oznaczanej przez i z odpowiednim indeksem określającym względem czego jest obliczany

moment bezwładności (np. i

x

– oznacza promień bezwładności masy względem osi x).

Ogólnie:

i

i

=

I

i

m

(7.10)

Promień bezwładności odpowiada odległości w której należałoby skupić całą masę, aby

moment bezwładności skupionej masy był równy momentowi bezwładności całej masy.

Pojęcia promienia bezwładności i

i

nie należy utożsamiać z odległością środka masy r

C

,

gdyż są to pojęcia całkowicie różne.

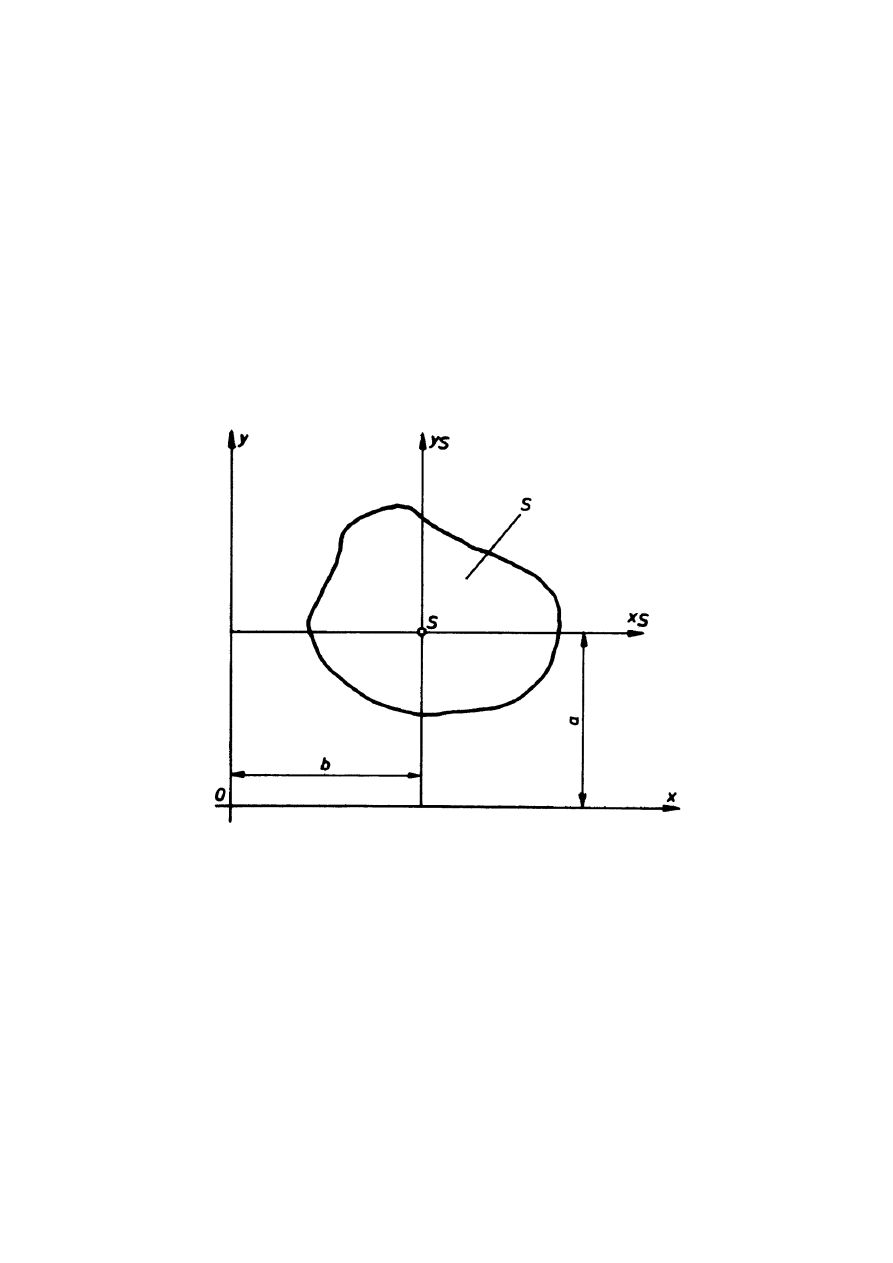
Rys. 7.3.

Dla układów obróconych (rys. 7.3) związki między momentami przedstawiają się w

sposób następujący:

J

x'

=

J

x

+ J

y

2

+

J

x

- J

y

2

cos2φ - J

xy

sin2φ ,

J

y'

=

J

x

+ J

y

2

-

J

x

- J

y

2

cos2φ + J

xy

sin2φ ,

(7.10)

J

x'y'

=

J

x

- J

y

2

sin2φ + J

xy

cos2φ .

gdzie:

φ – kąt między układami osi obróconych, mierzony od dodatniego kierunku osi x, odkładany

zgodnie z zasadami stosowanymi w trygonometrii.

Wzory (7.10) wyrażają szukane zależności między momentami bezwładności i dewiacji

dla dwóch układów osi współrzędnych o wspólnym początku układu współrzędnych.

Dodając stronami pierwsze dwa równania (7.10) łatwo zauważyć związek:

J

x

+ J

y

= J

x’

+ J

y’

= J

0

= const.

(7.11)

Widzimy, ze suma momentów bezwładności względem dwu wzajemnie prostopadłych

osi, przecinających się w danym punkcie O, nie zależy od kierunku tych osi (od kąta φ) i jest

równa biegunowemu momentowi bezwładności względem O.

Osiami głównymi pola figury płaskiej nazywamy układ prostokątnych osi, względem

których moment dewiacji danej figury jest równy zeru. Oznaczać je będziemy przez 1, 2.

Osie główne, których początek leży w środku ciężkości rozpatrywanej figury płaskiej,

nazywamy głównymi centralnymi osiami bezwładności.

Osie główne są w stosunku do dowolnie przyjętego układu osi x, y (rys. 7.4) obrócone o kąt φ

taki, że:

tg2φ = -

2 J

xy

J

x

- J

y

(7.12)

Otrzymujemy dwa pierwiastki φ

oI

oraz φ

oII

w przedziale (0; 2π). W celu rozstrzygnięcia, która

oś jest osią maksymalną momentu bezwładności a która minimalną, można skorzystać z

poniższych wzorów.

Różniczkując otrzymujemy:

oI

xy

x

J

d

J

d

o

2

sin

4

1

2

1

2

oII

xy

x

J

d

J

d

oII

2

sin

4

2

1

2

(7.13)

Ze wzorów (7.13) widać, że oś 1 maksymalnego momentu bezwładności tworzy z osią x

kąt ostry przy momencie J

xy

< 0, zaś kąt rozwarty przy momencie J

xy

> 0.

Osiowe momenty bezwładności wyznaczone względem osi głównych, tzw. główne

momenty bezwładności, mają wartości ekstremalne: moment względem jednej z nich jest

maksymalny który oznaczamy go przez J

1

, drugi – minimalny i oznaczamy go przez J

2

.

Wartości tych momentów wyznacza się z następujących wzorów:

J

1

= J

max

=

J

x

+ J

y

2

+

(

J

x

- J

y

2

)

2

+ J

xy

2

,

J

2

= J

min

=

J

x

+ J

y

2

-

(

J

x

- J

y

2

)

2

+ J

xy

2

,

(7.14)

gdzie:

J

x

, J

y

, J

xy

– momenty bezwładności oraz dewiacji względem dowolnie przyjętego układu osi

współrzędnych x, y układu o takim samym początku jak szukany układ osi głównych

(rys. 7.4).

Rys. 7.4.

Wzory (7.12) i (7.14) pozwalają wyznaczyć główne osie i główne momenty

bezwładności, jeżeli znamy momenty bezwładności i moment dewiacji względem dowolnych

osi x, y.