GEOMETRIA ANALITYCZNA
W PRZESTRZENI
(czyli bardziej po ludzku w 3D)
1. Podstawowe definicje.
Prostokątny układ współrzędnych Oxyz – uporządkowana trójka osi Ox, Oy, Oz wzajemnie prostopadłych o wspólnym
początku O i wspólnej jednostce.
Każdemu punktowi przyporządkowujemy uporządkowaną trójkę liczb x,y,z zwanych współrzędnymi punktu P (i na
odwrót), przy czym x,y,z są współrzędnymi rzutów prostokątnych punktu P odpowiednio na osie Ox, Oy, Oz.
Wektor
– uporządkowana para punktów, z których pierwszy to początek, a drugi punkt to koniec wektora.
, P – początek, – koniec,
Wektor zerowy
– wektor, którego początek i koniec pokrywają się:
.
Współrzędne wektora
,
:
.
Długość wektora
– długość odcinka
:
.
Kierunek niezerowego wektora
– kierunek prostej .
Zwrot niezerowego wektora
– ten zwrot (z dwu) prostej , w którym poprzedza .
Wektory równoległe
– wektory, które mają ten sam kierunek.
Wektory równe
– wektory, które mają ten sam kierunek, zwrot i długość.
Wektory przeciwne
– wektory, które mają ten sam kierunek i długość, zwroty przeciwne.
Suma wektorów
– wektor taki, że
Różnica wektorów
– suma wektorów .
Iloczyn wektora niezerowego
przez liczbę – wektor, który:
jest równoległy do
,
ma zwrot zgodny ze zwrotem
, gdy lub zwrot przeciwny, gdy ,
ma długość
.
Jeżeli
lub , to .
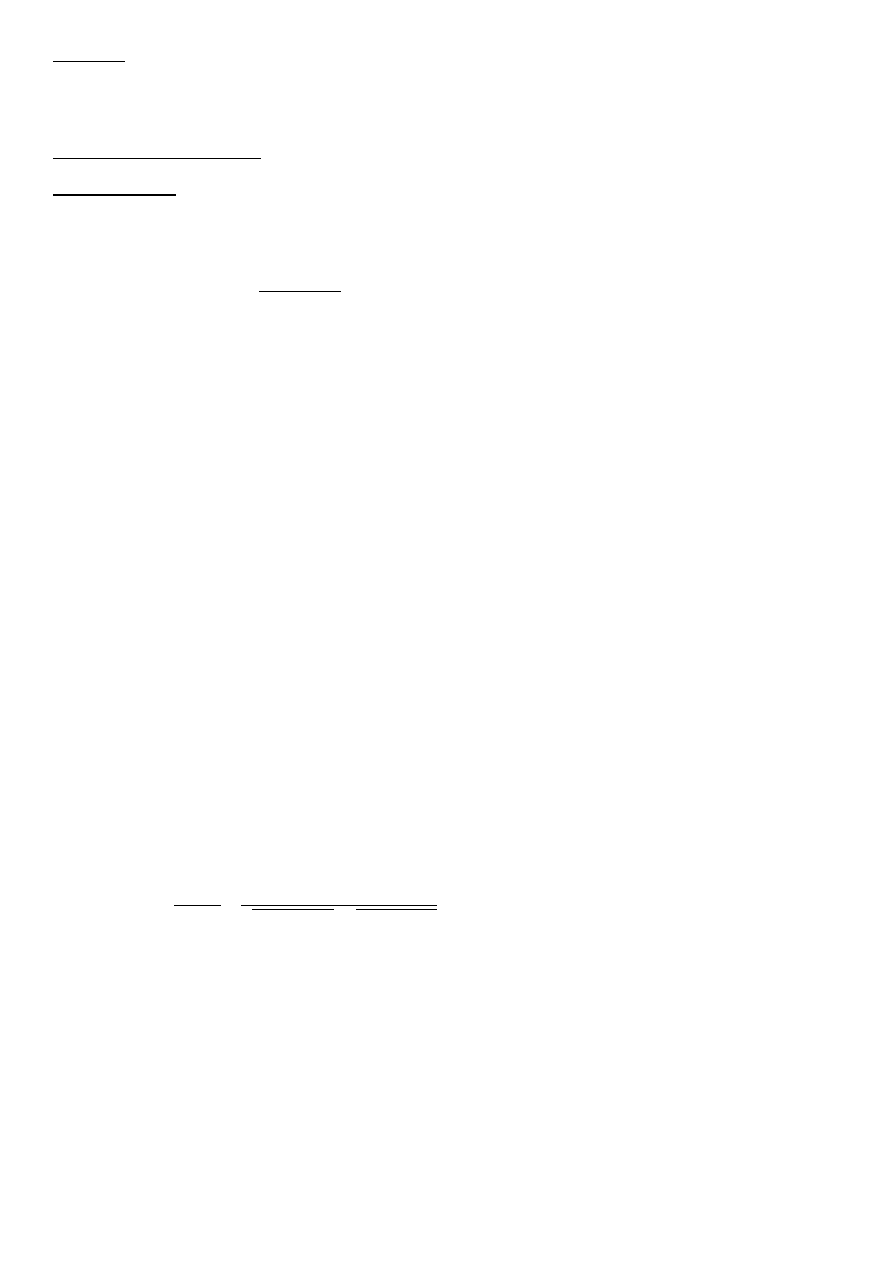
Wersor osi
– wektor o kierunku i zwrocie tej osi oraz długości 1. Niech
oznaczają odpowiednio wersory osi Ox,
Oy, Oz. Wtedy
.
Kąt wektorów niezerowych
– kąt wypukły między : .
Kąt wektora z osią – kąt wektora z wersorem tej osi.
TW.
Jeżeli
, to
a)
długość wektora
:
,
b)
,
c)
,
d)
,
e)
.
2. Iloczyn skalarny.
DEF
. Iloczynem skalarnym dwu niezerowych wektorów
nazywamy liczbę . Jeżeli
przynajmniej jeden z wektorów jest zerowy, to iloczyn skalarny jest 0.
TW.
Iloczyn skalarny ma własności
a)
,
b)
,
c)
dla ,
d)
.
TW. podstawowe o iloczynie skalarnym.
Jeżeli
,
, to
.
TW.
Jeżeli
oraz
,
, to
a)
,
3. Iloczyn wektorowy.
DEF.
Iloczynem wektorowym uporządkowanej pary niezerowych i nierównoległych wektorów
w układzie
współrzędnych Oxyz nazywamy wektor
taki, że
i)
wektor
jest prostopadły do obu wektorów ,
ii)
zwrot wektora
jest taki, by uporządkowana trójka wektorów
miała orientację zgodną z orientacją
układu Oxyz,
iii)
długość wektora
jest
.
Jeżeli przynajmniej jeden z wektorów jest zerowy lub wektory są równoległe, to ich iloczyn wektorowy jest wektorem
zerowym
.
b)
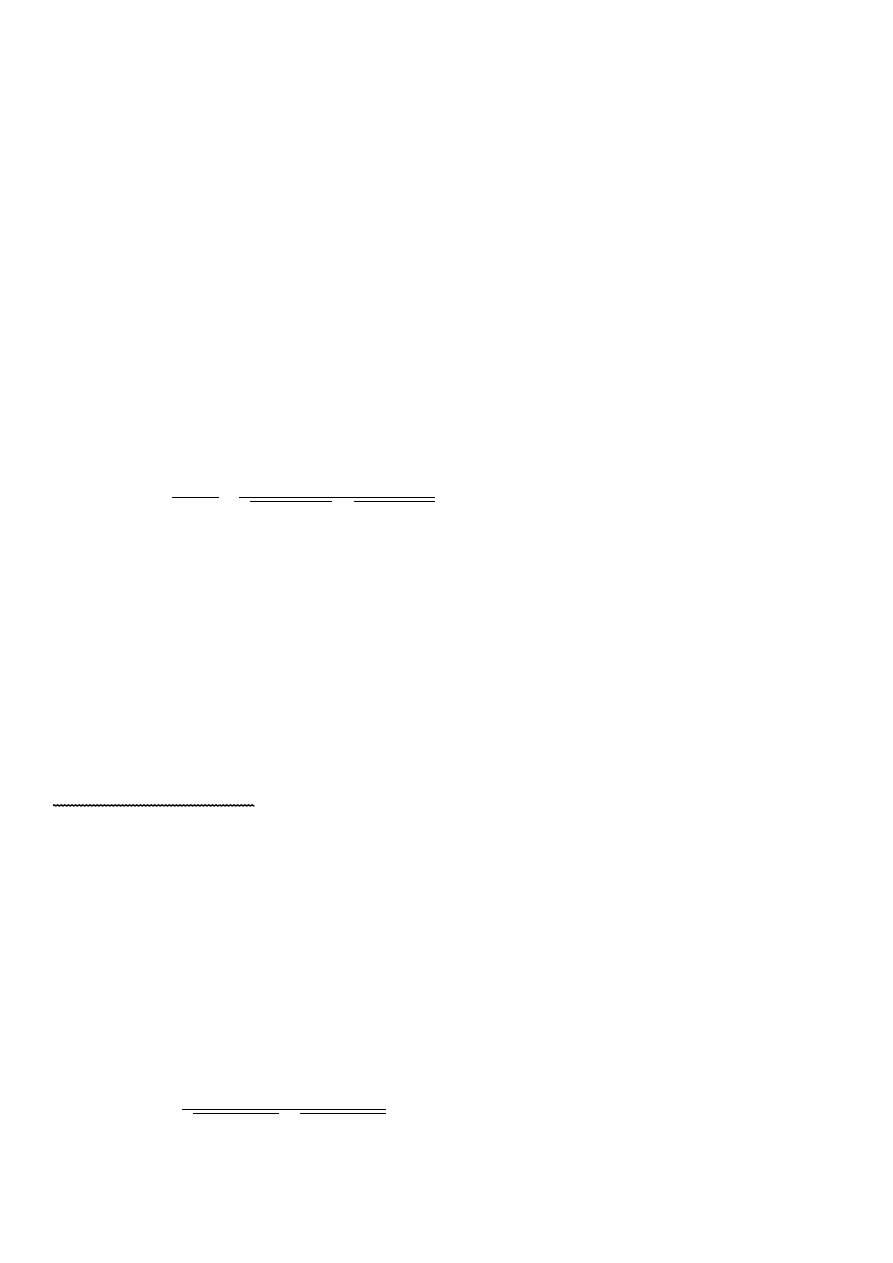
TW.
Iloczyn wektorowy ma własności
a)
,
b)
,
c)
dla ,
d)
.
TW. podstawowe o iloczynie wektorowym.
Jeżeli
,
, to
.
TW.
Jeżeli
oraz
,
, to
a)
,
4. Iloczyn mieszany.
5.
Płaszczyzna.
TW. Niech
będzie punktem płaszczyzny
, zaś
niezerowym wektorem (tzn.
)
prostopadłym do płaszczyzny
. Punkt
należy do płaszczyzny
wtedy i
tylko wtedy, gdy jego współrzędne
spełniają równanie
.
Równanie ogólne płaszczyzny:
,
gdzie
.
TW.
Załóżmy, że płaszczyzna
1
ma równanie
oraz płaszczyzna
2
:
. Wówczas:
a)
,
b)
,
c)
b)
TW.
Niech będzie dana płaszczyzna
o równaniu
oraz punkt
. Odległość
punktu
od płaszczyzny
wyraża się wzorem
DEF. Niech
będzie krawędzią (prostą) przecięcia dwu nierównoległych płaszczyzn
. Zbiór wszystkich
płaszczyzn zawierających krawędź
nazywamy pękiem płaszczyzn wyznaczonym przez płaszczyzny
.
TW.
Niech będą dane dwie nierównoległe płaszczyzny
1
:
,
2
:
.
Płaszczyzna
należy do pęku płaszczyzn wyznaczonego przez
wtedy i tylko wtedy, gdy istnieją liczby
takie, że
oraz równanie płaszczyzny
daje się zapisać:
.
Równanie
,
gdzie
, nazywamy równaniem pęku płaszczyzn wyznaczonego przez płaszczyzny
1
:
,
2
:
.
6. Prosta.
TW. Niech
będzie punktem prostej , zaś niezerowym wektorem (tzn.
)
równoległym do prostej
. Punkt należy do prostej wtedy i tylko wtedy, gdy jego współrzędne
spełniają równania
.
Powyższe równania noszą nazwę równań parametrycznych prostej
, – parametru, – współczynników
kierunkowych prostej
.
Równania kierunkowe prostej
:
gdzie
.
TW.
Niech płaszczyzny
1
:
i
2
:
mają wspólną krawędź . Punkt
należy do prostej wtedy i tylko wtedy, gdy współrzędne spełniają równania obu płaszczyzn tzn.:
Równania te noszą nazwę równań krawędziowych prostej
.
7.
Płaszczyzna i prosta.