1

Przykład 2.2 Belka wieloprzęsłowa II.

Dla statycznie wyznaczalnej belki wieloprzęsłowej, której sztywność zmienia się

odcinkowo, wyznaczyć zmianę kąta ugięcia (kąta obrotu przekroju poprzecznego) w
przegubie C i ugięcie w punkcie F.

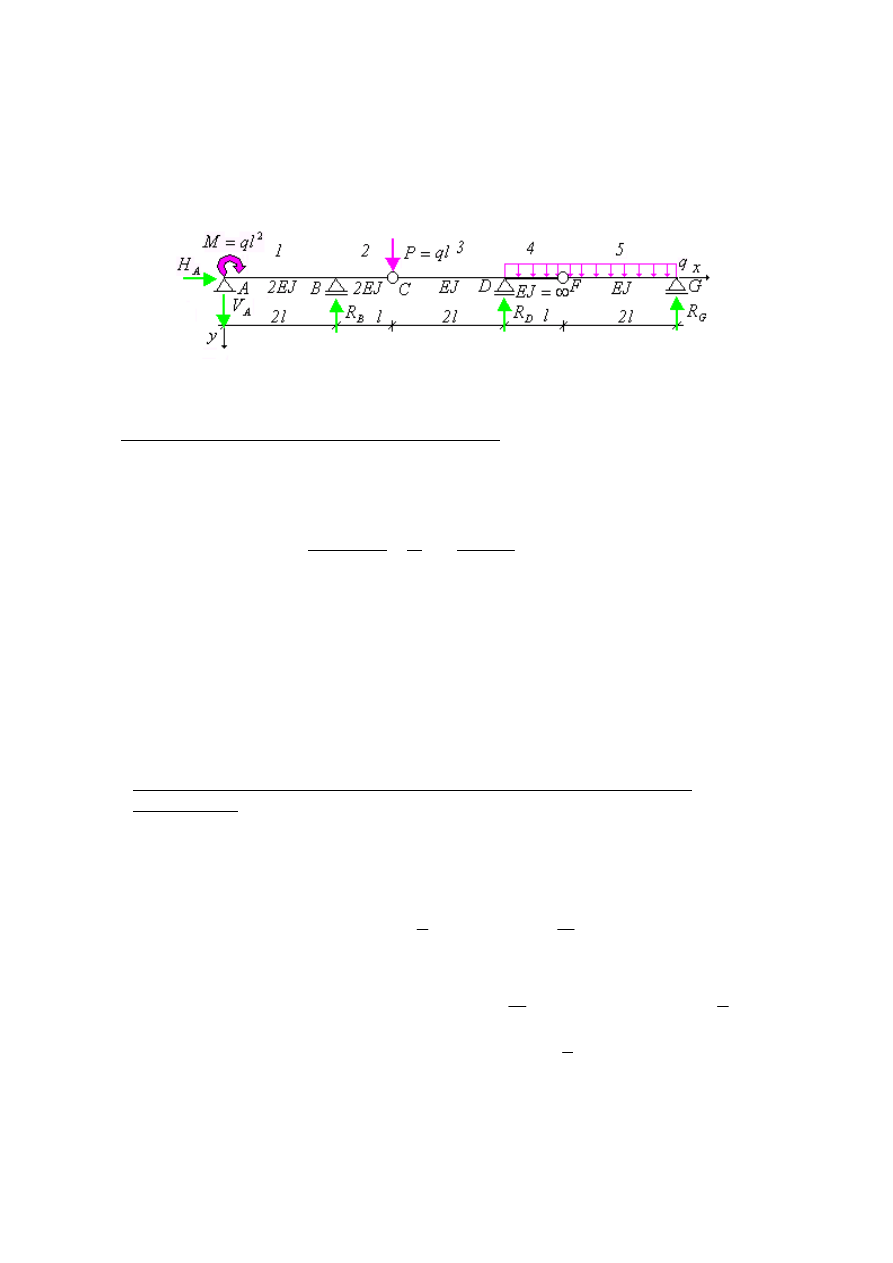
Rys. 1. Schemat statyczny belki

I. Wyznaczenie zmiany kąta ugięcia w przegubie C.

Zmianę kąta ugięcia wyznaczymy stosując metodę Maxwella-Mohra, korzystając ze

wzoru

∑∫

∑∫

=

=

=

=

5

1 0

1

5

1 0

1

1

i

il

zi

zi

zi

i

il

zi

i

i

zi

zi

C

dx

J

M

M

E

J

E

ds

M

M

θ

∆

(1)

gdzie:

l

C

p

C

C

θ

θ

θ

−

=

∆

- zmiana kąta ugięcia w przegubie C,

zi

M - moment gnący w i-tym przedziale belki od obciążenia zewnętrznego,

1
zi

M - moment gnący w i-tym przedziale belki od momentów jednostkowych, odpo-

wiadających poszukiwanemu przemieszczeniu, przyłożonych do prętów prze-
działów 2 i 3 nieskończenie blisko przegubu C,

i

l - długość i-tego przedziału belki o stałym module E.

1. Obliczenie reakcji i sporządzenie wykresu momentów gnących od obciążenia

zewnętrznego.

Z warunków równowagi dla belki wyznaczamy reakcje podpór

ql

R

l

l

q

l

R

M

G

G

FG

F

=

→

=

⋅

⋅

−

⋅

→

=

∑

0

2

2

0

ql

R

l

l

q

l

R

l

R

M

D

G

D

CG

C

4

11

0

2

7

3

5

2

0

=

→

=

⋅

⋅

−

⋅

+

⋅

→

=

∑

0

0

=

→

=

∑

A

ix

H

P

ql

R

l

R

l

l

q

l

R

l

P

l

R

M

M

B

G

D

B

A

8

7

0

8

2

13

3

5

3

2

0

=

→

=

⋅

+

⋅

⋅

−

⋅

+

⋅

−

⋅

+

−

→

=

∑

ql

V

R

l

q

R

P

R

V

P

A

G

D

B

A

iy

8

5

0

3

0

=

→

=

−

⋅

+

−

+

−

→

=

∑

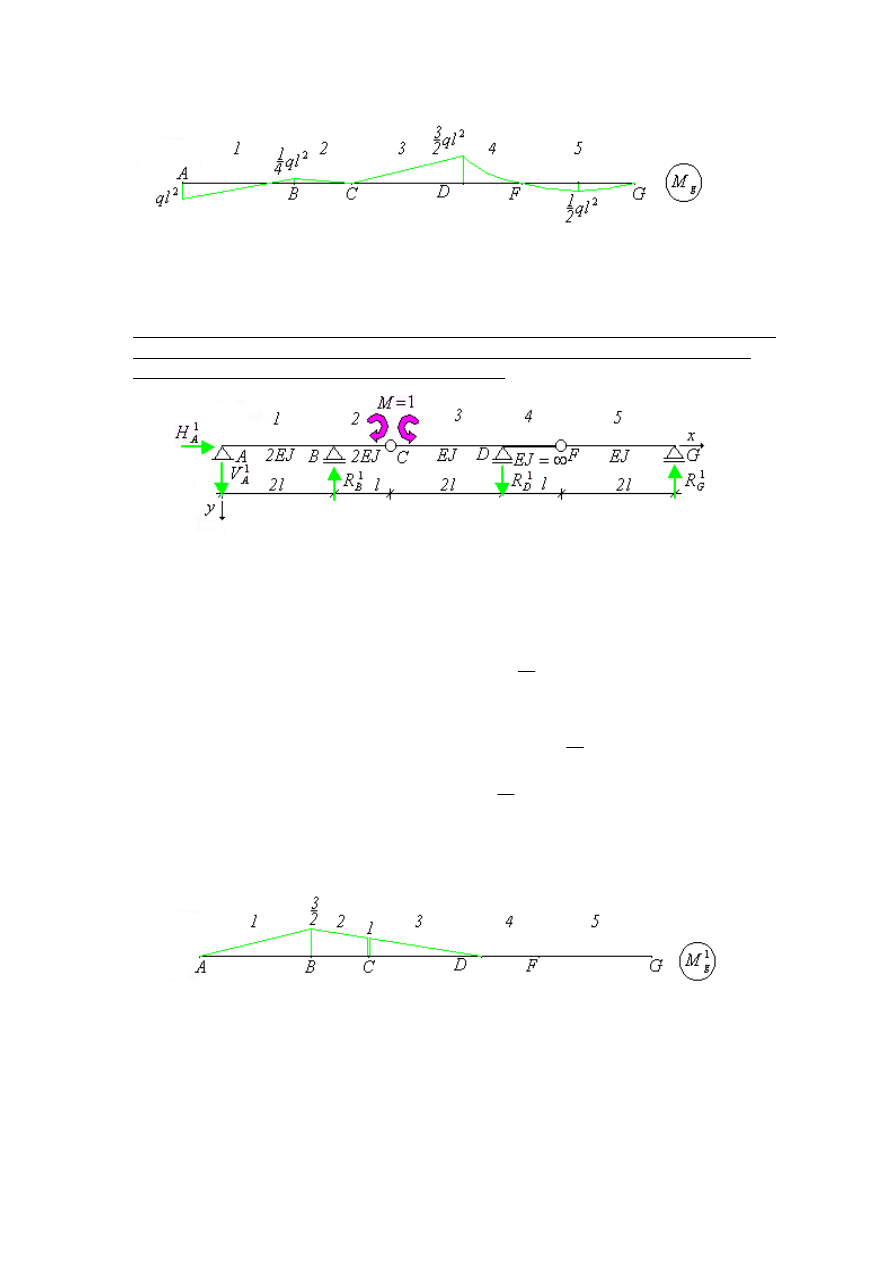
Wykorzystując przeprowadzone obliczenia sporządzamy wykres momentów gnących od

obciążenia zewnętrznego.

2

Rys. 3. Wykres momentów gnących od obciążenia zewnętrznego.

2. Obliczenie reakcji i sporządzenie wykresu momentów gnących od momentów jednostko-
wych, odpowiadających poszukiwanej zmianie kąta ugięcia, przyłożonych do prętów
przedziałów 2 i 3 nieskończenie blisko przegubu C.

Rys. 4. Schemat statyczny

Wyznaczamy reakcje podpór

0

0

0

1

1

1

=

→

=

⋅

→

=

∑

G

G

FG

F

R

l

R

M

l

R

l

R

l

R

M

D

G

D

CG

C

2

1

0

1

5

2

0

1

1

1

1

=

→

=

+

⋅

+

⋅

−

→

=

∑

0

0

1

1

=

→

=

∑

A

ix

H

P

l

R

l

R

l

R

l

R

M

B

G

D

B

A

4

5

0

5

1

1

2

0

1

1

1

1

1

=

→

=

⋅

+

⋅

−

+

−

⋅

→

=

∑

l

V

R

R

R

V

P

A

G

D

B

A

iy

4

3

0

0

1

1

1

1

1

1

=

→

=

−

+

−

→

=

∑

Wykorzystując przeprowadzone obliczenia sporządzamy wykres momentów gnących od

obciążenia jednostkowego.

Rys. 5. Wykres momentów gnących od momentów jednostkowych, odpowiadających
poszukiwanej zmianie kąta, przyłożonych do prętów przedziałów 2 i 3 nieskończenie blisko
przegubu C.

3

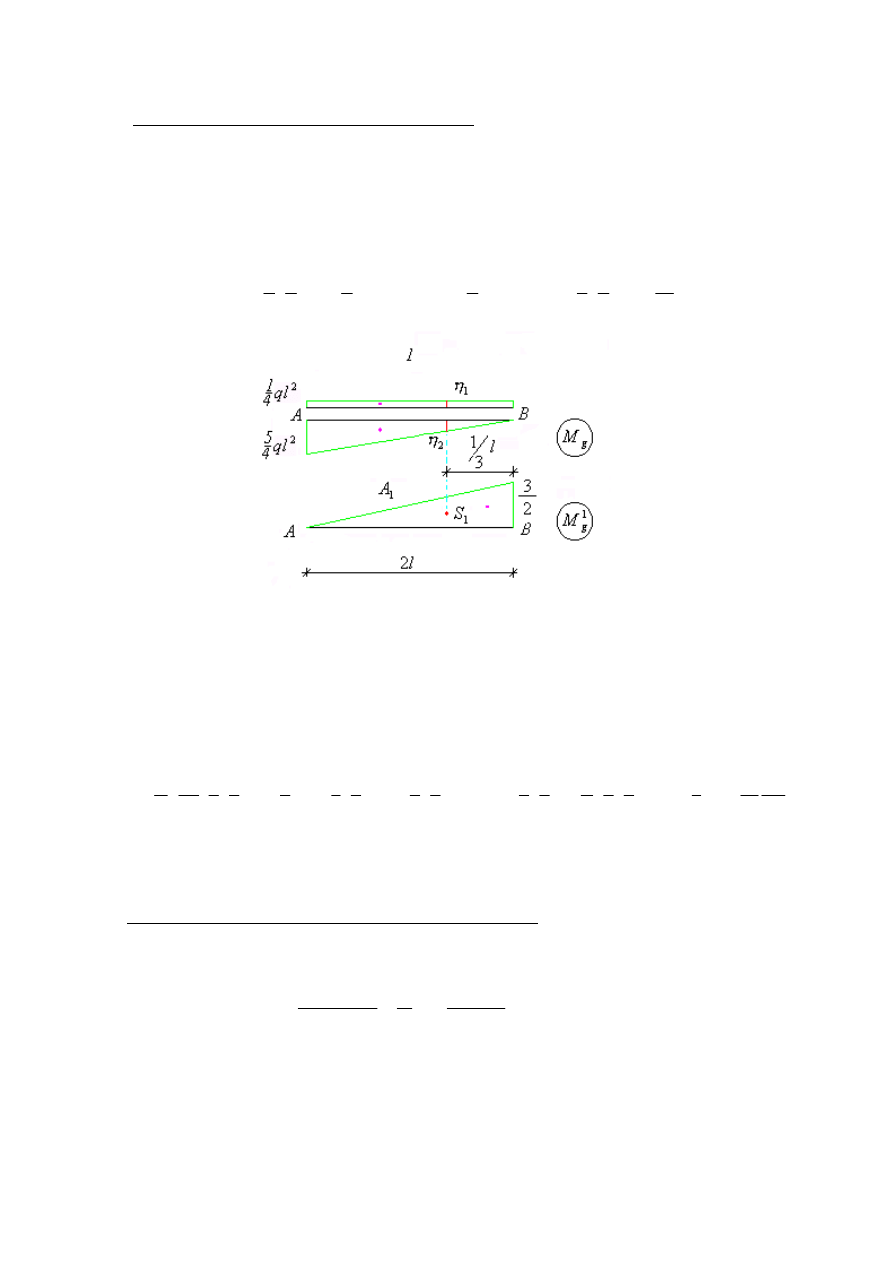
3. Obliczenie zmiany kąta ugięcia w przegubie C.

Całkę w przedziale 1 obliczymy mnożąc pole figury wykresu

1
g

M w przedziale 1 przez

rzędne w wykresach

g

M odpowiadające środkowi ciężkości figury wykresu

1
g

M w tym

przedziale. Pola powierzchni i odpowiadające im rzędne drugiego wykresu dla odciętej
odpowiadającej środkowi ciężkości figury pierwszego wykresu przedstawiono poniżej (patrz
rysunek 6).

2

2

2

2

1

1

12

5

4

5

3

1

4

1

2

3

2

2

3

2

1

ql

ql

ql

l

l

A

=

⋅

=

=

=

⋅

⋅

=

η

η

Rys. 6. Wykresy momentów gnących w przedziale 1

Podobnie w przedziale 2 i 3.
Ostatecznie wykorzystując wzór (1) i pamiętając o różnych sztywnościach belki w

poszczególnych przedziałach otrzymujemy

EJ

ql

l

ql

J

l

ql

ql

ql

l

J

E

C

3

2

2

2

2

24

11

1

3

1

2

2

3

2

1

1

2

1

3

2

1

4

1

2

1

4

5

3

1

4

1

2

2

3

2

1

2

1

1

=













⋅

⋅

⋅

⋅

⋅

+

























⋅

+

⋅

⋅

⋅

+













⋅

−

⋅

⋅

⋅

=

∆

θ

Otrzymany wynik końcowy ze znakiem plus oznacza, że zmiana kąta ugięcia w

przegubie C jest zgodna z założoną (Rys. 4).

II. Wyznaczenie przemieszczenia pionowego v punktu F.

Przemieszczenie pionowe wyznaczymy stosując metodę Maxwella-Mohra, ze wzoru

v

F

dx

J

M

M

E

J

E

ds

M

M

i

l

zi

zi

zi

i

l

zi

i

i

zi

zi

i

i

∑∫

∑∫

=

=

=

=

5

1 0

1

5

1 0

1

1

(3)

gdzie: v

F

- pionowe przemieszczenie punktu F,

zi

M - moment gnący w i-tym przedziale belki od obciążenia zewnętrznego,

1
zi

M - moment gnący w i-tym przedziale belki od pionowej siły jednostkowej, odpo-

wiadającej poszukiwanemu przemieszczeniu, przyłożonej w punkcie F,

4

i

l - długość i-tego przedziału belki o stałym module E.

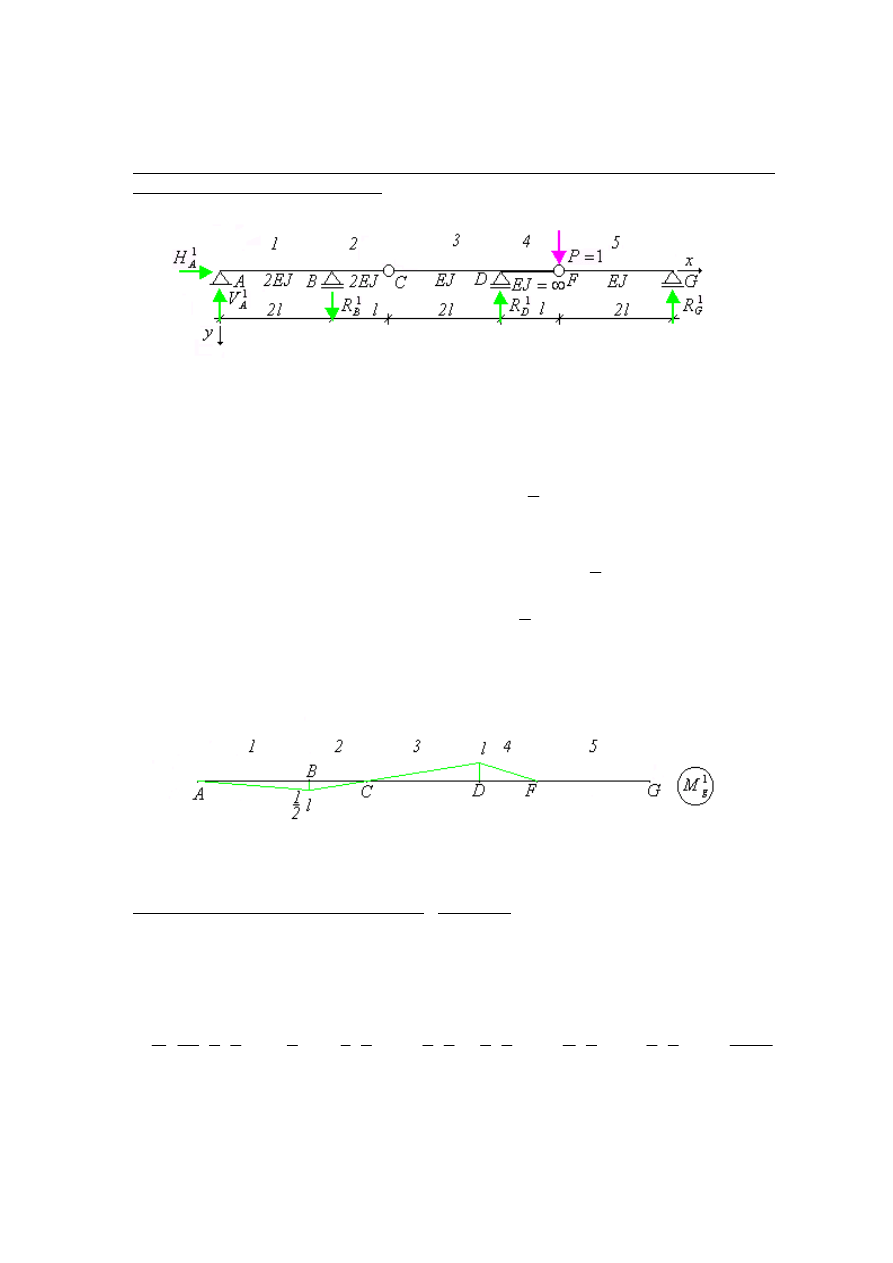
1. Obliczenie reakcji i sporządzenie wykresu momentów gnących od pionowej siły jednost-
kowej, przyłożonego w punkcie F.

Rys. 7. Schemat statyczny

Wyznaczamy reakcje podpór

0

0

0

1

1

1

=

→

=

⋅

→

=

∑

G

G

FG

F

R

l

R

M

2

3

0

3

1

5

2

0

1

1

1

1

=

→

=

⋅

−

⋅

+

⋅

→

=

∑

D

G

D

CG

C

R

l

l

R

l

R

M

0

0

1

1

=

→

=

∑

A

ix

H

P

4

3

0

8

5

2

6

1

0

1

1

1

1

1

=

→

=

⋅

+

⋅

+

⋅

−

⋅

−

→

=

∑

B

G

D

B

A

R

l

R

l

R

l

R

l

M

4

1

0

1

0

1

1

1

1

1

1

=

→

=

−

−

+

+

−

→

=

∑

A

G

D

B

A

iy

V

R

R

R

V

P

Wykorzystując przeprowadzone obliczenia sporządzamy wykres momentów gnących od

obciążenia jednostkowego.

Rys. 8. Wykres momentów gnących od pionowej siły jednostkowej, przyłożonej w punkcie F.

2. Obliczenie przemieszczenia pionowego v

F

punktu F.

Wartości całek w przedziale 4 (z uwagi na nieskończoną sztywność) i 5 (zerowe wykresy

momentów) są równe zeru. Ostatecznie wykorzystując wzór (1) i przeprowadzone obliczenia
otrzymujemy

v

F

EJ

ql

ql

l

l

J

ql

l

l

ql

ql

l

l

J

E

48

49

2

3

3

2

2

2

1

1

4

1

3

2

2

2

1

4

5

3

1

4

1

2

2

2

1

2

1

1

4

2

2

2

2

=













⋅

⋅

⋅

⋅

⋅

+













⋅

⋅

⋅

⋅

−













⋅

+

−

⋅

⋅

=

Otrzymany wynik końcowy ze znakiem plus oznacza, że zwrot wektora przemieszczenia jest
zgodny z założonym zwrotem siły jednostkowej (Rys. 7).