Podstawowe wielkości elektromagnetyczne

Indukcja elektromagnetyczna

ą

ograniczon

ię

powierzchn

cy

przenikają

y

magnetyczn

strumień

-

skojarzony

strumień

−

Ψ

określonym obwodem elektrycznym

φ

⋅

=

Ψ z

Strumień elektromagnetyczny

dS - elementarny wycinek powierzchni

indukcji

wektor

−

B

e

elementarn

ie

powierzchn

wszystkie

cych

przenikają

ych

elementarn

strumieni

wszystkich

suma

to

ie

powierzchn

skończoną

cy

przenikają

indukcji

wektora

strumień

S

B

S

d

B

S

−

⋅

=

∫

φ

S

d

B

S

d

B

d

ię

powierzchn

przez

indukcji

wektora

y

elementarn

strumień

−

= o

φ

zeru

równy

jest

zamkniętą

ię

powierzchn

dowolną

cy

przenikają

strumień

-

0

S

S

d

B

S

=

⋅

=

∫

φ

Podstawowe wielkości elektromagnetyczne

Prawo indukcji magnetycznej (Faradaya)

SEM indukowana w obwodzie jest równa co do wartości ze znakiem przeciwnym szybkości zmian
w czasie strumienia skojarzonego z tym obwodem.

dt

d

e

Ψ

−

=

V

l

B

dt

d

dt

d

e

⋅

⋅

−

=

−

=

Ψ

−

=

φ

Przepływ (SMM, amperozwoje)

Suma algebraiczna prądów przenikających obszar objęty krzywą zamkniętą zwana jest przepływem
przyporządkowanym tej krzywej.

prądu

gęstość

-

J

S

d

J

di

⋅

=

∫

⋅

=

⋅

=

Θ

S

z

i

S

d

J

Przenikalność magnetyczna

a

magnetyczn

ość

przenikaln

-

μ

r

μ

μ

μ

⋅

=

0

względna)

-

próżnia,

-

(

0

r

μ

μ

⎥⎦

⎤

⎢⎣

⎡

=

⋅

Ω

⋅

⋅

=

−

m

H

m

s

7

0

10

4

π

μ

∫

Θ

⋅

=

⋅

l

l

d

B

μ

Natężenie pola magnetycznego

ego

magnetyczn

pola

natężenia

wektor

-

H

μ

B

H

=

∫

∫

Θ

=

⋅

=

⋅

l

d

H

l

d

B

μ

Prawo przepływu

Całka liniowa wektora natężenia pola magnetycznego wzdłuż krzywej zamkniętej równa jest przepływowi obejmowanemu
przez tę krzywą.

∫

Θ

=

⋅

l

d

H

Podstawowe wielkości elektromagnetyczne

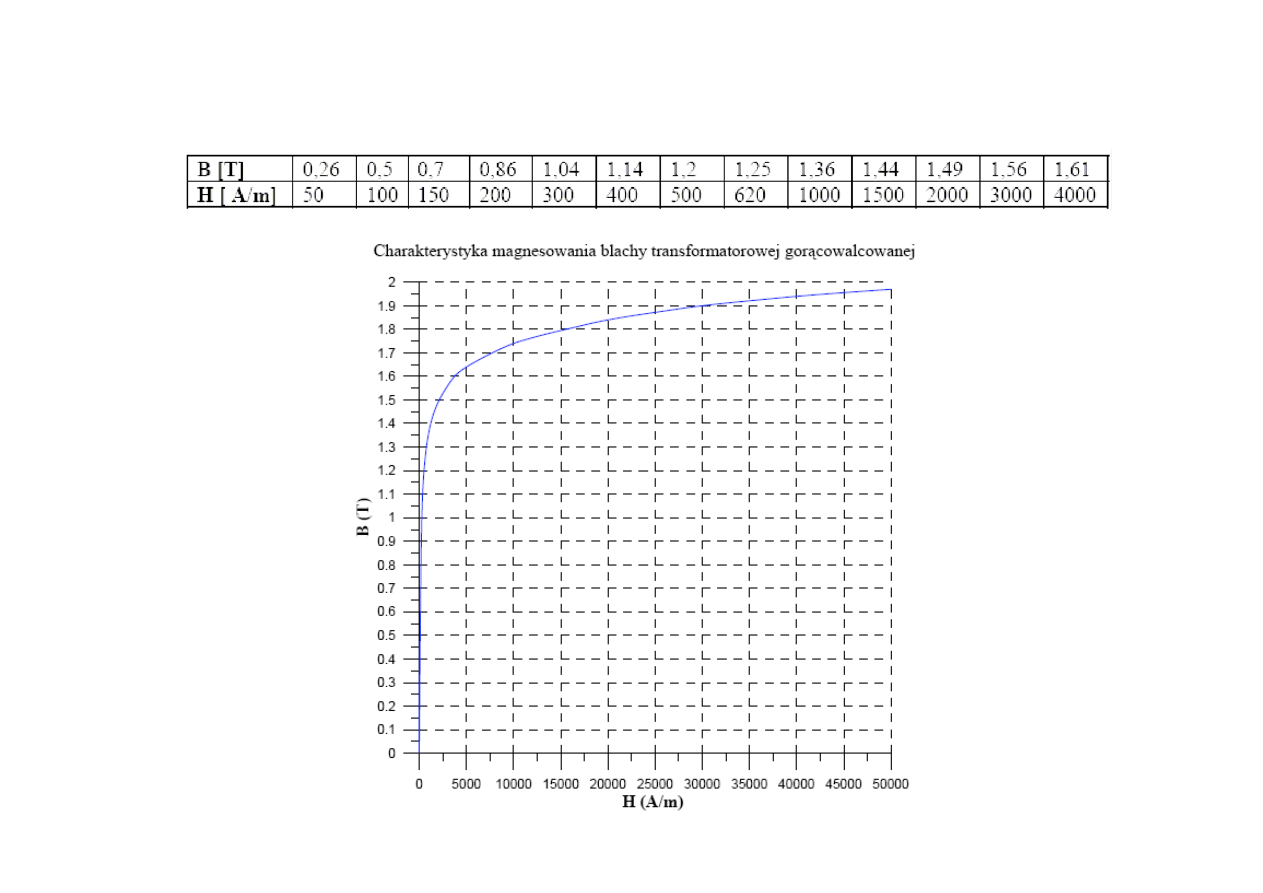
Charakterystyka magnesowania

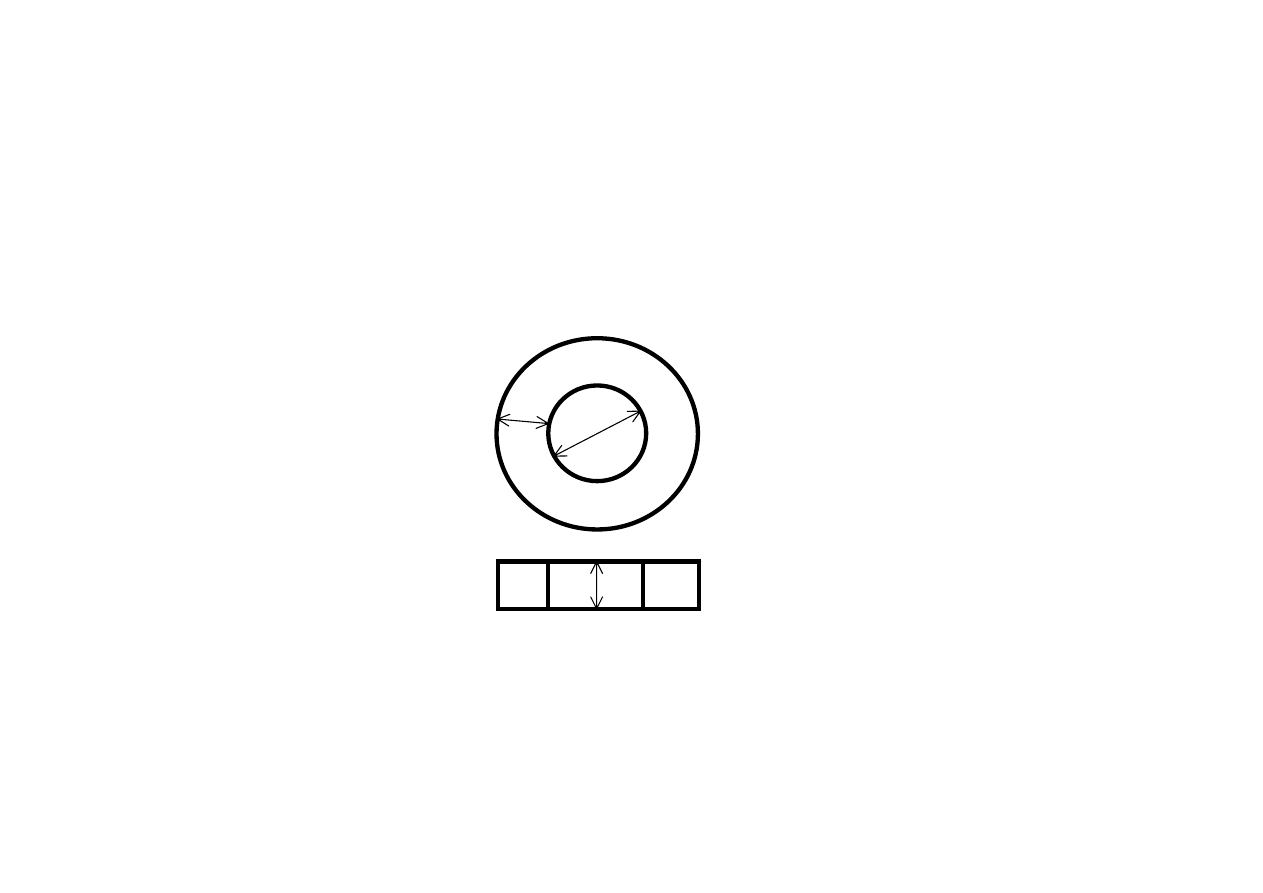
Na ferromagnetyczny rdzeń toroidalny o wymiarach a=10 mm, b=30 mm, c=80 mm
nawinięto uzwojenie o pewnej liczbie zwojów z. Uzwojenie zasilono napięciem
przemiennym U=127 V i częstotliwości f=50 Hz. Wytworzona indukcja w rdzeniu
wynosiła B=1,2 T.
Wiedząc, że prąd magnesujący wynosił I=110 mA obliczyć liczbę zwojów toroidu.

a

c

b

Zadanie 1

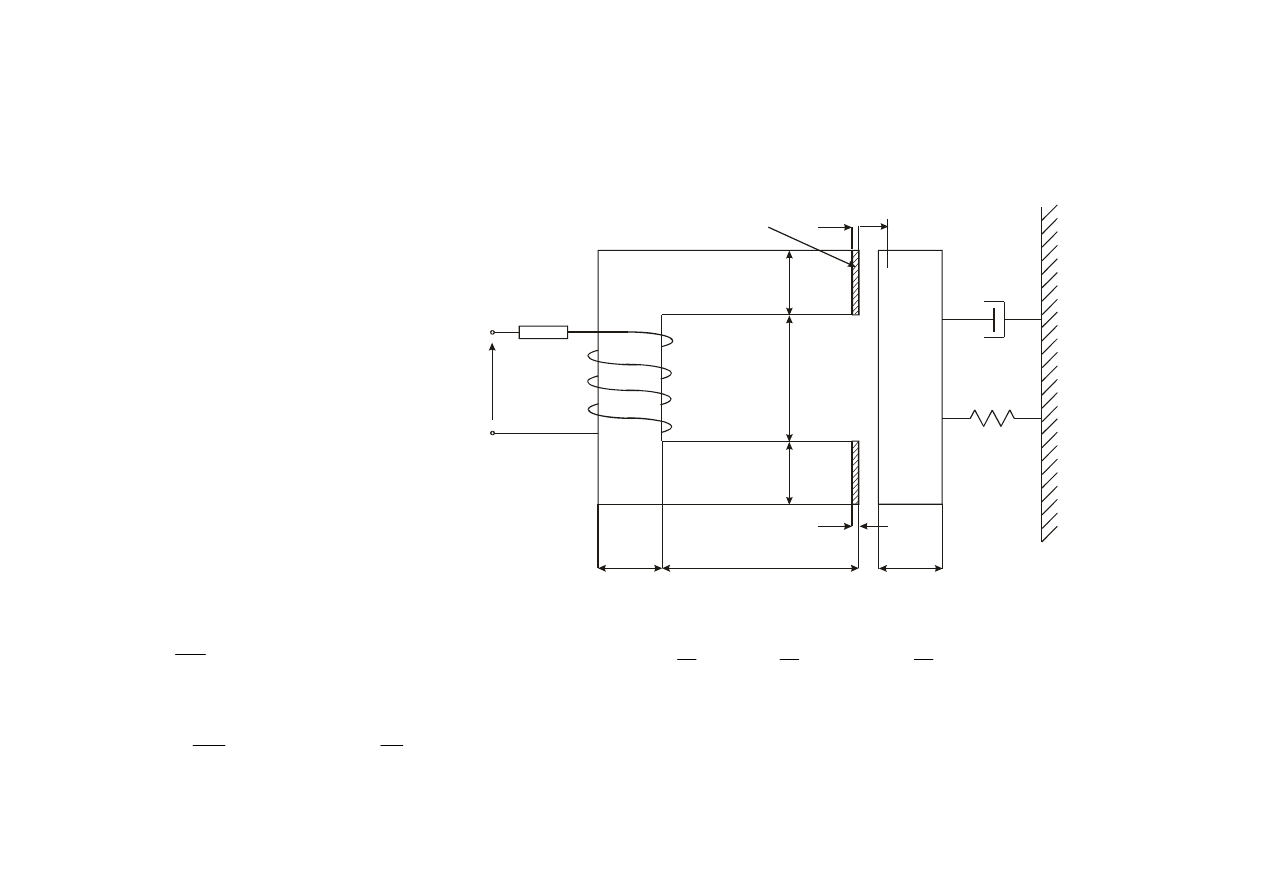
Rozwiązać układ znajdujący się na poniższym rysunku (stycznik).

Parametry dla poniższego układu:

m=0.25 kg

k=600 N/m

D=0.015 Ns/m

a=1 mm

b=3 mm

z=50

R=5

Ω

U=25 V

i

R

U

dt

d

⋅

−

=

Ψ

(

)

em

F

dt

dx

D

b

x

k

dt

x

d

m

−

⋅

−

−

⋅

−

=

⋅

2

2

Równania równowagi sił:

- elektryczne:

Zadanie 2

-mechaniczne

D

k

R

U(t)

Fe

a

x

20

60

20

20

40

20

a

mosiądz

( )

(

)

2

2

2

2

1

2

1

2

1

L

x

b

k

q

x

L

x

m

−

−

+

=

•

•

2

1

1

2

1

12

2

2

2

1

2

1

)

(

2

1

2

1

L

ϕ

ϕ

&

&

&

&

J

q

M

q

L

q

L

+

+

+

=

γ

J

1

δ

r

1

l

ϕ

1

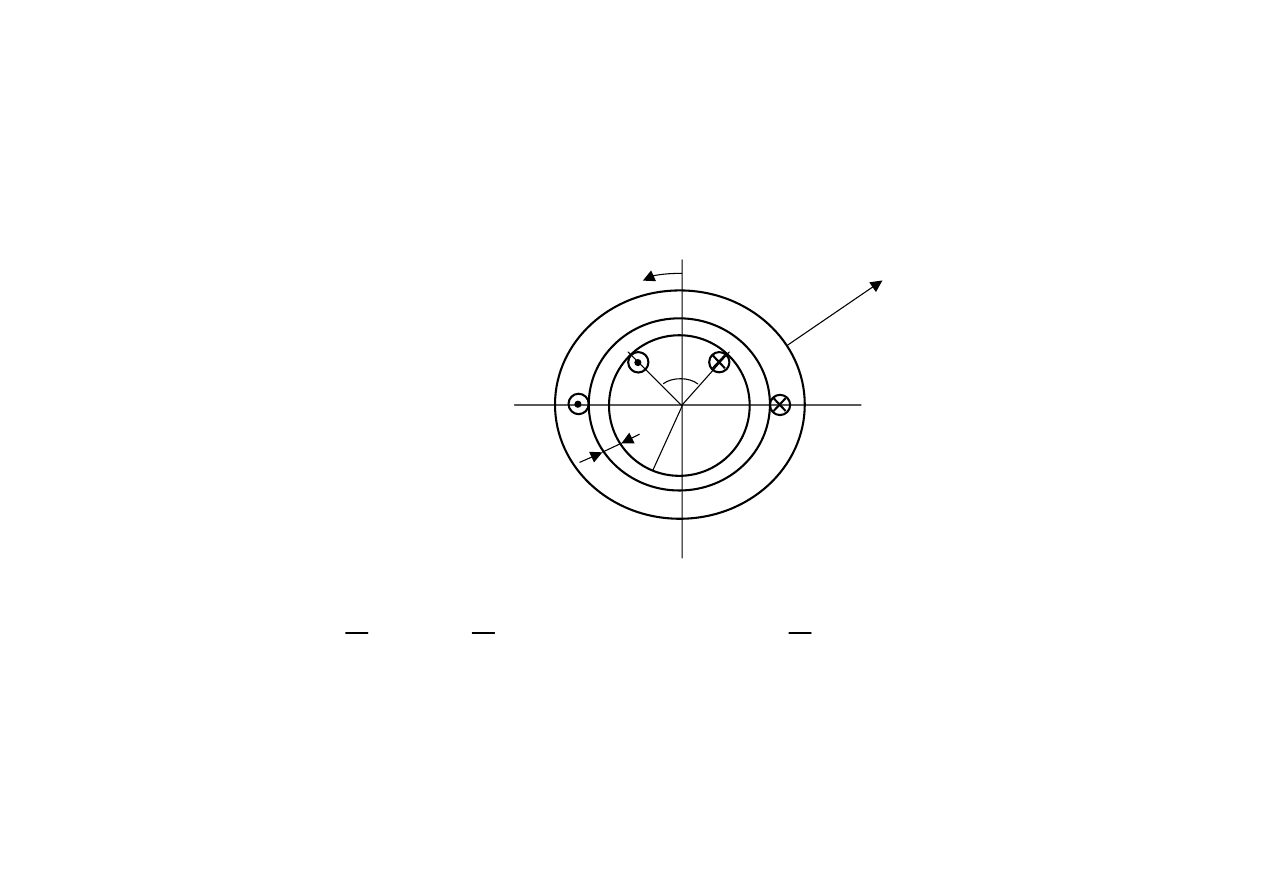
Zapisać równania ruchu i wyliczyć współczynniki indukcyjności własnej i wzajemnej.
Dane:
z

1

=z

2

=40

l

=0,2 m

r

1

=0,1 m

δ=0,001 m

γ=90

0

J

1

=10

-2

Nm

Zadanie 3