WPROWADZENIE

DO SZTUCZNEJ INTELIGENCJI

POLITECHNIKA WARSZAWSKA

WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

MEL

MEL

NS 586

Dr in

ż

. Franciszek Dul

© F.A. Dul 2007

18. UCZENIE SIĘ

NA PODSTWIE OBSERWACJI

© F.A. Dul 2007

NA PODSTWIE OBSERWACJI

Uczenie na podstawie obserwacji

Poka

ż

emy, w jaki sposób agent mo

ż

e

ulepszy

ć

swoje działania i zachowania

poprzez uczenie si

ę

na podstawie

poprzez uczenie si

ę

na podstawie

swoich własnych do

ś

wiadcze

ń

.

© F.A. Dul 2007

• Agenci ucz

ą

cy si

ę

• Uczenie indukcyjne
• Uczenie drzewa decyzyjnego
• Teoria uczenia - dlaczego to działa?

Plan rozdziału

© F.A. Dul 2007

Trzeba si

ę

uczy

ć

Obserwuj

ą

c

ś

rodowisko agent nie tylko zdobywa

wiedz

ę

o

ś

wiecie, ale tak

ż

e mo

ż

e ulepszy

ć

swoje

działania w przyszło

ś

ci.

Uczenie ma mie

ć

ró

ż

ne formy – mo

ż

e polega

ć

po prostu na gromadzeniu do

ś

wiadcze

ń

, ale mo

ż

e

tak

ż

e prowadzi

ć

do stworzenia ogólnych teorii,

na miar

ę

teorii Einsteina.

©

F.A. Dul 2007

na miar

ę

teorii Einsteina.

Rozpoczniemy od omówienia uczenia indukcyjnego
na podstawie obserwacji w oparciu o logik

ę

zda

ń

.

Odpowiemy te

ż

na pytanie, dlaczego uczenie działa?

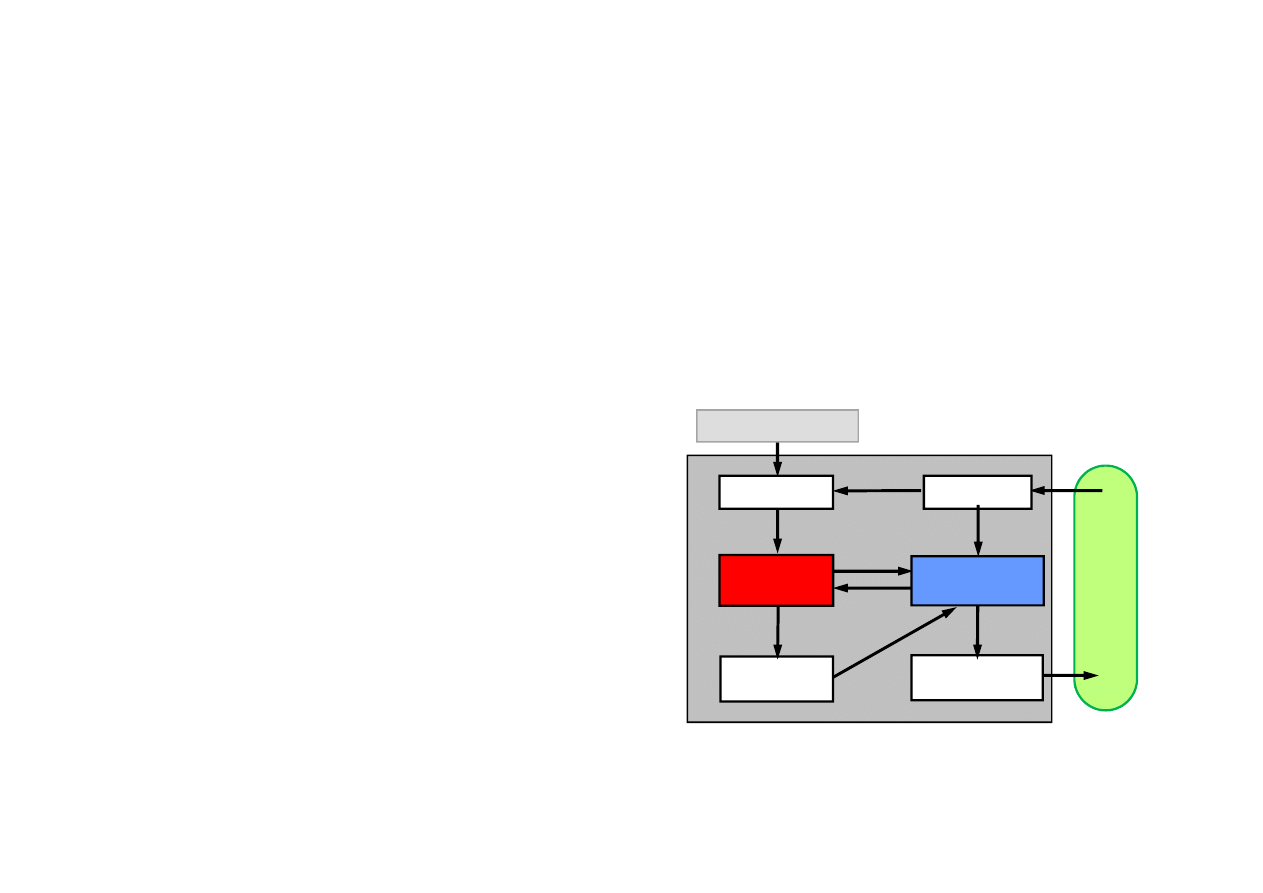
18.1. Formy uczenia

Agent ucz

ą

cy si

ę

posiada:

Standard jako

ś

ci

Agent musi si

ę

uczy

ć

, je

ż

eli musi działa

ć

w nieznanym

ś

rodowisku.

Uczenie jest metod

ą

konstruowania agenta polegaj

ą

c

ą

na skonfrontowaniu agenta z rzeczywisto

ś

ci

ą

zamiast

budowania dokładnego modelu jego działania.
Uczenie modyfikuje mechanizm podejmowania decyzji
agenta w celu polepszenia jego osi

ą

gów.

© F.A. Dul 2007

Agent ucz

ą

cy si

ę

posiada:

Ś

ro

d

o

w

is

k

o

Agent

Czujniki

Mechanizmy

wykonawcze

Generator

problemów

Krytyka

Sprz

ęż

enie

zwrotne

Zmiany

Wiedza

Cel

uczenia

Moduł

ucz

ą

cy si

ę

Moduł

decyzyjny

• moduł decyzyjny

, który

dokonuje wyboru działa

ń

na

podstawie obserwacji,

• moduł ucz

ą

cy si

ę

, który

modyfikuje moduł decyzyjny
tak, aby podejmował on lepsze
decyzje.

Moduły ucz

ą

ce si

ę

mog

ą

mie

ć

ró

ż

ne postacie, zale

ż

ne od typu

agenta który ma si

ę

uczy

ć

.

18.1. Formy uczenia

• Rodzaju elementów modułu decyzyjnego

które maj

ą

by

ć

uczone (odwzorowanie stan-działanie, reprezentacja cech

ś

rodowiska, model

ś

rodowiska i działa

ń

, u

ż

yteczno

ść

stanów,

u

ż

yteczno

ść

działa

ń

, cel),

• Reprezentacji

nauczanych elementów (refleksowa, logiczna,

probabilistyczna).

• Sprz

ęż

enia zwrotnego

które mo

ż

e by

ć

u

ż

yte do uczenia tych

elementów.

• Zakresu

wiedzy pocz

ą

tkowej

(apriorycznej) agenta.

Posta

ć

modułu ucz

ą

cego zale

ż

y od:

© F.A. Dul 2007`

• Zakresu

wiedzy pocz

ą

tkowej

(apriorycznej) agenta.

• Uczenie nadzorowane

(supervised learning): wyznaczenie

funkcji na podstawie przykładów ucz

ą

cych (danych i

odpowiedzi),

• Uczenie nienadzorowane

(unsupervised learning): wyznaczenie

funkcji na podstawie danych bez znajomo

ś

ci odpowiedzi.

• Uczenie ze wzmocnieniem

(reinforcement learning):

wyznaczenie funkcji na podstawie oceny wyników działania
agenta (najbardziej ogólne).

Sprz

ęż

enie zwrotne jest najwa

ż

niejszym czynnikiem

okre

ś

laj

ą

cym rodzaj uczenia:

18.2. Uczenie indukcyjne

Uczenie indukcyjne jest najprostsz

ą

form

ą

uczenia si

ę

.

Agent powinien nauczy

ć

si

ę

funkcji celu

f (target function).

Uczenie realizowane jest za pomoc

ą

wzorców

b

ę

d

ą

cych

parami (x, f(x)), x

∈

D.

Zbiór wzorców jest

zbiorem ucz

ą

cym

.

Zadanie uczenia indukcyjnego:

Znale

źć

hipotez

ę

h nale

żą

c

ą

do przestrzeni hipotez H

© F.A. Dul 2007

Znale

źć

hipotez

ę

h nale

żą

c

ą

do przestrzeni hipotez H

tak

ą

,

ż

e h przybli

ż

a f dla danego zbioru ucz

ą

cego

wzorców.

Dobra hipoteza h umo

ż

liwia

uogólnienie

- prawidłow

ą

klasyfikacj

ę

wzorca nie nale

żą

cego do zbioru ucz

ą

cego.

Uczenie indukcyjne jest bardzo uproszczonym sposobem
uczenia si

ę

, gdy

ż

:

• ignoruje wiedz

ę

aprioryczn

ą

posiadan

ą

przez agenta,

• zakłada,

ż

e dysponujemy zbiorem ucz

ą

cym.

××××

f(x)

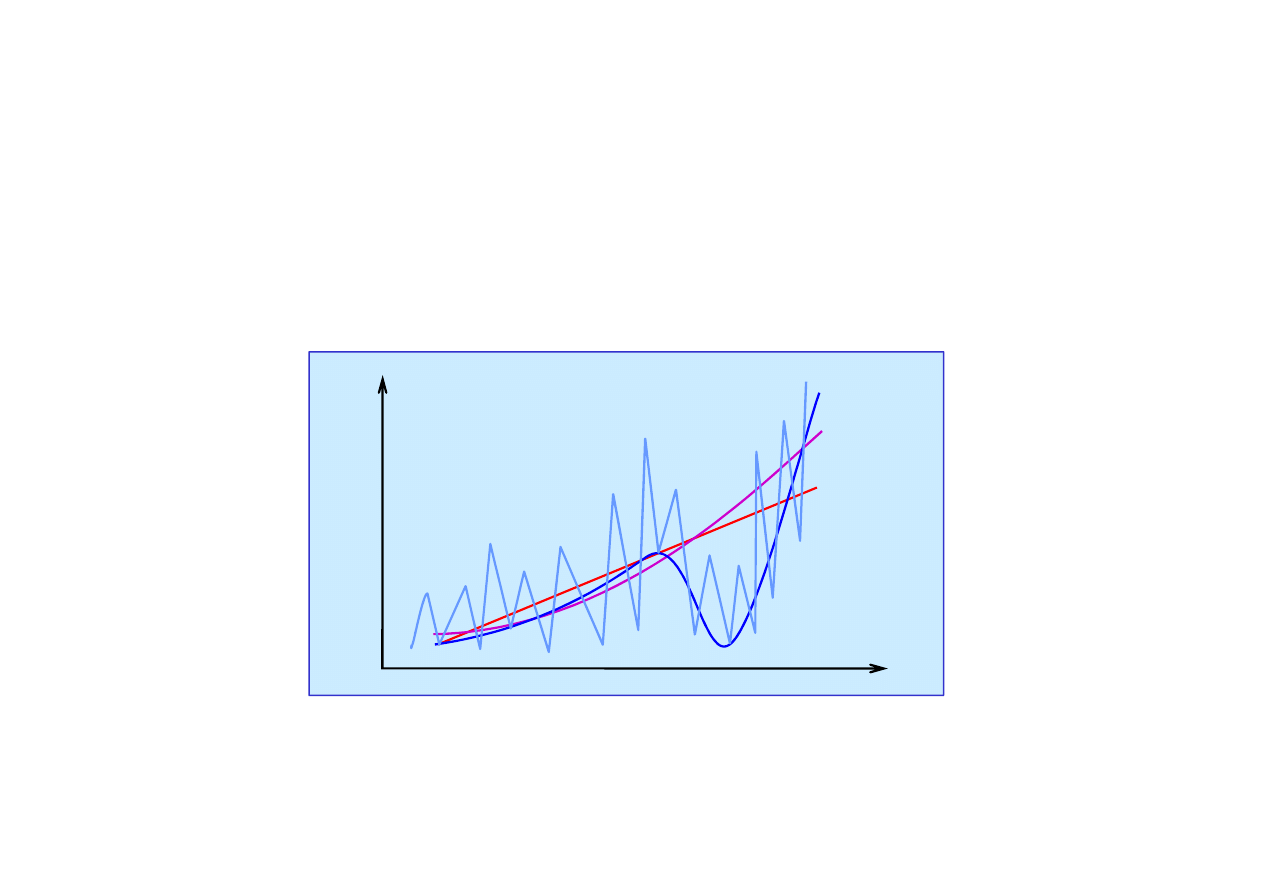
18.2. Uczenie indukcyjne

Metoda uczenia indukcyjnego

Hipoteza h jest

zgodna

(consistent) je

ż

eli pokrywa si

ę

z funkcj

ą

f dla wszystkich wzorców.

Dopasowanie hipotezy h tak, aby zgadzała si

ę

z funkcj

ą

celu

f na zbiorze ucz

ą

cym mo

ż

na osi

ą

gn

ąć

np. poprzez

dopasowanie krzywej (curve fitting).

h

1

= a

0

+ a

1

x

h

2

= a

0

+ a

1

x + a

2

x

2

h

5

= a

0

+ a

1

x + a

2

x

2

+ a

3

x

3

+ a

4

x

4

+ a

5

x

5

××××

××××

××××

××××

××××

××××

x

© F.A. Dul 2007

Któr

ą

zgodn

ą

hipotez

ę

nale

ż

y zatem wybra

ć

?

Brzytwa Ockhama

(Ockham’s razor): nale

ż

y wybra

ć

najprostsz

ą

hipotez

ę

zgodn

ą

z danymi.

h

1

= a

0

+ a

1

x

18.2. Uczenie indukcyjne

Identyfikacja jako uczenie indukcyjne

Identyfikacja parametryczna

polega na wyznaczeniu

parametrów p

danego

modelu M(x(t);p) tak, aby predykcja

stanu x(t) była zgodna z obserwacjami y(t

k

), np. w sensie

normy

Identyfikacja parametryczna jest wi

ę

c rodzajem uczenia

∑

=

∈

−

=

n

k

k

k

D

t

t

1

||

)

;

(

)

(

||

min

arg

q

x

y

p

q

© F.A. Dul 2007

Identyfikacja parametryczna jest wi

ę

c rodzajem uczenia

indukcyjnego, w którym funkcja celu dana jest niejawnie
poprzez model zale

ż

ny od parametrów.

Identyfikacja strukturalna

polega na wyznaczeniu struktury

modelu, np. w postaci grafu przepływu informacji, systemu
modeli przyczynowych, itp.

18.3. Uczenie drzew decyzyjnych

Drzewo decyzyjne jest struktur

ą

funkcyjn

ą

na wej

ś

ciu której

s

ą

atrybuty

, za

ś

na wyj

ś

ciu –

decyzja

.

Atrybuty oraz decyzja mog

ą

by

ć

dyskretne lub ci

ą

głe.

Drzewo decyzyjne stanowi jedn

ą

z mo

ż

liwych reprezentacji

hipotez.
Drzewo decyzyjne mo

ż

e reprezentowa

ć

moduł decyzyjny

agenta.
Uczenie drzew decyzyjnych jest jedn

ą

z najbardziej

© F.A. Dul 2007

Uczenie drzew decyzyjnych jest jedn

ą

z najbardziej

u

ż

ytecznych form uczenia.

Uczenie drzew decyzyjnych dyskretnych nazywa si

ę

klasyfikacj

ą

, za

ś

ci

ą

głych –

regresj

ą

.

Klasyfikacja boolowska u

ż

ywa warto

ś

ci Fałsz i Prawda.

Drzewo decyzyjne wyznacza decyzj

ę

na podstawie ci

ą

gu

testów.
Ka

ż

dy test dotyczy pewnego atrybutu, za

ś

li

ś

cie drzewa

okre

ś

laj

ą

wypracowane decyzje.

18.3. Uczenie drzew decyzyjnych

Przykład
Nale

ż

y zdecydowa

ć

czy czeka

ć

na stolik w restauracji

opieraj

ą

c si

ę

na nast

ę

puj

ą

cych atrybutach:

• Alternatywa

: czy w pobli

ż

u jest inna restauracja?

• Bar

: czy jest wygodny bar przy którym mo

ż

na poczeka

ć

?

• Pi

ą

tek/Sobota

: czy jest pi

ą

tek lub sobota?

• Głodny

: czy jeste

ś

my głodni?

• Klienci

: liczba osób w restauracji (Brak, Kilku, Pełno);

© F.A. Dul 2007

• Klienci

: liczba osób w restauracji (Brak, Kilku, Pełno);

• Cena

: rozpi

ę

to

ść

cen ($, $$, $$$);

• Deszcz

: czy pada na zewn

ą

trz?

• Rezerwacja

: czy dokonali

ś

my rezerwacji?

• Rodzaj

: rodzaj restauracji (francuska, włoska, tajska, Burger);

• Czas

: szacowany czas oczekiwania: 0-10, 10-30, 30-60, >60 min.

Decyzj

ę

okre

ś

la predykat

CzyCzeka

ć

b

ę

d

ą

cy funkcj

ą

atrybutów.

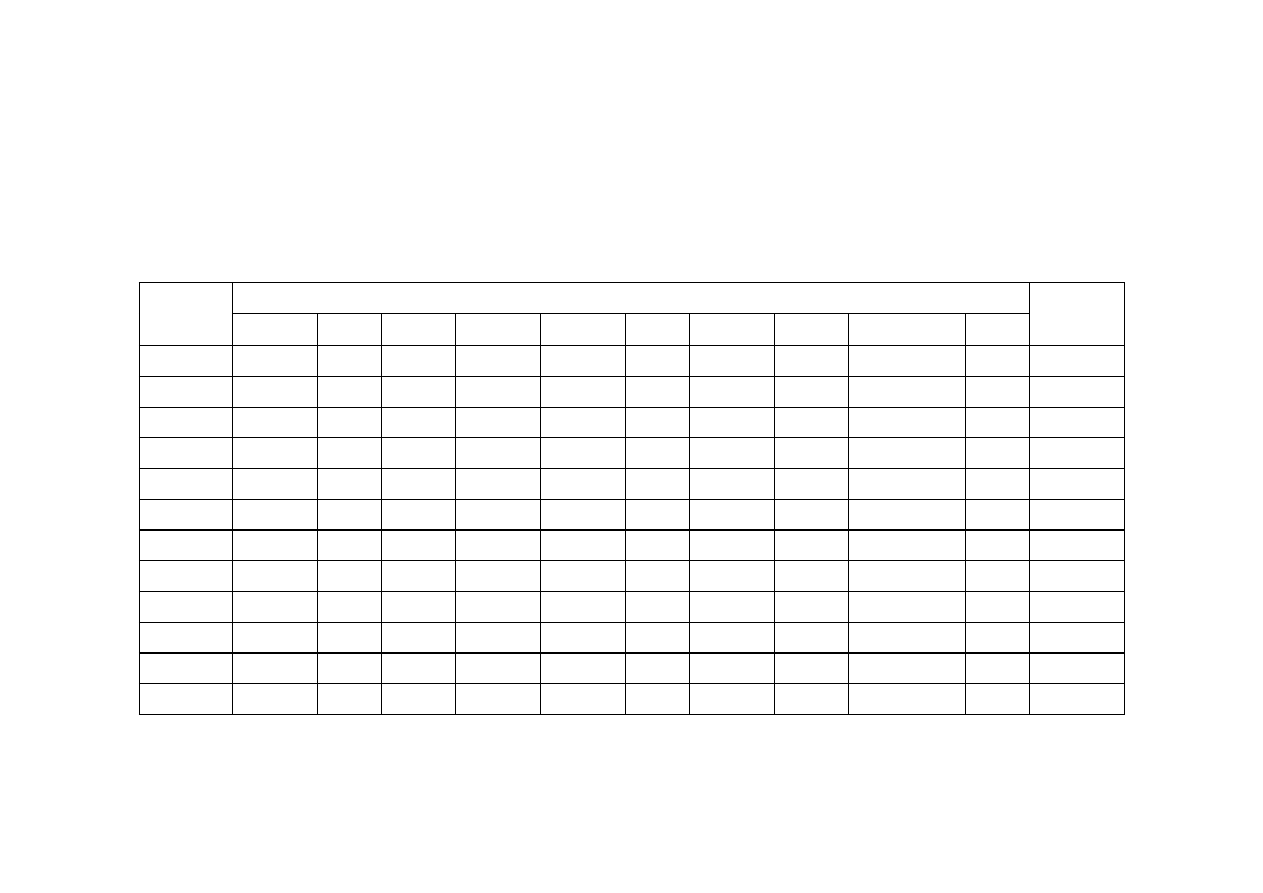
18.3. Uczenie drzew decyzyjnych

Reprezentacje oparte na atrybutach
Wzorce opisane s

ą

przez

warto

ś

ci atrybutów

(boolowskie,

dyskretne, ci

ą

głe).

Zbiór ucz

ą

cy

dla zadania oczekiwania na stolik w restauracji.

Atrybuty

Przykład

Altern.

Bar

Pt/Sob

Głodny

Klienci

Cena

Deszcz

Rezer.

Rodzaj

Czas

Cel
Czy

Czeka

ć

?

X

1

Tak

Nie

Nie

Tak

Kilku

$$$

Nie

Tak

Francuska

0-10

Tak

X

2

Tak

Nie

Nie

Tak

Pełno

$

Nie

Nie

Tajska

30-60

Nie

X

3

Nie

Tak

Nie

Nie

Kilku

$

Nie

Nie

Burger

0-10

Tak

X

Tak

Nie

Tak

Tak

Pełno

$

Nie

Nie

Tajska

10-30

Tak

© F.A. Dul 2007

Klasyfikacja

wzorców jest

pozytywna

(Tak) lub

negatywna

(Nie).

X

4

Tak

Nie

Tak

Tak

Pełno

$

Nie

Nie

Tajska

10-30

Tak

X

5

Tak

Nie

Tak

Nie

Pełno

$$$

Nie

Tak

Francuska

> 60

Nie

X

6

Nie

Tak

Nie

Tak

Kilku

$$

Tak

Tak

Włoska

0-10

Tak

X

7

Nie

Tak

Nie

Nie

Brak

$

Tak

Nie

Burger

0-10

Nie

X

8

Nie

Nie

Nie

Tak

Kilku

$$

Tak

Tak

Tajska

0-10

Tak

X

9

Nie

Tak

Tak

Nie

Pełno

$

Tak

Nie

Burger

> 60

Nie

X

10

Tak

Tak

Tak

Tak

Pełno

$$$

Nie

Tak

Włoska

10-30

Nie

X

11

Nie

Nie

Nie

Nie

Brak

$

Nie

Nie

Tajska

0-10

Nie

X

12

Tak

Tak

Tak

Tak

Pełno

$

Nie

Nie

Burger

30-60

Tak

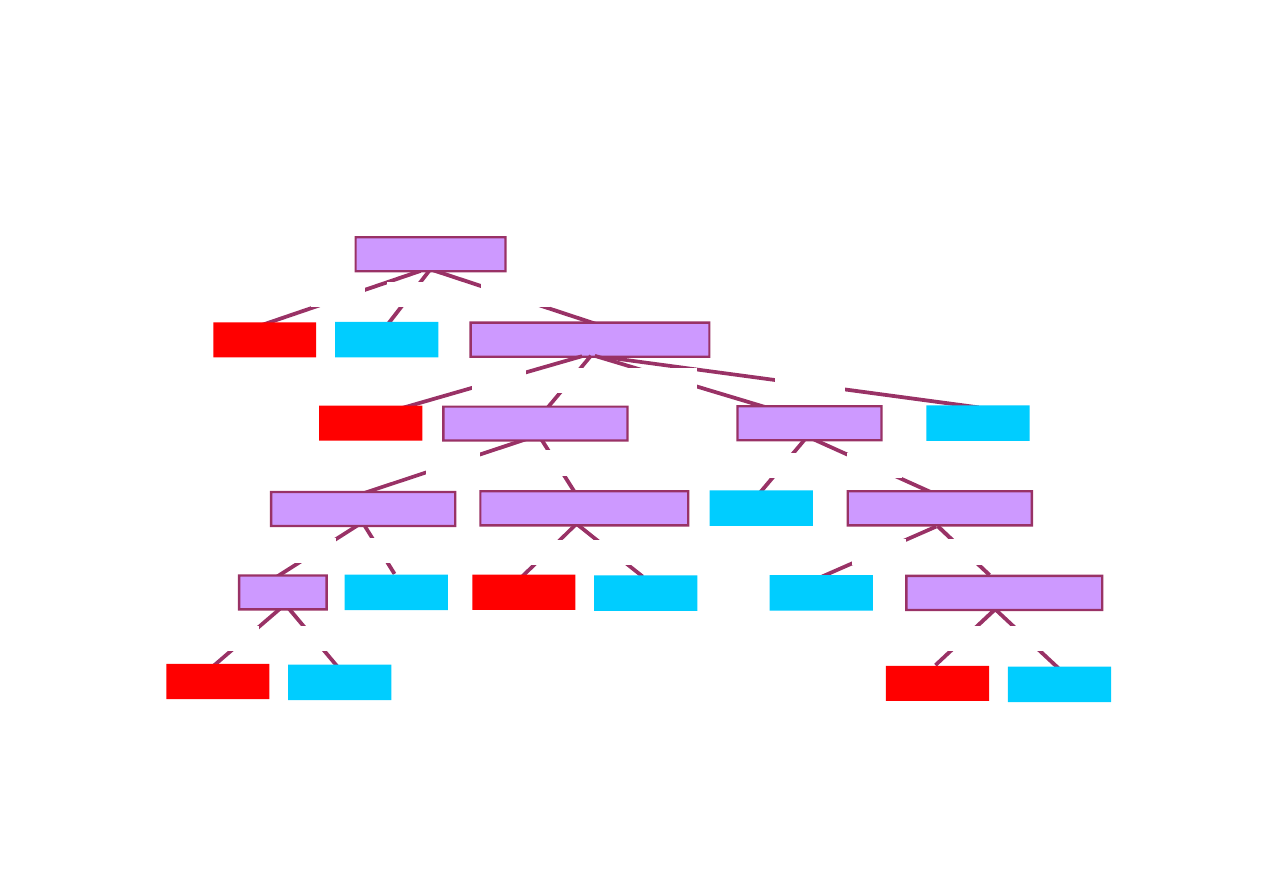
18.3. Uczenie drzew decyzyjnych

Drzewo decyzyjne

Drzewo decyzyjne dla zadania oczekiwania na stolik
w restauracji.

Klienci

CzasOczekiwania

Fałsz

Prawda

Brak

Kilku

Pełno

> 60

60-30

30-10

Alternatywa ?

Głodny?

Fałsz

0-10

Prawda

© F.A. Dul 2007

Rezerwacja ?

Pi

ą

tek/Sobota ?

PadaDeszcz ?

Bar ?

Nie

Tak

Fałsz

Prawda

Prawda

Fałsz

Prawda

Nie

Tak

Nie

Tak

Nie

Tak

Alternatywa ?

Prawda

Prawda

Fałsz

Prawda

Nie

Tak

Nie

Tak

Nie

Tak

Posta

ć

logiczna drzewa decyzyjnego

∀

s CzyCzeka

ć

(s)

⇔

⇔

⇔

⇔

( P

1

(s)

∨

P

2

(s)

∨

...

∨

P

m

(s) )

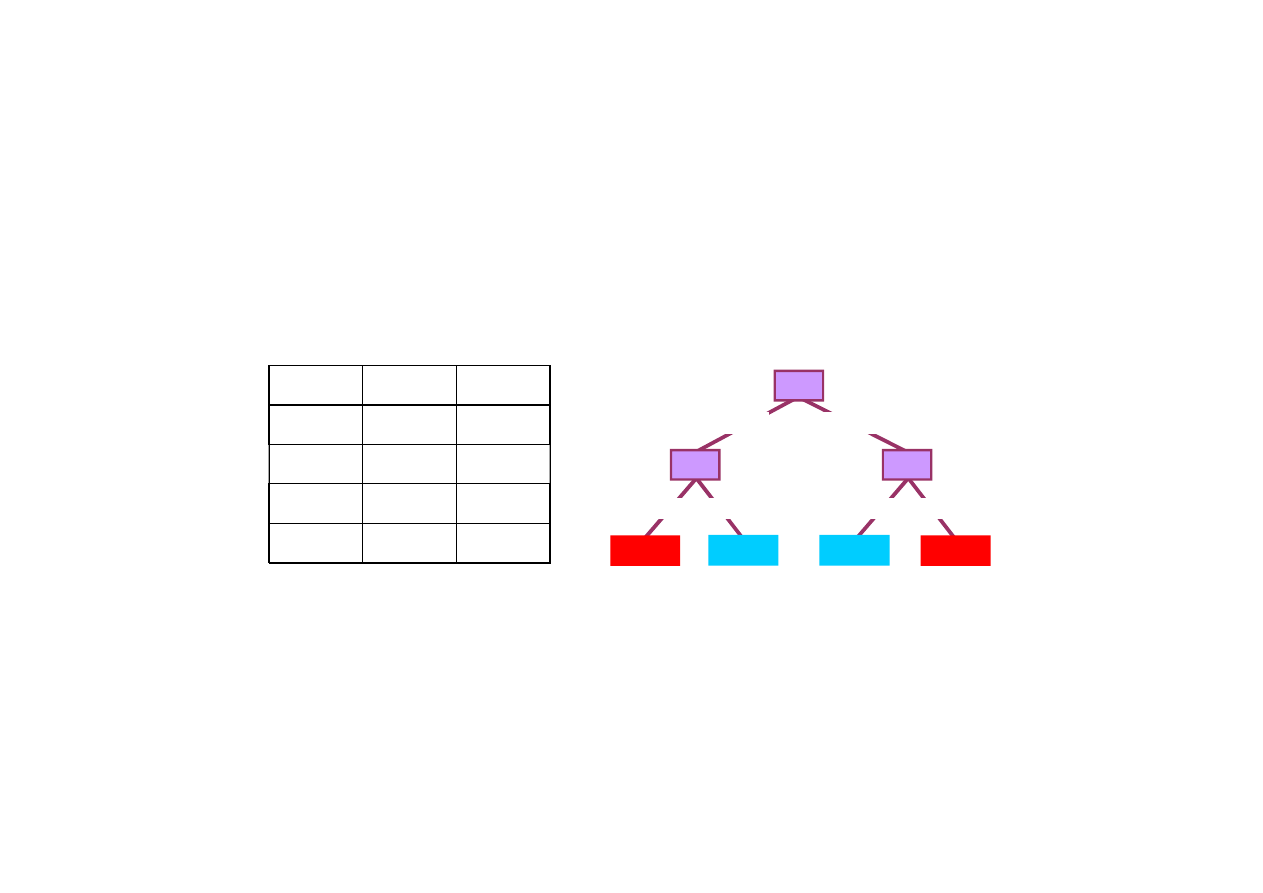
18.3. Uczenie drzew decyzyjnych

Ekspresyjno

ść

drzewa decyzyjnego

Drzewo decyzyjne mo

ż

e reprezentowa

ć

ka

ż

d

ą

funkcj

ę

atrybutów.
Funkcjom boolowskim lub wierszom tablic prawdy
odpowiadaj

ą

ś

cie

ż

ki do li

ś

ci.

Przykład

Drzewo decyzyjne dla funkcji logicznej XOR (eXclusive OR)

A

Fałsz

Prawda

A

B

A xor B

Fałsz

Fałsz

Prawda

© F.A. Dul 2007

Dla ka

ż

dego zbioru ucz

ą

cego mo

ż

na zbudowa

ć

trywialne

zgodne drzewo decyzyjne z jedn

ą

ś

cie

ż

k

ą

do li

ś

cia dla

ka

ż

dego wzorca.

Takie drzewo nie mo

ż

e jednak by

ć

uogólnione dla nowych

wzorców i mo

ż

e by

ć

bardzo wielkie.

Mo

ż

na jednak zbudowa

ć

bardziej zwarte drzewa decyzyjne.

B

Fałsz

Prawda

Fałsz

Prawda

B

Fałsz

Prawda

Fałsz

Prawda

Fałsz

Prawda

Fałsz

Prawda

Fałsz

Fałsz

Prawda

Prawda

Prawda

18.3. Uczenie drzew decyzyjnych

Drzewa decyzyjne s

ą

efektywne dla pewnych zada

ń

, a dla

innych nie.
Nie ma ogólnej efektywnej reprezentacji dowolnej funkcji.

Uzasadnienie

Liczba wszystkich funkcji boolowskich z n atrybutami jest
równa liczbie opisuj

ą

cych je tablic prawdy.

Ka

ż

da tablica prawdy ma 2

n

wierszy.

Warto

ść

funkcji opisuje 2

n

cyfr (kolumna tablicy prawdy).

© F.A. Dul 2007

Warto

ść

funkcji opisuje 2

n

cyfr (kolumna tablicy prawdy).

Liczba ró

ż

nych funkcji jest zatem równa

2

2n

.

Ju

ż

dla n = 6 atrybutów boolowskich liczba funkcji jest

równa

18,446,744,073,709,551,616 ~ 10

19

.

Mo

ż

na jednak efektywnie budowa

ć

drzewa decyzyjne

dla wielu problemów o znaczeniu praktycznym.

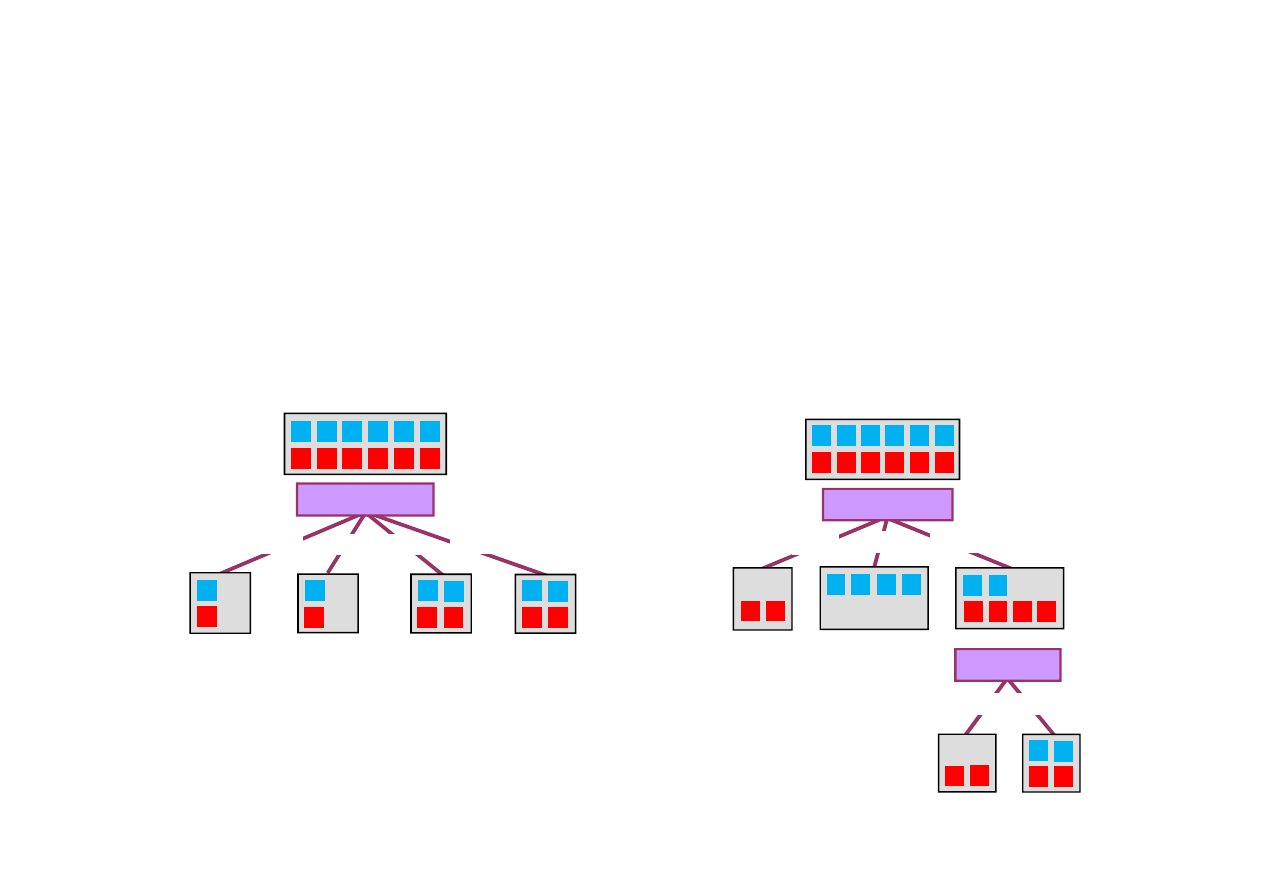
18.3. Uczenie drzew decyzyjnych

Uczenie drzewa decyzyjnego

Cel: zbudowa

ć

„małe” drzewo zgodne z wzorcami ucz

ą

cymi.

Idea: wybra

ć

rekursyjnie ”najwa

ż

niejsze" atrybuty jako

korzenie poddrzew.

1

3

4

6

8 12

1

3

4

6

8 12

Dobre atrybuty dziel

ą

zbiór wzorców na podzbiory które (w

przypadku idealnym) s

ą

w cało

ś

ci pozytywne lub negatywne.

Przykład

© F.A. Dul 2007

Włoska Tajska

2

5

7

9 10 11

6

10

4

2

8

11

Burger

Francuska

1

5

3

7

12

9

Rodzaj

Klienci

Brak

Kilku

Pełno

1

3

6

8

7 11

12

4

2

5

9 10

2

5

7

9 10 11

Nie

Tak

5

4

2

12

10

Głodny?

9

Rodzaj

jest złym atrybutem dziel

ą

cym,

gdy

ż

utworzone podzbiory s

ą

mieszane.

Klienci

s

ą

lepszym atrybutem jako korze

ń

drzewa, gdy

ż

dwa podzbiory s

ą

jednorodne.

18.3. Uczenie drzew decyzyjnych

Algorytm uczenia drzewa decyzyjnego DTL (Decision Tree
Learning)

© F.A. Dul 2007

18.3. Uczenie drzew decyzyjnych

Wybór atrybutów na podstawie teorii informacji
Ocena zdolno

ś

ci atrybutu do efektywnego podziału zbioru

ucz

ą

cego mo

ż

e by

ć

przeprowadzona za pomoc

ą

poj

ę

cia

pojemno

ś

ci informacyjnej

(entropii):

∑

=

−

=

n

i

i

i

n

v

P

v

P

v

P

v

P

I

1

2

1

)

(

log

)

(

))

(

),...,

(

(

Dla zbioru ucz

ą

cego zawieraj

ą

cego p wzorców pozytywnych

i n wzorców negatywnych entropia jest równa:

© F.A. Dul 2007

n

p

n

n

p

n

n

p

p

n

p

p

n

p

n

n

p

p

I

+

+

−

+

+

−

=

+

+

2

2

log

log

)

,

(

i n wzorców negatywnych entropia jest równa:

bit

I

1

2

1

log

2

1

2

1

log

2

1

)

12

6

,

12

6

(

2

2

=

−

−

=

Przykład Dla zadania restauracyjnego mamy p = 6, n = 6,
zatem entropia jest równa

18.3. Uczenie drzew decyzyjnych

Wzmocnienie informacyjne

Je

ż

eli atrybut A dzieli zbiór ucz

ą

cy E na podzbiory E

1

, … , E

m

,

które zawieraj

ą

p

i

oraz n

i

wzorców pozytywnych i negatywnych

to ilo

ść

informacji potrzebna do klasyfikacji wzorców jest równa

Wzmocnienie informacyjne

(Information Gain, IG) lub

zmniejszenie entropii atrybutu A wynosi

∑

=

+

+

+

+

=

m

i

i

i

i

i

i

i

i

i

n

p

n

n

p

p

I

n

p

n

p

A

R

1

)

,

(

)

(

© F.A. Dul 2007

zmniejszenie entropii atrybutu A wynosi

Wybór atrybutów przy budowie drzewa decyzyjnego nast

ę

puje

w kolejno

ś

ci okre

ś

lonej warto

ś

ciami ich wzmocnienia

informacyjnego.

)

(

)

,

(

)

(

A

R

n

p

n

n

p

p

I

A

IG

−

+

+

=

18.3. Uczenie drzew decyzyjnych

Przykład
Warto

ś

ci wzmocnienia informacyjnego dla atrybutów Klienci

i Rodzaj s

ą

równe:

bitów

0541

.

)]

6

4

,

6

2

(

12

6

)

0

,

1

(

12

4

)

1

,

0

(

12

2

[

1

)

(

=

+

+

−

=

I

I

I

Klienci

IG

bitów

0

)]

4

2

,

4

2

(

12

4

)

4

2

,

4

2

(

12

4

)

2

1

,

2

1

(

12

2

)

2

1

,

2

1

(

12

2

[

1

)

(

=

+

+

+

−

=

I

I

I

I

Rodzaj

IG

© F.A. Dul 2007

Warto

ść

IG(Klienci) jest wi

ę

ksza ni

ż

IG(Rodzaj) i dlatego

atrybut Klienci zostanie wybrany przez algorytm Decision Tree
Learning jako korze

ń

drzewa decyzyjnego.

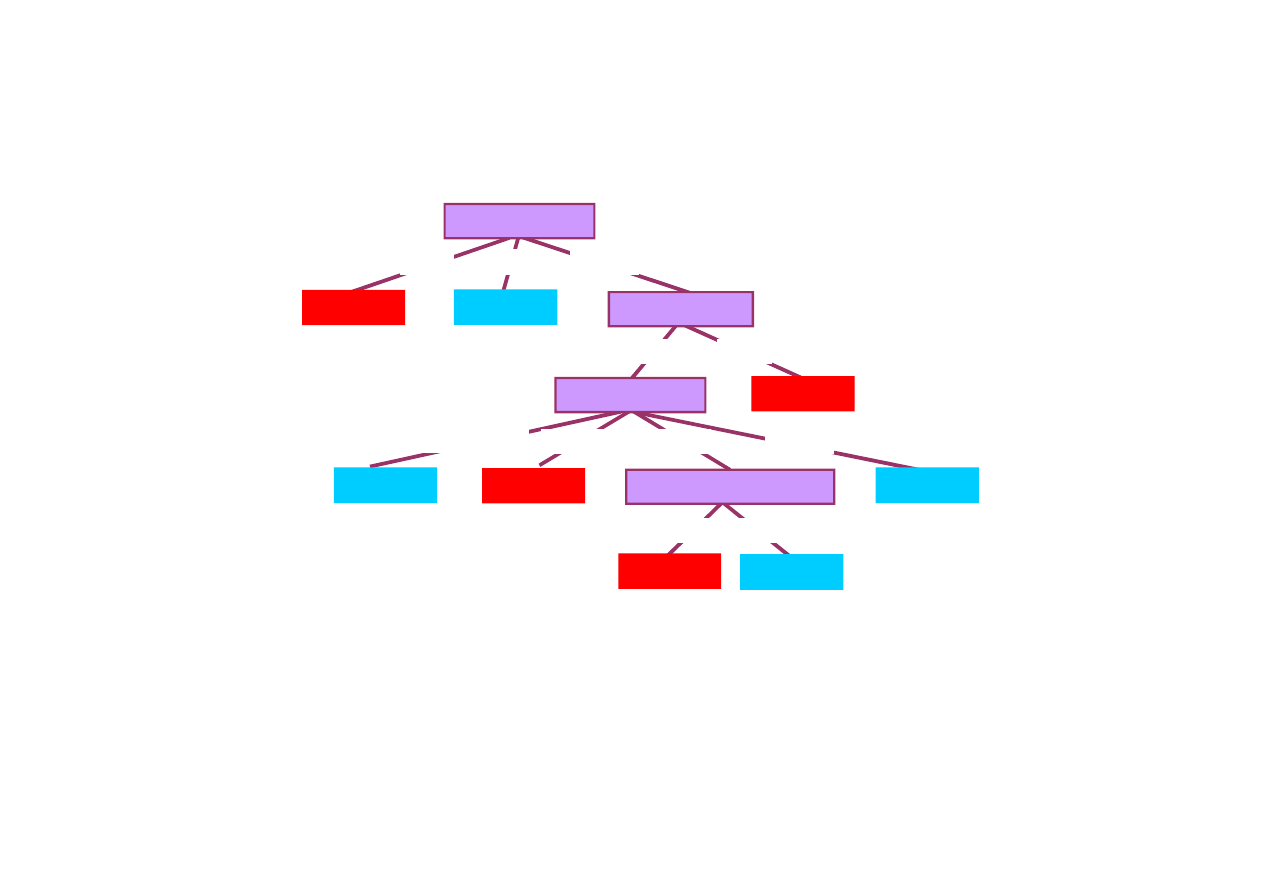
18.3. Uczenie drzew decyzyjnych

Nauczone drzewo decyzyjne

Drzewo decyzyjne nauczone na podstawie 12 wzorców.

Klienci

Fałsz

Prawda

Brak

Kilku

Pełno

Głodny?

Fałsz

Nie

Tak

Rodzaj

Francuska

Włoska

Tajska

Burger

© F.A. Dul 2007

Nauczone drzewo jest du

ż

o prostsze ni

ż

drzewo wyj

ś

ciowe.

Drzewo to ukazuje nieznan

ą

wcze

ś

niej własno

ść

- gotowo

ść

oczekiwania w weekendy na tajskie posiłki.
Drzewo odpowiadaj

ą

ce hipotezie h bli

ż

szej prawdziwej funkcji

f mo

ż

na uzyska

ć

na podstawie wi

ę

kszej ilo

ś

ci wzorców.

Pi

ą

tek/Sobota ?

Fałsz

Prawda

Nie

Tak

Fałsz

Prawda

Francuska

Włoska

Tajska

Prawda

Burger

18.3. Uczenie drzew decyzyjnych

Miara jako

ś

ci uczenia

Hipoteza h dobrze przybli

ż

a funkcj

ę

celu f je

ż

eli poprawnie

klasyfikuje wzorce nieznane wcze

ś

niej.

Metodologia oceny a posteriori jako

ś

ci uczenia:

• Zebra

ć

du

ż

y zbiór wzorców.

• Podzieli

ć

zbiór wzorców na

zbiór ucz

ą

cy

i

zbiór

testowy.

• Wyznaczy

ć

hipotez

ę

h za pomoc

ą

algorytmu ucz

ą

cego

© F.A. Dul 2007

• Wyznaczy

ć

hipotez

ę

h za pomoc

ą

algorytmu ucz

ą

cego

przy wykorzystaniu wzorców ze zbioru ucz

ą

cego.

• Wyznaczy

ć

udział poprawnie sklasyfikowanych

wzorców ze zbioru testowego przy u

ż

yciu hipotezy h.

• Powtórzy

ć

procedur

ę

dla zbiorów testowych o ró

ż

nych

wymiarach.

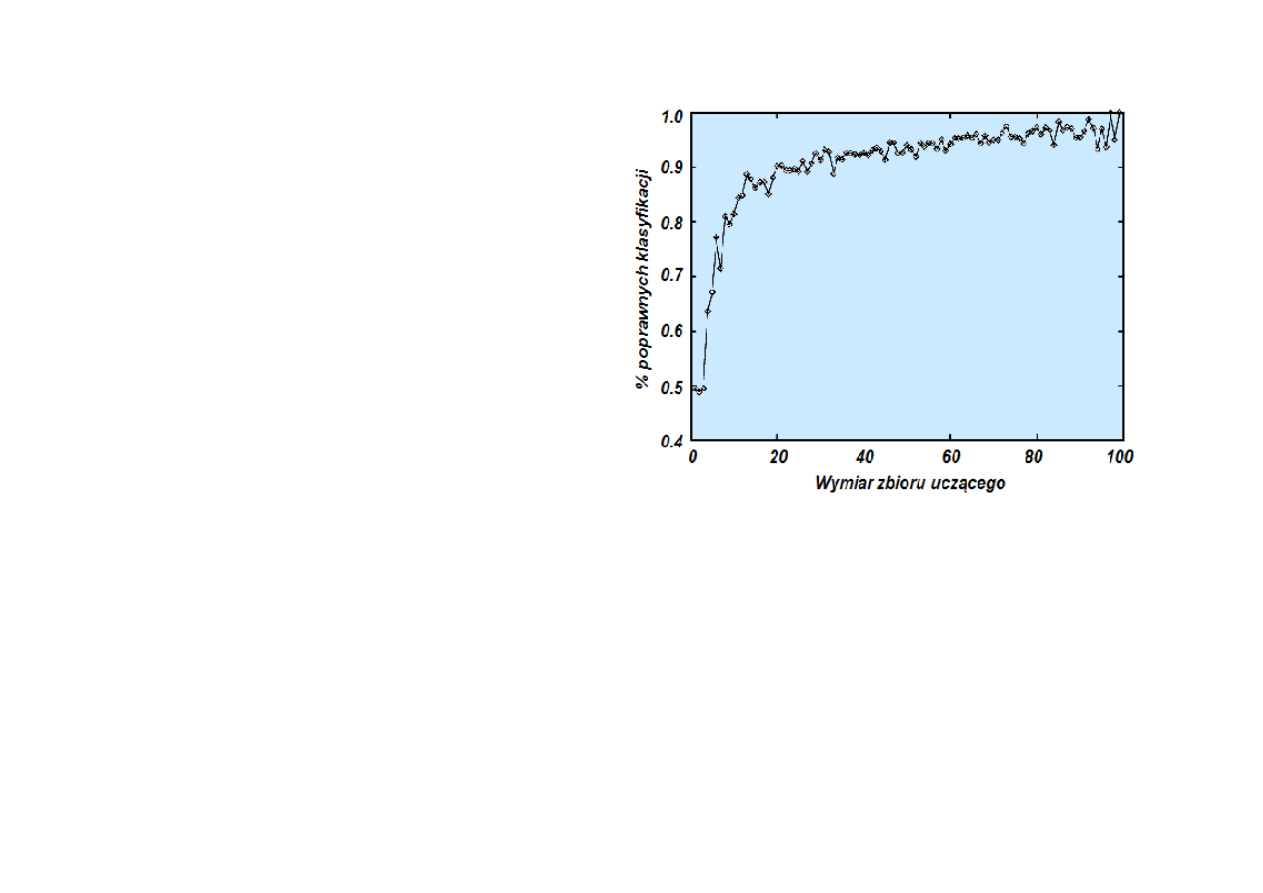
18.3. Uczenie drzew decyzyjnych

Krzywa ucz

ą

ca

obrazuje

udział poprawnych dopasowa

ń

wzorców ze zbioru testowego
w funkcji wymiaru zbioru
ucz

ą

cego.

Wraz ze wzrostem wymiaru
zbioru ucz

ą

cego wzrasta

stopie

ń

poprawno

ś

ci

klasyfikacji za pomoc

ą

hipotezy h.

© F.A. Dul 2007

hipotezy h.

Zagl

ą

danie

(peeking) jest bł

ę

dem uczenia polegaj

ą

cym

na „przeciekaniu” informacji ze zbioru testowego w trakcie
procesu nauczania.
Zagl

ą

danie powoduje spadek jako

ś

ci klasyfikacji za pomoc

ą

tak otrzymanej hipotezy.
Zagl

ą

daniu mo

ż

na zaradzi

ć

poprzez starann

ą

separacj

ę

zbiorów ucz

ą

cych i testowych.

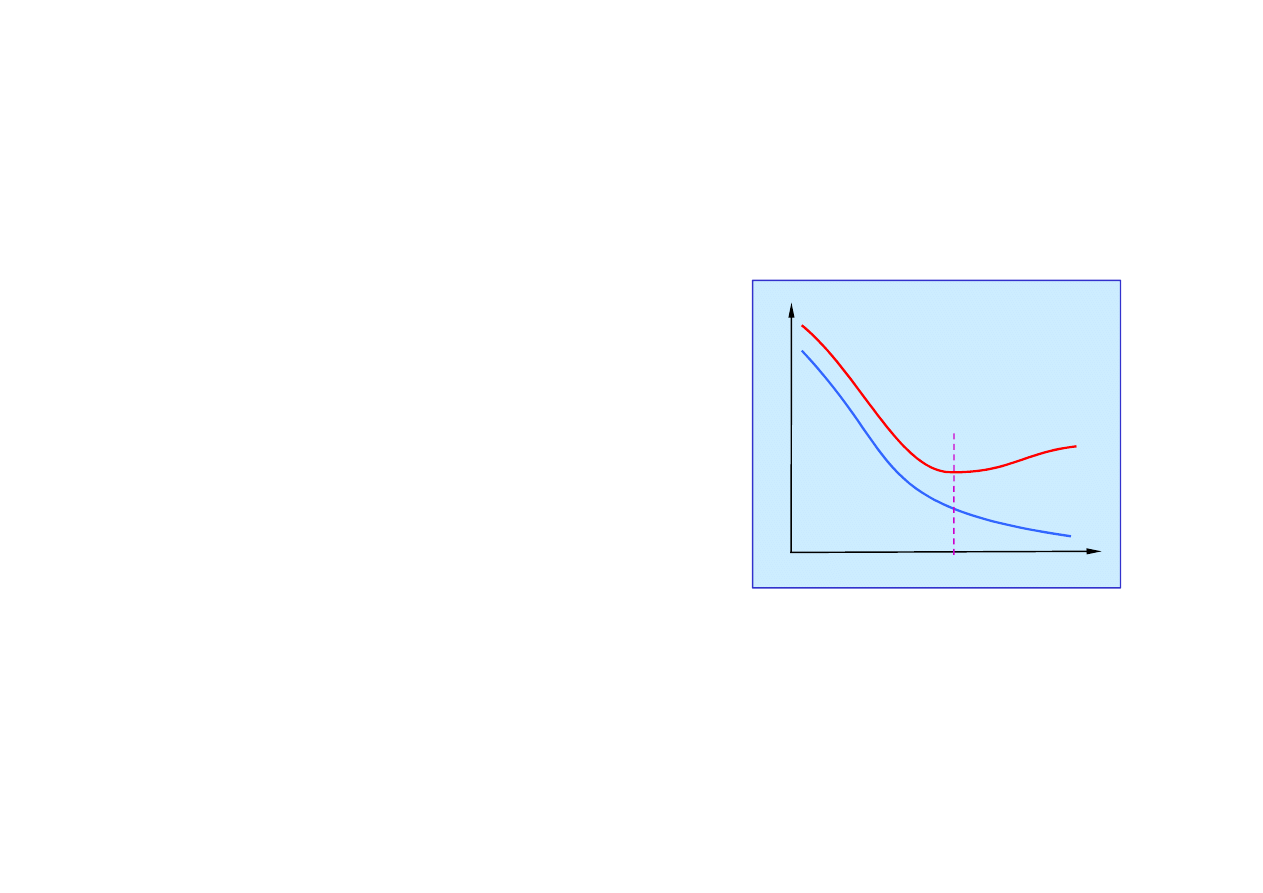
18.3. Uczenie drzew decyzyjnych

Przeuczenie (overfitting)

Gdy przestrze

ń

hipotez jest zbyt obszerna mo

ż

e wyst

ą

pi

ć

zjawisko

przeuczenia

.

Przeuczenie wyst

ę

puje najcz

ęś

ciej wtedy, gdy:

Pocz

ą

tek

przeuczenia

ε

• uczenie trwa zbyt długo,
• zbiór ucz

ą

cy jest za mały.

• u

ż

ywa si

ę

parametrów

nie zwi

ą

zanych przyczynowo

z funkcj

ą

celu.

© F.A. Dul 2007

n

Przy przeuczeniu bł

ą

d dopasowania

wzorców ze zbioru ucz

ą

cego spada,

za

ś

bł

ą

d dopasowania wzorców

ze zbioru testowego ro

ś

nie.

z funkcj

ą

celu.

Przeuczenia mo

ż

na unikn

ąć

przeprowadzaj

ą

c testy, np. wali-

dacji skro

ś

nej (cross-validation) czy wczesnego zako

ń

czenia.

Pozwalaj

ą

one stwierdzi

ć

, czy dalsze uczenie prowadzi

do otrzymania lepszych uogólnie

ń

.

Przeuczenie mo

ż

e wyst

ą

pi

ć

we wszystkich rodzajach uczenia.

18.4. Uczenie zespołowe

Uczenie zespołowe (ensemble learning) obejmuje zbiór hipotez.
Istota uczenia zespołowego polega na wyznaczeniu zbioru
hipotez a nast

ę

pnie ł

ą

czeniu wyników ich przewidywa

ń

.

Mo

ż

na zbudowa

ć

kilka drzew decyzyjnych na podstawie tego

samego (du

ż

ego) zbioru ucz

ą

cego i u

ż

y

ć

ich do klasyfikacji

poprzez

głosowanie

.

Głosowanie wi

ę

kszo

ś

ciowe umo

ż

liwia poprawienie jako

ś

ci

klasyfikacji, gdy

ż

prawdopodobie

ń

stwo bł

ę

dnej klasyfikacji

© F.A. Dul 2007

klasyfikacji, gdy

ż

prawdopodobie

ń

stwo bł

ę

dnej klasyfikacji

przez wi

ę

kszo

ść

drzew jest małe.

–

+

+

+

+

+

+

+

+

+

+

+

+

+

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

–

U

ż

ycie pi

ę

ciu hipotez zamiast jednej

redukuje prawdopodobie

ń

stwo bł

ę

dnej

klasyfikacji z 1/10 do 1/100.
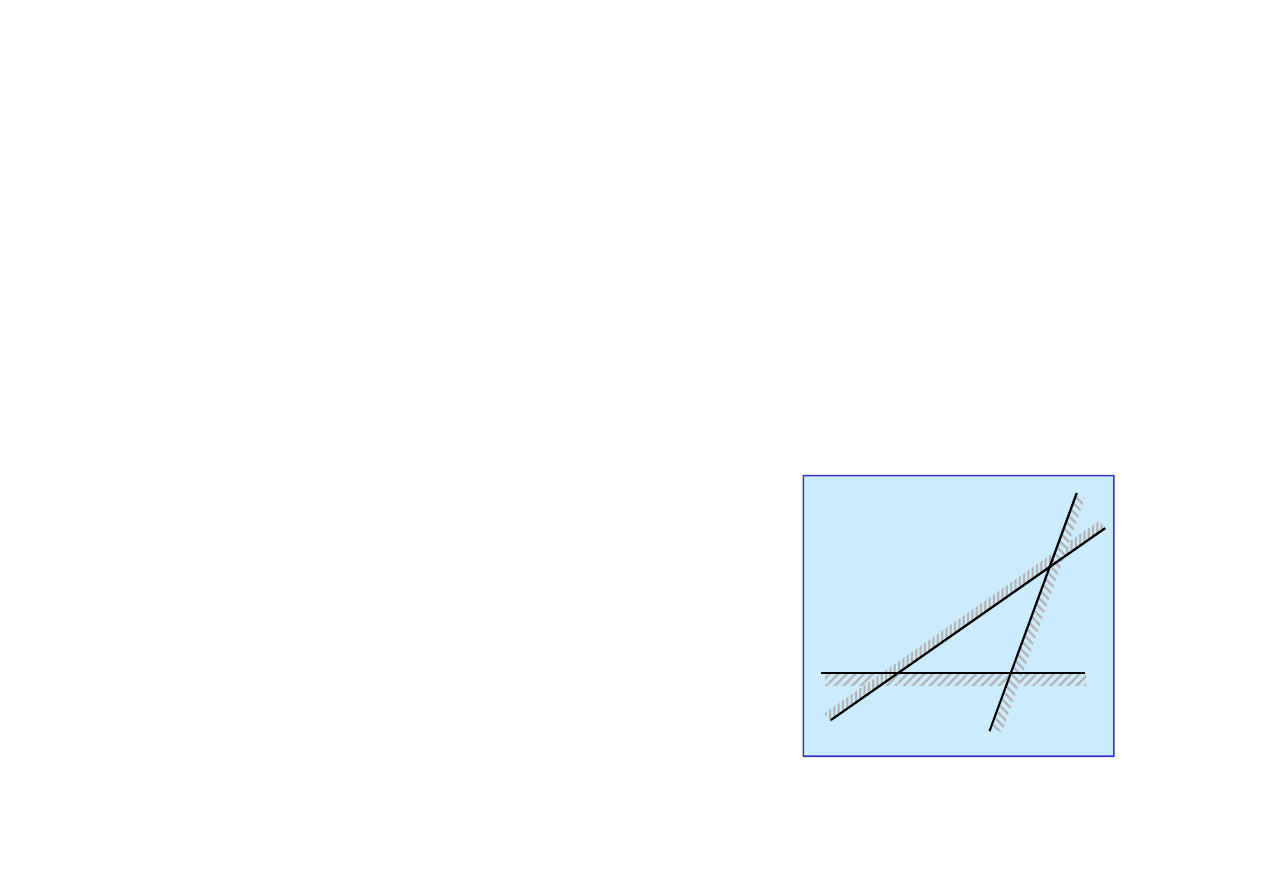
Uczenie zespołowe pozwala rozszerzy

ć

przestrze

ń

hipotez.

Trzy hipotezy pozwalaj

ą

kwalifikowa

ć

wzorce w obszarze, czego nie mo

ż

na

łatwo osi

ą

gn

ąć

przy pomocy pojedy

ń

czej hipotezy.

Najcz

ęś

ciej u

ż

ywan

ą

metod

ą

uczenia zespołowego jest

metoda wzmacniania (

boosting

).

18.4. Uczenie zespołowe

© F.A. Dul 2007

18.5. Obliczeniowa teoria uczenia

Dlaczego uczenie jest skuteczne?
Podstawowa zasada

obliczeniowej teorii uczenia:

Zła hipoteza zostanie prawie na pewno wykryta
na podstawie niewielkiej liczby przykładów ucz

ą

cych,

gdy

ż

jej przewidywania b

ę

d

ą

niewła

ś

ciwe.

Je

ż

eli hipoteza jest potwierdzona przez du

żą

liczb

ę

przykładów

ucz

ą

cych, to jest mało prawdopodobne aby była zła.

Taka hipoteza jest

prawdopodobnie w przybli

ż

eniu poprawna

© F.A. Dul 2007

Taka hipoteza jest

prawdopodobnie w przybli

ż

eniu poprawna

(probably approximately correct, PAC).

Algorytm PAC – algorytm ucz

ą

cy oparty na hipotezie PAC.

Zało

ż

enie podstawowe (o stacjonarno

ś

ci): zbiory ucz

ą

ce

i testowe s

ą

wybrane losowo i s

ą

niezale

ż

ne.

Zakłada si

ę

te

ż

,

ż

e przykłady ucz

ą

ce s

ą

typowe dla zadania

– nie s

ą

„dziwne” (np. trójkołowe samochody, itp.), gdy

ż

wówczas uogólnienia mog

ą

by

ć

niemiarodajne (np. przy

rozpoznawaniu samochodów).

18.5. Obliczeniowa teoria uczenia

Liczba przykładów ucz

ą

cych

Oznaczenia:

Bł

ą

d hipotezy h wzgl

ę

dem funkcji celu f

∈

H przy danym

zbiorze D jest to prawdopodobie

ń

stwo tego,

ż

e h ró

ż

ni si

ę

od f na pewnym przykładzie z D,

e(h) = P( h(x) ≠ f(x) | x

∈

D ).

• X – zbiór wszystkich mo

ż

liwych przykładów,

• D –

ź

ródło przykładów,

• H – zbiór mo

ż

liwych hipotez,

• N – liczba przykładów w zbiorze ucz

ą

cym.

© F.A. Dul 2007

e(h) = P( h(x) ≠ f(x) | x

∈

D ).

Hipoteza jest

poprawna w przybli

ż

eniu

, je

ż

eli

e(h) ≤

ε

,

ε

–

małe

.

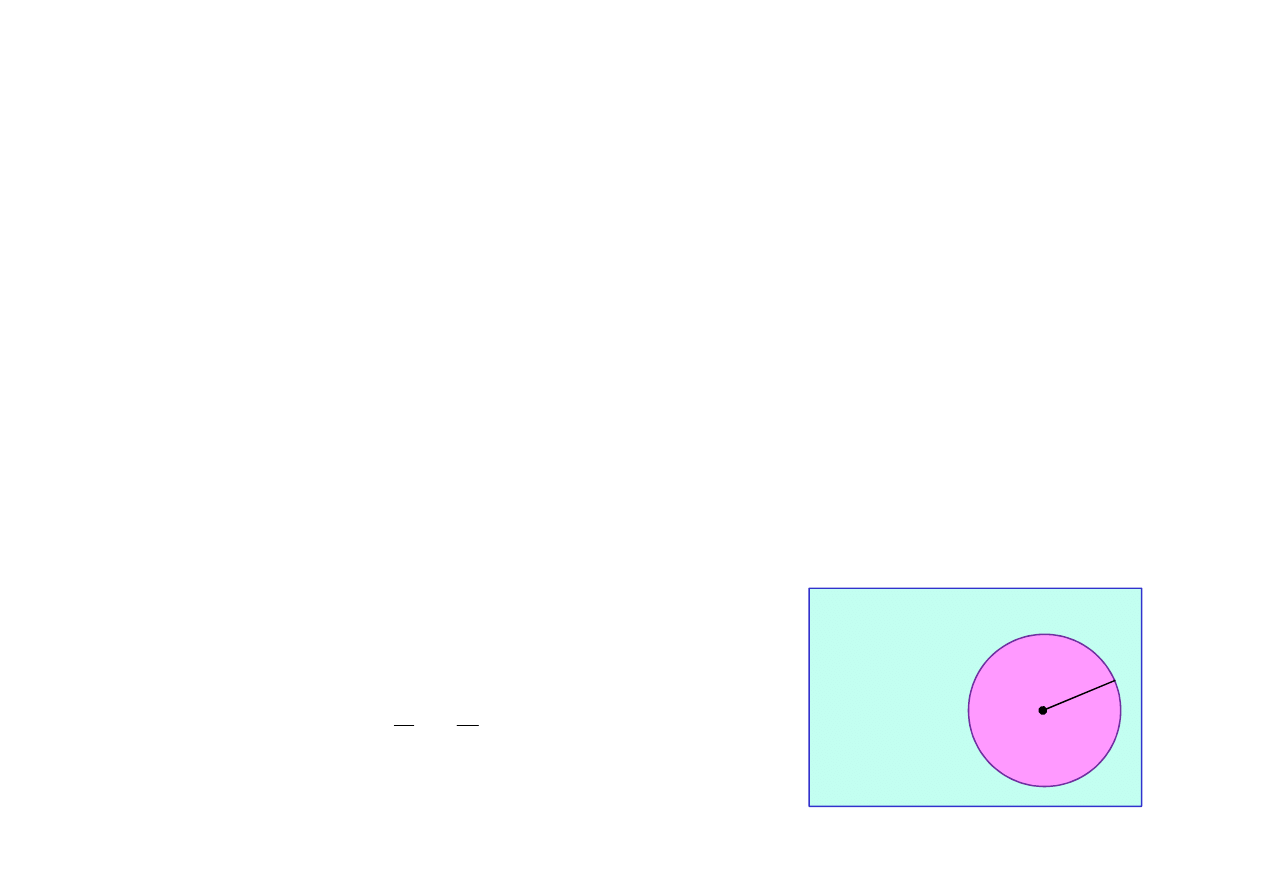
Hipotezy zgodne le

żą

w kole o

ś

rodku w f i promieniu

ε

.

f

ε

H

H

złe

Liczba N przykładów ucz

ą

cych dla

których wszystkie hipotezy zgodne b

ę

d

ą

w przybli

ż

eniu poprawne jest równa

|)

|

ln

1

(ln

1

H

+

≥

δ

ε

N

1-

δ

– prawdopodobie

ń

stwo,

ż

e bł

ą

d

hipotezy jest mniejszy ni

ż

ε

.

Uczenie agenta indukcyjnego

Uczenie indukcyjne to w istocie aproksymacja funkcji
na podstawie danych do

ś

wiadczalnych.

Uczenie drzew decyzyjnych ma charakter
identyfikacji strukturalnej – buduje si

ę

struktur

ę

drzewa na podstawie danych.

Agent ucz

ą

cy si

ę

indukcyjnie jest „tabula rasa”

– nie wie niczego o

ś

wiecie i niczego nie pami

ę

ta.

©

F.A. Dul 2007

– nie wie niczego o

ś

wiecie i niczego nie pami

ę

ta.

Mo

ż

e on znacznie podwy

ż

szy

ć

efektywno

ść

i jako

ść

uczenia poprzez wykorzystanie wiedzy wiedzy
posiadanej a priori.

Bardziej zaawansowany agent b

ę

dzie zatem

wykorzystywał

uczenie z wiedz

ą

.

Podsumowanie

• Uczenie jest niezb

ę

dne przy niepewnym

ś

rodowisku.

• Agent ucz

ą

cy si

ę

= moduł decyzyjny + moduł ucz

ą

cy si

ę

.

• Uczenie przybiera wiele form zale

ż

nych od struktury agenta

i rodzaju ucz

ą

cego sprz

ęż

enia zwrotnego.

• Uczenie indukcyjne wykorzystuje wzorce ucz

ą

ce - zbiór par

wej

ś

cie i wyj

ś

cie.

• Uczenie funkcji dyskretnej to klasyfikacja, za

ś

funkcji ci

ą

głej

to regresja.

• Uczenie indukcyjne polega na znalezieniu hipotezy zgodnej

• Uczenie indukcyjne polega na znalezieniu hipotezy zgodnej

z danymi wzorcami.

• Brzytwa Ochkama sugeruje wybór hipotezy najprostszej.
• Identyfikacja modelu jest form

ą

uczenia indukcyjnego.

• Drzewo decyzyjne uczy si

ę

przy wykorzystaniu

wzmocnienia informacyjnego.

• Przeuczenie polega na nadmiernym dopasowaniu hipotezy

do wzorców i prowadzi do bł

ę

dnych klasyfikacji.

• Jako

ść

uczenia wyra

ż

a si

ę

dokładno

ś

ci

ą

wzorców mierzon

ą

na zbiorze testowym (innym ni

ż

zbiór ucz

ą

cy).

©

F.A. Dul 2007