Politechnika Poznańska
Laboratorium Elektrotechniki
Elektrotechnika - laboratoria
Nazwisko i imię:
Dawid Kasprzak
Andrzej Ziegler
Krzysztof Zięntek
Adrian Tomczak
Semestr:
3
Wydział:
B M i Z
Kierunek:
M e c h a t ro n i k a
Grupa dziek./lab:
2 / 1
Temat ćwiczenia:
Pomiar mocy i energii w układach jednofazowych
Data wykonania ćwiczenia:
21.12.2010r.
Data i podpis prowadzącego:
Ocena:
Schemat układu do pomiaru mocy i energii odbiorników jednofazowych:
Wyniki pomiarów i obliczenia:
Pomiary
Obliczenia
Rodzaj
połączenia
U
[V]
I [A]
P1
[W]
t
[s]
n
[obr]
S
[VA]
Q
[var]
cos(fi)
A
[Wh]
C
[Wh/obr]
żarówka 200W
230 0,88
200 600
60,5 202,4
31,08 0,9881
33,33
0,55
rezystor R
230 0,90
203 600
68,0 207,0
40,50 0,9807
33,83
0,50
szeregowo RL
230 0,80
180 600
55,0 184,0
38,16 0,9783
30,00
0,55
szeregowo RC
230 0,90
202 600
65,0 207,0
45,22 0,9758
33,67
0,52
Przykładowe obliczenia:
Wszystkie przykładowe obliczenia przedstawione są dla pierwszego badanego elementu (żarówki
200W). Dla pozostałych elementów obliczenia są analogiczne.
Moc pozorna:
Moc bierna:
Moc bierną Q obliczamy z trójkąta mocy. Jest ot trójkąt prostokątny, możemy zatem skorzystad z
twierdzenia Pitagorasa i wyznaczyd zależnośd:
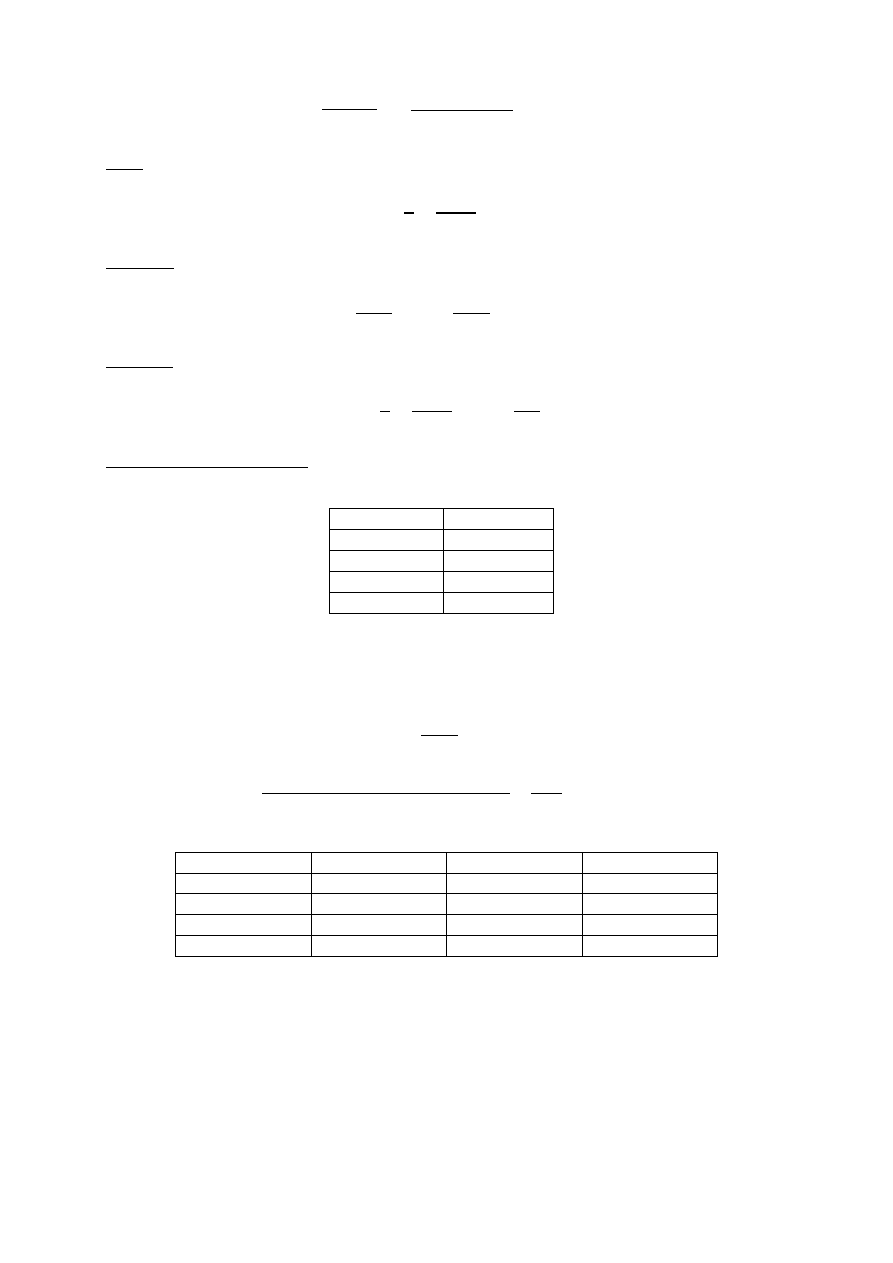
cosφ:
obliczamy podobnie jak moc bierną z trójkąta mocy, korzystając z zależności trygonometrycznej
Energia A:
Energię układu obliczamy z iloczynu
Energia C:
Energię, jaka przypada na jeden obrót obliczamy ze wzoru
Przeliczanie mocy na dżule *J+:
A [Wh]
A [J]
33,33
120000
33,83
121800
30,00
108000
33,67
121200
Użyty podczas doświadczenia licznik energii charakteryzował się napięciem U=220V, natężeniem
I=10A i częstotliwością f=50Hz. Licznik zlicza 1kWh na 1500 obrotów tarczy.
Przykład obliczeo:
Wyniki obliczeo zestawione w tabeli:
P1 [W]
n [obr]
A [Wh] obliczone
B [Wh] licznika
200
60,5
33,33
40,33333
203
68,0
33,83
45,33333
180
55,0
30,00
36,66667
202
65,0
33,67
43,33333
A – energia obliczona; B – energia zliczona przez licznik.
Okazuje się, że zużyta energia obliczona ze zmierzonej mocy jest mniejsza, niż ta, jaką zlicza licznik.
Należy jednak zauważyd, iż pomiar liczby obrotów nie jest bardzo dokładny, ponieważ obroty
mierzone w czasie 10min (600s) mierzone były z dokładnością do 0,5 obrotu – na tarczy były
zaznaczone 2 kreski.
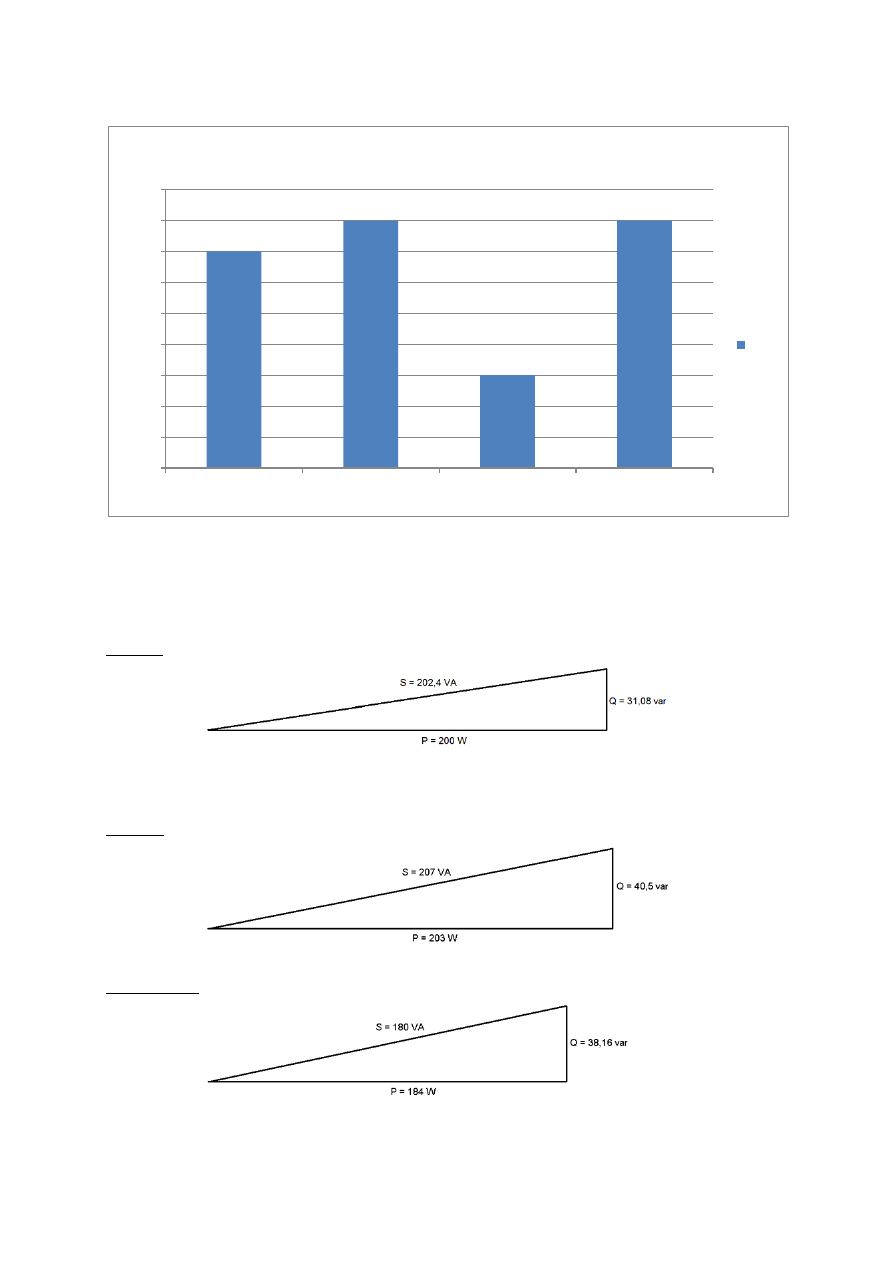
Wykresy prądów:
Trójkąty mocy:
Żarówka
Rezystor
Szeregowo RL
0,74
0,76
0,78
0,80
0,82
0,84
0,86
0,88
0,90
0,92
żarówka 200W
rezystor R
szeregowo RL
szeregowo RC
Zależnośd płynącego prądu od elementu
I [A]
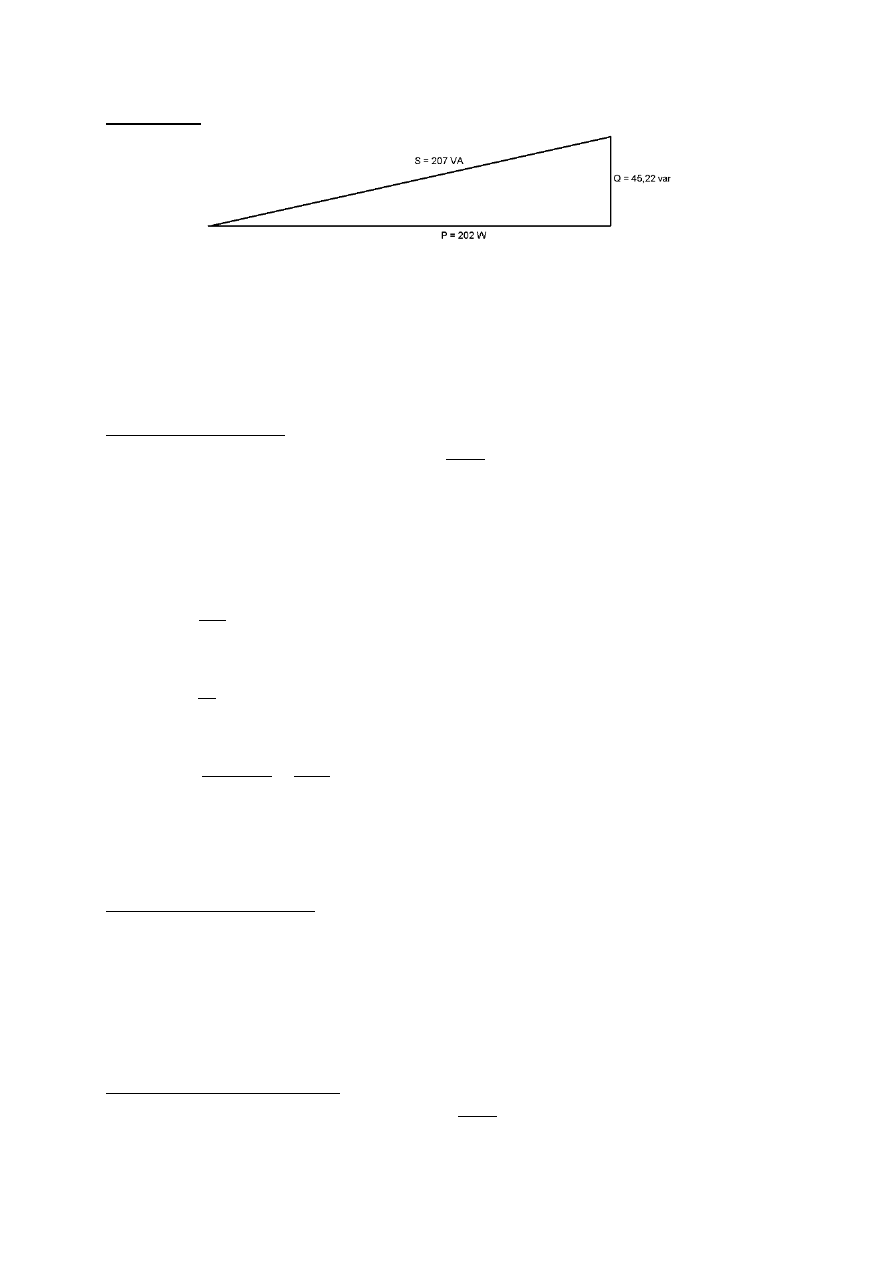
Szeregowo RC
Przeliczenie mocy na J dla wskazao licznika:
Dyskusja błędów:
Obliczanie stałej przyrządu:
Gdzie:
C
P
– stała przyrządu
W
max
– zakres przyrządu
α
max
– liczba działek
Dla woltomierza:
Dla amperomierza:
Dla watomierza:
Obliczanie wskazania miernika:
W
p
– wskazanie przyrządu
Wyniki obliczeo wskazao przyrządów przedstawiliśmy w tabeli z pomiarami (pomiary
odczytane z przyrządów znajdują się w załączonej karcie z wynikami pomiarów z dwiczenia).
Obliczamy błąd względny pomiaru:
δ
p
– błąd względny pomiaru
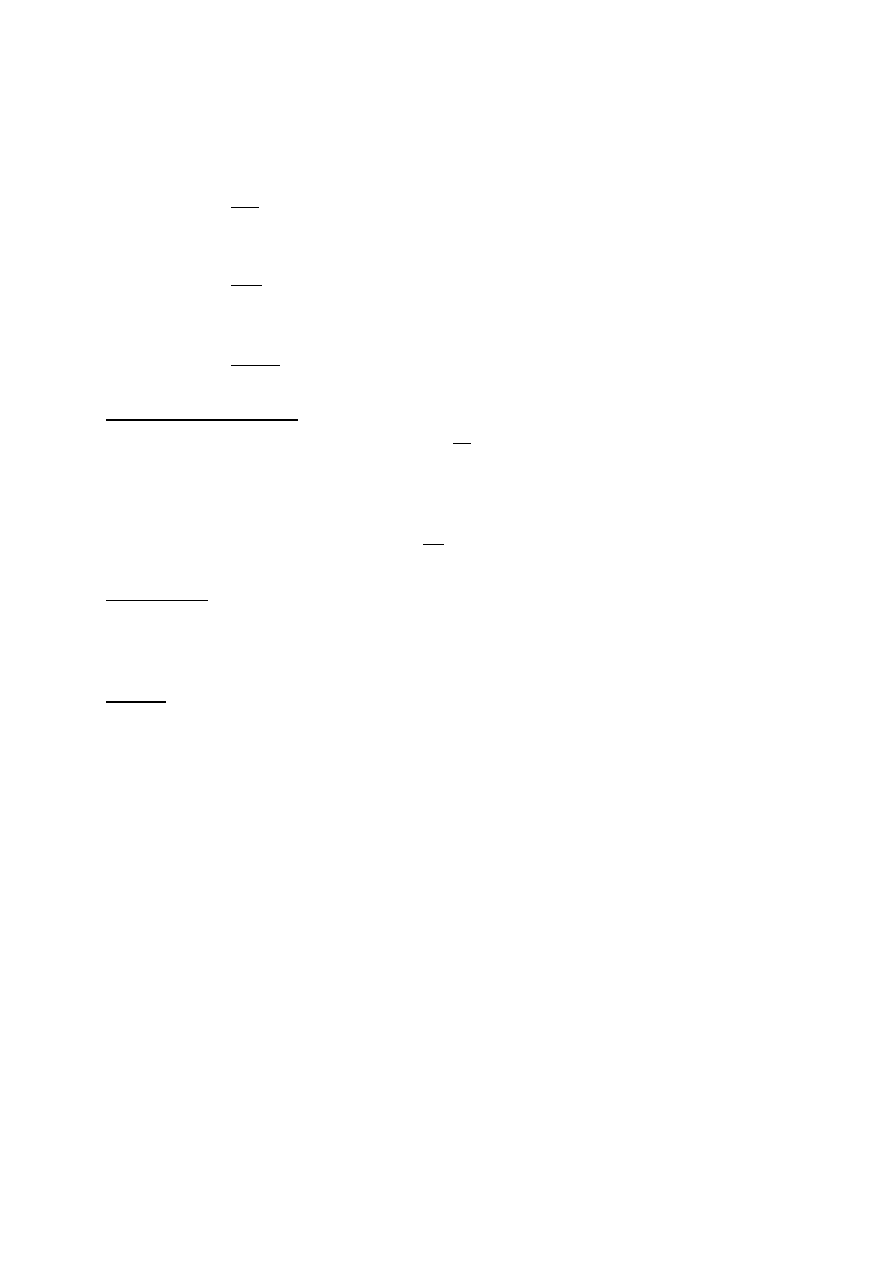
δ
kl
– klasa dokładności przyrządu
W
wsk
– wskazanie przyrządu
Dla woltomierza:
Dla amperomierza:
Dla watomierza:
Obliczanie czułości miernika:
S – czułośd miernika
np. dla amperomierza:
Błąd graniczny:
Δp
gr
– błąd graniczny
Wnioski:
Wartości rzeczywiste są różne od tych, które wskazałby licznik energii elektrycznej. Działa to niestety
na naszą niekorzyśd jako odbiorców energii elektrycznej. Różnica w otrzymanych wartościach wynosi
ok. 200Wh, co w skali roku powoduje znaczny wzrost kosztów tej energii. Użyty w dwiczeniu licznik
jest standardowym licznikiem energii elektrycznej stosowanym w wielu domostwach. Jego działanie
polega na pomiarze pobranej mocy czynnej P w czasie. Standardowe liczniki nie są zdolne do pomiaru
mocy biernej. W prostym obwodzie prądu przemiennego składającego się ze źródła i liniowego
obciążenia, zarówno prąd jak i napięcie są sinusoidalne. Jeżeli obciążenie jest całkowicie
rezystancyjne obydwie wielkości zmieniają polaryzację w tym samym czasie, natomiast kierunek
przepływu energii się nie zmienia. W takim przypadku moc całkowita równa jest mocy czynnej i nie
pojawia się potrzeba kompensacji mocy biernej. Widad to na przedstawionych wykresach (trójkątach
napięd). Jeżeli obciążenie jest czysto indukcyjne lub pojemnościowe, to napięcie i prąd są przesunięte
względem siebie w fazie o 90 stopni. Maksymalna wartośd napięcia przypada wtedy gdy prąd
przechodzi przez zero. W takim wypadku, przepływa tylko moc bierna, która nie dostarcza energii
obciążeniu. Rzeczywiste obciążenia mają charakter rezystancyjny, indukcyjny i pojemnościowy co
oznacza, że odbierają zarówno moc czynną jak i bierną. Elektrycy mierzą pobór mocy jako sumę tych
dwóch wielkości. Mimo tego, że moc bierna nie wykonuje pracy, to powoduje wzrost prądów
zasilających oraz nagrzewa urządzenia służące do przesyłu energii co z kolei prowadzi do większych
strat w przesyle energii. Stosunek mocy czynnej do mocy pozornej jest nazywany współczynnikiem
mocy. Jest on określany jako kosinus kąta pomiędzy wektorami napięcia i prądu - jego wartośd
została obliczona w tabeli. Współczynnik mocy równy jest 1 wtedy gdy napięcie i prąd są ze sobą w
fazie, a wynosi zero gdy obydwa wektory są przesunięte względem siebie o 90 stopni. Kondensatory
kompensują moc bierną, natomiast cewki i odbiorniki typu indukcyjnego generują pasożytniczą moc

bierną. Porównując moc bierną pojemnościową i bierną indukcyjną możemy w odpowiedni sposób
regulowad kąt między wektorem prądu, a wektorem napięcia. Na tym fundamentalnym mechanizmie
opiera się kontrola współczynnika mocy (kompensacja) - kondensatory włączane są do obwodu, aby
częściowo zlikwidowad moc bierną obciążenia. Dąży się do tego, aby współczynnik mocy odbiorców
energii elektrycznej był bliski jedności. Moc bierna nie transferuje energii. Dlatego na wykresie
wektorowym jest ona reprezentowana na osi urojonej. Właściwie przeprowadzona kompensacja
mocy biernej pozwala praktycznie w całości wyeliminowad comiesięczne opłaty za energię bierną. W
energetyce przemysłowej tylko niektórzy odbiorcy, głównie duże zakłady przemysłowe posiadają
specjalne liczniki mocy biernej. Odbiorca taki zobowiązany jest do dodatkowej opłaty za pobieraną
moc bierną.
W naszym przypadku cosφ wyszedł bardzo mały, głównie ze względu na to, że ustawienie pieca
(obciążenia rezystancyjnego) było niedobrane do wyznaczania mocy biernej (dlatego otrzymane
przez nas trójkąty mocy są takie płaskie).
Wskazania amperomierza są ponadto obarczone dużym błędem, ponieważ podczas wykonywania
dwiczenia wystąpił problem z doborem właściwego zakresu amperomierza (związany bezpośrednio z
brakiem odpowiedniego miernika). Widad to wyraźnie po obliczonej czułości amperomierza. Okazuje
się, że minimalna wartośd, do mierzenia której użyty przez nas amperomierz jest przystosowany to
2A, podczas gdy mierzone przez nas wartości nie przekraczały 1A.
Wyszukiwarka
Podobne podstrony:
El sprawko 5 id 157337 Nieznany
El sprawko 2
El sprawko 5
El sprawko 5
El sprawko 1
El sprawko 2333
El sprawko 6
El sprawko 2
El sprawko 5 id 157337 Nieznany
El sprawko 2
El sprawko 2
El sprawko 5
El sprawko 2333
El sprawko 4
El sprawko 1
El sprawko 2
sprawko EL EN PEM
więcej podobnych podstron