Z. Kąkol-Notatki do Wykładu z Fizyki

35-1

Wykład 35

35.

Lasery

35.1

Emisja spontaniczna

Jeden z postulatów Bohra mówił, że promieniowanie elektromagnetyczne zostaje

wysłane tylko wtedy gdy elektron poruszający się po orbicie o całkowitej energii E

j

zmienia swój ruch skokowo, tak że porusza się następnie po orbicie o energii E

k

. W ję-

zyku mechaniki kwantowej mówimy, że cząstka (elektron) przechodzi ze stanu wzbu-
dzonego (o wyższej energii) do stanu podstawowego emitując foton. Częstotliwość emi-
towanego promieniowania jest równa

h

E

E

v

k

j

−

=

Jak już widzieliśmy źródłem takiego promieniowania jest na przykład jednoatomowy
gaz pobudzony do świecenia metodą wyładowania elektrycznego (widmo liniowe).
Teoria kwantowa przewiduje, że elektron znajdujący się w stanie wzbudzonym

samoist-

nie

przejdzie do stanu podstawowego emitując foton. Zjawisko takie jest nazywane

emi-

sją spontaniczną

.

Jeżeli różnica energii wynosi kilka elektronowoltów (jak w atomie wodoru, gdzie
E

1

= -13.6 eV) to czas charakterystyczny dla procesu emisji spontanicznej ma wartość

rzędu 10

-8

s.

35.2

Absorpcja

Na gruncie modelu Bohra można łatwo zrozumieć własności widm emisyjnych ato-

mów jednoelektronowych. Można również zrozumieć widma absorpcyjne.
Ponieważ elektron musi mieć w atomie energię całkowitą równą jednej z energii dozwo-
lonych (stanu stacjonarnego) więc z padającego promieniowania może on absorbować
tylko określone porcje (kwanty) energii. Energia absorbowanych kwantów h

ν

musi być

równa różnicy pomiędzy energiami dozwolonych stanów tak więc linie widma absorp-
cyjnego mają te same częstotliwości (długości fal) co linie widma emisyjnego.
Doświadczenie pokazuje, że w chłodnym gazie atomy są w stanie podstawowym n = 1
więc procesy absorpcji odpowiadają serii Lymana. W bardzo wysokich temperaturach
atomy będą już w stanie n = 2 i możemy obserwować linie absorpcyjne serii Balmera
(widzialne).
Procesy wzbudzania atomów na wyższe poziomy energetyczne przez ich oświetlanie
nosi nazwę

pompowania optycznego

.

35.3

Emisja wymuszona

Teoria kwantowa mówi także, że oprócz

emisji spontanicznej

oraz procesów

ab-

sorpcji

występuje także inny proces, nazywany

emisją wymuszoną

.

Z. Kąkol-Notatki do Wykładu z Fizyki

35-2

Przypuśćmy, że atom znajduje się w stanie wzbudzonym E

j

i może emitować foton

o energii (E

j

- E

k

). Jeżeli taki atom zostanie oświetlony promieniowaniem, które zawiera

fotony o energii właśnie równej (E

j

- E

k

) to

prawdopodobieństwo wypromieniowania

przez atom energii wzrośnie

.

Takie zjawisko przyspieszenia wypromieniowania energii przez oświetlenie atomów
wzbudzonych odpowiednim promieniowaniem nazywane jest

emisją wymuszoną

.

Uwaga:

Foton wysyłany w procesie emisji wymuszonej ma taką samą fazę oraz taki sam

kierunek ruchu jak foton wymuszający

.

W emisji spontanicznej mamy do czynienia z fotonami, których fazy i kierunki są rozło-
ż

one przypadkowo. Emisja wymuszona stwarza szansę uzyskania promieniowania spój-

nego.
ś

eby móc przeanalizować możliwość takiej emisji musi wiedzieć jak atomy (cząsteczki)

układu obsadzają różne stany energetyczne tzn. ile jest w stanie podstawowym a ile w
stanach wzbudzonych.

35.4

Rozkład Boltzmana

Opis szczegółowy układu fizycznego złożonego z bardzo dużej liczby elementów jest
bardzo skomplikowany np. próba opisu ruchu jednej cząstki gazu w układzie zawierają-
cym 10

23

cząstek (1 mol).

Na szczęście do wyznaczenia podstawowych własności układu (wielkości mierzalnych)
takich jak temperatura, ciśnienie - informacje szczegółowe są na ogół niepotrzebne.
Jeśli do układu wielu cząstek zastosujemy ogólne zasady mechaniki (takie jak prawa
zachowania) to możemy zaniedbać szczegóły ruchu czy oddziaływań pojedynczych czą-
stek i podstawowe własności układu wyprowadzić z samych rozważań statystycznych.
Taki przykład już poznaliśmy. Jest nim związek pomiędzy własnościami gazu klasycz-
nego i rozkładem Maxwella prędkości cząsteczek gazu.
Funkcja rozkładu N(v) daje informację o prawdopodobieństwie, że cząsteczka ma pręd-
kość w przedziale v, v + d v. Znając funkcję N(v) możemy obliczyć takie wielkości jak
ś

rednia prędkość (pęd niesiony przez cząsteczki), średni kwadrat prędkości (energia ki-

netyczna) itp. a na ich podstawie obliczyć takie wielkości mierzalne jak ciśnienie (zwią-
zane z pędem) czy temperaturę (związaną z energią).
Spróbujemy teraz znaleźć rozkład prawdopodobieństwa z jakim cząstki układu zajmują
różne stany energetyczne.
W tym celu rozpatrzymy układ zawierający dużą liczbę cząstek, które znajdują się w
równowadze w temperaturze T. By osiągnąć ten stan równowagi cząstki muszą wymie-
niać energię ze sobą (poprzez zderzenia). Podczas tej wymiany ich energie będą fluktu-
ować, przyjmując wartości raz mniejsze raz większe od średniej.
ś

eby to zilustrować rozważmy układ, w którym cząstki mogą przyjmować jedną z na-

stępujących wartości energii E = 0,

∆

E, 2

∆

E, 3

∆

E, 4

∆

E..... .

Celem uproszczenia przyjmijmy, że układ ma zawiera tylko 4 cząstki oraz, że energia
całkowita układu ma wartość 3

∆

E.

Ponieważ te cztery cząstki mogą wymieniać energię między sobą, więc realizowany
może być każdy możliwy podział energii całkowitej 3

∆

E pomiędzy te obiekty. Na ry-

sunku poniżej pokazane są wszystkie możliwe podziały, które numerujemy indeksem i.
Uwaga: Obliczając ilość sposobów realizacji danego podziału traktujemy jako rozróż-
nialny podział, który można otrzymać z danego w drodze przestawiania cząstek pomię-

Z. Kąkol-Notatki do Wykładu z Fizyki

35-3

dzy różnymi stanami. Przestawienia cząstek w tym samym stanie energetycznym nie
prowadzą do nowych sposobów realizacji podziałów, bo nie można eksperymentalnie
odróżnić od siebie takich samych cząstek o tej samej energii. Wreszcie ostatnie założe-
nie: wszystkie sposoby podziału energii mogą wydarzyć się z tym samym prawdopodo-
bieństwem.

i

E=0

E=

∆

E

E=2

∆

E

E=3

∆

E

E=4

∆

E

liczba sposobów

realizacji podzia-

łu

P

i

1

1,2,3

4

1

1,2,4

3

4

4/20

1

1,3,4

2

1

2,3,4

1

2

1,2

3

4

2

1,2

4

3

2

1,3

2

4

2

1,3

4

2

2

1,4

2

3

2

1,4

3

2

12

12/20

2

2,3

1

4

2

2,3

4

1

2

2,4

1

3

2

2,4

3

1

2

3,4

1

2

2

3,4

2

1

3

1

2,3,4

3

2

1,3,4

4

4/20

3

3

1,2,4

3

4

1,2,3

n(E)

40/20

24/20

12/20

4/20

0/20

Obliczamy następnie n(E) czyli prawdopodobną ilość cząstek w danym stanie energe-
tycznym E.
Weźmy stan E = 0.
Dla podziału i = 1 mamy 3 cząstki a prawdopodobieństwo, że taki podział ma miejsce
wynosi 4/20.
Dla podziału i = 2 mamy 2 cząstki a prawdopodobieństwo, że taki podział ma miejsce
wynosi 12/20.
Wreszcie dla podziału i = 3 mamy 1 cząstkę a prawdopodobieństwo, że taki podział ma
miejsce wynosi 4/20.
Zatem prawdopodobna ilość obiektów w stanie E = 0 wynosi:

Z. Kąkol-Notatki do Wykładu z Fizyki

35-4

n(E) = 3 (4/20) + 2 (12/20) + 1 (4/20) = 40/20 = 2

Analogicznie obliczamy n(E) dla pozostałych wartości E (patrz ostatni wiersz tabeli).
Zauważmy, że suma tych liczb wynosi cztery, tak że jest równa całkowitej liczbie czą-
stek we wszystkich stanach energetycznych.
Wykres zależności n(E) jest pokazany na rysunku poniżej.
Ciągła krzywa na rysunku jest wykresem malejącej wykładniczo funkcji

0

)

(

E

E

Ae

E

n

−

=

(35.1)

Możemy teraz brać

∆

E coraz mniejsze (zwiększając ilość dozwolonych stanów) przy tej

samej co poprzednio wartości całkowitej energii. Oznacza to, że będziemy dodawać co-
raz więcej punktów do naszego wykresu, aż w granicy gdy

∆

E

→

0 przejdziemy do

funkcji ciągłej danej powyższym równaniem.
Potrzebujemy jeszcze znaleźć E

0

. Obliczenia te choć proste wykraczają poza ramy tego

wykładu. Wystarczy więc zapamiętać, że E

0

= kT, tzn. jest równa średniej energii układu

cząstek w temperaturze T.
Ostatecznie więc

kT

E

Ae

E

n

−

=

)

(

(35.2)

Jest to

rozkład Boltzmana

, który mówi, że prawdopodobna ilość cząstek układu w rów-

nowadze w temperaturze T, znajdujących się w stanie o energii E jest proporcjonalna do

kT

E

e

−

. Sposób wyboru stałej proporcjonalności A zależy od tego jaki układ rozważamy.

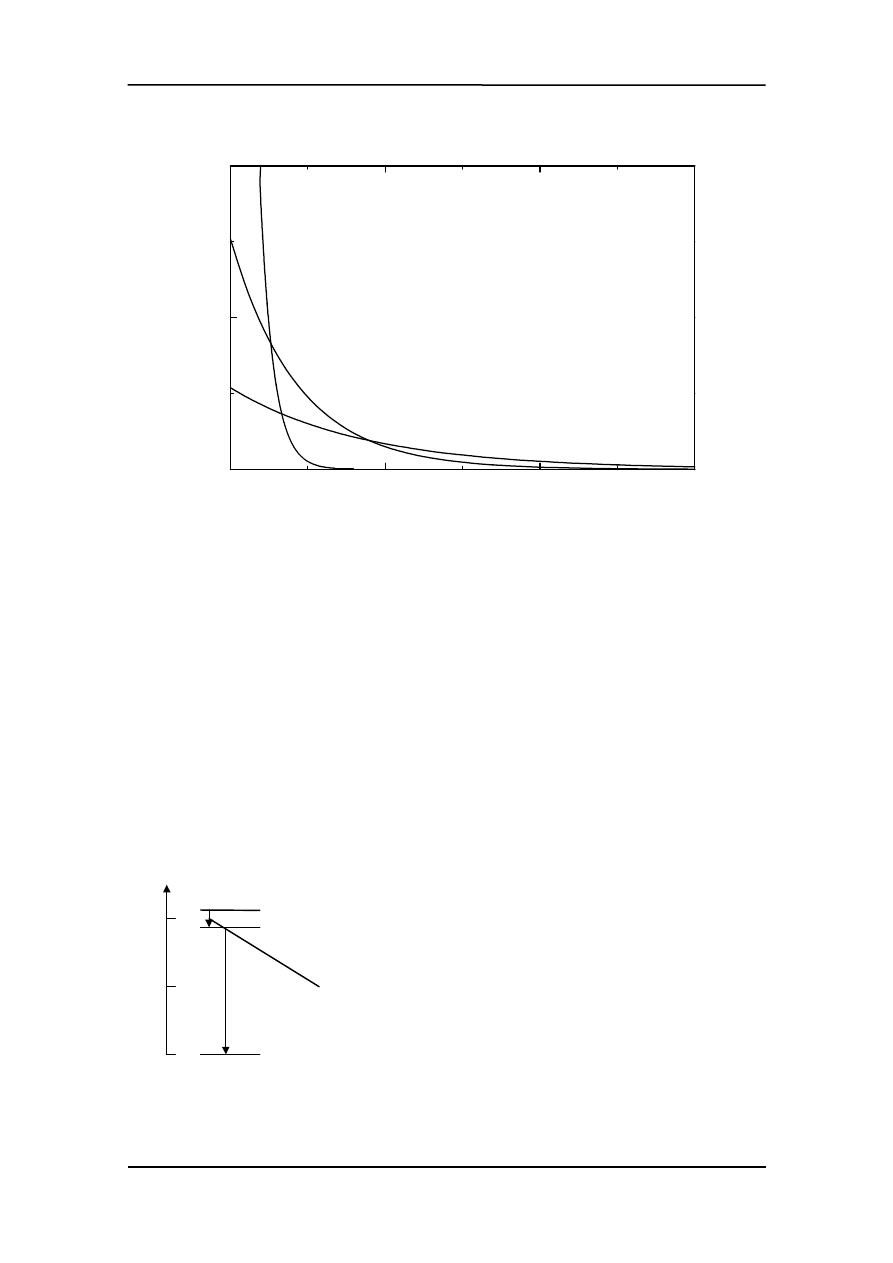
Poniżej pokazana jest zależność n(E) dla trzech różnych temperatur i trzech odpowied-
nich wartości stałej A.

2

1

0

4

∆

E

3

∆

E

2

∆

E

∆

E

n(E)

Z. Kąkol-Notatki do Wykładu z Fizyki

35-5

Widzimy, że stany o niższej energii są obsadzane z większym prawdopodobieństwem
niż stany o wyższym E.

35.5

Laser

Jeżeli więc układ będący w stanie równowagi oświetlimy odpowiednim promienio-

waniem to w takim układzie

absorpcja będzie przeważała nad emisją wymuszoną

.

ś

eby przeważała emisja wymuszona, to w wyższym stanie energetycznym musi się

znajdować więcej atomów (cząsteczek) niż w stanie niższym. Mówimy, że rozkład musi
być antyboltzmanowski.
Taki układ można przygotować na kilka sposobów min. za pomocą zderzeń z innymi
atomami lub za pomocą pompowania optycznego.

Ten pierwszy sposób jest wykorzysty-
wany w laserze helowo-neonowym.
Schemat poziomów energetycznych dla
tego lasera jest pokazany na rysunku
obok.
W tym laserze atomy neonu są wzbu-
dzane do na poziom E

n’

w trakcie zde-

rzeń ze wzbudzonymi atomami helu.
Przejście na poziom E

n

zachodzi wsku-

tek emisji wymuszonej. Następnie ato-
my neonu przechodzą szybko do stanu
podstawowego oddając energię w wyni-
ku zderzeń ze ściankami.

0

1

2

3

0

1

2

a - T = 1000 K
b - T = 5000 K
c - T = 10000 K

c

b

a

n

(

E

)

E (eV)

10

20

eV

E

n’

E

n

h

ν

=1.96 eV

λ

= 633 nm

E

1

Z. Kąkol-Notatki do Wykładu z Fizyki

35-6

d)

c)

b)

a)

Emisja wymuszona w laserze przedstawiona została na rysunkach poniżej.

Na rysunku (a) foton zostaje „wprowadzony”
do gazu. Foton wymusza emisję drugiego fo-
tonu przez wzbudzony atom (b). Przez układ
poruszają się dwa fotony. Wymuszona zostaje
kolejna emisja i już trzy fotony o tej samej
fazie poruszają się przez układ (c). Jeżeli na
końcach zbiornika znajdują się lustra to ten
proces będzie trwał aż wszystkie atomy wy-
promieniują nadmiar energii.
Jeżeli jedno z tych zwierciadeł będzie czę-
ś

ciowo przepuszczające to układ będzie

opuszczała wiązka spójna - wszystkie fotony
będą miały tę samą fazę.
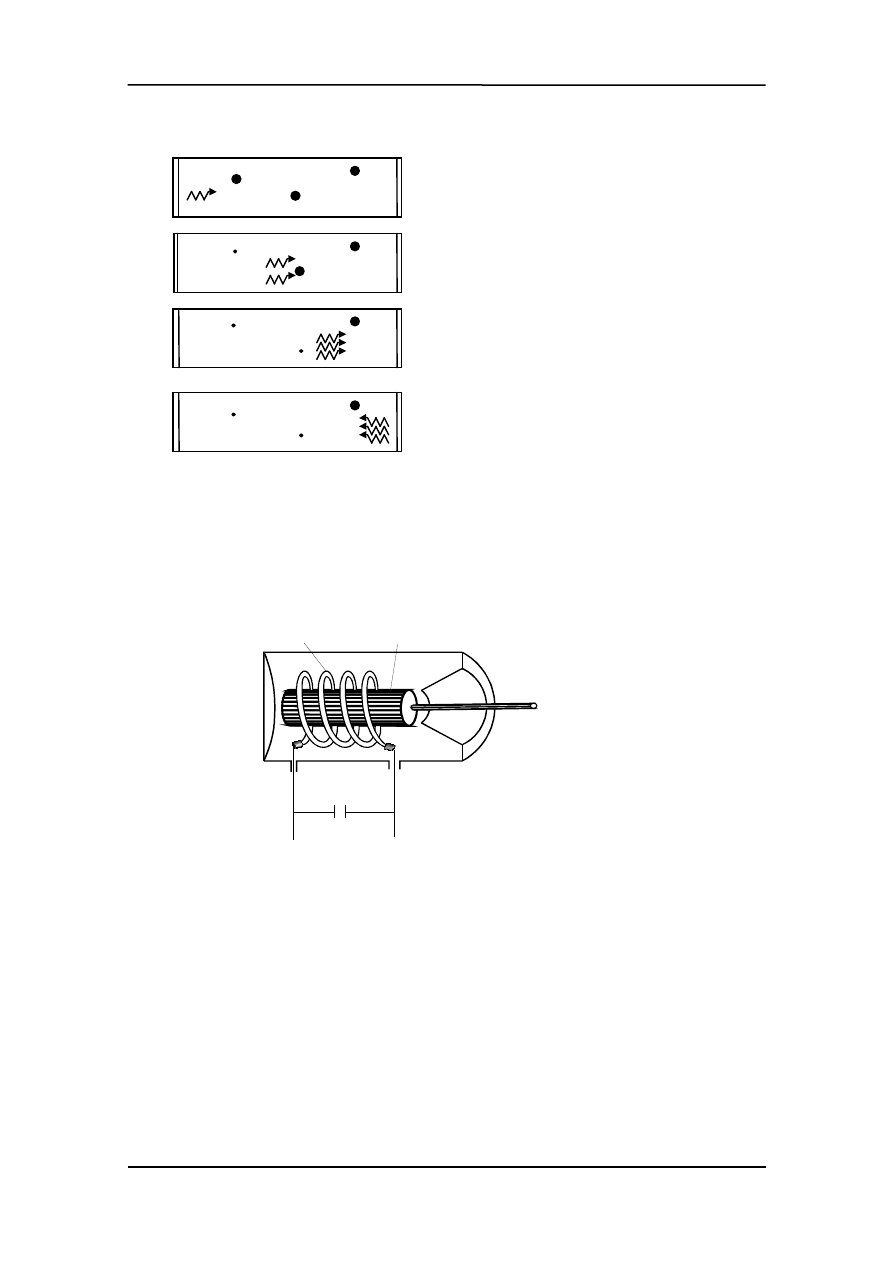
Inny sposób „odwrócenia” rozkładu boltzma-
nowskiego jest wykorzystany w laserze rubi-
nowym. Laser zbudowany na ciele stałym
składa się z pręta wykonanego z kryształu

Al

2

O

3

, w którym jonami czynnymi są jony z grupy ziem rzadkich. Na końcach pręta są

naniesione zwierciadła odbijające. Promieniowanie pompujące jest wytwarzane przez
lampę błyskową umieszczoną wokół kryształu tak jak pokazano na rysunku poniżej.

Od czasu uruchomienia pierwszego lasera tj. od 1960 roku technologia tych urządzeń
bardzo się rozwinęła. Obecnie działają zarówno lasery impulsowe jak i lasery o pracy
ciągłej. Ośrodkami czynnymi w laserach są gazy, ciała stałe i ciecze, a zakres długości
fal jest bardzo szeroki; od podczerwieni przez obszar widzialny aż do nadfioletu (ostat-
nio !!!).
Zastosowania laserów są wszechstronne. Przykładowo:

•

w odtwarzaczach i nagrywarkach (CD),

•

w dalmierzach, celownikach

•

przy obróbce mechanicznej

•

holografia

lampa
błyskowa

wi

ą

zka

ś

wiatła

laserowego

kryształ