Ewa KOTELA, Jacek LESZCZYŃSKI

Politechnika Częstochowska

Analiza jednowymiarowego przepływu ciepła przez przegrodę wypełnioną

materiałem granulowanym.

W pracy rozważa się przepływ ciepła przez przegrodę wypełnioną granulatem. Rozpatrywana jest

przegroda, której warstwę środkową stanowi komora wypełniona granulatem o znanych własnościach
fizycznych i geometrycznych, znanym rozkładzie ziaren oraz o określonym współczynniku przewodzenia
i wnikania ciepła. Ponadto praca zawiera wyniki symulacji komputerowych wpływu różnych parametrów,
zarówno komory z granulatem jak i samego granulatu na opór cieplny. Przedstawiono również wzór opisujący
strumień ciepła przepływający przez przegrodę, przy założeniu, że występuje jednowymiarowy przepływ ciepła,
ziarna materiału granulowanego są kulami i przyjmujemy stałą wartość temperatury powietrza wewnątrz
przestrzeni między ziarnami. Proponowane rozwiązanie umożliwia regulowanie oporu cieplnego wewnątrz
przegrody wypełnionej materiałem granulowanym.

Słowa kluczowe: przepływ ciepła, granulat, przegroda

WPROWADZENIE

Przepływ ciepła w materiałach granulowanych stanowi ciągłe wyzwanie dla grup

badawczych i przemysłu. Z fizycznego punktu widzenia można powiedzieć, że charakter
przepływu ciepła w granulacie zbliżony jest do przepływu ciepła w materiałach porowatych.
Ponieważ profil przepływu w samych materiałach sypkich jest trudny do ustalenia na drodze
zarówno teoretycznej jak i eksperymentalnej dlatego analiza przepływu w materiach sypkich
jest utrudniona. Szczególnie należy zwrócić uwagę na fakt wnikania ciepła z przestrzeni
międzyziarnowych, w których znajduje się powietrze, do ziaren. Wnikanie to ma bardzo silny
charakter ze względu na dwa procesy. Proces konwekcji mogący być wynikiem przepływu
płynu filtrującego materiał sypki oraz proces promieniowania w wyniku różnicy czwartych
potęg temperatur. W niniejszej pracy skoncentrowano się jedynie na jednowymiarowym
ustalonym przepływie ciepła przez dowolny materiał granulowany. W pracy zaproponowano
również formułę na obliczanie oporu cieplnego przy założeniu stałej temperatury gazu
wypełniającego przestrzenie między ziarnami.


JEDNOWYMIAROWY MODEL PRZEPŁYWU CIEPŁA

Realizując temat przepływu ciepła przez przegrody wypełnione materiałem

granulowanym za cel postawiono sobie dobranie odpowiednich parametrów, zarówno dla
granulatu jak i materiałów do budowy systemu ścianek, w celu utrzymania optymalnych

1

warunków temperaturowych po jednej stronie przegrody bez względu na warunki panujące po
drugiej stronie. Rozważa się przegrodę o zmiennym oporze cieplnym, która charakteryzuje się
tym, że wewnątrz niej znajduje się materiał granulowany o dużym współczynniku
przewodzenia

λ

zz

, natomiast niewielkim współczynniku wnikania ciepła z otoczenia dla tego

materiału α

zz

, którym może być np. guma piankowa, gazogips, żwir pumeksowy. Granulat jest

ograniczony po obu stronach systemem ścianek zewnętrznych. Ścianki te mają określone
szerokości

δ

j

i współczynniki przewodzenia ciepła

λ

j

. Przestrzenie między ziarnami materiału

granulowanego w wewnętrznej objętości komory określa współczynnik porowatości
przegrody

ε i współczynnik przewodzenia ciepła λ

g

dla powietrza filtrującego. Powietrze

przepływające między pustymi miejscami w przestrzeni wypełnionej materiałem
granulowanym wymienia ciepło zarówno z ziarnami granulatu jak i z przegrodami
ograniczającymi granulat.

Wymiana ciepła następuje w taki sposób, iż ciepło o znanej temperaturze po jednej stronie
przegrody przenika przez system kolejnych ścianek aż do komory wypełnionej materiałem
granulowanym, w której następuje modyfikacja wymiany ciepła spowodowana
oddziaływaniem powietrza zewnętrznego (doprowadzonego przez nas) o regulowanej
temperaturze T

p

i prędkości w

p

. W dalszej kolejności ciepło przenika przez system ścianek po

drugiej stronie przegrody, a ostatecznie zostaje oddane na drugą stronę przegrody kształtując
tam temperaturę T

2

.

Rys.1 Przekrój poprzeczny przegrody, na której dokonywano symulacji komputerowych

2

Zakładając, że występuje jednowymiarowy przepływ ciepła oraz ziarna materiału
granulowanego są kulami i przyjmując stałą wartość temperatury powietrza wewnątrz
przestrzeni między ziarnami można wyznaczyć strumień ciepła przepływający w kierunku od
zewnątrz do wewnątrz pomieszczenia jako

(

2

1

T

T

)

R

A

Q

−

⋅

=

•

(1.1)

gdzie

A

jest powierzchnią, przez którą płynie ciepło [m

2

],

T

1

jest temperaturą panującą na zewnątrz pomieszczenia [K],

T

2

jest temperaturą panującą wewnątrz pomieszczenia [K]

oraz

R

jest oporem cieplnym przegrody [(m

2

K)/W] określonym jako

(

)

(

)

∑

∑

=

=

⋅

−

+

⋅

+

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

+

+

+

+

=

2

1

1

3

2

1

1

36

1

1

i

n

j

p

zz

g

zz

pw

pz

j

j

i

V

A

R

δ

λ

ε

λ

ε

ε

π

α

α

α

ε

λ

δ

α

(1.2)

W powyższym wzorze przyjęto następujące oznaczenia:

α

i

-

współczynniki wnikania ciepła dla powietrza oddziałującego na ścianki zewnętrzną

i wewnętrzną, (i=1,2) [W/(m

2

K)]

α

pw

, α

pz

-

współczynniki wnikania ciepła dla powietrza filtrującego materiał granulowany

i oddziałującego na ścianki ograniczające ruch ziaren [W/(m

2

K)]

α

zz

-

współczynnik wnikania ciepła do ziaren dla powietrza filtrującego materiał granulowany

[W/(m

2

K)]

λ

g

-

współczynnik przewodzenia ciepła w powietrzu filtrującym materiał granulowany

[W/(mK)]

λ

j

-

współczynniki przewodzenia ciepła dla ścianek otaczających materiał granulowany,

(j=1,…,n) [W/(mK)]

λ

zz

-

współczynnik przewodzenia ciepła dla ziaren materiału granulowanego [W/(mK)]

δ

j

-

szerokości poszczególnych ścianek otaczających materiał granulowany, (j=1,…,n) [m]

δ

p

-

szerokość przegrody wypełnionej materiałem granulowanym [m]

ε

-

porowatość złoża powstałego z wypełnienia materiałem granulowanym wewnętrznej

komory przegrody [-]

V

-

objętość przegrody wypełnionej materiałem granulowanym [m

3

]

n - całkowita liczba ścianek otaczających materiał granulowany [-]


W dalszych rozważaniach zakłada się, że przegroda będzie składała się tylko z warstwy
granulatu. Ścianki ograniczające występować będą jedynie hipotetycznie, jak również nie

będzie doprowadzane do komory z materiałem granulowanym powietrze z zewnątrz (

).

p

Q

•

3

Współczynniki wnikania ciepła dla powietrza filtrującego materiał granulowany
i oddziałującego na przegrody ograniczające ruch ziaren, współczynnik wnikania ciepła do
ziaren dla powietrza filtrującego materiał granulowany, współczynnik porowatości,
powierzchnię przez, którą płynie ciepło, szerokość przegrody wypełnionej materiałem
granulowanym, współczynnik przewodzenia ciepła w powietrzu filtrującym materiał
granulowany, jak i współczynnik przewodzenia ciepła dla ziaren materiału granulowanego
dobiera się do uproszczonego wzoru (1.1), który pozwala wyznaczyć opór cieplny dla takiej
przegrody (rys.1).

(

)

(

)

p

zz

g

zz

pw

pz

V

A

R

δ

λ

ε

ελ

ε

π

α

α

α

ε

−

+

+

⎟

⎠

⎞

⎜

⎝

⎛

⋅

−

⋅

+

+

=

1

1

36

1

3

2

(1.3)

ANALIZA OTRZYMANYCH WYNIKÓW

Celem badań było ustalenie jak kształtuje się opór w zależności od czynników m.in.

materiału granulowanego. Dlatego na podstawie symulacji komputerowych wykonano
zestawienie danych, które prezentowane są na wykresach 1-4. Wyniki te zaprezentowano
w formie graficznej, aby lepiej zobrazować zachodzący proces.


Przedstawiony poniżej (rys.2) wykres zależności oporu cieplnego (R) od porowatości (

ε )

wykazuje, iż wraz ze wzrostem porowatości opór cieplny maleje niezależnie od
współczynnika przewodzenia ciepła dla ziaren materiału granulowanego (

zz

λ ). Wyraźnie

widać, że dla granulatu o współczynniku

1

,

0

=

zz

λ

W/mK opór cieplny utrzymuje się na

wyższym poziomie niż dla granulatów o wyższym współczynniku

zz

λ . Dalej obserwujemy,

że opór dla granulatów o współczynnikach przewodzenia ciepła wyższych od 0,6 W/mK
i przy porowatości ponad 0,5 utrzymuje się na poziomie 0,03 m

2

K/W.

4

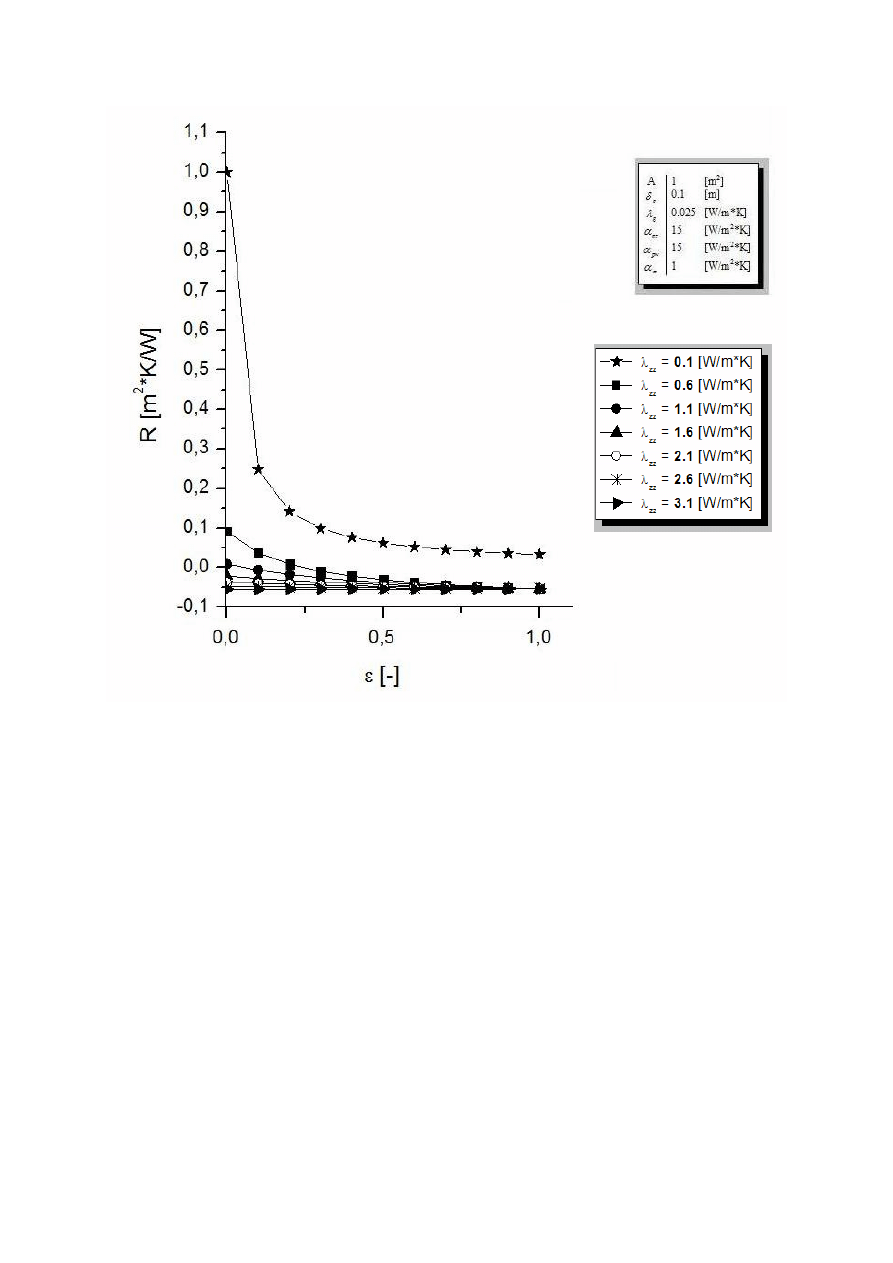
Rys.2 Zależność między porowatością, a oporem cieplnym pod wpływem zmieniającego się
współczynnika przewodzenia ciepła dla ziaren materiału granulowanego

Kolejny wykres (rys.3), zależności oporu cieplnego (R) od szerokości przegrody
z granulatem (

p

δ

) przedstawia, że w wyniku przepływu ciepła przez granulat nastąpił wzrost,

a następnie płynne obniżenie wartości oporu cieplnego (R) bez względu na współczynnik
przewodzenia ciepła dla ziaren materiału granulowanego (

zz

λ ) osiągając wartość

0,052 m

2

K/W dla szerokości przegrody (

p

δ

) powyżej 2,5 metra. Wyniki zmian oporu

cieplnego liczone zostały w odstępach 0,1 metra, przy równoczesnej zmianie współczynnika

zz

λ oraz przy określonych parametrach. Zastosowanie granulatu o różnym współczynniku

przewodzenia ciepła nie miało zdecydowanego wpływu na opór cieplny, gdy szerokość
przegrody przekraczała 1 metr. Na wykresie 3 można zauważyć, że przy zastosowaniu
granulatu o współczynniku

zz

λ =0,1 W/mK wartość oporu cieplnego wynosi maksymalnie

0,063m

2

K/W. Jest to najwyższa wartość jaką uzyskaliśmy przy określonych parametrach.

5

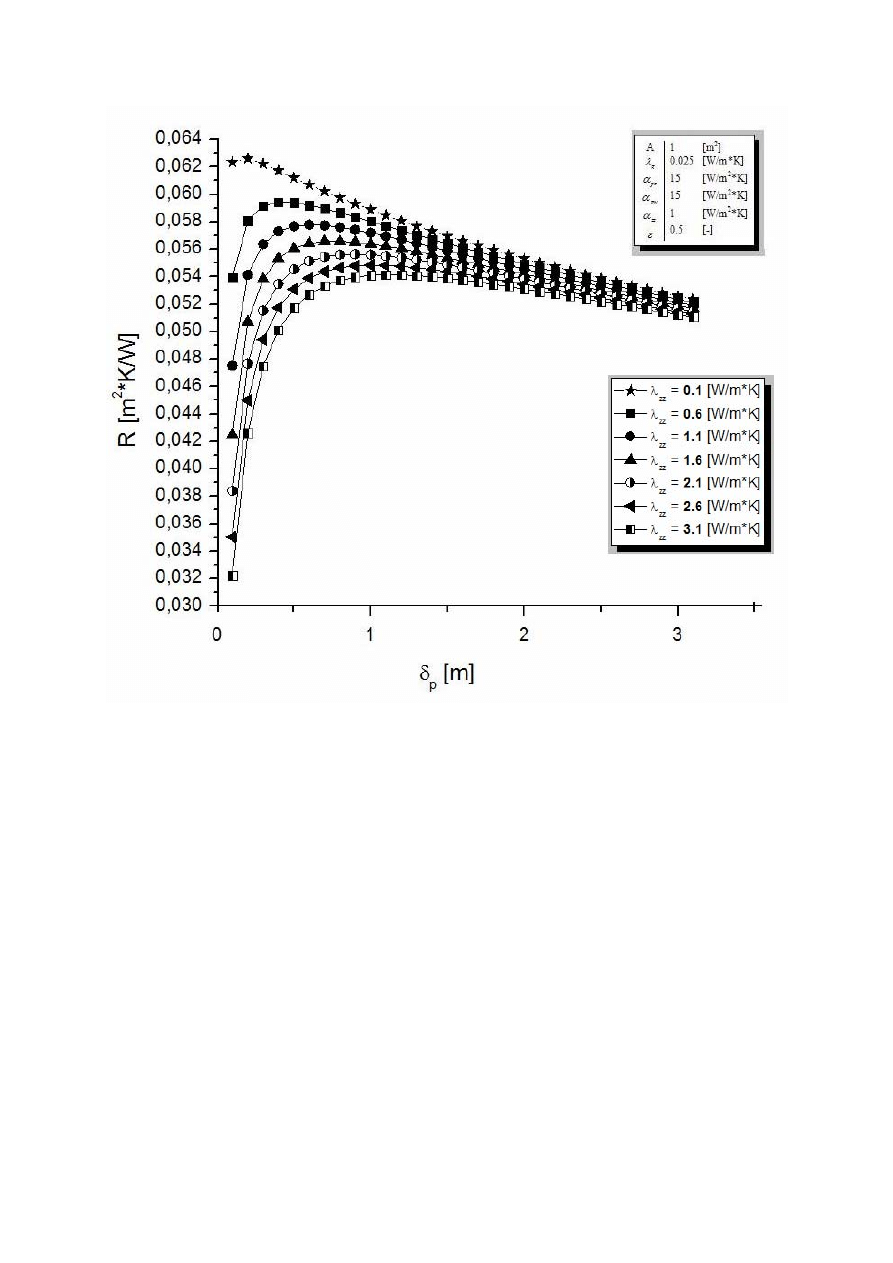
Rys.3 Zależność między szerokością przegrody z granulatem, a oporem cieplnym pod wpływem
zmieniającego się współczynnika przewodzenia ciepła dla ziaren materiału granulowanego

Na rysunku 4 pokazano z kolei zależność między oporem cieplnym (R), a szerokością
przegrody z granulatem zmieniając przy tym współczynnik porowatości. Jak można
zaobserwować opór cieplny dla porowatości 0,1 najpierw dość szybko rośnie wraz ze
wzrostem szerokości przegrody, aż do momentu w którym przegroda osiąga około 0,7 m.
I tak dla szerokości przegrody równej 0,7 m opór jest prawie 8 krotnie wyższy przy
współczynniku porowatości równym 0,1 niż przy porowatości 0,9. Następnie opór powoli
maleje. Podobnie zachowują się wartości oporu dla porowatości 0,2-0,4 z tym, że tutaj już
wzrost nie jest tak widoczny. Natomiast dla współczynnika porowatości powyżej 0,5
szerokość przegrody z granulatem nie wpływa w znaczącym stopniu na opór, którego
wartości utrzymują się praktycznie na jednym poziomie.

6

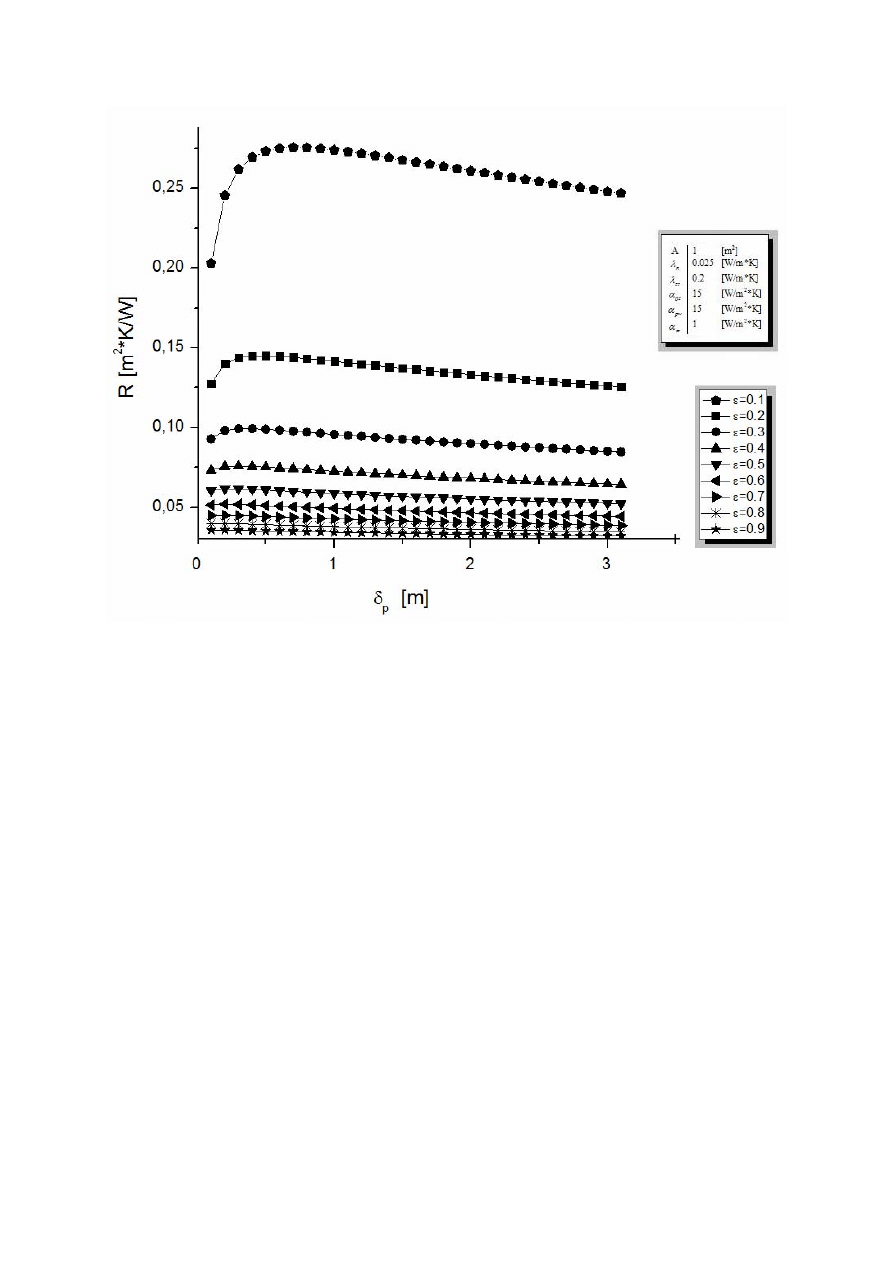
Rys.4 Zależność między szerokością przegrody z granulatem, a oporem cieplnym pod wpływem
zmieniającej się porowatości

Przedstawiony poniżej (rys.5) wykres zależności oporu cieplnego od współczynnika
przewodzenia ciepła dla ziaren materiału granulowanego (

zz

λ ) wykazuje, iż wpływ

współczynnika wnikania ciepła do ziaren dla powietrza filtrującego materiał granulowany
(

zz

α ) na opór cieplny zmniejsza się, gdy współczynnik

zz

λ wzrasta powyżej 40 W/mK przy

określonych parametrach. Wyraźnie widać, że przy niskim współczynniku

zz

α opór bardzo

szybko maleje wraz ze wzrostem współczynnika

zz

λ . Dalej obserwujemy, że czym wyższy

współczynnik

zz

α wartości oporu cieplnego przy wzroście

zz

λ coraz wolniej maleją zbliżając

się do zera.

7

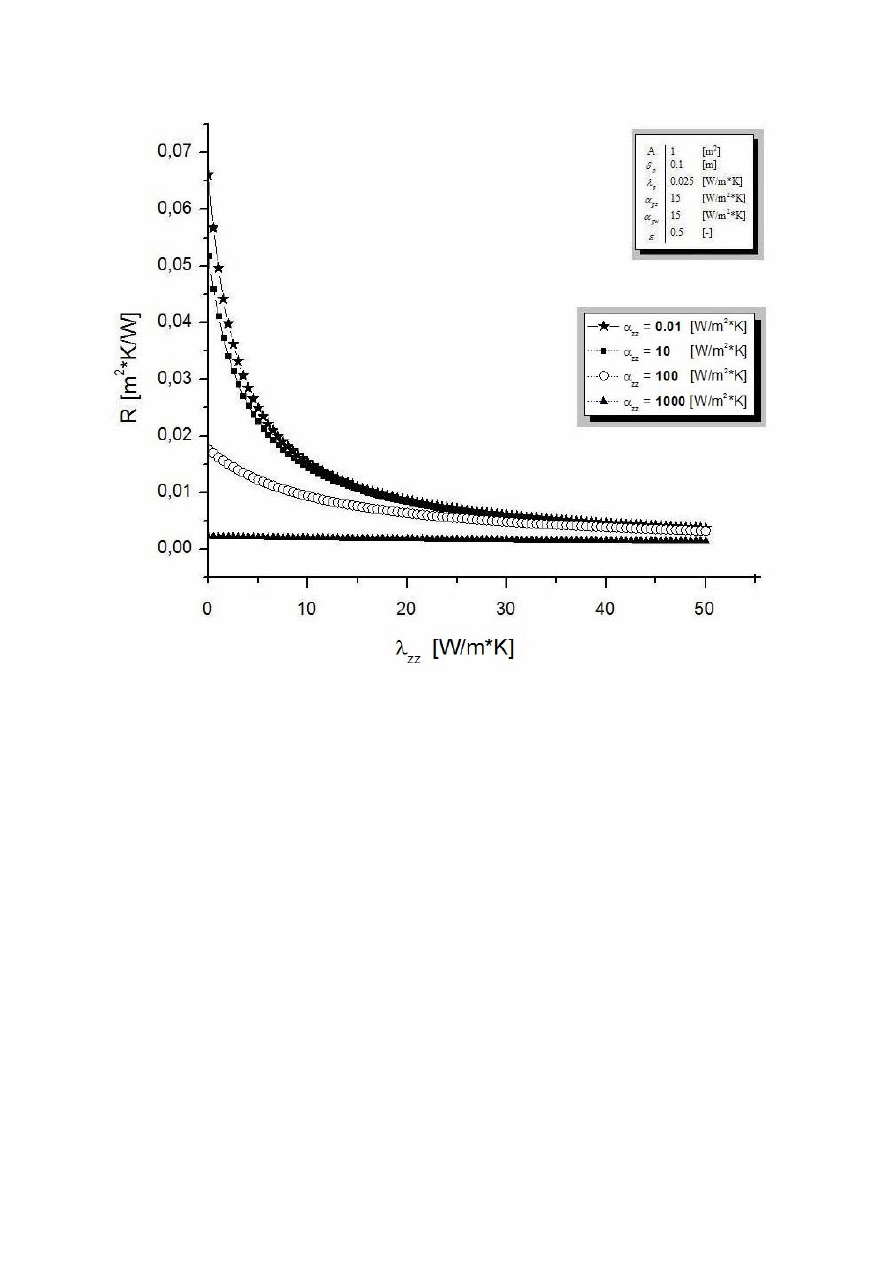
Rys.5 Zależność między współczynnikiem przewodzenia ciepła dla ziaren materiału granulowanego,
a oporem cieplnym pod wpływem zmieniającego się współczynnika wnikania ciepła do ziaren dla
powietrza filtrującego materiał granulowany

WNIOSKI KOŃCOWE

Celem przeprowadzonych prób było określenie jaki wpływ na opór cieplny, a przez to

na strumień ciepła mają parametry przegrody z granulatem oraz samego granulatu. Podczas
prób brano pod uwagę jedynie przepływ ciepła przez sam granulat. Nie doprowadzano
powietrza z zewnątrz do przegrody z granulatem jak również usunięto system ścianek
otaczających granulat. Ważnym elementem badań jest fakt, iż podczas prób, gdy badano
wpływ jednego parametru na opór cieplny, pozostałe przyjmowano za stałe. Obliczenia
wykonano przy założeniach, że przyjmujemy powierzchnię przez, którą płynie ciepło równą
1 m

2

, współczynnik przewodzenia ciepła w powietrzu filtrującym materiał granulowany

0.025 W/mK oraz współczynniki wnikania ciepła dla powietrza filtrującego materiał
granulowany i oddziałującego na przegrody ograniczające ruch ziaren 15 W/m

2

K. Na

podstawie symulacji komputerowych otrzymano wyniki, które zaprezentowano na wykresach
2-5.

8

Należy zwrócić uwagę, że

zz

λ ma znaczący wpływ na opór cieplny jedynie przy szerokości

przegrody z granulatem do około 1 m. Przy szerszych przegrodach wartość oporu zaczyna
maleć i bez względu na

zz

λ zbliża się do 0,052 m

2

K/W przy

p

δ

= 3m. Zaobserwowano

również, że porowatość wpływa w znacznym stopniu na wartości oporu przy zwiększającej
się przegrodzie (rys.3). Biorąc pod uwagę wykres 4 należy stwierdzić, że wpływ

zz

λ na opór

cieplny zanika, gdy szerokość przegrody z granulatem przekroczy 1 m. Można zaobserwować
również, że przy przyjętych parametrach najlepsze efekty daje przegroda o współczynniku
porowatości

ε =0,1. Spadek porowatości powoduje wzrost oporu, co skutkuje poprawą

izolacyjności cieplnej przegrody. Na wykresie 5 natomiast zanotowano istotny spadek oporu
cieplnego dla przegrody z granulatem o

zz

α z przedziału 0,01 – 10 W/m

2

K przy

wzrastającym współczynniku

zz

λ . Wraz ze wzrostem

zz

α spadek oporu stawał się

łagodniejszy. Przy

zz

α = 100000 W/m

2

K wartości oporu utrzymują się na poziomie bardzo

bliskim zera.

Przeprowadzone symulacje procesu przepływu ciepła przez przegrodę z materiałem
granulowanym wskazują jaki granulat należałoby dobrać oraz jaka powinna być szerokość
przegrody, aby uzyskać najlepsze efekty. Dużą skuteczność uzyskano (rys.2 i rys.4) przy
granulacie o współczynniku

zz

λ = 0,1 oraz przy ε =0,1. Przy doborze rodzaju granulatu

warto więc mieć na uwadze zarówno współczynniki przewodzenia, wnikania jak i wymiary
przegrody i porowatość. Proponowane rozwiązanie umożliwia regulowanie oporu cieplnego
wewnątrz przegrody wypełnionej materiałem granulowanym, co w dalszej kolejności pozwala
regulować strumień ciepła umożliwiając w ten sposób regulowanie temperatury.


Bibliografia:

[1] Kostowski E., Przepływ ciepła, Skrypty uczelniane nr 1293, Politechnika Śląska im. W. Pstrowskiego,
Gliwice 1986.
[2] Kowalczyk R., Ruch ciepła, 1999, WN-T, Warszawa.
[3] Leszczyński J., Kotela E., Błaszczyk T., Przegroda budowlana o zmiennym oporze cieplnym
i sposób zapewnienia komfortu cieplnego w pomieszczeniu, zgłoszenie patentowe
nr P.389926, 2009.
[4] Orzechowski Z., Przepływy dwufazowe jednowymiarowe ustalone adiabatycznie, PWN Warszawa 1990.
[5] Pogorzelski J.A. Zagadnienia cieplno-wilgotnościowe przegród budowlanych, Arkady, Warszawa, [w:]
Klemm P. (red.) „Budownictwo ogólne”, Tom 2, „Fizyka budowli”, s.103-364.
[6] Staniszewski B. Wymiana ciepła i wymienniki, Warszawa, PWN,1963.
[7] Strumiłło C., Ruch ciepła, Wyd. PŁ, Łódź, 1982.

9