4. ELEMENTY RACHUNKU OPERATOROWEGO

4.1 PRZEKSZTAŁCENIE LAPLACE’A

Def. 4.1.1 (transformata Laplace’a)
Niech funkcja f będzie określona na przedziale [0,



). Transformatę Laplace’a funkcji f oznaczamy symbolem F(s) lub L{f(t)} i

definiujemy wzorem



)

(s

F

L{f(t)}









0

)

(

dt

e

t

f

st

def

,

gdzie s jest zmienną rzeczywistą. Funkcję F(s) nazywamy także L-transformatą lub obrazem funkcji f(t).

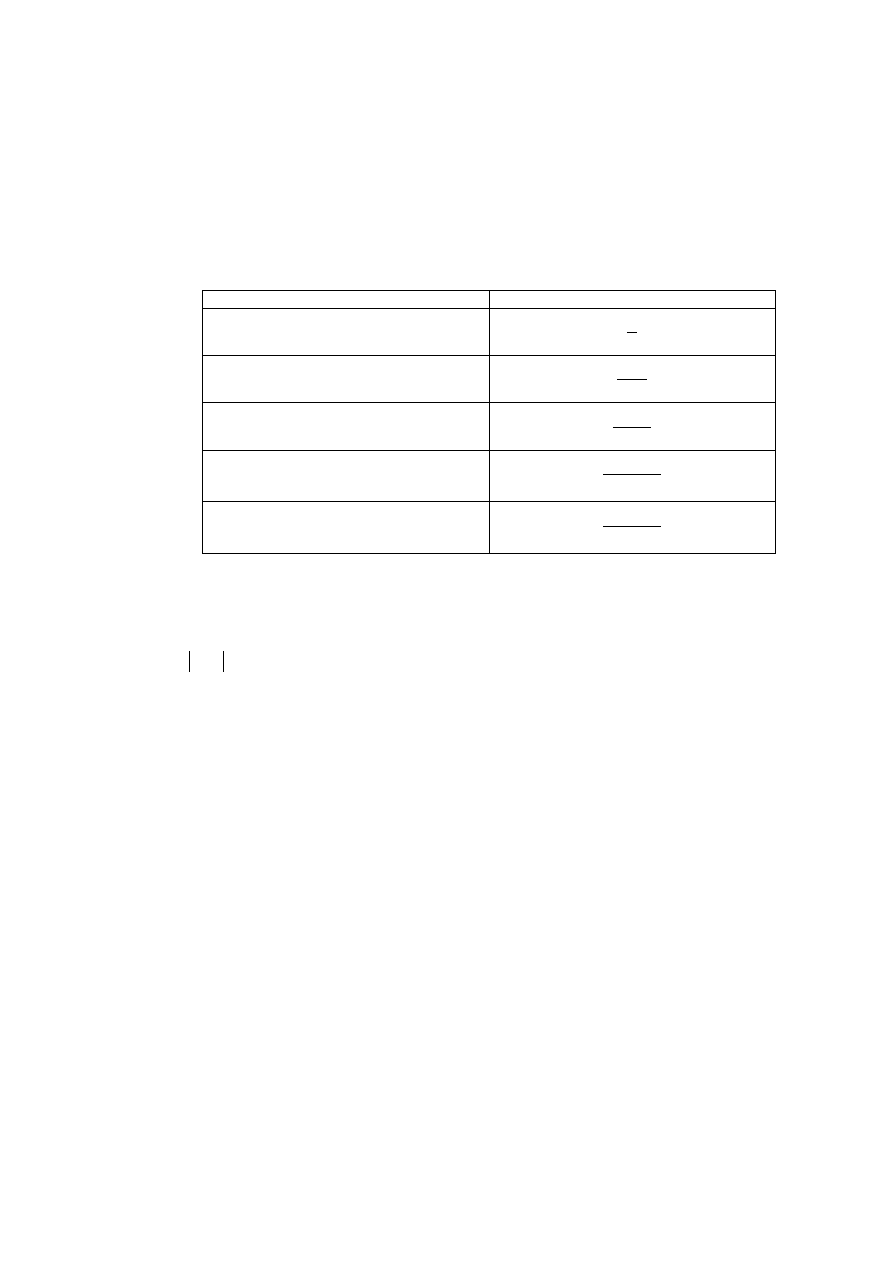
Fakt 4.1.2 (transformaty ważniejszych funkcji)

Funkcja

Transformata

1

s

1

n

t

1

!



n

s

n

t

e







s

1

t



sin

2

2







s

t



cos

2

2





s

s

Fakt 4.1.3 (warunki wystarczające istnienia transformaty Laplace’a)
Niech
1. funkcja

R

f





)

,

0

[

:

ma skończoną liczbę punktów nieciągłości pierwszego rodzaju na każdym przedziale [0,T], gdzie

T > 0;

2.

Ct

t

M

R

C

Me

t

f















)

(

0

0

.

Wtedy transformata Laplace’a L{f(t)} istnieje dla s > C.

Uwaga. Funkcję f spełniającą warunki 1. i 2. powyższego faktu będziemy nazywali oryginałem.

Fakt 4.1.4 (o liniowości przekształcenia Laplace’a)
Jeżeli istnieją transformaty Laplace’a funkcji f i g oraz c



R, to

1. istnieje transformata Laplace’a funkcji f + g oraz

L{f(t)+g(t)} = L{f(t)} + L{g(t)};

2. istnieje transformata Laplace’a funkcji cf oraz

L{cf(t)} = cL{f(t)}.

Fakt 4.1.5 (o jednoznaczności transformaty Laplace’a)
Jeżeli funkcje ciągłe

R

g

f





)

,

0

[

:

,

mają takie same transformaty Laplace’a: F(s) = G(s), to są równe na przedziale

[0,



).

4.2 METODA OPERATOROWA ROZWIĄZYWANIA RÓWNAŃ RÓŻNICZKOWYCH

Fakt 4.2.1 (transformata n-tej pochodnej)
Jeżeli funkcja f(t) oraz jej pochodne f’(t), f’’(t), ..., f

(n-1)

(t) są oryginałami, a ponadto funkcja ta ma na przedziale (0,



) ciągłą n-

tą pochodną, to istnieje transformata L{f(t)} oraz

L{f

(n)

(t)} =

= s

n

L{f(t)} – s

n-1

f(0

+

) – s

n-2

f’(0

+

) + ... – sf

(n-2)

(0

+

) – f

(n-1)

(0

+

) =

= s

n

F(s) – s

n-1

f(0

+

) – s

n-2

f’(0

+

) + ... – sf

(n-2)

(0

+

) – f

(n-1)

(0

+

),

gdzie F(s) = L{f(t)},

)

(

lim

)

0

(

0

t

f

f

t









,

)

(

'

lim

)

0

(

'

0

t

f

f

t









, ...,

)

(

lim

)

0

(

)

1

(

0

)

1

(

t

f

f

n

t

n













.

Uwaga. Jeżeli funkcje f(t), f’(t), ..., f

(n-1)

(t) są ciągłe prawostronnie w punkcie t

0

= 0, to f(0

+

) = f(0), f’(0

+

) = f’(0), ..., f

(n-1)

(0

+

) =

f

(n-1)

(0).

4.3 WŁASNOŚCI PRZEKSZTAŁCENIA LAPLACE’A


Fakt 4.3.1 (zmiana skali)
Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej



> 0

L{f(



t)} =

















s

F

1

,

gdzie F(s) oznacza obraz funkcji f(t).


Fakt 4.3.2 (o różniczkowaniu obrazu)
Jeżeli funkcja f(t) jest oryginałem, to

L{t

n

f(t)} =(-1)

n

F

(n)

(s)

,

gdzie F(s) oznacza obraz funkcji f(t).


Fakt 4.3.3 (o przesunięciu argumentów obrazu)
Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej a



R

L{e



t

f(t)} = F(s – a)

,

gdzie F(s) oznacza obraz funkcji f(t).


Fakt 4.3.4 (o przesunięciu argumentów oryginału)
Jeżeli funkcja f(t) jest oryginałem, to dla dowolnej stałej



> 0

L{1(t –



)f(t –



)} = e

-s



F(s)

,

gdzie F(s) oznacza obraz funkcji f(t).


Fakt 4.3.4 (o całkowaniu oryginału)
Jeżeli funkcja f(t) jest oryginałem, to

L

s

s

F

d

f

t

)

(

)

(

0





















,

gdzie F(s) oznacza obraz funkcji f(t).

Fakt 4.3.5 (transformaty ważniejszych funkcji c.d.)

Funkcja

Transformata

sh



t

2

2






s

ch



t

2

2





s

s

t

n

e



t

1

)

(

!





n

s

n



e



t

sin



t

2

2

)

(











s

e



t

cos



t

2

2

)

(













s

s

4.4 SPLOT FUNKCJI


Def. 4.4.1 (splot funkcji)
Niech funkcje f(t) i g(t) będą całkowalne na każdym przedziale [0,T], gdzie T > 0. Splot funkcji f(t) i g(t) oznaczamy
symbolem

)

(

)

(

t

g

t

f



i określamy wzorem









t

def

d

t

g

f

t

g

t

f

0

)

(

)

(

)

(

)

(







.

Fakt 4.4.2 (własności splotu funkcji)
Niech funkcje f(t), g(t), h(t) będą całkowalne na każdym przedziale [0,T], gdzie T > 0 i niech c



R. Wtedy

1.

)

(

)

(

)

(

)

(

t

f

t

g

t

g

t

f







;

2.





)

(

)

(

)

(

)

(

)

(

)

(

)

(

t

h

t

f

t

g

t

f

t

h

t

g

t

f













;

3.









)

(

)

(

)

(

)

(

)

(

)

(

t

h

t

g

t

f

t

h

t

g

t

f











;

4.









)

(

)

(

)

(

)

(

t

g

t

f

c

t

g

t

cf







.

Tw. 4.4.3 (wzór Borela)
Jeżeli funkcje f(t) i g(t) są oryginałami, to istniej transformata Laplace’a ich splotu oraz

L{

)

(

)

(

t

g

t

f



} = L{f(t)}



L{g(t)}.