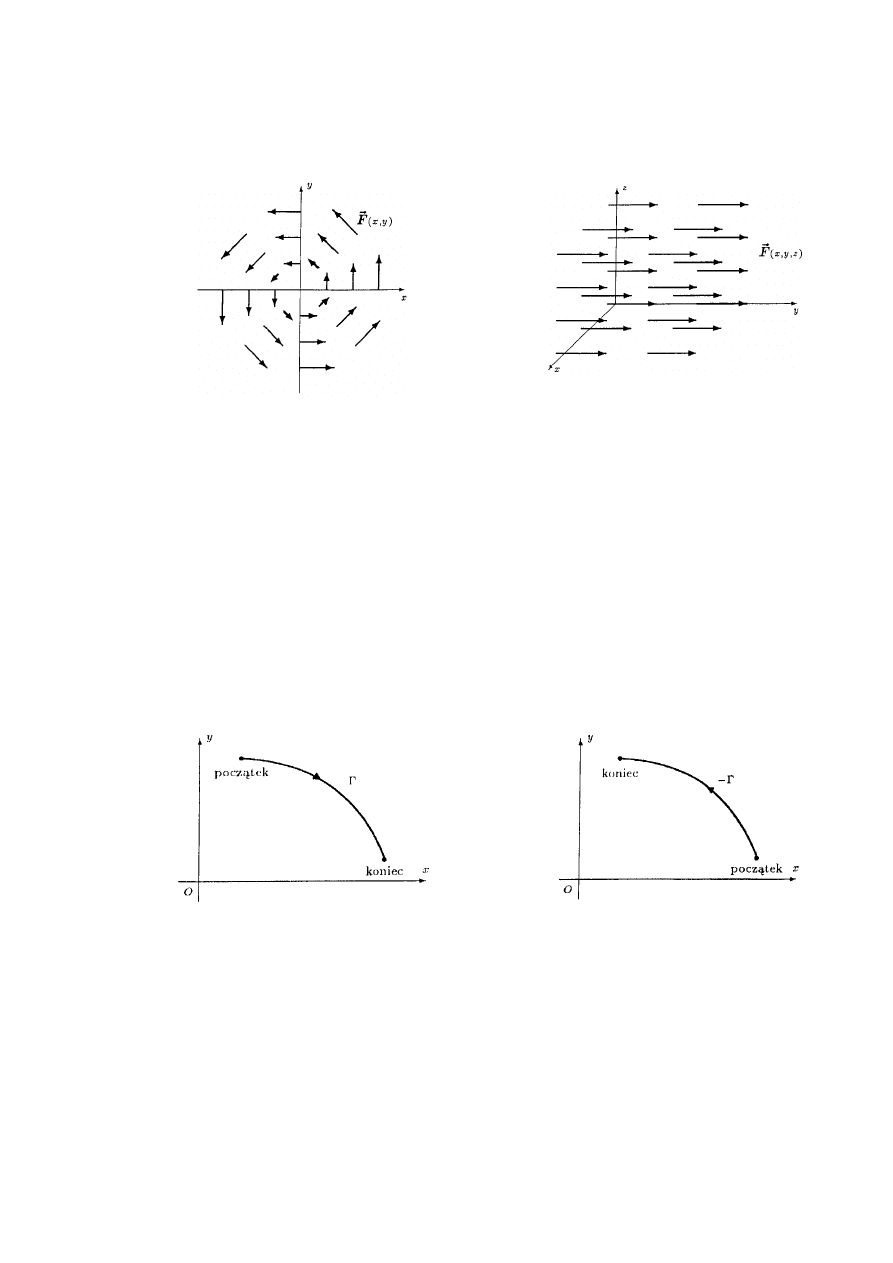
2. CAŁKI KRZYWOLINIOWE ZORIENTOWANE
2.1 DEFINICJE I WŁASNOŚCI CAŁEK KRZYWOLINIOWYCH ZORIENTOWANYCH
Def. 2.1.1 (pole wektorowe na płaszczyźnie i w przestrzeni)
a) Niech D będzie obszarem na płaszczyźnie. Polem wektorowym na D nazywamy funkcję wektorową
2
:
R
D
F
, gdzie
)
,
(
),
,
(
)
,
(
y
x
Q
y
x
P
y
x
F
dla (x,y)
D.
Rys. 2.1.1 Pole wektorowe na płaszczyźnie
Rys. 2.1.2 Pole wektorowe w przestrzeni
b) Niech V będzie obszarem w przestrzeni. Polem wektorowym na V nazywamy funkcję wektorową
3
:
R
D
F
, gdzie
)
,
,
(
),
,
(
),
,
(
)
,
,
(
z
y
x
R
y
x
Q
y
x
P
z
y
x
F
dla (x,y,z)
V.
c) Jeżeli funkcje P, Q lub P, Q, R są ciągłe odpowiednio na obszarach D lub V, to mówimy, że pole wektorowe
F
jest ciągłe
na tych obszarach.
d) Podobnie, jeżeli funkcje P, Q lub P, Q, R mają ciągłe wszystkie pochodne cząstkowe pierwszego rzędu odpowiednio na
obszarach D lub V, to mówimy, że pole wektorowe
F
jest różniczkowalne w sposób ciągły na tych obszarach.
Uwaga. Będziemy także pisali krótko
)
(
),
(
)
(
r
Q
r
P
r
F
, gdzie
)
,
(
y
x
r
lub
)
(
),
(
),
(
)
(
r
R
r
Q
r
P
r
F
, gdzie
)
,
,
(
z
y
x
r
.
Def. 2.1.2 (łuk zorientowany)
Łuk zwykły niezamknięty, na którym ustalono początek i koniec (kierunek) nazywamy łukiem zorientowanym. Łuk zoriento-
wany oznaczamy tym samym symbolem co łuk. Łuk o orientacji przeciwnej do orientacji łuku
oznaczamy przez –
. Jeżeli
ze wzrostem parametru łuku zorientowanego poruszamy się po nim w kierunku orientacji, to mówimy, że parametryzacja łuku
jest zgodna z jego orientacją.
Rys. 2.1.3 Łuk zorientowany
Rys. 2.1.4 Łuk -
o orientacji przeciwnej do
łuku zorientowanego
Oznaczenia w definicji całki krzywoliniowej zorientowanej
Niech
będzie łukiem zorientowanym na płaszczyźnie opisanym równaniem parametrycznym
]
,
[
),
(
t
t
r
r
, gdzie
)
,
(
y
x
r
oraz
)
(
),
(
)
(
t
y
t
x
t
r
. Zakładamy przy tym, że orientacja łuku
jest zgodna z jego parametryzacją. Wprowa-
dzamy następujące oznaczenia:
P = {t
0
, t
1
, ..., t
n
}, gdzie
= t
0
< t
1
< … < t
n
=
– podział odcinka [
,
] na n
N odcinków;
t
k
= t
k
– t
k-1
– długość k-tego odcinka podziału
P, 1
k
n;
(
P) = max{
t
k
: 1
k
n } – średnica podziału
P;
n
t
t
t
,
,
,
2
1
, gdzie
]
,
[
1
k
k
k
t
t
t
dla 1
k
n – zbiór punktów pośrednich podziału
P.
)
(
k
k
t
r
A
– punkty podziału łuku
indukowane przez podział
P, 0
k
n (A
0
jest początkiem, a A
n
końcem łuku zoriento-
wanego
);
)
(
),
(
)
,
(
)
(
k
k
k
k
k
k
t
y
t
x
y
x
t
r
r
– punkty pośrednie na łuku A
k-1
A
k
indukowane przez wybór punktów pośrednich podziału
P, 1
k
n;
)
,
(
)
(
)
(
1
k
k
k
k
k
y
x
t
r
t
r
r
, gdzie
)
(
)
(
1
k
k
k
t
x
t
x
x
,
)
(
)
(
1
k
k
k
t
y
t
y
y
, 1
k
n.
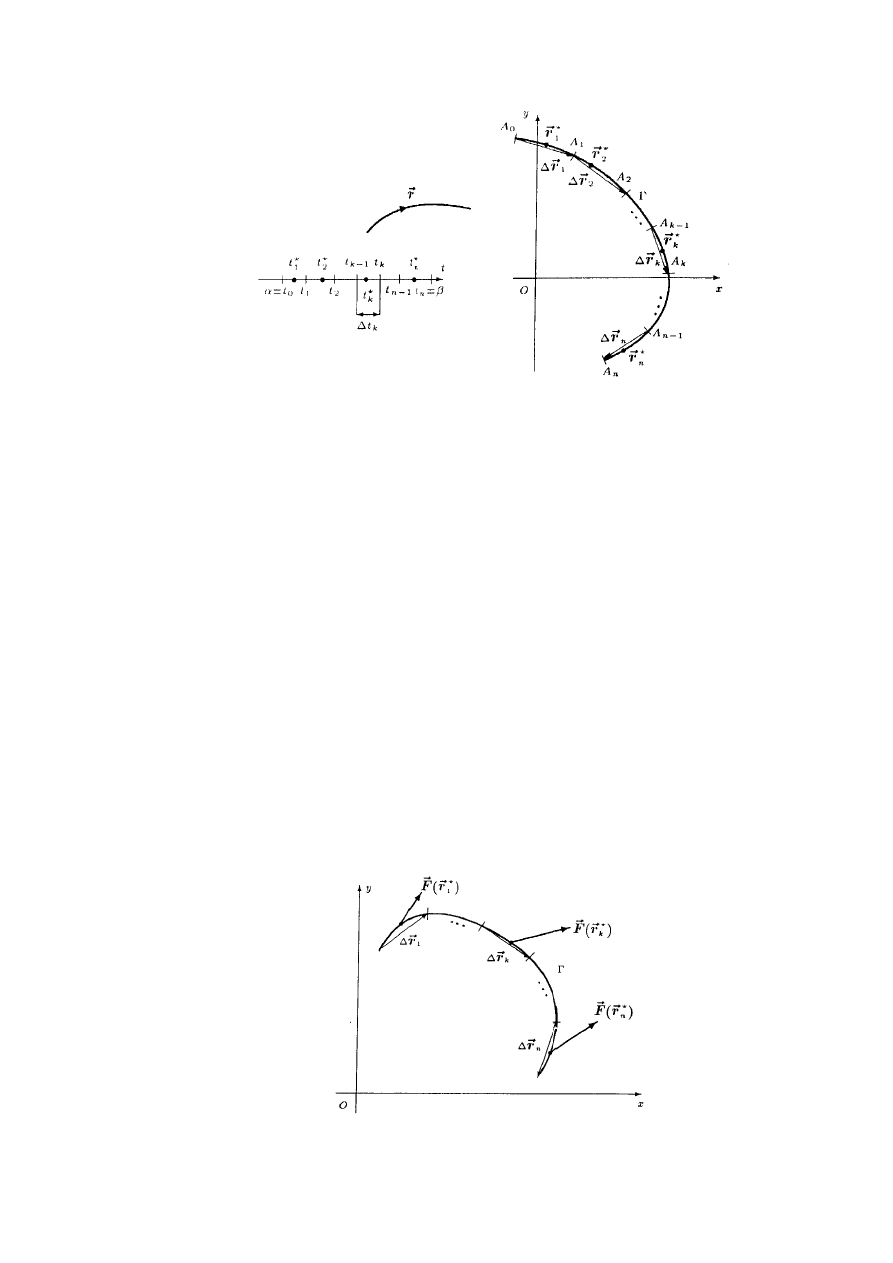
Rys. 2.1.5 Podział odcinka [
,
] i podział łuku zorientowanego
indukowany przez ten podział
Def. 2.1.3 (całka krzywoliniowa zorientowana)
Niech
)
,
(
Q
P
F
będzie polem wektorowym określonym na łuku zorientowanym
R
2
. Całkę krzywoliniową zoriento-
waną z pola wektorowego
F
po łuku
definiujemy wzorem:
n
k
k
k
k
k
k
k
def
y
y
x
Q
x
y
x
P
dy
y
x
Q
dx
y
x
P
1
0
)
(
)
,
(
)
,
(
lim
)
,
(
)
,
(
P
,
o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobu podziału P przedziału [
,
], ani od sposobu
wyboru punktów pośrednich
. Powyższą całkę oznaczamy krótko przez
dy
Q
dx
P
.
Uwaga. Całkę krzywoliniową zorientowaną z pola wektorowego
)
,
,
(
R
Q
P
F
po łuku
położonym w przestrzeni definiu-
jemy analogicznie i oznaczamy symbolem:
dz
z
y
x
R
dy
z
y
x
Q
dx
z
y
x
P
)
,
,
(
)
,
,
(
)
,
,
(
lub krótko
dz
R
dy
Q
dx
P
.
W zapisie wektorowym definicja całki krzywoliniowej zorientowanej z pola wektorowego
)
,
(
Q
P
F
lub pola wektorowego
)
,
,
(
R
Q
P
F
po łuku zorientowanym
położonym odpowiednio na płaszczyźnie lub w przestrzeni przyjmuje jednolitą
formę:
n
k
k
k
def
r
r
F
r
d
r
F
1
0
)
(
)
(
lim
)
(
P
,
gdzie
)
,
(
dy
dx
r
d
def
lub
)
,
,
(
dz
dy
dx
r
d
def
. Całkę krzywoliniową z pola wektorowego
F
po łuku
oznaczamy też krótko
symbolem
r
d
F
.
Rys. 2.1.6 Ilustracja do definicji całki krzywoliniowej zorientowanej w formie wektorowej
Def. 2.1.4 (całka krzywoliniowa po sumie łuków zorientowanych)

Niech łuk zorientowany
będzie sumą łuków niezamkniętch zorientowanych
1
,
2
, …,
m
, przy czym koniec łuku
k
jest
początkiem łuku
k+1
, 1
k
m – 1. Ponadto niech
F
będzie polem wektorowym określonym na łuku
. Całkę krzywoli-
niową zorientowaną z pola
F
po łuku
określamy wzorem:
m
r
d
F
r
d
F
r
d
F
r
d
F
def
...
2
1
,
o ile całki po prawej stronie znaku równości istnieją.
Uwaga. Jeżeli łuk zorientowany na płaszczyźnie jest zamknięty, to wtedy piszemy
w miejsce
.
Rys. 2.1.7 Ilustracje do definicji całki krzywoliniowej zorientowanej po sumie łuków
Tw. 2.1.5 (liniowość całki krzywoliniowej zorientowanej)
Jeżeli istnieją całki krzywoliniowe z pól wektorowych
F
i
G
po kawałkami gładkim łuku zorientowanym
oraz jeżeli c jest
stałą dowolną, to:
a) istnieje całka krzywoliniowa z pola wektorowego
G
F
po łuku
oraz
r
d
G
r
d
F
r
d
G
F
,
b) istnieje całka z pola wektorowego
F
c
po łuku
oraz
r
d
F
c
r
d
F
c
,
c) istnieje całka krzywoliniowa z pola wektorowego
F
po łuku o orientacji przeciwnej –
oraz
r
d
F
r
d
F
.
Tw. 2.1.6 (zależność między całkami krzywoliniowymi)
Niech pole wektorowe
)
,
(
Q
P
F
będzie ciągłe na łuku gładkim
. Wtedy
dl
y
x
y
x
Q
y
x
y
x
P
dy
y
x
Q
dx
y
x
P
)
,
(
cos
)
,
(
)
,
(
cos
)
,
(
)
,
(
)
,
(
,
gdzie
(x,y) oznacza kąt między wektorem stycznym do łuku
w punkcie (x,y) a dodatnią częścią osi Ox, natomiast
(x,y)
oznacza kąt między tym samym wektorem i dodatnią częścią osi Oy. Zakładamy przy tym, że zwrot wektora stycznego jest
zgodny z orientacją łuku
.
Uwaga. Prawdziwa jest także analogiczna równość dla całek krzywoliniowych po łuku położonym w przestrzeni. Równości te
niektórzy autorzy przyjmują jako definicję całki krzywoliniowej zorientowanej.
Rys. 2.1.8 Ilustracja do twierdzenia o zależności między dwoma rodzajami całek krzywoliniowych
2.2 ZAMIANA CAŁKI KRZYWOLINIOWEJ ZORIENTOWANEJ NA CAŁKĘ POJEDYNCZĄ
Tw. 2.2.1 (o zamianie całki krzywoliniowej na całkę pojedynczą)
a) Jeżeli
1. łuk
= {(x(t), y(t)) : t
[
,
]} jest niezamknięty i gładki,
2. orientacja łuku
jest zgodna z jego polaryzacją,

3. pole wektorowe
)
,
(
Q
P
F
jest ciągłe na
,
to
dt
t
y
t
y
t
x
Q
t
x
t
y
t
x
P
dy
y
x
Q
dx
y
x
P
)
(
)
(
),
(
)
(
)
(
),
(
)
,
(
)
,
(
/
/
.
b) Podobnie, jeżeli
1. łuk
= {(x(t), y(t), z(t)) : t
[
,
]}jest niezamknięty i gładki,
2. orientacja łuku
jest zgodna z jego polaryzacją,
3. pole wektorowe
)
,
,
(
R
Q
P
F
jest ciągłe na
,
to
dt
t
z
t
z
t
y
t
x
R
t
y
t
z
t
y
t
x
Q
t
x
t
z
t
y
t
x
P
dz
z
y
x
Q
dy
z
y
x
Q
dx
z
y
x
P
)
(
)
(
),
(
),
(
)
(
)
(
),
(
),
(
)
(
)
(
),
(
),
(
)
,
,
(
)
,
,
(
)
,
,
(
/
/
/
.
Uwaga. Powyższe wzory w formie wektorowej przyjmują jednolitą postać:
dt
t
r
t
r
F
r
d
r
F
)
(
)
(
)
(
/
,
gdzie
)
(t
r
r
jest parametryzacją łuku
oraz
)
(
),
(
)
(
/
/
/
t
y
t
x
t
r
lub
)
(
),
(
),
(
)
(
/
/
/
/
t
z
t
y
t
x
t
r
.
Jeżeli pole wektorowe
)
,
(
Q
P
F
jest ciągłe na łuku gładkim
opisanym równaniem y = y(x), gdzie a
x
b i orientacja
łuku
jest zgodna ze wzrostem zmiennej x, to
b
a
dx
x
y
x
y
x
Q
x
y
x
P
dy
y
x
Q
dx
y
x
P
)
(
)
(
,
)
(
,
)
,
(
)
,
(
/
.
2.3 NIEZALEŻNOŚĆ CAŁKI OD DROGI CAŁKOWANIA
Def. 2.3.1 (pole potencjalne, potencjał pola)
Pole wektorowe
F
określone na obszarze D nazywamy polem potencjalnym, gdy istnieje funkcja U: D
R taka, że
U
F
grad
.
Funkcję U nazywamy potencjałem pola wektorowego
F
.
Uwaga. Dla pola wektorowego na płaszczyźnie
)
,
(
Q
P
F
powyższy warunek ma postać
y
U
Q
x
U
P
,
.
Podobnie, dla pola wektorowego w przestrzeni
)
,
,
(
R
Q
P
F
, mamy
z
U
R
y
U
Q
x
U
P
,
,
.
Tw. 2.3.2 (całka krzywoliniowa z pola potencjalnego)
a) Niech
1. pole wektorowe
)
,
(
Q
P
F
będzie ciągłe na obszarze D
R
2
,
2. pole wektorowe
F
będzie potencjalne na obszarze D z potencjałem U.
Wtedy
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
1
1
2
2
)
,
(
)
,
(
2
2
1
1
y
x
U
y
x
U
y
x
U
dy
y
x
Q
dx
y
x
P
y
x
y
x
B
A
,
gdzie
B
A
jest dowolnym zorientowanym kawałkami gładkim łukiem o początku w punkcie A = (x
1
,y
1
) i końcu w punkcie
B = (x
2
,y
2
), całkowicie zawartym w obszarze D.
b) Podobnie, niech
1. pole wektorowe
)
,
,
(
R
Q
P
F
będzie ciągłe na obszarze V
R
3
,
2. pole wektorowe
F
będzie potencjalne na obszarze V z potencjałem U.
Wtedy
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
1
1
1
2
2
2
)
,
,
(
)
,
,
(
2
2
2
1
1
1
z
y
x
U
z
y
x
U
z
y
x
U
dz
z
y
x
R
dy
z
y
x
Q
dx
z
y
x
P
z
y
x
z
y
x
B
A
,

gdzie
B
A
jest dowolnym zorientowanym kawałkami gładkim łukiem o początku w punkcie A = (x
1
,y
1
,z
1
) i końcu w
punkcie B = (x
1
,y
1
,z
1
), całkowicie zawartym w obszarze V.
Uwaga. W formie wektorowej powyższe wzory przyjmują jednolitą postać:
)
(
)
(
)
(
A
U
B
U
r
U
r
d
U
B
A
B
A
grad
.
Inaczej mówiąc, całka zorientowana w polu potencjalnym nie zależy od drogi całkowania i jest równa różnicy potencjałów w
punktach końcowym i początkowym drogi całkowania. W szczególności w polu potencjalnym
F
mamy
0
r
d
F
,
gdzie
jest dowolnym łukiem zamkniętym zawartym w rozważanym obszarze.
Tw. 2.3.3 (warunek konieczny i wystarczający potencjalności pola)
a) Niech
1. obszar D
R
2
będzie wypukły,
2. pole wektorowe
)
,
(
Q
P
F
będzie różniczkowalne w sposób ciągły na D.
Wówczas pole wektorowe
F
jest potencjalne na D wtedy i tylko wtedy, gdy
)
,
(
)
,
(
y
x
x
Q
y
x
y
P
dla każdego punktu
D
y
x
)
,
(
.
b) Niech
1. obszar V
R
3
będzie wypukły,
2. pole wektorowe
)
,
,
(
R
Q
P
F
będzie różniczkowalne w sposób ciągły na V.
Wówczas pole wektorowe
F
jest potencjalne na V wtedy i tylko wtedy, gdy
)
,
,
(
)
,
,
(
z
y
x
x
Q
z
y
x
y
P
,
)
,
,
(
)
,
,
(
z
y
x
x
R
z
y
x
z
P
,
)
,
,
(
)
,
,
(
z
y
x
y
R
z
y
x
z
Q
dla każdego punktu
V
z
y
x
)
,
,
(
.
Uwaga. Zamiast wypukłości obszarów D i V można założyć, że są one obszarami jednospójnymi odpowiednio na płaszczyźnie
lub w przestrzeni.
Def. 2.3.4 (rotacja pola wektorowego)
Niech pole wektorowe
)
,
,
(
R
Q
P
F
będzie różniczkowalne w sposób ciągły na obszarze V
R
3
. Rotacją pola wektorowego
F
nazywamy pole wektorowe określone wzorem:
k
y
P
x
Q
j
x
R
z
P
i
z
Q
y
R
R
Q
P
z
y
x
k
j
i
F
def
rot
.
Fakt 2.3.5 (kryterium potencjalności pola wektorowego)
Pole wektorowe
)
,
,
(
R
Q
P
F
na obszarze V
R
3
jest potencjalne wtedy i tylko wtedy, gdy
0
rot
F
.
2.4 TWIERDZENIE GREENA
Def. 2.4.1 (znak orientacji)
Niech
będzie kawałkami gładkim łukiem zamkniętym (bez samoprzecięć) na płaszczyźnie, tzn. krzywą Jordana. Mówimy,
że orientacja łuku
jest dodatnia względem swego wnętrza D, gdy podczas ruchu łuku
w kierunku jego orientacji obszar D
leży cały czas po lewej stronie łuku. W przeciwnym przypadku mówimy, że orientacja łuku jest ujemna.
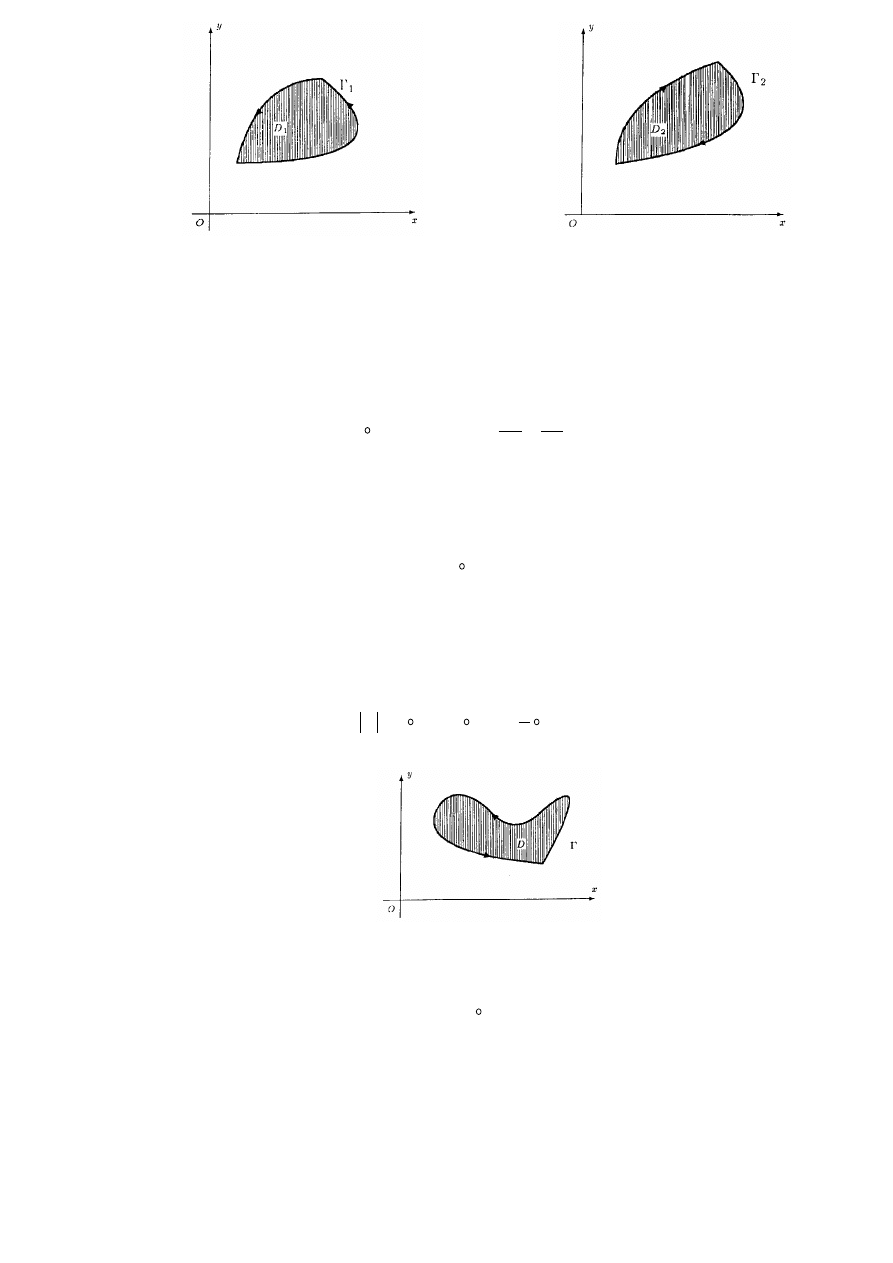
Rys. 2.4.1 Łuk
1
jest zorientowany dodatnio
względem obszaru D
1
Rys. 2.4.2 Łuk
2
jest zorientowany ujemnie
względem obszaru D
2
Tw. 2.4.2 (wzór Greena)
Niech
1. obszar domknięty D
R
2
będzie normalny względem obu osi układu,
2. brzeg
obszaru D będzie zorientowany dodatnio,
3. pole wektorowe
)
,
(
Q
P
F
będzie różniczkowalne w sposób ciągły na D.
Wtedy
D
dy
dx
y
P
x
Q
dy
Q
dx
P
.
Uwaga. Wzór Greena jest prawdziwy także dla obszaru D, który można podzielić na skończoną liczbę obszarów normalnych
(względem obu osi).
Def. 2.4.3 (cyrkulacja pola wektorowego)
Cyrkulacją pola wektorowego
F
po łuku zamkniętym zorientowanym
nazywamy całkę krzywoliniową zorientowaną
r
d
F
.
2.5 ZASTOSOWANIA CAŁEK KRZYWOLINIOWYCH ZORIENTOWANYCH
Fakt 2.5.1 (zastosowania w geometrii)
Pole obszaru D
R
2
ograniczonego łukiem zamkniętym kawałkami gładkim
, dodatnio zorientowanym względem obszaru
D, wyraża się wzorami:
ydx
xdy
xdy
ydx
D
2
1
.
Fakt 2.5.2 (zastosowania w fizyce)
1. Praca w polu wektorowym
F
wykonana wzdłuż łuku zorientowanego
, od punktu początkowego do końcowego, wy-
raża się wzorem:
r
d
F
W
.
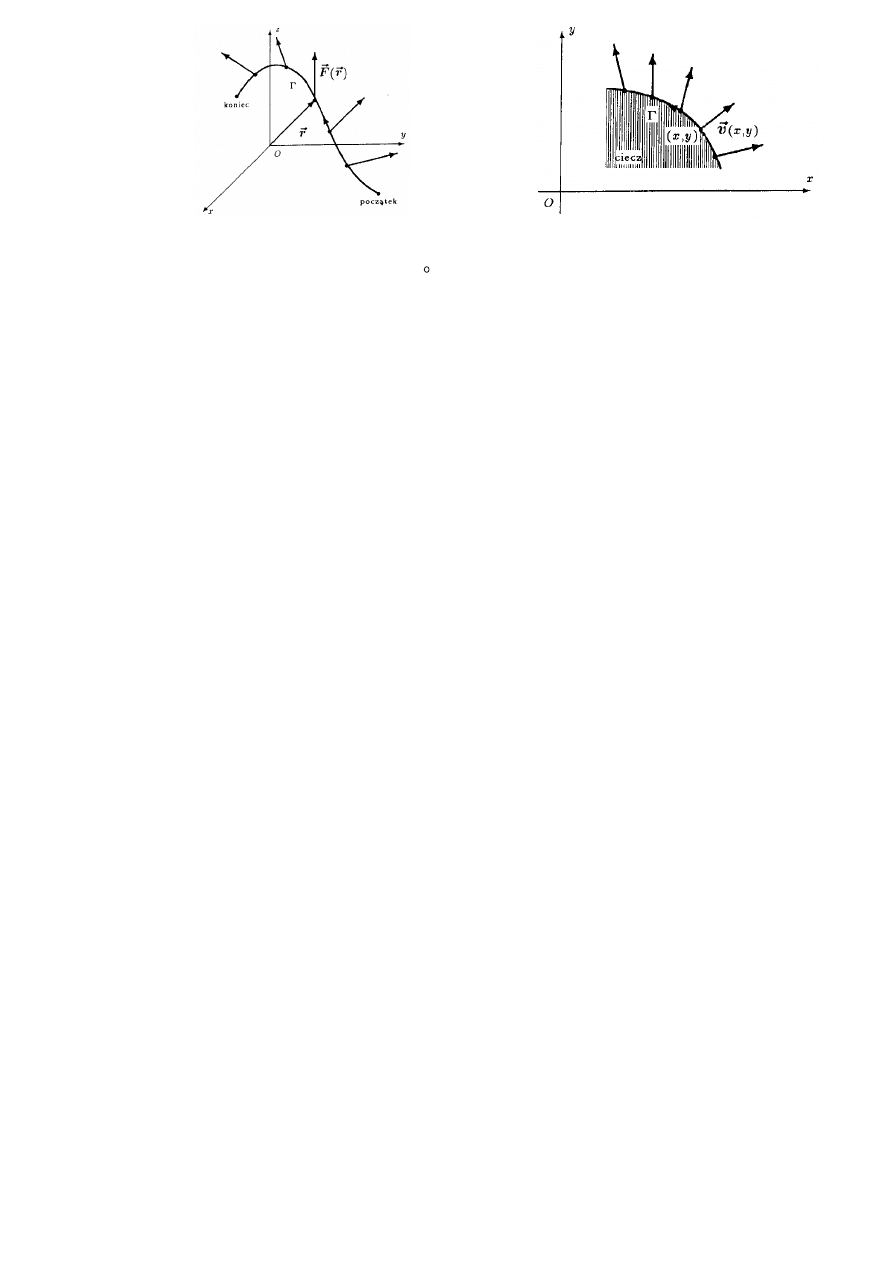
2. Ilość płaskiej (umownej) cieczy przepływającej w jednostce czasu przez łuk zorientowany
wyraża się wzorem:
dy
y
x
P
dx
y
x
Q
A
)
,
(
)
,
(
,
gdzie
)
,
(
),
,
(
)
,
(
y
x
Q
y
x
P
y
x
v
oznacza prędkość przepływu cieczy w punkcie (x,y) tego łuku.
Wyszukiwarka
Podobne podstrony:
,analiza matematyczna 2, calki Nieznany (6)
,analiza matematyczna 2, calki Nieznany (2)
,analiza matematyczna 2, calki Nieznany (5)
cw 13 Analiza Matematyczna (calki) id
,analiza matematyczna 2, elemen Nieznany (2)
Zadania z analizy matematycznej calki
ANALIZA MATEMATYCZNA CAŁKI KRZYWO LINIOWE
,analiza matematyczna 2, rownan Nieznany (2)
,analiza matematyczna 2, uklady Nieznany (2)
,analiza matematyczna 2, rownan Nieznany (3)
cw 13 Analiza Matematyczna (calki) id
,analiza matematyczna 2, elemen Nieznany (2)
więcej podobnych podstron