3. CAŁKI POWIERZCHNIOWE NIEZORIENTOWANE

3.1 PŁATY POWIERZCHNIOWE

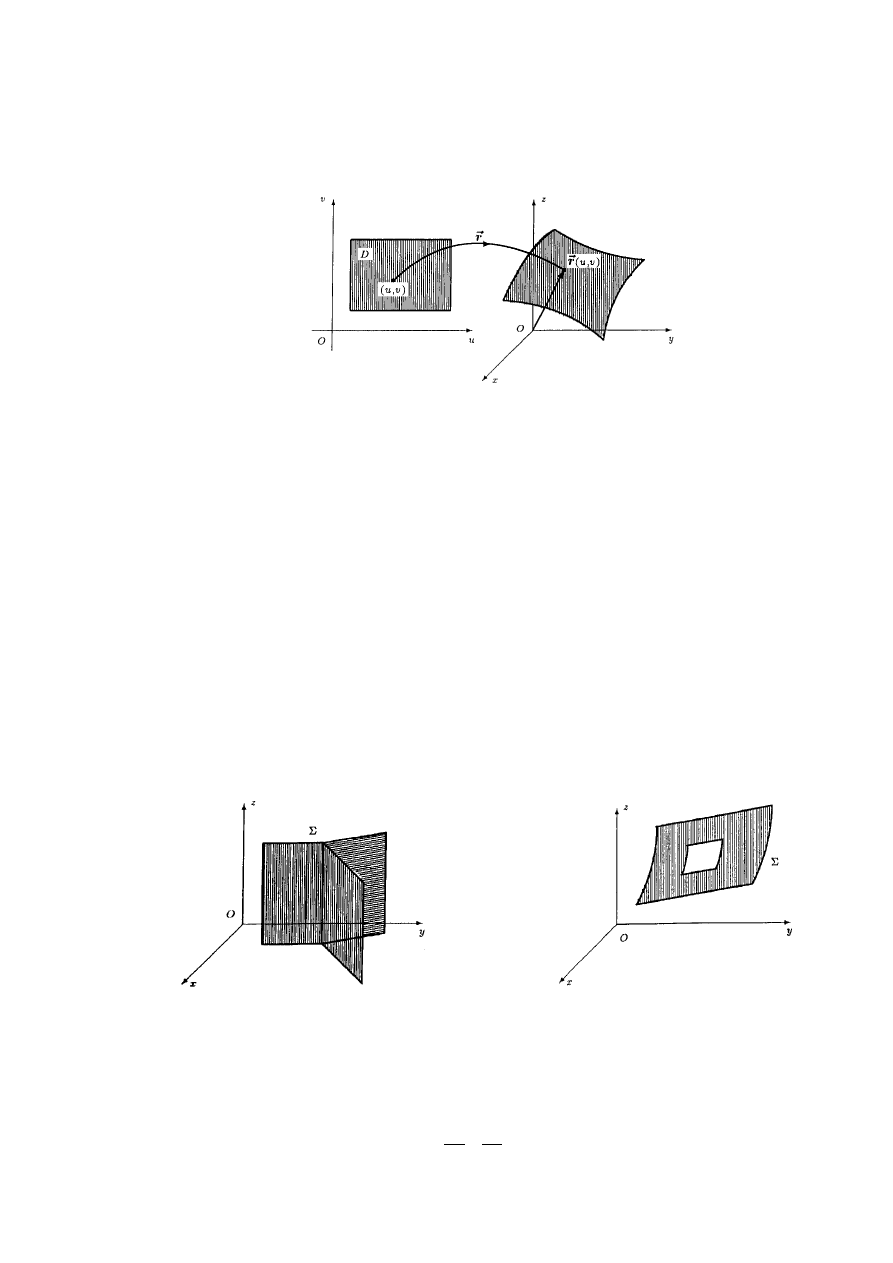
Def. 3.1.1 (funkcja wektorowa dwóch zmiennych w przestrzeni)
a) Niech D będzie obszarem na płaszczyźnie. Funkcją wektorową dwóch zmiennych w przestrzeni nazywamy odwzorowanie

3

:

R

D

r





. Funkcję taką będziemy zapisywać w postaci





)

,

(

),

,

(

),

,

(

)

,

(

v

u

z

v

u

y

v

u

x

v

u

r





, gdzie

D

v

u



)

,

(

.

Rys. 3.1.1 Funkcja wektorowa

3

:

R

D

r





b) Mówimy, że funkcja wektorowa

3

:

R

D

r





jest różnowartościowa, gdy dla dowolnych punktów (u

1

,v

1

), (u

2

,v

2

)



D

prawdziwa jest implikacja

)

,

(

)

,

(

)

,

(

)

,

(

2

2

1

1

2

2

1

1

v

u

r

v

u

r

v

u

v

u











.

c) Mówimy, że funkcja wektorowa

3

:

R

D

r





jest ciągła, gdy funkcje x, y, z są ciągłe na D.

d) Mówimy, że funkcja wektorowa

3

:

R

D

r





jest różniczkowalna w sposób ciągły, gdy funkcje x, y, z mają ciągłe

wszystkie pochodne cząstkowe pierwszego rzędu na obszarze D.

Def. 3.1.2 (płat powierzchniowy)
Niech

D

będzie

prostokątem

na

płaszczyźnie

oraz

niech

funkcja

wektorowa

3

:

R

D

r





,

gdzie





)

,

(

),

,

(

),

,

(

)

,

(

v

u

z

v

u

y

v

u

x

v

u

r





dla

D

v

u



)

,

(

, będzie ciągła i różnowartościowa na prostokącie D. Płatem powierzchnio-

wym nazywamy zbiór wartości funkcji wektorowej

r



, tj. zbiór:





D

v

u

v

u

r







)

,

(

:

)

,

(



.

Zbiór w przestrzeni taki, że każdy jego punkt ma otoczenie domknięte, które jest płatem prostym, nazywamy płatem po-
wierzchniowym.

Uwaga. Funkcję wektorową

r



lub układ funkcji x, y, z nazywamy parametryzacją płata



. Płat prosty można wyobrazić sobie

jako powyginany w przestrzeni prostokąt. Przy tym przekształcaniu prostokąta nie można rozrywać ani sklejać.

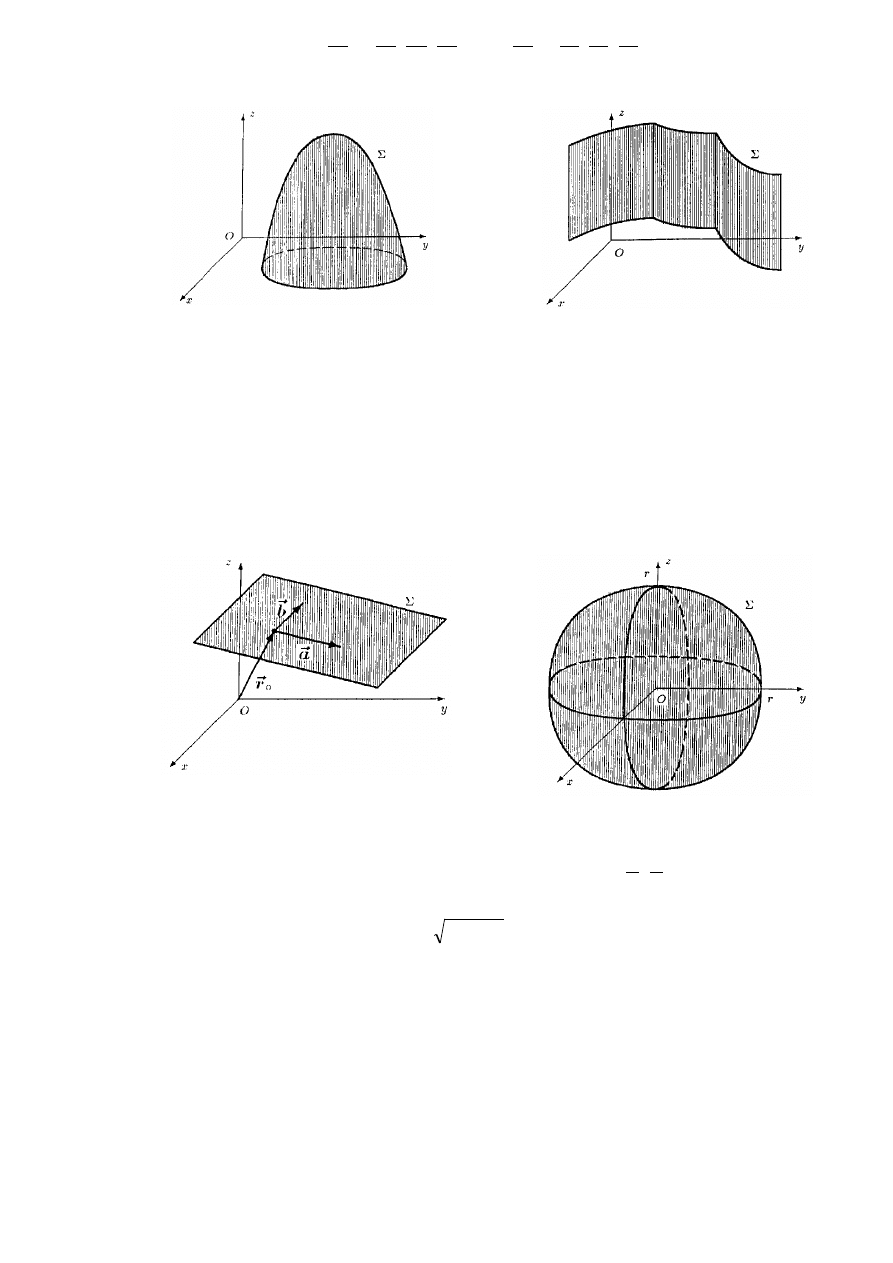
Rys. 3.1.2 Zbiór



nie jest płatem

powierzchniowym

Rys. 3.1.3 Zbiór



jest płatem

powierzchniowym

Def. 3.1.3 (płat powierzchniowy gładki)
Płat powierzchniowy





D

v

u

v

u

r







)

,

(

:

)

,

(



, gdzie D jest obszarem domkniętym z brzegiem kawałkami gładkim, a funkcja

wektorowa





)

,

(

),

,

(

),

,

(

)

,

(

v

u

z

v

u

y

v

u

x

v

u

r





jest różnowartościowa i różniczkowalna w sposób ciągły na obszarze D, nazy-

wamy płatem gładkim, gdy na obszarze D spełniony jest warunek

0



















v

r

u

r

,

gdzie































u

z

u

y

u

x

u

r

,

,



oraz































v

z

v

y

v

x

v

r

,

,



.

Płat, który można podzielić na skończoną liczbę płatów gładkich, nazywamy płatem kawałkami gładkim.

Rys. 3.1.4 Płat powierzchniowy gładki

Rys. 3.1.5 Płat powierzchniowy kawałkami gładki

Fakt 3.1.4 (równania parametryczne ważniejszych płatów powierzchniowych)
1. Płaszczyzna przechodząca przez punkt

)

,

,

(

0

0

0

0

z

y

x

r





i rozpięta na wektorach

)

,

,

(

1

1

1

z

y

x

a





,

)

,

,

(

2

2

2

z

y

x

b





ma

przedstawienie parametryczne:

R

v

R

u

vz

uz

z

z

uy

uy

y

y

vx

ux

x

x



































,

:

2

1

0

2

1

0

2

1

0

.

W formie wektorowej parametryzacja płaszczyzny ma postać:



R

v

R

u

b

v

a

u

r

r













,

:

0









.

2. Sfera o środku w początku układu współrzędnych i promieniu r > 0 ma przedstawienie parametryczne:































2

,

2

],

2

,

0

[

sin

cos

sin

cos

cos

:







v

u

v

r

z

v

u

r

y

v

u

r

x

.

3. Powierzchnia stożka określona równaniem

2

2

y

x

k

z





, gdzie

2

2

2

r

y

x





, ma przedstawienie parametryczne:



  

r

v

u

kv

z

u

v

y

u

v

x

,

0

,

2

,

0

sin

cos

:

























.

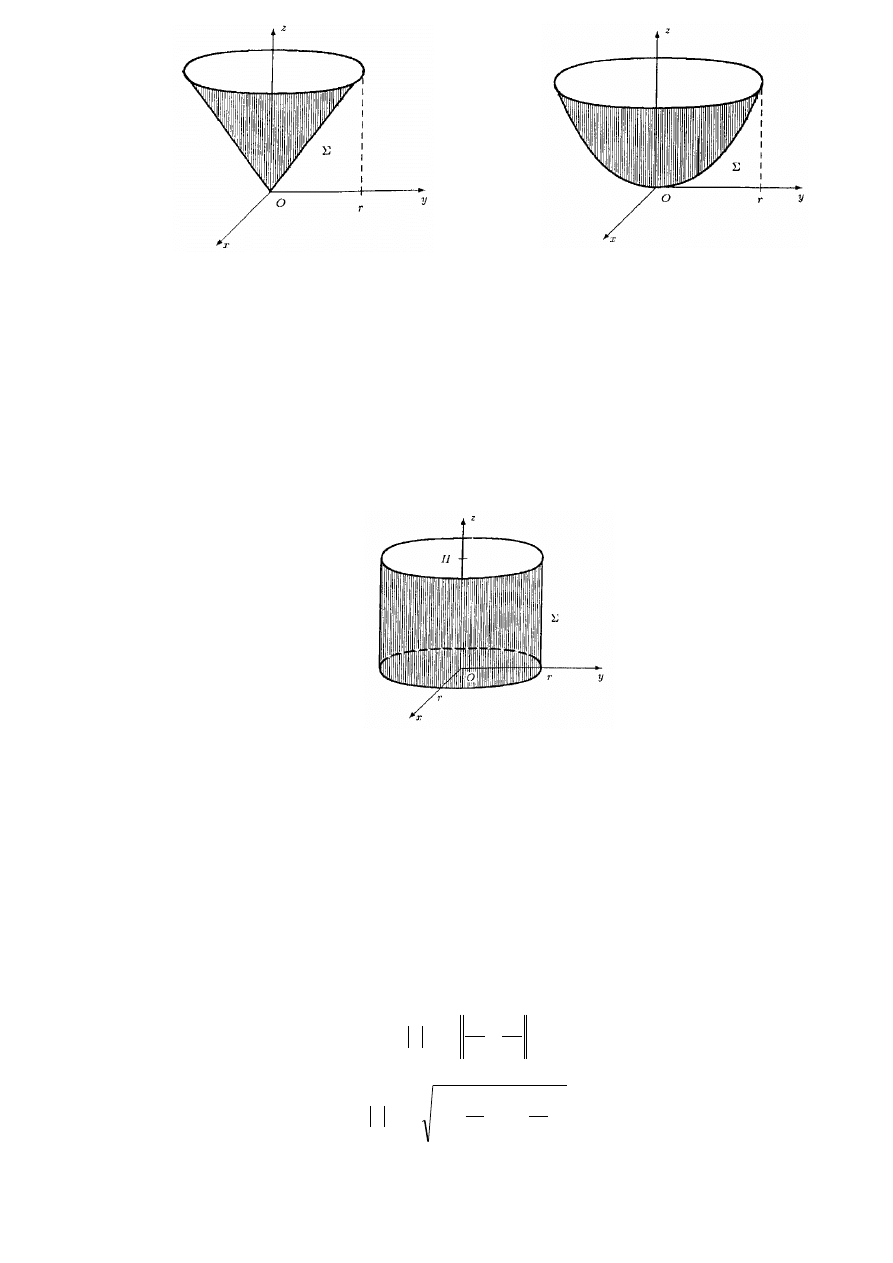
4. Powierzchnia paraboloidy obrotowej określona równaniem





2

2

y

x

k

z





, gdzie

2

2

2

r

y

x





, ma przedstawienie

parametryczne:



  

r

v

u

kv

z

u

v

y

u

v

x

,

0

,

2

,

0

sin

cos

:

2

























.

5. Powierzchnia walcowa opisana równaniem

2

2

2

r

y

x





, gdzie

H

z





0

, ma przedstawienie parametryczne:



 



H

v

u

v

z

u

r

y

u

r

x

,

0

,

2

,

0

sin

cos

:

























.

Uwaga. Równania fragmentów tych płatów powierzchniowych otrzymamy zmniejszając odpowiednio zakresy parametrów
u, v.

Fakt 3.1.5 (o postaci płatów powierzchniowych)
Płatami powierzchniowymi są wykresy funkcji ciągłych postaci:
1.

1

)

,

(

);

,

(

D

y

x

y

x

z

z





, gdzie D

1

jest obszarem na płaszczyźnie xOy,

2.

2

)

,

(

);

,

(

D

z

y

z

y

x

x





, gdzie D

2

jest obszarem na płaszczyźnie yOz,

3.

3

)

,

(

);

,

(

D

z

x

z

x

y

y





, gdzie D

3

jest obszarem na płaszczyźnie xOz.

Jeżeli funkcje te mają ciągłe pochodne cząstkowe pierwszego rzędu na rozważanych obszarach, to te płaty powierzchniowe są
gładkie.
Uwaga. Równania ważniejszych płatów powierzchniowych, które są wykresami funkcji postaci z = f(x,y) podane są w części
„Analiza matematyczna 2” w fakcie 3.2.5.

Tw. 3.1.6 (pole płata powierzchniowego)
Niech





D

v

u

v

u

r







)

,

(

:

)

,

(



będzie gładkim płatem powierzchniowym. Wtedy pole tego płata wyraża się wzorem:

















D

dv

du

v

r

u

r





.

Uwaga. Jeżeli płat gładki



jest wykresem funkcji z = z(x,y), gdzie (x,y)



D, to jego pole wyraża się wzorem:







































D

dy

dx

y

z

x

z

2

2

1

.

Analogicznie wyglądają wzory na pola płatów gładkich będących wykresami funkcji x = x(y,z) oraz y = y(x,z).

3.2 DEFINICJA I WŁASNOŚCI CAŁKI POWIERZCHNIOWEJ NIEZORIENTOWANEJ

Oznaczenia w definicji całki powierzchniowej niezorientowanej
Niech





D

v

u

v

u

r







)

,

(

:

)

,

(



będzie gładkim płatem powierzchniowym, zakładamy przy tym, że D jest domkniętym ob-

szarem regularnym na płaszczyźnie. Wprowadzamy następujące oznaczenia:
P = {



D

1

,



D

2

, ...,



D

n

}, – podział obszaru D na obszary regularne



D

k

(o rozłącznych wnętrzach), 1



k



n;

d

k

– średnica obszaru



D

k

, tj. kres górny odległości punktów zbioru



D

k

, 1



k



n;



(

P) = max{d

k

: 1



k



n } – średnica podziału

P;





)

,

(

,

)

,

(

),

,

(

2

2

1

1

















n

n

v

u

v

u

v

u



, gdzie

k

k

k

D

v

u







)

,

(

dla 1



k



n – zbiór punktów pośrednich podziału

P.



k

– część płata



odpowiadająca obszarowi



D

k

w podanej wyżej parametryzacji

r



, 1



k



n;

|



k

| – pole płata



k

, 1



k



n;

)

,

,

(







k

k

k

z

y

x

– punkt płata



k

odpowiadający punktowi

k

k

k

D

v

u







)

,

(

w podanej parametryzacji

r



, 1



k



n.

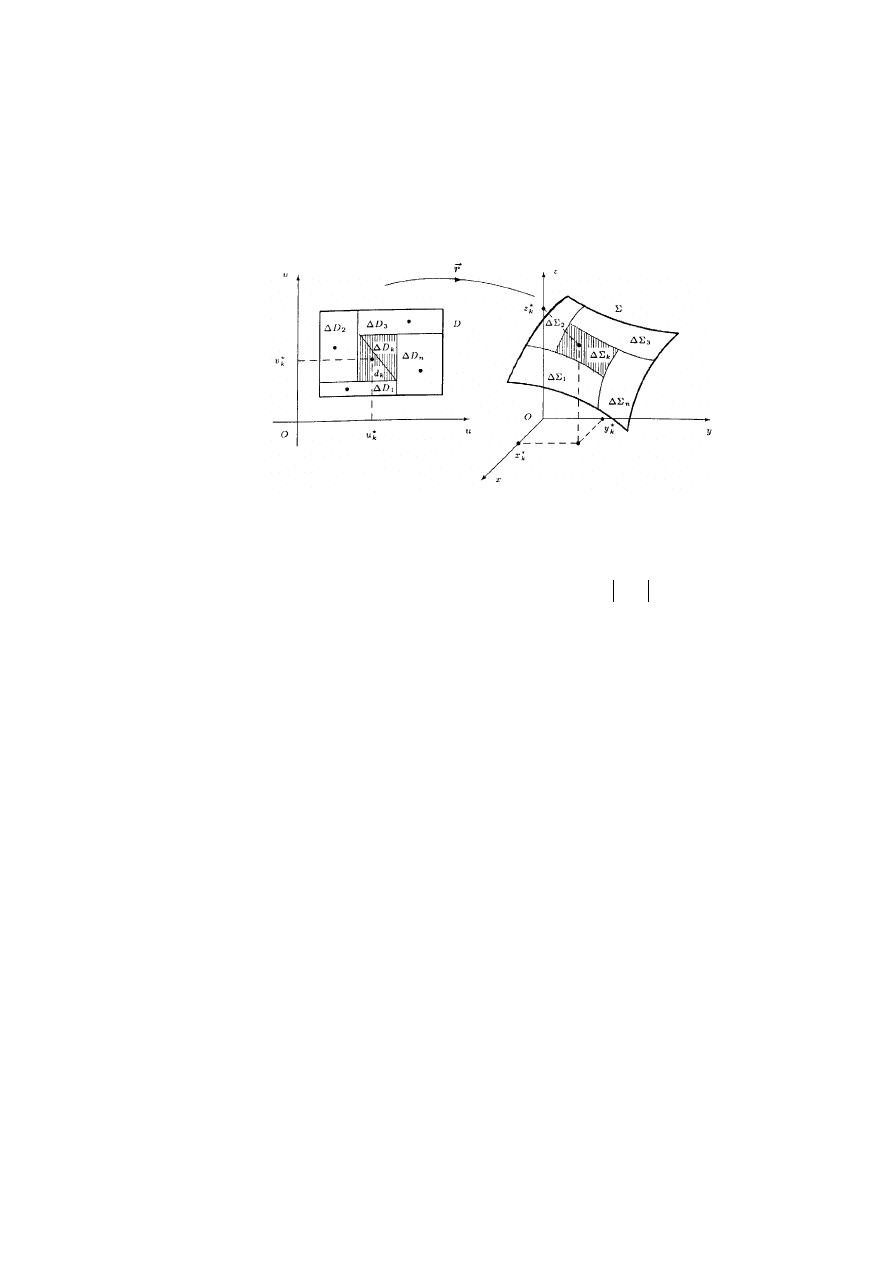
Rys. 3.2.1 Ilustracja do definicji całki powierzchniowej niezorientowanej

Def. 3.2.1 (całka powierzchniowa niezorientowana)
Niech



będzie płatem powierzchniowym gładkim oraz niech funkcja

R

f





:

będzie ograniczona. Całkę powierzchniową

niezorientowaną z funkcji f po płacie



definiujemy wzorem:

























n

k

k

k

k

k

def

z

y

x

f

dS

z

y

x

f

1

0

)

(

,

,

lim

)

,

,

(

P



,

o ile granica po prawej stronie znaku równości istnieje oraz nie zależy od sposobu podziału P obszaru D, ani od sposobu wy-
boru punktów pośrednich



.

Uwaga. Wartość całki powierzchniowej niezorientowanej nie zależy od sposobu parametryzacji płata. Całkę powierzchniową
niezorientowaną z funkcji f po płacie



oznaczamy krótko symbolem





dS

f

.

Def. 3.2.2 (całka powierzchniowa po płacie kawałkami gładkim)
Niech



będzie płatem kawałkami gładkim złożonym z płatów gładkich



1

,



2

, …,



m

oraz niech f będzie funkcją określoną i

ograniczoną na płacie



. Całkę powierzchniową niezorientowaną z funkcji f po płacie



definiujemy wzorem:;

























m

dS

f

dS

f

dS

f

dS

f

def

...

2

1

,

o ile całki po prawej stronie znaku równości istnieją.

Tw. 3.2.3 (liniowość całki powierzchniowej niezorientowanej)
Jeżeli funkcje f i g są całkowalne na kawałkami gładkim płacie powierzchniowym



oraz jeżeli c jest dowolną stałą, to:

a) funkcja f + g jest całkowalna na płacie



oraz



















dS

g

dS

f

dS

g

f

)

(

,

b) funkcja cf jest całkowalna na płacie



oraz











dS

f

c

dS

cf )

(

.

Def. 3.2.4 (całka powierzchniowa niezorientowana z funkcji wektorowej)
Niech



będzie kawałkami gładkim płatem powierzchniowym oraz niech funkcje P, Q, R będą całkowalne na



. Całkę po-

wierzchniową niezorientowaną po płacie



z funkcji wektorowej

)

,

,

(

R

Q

P

F





określamy wzorem:































dS

R

dS

Q

dS

P

dS

F

def

,

,



.

3.3 ZAMIANA CAŁKI POWIERZCHNIOWEJ NIEZORIENTOWANEJ NA CAŁKĘ PODWÓJNĄ

Tw. 3.3.1 (o zamianie całki powierzchniowej na całkę podwójną)
Jeżeli

1. obszar D



R

2

jest regularny,

2. płat





D

v

u

v

u

r







)

,

(

:

)

,

(



jest gładki,

3. funkcja

R

f





:

jest ciągła,

to





dv

du

v

r

u

r

v

u

r

f

dS

z

y

x

f

D

























)

,

(

)

,

,

(

.

Uwaga. Jeżeli płat gładki



jest wykresem funkcji z = z(x,y), gdzie (x,y)



D oraz funkcja f jest ciągła na



, to wzór na zamianę

całek przyjmuje postać:





dy

dx

y

x

y

z

y

x

x

z

y

x

z

y

x

f

dS

z

y

x

f

D

2

2

)

,

(

)

,

(

1

)

,

(

,

,

)

,

,

(









































.

Analogiczne wzory otrzymujemy w przypadku płatów powierzchniowych opisanych równaniami x = x(y,z) lub y = y(x,z).


3.4 ZASTOSOWANIA CAŁEK POWIERZCHNIOWYCH NIEZORIENTOWANYCH

Fakt 3.4.1 (zastosowania w geometrii)
Pole kawałkami gładkiego płata



wyraża się wzorem:









dS

.

Fakt 3.4.2 (zastosowania w fizyce)
1. Masa płata materialnego



o gęstości powierzchniowej masy



wyraża się wzorem:







dS

z

y

x

M

)

,

,

(



.

2. Momenty statyczne względem płaszczyzn układu współrzędnych płata materialnego



o gęstości powierzchniowej masy



wyrażają się wzorami:







dS

z

y

x

x

MS

yz

)

,

,

(



,







dS

z

y

x

y

MS

xz

)

,

,

(



,







dS

z

y

x

z

MS

xy

)

,

,

(



.

3. Współrzędne środka masy płata



o gęstości powierzchniowej masy



wyrażają się wzorami:

M

MS

x

yz

C



,

M

MS

y

xz

C



,

M

MS

z

xy

C



.

4. Momenty bezwładności względem osi oraz względem początku układu współrzędnych płata materialnego



o gęstości

powierzchniowej masy



wyrażają się wzorami:













dS

z

y

x

z

y

I

x

)

,

,

(

2

2



,













dS

z

y

x

z

x

I

y

)

,

,

(

2

2



,













dS

z

y

x

y

x

I

z

)

,

,

(

2

2



,















dS

z

y

x

z

y

x

I

)

,

,

(

2

2

2

0



.

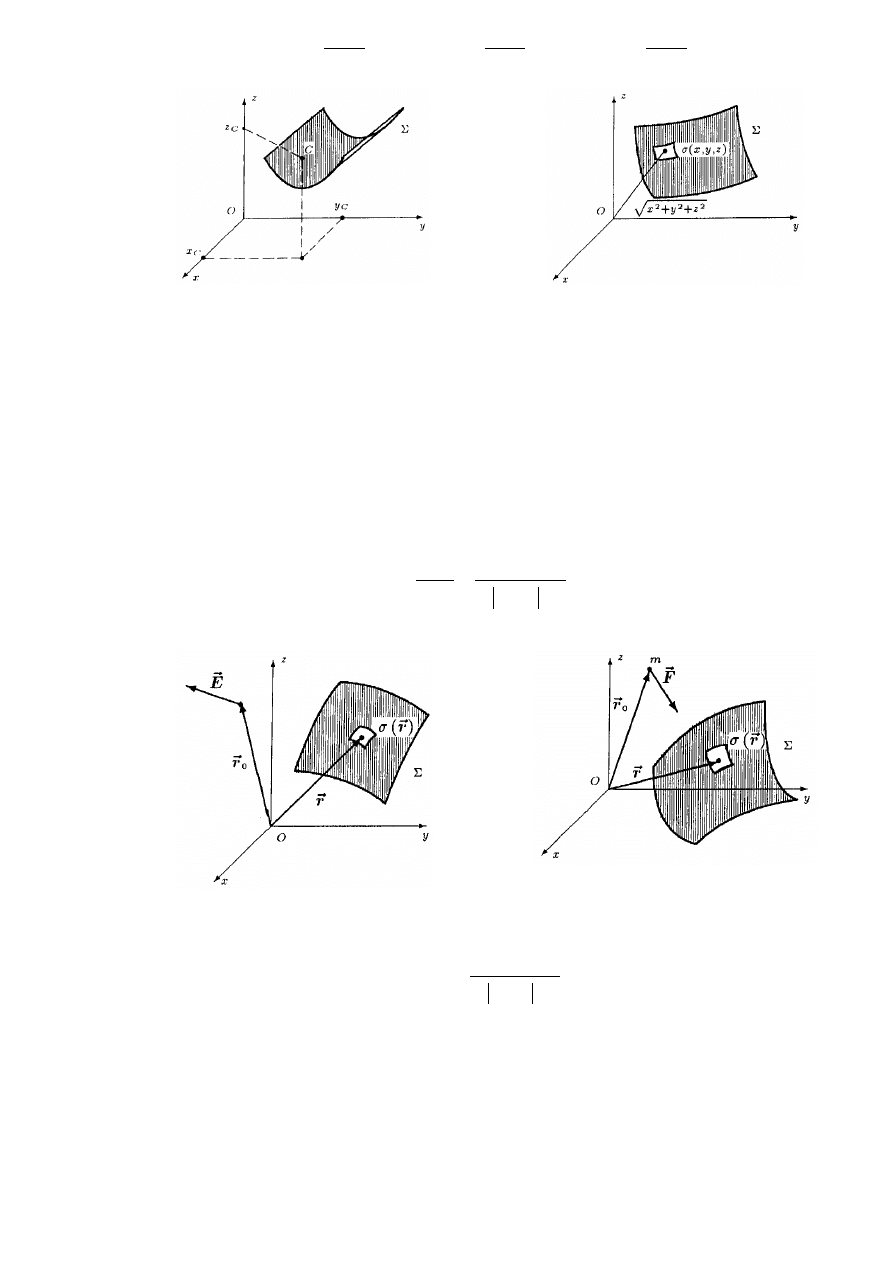
5. Natężenie pola elektrycznego w punkcie

0

r



pochodzące od ładunku elektrycznego rozłożonego na płacie



o gęstości

powierzchniowej ładunku



wyraża się wzorem:











dS

r

r

r

r

r

E

3

0

0

0

)

(

)

(

4

1

















,

gdzie



0

oznacza stałą dielektryczną próżni.

6. Siła przyciągania grawitacyjnego masy m skupionej w punkcie

0

r



przez płat materialny



o gęstości powierzchniowej

masy



wyraża się wzorem:

dS

r

r

r

r

r

Gm

F











3

0

0

)

(

)

(















,

gdzie G oznacza stałą grawitacji.

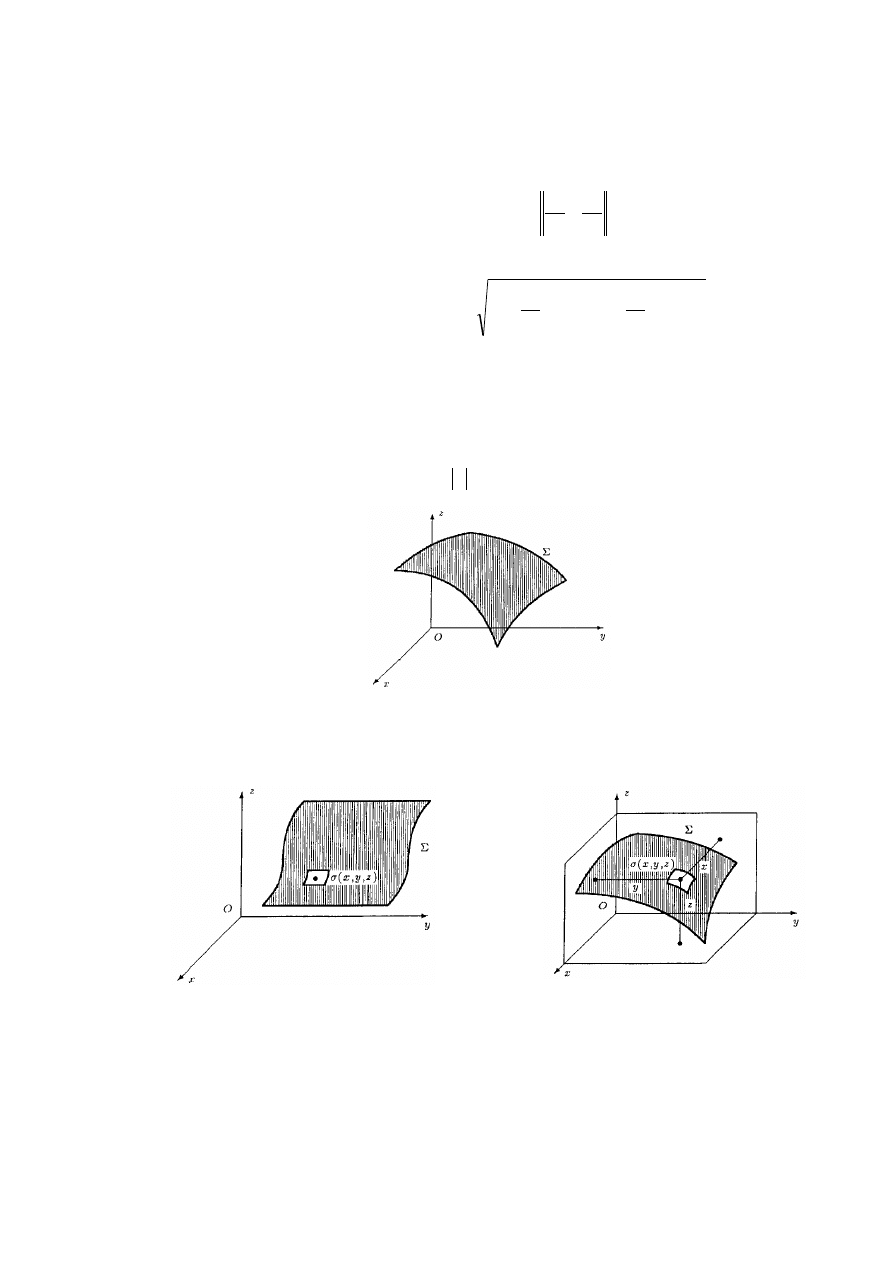
Fakt 3.4.3 (środki masy płatów symetrycznych)
1. Jeżeli płat powierzchniowy ma środek symetrii i gęstość powierzchniowa masy jest funkcją symetryczną względem tego

środka (np. jest stała), to środek masy płata pokrywa się z jego środkiem symetrii.

2. Jeżeli płat powierzchniowy ma oś lub płaszczyznę symetrii i gęstość powierzchniowa masy jest funkcją symetryczną

względem tej osi lub płaszczyzny (np. jest stała), to środek masy tego płata leży na jego osi lub płaszczyźnie symetrii.