Statystyczne modele komputerów

i systemów komputerowych

Wykład z Podstaw Informatyki

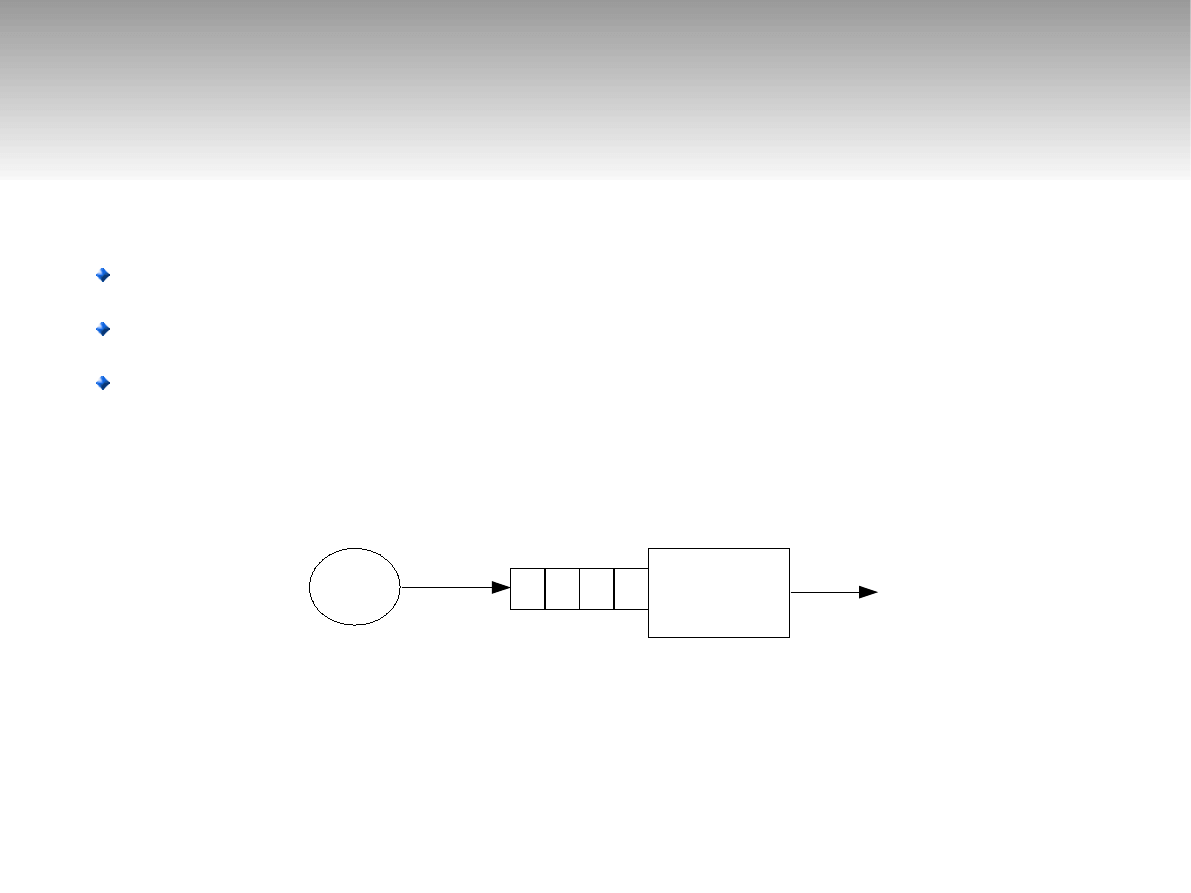
System M/M/1

Źródło zgłoszeń
Kolejka
Stanowisko obsługi

∞

λ

μ

Źródło zgłoszeń - parametry

Wymiar (skończenie- lub nieskończenie wy-
miarowe)
Rozkład odstępów czasu między generacją
kolejnych zgłoszeń ma rozkład wykładniczy

A  x=1−e

−

λx

Kolejka - parametry

Regulamin obsługi (FIFO)
Brak priorytetów

Stanowisko obsługi - parametry

Liczba kanałów obsługi – 1
Wykładniczy rozkład czasów obsługi

B  x=1−e

−

μx

Analiza pracy systemu M/M/1

Dane: λ,

μ

Szukane: E(n), E(k), E(s),

 E(

τ), E(w), E(v)

n, k, s – zmieniają się w czasie (kon-
kretne wartości występują z określonym
prawdopodobieństwem P

n

(t) )

W krótkim odcinku czasu dt może zajść
co najwyżej jedno zdarzenie danego
typu (proces Poissona)

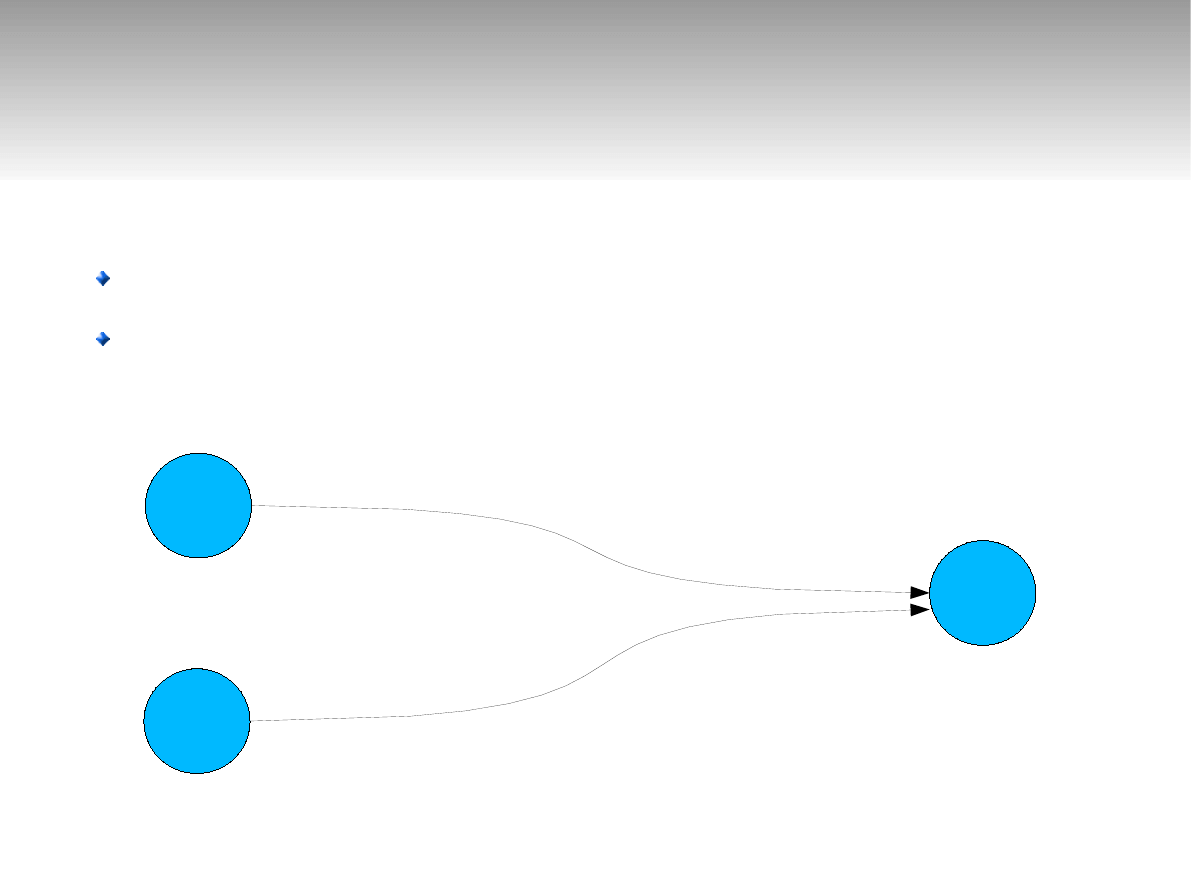
Analiza pracy systemu M/M/1

W chwili t+dt w systemie jest 0 zgłoszeń
Co było w chwili t

P

0

(t+dt)

P

0

(t)

P

1

(t)

1-λdt

(1-λdt)μdt

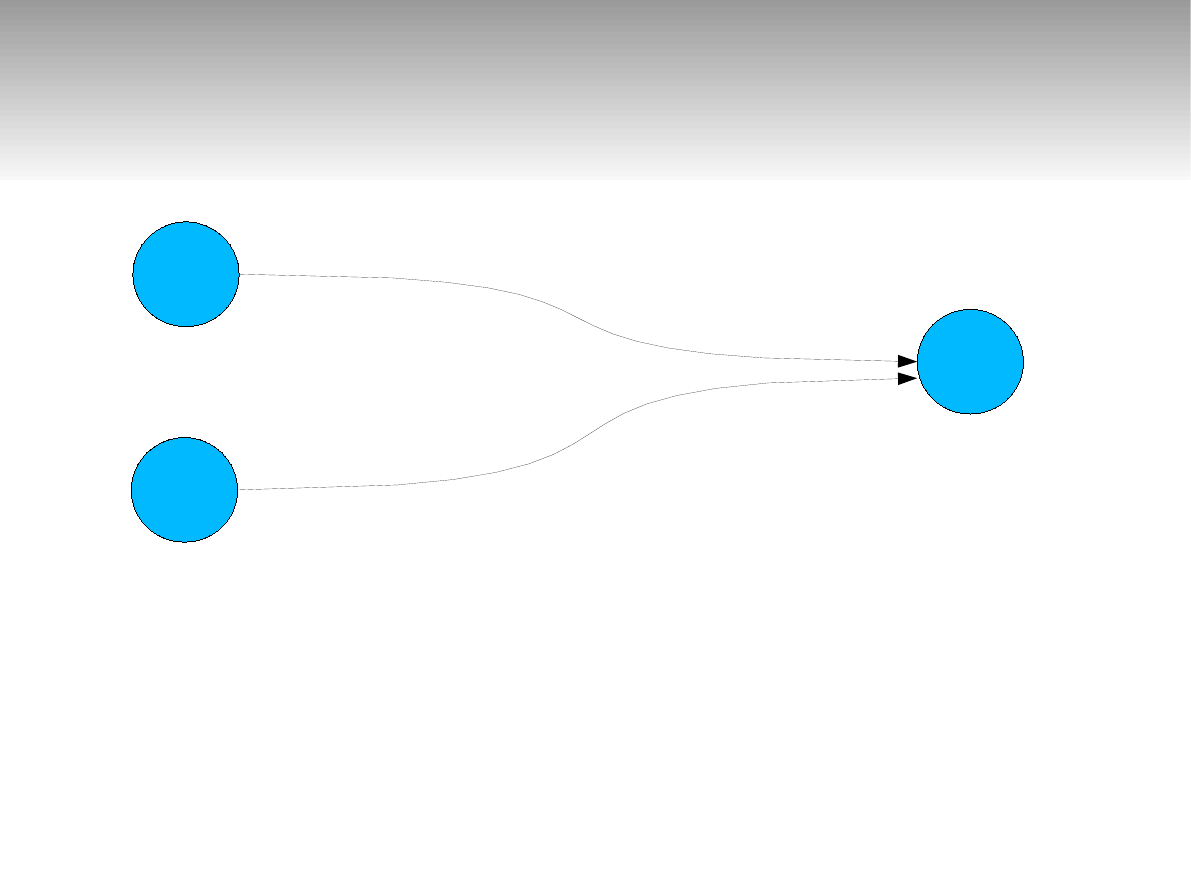
Analiza pracy systemu M/M/1

P

0

(t+dt)

P

0

(t)

P

1

(t)

1-λdt

(1-λdt)μdt

P

0



tdt =P

0



t⋅1−λ dtP

1



t⋅1−λ dt⋅μ dt

Analiza pracy systemu M/M/1

P

0



tdt =P

0



t⋅1−λ dtP

1



t⋅1−λ dt⋅μ dt

P

0



tdt =P

0



t−P

0



t ⋅λ dtP

1



t⋅μ dt− P

1



t ⋅λ μ dt

2

P

0



tdt −P

0



t=−P

0



t⋅λ dtP

1



t⋅μ dt−P

1



t⋅λ μ dt

2

P

0



tdt− P

0



t 

dt

=−

P

0



t ⋅λ P

1



t ⋅μ−P

1



t⋅λ μ dt

lim

dt  0

P

0



tdt− P

0



t 

dt

=−

P

0



t⋅λP

1



t ⋅μ

˙

P

0



t=−P

0



t⋅λP

1



t ⋅μ

0=−P

0

⋅

λP

1

⋅

μ

P

0

⋅

λ=P

1

⋅

μ

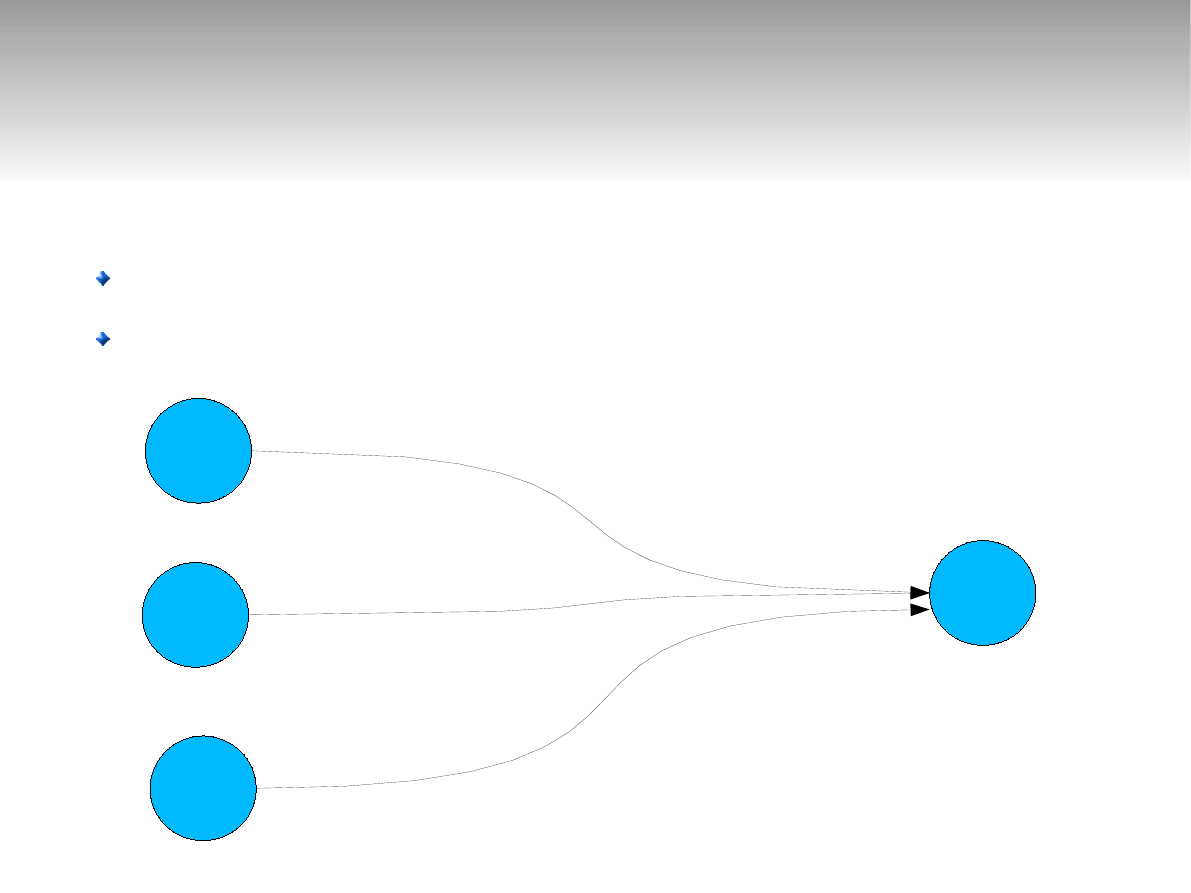
Analiza pracy systemu M/M/1

W chwili t+dt w systemie jest n zgłoszeń
Co było w chwili t

P

n

(t+dt)

P

n-1

(t)

P

n+1

(t)

λdt(1-μdt)

(1-λdt)μdt

P

n

(t)

(1-λdt)(1-μdt)+λdt μdt

Analiza pracy systemu M/M/1

P

n



tdt=P

n−1



t ⋅λdt⋅1− μdt  P

n



t⋅1− λdt ⋅1− μdt λdt⋅μdt 



P

n1



t⋅1−λdt ⋅μ dt

P

n



tdt=P

n−1



t ⋅λdt−P

n−1



t⋅λμdt

2



P

n



t−P

n



t⋅λ dt−P

n



t⋅μdt2⋅P

n



t ⋅λμdt

2



P

n1



t ⋅μ dt−P

n1



t⋅λ μdt

2

P

n



tdt −P

n



t 

dt

=

P

n−1



t ⋅λ−P

n−1



t⋅λμ dt−P

n



t⋅λ−P

n



t⋅μ2⋅P

n



t ⋅λμdt



P

n1



t⋅μ−P

n1



t⋅λ μdt

lim

dt  0

P

n



tdt −P

n



t

dt

=

P

n−1



t ⋅λ− P

n



t⋅λ−P

n



t ⋅μP

n1



t ⋅μ

Analiza pracy systemu M/M/1

lim

dt  0

P

n



tdt −P

n



t

dt

=

P

n−1



t ⋅λ− P

n



t⋅λ−P

n



t ⋅μP

n1



t ⋅μ

˙

P

n



t =P

n−1



t⋅λ−P

n



t ⋅λ−P

n



t⋅μP

n1



t⋅μ

0=P

n−1

⋅

λ−P

n

⋅

λ−P

n

⋅

μ P

n1

⋅

μ

P

n

⋅

μ−P

n−1

⋅

λ=P

n1

⋅

μ−P

n

⋅

λ

P

1

⋅

μ−P

0

⋅

λ=0

P

n

⋅

μ=P

n−1

⋅

λ

P

n

=

P

n−1

⋅

λ
μ

=

P

n−1

⋅

ρ=P

0

⋅

ρ

n

Analiza pracy systemu M/M/1

P

n

=

P

0

⋅

ρ

n

∑

n=0

∞

P

n

=

1

∑

n=0

∞

P

0

⋅

ρ

n

=

1

P

0

⋅

∑

n=0

∞

ρ

n

=

1

P

0

⋅

1

1− ρ

=

1

P

0

=

1− ρ

P

n

=

1− ρ⋅ρ

n

Analiza pracy systemu M/M/1 –

średnia liczba zgłoszeń

E  n=

∑

n=0

∞

n⋅P

n

=

∑

n=0

∞

n⋅1− ρ⋅ρ

n

=

1− ρ⋅

∑

n=0

∞

n⋅ρ

n

∑

n=0

∞

ρ

n

=

1



1− ρ

∑

n=0

∞

n⋅ρ

n −1

=−

−

1



1− ρ

2

∑

n=0

∞

n⋅ρ

n

=

ρ



1−ρ

2

E  n=1− ρ⋅

∑

n=0

∞

n⋅ρ

n

=

1− ρ⋅

ρ



1− ρ

2

=

ρ

1− ρ

Analiza pracy systemu M/M/1 –

średnia długość kolejki

E  k =

∑

n =2

∞



n−1⋅P

n

=

∑

n=2

∞



n−1⋅1− ρ⋅ρ

n

E  k=1− ρ⋅

∑

n= 2

∞

n⋅ρ

n

−

1− ρ⋅

∑

n= 2

∞

ρ

n

E k =1− ρ⋅

ρ



1− ρ

2

−

ρ−1− ρ⋅

1

1− ρ

−

ρ

E  k =1− ρ⋅

ρ−1− ρ

2



1− ρ

2

−

1− ρ⋅

1− ρ⋅1− ρ

1− ρ

E  k =

ρ

2

1− ρ

Analiza pracy systemu M/M/1 –

średnia zajętość stanowiska

E  s=1− P

0

=

1−1− ρ= ρ

E  s= E n−E  k =

ρ

1− ρ

−

ρ

2

1− ρ

=

ρ− ρ

2

1− ρ

=

ρ1− ρ

1− ρ

=

ρ

Analiza pracy systemu M/M/1 –

twierdzenie Little'a

E n=λ⋅E  τ

E  τ =

E n

λ

=

ρ

1−ρ

⋅

1

λ

=

λ

μ⋅1− ρ

⋅

1

λ

=

1

μ⋅1− ρ

E w=

E  k 

λ

=

ρ

μ⋅1− ρ

E v =

E s

λ

=

ρ
λ

=

1

μ

Analiza pracy systemu M/M/1 –

prawo ciągłości przepływu

A x=1−e

−

λ dt

∞

λ

μ

D x=?

d  x = ρ⋅b x1− ρ⋅a  x∗b x 

d  x = ρ⋅b x1− ρ⋅

∫

0

x

a τ b  x−τ dτ

d  x= ρ⋅μ e

−

μx



1− ρ⋅

∫

0

x

λ e

−

λτ

∗

μ e

−

μ x−τ 

dτ

d  x=λ e

−

λx

D  x=1−e

−

λx

=

A x

Sieci stanowisk M/M/1

Sieci otwarte
Sieci zamknięte

Sieci mieszane

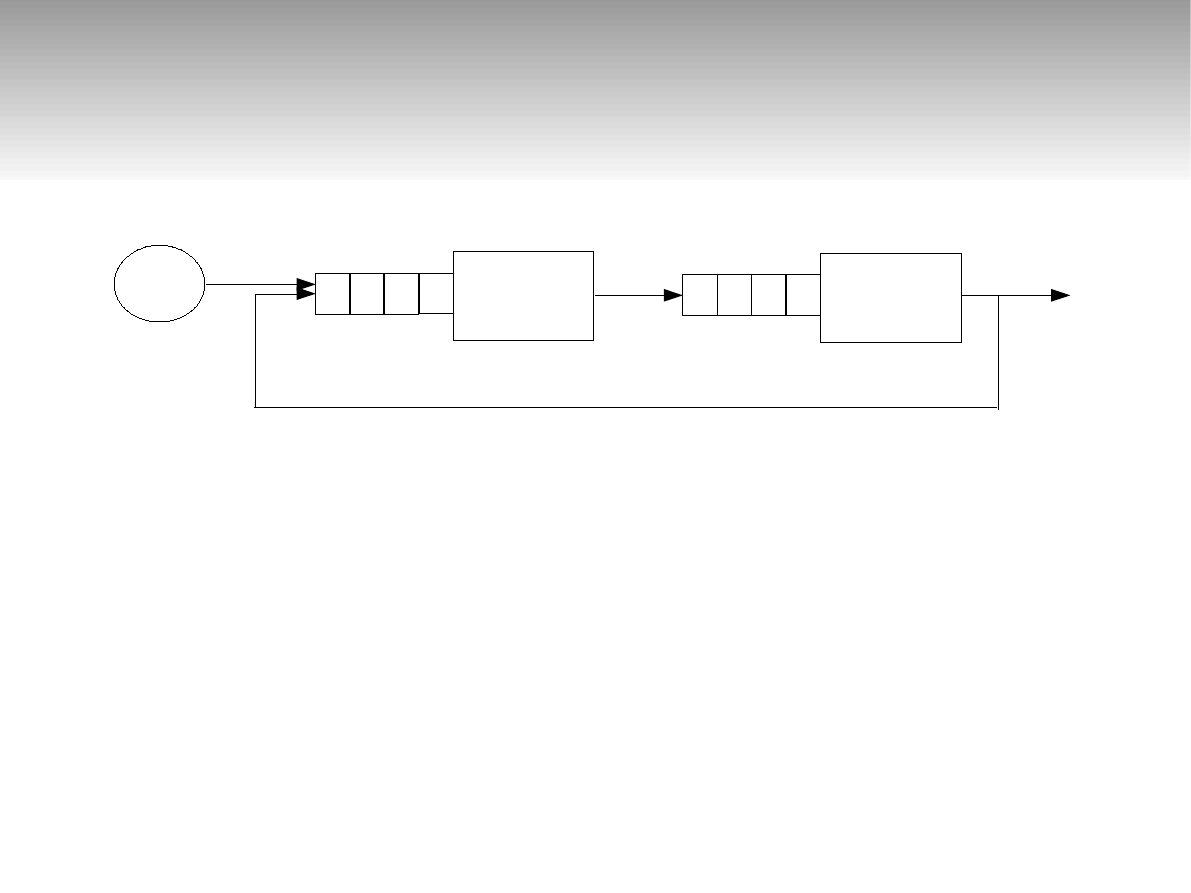
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

E(k

1

)=? E(k

2

)=? E(w)=?

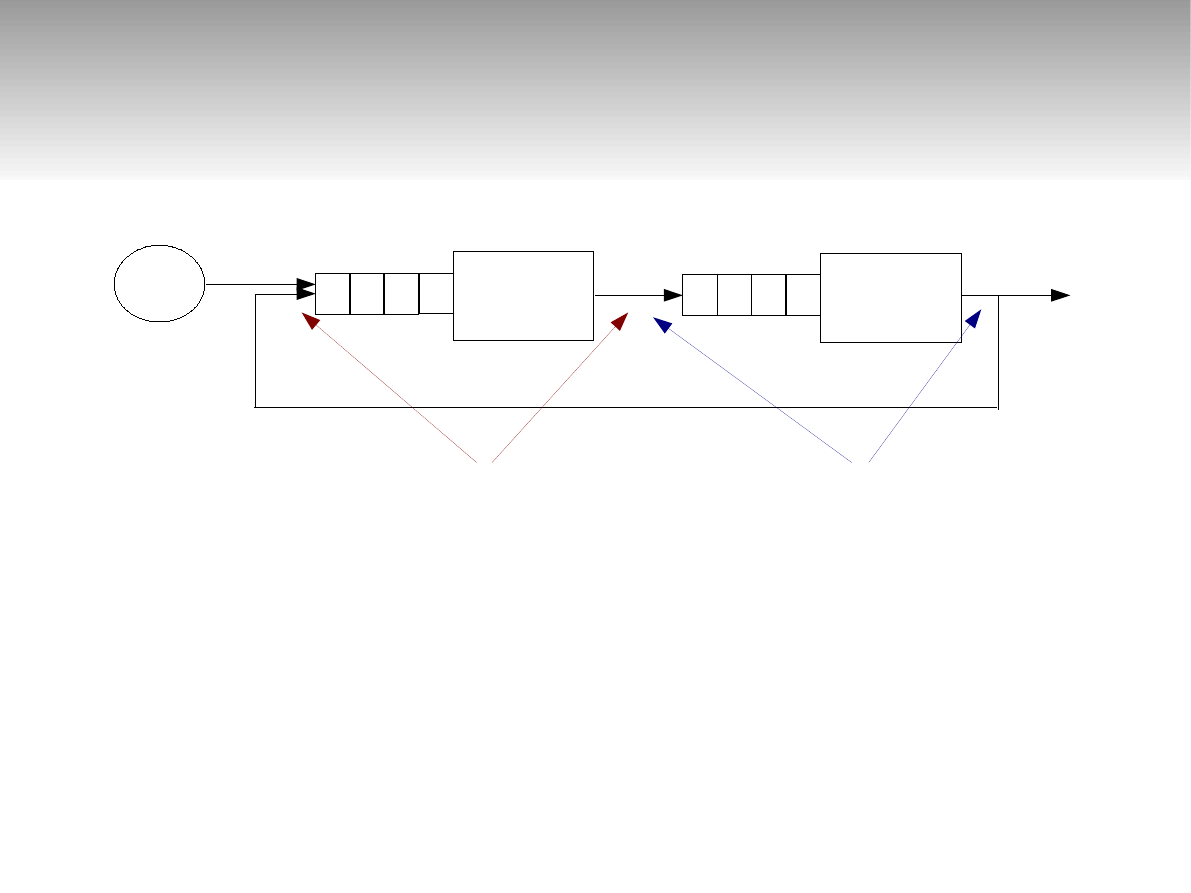
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

λ

1

λ

2

λ

1

=

λ

0



r

21

⋅

λ

2

λ

2

=

λ

1

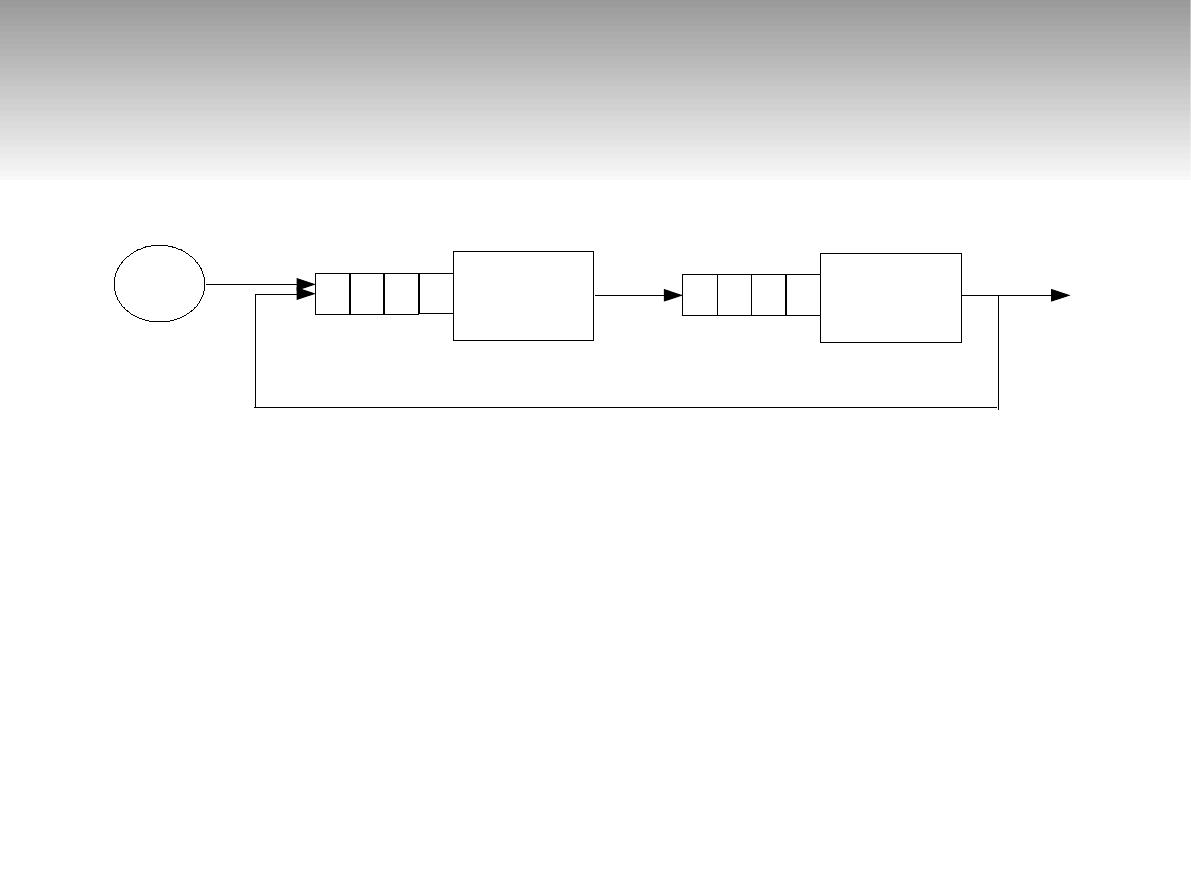
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

λ

1

=

λ

0



r

21

⋅

λ

1

λ

1

−

r

21

⋅

λ

1

=

λ

0

λ

1

−

0.5 λ

1

=

5

0.5 λ

1

=

5

λ

1

=

10

λ

2

=

λ

1

=

10

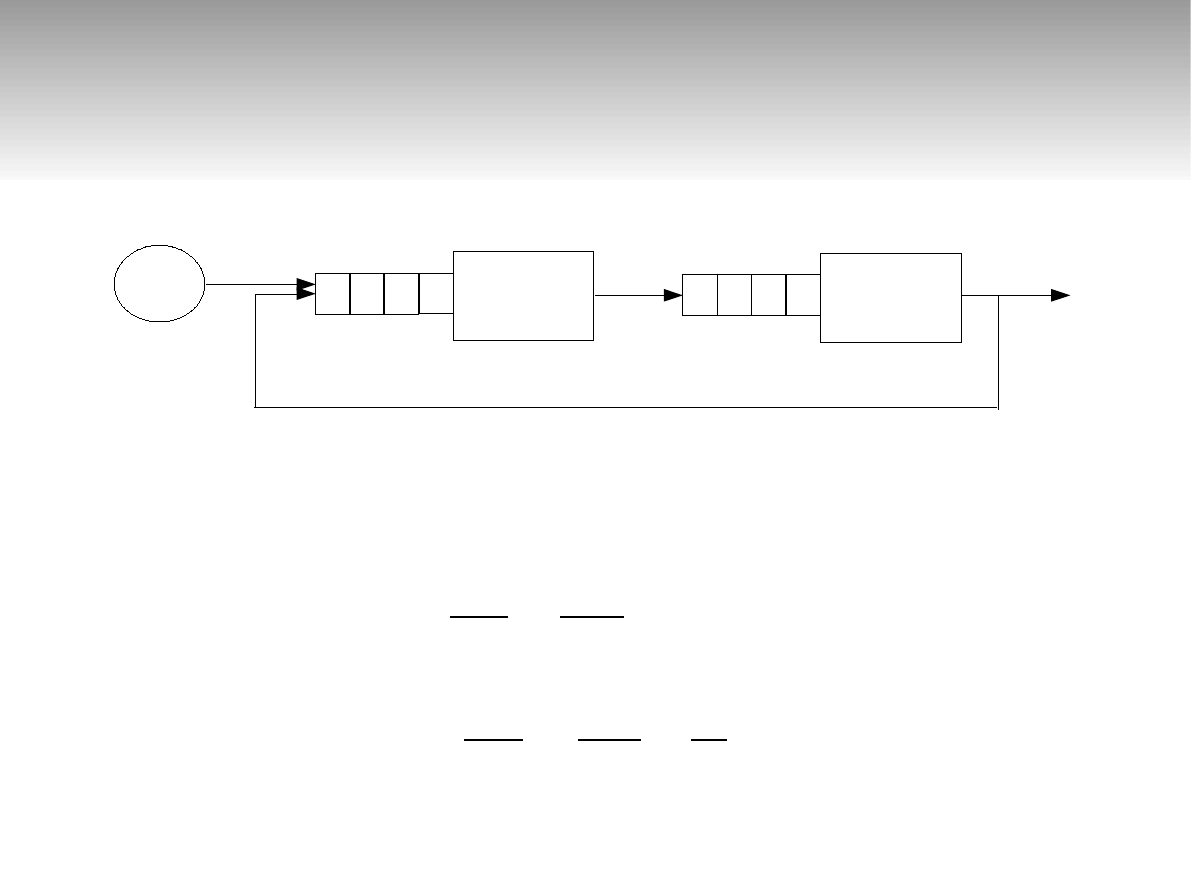
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

λ

2

=

λ

1

=

10

ρ

1

=

λ

1

μ

1

=

10
20

=

0,51

ρ

2

=

λ

2

μ

2

=

10

15

=

2
3



1

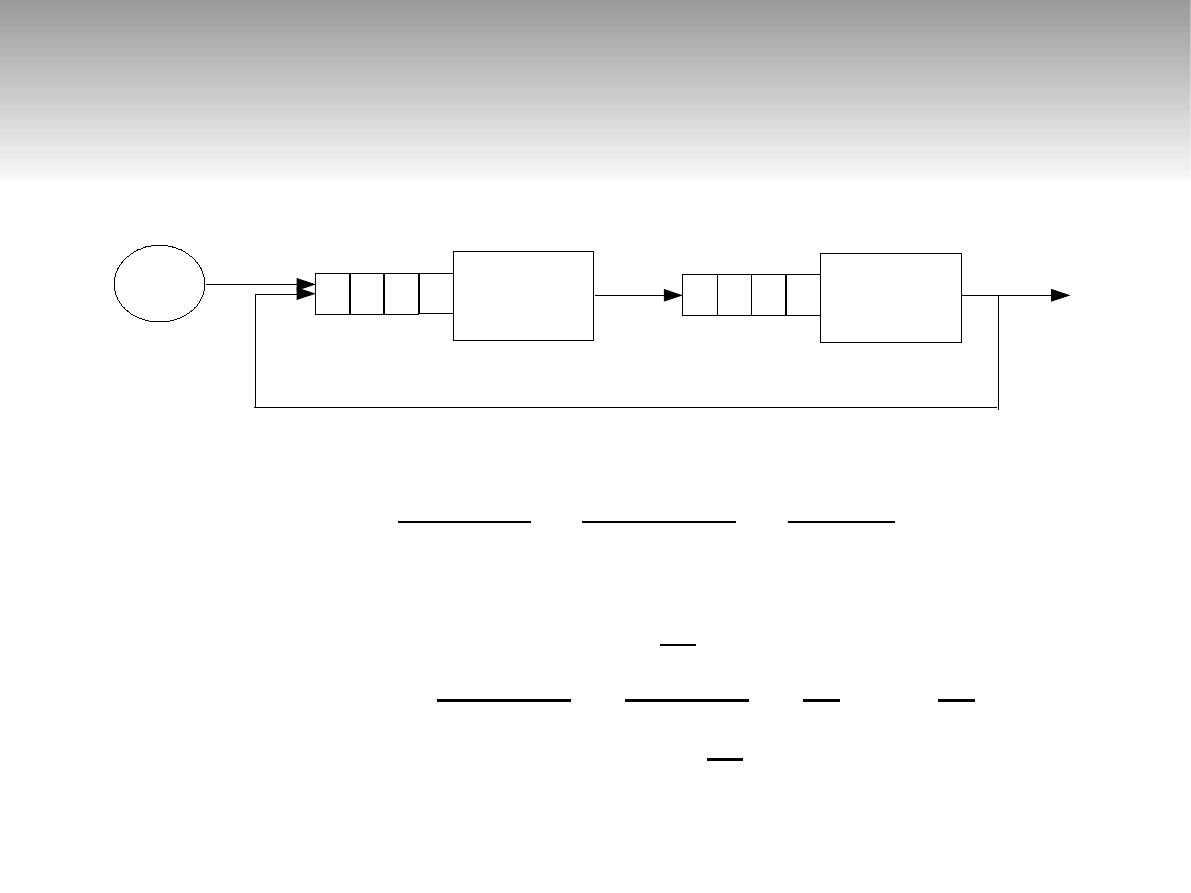
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

E  k

1

=

ρ

1

2

1− ρ

1

=

0,5

2

1−0,5

=

0,25

0,5

=

0,5

E  k

2

=

ρ

2

2

1− ρ

2

=

2
3

2

1−

2
3

=

4
9

⋅

3=

4
3

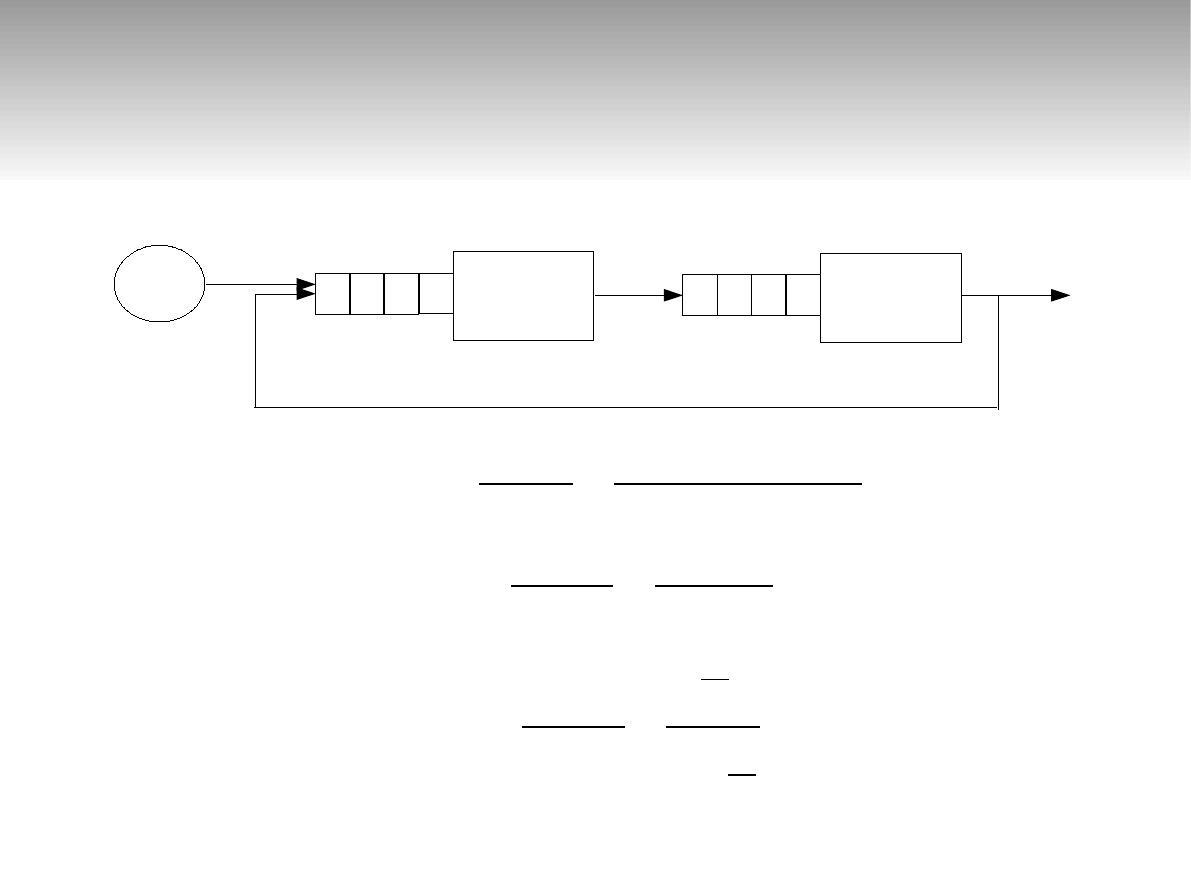
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

E  w=

E n

λ

0

=

E n

1



E  n

2



λ

0

E n

1

=

ρ

1

1− ρ

1

=

0,5

1−0,5

=

1

E  n

2

=

ρ

2

1− ρ

2

=

2
3

1−

2

3

=

2

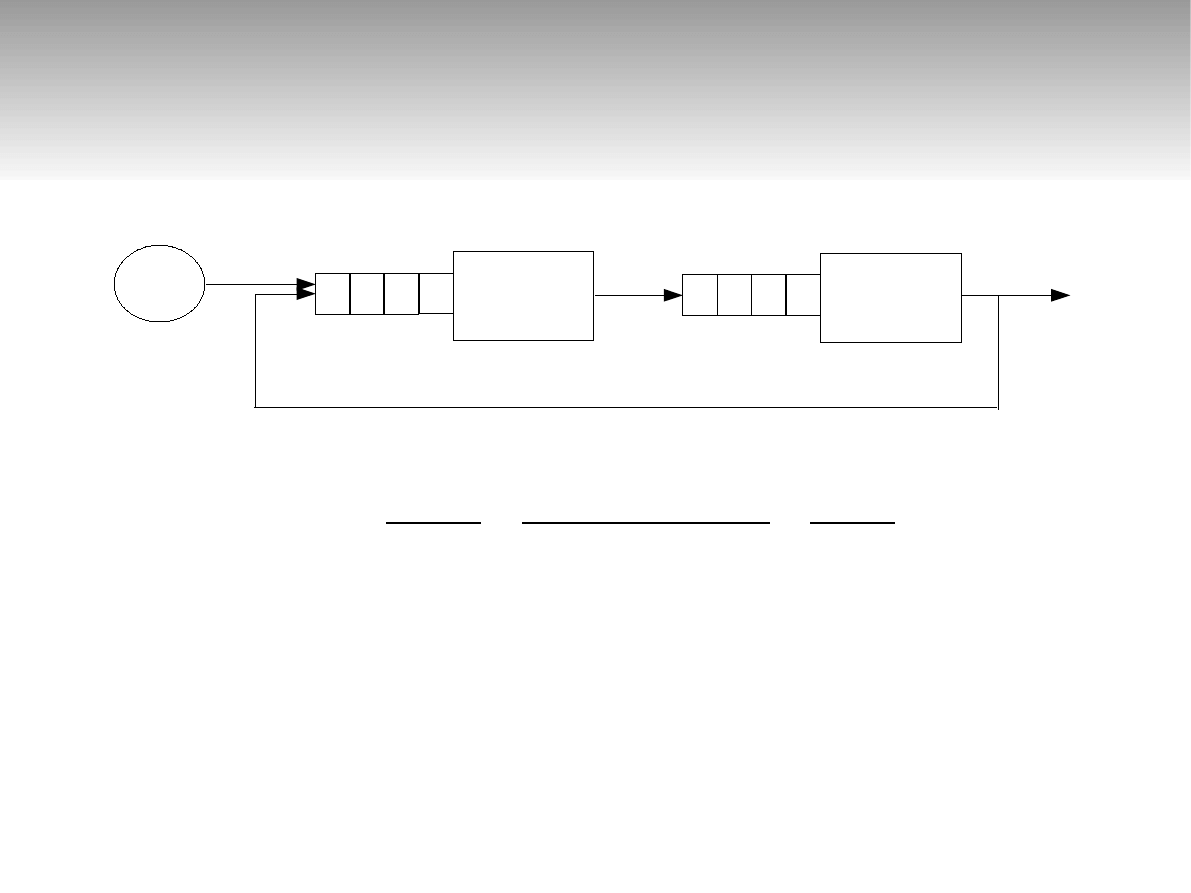
Sieci otwarte

∞

λ

0

=5

μ

1

=20

μ

2

=15

r

21

=0,5

E  w=

E n

λ

0

=

E n

1



E  n

2



λ

0

=

12

5

=

0,6

Sieci zamknięte

μ

1

=2

μ

2

=3

N=2

E(k

1

)=?

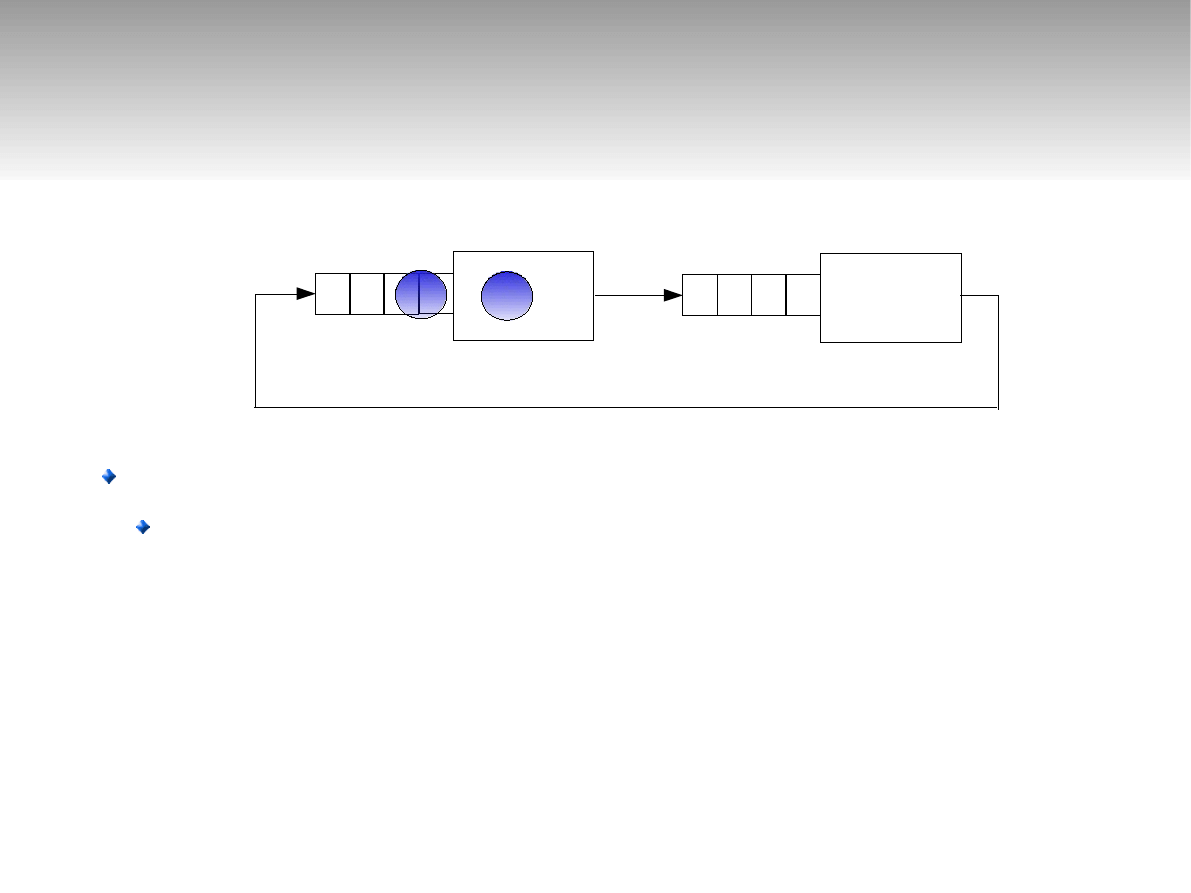
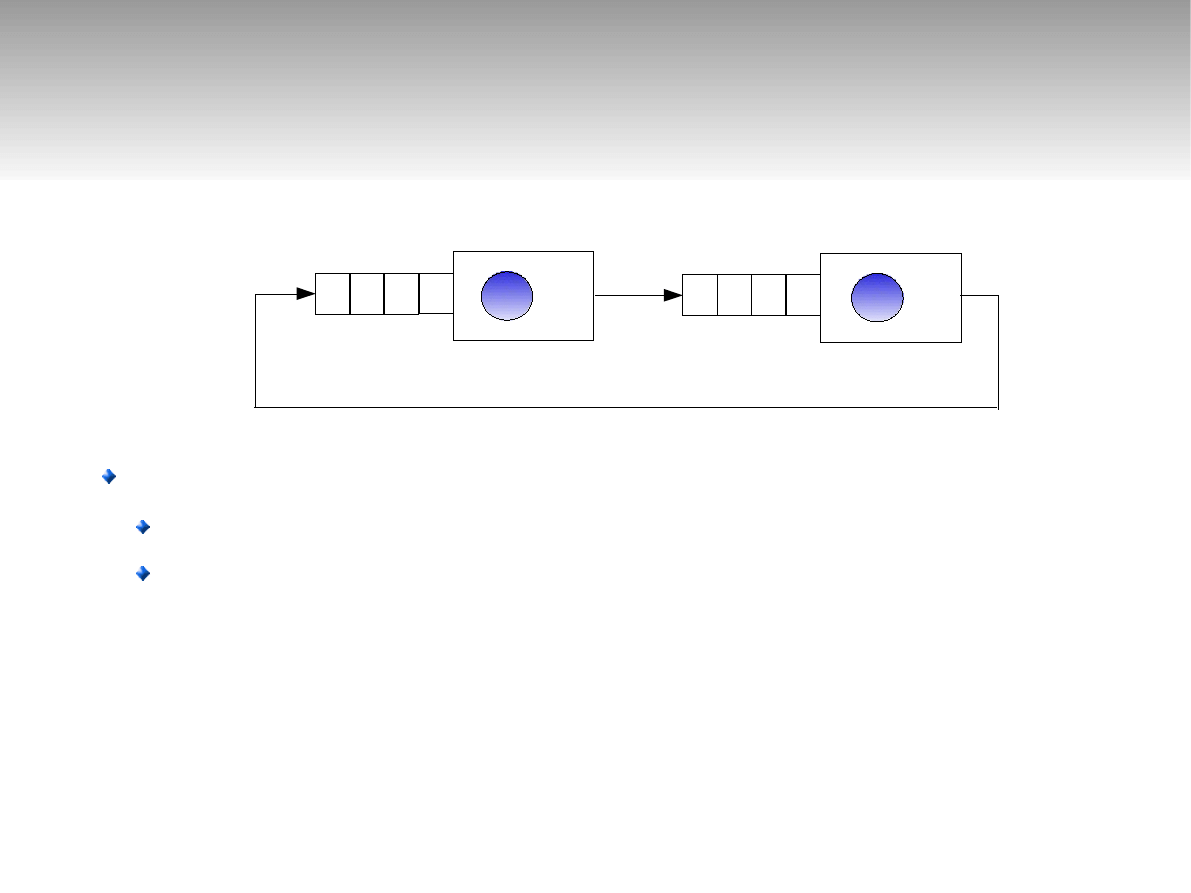
Sieci zamknięte

μ

1

=2

μ

2

=3

N=2

3 stany pracy

2 0

Sieci zamknięte

μ

1

=2

μ

2

=3

N=2

3 stany pracy

2 0

1 1

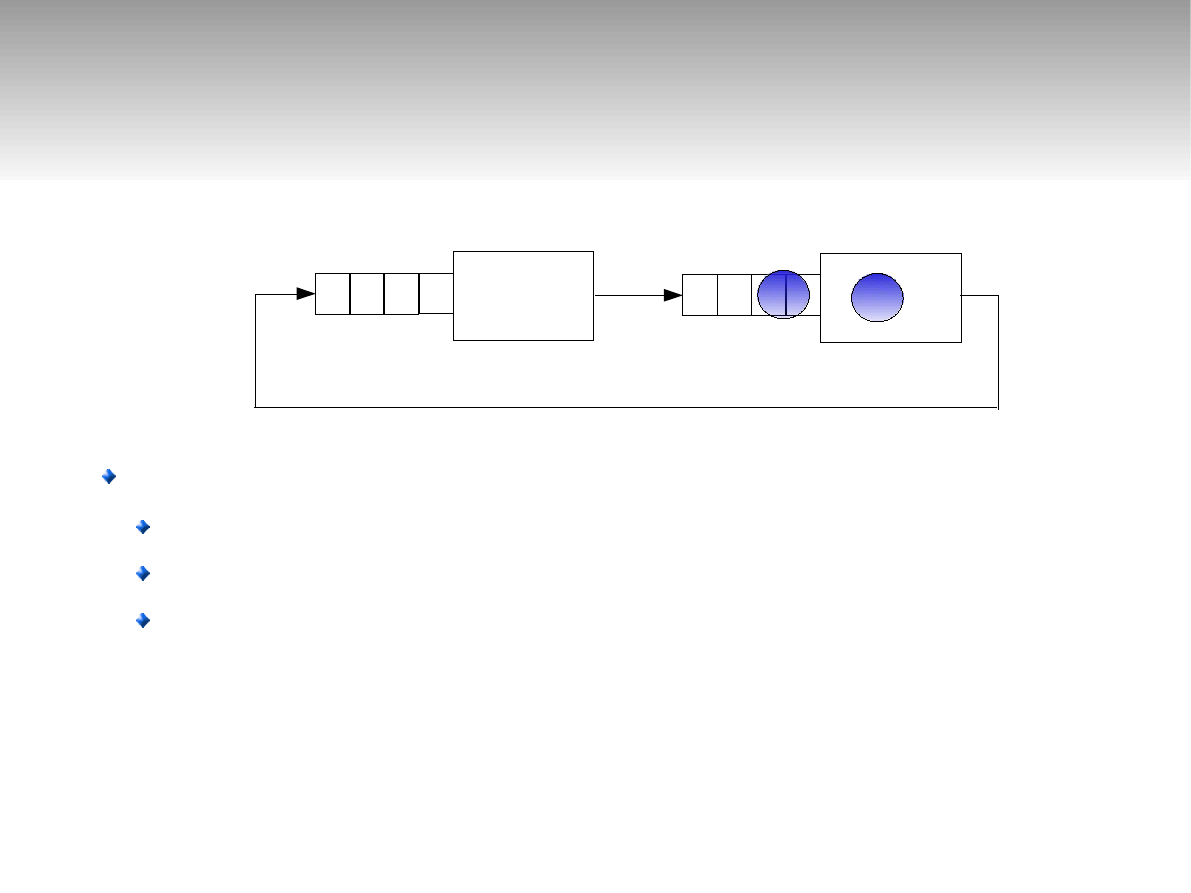
Sieci zamknięte

μ

1

=2

μ

2

=3

N=2

3 stany pracy

2 0

1 1

0 2

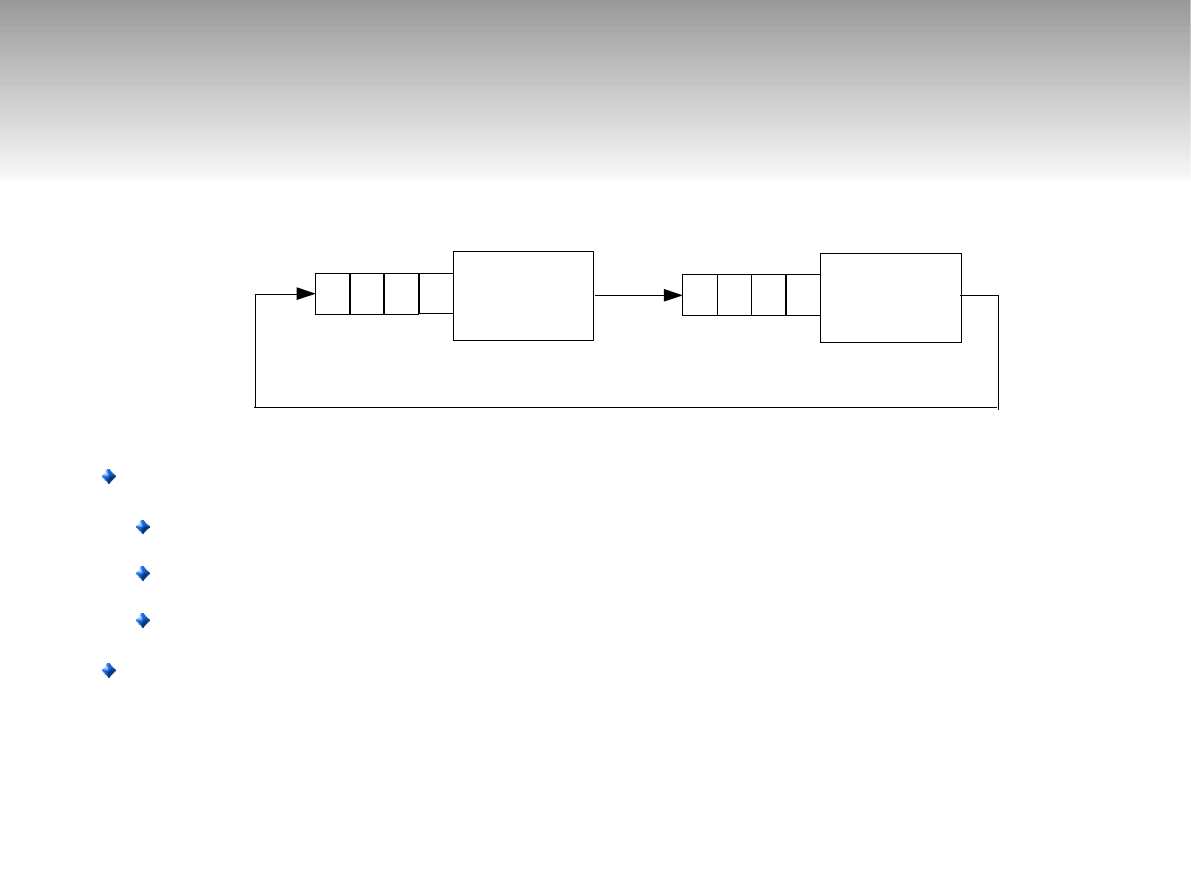
Sieci zamknięte

μ

1

=2

μ

2

=3

N=2

3 stany pracy

2 0

1 1

0 2

Oblicz prawdopodobieństwa każdego stanu

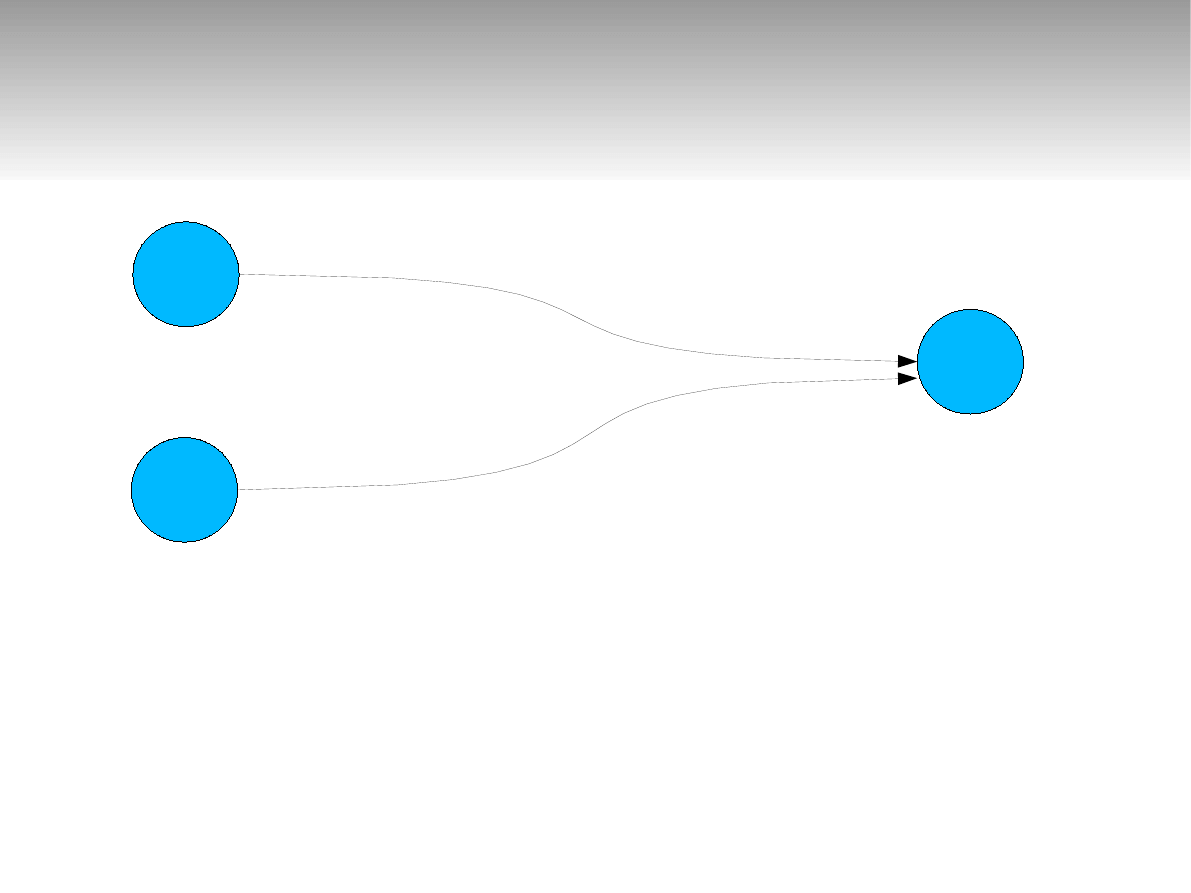
Sieci zamknięte

P

20

(t+dt)

P

20

(t)

P

11

(t)

1-μ

1

dt

(1-μ

1

dt)μ

2

dt

P

20



tdt =P

20



t⋅1− μ

1

dtP

11



t⋅1−μ

1

dt⋅μ

2

dt

Sieci zamknięte

P

20



tdt = P

20



t ⋅1−μ

1

dt P

11



t ⋅1− μ

1

dt ⋅μ

2

dt

P

20



tdt =P

20



t−P

20



t⋅μ

1

dtP

11



t⋅μ

2

dt−P

11



t⋅μ

1

μ

2

dt

2

P

20



tdt −P

20



t=−P

20



t⋅μ

1

dtP

11



t⋅μ

2

dt−P

11



t⋅μ

1

μ

2

dt

2

P

20



tdt −P

20



t

dt

=−

P

20



t  μ

1



P

11



t μ

2

−

P

11



t  μ

1

μ

2

dt

lim

dt 0

P

20



tdt −P

20



t

dt

=−

P

20



t  μ

1



P

11



t μ

2

˙

P

20



t=−P

20



t μ

1



P

11



t  μ

2

0=−P

20

μ

1



P

11

μ

2

P

20

μ

1

=

P

11

μ

2

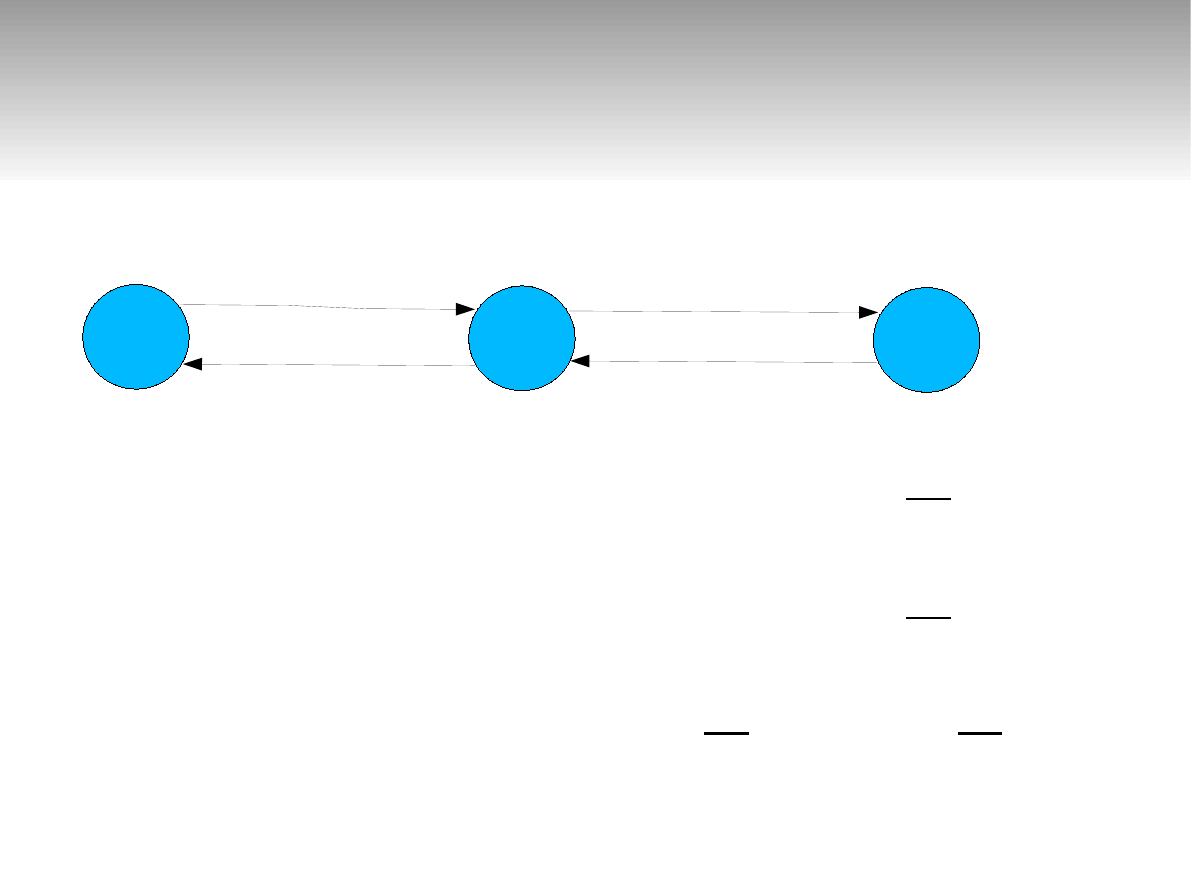
Sieci zamknięte

P

20

μ

1

P

20

μ

1

=

P

11

μ

2

P

02

μ

2

=

P

11

μ

1

P

20



P

11



P

02

=

1

P

11

P

02

μ

1

μ

2

μ

2

P

20

=

P

11

⋅

μ

2

μ

1

P

02

=

P

11

⋅

μ

1

μ

2

P

11

⋅

μ

2

μ

1



P

11



P

11

⋅

μ

1

μ

2

=

1

Sieci zamknięte

P

11

⋅

μ

2

μ

1



P

11



P

11

⋅

μ

1

μ

2

=

1

P

11

⋅

3

2



P

11



P

11

⋅

2
3

=

1

9 P

11



6 P

11



4 P

11

=

6

19 P

11

=

6

P

11

=

6

19

P

20

=

P

11

⋅

μ

2

μ

1

=

6

19

⋅

3
2

=

9

19

P

02

=

P

11

⋅

μ

1

μ

2

=

6

19

⋅

2
3

=

4

19

Sieci zamknięte

P

11

=

6

19

P

20

=

P

11

⋅

μ

2

μ

1

=

6

19

⋅

3
2

=

9

19

P

02

=

P

11

⋅

μ

1

μ

2

=

6

19

⋅

2
3

=

4

19

E k

1

=

1⋅P

20

=

9

19

Systemy sterowane przepływem

argumentów (Data Flow)

Wykład z Podstaw Informatyki

Definicja algorytmu

Uporządkowany zbiór operacji, których wy-
konanie prowadzi do rozwiązania dowolnego
zadania z pewnej klasy zadań
Pojedyncza operacja: Y = O( A, X )
Przykłady:

y = a + b

y = NWD( a, b )

Y = pierwiastki wielomianu W(x)

Y = liczby pierwsze mniejsze niż a

Układ sprzętowy realizujący algorytmy –
maszyna von Neumanna

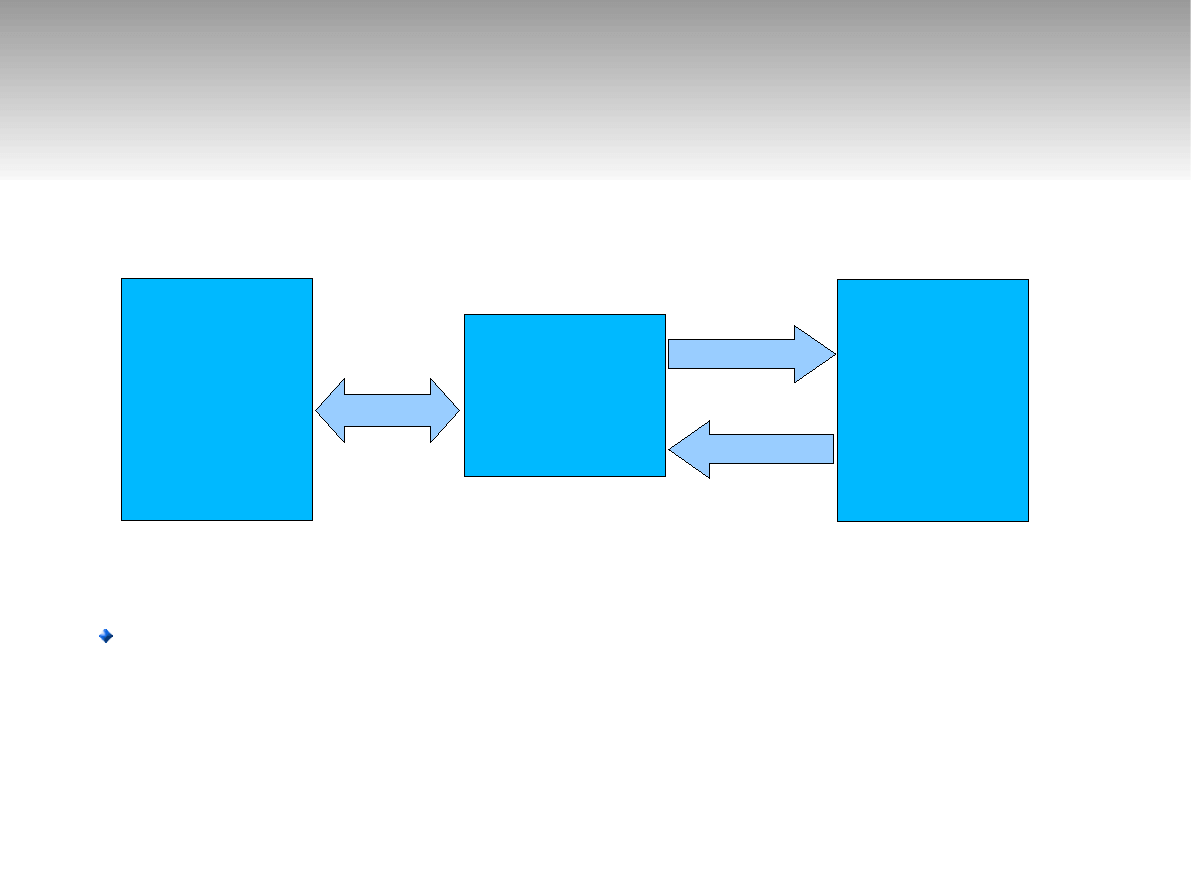
Maszyna von Neumanna

O wyborze rozkazu do wykonania decyduje
zawartość licznika rozkazów

Rozkazy

JAL

Dane

Definicja algorytmu

Uporządkowany zbiór operacji, których wy-
konanie prowadzi do rozwiązania dowolnego
zadania z pewnej klasy zadań
Kolejność wykonywania rozkazów nie jest
narzucona przez treść algorytmu
Rozkaz wykonywany, gdy tylko są wszystkie
potrzebne argumenty

Przykład

Zależności między operacjami i argumentami

A1

A2

A3

O1
O2
O3
O4

X
X

X

X

X

X

Operacje O1, O2, O3 i O4 należy wykonać kolejno

na odpowiednich argumentach

Argumenty A1, A2, A3 należy dostarczyć opera-

cjom aby umożliwić ich wykonanie

Kanoniczna postać algorytmu

Y = O( A, X )

Przykład

y1 = O1( a1 )
y2 = O2( a2, y1 )
y3 = O3( a3, y1 )

y4 = O4( y1, y2, y3 )

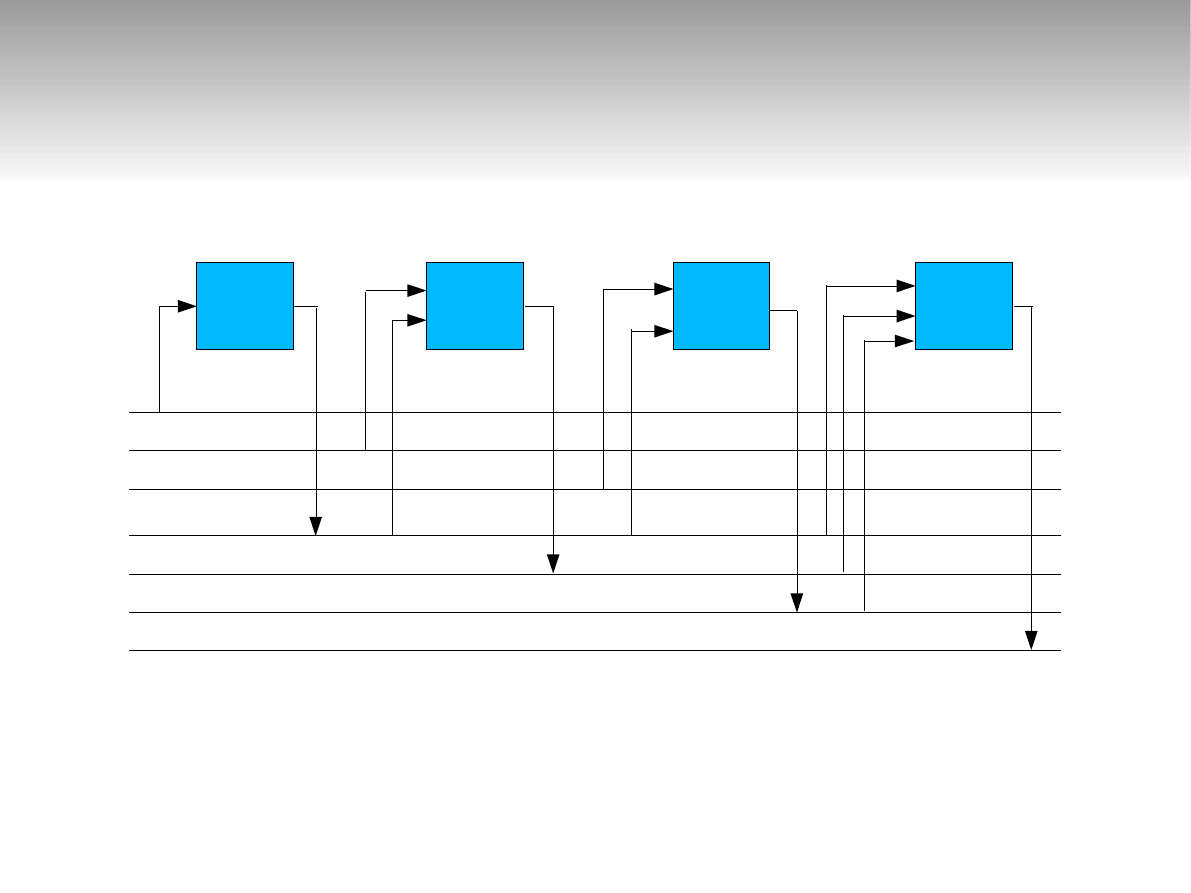
Realizacja algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

O1

O2

O3

O4

a1

a2

a3
y1

y2

y3

y4

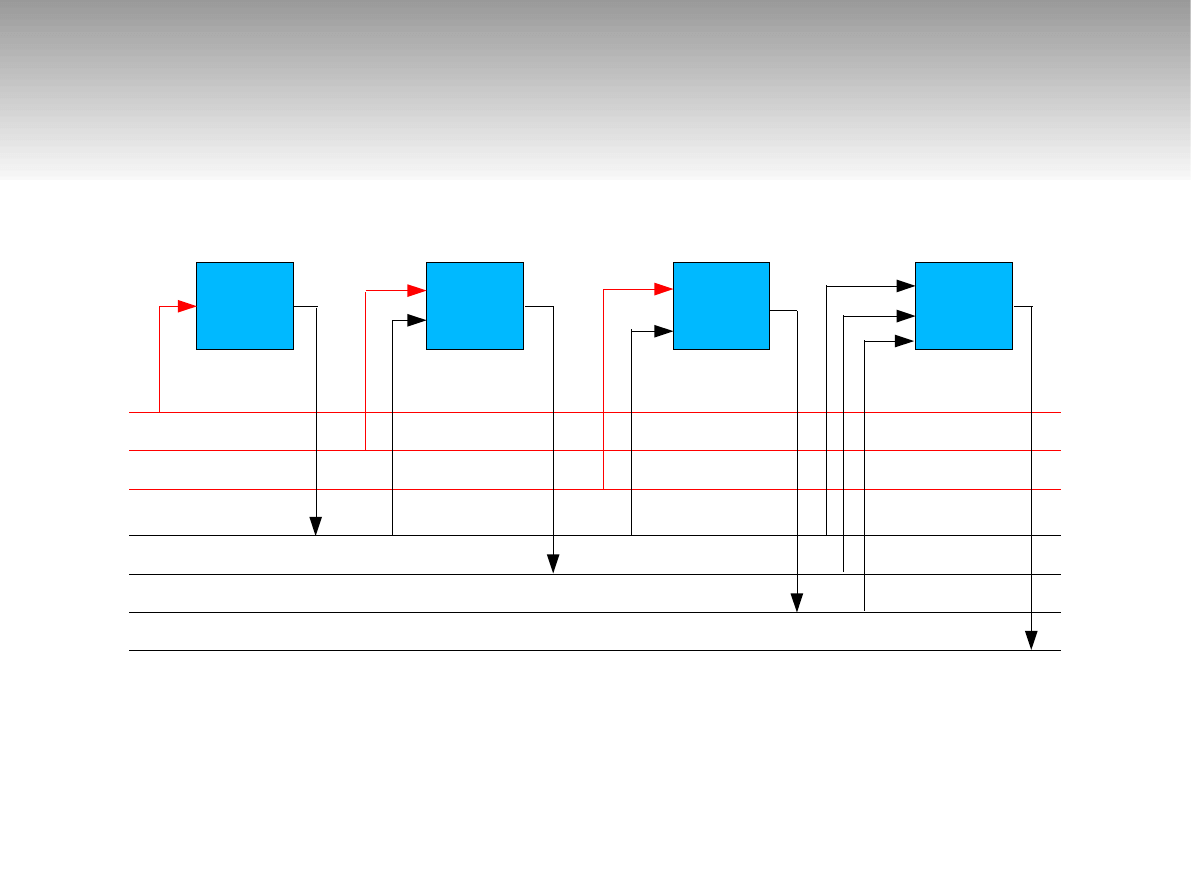
Realizacja algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

O1

O2

O3

O4

a1

a2

a3

y1

y2

y3

y4

Realizacja algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

O1

O2

O3

O4

a1

a2

a3
y1

y2

y3

y4

Realizacja algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

O1

O2

O3

O4

a1

a2

a3
y1

y2

y3

y4

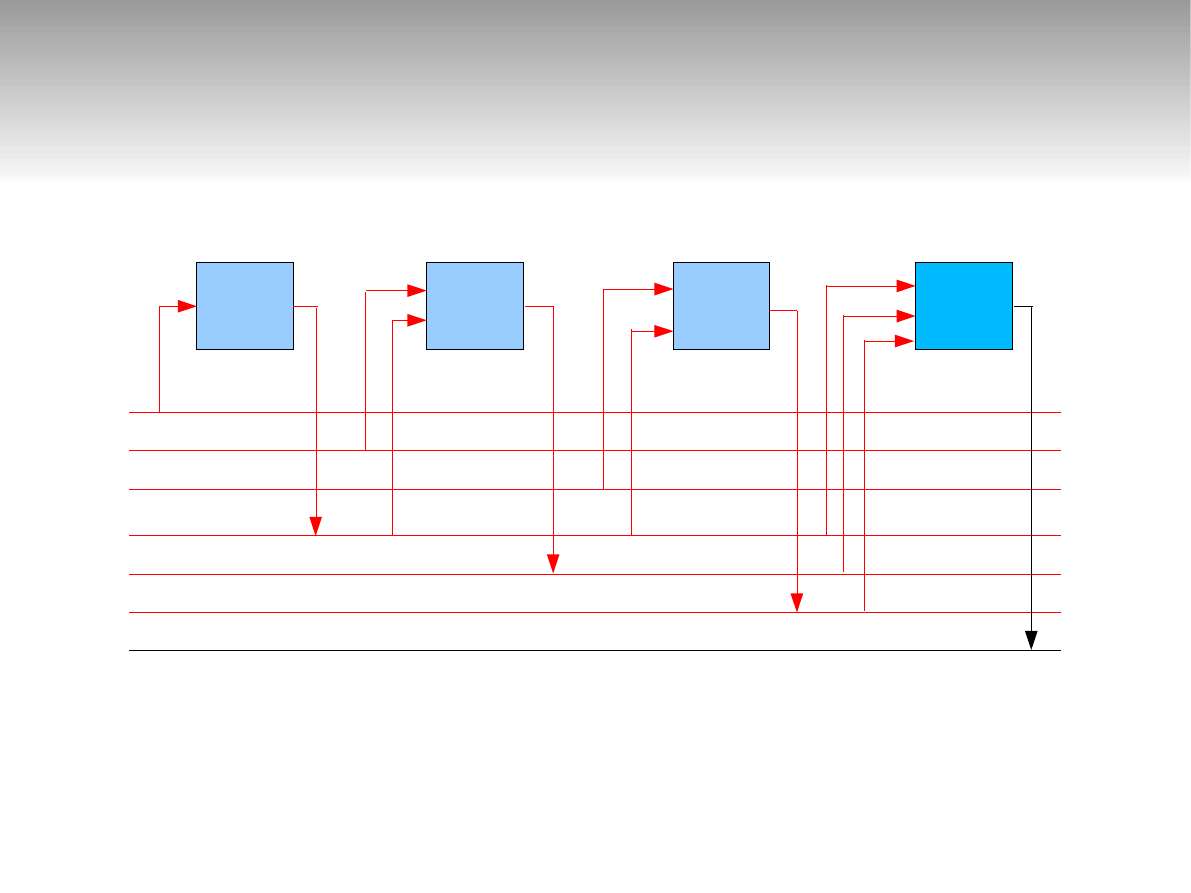
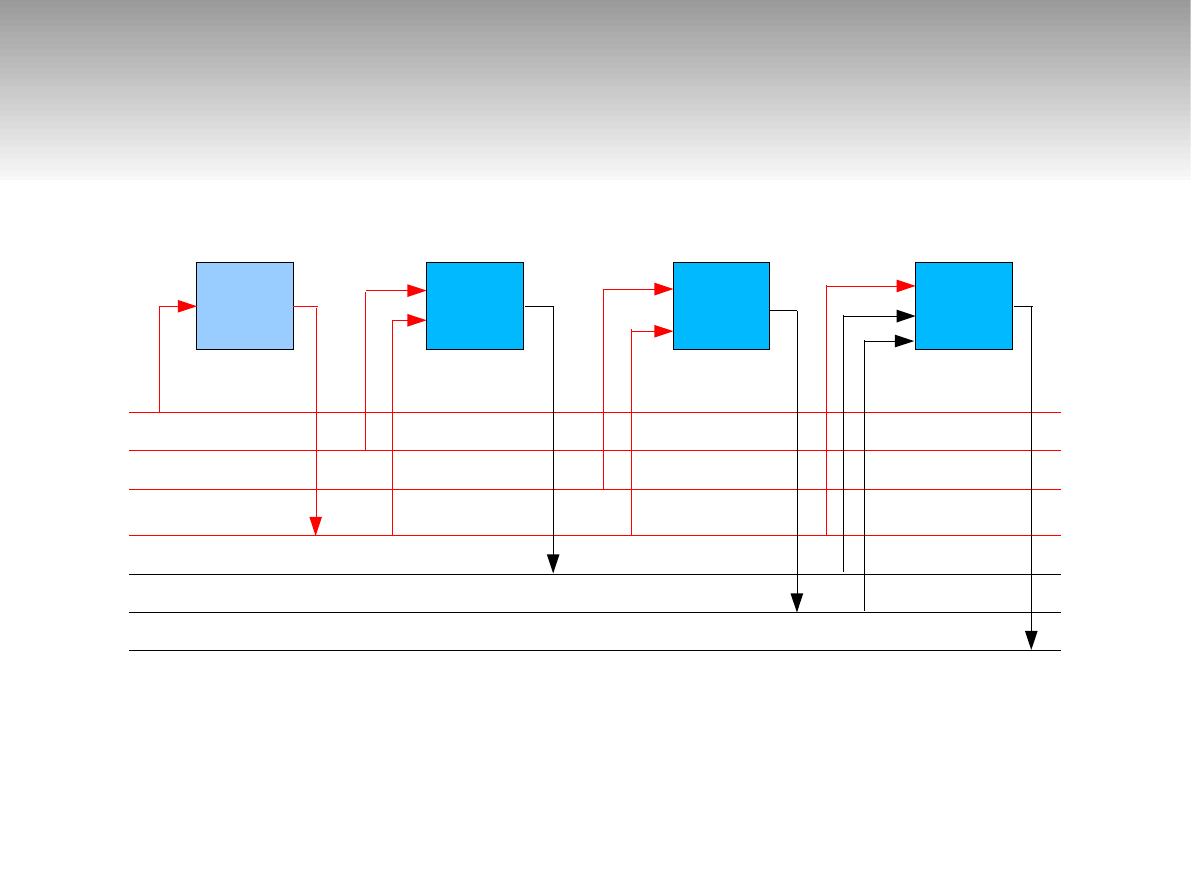
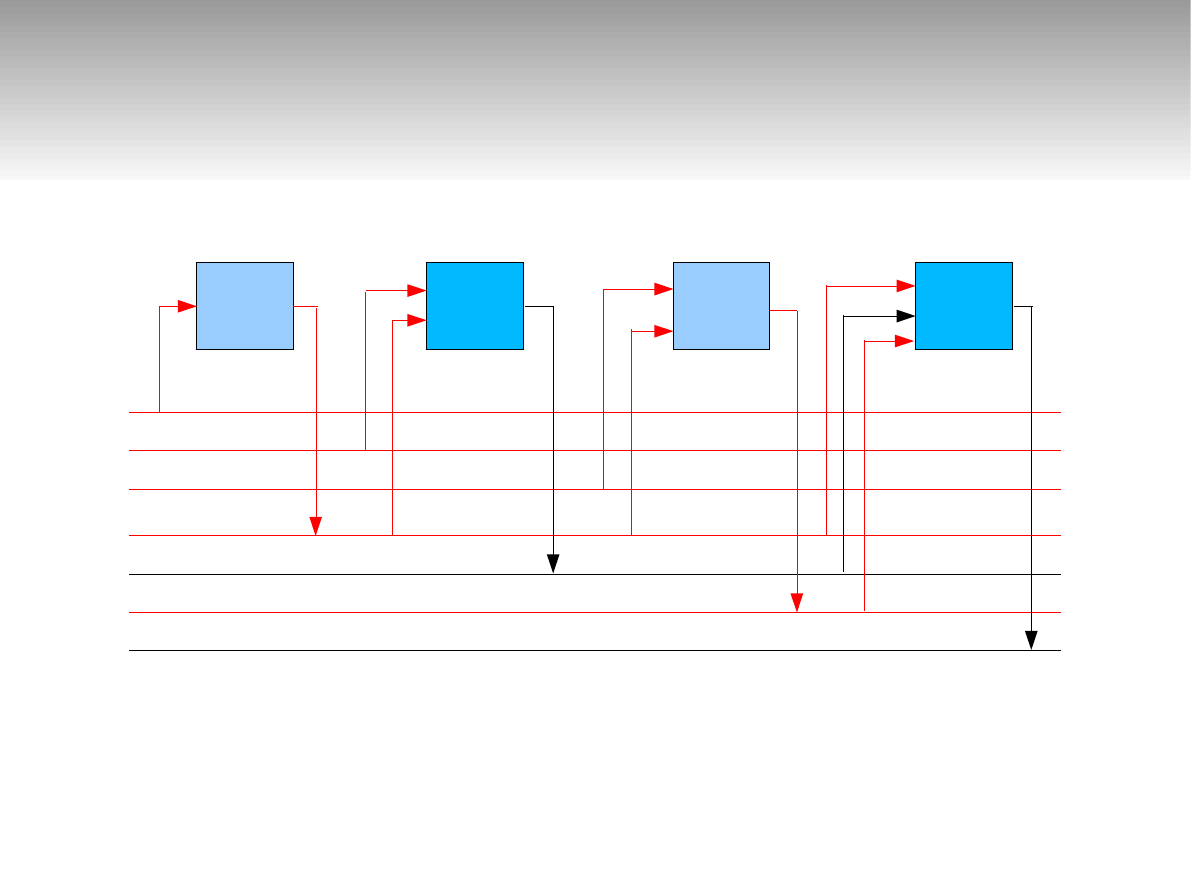
Realizacja algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

O1

O2

O3

O4

a1

a2

a3
y1

y2

y3

y4

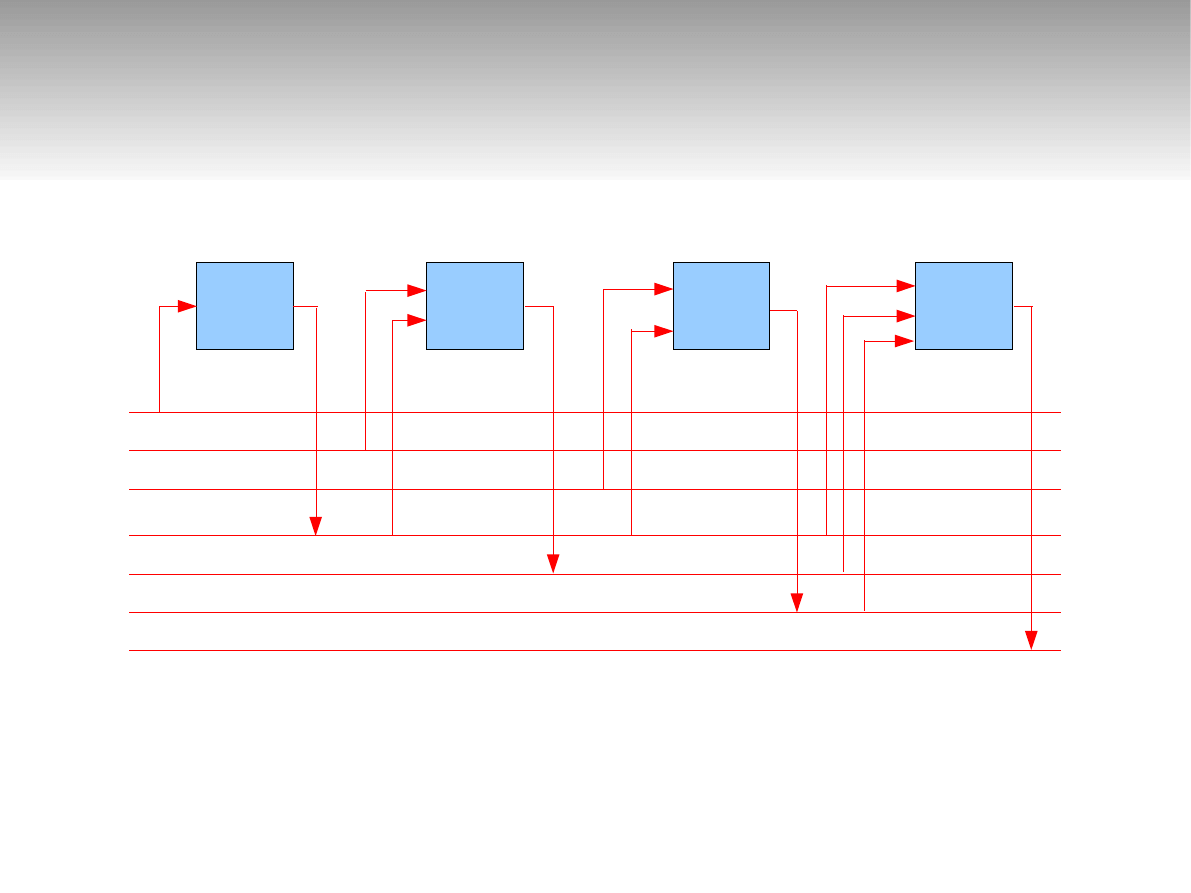
Realizacja algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

O1

O2

O3

O4

a1

a2

a3
y1

y2

y3

y4

Macierz zmiennych postaci kano-

nicznej algorytmu

y1 = O1( a1 )
y2 = O2( a2, y1 )

y3 = O3( a3, y1 )
y4 = O4( y1, y2, y3 )

y1

y2

y3

y4

y1

0

1

1

1

y2

0

0

0

1

y3

0

0

0

1

y4

0

0

0

0

Macierz zmiennych postaci kano-

nicznej algorytmu

y1

y2

y3

y4

y1

0

1

1

1

y2

0

0

0

1

y3

0

0

0

1

y4

0

0

0

0

Warunek wystarczający przepływu

laminarnego

y1

y2

y3

y4

y1

0

1

1

1

y2

0

0

0

1

y3

0

0

0

1

y4

0

0

0

0

Warunek konieczny i wystarczający

przepływu laminarnego

Macierz całkowicie zredukowana macierzą o
zerowej przekątnej
Funkcja redukująca: f

R

(A)=A

∙A+A

Redukcję przeprowadzić lg

2

n razy

Przykład

∣

0 1
1 0

∣

⋅

∣

0 1
1 0

∣



∣

0 1
1 0

∣

=

∣

1 0
0 1

∣



∣

0 1
1 0

∣

=

∣

1 1
1 1

∣

Koniec wykładów z PI

Dziękuję za uwagę

Egzamin

●

Przeprowadzony w semestrze letnim

●

2 niezależne części: pisemna i ustna

●

Każdą część można zdawać 3-krotnie (3
próby)

●

Obie części muszą być zaliczone

●

Ocena z danej części równa średniej arytme-
tycznej wszystkich prób

●

Wyjątek, gdy ostatnia próba zakończona co
najmniej oceną 4 – wtedy ocena ostatniej
próby jest oceną danej części

Egzamin - c.d.

●

Końcowa ocena z egzaminu – średnią oby-
dwu części

●

Ocena końcowa (k) z przedmiotu – średnią
ważoną ocen z zaliczeń ćwiczeń tablicowych
(t), laboratorium (l), pisemnej części egzami-
nu (p) i ustnej części egzaminu (u) według
wzoru:

k = 0,15 t + 0,15 l + 0,35 p + 0,35 u

Zwolnienia z egzaminu

●

Zwolnienie z całości egzaminu z oceną 5 -
zaliczenie ćwiczeń tablicowych w obydwu
semestrach (i laboratorium) na ocenę 5

●

Zwolnienie z części pisemnej – średnia
arytmetyczna zaliczeń ćwiczeń tablicowych
w obydwu semestrach co najmniej 4,5

●

Dodatkowy warunek – uzyskanie zaliczeń
w terminie przed datą rozpoczęcia sesji eg-
zaminacyjnej

Terminy egzaminów

●

Pisemne

●

Piątek 13 czerwca, godz. 15.00, sale A, B, C

●

Piątek 27 czerwca, godz. 14.00, sale A, B, C

●

26 września, godz. 8.30, sale A, B

●

Ustne – bez 2 ostatnich pytań z listy

●

Egzaminatorzy

●

dr inż. Alina Momot

●

dr inż. Małgorzata Bach

●

mgr inż. Ewa Płuciennik

●

dr inż. Robert Brzeski

●

dr inż. Paweł Kasprowski

●

mgr inż. Aleksander Chrószcz

●

mgr inż. Robert Tutajewicz

Na egzamin zabrać co najmniej 5 kartek

Konsultacje w sesji

●

Wtorek 10 czerwca 17.00 – 18.00

●

Wtorek 17 czerwca 17.00 – 19.00

●

Czwartek 19 czerwca 17.00 – 19.00

●

Wtorek 24 czerwca 17.00 – 18.00

●

Środa 25 czerwca 17.00 – 19.00

●

Czwartek 26 czerwca 10.00 – 11.00

●

Poniedziałek 30 czerwca 17.00 – 18.00

●

Dodatkowo egzamin ustny:

●

Czwartek 12 czerwca 19.00

I to już rzeczywiście koniec

Życzę udanej sesji