Z. Kąkol-Notatki do Wykładu z Fizyki

7-1

Wykład 7

7.

Praca i energia

7.1

Wstęp

Podstawowym zagadnieniem dynamiki jest określenie ruchu punktu, jeżeli znana

jest siła działająca na ten punkt. W pierwszym kroku wyznaczamy przyspieszenie

a = F/m

Gdy m i F stałe to a też jest stałe i wtedy możemy prosto obliczyć prędkość

v

=

v

0

+ at

i położenie

x =

v

0

t + at

2

/2

Zagadnienie jest bardziej złożone gdy F nie jest stała. Trzeba posługiwać się bardziej
skomplikowaną matematyką (całkowanie). Mamy często do czynienia z takimi siłami
np. siła grawitacji między dwoma ciałami zależy od ich odległości, siła wywierana przez
rozciągniętą sprężynę zależy od stopnia rozciągnięcia.
Postępowanie pozwalające określić ruch punktu prowadzi nas do pojęcia pracy, energii
i twierdzenia o pracy i energii. Zagadnienia związane z energią są tak istotne (szeroko
rozumiana ekonomia, ekologia, zasoby energii itd.), że ich znajomość jest konieczna dla
wszelkich rozważań zarówno ekonomicznych, technologicznych jak i społecznych. Pro-
blemy energii (jej różne formy ich konwersja itd.) będą odtąd przewijać się stale przez
wykłady. Z energią związana jest najważniejsza chyba zasada całej fizyki -

zasada za-

chowania energii

. Nakłada ona sztywne granice na przetwarzanie energii i jej wykorzy-

stanie. Będzie ona centralnym tematem większości działów fizyki omawianych na wy-
kładach. W mechanice zasada zachowania energii pozwala obliczać w bardzo prosty
sposób ruch ciał bez konieczności korzystania z zasad dynamiki Newtona.

7.2

Praca wykonana przez stałą siłę

W najprostszym przypadku, siła F jest stała, a punkt porusza się w kierunku działa-

nia siły. Wtedy

W = F·s = Fs cos

α

(7.1)

(Iloczyn dwóch wektorów daje liczbę).
Zastanówmy się czy kąt

α

może być różny od zera? Odpowiedź jest twierdząca bo stała

siła nie musi mieć kierunku zgodnego z kierunkiem ruchu punktu materialnego. Oczy-
wiście muszą działać jeszcze inne siły (ciężar, tarcie). Gdyby działała tylko jedna to
i tak ciało nie musiałoby poruszać się w kierunku jej działania np. rzut ukośny (tylko
grawitacja).
Wzór Fs cos

α

określa jedynie pracę wykonaną przy przemieszczaniu punktu przez jed-

ną siłę. Pracę wykonaną przez inne należy obliczyć oddzielnie i potem je zsumować.

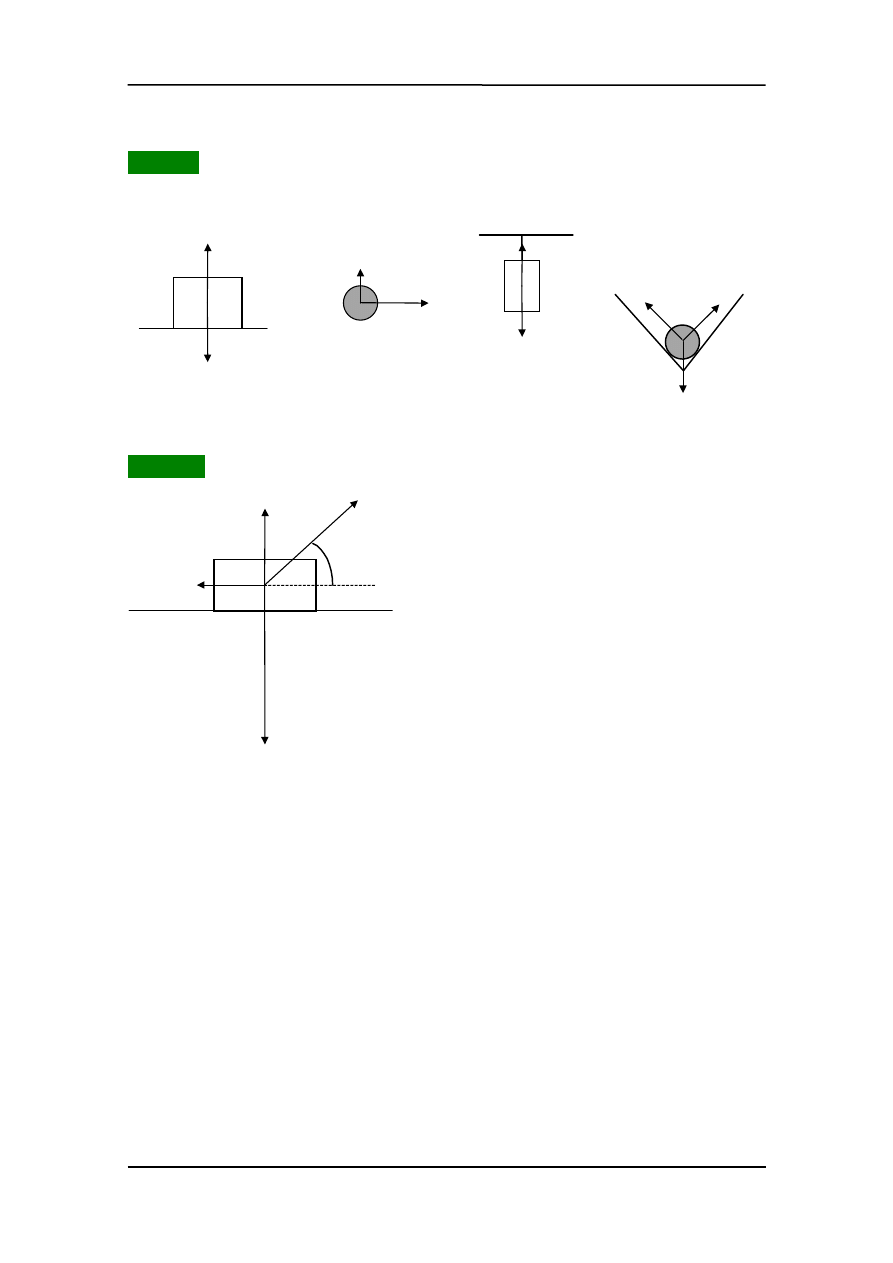
Z. Kąkol-Notatki do Wykładu z Fizyki

7-2

Zwróćmy uwagę, że gdy

α

= 0 otrzymujemy pierwszy wzór Fs. Gdy

α

= 90

°

to z rów-

nania wynika, że W = 0.

Przykłady

(a) i (b) W = 0 bo

α

= 90

°

, (c) i (d) bo przesunięcie s = 0.

Jednostką pracy jest w układzie SI dżul (J), 1J = 1N·1m.

Często używa się jednostki elektronowolt 1eV = 1.6·10

-19

J.

Przykład 2

Sanki o masie 5 kg są ciągnięte ze stałą pręd-
kością po poziomej powierzchni. Jaka praca
zostanie wykonana na drodze s = 9 m, jeśli
współczynnik tarcia kinetycznego wynosi 0.2,
a sznurek, za który ciągniemy tworzy kąt 45

°

z poziomem?
Pracę obliczamy z zależności:

W = Fs cos

α

Aby obliczyć pracę musimy znaleźć F. Z wa-
runku stałej prędkości (w kierunku pozio-
mym)

Fcos

α

- T = 0

a dla kierunku pionowego

Fsin

α

+R - mg = 0

Nacisk na podłoże (równy reakcji podłoża) wynosi mg - Fsin

α

, więc siła tarcia wynosi

T =

µ

(mg - Fsin

α

)

Te równania pozwalają wyliczyć F (eliminując T).

F =

µ

mg/(cos

α

+

µ

sin

α

)

więc praca

W = Fs cos

α

=

µ

mgs cos

α

/(cos

α

+

µ

sin

α

)

Q

R

F

v=const

Q

N

Q

R

1

R

2

a)

b)

c)

d)

mg

F

T

R

α

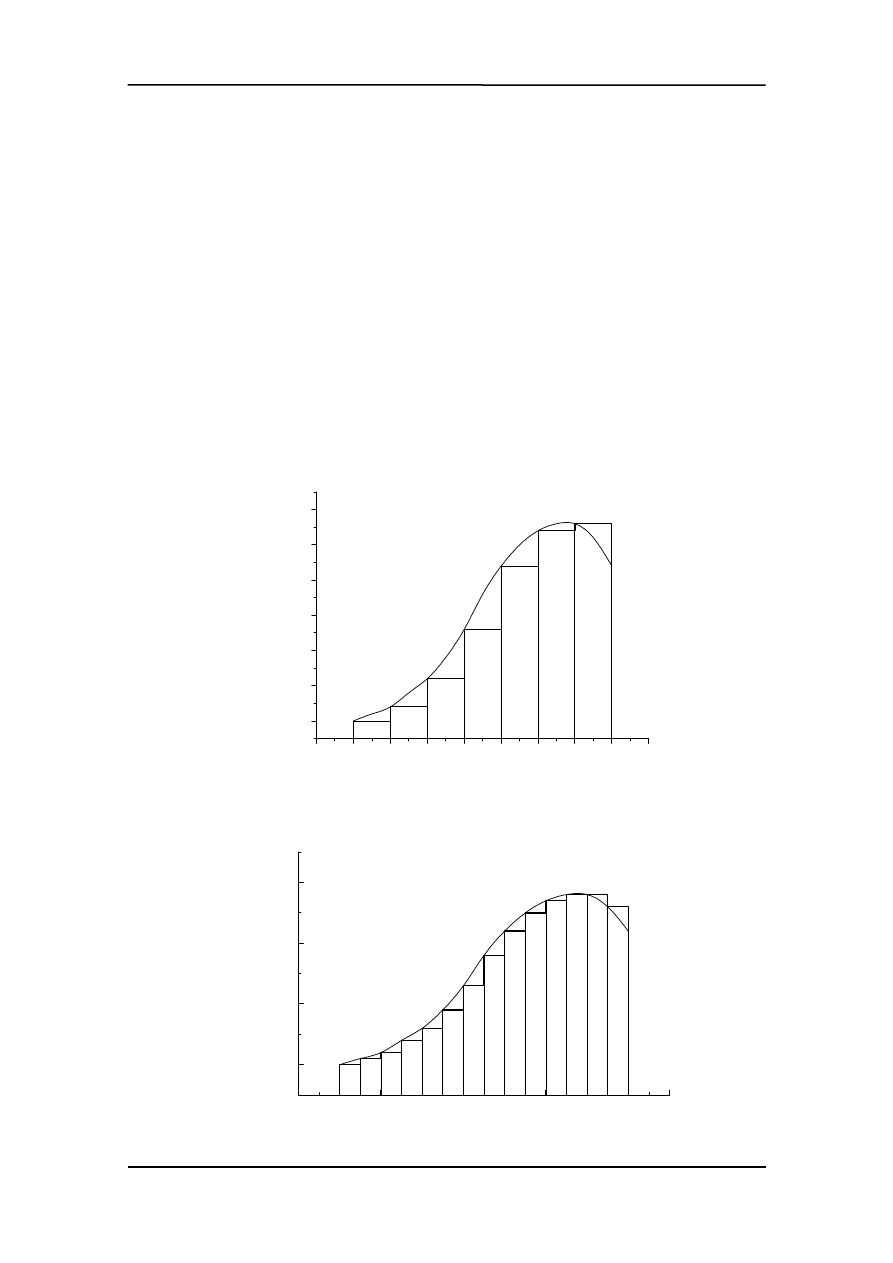
Z. Kąkol-Notatki do Wykładu z Fizyki

7-3

7.3

Praca wykonana przez siłę zmienną

Rozważmy teraz siłę będącą funkcją położenia F(x), której kierunek jest zgodny

z osią x. Szukamy pracy jaką wykona ta siła przy przesuwaniu ciała od położenia x

1

do

położenia x

2

. Jak skorzystać ze wzoru W = Fs cos

α

czyli co podstawić za F, skoro war-

tość jej zmienia się (rysunki poniżej)?
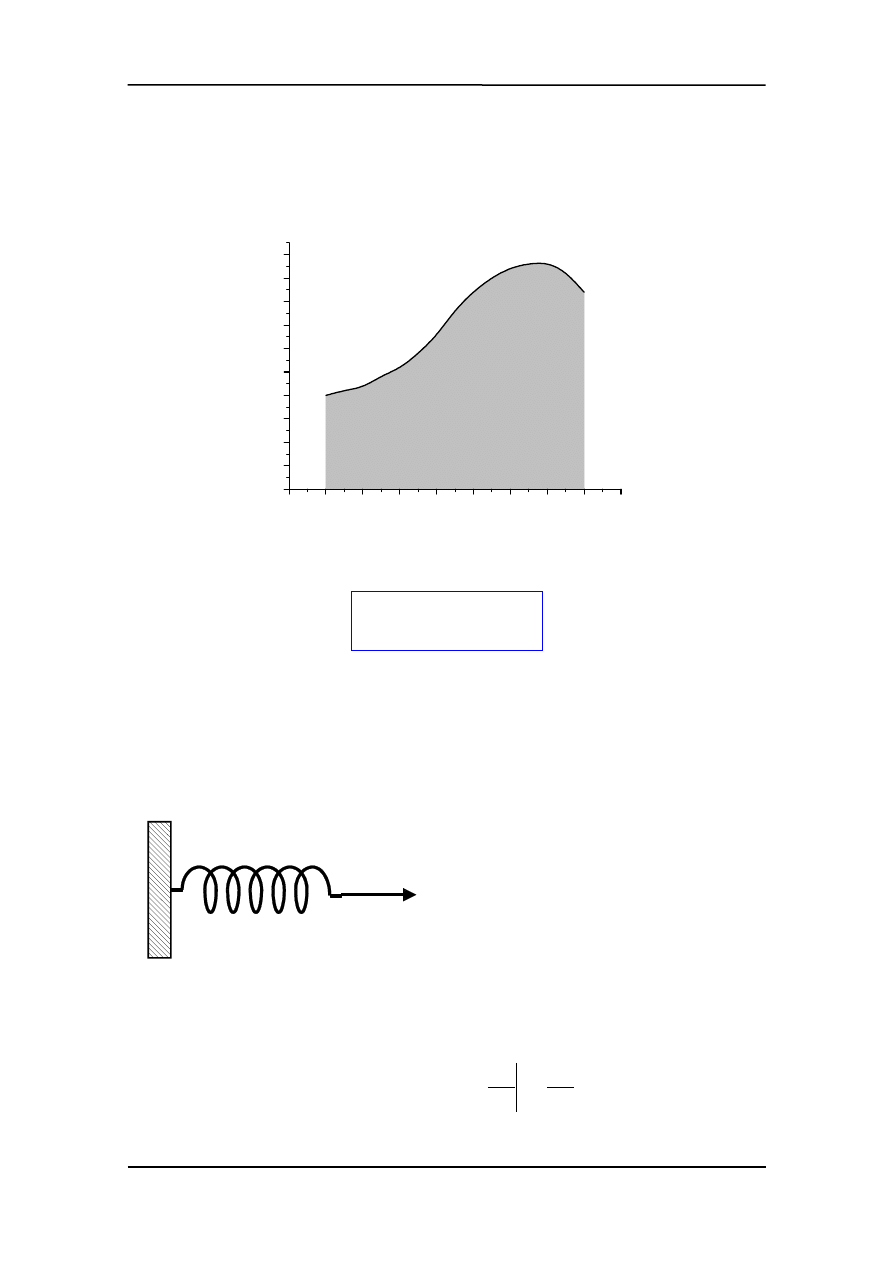
Zaczynamy od przybliżenia. Dzielimy całkowite przemieszczenie na n jednakowych od-
cinków

∆

x (rysunek poniżej). Wewnątrz takiego przedziału przyjmujemy (to jest to

przybliżenie), że siła jest stała (prawie) i możemy teraz policzyć pracę na tym odcinku

∆

x:

∆

W

i

= F

i

∆

x, gdzie F

i

jest wartością siły na tym odcinku. Zwróćmy uwagę, że od

strony czysto formalnej (geometria) liczenie pracy jest równoważne liczeniu sumy po-
wierzchni prostokątów o szerokości

∆

x i wysokości F

i

. Następnie możemy zsumować

prace na kolejnych odcinkach (zsumować pola prostokątów) i otrzymać pracę całkowitą.

∑

=

∆

=

n

i

i

x

F

W

1

ś

eby poprawić to przybliżenie dzielimy przedział (x

1

, x

2

) na więcej (mniejszych) od-

cinków

∆

x (patrz kolejny rysunek).

0

2

4

6

8

10

12

14

16

18

20

25

30

35

40

45

50

F

(

x)

X

0

2

4

6

8

10

12

14

16

18

20

30

40

50

F

(

x)

X

Z. Kąkol-Notatki do Wykładu z Fizyki

7-4

I teraz znowu powtarzamy procedurę sumowania. Przybliżenie jest lepsze bo siła ma

prawie stałą wartość wewnątrz "małych" przedziałów

∆

x (pola powierzchni prostokątów

bardziej pokrywają się z polem pod krzywą).

Widać, że rozwiązaniem problemu jest przejście (w granicy)

∆

x

→

0.

Stosujemy tę samą procedurę obliczając

∑

∫

=

∆

=

→

∆

2

1

2

1

d

lim

0

x

x

x

x

x

x

F

x

F

W

(7.2)

To jest definicja całki. Liczbowo odpowiada to liczeniu pola powierzchni pod krzywą
(w zadanym przedziale - granicach). Odpowiada to też z definicji liczeniu wartości
ś

redniej co zgadza się z intuicyjnym podejściem: W = F

ś

rednia

(x

2

– x

1

)

Trzeba więc albo umieć rozwiązać całkę (albo poszukać w tablicach) lub umieć obli-
czyć pole powierzchni pod krzywą co może być czasem łatwe.

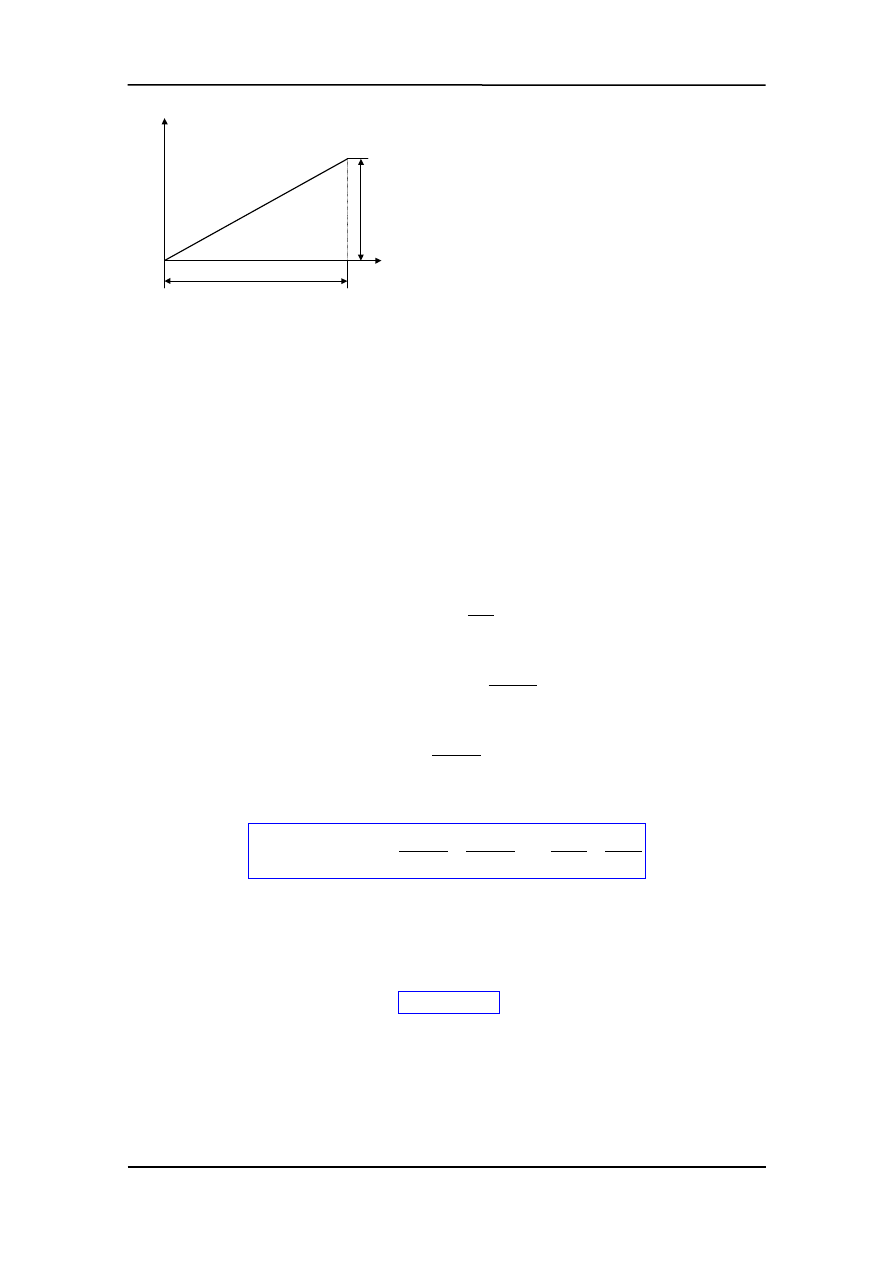
Np. rozważmy sprężynę zamocowaną
jednym końcem do ściany i rozciąganą
siłą F tak, że jej koniec przemieszcza się
o x. Siła wywierana przez sprężynę jest
siłą przywracającą równowagę i wynosi
F = -k x.
Aby rozciągnąć sprężynę musimy przy-
łożyć siłę równą co do wartości lecz
przeciwnie skierowaną. Tak więc F = k
x.

Teraz obliczmy pracę

∫

∫

=

=

=

=

x

x

x

kx

kx

x

kx

x

F

W

0

0

2

0

2

2

2

d

)

(

d

0

2

4

6

8

10

12

14

16

18

0

5

10

15

20

25

30

35

40

45

50

F

(

x)

X

F

Z. Kąkol-Notatki do Wykładu z Fizyki

7-5

Możemy też wprost obliczyć pole pod wykre-
sem F(x).

Pole powierzchni jest polem trójkąta i wynosi

P = (1/2) x·kx = (1/2) kx

2

i zgadza się z wynikiem uzyskanym z oblicze-
nia całki.
To był przypadek jednowymiarowy. Przypa-
dek 2 i 3-wymiarowy są w zasadzie swej roz-

patrywane podobnie ale matematycznie trudniejsze.

7.4

Energia kinetyczna i twierdzenie o pracy i energii

W przykładzie z sankami mieliśmy do czynienia z ruchem bez przyspieszenia.

Oznaczało to, że wypadkowa siła działająca na ciało wynosi zero. Teraz rozważmy
przypadek gdy ciało porusza się pod wpływem niezrównoważonej siły. Najprostszy
przypadek to stała siła czyli ruch ze stałym przyspieszeniem. Jaką pracę wykonuje ta siła
przy przemieszczeniu ciała na odległość x?
Zakładamy, że kierunek siły F i przyspieszenia a pokrywa się z kierunkiem osi x. Dla
stałego przyspieszenia mamy

2

2

0

at

t

x

+

=

v

oraz

t

a

at

0

0

v

v

v

v

−

=

⇒

+

=

co w połączeniu daje

t

x

2

0

v

v

+

=

Wykonana praca jest równa

2

2

2

2

0

2

0

0

v

v

v

v

v

v

m

m

t

t

m

x

ma

Fx

W

−

=













+













−

=

=

=

(7.3)

Połowę iloczynu masy ciała i kwadratu prędkości nazywamy

energią kinetyczną

.

Praca wykonana przez wypadkową siłę F działającą na punkt materialny jest równa
zmianie energii kinetycznej tego punktu

.

W = E

k

– E

k0

(7.4)

To jest twierdzenie o pracy i energii

.

Gdy nie ma zmiany wartości prędkości to nie ma zmiany energii kinetycznej tzn. nie jest
wykonywana praca (np. siła dośrodkowa). Z twierdzenia powyższego wynika, że jed-
nostki pracy i energii są takie same.

F(x)

x

F=kx

kx

x

Z. Kąkol-Notatki do Wykładu z Fizyki

7-6

7.5

Moc

Rozważmy czas w jakim wykonywana jest praca. Często interesuje nas

szybkość wy-

konania pracy

a nie jej wartość. To jest właśnie

moc

.

Moc średnia:

P

ś

rednia

= W/t

Moc chwilowa:

P = dW/dt

Oczywiście gdy moc jest stała w czasie to P

ś

rednia

= P.

Jednostką mocy jest wat. 1W = 1J/1s.
Dla celów praktycznych używa się kW (kilowatów) lub KM (koni mechanicznych przy
czym 1 KM

≈

(3/4) kW.