Project “The development of the didactic potential of Cracow University of Technology in the range of modern

construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

1

Exercise 4.2

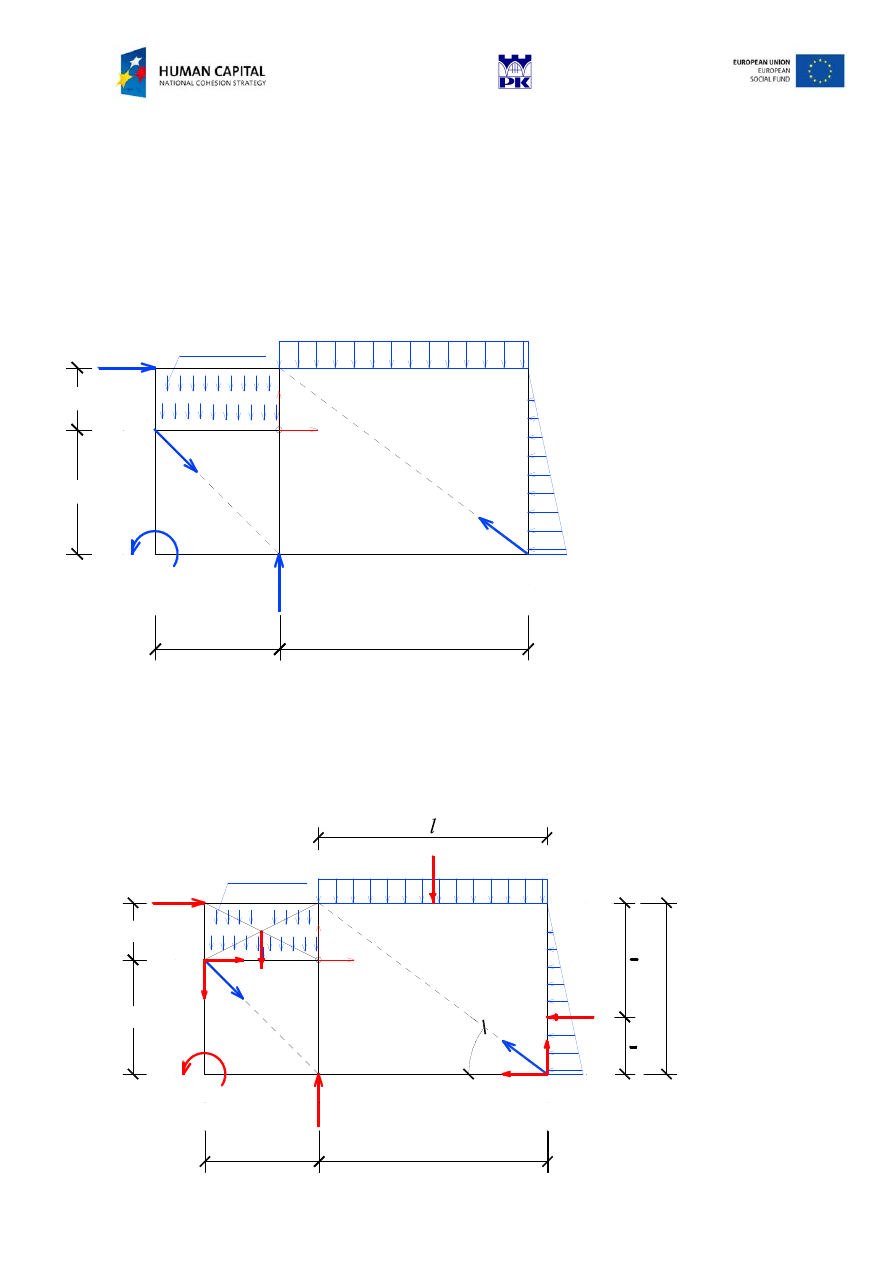
For a given planar force system find:

I

An equivalent coupe-force system at point A.

II.

The simplest equivalent force system. Draw the result of reduction on the figure.

q

1

=4 kN/m

17 kNm

q

2

=

2 kN/m

14 kN

10 kN

15 kN

3

2 kN

2m

4m

1m

2m

=3 kN/m2

A

x

y

The origin of the coordinate system is positioned at point A

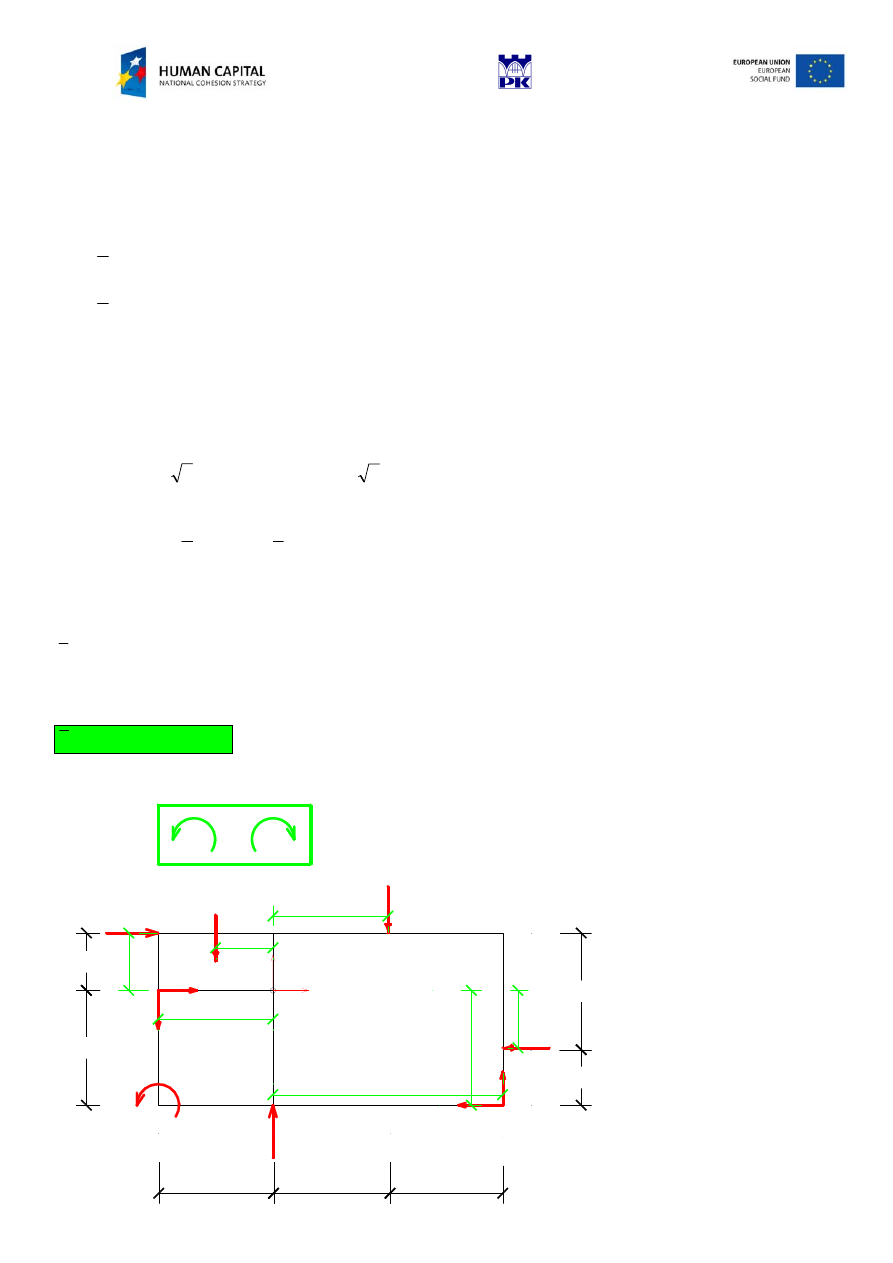
I. An equivalent couple-force system at point A

 Replacing the distributed loads by their resultants.

q

1

=4 kN/m

M

1

=17 kNm

q

2

=

2 kN/m

F

4

=14 kN

F

1

=10 kN

15 kN

3

2 kN

2m

4m

1m

2m

=3 kN/m2

A

x

y

F

6

F

5

W

1

W

2

2
3

*l

2

1
3

*l

2

W

3

F

2

F

3



1

l

2

construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

2

])

[

4

],

/

[

4

(

1

1

1

1

1

m

l

m

kN

q

l

q

W









]

[

16

]

[

4

]

/

[

4

1

kN

m

m

kN

W







])

3

[

],

/

[

2

(

2

1

2

2

2

2

2

m

l

m

kN

q

l

q

W









]

[

3

]

[

3

]

/

[

2

2

1

2

kN

m

m

kN

W









])

[

2

]

[

2

]

[

1

],

/

[

3

(

2

2

3

m

m

m

area

m

kN

area

W

















]

[

6

]

[

2

]

/

[

3

2

2

3

kN

m

m

kN

W







 Resolving the oblique forces into components

]

[

2

3

)

45

sin(

2

kN

F







,

]

[

2

3

)

45

cos(

3

kN

F







]

[

3

3

2

kN

F

F





Where:

5

4

)

cos(





,

5

3

)

sin(





(see the figure)

]

[

12

]

[

15

)

cos(

5

kN

kN

F









]

[

9

]

[

15

)

sin(

6

kN

kN

F









 Determining the sum vector

)

,

,

(

O

S

S

S

y

x



2

5

2

1

W

F

F

F

S

x









]

[

2 kN

S

x





3

1

6

4

3

W

W

F

F

F

S

y













]

[

2 kN

S

y





)

],

[

2

],

[

2

(

O

kN

kN

S







 Detrmining the total moment about point A

Project “The development of the didactic potential of Cracow University of Technology in the range of modern

M

1

F

4

F

1

2m

2m

1m

2m

A

x

y

F

6

F

5

W

1

W

2

W

3

F

2

F

3

r

F1

r

F3

r

F5

r

F6

r

W3

r

W1

2m

r

W2

+

-

1m

2m

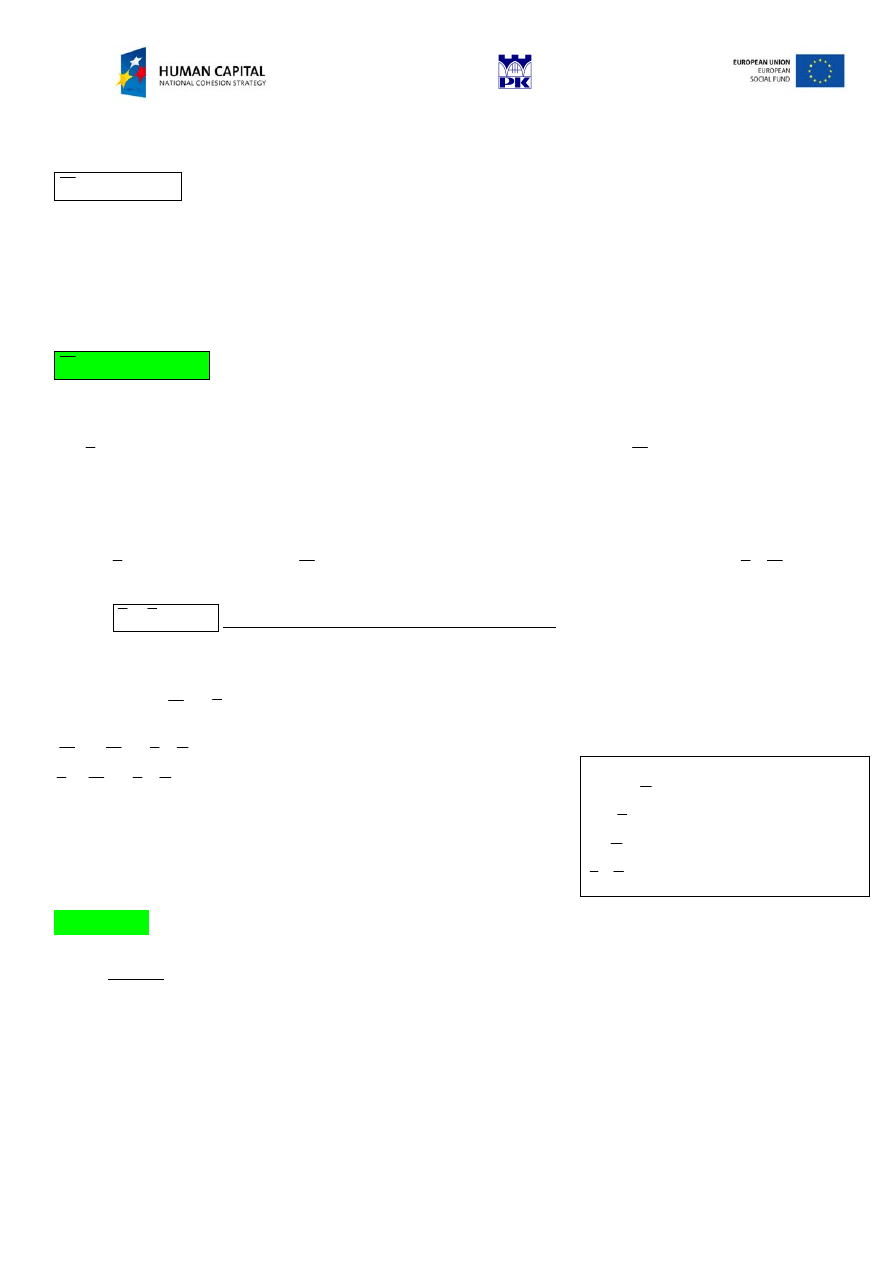
Project “The development of the didactic potential of Cracow University of Technology in the range of modern

construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

3

)

,

0

,

0

(

Az

A

M

M



(for a planar force system)

1

3

3

2

2

1

1

6

6

5

5

3

3

1

1

M

r

W

r

W

r

W

r

F

r

F

r

F

r

F

M

W

W

W

F

F

F

F

Az

































Remark: the moment of F

2

and F

4

about A equal zero, because their lines of action pass through that point.

]

[

4

]

[

17

]

[

1

]

[

6

]

[

1

]

[

3

]

[

2

]

[

16

]

[

4

]

[

9

]

[

2

]

[

12

]

[

2

]

[

3

]

[

1

]

[

10

kNm

kNm

m

kN

m

kN

m

kN

m

kN

m

kN

m

kN

m

kN

M

Az







































])

[

4

,

0

,

0

(

kNm

M

A





 Answer
The planar system of forces can be reduced at point A to a coupe-force system comprising one force

)

],

[

2

],

[

2

(

O

kN

kN

S







applied at point A, and one couple with a moment

])

[

4

,

0

,

0

(

kNm

M

A





,

II. The simplest equivalent system



)

],

[

2

],

[

2

(

O

kN

kN

S







,

])

[

4

,

0

,

0

(

kNm

M

A





hence the parameter of the system

0





A

M

S

k



0

0







k

S

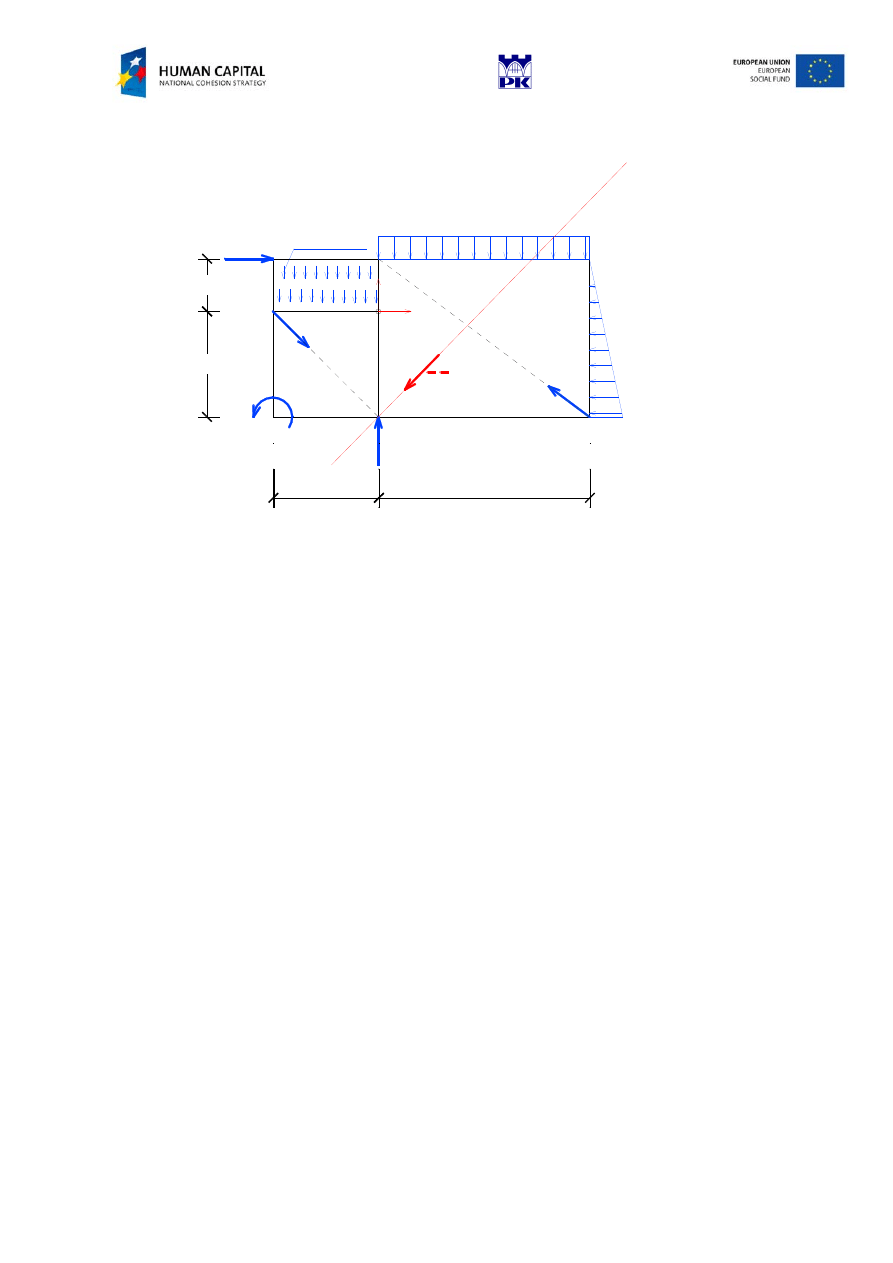
the system can be reduced to a resultant force.

 The equation of a central axis

0

);

,

,

(





P

M

z

y

x

P

P

A

S

M

M

A

p







)

0

,

,

(

)

0

,

,

(

int

)

0

,

0

,

0

(

int

y

x

P

A

vector

y

x

P

po

A

po







)

0

,

,

(

)

0

],

[

2

],

[

2

(

y

x

P

A

kN

kN

S











)

]

[

2

]

[

2

,

0

,

0

(

x

kN

y

kN

P

A

S













P

A

S

M

A







0

)

]

[

2

]

[

2

,

0

,

0

(

])

[

4

,

0

,

0

(

)

0

,

0

,

0

(

x

kN

y

kN

kNm















[

2

]

[

2

]

[

2

]

[

4

0

m

x

y

x

kN

y

kN

kNm

]



















]

[

2 m

x

y





the central axis (or the line of action of the resultant force.)

 Answer

The given planar system of forces can be reduced to a resultant force equal to the sum vector, acting along the
central

]

[

2 m

x

y





Project “The development of the didactic potential of Cracow University of Technology in the range of modern

construction” is co-financed by the European Union within the confines of the European Social Fund

and realized under surveillance of Ministry of Science and Higher Education.

4

q

1

=4 kN/m

17 kNm

q

2

=

2 kN/m

14 kN

10 kN

15 kN

3

2 kN

2m

4m

1m

2m

=3 kN/m2

A

x

y

y=

x-

2[

m

]

W=S(-2[kN ],-2[kN ])